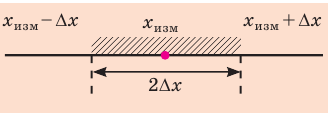
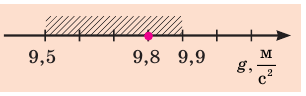
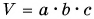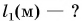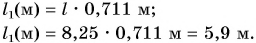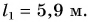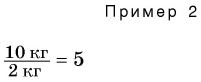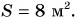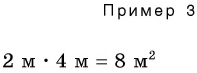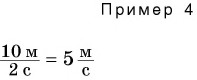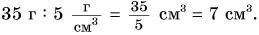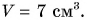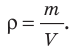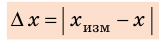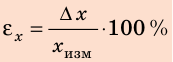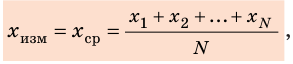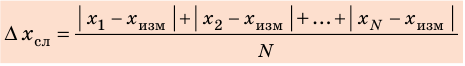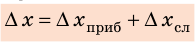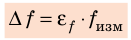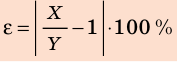Практически каждый раз при решении задач по математике, физике или другим дисциплинам приходится выбирать обозначения тех или иных величин. Среди них следует различать обозначения общепринятые (или даже устанавливаемые нормативными документами) и обозначения, выбор которых обычно выполняется самостоятельно, в зависимости от индивидуальных предпочтений. Есть также величины, обозначения которых в разных дисциплинах приняты свои. Есть обозначения международные, а есть – принятые различными в разных странах.
Как обозначается длина, ширина, высота, толщина, глубина
Обозначение длины в математике обычно зависит от того, какой объект в данном случае рассматривается: одномерный, двумерный или трехмерный. Если речь идёт об обозначении длины одномерного объекта (нити, проволоки и т.п.) или обозначении длины куска сортового проката (трубы, швеллера, двутавра и т.п.), то длина обычно обозначается буквой l (написанной курсивом, т.е. с наклоном, чтобы не было похоже на «единицу») или L. Если же речь идёт о двумерном объекте, в котором нужно обозначить не только длину, но и ширину, то обычно принимают одну из таких пар обозначений: a и b (а – длина, b — ширина), l и b (l – длина, b — ширина), l и h (l – длина, h — высота). Для обозначений могут быть использованы и соответствующие заглавные буквы, в литературе часто встречается сочетание L, B, H (L – длина, В – ширина, Н — высота). Эти же буквы приняты и в физике для обозначения длины, ширины, высоты объектов. Если же речь идёт о длине волны, то она обозначается строчной греческой буквой «лямбда».
Высота обозначается обычно буквой h (читается: [аш]). В технической литературе для обозначения высоты также используют букву Н (читается: [аш]). Этими же буквами (h, реже Н) обозначается глубина.
Толщина в физике обозначается либо строчной (маленькой) буквой s, либо греческой строчной буквой «дельта», с использованием (при необходимости) нижних индексов (обычно – числовых, соответствующих номеру слоя, т.е. 1, 2, 3, 4 и т.д.).
Вопросы «как в математике пишется длина», «как в математике пишется периметр», «как в математике пишется площадь» некорректны. Здесь уместно вместо слова «пишется» употребить слово «обозначается».
Как обозначается периметр
При решении задач по геометрии часто возникает необходимость обозначить периметр. Периметр в математике обозначается заглавной (т.е. большой) буквой Р (читается: [пэ]).
Как обозначается площадь
Обозначение площади в научно-технической литературе можно встретить различные. Поэтому и возникают вопросы «Как обозначается площадь в математике», «Как обозначается площадь в физике» и т.п. Ответ на вопрос о том, какой буквой обозначается площадь, зависит от конкретной дисциплины, о которой в данный момент идёт речь. В математике и в физике площадь обозначается буквой S заглавной (читается: [эс]). Так, в геометрии этой буквой обозначается площадь любых фигур (треугольника, прямоугольника, квадрата, ромба и т.п.). Если нужно в одной задаче обозначить площадь нескольких фигур, то используются нижние индексы. В качестве индекса могут быть использованы числа (1, 2, 3 и т.д.), т.е. площади обозначаются как S1, S2, S3 и т.д., а могут быть использованы сокращения от названия фигур (Sтр, Sпр, Sкв, Sр и т.п.). При необходимости обозначения в одной задаче площадей нескольких треугольников чаще в качестве нижнего индекса принимают обозначения этих треугольников (например, SABC, SMNP, SLPH со значком треугольника перед буквами ABC, MNP, LPH). В физике обозначается площадь поперечного сечения той же буквой S, при необходимости – с добавлением нижнего индекса (например, S1, S2, S3 и т.д.). Однако, в сопромате и в строительной механике буквой S (с добавлением индекса) обозначается не площадь, а статический момент площади относительно оси, а для обозначения площади в этих дисциплинах обычно используются буквы F (читается: [эф]) и A (читается: [а]).
Источники информации:
- Справочник по элементарной математике. Геометрия, тригонометрия, векторная алгебра/ Под ред. П.Ф. Фильчакова
- Яворский Б.М., Детлаф А.А., Лебедев А.К. Справочник по физике для инженеров и студентов вузов
- ru.wikipedia.org – список обозначений в физике
Ни для кого не секрет, что существуют специальные обозначения для величин в любой науке. Буквенные обозначения в физике доказывают, что данная наука не является исключением в плане идентификации величин при помощи особых символов. Основных величин, а также их производных, достаточно много, каждая из которых имеет свой символ. Итак, буквенные обозначения в физике подробно рассматриваются в данной статье.
Физика и основные физические величины
Благодаря Аристотелю начало употребляться слово физика, так как именно он впервые употребил этот термин, который в ту пору считался синонимом термина философия. Это связано с общностью объекта изучения — законы Вселенной, конкретнее — то, как она функционирует. Как известно, в XVI-XVII веках произошла первая научная революция, именно благодаря ей физика была выделена в самостоятельную науку.
Михаил Васильевич Ломоносов ввел в русский язык слово физика посредством издания учебника в переводе с немецкого — первого в России учебника по физике.
Итак, физика представляет собой раздел естествознания, посвященный изучению общих законов природы, а также материи, ее движение и структуре. Основных физических величин не так много, как может показаться на первый взгляд — их всего 7:
- длина,
- масса,
- время,
- сила тока,
- температура,
- количество вещества,
- сила света.
Конечно, у них есть свои буквенные обозначения в физике. Например, для массы выбран символ m, а для температуры — Т. Также у всех величин есть своя единица измерения: у силы света — кандела (кд), а у количества вещества единицей измерения является моль.
Производные физические величины
Производных физических величин значительно больше, чем основных. Их насчитывается 26, причем часто некоторые из них приписывают к основным.
Итак, площадь является производной от длины, объем — также от длины, скорость — от времени, длины, а ускорение, в свою очередь, характеризует быстроту изменения скорости. Импульс выражается через массу и скорость, сила — произведение массы и ускорения, механическая работа зависит от силы и длины, энергия пропорциональна массе. Мощность, давление, плотность, поверхностная плотность, линейная плотность, количество теплоты, напряжение, электрическое сопротивление, магнитный поток, момент инерции, момент импульса, момент силы — все они зависят от массы. Частота, угловая скорость, угловое ускорение обратно пропорциональны времени, а электрический заряд имеет прямую зависимость от времени. Угол и телесный угол являются производными величинами из длины.
Какой буквой обозначается напряжение в физике? Напряжение, которое является скалярной величиной, обозначается буквой U. Для скорости обозначение имеет вид буквы v, для механической работы — А, а для энергии — Е. Электрический заряд принято обозначать буквой q, а магнитный поток — Ф.
СИ: общие сведения
Международная система единиц (СИ) представляет собой систему физических единиц, которая основана на Международной системе величин, включая наименования и обозначения физических величин. Она принята Генеральной конференцией по мерам и весам. Именно эта система регламентирует буквенные обозначения в физике, а также их размерность и единицы измерения. Для обозначения используются буквы латинского алфавита, в отдельных случаях — греческого. Также возможно в качестве обозначения использование специальных символов.
Заключение
Итак, в любой научной дисциплине есть особые обозначения для различного рода величин. Естественно, физика не является исключением. Буквенных обозначений достаточно много: сила, площадь, масса, ускорение, напряжение и т. д. Они имеют свои обозначения. Существует специальная система, которая называется Международная система единиц. Считается, что основные единицы не могут быть математически выведены из других. Производные же величины получают при помощи умножения и деления из основных.
Переходя к физическим приложениям производной, мы будем использовать несколько иные обозначения те, которые приняты в физике.
Во-первых, меняется обозначение функций. В самом деле, какие функции мы собираемся дифференцировать? Этими функциями служат физические величины, зависящие от времени. Например, координата тела x(t) и его скорость v(t) могут быть заданы формулами:
(читается ¾икс с точкой¿).
Имеется ещё одно обозначение производной, очень распространённое как в математике, так и в физике:
|
производная функции x(t) |
|
(читается ¾дэ икс по дэ тэ¿).
Остановимся подробнее на смысле обозначения (1.16
). Математик понимает его двояко либо как предел:
либо как дробь, в знаменателе которой стоит приращение времени dt, а в числителе так называемый дифференциал dx функции x(t). Понятие дифференциала не сложно, но мы не будем его сейчас обсуждать; оно ждёт вас на первом курсе.
Физик, не скованный требованиями математической строгости, понимает обозначение (1.16
) более неформально. Пусть dx есть изменение координаты за время dt. Возьмём интервал dt настолько маленьким, что отношение dx=dt близко к своему пределу (1.17
) с устраивающей нас точностью.
И тогда, скажет физик, производная координаты по времени есть попросту дробь, в числителе которой стоит достаточно малое изменение координаты dx, а в знаменателе достаточно малый промежуток времени dt, в течение которого это изменение координаты произошло.
Такое нестрогое понимание производной характерно для рассуждений в физике. Далее мы будем придерживаться именно этого физического уровня строгости.
Производная x(t) физической величины x(t) снова является функцией времени, и эту функцию снова можно продифференцировать найти производную производной, или вторую производную функции x(t). Вот одно обозначение второй производной:
вторая производная функции x(t)
обозначаетсяx (t)
(читается ¾икс с двумя точками¿), а вот другое:
вторая производная функции x(t)
обозначаетсяdt
2
(читается ¾дэ два икс по дэ тэ квадрат¿ или ¾дэ два икс по дэ тэ дважды¿).
Давайте вернёмся к исходному примеру (1.13
) и посчитаем производную координаты, а заодно посмотрим на совместное использование обозначений (1.15
) и (1.16
):
x(t) = 1 + 12t 3t2
)
x(t) = dt
d
(1 + 12t 3t2
) = 12 6t:
(Символ дифференцирования dt
d
перед скобкой это всё равно что штрих сверху за скобкой в прежних обозначениях.)
Обратите внимание, что производная координаты оказалась равна скорости (1.14
). Это не случайное совпадение. Связь производной координаты со скоростью тела будет выяснена в следующем разделе ¾Механическое движение¿.
1.1.7
Предел векторной величины
Физические величины бывают не только скалярными, но и векторными. Соответственно, часто нас интересует скорость изменения векторной величины то есть, производная вектора. Однако прежде чем говорить о производной, нужно разобраться с понятием предела векторной величины.
Рассмотрим последовательность векторов ~u1
; ~u2
; ~u3
; : : : Сделав, если необходимо, параллельный перенос, сведём их начала в одну точку O (рис.1.5
):
|
Рис. 1.5. lim ~un |
|||||||||
|
Концы векторов обозначим A1 |
|||||||||
Предположим, что последовательность точек A1
; A2
; A3
; : : : ¾втекает¿2
в точку B:
lim An
= B:
Обозначим ~v = OB. Мы скажем тогда, что последовательность синих векторов ~un
стремится к красному вектору ~v, или что вектор ~v является пределом последовательности векторов ~un
:
~v = lim ~un
:
2
Вполне достаточно интуитивного понимания этого ¾втекания¿, но вас, быть может, интересует более строгое объяснение? Тогда вот оно.
Пусть дело происходит на плоскости. ¾Втекание¿ последовательности A1
; A2
; A3
; : : : в точку B означает следующее: сколь бы малый круг с центром в точке B мы ни взяли, все точки последовательности, начиная с некоторой, попадут внутрь этого круга. Иными словами, вне любого круга с центром B имеется лишь конечное число точек нашей последовательности.
А если дело происходит в пространстве? Определение ¾втекания¿ модифицируется незначительно: нужно лишь заменить слово ¾круг¿ на слово ¾шар¿.
Предположим теперь, что концы синих векторов на рис. 1.5
пробегают не дискретный набор значений, а непрерывную кривую (например, указанную пунктирной линией). Таким образом, мы имеем дело не с последовательностью векторов ~un
, а с вектором ~u(t), который меняется со временем. Это как раз то, что нам и нужно в физике!
Дальнейшее объяснение почти такое же. Пусть t стремится к некоторому значению t0
. Если
при этом концы векторов ~u(t) ¾втекают¿ в некоторую точку B, то мы говорим, что вектор
~v = OB является пределом векторной величины ~u(t):
t!t0
1.1.8
Дифференцирование векторов
Выяснив, что такое предел векторной величины, мы готовы сделать следующий шаг ввести понятие производной вектора.
Предположим, что имеется некоторый вектор ~u(t), зависящий от времени. Это означает, что длина данного вектора и его направление могут меняться с течением времени.
По аналогии с обычной (скалярной) функцией вводится понятие изменения (или приращения) вектора. Изменение вектора ~u за время t есть векторная величина:
~u = ~u(t + t) ~u(t):
Обратите внимание, что в правой части данного соотношения стоит разность векторов. Изменение вектора ~u показано на рис. 1.6
(напомним, что при вычитании векторов мы сводим их начала в одну точку, соединяем концы и ¾укалываем¿ стрелкой тот вектор, из которого производится вычитание).
~u(t) ~u
Рис. 1.6. Изменение вектора
Если промежуток времени t достаточно мал, то и вектор ~u за это время меняется мало (в физике, по крайней мере, так считается всегда). Соответственно, если при t ! 0 отношение~u= t стремится к некоторому пределу, то этот предел называется производной вектора ~u:
При обозначении производной вектора мы не будем использовать точку сверху (так как символ ~u_
не слишком хорошо смотрится) и ограничиваемся обозначением (1.18
). Но для производной скаляра мы, разумеется, свободно используем оба обозначения.
Напомним, что d~u=dt это символ производной. Его можно понимать и как дробь, в числителе которой стоит дифференциал вектора ~u, соответствующий промежутку времени dt. Выше мы не стали обсуждать понятие дифференциала, так как в школе его не проходят; не будем обсуждать дифференциал и здесь.
Однако на физическом уровне строгости производную d~u=dt можно считать дробью, в знаменателе которой стоит очень малый интервал времени dt, а в числителе соответствующее малое изменение d~u вектора ~u. При достаточно малом dt величина данной дроби отличается от
предела в правой части (1.18
) столь мало, что с учётом имеющейся точности измерений этим отличием можно пренебречь.
Этого (не вполне строгого) физического понимания производной нам окажется вполне достаточно.
Правила дифференцирования векторных выражений во многом аналогичны правилам дифференцирования скаляров. Нам понадобятся лишь самые простые правила.
1. Постоянный скалярный множитель выносится за знак производной: если c = const, то
d(c~u) = c
d~u:
dt dt
Мы используем это правило в разделе ¾Импульс¿, когда второй закон Ньютона
2. Постоянный векторный множитель выносится за знак производной: если ~c = const, то dt
d
(x(t)~c) = x(t)~c:
3. Производная суммы векторов равна сумме их производных:
dt
d
(~u + ~v) =d~u
dt
+d~v
dt
:
Последними двумя правилами мы будем пользоваться неоднократно. Посмотрим, как они работают в важнейшей ситуации дифференцирования вектора при наличии в пространстве прямоугольной системы координат OXY Z (рис. 1.7
).
Рис. 1.7. Разложение вектора по базису
Как известно, любой вектор ~u единственным образом раскладывается по базису единичных
векторов ~
,~
,~
: i j k
~u = ux
i + uy
j + uz
k:
Здесь ux
, uy
, uz
проекции вектора ~u на координатные оси. Они же являются координатами вектора ~u в данном базисе.
Вектор ~u в нашем случае зависит от времени, а это значит, что его координаты ux
, uy
, uz
являются функциями времени:
|
~u(t) = ux |
Uy |
Uz |
Дифференцируем это равенство. Сначала пользуемся правилом дифференцирования суммы:
|
ux |
uy |
uz |
|||||||||||
|
Затем выносим постоянные векторы за знак производной: |
|||||||||||||
|
Ux |
Таким образом, если вектор ~u имеет координаты (ux
; uy
; uz
), то координаты производной d~u=dt являются производными координат вектора ~u, а именно (ux
; uy
; uz
).
Ввиду особой важности формулы (1.20
) дадим более непосредственный её вывод. В момент времени t + t согласно (1.19
) имеем:
~u(t + t) = ux
(t + t) i + uy
(t + t) j + uz
(t + t)k:
Напишем изменение вектора ~u:
~u = ~u(t + t) ~u(t) =
Ux
(t + t) i + uy
(t + t) j + uz
(t + t)k ux
(t) i + uy
(t) j + uz
(t)k =
|
= (ux |
||||||||||
|
Ux |
||||||||||
|
Делим обе части полученного равенства на t: |
||||||||||
|
T |
t |
В пределе при t ! 0 дроби ux
= t, uy
= t, uz
= t переходят соответственно в производные ux
, uy
, uz
, и мы снова получаем соотношение (1.20
):
Ux
i + uy
j + uz
k.
Изучение физики в школе длится несколько лет. При этом ученики сталкиваются с проблемой, что одни и те же буквы обозначают совершенно разные величины. Чаще всего этот факт касается латинских букв. Как же тогда решать задачи?
Пугаться такого повтора не стоит. Ученые постарались ввести их в обозначение так, чтобы одинаковые буквы не встретились в одной формуле. Чаще всего ученики сталкиваются с латинской n. Она может быть строчной или прописной. Поэтому логично возникает вопрос о том, что такое n в физике, то есть в определенной встретившейся ученику формуле.
Что обозначает прописная буква N в физике?
Чаще всего в школьном курсе она встречается при изучении механики. Ведь там она может быть сразу в дух значениях — мощность и сила нормальной реакции опоры. Естественно, что эти понятия не пересекаются, ведь используются в разных разделах механики и измеряются в разных единицах. Поэтому всегда нужно точно определить, что такое n в физике.
Мощность — это скорость изменения энергии системы. Это скалярная величина, то есть просто число. Единицей ее измерения служит ватт (Вт).
Сила нормальной реакции опоры — сила, которая оказывает действие на тело со стороны опоры или подвеса. Кроме числового значения, она имеет направление, то есть это векторная величина. Причем она всегда перпендикулярна поверхности, на которую производится внешнее воздействие. Единицей измерения этой N является ньютон (Н).
Что такое N в физике, помимо уже указанных величин? Это может быть:
постоянная Авогадро;
увеличение оптического прибора;
концентрация вещества;
число Дебая;
полная мощность излучения.
Что может обозначать строчная буква n в физике?
Список наименований, которые могут за ней скрываться, достаточно обширен. Обозначение n в физике используется для таких понятий:
показатель преломления, причем он может быть абсолютным или относительным;
нейтрон — нейтральная элементарная частица с массой незначительно большей, чем у протона;
частота вращения (используется для замены греческой буквы «ню», так как она очень похожа на латинскую «вэ») — число повторения оборотов за единицу времени, измеряется в герцах (Гц).
Что означает n в физике, кроме уже указанных величин? Оказывается, за ней скрываются основное квантовое число (квантовая физика), концентрация и постоянная Лошмидта (молекулярная физика). Кстати, при вычислении концентрации вещества требуется знать величину, которая также записывается латинской «эн». О ней будет идти речь ниже.
Какая физическая величина может быть обозначена n и N?
Ее название происходит от латинского слова numerus, в переводе оно звучит как «число», «количество». Поэтому ответ на вопрос о том, что значит n в физике, достаточно прост. Это количество любых предметов, тел, частиц — всего, о чем идет речь в определенной задаче.
Причем «количество» — одна из немногих физических величин, которые не имеют единицы измерения. Это просто число, без наименования. Например, если в задаче идет речь о 10 частицах, то n будет равно просто 10. Но если получается так, что строчная «эн» уже занята, то использовать приходится прописную букву.
Формулы, в которых фигурирует прописная N
Первая из них определяет мощность, которая равна отношению работы ко времени:
В молекулярной физике имеется такое понятие, как химическое количество вещества. Обозначается греческой буквой «ню». Чтобы его сосчитать, следует разделить количество частиц на число Авогадро :
Кстати, последняя величина тоже обозначается столь популярной буквой N. Только у нее всегда присутствует нижний индекс — А.
Чтобы определить электрический заряд, потребуется формула:
Еще одна формула с N в физике —
частота колебаний. Чтобы ее сосчитать, нужно их число разделить на время:
Появляется буква «эн» в формуле для периода обращения:
Формулы, в которых встречается строчная n
В школьном курсе физики эта буква чаще всего ассоциируется с показателем преломления вещества. Поэтому важным оказывается знание формул с ее применением.
Так, для абсолютного показателя преломления формула записывается следующим образом:
Здесь с — скорость света в вакууме, v — его скорость в преломляющей среде.
Формула для относительного показателя преломления несколько сложнее:
n 21 = v 1: v 2 = n 2: n 1 ,
где n 1 и n 2 — абсолютные показатели преломления первой и второй среды, v 1 и v 2 — скорости световой волны в указанных веществах.
Как найти n в физике? В этом нам поможет формула, в которой требуется знать углы падения и преломления луча, то есть n 21 = sin α: sin γ.
Чему равно n в физике, если это показатель преломления?
Обычно в таблицах приводятся значения для абсолютных показателей преломления различных веществ. Не стоит забывать, что эта величина зависит не только от свойств среды, но и от длины волны. Табличные значения показателя преломления даются для оптического диапазона.
Итак, стало ясно, что такое n в физике. Чтобы не осталось каких-либо вопросов, стоит рассмотреть некоторые примеры.
Задача на мощность
№1.
Во время пахоты трактор тянет плуг равномерно. При этом он прилагает силу 10 кН. При таком движении в течение 10 минут он преодолевает 1,2 км. Требуется определить развиваемую им мощность.
Перевод единиц в СИ.
Начать можно с силы, 10 Н равны 10000 Н. Потом расстояние: 1,2 × 1000 = 1200 м. Осталось время — 10 × 60 = 600 с.
Выбор формул.
Как уже было сказано выше, N = А: t. Но в задаче нет значения для работы. Для ее вычисления пригодится еще одна формула: А = F × S. Окончательный вид формулы для мощности выглядит так: N = (F × S) : t.
Решение.
Вычислим сначала работу, а потом — мощность. Тогда в первом действии получится 10 000 × 1 200 = 12 000 000 Дж. Второе действие дает 12 000 000: 600 = 20 000 Вт.
Ответ.
Мощность трактора равна 20 000 Вт.
Задачи на показатель преломления
№2.
Абсолютный показатель преломления у стекла равен 1,5. Скорость распространения света в стекле меньше, чем в вакууме. Требуется определить, во сколько раз.
В СИ переводить данные не требуется.
При выборе формул остановиться нужно на этой: n = с: v.
Решение.
Из указанной формулы видно, что v = с: n. Это значит, что скорость распространения света в стекле равна скорости света в вакууме, деленному на показатель преломления. То есть она уменьшается в полтора раза.
Ответ.
Скорость распространения света в стекле меньше, чем в вакууме, в 1,5 раза.
№3.
Имеются две прозрачные среды. Скорость света в первой из них равна 225 000 км/с, во второй — на 25 000 км/с меньше. Луч света идет из первой среды во вторую. Угол падения α равен 30º. Вычислить значение угла преломления.
Нужно ли переводить в СИ? Скорости даны во внесистемных единицах. Однако при подстановке в формулы они сократятся. Поэтому переводить скорости в м/с не нужно.
Выбор формул, необходимых для решения задачи.
Потребуется использовать закон преломления света: n 21 = sin α: sin γ. А также: n = с: v.
Решение.
В первой формуле n 21 — это отношение двух показателей преломления рассматриваемых веществ, то есть n 2 и n 1 . Если записать вторую указанную формулу для предложенных сред, то получатся такие: n 1 = с: v 1 и n 2 =с: v 2 . Если составить отношение двух последних выражений, получится, что n 21 = v 1: v 2 . Подставив его в формулу закона преломления, можно вывести такое выражение для синуса угла преломления: sin γ = sin α × (v 2: v 1).
Подставляем в формулу значения указанных скоростей и синуса 30º (равен 0,5), получается, что синус угла преломления равен 0,44. По таблице Брадиса получается, что угол γ равен 26º.
Ответ.
Значение угла преломления — 26º.
Задачи на период обращения
№4.
Лопасти ветряной мельницы вращаются с периодом, равным 5 секундам. Вычислите число оборотов этих лопастей за 1 час.
Переводить в единицы СИ нужно только время 1 час. Оно будет равно 3 600 секундам.
Подбор формул
. Период вращения и число оборотов связаны формулой Т = t: N.
Решение.
Из указанной формулы число оборотов определяется отношением времени к периоду. Таким образом, N = 3600: 5 = 720.
Ответ.
Число оборотов лопастей мельницы равно 720.
№5.
Винт самолета вращается с частотой 25 Гц. Какое время потребуется винту, чтобы совершить 3 000 оборотов?
Все данные приведены с СИ, поэтому переводить ничего не нужно.
Необходимая формула
: частота ν = N: t. Из нее необходимо только вывести формулу для неизвестного времени. Оно является делителем, поэтому его полагается находить делением N на ν.
Решение.
В результате деления 3 000 на 25 получается число 120. Оно будет измеряться в секундах.
Ответ.
Винт самолета совершает 3000 оборотов за 120 с.
Подведем итоги
Когда ученику в задаче по физике встречается формула, содержащая n
или
N, ему нужно
разобраться с двумя моментами. Первый — из какого раздела физики приведено равенство. Это может быть ясно из заголовка в учебнике, справочнике или слов учителя. Потом следует определиться с тем, что скрывается за многоликой «эн». Причем в этом помогает наименование единиц измерения, если, конечно, приведено ее значение.
Также допускается еще один вариант: внимательно посмотрите на остальные буквы в формуле. Возможно, они окажутся знакомыми и дадут подсказку в решаемом вопросе.
Построение чертежей — дело непростое, но без него в современном мире никак. Ведь чтобы изготовить даже самый обычный предмет (крошечный болт или гайку, полку для книг, дизайн нового платья и подобное), изначально нужно провести соответствующие вычисления и нарисовать чертеж будущего изделия. Однако часто составляет его один человек, а занимается изготовлением чего-либо по этой схеме другой.
Чтобы не возникло путаницы в понимании изображенного предмета и его параметров, во всем мире приняты условные обозначения длины, ширины, высоты и других величин, применяемых при проектировании. Каковы они? Давайте узнаем.
Величины
Площадь, высота и другие обозначения подобного характера являются не только физическими, но и математическими величинами.
Единое их буквенное обозначение (используемое всеми странами) было уставлено в середине ХХ века Международной системой единиц (СИ) и применяется по сей день. Именно по этой причине все подобные параметры обозначаются латинскими, а не кириллическими буквами или арабской вязью. Чтобы не создавать отдельных трудностей, при разработке стандартов конструкторской документации в большинстве современных стран решено было использовать практически те же условные обозначения, что применяются в физике или геометрии.
Любой выпускник школы помнит, что в зависимости от того, двухмерная или трехмерная фигура (изделие) изображена на чертеже, она обладает набором основных параметров. Если присутствуют два измерения — это ширина и длина, если их три — добавляется еще и высота.
Итак, для начала давайте выясним, как правильно длину, ширину, высоту обозначать на чертежах.
Ширина
Как было сказано выше, в математике рассматриваемая величина является одним из трех пространственных измерений любого объекта, при условии что его замеры производятся в поперечном направлении. Так чем знаменита ширина? Обозначение буквой «В» она имеет. Об этом известно во всём мире. Причем, согласно ГОСТу, допустимо применение как заглавной, так и строчной латинских литер. Часто возникает вопрос о том, почему именно такая буква выбрана. Ведь обычно сокращение производится по первой греческого или английского названия величины. При этом ширина на английском будет выглядеть как «width».
Вероятно, здесь дело в том, что данный параметр наиболее широкое применение изначально имел в геометрии. В этой науке, описывая фигуры, часто длину, ширину, высоту обозначают буквами «а», «b», «с». Согласно этой традиции, при выборе литера «В» (или «b») была заимствована системой СИ (хотя для других двух измерений стали применять отличные от геометрических символы).
Большинство полагает, что это было сделано, дабы не путать ширину (обозначение буквой «B»/«b») с весом. Дело в том, что последний иногда именуется как «W» (сокращение от английского названия weight), хотя допустимо использование и других литер («G» и «Р»). Согласно международным нормам системы СИ, измеряется ширина в метрах или кратных (дольных) их единицах. Стоит отметить, что в геометрии иногда также допустимо использовать «w» для обозначения ширины, однако в физике и остальных точных науках такое обозначение, как правило, не применяется.
Длина
Как уже было указано, в математике длина, высота, ширина — это три пространственных измерения. При этом, если ширина является линейным размером в поперечном направлении, то длина — в продольном. Рассматривая ее как величину физики можно понять, что под этим словом подразумевается численная характеристика протяжности линий.
В английском языке этот термин именуется length. Именно из-за этого данная величина обозначается заглавной или строчной начальной литерой этого слова — «L». Как и ширина, длина измеряется в метрах или их кратных (дольных) единицах.
Высота
Наличие этой величины указывает на то, что приходится иметь дело с более сложным — трехмерным пространством. В отличие от длины и ширины, высота численно характеризует размер объекта в вертикальном направлении.
На английском она пишется как «height». Поэтому, согласно международным нормам, ее обозначают латинской литерой «Н»/«h». Помимо высоты, в чертежах иногда эта буква выступает и как глубины обозначение. Высота, ширина и длина — все все эти параметры измеряются в метрах и их кратных и дольных единицах (километры, сантиметры, миллиметры и т. п.).
Радиус и диаметр
Помимо рассмотренных параметров, при составлении чертежей приходится иметь дело и с иными.
Например, при работе с окружностями возникает необходимость в определении их радиуса. Так именуется отрезок, который соединяет две точки. Первая из них является центром. Вторая находится непосредственно на самой окружности. На латыни это слово выглядит как «radius». Отсюда и строчная или заглавная «R»/«r».
Чертя окружности, помимо радиуса часто приходится сталкиваться с близким к нему явлением — диаметром. Он также является отрезком, соединяющим две точки на окружности. При этом он обязательно проходит через центр.
Численно диаметр равен двум радиусам. По-английски это слово пишется так: «diameter». Отсюда и сокращение — большая или маленькая латинская буква «D»/«d». Часто диаметр на чертежах обозначают при помощи перечеркнутого круга — «Ø».
Хотя это распространенное сокращение, стоит иметь в виду, что ГОСТ предусматривает использование только латинской «D»/«d».
Толщина
Большинство из нас помнят школьные уроки математики. Ещё тогда учителя рассказывали, что, латинской литерой «s» принято обозначать такую величину, как площадь. Однако, согласно общепринятым нормам, на чертежах таким способом записывается совсем другой параметр — толщина.
Почему так? Известно, что в случае с высотой, шириной, длиной, обозначение буквами можно было объяснить их написанием или традицией. Вот только толщина по-английски выглядит как «thickness», а в латинском варианте — «crassities». Также непонятно, почему, в отличие от других величин, толщину можно обозначать только строчной литерой. Обозначение «s» также применяется при описании толщины страниц, стенок, ребер и так далее.
Периметр и площадь
В отличие от всех перечисленных выше величин, слово «периметр» пришло не из латыни или английского, а из греческого языка. Оно образовано от «περιμετρέο» («измерять окружность»). И сегодня этот термин сохранил свое значение (общая длина границ фигуры). Впоследствии слово попало в английский язык («perimeter») и закрепилось в системе СИ в виде сокращения буквой «Р».
Площадь — это величина, показывающая количественную характеристику геометрической фигуры, обладающей двумя измерениями (длиной и шириной). В отличие от всего перечисленного ранее, она измеряется в квадратных метрах (а также в дольных и кратных их единицах). Что касается буквенного обозначения площади, то в разных сферах оно отличается. Например, в математике это знакомая всем с детства латинская литера «S». Почему так — нет информации.
Некоторые по незнанию думают, что это связано с английским написанием слова «square». Однако в нем математическая площадь — это «area», а «square» — это площадь в архитектурном понимании. Кстати, стоит вспомнить, что «square» — название геометрической фигуры «квадрат». Так что стоит быть внимательным при изучении чертежей на английском языке. Из-за перевода «area» в отдельных дисциплинах в качестве обозначения применяется литера «А». В редких случаях также используется «F», однако в физике данная буква означает величину под названием «сила» («fortis»).
Другие распространенные сокращения
Обозначения высоты, ширины, длины, толщины, радиуса, диаметра являются наиболее употребляемыми при составлении чертежей. Однако есть и другие величины, которые тоже часто присутствуют в них. Например, строчное «t». В физике это означает «температуру», однако согласно ГОСТу Единой системы конструкторской документации, данная литера — это шаг (винтовых пружин, и подобного). При этом она не используется, когда речь идет о зубчатых зацеплениях и резьбе.
Заглавная и строчная буква «A»/«a» (согласно все тем же нормам) в чертежах применяется, чтобы обозначать не площадь, а межцентровое и межосевое расстояние. Помимо различных величин, в чертежах часто приходится обозначать углы разного размера. Для этого принято использовать строчные литеры греческого алфавита. Наиболее применяемые — «α», «β», «γ» и «δ». Однако допустимо использовать и другие.
Какой стандарт определяет буквенное обозначение длины, ширины, высоты, площади и других величин?
Как уже было сказано выше, чтобы не было недопонимания при прочтении чертежа, представителями разных народов приняты общие стандарты буквенного обозначения. Иными словами, если вы сомневаетесь в интерпретации того или иного сокращения, загляните в ГОСТы. Таким образом вы узнаете, как правильно обозначается высота, ширины, длина, диаметр, радиус и так далее.
👋 Привет Лёва
Середнячок
40/250
Задать вопрос

киря138
+10
Решено
7 лет назад
Физика
1 — 4 классы
как обозначается ширина длина высота в физике
Смотреть ответ
1
Ответ
5
(2 оценки)
2
аожвозплеалм
7 лет назад
Светило науки — 13 ответов — 0 раз оказано помощи
длина -а . ширина — b . высота — с
(2 оценки)
https://vashotvet.com/task/7971052
Физика > Длина
Длина в физике – физическая мера. Узнайте, как обозначается длина в физике, формула, как найти длину, какой буквой делают обозначение, единица измерения.
Длина отображает физическое измерение дистанции, которая в системе единиц отображена в метрах.
Задача обучения
- Различать СИ (система единиц) и обычные единицы длины.
Основные пункты
- Единицей СИ выступает метр.
- Один метр – дистанция, которую свет преодолевает в вакууме за 1/299 792 458 секунды.
- Единицы на счетчике разработаны вокруг числа 10.
Термин
Длина – физическая удаленность между объектами.
Давайте разберемся в том, что собою представляет длина в физике. Длина – измерение физической дистанции. Многие характеристики наблюдения строятся на определении длины. От нее зависит дистанция между объектами, степень силы, оказываемая объектом, и скорость перемещения. Чтобы точно описать длину, необходимо полагаться на общепринятую единицу измерения в физике.
Известно, что в различных частях мира используют разные единицы измерения длины (например, в США – дюйм). Обычно, если речь идет о региональном масштабе, то проблем не возникает. Но при сотрудничестве между странами появляются нестыковки. Именно поэтому возникла необходимость в стандартной единице измерения, принятой на международном уровне. Таким образом, выбор пал на метр, потому что он лучше всего сотрудничает со скоростью света.
Один метр вычисляет дистанцию, которую свет преодолевает за 1/299 792 458 секунды. Все показатели основываются на счетчике с кратностью в 10. Например, 1 км = 1000 м.
| Длина | |
 |
|
| Размерность |
L |
|---|---|
| Единицы измерения | |
| СИ |
м |
| СГС |
см |
Длина
Длина — физическая величина, числовая характеристика протяжённости линий. В узком смысле под длиной понимают линейный размер предмета в продольном направлении (обычно это направление наибольшего размера), то есть расстояние между его двумя наиболее удалёнными точками, измеренное горизонтально, в отличие от высоты, которая измеряется в вертикальном направлении, а также ширины или толщины, которые измеряются поперёк объекта (под прямым углом к длине). В физике термин «длина» обычно используется как синоним «расстояния» и обозначается 

Размерность длины — dim l = L. В ряду других пространственных величин длина — это величина единичной размерности, тогда как площадь — двухмерная, объём — трёхмерная. В большинстве систем измерений единица длины — одна из фундаментальных единиц измерения, на основе которых образуются другие единицы. В международной системе единиц (СИ) за единицу длины принят метр.
Содержание
- 1 Единицы измерения длины
- 1.1 Метрическая система
- 1.2 Британская/Американская система
- 1.3 Старорусская система
- 1.3.1 См. также
- 1.4 Древнегреческая система
- 1.5 Мусульманская система
- 1.6 Типографическая система
- 1.7 Морская система
- 1.8 Единицы, применяемые в астрономии
- 2 Средства измерений длины, расстояния
- 2.1 Измерительные инструменты и меры
- 2.2 Измерительные приборы
- 2.3 Другие средства
- 3 См. также
- 4 Примечания
Единицы измерения длины
Относительные размеры
объектов, м.
-20 —
–
-18 —
–
-16 —
–
-14 —
–
-12 —
–
-10 —
–
-8 —
–
-6 —
–
-4 —
–
-2 —
–
0 —
–
2 —
–
4 —
–
6 —
–
8 —
–
10 —
–
12 —
–
14 —
–
16 —
–
18 —
–
20 —
–
22 —
–
24 —
–
26 —
–
28 —
–
30 —
Метрическая система
Метрическая система считается самой удобной из всех придуманных из-за своей простоты. В основе метрической системы лежит единица измерения метр. Все остальные единицы измерения являются кратными степеням десяти от метра (например, километр — это 10³ метров и т. п.), что позволяет облегчить подсчёты. До 1960 года у метра был специальный эталон, ныне хранящийся в Париже. Сегодня, по определению, метр равен расстоянию, которое проходит свет в вакууме за 1/299 792 458 долю секунды.
Британская/Американская система
Исходными английскими мерами длины были миля, ярд, фут и дюйм. Миля пришла в Англию из Древнего Рима, где она определялась как тысяча двойных шагов вооружённого римского воина.
- Лига (лье)
- Фурлонг
- Чейн
- Род
- Линк
- Ладонь
- Линия
Старорусская система
В Древней Руси мерой длины, веса и т. п. являлся человек. На это указывают названия мер длины: локоть (расстояние от конца вытянутого среднего пальца руки или сжатого кулака до локтевого сгиба), пядь (расстояние между вытянутым большим и указательным пальцами руки), сажень (расстояние от конца пальцев одной руки до конца пальцев другой) и другие[1].
В частности, аршин был связан с длиной человеческого шага. Однако необходимость унификации систем измерений с британской в связи с развитием международной торговли потребовала введения во времена Петра I так называемого «казённого аршина». Это была мерная линейка с металлическими наконечниками с государственным клеймом. Казённый аршин равнялся 28 английским дюймам и делился на 16 вершков.[2]
См. также
- Миля
- Межевая верста
- Верста
- Косая сажень
- Маховая сажень
- Пядь
Древнегреческая система
- Дактиль (единица измерения)
- Кондилос
- Оргия
- Палайста
- Пекис
- Плетр
- Подес
- Стадий, или «стадия»
- Эпидама
Мусульманская система
- Ангушт или Асба (аналог дюйма)
- Пай (аналог фута)
- Ба или кама, равная приблизительно 2 м
- Касаба или наб
- Фарсах или парасанг, равный трём милям по 1000 Ба, или 6 км
- Барид, равный четырём фарсахам[3]
Типографическая система
- Цицеро
- Пункт
Морская система
Морская система измерения длины привязана к размеру планеты Земля. В качестве основной единицы измерения принята морская миля, равная длине одной минуты (1/60 градуса) дуги меридиана земного эллипсоида. Длина морской мили является величиной переменной, зависящей от широты. Ее численное значение составляет от 1843 метров на экваторе до 1861,6 метров на полюсах.
Международная морская миля составляет 1852 м, в отличие от морской мили Британской системы (1853,184 м). Для измерения меньших размеров применяют кабельтов — 1/10 морской мили, или 185,2 м (округлённо — 185 м).[4]
Единицы, применяемые в астрономии
- Астрономическая единица
- Световой год
- Парсек
Средства измерений длины, расстояния
Измерительные инструменты и меры
- Линейка
- Концевая мера
- Штангенинструмент
- Рулетка (инструмент)
- Микрометр (инструмент)
- Индикатор часового типа
- Калибр (инструмент)
- Толщиномер
Измерительные приборы
- Высотомер
- Радиовысотомер
- Дальномер
- Радиодальномер
- Интерференционные толщиномеры (ультразвуковые, лазерные, радиационные)
Другие средства
- Большие расстояния в навигации определяются при помощи средств радионавигационных систем или спутниковых систем
- Очень маленькие расстояния измеряются с помощью измерительных микроскопов
См. также
- Длина кривой
- Мера
- Объём
- Площадь
- Высота
- Глубина
Примечания
- ↑ Меры длины
- ↑ Отечественные компании переходят на исторические меры длины
- ↑ Власов А.Д., Мурин Б.П. Единицы физических величин в науке и технике: Справочник. — М.: Энергоатомиздат, 1990. — С. 176. — ISBN 5-283-03966-8
- ↑ Учебник по навигации
Категории:
- Физические величины по алфавиту
- Метрология
Wikimedia Foundation.
2010.
Содержание:
Явления природы и свойства тел в физике описывают с помощью терминов, например: движение, траектория, состояние спокойствия. Описывая движение (рис. 4.1), можно указать, куда движется тело (вперед, назад или вверх), большое оно или маленькое; движется по пря-мой или поворачивает (влево или вправо), а может, вообще не движется. Такая характеристика движения является качественной.
Нас интересуют и количественные характеристики: с какой скоростью двигался автомобиль, какое расстояние он проехал. Количественной характеристикой тела или явления является физическая величина. Физическая величина описывает определенное свойство тела или явления. Она характеризуется числовым значением и единицей измерения. Например: автомобиль проехал путь в 30 километров. Сокращенно можно записать S = 30 км.
Каждая физическая величина имеет свое на-звание и символ, которым она обозначается.
Чтобы описать явление падения определенного тела, можно применить такие физические величины, как масса тела, высота, время падения. Физические величины обычно обозначают латинскими или греческими буквами. Массу тела обозначают буквой «m», высоту – буквой «h», время – буквой «t». Например, если тело массой 2 килограмма упало с высоты 5 метров за одну секунду, то пишут: m = 2 кг, h = 5 м, t = 1 с, употребляя общепринятые сокращения: кг – килограмм, м – метр, с – секунда.
Если нас интересует единица измерения физической величины, а не ее числовое значение, то эту величину пишут в квадратных скобках. Например, диаметр трубы составляет d = 3,2 см, а название единицы измерения (размерность): [d] =см.
Почему нужно измерять:
Начертите на листе бумаги горизонтальный отрезок. Потом проведите от середины этого отрезка перпендикулярный к нему отрезок такой же длины «на глаз». Измерьте длину отрезков линейкой, и вы убедитесь, что вертикальный отрезок короче. Вот почему нужно проводить измерения.
Средства измерения
Прямые измерения физических величин осуществляют с помощью приборов. Длину измеряют линейкой, время – с помощью часов, массу – на весах. Для определения размеров очень малых тел или больших расстояний используют более сложные приборы. Измерить физическую величину – значит сравнить ее с определенной мерой, которая является копией общепринятого образца-эталона. Эталонов немного, и хранятся они в специальных метрологических лабораториях.
История:
Для измерения времени использовали вытекание или капанье воды в сосуд с делениями или пересыпание песка – водяные или песочные часы (рис. 4.2). Движение Солнца по небу давало возможность измерять время с помощью солнечных часов (рис. 4.3). Такими часами люди пользовались несколько тысячелетий, однако они имели существенный недостаток – были довольно неточными.
Рис. 4.3. Солнечные часы
В настоящее время появились очень точные кварцевые часы, которые отсчитывают время в на-ручных часах, мобильном телефоне или компьютере. Для потребностей навигации и науки используют атомные часы, которые «ходят» настолько точно, что допускают ошибку в одну секунду за 500 000 лет!
Для измерения длины надо иметь образец, дли-на которого соответствует общепринятым единицам измерения. Сейчас это 1 м. Эталон (образец) метра хранится в метрологических лабораториях, главная из которых находится в г. Севре (Франция). Измерить длину можно еще и в других единицах измерения – канцелярскими скрепками, например, или спичками и сказать: мой рост составляет 80 скрепок или 36 спичечных коробков. Однако у других людей скрепки или спички могут оказаться другого размера, что усложнит обмен информацией. В давние времена так и было: пользовались футами (длина ступни – 30 см), дюймами (длина последней фаланги большого пальца, приблизительно 2,5 см), ярдами, пядями, саженями, локтями.
Инициаторами перехода на метрическую систему единиц были французы. Согласно договоренности, один метр определили как одну сорокамиллионную часть длины меридиана, который проходит через Париж. Для определения длины меридиана достаточно было измерять его часть, которая простирается от юга Испании до севера Норвегии. Начался этот процесс во время Великой французской революции. Днем рождения метрической системы мер считают 10 декабря 1799 г.
На территории нашей страны метрическая система мер была введена специальным декретом 14 сентября в 1918 г. Переход на новые стандарты измерений связан с изменением привычек, необходимостью переиздания справочников, переоборудования метрических лабораторий, с переподготовкой персонала и тому подобным. Все это стоит довольно дорого. США, например, переход на новые стандарты обошелся в 11 млрд. долларов.
Международная система единиц измерения – СИ
В связи с потребностью международного сотрудничества в 1960 году большинство стран мира подписали соглашение о единой Международной системе еди-ниц измерения SI – Systeme International (на русском языке – СИ).
Рис. 4.4. Эталон метра хранится в Международном бюро мер и весов в Париже
Рис. 4.5. Эталон килограмма
В СИ есть 7 основных единицы измерения, которые обеспечены соответствующими эталонами. Остальные единицы измерения могут быть выражены через основные единицы. Для начала нам понадобятся три основные единицы: метр, килограмм и секунда.
Эталон метра изображен на рис. 4.4. Это рельс определенного профиля, длина которого составляет одну сорокамиллионную часть меридиана, проходящего через Париж. Первый эталон метра был изготовлен во Франции в 1795 году.
В 1983 году эталон длины был изменен: теперь метр определен как расстояние, которое проходит свет в вакууме за 1/299 792 458 долю секунды.
Эталон килограмма – цилиндр из платиново-иридиевого сплава, высота которого равна его диаметру и составляет 39 мм (рис. 4.5).
С эталоном секунды вы ознакомитесь в 11 классе.
Таблица 4.1
| Величина | Символ | Размерность | |
| рус. | междунар. | ||
| Длина | l | м | m |
| Масса | m | кг | kg |
| Время | t | с | s |
| Площадь | S, | м2 | m2 |
| Объем | V | м3 | m3 |
| Скорость | v | м/с | m/s |
Площадь в СИ измеряют в м2 (квадратные метры), объем – в м3 (кубические метры).
В таблице 4.1 единицы площади, объема и скорости являются производны-ми единицами, их размерности происходят от основных единиц измерения.
В расчетах используют также кратные и дольные единицы.
Кратные единицы – это единицы, которые больше основных единиц в 10, 100, 1000 и больше раз. Например: 1 дм = 10 см = 101 см, 1 м = 100 см = 102 см, 1 км = 1000 м = 103 м, 1 кг = 1000 г = 103 г.
Дольные единицы – это единицы, которые меньше основных единиц в 10, 100, 1000 и больше раз: 1 см = 0,01 м = 10–2 м, 1 мм = 0,1 см = 10–1 см.
С единицами времени несколько иначе: 1 мин. = 60 с, 1 час = 3600 с. Дольными являются лишь 1 мс (миллисекунда) = 0,001 с = 10–3 с и 1 мкс (микросекунда)= = 0,000001 с = 10–6 с.
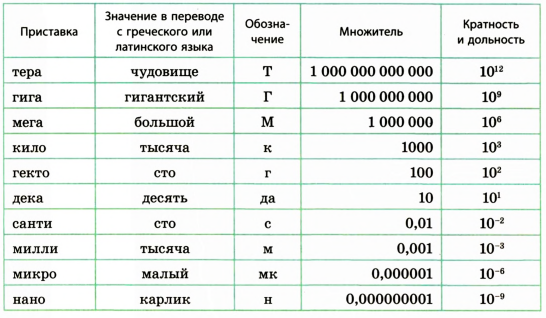
Для обозначения кратных и дольных единиц используют приставки (табл. 4.2).
Таблица 4.2 Приставки для обозначения кратных и дольных единиц
| Кратность | Приставка | Обозначение | Пример | ||
| русское | международное | русское | международное | ||
| 102 | гекто | hecto | г | h | 5 гПа (гектопаскаль) = = 500 Па |
| 103 | кило | kilo | к | k | 6 кг (килограмм) = 6000 г |
| 106 | мега | mega | М | M | 2 МДж (мегаджоуль) = = 2 000 000 Дж |
| 109 | гига | giga | Г | G | 1 ГГц (гигагерц) = = 1 000 000 000 Гц |
| Дольность | |||||
| 10–1 | деци | deci | д | d | дм – дециметр |
| 10–2 | санти | centi | с | c | см – сантиметр |
| 10–3 | милли | milli | м | м | мл – миллилитр |
| 10–6 | микро | micro | мк | µ | мкм – микрометр, микрон |
| 10–9 | нано | nano | н | n | нм – нанометр |
Итоги
- Физические величины количественно описывают свойства тел и явлений.
- Физические величины характеризуются названием, символом, числовым значением и единицей измерения.
- В международной системе единиц измерения (СИ) основные механические единицы измерения физических величин – метр, килограмм и секунда.
- Измерить физическую величину – значит сравнить ее с мерой-эталоном.
Физические величины
Физические тела и явления характеризуют физическими величинами. Некоторые из них вам уже знакомы из курса природоведения: это длина, площадь, объем, масса, сила. Рассмотрим их подробнее.
В науке используют единицы физических величин, определенные Международной системой единиц, которую сокращенно называют1 SI — от английских слов System International, что означает «международная система».
Длина, Площадь, Объем
Длиной характеризуют физические тела и, например, путь, пройденный телом за время его движения. За единицу длины в SI принят2 I метр (м).
На линейках и мерных лентах (рулетках) нанесены деления, обозначающие сотые и тысячные доли метра — сантиметры и миллиметры (рис. 3.1).
Единицы площади и объема определяют с помощью единицы длины: единицей площади является I м2 (площадь квадрата со стороной I м), а единицей объема — I м3 (объем куба с ребром I м).
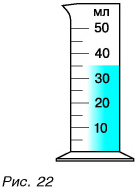
Объем жидкости измеряют с помощью измерительных цилиндров, называемых часто мензурками (рис. 3.2). Длину, площадь и объем задают их числовыми значениями. Физические величины, которые задают только числовыми значениями, называют скалярными.
Время
Всякое физическое явление длится в течение определённого промежутка времени. За единицу времени в S1 принята 1 секунда (с), 60 с составляют 1 минуту (мун), а 60 минут — 1 час (ч).
Время измеряют часами (рис. 3.3). Они представляют собой обычно устройства, в которых повторяется определенный процесс. Например, в маятниковых часах повторяются колебания маятника. Сегодня чаще используют кварцевые часы, в которых колеблются крошечные кристаллы кварца.
Перемещение и скорость
При движении тело изменяет свое положение в пространстве.
Перемещением тела называют направленный отрезок, проведенный из начального положения тела в его конечное положение.
Перемещение задают числовым значением (длиной указанного отрезка) и направлением. Физические величины, которые характеризуют числовым значением и направлением, называют векторными:
Значение векторной величины называют ее модулем.
Векторную величину обозначают буквой со стрелкой, а модуль — той же буквой без стрелки. Так, перемещение обычно обозначают 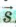

Скоростью тела называют физическую величину, равную отношению перемещения тела к промежутку времени, в течение которого произошло это перемещение.
Скорость, как и перемещение, является векторной величиной, то есть ее характеризуют модулем и направлением. Например, скорости двух встречных автомобилей могут быть равными по модулю, но направлены они противоположно. Скорость обозначают обычно 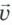
Единицей скорости в SI является 1 метр в секунду (м/с). Тело, которое движется с такой скоростью, за 1 с перемещается на 1 м, — это скорость прогулки. Рекорд скорости в беге — чуть больше 10 м/с.
Скорость современных реактивных самолетов достигает почти километра в секунду (км/с), а космических кораблей — даже больше 10 км/с. Но ни одно тело не может двигаться со скоростью, превышающей скорость света в вакууме, которая равна примерно 300 000 км/с.
Для измерения скорости автомобилей и мотоциклов используют спидометры1 (рис. 3.4-3.6). Они показывают обычно скорость в километрах в час (км/ч). Вы, наверное, замечали, что во время движения автомобиля стрелка спидомстра обычно «покачивается». Дело в том, что скорость автомобиля при движении обычно изменяется.
Масса
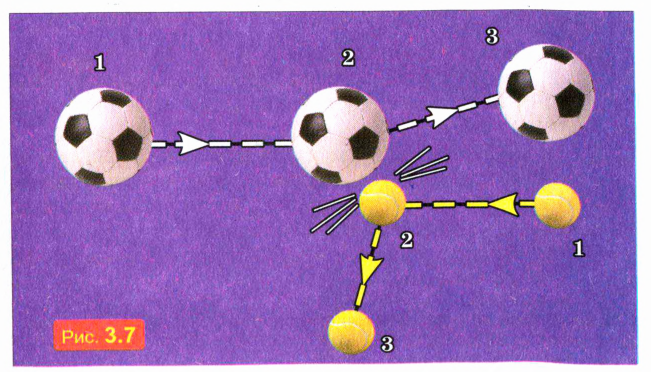
Каждое физическое тело имеет определенную массу. Массы двух тел можно сравнить, измерив, как изменяются их скорости при взаимодействии друг с другом: скорость тела большей массы изменяется меньше, чем скорость тела меньшей массы.
Например, на рис. 3.7 схематически показано столкновение, футбольного и теннисного мячей (цифры обозначают положение мячей в три последовательных момента времени). Мы видим, что при столкновении скорость футбольного мяча изменилась намного меньше, чем скорость теннисного. Значит, масса футбольного мяча намного больше массы теннисного мяча.
Далее мы расскажем о намного более простом способе измерения массы тел, который обычно и используют на практике.
Единицей массы в S1 является 1 килограмм (кг). Это примерно масса одного литра воды. Международный эталон килограмма представляет собой металлический цилиндр из специального сплава.
Сила
Мерой взаимодействия тел является сила: чем больше сила, действующая на тело, тем больше изменяется скорость этого тела за 1 с. Сила является векторной величиной: ее задают числовым значением и направлением. На рисунках силу обозначают стрелкой, начало которой находится в точке приложения силы.
Единицу силы в честь Ньютона назвали ньютоном (Н)1. Сила в 1 Н, приложенная к движущемуся телу массой 1 кг в направлении движения тела, увеличивает его скорость за каждую секунду на 1 м/с,
Чтобы вы представили себе, что такое сила в 1 Н, приведем пример: когда вы держите полное ведро воды, то прикладываете к нему силу, равную примерно 100 Н. При этом приложенная вами сила уравновешивает силу, с которой Земля притягивает то же самое ведро с водой.
Силу, с которой Земля притягивает предметы, называют силой тяжести. В многочисленных опытах было установлено, что сила тяжести, действующая на тело, пропорциональна его массе.
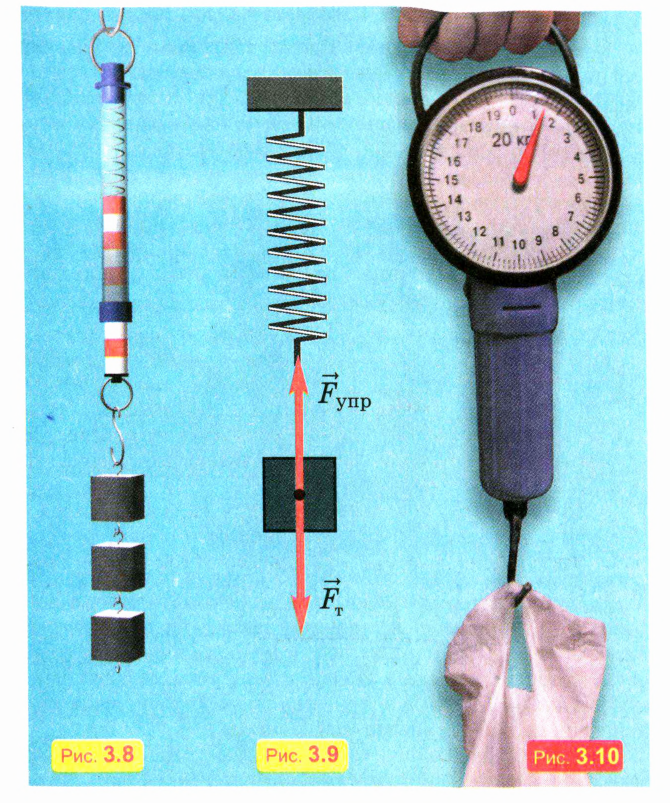
Силу измеряют динамометром2. На рис. 3.8 показан пружинный динамометр, действие которого основано на том, что удлинение пружины пропорционально значению растягивающей ее силы.
На рис. 3.9 схематически изображены силы, действующие на тело, подвешенное к динамометру: это сила тяжести со стороны Земли и сила упругости со стороны пружины. Если тело находится в покое, сила упругости уравновешивает силу тяжести, то есть направлена противоположно ей и равна ей по модулю.
Значит, по удлинению пружины в этом случае можно найти значение силы тяжести. А это, в свою очередь, позволяет рассчитать массу тела, поскольку сила тяжести пропорциональна массе тела.
Таким образом, массу тела можно найти с помощью взвешивания. Пружинные весы (рис. 3.10) — это динамометр, шкала которого размечена (проградуирована) так, что она показывает массу подвешенного груза.
Что называется физической величиной
Издавна люди для более точного описания каких-нибудь событий, явлений, свойств тел и веществ используют их характеристики. Например, сравнивая тела, которые нас окружают, мы говорим, что книга меньше, чем книжный шкаф, а конь больше кошки. Это означает, что объем коня больше объема кошки, а объем книги меньше объема шкафа.
Объем — пример физической величины, которая характеризует общее свойство тел занимать ту или иную часть пространства (рис. 1.15, а). При этом числовое значение объема каждого из тел индивидуально.
Рис. 1.15. Для характеристики свойства тел занимать ту или иную часть пространства мы используем физическую величину объем (а, б), для характеристики движения — скорость (б, в)
Общая характеристика многих материальных объектов или явлений, которая может приобретать индивидуальное значение для каждого из них, называется физической величиной.
Еще одним примером физической величины может служить известное вам понятие «скорость*. Все движущиеся тела изменяют свое положение в пространстве с течением времени, однако быстрота этого изменения для каждого тела различна (рис. 1.15, б, в). Так, самолет за 1 с полета успевает изменить свое положение в пространстве на 250 м, автомобиль — на 25 м, человек — на 1 м, а черепаха — всего на несколько сантиметров. Поэтому физики и говорят, что скорость — это физическая величина, которая характеризует быстроту движения.
Нетрудно догадаться, что объем и скорость,— это далеко не все физические величины, которыми оперирует физика. Масса, плотность, сила, температура, давление, напряжение, освещенность — это лишь малая часть тех физических величин, с которыми вы познакомитесь, изучая физику.
Что означает измерить физическую величину
Для того чтобы количественно описать свойства какого-либо материального объекта или физического явления, необходимо установить значение физической величины, которая характеризует данный объект или явление.
Значение физических величин получают путем измерений (рис. 1.16— 1.19) или вычислений.
Измерить физическую величину — значит сравнить ее с однородной величиной, принятой за единицу.
Приведем пример из художественной литературы: «Пройдя шагов триста по берегу реки, маленький отряд вступил под своды дремучего леса, извилистыми тропами которого им надо было странствовать на протяжении десяти дней*. (Ж. Верн «Пятнадцатилетний капитан*)
Герои романа Ж. Верна измеряли пройденный путь, сравнивая его с шагом, то есть единицей измерения служил шаг. Таких шагов оказалось триста. В результате измерения было получено числовое значение (триста) физической величины (пути) в избранных единицах (шагах).
Рис. 1.20. Если бабушка и внук будут измерять расстояние в шагах. то они всегда будут получать разные результаты
Очевидно, что выбор такой единицы не позволяет сравнивать результаты измерений, полученные разными людьми, поскольку длина шага у всех разная (рис. 1.20). Поэтому ради удобства и точности люди давным-давно начали договариваться о том, чтобы измерять одну и ту же физическую величину одинаковыми единицами. Ныне в большинстве стран мира действует принятая в I960 году Международная система единиц измерения, которая носит название «Система Интернациональная* (СИ) (рис. 1.21).
В этой системе единицей длины является метр (м), времени — секунда (с); объем измеряется в метрах кубических (м3), а скорость — в метрах в секунду (м/с). Об остальных единицах СИ вы узнаете позже.
Кратные и дольные единицы
Из курса математики вы знаете, что для сокращения записи больших и малых значений разных величин пользуются кратными и дольными единицами.
Кратные единицы — это единицы, которые больше основных единиц в 10, 100, 1000 и более раз.
Дольные единицы — это единицы, которые меньше основных в 10, 100, 1000 и более раз.
Для записи кратных и дольных единиц используют приставки. Например, единицы
Рис. 1.21. Основные единицы Международной системы (СИ)
длины, кратные одному метру,— это километр (1000 м), декаметр (10 м). Единицы длины, дольные одному метру,— это дециметр (0,1 м), сантиметр (0,01 м), микрометр (0,000001 м) и так далее.
В таблице приведены наиболее часто употребляемые приставки.
Приставки, служащие для образования кратных и дольных единиц
Измерительные приборы
Измерение физических величин ученые проводят с помощью измерительных приборов. Простейшие из них — линейка, рулетка — служат для измерения расстояния и линейных размеров тела. Вам также хорошо известны такие измерительные приборы, как часы — прибор для измерения времени, транспортир — прибор для измерения углов на плоскости, термометр — прибор для измерения температуры и некоторые другие (рис. 1.22, с. 20). Со многими измерительными приборами вам еще предстоит познакомиться.
Большинство измерительных приборов имеют шкалу, которая обеспечивает возможность измерения. Кроме шкалы, на приборе указывают единицы, в которых выражается измеренная данным прибором величина*.
По шкале можно установить две наиболее важные характеристики прибора: пределы измерения и цену деления.
Пределы измерения — это наибольшее и наименьшее значения физической величины, которые можно измерить данным прибором.

————————————————
Цена деления — это значение наименьшего деления шкалы измерительного прибора.
Например, верхний предел измерений медицинского термометра (рис. 1.23) равен 42 °С, нижний — 34 °С, а цена деления шкалы этого термометра составляет 0,1 °С.
Напоминаем: чтобы определить цену деления шкалы любого прибора, необходимо разность двух любых значений величин, указанных на шкале, разделить на количество делений между ними.
Итоги:
Общая характеристика материальных объектов или явлений, которая может приобретать индивидуальное значение для каждого из них, называется физической величиной.
Измерить физическую величину — значит сравнить ее с однородной величиной, принятой за единицу.
В результате измерений мы получаем значение физических величин.
Говоря о значении физической величины, следует указать ее числовое значение и единицу.
Для измерения физических величин пользуются измерительными приборами.
Для сокращения записи числовых значений больших и малых физических величин используют кратные и дольные единицы. Они образуются с помощью приставок.
Точность измерений
Теперь вы знаете, что означает измерить физическую величину. И в повсе дневной жизни вам уже приходилось выполнять множество простейших измерений. Но насколько точными были ваши измерения? Можно ли получить абсолютно точное значение физической величины?
Попробуем разобраться в этих непростых вопросах.
Оцениваем размеры и проверяем результат:
Начнем с проверки вашего глазомера.
Оцените на глаз длину иглы, изображенной на рис 1.24. А теперь давайте проверим, насколько результат вашей оценки соответствует действительности, то есть измерим длину той же иглы с помощью линейки. Для этого:
- — приложим линейку к игле так, чтобы «ноль» на ее шкале совпал с одним концом иглы (рис. 1.25);
- — определим значение деления шкалы, напротив которого расположен ее другой конец.
Мы видим, что он расположен возле отметки 5 см. Отсюда делаем вывод, что длина иглы около 5 см. Если результат вашей предварительной оценки совпадает с этим значением, то у вас хороший глазомер. Определить на глаз размер более точно нам не удастся.
Результат измерений:
Если нам нужен более точный результат, придется обратить внимание на то, что кончик иглы немного более чем на два миллиметра выступает за отметку 5 см. Итак, более точная длина иглы — 5,2 см, или 52 мм.
Вы можете возразить, что это тоже неточно.
Да, неточно! Именно поэтому принято всегда указывать точность, с которой выполнено измерение.
В первом случае наше измерение выполнено с точностью до 1 см, а во втором — с точностью до 0,1 см.
Чтобы произвести еще более точное измерение, необходимо учесть длину той части иглы, которая выступает за отметку 52 мм, и тогда точность повысится до 0,01 см. Но для этого нам придется использовать измерительный прибор с еще меньшей ценой деления, то есть более точный, но даже тогда мы не можем утверждать, что измерили иглу совершенно точно.
Причин для этого достаточно: это и несовершенство конструкции прибора, и погрешности, которые возникают при проведении опыта (например, начало иглы невозможно абсолютно точно совместить с «нулем» линейки). Таким образом, даже если измерение проводится более тщательно и с помощью более совершенного прибора, точность возрастает, но погрешностей все равно не избежать.
Чтобы уменьшить погрешность, измерение можно выполнить несколько раз, а затем вычислить среднее значение всех полученных результатов (наити их среднее арифметическое).
Точность измерений
Однако не следует думать, что чем точнее измерение, тем лучше: излишняя точность не всегда целесообразна.
Предположим, что вместо длины иглы вам необходимо измерить длину крышки стола. В этом случае нет необходимости учитывать десятые и сотые доли миллиметра, поскольку, измеряя длину стола в разных местах, мы получим величины, отличающиеся на несколько миллиметров. Поэтому долями миллиметра в этом случае можно пренебречь. Также нет смысла измерять длину стены с точностью до одного миллиметра (рис. 1.26).
Из этого можно сделать вывод, что необходимую точность измерения определяет цель эксперимента.
Чаще всего важно не значение погрешности, а то, какую часть от всей измеренной величины составляет возможная погрешность.
Если портной, выкраивая брюки, ошибется на 1 мм, вы этого даже не заметите. А вот если, втягивая нить в ушко иглы, он всякий раз будет ошибаться на 1 мм (рис. 1.27), то едва ли брюки вообще когда-либо будут сшиты.
Роль измерений в физике. Прямые и косвенные измерения
Наука начинается с тех пор, как начинают измерять… Д. И. Менделеев
Вдумайтесь в слова известного ученого. Из них ясна роль измерений в любой науке, особенно в физике. Но, кроме того, измерения важны в практической жизни. Можете ли вы представить свою жизнь без измерений времени, массы, длины, скорости движения, расхода электроэнергии и т. д.?
Как измерить физическую величину? Для этой цели используются измерительные приборы. Некоторые из них вам уже известны. Это разного вида линейки, часы, термометры, весы, транспортиры и др.
Измерительные приборы бывают цифровые и шкальные. В цифровых приборах результат измерений определяется цифрами. Это электронные приборы — часы, термометр, счетчик электроэнергии (рис. 19) и др.
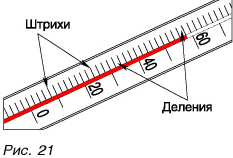
Линейка, стрелочные часы, термометр бытовой, весы, транспортир (рис. 20) — это шкальные приборы. Они имеют шкалу. По ней определяется результат измерений. Вся шкала расчерчена штрихами на деления (рис. 21). Одно деление это не один штрих, как иногда ошибочно считают некоторые учащиеся, а промежуток между двумя ближайшими штрихами. На рисунке 22 на шкале мензурки от значения 10 мл до значения 20 мл два деления, но три штриха. Приборы, которые мы будем использовать в лабораторных работах, в основном шкальные.
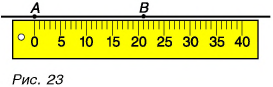
Что значит измерить физическую величину? Измерить физическую величину — значит сравнить ее с однородной величиной, принятой за единицу. Например, чтобы измерить длину отрезка прямой между точками A и В, нужно приложить линейку и по ее шкале (рис. 23) определить, сколько миллиметров укладывается между точками А и В. Однородной величиной, с которой проводилось сравнение длины отрезка АВ, в данном случае была длина, равная 1 мм.
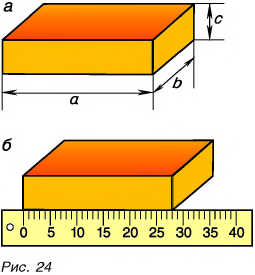
Если физическая величина измеряется непосредственно путем снятия данных со шкалы прибора, то такое измерение называют прямым. Например, приложив линейку к разным ребрам бруска, мы определим его длину а, ширину b и высоту с (рис. 24, а). Значение длины, ширины и высоты мы определили непосредственно, сняв данные со шкалы линейки. Из рисунка 24, б следует: a = 28 мм. Это прямое измерение.
А как определить объем бруска? Надо провести прямые измерения его длины а, ширины b и высоты с, а затем по формуле
вычислить объем бруска.
В этом случае мы говорим, что объем бруска определили по формуле, т. е. косвенно, и измерение объема называется косвенным измерением.
В физике измерения физических величин чаще всего косвенные. В дальнейшем вы убедитесь в этом сами.
Главные выводы:
- Измерительные приборы бывают цифровые и шкальные.
- При прямых измерениях физическая величина определяется непосредственно по шкале прибора.
- При косвенных измерениях физическая величина определяется по формуле.
Для любознательных:
Изучая строение человеческого тела и работу его органов, ученые проводят множество измерений. Оказывается, в человеке массой примерно 70 кг около 6 л крови. Сердце человека в спокойном состоянии сокращается 60—80 раз в минуту. За одно сокращение оно выбрасывает в среднем 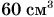
В течение суток кровь человека около 360 раз проходит через почки, очищаясь там от вредных веществ. Общая протяженность почечных кровеносных сосудов составляет приблизительно 18 км. Ведя здоровый образ жизни, мы помогаем нашему организму работать без сбоев!
Единицы измерения физических величин
Чтобы решить, как быстрее доехать до вокзала — на трамвае или на такси, сравнивают скорости движения этих транспортных средств. Скорость — физическая величина. Она количественно описывает физическое явление — движение. Если скорость автомобиля 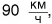
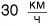
В физике для описания физических явлений и свойств используется множество физических величин: длина, сила, давление и др. Каждая физическая величина имеет символическое обозначение, числовое значение и единицу измерения. Например, длина бруска 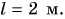
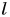
Исторически сложилось так, что у разных народов и государств единицы измерения одних и тех же физических величин различались. Часто это были единицы, соответствующие размерам частей тела человека, массе семени бобов и т. д. Пользоваться такими единицами было неудобно, особенно в торговле между разными государствами.
Например, в Англии для измерения длины использовался фут (1 фут = 30,5 см), а на Руси — аршин (1 аршин = 71,1 см) (рис. 30). Нужно было упорядочить систему единиц, сделать ее удобной в использовании всеми странами. В 1960 г. ввели единую Международную систему единиц (сокращенно СИ — Систему Интернациональную). Ею пользуется большинство стран. Основными единицами в СИ являются: метр (м) — для длины, килограмм (кг) — для массы, секунда (с) — для промежутка времени, Кельвин (К) — для температуры.
Но всегда ли удобно измерять время в секундах, а длину — в метрах? Оказывается, нет. Например, время движения поезда из Минска в Москву измеряют в часах (ч), а путь — в километрах (км). Единицы 1 ч и 1 км — это неосновные (кратные) единицы СИ. Между основными и неосновными единицами существует связь. Так, 1 км = 1000 м, 1 ч = 3600 с.
Основные единицы измерения имеют эталоны. Эталоны хранятся в г. Севре (Франция) в Международном бюро мер и весов. На рисунке 31 приведен эталон килограмма — цилиндр из плати но-иридиевого сплава. По эталону делают копии, которыми пользуются разные страны. Позже вы познакомитесь с эталонами других единиц измерения.
Для любознательных
Эталонная база страны обеспечивает единство измерений и является частью национального достояния. В Беларуси, как и в других странах, ведется работа по исследованию и созданию эталонных комплексов. В Белорусском государственном институте метрологии созданы эталоны массы, времени (см. рис.), температуры и др.
Главные выводы
- Каждая физическая величина имеет символическое обозначение, числовое значение и единицу измерения.
- Основными единицами СИ являются: метр, килограмм, секунда, Кельвин и др.
- Основные единицы измерения имеют свои эталоны.
Пример №1
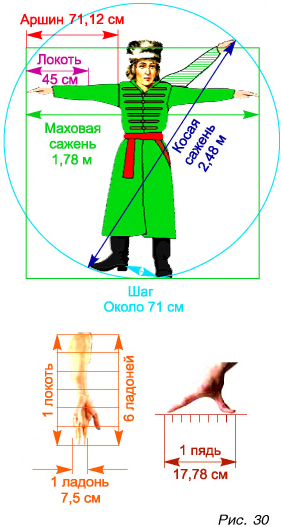
В одной из книг немецкого путешественника XVII в. есть такие строки: «Шелковая материя, привозимая с Востока, называется русскими «китайкой», и каждый кусок содержит ни больше ни меньше как восемь с четвертью аршин». Сколько метров в куске материи?
Дано:
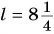
1 аршин = 71,1 см = 0,711 м
Решение
Так как 1 аршин = 71,1 см = 0,711 м, то длина восьми с четвертью аршин в метрах будет равна:
Ответ:
- Заказать решение задач по физике
Действия над физическими величинами
В математике можно складывать, вычитать и сравнивать любые числа. А какие действия можно производить над физическими величинами?
Действия сложения, вычитания и сравнения над физическими величинами можно производить только в том случае, если они однородны, т. е. представляют одну и ту же физическую величину.
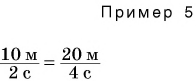
Мы можем складывать длину с длиной, вычитать из массы массу, сравнивать промежуток времени с промежутком времени (пример 1). Смешно и нелепо было бы складывать 4 м и 5 кг или вычитать 30 с из 9 кг. А вот умножать и делить можно как однородные, так и разные физические величины.
В примере 2 делятся не только числовые значения (10 : 2 = 5), но и единицы физических величин (кг : кг = 1). Результат показывает, во сколько раз одна физическая величина (масса) больше другой.
В примере 3 умножаются числовые значения 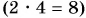
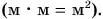
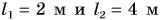
В примере 4 в результате деления двух разных физических величин — длины 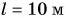
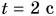
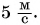
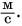
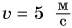
В примере 5 знак равенства относится не только к числовым значениям, но и к единицам. Знак равенства поставить нельзя, если сравнить 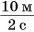
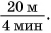
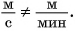
Для любознательных:
Большие единицы времени — год и сутки — дала нам сама природа. Но час, минута и секунда появились благодаря человеку.
Принятое в настоящее время деление суток восходит к глубокой древности. В Вавилоне применялась не десятичная, а шестидесятеричная система счисления. Поскольку 60 делится без остатка на 12, сутки у вавилонян состояли из 12 равных частей. В Древнем Египте было введено деление суток на 24 часа. Позже появились минуты и секунды. То, что в 1 часе 60 минут, а в 1 минуте 60 секунд, — наследие шестидесятеричной системы счисления Вавилона.
Главные выводы:
- Складывать, вычитать и сравнивать можно только однородные физические величины.
- Умножение и деление разнородных величин приводит к появлению новой физической величины.
Пример №2
Выберите значения физических величин, которые можно складывать: 120 г, 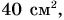
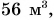
Решение
Однородными физическими величинами в данном случае являются массы тел: 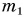
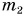
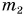
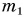
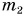
Следовательно, m = 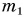
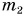
Ответ: результатом сложения является масса m = 168 г.
Пример №3
Определите физические величины, получившиеся в результате
выполнения следующих действий: 1) 35 г : 5 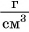
Решение
1) Найдем отношение двух физических величин, разделив их числовые значения и единицы:
Мы получили физическую величину — объем
2) Чтобы умножить две однородные физические величины, необходимо выразить их в одних единицах, например в сантиметрах (см):
Мы получили физическую величину — площадь
Ответ: 1) в результате деления двух физических величин разного рода (массы и плотности) получена третья физическая величина — объем 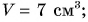
физические величины и их измерение
Чем отличается язык физики (и любой другой точной науки) от обычного? язык физики интернационален: он создавался лучшими умами человечества, его однозначно понимают в любом уголке нашей планеты. язык физики объективен: каждое его понятие однозначно, оно имеет один смысл, который может измениться (чаще всего — расшириться) только благодаря опытам. Как и методы научного познания, язык физики родился из практики.
Что такое физическое исследование и каковы его методы
Вспомним, с чего начинается исследовательская работа ученых. Прежде всего — это наблюдение за определенным явлением (телом или материалом) и размышления над его сущностью.
Наблюдение — это восприятие природы с целью получения первичных данных для последующего анализа. Далеко не всегда наблюдения приводят к правильным выводам. Поэтому, чтобы опровергнуть или подтвердить собственные выводы, ученые проводят физические исследования.
Физическое исследование — это целенаправленное изучение явлений и свойств природы средствами физики.
| Методы физических исследований | |
|---|---|
| экспериментальный | теоретический |
| Эксперимент — исследование физического явления в условиях, находящихся под контролем исследователя. В своей основе физика является экспериментальной наукой: большинство ее законов основаны на фактах, установленных опытным путем. | Анализ данных, полученных в результате экспериментов, формулирование законов природы, объяснение конкретных явлений и свойств на основе этих законов, а главное — предвидение и теоретическое обоснование (с широким использованием математики) еще не известных явлений и свойств. |
Какие наблюдения, теоретические и экспериментальные исследования вы провели бы, чтобы исследовать свечение обычной лампы накаливания?
Теоретические исследования проводят не с конкретным физическим телом, а с его идеализированным аналогом — физической моделью, которая должна учитывать только некоторые основные свойства исследуемого тела. Так, изучая движение автомобиля, мы иногда используем его физическую модель — материальную точку (рис. 2.1, а).
Эту модель используют, если размеры тела не существенны для теоретического описания, то есть в модели «материальная точка» учитывается только масса тела, а его форма и размеры во внимание не принимаются. А вот если нужно выяснить, как на движение автомобиля влияет сопротивление воздуха, целесообразно применить уже другую физическую модель — она должна учитывать и форму, и размеры автомобиля (рис. 2.1, б), но может не учитывать, например, размещение пассажиров в салоне. Чем больше выбрано соответствующих параметров для исследования физической системы «автомобиль», тем точнее можно предвидеть «поведение» этой системы.
Рис. 2.1. Определяя скорость и время движения автомобиля, можно применять физическую модель «материальная точка» (а); выясняя аэродинамические свойства автомобиля, эту физическую модель применять нельзя (б)
Целесообразно ли использовать физическую модель «материальная точка», если инженеры должны рассчитать устойчивость автомобиля?
Как измерить физическую величину
Описывая, например, движение автомобиля, мы используем определенные количественные характеристики: скорость, ускорение, время движения, силу тяги, мощность и т. п.
Из предыдущего курса физики вы знаете, что количественную меру свойства тела, физического процесса или явления называют физической величиной. Значение физической величины устанавливают в ходе измерений, которые, в свою очередь, бывают прямые и косвенные. При прямых измерениях величину сравнивают с ее единицей (метром, секундой, килограммом, ампером и т. п.) с помощью измерительного прибора, проградуированного в соответствующих единицах (рис. 2.2).
Рис. 2.2. Современные приборы для прямого измерения температуры (а); массы (б); скорости движения (в)
Назовите несколько физических величин, значения которых вы находили с помощью прямых измерений. В каких единицах измеряют эти величины? какими приборами? При косвенных измерениях величину вычисляют по результатам прямых измерений других величин, связанных с измеряемой величиной некоторой функциональной зависимостью. Так, чтобы найти среднюю плотность ρ тела, нужно с помощью весов измерить массу m тела, с помощью, например, мензурки измерить его объем V, а затем массу разделить на объем:
Построение системы единиц
В конце XVIII в., после Великой французской революции, перед французскими учеными была поставлена задача создать систему единиц на научной основе. В результате появилась метрическая система единиц. В 1960 г. была создана Международная система единиц CИ, которая со временем стала в мире доминирующей.
Основные единицы СИ
- килограмм (1 кг, 1 kg) единица массы
- метр (1 м, 1 m) единица длины
- секунда (1 с, 1 s) единица времени
- ампер (1 А, 1 А) единица силы тока
- моль (1 моль, 1 mol) единица количества вещества
- кельвин (1 К, 1 K) единица температуры
- кандела (1 кд, 1 kd) единица силы света
Исторически единицы физических величин связывали с определенными телами или природными процессами. Так, 1 метр был связан с размерами планеты Земля, 1 килограмм — с определенным объемом воды, 1 секунда — с суточным вращением Земли. Позже для каждой единицы был создан эталон — средство (или комплекс средств) для воспроизведения и хранения единицы физической величины. Основные эталоны хранились (и хранятся сейчас) в Международном бюро мер и весов (г. Севр, Франция).
Сейчас все большее распространение получают методы построения системы единиц, основанные на особенностях излучения и распространения электромагнитных волн, а также на фундаментальных физических константах. Рассмотрим основные этапы создания системы единиц на примерах метра и килограмма.
Напомним, что для удобства записи больших и малых значений физических величин используют кратные и дольные единицы. Кратные единицы больше основных единиц в 10, 100, 1000 и более раз. Дольные единицы меньше основных единиц в 10, 100, 1000 и более раз.
Названия кратных и дольных единиц включают в себя специальные префиксы. Например, километр (1000 м, или 103 м) — кратная единица длины, миллиметр (0,001 м, или 10–3 м) — дольная единица длины (см. табл. 1).
Таблица 1. Префиксы для образования названий кратных и дольных единиц
| Префикс | Символ | Множитель |
| атто- | а | 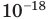 |
| фемто- | ф | 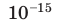 |
| пико- | п | 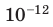 |
| нано- | н | 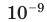 |
| микро- | мк | 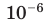 |
| милли- | м | 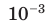 |
| санти- | с | 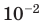 |
| кило- | к | 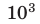 |
| мега- | М | 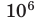 |
| гига- | Г | 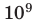 |
| тера- | Т | 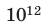 |
| пета | п | 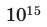 |
| экса | е | 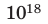 |
Погрешности измерений
При измерении любой физической величины обычно выполняют три последовательные операции: 1) выбор, проверка и установка прибора (приборов); 2) снятие показаний прибора (приборов); 3) вычисление искомой величины по результатам измерений (при косвенных измерениях); 4) оценка погрешности.
Например, нужно измерить на местности расстояние около 5 м. Разумеется, что для этого не следует брать ученическую линейку, — удобнее воспользоваться рулеткой. Все приборы имеют определенную точность. Расстояние в 5 м, как правило, не требуется определять с точностью до миллиметра, поэтому шкала рулетки может и не содержать соответствующих делений.
Рис. 2.3. Штангенциркуль. Точность измерения изображенным прибором — сотые доли миллиметра
А вот если для ремонта лабораторного крана необходимо определить размер шайбы, целесообразно воспользоваться штангенциркулем (см. рис. 2.3). Однако даже с помощью сверхточного прибора нельзя выполнить измерения абсолютно точно. Всегда есть погрешности измерений — отклонение значения измеренной величины от ее истинного значения. Модуль разности между измеренным (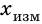
Отношение абсолютной погрешности к измеренному значению измеряемой величины называют относительной погрешностью измерения 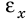
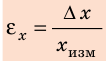
Погрешности при измерениях бывают случайные и систематические.
Случайные погрешности
Случайные погрешности связаны с процессом измерения: измеряя расстояние рулеткой, невозможно проложить ее идеально ровно; отсчитывая секундомером время, прибор невозможно мгновенно включить и выключить и т. д. Чтобы результаты были более точными, измерения проводят несколько раз и определяют среднее значение измеряемой величины:
где 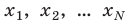
Если измерение проводилось один раз, будем считать, что случайная погрешность равна половине цены деления шкалы прибора.
Систематические погрешности
Систематические погрешности связаны прежде всего с выбором прибора: невозможно найти рулетку с идеально точной шкалой, идеально равноплечие рычаги и т. п. Систематические погрешности определяются классом точности прибора, поэтому их часто называют погрешностями прибора. В процессе эксплуатации точность приборов может снижаться, поэтому их необходимо периодически калибровать при помощи специального оборудования. Абсолютные погрешности некоторых приборов, используемых в школе, приведены в табл. 2. Если используются другие приборы, будем считать, что абсолютная погрешность прибора равна половине цены деления его шкалы.
Абсолютная погрешность прямого измерения (∆x) учитывает как систематическую погрешность, связанную с прибором (
Обратите внимание! Приведенные формулы очень упрощены. Ученые используют более сложные методы расчетов погрешностей.
Таблица 2. Абсолютные погрешности некоторых физических приборов
| Физический прибор | Цена деления шкалы прибора | Абсолютная погрешность прибора |
| Линейка ученическая | 1 мм | ±1 мм |
| Лента измерительная | 0,5 см | ±0,5 см |
| Штангенциркуль | 0,1 мм | ±0,05 мм |
| Цилиндр измерительный | 1 мл | ±1 мл |
| Секундомер | 0,2 с | ±1 с за 30 мин |
| Динамометр учебный | 0,1 Н | ±0,05 Н |
| Термометр лабораторный | 1 °С | ±1 °С |
Как определить погрешности косвенных измерений
Многие физические величины невозможно измерить непосредственно. Их косвенное измерение включает два этапа: 1) методом прямых измерений находят значения определенных величин, например x, y; 2) по соответствующей формуле вычисляют искомую величину f. Как в таком случае определить абсолютную ∆f и относительную 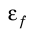
- Относительную погрешность определяют по специальным формулам (см. табл. 3).
- Абсолютную погрешность определяют по относительной погрешности:
- Если эксперимент проводят, чтобы выяснить, выполняется ли некое равенство (например, X Y= ), то относительную погрешность экспериментальной проверки равенства X Y= можно оценить по формуле:
Таблица 3. Некоторые формулы для определения относительной погрешности
| Функциональная зависимость | Относительная погрешность |
|---|---|
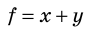 |
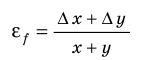 |
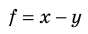 |
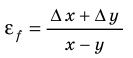 |
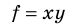 |
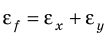 |
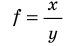 |
|
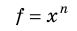 |
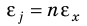 |
Как правильно записать результаты
Абсолютная погрешность эксперимента определяет точность, с которой имеет смысл вычислять измеряемую величину. Абсолютную погрешность ∆x обычно округляют до одной значащей цифры с завышением, а результат измерения xизм — до величины разряда, оставшегося после округления в абсолютной погрешности. Окончательный результат х записывают в виде:
Абсолютная погрешность — положительная величина, поэтому 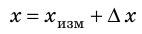
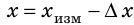
Рис. 2.4. Абсолютная погрешность измерения определяет интервал, в котором находится истинное значение измеряемой величины
Пример. Пусть измеряли ускорение свободного падения (g). После обработки экспериментальных данных получили: 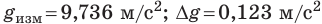
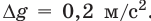
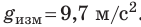
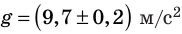
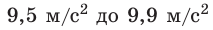
Рис. 2.5. Табличное значение: 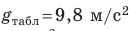
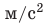
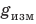
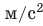
- Точность измерений и погрешности
- Определение площади и объема
- Связь физики с другими науками
- Макромир, мегамир и микромир в физике
- Что изучает физика
- Как зарождалась физика
- Единая физическая картина мира
- Физика и научно-технический прогресс
Длина — расстояние от точки до точки, измерение кривой: для отрезка прямой длина — расстояние между его концами, для ломаной — сумма длин ее звеньев, для других кривых — верхняя граница длины ломаной линии, вписанной в эту кривую.
В физике длина обозначается в основном буквами L или l (от англ. Length). Единицей измерения длины в системе СИ является метр, в системе СГС — сантиметр.
Линейные размеры тела[править]
Термин длина употребляется также для обозначения одного из линейных размеров тела. Если тело имеет форму параллелепипеда, то стороны этого параллелепипеда обычно называют длиной, шириной и толщиной. Наибольшая (самая длинная) из сторон — длина. Учитывая ориентацию предмета относительно поверхности Земли, его стороны можно назвать высотой, длиной и толщиной (или шириной). В этом случае длина — большая из горизонтальных сторон. Реки имеют длину русла, ширину и глубину.
Единицы измерения[править]
Стандартной единицей длины в международной системе единиц СИ является метр и его кратные и частные производные: сантиметр, километр, миллиметр, микрометр, нанометр и др. В некоторых странах (США, Великобритания) и профессиях (полиграфия, морское дело) принято использовать традиционные единицы длины, такие как мили или ярды.
Длина в специальной теории относительности[править]
Согласно специальной теории относительности, длина любого тела движущегося выглядит меньше по направлению движения этого тела по сравнению с длиной в собственной системе отсчета этого тела. Если длина тела в собственной системе отсчета равна 
,
где v — скорость подвижной системы, c — скорость света. Это явление называется лоренцовым сокращением длины.
См. также[править]
- Планковская длина
Источники[править]
- ↑ Жданов В. І. Вступ до теорії відносності. — К.: ВПЦ «Київський університет», 2008. — 290 с. (укр.)