Двугранный угол и линейный угол двугранного угла
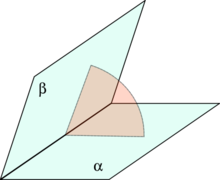
Двугранный угол трёх векторов (как внешний сферический угол)
Двугранный угол — пространственная геометрическая фигура, образованная двумя полуплоскостями, исходящими из одной прямой, а также часть пространства, ограниченная этими полуплоскостями.[1]
Определения и свойства
Полуплоскости называются гранями двугранного угла, а их общая прямая — ребром.
Прямой угол в двугранном угле, равном 45 градусов (анимация)
Двугранные углы измеряются линейным углом, то есть углом, образованным пересечением двугранного угла с плоскостью, перпендикулярной к его ребру. Таким образом, чтобы измерить двугранный угол, можно взять любую точку на его ребре и перпендикулярно ребру провести из неё лучи в каждую из граней. Линейный угол между этими двумя лучами и будет равен по величине двугранному углу. Если один из лучей не перпендикулярен ребру, то величина линейного угла между лучами в общем случае будет отлична от величины двугранного угла. Например, в любой двугранный угол (в том числе больший 90 градусов) можно поместить прямой угол так, чтобы его вершина лежала на ребре двугранного угла, а стороны принадлежали его граням. В этом легко убедиться, размещая угольник в приоткрытой книге.
У всякого многогранника, правильного или неправильного, выпуклого или вогнутого, есть двугранный угол на каждом ребре.
Величины двугранных углов правильных многогранников:
| Название | точный двугранный угол в радианах | приближённое значение в градусах |
|---|---|---|
| Тетраэдр | arccos(1/3) | 70.53° |
| Гексаэдр или куб | π/2 | 90°(точн.) |
| Октаэдр | π − arccos(1/3) | 109.47° |
| Додекаэдр | 2·arctg(φ) | 116.56° |
| Икосаэдр | 2·arctg(φ + 1) | 138.19° |
где φ = (1 + √5)/2 — золотое сечение.
Вариации и обобщения
- Двугранным углом также называется пересечение двух полупространств в
-мерном Евклидовом пространстве.
Примечания
- ↑ Д-Коо // «Математическая энциклопедия» / Главный редактор И. М. Виноградов. — М.: «Советская энциклопедия», 1979. — Т. 2. — С. 50. — 1104 с. — (51[03] М34). — 148 800 экз.
См. также
- Угол
- Многогранный угол
- Телесный угол
- Трехгранный угол
Ссылки
Двугранный угол: тематические медиа-файлы на Викискладе
Если в плоскости γ провести две пересекающиеся прямые АК и BN в точке М, то плоскость разделится ими на 4 области, которые образуют 4 «плоских » угла.
Аналогично две пересекающиеся плоскости γ и β по прямой АВ, делят пространство на 4 области и образуют 4 двугранных угла.
Определение. Двугранный угол – это фигура, образованная прямой АВ и двумя полуплоскостями с общей границей АВ, не принадлежащей одной плоскости.
Полуплоскости, образующие двугранный угол, называются гранями двугранного угла.
Общая для граней прямая АВ (граница полуплоскостей) называется ребром двугранного угла.
Обозначение: KABL, где K и L-это точки, лежащие в разных гранях, а АВ – ребро двугранного угла.
Моделью двугранного угла являются:
- стена комнаты с полом или потолком;
- двускатная крыша;
- полураскрытая книга;
- открытка со сгибом.
Измерение двугранных углов сводится к измерению линейных углов.
Определение. Линейным углом двугранного угла называется плоский угол, образованный двумя лучами, которые лежат в гранях этого двугранного угла и перпендикулярны его ребру.
Все линейные углы данного двугранного угла равны между собой.
За величину двугранного угла принимают величину его линейного угла.
Выражение двугранный угол равен ᵠ означает, что величина соответствующего линейного угла равна ᵠ.
Двугранный угол называется прямым (острым, тупым), если он равен 90°(меньше 90°, больше 90°)
Если Вам понравилась информация и появилось желание поддержать нас, Вы можете:
- отправить денежный перевод с карты на карту мгновенно и без комиссий по ссылке . Ссылка на перевод . В поле «Добавьте комментарий» необходимо указать «в дар» или «подарок».
- оставить комментарий ниже.
×òî òàêîå «ÄÂÓÃÐÀÍÍÛÉ ÓÃÎË»? Êàê ïðàâèëüíî ïèøåòñÿ äàííîå ñëîâî. Ïîíÿòèå è òðàêòîâêà.
ÄÂÓÃÐÀÍÍÛÉ ÓÃÎË
ôèãóðà â ïðîñòðàíñòâå, îáðàçîâàííàÿ äâóìÿ ïîëóïëîñêîñòÿìè, èñõîäÿùèìè èç îäíîé ïðÿìîé, à òàêæå ÷àñòü ïðîñòðàíñòâà, îãðàíè÷åííàÿ ýòèìè ïîëóïëîñêîñòÿìè (ðèñ.). Ïîëóïëîñêîñòè ãðàíÿìè Ä. ó., à èõ îáùàÿ ïðÿìàÿ ðåáðîì. Ä. ó. èçìåðÿåòñÿ ëèíåéíûì óãëîì, ò.å. óãëîì åå ìåæäó äâóìÿ ïåðïåíäèêóëÿðàìè ê ðåáðó, âûõîäÿùèìè èç îäíîé òî÷êè è ëåæàùèìè â ðàçíûõ ãðàíÿõ, èëè, èíà÷å, óãëîì, îáðàçîâàííûì ïåðåñå÷åíèåì Ä. ó. ïëîñêîñòüþ, ïåðïåíäèêóëÿðíîé ê ðåáðó.
ÄÂÓÃÐÀÍÍÛÉ ÓÃÎË — ÄÂÓÃÐÀÍÍÛÉ óãîë — ôèãóðà, îáðàçîâàííàÿ äâóìÿ ïîëóïëîñêîñòÿìè (ãðàíÿìè äâóãðàííîãî óãëà), èñõîäÿùèìè … Áîëüøîé ýíöèêëîïåäè÷åñêèé ñëîâàðü
ÄÂÓÃÐÀÍÍÛÉ ÓÃÎË — — ôèãóðà â ïðîñòðàíñòâå, îáðàçîâàííàÿ äâóìÿ ïîëóïëîñêîñòÿìè, èñõîäÿùèìè èç îäíîé ïðÿìîé, à òàêæå ÷… Ìàòåìàòè÷åñêàÿ ýíöèêëîïåäèÿ
→
двугранный — прилагательное, именительный п., муж. p., ед. ч.
↳
двугранный — прилагательное, винительный п., муж. p., ед. ч.
Часть речи: прилагательное
Положительная степень:
| Единственное число | Множественное число | |||
|---|---|---|---|---|
| Мужской род | Женский род | Средний род | ||
| Им. |
двугранный |
двугранная |
двугранное |
двугранные |
| Рд. |
двугранного |
двугранной |
двугранного |
двугранных |
| Дт. |
двугранному |
двугранной |
двугранному |
двугранным |
| Вн. |
двугранного двугранный |
двугранную |
двугранное |
двугранные двугранных |
| Тв. |
двугранным |
двугранною двугранной |
двугранным |
двугранными |
| Пр. |
двугранном |
двугранной |
двугранном |
двугранных |
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
Рис. (1). Ноутбук.
Двугранный угол — это часть пространства, заключённая между двумя полуплоскостями, имеющими одну общую границу.
Рис. (2). Две пересекающиеся плоскости.
Если в пространстве пересекаются две плоскости, получаются четыре двугранных угла (аналогично как при пересечении двух прямых получаются четыре угла). Рассмотрим один из них.
Рис. (3). Двугранный угол.
Полуплоскости
α
и
β
, образующие двугранный угол, называются его гранями.
Общая прямая (a) этих граней называется ребром двугранного угла.
Выберем на ребре (a) двугранного угла произвольную точку (C) и проведём две пересекающиеся прямые
AC⊥a
и
BC⊥a
, а через эти прямые — плоскость
γ
перпендикулярно ребру (a).
Рис. (4). Линейный угол двугранного угла.
Линии пересечения (AC) и (BC) полуплоскостей
α
и
β
с плоскостью
γ
образуют некоторый угол
∡ACB
. Этот угол называется линейным углом двугранного угла. Величина линейного угла не зависит от выбора точки (C) на ребре (a).
Обрати внимание!
Величина двугранного угла (0° <)
∡ACB
(< 180°).
Если плоскости параллельны, то угол между ними равен (0°) по определению.
Если при пересечении плоскостей один из двугранных углов составляет (90°), то три остальных угла — тоже (90°). Эти плоскости называют перпендикулярными.
Следующие теоремы, которые здесь приведём без доказательств, могут пригодиться при решении задач.
1. Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны.
2. Плоскость, перпендикулярная прямой, по которой пересекаются две плоскости, перпендикулярна каждой из этих плоскостей.
3. Если две плоскости перпендикулярны, и в одной из них прямая проведена перпендикулярно линии пересечения плоскостей, то эта прямая перпендикулярна второй плоскости.
Многогранные углы
Объясним понятие многогранных углов.
Представим несколько лучей в пространстве с общим началом. Их можно представить тоже как часть линий пересечения плоскостей — трёх, четырёх или больше — и назвать рёбрами многогранного угла.

Рис. (5). Трёхгранный угол.

Рис. (6). Четырёхгранный угол.
Рис. (7). Пятигранный угол.
Каждые два луча образуют угол, который называют плоским углом многогранного угла.
Обрати внимание!
Каждый плоский угол трёхгранного угла меньше суммы двух других плоских углов.
Сумма плоских углов многогранного угла меньше (360°).
Источники:
Рисунки 2-7. Плоскости, углы, © ЯКласс.
§ 14.Двугранные углы. Угол между двумя плоскостями
14.1. Двугранный угол и его измерение
Рассмотрим два полупространства, образованные непараллельными плоскостями. Пересечение этих полупространств назовём двугранным углом.
Прямую, по которой пересекаются плоскости — границы полупространств, называют ребром двугранного угла, а полуплоскости этих плоскостей, образующие двугранный угол, — гранями двугранного угла.
Двугранный угол с гранями α, β и ребром a обозначают αaβ. Можно использовать и такие обозначения двугранного угла, как K(AB)T; α(AB)β (рис. 94, 95).
Рис. 94
Рис. 95
Рис. 96
Замечание. Иногда говорят, что двугранный угол αaβ образован двумя полуплоскостями α и β, имеющими общую граничную прямую a.
Фигуры, образованные двумя страницами одной книги, двумя соседними гранями куба, — модели двугранного угла.
Для измерения двугранного угла введём понятие его линейного угла. На ребре a двугранного угла αaβ отметим произвольную точку O и в гранях α и β проведём из точки O соответственно лучи OA и OB, перпендикулярные ребру a (рис. 96, а). Угол AOB, образованный этими лучами, называется линейным углом двугранного угла αaβ.
Так как OA ⊥ a и OB ⊥ a, то плоскость AOB перпендикулярна прямой a. Это означает, что линейный угол двугранного угла есть пересечение данного двугранного угла и плоскости, перпендикулярной его ребру.
Вследствие произвольного выбора точки O на ребре двугранного угла заключаем, что двугранный угол имеет бесконечное множество линейных углов. Докажем, что все они равны. Действительно, рассмотрим два линейных угла AOB и A1O1B1 двугранного угла αaβ (рис. 96, б). Лучи OA и O1A1 лежат в одной грани α и перпендикулярны прямой a — ребру двугранного угла, поэтому они сонаправлены. Аналогично получаем, что сонаправлены лучи OB и O1B1. Тогда ∠ AOB = ∠ A1O1B1 (как углы с сонаправленными сторонами).
Таким образом, нами доказана теорема.

Иначе говоря, все линейные углы данного двугранного угла равны между собой.
Это позволяет ввести следующее определение.
Определение. Величиной двугранного угла называется величина его линейного угла.
Рис. 97
Величина двугранного угла, измеренная в градусах, принадлежит промежутку (0°; 180°).
На рисунке 97 изображён двугранный угол, градусная мера (величина) которого равна 30°. В этом случае также говорят, что двугранный угол равен тридцати градусам.
Двугранный угол является острым (рис. 98, а), прямым (рис. 98, б) или тупым (рис. 98, в), если его линейный угол соответственно острый, прямой или тупой.
Рис. 98
Заметим, что аналогично тому, как и на плоскости, в пространстве определяются смежные (рис. 99, а) и вертикальные (рис. 99, б) двугранные углы. При этом справедливы и аналогичные теоремы о величинах этих углов.
Попробуйте доказать самостоятельно следующие два утверждения, важные для решения задач.
На гранях двугранного угла величины α взяты точки A и B; A1 и B1 — проекции этих точек на ребро двугранного угла; AA1 = a; BB1 = b; A1B1 = h. Тогда
AB = 
Рис. 99
Если внутри двугранного угла величины α взята точка на расстояниях a и b от граней двугранного угла, то её расстояние от ребра двугранного угла равно 
14.2. Угол между двумя плоскостями
Две пересекающиеся плоскости образуют четыре двугранных угла с общим ребром (рис. 100). Если величина одного из них равна ϕ, то величины трёх остальных равны соответственно 180° – ϕ, ϕ, 180° – ϕ (почему?). Наименьшая из этих величин принимается за величину угла между данными пересекающимися плоскостями.
Определение. Углом между двумя пересекающимися плоскостями называется наименьший из двугранных углов, образованных при их пересечении.
Угол между параллельными или совпадающими плоскостями полагается считать равным нулю.
Если величина угла между плоскостями α и β равна ϕ, то пишут: 
Рис. 100
Так как двугранный угол измеряется своим линейным углом, то из выше приведённого определения следует, что угол между пересекающимися плоскостями равен углу между пересекающимися прямыми, лежащими в этих плоскостях и перпендикулярными к линии их пересечения (см. рис. 100). Это означает, что величина угла между плоскостями принадлежит промежутку [0°; 90°].
Рис. 101
ЗАДаЧа. Отрезок DM длиной 3,2 перпендикулярен плоскости ромба ABCD (∠ ADC — тупой). Диагонали ромба равны 12 и 16. Найти углы между плоскостями:
а) ABC и MBC; б) AMD и CMD.
Решение. а) Пусть DE — высота ромба ABCD (рис. 101). Тогда по теореме о трёх перпендикулярах ME ⊥ BC и ∠ DEM = ϕ — линейный угол двугранного угла, образованного плоскостями ABC и MBC. Найдём величину этого угла.
По условию задачи DM ⊥ (ABC), поэтому ⧌ MDE — прямоугольный, значит, tg ϕ = 



Учитывая, что S = 






б) Так как отрезок DM — перпендикуляр к плоскости ромба ABCD, то AD ⊥ DM, CD ⊥ DM, значит, ∠ ADC = ψ — линейный угол двугранного угла, образованного пересекающимися плоскостями ADM и CDM. Найдём этот угол.
В треугольнике ACD по теореме косинусов находим
cos ψ = 


откуда ψ = arccos 
Ответ: а) arctg 

From Wikipedia, the free encyclopedia
This article is about the geometry term. For other uses, see Dihedral.
Angle between two half-planes (α, β, pale blue) in a third plane (red) which cuts the line of intersection at right angles
A dihedral angle is the angle between two intersecting planes or half-planes. In chemistry, it is the clockwise angle between half-planes through two sets of three atoms, having two atoms in common. In solid geometry, it is defined as the union of a line and two half-planes that have this line as a common edge. In higher dimensions, a dihedral angle represents the angle between two hyperplanes.
The planes of a flying machine are said to be at positive dihedral angle when both starboard and port main planes (commonly called wings) are upwardly inclined to the lateral axis. When downwardly inclined they are said to be at a negative dihedral angle.
Mathematical background[edit]
When the two intersecting planes are described in terms of Cartesian coordinates by the two equations
the dihedral angle, 
and satisfies 
Alternatively, if nA and nB are normal vector to the planes, one has
where nA · nB is the dot product of the vectors and |nA| |nB| is the product of their lengths.[1]
The absolute value is required in above formulas, as the planes are not changed when changing all coefficient signs in one equation, or replacing one normal vector by its opposite.
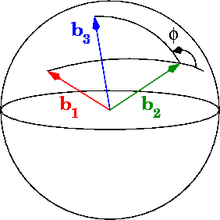
However the absolute values can be and should be avoided when considering the dihedral angle of two half planes whose boundaries are the same line. In this case, the half planes can be described by a point P of their intersection, and three vectors b0, b1 and b2 such that P + b0, P + b1 and P + b2 belong respectively to the intersection line, the first half plane, and the second half plane. The dihedral angle of these two half planes is defined by
,
and satisfies 




In polymer physics[edit]
In some scientific areas such as polymer physics, one may consider a chain of points and links between consecutive points. If the points are sequentially numbered and located at positions r1, r2, r3, etc. then bond vectors are defined by u1=r2−r1, u2=r3−r2, and ui=ri+1−ri, more generally.[2] This is the case for kinematic chains or amino acids in a protein structure. In these cases, one is often interested in the half-planes defined by three consecutive points, and the dihedral angle between two consecutive such half-planes. If u1, u2 and u3 are three consecutive bond vectors, the intersection of the half-planes is oriented, which allows defining a dihedral angle that belongs to the interval (−π, π]. This dihedral angle is defined by[3]
or, using the function atan2,
This dihedral angle does not depend on the orientation of the chain (order in which the point are considered) — reversing this ordering consists of replacing each vector by its opposite vector, and exchanging the indices 1 and 3. Both operations do not change the cosine, but change the sign of the sine. Thus, together, they do not change the angle.
A simpler formula for the same dihedral angle is the following (the proof is given below)
or equivalently,
This can be deduced from previous formulas by using the vector quadruple product formula, and the fact that a scalar triple product is zero if it contains twice the same vector:
Given the definition of the cross product, this means that 



In stereochemistry[edit]
Free energy diagram of n-butane as a function of dihedral angle.
In stereochemistry, a torsion angle is defined as a particular example of a dihedral angle, describing the geometric relation of two parts of a molecule joined by a chemical bond.[4][5] Every set of three non-colinear atoms of a molecule defines a half-plane. As explained above, when two such half-planes intersect (i.e., a set of four consecutively-bonded atoms), the angle between them is a dihedral angle. Dihedral angles are used to specify the molecular conformation.[6] Stereochemical arrangements corresponding to angles between 0° and ±90° are called syn (s), those corresponding to angles between ±90° and 180° anti (a). Similarly, arrangements corresponding to angles between 30° and 150° or between −30° and −150° are called clinal (c) and those between 0° and ±30° or ±150° and 180° are called periplanar (p).
The two types of terms can be combined so as to define four ranges of angle; 0° to ±30° synperiplanar (sp); 30° to 90° and −30° to −90° synclinal (sc); 90° to 150° and −90° to −150° anticlinal (ac); ±150° to 180° antiperiplanar (ap). The synperiplanar conformation is also known as the syn— or cis-conformation; antiperiplanar as anti or trans; and synclinal as gauche or skew.
For example, with n-butane two planes can be specified in terms of the two central carbon atoms and either of the methyl carbon atoms. The syn-conformation shown above, with a dihedral angle of 60° is less stable than the anti-conformation with a dihedral angle of 180°.
For macromolecular usage the symbols T, C, G+, G−, A+ and A− are recommended (ap, sp, +sc, −sc, +ac and −ac respectively).
Proteins[edit]
Depiction of a protein, showing where ω, φ, & ψ refer to.
A Ramachandran plot (also known as a Ramachandran diagram or a [φ,ψ] plot), originally developed in 1963 by G. N. Ramachandran, C. Ramakrishnan, and V. Sasisekharan,[7] is a way to visualize energetically allowed regions for backbone dihedral angles ψ against φ of amino acid residues in protein structure.
In a protein chain three dihedral angles are defined:
- ω (omega) is the angle in the chain Cα − C’ − N − Cα,
- φ (phi) is the angle in the chain C’ − N − Cα − C’
- ψ (psi) is the angle in the chain N − Cα − C’ − N (called φ′ by Ramachandran)
The figure at right illustrates the location of each of these angles (but it does not show correctly the way they are defined).[8]
The planarity of the peptide bond usually restricts ω to be 180° (the typical trans case) or 0° (the rare cis case). The distance between the Cα atoms in the trans and cis isomers is approximately 3.8 and 2.9 Å, respectively. The vast majority of the peptide bonds in proteins are trans, though the peptide bond to the nitrogen of proline has an increased prevalence of cis compared to other amino-acid pairs.[9]
The side chain dihedral angles are designated with χn (chi-n).[10] They tend to cluster near 180°, 60°, and −60°, which are called the trans, gauche−, and gauche+ conformations. The stability of certain sidechain dihedral angles is affected by the values φ and ψ.[11] For instance, there are direct steric interactions between the Cγ of the side chain in the gauche+ rotamer and the backbone nitrogen of the next residue when ψ is near -60°.[12] This is evident from statistical distributions in backbone-dependent rotamer libraries.
Converting from dihedral angles to Cartesian coordinates in chains[edit]
It is common to represent polymers backbones, notably proteins, in internal coordinates; that is, a list of consecutive dihedral angles and bond lengths. However, some types of computational chemistry instead use cartesian coordinates. In computational structure optimization, some programs need to flip back and forth between these representations during their iterations. This task can dominate the calculation time. For processes with many iterations or with long chains, it can also introduce cumulative numerical inaccuracy. While all conversion algorithms produce mathematically identical results, they differ in speed and numerical accuracy.[13][non-primary source needed]
Geometry[edit]
Every polyhedron has a dihedral angle at every edge describing the relationship of the two faces that share that edge. This dihedral angle, also called the face angle, is measured as the internal angle with respect to the polyhedron. An angle of 0° means the face normal vectors are antiparallel and the faces overlap each other, which implies that it is part of a degenerate polyhedron. An angle of 180° means the faces are parallel, as in a tiling. An angle greater than 180° exists on concave portions of a polyhedron.
Every dihedral angle in an edge-transitive polyhedron has the same value. This includes the 5 Platonic solids, the 13 Catalan solids, the 4 Kepler–Poinsot polyhedra, the two quasiregular solids, and two quasiregular dual solids.
Law of cosines for dihedral angle[edit]
Given 3 faces of a polyhedron which meet at a common vertex P and have edges AP, BP and CP, the cosine of the dihedral angle between the faces containing APC and BPC is:[14]
This can be deduced from Spherical law of cosines
See also[edit]
- Atropisomer
References[edit]
- ^ «Angle Between Two Planes». TutorVista.com. Retrieved 2018-07-06.
- ^ Kröger, Martin (2005). Models for polymeric and anisotropic liquids. Springer. ISBN 3540262105.
- ^ Blondel, Arnaud; Karplus, Martin (7 Dec 1998). «New formulation for derivatives of torsion angles and improper torsion angles in molecular mechanics: Elimination of singularities». Journal of Computational Chemistry. 17 (9): 1132–1141. doi:10.1002/(SICI)1096-987X(19960715)17:9<1132::AID-JCC5>3.0.CO;2-T.
- ^ IUPAC, Compendium of Chemical Terminology, 2nd ed. (the «Gold Book») (1997). Online corrected version: (2006–) «Torsion angle». doi:10.1351/goldbook.T06406
- ^ IUPAC, Compendium of Chemical Terminology, 2nd ed. (the «Gold Book») (1997). Online corrected version: (2006–) «Dihedral angle». doi:10.1351/goldbook.D01730
- ^ Anslyn, Eric; Dennis Dougherty (2006). Modern Physical Organic Chemistry. University Science. p. 95. ISBN 978-1891389313.
- ^ Ramachandran, G. N.; Ramakrishnan, C.; Sasisekharan, V. (1963). «Stereochemistry of polypeptide chain configurations». Journal of Molecular Biology. 7: 95–9. doi:10.1016/S0022-2836(63)80023-6. PMID 13990617.
- ^ Richardson, J. S. (1981). «The Anatomy and Taxonomy of Protein Structure». Anatomy and Taxonomy of Protein Structures. Advances in Protein Chemistry. Vol. 34. pp. 167–339. doi:10.1016/S0065-3233(08)60520-3. ISBN 9780120342341. PMID 7020376.
- ^ Singh J, Hanson J, Heffernan R, Paliwal K, Yang Y, Zhou Y (August 2018). «Detecting Proline and Non-Proline Cis Isomers in Protein Structures from Sequences Using Deep Residual Ensemble Learning». Journal of Chemical Information and Modeling. 58 (9): 2033–2042. doi:10.1021/acs.jcim.8b00442. PMID 30118602. S2CID 52031431.
- ^ «Side Chain Conformation».
- ^ Dunbrack, RL Jr.; Karplus, M (20 March 1993). «Backbone-dependent rotamer library for proteins. Application to side-chain prediction». Journal of Molecular Biology. 230 (2): 543–74. doi:10.1006/jmbi.1993.1170. PMID 8464064.
- ^ Dunbrack, RL Jr; Karplus, M (May 1994). «Conformational analysis of the backbone-dependent rotamer preferences of protein sidechains». Nature Structural Biology. 1 (5): 334–40. doi:10.1038/nsb0594-334. PMID 7664040. S2CID 9157373.
- ^ Parsons, J.; Holmes, J. B.; Rojas, J. M.; Tsai, J.; Strauss, C. E. (2005), «Practical conversion from torsion space to cartesian space for in silico protein synthesis», Journal of Computational Chemistry, 26 (10): 1063–1068, doi:10.1002/jcc.20237, PMID 15898109, S2CID 2279574
- ^ «dihedral angle calculator polyhedron». www.had2know.com. Archived from the original on 25 November 2015. Retrieved 25 October 2015.
External links[edit]
- The Dihedral Angle in Woodworking at Tips.FM
- Analysis of the 5 Regular Polyhedra gives a step-by-step derivation of these exact values.
From Wikipedia, the free encyclopedia
This article is about the geometry term. For other uses, see Dihedral.
Angle between two half-planes (α, β, pale blue) in a third plane (red) which cuts the line of intersection at right angles
A dihedral angle is the angle between two intersecting planes or half-planes. In chemistry, it is the clockwise angle between half-planes through two sets of three atoms, having two atoms in common. In solid geometry, it is defined as the union of a line and two half-planes that have this line as a common edge. In higher dimensions, a dihedral angle represents the angle between two hyperplanes.
The planes of a flying machine are said to be at positive dihedral angle when both starboard and port main planes (commonly called wings) are upwardly inclined to the lateral axis. When downwardly inclined they are said to be at a negative dihedral angle.
Mathematical background[edit]
When the two intersecting planes are described in terms of Cartesian coordinates by the two equations
the dihedral angle, 
and satisfies 
Alternatively, if nA and nB are normal vector to the planes, one has
where nA · nB is the dot product of the vectors and |nA| |nB| is the product of their lengths.[1]
The absolute value is required in above formulas, as the planes are not changed when changing all coefficient signs in one equation, or replacing one normal vector by its opposite.
However the absolute values can be and should be avoided when considering the dihedral angle of two half planes whose boundaries are the same line. In this case, the half planes can be described by a point P of their intersection, and three vectors b0, b1 and b2 such that P + b0, P + b1 and P + b2 belong respectively to the intersection line, the first half plane, and the second half plane. The dihedral angle of these two half planes is defined by
,
and satisfies 




In polymer physics[edit]
In some scientific areas such as polymer physics, one may consider a chain of points and links between consecutive points. If the points are sequentially numbered and located at positions r1, r2, r3, etc. then bond vectors are defined by u1=r2−r1, u2=r3−r2, and ui=ri+1−ri, more generally.[2] This is the case for kinematic chains or amino acids in a protein structure. In these cases, one is often interested in the half-planes defined by three consecutive points, and the dihedral angle between two consecutive such half-planes. If u1, u2 and u3 are three consecutive bond vectors, the intersection of the half-planes is oriented, which allows defining a dihedral angle that belongs to the interval (−π, π]. This dihedral angle is defined by[3]
or, using the function atan2,
This dihedral angle does not depend on the orientation of the chain (order in which the point are considered) — reversing this ordering consists of replacing each vector by its opposite vector, and exchanging the indices 1 and 3. Both operations do not change the cosine, but change the sign of the sine. Thus, together, they do not change the angle.
A simpler formula for the same dihedral angle is the following (the proof is given below)
or equivalently,
This can be deduced from previous formulas by using the vector quadruple product formula, and the fact that a scalar triple product is zero if it contains twice the same vector:
Given the definition of the cross product, this means that 



In stereochemistry[edit]
Free energy diagram of n-butane as a function of dihedral angle.
In stereochemistry, a torsion angle is defined as a particular example of a dihedral angle, describing the geometric relation of two parts of a molecule joined by a chemical bond.[4][5] Every set of three non-colinear atoms of a molecule defines a half-plane. As explained above, when two such half-planes intersect (i.e., a set of four consecutively-bonded atoms), the angle between them is a dihedral angle. Dihedral angles are used to specify the molecular conformation.[6] Stereochemical arrangements corresponding to angles between 0° and ±90° are called syn (s), those corresponding to angles between ±90° and 180° anti (a). Similarly, arrangements corresponding to angles between 30° and 150° or between −30° and −150° are called clinal (c) and those between 0° and ±30° or ±150° and 180° are called periplanar (p).
The two types of terms can be combined so as to define four ranges of angle; 0° to ±30° synperiplanar (sp); 30° to 90° and −30° to −90° synclinal (sc); 90° to 150° and −90° to −150° anticlinal (ac); ±150° to 180° antiperiplanar (ap). The synperiplanar conformation is also known as the syn— or cis-conformation; antiperiplanar as anti or trans; and synclinal as gauche or skew.
For example, with n-butane two planes can be specified in terms of the two central carbon atoms and either of the methyl carbon atoms. The syn-conformation shown above, with a dihedral angle of 60° is less stable than the anti-conformation with a dihedral angle of 180°.
For macromolecular usage the symbols T, C, G+, G−, A+ and A− are recommended (ap, sp, +sc, −sc, +ac and −ac respectively).
Proteins[edit]
Depiction of a protein, showing where ω, φ, & ψ refer to.
A Ramachandran plot (also known as a Ramachandran diagram or a [φ,ψ] plot), originally developed in 1963 by G. N. Ramachandran, C. Ramakrishnan, and V. Sasisekharan,[7] is a way to visualize energetically allowed regions for backbone dihedral angles ψ against φ of amino acid residues in protein structure.
In a protein chain three dihedral angles are defined:
- ω (omega) is the angle in the chain Cα − C’ − N − Cα,
- φ (phi) is the angle in the chain C’ − N − Cα − C’
- ψ (psi) is the angle in the chain N − Cα − C’ − N (called φ′ by Ramachandran)
The figure at right illustrates the location of each of these angles (but it does not show correctly the way they are defined).[8]
The planarity of the peptide bond usually restricts ω to be 180° (the typical trans case) or 0° (the rare cis case). The distance between the Cα atoms in the trans and cis isomers is approximately 3.8 and 2.9 Å, respectively. The vast majority of the peptide bonds in proteins are trans, though the peptide bond to the nitrogen of proline has an increased prevalence of cis compared to other amino-acid pairs.[9]
The side chain dihedral angles are designated with χn (chi-n).[10] They tend to cluster near 180°, 60°, and −60°, which are called the trans, gauche−, and gauche+ conformations. The stability of certain sidechain dihedral angles is affected by the values φ and ψ.[11] For instance, there are direct steric interactions between the Cγ of the side chain in the gauche+ rotamer and the backbone nitrogen of the next residue when ψ is near -60°.[12] This is evident from statistical distributions in backbone-dependent rotamer libraries.
Converting from dihedral angles to Cartesian coordinates in chains[edit]
It is common to represent polymers backbones, notably proteins, in internal coordinates; that is, a list of consecutive dihedral angles and bond lengths. However, some types of computational chemistry instead use cartesian coordinates. In computational structure optimization, some programs need to flip back and forth between these representations during their iterations. This task can dominate the calculation time. For processes with many iterations or with long chains, it can also introduce cumulative numerical inaccuracy. While all conversion algorithms produce mathematically identical results, they differ in speed and numerical accuracy.[13][non-primary source needed]
Geometry[edit]
Every polyhedron has a dihedral angle at every edge describing the relationship of the two faces that share that edge. This dihedral angle, also called the face angle, is measured as the internal angle with respect to the polyhedron. An angle of 0° means the face normal vectors are antiparallel and the faces overlap each other, which implies that it is part of a degenerate polyhedron. An angle of 180° means the faces are parallel, as in a tiling. An angle greater than 180° exists on concave portions of a polyhedron.
Every dihedral angle in an edge-transitive polyhedron has the same value. This includes the 5 Platonic solids, the 13 Catalan solids, the 4 Kepler–Poinsot polyhedra, the two quasiregular solids, and two quasiregular dual solids.
Law of cosines for dihedral angle[edit]
Given 3 faces of a polyhedron which meet at a common vertex P and have edges AP, BP and CP, the cosine of the dihedral angle between the faces containing APC and BPC is:[14]
This can be deduced from Spherical law of cosines
See also[edit]
- Atropisomer
References[edit]
- ^ «Angle Between Two Planes». TutorVista.com. Retrieved 2018-07-06.
- ^ Kröger, Martin (2005). Models for polymeric and anisotropic liquids. Springer. ISBN 3540262105.
- ^ Blondel, Arnaud; Karplus, Martin (7 Dec 1998). «New formulation for derivatives of torsion angles and improper torsion angles in molecular mechanics: Elimination of singularities». Journal of Computational Chemistry. 17 (9): 1132–1141. doi:10.1002/(SICI)1096-987X(19960715)17:9<1132::AID-JCC5>3.0.CO;2-T.
- ^ IUPAC, Compendium of Chemical Terminology, 2nd ed. (the «Gold Book») (1997). Online corrected version: (2006–) «Torsion angle». doi:10.1351/goldbook.T06406
- ^ IUPAC, Compendium of Chemical Terminology, 2nd ed. (the «Gold Book») (1997). Online corrected version: (2006–) «Dihedral angle». doi:10.1351/goldbook.D01730
- ^ Anslyn, Eric; Dennis Dougherty (2006). Modern Physical Organic Chemistry. University Science. p. 95. ISBN 978-1891389313.
- ^ Ramachandran, G. N.; Ramakrishnan, C.; Sasisekharan, V. (1963). «Stereochemistry of polypeptide chain configurations». Journal of Molecular Biology. 7: 95–9. doi:10.1016/S0022-2836(63)80023-6. PMID 13990617.
- ^ Richardson, J. S. (1981). «The Anatomy and Taxonomy of Protein Structure». Anatomy and Taxonomy of Protein Structures. Advances in Protein Chemistry. Vol. 34. pp. 167–339. doi:10.1016/S0065-3233(08)60520-3. ISBN 9780120342341. PMID 7020376.
- ^ Singh J, Hanson J, Heffernan R, Paliwal K, Yang Y, Zhou Y (August 2018). «Detecting Proline and Non-Proline Cis Isomers in Protein Structures from Sequences Using Deep Residual Ensemble Learning». Journal of Chemical Information and Modeling. 58 (9): 2033–2042. doi:10.1021/acs.jcim.8b00442. PMID 30118602. S2CID 52031431.
- ^ «Side Chain Conformation».
- ^ Dunbrack, RL Jr.; Karplus, M (20 March 1993). «Backbone-dependent rotamer library for proteins. Application to side-chain prediction». Journal of Molecular Biology. 230 (2): 543–74. doi:10.1006/jmbi.1993.1170. PMID 8464064.
- ^ Dunbrack, RL Jr; Karplus, M (May 1994). «Conformational analysis of the backbone-dependent rotamer preferences of protein sidechains». Nature Structural Biology. 1 (5): 334–40. doi:10.1038/nsb0594-334. PMID 7664040. S2CID 9157373.
- ^ Parsons, J.; Holmes, J. B.; Rojas, J. M.; Tsai, J.; Strauss, C. E. (2005), «Practical conversion from torsion space to cartesian space for in silico protein synthesis», Journal of Computational Chemistry, 26 (10): 1063–1068, doi:10.1002/jcc.20237, PMID 15898109, S2CID 2279574
- ^ «dihedral angle calculator polyhedron». www.had2know.com. Archived from the original on 25 November 2015. Retrieved 25 October 2015.
External links[edit]
- The Dihedral Angle in Woodworking at Tips.FM
- Analysis of the 5 Regular Polyhedra gives a step-by-step derivation of these exact values.
План урока:
Понятие двугранного угла и угла между плоскостями
Перпендикулярность плоскостей
Прямоугольный параллелепипед
Трехгранный угол
Многогранный угол
Типичные задачи на углы между плоскостями
Понятие двугранного угла и угла между плоскостями
Напомним, что в планиметрии углом называют фигуру, состоящую из точки и двух лучей, выходящих из нее. Сама точка именуется вершиной угла, а лучи – сторонами угла.
По аналогии в стереометрии рассматривается схожая фигура – двугранный угол. Он состоит из двух полуплоскостей, которые исходят из одной прямой. Каждая из этих полуплоскостей именуется гранью двугранного угла, а их общая прямая – это ребро двугранного угла.
Для обозначения двугранного угла достаточно указать две точки на его ребре, а также ещё по одной точке на каждой грани. Например, на следующем рисунке показан угол САВD:
Двугранные углы часто встречаются в обычной жизни. Например, его образуют двухскатные крыши домов. В стереометрии двугранные угла можно найти в любом многограннике.
Двугранные углы можно измерять. Для этого надо выбрать произвольную точку на ребре угла и на каждой грани построить перпендикуляр, проходящий через эту точку. Через эти два перпендикуляра можно построить единственную плоскость. Угол между двумя перпендикулярами и принимается за величину двугранного угла.
Отдельно отметим, что плоскость, проходящая через перпендикуляры (на рисунке выше это γ) перпендикулярна ребру угла АВ. Это вытекает из признака перпендикулярности прямой и плоскости. Действительно, АВ⊥ВС и АВ⊥BD, поэтому и АВ⊥γ. Построенный угол ∠СBD называют линейным углом двугранного угла.
Понятно, что в каждом двугранном угле можно построить сколько угодно линейных углов:
Здесь помимо ∠ВСD построены линейные углы ∠В’С’D’ и ∠В’’С’’D’’. Однако все эти углы имеют одинаковую градусную меру. Сравним, например, ∠ВСD и ∠В’С’D’. Так как BD⊥AB и B’D’⊥АВ, то BD||B’D’. Аналогично можно прийти к выводу, что ВС||B’C’. Получаем, что стороны углов ∠ВСD и ∠В’С’D’ – это сонаправленные лучи, а потому ∠ВСD и ∠В’С’D’ одинаковы.
Двугранные углы, как и обычные углы, можно разделить на острые (их градусная мера меньше 90°), прямые (они в точности равны 90°) и тупые (которые больше 90°).
Если две плоскости пересекаются, то они образуют сразу 4 двугранных угла. Если среди них есть острый угол, то его величина считается углом между плоскостями. Если же все образуется 4 прямых двугранных угла, то угол между плоскостями принимается равным 90°.
Перпендикулярность плоскостей
В частном случае, когда угол составляет 90°, говорят, что пересекающиеся плоскости перпендикулярны.
Перпендикулярны друг другу пол и стены в доме, смежные грани кубика, стенки коробки. Существует особый признак перпендикулярности плоскостей.
Действительно, пусть плоскости α и β пересекаются по линии n, и в β есть такая прямая m, что m⊥α. Тогда m и n должны пересекаться в какой-нибудь точке К. Проведем в плоскости α через К прямую р, перпендикулярную n. Ясно, что m⊥р, ведь m⊥α. Получается, угол между m и р как раз и является углом между плоскостями α и β, ведь m⊥n и р⊥n. И этот угол равен 90°, ведь m⊥p, ч т. д.
Из доказанного признака вытекает следующее утверждение:
Прямоугольный параллелепипед
Ранее мы уже узнали про параллелепипед. Это фигура с 6 гранями, каждая из которых представляет собой параллелограмм. Особый интерес представляет его частный случай – прямоугольный параллелепипед.
Такую форму имеют многие шкафы, другие предметы мебели, коробки для обуви, небоскребы. Изображают прямоугольный параллелепипед так:
Для обозначения вершин параллелепипеда применяют латинские буквы. Очень часто для вершин одной грани используют 4 буквы без индекса (на рисунке выше это А, В, С, D), а другие 4 вершины обозначают такими же буквами, но с нижним индексом 1: А1, B1, C1 и D1. При этом одноименные вершины (например, А и А1) находятся на одном ребре, которое располагается на рисунке вертикально.
Докажем некоторые свойства прямоугольного параллелепипеда.
Например, ребро АD пересекается с гранями АВВ1А1 и CDD1C1. Значит, оно перпендикулярно этим граням (точнее говоря, оно перпендикулярно плоскостям, проходящим через эти грани). Действительно, AD⊥DC, ведь ∠ADC является углом в прямоугольнике АВСD и потому он прямой. Аналогично и AD⊥DD1, ведь и ADD1A1 – прямоугольник. Получается, что ребро AD перпендикулярно 2 прямым в грани CDD1C1 (которые при этом пересекаются), и потому оно перпендикулярно и всей грани. То же самое можно продемонстрировать для любого ребра прямоугольного параллелепипеда и любой грани, которую она пересекает.
Эти грани пересекаются по ребру А1D1. Этому ребру в свою очередь перпендикулярны ребра АА1 и А1В1, лежащие в гранях ADD1A1 и A1D1C1B1. Значит, ∠АА1В1 и будет углом между этими гранями. Но он составляет 90°, то есть грани перпендикулярны, ч. т. д.
Хотя у прямоугольного параллелепипеда есть 12 граней, многие из них имеют одинаковую длину. Поэтому для описания размеров этой фигуры достаточно указать только три параметра. Обычно их называют длиной, шириной и высотой:
Эти параметры также называют измерениями прямоугольного параллелепипеда. Зная их, можно вычислить длину диагонали прямоугольного параллелепипеда. Для этого используется следующая теорема:
Действительно, пусть есть прямоугольный параллелепипед АВСDA1B1C1D1. Назовем ребро AD его длиной, АВ – шириной, а ВВ1 – высотой. Пусть необходимо найти длину диагонали В1D:
Сначала построим отрезок BD и рассмотрим ∆ABD. Он прямоугольный, и потому для него верна теорема Пифагора:
Теперь перейдем к ∆В1ВD. Так как ребро BB1 перпендикулярно грани ABCD, то ∠В1ВD – прямой. Тогда и ∆В1ВD – прямоугольный, а потому и для него можно записать теорему Пифагора:
Дополнительно отметим уже известный нам факт, что тот прямоугольный параллелепипед, у которого все стороны одинаковы, именуется кубом. Можно дать и такое определение куба:
Трехгранный угол
Выберем в пространстве произвольную точку K. Далее из нее проведем три луча КА, КВ и КС так, чтобы они не находились в одной плоскости:
В результате мы получили фигуру, которую именуют трехгранным углом. Она состоит их трех плоских углов: ∠АКС, ∠АКВ и ∠ВКС. Эти углы так и называются – плоские углы трехгранного угла. Сам же трехгранный угол обозначают четырьмя буквами: КАВС. Обратите внимание, что через каждую пару лучей КА, КВ и КС можно провести плоскость. Таким образом, название «трехгранный» угол показывает, что в точке К сходятся три грани. Чаще всего в стереометрии такой угол возникает при рассмотрении вершин тетраэдра, в котором есть сразу четыре трехгранных угла:
Доказательство. Пусть в пространстве из точки D выходят лучи AD, BD и CD. Важно понимать, что мы можем свободно «передвигать» точки А, В и С по лучам, и величина плоских углов при этом меняться не будет. Если среди плоских углов нет наибольшего, то теорема очевидно выполняется. Поэтому надо рассмотреть лишь случай, когда один из углов – наибольший. Пусть им будет ∠BDC:
Это возможно сделать, ведь ∠BDC > AD, поэтому внутри ∠BDC можно провести луч DK. Далее «сместим» точку А на луче АD так, чтобы DK = AD. Естественно, что при этом плоские углы трехгранного угла никак не изменятся, также как останется верным равенство
Сравним ∆ADC и ∆DKC. У них есть общая сторона DC, одинаковы стороны DK и AD, а также совпадают углы между ними. Значит, эти треугольники равны, и тогда можно записать, что:
Теперь сравним ∆ABD и ∆DBK. У них BD – общая сторона, а DK = AD. При этом BK < AB. В таком случае против меньшей стороны будет лежать меньший угол (смотри примечание после доказательства), то есть
Именно это неравенство и необходимо было доказать.
Примечание. В ходе доказательства было использовано утверждение, что если у двух треугольников две стороны одинаковы, в третьи стороны отличаются, то против меньшей третьей стороны будет располагаться меньший угол:
Это утверждение часто не рассматривается в курсе планиметрии, поэтому есть смысл доказать его отдельно. Действительно, пусть есть ∆АВС и ∆А’B’C’, АС = А’C’ и АВ = A’B’, а СВ < C’B’. Надо показать, что ∠А <∠A’. Для этого выразим стороны СВ и C’B’ (а точнее говоря, их квадраты) с помощью теоремы косинусов:
Из последнего неравенства на основе определения косинуса для углов из интервала от 0° до 180° вытекает, что и
Многогранный угол
Возможен случай, когда из одной точки в пространстве выходят не три, а большее количество лучей, причем образуемые ими углы не располагаются в единой плоскости. Такая фигура именуется многогранным углом. Трехгранный угол можно считать его частным случаем. Также его частными случаями будут четырехгранный угол, пятигранный угол, шестигранный угол и т. д.
Более наглядна следующая демонстрация многогранного угла. Построим на плоскости α произвольный многоугольник. Далее выберем какую-нибудь точку вне плоскости α и соединим ее с вершинами многоугольника с помощью лучей. При этом у нас как раз получится многогранный угол. Если, например, в качестве многоугольника мы использовали пятиугольник, то и получим мы пятигранный угол:
Важно отметить, что в данном случае состоит многогранный угол именно из лучей КА1, КА2, КА3…, а не из одноименных отрезков. То есть многогранный угол – это ни в коем случае не многогранник КА1А2А3А4А5, у него есть только одна вершина – точка К. Многогранник КА1А2А3А4А5 – это пирамида, такая фигура изучается в курсе стереометрии чуть позже. Многоугольник А1А2А3А4А5 – это сечение многогранного угла. Углы ∠А1КА2, ∠А2КА3, ∠А3КА4… – это плоские углы многогранного угла.
Заметим, что на исходный многоугольник на плоскости может быть как выпуклым, так и невыпуклым. Соответственно и многогранный угол может быть как выпуклым, так и невыпуклым:
Так как любой треугольник – это выпуклый многоугольник, то и любой трехгранный угол является выпуклым. В выпуклом угле все его точки лежат по одну сторону от любой плоскости, проходящей, через какие-нибудь два смежных луча угла. Вообще любое сечение многогранного угла представляет собой выпуклый многоугольник.
Докажем важное утверждение:
Для доказательства возьмем произвольный многогранный угол и проведем в нем сечение А1А2А3…Аn, которое будет являться выпуклым многоугольником:
В последнем равенстве в каждой скобке стоят по два плоских угла в тех трехгранных углах, вершины которых совпадают с вершинами многоугольника А1А2А3…Аn. В предыдущей теореме мы выяснили, что эта сумма меньше третьего плоского угла, то есть
В правой части в скобках стоит сумма углов выпуклого n-угольника А1А2А3…Аn. Она, как мы знаем, составляет 180°•(n – 2), то есть
Последнее неравенство и необходимо было доказать.
Типичные задачи на углы между плоскостями
В школьной практике почти не встречаются задачи с многогранными углами, поэтому достаточно понимания и двугранного угла.
Задание. У тетраэдра ABCD все ребра одинаковы. Найдите величину двугранного угла между плоскостями АВС и АСD.
Решение. Отметим на ребре АС точку М, которая является его серединой:
Заметим, что плоскости АВС и АСD пересекаются по прямой АС. Раз все ребра тетраэдра одинаковы, то ∆АВС и ∆АСD – равносторонние. DM и BM – это медианы в ∆АВС и ∆АСD соответственно, ведь M – середина АС. Но раз треугольники равносторонние, то они одновременно являются и высотами, то есть BM⊥AC и DM⊥АС. Тогда ∠DMB как раз и представляет собой линейный угол двугранного угла BАСD. То есть именно его значение нам и надо вычислить (если, конечно, он окажется не больше 90°).
Пусть ребра тетраэдра имеют длину а. Тогда АМ вдвое короче. Найдем из прямоугольного ∆АМD длину MD:
Задание. Двугранный угол равен φ, меньший 90°. На одной из его граней отмечена точка К, которая находится на расстоянии d от другой грани. Каково расстояние между точкой К и ребром двугранного угла?
Решение. Пусть угол образован плоскостями α и β. Опустим из K два перпендикуляра – один на плоскость β в точку Н, а другой на линию пересечения плоскостей в точку Р:
По условию задачи ∠НРК = φ, а HK = d. Нам же надо найти РК. Это можно сделать, применив определение синуса к ∆РНК:
Задание. Верно ли, что плоскость, пересекающая две параллельные плоскости, образует с ними одинаковые углы?
Решение. Пусть есть параллельные друг другу плоскости α и β, а пересекает их плоскость γ. Линию пересечения α и γ обозначим как n, и такую же линию для β и γ обозначим как m:
Заметим, что m и n располагаются в одной плоскости γ и при этом не пересекаются, в противном случае у α и β нашлась бы общая точка, которой быть не должно. Значит, m||n.
Далее проведем в γ прямую р, перпендикулярную n. Раз m||n и р⊥n, то и р⊥m. То есть р – общий перпендикуляр для m и n.
Далее в α через точку пересечения n и p проведем прямую k, перпендикулярную n. Ясно, что k||β. После уже через точку пересечения m и p построим такую прямую k’, что k||k’:
Так как k||β и k||k’, то прямая k’ будет принадлежать плоскости β (по теореме 6 из этого урока). Так как k||k’, m||n и n⊥k, то по теореме о сонаправленных лучах можно утверждать, что и m⊥k’. Тогда углы, отмеченные на рисунке синим цветом – это и есть линейные углы двугранных углов. Они одинаковы, так как являются соответственными при секущей р и параллельных прямых k и k’. Если же двугранные углы равны, то одинаковы и углы между плоскостями, ч. т. д.
Примечание. Доказанный факт можно сформулировать в виде теоремы:
Она может быть использована при решении некоторых сложных задач.
Задание. В прямоугольном ∆АВС АВ и АС – катеты с длиной 7 и 24 соответственно. Через гипотенузу проведена плоскость β, образующая с плоскостью АВС угол 30°. Каково расстояние между точкой А и плоскостью β?
Решение.
Опустим из А перпендикуляр АН на β. Это и будет искомое нами расстояние. Также в ∆АВС построим высоту AD. Заметим, что раз АН⊥β, то по определению и АН⊥HD. Можно сказать, что HD – это проекция AD на β. Раз прямая ВС перпендикулярна наклонной AD, то она одновременно будет перпендикулярна и наклонной HD по обратной теореме о трех перпендикулярах.
Плоскости АВС и β пересекаются по прямой ВС, АD⊥ВС и HD⊥BC. Получается, что ADH – это как раз угол между АВС и β, и по условию он составляет 30°.
По теореме Пифагора вычислим гипотенузу ВС:
Теперь перейдем к ∆AHD. Он также прямоугольный (∠Н = 90°). Используем для него тригонометрию:
Задание. Известны измерения прямоугольного параллелепипеда. Его длина составляет 90 см, ширина – 20 см, а высота – 60 см. Какова длина диагонали такого параллелепипеда?
Решение. Обозначим измерения буквами а, b, с, а диагональ буквой d. Достаточно просто воспользоваться формулой:
Далее рассмотрим несколько задач, в которых надо найти угол между плоскостями, находящимися в кубе с ребром, чья длина составляет единицу.
Задание. Вычислите угол между гранью ADHЕ и сечением АBGН:
Решение. Заметим, что сечение АВGH содержит прямую АВ. Но АВ – это перпендикуляр к АЕНD. Если АВGH содержит перпендикуляр к ADH, то эти две плоскости перпендикулярны, и угол между ними составляет 90°.
Ответ: 90°.
Задание. Определите угол между гранью ADHE и сечением ADGF:
Решение. Две рассматриваемые плоскости пересекаются по ребру AD. Ребра DH и AD перпендикулярны как стороны квадрата. Так как AD – это перпендикуляр к грани СDHG, то AD⊥DG. Получается, что ∠HDG – это и есть искомый угол. Его величина равна 45°, ведь это угол между диагональю квадрата и его стороной.
Ответ: 45°.
Задание. Вычислите угол между сечениями АВGH и EFCD:
Решение. Пересекаются эти две плоскости по прямой KP, где K и P – точки пересечения диагоналей квадратов BFGH и AEHD. Докажем, что отрезки KG и KC перпендикулярны KP.
Действительно, рассмотрим четырехугольник АВGH. Ребра АВ и GH перпендикулярны граням AEHD и BFGH, поэтому все углы в АВGH – прямые, то есть это прямоугольник и BG||AH. Теперь рассмотрим четырехугольник АВKP. Стороны BK и AP параллельны и равны как половины равных отрезков BG и AH. Значит, BKAP – параллелограмм. Но в нем есть прямые углы ∠В и ∠А, поэтому BKAP – прямоугольник. Аналогично можно показать, что и KGHP – прямоугольник. Это и приводит к выводу о том, что KG⊥KP и PH⊥KP. Поэтому ∠СKG и является искомым углом между сечениями. Он является углом между диагоналями квадрата, то есть равен 90°.
Ответ: 90°.
Задание. Найдите угол между сечением AFH и гранью AEHD:
Решение. Обозначим середину диагонали AH буквой K. Докажем ∠EKF – искомый нами угол:
Действительно, плоскости AHD и AFH пересекаются по прямой AH. EK – медиана в равнобедренном ∆AEH с основанием AH, поэтому она также является и высотой, то есть EK⊥AH. AF и FH – диагонали в равных квадратах ABFE и EFGH, поэтому эти диагонали одинаковы. Значит, ∆AFH – равнобедренный, и поэтому его медиана FK также перпендикулярна основанию AH. Получается, что ∠EKF и является искомым. Вычислить его можно из ∆EKF.
Сначала найдем длину EK. В прямоугольном ∆AEK ∠KAE составляет 45° (угол между диагональю и стороной квадрата), поэтому
Задание. Вычислите угол между гранью BCGF и сечением AFH:
Решение. Вспомним, что в предыдущей задаче мы уже вычислили угол между гранью АЕHD и тем же сечением АFH. Но грани AEHD и BCFG параллельны, поэтому АFH должна пересекаться их под одним и тем же углом. Поэтому ответ этой задачи совпадает с ответом к предыдущей задаче.
Ответ: ≈ 54,74°.
Задание. Чему равен угол между сечениями АСH и AFGH?
Решение. Пусть диагонали СН и DG пересекаются в точке К. Точка K будет принадлежать обоим сечениям, как и точка А. Значит, сечения пересекаются по линии АК. Проведем в сечении AFGH через точку K прямую, перпендикулярны АК и пересекающую FG в какой-то точке Р (позже мы убедимся, что прямая действительно должна пересекать отрезок FG):
Докажем, что ∠CPK и является углом между сечениями. Мы специально провели РК так, что РК⊥АК. Теперь посмотрим на ∆АСН. Он равносторонний, ведь его стороны АС, СН и DH – это диагонали равных квадратов (граней куба). Прямая АК – медиана, ведь K – точка пересечения диагоналей квадрата СDHG, которая делит диагонали пополам. Но раз ∆АСН равносторонний, то его медиана – это ещё и высота, то есть АК⊥РК. Итак, АК⊥СК и АК⊥РК, поэтому ∠CPK – это угол между сечениями. Для его вычисления необходимо найти все стороны в ∆РСК и далее применить теорему косинусов.
Проще всего найти СК. ∆СKD – прямоугольный (∠К = 90°), а ∠СDK составляет 45° (угол между стороной и диагональю в квадрате). Тогда можно записать, что
Отдельно отметим, что отрезки GK и KD имеют такую же длину, ведь диагонали в квадрате (а значит и их половины) одинаковы.
Для нахождения РК покажем отдельно плоскость AFG, то есть красное сечение:
Обозначим ∠KAD как φ. Тогда ∠АКD будет составлять 90 – φ. Углы ∠АКD, ∠АKP и ∠PKG в сумме дают 180°, что позволяет найти ∠PKG:
Получилось, что у ∆АКD и ∆PKG есть по два одинаковых угла (φ и 90°). Значит, они подобны. Составим такую пропорцию:
Теперь можно вернуться ко всему кубу и найти отрезок РС. Здесь снова можно применить теорему Пифагора, но уже к ∆PCG:
Теперь для ∆PCK мы можем записать теорему косинусов
Неожиданно мы доказали, что два построенных сечения перпендикулярны друг другу. Прийти к этому выводу можно было и иначе. Достаточно было бы показать, что прямая CH – это перпендикуляр к сечению AFGD. Попробуйте сделать это самостоятельно.
Ответ: 90°.
Задание. Вычислите угол между сечениями BDHF и ADGF:
Решение. У сечений общими являются точки F и D. Значит, именно по прямой FD они пересекаются.
Опустим в синей сечении BDHF перпендикуляр на FD, который упадет в некоторую точку K:
Докажем, что отрезок GK также перпендикулярен FD. Действительно, BK – это высота в ∆BDF. Но ∆BDF и ∆GDF равны, ведь они одинаковы все три стороны (FD – общая сторона, BF и FG – ребра куба, BD и DG – диагонали на гранях куба). В равных треугольниках высоты должны делить стороны на равные отрезки, поэтому высота, опущенная из G на FD, также разделит FD на отрезки FK и KD. То есть она просто упадет в точку K. Это и значит, что KG – высота. Получается, что нам надо вычислить ∠BKG.
Сначала найдем длину диагоналей BD и BG. Можно применить теорему Пифагора для ∆BFG:
KG имеет ту же длину, ведь KG и BK – одинаковые высоты в равных треугольниках ∆BDF и ∆GDF.
Теперь используем теорему косинусов для ∆BKG:
Мы вычислили двугранный угол, но он оказался больше 90°. Это значит, угол между плоскостями равен не 120°, а 180° – 120°, то есть 60°.
Ответ: 60°.
Сегодня мы познакомились с понятием двугранного угла, научились вычислять углы между плоскостями. В частном случае вместо вычисления угла можно просто доказать перпендикулярность плоскостей.
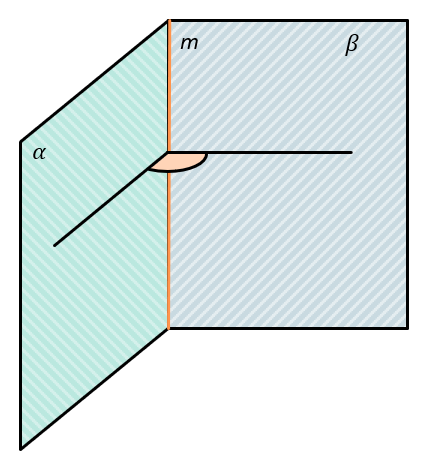
Двугранный угол
Двугранный угол – это геометрическая фигура, образованная двумя полуплоскостями и прямой между ними.
(alpha cap beta = m)
Стороны двугранного угла – полуплоскости, из которых он состоит.
Ребро двугранного угла – прямая, по которой пересекаются его стороны.
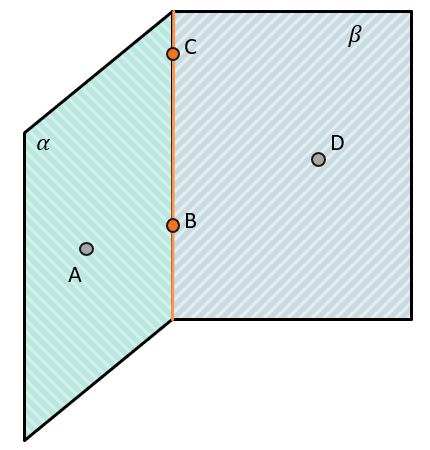
Двугранный угол обозначается четырьмя точками, принадлежавшими сторонам и ребру, например ABCD. При чем таким образом, что через первые три точки можно провести одну плоскость (АВС), через три последние точки вторую (BCD), а точки посередине (ВС) принадлежат обеим плоскостям, т.е. образуют ребро угла:
(left. begin{matrix} \ A, B, C in a \ A, B, C in beta \ \ end{matrix} right} Longrightarrow a cap beta = BC Longrightarrow ABCD — (alphahat{}beta))
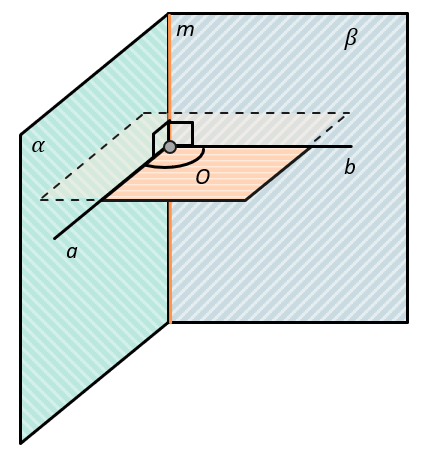
Градусная мера двугранного угла определяется его линейным углом.
Линейный угол двугранного угла – это угол между перпендикулярами к его ребру.
(left. begin{matrix} \ a,bbot m \ a in alpha \ b in beta \ a cap b cap m = O \ \ end{matrix} right} Longrightarrow left( ahat{}b right) = (alphahat{}beta))
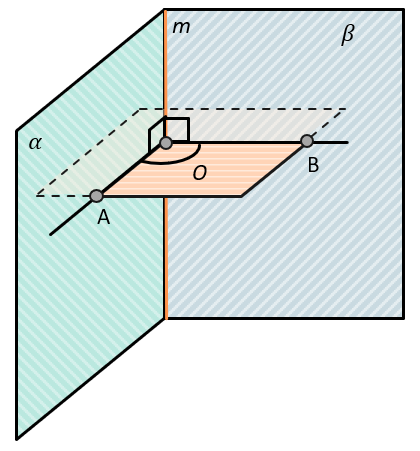
Все линейные углы двугранного угла равны – это значит, что мы можем взять абсолютно любой линейный угол на и его градусная мера будет равна градусной мере самого двугранного угла.
Так же линейный угол двугранного угла можно обозначать через точки, лежащие на прямых a и b, например:
(angle AOB = (alphahat{}beta))


 -мерном Евклидовом пространстве.
-мерном Евклидовом пространстве.





























![{displaystyle (mathbf {u} _{1}times mathbf {u} _{2})times (mathbf {u} _{2}times mathbf {u} _{3})=[(mathbf {u} _{2}times mathbf {u} _{3})cdot mathbf {u} _{1}]mathbf {u} _{2}-[(mathbf {u} _{2}times mathbf {u} _{3})cdot mathbf {u} _{2}]mathbf {u} _{1}=[(mathbf {u} _{2}times mathbf {u} _{3})cdot mathbf {u} _{1}]mathbf {u} _{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/78dfd079ef2f25bdd1f87bcbd9d208c2af4ca75b)