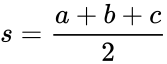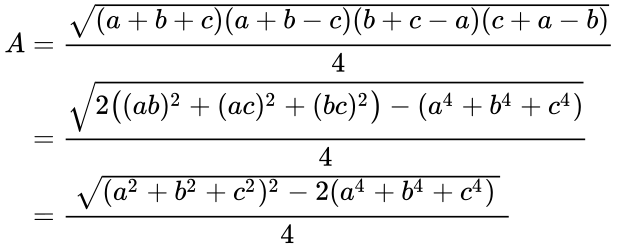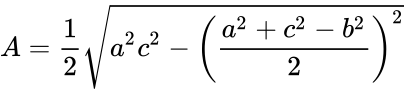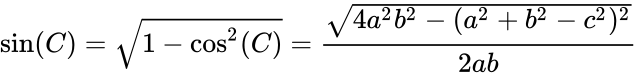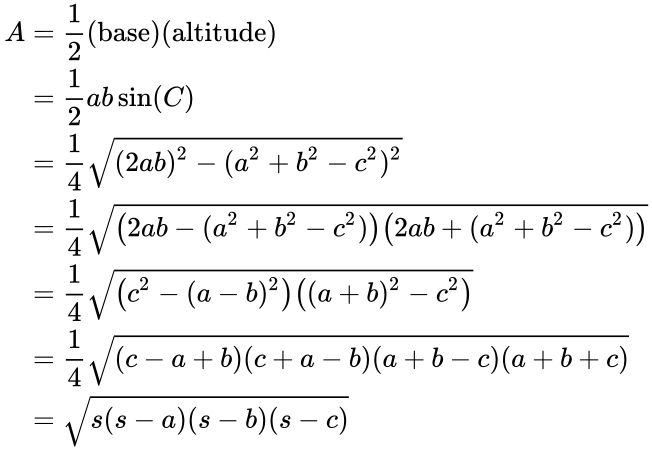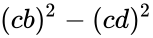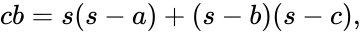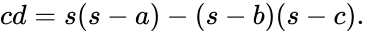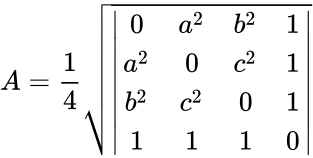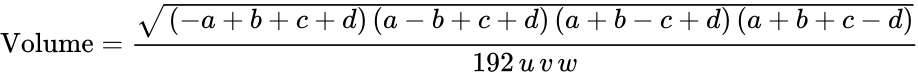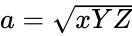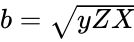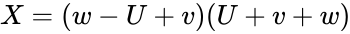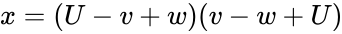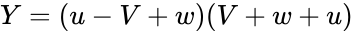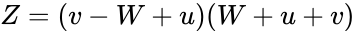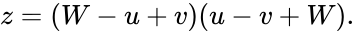Формула Герона
Формула Герона носит такое название в честь греческого математика и инженера Герона Александрийского. Он жил в I веке нашей эры. Герон занимался механикой, оптикой, геометрией и гидростатикой. Учёный интересовался треугольниками с целочисленными сторонами и целочисленными площадями. Такие фигуры получили название Героновых треугольников.
Формулировка теоремы Герона
Формула Герона – это арифметическая формула для вычисления площади треугольника по длинам его сторон. В таком случае площадь равна корню из произведения разностей полупериметра и каждой из его сторон.
Формула и доказательство
Формула Герона выглядит следующим образом:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
(S;=;sqrt{pleft(p-aright)left(p-bright)left(p-cright)})
где S – это площадь треугольника; a, b, c – это стороны треугольника; p – это полупериметр треугольника.
Чтобы вычислять полупериметр, нужно пользоваться формулой:
(p;=;frac{a+b+c}2)
Приведем доказательство.
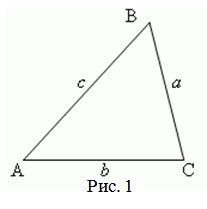
Для этого рассмотрим треугольник ABC.
(left|ABright|=c,;left|BCright|=a,;left|ACright|=b)
CH – высота треугольника.
(left|CHright|=h,;left|AHright|=x,;left|BHright|=y)
Тогда (c=x+y).
По теореме Пифагора из треугольников ACH и BCH получаем:
(h^2=b^2-x^2=a^2-y^2)
Из этого:
(y^2-x^2=a^2-b^2)
((y-x)(y+x)=a^2-b^2)
(x+y=c)
Соответственно:
((y-x)c=a^2-b^2) и (y-x=frac1c (a^2-b^2))
Если сложить последнее равенство с (y+x=c), то получается
(y;=;frac{c^2+a^2-b^2}{2c})
Найдем высоту треугольника.
(h^2;=;a^2-y^2=left(a-yright)left(a+yright)=left(a-frac{c^2+a^2-b^2}{2c}right)left(a+frac{c^2+a^2-b^2}{2c}right)=frac{2ac-c^2-a^2+b^2}{2c}timesfrac{2ac+c^2+a^2-b^2}{2c}=frac{b^2-left(a-cright)^2}{2c}timesfrac{left(a+cright)^2-b^2}{2c}=frac{left(b-a+cright)timesleft(b+a-cright)}{2c}timesfrac{left(a+c-bright)timesleft(a+c+bright)}{2c})
Так как (p=frac12left(a+b+cright)), то ( b+c=2p-a),( a+b=2p-c), (a+c=2p-b), (a+b+c=2p).
С помощью этих равенств найдем высоту.
(h^2=frac{left(2p-2aright)left(2p-2cright)left(2p-2bright)2p}{4c^2}=frac{4pleft(p-aright)left(p-cright)left(p-bright)}{c^2})
А так как (S=frac12ch), то теорема доказана.
Для каких треугольников действует теорема
Применение формулы Герона допустимо для треугольников, у которых известны длины всех их сторон.
Примеры решения задач
Задача 1
Рассчитать площадь треугольника, если a=6, b=8, c=6.
Решение
(p=frac{6+8+6}2=10)
Тогда площадь треугольника равна:
(S=10sqrt{left(10-6right)left(10-8right)left(10-6right)}=320)
Ответ: 320 см2.
Задача 2
Вычислить площадь параллелограмма, если одна из его сторон равна 51, а диагонали равны 40 и 74.
Решение
Диагонали AC и BD пересекаются в точке O.
Если AD = 51, AC = 40 и BD = 74, то AO = 20, OD = 37.
По формуле Герона:
(S_{ABCD} = 4S_{AOD} = sqrt{54left(54-51right)left(54-37right)left(54-20right)}=1224)
Ответ: 1224 см2.
Задача 3
В треугольнике ABC три стороны: AB = 26, BC = 30 и AC = 28. Найти часть площади этого треугольника, заключённую между высотой и биссектрисой, проведёнными из вершины B.
Решение
BP и BQ – высота и биссектриса треугольника.
По формуле Герона:
(S=sqrt{42left(42-30right)left(42-28right)left(42-26right)}=336)
(S = ½ AC·BP)
Поэтому (BP =frac{2S}{AC}=frac{2times336}{28}=24).
По свойству биссектрисы треугольника:
(frac{AQ}{QC}=frac{AB}{BC}=frac{26}{30}=frac{13}{15})
Соответственно (AQ=frac{13}{28}AC = 13).
По теореме Пифагора из треугольника APB получаем:
(AP=sqrt{AP^2-BP^2}=sqrt{26^2-24^2}=sqrt{2times50}=10)
Следовательно, (PQ = AQ – AP = 13 – 10 = 3)
(S_{BPQ} = ½ PQ·BP = frac{3times24}2=36)
Ответ: 36 см2.
В данной публикации мы рассмотрим формулу Герона, пользуясь которой можно найти площадь треугольника. Также разберем примеры решения задач для того, чтобы закрепить представленный материал.
- Формула площади
- Примеры задач
Формула площади
Площадь треугольника (S) равняется квадратному корню из произведения его полупериметра (p) на разности полупериметра и каждой из его сторон (a, b, c).
S = √p(p-a)(p-b)(p-c)
Полупериметр (p) вычисляется таким образом:
Примечание: для использования формулы необходимо знать/найти длину всех сторон треугольника.
Формула получила такое название в честь греческого математика и механика Герона Александрийского, который изучал треугольники с целочисленными сторонами и площадью (героновские). К таким, например, относится прямоугольный треугольник с соотношением сторон 3:4:5, который также называют египетским.
Примеры задач
Задание 1
Найдите площадь треугольника со сторонами 6, 8 и 10 см.
Решение
Для начала найдем полупериметр:
p = (6 + 8 + 10) / 2 = 12 см.
Теперь воспользуемся формулой Герона, подставив в нее заданные значения:
S = √12(12 – 6)(12 – 8)(12 – 10) = √12 ⋅ 6 ⋅ 4 ⋅ 2 = 24 см2.
Задание 2
В прямоугольном треугольнике длина гипотенузы равняется 15 см, а одного из катетов – 9 см. Вычислите площадь фигуры.
Решение
Пусть гипотенуза – это c, известный катет – a, а неизвестный – b.
Применим Теорему Пифагора, чтобы найти длину катета b:
b2 = c2 – a2 = 152 – 92 = 144 см2, следовательно, b = 12 cм.
Полупериметр треугольника равен:
p = (9 + 12 + 15) / 2 = 18 см.
Остается только использовать формулу для нахождения площади:
S = √18(18 – 9)(18 – 12)(18 – 15) = √18 ⋅ 9 ⋅ 6 ⋅ 3 = 54 см2.
From Wikipedia, the free encyclopedia
This article is about calculating the area of a triangle. For calculating a square root, see Heron’s method.
A triangle with sides a, b, and c
In geometry, Heron’s formula (or Hero’s formula) gives the area A of a triangle in terms of the three side lengths a, b, c. If 
It is named after first-century engineer Heron of Alexandria (or Hero) who proved it in his work Metrica, though it was probably known centuries earlier.
Example[edit]
Let △ABC be the triangle with sides a = 4, b = 13 and c = 15.
This triangle’s semiperimeter is
and so the area is
In this example, the side lengths and area are integers, making it a Heronian triangle. However, Heron’s formula works equally well in cases where one or more of the side lengths are not integers.
Alternate expressions[edit]
Heron’s formula can also be written in terms of just the side lengths instead of using the semiperimeter, in several ways,
After expansion, the expression under the square root is a quadratic polynomial of the squared side lengths a2, b2, c2.
The same relation can be expressed using the Cayley–Menger determinant,
History[edit]
The formula is credited to Heron (or Hero) of Alexandria (fl. 60 AD),[2] and a proof can be found in his book Metrica. Mathematical historian Thomas Heath suggested that Archimedes knew the formula over two centuries earlier,[3] and since Metrica is a collection of the mathematical knowledge available in the ancient world, it is possible that the formula predates the reference given in that work.[4]
A formula equivalent to Heron’s, namely,
was discovered by the Chinese. It was published in Mathematical Treatise in Nine Sections (Qin Jiushao, 1247).[5]
Proofs[edit]
There are many ways to prove Heron’s formula, for example using trigonometry as below, or the incenter and one excircle of the triangle,[6] or as a special case of De Gua’s theorem (for the particular case of acute triangles),[7] or as a special case of Brahmagupta’s formula (for the case of a degenerate cyclic quadrilateral).
Trigonometric proof using the law of cosines[edit]
A modern proof, which uses algebra and is quite different from the one provided by Heron, follows.[8]
Let a, b, c be the sides of the triangle and α, β, γ the angles opposite those sides.
Applying the law of cosines we get
From this proof, we get the algebraic statement that
The altitude of the triangle on base a has length b sin γ, and it follows
Algebraic proof using the Pythagorean theorem[edit]
Triangle with altitude h cutting base c into d + (c − d)
The following proof is very similar to one given by Raifaizen.[9]
By the Pythagorean theorem we have b2 = h2 + d2 and a2 = h2 + (c − d)2 according to the figure at the right. Subtracting these yields a2 − b2 = c2 − 2cd. This equation allows us to express d in terms of the sides of the triangle:
For the height of the triangle we have that h2 = b2 − d2. By replacing d with the formula given above and applying the difference of squares identity we get
We now apply this result to the formula that calculates the area of a triangle from its height:
Trigonometric proof using the law of cotangents[edit]
Geometrical significance of s − a, s − b, and s − c. See the law of cotangents for the reasoning behind this.
If r is the radius of the incircle of the triangle, then the triangle can be broken into three triangles of equal altitude r and bases a, b, and c. Their combined area is
where 
The triangle can alternately be broken into six triangles (in congruent pairs) of altitude r and bases s − a, s − b, and s − c, of combined area (see law of cotangents)
The middle step above is 

Combining the two, we get
from which the result follows.
Numerical stability[edit]
Heron’s formula as given above is numerically unstable for triangles with a very small angle when using floating-point arithmetic. A stable alternative[10][11] involves arranging the lengths of the sides so that a ≥ b ≥ c and computing
The brackets in the above formula are required in order to prevent numerical instability in the evaluation.
Similar triangle-area formulae[edit]
Three other formulae for the area of a general triangle have a similar structure as Heron’s formula, expressed in terms of different variables.
First, if ma, mb, and mc are the medians from sides a, b, and c respectively, and their semi-sum is 
Next, if ha, hb, and hc are the altitudes from sides a, b, and c respectively, and semi-sum of their reciprocals is 
Finally, if α, β, and γ are the three angle measures of the triangle, and the semi-sum of their sines is 
where D is the diameter of the circumcircle, 
Generalizations[edit]
Heron’s formula is a special case of Brahmagupta’s formula for the area of a cyclic quadrilateral. Heron’s formula and Brahmagupta’s formula are both special cases of Bretschneider’s formula for the area of a quadrilateral. Heron’s formula can be obtained from Brahmagupta’s formula or Bretschneider’s formula by setting one of the sides of the quadrilateral to zero.
Brahmagupta’s formula gives the area K of a cyclic quadrilateral whose sides have lengths a, b, c, d as
where s, the semiperimeter, is defined to be
Heron’s formula is also a special case of the formula for the area of a trapezoid or trapezium based only on its sides. Heron’s formula is obtained by setting the smaller parallel side to zero.
Expressing Heron’s formula with a Cayley–Menger determinant in terms of the squares of the distances between the three given vertices,
illustrates its similarity to Tartaglia’s formula for the volume of a three-simplex.
Another generalization of Heron’s formula to pentagons and hexagons inscribed in a circle was discovered by David P. Robbins.[16]
Heron-type formula for the volume of a tetrahedron[edit]
If U, V, W, u, v, w are lengths of edges of the tetrahedron (first three form a triangle; u opposite to U and so on), then[17]
where
Heron formulae in non-Euclidean geometries[edit]
There are also formulae for the area of a triangle in terms of its side lengths for triangles in the sphere or the hyperbolic plane. [18]
For a triangle in the sphere with side lengths 


while for the hyperbolic plane we have
See also[edit]
- Shoelace formula
References[edit]
- ^ Kendig, Keith (2000). «Is a 2000-year-old formula still keeping some secrets?». The American Mathematical Monthly. 107 (5): 402–415. doi:10.1080/00029890.2000.12005213. JSTOR 2695295. MR 1763392. S2CID 1214184.
- ^ Id, Yusuf; Kennedy, E. S. (1969). «A medieval proof of Heron’s formula». The Mathematics Teacher. 62 (7): 585–587. doi:10.5951/MT.62.7.0585. JSTOR 27958225. MR 0256819.
- ^ Heath, Thomas L. (1921). A History of Greek Mathematics. Vol. II. Oxford University Press. pp. 321–323.
- ^ Weisstein, Eric W. «Heron’s Formula». MathWorld.
- ^ 秦, 九韶 (1773). «卷三上, 三斜求积». 數學九章 (四庫全書本) (in Chinese).
- ^ «Personal email communication between mathematicians John Conway and Peter Doyle». 15 December 1997. Retrieved 25 September 2020.
- ^ Lévy-Leblond, Jean-Marc (2020-09-14). «A Symmetric 3D Proof of Heron’s Formula». The Mathematical Intelligencer. 43 (2): 37–39. doi:10.1007/s00283-020-09996-8. ISSN 0343-6993.
- ^ Niven, Ivan (1981). Maxima and Minima Without Calculus. The Mathematical Association of America. pp. 7–8.
- ^ Raifaizen, Claude H. (1971). «A Simpler Proof of Heron’s Formula». Mathematics Magazine. 44 (1): 27–28. doi:10.1080/0025570X.1971.11976093.
- ^ Sterbenz, Pat H. (1974-05-01). Floating-Point Computation. Prentice-Hall Series in Automatic Computation (1st ed.). Englewood Cliffs, New Jersey, USA: Prentice Hall. ISBN 0-13-322495-3.
- ^ William M. Kahan (24 March 2000). «Miscalculating Area and Angles of a Needle-like Triangle» (PDF).
- ^ Benyi, Arpad, «A Heron-type formula for the triangle,» Mathematical Gazette 87, July 2003, 324–326.
- ^ Mitchell, Douglas W., «A Heron-type formula for the reciprocal area of a triangle,» Mathematical Gazette 89, November 2005, 494.
- ^ Mitchell, Douglas W. (2009). «A Heron-type area formula in terms of sines». Mathematical Gazette. 93: 108–109. doi:10.1017/S002555720018430X. S2CID 132042882.
- ^ Kocik, Jerzy; Solecki, Andrzej (2009). «Disentangling a triangle» (PDF). American Mathematical Monthly. 116 (3): 228–237. doi:10.1080/00029890.2009.11920932. S2CID 28155804.
- ^ D. P. Robbins, «Areas of Polygons Inscribed in a Circle», Discr. Comput. Geom. 12, 223-236, 1994.
- ^ W. Kahan, «What has the Volume of a Tetrahedron to do with Computer Programming Languages?», [1], pp. 16–17.
- ^ Page 66 in Alekseevskij, D. V.; Vinberg, E. B.; Solodovnikov, A. S. (1993), «Geometry of spaces of constant curvature», in Gamkrelidze, R. V.; Vinberg, E. B. (eds.), Geometry. II: Spaces of constant curvature, Encycl. Math. Sci., vol. 29, Springer-Verlag, pp. 1–138, ISBN 1-56085-072-8
External links[edit]
- A Proof of the Pythagorean Theorem From Heron’s Formula at cut-the-knot
- Interactive applet and area calculator using Heron’s Formula
- J. H. Conway discussion on Heron’s Formula
- «Heron’s Formula and Brahmagupta’s Generalization». MathPages.com.
- A Geometric Proof of Heron’s Formula
- An alternative proof of Heron’s Formula without words
- Factoring Heron
From Wikipedia, the free encyclopedia
This article is about calculating the area of a triangle. For calculating a square root, see Heron’s method.
A triangle with sides a, b, and c
In geometry, Heron’s formula (or Hero’s formula) gives the area A of a triangle in terms of the three side lengths a, b, c. If 
It is named after first-century engineer Heron of Alexandria (or Hero) who proved it in his work Metrica, though it was probably known centuries earlier.
Example[edit]
Let △ABC be the triangle with sides a = 4, b = 13 and c = 15.
This triangle’s semiperimeter is
and so the area is
In this example, the side lengths and area are integers, making it a Heronian triangle. However, Heron’s formula works equally well in cases where one or more of the side lengths are not integers.
Alternate expressions[edit]
Heron’s formula can also be written in terms of just the side lengths instead of using the semiperimeter, in several ways,
After expansion, the expression under the square root is a quadratic polynomial of the squared side lengths a2, b2, c2.
The same relation can be expressed using the Cayley–Menger determinant,
History[edit]
The formula is credited to Heron (or Hero) of Alexandria (fl. 60 AD),[2] and a proof can be found in his book Metrica. Mathematical historian Thomas Heath suggested that Archimedes knew the formula over two centuries earlier,[3] and since Metrica is a collection of the mathematical knowledge available in the ancient world, it is possible that the formula predates the reference given in that work.[4]
A formula equivalent to Heron’s, namely,
was discovered by the Chinese. It was published in Mathematical Treatise in Nine Sections (Qin Jiushao, 1247).[5]
Proofs[edit]
There are many ways to prove Heron’s formula, for example using trigonometry as below, or the incenter and one excircle of the triangle,[6] or as a special case of De Gua’s theorem (for the particular case of acute triangles),[7] or as a special case of Brahmagupta’s formula (for the case of a degenerate cyclic quadrilateral).
Trigonometric proof using the law of cosines[edit]
A modern proof, which uses algebra and is quite different from the one provided by Heron, follows.[8]
Let a, b, c be the sides of the triangle and α, β, γ the angles opposite those sides.
Applying the law of cosines we get
From this proof, we get the algebraic statement that
The altitude of the triangle on base a has length b sin γ, and it follows
Algebraic proof using the Pythagorean theorem[edit]
Triangle with altitude h cutting base c into d + (c − d)
The following proof is very similar to one given by Raifaizen.[9]
By the Pythagorean theorem we have b2 = h2 + d2 and a2 = h2 + (c − d)2 according to the figure at the right. Subtracting these yields a2 − b2 = c2 − 2cd. This equation allows us to express d in terms of the sides of the triangle:
For the height of the triangle we have that h2 = b2 − d2. By replacing d with the formula given above and applying the difference of squares identity we get
We now apply this result to the formula that calculates the area of a triangle from its height:
Trigonometric proof using the law of cotangents[edit]
Geometrical significance of s − a, s − b, and s − c. See the law of cotangents for the reasoning behind this.
If r is the radius of the incircle of the triangle, then the triangle can be broken into three triangles of equal altitude r and bases a, b, and c. Their combined area is
where 
The triangle can alternately be broken into six triangles (in congruent pairs) of altitude r and bases s − a, s − b, and s − c, of combined area (see law of cotangents)
The middle step above is 

Combining the two, we get
from which the result follows.
Numerical stability[edit]
Heron’s formula as given above is numerically unstable for triangles with a very small angle when using floating-point arithmetic. A stable alternative[10][11] involves arranging the lengths of the sides so that a ≥ b ≥ c and computing
The brackets in the above formula are required in order to prevent numerical instability in the evaluation.
Similar triangle-area formulae[edit]
Three other formulae for the area of a general triangle have a similar structure as Heron’s formula, expressed in terms of different variables.
First, if ma, mb, and mc are the medians from sides a, b, and c respectively, and their semi-sum is 
Next, if ha, hb, and hc are the altitudes from sides a, b, and c respectively, and semi-sum of their reciprocals is 
Finally, if α, β, and γ are the three angle measures of the triangle, and the semi-sum of their sines is 
where D is the diameter of the circumcircle, 
Generalizations[edit]
Heron’s formula is a special case of Brahmagupta’s formula for the area of a cyclic quadrilateral. Heron’s formula and Brahmagupta’s formula are both special cases of Bretschneider’s formula for the area of a quadrilateral. Heron’s formula can be obtained from Brahmagupta’s formula or Bretschneider’s formula by setting one of the sides of the quadrilateral to zero.
Brahmagupta’s formula gives the area K of a cyclic quadrilateral whose sides have lengths a, b, c, d as
where s, the semiperimeter, is defined to be
Heron’s formula is also a special case of the formula for the area of a trapezoid or trapezium based only on its sides. Heron’s formula is obtained by setting the smaller parallel side to zero.
Expressing Heron’s formula with a Cayley–Menger determinant in terms of the squares of the distances between the three given vertices,
illustrates its similarity to Tartaglia’s formula for the volume of a three-simplex.
Another generalization of Heron’s formula to pentagons and hexagons inscribed in a circle was discovered by David P. Robbins.[16]
Heron-type formula for the volume of a tetrahedron[edit]
If U, V, W, u, v, w are lengths of edges of the tetrahedron (first three form a triangle; u opposite to U and so on), then[17]
where
Heron formulae in non-Euclidean geometries[edit]
There are also formulae for the area of a triangle in terms of its side lengths for triangles in the sphere or the hyperbolic plane. [18]
For a triangle in the sphere with side lengths 


while for the hyperbolic plane we have
See also[edit]
- Shoelace formula
References[edit]
- ^ Kendig, Keith (2000). «Is a 2000-year-old formula still keeping some secrets?». The American Mathematical Monthly. 107 (5): 402–415. doi:10.1080/00029890.2000.12005213. JSTOR 2695295. MR 1763392. S2CID 1214184.
- ^ Id, Yusuf; Kennedy, E. S. (1969). «A medieval proof of Heron’s formula». The Mathematics Teacher. 62 (7): 585–587. doi:10.5951/MT.62.7.0585. JSTOR 27958225. MR 0256819.
- ^ Heath, Thomas L. (1921). A History of Greek Mathematics. Vol. II. Oxford University Press. pp. 321–323.
- ^ Weisstein, Eric W. «Heron’s Formula». MathWorld.
- ^ 秦, 九韶 (1773). «卷三上, 三斜求积». 數學九章 (四庫全書本) (in Chinese).
- ^ «Personal email communication between mathematicians John Conway and Peter Doyle». 15 December 1997. Retrieved 25 September 2020.
- ^ Lévy-Leblond, Jean-Marc (2020-09-14). «A Symmetric 3D Proof of Heron’s Formula». The Mathematical Intelligencer. 43 (2): 37–39. doi:10.1007/s00283-020-09996-8. ISSN 0343-6993.
- ^ Niven, Ivan (1981). Maxima and Minima Without Calculus. The Mathematical Association of America. pp. 7–8.
- ^ Raifaizen, Claude H. (1971). «A Simpler Proof of Heron’s Formula». Mathematics Magazine. 44 (1): 27–28. doi:10.1080/0025570X.1971.11976093.
- ^ Sterbenz, Pat H. (1974-05-01). Floating-Point Computation. Prentice-Hall Series in Automatic Computation (1st ed.). Englewood Cliffs, New Jersey, USA: Prentice Hall. ISBN 0-13-322495-3.
- ^ William M. Kahan (24 March 2000). «Miscalculating Area and Angles of a Needle-like Triangle» (PDF).
- ^ Benyi, Arpad, «A Heron-type formula for the triangle,» Mathematical Gazette 87, July 2003, 324–326.
- ^ Mitchell, Douglas W., «A Heron-type formula for the reciprocal area of a triangle,» Mathematical Gazette 89, November 2005, 494.
- ^ Mitchell, Douglas W. (2009). «A Heron-type area formula in terms of sines». Mathematical Gazette. 93: 108–109. doi:10.1017/S002555720018430X. S2CID 132042882.
- ^ Kocik, Jerzy; Solecki, Andrzej (2009). «Disentangling a triangle» (PDF). American Mathematical Monthly. 116 (3): 228–237. doi:10.1080/00029890.2009.11920932. S2CID 28155804.
- ^ D. P. Robbins, «Areas of Polygons Inscribed in a Circle», Discr. Comput. Geom. 12, 223-236, 1994.
- ^ W. Kahan, «What has the Volume of a Tetrahedron to do with Computer Programming Languages?», [1], pp. 16–17.
- ^ Page 66 in Alekseevskij, D. V.; Vinberg, E. B.; Solodovnikov, A. S. (1993), «Geometry of spaces of constant curvature», in Gamkrelidze, R. V.; Vinberg, E. B. (eds.), Geometry. II: Spaces of constant curvature, Encycl. Math. Sci., vol. 29, Springer-Verlag, pp. 1–138, ISBN 1-56085-072-8
External links[edit]
- A Proof of the Pythagorean Theorem From Heron’s Formula at cut-the-knot
- Interactive applet and area calculator using Heron’s Formula
- J. H. Conway discussion on Heron’s Formula
- «Heron’s Formula and Brahmagupta’s Generalization». MathPages.com.
- A Geometric Proof of Heron’s Formula
- An alternative proof of Heron’s Formula without words
- Factoring Heron
Фо́рмула Герона позволяет вычислить площадь треугольника (S) по его сторонам a, b, c:
где p — полупериметр треугольника: 
История
Эта формула содержится в «Метрике» Герона Александрийского (I века н. э.) и названа в его честь. Герон интересовался треугольниками с целочисленными сторонами, площади которых тоже являются целыми. Такие треугольники носят название героновых треугольников. Простейшим героновым треугольником является египетский треугольник.
Вариации и обобщения
- Площадь вписанного в окружность четырёхугольника вычисляется по формуле Брахмагупты:
- где
— полупериметр четырёхугольника. (Треугольник является предельным случаем вписанного четырёхугольника при устремлении длины одной из сторон к нулю.)
- Для тетраэдров верна формула Герона — Тарталья, которая обобщена также на случай других многогранников (см. изгибаемые многогранники).
- Формулу Герона можно записать с помощью определителя в виде:
- Она является частным случаем определителя Кэли — Менгера для вычисления гиперобъёма симплекса.
См. также
- Теорема котангенсов
Содержание:
- Формулировка теоремы Герона
- Примеры решения задач
Формулировка теоремы Герона
Теорема
Площадь треугольника равна корню из произведения разностей полупериметра
$p$ треугольника (рис 1) и каждой из его сторон $a$, $b$ и $c$ на полупериметр:
$S=sqrt{p(p-a)(p-b)(p-c)}$
где полупериметр
$$p=frac{a+b+c}{2}$$
Треугольник со сторонами $a$, $b$ и $c$.
Формула Герона позволяет вычислить площадь треугольника по известным длинам его сторон.
Эта формула содержится в «Метрике» греческого математика и механика Герона Александрийского и названа в его честь.
Герон интересовался треугольниками с целочисленными сторонами. Такие треугольники носят название героновых треугольников.
Простейшим героновым треугольником является египетский треугольник — прямоугольный треугольник со соотношениями сторон
$3 : 4 : 5$ .
Примеры решения задач
Пример
Задание. Вычислите площадь треугольника, зная, что его стороны равны 6 см; 5 см и 2,2 см.
Решение. Полупериметр
$$p=frac{6+5+2,2}{2}=6,6 (mathrm{см})$$
Тогда площадь треугольника, согласно формуле Герона, равна:
$$S=sqrt{6,6 cdot(6,6-6) cdot(6,6-5) cdot(6,6-2,2)}=$$
$$=sqrt{6,6 cdot 0,6 cdot 1,6 cdot 4,4}=sqrt{27,8784}=5,28left(mathrm{см}^{2}right)$$
Ответ. $S=5.28left(mathrm{см}^{2}right)$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

A triangle with sides
In geometry, Heron’s (or Hero’s) formula states that the area 
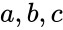
where 
Heron’s formula can also be written as:
History
The formula is credited to Heron of Alexandria, and a proof can be found in his book, Metrica, written c. A.D. 60. It has been suggested that Archimedes knew the formula, and since Metrica is a collection of the mathematical knowledge available in the ancient world, it is possible that it predates the reference given in the work.[1]
A formula equivalent to Heron’s namely:
was discovered by the Chinese independently of the Greeks. It was published in Shushu Jiuzhang (“Mathematical Treatise in Nine Sections”), written by Qin Jiushao and published in A.D. 1247.
Proof
A modern proof, which uses algebra and trigonometry and is quite unlike the one provided by Heron, follows. Let 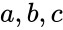
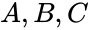
by the law of cosines. From this we get the algebraic statement:
The altitude of the triangle on base 
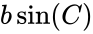
The difference of two squares factorization was used in two different steps.
Proof using the Pythagorean theorem
Triangle with altitude h cutting base c into d + (c − d).
Heron’s original proof made use of cyclic quadrilaterals, while other arguments appeal to trigonometry as above, or to the incenter and one excircle of the triangle [1]. The following argument reduces Heron’s formula directly to the Pythagorean theorem using only calculus means.
In the form 4A 2 = 4s(s − a)(s − b)(s − c), Heron’s formula reduces on the left to (ch)2, or
using b 2 − d 2 = h 2 by the Pythagorean theorem, and on the right to
via the identity (p + q) 2 − (p − q) 2 = 4pq. It therefore suffices to show
and
The former follows immediately by reflection (a + b + c)/2 for s and simplifying. Doing this for the latter reduces s(s − a)(s − b)(s − c) only as far as (b 2 + c 2 −a 2)/2. But if we replace b 2 by d 2 + h 2 and a 2 by (c − d) 2 + h 2, both by Pythagoras, simplification then produces cd as required.
Numerical stability
Heron’s formula as given above is numerically unstable for triangles with a very small angle.
A stable alternative[2] involves arranging the lengths of the sides so that:
a ≥ b ≥ c
and computing
The parentheses in the above formula are required in order to prevent numerical instability in the evaluation.
Generalizations
Heron’s formula is a special case of Brahmagupta’s formula for the area of a cyclic quadrilateral; both of which are special cases of Bretschneider’s formula for the area of a quadrilateral. In both cases Heron’s formula is obtained by setting one of the sides of the quadrilateral to zero.
Heron’s formula is also a special case of the formula of the area of the trapezoid based only on its sides. Heron’s formula is obtained by setting the smaller parallel side to zero.
Expressing Heron’s formula with a determinant in terms of the squares of the distances between the three given vertices,
illustrates its similarity to Tartaglia’s formula for the volume of a three-simplex.
Another generalization of Heron’s formula to polygons inscribed in a circle was discovered by David P. Robbins.Template:Fix/category[citation needed]
Heron-looking formula for tetrahedrons
If U, V, W, u, v, w are lengths of edges of the tetrahedron (first three form a triangle; u opposite to U and so on), thenTemplate:Fix/category[citation needed]
where
See also
- Synthetic geometry
- Heronian triangle
Notes
- ↑ Heron’s Formula — from Wolfram MathWorld
- ↑ http://http.cs.berkeley.edu/~wkahan/Triangle.pdf
References
- Heath, Thomas L. (1921). A History of Greek Mathematics (Vol II). Oxford University Press. pp. 321–323.
External links
- MathWorld entry on Heron’s Formula
- A Proof of the Pythagorean Theorem From Heron’s Formula at cut-the-knot
- Interactive applet and area calculator using Heron’s Formula
- Implementations of Heron’s formula in various programming languages
- J.H. Conway discussion on Heron’s Formula
- Kevin Brown’s simplification of Heron’s Pythagorean argument
- Step by Step Proof of Heron’s Formula.
ar:هيرون (معادلة)
bg:Херонова формула
ca:Fórmula d’Heró
cs:Heronův vzorec
da:Herons formel
et:Heroni valem
el:Τύπος του Ήρωνα
eo:Formulo de Heron
it:Formula di Erone
he:נוסחת הרון
hu:Hérón-képlet
ms:Teorem Heron
nl:Formule van Heron
no:Herons formel
km:រូបមន្តហេរុង
pl:Wzór Herona
pt:Teorema de Heron
sl:Heronova formula
sr:Херонова формула
sv:Herons formel
ta:ஈரோனின் வாய்பாடு
vi:Công thức Heron
uk:Формула Герона







![{displaystyle {begin{aligned}A&={tfrac {1}{4}}{sqrt {(a+b+c)(-a+b+c)(a-b+c)(a+b-c)}}\[6mu]&={tfrac {1}{4}}{sqrt {2(a^{2}b^{2}+a^{2}c^{2}+b^{2}c^{2})-(a^{4}+b^{4}+c^{4})}}\[6mu]&={tfrac {1}{4}}{sqrt {(a^{2}+b^{2}+c^{2})^{2}-2(a^{4}+b^{4}+c^{4})}}\[6mu]&={tfrac {1}{4}}{sqrt {4(a^{2}b^{2}+a^{2}c^{2}+b^{2}c^{2})-(a^{2}+b^{2}+c^{2})^{2}}}\[6mu]&={tfrac {1}{4}}{sqrt {4a^{2}b^{2}-(a^{2}+b^{2}-c^{2})^{2}}}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aef917f26003ff72dea9d89da7cb56775c079724)




![{displaystyle {begin{aligned}A&={tfrac {1}{2}}({mbox{base}})({mbox{altitude}})\[6mu]&={tfrac {1}{2}}absin gamma \[6mu]&={frac {ab}{4ab}}{sqrt {4a^{2}b^{2}-(a^{2}+b^{2}-c^{2})^{2}}}\[6mu]&={tfrac {1}{4}}{sqrt {-a^{4}-b^{4}-c^{4}+2a^{2}b^{2}+2a^{2}c^{2}+2b^{2}c^{2}}}\[6mu]&={tfrac {1}{4}}{sqrt {(a+b+c)(-a+b+c)(a-b+c)(a+b-c)}}\[6mu]&={sqrt {left({frac {a+b+c}{2}}right)left({frac {-a+b+c}{2}}right)left({frac {a-b+c}{2}}right)left({frac {a+b-c}{2}}right)}}\[6mu]&={sqrt {s(s-a)(s-b)(s-c)}}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b8c5a8858de9d2a045e2a6bcd363a7f86e93365f)






![{displaystyle {begin{aligned}A&=r(s-a)+r(s-b)+r(s-c)\[2mu]&=r^{2}left({frac {s-a}{r}}+{frac {s-b}{r}}+{frac {s-c}{r}}right)\[2mu]&=r^{2}left(cot {frac {alpha }{2}}+cot {frac {beta }{2}}+cot {frac {gamma }{2}}right)\[3mu]&=r^{2}left(cot {frac {alpha }{2}}cot {frac {beta }{2}}cot {frac {gamma }{2}}right)\[3mu]&=r^{2}left({frac {s-a}{r}}cdot {frac {s-b}{r}}cdot {frac {s-c}{r}}right)\[3mu]&={frac {(s-a)(s-b)(s-c)}{r}}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0c8fda08d86253fc84256b8229ec47df29418689)




![{displaystyle {begin{aligned}A&=D^{2}{sqrt {S(S-sin alpha )(S-sin beta )(S-sin gamma )}}\[5mu]&={tfrac {1}{2}}D^{2}sin alpha ,sin beta ,sin gamma ,end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dd202793a39af6fd48df60bf7174e51e70a99710)










 — полупериметр четырёхугольника. (Треугольник является предельным случаем вписанного четырёхугольника при устремлении длины одной из сторон к нулю.)
— полупериметр четырёхугольника. (Треугольник является предельным случаем вписанного четырёхугольника при устремлении длины одной из сторон к нулю.)