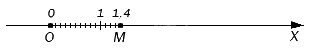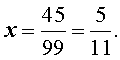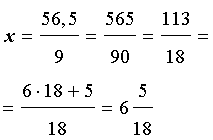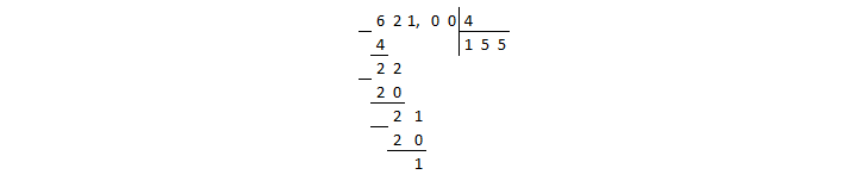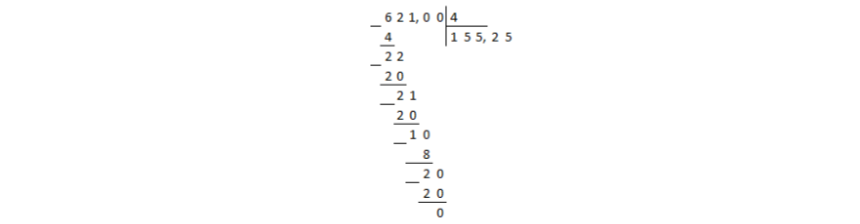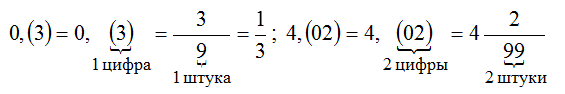Данный материал мы посвятим такой важной теме, как десятичные дроби. Сначала определимся с основными определениями, приведем примеры и остановимся на правилах десятичной записи, а также на том, что из себя представляют разряды десятичных дробей. Далее выделим основные виды: конечные и бесконечные, периодические и непериодические дроби. В финальной части мы покажем, как точки, соответствующие дробным числам, расположены на оси координат.
Что такое десятичная запись дробных чисел
Так называемая десятичная запись дробных чисел может быть использована как для натуральных, так и для дробных чисел. Она выглядит как набор из двух и более цифр, между которыми есть запятая.
Десятичная запятая нужна для того, чтобы отделять целую часть от дробной. Как правило, последняя цифра десятичной дроби не бывает нулем, за исключением случаев, когда десятичная запятая стоит сразу после первого же нуля.
Какие можно привести примеры дробных чисел в десятичной записи? Это может быть 34,21, 0,35035044, 0,0001, 11 231 552,9 и др.
В некоторых учебниках можно встретить использование точки вместо запятой (5.67, 6789.1011 и др.) Это вариант считается равнозначным, но он более характерен для англоязычных источников.
Определение десятичных дробей
Основываясь на указанном выше понятии десятичной записи, мы можем сформулировать следующее определение десятичных дробей:
Десятичные дроби представляют собой дробные числа в десятичной записи.
Для чего нам нужна запись дробей в такой форме? Она дает нам некоторые преимущества перед обыкновенными, например, более компактную запись, особенно в тех случаях, когда в знаменателе стоят 1000, 100, 10 и др. или смешанное число. Например, вместо 610 мы можем указать 0,6, вместо 2510000 – 0, 0023, вместо 5123100 – 512,03.
О том, как правильно представить в десятичном виде обыкновенные дроби с десятками, сотнями, тысячами в знаменателе, будет рассказано в рамках отдельного материала.
Как правильно читать десятичные дроби
Существуют некоторые правила чтения записей десятичных дробей. Так, те десятичные дроби, которым соответствуют их правильные обыкновенные эквиваленты, читаются почти так же, но с добавлением слов «ноль десятых» в начале. Так, запись 0,14, которой соответствует 14100, читается как «ноль целых четырнадцать сотых».
Если же десятичной дроби можно поставить в соответствие смешанное число, то она читается тем же образом, как и это число. Так, если у нас есть дробь 56,002, которой соответствует 5621000, мы читаем такую запись как «пятьдесят шесть целых две тысячных».
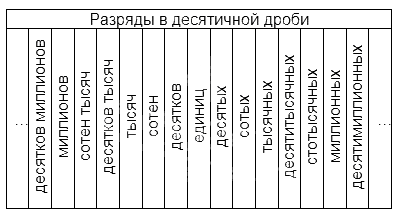
Что такое разряды в десятичных дробях
Значение цифры в записи десятичной дроби зависит от того, на каком месте она расположена (так же, как и в случае с натуральными числами). Так, в десятичной дроби 0,7 семерка – это десятые доли, в 0,0007 – десятитысячные, а в дроби 70 000,345 она означает семь десятков тысяч целых единиц. Таким образом, в десятичных дробях тоже существует понятие разряда числа.
Названия разрядов, расположенных до запятой, аналогичны тем, что существуют в натуральных числах. Названия тех, что расположены после, наглядно представлены в таблице:
Разберем пример.
У нас есть десятичная дробь 43,098. У нее в разряде десятков находится четверка, в разряде единиц тройка, в разряде десятых – ноль, сотых – 9, тысячных – 8.
Принято различать разряды десятичных дробей по старшинству. Если мы движемся по цифрам слева направо, то мы будем идти от старших разрядов к младшим. Получается, что сотни старше десятков, а миллионные доли младше, чем сотые. Если взять ту конечную десятичную дробь, которую мы приводили в качестве примера выше, то в ней старшим, или высшим будет разряд сотен, а младшим, или низшим – разряд 10-тысячных.
Любую десятичную дробь можно разложить по отдельным разрядам, то есть представить в виде суммы. Это действие выполняется так же, как и для натуральных чисел.
Попробуем разложить дробь 56,0455 по разрядам.
У нас получится:
56,0455 =50+6+0,4+0,005+0,0005
Если мы вспомним свойства сложения, то сможем представить эту дробь и в других видах, например, как сумму 56+0,0455, или 56,0055+0,4 и др.
Что такое конечные десятичные дроби
Все дроби, о которых мы говорили выше, являются конечными десятичными дробями. Это означает, что количество цифр, расположенное у них после запятой, является конечным. Выведем определение:
Конечные десятичные дроби представляют собой вид десятичных дробей, у которых после знака запятой стоит конечное число знаков.
Примерами таких дробей могут быть 0,367, 3,7, 55,102567958, 231 032,49 и др.
Любую из этих дробей можно перевести либо в смешанное число (если значение их дробной части отличается от нуля), либо в обыкновенную дробь (при нулевой целой части). Тому, как это делается, мы посвятили отдельный материал. Здесь просто укажем пару примеров: так, конечную десятичную дробь 5,63 мы можем привести к виду 563100, а 0,2 соответствует 210 (или любая другая равная ей дробь, например, 420 или 15.)
Но обратный процесс, т.е. запись обыкновенной дроби в десятичном виде, может быть выполнен не всегда. Так, 513 нельзя заменить на равную дробь с знаменателем 100, 10 и др., значит, конечная десятичная дробь из нее не получится.
Основные виды бесконечных десятичных дробей: периодические и непериодические дроби
Мы указывали выше, что конечные дроби называются так потому, что после запятой у них стоит конечное число цифр. Однако оно вполне может быть и бесконечным, и в этом случае сами дроби также будут называться бесконечными.
Бесконечными десятичными дробями называются такие, у которых после запятой стоит бесконечное количество цифр.
Очевидно, что полностью такие числа записаны быть просто не могут, поэтому мы указываем лишь часть из них и дальше ставим многоточие. Это знак говорит о бесконечном продолжении последовательности знаков после запятой. Примерами бесконечных десятичных дробей могут быть 0,143346732…, 3,1415989032…, 153,0245005…, 2,66666666666…, 69,748768152…. и т.д.
В «хвосте» такой дроби могут стоять не только случайные на первый взгляд последовательности цифр, но постоянное повторение одного и того же знака или группы знаков. Дроби с чередованием после десятичной запятой называются периодическими.
Периодическими десятичными дробями называются такие бесконечные десятичные дроби, у которых после запятой повторяется одна цифра или группа из нескольких цифр. Повторяющаяся часть называется периодом дроби.
К примеру, для дроби 3,444444…. периодом будет цифра 4, а для 76, 134134134134… – группа 134.
Какое же минимальное количество знаков допустимо оставить в записи периодической дроби? Для периодических дробей достаточно будет записать весь период один раз в круглых скобках. Так, дробь 3,444444…. правильно будет записать как 3,(4), а 76, 134134134134…– как 76,(134).
В целом записи с несколькими периодами в скобках будут иметь точно такой же смысл: к примеру, периодическая дробь 0,677777 – это то же самое, что 0,6(7) и 0,6(77) и т.д. Также допустимы записи вида 0,67777(7), 0,67(7777) и др.
Во избежание ошибок введем однообразие обозначений. Условимся записывать только один период (максимально короткую последовательность цифр), который стоит ближе всего к десятичной запятой, и заключать его в круглые скобки.
То есть для указанной выше дроби основной будем считать запись 0,6(7), а, например, в случае с дробью 8,9134343434 будем писать 8,91(34).
Если знаменатель обыкновенной дроби содержит простые множители, не равные 5 и 2, то при переводе в десятичную запись из них получатся бесконечные дроби.
В принципе, любую конечную дробь мы можем записать в виде периодической. Для этого нам просто нужно добавить справа бесконечно много нулей. Как это выглядит в записи? Допустим, у нас есть конечная дробь 45,32. В периодическом виде она будет выглядеть как 45,32(0). Это действие возможно потому, что добавление нулей справа в любую десятичную дробь дает нам в результате равную ей дробь.
Отдельно следует остановиться на периодических дробях с периодом 9, например, 4,89 (9), 31,6(9). Они являются альтернативной записью схожих дробей с периодом 0, поэтому их часто заменяют при письме именно дробями с нулевым периодом. При этом к значению следующего разряда добавляют единицу, а в круглых скобках указывают (0). Равенство получившихся чисел легко проверить, представив их в виде обыкновенных дробей.
К примеру, дробь 8,31(9) можно заменить на соответствующую ей дробь 8,32(0). Или 4,(9)=5,(0)=5.
Бесконечные десятичные периодические дроби относятся к рациональным числам. Иначе говоря, любую периодическую дробь можно представить в виде обыкновенной, и наоборот.
Существуют и дроби, у которых после запятой бесконечно повторяющаяся последовательность отсутствует. В таком случае их называют непериодическими дробями.
К непериодическим десятичным дробям относятся те бесконечные десятичные дроби, в которых после запятой не содержится периода, т.е. повторяющейся группы цифр.
Иногда непериодические дроби выглядят очень похожими на периодические. Например, 9,03003000300003… на первый взгляд кажется имеющей период, однако подробный анализ знаков после запятой подтверждает, что это все же непериодическая дробь. С такими числами надо быть очень внимательным.
Непериодические дроби относятся к иррациональным числам. В обыкновенные дроби их не переводят.
Основные действия с десятичными дробями
С десятичными дробями можно производить следующие действия: сравнение, вычитание, сложение, деление и умножение. Разберем каждое из них отдельно.
Сравнение десятичных дробей может быть сведено к сравнению обыкновенных дробей, которые соответствуют исходным десятичным. Но бесконечные непериодические дроби свести к такому виду нельзя, а перевод десятичных дробей в обыкновенные зачастую является трудоемкой задачей. Как же быстро произвести действие сравнения, если нам нужно сделать это по ходу решения задачи? Удобно сравнивать десятичные дроби по разрядам таким же образом, как мы сравниваем натуральные числа. Этому методу мы посвятим отдельную статью.
Чтобы складывать одни десятичные дроби с другими, удобно использовать метод сложения столбиком, как для натуральных чисел. Чтобы складывать периодические десятичные дроби, необходимо предварительно заменить их обыкновенными и считать по стандартной схеме. Если же по условиям задачи нам надо сложить бесконечные непериодические дроби, то нужно перед этим округлить их до некоторого разряда, а потом уже складывать. Чем меньше разряд, до которого мы округляем, тем выше будет точность вычисления. Для вычитания, умножения и деления бесконечных дробей предварительное округление также необходимо.
Нахождение разности десятичных дробей обратно действию сложения. По сути, с помощью вычитания мы можем найти такое число, сумма которого с вычитаемой дробью даст нам уменьшаемую. Подробнее об этом расскажем в рамках отдельного материала.
Умножение десятичных дробей производится так же, как и для натуральных чисел. Для этого тоже подходит метод вычисления столбиком. Это действие с периодическими дробями мы опять же сводим к умножению обыкновенных дробей по уже изученным правилам. Бесконечные дроби, как мы помним, надо округлить перед подсчетами.
Процесс деления десятичных дробей является обратным процессу умножения. При решении задач мы также пользуемся подсчетами в столбик.
Положение десятичных дробей на оси координат
Можно установить точное соответствие между конечной десятичной дробью и точкой на оси координат. Выясним, как отметить точку на оси, которая будет точно соответствовать необходимой десятичной дроби.
Мы уже изучали, как построить точки, соответствующие обыкновенным дробям, а ведь десятичные дроби можно привести к такому виду. Например, обыкновенная дробь 1410 – это то же самое, что и 1,4, поэтому соответствующая ей точка будет удалена от начала отсчета в положительном направлении ровно на такое же расстояние:
Можно обойтись без замены десятичной дроби на обыкновенную, а взять на основу метод разложения по разрядам. Так, если нам надо отметить точку, координата которой будет равна 15,4008, то мы предварительно представим это число в виде суммы 15+0,4+,0008. Для начала отложим от начала отсчета 15 целых единичных отрезков в положительном направлении, потом 4 десятых доли одного отрезка, а потом 8 десятитысячных долей одного отрезка. В итоге мы получим точку координат, которой соответствует дробь 15,4008.
Для бесконечной десятичной дроби лучше пользоваться именно этим способом, поскольку он позволяет приблизиться к нужной точке сколь угодно близко. В некоторых случаях можно построить и точное соответствие бесконечной дроби на оси координат: так, 2=1,41421…, и с этой дробью может быть соотнесена точка на координатном луче, удаленная от 0 на длину диагонали квадрата, сторона которого будет равна одному единичному отрезку.
Если мы находим не точку на оси, а десятичную дробь, соответствующую ей, то это действие называется десятичным измерением отрезка. Посмотрим, как правильно это сделать.
Допустим, нам нужно попасть от нуля в заданную точку на оси координат (или максимально приблизиться в случае с бесконечной дробью). Для этого мы постепенно откладываем единичные отрезки от начала координат, пока не попадем в нужную точку. После целых отрезков при необходимости отмеряем десятые, сотые и более мелкие доли, чтобы соответствие было максимально точным. В итоге мы получили десятичную дробь, которая соответствует заданной точке на оси координат.
Выше мы приводили рисунок с точкой M. Посмотрите на него еще раз: чтобы попасть в эту точку, нужно отмерить от нуля один единичный отрезок и четыре десятых доли от его, поскольку этой точке соответствует десятичная дробь 1,4.
Если мы не можем попасть в точку в процессе десятичного измерения, то значит, что ей соответствует бесконечная десятичная дробь.
Математика
6 класс
Урок № 73
Бесконечные периодические десятичные дроби
Перечень рассматриваемых вопросов:
– понятие бесконечной периодической десятичной дроби;
– преобразование обыкновенных дробей в бесконечные периодические дроби;
– действия с периодическими дробями.
Тезаурус
Бесконечная периодическая десятичная дробь – это дробь, у которой одна цифра или группа цифр повторяются. Повторяющаяся группа цифр называется периодом и записывается в скобках.
Любое рациональное число p/q можно разложить в периодическую десятичную дробь.
Любая периодическая дробь есть десятичное разложение некоторого рационального числа.
Список литературы
Обязательная литература:
1. Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017, стр. 258.
Дополнительная литература:
1. Чулков П. В. Математика: тематические тесты.5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина – М.: Просвещение, 2009, стр. 142.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин – М.: Просвещение, 2014, стр. 95.
Теоретический материал для самостоятельного изучения
Обыкновенную дробь можно разложить в конечную десятичную, если в знаменателе нет простых множителей, кроме 2 и 5.
Вы уже знаете, как это сделать.
1. Умножить числитель и знаменатель на одно и то же число, чтобы привести к знаменателю 10, 100, 1000 и т. д.;
2. Выполнить деление числителя на знаменатель.
Пример 1. Умножили числитель и знаменатель на 2.
Пример 2. Сначала сократили дробь.
Пример 3. Выполнили деление 3 на 125.
Рассмотрим примеры, когда привести к знаменателю 10, 100 и т. д. нельзя. Возможно только деление числителя на знаменатель.
Заметим, что при делении получаются повторяющиеся остатки и, соответственно, повторяющиеся цифры в частном. Из-за этого процесс деления бесконечен. Отсюда происходит бесконечная десятичная дробь.
Рассмотрим другие примеры.
Повторяющиеся цифры 3; 27; 6 называют периодом дроби. Бесконечные десятичные дроби 0,333…; 0,2727…; 0,1666… называют периодическими.
Записывают так:
0,(3)
0,(27)
0,1(6)
Читают так:
«Нуль целых и три в периоде»
«Нуль целых и 27 в периоде»
«Нуль целых одна десятая и шесть в периоде»
Периодическая дробь – это бесконечная десятичная дробь, у которой, начиная с некоторого десятичного знака, повторяется одна и та же цифра или несколько цифр (период дроби).
Отметим, что любое рациональное число p/q разлагается в периодическую десятичную дробь.
Любая периодическая дробь есть десятичное разложение некоторого рационального числа.
Замечание. При делении уголком десятичное разложение с периодом 9 не возникает.
Далее рассмотрим, как выполняются действия с периодическими дробями?
1. Сравните дроби
1/3 и 0,3
Запишем дробь 1/3 в виде бесконечной периодической дроби 0,333…
Запишем дробь 0,3 в следующем виде 0,300… Приписывая бесконечно много нулей, мы превращаем конечную дробь в равную ей бесконечную периодическую дробь с периодом 0.
Теперь можем сравнить: 0,333… > 0,300…
2. Разложите обыкновенную дробь в бесконечную периодическую десятичную дробь, округлите до десятых.
1/3 = 0,333… ≈ 0,3
5/9 = 0,555… ≈ 0,6
Разбор заданий тренировочного модуля
Задание 1
Представьте в виде периодической дроби. В ответе укажите её период.
период 6
период 4
период 18
период 6
Ответ: 6; 4; 18; 6.
Задание 2
Используя предыдущие задания, запишите периодическую дробь в виде обыкновенной дроби: 0,(3); 0,(5); 0,(6).
0,(3)
0,(5)
0,(6)
Ответ:
Задание 3 ⃰ (повышенного уровня сложности)
Задача: периодическую дробь 0,(1) записать в виде обыкновенной дроби.
Пусть х = 0,(1) = 0,111…
Умножим обе части на 10.
Получим
10 ∙ х = 1,111…
Найдём разность
10 ∙ х – х = 1,111… – 0,111…
Получим
9 ∙ х = 1
Значит,
Ответ:.
Бесконечные периодические и непериодические десятичные дроби
Содержание
Бесконечные периодические и непериодические десятичные дроби
В десятичной записи конечной десятичной дроби после запятой стоит конечное число десятичных знаков.
В десятичной записи бесконечной десятичной дроби после запятой стоит бесконечное число десятичных знаков.
Бесконечные десятичные дроби бывают периодическими и непериодическими.
Бесконечной периодической десятичной дробью называют такую дробь, десятичные знаки которой, начиная с некоторого, представляют собой повторение одной и той же группы цифр, состоящей или из одной цифры, отличной от 0 и 9 , или из нескольких цифр, причем последовательность цифр при повторении в этой группе не изменяется.
Повторяющаяся группа цифр называется периодом бесконечной периодической десятичной дроби.
Для обозначения периода десятичной дроби используют круглые скобки.
Например,
2,616161… = 2,(61) ;
53222222… = 5,3(2) .
ЗАМЕЧАНИЕ. Еще раз подчеркнем, что период бесконечной десятичной дроби не может состоять из одной или нескольких цифр 0 и не может состоять из одной или нескольких цифр 9 .
Бесконечная десятичная дробь, не являющаяся периодической, называется непериодической.
Алгоритм обращения бесконечной периодической десятичной дроби в простую дробь
Разберем алгоритм обращения бесконечной периодической десятичной дроби в простую дробь на примере решений следующих задач.
ЗАДАЧА 1. Обратить периодическую дробь
0,(45)
в простую дробь.
РЕШЕНИЕ. Если ввести обозначение
x = 0,(45) = 0,4545… ,
то, умножив это соотношение на 100 , получим:
100x = 45,4545… .
При этом
100x – x = 99 x =
= 45,0000… = 45.
Следовательно,
ОТВЕТ: .
ЗАДАЧА 2. Обратить периодическую дробь
6,2(7)
в простую дробь.
РЕШЕНИЕ. Если ввести обозначение
x = 6,2(7) = 6,2777… ,
то, умножив это соотношение на 10 , получим:
10x = 62,7777… .
При этом
10x – x = 9x =
= 62,7777… – 6,2777… =
= 56,5.
Следовательно,
ОТВЕТ: .
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Бесконечные десятичные дроби
Десятичные дроби после запятой могут содержать бесконечное количество цифр.
Бесконечные десятичные дроби — это десятичные дроби, в записи которых находится бесконечное число цифр.
Бесконечную десятичную дробь практически невозможно записать полностью, поэтому при их записи ограничиваются только некоторым конечным количеством цифр после запятой, после чего ставят многоточие, которое указывает на бесконечно продолжающуюся последовательность цифр.
Пример 1
Например, $0,443340831dots ; 3,1415935432dots ; 135,126730405dots ; 4,33333333333dots ; 676,68349349dots$.
Рассмотрим последние две бесконечные десятичные дроби. В дроби $4,33333333333dots$ бесконечно повторяется цифра $3$, а в дроби $676,68349349dots$ с третьего знака после запятой повторяется группа цифр $3$, $4$ и $9$. Подобные бесконечные десятичные дроби называются периодическими.

Профориентация для студентов
Поможем определиться с профессией, окажем помощь в профессиональном самоопределении и трудоустройстве
Пройти профориентацию
Периодические десятичные дроби
Периодические десятичные дроби (или периодические дроби) — это бесконечные десятичные дроби, в записи которых с некоторого знака после запятой бесконечно повторяется какая-нибудь цифра или их группа, которая называется периодом дроби}.
Пример 2
Например, период периодической дроби $4,33333333333dots$ — цифра $3$, а период дроби $676,68349349dots$ — группа цифр $349$.
Для краткости записи бесконечных периодических десятичных дробей принято период записывать один раз, заключив его в круглые скобки. Например, периодическую дробь $4,33333333333dots$ записывают $4,(3)$, а периодическую дробь $676,68349349dots$ записывают $676,68(349)$.
Бесконечные десятичные периодические дроби получают при переводе обыкновенных дробей, знаменатели которых содержат простые множители, кроме $2$ и $5$, в десятичные дроби.
Любая конечная десятичная дробь (и целое число) может быть записана в виде периодической дроби, для чего достаточно справа дописать бесконечное количество цифр $0$.
«Периодические десятичные дроби» 👇
Пример 3
Например, конечная десятичная дробь $45,12$ может быть записана в виде периодической дроби как $45,12(0)$, а целое число $(74)$ в виде бесконечной периодической десятичной дроби будет иметь вид $74(0)$.
В случае периодических дробей, которые имеют период 9, используют переход к другой записи периодической дроби с периодом $0$. Только для этого период 9заменяют периодом $0$, при этом значение следующего по старшинству разряда увеличивается на $1$.
Пример 4
Например, периодическую дробь $7,45(9)$ можно заменить периодической дробью $7,46(0)$ или равной ей десятичной дробью $7,46$.
Бесконечные десятичные периодические дроби представляются рациональными числами. Другими словами, любая периодическая дробь может быть переведена в обыкновенную дробь, а любая обыкновенная дробь может быть представлена в виде периодической дроби.
Перевод обыкновенных дробей в конечные и бесконечные периодические десятичные дроби
В десятичную дробь можно перевести не только обыкновенные дроби со знаменателями $10, 100, dots$.
В некоторых случаях исходную обыкновенную дробь можно легко привести к знаменателю $10$, $100$ или $1 000$, после чего можно полученную дробь представить в виде десятичной дроби.
Пример 5
Чтобы дробь $frac{3}{5}$ }привести к дроби со знаменателем $10$, нужно числитель и знаменатель дроби умножить на $2$, после чего получим $frac{6}{10}$, которую не составит труда перевести в десятичную дробь $0,6$.
Для остальных случаев используется другой способ перевода обыкновенной дроби в десятичную}:
-
числитель нужно заменить десятичной дробью с любым числом нулей после десятичной запятой;
-
разделить числитель дроби на знаменатель (деление выполняется как деление натуральных чисел в столбик, а в частном ставят десятичную запятую после окончания деления целой части делимого).
Пример 6
Перевести обыкновенную дробь $frac{621}{4}$ в десятичную дробь.
Решение.
Число $621$ в числителе представим в виде десятичной дроби. Для этого добавим десятичную запятую и для начала два нуля после нее. Далее при необходимости можно буде добавить нули еще. Итак, получили $621,00$.
Выполним деление числа $621,00$ на $4$ в столбик:
Рисунок 1.
Деление дошло до десятичной запятой в делимом, а остаток при этом получили не нулевой. В таком случае в частном ставится десятичная запятая и продолжается деление столбиком, не взирая на запятые:
Рисунок 2.
В остатке получили нуль, значит деление окончено.
Ответ: $155,25$.
Возможен случай, когда при делении числителя и знаменателя обыкновенной дроби в остатке $0$ так и не получается. В этом случае деление можно продолжать бесконечно. Начиная с определенного момента остатки от деления периодически повторяются, а значит повторяются и цифры в частном. Из этого можно сделать вывод, что данная обыкновенная дробь переведется в бесконечную периодическую десятичную дробь.
Пример 7
Перевести обыкновенную дробь $frac{19}{44}$ в десятичную дробь.
Решение.}
Для перевода обыкновенной дроби в десятичную выполним деление в столбик:
Рисунок 3.
При делении повторяются остатки $8$ и $36$, а в частном также повторяются цифры $1$ и $8$. Итак, исходную обыкновенную дробь $frac{19}{44}$ перевели в периодическую дробь $frac{19}{44}=0,43181818dots =0,43(18)$.
Ответ: $0,43(18)$.
Общий вывод о переводе обыкновенных дробей в десятичные:
-
если знаменатель можно разложить на простые множители, среди которых будут присутствовать только числа $2$ и $5$, то такую дробь можно перевести в конечную десятичную дробь;
-
если кроме чисел $2$ и $5$ в разложении знаменателя присутствуют другие простые числа, то такая дробь переводится в бесконечную десятичную периодическую дробь.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Бесконечные периодические десятичные дроби – это дроби, у которых одна цифра или группа цифр повторяются.
Примеры: 0,66666666666666…; 0,33333333333333…; 0,68181818181818…
Повторяющаяся группа цифр называется периодом и записывается в скобках.
Примеры: 0,(6); 0,(3); 0,6(81).
Получить периодическую дробь можно тогда, когда при делении числителя на знаменатель получаются повторяющиеся остатки. Именно повторяющиеся остатки делают процесс деления бесконечным, что приводит к появлению бесконечной периодической дроби.
Пример 1. Разделить 1 на 3: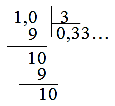
- Записывается. Обычно бесконечные периодические дроби записывают сокращенно: сначала записывают целую часть, затем ставят запятую и в скобках указывают период (цифру, которая повторяется).
- Читается. Бесконечные периодические дроби читаются так: «ноль целых и три в периоде»
Пример 2. Разделить 5 на 11:
При делении мы постоянно получаем остаток 5 или 6. Затем приписываем к остатку 0 и делим 50 или 60 на 11. В результате мы получаем повторяющиеся остатки, поэтому деление 5 на 11 будет выполняться бесконечно.
- Записывается: 0,(45).
- Читается: «ноль целых и сорок пять в периоде»
Виды периодических дробей
Периодические дроби бывают двух видов: чистые и смешанные.
- Чистые — дроби, у которых период начинается сразу после запятой.
Примеры: 0,(3); 0,(5); 0,(6). - Смешанные — дроби, у которых период начинается после некоторого количества не повторяющихся цифр.
Примеры: 0,52(3); 0,16(5); 0,31(6)
Чтобы записать периодическую дробь в виде десятичной дроби, нужно округлить эту дробь до нужного разряда. Как округлять, можно прочитать в статье «Правила округления чисел«
Примеры округления:
Округлить 0,(3) до сотых. Получаем 0,333333…≈ 0,33.
Округлить 6,31(6) до тысячных. Получаем 6,31666666… ≈ 6,317
Перевод периодической дроби в обыкновенную
✅ Для чистой периодической дроби
Чтобы перевести чистую периодическую дробь в обыкновенную дробь, нужно
➤ в числитель обыкновенной дроби записать период периодической дроби,
➤ в знаменатель обыкновенной дроби записать некоторое количество девяток, при этом, количество девяток должно быть равно количеству цифр в периоде периодической дроби.
Пример 1: перевести 0,(3) в обыкновенную дробь.
В периодической дроби 0,(3) период состоит из одной цифры 3, поэтому в числителе записываем одну тройку, а в знаменателе — одну девятку. Полученную дробь можно сократить на 3, тогда получим обыкновенную дробь 1/3.
Пример 2. Перевести 0,(45) в обыкновенную дробь.
В периодической дроби 0,(45) период состоит из двух цифр, поэтому в числителе записываем 45, а в знаменателе — 99. Полученную дробь можно сократить на 9, тогда получим обыкновенную дробь 5/11.
✅ Для смешанной периодической дроби
Чтобы перевести смешанную периодическую дробь в обыкновенную дробь, нужно
- в числителе записать разность:
- уменьшаемое — все цифры, стоящие после запятой, в том числе в периоде,
- вычитаемое — цифры, стоящие между запятой и первым периодом периодической дроби.
- в знаменателе записать некоторое количество девяток и нулей.
- количество девяток должно быть равно количеству цифр в периоде периодической дроби,
- количество нулей должно быть равно количеству цифр между запятой и периодом периодической дроби.
Пример 3: перевести 0,31(6) в обыкновенную дробь.
➤ В числителе запишем разность разность:
уменьшаемое — все цифры, стоящие после запятой, включая и период = 316
вычитаемое — цифры, стоящие между запятой и периодом = 31
получаем числитель = (316-31).
➤ В знаменателе запишем некоторое количество девяток и нулей.
количество девяток равно количеству цифр в периоде периодической дроби 0,31(6) — одна девятка
количество нулей равно количеству цифр между запятой и периодом — два нуля.
получаем знаменатель = 900. Получили дробь, которую можно сократить.
|
316-31 900 |
= |
285 900 |
= |
285:15 900:15 |
= |
19 60 |
Пример 4. перевести 0,72(62) в обыкновенную дробь.
➤ В числителе: уменьшаемое = 7262, вычитаемое = 72, получаем числитель = (7262-72).
➤ В знаменателе: 2 цифры в периоде (99), две цифры между запятой и периодом (00), получаем 9900.
Получили дробь, которую можно сократить.
|
7262-72 9900 |
= |
7190 9900 |
= |
7190:10 9900:10 |
= |
719 990 |
Определение
Бесконечная десятичная дробь, у которой одна или несколько цифр повторяются в одной и той же
последовательности, называется периодической десятичной дробью.
Например. $0,1234444444 ldots ; 12,453737373737 ldots$
Повторяющиеся цифры — период — для сокращения записи пишут в круглых скобках.
Например. $0,12344444444 ldots=0,123(4)$ ;
$12,453737373737 ldots=12,45(37)$
Определение
Чистой периодической дробью называется периодическая дробь, у которой период начинается сразу после запятой.
Например. $2,4949 ldots=2,(49)$
Определение
Смешанной периодической дробью называется такая десятичная дробь, у которой между запятой и
периодом есть не менее одной неповторяющейся бесконечное число раз цифры.
Например. $0,11232323 ldots=0,11(23)$ ;
$1,54444 . .=1,5(4)$
Чтобы обратить чистую периодическую дробь в обыкновенную, достаточно записать числителем ее период,
а в знаменателе записать столько девяток, сколько цифр в периоде.
Чтобы записать смешанную периодическую дробь в виде обыкновенной, надо из числа, стоящего до второго
периода вычесть число, стоящее до первого периода, результат записать в
числителе; в
знаменатель записать
число, содержащее столько девяток, сколько цифр в периоде, и столько нулей в конце, сколько цифр между
запятой и периодом.
Например. Запишем дробь $2,34(2)$ в виде обыкновенной
Читать первую тему — понятие дроби и виды дробей,
раздела дроби.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

§ 1.1. Бесконечные десятичные дроби
Рациональные (в частности, целые) числа и их свойства считаются известными из школы. Рациональные числа можно сравнивать (т. е. для них введены понятия “равно”, “больше” и “меньше”), определены арифметические действия над рациональными числами – сложение, вычитание, умножение и деление.
Но рациональных чисел недостаточно даже для задач элемен-
тарной математики. Так, длина диагонали квадрата со стороной 1 p
равна 2, а это число иррациональное, т. е. не рациональное. Не является рациональным и число , выражающее длину окружности диаметра 1.
Напомним, что такое числовая прямая. На горизонтально расположенной прямой выбирают начальную точку O и единичный отрезок OE, отложенный вправо от точки O. Точке O ставится в соответствие число 0, точке E – число 1. Откладывая вправо от точки E шаг за шагом единичный отрезок, получают точки, соответствующие натуральным числам 2; 3; : : : , а откладывая единичный отрезок влево от точки O, – точки, соответствующие целым отрицательным числам 1; 2; : : : .
Затем строятся точки, соответствующие рациональным числам. При n = 2; 3; : : : отрезок OE делят на n равных частей и чтобы получить точку, соответствующую положительному рациональному числу m=n, вправо от точки O откладывают m раз отрезок длины 1=n. Точно также для отрицательных рациональных чисел находят соответствующие им точки слева от точки O.
Таким образом, каждому рациональному числу поставлена в соответствие точка на числовой прямой. Но при этом не каждой точке числовой прямой соответствует рациональное число. На-
пример, нет рационального числа, соответствующего точке, рас- p
положенной справа от O на расстоянии 2.
В этой главе рациональные числа будут пополнены до множества действительных чисел, в результате каждой точке числовой
7

|
8 |
Гл. 1. Действительные числа |
|||||
прямой будет соответствовать число, а каждому числу – точка на прямой.
Такое пополнение рациональных чисел можно осуществить разными способами. Мы сделаем это, используя бесконечные десятичные дроби. Такой способ был намечен в школе, но сейчас все рассуждения будут проведены заново.
Отметим, что определение действительных чисел как бесконечных десятичных дробей восходит к К. Вейерштрассу.
Построим десятичную дробь, соответствующую произвольной точке A числовой прямой.
Пусть точка A расположена справа от точки O и не отвечает натуральному числу. Найдём целые числа a0 и a0+1, между которыми лежит точка A. В качестве целой части десятичной дроби, соответствующей точке A, берём a0.
Далее отрезок между точками a0 и a0 + 1 делим на 10 равных частей и приписываем этим частям слева направо цифры от 0 до 9. Среди полученных промежутков длины 1/10 находим тот, внутри которого находится точка A (случай, когда A оказывается одной из точек деления, обсудим позднее) и в качестве первого десятичного знака искомой дроби берём цифру, приписанную этому промежутку. Продолжая этот процесс, получим (при условии, что A не оказывается точкой деления) бесконечную десятичную дробь, соответствующую точке A.
Рассмотрим теперь случай, когда точка A оказалась одной из точек деления. Пусть, например, A расположена как на рисунке:
|
0 |
1 |
2 |
9 |
||||||
|
a |
A |
a +1 |
|||||||
|
0 |
0 |
Точкам на промежутке, примыкающем к A справа, в качестве первого десятичного знака мы приписали цифру 2, а на промежутке, примыкающем слева, – цифру 1. По поводу самих точек деления нужно решить, к какому промежутку их относить: лежащему справа или лежащему слева. Если точки деления относить к
|
§ 1.1. Бесконечные десятичные дроби |
9 |
правым промежуткам, то для точки A на рисунке получим a0; 2, а все остальные десятичные знаки – ноли, т. е. получим a0; 2000 : : : . Если точки деления относить к левым промежуткам, то для точки A получим a0; 1, а все остальные десятичные знаки – девятки,
т.е. получим a0; 1999 : : : = a0; 1(9).
Взависимости от договоренности, относить точки деления к правым или к левым промежуткам, для точек, соответствующих натуральным числам, также получим две бесконечные десятичные дроби. У одной из них все десятичные знаки ноли, а у другой целая часть на единицу меньше, а все десятичные знаки – девятки.
Для точек числовой прямой слева от точки O пишем перед дробью знак минус, а затем подобным образом находим числа a0; a1; a2; : : : , определяющие соответствующую бесконечную десятичную дробь a0; a1a2 : : : .
Таким образом, для всех точек числовой прямой (кроме начальной точки O), которые оказываются точками деления, возможны две записи – с нолем в периоде (т. е. в виде целого числа или конечной десятичной дроби) или с девяткой в периоде. Для остальных точек бесконечная десятичная дробь определяется однозначно.
Чтобы каждой точке числовой прямой соответствовала единственная бесконечная десятичная дробь, уславливаются не различать получающиеся при указанном построении дроби с 0 и с 9 в периоде. Обычно в каждом рассуждении используют дроби только с нолем или только с девяткой в периоде.
Поставим обратную задачу – для заданной бесконечной десятичной дроби a0; a1a2 : : : найти соответствующую ей точку числовой прямой.
По знаку дроби и числу a0 находим два идущих подряд целых числа, между которыми должна располагаться искомая точка. Затем, разбив промежуток между этими точками на 10 равных частей, по числу a1 находим тот из полученных промежутков длины 1=10, которому должна принадлежать наша точка.
Продолжая шаг за шагом это построение, получим последовательность промежутков, каждый из которых содержится в предыдущем, а длина его в 10 раз меньше. Искомая точка должна принадлежать всем этим промежуткам.
|
10 |
Гл. 1. Действительные числа |
Но обязательно ли существует такая точка, мы сейчас не знаем. В дальнейшем на этот вопрос будет получен положительный ответ.
Всё сказанное о бесконечных десятичных дробях следует рассматривать как наводящие соображения к тому, чтобы назвать числами бесконечные десятичные дроби.
Определение. Действительными (вещественными) числами называют бесконечные десятичные дроби a0; a1a2 : : : , где выбран определённый знак: “+” или “ ”, a0 – натуральное число или нуль, а все десятичные знаки a1; a2; : : : – цифры от 0 до 9. При этом дробь a0; a1 : : : am(9), где am 6= 9, определяет то же число, что и дробь a0; a1 : : : am 1d000 : : : , у которой m-й десятичный знак d равен am + 1.
Действительные числа будем обозначать буквами и писать a = a0; a1a2 : : : , опуская обычно при этом знак +. Число 0 записывают как бесконечную дробь 0; 000 : : : , которую можно снабдить и знаком + и знаком , но как правило этой дроби знак не приписывают.
При записи чисел a; b; c; : : : в виде бесконечных десятичных дробей для обозначения десятичных знаков будем использовать эти же буквы с индексами:
a = a0; a1a2 : : : ; b = b0; b1b2 : : : ; c = c0; c1c2 : : : :
Для каждого числа a = a0; a1a2 : : : вводится число a, которое отличается от a только знаком, т. е. a := a0; a1a2 : : : . На числовой прямой точки, соответствующие числам a и a, расположены симметрично относительно начальной точки O.
Выясним, как соотносятся рациональные и действительные числа.
Рациональные числа представимы в виде дроби mn , где m – целое число, а n – натуральное.
Будем для определённости считать, что m > 0. Разделив m на n “уголком”, получим либо конечную десятичную дробь, которую можно записать в виде бесконечной дроби с 0 в периоде, либо бесконечную десятичную дробь, которая обязательно будет периодической.
В самом деле, остатками при делении на n могут быть только числа 1; 2; : : : ; n 1. Рассмотрим остатки, которые получаются при делении m на n после того, как все значащие цифры числа m
Соседние файлы в папке Лекции, матан
- #
- #