Как написать что точка принадлежит окружности

Перейти к содержанию

var x,y,r,h: real;

begin

    write('координаты точки: ');

    readln(x,y);

    write('радиус круга: ');

    readln(r);

    h := sqrt(x*x + y*y);

    if h > r then writeln('Точка не принадлежит кругу')

    else writeln('Точка принадлежит кругу');

end.

координаты точки: -1 -2

радиус круга: 5

Точка принадлежит кругу

#include 

#include 

main() {

    float x,y,r,h;

    printf("Координаты точки: ");

    scanf("%f%f", &x,&y);

    printf("Радиус круга: ");

    scanf("%f", &r);

    h = sqrt(x*x + y*y);

    printf("Гипотенуза равна %.2f. ", h);

    if (h > r) printf("Точка не принадлежит кругу.n");

    else printf("Точка принадлежит кругу.n");

}

Координаты точки: 4 5

Радиус круга: 10

Гипотенуза равна 6.40. Точка принадлежит кругу.

from math import sqrt

 
x = float(input("x="))

y = float(input("y="))

r = float(input("r="))

h = sqrt(x**2 + y**2)

print("Расстояние до точки от начала координат равно %.2f" % h)

if h > r:

    print("точка находится за пределами круга")

else:

    print("точка принадлежит кругу")

x=10

y=-3

r=5

Расстояние до точки от начала координат равно 10.44

точка находится за пределами круга

алг точка_круг

нач

  вещ x,y,r,h

  вывод "Координаты точки: "

  ввод x,y

  вывод "Радиус круга: "

  ввод r

  h := sqrt(x**2 + y**2)

  если h > r то вывод "Не принадлежит"

   иначе вывод "Принадлежит"

  все

кон

Координаты точки: 1.6 -2.1

Радиус круга: 4

Принадлежит

input "x=", x

input "y=", y

input "r=", r

h = sqrt(x^2 + y^2)

if h > r then

        print "Не принадлежит"

else

        print "Принадлежит"

endif

Определение принадлежности точки кругу с центром в начале координат

Вводятся координаты (x;y) точки и радиус круга ( r ). Определить принадлежит ли данная точка кругу, если его центр находится в начале координат.

Будем считать, что точка принадлежит кругу, если находится внутри его или на его окружности.

Из любой точки координатной плоскости можно провести отрезок к началу координат. Если длина этого отрезка больше радиуса круга, то точка лежит за пределами круга и, следовательно, не принадлежит ему. Если же отрезок, соединяющий точку и начало координат, меньше радиуса круга с центром в начале координат или равен ему, то точка будет принадлежать кругу.

Отрезок между любой точкой и нулевой точкой (началом координат) является гипотенузой прямоугольного треугольника, катеты которого равны значениям x и y координаты данной точки.

Таким образом задача сводится по-сути к двум действия:

1. Нахождение длины отрезка между точкой и началом координат по теореме Пифагора (квадрат длины гипотенузы равен сумме квадратов длин катетов).
2. Сравнению полученного значения с радиусом круга.

Pascal

Определение принадлежности точки кругу с центром в начале координат паскаль

Язык Си

Для gcc компилировать с ключом -lm.

Python

Определение принадлежности точки кругу с центром в начале координат Python

Уравнение окружности.

Аналитическая геометрия дает единообразные приемы решения геометрических задач. Для этого все заданные и искомые точки и линии относят к одной системе координат.

В системе координат можно каждую точку охарактеризовать ее координатами, а каждую линию – уравнением с двумя неизвестными, графиком которого эта линия является. Таким образом геометрическая задача сводится к алгебраической, где хорошо отработаны все приемы вычислений.

Окружность есть геометрическое место точек с одним определенным свойством (каждая точка окружности равноудалена от одной точки, называется центром). Уравнение окружности должно отражать это свойство, удовлетворять этому условию.

Геометрическая интерпретация уравнения окружности – это линия окружности.

Если поместить окружность в систему координат, то все точки окружности удовлетворяют одному условию – расстояние от них до центра окружности должно быть одинаковым и равным окружности.

Окружность с центром в точке А и радиусом R поместим в координатную плоскость.

Если координаты центра (а;b), а координаты любой точки окружности (х; у), то уравнение окружности имеет вид:

Если квадрат радиуса окружности равен сумме квадратов разностей соответствующих координат любой точки окружности и ее центра, то это уравнение является уравнением окружности в плоской системе координат.

Если центр окружности совпадает с точкой начала координат, то квадрат радиуса окружности равен сумме квадратов координат любой точки окружности. В этом случае уравнение окружности принимает вид:

Следовательно, любая геометрическая фигура как геометрическое место точек определяется уравнением, связывающим координаты ее точек. И наоборот, уравнение, связывающее координаты х и у, определяют линию как геометрическое место точек плоскости, координаты которых удовлетворяют данному уравнению.

Примеры решения задач про уравнение окружности

Задача. Составить уравнение заданной окружности

Составьте уравнение окружности с центром в точке O (2;-3) и радиусом 4.

Решение.
Обратимся к формуле уравнения окружности:
R 2 = (x- a ) 2 + (y- b ) 2

Подставим значения в формулу.
Радиус окружности R = 4
Координаты центра окружности (в соответствии с условием)
a = 2
b = -3

Получаем:
(x — 2 ) 2 + (y — ( -3 )) 2 = 4 2
или
(x — 2 ) 2 + (y + 3 ) 2 = 16 .

Задача. Принадлежит ли точка уравнению окружности

Проверить, принадлежит ли точка A(2;3) уравнению окружности (x — 2) 2 + (y + 3) 2 = 16.

Решение.
Если точка принадлежит окружности, то ее координаты удовлетворяют уравнению окружности.
Чтобы проверить, принадлежит ли окружности точка с заданными координатами, подставим координаты точки в уравнение заданной окружности.

В уравнение ( x — 2) 2 + ( y + 3) 2 = 16
подставим, согласно условию, координаты точки А(2;3), то есть
x = 2
y = 3

Проверим истинность полученного равенства
( x — 2) 2 + ( y + 3) 2 = 16
( 2 — 2) 2 + ( 3 + 3) 2 = 16
0 + 36 = 16 равенство неверно

Таким образом, заданная точка не принадлежит заданному уравнению окружности.

Принадлежит ли точка кругу?

Определить, принадлежит ли точка с координатами (x; y) кругу радиуса R с центром в начале координат.

Пользователь вводит координаты точки и радиус круга.

Если выбрать точку на координатной плоскости, то можно увидеть, что проекции ее координат на оси x и y являются катетами прямоугольного треугольника. А гипотенуза этого прямоугольного треугольника как раз показывает расстояние от начала координат до точки. Таким образом, если длина гипотенузы будет меньше радиуса круга, то точка будет принадлежать кругу; иначе она будет находится за его пределами.

Длину гипотенузы вычисляется по теореме Пифагора: квадрат гипотенузы равен сумме квадратов катетов. Откуда гипотенуза равна квадратному корню из суммы квадратов катетов.

Пример выполнения программы:

Обратите внимание, можно вводить отрицательные координаты. При возведении в квадрат все-равно будет получено положительное число.

Уравнение окружности.

Аналитическая геометрия дает единообразные приемы решения геометрических задач. Для этого все заданные и искомые точки и линии относят к одной системе координат.

В системе координат можно каждую точку охарактеризовать ее координатами, а каждую линию – уравнением с двумя неизвестными, графиком которого эта линия является. Таким образом геометрическая задача сводится к алгебраической, где хорошо отработаны все приемы вычислений.

Окружность есть геометрическое место точек с одним определенным свойством (каждая точка окружности равноудалена от одной точки, называется центром). Уравнение окружности должно отражать это свойство, удовлетворять этому условию.

Геометрическая интерпретация уравнения окружности – это линия окружности.

Если поместить окружность в систему координат, то все точки окружности удовлетворяют одному условию – расстояние от них до центра окружности должно быть одинаковым и равным окружности.

Окружность с центром в точке А и радиусом R поместим в координатную плоскость.

Если координаты центра (а;b), а координаты любой точки окружности (х; у), то уравнение окружности имеет вид:

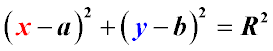
Если квадрат радиуса окружности равен сумме квадратов разностей соответствующих координат любой точки окружности и ее центра, то это уравнение является уравнением окружности в плоской системе координат.

Если центр окружности совпадает с точкой начала координат, то квадрат радиуса окружности равен сумме квадратов координат любой точки окружности. В этом случае уравнение окружности принимает вид:

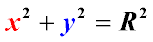
Следовательно, любая геометрическая фигура как геометрическое место точек определяется уравнением, связывающим координаты ее точек. И наоборот, уравнение, связывающее координаты х и у, определяют линию как геометрическое место точек плоскости, координаты которых удовлетворяют данному уравнению.

Примеры решения задач про уравнение окружности

Задача. Составить уравнение заданной окружности

Составьте уравнение окружности с центром в точке O (2;-3) и радиусом 4.

Решение.
Обратимся к формуле уравнения окружности:
R² = (x-a)² + (y-b)²

Подставим значения в формулу.
Радиус окружности R = 4
Координаты центра окружности (в соответствии с условием)
a = 2
b = -3

Получаем:
(x — 2)² + (y — (-3))² = 4²
или
(x — 2)² + (y + 3)² = 16.

Задача. Принадлежит ли точка уравнению окружности

Проверить, принадлежит ли точка A(2;3) уравнению окружности (x — 2)² + (y + 3)² = 16.

Решение.
Если точка принадлежит окружности, то ее координаты удовлетворяют уравнению окружности.
Чтобы проверить, принадлежит ли окружности точка с заданными координатами, подставим координаты точки в уравнение заданной окружности.

В уравнение (x — 2)² + (y + 3)² = 16
подставим, согласно условию, координаты точки А(2;3), то есть
x = 2
y = 3

Проверим истинность полученного равенства
(x — 2)² + (y + 3)² = 16
(2 — 2)² + (3 + 3)² = 16
0 + 36 = 16 равенство неверно

Таким образом, заданная точка не принадлежит заданному уравнению окружности.

0
 

 Площадь геометрической фигуры |

Описание курса

| Задачи про окружность 

Вводятся координаты (x;y) точки и радиус круга ( r ). Определить принадлежит ли данная точка кругу, если его центр находится в начале координат.

Будем считать, что точка принадлежит кругу, если находится внутри его или на его окружности.

Из любой точки координатной плоскости можно провести отрезок к началу координат. Если длина этого отрезка больше радиуса круга, то точка лежит за пределами круга и, следовательно, не принадлежит ему. Если же отрезок, соединяющий точку и начало координат, меньше радиуса круга с центром в начале координат или равен ему, то точка будет принадлежать кругу.

Отрезок между любой точкой и нулевой точкой (началом координат) является гипотенузой прямоугольного треугольника, катеты которого равны значениям x и y координаты данной точки.

Таким образом задача сводится по-сути к двум действия:

1. Нахождение длины отрезка между точкой и началом координат по теореме Пифагора (квадрат длины гипотенузы равен сумме квадратов длин катетов).
2. Сравнению полученного значения с радиусом круга.

Окружность — это линия на плоскости, каждая точка которой расположена на одинаковом расстоянии от центра окружности. Это расстояние называется радиус и в записях обозначается буквой R .
Центр окружности обозначают буквой O.

Окружность разделяет плоскость на две части, внутреннюю и внешнюю. Внутренняя часть, включающая саму окружность, называется кругом. (Наведите курсор на рисунок.)

Точка O — это центр и круга и окружности.

Отрезки OA, OB, и OC — это радиусы, их длины равны. Отрезок BC, проходящий через центр окружности (круга) называется диаметром и обозначается буквой D. Диаметр разделяет круг на два полукруга, а окружность на две полуокружности.

Диаметр равен двум радиусам, это хорошо видно на рисунке.

BC = OC + OB , так как BC = D а OC = OB = R , то

Точки A и B делят окружность на две части, которые называются дугами, а точки A и B концами этих дуг.

Дуга окружности — это часть окружности ограниченная двумя точками.

На рисунке точки B и C разделили окружность на две дуги, голубую и зеленую.

Записать их названия мы можем так:

BC (дуга BC) — в данном случае речь может идти как о голубой так и о зеленой;

BAC (дуга BAC) — в данном случае речь идет именно о зеленой дуге.

Выберите верные утверждения, исходя из рисунка:

1) Точки C, B и E не принадлежат кругу.

2) Точки D, B и O принадлежат окружности.

3) Точки A, B и O принадлежат кругу. Неверно. Точка B принадлежат кругу, так как окружность часть круга. Неверно. Точка O центр окружности, но не лежит на ней. 1) Точка О является центром и окружности, и круга.

2) Точка О является центром окружности, но не центром круга.

3) Точки D и B не принадлежат окружности. 1) Точки B и D не принадлежат кругу.

2) Точки A, B, D и O принадлежат кругу.

3) Точки B, D и E принадлежат кругу. Неверно. Точка О является центром и окружности, и круга. Неверно. Точки D и B принадлежат окружности. Неверно. Точки B и D принадлежат кругу, так как лежат на окружности, а она часть круга. 1) Точки B и D разделяют окружность на 4 дуги.

2) Точки B и D разделяют окружность на 3 дуги.

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

Окружность – это множество точек, равноудаленных от заданной точки (точки О), которую называют центром окружности. Окружность разделит плоскость на 2 части. Ту часть плоскости, которая лежит внутри окружности вместе с самой окружностью, называют кругом. Точка О является как центром окружности, так и центром круга (рис. 2).

Рис. 2. Окружность и круг

Взаимное расположение окружности и точки

Точки могут лежать на окружности, т. е. принадлежать окружности. Точки А и В принадлежат окружности с центром в точке О (Рис. 3); точки О, Е и D не принадлежат окружности с центром в точке О; точки О, Е, А, В принадлежат кругу с центром в точке О, а точка D не принадлежит этому кругу.

Рис. 3. Окружность и круг с центром в точке О

Точки А и В делят окружность на две части (рис. 4), каждую из которых называют дугой окружности; точки А и В – концами дуг.

Рис. 4. Окружность

Дуга, радиус, хорда, диаметр окружности

Дуга окружности – это часть окружности, ограниченная двумя точками. Пример. На окружности с центром в точке О отмечены точки А, В и С. Назовите дуги, на которые эти дуги делят окружность. Дуги с концами в точках А и В: дуга АВ, дуга АСВ. Дуги с концами в точках В и С: дуга ВС, дуга ВАС. Дуги с концами в точках А и С: дуга АС, дуга АВС. Отрезки ОА, ОВ соединяют центр окружности с точками, лежащими на окружности. Их называют радиусами (рис. 5).

Рис. 5. Радиусы окружности

Радиус – это расстояние от центра окружности до любой точки окружности. Радиусы одной окружности равны. Обозначают радиусы R или r. Отрезок, соединяющий две точки окружности, называют хордой. Хорду, проходящую через центр окружности, называют диаметром. Обозначают: d или D. Свойства диаметра: 1. диаметр – самая большая хорда. 2. d = 2R. Диаметр делит круг на два полукруга, а окружность – на две полуокружности

Задача 1

Постройте окружность с центром в точке О и радиусом 4 см. Постройте прямую а так, чтобы она пересекла окружность в двух точках А и В (рис. 6). На каком расстоянии от центра окружности находятся точки А и В?

Рис. 6. Окружность с центром в точке О и радиусом 4 см

Так как расстояние между двумя точками – это длина отрезка с концами в этих точках, то нам необходимо найти длины отрезков ОА и ОВ. По определению отрезки ОА и ОВ – радиусы одной и той же окружности. Тогда ОА = ОВ = R= 4 см. Значит, на расстоянии 4 см находятся точки А и В от центра окружности.

Задача 2

Постройте отрезок АВ, равный 4 см. Постройте первую окружность с центром в точке А радиусом 3 см, и другую окружность с центром в точке В радиусом 2 см. Назовите точки пересечения окружностей точками Е и С (рис. 7). Чему равны длины отрезков АЕ, АС, ЕВ и ВС?

Рис. 7. Отрезок АВ

По определению, отрезок АЕ, АС – это радиусы первой окружности. АЕ = АС =

Рис. 8. Точки, удаленные от концов отрезка на 3 см

Список литературы

1. Н.Я. Виленкин. Учебник для 5 кл. общеобразовательных учреждений/ 17-е изд. – М.: Мнемозина, 2005.
2. Шевкин А.В. Текстовые задачи по математике: 5–6. – М.: Илекса, 2011. – 106 с.
3. Ершева А.П., Голобородько В.В. Вся школьная математика в самостоятельных и контрольных работах. Математика 5–6. – М.: Илекса, 2006. – 432 с.
4. Н.Н. Хлевнюк, М.В. Иванова. Формирование вычислительных навыков на уроках математики. 5–9 классы. – М.: Илекса, 2011. – 248 с.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

Домашнее задание

Учебник математики. 5 класс. Н.Я. Виленкин. № 850–856.

Если вы нашли ошибку или неработающую ссылку, пожалуйста, сообщите нам – сделайте свой вклад в развитие проекта.