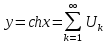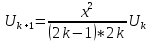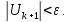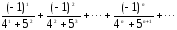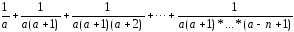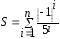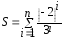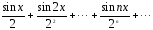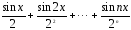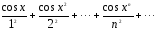План урока:
Понятие циклического алгоритма
Программирование циклического алгоритма
Операторы цикла
Решение задач с использованием операторов while, repeat, for
Понятие циклического алгоритма
В жизни людей очень часто встречаются циклы. Будь то жизнь маленького ребёнка или взрослого человека, а то и пожилых людей. Эти циклы можно расписать как выполнение одних и тех же действий, пока выполняется определённое условие. К примеру, взрослый человек находится на работе до момента, когда наступит время его ухода. И так изо дня в день, однако, есть и исключения в виде выходных. В жизни детей можно привести такой пример, как обязанность каждый день ходить в школу до момента, когда наступят выходные или каникулы.
Циклические алгоритмы – это алгоритмы, в которых некоторая часть операций повторяется многократно.
Цикл – конструкция с оператором, который повторяется определённое или неопределённое заранее количество раз. Действия, выполняющиеся последовательно внутри цикла, называют телом цикла.
В разных средах программирования циклические конструкции могут быть реализованы по-разному, но неизменным остается главный признак, отличающий циклы от линейных операций и ветвлений – возможность перемещения по программе не только «сверху-вниз», но и «снизу-вверх», для возврата к уже выполненным ранее действиям.
Циклы разделяют на три типа в зависимости от метода организации повторений:
- Цикл, в котором задано условие окончания работы;
- Когда известно условие продолжения работы цикла;
- Когда известно число повторений цикла.
Программирование циклического алгоритма
Выбрав среду программирования Паскаль необходимо познакомиться с операторами, с помощью которых можно разработать программу с циклом. Ими являются while, repeat, for. Оператор while был разобран ещё на прошлом уроке, однако забывать о нём нельзя.
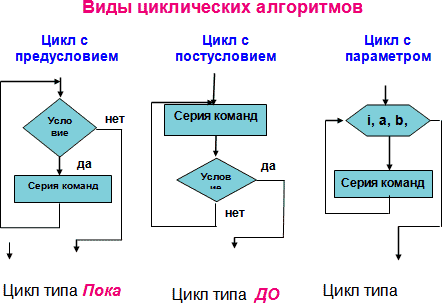
Цикл с предусловием
Цикл с предусловием реализует циклический алгоритм, записанный на языке программирования, с использованием определённого условия, истинность которого проверяется перед каждой итерацией цикла. Выполнение цикла прекращается, когда условие становится ложным.
Цикл с постусловием
Цикл с постусловием – это алгоритм циклической структуры, в котором проверка условия продолжения осуществляется после выполнения тела цикла.
Тело цикла с постусловием всегда выполняется как минимум один раз, независимо от истинности или ложности условия. Это его ключевое отличие от цикла с предусловием.
Такие циклы удобны, когда в условии используется результат выполнения тела цикла. Например, если мы хотим найти в тексте слово «стоп», мы должны сначала прочитать очередное слово, и только потом проверить, является ли оно искомым или следует продолжить поиск.

Цикл с заданным числом повторений
Этот вид цикла вместо логического условия выполнения использует параметр (счетчик) – специальную переменную, которая на каждом шаге цикла получает очередное значение из определенного диапазона. Цикл повторяется до тех пор, пока не будут перебраны все элементы диапазона. Таким образом, определяя диапазон, мы определяем заранее заданное число повторений.
Операторы цикла
Для программирования циклических алгоритмов и корректного выполнения программ с их использованием, необходимо знать операторы цикла. Чаще всего, в языке Паскаль используют операторы цикла: for, repeat и while. Разберем их подробнее.
Оператор while
Оператор while используется, когда нужно создать цикл с предусловием. Его схема в циклическом алгоритме выглядит следующим образом:
Если переводить его дословно, то можно сказать, что он работает по принципу «пока <условие> выполнять действие <оператор 1>», а заканчивается при переходе программы на слово end. Перед выполнением операторов внутри цикла условие обязательно проверяется и уже дальше, в зависимости от его истинности, программа либо выполняет тело цикла, либо переходит к последующим операторам.
Решение задач с использованием оператора while
Для более чёткого понимания решения задач нужно разобрать циклические алгоритмы, примеры которых приведены в решениях.
Задача 1. На вход подаются целые числа. До тех пор, пока не будет введено число, которое больше 17, программа должна вывести сумму полученного числа и числа 8. Когда вводимое число будет больше 17, то после выполнения программы цикл завершается.
Решение.
Шаг 1. Для начала необходимо дать программе название.
Шаг 2. Учитывая, что на вход подаётся целое число, указать тип данных, в данном случае – integer.
Шаг 3. Запись командного блока. Нужно написать слово, обозначающее начало, begin.
Шаг 4. Нужно дать переменной a значение 1, чтобы цикл начался автоматически.
Шаг 5. Запись цикла. Поскольку известно условие окончания работы, для этой задачи необходимо написать «пока a меньше или равно 17» и сделать переход к последующим операторам путём написания составного цикла.
Шаг 6. Первоначальный вывод программы. Необходимо написать то, что программа будет выдавать в первую очередь. В данном случае, она будет запрашивать целое число, запрос так и пишется: «Введите целое число: » .
Шаг 7. Запись необходимых операторов. Используя оператор readln программа считывает данные и переводит курсор на новую строку. Далее она производит операции над поступившими данными.
Шаг 8. Запись суммы. Исходя из условия задачи необходимо сделать так, чтобы программа выводила сумму входящего числа и числа 8. Осуществить это можно используя оператор writeln.
Шаг 9. Запись вывода программы после цикла. После того, как программа выполнит свою работу в цикле, необходимо показать, что она из него вышла. Можно просто попрощаться, как в данном случае.
Шаг 10. Проверка правильности записи алгоритма. В конце программного блока, после слова end нельзя забывать точку, её обязательно нужно поставить.
Оператор repeat
Оператор цикла repeat until используется для создания циклического алгоритма с постусловием. Его схема выглядит так:
Дословно оператор Паскаля repeat можно перевести как «повторяй <оператор 1>, до <условие>». В зависимости от истинности условия, либо происходит переход на повторение «оператора 1», либо осуществляется выход из цикла к последующим операторам.
Оператор repeat имеет два важных отличия от оператора while:
- в операторе repeat сначала выполняется тело, а затем проверяется условие;
- в операторе repeat прописывается условие завершения цикла, тогда как в операторе while – условие его продолжения.
Решение задач с использованием оператора repeat
Задача 1. Придумать алгоритм и написать по нему программу, результатом выполнения которой будет вывод последовательности натуральных чисел от 1 до введенного пользователем числа.
Решение.
Шаг 1. Название программы. В данном случае — «задача 1».
Шаг 2. Учитывая, что на вход подаются целые числа, требуется указать тип данных – integer.
Шаг 3. Командный блок. Запись начального слова begin.
Шаг 4. Вывод запроса программы. Поскольку программе необходимо целое число, нужно попросить пользователя ввести его. Осуществляется это с помощью процедуры writeln и текста «Введите целое число, которое больше 1: ».
Шаг 5. Необходимо присвоить переменной i значение 1 для того, чтобы последовательность начиналась с натурального числа.
Шаг 6. Запись цикла. Учитывая, что используется цикл с постусловием, необходимо сначала записать оператор, который будет повторяться, затем увеличить i на 1, чтобы образовывалась последовательность, и уже после этого прописать условие повторения. В данной задаче цикл перестаёт повторяться тогда, когда переменная i принимает значение больше введённого числа, которое является последним членом последовательности.
Шаг 7. Проверка программы на правильность в выводе. В результате своей работы программа должна вывести последовательность натуральных чисел от 1 до n, через пробел.
Оператор for
Используя оператор for можно задать нужное количество повторений одних и тех же действий. По-другому его называют оператором циклов с известным числом повторений. Он имеет два соединительных слова – это to и downto. Различие между ними в том, что при использовании первого к предыдущему значению переменной цикла прибавляется единица, а при написании второго – вычитается единица. Схемы оператора имеют следующий вид:
Дословно его можно перевести как «для переменной в значении от начального к конечному выполнять <оператор 1> ».
Решение задач с использованием оператора for
Рассмотреть пример с оператором for можно при написании короткого алгоритма для следующей задачи.
Задача 1. Напишите на одном из языков программирование алгоритм, который выводит квадраты чисел от 1 до 10.
Решение.
Шаг 1. Необходимо дать программе название.
Шаг 2. Поскольку на вход числа не подаются, тип указывается в зависимости от данных, которые изначально находятся в программе. В данном случае – это целые числа.
Шаг 3. Запись блока с командами алгоритма.
Шаг 4. Перебор последовательности чисел осуществляется в цикле for, в котором счетчик i пробегает значения от 1 до 10, а расчет и вывод квадратов осуществляется в процедуре write.
Решение задач с использованием операторов while, repeat, for
Задача 1 Разработать алгоритм программы, которая выведет таблицу умножения чисел от 1 до 10 на 9.
Решение
Для решения можно написать два вида кода. Однако, этапы разработки программы, задачи, которые ей необходимо выполнить, очень похожи на прошлые примеры, и она ничем не отличается от решения обычной задачи. Поскольку различие в этих двух кодах лишь в использованном операторе while и for, то рассматривать их по-отдельности нет смысла. Последовательность написания первого кода выглядит так:
Шаг 1. Нужно назвать программу.
Шаг 2. Так как пользователь не вводит никаких данных, то их можно ввести в сам код программы. Тип используемых данных в данном случае – это integer.
Шаг 3. Написание команд. Изначально нужно сделать так, чтобы программа вывела название того, для чего она предназначена. В данной задаче это «Таблица умножения на 9».
Шаг 4. Запись цикла for. С помощью него программа будет последовательно умножать числа от 1 до 10 на 9 и составлять таблицу умножения путём вывода каждого значения по схеме «9x, i, =, p», где i – умножаемое на 9 число, p – результат произведения 9 и i.
Шаг 6. Программа завершает свою работу. Необходимо проверить правильность выведенных данных и, если это необходимо, поправить код для более корректной работы.
В этой статье будет рассмотрена работа циклического алгоритма — что это, как он работает, какие виды существуют. Также будут рассмотрены примеры циклических алгоритмов в разных языках программирования.
Прежде чем приступить к основной теме статьи, следует прояснить терминологию вопроса и рассмотреть основные определения:
— цикл — вид управляющей конструкции в языках программирования. Он позволяет организовать многократное исполнение определённого набора инструкций (последовательность действий, при котором выполняется тело цикла);
— тело цикла — последовательность инструкций, обеспечивающая их многократное исполнение;
— итерация — однократное исполнение тела цикла;
— условие выхода (условие окончания) — выражение, которое определяет, станет ли в очередной раз выполняться итерация либо произойдёт завершение цикла;
— счётчик цикла — переменная, которая сохраняет номер итерации.
Счётчик не обязательно должен содержаться в цикле и счётчик совсем не обязательно должен быть один, то есть условие выхода порой зависит от нескольких изменяемых переменных. Вдобавок к этому, условие выхода иногда зависит от внешних условий (как пример — наступление определённого времени).
Работа любого цикла вне зависимости от его вида включает в себя:
— первоначальную инициализацию циклических переменных;
— проверку условия выхода из цикла;
— выполнение тела;
— обновление циклической переменной на каждой итерации.
Многие языки программирования предоставляют разработчику средства, обеспечивающие досрочное завершение цикла (выход из него вне зависимости от истинности условия выхода).
Виды циклических алгоритмов
Безусловные циклы
В некоторых программах и линейных алгоритмах на компьютерах выход из циклов не предусмотрен логикой. Эти циклы называются безусловными (другое название — бесконечные). При написании таких алгоритмов для решения поставленных задач специальных синтаксических средств не используют (они часто и не предусмотрены). На практике вполне достаточно конструкций, которые предназначены для формирования обычных (условных) циклов. Чтобы обеспечить бесконечное повторение, проверка условия или исключается (LOOP…END LOOP, язык программирования Ада), или заменяется константным значением (while true do …, Pascal).
Теперь следует рассмотреть группу циклов с условием.
Циклический алгоритм с предусловием
При наличии предусловия цикл выполняется до тех пор, пока истинно определённое условие, которое указано перед началом. Данное условие проверяется ещё до выполнения тела, в результате чего тело алгоритма может вообще ни разу не выполнится (пример такой ситуации с нулевым количеством итераций — условие изначально ложно). Что касается применения и реализации, то во многих процедурных языках программирования такой алгоритм реализуется с помощью оператора while.
Циклический алгоритм с постусловием
В данном случае проверка условия происходит уже после выполнения тела. Это означает, что тело цикла хотя бы раз, да выполнится. В Pascal такой алгоритм реализуется посредством оператора repeat..until, в языке программирования Си — с помощью do…while.
В зависимости от языка, трактовка условий бывает разной. В том же Pascal речь идёт об условии выхода (работа линейного алгоритма завершится, когда условие истинно; «цикл до»), а в вышеупомянутом Си можно говорить об условии продолжения (цикл завершится, когда условие ложно; «цикл пока»).
Циклический алгоритм с выходом из середины
Это самая общая форма условного линейного алгоритма. Синтаксически оформляется посредством 3-х конструкций:
— начало цикла,
— конец,
— команда выхода.
Конструкция начала обеспечивает маркировку программной точки, где начинается тело, конструкция конца — где тело заканчивается. Внутри циклического алгоритма присутствует команда, обеспечивающая выход — цикл оканчивается, а управление передаётся оператору, следующему за конструкцией конца.
Если сравнивать этот алгоритм с вышеупомянутыми, то он имеет особенность: часть тела, которая расположена после начала и до команды выхода, выполнится всегда, а часть тела, расположенная после команды выхода, при последней итерации не выполнится.
Чтобы организовать выход из середины, в некоторых языках программирования необходимо использовать специальные конструкции. В Ада это LOOP…END LOOP и команда EXIT либо EXIT WHEN:
Внутри этого алгоритма может находиться любое число команд выхода обоих типов — как EXIT WHEN (используется, если проверяется лишь условие выхода), так и просто EXIT (используется, если выход осуществляется в одной из вариаций сложного условного оператора).
В некоторых языках специальные конструкции для выхода из середины отсутствуют. В таких случаях смоделировать выход можно, используя любой условный цикл и оператор досрочного выхода (тот же break в Си) или goto — оператор безусловного перехода.
Циклический алгоритм cо счётчиком
При реализации этого алгоритма на компьютере определённая переменная меняет своё значение с некоторым шагом (она имеет заданное начальное и конечное значения), причём для каждого значения переменной тело цикла выполнится хотя бы раз. Во многих процедурных языках программирования алгоритм со счётчиком реализуется с помощью оператора for. В нём указывается счётчик (его ещё называют переменной цикла), определённое число проходов (граничное значение счётчика) и, в некоторых случаях, шаг изменения счётчика. В качестве примера — циклический алгоритм со счётчиком в языке программирования Оберон-2:
Хотите знать про алгоритмы больше? Записывайтесь на специализированные курсы в OTUS!
Источник — https://dic.academic.ru/dic.nsf/ruwiki/1188296.
Алгоритм циклической структуры
Алгоритм циклической структуры
Как вы помните, любой алгоритм можно составить из нескольких базовых структур. В простейшей — линейной — команды выполняются однократно в той последовательности, как записаны. Если на каком-то этапе исполнитель должен выбирать один вариант из нескольких, используют разветвленную структуру. Но чаще всего автоматизируют те действия, которые нужно выполнять много раз подряд. И здесь на помощь приходит циклическая структура.
В алгоритме циклической структуры (цикле) серия команд (тело цикла) повторяется многократно. При этом нужно указать, либо сколько раз исполнитель должен выполнить тело цикла, либо при каком условии исполнитель будет повторять тело цикла еще раз.
Разновидности циклической структуры
Разновидности циклической структуры
Задается количество повторений
Цикл с параметром
Задается условие продолжения/окончания повторений
блок-схема
фрагмент программы
for i:=1 to 10 do
write(i, ‘ ‘);
Результат:
1 2 3 4 5 6 7 8 9 10
for k:=8 downto 1 do
write(k*k, ‘ ‘);
n:=1;
while n < 100 do
begin
write(n, ‘ ‘);
n:=n*2;
end;
Результат:
1 2 4 8 16 32 64
m:=1;
repeat
write(m, ‘ ‘);
m:=m*3;
until m > 500;
Результат:
1 3 9 27 81 243
Результат:
64 49 36 25 16 9 4 1
(В примерах фрагментов программ ключевые слова операторов цикла выделены полужирным шрифтом).
Если тело цикла состоит более чем из одной команды, в операторах for…to…do и while…do ее необходимо, как и в условном операторе, заключать в операторные скобки begin…end (см. пример цикла с предусловием).
При составлении циклического алгоритма, нужно…
При составлении циклического алгоритма, нужно…
- Определить, какая последовательность действий должна повторяться.
- Выяснить, что будет известно о количестве повторений тела цикла до начала цикла.
- Если число повторений известно, можно использовать цикл с параметром.
- Если тело цикла обязательно выполняется хотя бы один раз, можно использовать цикл с постусловием.
- Если число повторений неизвестно и может быть нулевым, необходимо использовать цикл с предусловием.
- Определить пределы изменения параметра (для цикла с параметром) либо условие повторения/окончания (для циклов с условием).
- Определить, значения каких переменных должны быть известны до начала цикла (особое внимание обратить на переменные, входящие в условие оператора цикла с предусловием). Операторы для ввода или вычисления этих переменных должны быть записаны до заголовка цикла.
- Записать алгоритм на языке программирования.
- Подобрать данные для тестирования программы (предусмотреть несколько наборов данных, в том числе для предельных случаев, например, для случая, когда тело цикла с предусловием не должно выполняться ни разу).
Цель: изучение алгоритмической структуры циклы, создание моделей и алгоритмов для решения практических задач.
Ход урока
I. Актуализация знаний
- Повторить понятие алгоритма, основные конструкции алгоритмического языка.
- Уметь разрабатывать математическую модель, алгоритм и блок схему решения задачи.
- Иметь понятие о языках программирования и их назначении.
- Уметь работать в среде программирования.
- Знать структуры программы.
- Уметь записывать выражения, содержащие числовые и символьные величины.
- Знать структуры операторов и особенности их работы.
- Уметь применять операторы при написании программ с линейными и ветвящимися структурами.
- Уметь на компьютере создавать и запускать программы на отладку.
II. Теоретический материал урока
Большинство практических задач требует многократного повторения одних и тех же действий, т. е. повторного использования одного или нескольких операторов. (Презентация)
Пусть требуется ввести и обработать последовательность чисел. Если чисел всего пять, можно составить линейный алгоритм. Если их тысяча, записать линейный алгоритм можно, но очень утомительно и нерационально. Если количество чисел к моменту разработки алгоритма неизвестно, то линейный алгоритм принципиально невозможен.
Другой пример. Чтобы найти фамилию человека в списке, надо проверить первую фамилию списка, затем вторую, третью и т.д. до тех пор, пока не будет найдена нужная или не будет достигнут конец списка. Преодолеть подобные трудности можно с помощью циклов.
Циклом называется многократно исполняемый участок алгоритма (программы). Соответственно циклический алгоритм — это алгоритм, содержащий циклы.
Различают два типа циклов: с известным числом повторений и с неизвестным числом повторений. При этом в обоих случаях имеется в виду число повторений на стадии разработки алгоритма.
Существует 3 типа циклических структур:
- Цикл с предусловием;
- Цикл с послеусловием;
- Цикл с параметром;
Иначе данные структуры называют циклами типа «Пока», «До», «Для».
Графическая форма записи данных алгоритмических структур:
Цикл с предусловием (иначе цикл пока) имеет вид:
| Форматы записи операторов алгоритма | Блок-схема | Форматы записи операторов на Паскале |
| Пока (условие) нц серия команд кц |
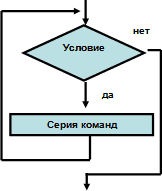 |
while условие do begin серия команд; end; |
где
условие – выражение логического типа.
Цикл может не выполняться ни разу, если значение логического выражения сразу же оказывается ложь.
Серия команд, находящихся между begin и end, выполняются до тех пор, пока условие истинно.
Для того чтобы цикл завершился, необходимо, чтобы последовательность инструкций между BEGIN и END изменяла значение переменных, входящих в условие.
Цикл с постусловием (иначе цикл до) имеет вид:
| Форматы записи операторов алгоритма | Блок-схема | Форматы записи операторов на Паскале |
| В алгоритмическом языке нет команды которая могла бы описать данную структуру, но ее можно выразить с помощью других команд (Например, ветвления). | 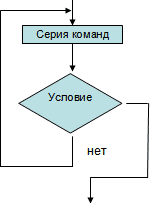 |
repeat серия команд until условие |
где
условие – выражение логического типа.
Обратите внимание:
Последовательность инструкций между repeat и until всегда будет выполнено хотя бы один раз;
Для того чтобы цикл завершился, необходимо, чтобы последовательность операторов между repeat и until изменяла значения переменных, входящих в выражение условие.
Инструкция repeat, как и инструкция while, используется в программе, если надо провести некоторые повторяющиеся вычисления (цикл), однако число повторов заранее не известно и определяется самим ходом вычисления.
Цикл с параметром (иначе цикл для) имеет вид:
| Форматы записи операторов алгоритма | Блок-схема | Форматы записи операторов на Паскале |
| Для i от а до b шаг h делай Нц Серия команд кц |
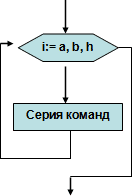 |
h = +1 for i:= a to b do begin серия команд end; h = -1 for i:= b downto a do begin Cерия команд; end; |
где
i – параметр цикла;
a – начальное значение цикла;
b – конечное значение цикла;
h – шаг изменения параметра.
Структура данного цикла иначе называют циклом i раз.
Эта команда выполняется таким образом: параметру i присваивается начальное значение а, сравнивается с конечным значением b и, если оно меньше или равно конечному значению b, выполняется серия команд. Параметру присваивается значение предыдущего, увеличенного на величину h – шага изменения параметра и вновь сравнивается с конечным значением b.
На языке программирования Паскаль шаг изменения параметра может быть равным одному или минус одному.
Если между begin и end находится только один оператор, то операторные скобки можно не писать. Это правило работает для цикла типа «Пока» и «Для».
Рассмотрим пример решения задач с использованием данных структур
Пример.
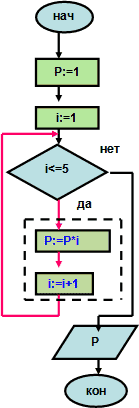
Вычислить произведение чисел от 1 до 5 используя различные варианты цикла
Математическая модель:
Р= 1· 2· 3· 4· 5=120
Составим алгоритм в виде блок-схемы.
Для проверки правильности алгоритма заполним трассировочную таблицу.
| Шаг | Операция | Р | i | Проверка условия |
| 1 | P:=1 | 1 | ||
| 2 | i:=1; | 1 | 1 | |
| 3 | i<=5 P:=P*I i:=i+1 |
1 | 1 | 1<=5, да (истина) |
| 4 | i<=5 P:=P*I i:=i+1 |
2 | 2 | 2<=5, да (истина) |
| 5 | i<=5 P:=P*I i:=i+1 |
6 | 3 | 3<=5, да (истина) |
| 6 | i<=5 P:=P*I i:=i+1 |
24 | 4 | 4<=5, да (истина) |
| 7 | i<=5 P:=P*I i:=i+1 |
120 | 5 | 5<=5, да (истина) |
| 8 | i<=5 P:=P*I i:=i+1 |
6<=5, нет (ложь) |
Проверка условия происходит в несколько шагов: проверка условия и выполнение команд на одной из ветвей. Поэтому в трассировочной таблице записываются не команды алгоритма, а отдельные операции, выполняемые компьютером на каждом шаге.
Шаг первый: Р присваивается значение один.
Шаг второй: i присваивается значение один.
Шаг третий: при i равном единице проверяем условие один меньше или равен пяти, да, условие истинно, значит Р присваивается значение один умноженное на один, будет два. Для i: один плюс один, будет два.
Шаг четвертый: при i равном двум проверяем условие два меньше или равен пяти, да, условие истинно, значит Р присваивается значение 2 умноженное на один, будет 2. Для i: два плюс один, будет три.
Шаг пятый: при i равном трем проверяем условие три меньше или равен пяти, да, условие истинно, значит Р присваивается значение два умноженное на три, будет шесть. Для i: три плюс один, будет четыре.
Шаг шестой: при i равном четырем проверяем условие четыре меньше или равен пяти, да, условие истинно, значит Р присваивается значение шесть умноженное на четыре, будет двадцать четыре. Для i: четыре плюс один, будет пять.
Шаг седьмой: при i равном пяти проверяем условие пять меньше или равен пяти, да ,условие истинно, значит Р присваивается значение двадцать четыре умноженное на пять, будет сто двадцать. Для i: пять плюс один, будет шесть.
Шаг восьмой: при i равном шести проверяем условие шесть меньше или равен пяти, нет, условие ложно, тогда мы выходим из цикла, а в результате получаем последнее значение равное сто двадцати.
Program Pr1;
Var i: integer;
Begin
P:=1;
i:=1;
While i<=5 do
begin
P:=P*i;
i:=i+1;
end;
Write (‘P=’, P);
end.
Для цикла с постусловием построим блок-схему и трассировочную таблицу. (слайд16)
В результате получаем последнее значение равное сто двадцати на седьмом шаге
И для Цикла с параметром построим блок-схему и трассировочную таблицу. (слайд17)
В результате получаем последнее значение равное сто двадцати на шестом шаге
Задача:
Вывести на экран числа от 1 до 5 в:
- прямом порядке;
- обратном порядке.
Математическая модель:
- 1 2 3 4 5;
- 5 4 3 2 1.
Блок-схема и программа решения задачи представлена для чисел в прямом порядке и обратном порядке.
(слайд 21)
Запишем рассмотренные алгоритмы на языке программирования Паскаль.
(слайд 22)
III. Подведение итогов урока
И так мы рассмотрели следующие вопросы:
- Алгоритмическая структура цикл;
- Виды алгоритмических структур:
- Цикл с предусловием;
- Цикл с послеусловием;
- Цикл с параметром;
- Рассмотрели способы записи данных структур;
- Разобрали примеры решения задач с помощью этих структур.
Занятие 4. Графическая реализация циклического алгоритма
В рассмотрении циклического алгоритма следует выделить несколько понятий.
Тело цикла – это набор инструкций, предназначенный для многократного выполнения.
Итерация – это единичное выполнение тела цикла.
Переменная цикла – это величина, изменяющаяся на каждой итерации цикла.
Каждый цикл должен содержать следующие необходимые элементы:
- первоначальное задание переменной цикла,
- проверку условия,
- выполнение тела цикла,
- изменение переменной цикла.
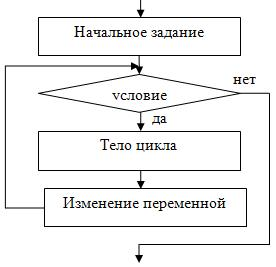
Циклы бывают двух видов – с предусловием и с постусловием. В цикле с предусловием сначала проверяется условие входа в цикл, а затем выполняется тело цикла, если условие верно. Цикл с предусловием представлен на рис. 2.9. Цикл с предусловием также может быть задан с помощью счетчика. Это удобно в тех случаях, когда точно известно количество итераций. В общем виде блок-схема, реализующая цикл с предусловием, представлена ниже. Сначала задается начальное значение переменной цикла, затем условие входа в цикл, тело цикла и изменение переменной цикла. Выход из цикла осуществляется в момент проверки условия входа в цикл, когда оно не выполняется, т.е. условие ложно. Цикл с предусловием может ни разу не выполниться, если при первой проверке условия входа в цикл оно оказывается ложным.
Рис.
2.9.
Циклический алгоритм с предусловием в общем виде
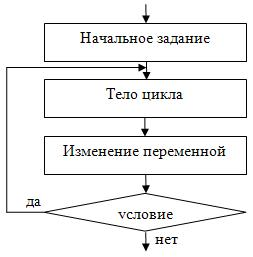
В цикле с постусловием сначала выполняется тело цикла, а потом проверяется условие. Циклический алгоритм с постусловием представлен на рис. 2.10.
Рис.
2.10.
Циклический алгоритм с постусловием в общем виде
Если условие верно, то итерация повторяется, если же неверно, то осуществляется выход из цикла. В отличие от цикла с предусловием, любой цикл с постусловием всегда выполнится хоть раз.
Примечание. Как видно из представленных блок-схем для циклов с предусловием и постусловием, условие записывается внутри блока условия (формы ромба), как и в разветвляющемся алгоритме. Принципиальная разница между разветвляющимся и циклическим алгоритмами при графической реализации состоит в том, что в циклическом алгоритме в обязательном порядке присутствует стрелка, идущая наверх. Именно эта стрелка обеспечивает многократный повтор тела цикла.
Приведем простейшие примеры, соответствующие циклическому алгоритму.
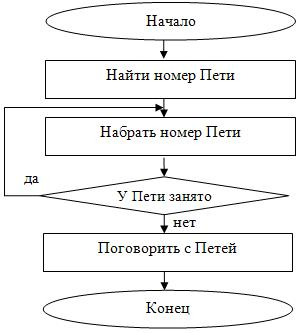
Пример 7. Вася звонит Пете, но у Пети может быть занята линия. Составить блок-схему действий Васи в этом случае.
Решение. Когда телефонная линия занята, то необходимо снова и снова набирать номер, пока Петя не закончит предыдущий разговор, и телефонная линия не окажется вновь свободной. Блок-схема представлена на рис. 2.11.
Рис.
2.11.
Блок-схема для примера 7
Здесь тело цикла состоит из одного действия «Набрать номер Пети», т.к. именно это действие следует повторять, пока линия будет занята. Под итерацией цикла понимается очередная попытка дозвониться до Пети. Как таковой переменной цикла здесь нет, т.к. ситуация взята из жизни. Выход из цикла происходит в тот момент, когда условие «У Пети занято» стало неверным, т.е. телефонная линия свободна – действительно, нет необходимости больше набирать номер Пети. В данном примере применен цикл с постусловием, т.к. сначала необходимо набрать номер Пети, ведь иначе мы не можем ответить на вопрос – занята ли линия у Пети.
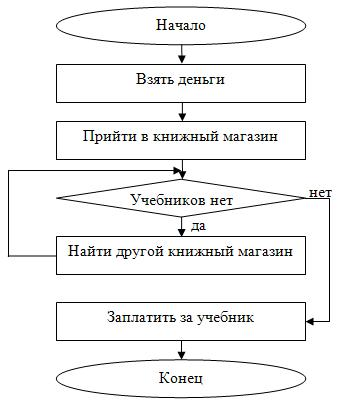
Пример 8. Ученику требуется купить учебник. Составить блок-схему, описывающую действия ученика в случае, если учебника нет в ряде магазинов.
Решение. Действия ученика в данном примере очевидны: когда он приходит в первый и любой последующий магазины, то возможны два варианта – учебник имеется в наличии или учебника нет в продаже. Если учебника нет в продаже, то ученику следует пойти в другой книжный магазин и спросить данный учебник, и т.д. пока учебник не будет куплен, т.к. перед учеником стоит конечная цель – купить учебник. Мы будем использовать цикл с предусловием, т.к. сначала требуется найти магазин, имеющий в наличии данный учебник. Цикл будет выполняться, пока условие «В данном магазине нет учебника» будет верным, а выход из цикла осуществится, когда условие станет ложным, т.е. когда ученик придет в магазин, в котором есть данный учебник. Действительно, в этом случае ученик купит нужный ему учебник и не будет больше искать книжные магазины. Результат блок-схемы представлен на рис. 2.12.
Рис.
2.12.
Блок-схема для примера 8
Здесь тело цикла состоит из одного действия «Найти другой книжный магазин». Переменной цикла в явном виде нет, но можно подразумевать номер магазина, в который пришел ученик в очередной раз. Как любой другой цикл с предусловием, данный цикл может ни разу не выполниться (не иметь итераций), если в первом же магазине окажется нужный учебник.
Примечание. Если в данную задачу добавить условие выбора учебника в жесткой или мягкой обложке, как в примере 5, то оно появится после выхода из цикла. На реализацию циклического алгоритма данное условие не повлияет.
Пример 9. Даны числа 

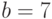






Решение. В отличие от примеров 3 и 6 здесь число 






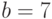
Рис.
2.13.
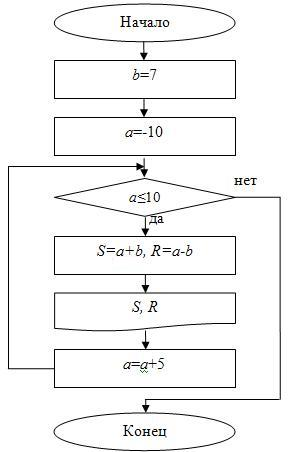
Блок-схема для примера 9 (с предусловием)
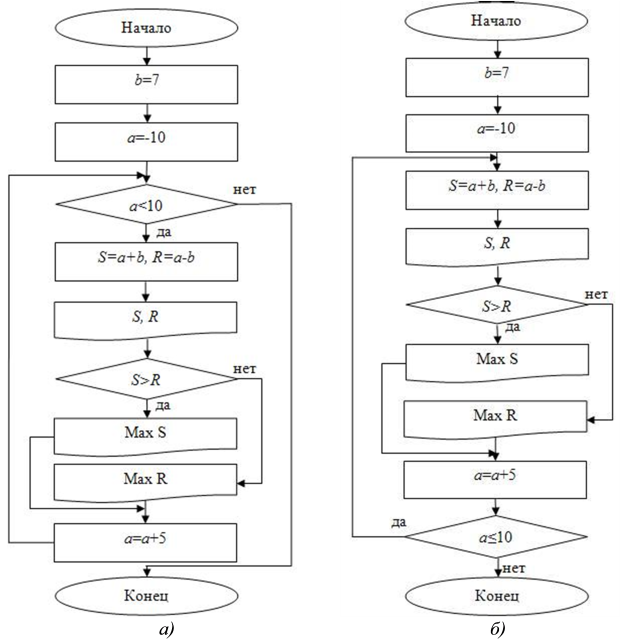
Тело цикла состоит из нескольких действий: вычисление суммы, вычисление разности и вывод полученных данных на экран. Таким образом, у нас получится несколько значений сумм и разностей, т.к. 

Данная задача может быть сделана и с циклом с предусловием, и с постусловием. В этом случае тело цикла, условие и изменение переменной цикла будут такими же, как и в цикле с предусловием, но сначала необходимо выполнить тело цикла, а потом проверить условие для выполнения следующей итерации.
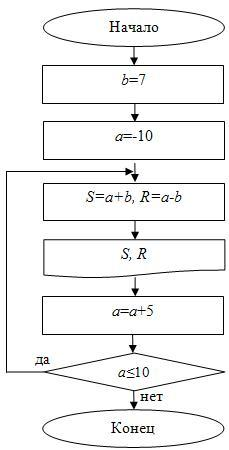
Приведем блок-схему, использующую цикл с постусловием, на рис. 2.14.
Рис.
2.14.
Блок-схема для примера 9 (с постусловием)
В данной задаче также могут быть соединены циклический и разветвляющийся алгоритмы, если по условию задачи требуется сравнить полученные значения суммы и разности, как в примере 6. В этом случае цикл можно реализовать как с предусловием, так и с постусловием, а сравнение суммы и разности добавится внутрь тела цикла, т.к. следует сравнить между собой все полученные суммы и разности. Организация самого цикла останется прежней. Приведем на рис. 2.15а блок-схему с предусловием, а на рис. 2.15б блок-схему с постусловием.
Рис.
2.15.
Блок-схема с ветвлением для примера 9: а) с предусловием, б) с постусловием
ЛЕКЦИЯ
№ 2. Алгоритмы циклической структуры.
Цель лекции:
Приобретение навыков
построения алгоритмов циклической
структуры.
Базовая
структура цикл. Обеспечивает
многократное выполнение некоторой
совокупности действий, которая называется
телом цикла. Используется при решении
задач табулирования и построения
графиков функций, вычисления сумм и
произведений (конечных и бесконечных),
решения уравнений и т.п. Алгоритмы,
реализующие такие вычисления, называют
циклическими, а повторяющиеся участки
вычислений — циклами. Использование
циклов позволяет выполнять большие
объемы вычислений при помощи компактных
программ. Структура цикл существует в
трех вариантах: цикл с предусловием
(цикл ПОКА), цикл с постусловием (цикл
ДО) и цикл с параметром. На рисунке 10
изображен цикл с предусловием, а на
рисунке 11 – цикл с постусловием, которые
называют условными циклическими
алгоритмами
|
. Рисунок |
Рисунок |
Эти циклы
взаимозаменяемы и обладают некоторыми
отличиями.
-
в цикле с предусловием условие проверяется
до тела цикла, в цикле с постусловием
– после тела цикла; -
в цикле с постусловием тело цикла
выполняется хотя бы один раз, в цикле
с предусловием тело цикла может не
выполниться ни разу; -
в цикле с предусловием проверяется
условие продолжения цикла, в цикле с
постусловием – условие выхода из цикла.
При написании условных циклических
алгоритмов следует помнить следующее.
Во-первых, чтобы цикл имел шанс когда-нибудь
закончиться, содержимое его тела должно
обязательно влиять на условие цикла.
Во-вторых, условие должно состоять из
корректных выражений и значений,
определенных еще до первого выполнения
тела цикла.
Кроме того, существует безусловный
циклический алгоритм (рисунок 2.3),
который удобно использовать, если
известно, сколько раз необходимо
выполнить тело цикла.
|
Рисунок |
Типичным примером такого алгоритма
является алгоритм решения задачи
табулирования функции одной переменной.
Пример. Вычислить значения функции
у = f(x) некоторой переменной х,
изменяющейся от начального значения
хо до конечного xk
с постоянным шагом h. Эта задача
реализуется с помощью цикла с заданным
количеством повторений, которое
определяется как n
=mod((xk—xo)/h)+1.
Процедура вычислений сводится к
следующему: вычисляется значение у
для начального значения x,
равного x0.
Затем х увеличивается на значение
шага h, и для него вычисляется значение
у. Последний этап повторяется до
тех пор, пока х не превысит конечного
значения xk.
(Схема алгоритма решения задачи приведена
на рисунке 2.4). Переменная х
называется параметром цикла. Назначение
блоков 1, 2 и 8 ясно из схемы алгоритма.
В блоке 3 осуществляется подготовка
цикла -присвоение начального значения
хо параметру цикла
х. Блоки 4 и 5 представляют собой тело
цикла, т. е. участок вычислений,
повторяющихся при различных значениях
параметра цикла. В блоке 6 текущее
значение параметра цикла x
увеличивается на значение шага h.
Результат операции х+h присваивается
переменной x, предыдущее
значение х при этом стирается. В
блоке 7 проверяется условие продолжения
цикла. При выполнении условия х<=xk
цикл повторяется, при невыполнении —
повторение цикла прекращается, т. е.
осуществляется выход из цикла.
|
Рисунок |
Рисунок |
C использованием блока
модификации схема алгоритма имеет
вид, приведенный на рисунке 2.5. Блок
модификации 3 помещается в начале цикла
и выполняет те же функции, что и блоки
3, 6, 7 в схеме на рисунке 2.4. Запись х
= xо, xk,
h, помещенная в блоке модификации,
представляет собой заголовок цикла
и предписывает следующие действия:
«Для x, изменяющегося
от x0 до
xk
с шагом h, выполнить операции,
указанные в блоках, следующих за блоком
модификации, и ограниченные линией,
входящей слева в блок модификации».
Выход из цикла обозначается линией
связи, выходящей справа из блока
модификации. Если величины x0,
xk,
h представлены в блоке модификации
константами, например x
= 0,50,1, то при значении шага, равном
единице, его запись можно опустить:
х=0, 50
Оформление схем циклических алгоритмов
с использованием блока модификации
является предпочтительным.
Рассмотрим использование алгоритмов
циклической структуры на конкретных
примерах.
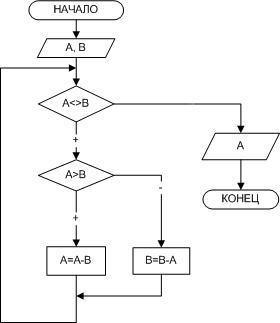
Пример 1. Найти наибольший общий
делитель (НОД) двух натуральных чисел
А и В. Входные данные: А и В. Выходные
данные: А – НОД.
Для решения поставленной задачи
воспользуемся алгоритмом Евклида: будем
уменьшать каждый раз большее из чисел
на величину меньшего до тех пор, пока
оба значения не станут равными.
В блок–схеме решения задачи, представленной
на рис. 2.6, для решения поставленной
задачи используется цикл с предусловием,
то есть тело цикла повторяется до тех
пор, пока А не равно В.
Рисунок
2.6-Поиск наибольшего общего делителя
двух чисел
Рисунок
2.6 — Поиск наибольшего общего делителя
двух чисел
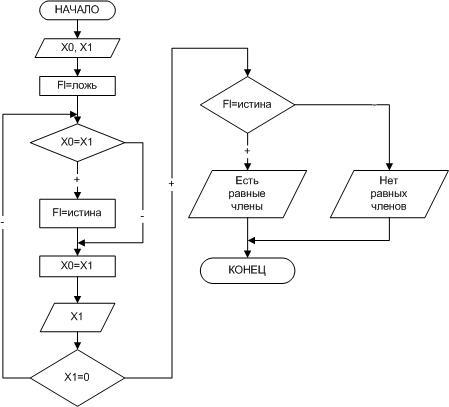
Пример 2. Вводится последовательность
чисел, 0 – конец последовательности.
Определить, содержит ли последовательность
хотя бы два равных соседних числа.
Рисунок
2.7- Поиск равных соседних элементов
последовательности
Входные данные: X0 – текущий
член последовательности, X1 –
следующий член последовательности.
Выходные данные: сообщение о наличии
в последовательности двух равных
соседних элементов.
Вспомогательные переменные: Fl
– логическая переменная, сохраняет
значение «истина», если в последовательности
есть равные рядом стоящие члены и «ложь»
— иначе.
Блок–схема решения задачи приведена
на рисунке. 2.7. Применение здесь цикла
с постусловием обосновано тем, что
необходимо вначале сравнить два
элемента последовательности, а затем
принять решение об окончании цикла.
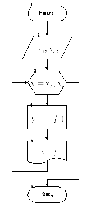
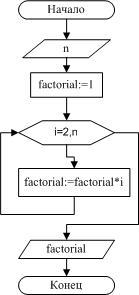
Пример 3.Вычислить факториал числа
N (N!=1*2*3 …*N).
Входные данные: N– целое число, факториал
которого необходимо вычислить.
Выходные данные: factorial– значение
факториала числа N, произведение чисел
от 1 до N, целое число.
Промежуточные данные: i– целочисленная
переменная, принимающая значения от 2
до N с шагом 1, параметр цикла. Блок-схема
приведена на рисунке 2.8.
Рисунок
2.8 — Вычисление факториала
Итак, вводится число N. Переменной
factorial, предназначенной для хранения
значения произведения последовательности
чисел, присваивается начальное значение,
равное единице. Затем организуется
цикл, параметром которого выступает
переменная i. Если значение параметра
цикла меньше или равно N, то выполняется
оператор тела цикла, в котором из участка
памяти с именем factorial считывается
предыдущее значение произведения,
умножается на текущее значение параметра
цикла, а результат снова помещается
участок памяти с именем factorial. Когда
параметр i становится больше N, цикл
заканчивается, и на печать выводится
значение переменой factorial, которая была
вычислена в теле цикла.
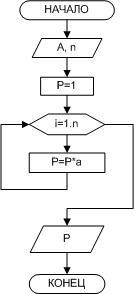
Пример 4.
Вычислить an(n>0).
Входные данные: a – вещественное
число, которое необходимо возвести в
целую положительную степень n.
Выходные данные: p (вещественное
число) – результат возведения вещественного
числа a в целую положительную степень
n.
Рисунок
2.9 — Возведение вещественного числа в
целую степень
Промежуточные данные: i–
целочисленная переменная, принимающая
значения от 1 до n с шагом 1, параметр
цикла. Известно, что для того, чтобы
получить целую степень n числа
a, нужно умножить его само на себя
n раз. Результат этого умножения
будет храниться в участке памяти с
именем p. При выполнении очередного
цикла из этого участка предыдущее
значение будет считываться, умножаться
на основание степени a и снова
записываться в участок памяти p.
Цикл выполняется n раз.
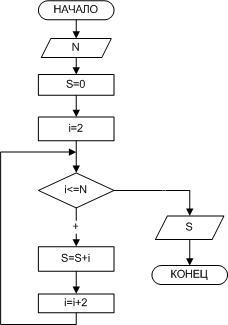
Пример
5.Вычислить
сумму натуральных четных чисел, не
превышающих N.
Входные данные: N – целое число.
Выходные данные: S – сумма четных чисел.
Промежуточные данные: i – переменная,
принимающая значения от 2 до N с шагом
2, следовательно, также имеет целочисленное
значение.
Рисунок
2.10 — Вычисление суммы четных, натуральных
чисел
При сложении нескольких чисел
необходимо накапливать результат
в определенном участке памяти, каждый
раз считывая из этого участка предыдущее
значение суммы и прибавляя к нему
следующее слагаемое. Для выполнения
первого оператора накапливания
суммы из участка памяти необходимо
взять такое число, которое не влияло
бы на результат сложения. Т.е. перед
началом цикла переменной, предназначенной
для накапливания суммы, необходимо
присвоить значение нуль.
Пример 6. Дано натуральное число
N. Определить К – количество делителей
этого числа, не превышающих его (N=12, его
делители 1, 2, 3, 4, 6, K=5).
Входные данные: N – целое число.
Выходные данные: целое число K – количество
делителей N.
Промежуточные данные: i – параметр
цикла, возможные делители числа N.
Рисунок
2.11 — Определение количества делителей
натурального числа
В блок-схеме, изображенной на
рисунке 2.11, реализован следующий
алгоритм: в переменную K, предназначенную
для подсчета количества делителей
заданного числа, помещается значение,
которое не влияло бы на результат, т.е.
нуль. Далее организовывается цикл, в
котором изменяющийся параметр i
выполняет роль возможных делителей
числа N. Если заданное число делится
нацело на параметр цикла, это означает,
что i является делителем N, и значение
переменной K следует увеличить на
единицу. Цикл необходимо повторить N/2
раз.
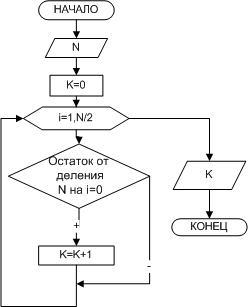
Пример 7.Дано натуральное число N.
Определить, является ли оно простым.
Натуральное число N называется простым,
если оно делится нацело без остатка
только на единицу и N. Число 13 – простое,
так как делится только на 1 и 13, N=12 не
является простым, так как делится на 1,
2, 3, 4, 6 и 12.
Входные данные: N – целое число. Выходные
данные: сообщение.
Промежуточные данные: i – параметр
цикла, возможные делители числа N.
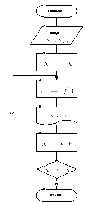
Рисунок 2.12 —
Определение простого числа
Алгоритм решения этой задачи (рисунок
2.12) заключается в том, что число N делится
на параметр цикла i, изменяющийся
в диапазоне от 2 до N/2. Если среди
значений параметра не найдется ни
одного числа, делящего заданное
число нацело, то N – простое число, иначе
оно таковым не является. Обратите
внимание на то, что в алгоритме
предусмотрено два выхода из цикла.
Первый естественный, при исчерпании
всех значений параметра, а второй —
досрочный. Нет смысла продолжать
цикл, если будет найден хотя бы один
делитель из указанной области изменения
параметра.
Пример 8. Вычислить значения
функции
используя рекуррентную
(k=1,2,3,…) формулу. Вычисления
прекратить при выполнении условия
Определить количество итераций.
Начальные значения параметров равны
U1=1; x=5.5; точность ε принять
равной 10-4.
Входные данные: U – начальное приближение,
х, E – точность (ε).
Выходные данные: y — значение вычисленной
функции, k — количество итераций.
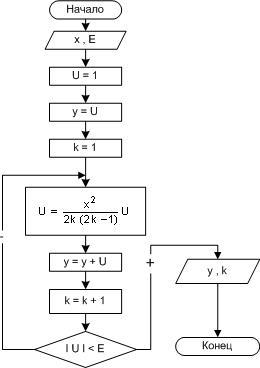
Рисунок
2.13 — Вычисление суммы значений функции
с заданной точностью
Пример 9. Дано натуральное число N.
Определить самую большую цифру и ее
позицию в числе (N=573863, наибольшей
является цифра 8, ее позиция –
четвертая слева).
Входные данные: N – целое число.
Выходные данные: max – значение наибольшей
цифры в числе, pos – позиция этой цифры
в числе.
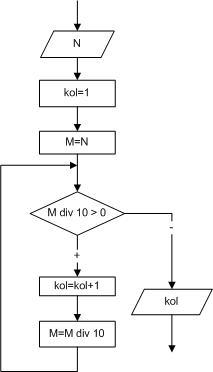
Рисунок 2.14 —
Определение количества цифр в числе
Промежуточные данные: i – параметр
цикла, kol – количество цифр в числе, M –
переменная для временного хранения
значения N.
Рисунок2.15
— Определение максимальной цифры в
числе и ее позиции
Разобьем решение этой задачи на два
этапа. Вначале найдем количество цифр
в заданном числе (рисунок 2.14), а затем
определим наибольшую цифру и ее позицию
(рисунок 2.15). Для того, чтобы подсчитать
количество цифр в числе, необходимо
определить, сколько раз заданное
число можно разделить на десять
нацело. Если цифры числа известны,
определить наибольшую из них не
составит труда. Алгоритм поиска
максимального значения в некоторой
последовательности цифр заключается
в следующем. В ячейку, в которой будет
храниться максимальный элемент (max),
записывают значение, меньшее любого из
элементов последовательности (в нашем
случае max=-1, так как цифры числа находятся
в диапазоне от 0 до 9). Затем сравнивают
элементы последовательности со
значением ячейки max, если найдется
элемент, превышающий значение
предполагаемого максимума, то ячейке
max необходимо присвоить значение
этого элемента и, соответственно,
запомнить его номер в последовательности
(в нашем случае переменной pos присваивается
значение параметра цикла i).
В алгоритме поиска минимума вначале
в переменную min записываем значение,
заранее большее любого элемента
последовательности. Затем все элементы
последовательности сравниваем с
min, если встретится значение меньшее,
чем min, переписываем его в переменную
min
Задания по циклическим алгоритмам
Вариант 1
1.
Hе используя стандаpтные функции (за
исключением abs), вычислить сумму
следующего pяда с заданной точностью
Е>0 (Е вводится с клавиатуры):
2.
Даны целые числа K и N (N >
0). Вывести N раз число K.
3. Даны положительные
числа A и B (A > B). На
отрезке длины A размещено максимально
возможное количество отрезков длины B
(без наложений). Не используя операции
умножения и деления, найти длину незанятой
части отрезка A.
Вариант 2
1.
Hе используя стандаpтные функции,
вычислить сумму n первых членов следующего
pяда (n вводится с клавиатуры):
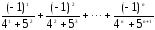
2. Даны два целых числа
A и B (A < B). Вывести в
порядке возрастания все целые числа,
расположенные между A и B (включая
сами числа A и B), а также количество
N этих чисел.
3. Даны положительные
числа A и B (A > B). На
отрезке длины A размещено максимально
возможное количество отрезков длины B
(без наложений). Не используя операции
умножения и деления, найти количество
отрезков B, размещенных на отрезке
A.
Вариант 3
1
Дано действительное число х. Hе
используя стандаpтные функции (за
исключением abs),вычислить сумму следующего
pяда с заданной точностью Е>0 (Е, x
вводятся с клавиатуры):
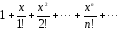
2.
Даны два целых числа A и B (A
< B). Вывести в порядке убывания все
целые числа, расположенные между A
и B (не включая числа A и B), а
также количество N этих чисел.
3. Даны целые положительные
числа N и K. Используя только
операции сложения и вычитания, найти
частное от деления нацело N на K,
а также остаток от этого деления.
Вариант 4
1.
Дано действительное число х. Hе
используя стандаpтные функции, вычислить
сумму n первых членов следующего pяда
(n, х вводятся с клавиатуры):

2. Дано вещественное
число — цена 1 кг конфет. Вывести стоимость
1, 2, … , 10 кг конфет.
3. Дано целое число N
(> 0). Если оно является степенью числа
3, то вывести True, если не является —
вывести False.
Вариант 5
1
Дано действительное число х. Hе
используя стандаpтные функции (за
исключением abs), вычислить сумму следующего
pяда с заданной точностью Е>0 (Е, x
вводятся с клавиатуры):
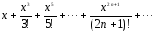
2.
Дано вещественное число — цена 1 кг
конфет. Вывести стоимость 0.1, 0.2, … , 1 кг
конфет.
3. Дано целое число N
(> 0), являющееся некоторой степенью
числа 2: N = 2K. Найти целое
число K — показатель этой степени.
Вариант 6
1.
Дано действительное число х. Hе
используя стандаpтные функции, вычислить
сумму n первых членов следующего pяда
(n, х вводятся с клавиатуры):
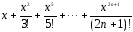
2. Дано вещественное
число — цена 1 кг конфет. Вывести стоимость
1.2, 1.4, … , 2 кг конфет.
3. Дано целое число N
(> 0). Найти наименьшее целое положительное
число K, квадрат которого превосходит
N: K2 > N. Функцию
извлечения квадратного корня не
использовать.
Вариант 7
1
Дано действительное число х. Hе
используя стандаpтные функции (за
исключением abs), вычислить сумму следующего
pяда с заданной точностью Е>0 (Е, x
вводятся с клавиатуры):
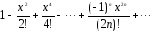
.2.
Даны два целых числа A и B (A
< B). Найти сумму всех целых чисел
от A до B включительно.
3. Дано целое число N
(> 0). Найти наибольшее целое число K,
квадрат которого не превосходит N:
K2 N.
Функцию извлечения квадратного корня
не использовать.
Вариант 8
1.
Дано действительное число х. Hе
используя стандаpтные функции, вычислить
сумму n первых членов следующего pяда
(n, х вводятся с клавиатуры):

2. Даны два целых числа
A и B (A < B). Найти
произведение всех целых чисел от A
до B включительно.
3. Дано целое число N
(> 1). Найти наименьшее целое число K,
при котором выполняется неравенство
3K > N.
Вариант 9
1.
Hе используя стандаpтные функции,
вычислить сумму n первых членов следующего
pяда (n вводится с клавиатуры):

2. Даны два целых числа
A и B (A < B). Найти сумму
квадратов всех целых чисел от A до
B включительно.
3. Дано целое число N
(> 1). Найти наибольшее целое число K,
при котором выполняется неравенство
3K < N.
Вариант 10
1.
Дано натуральное число. Получить число,
получаемое при прочтении его цифр справа
налево.
2.
Дано натуральное число n и
действительное число а. Вычислить n
первых членов следующего pяда (n, a вводится
с клавиатуры):

3. Начальный вклад в
банке равен 1000 руб. Через каждый месяц
размер вклада увеличивается на P
процентов от имеющейся суммы (P —
вещественное число, 0 < P < 25). По
данному P определить, через сколько
месяцев размер вклада превысит 1100 руб.,
и вывести найденное количество месяцев
K (целое число) и итоговый размер
вклада S (вещественное число).
Вариант 11
1.
Дано действительное число a.
Вычислить сумму следующего pяда с
заданной точностью Е>0 (Е, a вводятся
с клавиатуры):
.
2. Дано целое число N
(> 0). Найти сумму
N2 + (N + 1)2 + (N + 2)2
+ … + (2·N)2
(целое число).
3. Даны положительные
числа A, B, C. На прямоугольнике
размера A B
размещено максимально возможное
количество квадратов со стороной C
(без наложений). Найти количество
квадратов, размещенных на прямоугольнике.
Вариант 12
-
Hе используя стандаpтные функции (за
исключением abs), вычислить сумму
следующего pяда с заданной точностью
Е>0 (Е вводится с клавиатуры):.
2. Дано целое число N
(> 0). Найти квадрат данного числа,
используя для его вычисления следующую
формулу:
N2 = 1 + 3 + 5 + … + (2·N – 1).
После добавления к сумме каждого
слагаемого выводить текущее значение
суммы (в результате будут выведены
квадраты всех целых чисел от 1 до N).
3.
Найти 10 первых натуральных чисел,
оканчивающихся на цифру «7», кратных
числу 9 и больших 100.
Вариант 13
1.
Hе используя стандаpтные функции,
вычислить сумму n первых членов следующего
pяда (n вводится с клавиатуры):.
.
2. Дано вещественное
число A и целое число N (> 0).
Используя один цикл, вывести все целые
степени числа A от 1 до N.
3. Дано целое число N
(> 0). С помощью операций деления нацело
и взятия остатка от деления определить,
имеются ли в записи числа N нечетные
цифры. Если имеются, то вывести True, если
нет — вывести False.
Вариант 14
1.
Hе используя стандаpтные функции
(за исключением abs), вычислить сумму
следующего pяда с заданной точностью
Е>0 (Е вводится с клавиатуры):.
2. Дано вещественное
число A и целое число N (> 0).
Используя один цикл, найти сумму
1 + A + A2 + A3 + … +
AN.
3. Дано целое число N
(> 0). Используя операции деления нацело
и взятия остатка от деления, вывести
все его цифры, начиная с самой правой
(разряда единиц).
Вариант 15
-
Hе используя стандаpтные функции,
вычислить сумму n первых членов следующего
pяда (n вводится с клавиатуры):.
2.
Дано вещественное число A и целое
число N (> 0). Найти A в степени
N:
AN = A·A· … ·A
(числа A перемножаются N раз).
3. Дано целое число N
(> 1). Если оно является простым, то
есть не имеет положительных делителей,
кроме 1 и самого себя, то вывести True,
иначе вывести False.
Вариант 16
1.
Дано действительное число x. Hе
используя стандаpтные функции (за
исключением abs и sin), вычислить сумму
следующего pяда с заданной точностью
Е>0 (Е,x вводятся с клавиатуры):.
.
2. Дано вещественное
число A и целое число N (> 0).
Используя один цикл, найти значение
выражения
1 – A + A2 – A3 + …
+ (–1)N·AN.
Условный оператор не использовать.
3. Спортсмен-лыжник
начал тренировки, пробежав в первый
день 10 км. Каждый следующий день он
увеличивал длину пробега на P
процентов от пробега предыдущего дня
(P — вещественное, 0 < P < 50). По
данному P определить, после какого
дня суммарный пробег лыжника за все дни
превысит 200 км, и вывести найденное
количество дней K (целое) и суммарный
пробег S (вещественное число).
Вариант 17
1.
Дано действительное число x. Hе
используя стандаpтные функции (за
исключением abs и sin), вычислить сумму n
первых слагаемых следующего pяда (x
вводятся с клавиатуры): .
.
2. Дана последовательность целых чисел,
оканчивающаяся числом 9999. Количество
чисел в последовательности не меньше
двух. Определить, есть ли в ней хотя бы
одна пара «соседних» четных чисел. В
случае положительного ответа определить
их порядковые номера.
3.
Дано целое число N (> 0). С помощью
операций деления нацело и взятия остатка
от деления определить, имеется ли в
записи числа N цифра «2». Если имеется,
то вывести True, если нет — вывести False.
Вариант 18
1. Дано действительное число x. Hе используя
стандаpтные функции (за исключением abs
и cos), вычислить сумму следующего pяда с
заданной точностью Е>0 (Е,x вводятся с
клавиатуры):.
2. Дано целое число N
(> 1) и две вещественные точки на числовой
оси: A, B (A < B). Отрезок
[A, B] разбит на N равных
отрезков. Вывести H — длину каждого
отрезка, а также набор точек
3.
Дано натуральное число. Выяснить,
является ли оно простым (простым
называется натуральное число, большее
1, не имеющее других делителей, кроме
единицы и самого себя).
Вариант 19
1. Дано действительное число x. Hе используя
стандаpтные функции (за исключением abs
и cos), вычислить сумму n первых слагаемых
следующего pяда (x вводятся с клавиатуры):
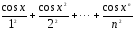
.
2. Дано целое число N
(> 0). Используя операции деления нацело
и взятия остатка от деления, найти
количество и сумму его цифр.
3.
Имеется список учащихся класса с
указанием роста каждого из них. Выяснить,
перечислены ли ученики в списке в порядке
убывания их роста.
Вариант 20
1.
Дано натуральное число. Выяснить,
является ли оно палиндромом («перевертышем»),
т.е. числом, десятичная запись которого
читается одинаково слева направо и
справа налево
2. Hе используя
cтандаpтные функции, вычислить сумму n
первых членов следующего pяда (n вводится
с клавиатуры):
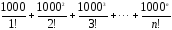
3. Дана последовательность ненулевых
целых чисел, оканчивающаяся нулем.
Определить, сколько раз в этой
последовательности меняется знак.
(Например, в последовательности 10, –4,
12, 56, –4 знак меняется 3 раза.)