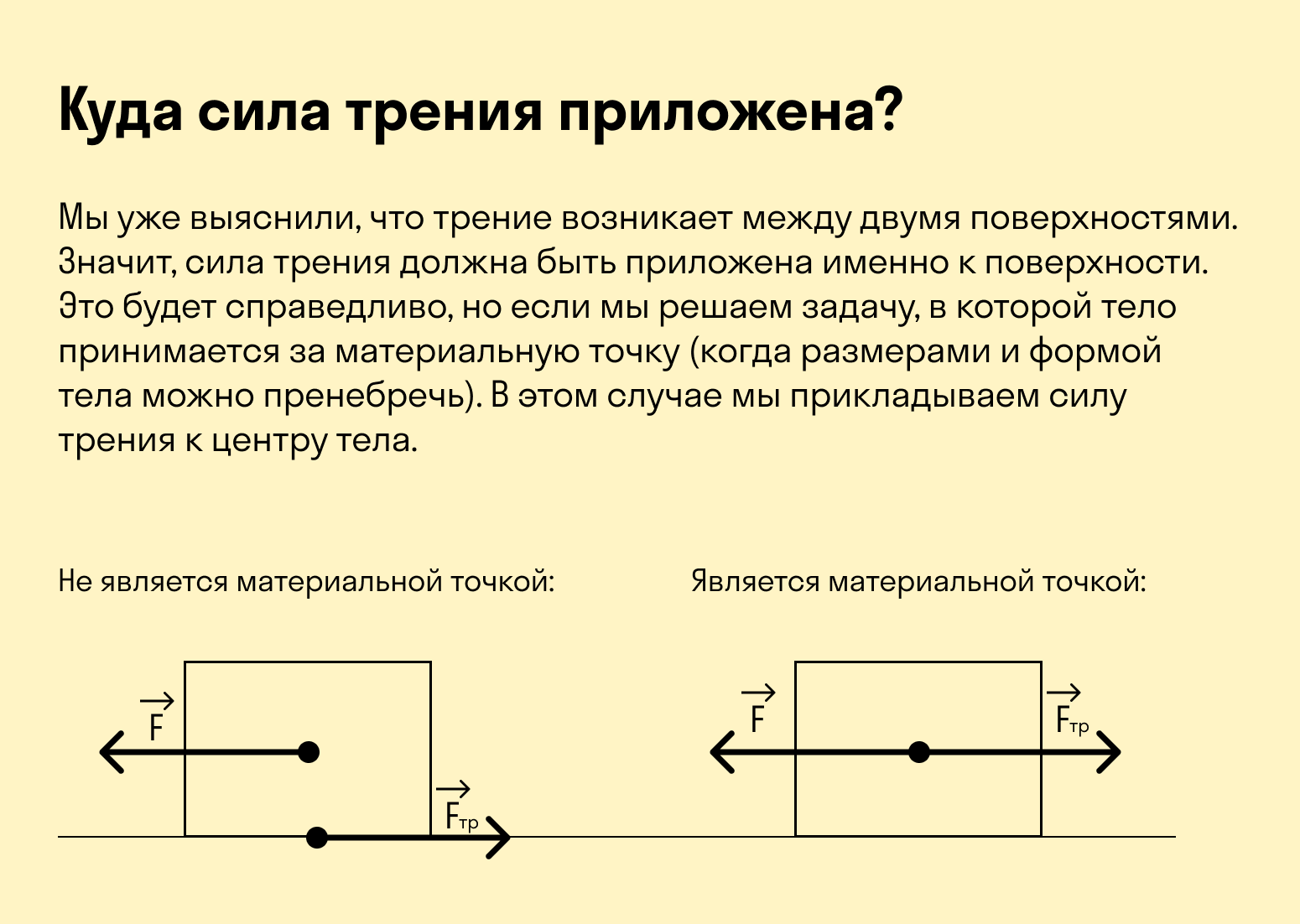
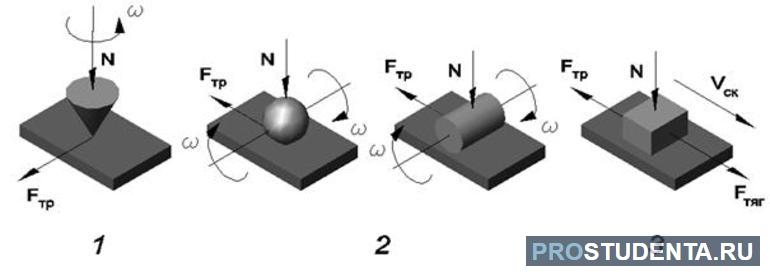
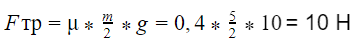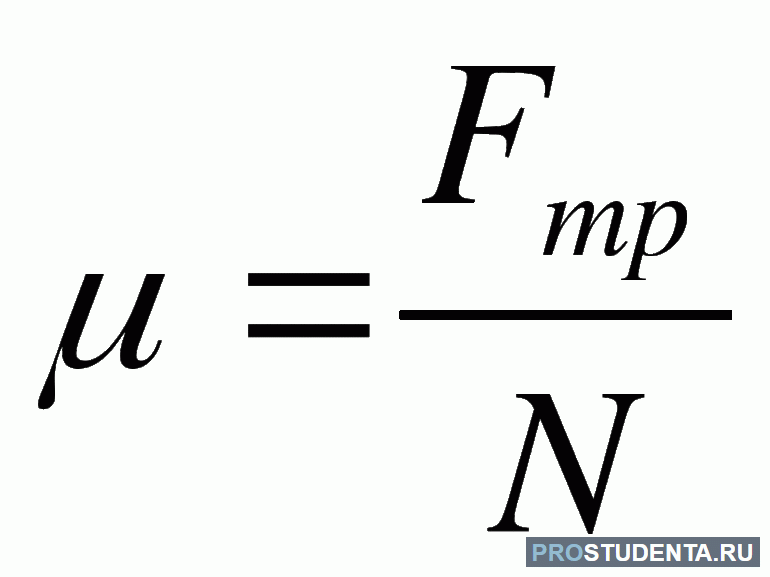Сила трения: величина, направление
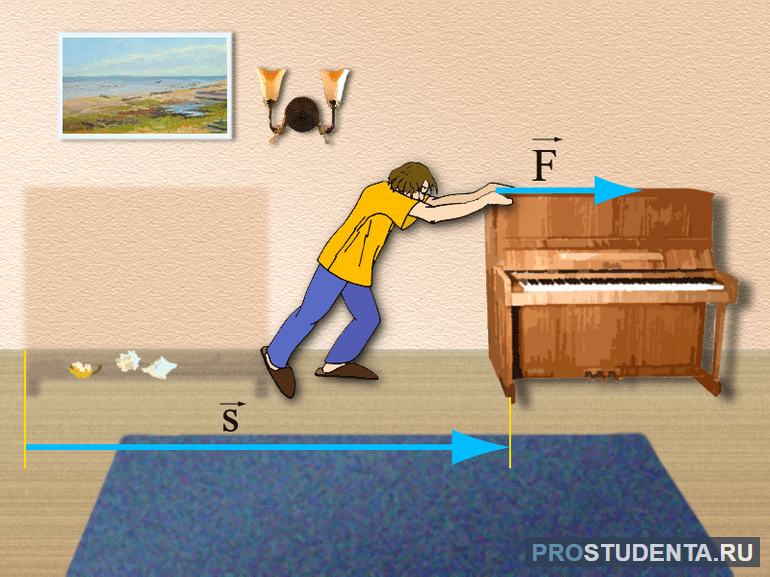
С силой трения вы сталкиваетесь буквально каждую секунду. Каждый раз, когда вы взаимодействуете с любой поверхностью — идете по асфальту, сидите на стуле, пьете чай из чашки — на вас действует сила трения.
Трение — это и есть взаимодействие в плоскости соприкосновения двух поверхностей.
Чтобы перевести трение на язык физики, вводится понятие сила трения.
Сила трения — это величина, которая характеризует процесс трения по величине и направлению.
Измеряется сила трения, как и любая сила — в Ньютонах.
Возникает сила трения по двум причинам:
- Различные шероховатости, царапины и прочие «несовершенства» поверхностей. Эти дефекты задевают друг друга при соприкосновении и создается сила, тормозящая движение.
- Когда контактирующие поверхности практически гладкие (до идеала довести невозможно, но стремиться к нему — значит устремлять силу трения к нулю), то расстояние между ними становится минимальным. В этом случае возникает взаимное притяжение молекул вещества этих поверхностей. Притяжение обусловлено взаимодействием между электрическими зарядами атомов. В связи с этим можно часто услышать формулировку «Сила трения — сила электромагнитной природы»
Направлена сила трения всегда против скорости тела. В этом плане все просто, но всегда есть вопрос:
В задачах часто пишут что-то вроде: «Поверхность считать идеально гладкой». Это значит, что сила трения в данной задаче отсутствует. Да, в реальной жизни это невозможно, но во имя красивой математической модели трением часто пренебрегают.
Не переживайте из-за этой несправедливости, а просто решайте задачи без трения, если увидели словосочетание «гладкая поверхность».
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Пятерка по физике у тебя в кармане!
Решай домашку по физике на изи. Подробные решения помогут разобраться в сложной теме и получить пятерку!
Сухое и вязкое трение
Есть очень большая разница между вашим соприкосновением с водой в бассейне во время плавания и соприкосновением между асфальтом и колесами вашего велосипеда.
В случае с плаванием мы имеем дело с вязким трением — явлением сопротивления при движении твердого тела в жидкости или воздухе. Самолет тоже подвергается вязкому трению и вон тот наглый голубь из вашего двора.
А вот сухое трение — это явление сопротивления при соприкосновении двух твердых тел. Например, если школьник ерзает на стуле или злодей из фильма потирает ладоши — это будет сухое трение.
А если злодей чистоплотный и потирает ладоши, капнув на них антисептик?
Тогда это вязкое трение, не смотря на то, что руки — твердые тела. В данном случае есть влажная прослойка.
Вязкое трение в школьном курсе физики не рассматривается подробно, а вот сухое — разбирают вдоль и поперек. У сухого трения также есть разновидности, давайте о них поговорим.
Трение покоя
Если вы решите сдвинуть с места грузовик, вряд ли у вас это получится. Не то, чтобы мы в вас не верим — просто это невозможно сделать из-за того, что масса человека во много раз меньше массы грузовика, да еще и сила трения мешает это сделать. Мир жесток, что тут поделать.
В случае, когда сила трения есть, но тело не двигается с места, мы имеем дело с силой трения покоя.
Сила трения покоя равна силе тяги. Например, если вы пытаетесь сдвинуть с места санки, действуя на них с силой тяги 10 Н, то сила трения будет равна 10 Н.
Сила трения покоя
Fтр = Fтяги
Fтр — сила трения покоя [Н]
Fтяги — сила тяги [Н]
Немного потренируемся!
Задача
Найти силу трения покоя для тела, на которое действуют сила тяги в 4 Н.
Решение:
Тело покоится, значит
Fтр = Fтяги = 4 Н
Ответ: сила трения равна 4 Н.
Трение скольжения
А теперь давайте скользить на коньках по льду. Каток достаточно гладкий, но, как мы уже выяснили, сила трения все равно будет присутствовать и вычисляться будет по формуле:
Сила трения скольжения
Fтр = μN
Fтр — сила трения скольжения [Н]
μ — коэффициент трения [—]
N — сила реакции опоры [Н]
Сила трения, которую мы получим по этой формуле будет максимально возможной — то есть больше уже некуда.
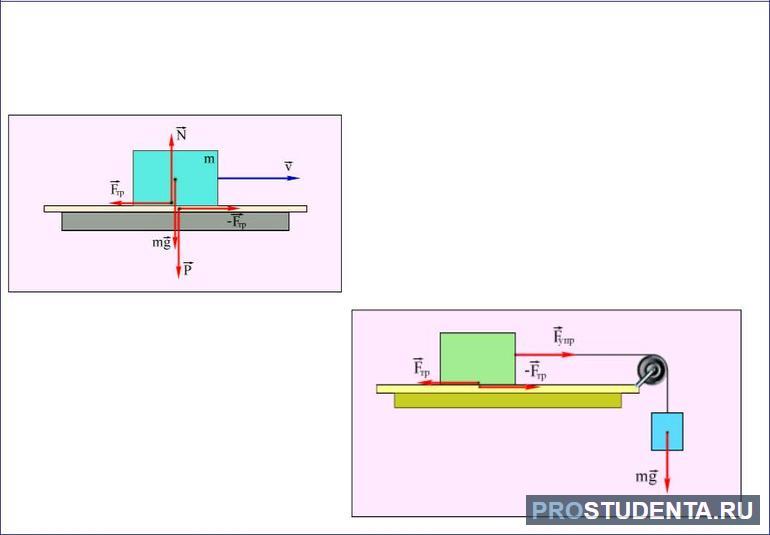
Сила реакции опоры — это сила, с которой опора действует на тело. Она численно равна силе нормального давления и противоположна по направлению.
Сила нормального давления — это то же самое, что и вес тела?
Не совсем. Сила нормального давления направлена всегда перпендикулярно поверхности (нормаль — перпендикуляр к поверхности). Вес не обязательно направлен перпендикулярно поверхности.
В рамках школьного курса вес всегда направлен перпендикулярно поверхности, поэтому силу реакции опоры можно численно приравнивать к весу.
Подробнее про вес тела читайте в нашей статье😇
Также, если тело находится на горизонтальной поверхности, сила реакции опоры будет равна силе тяжести: N = mg.
Коэффициент трения — это характеристика поверхности. Он определяется экспериментально, не имеет размерности и показывает, насколько поверхность гладкая — чем больше коэффициент, тем более шероховатая поверхность. Коэффициент трения положителен и чаще всего меньше единицы.
Будем бдительны!
Из формулы не следует зависимость силы трения от площади соприкосновения. Например, если вы положите брусок на один бок и протащите по столу, а потом перевернете на другой, не равный по площади, и сделаете то же самое — сила трения не изменится.
Задача 1
Масса котика, лежащего на столе, составляет 5 кг. Коэффициент трения µ = 0,2. К коту прилагают внешнюю силу, равную 2,5 Н. Какая сила трения при этом возникает?
Решение:
По условию данной задачи невозможно понять, двигается наш котик или нет. Решение о том, приравниваем ли мы к силе тяги силу трения, принять сразу нельзя. В таких случаях нужно все-таки рассчитать по формуле:
F = μN
Так как котик лежит на горизонтальной поверхности, сила реакции опоры в данном случае равна силе тяжести: N = mg.
F = μmg = 0,2 · 5 · 10 = 10Н
Мы получили максимально возможную силу трения. Внешняя сила по условию задачи меньше максимальной. Это значит, что котик находится в покое. Сила трения уравновешивает внешнюю силу. Следовательно, она равняется 2,5 Н.
Ответ: возникает сила трения величиной 2,5 Н
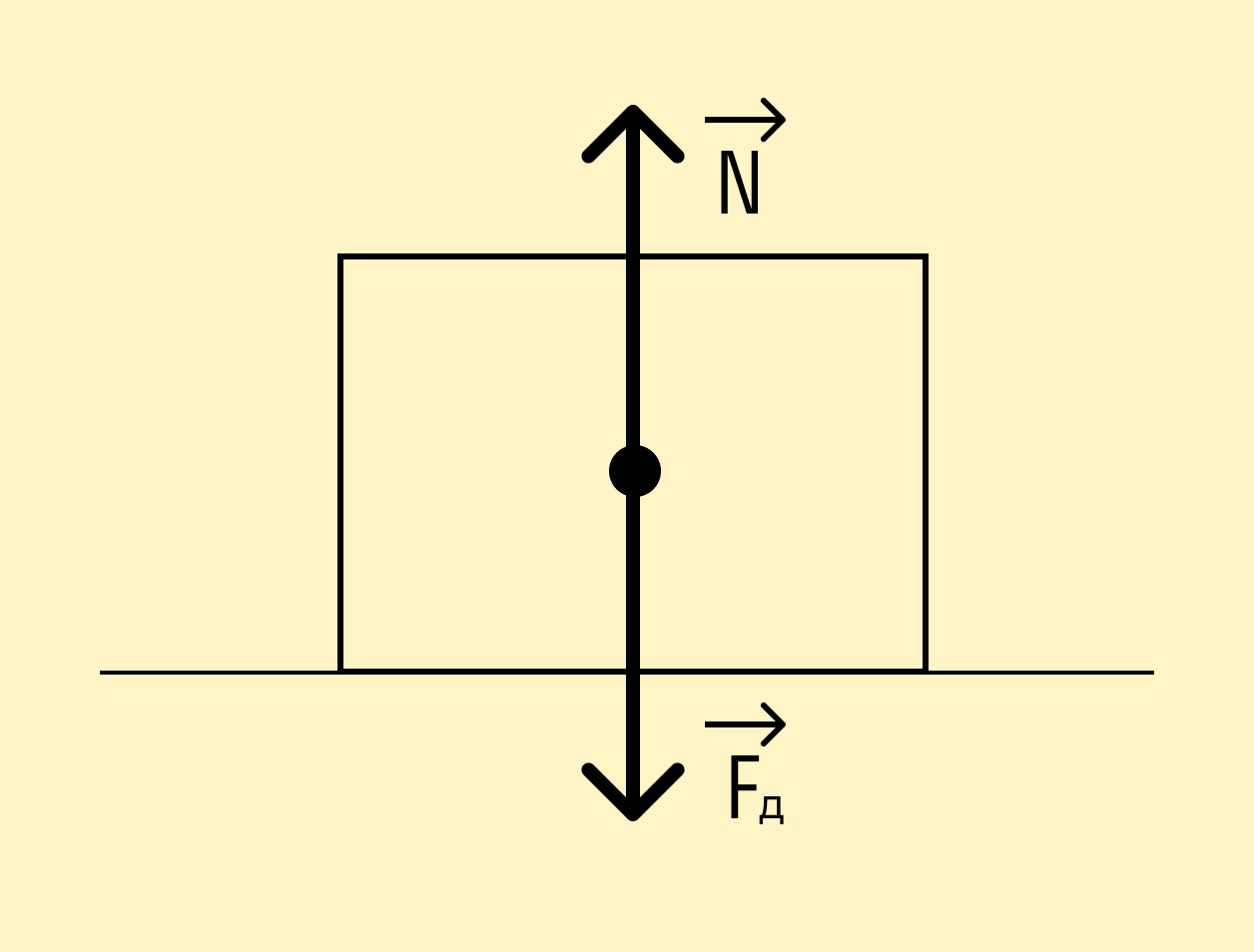
Задача 2
Барсук скользит по горизонтальной плоскости. Найти коэффициент трения, если сила трения равна 5 Н, а сила давления тела на плоскость — 20 Н.
Решение:
В данной задаче нам известно, что барсучок скользит. Значит нужно воспользоваться формулой:
Fтр = μN
Так как барсук находится на горизонтальной поверхности, сила реакции опоры в данном случае равна силе давления на плоскость: N = Fд.
Fтр = μFд
Выражаем коэффициент трения:
μ = Fтр / Fд = 5 / 20 = 0,25
Ответ: коэффициент трения равен 0,25
Задача 3
Пудель вашей бабушки массой 5 кг скользит по горизонтальной поверхности. Сила трения скольжения равна 20 Н. Найдите силу трения, если пудель сильно похудеет, и его масса уменьшится в два раза, а коэффициент трения останется неизменным.
Решение:
В данной задаче нам известно, что пудель скользит. Значит, нужно воспользоваться формулой:
Fтр = μN
Так как пудель находится на горизонтальной поверхности, сила реакции опоры в данном случае равна силе тяжести: N = mg.
Fтр = μmg
Выразим коэффициент трения:
μ = Fтр / mg = 20 / 5 · 10 = 0,4
Теперь рассчитаем силу трения для массы, меньшей в два раза:
Ответ: сила трения будет равна 10 Н.
Задача 4
Ученик провел эксперимент по изучению силы трения скольжения, перемещая брусок с грузами равномерно по горизонтальным поверхностям с помощью динамометра.
Результаты экспериментальных измерений массы бруска с грузами m, площади соприкосновения бруска и поверхности S и приложенной силы F представлены в таблице.
Какие утверждения соответствуют результатам проведенных экспериментальных измерений? Из предложенного перечня утверждений выберите два правильных.
-
Коэффициенты трения скольжения во втором и третьем опытах равны.
-
Коэффициент трения скольжения между бруском и деревянной рейкой больше коэффициента трения скольжения между бруском и пластиковой рейкой.
-
Сила трения скольжения зависит от площади соприкосновения бруска и поверхности.
-
Сила трения скольжения зависит от рода соприкасающейся поверхности.
Решение:
Подробно рассмотрим каждое утверждение.
-
В данном случае сила реакции опоры равна силе тяжести. Значит Fтр = μN = μmg.
Выразим коэффициент трения скольжения:
μ = Fтр / mgКоэффициент трения скольжения во втором опыте равен 0,4 / (0,2 · 10) = 0,2.
В третьем опыте — 0,4 / (0,1 · 10) = 0,4.
Следовательно, утверждение «Коэффициенты трения скольжения во втором и третьем опытах равны» неверно.
-
Как и в первом утверждении, коэффициент трения будет вычисляться по формуле:
μ = Fтр / mgДля деревянной рейки μ = Fтр / mg = 0,8 / 0,2 · 10 = 0,4
Для пластиковой рейки μ = Fтр / mg = 4,8 / 0,2 · 10 = 0,2
Следовательно утверждение «Коэффициент трения скольжения между бруском и деревянной рейкой больше коэффициента трения скольжения между бруском и пластиковой рейкой» верно.
-
Согласно формуле Fтр = μN, сила трения не зависит от площади поверхности соприкосновения. Значит утверждение «Сила трения скольжения зависит от площади соприкосновения бруска и поверхности» неверно.
-
Если проанализировать первый и второй эксперимент, можно увидеть, что при прочих равных данных сила меняется. Это значит, что утверждение «Сила трения скольжения зависит от рода соприкасающейся поверхности» верно.
Ответ: 25
Онлайн-курсы физики в Skysmart не менее увлекательны, чем наши статьи!
Трение качения
Про колесо совершенно точно нельзя сказать, что оно скользит или покоится. При этом сила трения явно возникает, так как существует соприкосновение двух поверхностей.
В этом случае мы говорим о трении качения — сопротивлению движения, если одно тело катится по поверхности другого. При равных силах нормального давления сила трения скольжения больше силы трения качения. Это явление часто используют, например, ставя колесики на чемодан. Да и вообще, ставя колесики куда угодно.
Сила трения качения
Fтр = (λN)/R
Fтр — сила трения качения [Н]
λ — коэффициент трения качения [м]
N — сила реакции опоры [Н]
R — радиус колеса [м]
Задачи на трение качения встречаются только в задачах высокого уровня сложности (например, в олимпиадах). Однако на формулу посмотреть полезно, даже если вы не планируете покорять самую высокую вершину.
Если приглядеться, она очень похожа на формулу трения скольжения, только в знаменателе появляется радиус. Если мы будем увеличивать знаменатель, то сила трения будет уменьшаться. То есть, чем больше радиус колеса, тем меньше трение.
Ладно, давайте все-таки решим задачу на силу трения качения — только никому об этом не рассказывайте 😉
Задача
Какого радиуса понадобится установить колесо, чтобы уменьшить силу трения, равную 17 Н — на 5 Н. При коэффициенте трения 0,6 мм и силе нормального давления тела равной 10 кН.
Решение:
Берем формулу силы трения качения:
Fтр = (λN)/R
Выражаем из нее радиус:
R = (λN)/Fтр
Коэффициент трения качения и сила нормального давления нам даны, а чтобы найти силу трения, нам нужно вычесть из начальной силы трения ее изменение:
Fтр 2 = Fтр 1 − ΔFтр = 17 − 5 = 12Н
Подставляем числа в формулу, предварительно переведя их в СИ:
СИ — международная система единиц. «Перевести в СИ» означает перевод всех величин в метры, килограммы, секунды и другие единицы измерения без приставок. Исключение составляет килограмм с приставкой «кило».
R = (λN)/Fтр = 0,0006 · 10 000 / 12 = 0,5 м
Ответ: необходимо поставить колесо радиусом 0,5 м.
Избавиться от трения: возможно ли это
Итак, идеально гладких поверхностей в реальной жизни не бывает. Это значит, что стараясь делать поверхность идеально гладкой — например, натирая ее миллион часов супер-мелкой наждачной бумагой — мы минимизируем трение, но не избавляемся от него.
Но это не значит, что способов избавиться от трения не существует. Например, вполне себе реальны поезда на магнитных подушках. Благодаря магнитному полю, которое создается между рельсом и вагоном, поезд как будто бы парит. Так он ликвидирует соприкосновение различных поверхностей, из-за которого и создается трение.

{mu = dfrac{F_{тр}}{mg}}
Ускорение свободного падения g
Приводим 2 варианта нахождения коэффициента трения — зная силу трения и массу тела или зная угол наклона. Для обоих вариантов вы найдете удобные калькуляторы и формулы для расчета.
Коэффициент трения представляет собой безразмерную скалярную величину, которая равна отношению силы трения между двумя телами и силы, прижимающей их друг к другу, во время или в начале скольжения.
Коэффициент трения чаще всего обозначают греческой буквой µ («мю»).
Следует помнить, что коэффициент трения (μ) величина безразмерная, то есть не имеет единицы измерения.
Коэффициент трения зависит от качества обработки трущихся поверхностей, скорости движения тел относительно друг друга и материала соприкасающихся поверхностей. В большинстве случаев коэффициент трения находится в пределах от 0,1 до 0,5 (см. таблицу).
Содержание:
- калькулятор коэффициента трения
- формула коэффициента трения через силу трения и массу
- формула коэффициента трения через угол наклона
- таблица коэффициентов трения
- примеры задач
Формула коэффициента трения через силу трения и массу
mu = dfrac{F_{тр}}{mg}
Fтр — сила трения
m — масса тела
g — ускорение свободного падения (в большинстве задач можно принять g=9.81 м/с²)
Формула коэффициента трения через угол наклона
mu = tg(alpha)
α — угол наклона
Таблица коэффициентов трения скольжения для разных пар материалов
| Трущиеся материалы (при сухих поверхностях) | Коэффициенты трения | |
|---|---|---|
| покоя | при движении | |
| Резина по сухому асфальту | 0,95-1,0 | 0,5-0,8 |
| Резина по влажному асфальту | 0,25-0,75 | |
| Алюминий по алюминию | 0,94 | |
| Бронза по бронзе | 0,20 | |
| Бронза по чугуну | 0,21 | |
| Дерево по дереву (в среднем) | 0,65 | 0,33 |
| Дерево по камню | 0,46-0,60 | |
| Дуб по дубу (вдоль волокон) | 0,62 | 0,48 |
| Дуб по дубу (перпендикулярно волокнам) | 0,54 | 0,34 |
| Железо по железу | 0,15 | 0,14 |
| Железо по чугуну | 0,19 | 0,18 |
| Железо по бронзе (слабая смазка) | 0,19 | 0,18 |
| Канат пеньковый по деревянному барабану | 0,40 | |
| Канат пеньковый по железному барабану | 0,25 | |
| Каучук по дереву | 0,80 | 0,55 |
| Каучук по металлу | 0,80 | 0,55 |
| Кирпич по кирпичу (гладко отшлифованные) | 0,5-0,7 | |
| Колесо со стальным бандажем по рельсу | 0,16 | |
| Лед по льду | 0,05-0,1 | 0,028 |
| Метал по аботекстолиту | 0,35-0,50 | |
| Метал по дереву (в среднем) | 0,60 | 0,40 |
| Метал по камню (в среднем) | 0,42-0,50 | |
| Метал по металу (в среднем) | 0,18-0,20 | |
| Медь по чугуну | 0,27 | |
| Олово по свинцу | 2,25 | |
| Полозья деревянные по льду | 0,035 | |
| Полозья обитые железом по льду | 0,02 | |
| Резина (шина) по твердому грунту | 0,40-0,60 | |
| Резина (шина) по чугуну | 0,83 | 0,8 |
| Ремень кожаный по деревянному шкиву | 0,50 | 0,30-0,50 |
| Ремень кожаный по чугунному шкиву | 0,30-0,50 | 0,56 |
| Сталь по железу | 0,19 | |
| Сталь(коньки) по льду | 0,02-0,03 | 0,015 |
| Сталь по райбесту | 0,25-0,45 | |
| Сталь по стали | 0,15-0,25 | 0,09 (ν = 3 м/с)
0,03 (ν = 27 м/с) |
| Сталь по феродо | 0,25-0,45 | |
| Точильный камень (мелкозернистый) по железу | 1 | |
| Точильный камень (мелкозернистый) по стали | 0,94 | |
| Точильный камень (мелкозернистый) по чугуну | 0,72 | |
| Чугун по дубу | 0,65 | 0,30-0,50 |
| Чугун по райбесту | 0,25-0,45 | |
| Чугун по стали | 0,33 | 0,13 (ν = 20 м/с) |
| Чугун по феродо | 0,25-0,45 | |
| Чугун по чугуну | 0,15 |
Примеры задач на нахождение коэффициента трения
Задача 1
Найдите коэффициент трения между полом и ящиком массой 20 кг, который равномерно двигают с силой 50 Н.
Решение
Для решения задачи воспользуемся формулой.
mu = dfrac{F_{тр}}{mg} = dfrac{50}{20 cdot 9.81} = dfrac{50}{196.2} approx 0.25484
Ответ: approx 0.25484
С помощью калькулятора удобно проверить ответ.
Задача 2
Найдите коэффициент трения если угол наклона 30°.
Решение
Для решения этой задачи воспользуемся второй формулой.
mu = tg(alpha) = tg(30°) approx 0.57735
Ответ: approx 0.57735
Проверим полученный ответ с помощью калькулятора .
Сила трения. Коэффициент трения
- Причины возникновения трения
- Трение покоя
- Трение скольжения
- Трение качения
- Задачи
- Лабораторная работа №8. Измерение коэффициента трения скольжения
п.1. Причины возникновения трения
При движении одного тела по поверхности другого всегда возникает сила, направленная противоположно направлению скорости и замедляющая движение. Эта сила называется силой трения.
По своей природе сила трения отличается от силы тяготения и силы упругости, которые были рассмотрены в предыдущих параграфах.
Причины возникновения силы трения можно разделить на два класса: 1) шероховатость поверхностей контактирующих тел; 2) взаимное притяжение молекул при контакте.
Неровности поверхностей проявляются на макроуровне и видны невооруженным глазом или в оптический микроскоп. Их влияние можно уменьшить, если отполировать поверхности или нанести смазку.
Взаимное притяжение молекул проявляется на микроуровне и приводит к тому, что даже на идеально отполированных поверхностях не удается избежать трения, когда частицы одного тела перемещаются относительно частиц другого.
Сила трения – это сумма межмолекулярных сил, возникающих при деформациях и изломах контактирующих поверхностей за счет разрыва межмолекулярных связей.
Сила трения направлена вдоль поверхностей контактирующих тел.
Как и сила упругости, сила трения имеет электромагнитную природу и связана с межмолекулярным взаимодействием.
Но в отличие от силы упругости, причиной силы трения является разрыв межмолекулярных связей. Кроме того, если сила упругости всегда направлена перпендикулярно поверхностям контактирующих тел, то сила трения всегда направлена вдоль этих поверхностей.
В зависимости от характера движения контактирующих тел различают трение покоя, трение скольжения и трение качения.
п.2. Трение покоя
Сила трения, возникающая при относительной скорости двух контактирующих тел равной нулю, называется силой трения покоя.
Сила трения покоя равна по модулю приложенной силе и направлена в сторону, противоположную возможному движению тела, параллельно контактирующим поверхностям.
Если параллельно поверхности контакта на тело не действует сила, сила трения покоя равна нулю. Максимальное значение силы трения, при котором тело все ещё неподвижно, называется максимальной силой трения покоя.
Пример изменения силы трения покоя
 |
Сила трения покоя равна приложенной силе, которая все ещё не приводит тело в движение. Допустим, что мы прикладываем к шкафу последовательно силу 100 Н, 200 Н, 300 Н, и он начинает равномерно двигаться только при 300 Н. Как только тело начинает скользить, на него уже действует сила трения скольжения. Получаем: |
||
| Приложенная сила, Н | Движение | Сила трения покоя, Н | Сила трения скольжения, Н |
| 100 | Нет | 100 | — |
| 200 | Нет | 200 | — |
| 300 | Есть, равномерное | — | 300 |
п.3. Трение скольжения
Силу трения, возникающую в результате движения одного тела по поверхности другого, называют силой трения скольжения.
Сила трения скольжения всегда направлена в сторону, противоположную перемещению тела («тормозит» движение).
 |
Если тело расположено на горизонтальной опоре, сила тяжести (mg), действующая на него, равна по величине силе реакции опоры (N) (см. §22 данного справочника). Сила трения направлена противоположно силе тяги. |
Сила трения скольжения прямо пропорциональна силе реакции опоры: $$ F_{text{тр}}=mu N $$ Коэффициент (mu) называют коэффициентом трения скольжения; величина (mu) зависит от материала трущихся тел и состояния их поверхностей.
Значения коэффициентов трения скольжения для различных поверхностей приводятся в справочных таблицах.
При проектировании и разработке машин и механизмов коэффициенты трения скольжения для отдельных узлов определяются в специальных лабораториях.
п.4. Трение качения
Сила трения, возникающая при качении одного тела по поверхности другого, называется силой трения качения.
Сила трения качения значительно меньше силы трения скольжения.
 |
Уменьшение трения за счет качения используется в шариковых и роликовых подшипниках. Первый подшипник качения был установлен в опоре ветряка, построенного в Англии в 1780 г. Этот подшипник состоял из двух литых чугунных дорожек качения, между которыми находилось 40 чугунных шаров. Сегодня подшипники являются незаменимой деталью во всех подвижных конструкциях; они уменьшают износ трущихся деталей и снижают потери энергии на нагрев из-за трения. |
п.5. Задачи
Задача 1. Найдите коэффициент трения между шинами автомобиля и дорогой, если при равномерном движении по прямолинейному участку двигатель развивает силу тяги, равную 30 кН. Масса автомобиля 6 т.
Дано:
(m=6 text{т}=6cdot 10^3 text{кг})
(F_{text{тяги}}=30 text{кН}=3cdot 10^4 text{Н})
(gapprox 10 text{м/с}^2)
__________________
(mu-?)
Коэффициент трения $$ mu=frac{F_{text{тр}}}{N}. $$ При равномерном движении скорость постоянна и ускорение (overrightarrow{a}=0). По второму закону Ньютона, равнодействующая горизонтальных сил равна нулю $$ overrightarrow{F_{text{тр}}}+ overrightarrow{F_{text{тяги}}}=0. $$ Значит, сила трения и сила тяги равны по модулю: $$ F_{text{тр}}=F_{text{тяги}}. $$ Сила реакции горизонтальной опоры равна силе тяжести, действующей на автомобиль: $$ n=mg. $$ Получаем: $$ mu=frac{F_{text{тр}}}{N}= frac{F_{text{тяги}}}{mg}, mu=frac{3cdot 10^4}{6cdot 10^3cdot 10}=0,5. $$ Ответ: 0,5
Задача 2. Деревянный брусок массой 3 кг равномерно тянут по горизонтальной деревянной доске с помощью динамометра. Жесткость пружины динамометра равна 3 Н/см, коэффициент трения дерева об дерево 0,3. На сколько сантиметров растянется пружина?
Дано:
(m=3 text{кг})
(k=3frac{text{Н}}{text{см}}=frac{3 text{Н}}{0,01 text{м}}=300frac{text{Н}}{text{м}})
(mu=0,3)
(gapprox 10 text{м/с}^2)
__________________
(Delta l-?)
Показания динамометра – это сила упругости, равная силе тяги. При равномерном движении сила тяги равна по модулю силе трения. Поэтому begin{gather*} F_{text{упр}}=kDelta l=F_{text{тр}}=mu N=mu mgRightarrow kDelta l=mu mg end{gather*} Получаем: $$ Delta l=frac{mu mg}{k}, Delta l=frac{0,3cdot 3cdot 10}{300}=0,03 (text{м})=3 (text{см}) $$ Ответ: 3 см.
Задача 3. Автомобиль движется по горизонтальному участку дороги со скоростью 72 км/ч. Рассчитайте время торможения и тормозной путь до полной остановки, если коэффициент трения колес о дорогу равен 0,4.
Дано:
(v_1=72frac{text{км}}{text{ч}}=20frac{text{м}}{text{с}})
(mu=0,4)
(v_2=0)
(gapprox 10 text{м/с}^2)
__________________
(t, s-?)
Автомобиль тормозит за счет силы трения. По второму закону Ньютона begin{gather*} F_{text{тр}}=ma. end{gather*} С другой стороны на горизонтальной дороге $$ F_{text{тр}}=mu N=mu mg. $$ Получаем: $$ ma=mu mgRightarrow a=mu g. $$ По определению ускорения $$ a=frac{v_2-v_1}{t}. $$ Т.к. (v_2=0), ускорение отрицательное.
Модуль ускорения $$ |a|=frac{v_1}{t}=mu gRightarrow t=frac{v_1}{mu g} $$ Время торможения прямо пропорционально скорости и обратно пропорционально коэффициенту трения. $$ t=frac{20}{0,4cdot 10}=5 (text{с}) $$ Найдем тормозной путь $$ s=v_1t+frac{at^2}{2}=v_1t+ left(frac{overbrace{v_2}^{=0}-v_1}{t}right)frac{t^2}{2}=v_1t -frac{v_1t}{2}=frac{v_1t}{2}=frac{v_1t}{2}cdot frac{v_1}{mu g}=frac{v_1^2}{2mu g} $$ Тормозной путь прямо пропорционален квадрату(!) скорости и обратно пропорционален коэффициенту трения. $$ s=frac{20^2}{2cdot 0,4cdot 10}=50 (text{м}) $$ Ответ: 5 с; 50 м.
п.6. Лабораторная работа №8. Измерение коэффициента трения скольжения
Цель работы
Научиться измерять силу трения скольжения и определять коэффициент трения скольжения. Изучить зависимость коэффициента трения скольжения от материалов соприкасающихся тел и от площади опоры движущегося тела.
Теоретические сведения
 |
При (v=const) (равномерное движение) получаем По вертикали (moverrightarrow{g}=-overrightarrow{N}). Модули этих сил равны По горизонтали (overrightarrow{F_{text{тр}}}=-overrightarrow{F_{text{тяги}}}). Модули этих сил равны $$ F_{text{тяги}}=F_{text{тр}}=mu N=mu mg $$ |
Если тело перемещать с помощью динамометра, то сила упругости, возникающая в пружине, будет равна силе тяги. Т.е., сила тяги непосредственно измеряется динамометром.
В работе используются стандартные лабораторные грузики массой 100 г.
Измерив силу тяги и зная массу перемещаемого тела, рассчитываем коэффициент трения: $$ mu=frac{F_{text{тяги}}}{mg} $$
Для расчетов используем стандартное значение (g=9,80665 text{м/с}^2).
Погрешность для прямых измерений (F_{text{тяги}}) определяется как половина цены деления динамометра. Погрешность для массы определяется по маркировке грузиков и бруска, (Delta m=2 text{г}) для (m=100 text{г}), т.е. (delta_m=2text{%}).
Погрешность эксперимента (delta_e) рассчитывается как средняя арифметическая по результатам измерений и вычислений.
Приборы и материалы
Лабораторный динамометр на 5 Н; набор грузиков по 100 г; деревянный брусок с крючком 100 г; деревянная доска; наждачная бумага.
Ход работы
1. Прикрепите динамометр к бруску, положите доску горизонтально, поставьте брусок самой большой по площади гранью слева на доску.
2. Перемещая брусок слева направо по доске, добейтесь равномерного скольжения (со стабильными показаниями динамометра). Снимите показания динамометра и запишите.
3. Повторите эксперимент, нагружая брусок одним, двумя, тремя и четырьмя грузиками.
4. Рассчитайте коэффициент трения дерева об дерево, определите относительную и абсолютную погрешности эксперимента.
5. Повторите эксперимент, перемещая брусок по доске, обмотанной наждачной бумагой. Найдите коэффициент трения дерева об наждак, определите относительную и абсолютную погрешности эксперимента.
6. Снимите наждачную бумагу и повторите эксперимент для трения дерева об дерево. Однако на этот раз брусок должен опираться на меньшую по площади грань. Рассчитайте коэффициент трения дерева об дерево в этом случае.
7. Сравните полученные коэффициенты трения, сделайте выводы о зависимости коэффициента трения от материала соприкасающихся поверхностей и от площади опоры движущегося тела.
Результаты измерений и вычислений
Цена деления динамометра (d=0,1 text{Н}).
Таблица для расчета коэффициента трения скольжения дерева об дерево
| Опыт | (m, text{кг}) | (F_{text{тяги}}, text{Н}) | (mu=frac{F_{text{тяги}}}{mg}) | (Delta=|mu-mu_{text{ср}}|) | |
| 1 | Брусок | 0,1 | 0,3 | 0,306 | 0,026 |
| 2 | Брусок + 1 грузик | 0,2 | 0,7 | 0,357 | 0,025 |
| 3 | Брусок + 2 грузика | 0,3 | 1,0 | 0,340 | 0,008 |
| 4 | Брусок + 3 грузика | 0,4 | 1,3 | 0,331 | 0,001 |
| 5 | Брусок + 4 грузика | 0,5 | 1,6 | 0,326 | 0,006 |
| Всего | — | — | 1,660 | 0,065 |
Среднее значение коэффициента трения $$ mu_{text{ср}}=frac{1,660}{5}=0,332 $$ Среднее значение абсолютного отклонения $$ Delta =frac{0,065}{5}=0,013 $$ Относительная погрешность begin{gather*} delta=frac{0,013}{0,332}cdot 100text{%}approx 3,9text{%}\[7pt] mu_{text{дд}}=(0,332pm 0,013), delta_mu=3,9text{%} end{gather*}
Таблица для расчета коэффициента трения скольжения дерева об наждак
| Опыт | (m, text{кг}) | (F_{text{тяги}}, text{Н}) | (mu=frac{F_{text{тяги}}}{mg}) | (Delta=|mu-mu_{text{ср}}|) | |
| 1 | Брусок | 0,1 | 0,6 | 0,612 | 0,039 |
| 2 | Брусок + 1 грузик | 0,2 | 1,1 | 0,561 | 0,012 |
| 3 | Брусок + 2 грузика | 0,3 | 1,7 | 0,578 | 0,005 |
| 4 | Брусок + 3 грузика | 0,4 | 2,2 | 0,561 | 0,012 |
| 5 | Брусок + 4 грузика | 0,5 | 2,7 | 0,551 | 0,022 |
| Всего | — | — | 2,862 | 0,090 |
Среднее значение коэффициента трения $$ mu_{text{ср}}=frac{2,862}{5}approx 0,572 $$ Среднее значение абсолютного отклонения $$ Delta =frac{0,090}{5}=0,018 $$ Относительная погрешность begin{gather*} delta=frac{0,018}{0,572}cdot 100text{%}approx 3,1text{%}\[7pt] mu_{text{дн}}=(0,572pm 0,018), delta_mu=3,1text{%} end{gather*}
Таблица для расчета коэффициента трения скольжения дерева об дерево (узкая грань)
| Опыт | (m, text{кг}) | (F_{text{тяги}}, text{Н}) | (mu=frac{F_{text{тяги}}}{mg}) | (Delta=|mu-mu_{text{ср}}|) | |
| 1 | Брусок | 0,1 | 0,35 | 0,357 | 0,011 |
| 2 | Брусок + 1 грузик | 0,2 | 0,7 | 0,357 | 0,011 |
| 3 | Брусок + 2 грузика | 0,3 | 1,0 | 0,340 | 0,006 |
| 4 | Брусок + 3 грузика | 0,4 | 1,3 | 0,331 | 0,015 |
| 5 | Брусок + 4 грузика | 0,5 | 1,7 | 0,347 | 0,000 |
| Всего | — | — | 1,732 | 0,043 |
Среднее значение коэффициента трения $$ mu_{text{ср}}=frac{1,732}{5}approx 0,346 $$ Среднее значение абсолютного отклонения $$ Delta =frac{0,043}{5}approx 0,009 $$ Относительная погрешность begin{gather*} delta=frac{0,009}{0,346}cdot 100text{%}approx 2,5text{%}\[7pt] mu ‘_{text{дд}}=(0,346pm 0,009), delta_mu=2,5text{%} end{gather*}
Выводы
На основании проделанной работы можно сделать следующие выводы.
В работе исследовалась зависимость коэффициента трения скольжения от поверхностей, из которых изготовлены соприкасающиеся тела.
Для скольжения дерева об дерево был получен коэффициент begin{gather*} mu_{text{дд}}=(0,332pm 0,013), delta_mu=3,9text{%} end{gather*}
Для скольжения дерева об наждак был получен коэффициент begin{gather*} mu_{text{дн}}=(0,572pm 0,018), delta_mu=3,1text{%}\[7px] mu_{text{дн}}gt mu_{text{дд}} end{gather*}
Наждак является более шероховатой поверхностью и сила трения на ней больше.
Коэффициент трения скольжения сильно зависит от материалов соприкасающихся поверхностей.
Также в работе исследовалась зависимость коэффициента трения скольжения от площади опоры движущегося тела. Брусок выставлялся на более узкую грань, и изучалось скольжение дерева об дерево в этом случае. Был получен коэффициент begin{gather*} mu’_{text{дд}}=(0,346pm 0,009), delta_mu=2,5text{%} end{gather*} Поскольку begin{gather*} 0,319le mu_{text{дд}}le 0,345 0,337le mu’_{text{дд}}le 0,355 end{gather*} Полученные отрезки значений перекрываются.
Таким образом, в рамках погрешности эксперимента коэффициент трения скольжения не зависит от площади опоры движущегося тела.
Трения коэффициент
- Трения коэффициент
-
отношение силы трения F к реакции Т, направленной по нормали к поверхности касания, возникающей при приложении нагрузки, прижимающей одно тело к другому: f = F/T. Т. к. — характеристика, применяемая при выполнении технических расчётов, характеризующих фрикционное взаимодействие двух тел (см. Трение внешнее).
В зависимости от вида перемещения одного тела по другому различают: Т.к. при сдвиге — скольжении и Т.к. при качении. В свою очередь, при скольжении в зависимости от величины тангенциальной силы (см. рис. при ст. Трение внешнее) различают коэффициент неполного трения скольжения, коэффициент трения покоя и коэффициент трения скольжения. Все эти Т.к. могут изменяться в широких пределах в зависимости от шероховатости и волнистости поверхностей, характера плёнок, покрывающих поверхности. Для протяжённого контакта они мало изменяются с изменением нагрузки.
В зависимости от величины коэффициент трения скольжения пары трения делят на 2 группы: фрикционные материалы, имеющие большой Т. к.— обычно 0,3—0,35, редко 0,5—0,6, и антифрикционные, имеющие Т. к. без смазки 0,15—0,12, при граничной смазке 0,1—0,05.
Сопротивление свободному качению твёрдого тела (например, колеса) характеризуют коэффициентом сопротивления перекатыванию fk = T•rd/Ik [см], где Т — нормальная составляющая реакции колеса на опору; rd — динамический радиус качения; Ik — нормальная нагрузка на колесе. Если на колесо действуют ведущий или тормозной моменты, то коэффициент сцепления ψ колеса с дорожным покрытием определяется равенством: ψ = Tx/Ik, где Tx — неполная сила трения скольжения, возникающая между катящимся колесом и дорогой. Коэффициенты fk и ψ существенно зависят от природы трущихся тел, характера покрывающих их плёнок и скорости качения. Обычно для металлов (сталь по стали) fk = 0,001—0,002 см. При движении автомобиля со скоростью 80 км/час Т. к. колёс по асфальту fk = 0,02 см и резко возрастает с увеличением скорости. Коэффициент сцепления ψ на сухом асфальте доходит у автомобильных колёс до 0,8, а при наличии плёнки воды снижается до 0,2—0,1.
И. В. Крагельский.
Большая советская энциклопедия. — М.: Советская энциклопедия.
1969—1978.
Полезное
Смотреть что такое «Трения коэффициент» в других словарях:
-
ТРЕНИЯ КОЭФФИЦИЕНТ — величина, характеризующая трение внешнее. В зависимости от вида перемещения одного тела по другому различают Т … Физическая энциклопедия
-
Трения коэффициент — … Википедия
-
КОЭФФИЦИЕНТ — (от лат. co совместно и efficiens производящий) множитель, обычно выражаемый цифрами. Если произведение содержит одну или несколько переменных (или неизвестных) величин, то коэффициентом при них называют также произведение всех постоянных, в т. ч … Большой Энциклопедический словарь
-
КОЭФФИЦИЕНТ (множитель) — КОЭФФИЦИЕНТ (от лат. co совместно и efficiens производящий), множитель, обычно выражаемый цифрами. Если произведение содержит одну или несколько переменных (или неизвестных) величин, то коэффициентом при них называют также произведение всех… … Энциклопедический словарь
-
Коэффициент — [coefficient, factor, ratio] числовой множитель в буквенном или числовом уравнении функциональной зависимости коэффициента известный множитель при той или иной степени неизвестного или постоянный множитель при переменной величине. Многие… … Энциклопедический словарь по металлургии
-
коэффициент — а; м. [от лат. coefficiens (coefficientis) содействующий] 1. Числовой (или буквенный) множитель в алгебраическом выражении. 2. Величина, определяющая какое л. свойство физического тела. К. трения. К. расширения. К. полезного действия (отношение… … Энциклопедический словарь
-
коэффициент эффективности — [efficiency factor] относительный качественный показатель, характеризующий достигнутый уровень экономической эффективности; отношение экономического результата (например, суммы прибыли или экономии от снижения себестоимости продукции и т. п.).… … Энциклопедический словарь по металлургии
-
коэффициент циклической перегрузки — [cyclic overload ratio] отношение приложенного напряжения (I.) к пределу выносливости материала (образца, полуфабриката, изделия); Смотри также: Коэффициент фабрикационный коэффициент … Энциклопедический словарь по металлургии
-
коэффициент форсирования — [boosting ratio] отношение максимальной тепловой мощности к средней в печах периодического действия; Смотри также: Коэффициент фабрикационный коэффициент температурный коэффициент сопротивления … Энциклопедический словарь по металлургии
-
коэффициент уширения — [spread ratio] показатель деформации, равный отношению ширины полосы после деформации к ее ширине до деформации; Смотри также: Коэффициент фабрикационный коэффициент температурный … Энциклопедический словарь по металлургии
Процесс взаимодействия тел при их относительном движении можно отобразить с помощью формулы трения скольжения. Коэффициент определяется только путём проведённых исследований. Изучением процессов трения занимается раздел физики, который называется трибологией (механикой фрикционного взаимодействия). Определяемый коэффициент является совокупной характеристикой пары материалов, которые не зависят от площади соприкосновения тел.
Оглавление:
- Краткое описание
- Сила трения скольжения
- Правила расчёта
- Измерительные манипуляции
- Основные характеристики
- Практическое значение
- Ключевые нюансы
Процесс взаимодействия тел при их относительном движении можно отобразить с помощью формулы трения скольжения. Коэффициент определяется только путём проведённых исследований. Изучением процессов трения занимается раздел физики, который называется трибологией (механикой фрикционного взаимодействия). Определяемый коэффициент является совокупной характеристикой пары материалов, которые не зависят от площади соприкосновения тел.
Краткое описание
Трение можно рассматривать как способ взаимодействия двух объектов. Но у этого процесса есть свои нюансы. Между двумя объектами трение возникает только в результате их соприкосновения с определённой площадью поверхности. Этот процесс попадает под действие третьего закона Ньютона.
Например, если взять 2 небольших бруска из дерева и просто их передвигать, то в итоге можно наблюдать соприкосновение по площадям. Во время эксперимента можно заметить, что двигать предметами относительно друг друга гораздо сложнее, нежели совершать с ними какие-либо манипуляции в воздухе. Именно в этом случае в действие вступает закон трения.
В третьем законе Ньютона описано правило, которое касается того, что по модулю силы равны, но направлены совершенно в разные стороны. Получается, что сила μ является векторной величиной. Этот процесс имеет электромагнитную природу. Трение возникает в результате того, что молекулы и атомы тел, участвующих в соприкосновении, начинают взаимодействовать друг с другом. На этом правиле основано много задач по физике. Латинской буквой k или греческой μ обозначается коэффициент трения.
Сила трения скольжения
Коэффициент трения скольжения показывает отношение μ к силе давления на поверхность. Это правило изучают на уроках физики в 10 классе. Силы трения всегда воздействуют на объекты. Они возникают в результате соприкосновения твёрдых тел, газов и жидкостей, подчиняются закону Ньютона.
Для решения сложных задач нужно понимать, что направление силы трения противоположно движению объекта и факторам, которые стремятся изменить его положение. Исключений не предусмотрено. О процессе трения скольжения можно говорить только тогда, когда тело движется относительно другого объекта. Конечные результаты во многом зависят от следующих факторов:
- скорости движения;
- коэффициента трения скольжения (µ), от которого напрямую зависят свойства, а также состояние поверхностей соприкосновения;
- силы нормальной реакции опоры (N→).
Итоговый коэффициент во многом зависит от свойств задействованного материала.
Например, чем шероховатее будет поверхность, тем больше станет значение μ. У скользких оснований коэффициент окажется минимальным. Трение во многом зависит от скорости, но этим значением часто пренебрегают, если речь не идет о точных измерениях. По этой причине показатель μ является постоянным.
Правила расчёта
С максимальной точностью силу трения скольжения можно определить с помощью формулы F = µ* N. Значение N рассчитывается как производное массы тела на ускорение свободного падения. Учитывается также косинус угла к поверхности: N = m * g * cosa. Формула коэффициента трения скольжения выглядит следующим образом: µ = F/N.
На уроках физики можно узнать, что для основного количества всех пар материалов коэффициент рассчитывается во время опытов. Значение находится в пределах от 0,1 до 0,5. В такой ситуации μ будет являться переменной величиной.
В физике используются специальные таблицы, в которых указаны переменные величины для каждого из материалов. Но эти данные являются актуальными только при соблюдении определённых условий. Если нужно получить максимально точный результат, тогда следует самостоятельно выполнить расчёты для конкретной ситуации.
Измерительные манипуляции
Динамометр используется для измерения реальных показателей механической силы. Этот прибор включает в себя силовой элемент (пружину) и отчётное звено (линейку). Принцип использования стандартного пружинного динамометра прост. На прибор воздействует сила, которая растягивает либо сжимает упругое звено. Полученное значение фиксируется при помощи измерительной части.
Чтобы правильно найти величину μ, которая передаётся на брусок в процессе его движения по конкретной поверхности, нужно постараться прикрепить к объекту динамометр. Необходимо потянуть устройство за пружину в горизонтальной плоскости.
Чтобы полученный результат не имел погрешностей, нужно следить за тем, чтобы прибор перемещался максимально равномерно и с постоянной скоростью.
На анализируемую величину будут действовать сразу 2 силы, одна из которых препятствует движению бруска, а вторая старается снизить вероятность деформации пружины. Так как движение динамометра равномерное, силы имеют одинаковое значение и уравновешивают друг друга. На измерительной шкале регистрируется показатель упругости пружины, из-за чего полученная величина и будет искомой цифрой.
Проведённый опыт может доказать, что итоговое значение μ во многом зависит от веса задействованного объекта. Если применить дополнительный груз и повторить исследование, тогда можно заметить, что значение на линейке увеличится.
Основные характеристики
Сила трения может рассматриваться как процесс, который возникает в результате соприкосновения двух объектов и препятствует их относительному движению. Основными причинами трения являются специфическая шероховатость трущихся поверхностей и взаимодействие имеющихся молекул. Существует определённый характер фрикционного взаимодействия, который принято делить на несколько категорий:
- Граничное. В области контакта содержатся участки и слои разной природы (например, жидкость, оксидные плёнки). Это самый распространённый случай, когда дело касается скольжения.
- Сухое. Взаимодействующие твёрдые тела не разделены между собой дополнительными слоями. На практике крайне редко фиксируются ситуации, которые свойственны сухому трению. Для этого случая характерно наличие большого значения μ в состоянии покоя.
- Жидкостное. Задействованные тела разделены слоем твёрдого тела (например, порошок графита), газом либо жидкостью. Эта ситуация чаще всего фиксируется при трении качения. Твёрдые тела погружены в жидкость, а величина μ отличается вязкой средой.
- Смешанное. Зона контакта содержит участки жидкостного и сухого трения.
- Вязкоупругое. Решающую роль играет внутреннее трение в смазывающем материале. Это фрикционное взаимодействие возникает при увеличении относительных скоростей перемещения.
Многочисленные исследования показали, что для многих пар материалов итоговое значение µ не превышает 1. В противном случае можно говорить, что между контактирующими телами присутствует сила адгезии.
Для решения элементарных задач используется следующая формула: µ = (F + F adhesion)/ N. Значение μ измеряется стандартным образом, никакие дополнительные буквы для обозначения полученного результата не используются (указываются только цифры).
Практическое значение
Трение играет отрицательную роль во многих механизмах, например, в транспортных средствах, двигателях внутреннего сгорания, зубчатых шестеренках. Негативное значение сказывается на снижении коэффициента полезного действия механизма. Смазки, масла на синтетической и натуральной основе позволяют существенно уменьшить силу трения. На многих широко распространённых деталях присутствует защитное напыление.
Если речь идет о миниатюризации МЭМС (микроэлектромеханических систем) и НЭМС (наноэлектромеханических систем), тогда показатель μ будет существенно увеличиваться. Для решения этих проблем используется усовершенствованный подход в рамках трибологии.
Благодаря трению объекты могут перемещаться. Например, при ходьбе неизбежным является сцепление стопы с полом, из-за чего человек отталкивается от поверхности и движется дальше. Аналогичным образом происходит сцепление колёс транспортного средства с дорогой. Для повышения эксплуатационных характеристик автомобилей выпускаются инновационные формы и специальные разновидности резины для колёс. На спортивные машины устанавливают универсальные антикрылья, которые прижимают транспортное средство к трассе.
Ключевые нюансы
Сила трения имеет место и при качении какого-либо тела. Но этим параметром часто пренебрегают, так как итоговые показатели недостаточно велики, чтобы брать их в расчёт. Такой подход позволяет упростить процесс решения различных задач. Но даже в этом случае можно сохранить высокую степень точности итогового результата.
Для закрепления полученных знаний можно изучить пример решения задачи по физике. На пол поставили ящик весом 7 кг. Между этим объектом и напольным покрытием значение μ составляет 0,3. К ящику прикладывают силу, которая соответствует 14 Н. Нужно совершить необходимые расчёты, чтобы понять, можно ли сдвинуть объект с места. Для определения силы реакции необходимо массу ящика умножить на ускорение:
- N = m * g.
- N = 10 кг * 9,8 м/с² = 98 кг * м/с² = 98 Н.
- F = k * N.
- F = 0,3 * 98 Н = 29,4 Н.
Полученный результат позволяет сделать вывод, что ящик останется на прежнем месте. Это связано с тем, что итоговое значение превышает усилия, приложенные к объекту: 29,4 Н > 14 Н.
Силы трения имеют большое значение в жизни людей и животных.
Благодаря этому явлению человек может ходить и держать в руках различные предметы. За счёт действия закона сцепления на скалах удерживаются огромные валуны и не падают в пропасть, а плетущиеся растения тянутся к солнечному свету и скрепляются с ближайшей опорой.
Люди и животные от природы умеют избавляться от негативного воздействия торможения. К примеру, всё тело рыбы покрыто специальной слизью, что позволяет существенно уменьшить трение о воду. Человек при работе с техникой научился использовать различные смазывающие материалы, благодаря чему увеличивается срок эксплуатации, а также качество работы устройства.