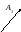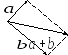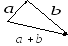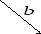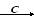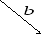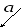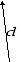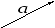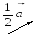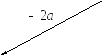Как написать коллинеарность векторов - Правописание и грамматика

Ученики 9-го класса, помимо понятия вектора, должны знать, что такое коллинеарные векторы, а также условия коллинеарности векторов.

Вектор — это направленный отрезок. Вектор обозначается двумя заглавными латинскими буквами со стрелочкой над ними

или одной маленькой со стрелочкой над ней

Нулевой вектор — вектор, начало которого совпадает с концом. То есть в геометрической интерпретации это просто точка.

Теперь, когда мы вспомнили базовые понятия, можно переходить к определению коллинеарных векторов.

Что значит «коллинеарные векторы»

Коллинеарные векторы — это ненулевые векторы, лежащие на одной прямой или на параллельных прямых. Причем считается, что нулевой вектор коллинеарен каждому другому вектору. То есть, попросту говоря, коллинеарность — это параллельность векторов. Если векторы

и
коллинеарны, то это записывают так:
.

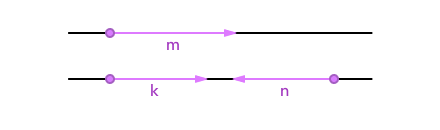
Коллинеарные векторы можно разделить по направлению на две группы: сонаправленные и противоположно направленные.

Векторы
и
лежат на параллельных прямых, а также имеют одно направление, поэтому
и
— сонаправленные векторы:
.

Векторы
и
лежат на параллельных прямых, но имеют разное направление, поэтому
и
— противоположно направленные векторы:
.

Задача № 1

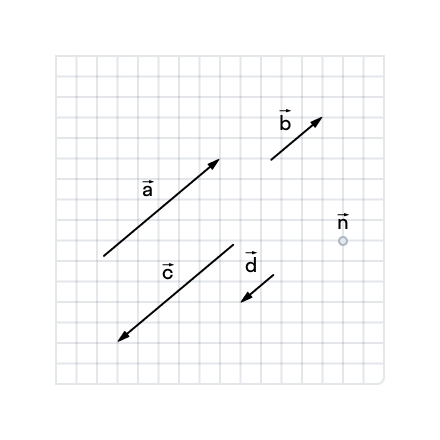
Найдите сонаправленные и противоположно направленные векторы.

Благодаря клетчатому фону мы можем определить, что все векторы на рисунке коллинеарны, то есть лежат на параллельных прямых. Осталось посмотреть на направление векторов и сделать выводы:

Но не забываем о нулевом векторе
— он будет сонаправлен с каждым вектором.

Но согласитесь, что визуальная оценка параллельности не самая точная вещь на планете, а математика славится своей точностью и четкостью. Поэтому возникает вопрос: как проверить коллинеарность векторов алгебраическими способами? Для этого существуют признаки коллинеарности векторов. Рассмотрим их.

Получай лайфхаки, статьи, видео и чек-листы по обучению на почту

Реши домашку по математике на 5.

Подробные решения помогут разобраться в самой сложной теме.

Признаки коллинеарности векторов

Первый критерий коллинеарности векторов: векторы
и
коллинеарны, если
.
Второй критерий коллинеарности векторов: два вектора коллинеарны, если отношения их координат равны.

Но здесь важно понимать, что это условие параллельности векторов работает только для всех ненулевых координат. Значит, если хотя бы один компонент вектора равен нулю, то правило неприменимо.
Третий критерий коллинеарности векторов, который могут применять одиннадцатиклассники, взрослые и все, кто увлечен математикой: два ненулевых вектора коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору.

Применим условия коллинеарности векторов при решении задач.

Задача № 2

Докажите, что векторы
и
коллинеарны.

У нас с вами есть два способа определить или доказать коллинеарность векторов, однако в координатах каждого вектора есть нули — значит, подходит только первый критерий, который еще называется свойством коллинеарных векторов: если
, то
.

Для начала определим
. А теперь проверим, выполняется ли условие
:

, значит,
. Что и требовалось доказать.

Задача № 3

Какие из векторов
,
и
коллинеарны?

А здесь очень удобно использовать второй критерий коллинеарности векторов, который звучит так: отношения соответствующих координат коллинеарных векторов равны.

Проверим коллинеарность векторов
и
: должно выполняться условие
, т. е.
— верно, значит,
.
Проверим коллинеарность векторов
и
: должно выполняться условие
, т. е.
— неверно, значит,
и
неколлинеарны.
Проверим коллинеарность векторов
и
: должно выполняться условие
, т. е.
— неверно, значит,
и
неколлинеарны.

Задача № 4

Определите, при каком значении k векторы
и
коллинеарны.

Так как по условию векторы должны быть коллинеарны, а в их координатах не содержится нуля, то можно использовать второй критерий коллинеарности, а именно — должно выполняться условие
, то есть
.

По свойству пропорции выразим k:

;

k = 27.

Значит, при k = 27 векторы
и
коллинеарны.

Если же вам нужно проверить коллинеарность векторов в пространстве, а не на плоскости, то все эти условия продолжают работать, но помните, что к проверке присоединяется третья координата векторов. Рассмотрим пару примеров.

Задача № 5

Докажите, что векторы
и
коллинеарны.

Поступим аналогично решению в задаче 2 — применим первый критерий, который еще называется свойством коллинеарных векторов, т. е. если
, то
.

Для начала определим
. А теперь проверим, выполняется ли условие
:

, значит,
. Что и требовалось доказать.

Задача № 6

Определите, при каких значениях k и f векторы
и
коллинеарны.

Аналогично задаче 4: так как по условию векторы должны быть коллинеарны и в их координатах не содержится нуля, то можно использовать второй критерий коллинеарности. А именно — должно выполняться условие
, то есть
.

Рассмотрим первую и вторую дроби, по свойству пропорции выразим k:

;

k = 27.

Рассмотрим первую и третью дроби, по свойству пропорции выразим f:

;

f = 2.

Значит, при k = 27 и f = 2 векторы
и
коллинеарны.

Векторы — удивительная тема, с помощью которой можно решить многие физические задачи, легко и просто доказать самые сложные геометрические теоремы. Сегодня вы узнали, какие векторы называются коллинеарными, но это лишь один аспект большой главы о векторах. Чтобы узнать остальные действия с векторами, познакомиться с интересными задачами и способами решений, приходите на онлайн-курсы математики для детей в Skysmart.

Источник

Условия коллинеарности векторов

Два вектора будут коллинеарны при выполнении любого из этих условий:

Условие коллинеарности векторов 1. Два вектора a и b коллинеарны, если существует число n такое, что

a = n · b

Условия коллинеарности векторов 2. Два вектора коллинеарны, если отношения их координат равны.

N.B. Условие 2 неприменимо, если один из компонентов вектора равен нулю.

Условия коллинеарности векторов 3. Два вектора коллинеарны, если их векторное произведение равно нулевому вектору.

N.B. Условие 3 применимо только для трехмерных (пространственных) задач.

Доказательство третего условия коллинеарности

Пусть есть два коллинеарные вектора a = {a_x; a_y; a_z} и b = {na_x; na_y; na_z}. Найдем их векторное произведение

a × b =

ijk
a_xa_ya_z
b_xb_yb_z

= i (a_yb_z — a_zb_y) — j (a_xb_z — a_zb_x) + k (a_xb_y — a_yb_x) =

= i (a_yna_z — a_zna_y) — j (a_xna_z — a_zna_x) + k (a_xna_y — a_yna_x) = 0i + 0j + 0k = 0

Примеры задач на коллинеарность векторов

Примеры задач на коллинеарность векторов на плоскости

Пример 1. Какие из векторов a = {1; 2}, b = {4; 8}, c = {5; 9} коллинеарны?

Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности, которое в случае плоской задачи для векторов a и b примет вид:

Значит:

Вектора a и b коллинеарны т.к.	1	=	2	.
4	8

Вектора a и с не коллинеарны т.к.	1	≠	2	.
5	9

Вектора с и b не коллинеарны т.к.	5	≠	9	.
4	8

Пример 2. Доказать что вектора a = {0; 3} и b = {0; 6} коллинеарны.

Решение: Так как вектора содержат компоненты равные нулю, то воспользуемся первым условием коллинеарности, найдем существует ли такое число n при котором:

b = na.

Для этого найдем ненулевой компонент вектора a в данном случае это a_y. Если вектора колинеарны то

n =	b_y	=	6	= 2
a_y	3

Найдем значение na:

na = {2 · 0; 2 · 3} = {0; 6}

Так как b = na, то вектора a и b коллинеарны.

Пример 3. найти значение параметра n при котором вектора a = {3; 2} и b = {9; n} коллинеарны.

Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности

Значит:

Решим это уравнение:

Ответ: вектора a и b коллинеарны при n = 6.

Примеры задач на коллинеарность векторов в пространстве

Пример 4. Какие из векторов a = {1; 2; 3}, b = {4; 8; 12}, c = {5; 10; 12} коллинеарны?

Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности, которое в случае пространственной задачи для векторов a и b примет вид:

a_x	=	a_y	=	a_z	.
b_x	b_y	b_z

Значит:

Вектора a и b коллинеарны т.к.
14 = 28 = 312

Вектора a и с не коллинеарны т.к.
15 = 210 ≠ 312

Вектора с и b не коллинеарны т.к.
54 = 108 ≠ 1212

Пример 5. Доказать что вектора a = {0; 3; 1} и b = {0; 6; 2} коллинеарны.

b = na.

Для этого найдем ненулевой компонент вектора a в данном случае это a_y. Если вектора колинеарны то

n =	b_y	=	6	= 2
a_y	3

Найдем значение na:

na = {2 · 0; 2 · 3; 2 · 1} = {0; 6; 2}

Так как b = na, то вектора a и b коллинеарны.

Пример 6. найти значение параметров n и m при которых вектора a = {3; 2; m} и b = {9; n; 12} коллинеарны.

a_x	=	a_y	=	a_z	.
b_x	b_y	b_z

Значит:

3	=	2	=	m
9	n	12

Из этого соотношения получим два уравнения:

Решим эти уравнения:

Ответ: вектора a и b коллинеарны при n = 6 и m = 4.

Источник

В статье ниже рассмотрим условия, при которых векторы считаются коллинеарными, а также разберем тему на конкретных примерах. И, прежде чем приступить к обсуждению, напомним некоторые определения.

Определение 1

Коллинеарные векторы – ненулевые векторы, лежащие на одной прямой или на параллельных прямых. Нулевой вектор считается коллинеарным любому другому.

Данное определение дает возможность убедиться в коллинеарности векторов в их геометрическом отображении, однако точность такого способа может иметь погрешности, например, в зависимости, от качества самого чертежа. Поэтому обратимся к алгебраическому толкованию: сформируем условие, которое будет явным признаком коллинеарности.

Согласно схемам операций над векторами умножение вектора на некоторое заданное число приводит к соответствующему сжатию или растяжению вектора при сохранении или смене направления. Тогда вектор b→=λ·a→ коллинеарен вектору a→ , где λ – некоторое действительное число. Справедливым будет и обратное утверждение: если вектор b→ коллинеарен вектору a→, его можно представить в виде λ·a→. Это является необходимым и достаточным условием коллинеарности двух ненулевых векторов.

Определение 2

Для коллинеарности двух векторов необходимо и достаточно, чтобы они были связаны равенствами: b→=λ·a→ или a→=μ·b→, μ∈R

Координатная форма условия коллинеарности векторов

Исходные данные: вектор a→ задан в некоторой прямоугольной системе координат на плоскости и имеет координаты (ax, ay), тогда, согласно полученному выше условию, вектор b→=λ·a→ имеет координаты (λ·ax, λ·ay).

По аналогии: если вектор a→ задан в трехмерном пространстве, то он будет представлен в виде координат a=(ax, ay, az) , а вектор b→=λ·a→ имеет координаты (λ·ax, λ·ay, λ·az). Из полученных утверждений следуют условия коллинеарности двух векторов в координатном толковании.

Определение 3

Для коллинеарности двух ненулевых векторов на плоскости необходимо и достаточно, чтобы их координаты были связаны соотношениями: bx=λ·axby=λ·ay или ax=μ·bxay=μ·by
Для коллинеарности двух ненулевых векторов в пространстве необходимо и достаточно, чтобы их координаты были связаны соотношениями: bx=λ·axby=λ·ay bz=λ·azили ax=μ·bxay=μ·by az=μ·bz

Мы можем также получить еще одно условие коллинеарности векторов, опираясь на понятие их произведения.

Если ненулевые векторы a→=(ax, ay, az) и b→=(bx, by, bz) коллинеарны, то согласно векторному определению произведения a→×b→=0→. И это также соответствует равенству: i→j→k→axayazbxbybz=0→, что, в свою очередь, возможно только тогда, когда заданные векторы связаны соотношениями b→=λ·a→ и a→=μ·b→ , где μ — произвольное действительное число (на основании теоремы о ранге матрицы), что указывает на факт коллинеарности векторов.

Определение 4

Два ненулевых вектора коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору.

Рассмотрим применение условия коллинеарности на конкретных примерах.

Пример 1

Исходные данные: векторы a→=(3-22, 1) и b→=(12+1, 2+1) . Необходимо определить, коллинеарны ли они.

Решение

Выполним задачу, опираясь на условие коллинеарности векторов на плоскости в координатах: bx=λ·axby=λ·ay Подставив заданные значения координат, получим: bx=λ·ax⇔12+1=λ·(3-22)⇒λ=1(2+1)·(3-22)=132-4+3-22=12-1by=λ·ay⇔2+1=12-1·1⇔(2+1)·(2-1)=1 ⇔1≡1

Т.е. b→=12-1·a→, следовательно, заданные векторы коллинеарны.

Ответ: заданные векторы коллинеарны.

Пример 2

Исходные данные: векторы a→=(1, 0, -2) и b→=(-3, 0, 6) . Необходимо убедиться в их коллинеарности.

Решение

Т.к. bx=λ·axby=λ·ay bz=λ·az⇔-3=-3·10=-3·06=-3·(-2) , то верным будет равенство: b→=-3·a→ , что является необходимым и достаточным условием коллинеарности. Таким образом, заданные векторы коллинеарны.

Найдем также векторное произведение заданных векторов и убедимся, что оно равно нулевому вектору: a→×b→=i→j→k→axayazbxbybz=i→j→k→10-2-306=i→·0·6+j→·(-2)·(-3)+k→·1·0-k→·0·(-3)-j→·1·6-i→·(-2)·0=0→Ответ: заданные векторы коллинеарны.

Пример 3

Исходные данные: векторы a→=(2, 7) и b→=(p, 3) . Необходимо определить, при каком значении p заданные векторы будут коллинеарны.

Решение

Согласно выведенному выше условию, векторы коллинеарны, если

b→=λ·a→⇔bx=λ·axby=λ·ay⇔p=λ·23=λ·7

тогда λ=37, а p=λ·2⇔p=67 .

Ответ: при p=67 заданные векторы коллинеарны.

Также распространены задачи на нахождения вектора, коллинеарного заданному. Решаются они без затруднений, основываясь на условии коллинеарности: : достаточным будет взять произвольное действительное число λ и определить вектор, коллинеарный данному.

Пример 4

Исходные данные: вектор a→=(2, -6) . Необходимо найти любой ненулевой вектор, коллинеарный заданному.

Решение

Ответом может послужить, например, 12·a→=(1, -3) или вектор 3·a→=(6, -18) .

Ответ: вектор, коллинеарный заданному имеет координаты (1, -3).

Пример 5

Исходные данные: вектор a→=(3, 4, -5) . Необходимо определить координаты вектора единичной длины, коллинеарного заданному.

Решение

Вычислим длину заданного вектора по его координатам: a→=ax2+bx2+cx2=32+42+(-5)2=52 Разделим каждую из заданных координат на полученную длину и получим единичный вектор, коллинеарный данному: 1a→·a→=(352, 452,- 12)

Ответ: (352, 452,- 12)

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

Источник

Любовь Петровна Гаврилюк

Эксперт по предмету «Геометрия»

Задать вопрос автору статьи

Понятие коллинеарности векторов

Чтобы понять, что значит коллинеарные векторы, сперва надо разобраться, что является геометрическим вектором. Для этого сначала введем понятие отрезка.

Определение 1

Отрезком будем называть такую часть прямой, которая ограничена точками с двух сторон.

Концами отрезка будем называть точки, которые его ограничивают.

Для введения определения вектора один из концов отрезка назовем его началом.

Определение 2

Вектором (направленным отрезком) будем называть такой отрезок, у которого обозначено, какая граничная точка его начало, а какая является его концом.

IT Профессия «Разработчик ПО»

Получишь знания, необходимые в работе, соберешь портфолио из собственных проектов и начнешь получать $$

Узнать подробнее

Обозначение: $overline{AB}$ — вектор $AB$, имеющий начало в точке $A$, а конец в точке $B$.

Иначе одной маленькой буквой: $overline{a}$ (рис. 1).

Рисунок 1. Обозначение векторов. Автор24 — интернет-биржа студенческих работ

Определение 3

Нулевым вектором будем называть любую точку, которая принадлежит плоскости.

Обозначение: $overline{0}$.

Далее рассмотрим, какие векторы называются коллинеарными.

Определение 4

Два ненулевых вектора будем называть коллинеарными, если они лежат на одной и той же прямой. Кроме того, понятие коллинеарность наблюдается в случается параллельности векторов (рис.2).

«Как найти вектор, коллинеарный вектору» 👇

Рисунок 2. Коллинеарность векторов. Автор24 — интернет-биржа студенческих работ

Также введем определение векторного произведения, которое будет нам необходимо далее.

Определение 5

Векторным произведением двух векторов будем называть такой вектор, который будет перпендикулярен обоим данным векторам, и его длина будет равняться произведению длин этих векторов с синусом угла между данными векторами, а также этот вектор с двумя начальными имеют ту же ориентацию, как и декартова система координат.

Обозначение: $overline{α}хoverline{β}$.

Чтобы найти векторное произведение, будем пользоваться формулой

$overline{α}хoverline{β}=begin{vmatrix}overline{i}&overline{j}&overline{k}\α_1&α_2&α_3\β_1&β_2&β_3end{vmatrix}$

Признак коллинеарности через пропорциональность или как определить коллинеарность векторов по координатам

Теорема 1

Главное условие коллинеарности векторов: чтобы ненулевые векторы были коллинеарны между собой, необходимо, чтобы их соответствующие координаты были пропорциональны друг другу.

Доказательство.

Необходимость: Пусть нам даны векторы $overline{α}$ и $overline{β}$, которые имеют координаты $(α_1,α_2,α_3)$ и $(β_1,β_2,β_3)$, соответственно, причем они коллинеарны друг другу. Тогда нам нужно доказать следующие равенства

$α_1=rβ_1$, $α_2=rβ_2$, $α_3=rβ_3$

Так как векторы $overline{α}$ и $overline{β}$ коллинеарны, то они будут либо сонаправленными, либо противоположно направленными. Без ограничения общности, будем считать, что они будут сонаправлены, то есть $overline{α}↑↑overline{β}$. Умножим один из этих векторов на действительное, большее нуля, число $r$, так, чтобы длины векторов $roverline{α}$ и $overline{β}$ были равны между собой. По определению умножения векторов на число, получим, что $roverline{α}↑↑overline{β}$. Но тогда, по определению равенства векторов, получим, что $roverline{α}=overline{β}$. Из этого равенства получим, что

$α_1=rβ_1$, $α_2=rβ_2$, $α_3=rβ_3$

Достаточность: Пусть верны равенства $α_1=rβ_1$, $α_2=rβ_2$, $α_3=rβ_3$. Докажем, что векторы $overline{α}$ и $overline{β}$ будут коллинеарными.

Из данных равенств следует, что $roverline{α}=overline{β}$.

Имеются два случая:

$r lt 0$

В этом случае, по определению умножения вектора на число, получим, что $roverline{α}↑↓overline{β}$.
$r >0$

В этом случае получим, что $roverline{α}↑↑overline{β}$.

Тогда, в обоих случаях получаем доказательство коллинеарности векторов $overline{α}$ и $overline{β}$.

Ответ: теорема доказана.

Пример 1

Как проверить коллинеарность векторов $(3,-1)$ и $(9,-3)$.

Доказательство.

Разложим второй вектор:

$(9,-3)=(3cdot 3,3cdot (-1) )=3(3,-1)$

Получаем, что координаты этих векторов пропорциональны друг другу, что, по теореме 1, и доказывает наше утверждение.

Признаки и свойства коллинеарности векторов через их произведение

Теорема 2

Чтобы ненулевые векторы были коллинеарны между собой, необходимо и достаточно, чтобы их векторное произведение было равно нулевому вектору.

Доказательство.

Так как векторы коллинеарны, то, по теореме 1, верны равенства

$α_1=rβ_1$, $α_2=rβ_2$, $α_3=rβ_3$

Найдем $overline{α}хoverline{β}$ по формуле

$overline{α}хoverline{β}=begin{vmatrix}overline{i}&overline{j}&overline{k}\α_1&α_2&α_3\β_1&β_2&β_3end{vmatrix}=begin{vmatrix}overline{i}&overline{j}&overline{k}\rβ_1&rβ_2&rβ_3\β_1&β_2&β_3end{vmatrix}=rbegin{vmatrix}overline{i}&overline{j}&overline{k}\β_1&β_2&β_3\β_1&β_2&β_3end{vmatrix}=rcdot overline{0}=overline{0}$

Достаточность: Пусть верно равенство $overline{α}хoverline{β}=overline{0}$, докажем, что векторы $overline{α}$ и $overline{β}$ коллинеарны. Так как векторное произведение равняется $overline{0}$, то его длина также равняется нулю. Следовательно, угол между $overline{α}$ и $overline{β}$ равняется $180^circ$ или $0^circ$. То есть, чтобы они были коллинеарны, векторы должны лежать на одной или параллельных прямых.

Теорема доказана.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

Содержание:

Формула
Примеры нахождения коллинеарного вектора

Формула

Для того чтобы вектор
$bar{a}=left(a_{x} ; a_{y}right)$ был коллинеарным вектору $bar{b}=left(b_{x} ; b_{y}right)$ необходимо, чтобы их соответствующие
координаты были пропорциональны, то есть их координаты удовлетворяли условию

$$frac{a_{x}}{b_{x}}=frac{a_{y}}{b_{y}}$$

Если векторы заданны в пространстве своими координатами:
$bar{a}=left(a_{x} ; a_{y} ; a_{z}right), bar{b}=left(b_{x} ; b_{y} ; b_{z}right)$, тогда условие коллинеарности имеет вид:

$$frac{a_{x}}{b_{x}}=frac{a_{y}}{b_{y}}=frac{a_{z}}{b_{z}}$$

Примеры нахождения коллинеарного вектора

Пример

Задание. Даны два вектора
$bar{a}=(2 ;-3)$ и $bar{b}=(-1 ; m)$. При каком значении
$m$ эти векторы будут коллинеарными?

Решение. Для того чтобы векторы
$bar{a}$ и
$bar{b}$ были коллинеарными необходимо,
чтобы их координаты были пропорциональными, то есть удовлетворяли условию:

$$frac{a_{x}}{b_{x}}=frac{a_{y}}{b_{y}}$$

Подставим координаты заданных векторов в это равенство и найдем значение
$m$:

$$frac{2}{-1}=frac{-3}{m}$$

По пропорции имеем:

$$2 cdot m=(-1) cdot(-3) Rightarrow 2 cdot m=3 Rightarrow m=frac{3}{2}=1,5$$

Ответ. Векторы
$bar{a}$ и
$bar{b}$ будут коллинеарными при
$m=1,5$

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Заданы два вектора
$bar{a}=(4 ;-m ; 1)$ и $bar{b}=(2 ;-3 ; n)$. При каких значениях
$m$ и
$n$ векторы
$bar{a}$ и
$bar{b}$ будут коллинеарными?

Решение. Для того чтобы векторы
$bar{a}$ и
$bar{b}$ были коллинеарными необходимо, чтобы их координаты
были пропорциональными, то есть чтобы выполнялись следующие равенства:

$$frac{4}{2}=frac{-m}{-3}=frac{1}{n}$$

А тогда значения неизвестных параметров
$m$ и
$n$ находим из равенств

$$frac{m}{3}=2 Rightarrow m=6$$
$$frac{1}{n}=2 Rightarrow n=frac{1}{2}=0,5$$

Ответ. Векторы
$bar{a}$ и
$bar{b}$ будут коллинеарными при
$m=6$ и $n=0,5$

Читать дальше: как найти вектор перпендикулярный вектору.

Источник

Необходимо
проверить набор всех формул.:

В
редакторе формул в кнопке «размер»
выбрать «определить размер» и
выставить:

обычный 12пт

крупный индекс
70%

мелкий индекс 50%

крупный символ 100%

мелкий символ 100%

Греческие
буквы (φ, α, β…) и русский текст должны
быть без наклона, т.е в редакторе формул
в кнопке «стили» надо выбрать для
них «текст», всё остальное набираем
в стиле «математический»
Все
векторы должны сверху иметь стрелку
(т.е. знак вектора).
Сохранить
текст для версии Word
2003.

1.1.
Вектор
– это направленный отрезок (или, другими
словами, упорядоченная пара точек).

Для
вектора принято обозначение
,
где точка– начало, точка– конец вектора.

1.2.
Длиной
(модулем) вектора

называется расстояние между началом
вектора и его концом. Обозначается.

1.3.
Вектор, у
которого совпадают начало и конец,
называют нулевым
вектором и
обозначают
.

2. Коллинеарные и компланарные векторы

2.1.
Векторы,
лежащие на одной прямой или на параллельных
прямых, называются коллинеарными.

Коллинеарность
векторов принято обозначать
.
Если хотят подчеркнуть сонаправленность
коллинеарных векторов, пишут,
если же коллинеарные векторы противоположно
ориентированы, принята запись.
Нулевой вектор принято считать
коллинеарным любому вектору.

2.2.
Совокупность трех и более векторов,
лежащих в одной плоскости или параллельных
одной плоскости, называют компланарной.

Например,
на рис. 1 тройки векторов
иявляются компланарными, тройка– не компланарна. А векторыи–
коллинеарны,и–
коллинеарны, причем,,.

Рис. 1

3. Линейные операции над векторами

3.1. Суммой векторов
иназывается вектор, который находится
либо по правилу параллелограмма (рис.
2), либо по правилу треугольника (рис.
3). В первом случае для нахождения суммы
оба вектора откладываются от одной
точки, на этих векторах строится
параллелограмм. Тогда сумма данных
векторов есть вектор, начало которого
совпадает с началами обоих векторов-слагаемых
и направленный по диагонали параллелограмма
(рис. 2). Чтобы найти сумму двух векторов
ипо правилу треугольника, нужно расположить
векторы последовательно (от конца
вектора
отложить вектор
).
Тогда их сумма – это вектор, начало
которого совпадает с началом первого
вектора (вектора
),
а конец совпадает с концом второго
вектора (вектора
)(рис.
3).

Рис. 2
Рис. 3

3.2. Сумму любого числа векторовнаходят по правилу многоугольника (рис.
4).

Рис. 4

По правилу многоугольника путем
параллельного переноса начало каждого
последующего вектора помещают в конец
предыдущего. Вектор
получен путем соединения начала первого
вектора и конца последнего вектора.

3.3. Произведением вектора
на числоназывается вектор,
удовлетворяющий условиям:

1.
,
если>
0;

,
если<
0.

2.
.

3.
.

При этом
принята запись
.

На рис.5 изображены векторы
.

Рис. 5

4. Базис. Разложение вектора по базису

4.1. Базисом на плоскостиназывают
пару ненулевых неколлинеарных векторов.

4.2. Разложить векторпо базисуи–
значит представить векторв виде

где
– некоторые числа, которые называютсякоординатамивекторав базисеи.

4.3. Два вектора коллинеарны, если их
координаты пропорциональны.

Например, в пространстве векторы
и– коллинеарны, так как,
где.
Векторыина плоскости не коллинеарны, так как,
а значит, они образуют базис.

4.4. Если известны координаты началаи координаты концавектора,
то его координаты находятся по формуле

4.5. Если вектор
на плоскости задан своими координатами,
то его длина находится по формуле

В
пространстве длина вектора
вычисляется по
формуле

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

В данной публикации мы рассмотрим, какие векторы называются коллинеарными и перечислим условия, при которых они являются таковыми. Также разберем примеры решения задач по этой теме.

Условия коллинеарности векторов
Примеры задач

Условия коллинеарности векторов

Векторы, лежащие на одной или нескольких параллельных прямых, называются коллинеарными.

Два вектора коллинеарны, если выполняется одно из условий ниже:

1. Существует такое число n, при котором a · n = b.

2. Отношения координат векторов равны. Но данное условие не может применяться, если одна из координат равняется нулю.

3. Векторное произведение равно нулевому вектору (применимо только для трехмерных задач).

Примеры задач

Задание 1
Даны векторы a = {2; 5}, b = {3; 7} и c = {6; 15}. Определим, есть ли среди них коллинеарные.

Решение:
У заданных векторов нет нулевых координат, значит мы можем применить второе условие коллинеарности.

Следовательно, коллинеарными являются только векторы a и c.

Задание 2
Выясним, при каком значении n векторы a = {4; 10} и b = {2; n} коллинеарны.

Решение:
Т.к. среди координат нет нулей, согласно второму условию мы можем составить их соотношение, чтобы рассчитать недостающий элемент.

Значит, n = 2 · 10 : 4 = 5.

Источник