Как написать коротко математика - Правописание и грамматика

Как писать короткие.

На этой странице находится вопрос Как писать короткие?. Здесь же – ответы на него,
и похожие вопросы в категории Математика, которые можно найти с помощью
простой в использовании поисковой системы. Уровень сложности вопроса
соответствует уровню подготовки учащихся 1 — 4 классов. В комментариях,
оставленных ниже, ознакомьтесь с вариантами ответов посетителей страницы. С
ними можно обсудить тему вопроса в режиме on-line. Если ни один из
предложенных ответов не устраивает, сформулируйте новый вопрос в поисковой
строке, расположенной вверху, и нажмите кнопку.

Источник

Для того, чтобы наглядно представить задачу и облегчить себе процесс ее решения, составляется краткая запись условия задачи. В краткой записи фиксируются величины, числа – данные и искомые, а также некоторые слова, показывающие, о чем говорится в задаче: «было», «положили», «стало» и т. п. и знаки, означающие отношения: «больше», «меньше», «одинаково» и т. п.

Краткую запись задачи можно выполнять в виде опорной схемы, таблицы, чертежа, с помощью геометрических фигур.

Для того чтобы краткая запись в максимальной степени способствовала решению задачи, нужно:

1) Краткую запись составлять на основе анализа текста задачи;
2) В краткой записи должно быть минимальное количество условных обозначений;
3) Количество вопросительных знаков в краткой записи должно соответствовать количеству действий в задаче;
4) Форму краткой записи выбирать такую, чтобы она более наглядно представляла условие задачи.

Основные виды краткой записи в начальной школе

Краткая запись в зависимости от типа задач:

Выберите страницу:

Возможны вариации перечисленных вариантов краткой записи в зависимости от условия задачи. Возможна и запись в виде таблиц и рисунков.

Примеры задач:

— Витя собрал коллекцию из 18 камней и разложил на коробки поровну. Сколько камней в каждой банке?

Простая задача на деление на равные части, оформляем такие задачи в виде таблицы

В 1 коробке Количество коробок Всего камней
? к. 3 к. 18 к.

— 8 приглашений разложили в конверты, по 2 в каждый. Сколько использовали конвертов?

В 1 конверте Количество конвертов Всего приглашений
2 пр. ? к. 8 пр.

— Трое друзей решили сложится поровну и купить мяч стоимостью 60 рублей. Сколько денег должен дать каждый из них?

На 1 чел. денег Количество чел. Всего денег
поровну 3 чел. 60 руб.

— Одну деталь мастер должен делать за 45 мин, а делает за 38 мин. Сколько времени сэкономит мастер, когда он сделает 8 деталей?

Составная задача на разностное сравнение, лучше оформить в виде таблицы.

— Вера посадила 9 луковиц, по 3 луковицы в ряд. Сколько получилось рядов?

Это простая задача на деление по содержанию. Такую задачу нагляднее оформить картинкой.

— В детский сад привезли два бидона с молоком, по 20 л в каждом. За завтраком дети выпили 12 л молока. Сколько литров молока осталось?

Задача на нахождение остатка.

Было — 20 л и 20 л
Выпили — 12 л
Осталось — ? л

— В куске ткани было 24 м ткани. Из 10 м этой ткани сшили одинаковые детские костюмы, а из остальной ткани-7 одинаковых детских пальто. Сколько метров ткани расходовали на одно пальто.

Было -24 м
Израсходовали — 10 м
Осталось — 7 к. по ? м

— Когда брат полил 5 грядок, а сестра -3 грядки, им осталось полить 4 грядки. Сколько всего грядок должны полить дети?

Было — ? гр.
Полили — 5 гр. и 3 гр.
Осталось — 4 гр.

— В парк привезли 33 куста роз. Когда на нескольких клумбах посадили по 6 кустов, то осталось еще 15 кустов. Сколько было клумб?

Было — 33 к.
Посадили — ? кл. по 6 к.
Осталось — 15 к.

— В прятки играли 12 ребят. К ним присоединились 3 девочки и 4 мальчика. Сколько всего ребят стали играть в прятки?

Было — 12 р.
Пришли — 3 д. и 4 м.
Стало — ? р.

— У Саши было 6 наклеек. Он подарил другу 2 наклейки. Потом Саша купил еще 5 наклеек. Сколько наклеек стало у Саши?

Было — 6 н.
Подарил — 2 н.
Купил — 5 н.
Стало — ? н.

— На полянке паслись 14 коров, а овец на 10 больше. Сколько животных паслись на полянке?

— В первый день вырыли 5м траншеи, во второй на 3м меньше, чем в первый, в третий на 1м больше, чем во второй. На сколько больше вырыли траншей в первый и во второй день вместе, чем в третий?

— На двух полках было 17 кг меда. Со второй полки продали 5 кг и на 2 полках стало поровну. Сколько кг меда было на 1 полке?

Нагляднее представит задачу запись в виде схемы.

Пояснения к решению задач

Эта форма работы над составной задачей предусматривает проверку умения учащихся по данным действиям решения задачи пояснить, на какой вопрос и с какой целью отвечает действие. Таким образом, в конце каждого действия пишем пояснение, что именно мы нашли этим действием. Такая форма работы помогает учащимся увидеть другие отношения, вести необходимую цепочку логических рассуждений, анализировать и делать выводы.

Ответ задачи

Если использовались пояснения, ответ можно записать кратко. Если же не использовались, пишем полный ответ.

Источник

Математика

Оформление задач также требует соблюдения принятых норм. Краткая запись условия задач оформляется в соответствии их вида. «Главные» слова пишутся с большой буквы.

В 1-4 классах нет необходимости писать слово «Решение».

Существует несколько форм записи решения задач: по действиям, по действиям с письменными пояснениями, по действиям с записью вопроса, выражением, уравнением.

Например: по действиям

Задача: У школьницы было 38 руб. Она купила 4 конверта по 5 руб., а на остальные деньги несколько открыток по 3 руб. Сколько открыток купила школьница?

1. 4 * 5 = 20 (руб.)

2. 38 – 20 = 18 (руб.)

3. 18 : 3 = 6 (откр.)

Ответ: 6 открыток купила школьница.

Например: по действиям с пояснениями

1. 4 * 5 = 20 (руб.) потратила на открытки

2. 38 – 20 = 18 (руб.) осталось денег

3. 18 : 3 = 6 (откр.) купила открыток

Ответ: 6 открыток купила школьница.

Например: по действиям с вопросами

1. Сколько денег потратила школьница на конверты?

4 * 5 = 20 (руб.)

2. Сколько денег осталось у школьницы?

38 – 20 = 18 (руб.)

3. Сколько открыток купила школьница

18 : 3 = 6 (откр.)

Ответ: 6 открыток купила школьница.

Например: выражением

(38 – 4 * 5 ) : 3 = 6 (откр.)

Ответ: 6 открыток купила школьница.

Например: уравнением

4 * 5 + х * 3 = 38

20 + х * 3 = 38

х * 3 = 38 – 20

х * 3 = 18

х = 18 : 3

х = 6

20 18

4 * 5 + 6 * 3 = 38

Ответ: 6 открыток купила школьница.

Слово «Ответ» пишется с заглавной буквы под решением. В первом классе ответ записывается кратко. Позднее учащиеся должны писать полный ответ.

Ответ: всего купили 10 мячей.

________________________________________________________________

Напомним, что в математике при сокращении наименований единиц измерений точки не ставятся.

Например: мм, м, см, ч, мин, км, кг, г и др.

________________________________________________________________

При оформлении решения выражений на порядок действий следует требовать от учащихся соблюдения следующих норм:

— записать выражение полностью;

— указать цифрами над знаками порядок действий;

— расписать выполняемые действия по порядку (применяя устные или письменные приемы вычислений), отступив вниз одну клетку;

— записать окончательное значение выражения.

Например :

3450-145*2+1265:5=3413

1)145*2=290

2) _1265 5 3) _3450 4) + 3160

_ 26 3160 3413

_ 15

________________________________________________________________

Приводим образцы оформления сложных уравнений, как это требуют учителя математики в средней школе.

627+123-56*2=638

Все письменные вычисления выполняются справа от уравнения.

________________________________________________________________

Оформлению записи задач геометрического типа

Все чертежи выполняются простым карандашом по линейке. Измерения можно подписывать ручкой. Обозначения буквами выполняются печатным шрифтом, прописными буквами латинского алфавита.

Слова длина, ширина прямоугольника не допускается обозначать кратко латинскими буквами.

Длина прямоугольника 12 см , его ширина равна 6 см . Вычислите периметр и площадь прямоугольника.

Образец краткой записи и решения задачи:

Дано: АВСД

а=12 см

в=6 см

Найти: Р , S

Р= (а+ в) *2

Р = (12+6)*2=36 (см)

S = a * в

S = 12*6=72 (см 2 )

Ответ: Р =36 см, S =72 см 2

Письмовник

Сокращения должны быть понятны читателю. Большое число необщепринятых сокращений затрудняет чтение текста. При усечении слова оставшаяся часть должна позволять легко и безошибочно восстанавливать полное слово, например: филос., филол., не фил.

Нежелательны сокращения, совпадающие по написанию с другими. Такие сокращения допустимы только в том случае, если контекст подсказывает, какое именно слово или словосочетание сокращено.

Сокращения должны быть единообразными. Принцип единообразия выдерживается, когда сокращаются (или не сокращаются) все однотипные слова. Форма сокращения при этом должна быть одинаковой.

Где найти правила сокращения слов?

Здесь можно найти многие общеупотребительные сокращения:

Приводим список некоторых общепринятых сокращений:

адм.-терр. административно-территориальный

акад. академик, академия

а. л. и авт. л. авторский лист

а/о акционерное общество, автономный округ, автономная область

б-ка библиотека

в. век, вв. века

вкз. вокзал

в/о вечернее отделение

вост.-европ. восточноевропейский

г. год; гора

гг. годы; горы

г. и г-н господин

гг. и г-да господа

г. и г-жа госпожа

г. и гор. город

гос. государственный

гос-во государство

гр. и гр-ка гражданка

гр. и гр-н гражданин

гр-не граждане

деп. департамент; депутат

дисс. диссертация

д. о. и д/о дом отдыха

д/о дневное отделение

дол. долина

долл. доллар

ежедн. ежедневный

ж. и жен. женский

ж. д. и ж/д железная дорога

ж.-д. и ж/д железнодорожный

зап. и з. западный

зап.-европ. западноевропейский

заруб. зарубежный

з. к. и з/к заключенный

з/о заочное отделение

изд-во издательство

ин. и иностр. иностранный

ин-т и инст. институт

и. о. исполняющий обязанности; имя и отчество

и т. д. и так далее

и т. п. и тому подобное, и тому подобные

и т. д. и т. п. и так далее и тому подобное

канд. и к. кандидат

кг килограмм

м. и муж. мужской

Мб и Мбайт мегабайт

мб миллибар

мин. министр

мин-во и мин. министерство

мин. и м. минута (Написание этого сокращения с точкой зафиксировано в «Русском орфографическом словаре» РАН; согласно ГОСТу, это сокращение должно быть написано без точки. – Прим. ред.)

мин. и миним. минимальный

мм миллиметр

моск. московский

нед. неделя

п. параграф, пункт

пп. параграфы, пункты

пер. и п. переулок

п/я почтовый ящик

просп., пр. и пр-т проспект

р. и руб. рубль

с. и сек. секунда

с. и стр. страница

см сантиметр

СПб. Санкт-Петербург

т. том, тт. тома

т. и тел. телефон

т. и тов. товарищ

т. и тыс. тысяча

т/к телеканал

Ф. И. О. и ф. и. о. фамилия, имя, отчество

ч. час (Написание этого сокращения с точкой зафиксировано в «Русском орфографическом словаре» РАН; согласно ГОСТу, это сокращение должно быть написано без точки. – Прим. ред.)

Как правильно сокращать названия предметов при заполнении дневника?

Названия многих учебных предметов не помещаются полностью в графу дневника. Тогда применяем некоторые сокращения. Сокращают название предмета до согласной буквы.
Например:

математика — матем.
русский язык — рус. яз.
история — ист.
информатика — информ.
физкультура — физкульт.
трудовое обучение — труд
английский язык — англ. яз.
литературное чтение — лит. чт.
окружающий мир — окр. мир

Источник

Скачать материал

Сейчас обучается 58 человек из 31 региона

Сейчас обучается 75 человек из 31 региона

Сейчас обучается 53 человека из 23 регионов

Описание презентации по отдельным слайдам:

1 слайд

Памятка по оформлению
краткой записи к задачам
1-2 класс

Выполнила:
учитель начальных классов
Баратова Г.Р.
2 слайд

Содержание
Простые задачи
Нахождение суммы 1 2 3
Увеличение числа на несколько единиц 4
Уменьшение числа на несколько единиц 5
Нахождение неизвестного слагаемого 6 7
Нахождение остатка 8
Нахождение неизвестного вычитаемого 9
Нахождение неизвестного уменьшаемого 10
Разностное сравнение 11 12

Составные задачи
Нахождение суммы 13 14 15 16
Нахождение остатка 17 18
Нахождение неизвестного слагаемого 19 20
Нахождение неизвестного вычитаемого 21 22 23
Нахождение третьего слагаемого 24
Нахождение неизвестного уменьшаемого 25 26
Разностное сравнение 27 28 29
3 слайд

Аня вымыла 5 тарелок, а Миша вымыл 4 тарелки. Сколько всего тарелок вымыли дети?
Аня – 5 т.
? т.
Миша – 4 т.
5 + 4 = 9 (т.)
Ответ: 9 тарелок вымыли дети.
Задача №1
4 слайд

На стоянке было 2 грузовика. Вечером приехало ещё 5 грузовиков Сколько всего грузовиков на стоянке?
Было – 2 г.
Приехало – 5 г.
Стало – ? г.
2 + 5 = 7 (г.)
Ответ: 7 грузовиков всего на стоянке.
Задача №2
5 слайд

На опушке леса росло 5 клёнов и 4 тополя, а сосен росло столько, сколько клёнов и тополей вместе. Сколько сосен росло на опушке леса?
Клёнов – 5 д.
Тополей – 4 д.
Сосен – ? д., К. + Т.
5 + 4 = 9 (д.)
Ответ: 9 сосен росло на опушке леса.
Задача №3
6 слайд

У Васи 7 марок, а у Егора на 3 марки больше. Сколько марок у Егора?
Вася – 7 м.
Егор – ? м., на 3 м. >
7 + 3 = 10 (м.)
Ответ: 10 марок у Егора.
Задача №4
7 слайд

В первой группе 10 учеников, а во второй на 3 ученика меньше. Сколько учеников во второй группе?
В I г. – 10 уч.
Во II г. – ? уч., на 3 уч. <
10 – 3 = 7 (уч.)
Ответ: 7 учеников во второй группе.
Задача №5
8 слайд

У Ани было 9 роз. 5 розовых, остальные белые. Сколько белых роз было у Ани?
Розовые – 5 р.
9 р.
Белые – ? р.
9 – 5 = 4 (р.)
Ответ: 4 белые розы были у Ани.
Задача №6
9 слайд

Дед Мазай вёз на своей лодке 5 зайцев. Он подобрал ещё несколько зайцев, и их стало 8. Сколько зайцев подобрал дед Мазай?
Было – 5 з.
Подобрал – ? з.
Стало – 8 з.
8 – 5 = 3 (з.)
Ответ: 3 зайца подобрал дед Мазай.
Задача №7
10 слайд

На проводах сидели 9 ворон. 5 ворон улетели. Сколько ворон осталось?
Было – 9 в.
Улетели – 5 в.
Осталось – ? в.
9 – 5 = 4 (в.)
Ответ: 4 вороны осталось.
Задача № 8
11 слайд

На кустике висело 7 ягод клубники. Когда несколько ягод созрело и упало, осталось 5 ягод. Сколько ягод созрело и упало?
Было – 7 яг.
Упало – ? яг.
Осталось – 5 яг.
7 – 5 = 2 (яг.)
Ответ: 2 ягоды созрело и упало.
Задача № 9
12 слайд

В зоопарке несколько медведей. Когда трёх медведей перевезли в другой зоопарк, осталось 6 медведей. Сколько медведей было в зоопарке первоначально?
Было – ? м.
Перевезли – 3 м.
Осталось – 6 м.
3 + 6 = 9 (м.)
Ответ: 9 медведей было в зоопарке первоначально.
Задача № 10
13 слайд

Один мальчик поймал 8 крабов, а другой 3 краба. На сколько крабов первый мальчик поймал больше второго?
I м. – 8 к.
на ? >
II м. – 3 к.
8 – 3 = 5 (к.)
Ответ: на 5 крабов первый мальчик поймал больше, чем второй.
Задача № 11
14 слайд

Один арбуз весит 5 кг, а другой 8 кг. На сколько килограммов один арбуз легче другого?
I ар. – 5 кг
на ? <
II ар. – 8 кг
8 – 5 = 3 (кг)
Ответ: на 3 килограмма один арбуз легче другого.
Задача № 12
15 слайд

На пришкольном участке 6 берёз, а лип на 4 меньше. Сколько всего деревьев на пришкольном участке?
Берёз – 6 д.
? д.
Лип – ?д., на 4 д.
Ответ: 8 деревьев всего на пришкольном участке.
Задача № 13
1) 6 – 4 = 2 (д.) – лип
2) 6 + 2 = 8 (д.)
16 слайд

В шкафу стоят 2 кастрюли, сковородок на 3 больше, а ваз столько, сколько кастрюль и сковородок вместе. Сколько ваз стоит в шкафу?
Кастрюли – 2 шт.
Сковородки – ? шт., на 3 шт. >
Вазы – ? шт., К. + С.
Ответ: 7 ваз стоит в шкафу.
Задача № 14
1) 2 + 3 = 5 (шт.) – сковородок
2) 2 + 5 = 7 (шт.)
17 слайд

У Тани 3 яблока, груш на 2 больше, чем яблок, а персиков на 4 меньше, чем груш. Сколько всего фруктов у Тани?
Яблоки – 3 шт.
Груши – ? шт., на 2 шт. > ? шт.
Персики – ? шт., на 4 шт. <
Ответ: 8 фруктов всего у Тани.
Задача № 15
1) 3 + 2 = 5 (шт.) – груш
2) 5 – 4 = 1 (шт.) – персиков
3) 3 + 5 = 7 (шт.) – яблок и груш вместе
4) 7 + 1 = 8 (шт.)
18 слайд

Жёлтых – 17 к.
Зелёных – ? к., на 6 к. < ? к.
Красных – ? к., на 12 к. >
В коробке 17 жёлтых кубиков, зелёных на 6 меньше, чем жёлтых, а красных на 12 больше, чем зелёных и жёлтых кубиков вместе. Сколько всего кубиков в коробке?
Ответ: 68 кубиков всего в коробке.
Задача № 16
1) 17 – 6 = 11 (к.) – зелёных
2) 17 + 11 = 28 (к.) – жёлтых и зелёных вместе
3) 28 + 12 = 40 (к.) – красных
4) 28 + 40 = 68 (к.)
19 слайд

Было – 4 г. и 6 г.
Израсходовали – 8 г.
Осталось – ? г.
Нашли 4 белых гриба и 6 подосиновиков. 8 грибов пошло на суп. Сколько грибов осталось?
Ответ: 2 гриба осталось.
Задача № 17
1) 4 + 6 = 10 (г.) – было
2) 10 – 8 = 2 (г.)
20 слайд

Было – 23 р.
Подарил – 6 р. и 4 р.
Осталось – ? р.
У Феди в аквариуме плавали 23 рыбки? Мальчик подарил 6 рыбок Ване и 4 рыбки Максиму. Сколько рыбок осталось в аквариуме у Феди?
Ответ: 13 рыбок осталось в аквариуме у Феди.
Задача № 18
1) 6 + 4 = 10 (р.) – подарил
2) 23 – 10 = 13 (р.)
21 слайд

Было – 22 п. и 13 п.
Прилетело – ? п.
Стало – 49 п.
На поле сидело 22 воробья и 13 синичек. Когда прилетело ещё несколько птиц, их стало 49. Сколько птиц прилетело?
Ответ: 14 птиц прилетело.
Задача № 19
1) 22 + 13 = 35 (п.) – было
2) 49 – 35 = 14 (п.)
22 слайд

Было – 6 к.
Причалило – 3 к. и ? к.
Стало – 19 к.
У причала стояло 6 катеров. Утром причалило 3 катера и несколько катеров причалило вечером, и после этого у причала стало 19 катеров. Сколько катеров причалило вечером?
Ответ: 10 катеров причалило вечером.
Задача № 20
1) 19 – 6 = 13 (к.) – причалило всего
2) 13 – 3 = 10 (к.)
23 слайд

Было – 7 б. и 3 б.
Улетело –? б.
Осталось – 5 б.
Маша увидела 7 белых и 3 пёстрых бабочек. Когда несколько бабочек улетело, их осталось 5. Сколько бабочек улетело?
Ответ: 5 бабочек улетело.
Задача № 21
1) 7 + 3 = 10 (б.) – было
2) 10 – 5 = 5 (б.)
24 слайд

Было – 20 в.
Улетели – 10 в. и ? в.
Осталось – 6 в.
На аэродроме было 20 вертолётов. Утром улетело 10 вертолётов. Сколько вертолётов улетело днём, если к вечеру их осталось 6?
Ответ: 4 вертолёта улетело днём.
Задача № 22
1) 20 – 6 = 14 (в.) – улетели всего
2) 14 – 10 = 4 (в.)
25 слайд

Было – 9 г.
Завяли – ? г.
Осталось – 2 г. и 3 г.
В букете было 9 гвоздик. Когда несколько гвоздик завяли, остались 2 красные и 3 розовые гвоздики. Сколько гвоздик завяло?
Ответ: 4 гвоздики завяло.
Задача № 23
1) 2 + 3 = 5 (г.) – осталось
2) 9 – 5 = 4 (г.)
26 слайд

В трёх классах на окнах стоят 35 горшков с цветками. В первом классе 11 горшков, во втором 13. Сколько горшков с цветками стоит в третьем классе?
Ответ: 11 горшков с цветками стоят в третьем классе.
Задача № 24
1)11 + 13 = 24(г.) – в I и II классах
2)35 – 24 = 11(г.)
I к. – 11 г..
II к. – 13 г. 35 г.
III к. – ? г.
27 слайд

Бабушка испекла блины. Папа съел 15 блинов, мама 10. Сколько всего блинов испекла бабушка, если осталось 22 блина?
Ответ: 47 блинов всего испекла бабушка.
Задача № 25
1)15 + 10 = 25(б.) – съели
2)25 + 22 = 47 (б.)
Было – ? б.
Съели – 15 б. и 10 б.
Осталось – 22 б.
28 слайд

В пенале лежали карандаши. Когда туда положили ещё 3 простых и 7 цветных карандашей, их стало 22. Сколько карандашей лежало в пенале сначала?
Ответ: 12 карандашей лежало в пенале сначала.
Задача № 26
1)3 + 7 = 10 (к.) – положили
2)22 – 10 = 12 (к.)
Было – ? к.
Положили – 3 к. и 7 к.
Стало – 22 к.
29 слайд

В зале музея 18 картин. Из них 6 пейзажей, а остальные портреты. На сколько больше портретов, чем пейзажей?
Ответ: на 6 портретов больше, чем пейзажей.
Задача № 27
1) 18 – 6 = 12 (к.) – портреты
2)12 – 6 = 6 (к.)
Пейзажи – 6 к.
18 к. на ? >
Портреты – ? к.
30 слайд

В саду 15 кустов малины, кустов крыжовника на 3 меньше, чем малины, а кустов смородины на 11 больше, чем малины. На сколько меньше кустов смородины, чем крыжовника и малины вместе?
Ответ: на 1 куст меньше смородины, чем крыжовника и малины вместе.
Задача № 28
1) 15 – 3 = 12 (к.) – крыжовника
2) 15 + 11 = 26 (к.) – смородины
3) 15 + 12 = 27 (к.) – малины и крыжовника вместе
4) 27 – 26 = 1 (к.)
Малина – 15 к.
Крыжовник – ? к., на 3 к. < на ? <
Смородина – ? к., на 11 к. >
31 слайд

Над полянкой кружились 8 пчёл и 11 стрекоз. 15 из них сели на цветы. На сколько больше насекомых село на цветы, чем продолжало кружиться?
Ответ: на 11 насекомых больше село на цветы, чем продолжало кружиться.
Задача № 29
1) 8 + 11 = 19 (н.) – было
2) 19 – 15 = 4 (н.) – осталось
3) 15 – 4 = 11 (н.)
Было – 8 н. и 11 н.
Сели – 15 н.
Осталось – ? н.
на ? >
32 слайд

http://files.vector-images.com/clipart/crab_mhk1.gif- краб
http://files.vector-images.com/clipart/birch1.gif — берёза
http://files.vector-images.com/clipart/vase_shlp1.gif — ваза
http://files.vector-images.com/clipart/apples-lo-252.gif — яблоки
http://i023.radikal.ru/0801/c2/2f07708f837c.jpg- — кубики
http://files.vector-images.com/clipart/mushroom_shlp1.gif — гриб
http://files.vector-images.com/clipart/aquarium2.gif — аквариум
http://static.freepik.com/image/th/11-936.jpg — птица
http://www.clipartov.net/images/mini/07/0000006490.jpg — катер
http://files.vector-images.com/clipart/butterfly_shlp2.gif- бабочка
http://files.vector-images.com/clipart/helicopter_vsl5.gif- вертолёт
http://files.vector-images.com/clipart/carnation_oa1.gif- гвоздика
http://files.vector-images.com/clipart/rose_oa6.gif- роза
Используемые источники

Узорова О. В. Нефедова Е. А. 2518 задач по математике 1 -4 классы
Издательство «Астрель», 2009
http://files.vector-images.com/clipart/flower_shlp2.gif- цветок в горшке
33 слайд

http://files.vector-images.com/clipart/mardigras_001.gif- блины
http://files.vector-images.com/clipart/pencil_shlp2.gif- карандаш
http://cartoonclipartfree.com/Cliparts_Free/Gegenstaende_Free/Cartoon-Clipart-Free-78.gif- картина
http://img-fotki.yandex.ru/get/5813/119528728.d09/0_a241c_e903c84b_XL- куст малины
http://files.vector-images.com/clipart/insect_mhl2.gif- стрекоза
http://files.vector-images.com/clipart/kitchen_prg28.gif — тарелки
http://files.vector-images.com/clipart/hare1.gif- заяц
http://files.vector-images.com/clipart/schoolboy_gk12.gif- ученик
http://files.vector-images.com/clipart/truck6.gif- грузовик
http://files.vector-images.com/clipart/pine1.gif- сосна
http://www.vectory.ru/products_pictures/vorona00712.gif — ворона
http://img.cliparto.com/pic/s/187502/3202247-postage-stamp.jpg- марка
http://files.vector-images.com/clipart/strawberry_hr1.gif- клубника
http://4-8class-math-forum.ru/i/p/6-1-6-b522.gif- 1 слайд
http://files.vector-images.com/clipart/bear8.gif — медведь
http://files.vector-images.com/clipart/watermelon_okh1.gif- арбуз

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 144 655 материалов в базе

Выберите категорию:
Выберите учебник и тему

Выберите класс:
Тип материала:
- Все материалы
- Статьи
- Научные работы
- Видеоуроки
- Презентации
- Конспекты
- Тесты
- Рабочие программы
- Другие методич. материалы

Найти материалы

Другие материалы

27.12.2015
3055
19

Рейтинг:
1 из 5

27.12.2015
1863
6

27.12.2015
523
0

27.12.2015
1073
1

Рейтинг:
1 из 5

27.12.2015
16541
173

27.12.2015
569
0

Рейтинг:
5 из 5

27.12.2015
4296
10

Вам будут интересны эти курсы:

Курс повышения квалификации «Возрастные особенности детей младшего школьного возраста»
Курс повышения квалификации «Роль педагога в реализации концепции патриотического воспитания школьников в образовательном процессе в свете ФГОС»
Курс повышения квалификации «Использование мини-проектов в школьном: начальном, основном и среднем общем и среднем профессиональном естественнонаучном образовании в условиях реализации ФГОС»
Курс повышения квалификации «Воспитание и социализация учащихся в условиях реализации ФГОС»
Курс повышения квалификации «Сопровождение детского отдыха: от вожатого до руководителя детского лагеря»
Курс повышения квалификации «Система образовательной организации в начальном общем образовании в условиях реализации ФГОС»
Курс повышения квалификации «Тайм-менеджмент — персональная эффективность преподавателя»
Курс профессиональной переподготовки «Организация инклюзивного обучения в сфере образования»
Курс повышения квалификации «Теория и практика инклюзивного обучения в образовательной организации в условиях реализации ФГОС»
Курс повышения квалификации «Мотивационное сопровождение учебного процесса младших школьников «группы риска» в общеобразовательном учреждении»
Курс повышения квалификации «Психолого-педагогическая диагностика в современном образовательном процессе»
Курс повышения квалификации «Применение современных педагогических технологий в образовательном процессе в условиях реализации ФГОС»
Курс повышения квалификации «Организация работы с обучающимися с ограниченными возможностями здоровья (ОВЗ) в соответствии с ФГОС»
Курс профессиональной переподготовки «Оказание психолого-педагогической помощи лицам с ОВЗ»

Источник

Образцы оформления задачи

1. Задачи на нахождение суммы

В вопросе задач такого типа всегда есть «Сколько всего?»

На школьном участке ребята посадили 7 лип и 4 клёна.

Сколько всего деревьев посадили ребята?

2. Задачи на нахождение остатка

В вопросе «Сколько … осталось?»

Мама с Юлей посадили 7 кустов смородины. Затем они полили 4 куста.

Сколько кустов смородины осталось полить?

3. Задачи на увеличение или уменьшение числа на несколько единиц

В условии «на … больше«

Папа с Володей собирали грибы. Папа нашёл 8 грибов, а Володя на 3 гриба больше.

Сколько грибов нашёл Володя?

В условии «на … меньше«

У Ани было 10 рублей, а у Оли на 2 рубля меньше.

Сколько денег было у Оли?

4. Задачи на разностное сравнение

В вопросе «На сколько больше…?»

Краски стоят 15 рублей, а альбом 8 рублей.

На сколько рублей краски дороже альбома?

«На сколько меньше…?»

Дыня весит 3 кг, а арбуз 7 кг.

На сколько кг дыня легче арбуза?

5. Задачи на нахождение неизвестного слагаемого

В условии «Было…Стало…»

В вопросе «Сколько добавили?»

У Саши было 4 карандаша. Когда ему купили еще несколько карандашей, у него их стало 9.

Сколько карандашей купили Саше?

6. Задачи на нахождение неизвестного вычитаемого

В условии «Было… Осталось…»

В вопросе «Сколько уехало?»

«Сколько человек вышло?»

В гараже было 9 машин. Когда несколько машин уехало, в гараже осталось 5 машин.

Сколько машин уехало?

7. Задачи на нахождение неизвестного уменьшаемого

В условии «Убрали… Осталось…»

В вопросе «Сколько было сначала?»

После того, как Дима отдал 2 свои машинки младшему брату, у него осталось 6 машинок.

Сколько машинок было у Димы сначала?

Задачи в 2 и 3 действия

Первый вид

Бабушка испекла пончики и разложила их по тарелкам. На первую тарелку она положила 5 пончиков, а на вторую на вторую на 2 пончика меньше.

Сколько всего пончиков испекла бабушка?

Второй вид

В классе два маленьких аквариума. В первом аквариуме 4 рыбки, а во втором — на 2 рыбки больше.

Сколько рыбок в двух аквариумах?

Третий вид

У Тани было 10 тетрадей. Она использовала 4 тетради.

На сколько больше тетрадей осталось, чем Таня использовала?

Четвёртый вид

У Юры было 12 счетных палочек. Для решения примеров он использовал сначала 3, а потом еще 4 палочки.

Сколько палочек у него осталось?

или

У Вани было 20 рублей. На покупку карандаша и ручки он истратил 6 и 8 рублей.

Сколько рублей осталось у Вани?

Задачи с составлением таблиц по их условию:

I тип:

На 3 одинаковые шторы израсходовали 18 м ткани. Сколько таких штор можно сшить из 30 м такой же ткани?

II тип:

В двух одинаковых пакетах 4 кг муки. Сколько килограммов муки в пяти таких пакетах?

Задачи с составлением рисунка по условию:

Два года назад Юле было 10 лет. Сколько лет будет Юле через 6 лет?

Источник

При решении задач в начальной школе, да и не только, записывают краткую запись. Хочу поделиться своим мнением о краткой записи.

Краткая запись. Зачем нужна краткая запись?

Краткая запись — это коротко записанное условие задачи, последним в краткой записи пишется вопрос к задаче. Следующий этап-решение. После него ответ.

Для чего нужна краткая запись? Раньше считалось для облегчения выбора действия, чтобы найти неизвестную величину. Но так ли это?

«В школе старшего сына на уроках математики мучают некоей краткой записью задач»… Это мнения родителей и я с ним согласна.

Когда я получала педагогическое образование, краткая запись при решении задачи была обязательна (мы писали виды краткой записи: фигурная скобка – сколько всего; стрелочка к большей (меньшей) величине – на столько больше (меньше); было, взяли, осталось… и т.д. ) Например:

Вот фрагмент урока по теме «Краткая запись».

« На проводах сидело 20 ласточек. Из них улетело 5 ласточек. Сколько ласточек осталось на проводах?

У.: — Назовите условие этой задачи?

— Назовите требование этой задачи? (Вопрос задачи.)

— Давайте вернемся к условию этой задачи. О чем говорится? Ласточки что делали?

— Давайте составим краткую запись.

Сидело- 20 л.

Улетело – 5 л.

Осталось — ? л.

У.: — Как вы думаете, когда есть краткая запись задачи, решать саму задачу легче будет?«

Я, Сафонова Ирина Евгеньевна, учитель начальных классов, думаю, что НЕТ, исходя из опыта работы, личного опыта (выполняя домашние задания со своими собственными детьми)!

Шло время, увеличивался стаж работы, приходило осознание методик, приобретённых в институте и я стала понимать, что дети обладающие гибкостью ума, легко составляют краткую запись и способ действия выбирают правильно, находя неизвестную величину. А самое главное, что этим детям и краткая запись не нужна, они и без краткой записи выбирают правильное действие для нахождения неизвестного!

А ведь мы, учителя, должны дать «костыль» — опору, тем ученикам, которые не обладают гибкостью ума, а эти ученики, как правило, и краткую запись составить не могут! А увидев, краткую запись (смотрите выше), стрелочки, скобочки, идущие непонятно куда, что-то соединяющие, дети, не умеющие решать задачи, просто теряются, не понимая, что записано в этой записи и теряют интерес к этому заданию! Получается для этих детей задача — это непреодолимое препятствие. Во-первых, как-то надо краткую запись составить. Во- вторых, выбрать правильное действие, чтобы найти неизвестную величину.

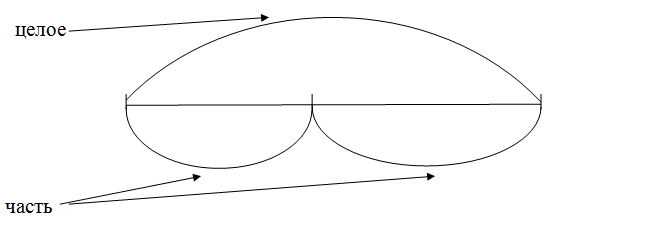
Выход из этой ситуации я нашла, работая в системе развивающего обучения «Эльконина — Давыдова» и особенно мне нравится краткая запись, а точнее схема (модели, чертёж) в математике Петерсон! Это изображение величин отрезками. Для решения всех простых задач надо знать только два правила: как найти целое и как найти часть. И ко всем этим задачам подходит одна схема.

Примеры задач, к которым составляется такая схема:

1.На проводах сидело 20 ласточек. Из них улетело 5 ласточек. Сколько ласточек осталось на проводах?

2. У Тани 5 яблок, у её сестры Вали 7 яблок. Сколько яблок у Тани и Вали вместе?

3. На стоянке стояли машины. После того как уехало 17 машин, на стоянке осталось 9 машин. Сколько машин стояло на стоянке?

И точно такой же подход к простейшим задачам на умножение и деление. Одним словом, кто хочет дать «костыль» при решении задач слабому ученику, рекомендую работать со схемой.

Источник

Матема́тика (от др.-греч. μάθημα — изучение, наука) — наука о структурах, порядке и отношениях, которая исторически сложилась на основе операций подсчёта, измерения и описания форм реальных объектов^[1]. Математические объекты создаются путём идеализации свойств реальных или других математических объектов и записи этих свойств на формальном языке. Математика не относится к естественным наукам, но широко используется в них как для точной формулировки их содержания, так и для получения новых результатов^[2]. Математика — фундаментальная наука, предоставляющая (общие) языковые средства другим наукам; тем самым она выявляет их структурную взаимосвязь и способствует нахождению самых общих законов природы^[3].

Содержание

1 Основные сведения
2 Этимология
3 Определения
4 Разделы математики
5 Обозначения
6 Краткая история
7 Философия математики
- 7.1 Цели и методы
- 7.2 Основания
  - 7.2.1 Теоретико-множественный подход
  - 7.2.2 Логицизм
  - 7.2.3 Формализм
  - 7.2.4 Интуиционизм
  - 7.2.5 Конструктивная математика
8 Основные темы
- 8.1 Числа
- 8.2 Преобразования
- 8.3 Структуры
- 8.4 Пространственные отношения
- 8.5 Дискретная математика
9 Коды в системах классификации знаний
10 Онлайновые сервисы
11 См. также
12 Примечания
13 Литература
14 Ссылки

Основные сведения

Идеализированные свойства исследуемых объектов либо формулируются в виде аксиом, либо перечисляются в определении соответствующих математических объектов. Затем по строгим правилам логического вывода из этих свойств выводятся другие истинные свойства (теоремы). Эта теория в совокупности образует математическую модель исследуемого объекта. Таким образом первоначально, исходя из пространственных и количественных соотношений, математика получает более абстрактные соотношения, изучение которых также является предметом современной математики.

Традиционно математика делится на теоретическую, выполняющую углублённый анализ внутриматематических структур, и прикладную, предоставляющую свои модели другим наукам и инженерным дисциплинам, причём некоторые из них занимают пограничное с математикой положение. В частности, формальная логика может рассматриваться и как часть философских наук, и как часть математических наук; механика — и физика, и математика; информатика, компьютерные технологии и алгоритмика относятся как к инженерии, так и к математическим наукам и т. д. В литературе было предложено много различных определений математики (см. ниже).

Этимология

Слово «математика» произошло от др.-греч. μάθημα (máthēma), что означает изучение, знание, наука, и др.-греч. μαθηματικός (mathēmatikós), первоначально означающего восприимчивый, успевающий^[4], позднее относящийся к изучению, впоследствии относящийся к математике. В частности, μαθηματικὴ τέχνη (mathēmatikḗ tékhnē), на латыни ars mathematica, означает искусство математики.

В текстах на русском языке слово «математика» или «мафематика» встречается по крайней мере с XVII века, например, у Николая Спафария в «Книге избранной вкратце о девяти мусах и о седмих свободных художествах» (1672 год)^[5]

Определения

Одно из первых определений предмета математики дал Декарт^[6]:

К области математики относятся только те науки, в которых рассматривается либо порядок, либо мера и совершенно не существенно, будут ли это числа, фигуры, звёзды, звуки или что-нибудь другое, в чём отыскивается эта мера. Таким образом, должна существовать некая общая наука, объясняющая всё относящееся к порядку и мере, не входя в исследование никаких частных предметов, и эта наука должна называться не иностранным, но старым, уже вошедшим в употребление именем Всеобщей математики.

В советское время классическим считалось определение из БСЭ^[7], данное А. Н. Колмогоровым:

Математика… наука о количественных отношениях и пространственных формах действительного мира.

Это определение Энгельса^[8]; правда, далее Колмогоров поясняет, что все использованные термины надо понимать в самом расширенном и абстрактном смысле.

Формулировка Бурбаки^[9]:

Сущность математики… представляется теперь как учение об отношениях между объектами, о которых ничего не известно, кроме описывающих их некоторых свойств,— именно тех, которые в качестве аксиом положены в основание теории… Математика есть набор абстрактных форм — математических структур.

Приведём ещё несколько современных определений.

Современная теоретическая («чистая») математика — это наука о математических структурах, математических инвариантах различных систем и процессов^[10].

Математика — наука, предоставляющая возможность исчисления моделей, приводимых к стандартному (каноническому) виду. Наука о нахождении решений аналитических моделей (анализ) средствами формальных преобразований^[11].

Герман Вейль пессимистически оценил возможность дать общепринятое определение предмета математики:

Вопрос об основаниях математики и о том, что представляет собой в конечном счёте математика, остаётся открытым. Мы не знаем какого-то направления, которое позволит в конце концов найти окончательный ответ на этот вопрос, и можно ли вообще ожидать, что подобный «окончательный» ответ будет когда-нибудь получен и признан всеми математиками.

«Математизирование» может остаться одним из проявлений творческой деятельности человека, подобно музицированию или литературному творчеству, ярким и самобытным, но прогнозирование его исторических судеб не поддаётся рационализации и не может быть объективным^[12].

Разделы математики

1. Математика как учебная дисциплина подразделяется в Российской Федерации на элементарную математику, изучаемую в средней школе и образованную дисциплинами:

арифметика,
элементарная алгебра
элементарная геометрия: планиметрия и стереометрия
теория элементарных функций и элементы анализа

и высшую математику, изучаемую на нематематических специальностях вузов. Дисциплины, входящие в состав высшей математики, варьируются в зависимости от специальности.

Программа обучения по специальности математика^[13] образована следующими учебными дисциплинами:

Математический анализ
Алгебра
Аналитическая геометрия
Линейная алгебра и геометрия
Дискретная математика
Математическая логика
Дифференциальные уравнения
Дифференциальная геометрия
Топология
Функциональный анализ и интегральные уравнения
Теория функций комплексного переменного
Уравнения в частных производных (вместо этого курса физикам читаются Методы математической физики)
Теория вероятностей
Математическая статистика
Теория случайных процессов
Вариационное исчисление и методы оптимизации
Методы вычислений, то есть численные методы
Теория чисел

2. Математика как специальность научных работников Министерством образования и науки Российской Федерации^[14] подразделяется на специальности:

Вещественный, комплексный и функциональный анализ
Дифференциальные уравнения, динамические системы и оптимальное управление
Математическая физика
Геометрия и топология
Теория вероятностей и математическая статистика
Математическая логика, алгебра и теория чисел
Вычислительная математика
Дискретная математика и математическая кибернетика

3. Для систематизации научных работ используется раздел «Математика»^[15] универсальной десятичной классификации (УДК).

4. Американское математическое общество (AMS) выработало свой стандарт для классификации разделов математики. Он называется Mathematics Subject Classification. Этот стандарт периодически обновляется. Текущая версия — это MSC 2010. Предыдущая версия — MSC 2000.

Обозначения

Вследствие того, что математика работает с чрезвычайно разнообразными и довольно сложными структурами, система обозначений также очень сложна. Современная система записи формул сформировалась на основе европейской алгебраической традиции, а также математического анализа (понятия функции, производной и т. д.). Геометрия испокон века пользовалась наглядным (геометрическим же) представлением. В современной математике распространены также сложные графические системы записи (например, коммутативные диаграммы), нередко также применяются обозначения на основе графов.

Краткая история

Академиком А. Н. Колмогоровым предложена такая структура истории математики:

Период зарождения математики, на протяжении которого был накоплен достаточно большой фактический материал;
Период элементарной математики, начинающийся в VI—V веках до н. э. и завершающийся в конце XVI века («Запас понятий, с которыми имела дело математика до начала XVII века, составляет и до настоящего времени основу „элементарной математики“, преподаваемой в начальной и средней школе»);
Период математики переменных величин, охватывающий XVII—XVIII века, «который можно условно назвать также периодом „высшей математики“»;
Период современной математики — математики XIX—XX века, в ходе которого математикам пришлось «отнестись к процессу расширения предмета математических исследований сознательно, поставив перед собой задачу систематического изучения с достаточно общей точки зрения возможных типов количественных отношений и пространственных форм».

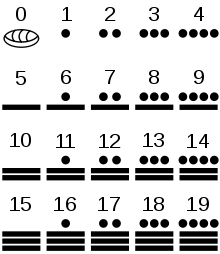
Цифры майя

Развитие математики началось вместе с тем, как человек стал использовать абстракции сколько-нибудь высокого уровня. Простая абстракция — числа; осмысление того, что два яблока и два апельсина, несмотря на все их различия, имеют что-то общее, а именно занимают обе руки одного человека, — качественное достижение мышления человека. Кроме того, что древние люди узнали, как считать конкретные объекты, они также поняли, как вычислять и абстрактные количества, такие, как время: дни, сезоны, года. Из элементарного счёта естественным образом начала развиваться арифметика: сложение, вычитание, умножение и деление чисел.

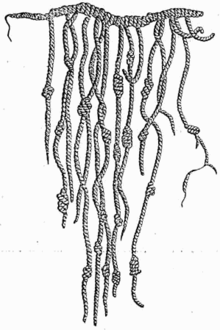
Развитие математики опирается на письменность и умение записывать числа. Наверно, древние люди сначала выражали количество путём рисования чёрточек на земле или выцарапывали их на древесине. Древние инки, не имея иной системы письменности, представляли и сохраняли числовые данные, используя сложную систему верёвочных узлов, так называемые кипу. Существовало множество различных систем счисления. Первые известные записи чисел были найдены в папирусе Ахмеса, созданном египтянами Среднего царства. Индская цивилизация разработала современную десятичную систему счисления, включающую концепцию нуля.

Исторически основные математические дисциплины появились под воздействием необходимости вести расчёты в коммерческой сфере, при измерении земель и для предсказания астрономических явлений и, позже, для решения новых физических задач. Каждая из этих сфер играет большую роль в широком развитии математики, заключающемся в изучении структур, пространств и изменений.

Философия математики

Цели и методы

Математика изучает воображаемые, идеальные объекты и соотношения между ними, используя формальный язык. В общем случае математические понятия и теоремы не обязательно имеют соответствие чему-либо в физическом мире. Главная задача прикладного раздела математики — создать математическую модель, достаточно адекватную исследуемому реальному объекту. Задача математика-теоретика — обеспечить достаточный набор удобных средств для достижения этой цели.

Содержание математики можно определить как систему математических моделей и инструментов для их создания. Модель объекта учитывает не все его черты, а только самые необходимые для целей изучения (идеализированные). Например, изучая физические свойства апельсина, мы можем абстрагироваться от его цвета и вкуса и представить его (пусть не идеально точно) шаром. Если же нам надо понять, сколько апельсинов получится, если мы сложим вместе два и три, — то можно абстрагироваться и от формы, оставив у модели только одну характеристику — количество. Абстракция и установление связей между объектами в самом общем виде — одно из главных направлений математического творчества.

Другое направление, наряду с абстрагированием — обобщение. Например, обобщая понятие «пространство» до пространства n-измерений. «Пространство , при является математической выдумкой. Впрочем, весьма гениальной выдумкой, которая помогает математически разбираться в сложных явлениях».^[16]

Изучение внутриматематических объектов, как правило, происходит при помощи аксиоматического метода: сначала для исследуемых объектов формулируются список основных понятий и аксиом, а затем из аксиом с помощью правил вывода получают содержательные теоремы, в совокупности образующие математическую модель.

Основания

Вопрос сущности и оснований математики обсуждался со времён Платона. Начиная с XX века наблюдается сравнительное согласие в вопросе, что надлежит считать строгим математическим доказательством, однако отсутствует согласие в понимании того, что в математике считать изначально истинным. Отсюда вытекают разногласия как в вопросах аксиоматики и взаимосвязи отраслей математики, так и в выборе логических систем, которыми следует при доказательствах пользоваться.

Помимо скептического, известны нижеперечисленные подходы к данному вопросу.

Теоретико-множественный подход

Предлагается рассматривать все математические объекты в рамках теории множеств, чаще всего с аксиоматикой Цермело — Френкеля (хотя существует множество других, равносильных ей). Данный подход считается с середины XX века преобладающим, однако в действительности большинство математических работ не ставят задач перевести свои утверждения строго на язык теории множеств, а оперируют понятиями и фактами, установленными в некоторых областях математики. Таким образом, если в теории множеств будет обнаружено противоречие, это не повлечёт за собой обесценивание большинства результатов.

Логицизм

Данный подход предполагает строгую типизацию математических объектов. Многие парадоксы, избегаемые в теории множеств лишь путём специальных уловок, оказываются невозможными в принципе.

Формализм

Данный подход предполагает изучение формальных систем на основе классической логики.

Интуиционизм

Интуиционизм предполагает в основании математики интуиционистскую логику, более ограниченную в средствах доказательства (но, как считается, и более надёжную). Интуиционизм отвергает доказательство от противного, многие неконструктивные доказательства становятся невозможными, а многие проблемы теории множеств — бессмысленными (неформализуемыми).

Конструктивная математика

Конструктивная математика — близкое к интуиционизму течение в математике, изучающее конструктивные построения^{[прояснить]}. Согласно критерию конструктивности — «существовать — значит быть построенным».^[17] Критерий конструктивности — более сильное требование, чем критерий непротиворечивости.^[18]

Основные темы

Числа

Понятие «число» первоначально относилось к натуральным числам. В дальнейшем оно было постепенно распространено на целые, рациональные, действительные, комплексные и другие числа.

Числа — Натуральные числа — Целые числа — Рациональные числа — Вещественные числа — Комплексные числа — Гиперкомплексные числа — Кватернионы — Октонионы — Седенионы — Гиперреальные числа — Сюрреальные числа — p-адические числа — Математические постоянные — Названия чисел — Бесконечность — Базы

Числовые системы
Счётные множества	Натуральные числа () • Целые () • Рациональные () • Алгебраические () • Периоды • Вычислимые • Арифметические
Вещественные числа и их расширения	Вещественные () • Комплексные () • Кватернионы () • Числа Кэли (октавы, октонионы) () • Седенионы () • Альтернионы • Процедура Кэли — Диксона • Дуальные • Гиперкомплексные • Суперреальные • Гиперреальные • Surreal number (англ.)
Другие числовые системы	Кардинальные числа • Порядковые числа (трансфинитные, ординал) • p-адические • Супернатуральные числа
См. также	Двойные числа • Иррациональные числа • Трансцендентные • Числовой луч • Бикватернион

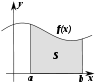
Преобразования


Арифметика	Дифференциальное и интегральное исчисление	Векторный анализ	Анализ
$frac{d^2}{dx^2} y = frac{d}{dx} y + c$
Дифференциальные уравнения	Динамические системы	Теория хаоса

Арифметика — Векторный анализ — Анализ — Теория меры — Дифференциальные уравнения — Динамические системы — Теория хаоса — Перечень функций

Структуры

Теория множеств — Абстрактная алгебра — Теория групп — Алгебраические структуры — Алгебраическая геометрия — Теория чисел — Топология — Линейная алгебра — Универсальная алгебра — Теория категорий — Теория последовательностей

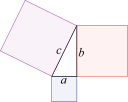
Пространственные отношения

Более наглядные подходы в математике.


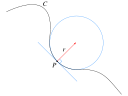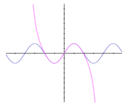
Геометрия	Тригонометрия	Дифференциальная геометрия

Топология	Фракталы

Геометрия — Тригонометрия — Алгебраическая геометрия — Топология — Дифференциальная геометрия — Дифференциальная топология — Алгебраическая топология — Линейная алгебра — Фракталы

Дискретная математика

Дискретная математика включает средства, которые применяются над объектами, способными принимать только отдельные, не непрерывные значения.

Комбинаторика — Теория множеств — Теория решёток — Математическая логика — Теория вычислимости— Криптография — Теория функциональных систем — Теория графов — Теория алгоритмов — Логические исчисления — Информатика

Коды в системах классификации знаний

УДК 51
Государственный рубрикатор научно-технической информации (ГРНТИ) (по состоянию на 2001 год): 27^[19]

Онлайновые сервисы

Существует большое число сайтов, предоставляющих сервис для математических расчётов. Большинство из них англоязычные.^[20] Из русскоязычных можно отметить сервис математических запросов поисковой системы Nigma.

См. также

Международный конгресс математиков
Классические проблемы математики
Открытые математические проблемы
Философия математики

Популяризаторы науки

Перельман, Яков Исидорович
Гарднер, Мартин

Примечания

↑ Энциклопедия Britannica
↑ Webster’s Online Dictionary
↑ Глава 2. Математика как язык науки. Сибирский открытый университет. Архивировано из первоисточника 2 февраля 2012. Проверено 5 октября 2010.
↑ Большой древнегреческий словарь (αω)
↑ Словарь русского языка XI—XVII вв. Выпуск 9 / Гл. ред. Ф. П. Филин. — М.: Наука, 1982. — С. 41.
↑ Декарт Р. Правила для руководства ума. М.-Л.: Соцэкгиз, 1936.
↑ См.: Математика БСЭ
↑ Маркс К., Энгельс Ф. Сочинения. 2-е изд. Т. 20. С. 37.
↑ Бурбаки Н. Архитектура математики. Очерки по истории математики / Перевод И. Г. Башмаковой под ред. К. А. Рыбникова. М.: ИЛ, 1963. С. 32, 258.
↑ Казиев В. М. Введение в математику
↑ Мухин О. И. Моделирование систем Учебное пособие. Пермь: РЦИ ПГТУ.
↑ Герман Вейль // Клайн М. Математика. Утрата определённости. — М.: Мир, 1984. — С. 16.
↑ Государственный образовательный стандарт высшего профессионального образования. Специальность 01.01.00. «Математика». Квалификация — Математик. Москва, 2000 (Составлено под руководством О. Б. Лупанова)
↑ Номенклатура специальностей научных работников, утверждённая приказом Минобрнауки России от 25.02.2009 № 59
↑ УДК 51 Математика
↑ Я. С. Бугров, С. М. Никольский. Элементы линейной алгебры и аналитической геометрии. М.: Наука, 1988. С. 44.
↑ Н. И. Кондаков. Логический словарь-справочник. М.: Наука, 1975. С. 259.
↑ Г. И. Рузавин. О природе математического знания. М.: 1968.
↑ http://www.gsnti-norms.ru/norms/common/doc.asp?0&/norms/grnti/gr27.htm
↑ Например: http://mathworld.wolfram.com

Литература

Энциклопедии

Математика // Энциклопедический словарь Брокгауза и Ефрона: В 86 томах (82 т. и 4 доп.). — СПб., 1890—1907.
Россия/Русская наука/Математика // Энциклопедический словарь Брокгауза и Ефрона: В 86 томах (82 т. и 4 доп.). — СПб., 1890—1907.
Математическая энциклопедия (в 5-ти томах), 1980-е гг. // Общие и специальные справочники по математике на EqWorld
Кондаков Н. И. Логический словарь-справочник. М.: Наука, 1975.
Энциклопедия математических наук и их приложений (нем.) 1899—1934 гг. (крупнейший обзор литературы XIX века)

Справочники

Г. Корн, Т. Корн. Справочник по математике для научных работников и инженеров М., 1973 г.

Книги

Клайн М. Математика. Утрата определённости. — М.: Мир, 1984.
Клайн М. Математика. Поиск истины. М.: Мир, 1988.
Клейн Ф. Элементарная математика с точки зрения высшей.

Том I. Арифметика. Алгебра. Анализ М.: Наука, 1987. 432 с.
Том II. Геометрия М.: Наука, 1987. 416 с.

Курант Р., Г. Роббинс. Что такое математика? 3-e изд., испр. и доп. — М.: 2001. 568 с.
Писаревский Б. М., Харин В. Т. О математике, математиках и не только. — М.: Бином. Лаборатория знаний, 2012. — 302 с.
Пуанкаре А. Наука и метод (рус.) (фр.)

Занимательная математика

Бобров С. П. Волшебный двурог М.: Детская литература, 1967. 496 с.
Дьюдени Г. Э. Кентерберийские головоломки; 200 знаменитых головоломок мира; Пятьсот двадцать головоломок
Кэррол Л. История с узелками; Логическая игра
Таунсенд Чарлз Барри. Звёздные головоломки; Самые весёлые головоломки; Самые трудные головоломки из старинных журналов
Перельман Я.И. Занимательная математика

Ссылки

	Портал «Математика»
	Математика в Викисловаре^?
	Математика в Викицитатнике^?
	Математика в Викитеке^?
	Математика на Викискладе^?
	Математика в Викиновостях^?

Видеолекция

История математики

Образовательные сайты

http://www.math.ru/
МЦНМО
Математические этюды
Мир математических уравнений
Сообщество свободного математического моделирования

Дискуссионные математические форумы

Математический форум мехмата МГУ
Математический форум Math Help Planet

Судьба математической науки

В. А. Успенский: Апология математики (+окончание).
МАТЕМАТИКИ ИСТОРИЯ

Наука
Научные направления Гуманитарные • Естественные • Общественные • Прикладные • Технические • Точные
Астрономия • Биология • География • Геология • Информатика • История • Лингвистика • Математика • Медицина • Психология • Политология • Социология • Физика • Филология • Химия • Экономика • Юриспруденция
Список академических дисциплин

Источник