Как написать периметр квадрата - Правописание и грамматика

Основные определения

Квадратом принято называть правильный четырёхугольник, у которого равны все углы и стороны. Это частный случай прямоугольника, из-за чего можно заметить схожесть некоторых алгоритмов.

Периметр — это сумма длин всех сторон многоугольника. Общепринятое обозначение — заглавная латинская буква P. Под «P» удобно писать маленькими буквами название фигуры, чтобы не запутаться в задачах по ходу решения.

Если длины заданы в разных единицах измерения, мы не сможем узнать периметр квадрата. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.

В чем измеряется периметр:

миллиметр (мм);
сантиметр (см);
дециметр (дм);
метр (м);
километр (км) и другие единицы измерения длины.

Получай лайфхаки, статьи, видео и чек-листы по обучению на почту

Реши домашку по математике на 5.

Подробные решения помогут разобраться в самой сложной теме.

Формула нахождения периметра квадрата

Как находится периметр квадрата, всегда зависит от исходных данных. Рассмотрим две формулы, которые проходят во 2 и 3 классе.

Если известна длина стороны

P = a + a + a + a, где a — сторона.

Так как все стороны фигуры равны, можно использовать формулу в таком виде: P = 4 × a

Если известна длина диагонали

P = d × 2 × √2, где d — диагональ.

Диагональ — это отрезок, который соединяет противоположные стороны фигуры.

Математика, как и любой другой предмет не сразу дается легко. Сложности могут возникать из-за неумения быстро делать простые арифметические действия — именно поэтому полезно практиковаться в решении примеров как можно чаще. Давайте сделаем это прямо сейчас!

Решение задач

1. Найти периметр квадрата, диагональ которого равняется √4 см

Как решаем:

Воспользуемся формулой P = d × 2 × √2;
P = √4 × 2 × √2.

Ответ: 4√2 см.

2. Найти периметр квадрата со стороной 97 мм. Записать ответ в сантиметрах

Как решаем:

Воспользуемся формулой P = 4 × a;
P = 4 × 97.

Ответ: 38,8 см.

3. Периметр квадрата 48 см. Чему равна его сторона?

Как решаем:

Воспользуемся формулой P = 4 × a;
Значит a = P : 4;
a = 48 : 4.

Ответ: 12 см.

4. Периметр квадрата 20 см. Как найти его площадь?

Как решаем:

Воспользуемся формулой P = 4 × a;
Тогда a = P : 4;
a = 20 : 4 = 5 см;
Воспользуемся формулой S = a × a;
Значит S = 5 × 5.

Ответ: 25 см².

Онлайн-школа Skysmart приглашает детей и подростков на курсы по математике — за интересными задачами, новыми прикладными знаниями и хорошими оценками!

Источник

Запомните!

Периметр — это сумма длин всех сторон многоугольника.

Иногда для вычисления периметра геометрических фигур используются специальные формулы,
в которых периметр обозначается заглавной латинской буквой «P».

Периметр измеряется в единицах длины: мм, см, м, км и т.д.

При нахождении периметра мы рекомендуем писать название фигуры маленькими
буквами под знаком «P», чтобы не забывать чей периметр вы находите.

Запомните!

Периметр прямоугольника — это сумма длины и ширины, умноженная на «2».

P = (a + b) · 2

,
где «a» — длина прямоугольника, «b» — ширина прямоугольника.

Стороны прямоугольника, которые лежат друг против друга (противолежащие), мы
называем длиной и шириной.

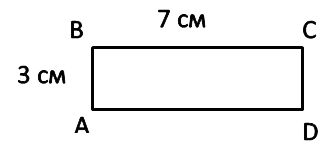
AB = 3 см, BC = 7 см

P_ABCD = (AB + BC) · 2
P_ABCD = (7 + 3) · 2 = 10 · 2 = 20 (см)

Запомните!

Периметр квадрата — это длина стороны квадрата, умноженная на «4».

P = a · 4

, где a — длина стороны квадрата.

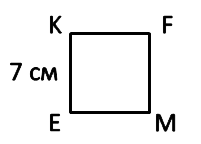
KE = 7 см

P_EKFM = 4 · KE
P_EKFM = 4 · 7 = 28 (см)

Как найти периметр многоугольника

Периметр любого многоугольника (в том числе и периметр треугольника)
рассчитывается по определению периметра.
Для этого надо просто сложить длины всех сторон многоугольника.

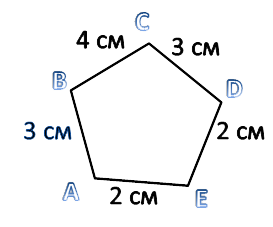
P_ABCDE = AB + BC + CD + DE + EA = 3 + 4 + 3 + 2 + 2 = 14 (см)

Источник

Загрузить PDF

Периметр двумерной фигуры – это общая длина ее границы, равная сумме длин сторон фигуры.^[1] Квадрат – это фигура с четырьмя сторонами одинаковой длины, которые пересекаются под углом 90°.^[2] Так как в квадрате все стороны имеют одинаковую длину, то вычислить его периметр очень легко. Эта статья расскажет вам, как вычислить периметр квадрата по одной данной стороне, по данной площади и по данному радиусу окружности, описанной вокруг квадрата.

1

Формула для вычисления периметра квадрата: P = 4s, где s – длина стороны квадрата.
2
Определите длину одной стороны квадрата и умножьте ее на 4, чтобы найти периметр. Чтобы определить длину стороны, измерьте ее линейкой или посмотрите ее значение в учебнике (задаче). Вот некоторые примеры вычисления периметра:
- Если сторона квадрата равна 4, то P = 4 * 4 = 16.
- Если сторона квадрата равна 6, то P = 4 * 6 = 36.
Реклама

1

Формула для вычисления площади квадрата. Площадь любого прямоугольника (а квадрат – это частный случай прямоугольника) равна произведению его длины на его ширину.^[3] Поскольку длина и ширина квадрата равны, то его площадь вычисляется по формуле: A = s*s = s², где s – длина стороны квадрата.
2
Извлеките квадратный корень из значения площади, чтобы найти сторону квадрата. Для этого в большинстве случаев воспользуйтесь калькулятором (введите значение площади и нажмите клавишу «√»). Вы также можете вычислить квадратный корень вручную.
- Если площадь квадрата равна 20, то его сторона равна: s = √20 = 4,472.
- Если площадь квадрата равна 25, то s = √25 = 5.
3
Умножьте найденную сторону на 4, чтобы найти периметр. Вычисленное значение стороны подставьте в формулу для нахождения периметра: P = 4s. Вы найдете периметр квадрата.
- В нашем первом примере: P = 4 * 4,472 = 17,888.
- Периметр квадрата, площадь которого равна 25, а сторона равна 5, равен Р = 4 * 5 = 20.
Реклама

1

Вписанный квадрат – это квадрат, вершины которого лежат на окружности.^[4]
2

Отношение между радиусом окружности и длиной стороны квадрата. Расстояние от центра описанной окружности до вершины вписанного в нее квадрата равно радиусу окружности. Чтобы найти сторону квадрата s, необходимо диагональю разделить квадрат на 2 прямоугольных треугольника. Каждый из этих треугольников будет иметь равные стороны a и b и общую гипотенузу с, равную удвоенному радиусу описанной окружности (2r).
3
Воспользуйтесь теоремой Пифагора, чтобы найти сторону квадрата. Теорема Пифагора гласит, что в любом прямоугольном треугольнике с катетами а и b и гипотенузой с: a² + b² = c².^[5] Так как в нашем случае а = b (не забывайте, что мы рассматриваем квадрат!), и мы знаем, что с = 2r, то мы можем переписать и упростить это уравнение:
- a² + a² = (2r)²«‘; теперь упростим это уравнение:
- 2a² = 4(r)²; теперь разделим обе стороны уравнения на 2:
- (a²) = 2(r)²; теперь извлечем квадратный корень из обеих сторон уравнения:
- a = √(2r). Таким образом, s = √(2r).
4

Умножьте найденную сторону квадрата на 4, чтобы найти его периметр. В этом случае периметр квадрата: P = 4√(2r). Эту формулу можно переписать так: Р = 4√2 * 4√r = 5,657r, где r – радиус описанной окружности.^[6]
5
Пример. Рассмотрим квадрат, вписанный в окружность радиусом 10. Это означает, что диагональ квадрата равна 2 * 10 = 20. Используя теорему Пифагора, мы получим: 2(a²) = 20², то есть 2a² = 400. Теперь разделим обе стороны уравнения на 2 и получим: a² = 200. Теперь извлечем квадратный корень из обеих сторон уравнения и получим: а = 14,142. Умножим это значение на 4 и вычислим периметр квадрата: P = 56,57.
- Обратите внимание, что вы могли бы получить тот же результат, просто умножив радиус (10) на 5,657: 10 * 5,567 = 56,57; но такой метод трудно запомнить, поэтому лучше пользоваться процессом вычисления, описанным выше.
Реклама

Об этой статье

Эту страницу просматривали 410 873 раза.

Была ли эта статья полезной?

Источник

Запомните!

Периметр — это сумма длин всех сторон многоугольника.

Периметр измеряется в единицах длины: мм, см, м, км и т.д.

Запомните!

Периметр прямоугольника — это сумма длины и ширины, умноженная на «2».

P = (a + b) · 2

,
где «a» — длина прямоугольника, «b» — ширина прямоугольника.

Стороны прямоугольника, которые лежат друг против друга (противолежащие), мы
называем длиной и шириной.

AB = 3 см, BC = 7 см

P_ABCD = (AB + BC) · 2
P_ABCD = (7 + 3) · 2 = 10 · 2 = 20 (см)

Запомните!

Периметр квадрата — это длина стороны квадрата, умноженная на «4».

P = a · 4

, где a — длина стороны квадрата.

KE = 7 см

P_EKFM = 4 · KE
P_EKFM = 4 · 7 = 28 (см)

Как найти периметр многоугольника

P_ABCDE = AB + BC + CD + DE + EA = 3 + 4 + 3 + 2 + 2 = 14 (см)

Периметр – это геометрический термин, который часто встречается в задачах. Чтобы понять, что такое периметр, следует нарисовать произвольный многоугольник и вооружиться линейкой. В переводе с греческого языка этот термин обозначает «измеряю вокруг».

Как вычислить периметр

Периметр обозначается латинской буквой P. Его можно измерить в сантиметрах, миллиметрах, метрах или дециметрах. Чтобы узнать периметр, следует измерить длину всех сторон многоугольника. Полученные значения нужно сложить. Итоговая сумма и станет ответом на вопрос: «Чему равен периметр многоугольника».

Периметр – это длина линий, которые ограничивают замкнутую фигуру (квадрат, прямоугольник, треугольник и др.).

Например, перед вами многоугольник со сторонами 10, 12, 13 и 11 см. Складываем вышеназванные числа (10+12+13+11) и получаем сумму 46. Это и есть периметр многоугольника.

Для удобства вычисления периметра в геометрии существует ряд формул. Каждая формула соответствует определенной фигуре.

Периметр и площадь квадрата

Это сумма его четырех сторон. Как мы знаем, все стороны квадрата имеют равный размер. Поэтому мы можем узнать периметр квадрата, умножив длину его стороны на четыре:

P= a*4

P= a+a+a+a

Например, перед нами квадрат со стороной 10 см.

P= 10*4

P=40

Ответ: 40 см

P= 10+10+10+10

P=40

Ответ: 40 см

Чтобы разобраться, что такое периметр и площадь, следует уяснить, что периметр вычисляет длину контура фигуры, а площадь – размер всей ее поверхности.

Чтобы узнать площадь квадрата, необходимо воспользоваться простой формулой:

S= a*a

S=a²

S – это площадь, а – сторона квадрата.

Например, в задаче указано, что длина стороны квадрата составляет 10см.

S=10*10

S= 100см²

Ответ: 100см²

Периметр и площадь прямоугольника

Стороны прямоугольника, находящиеся друг напротив друга и имеющие одинаковую длину, называются противолежащими. Это длина и ширина, они условно обозначаются латинскими буквами a и b. Формула для вычисления периметра прямоугольника выглядит так:

P= (a+b)*2

Используя эту формулу, мы сначала находим сумму ширины и длины, а затем умножаем ее на два.

Например, перед нами прямоугольник, имеющий длину 6 см и ширину 2 см.

P= (6+2) * 2

P= 16

Ответ: 16 см

Чтобы узнать площадь прямоугольника, следует длину умножить на ширину. Формула выглядит так:

S= a*b

Например, в условиях задачи сказано, что прямоугольник имеет длину 5 см и ширину 2см. Меняем буквы a и b на указанные числа.

S= 5*2

S=10см²

Ответ: 10 см²

Периметр круга (длина окружности)

Каждый круг имеет центр. Расстояние от центра круга до любой точки, расположенной на окружности, имеет название радиус круга. Часто ученики путают понятия «круг» и «окружность» и пытаются определить площадь окружности. Это серьезная ошибка. Следует разделить в голове понятия «круг» и «окружность». У окружности нет и не может быть площади, у нее есть только длина.

Чтобы найти периметр круга, следует вычислить длину его окружности. Существует формула для нахождения длины окружности:

L = 2πr

L= 2πd

L – длина окружности

π – это число «пи», математическая константа. Она равна отношению длины окружности к длине ее диаметра. Древнее название числа «пи» – лудольфово число. Это число иррационально, его десятичное представление после точки никогда не заканчивается.

π = 3.141 592 653 589 793 238 462 643 383 279 502

Для удобства вычислений обычно используют значение 3.14

R – это радиус окружности

D – Диаметр окружности

Итак, чтобы определить периметр круга, надо найти произведение радиуса и 2π. Если в задаче указан диаметр, то

Например, перед нами круг с радиусом 3 см. Найдем его периметр.

L= 2*3,14*3

L=6π

L=6*3.14

L = 18.84 см

P_к= 18,84 см

Ответ: 18.84 см

Отличие периметра от площади

Площадь – это размер поверхности фигуры, а периметр – это сумма ее границ.

Площадь всегда измеряется в квадратных единицах (см², м², мм²). Периметр измеряется в единицах длины – в сантиметрах, миллиметрах, метрах, дециметрах.

Hello there! Do you know if they make any plugins to help with SEO? I’m trying to get my blog to rank for some

สล็อตออนไลน์ เว็บตรง เว็บสล็อตไม่ผ่านเอเย่นต์ 2021 ไม่มีขั้นต่ำ เว็บใหญ่สล็อตเว็บหลัก G2G1XBET เว็บใหม่สล็อตแตกง่าย

I do believe all the ideas you have introduced for your post. They are very convincing and can definitely work. Still,

Чего-то супер не обычного они не несут Чехлы Для Авто Просто концепция производства и использования немного другая

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Основные определения

В чем измеряется периметр:

миллиметр (мм);
сантиметр (см);
дециметр (дм);
метр (м);
километр (км) и другие единицы измерения длины.

Формула нахождения периметра квадрата

Если известна длина стороны

P = a + a + a + a, где a — сторона.

Так как все стороны фигуры равны, можно использовать формулу в таком виде: P = 4 × a

Если известна длина диагонали

P = d × 2 × √2, где d — диагональ.

Диагональ — это отрезок, который соединяет противоположные стороны фигуры.

Решение задач

1. Найти периметр квадрата, диагональ которого равняется √4 см

Как решаем:

Воспользуемся формулой P = d × 2 × √2;
P = √4 × 2 × √2.

Ответ: 4√2 см.

2. Найти периметр квадрата со стороной 97 мм. Записать ответ в сантиметрах

Как решаем:

Воспользуемся формулой P = 4 × a;
P = 4 × 97.

Ответ: 38,8 см.

3. Периметр квадрата 48 см. Чему равна его сторона?

Как решаем:

Воспользуемся формулой P = 4 × a;
Значит a = P : 4;
a = 48 : 4.

Ответ: 12 см.

4. Периметр квадрата 20 см. Как найти его площадь?

Как решаем:

Воспользуемся формулой P = 4 × a;
Тогда a = P : 4;
a = 20 : 4 = 5 см;
Воспользуемся формулой S = a × a;
Значит S = 5 × 5.

Ответ: 25 см².

0 интересует

0 не интересует

ответил

17 Март, 18

от
Elechka124_zn

(92 баллов)

Лучший ответ

Формула периметра? формула периметра прямоугольника

Периметр равен =(одна сторона + вторая сторона) * на 2.

Р = (а+в)*2

Источник

The perimeter of square is defined as the total length of the boundaries of that square. The perimeter of any shape can be obtained in the same pattern, that is, finding the total length of the shape’s boundary. A square is a closed regular polygon. In a square, all sides are equal, and all angles are 90° each. It is a 2-dimensional figure. It is a special type of quadrilateral. Since all the sides of the square are equal, the perimeter of the square can be obtained by adding all the sides or by multiplying one side by 4. Let’s learn about the perimeter of square in detail,

What is Perimeter of Square?

The perimeter of any closed geometrical shape is obtained by finding the total length of the boundaries of its shape. Perimeter is the length that outlines the shape of the 2-D figures. The 2D figures include squares, rectangles, triangles, and circles. The perimeter and area of 2-D shapes are considered, and volume is obtained for 3-d shapes. The perimeter can be found for irregular shapes as well. Below are some of the terms used in 2-D shape:

Vertices: They are the endpoints of a shape.
Edge/Side: A line segment joining two adjacent vertices.
Diagonals: A line segment joining two nonadjacent vertices.
Area: Area is the space occupied by a figure.
Perimeter: Perimeter is the total length of the boundary of the figure.
Angles: The point where two sides meet is the angle often measured in degrees or radians.

Perimeter of Square Formula

The perimeter of square formula can be calculated using the side length of the square. If the side of the square is represented as “a”, the formula for perimeter of square can be expressed as,

Perimeter (P) = 4 × Side = 4 × a

As shown above, the perimeter of square is 4 times the length of its sides as all sides are equal in a square. The unit for the perimeter of square is the unit used for length. It is measured in meters (m), centimeters (cm), inches (in), etc.

Example: Calculate the perimeter of a square having a side of 8cm.

Solution:

Perimeter of square = 4 × side

P = 4 × 8

P = 32 cm.

Derivation of Perimeter of Square

In order to find the perimeter of closed geometrical shape, the length of all the boundaries should be added. Similarly, to derive the perimeter of square, we are required to add all the sides of the square, assume the length of the sides is denoted as “a”,

Perimeter = a + a + a + a

Perimeter of square = 4a

Where a is the side of the square.

How to Find the Perimeter of a Square?

Perimeter is the length of the boundary. It is often known as the distance around a closed 2D figure. The perimeters can be different according to the shapes given. The perimeter of a square can be calculated using side length, and there are cases when the side length is not given, then the perimeter of square can be obtained using diagonal and area. Therefore, the perimeter of square can be calculated using three methods,

Using side length
Using diagonal
Using area

Perimeter of Square using Side Length

The below-given steps can be used to find the perimeter of square using side length,

Measure the side of the square.
Multiply the side length by 4.
Express the perimeter obtained in the respective unit.

Perimeter of Square using Diagonal

However, if the side of the square is not given, but the diagonal is given, then the formula becomes,

Diagonal of a square (d) = √2 × side

Therefore, the Perimeter of square is,

P = 4 × (Diagonal/√2)

The below-given steps can be used to find the area of the perimeter of square using diagonals,

Measure the diagonal of the square.
Calculate the perimeter of the square using the formula, P = 4 × (Diagonal/√2).

Example: Find the perimeter of the diagonal is 4√2 m.

Solution:

The Perimeter of square is,

P = 4 × (Diagonal/√2)

= 4 × (4√2/√2)

= 16 m

Perimeter of Square using Area

When the area of square is given, let us assume the area of square is A. As we all know, Area = (side)²

Therefore, the perimeter of the square is,

Perimeter = 4 × √A

The below-given steps can be used to find the area of the perimeter of square using area,

Measure the area of the square.
Calculate the area of the square using the formula, Perimeter = 4 × √Area.

Example: Find the perimeter if the area of the square is 49 square units.

Solution:

The Perimeter of square is,

P = 4 × √Area

= 4 × √49

= 28 units

Solved Examples on Perimeter of Square

Example 1: Find the perimeter of the square if the side given is 4 units.

Solution:

The Perimeter of square is,

P = 4 × side

= 4 × 4

= 16 units

Example 2: Find the side and perimeter of the square if the diagonal given is 2√2 cm.

Solution:

Side = Diagonal/√2

= 2√2/√2

= 2 cm

Perimeter of square = 4×side

= 8 cm

Example 3: Find the side of the perimeter of the given square is √2.

Solution:

Perimeter = side × 4

√2 = side × 4

Therefore,

Side = √2/4

Example 4: Find the diagonal if the perimeter of the square is 3√2 cm.

Solution:

Perimeter = 4 × (diagonal/√2)

(3√2 × √2 ) /4 = diagonal

Diagonal = 1.5 cm

Example 5: Find the perimeter if the area given is 25 sq units.

Solution:

Perimeter = 4√Area

= 4√25

= 20 units

Example 6: Find the area and perimeter of the square if its side is 3 units.

Solution:

Perimeter = 4×side

= 4 × 3

= 12 units

Area = (Side)²

= (3)²

= 9 sq units

FAQs on Perimeter of Square

Question 1: What is the perimeter of the square formula?

Answer:

The perimeter of square is defined as the total length of its boundaries. The formula for perimeter of square is,

P = 4 × Side.

Question 2: What is the unit of the perimeter of square?

Answer:

The units used for perimeter of square is the units used for length. The units used are meter (m), centimeter (cm), inches (in), etc.

Question 3: What is the area and perimeter of square?

Answer:

The perimeter of square is defined as the total length of its boundaries. The formula for perimeter of square is,

P = 4 × Side.

The space covered in 2-dimensional space by the square is called as area of a square. The formula used for area of square is,

A = Side²

Question 4: How to find the side length of the square when perimeter is given?

Answer:

In order to find the side length of square, first note down the formula for perimeter of square.

P = 4 × Side

Side = P/4

Hence, to find side length of square when perimeter is given, divide the perimeter by 4.

Perimeter of Rectangle

Perimeter of Triangle

Circumference of a Circle

Источник

What is Perimeter of Square?

Vertices: They are the endpoints of a shape.
Edge/Side: A line segment joining two adjacent vertices.
Diagonals: A line segment joining two nonadjacent vertices.
Area: Area is the space occupied by a figure.
Perimeter: Perimeter is the total length of the boundary of the figure.
Angles: The point where two sides meet is the angle often measured in degrees or radians.

Perimeter of Square Formula

The perimeter of square formula can be calculated using the side length of the square. If the side of the square is represented as “a”, the formula for perimeter of square can be expressed as,

Perimeter (P) = 4 × Side = 4 × a

Example: Calculate the perimeter of a square having a side of 8cm.

Solution:

Perimeter of square = 4 × side

P = 4 × 8

P = 32 cm.

Derivation of Perimeter of Square

Perimeter = a + a + a + a

Perimeter of square = 4a

Where a is the side of the square.

How to Find the Perimeter of a Square?

Using side length
Using diagonal
Using area

Perimeter of Square using Side Length

The below-given steps can be used to find the perimeter of square using side length,

Measure the side of the square.
Multiply the side length by 4.
Express the perimeter obtained in the respective unit.

Perimeter of Square using Diagonal

However, if the side of the square is not given, but the diagonal is given, then the formula becomes,

Diagonal of a square (d) = √2 × side

Therefore, the Perimeter of square is,

P = 4 × (Diagonal/√2)

The below-given steps can be used to find the area of the perimeter of square using diagonals,

Measure the diagonal of the square.
Calculate the perimeter of the square using the formula, P = 4 × (Diagonal/√2).

Example: Find the perimeter of the diagonal is 4√2 m.

Solution:

The Perimeter of square is,

P = 4 × (Diagonal/√2)

= 4 × (4√2/√2)

= 16 m

Perimeter of Square using Area

When the area of square is given, let us assume the area of square is A. As we all know, Area = (side)²

Therefore, the perimeter of the square is,

Perimeter = 4 × √A

The below-given steps can be used to find the area of the perimeter of square using area,

Measure the area of the square.
Calculate the area of the square using the formula, Perimeter = 4 × √Area.

Example: Find the perimeter if the area of the square is 49 square units.

Solution:

The Perimeter of square is,

P = 4 × √Area

= 4 × √49

= 28 units

Solved Examples on Perimeter of Square

Example 1: Find the perimeter of the square if the side given is 4 units.

Solution:

The Perimeter of square is,

P = 4 × side

= 4 × 4

= 16 units

Example 2: Find the side and perimeter of the square if the diagonal given is 2√2 cm.

Solution:

Side = Diagonal/√2

= 2√2/√2

= 2 cm

Perimeter of square = 4×side

= 8 cm

Example 3: Find the side of the perimeter of the given square is √2.

Solution:

Perimeter = side × 4

√2 = side × 4

Therefore,

Side = √2/4

Example 4: Find the diagonal if the perimeter of the square is 3√2 cm.

Solution:

Perimeter = 4 × (diagonal/√2)

(3√2 × √2 ) /4 = diagonal

Diagonal = 1.5 cm

Example 5: Find the perimeter if the area given is 25 sq units.

Solution:

Perimeter = 4√Area

= 4√25

= 20 units

Example 6: Find the area and perimeter of the square if its side is 3 units.

Solution:

Perimeter = 4×side

= 4 × 3

= 12 units

Area = (Side)²

= (3)²

= 9 sq units

FAQs on Perimeter of Square

Question 1: What is the perimeter of the square formula?

Answer:

The perimeter of square is defined as the total length of its boundaries. The formula for perimeter of square is,

P = 4 × Side.

Question 2: What is the unit of the perimeter of square?

Answer:

The units used for perimeter of square is the units used for length. The units used are meter (m), centimeter (cm), inches (in), etc.

Question 3: What is the area and perimeter of square?

Answer:

The perimeter of square is defined as the total length of its boundaries. The formula for perimeter of square is,

P = 4 × Side.

The space covered in 2-dimensional space by the square is called as area of a square. The formula used for area of square is,

A = Side²

Question 4: How to find the side length of the square when perimeter is given?

Answer:

In order to find the side length of square, first note down the formula for perimeter of square.

P = 4 × Side

Side = P/4

Hence, to find side length of square when perimeter is given, divide the perimeter by 4.

Perimeter of Rectangle

Perimeter of Triangle

Circumference of a Circle

Источник

В данной публикации мы рассмотрим, каким образом можно посчитать периметр квадрата и разберем примеры решения задач.

Формула вычисления периметра
- По длине стороны
- По длине диагонали
Примеры задач

Формула вычисления периметра

По длине стороны

Периметр (P) квадрата равняется сумме длин его сторон.

P = a + a + a + a

Так как все стороны квадрата равны, формулу можно представить в виде произведения:

P = 4 ⋅ a

По длине диагонали

Периметр (P) квадрата равен произведению длины его диагонали на число 2√2:

P = d ⋅ 2√2

Данная формула следует из соотношения длин стороны (a) и диагонали (d) квадрата:
d = a√2.

Примеры задач

Задание 1
Найдите периметр квадрата, если его сторона равна 6 см.

Решение:
Используем формулу, в которой участвует значение стороны:
P = 6 см + 6 см + 6 см + 6 см = 4 ⋅ 6 см = 24 см.

Задание 2
Найдите периметр квадрата, диагональ которого равняется √2 см.

Решение 1:
С учетом известной нам величины воспользуемся второй формулой:
P = √2 см ⋅ 2√2 = 4 см.

Решение 2:
Выразим длину стороны через диагональ:
a = d / √2 = √2 см / √2 = 1 см.

Теперь, используя первую формулу, получаем:
P = 4 ⋅ 1 см = 4 см.

Источник

Основные определения

Формула нахождения периметра квадрата

Если известна длина стороны

Если известна длина диагонали

Решение задач

1. Найти периметр квадрата, диагональ которого равняется √4 см

2. Найти периметр квадрата со стороной 97 мм. Записать ответ в сантиметрах

3. Периметр квадрата 48 см. Чему равна его сторона?

4. Периметр квадрата 20 см. Как найти его площадь?

Как найти периметр многоугольника

Похожие статьи

Об этой статье

Была ли эта статья полезной?

Как найти периметр многоугольника

Как вычислить периметр

Периметр и площадь квадрата

Периметр и площадь прямоугольника

Периметр круга (длина окружности)

Отличие периметра от площади

Основные определения

Формула нахождения периметра квадрата

Если известна длина стороны

Если известна длина диагонали

Решение задач

1. Найти периметр квадрата, диагональ которого равняется √4 см

2. Найти периметр квадрата со стороной 97 мм. Записать ответ в сантиметрах

3. Периметр квадрата 48 см. Чему равна его сторона?

4. Периметр квадрата 20 см. Как найти его площадь?

What is Perimeter of Square?

Perimeter of Square Formula

Derivation of Perimeter of Square

How to Find the Perimeter of a Square?

Perimeter of Square using Side Length

Perimeter of Square using Diagonal

Perimeter of Square using Area

Solved Examples on Perimeter of Square

FAQs on Perimeter of Square

Read More

What is Perimeter of Square?

Perimeter of Square Formula

Derivation of Perimeter of Square

How to Find the Perimeter of a Square?

Perimeter of Square using Side Length

Perimeter of Square using Diagonal

Perimeter of Square using Area

Solved Examples on Perimeter of Square

FAQs on Perimeter of Square

Read More

Формула вычисления периметра

По длине стороны

По длине диагонали

Примеры задач