Как написать пятиугольник - Правописание и грамматика

Download Article

A regular pentagon is a five-sided polygon with sides of equal length and interior angles of 108° (3π/5 rad). Because 5 is a Fermat prime, you can construct a regular pentagon using only a straightedge and compass.

1

Draw a line segment AB.^[1]
2

Draw two circles, 1 and 2, centred at A and B, both with radius AB. The points where they intersect each other are C and D.^[2]

Advertisement
3

Connect C and D.
4

Draw circle 3 with centre C and radius AB. Circle 3 intersects circles 1 and 2 in E and F respectively. It also intersects line segment DC in G.^[3]
5

Connect E and F with G. Extend these lines far enough so they intersect circles 1 and 2. Call these new intersection points H and I.
6

Draw circles 4 and 5 centred at H and I with radius AB. Name the upper intersection point J.^[4]
7

Connect A, B, I, J and H.^[5]
8

Trace the pentagon in ink or another colour and erase any construction lines (if needed).

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

Place a piece of cardboard or a book under your paper to prevent the compasses from slipping.
Use a sharp pencil for increased precision.

Thanks for submitting a tip for review!

References

About This Article

Thanks to all authors for creating a page that has been read 73,447 times.

Did this article help you?

Don’t miss out! Sign up for

wikiHow’s newsletter

You’re all set!

Источник

Download Article

1

Draw a line segment AB.^[1]
2

Draw two circles, 1 and 2, centred at A and B, both with radius AB. The points where they intersect each other are C and D.^[2]

Advertisement
3

Connect C and D.
4

Draw circle 3 with centre C and radius AB. Circle 3 intersects circles 1 and 2 in E and F respectively. It also intersects line segment DC in G.^[3]
5

Connect E and F with G. Extend these lines far enough so they intersect circles 1 and 2. Call these new intersection points H and I.
6

Draw circles 4 and 5 centred at H and I with radius AB. Name the upper intersection point J.^[4]
7

Connect A, B, I, J and H.^[5]
8

Trace the pentagon in ink or another colour and erase any construction lines (if needed).

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

Place a piece of cardboard or a book under your paper to prevent the compasses from slipping.
Use a sharp pencil for increased precision.

Thanks for submitting a tip for review!

References

About This Article

Thanks to all authors for creating a page that has been read 73,447 times.

Did this article help you?

Don’t miss out! Sign up for

wikiHow’s newsletter

You’re all set!

Источник

Построение пятиугольника рассмотрим подробно:

Чертим необходимую окружность;
Строим вспомогательную окружность такого же размера;
Соединяем точки пересечения прямой линией, полученные при построении вспомогательной окружности;
Соединяем пересечение прямой линии с осью первоначальной окружности;
От полученной точки ведем отрезок к верхней точки пересечения окружности и оси;
Полученный отрезок есть ни что иное как радиус 2-й вспомогательной окружности;
Соединяем прямой линией от верхней точки пересечения с осью к точки пересечения вспомогательной окружности с горизонтальной осью. Полученная прямая и есть необходимый нам радиус для построения пятиугольника;
Строим «засечки» с первоначальной окружностью;
Соединяем полученные точки пересечения.

Вы можете посмотреть построение пятиугольника в видео:

Посмотрите примеры чертежей

Источник

Как построить и нарисовать правильный пятиугольник по окружности

Правильный пятиугольник представляет собой геометрическую фигуру, которая образовывается пересечением пяти прямых, создающих пять одинаковых углов. Такая фигура носит название — пентагон. С пятиугольником тесно связана работа художников — их рисунки строятся на основе правильных геометрических фигур. Для этого необходимо знать то, как быстро построить пентагон.

Чем интересна эта фигура? Форму пентагона имеет здание Министерства обороны Соединенных Штатов Америки. Это можно увидеть на фото, сделанных с высоты полета. В природе не существует кристаллов и камней, форма которых напоминала бы пентагон. Только в этой фигуре количество граней совпадает с числом диагоналей.

Параметры правильного пятиугольника

Прямоугольный пятиугольник, как и каждая фигура в геометрии, имеет свои параметры. Зная необходимые формулы, можно рассчитать эти параметры, что облегчит процесс построения пентагона. Способы и формулы расчетов:

сумма всех углов в многоугольниках равна 360 градусам. В правильном пятиугольнике все углы равны, соответственно, центральный угол находится таким способом: 360/5 = 72 градуса;
внутренний угол находится таким образом: 180*(n -2)/ n = 180*(5−2)/5 = 108 градусов. Сумма всех внутренних углов: 108*5 = 540 градусов.

Сторона пентагона находится с помощью параметров, которые уже даны в условии задачи:

если вокруг пятиугольника описана окружность и известен ее радиус, сторона находится по такой формуле: a = 2*R*sin (α/2) = 2*R*sin (72/2) = 1,1756*R.
Если известен радиус вписанной в пентагон окружности, то формула расчета стороны многоугольника: 2*r*tg (α/2) = 2*r*tg (α/2) = 1,453*r.
При известной величине диагонали пентагона его сторона рассчитывается таким образом: а = D/1,618.

Площадь пентагона так же, как и его сторона, зависит от уже найденных параметров:

с помощью известного радиуса вписанной окружности площадь находится так: S = (n*a*r)/2 = 2,5*a*r.
описанная вокруг пятиугольника окружность позволяет найти площадь по такой формуле: S = (n*R2*sin α)/2 = 2,3776*R2.
в зависимости от стороны пентагона: S = (5*a2*tg 54°)/4 = 1,7205* a2.

Построение пентагона

Построить правильный пятиугольник можно с помощью линейки и циркуля, на основе вписанной в него окружности или одной из сторон.

Как начертить пятиугольник на основе вписанной окружности? Для этого необходимо запастись циркулем и линейкой и сделать такие шаги:

Сначала необходимо начертить окружность с центром О, после чего на ней выбрать точку, А — вершину пентагона. От центра к вершине проводится отрезок.
Затем строится перпендикулярная прямой ОА отрезок, который также проходит через О — центр окружности. Его пересечение с окружностью обозначается точкой В. Отрезок О. В. делится пополам точкой С.
Точка С станет центром новой окружности, проходящей через А. Точка D — это ее пересечение с прямой ОВ в границах первой фигуры.
После этого проводится третья окружность через D, центром которой является точка А. Она пересекается с первой фигурой в двух точках, их необходимо обозначить буквами Е и F.
Следующая окружность имеет центр в точке Е и проходит через А, а ее пересечение с первоначальной находится в новой точке G.
Последняя окружность в этом рисунке проводится через точку, А с центром F. На ее пересечении с начальной ставится точка Н.
На первой окружности после всех проделанных шагов появились пять точек, которые необходимо соединить отрезками. Таким образом получился правильный пятиугольник АЕ G Н F.

Как построить правильный пятиугольник иным способом? С помощью линейки и циркуля пентагон можно построить немного быстрее. Для этого необходимо:

Cначала необходимо с помощью циркуля нарисовать окружность, центр которой — точка О.
Чертится радиус ОА — отрезок, который откладывается на окружность. Его делят пополам точкой В.
Перпендикулярно радиусу ОА начерчивается отрезок ОС, точки В и С соединяются прямой.
Следующим шагом является отложение длины отрезка ВС с помощью циркуля на диаметральной линии. Перпендикулярно отрезку ОА появляется точка D. Точки В и D соединяются, образуя новый отрезок.
Для того, чтобы получить величину стороны пентагона, необходимо соединить точки С и D.
D с помощью циркуля переносится на окружность и обозначается точкой Е. Соединив Е и С, можно получить первую сторону правильного пятиугольника. Следуя этой инструкции можно узнать о том, как быстро построить пятиугольник с равными сторонами, продолжая построение остальных его сторон подобно первой.

Интересные факты

В пятиугольнике с одинаковыми сторонами диагонали равны и образуют пятиконечную звезду, которая называется пентаграммой. Золотое сечение — это отношение величины диагонали к стороне пентагона.

Пентагон непригоден для полного заполнения плоскости. Использование любого материала в этой форме оставляет промежутки или образует наложения. Хотя природных кристаллов этой формы не существует в природе, но при образовании льда на поверхности гладких медных изделий возникают молекулы в виде пентагона, которые соединены в цепочки.

Наиболее простой способ получить правильный пятиугольник из полоски бумаги — завязать ее узлом и немного придавить. Этот способ полезен для родителей детей-дошкольников, которые хотят научить своих малышей распознавать геометрические фигуры.

Видео

Посмотрите, как можно быстро начертить пятиугольник.

Построение правильного пятиугольника

Первый способ — по данной стороне S с помощью транспортира.

Проводим прямую и откладываем на ней AB = S; принимаем эту линию за радиус и этим радиусом из точек A и В описываем дуги: далее с помощью транспортира строим в этих точках углы в 108°, стороны которых пересекутся с дугами в точках С и D; из этих точек радиусом АВ = 5 описываем дуги, которые пересекутся в Е, и прямыми линиями соединяем точки Л, С, Е, D, В.

Полученный пятиугольник — искомый.

Первый способ построения пятиугольника

Второй способ. Проведем окружность радиусом r. Из точки А циркулем проводим дугу радиуса AM до пересечения в точках В и С с окружностью. Соединяем В и С линией, которая пересечет горизонтальную ось в точке Е.

Затем из точки Е проводим дугу, которая пересечет горизонтальную линию в точке О. Описываем, наконец, из точки F дугу, которая пересечет окружность в точках Н и К. Отложив по окружности расстояние FO = FH = FK пять раз и соединив точки деления линиями, получим правильный пятиугольник.

Второй способ построения пятиугольника

Третий способ. В данный круг вписать правильный пятиугольник. Проводим два взаимно перпендикулярных диаметра АВ и МС. Делим радиус АО точкой Е пополам. Из точки Е, как из центра, проводим дугу окружности радиуса ЕМ и засекаем ею диаметр АВ в точке F. Отрезок MF равен стороне искомого правильного пятиугольника. Раствором циркуля, равным MF, делаем засечки N₁, Р₁, Q₁, К₁ и соединяем их прямыми.

Третий способ построения пятиугольника

На рисунке построен шестиугольник по данной стороне.

Построение шестиугольника

Прямой АВ = 5, как радиусом, из точек А и В описываем дуги, которые пересекутся в С; из этой точки тем же радиусом описываем окружность, на которой сторона А В отложится 6 раз.

Шестиугольник ADEFGB — искомый.

«Отделка комнат при ремонте»,
Н.П.Краснов

Правильный пятиугольник — построение, свойства и формулы

Бывают задачи на построение и нахождение некоторых геометрических параметров правильного пятиугольника. Построить фигуру непросто. Для этого математики рекомендуют несколько методик, позволяющих выполнить операцию более точно или за короткий промежуток времени. У фигуры есть свойства, а также формулы, позволяющие найти ее геометрические характеристики.

Точное построение фигуры

Специалисты рекомендуют некоторую последовательность действий, по которым построить правильный пятиугольник очень просто. Для операции необходимы обыкновенная тетрадь в клеточку, циркуль, карандаш, резинка и линейка. Следует выполнить некоторые шаги:

Построить окружность с центром в некоторой точке О.

Провести два диаметра. Они должны пересекаться под прямым углом.

Поставить точку V (пересечение окружности с одним из диаметров), которая является вершиной фигуры.

По левой стороне поставить точку D. Это пересечение диаметра (оси симметрии) с окружностью.

Отметить на отрезке OD точку А, которая делит его пополам.

Выполнить построение вспомогательной окружности, центром которой является точка, полученная в 5 пункте. Кроме того, круг с радиусом CV должен проходить через V.

Точку, полученную при пересечении диаметра и окружности, нужно обозначить литерой B.

Нарисовать окружность с радиусом, равным CV, из точки V.

Отметить пересечение круга с первой окружностью, центром которой является точка О. Искомое место пересечения обозначить литерой F (вторая вершина пентагона).

Поставить иглу циркуля в точку F и провести окружность через Е.

Обозначить пересечение окружностей с центрами в F и O точкой G, которая будет вершиной пентагона.

Аналогичным образом проделать шаг 11, только центр выбрать не в F, а в G. Полученную точку следует обозначить литерой H (последняя вершина фигуры).

Соединить пять точек (СVEFG) между собой с помощью линейки.

Если все пункты алгоритма выполнены правильно, то должен получиться пентагон, изображенный на рисунке 1:

Этот способ следует применять для точных построений и чертежей деталей. Однако для решения задач, в которых необходимо схематически изобразить пятиугольник, этот вариант не подойдет.

Алгоритм Биона

Прием Биона является менее точным методом, чем первый. Он позволяет построить любой правильный многоугольник, вписанный в произвольный круг. Для операции необходимо воспользоваться алгоритмом (шаблоном) Биона, имеющим такой вид:

Начертить окружность с центром в точке О и радиусом R.

Провести в ней диаметр АD.

Построить правильный (равносторонний) треугольник с одной из сторон, равной диаметру.

Поделить диаметр на несколько равных частей (АС = СE = ED), количество которых вычисляется по формуле: (n — 2). Переменная «n» эквивалентна количеству граней правильного многоугольника, то есть n = 3. Соотношение можно записать следующей зависимостью: АС = [1 / (n — 2)] * AD = AD / 3.

Провести из точек С и Е прямые, перпендикулярные диаметру.

Точки пересечения прямых с окружностью обозначить F и G.

Если соединить точки, то получится пентагон ABDFG.

Погрешность построения многоугольника с 5, 7, 9 и 10 сторонами при использовании алгоритма довольно маленькая. Ее значения равно 3,2%. Однако при n>10 погрешность составляет не более 11%.

Приближенные методы

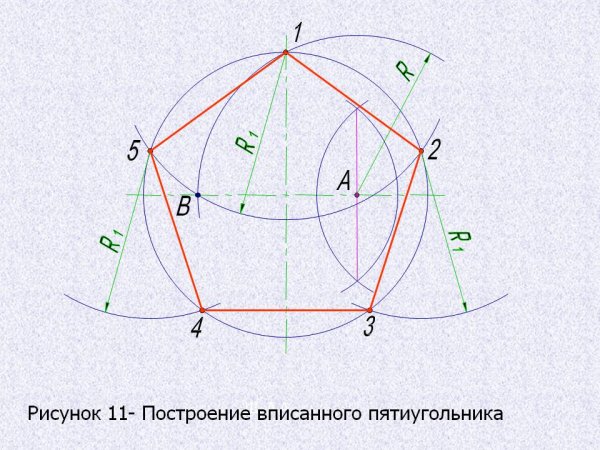
Существует несколько методов, позволяющих приближенно изобразить фигуру. Однако оптимальным является построение пентагона (рис. 2), используя две окружности (описанную и вписанную).

Метод известного математика А. Дюрера является оптимальным среди остальных, поскольку на построение затрачивается минимальное количество времени. Для его реализации следует выполнить определенные шаги алгоритма Дюрера:

Начертить произвольную окружность с центром в точке О.

Не вынимая иглу циркуля из точки О, выполнить построение другой окружности. Ее радиус нужно уменьшить таким образом, чтобы общий радиус R был равен стороне пятиугольника.

Отметить на окружности с большим радиусом две произвольные точки. При этом следует руководствоваться правилом: прямая, проходящая через них, должна касаться малой окружности в одной точке (касательная).

Отметить следующую точку, чтобы можно было соединить ее с предыдущей. Правило при этом должно соблюдаться.

Аналогично проделать операции с другими сторонами пентагона.

Существует еще один метод — построение пятиугольника из десятиугольника, который вписан в окружность. Для этого следует соединить его вершины через одну. Однако способ рекомендуется применять только в том случае, когда исходная фигура уже имеется. Кстати, его следует строить также методом А. Дюрера.

Математики рекомендуют еще один простой способ. Для его реализации необходимо начертить окружность с диаметром АD. После этого его нужно поделить на 3 равные части, то есть AB = BC = CD. Затем из точки С следует опустить перпендикуляры на окружность. Обозначить места пересечения точками E и F. Проделать такую же процедуру с точкой B, обозначив пересечения точками G и H. Остается лишь соединить все точки отрезками.

Признаки и свойства

Не всегда получается верно идентифицировать пятиугольник. Для этого математики предлагают признаки, которые применимы только к правильной фигуре. К ним можно отнести следующие:

Стороны равны между собой.

Любой угол правильного пятиугольника равен остальным его углам.

Следует отметить, что признаки справедливы для любого правильного многогранника. Пять осей симметрии имеет правильный пятиугольник (сколько сторон, столько и осей). Пентагон обладает некоторыми свойствами, которые будут очень полезны при решении задач. К ним можно отнести следующие:

Равенство сторон.

Углы равны по 108 градусов.

Центры вписанной и описанной окружностей совпадают.

Сумма внутренних углов равна 180 * (5 — 2) = 540 (градусов), а внешних — 360.

Количество диагоналей соответствует 5.

Значение площади кольца, которое образуется между вписанным и описанным кругами, эквивалентно произведению квадрата длины стороны на константу Pi / 4.

Биссектрисы, проведенные через центр, равны.

Диагонали — трисектрисы внутренних углов. Одна диагональ делит его на 1/3 и 2/3 части.

Отношение диагонали к стороне эквивалентно «золотому сечению» и равно [1 + 5^(1/2)] / 2.

Однако свойств недостаточно при решении задач, поскольку существуют некоторые формулы и соотношения для нахождения основных параметров пентагона.

Расчет параметров

С помощью соотношений можно легко найти необходимые характеристики любой фигуры. Однако в некоторых источниках не указаны условные обозначения известного параметра пентагона. Это существенно затрудняет понимание формулы, а также ее дальнейшее использование. Перед изучением следует нарисовать фигуру и обозначить некоторые величины, которыми могут быть диагонали, стороны, апофемы и радиусы.

Рекомендуется использовать различные литеры или буквенные обозначения. Недопустимо пронумеровывать вершины, поскольку при вычислениях можно ошибиться. Нельзя использовать вместо букв цифры при обозначениях. Например, пентагон ABCDE является правильной записью. Допускается применение чисел в индексах, а именно, в пятиугольнике правильного типа ABCDE при пересечении его диагоналей образовался пентагон A1B1C1D1E1.

Математики рекомендуют обозначать только промежуточные фигуры или их проекции литерами с индексами. Для каждой новой фигуры следует вводить другие обозначения. Не следует использовать зарезервированные переменные. Например, центр окружности в точке P является недопустимой записью, поскольку такой буквой обозначается периметр.

Условные обозначения

Для нахождения основных величин пентагона следует обозначить некоторые его параметры. Фигура имеет следующие обозначения:

Сторона: a.

Радиус вписанной и описанной окружностей: r и R соответственно.

Площадь: S.

Периметр и полупериметр: P и p соответственно.

Диагональ: d.

Отношение золотого сечения: Ф.

Значения сторон равны между собой. Площадь правильного пятиугольника — характеристика двумерной фигуры, которая показывает ее размерность. Периметром называется сумма всех 5 сторон. Полупериметр вычисляется по следующему соотношению: p = P / 2. Диагонали — отрезки, проведенные из одной вершины к противоположной (несмежной).

Соотношения и формулы

После обозначений следует переходить к рассмотрению основных формул, при помощи которых можно вычислять параметры фигуры. Сторону можно найти, воспользовавшись такими соотношениями:

a = 2r * tg(36).

a = 2R * sin(36).

a = R * [(5 — (5)^(1/2)) / 2]^(1/2).

Радиус вписанной окружности в пентагон можно найти, используя тригонометрические функции. Однако существует также формула, позволяющая вычислить приближенное значение. Это необходимо в том случае, когда под рукой нет специального онлайн-калькулятора, компьютера или таблиц Брадиса. Формулы для нахождения радиуса вписанной окружности:

r = a / (2tg(36)).

r = a * [5^(1/2) * [5 + 2 * 5^(1/2)]^(1/2) / 10].

Математики также рекомендуют описать вокруг пентагона окружность. Это расширит возможности по поиску его основных характеристик. Однако ее радиус следует вычислить. Формулы для его нахождения выглядят таким образом:

R = a / (2sin(36)).

R = a * [10^(1/2) * [5 + 5^(1/2)]^(1/2) / 10] = (5^(1/2) — 1) * r.

Периметр определяется просто: Р = 5а. Значение полупериметра эквивалентно половине периметра, то есть p = P / 2 = 5a / 2 = 2,5a. Площадь можно найти, используя такие формулы:

S = (5a^2 / 4) * ctg(36).

S = 5r^2 * tg(36).

S = 2,5 * R^2 * sin(72).

S = (5/12) * R * d.

Высота правильного пятиугольника (h) — отрезок, проведенный из центра на любую из сторон. Она делит ее на две равные части, поскольку является биссектрисой и медианой равнобедренного треугольника. У последнего две стороны — радиусы описанной окружности, а третья — сторона пентагона. Высота называется также апофемой и проекцией на «а». Вычисляется ее значение по формуле h = a * tg(72) / 2.

Величина Ф является отношением площади пентагона (S) к площади (S1) правильного пятиугольника, полученного при пересечении диагоналей первого: S / S1 = Ф^4 = 3Ф + 2 = (3 * 5^(1/2) + 7) / 2. Длина диагонали находится по такому соотношению: d = [Ф * 5^(1/2) * R]^(1/2).

Таким образом, при решении задач необходимо знать основные признаки, свойства, соотношения и формулы для нахождения основных характеристик пентагона. Практика обязательна, поскольку теоретические знания без практического применения бесполезны.

источники:

http://www.ktovdome.ru/otdelka_komnat_pri_remonte/351/10813.html

http://sprint-olympic.ru/uroki/geometrija/85022-pravilnyi-piatiygolnik-postroenie-svoistva-i-formyly.html

Источник

Построение правильного пятиугольника вписанного в окружность

Как начертить правильный пятиугольник в окружности

Как построить пятиугольник циркулем

Как построить правильный пятиугольник

Равносторонний пятиугольник чертеж

Как построить правильный 5 угольник

Построение правильного пятиугольника с помощью циркуля

Как построить правильный 5 угольник

Пятиугольник Рело

Построение правильного пятиугольника в окружности

Как построить правильный 5 угольник

Как построить пятиугольник в окружности

Равносторонний пятиугольник чертеж

Рисование звезды циркулем

Начертить пятиугольник

Построение правильного пятиугольника в окружности

Равносторонний пятиугольник чертеж

Построение правильных многоугольников

Равносторонний пятиугольник

Построение правильнихмногоугольников

Пятиугольник в виде домика

Восьмиугольник правильный чертеж

Правильный пятиугольник на клеточной бумаге

Геометрия построение пятиугольника

Равносторонний пятиугольник чертеж

Как начертить правильный шестиугольник

Как начертить 5 угольник

Правильный шестиугольник чертеж

Регулярный пятиугольник

Пентаграмма Пифагора

Как начертить правильный шестиугольник

Построение правильных многоугольников

Многоугольники пятиугольник

Равносторонний пятиугольник

Правильный пятиугольник на клеточной бумаге

Шестиугольника начерти два 2 пятиугольника

Правильный пятиугольник внутренний пятиугольник

Шестиугольник разделить на 2 пятиугольника

Пятиугольник со стороной 4 см

Правельнвц многоугольника

Треугольник четырехугольник пятиугольник

Пятиугольник и шестиугольник

Правильный 5 угольник

Центр правильного пятиугольника

Геометрические фигуры семиугольник

Вписанный правильный восьмиугольник

Пятиугольник в круге с помощью циркуля

Гексагон Призма

Как построить пятиугольник циркулем

Осевая симметрия пятиугольника построение

Пятиугольник вписанный в окружность построение

Пентагон форма пятиугольника

Семиугольник чертеж

Пятиугольник вписанный в квадрат

Правильный 5 ти угольник

Построение пятиугольника циркулем

Пятиугольник ABCDE

Начертить правильный шестиугольник

Произвольный пятиугольник

Правильный пятиугольник построение

Пятиугольник со стороной 3 см

Равносторонний пятиугольник чертеж

Построение пятиугольника

Правильный пятиугольник вписанный в окружность

Источник

Содержание

Точное построение фигуры
Алгоритм Биона
Приближенные методы
Признаки и свойства
Расчет параметров
- Условные обозначения
- Соотношения и формулы

Точное построение фигуры

Построить окружность с центром в некоторой точке О.

Провести два диаметра. Они должны пересекаться под прямым углом.

Поставить точку V (пересечение окружности с одним из диаметров), которая является вершиной фигуры.

По левой стороне поставить точку D. Это пересечение диаметра (оси симметрии) с окружностью.

Отметить на отрезке OD точку А, которая делит его пополам.

Точку, полученную при пересечении диаметра и окружности, нужно обозначить литерой B.

Нарисовать окружность с радиусом, равным CV, из точки V.

Поставить иглу циркуля в точку F и провести окружность через Е.

Обозначить пересечение окружностей с центрами в F и O точкой G, которая будет вершиной пентагона.

Соединить пять точек (СVEFG) между собой с помощью линейки.

Если все пункты алгоритма выполнены правильно, то должен получиться пентагон, изображенный на рисунке 1:

Этот способ следует применять для точных построений и чертежей деталей. Однако для решения задач, в которых необходимо схематически изобразить пятиугольник, этот вариант не подойдет.

Алгоритм Биона

Начертить окружность с центром в точке О и радиусом R.

Провести в ней диаметр АD.

Построить правильный (равносторонний) треугольник с одной из сторон, равной диаметру.

Провести из точек С и Е прямые, перпендикулярные диаметру.

Точки пересечения прямых с окружностью обозначить F и G.

Если соединить точки, то получится пентагон ABDFG.

Погрешность построения многоугольника с 5, 7, 9 и 10 сторонами при использовании алгоритма довольно маленькая. Ее значения равно 3,2%. Однако при n>10 погрешность составляет не более 11%.

Приближенные методы

Начертить произвольную окружность с центром в точке О.

Отметить следующую точку, чтобы можно было соединить ее с предыдущей. Правило при этом должно соблюдаться.

Аналогично проделать операции с другими сторонами пентагона.

Признаки и свойства

Стороны равны между собой.

Любой угол правильного пятиугольника равен остальным его углам.

Равенство сторон.

Углы равны по 108 градусов.

Центры вписанной и описанной окружностей совпадают.

Сумма внутренних углов равна 180 * (5 — 2) = 540 (градусов), а внешних — 360.

Количество диагоналей соответствует 5.

Биссектрисы, проведенные через центр, равны.

Диагонали — трисектрисы внутренних углов. Одна диагональ делит его на 1/3 и 2/3 части.

Отношение диагонали к стороне эквивалентно «золотому сечению» и равно [1 + 5^(1/2)] / 2.

Однако свойств недостаточно при решении задач, поскольку существуют некоторые формулы и соотношения для нахождения основных параметров пентагона.

Расчет параметров

Условные обозначения

Сторона: a.

Радиус вписанной и описанной окружностей: r и R соответственно.

Площадь: S.

Периметр и полупериметр: P и p соответственно.

Диагональ: d.

Отношение золотого сечения: Ф.

Соотношения и формулы

a = 2r * tg(36).

a = 2R * sin(36).

a = R * [(5 — (5)^(1/2)) / 2]^(1/2).

r = a / (2tg(36)).

r = a * [5^(1/2) * [5 + 2 * 5^(1/2)]^(1/2) / 10].

R = a / (2sin(36)).

R = a * [10^(1/2) * [5 + 5^(1/2)]^(1/2) / 10] = (5^(1/2) — 1) * r.

S = (5a^2 / 4) * ctg(36).

S = 5r^2 * tg(36).

S = 2,5 * R^2 * sin(72).

S = (5/12) * R * d.

ГеометрияСвойства диагоналей ромба — основные формулы и доказательство теоремы

ГеометрияДодекаэдр — свойства, вид и структура двенадцатигранника

Источник