Как написать пятнашки на java

Время на прочтение
9 мин

Количество просмотров 17K

«Пятнадцать», или «Пятнашка» — отличный пример простой логической игры, популярной во всем мире. Для того чтобы решить головоломку, необходимо расставить квадратики с цифрами по порядку, от меньшего к большему. Это непросто, но интересно.

В сегодняшнем туториале показываем, как разработать «Пятнашку» на Java 8 с Eclipse. Для разработки UI мы будем использовать Swing API.

Напоминаем: для всех читателей «Хабра» — скидка 10 000 рублей при записи на любой курс Skillbox по промокоду «Хабр».

Skillbox рекомендует: Образовательный онлайн-курс «Профессия Java-разработчик».

Проектирование игры

На этом этапе нужно определить свойства:

• Size — размер игрового поля;
• nbTiles — количество пятнашек в поле. nbTiles = size*size — 1;
• Tiles — пятнашка, которая представляет собой одномерный массив целых чисел. Каждая из пятнашек получит уникальное значение в диапазоне [0, nbTiles]. Ноль обозначает пустой квадрат;
• blankPos — позиция пустого квадрата.

Логика игры

Нужно определить метод сброса (reset), используемый для инициализации новой игровой позиции. Так мы устанавливаем значение для каждого элемента массива пятнашек. Ну а потом помещаем blankPos в последнюю позицию массива.

Также нужен метод shuffle для перетасовки массива пятнашек. Мы не включаем пустую пятнашку в процесс перетасовки, чтобы оставить ее в прежнем положении.

Поскольку только половина возможных стартовых позиций головоломки имеет решение, нужно проверить получившийся результат перемешивания, чтобы убедиться в том, что текущий расклад вообще решаем. Чтобы это сделать, определяем метод isSolvable.

Если конкретной пятнашке предшествует пятнашка с более высоким значением, это считается инверсией. Когда пустая пятнашка находится на своем месте, число инверсий должно быть четным, чтобы головоломка была разрешимой. Итак, мы подсчитываем количество инверсий и возвращаем true, если число четное.

Затем важно определить метод isSolved, чтобы проверить, решен ли наш расклад Game Of Fifteen. Сначала мы смотрим, где находится пустая пятнашка. Если в начальной позиции, то текущий расклад — новый, не решенный ранее. Затем мы перебираем плитки в обратном порядке, и, если значение пятнашки отличается от соответствующего индекса +1, возвращаем false. В противном случае в конце метода пора вернуть true, потому что головоломка уже решена.

Еще один метод, который нужно определить, — newGame. Он требуется для создания нового экземпляра игры. Для этого мы сбрасываем игровое поле, затем перетасовываем его и продолжаем до тех пор, пока игровая позиция не будет разрешима.

Вот пример кода с ключевой логикой пятнашек:

private void newGame() {
  do {
    reset(); // reset in initial state
    shuffle(); // shuffle
  } while(!isSolvable()); // make it until grid be solvable
 
  gameOver = false;
}
 
private void reset() {
  for (int i = 0; i < tiles.length; i++) {
    tiles[i] = (i + 1) % tiles.length;
  }
 
  // we set blank cell at the last
  blankPos = tiles.length - 1;
}
 
private void shuffle() {
  // don't include the blank tile in the shuffle, leave in the solved position
  int n = nbTiles;
 
  while (n > 1) {
    int r = RANDOM.nextInt(n--);
    int tmp = tiles[r];
    tiles[r] = tiles[n];
    tiles[n] = tmp;
  }
}
 
// Only half permutations of the puzzle are solvable/
// Whenever a tile is preceded by a tile with higher value it counts
// as an inversion. In our case, with the blank tile in the solved position,
// the number of inversions must be even for the puzzle to be solvable
private boolean isSolvable() {
  int countInversions = 0;
 
  for (int i = 0; i < nbTiles; i++) {
    for (int j = 0; j < i; j++) {
      if (tiles[j] > tiles[i])
        countInversions++;
    }
  }
 
  return countInversions % 2 == 0;
}
 
private boolean isSolved() {
  if (tiles[tiles.length - 1] != 0) // if blank tile is not in the solved position ==> not solved
    return false;
 
  for (int i = nbTiles - 1; i >= 0; i--) {
    if (tiles[i] != i + 1)
      return false;
  }
 
  return true;
}

Наконец, нужно запрограммировать движение пятнашек в массиве. Этот код будет вызываться позже посредством обратного вызова (callback), чтобы реагировать на движение курсора. Наша игра будет поддерживать несколько перемещений плиток одновременно. Таким образом, после того как мы конвертировали нажатую позицию на экране в пятнашку, мы получаем позицию пустой пятнашки и ищем направление движения для поддержки нескольких ее перемещений одновременно.

Вот пример кода:

// get position of the click
int ex = e.getX() - margin;
int ey = e.getY() - margin;
 
// click in the grid ?
if (ex < 0 || ex > gridSize  || ey < 0  || ey > gridSize)
  return;
 
// get position in the grid
int c1 = ex / tileSize;
int r1 = ey / tileSize;
 
// get position of the blank cell
int c2 = blankPos % size;
int r2 = blankPos / size;
 
// we convert in the 1D coord
int clickPos = r1 * size + c1;
 
int dir = 0;
 
// we search direction for multiple tile moves at once
if (c1 == c2  &&  Math.abs(r1 - r2) > 0)
  dir = (r1 - r2) > 0 ? size : -size;
else if (r1 == r2 && Math.abs(c1 - c2) > 0)
  dir = (c1 - c2) > 0 ? 1 : -1;
 
if (dir != 0) {
  // we move tiles in the direction
  do {
    int newBlankPos = blankPos + dir;
    tiles[blankPos] = tiles[newBlankPos];
    blankPos = newBlankPos;
  } while(blankPos != clickPos);
 
tiles[blankPos] = 0;

Разрабатываем UI на Swing API

Самое время заняться интерфейсом. Сначала берем класс Jpanel. Потом на поле рисуем пятнашки — для расчета размеров каждой воспользуемся данными, заданными в параметре конструктора игры:

gridSize = (dim  -  2 * margin);
tileSize = gridSize / size;

Margin также является параметром, заданным в конструкторе игры.

Теперь нужно определить метод drawGrid для отрисовки сетки и пятнашек на экране. Анализируем массив пятнашек и конвертируем координаты в координаты пользовательского интерфейса. Затем прорисуем каждую пятнашку с соответствующим номером в центре:

private void drawGrid(Graphics2D g) {
  for (int i = 0; i < tiles.length; i++) {
    // we convert 1D coords to 2D coords given the size of the 2D Array
    int r = i / size;
    int c = i % size;
    // we convert in coords on the UI
    int x = margin + c * tileSize;
    int y = margin + r * tileSize;
 
    // check special case for blank tile
    if(tiles[i] == 0) {
      if (gameOver) {
        g.setColor(FOREGROUND_COLOR);
        drawCenteredString(g, "u2713", x, y);
      }
 
      continue;
    }
 
    // for other tiles
    g.setColor(getForeground());
    g.fillRoundRect(x, y, tileSize, tileSize, 25, 25);
    g.setColor(Color.BLACK);
    g.drawRoundRect(x, y, tileSize, tileSize, 25, 25);
    g.setColor(Color.WHITE);
 
    drawCenteredString(g, String.valueOf(tiles[i]), x , y);
  }
}

Наконец, переопределим метод paintComponent, являющийся производным класса JPane. Затем используем метод drawGrid, а после — метод drawStartMessage для отображения сообщения, предлагающего кликнуть для запуска игры:

private void drawStartMessage(Graphics2D g) {
  if (gameOver) {
    g.setFont(getFont().deriveFont(Font.BOLD, 18));
    g.setColor(FOREGROUND_COLOR);
    String s = "Click to start new game";
    g.drawString(s, (getWidth() - g.getFontMetrics().stringWidth(s)) / 2,
        getHeight() - margin);
  }
}
 
private void drawCenteredString(Graphics2D g, String s, int x, int y) {
  // center string s for the given tile (x,y)
  FontMetrics fm = g.getFontMetrics();
  int asc = fm.getAscent();
  int desc = fm.getDescent();
  g.drawString(s,  x + (tileSize - fm.stringWidth(s)) / 2,
      y + (asc + (tileSize - (asc + desc)) / 2));
}
 
@Override
protected void paintComponent(Graphics g) {
  super.paintComponent(g);
  Graphics2D g2D = (Graphics2D) g;
  g2D.setRenderingHint(RenderingHints.KEY_ANTIALIASING, RenderingHints.VALUE_ANTIALIAS_ON);
  drawGrid(g2D);
  drawStartMessage(g2D);
}

Реагируем на действия пользователя в UI

Для того чтобы игра шла своим чередом, необходимо обрабатывать действия пользователя в UI. Для этого добавляем имплементацию MouseListener на Jpanel и код для перемещения пятнашек, уже показанный выше:

addMouseListener(new MouseAdapter() {
  @Override
  public void mousePressed(MouseEvent e) {
    // used to let users to interact on the grid by clicking
    // it's time to implement interaction with users to move tiles to solve the game !
    if (gameOver) {
      newGame();
    } else {
      // get position of the click
      int ex = e.getX() - margin;
      int ey = e.getY() - margin;
 
      // click in the grid ?
      if (ex < 0 || ex > gridSize  || ey < 0  || ey > gridSize)
        return;
 
      // get position in the grid
      int c1 = ex / tileSize;
      int r1 = ey / tileSize;
 
      // get position of the blank cell
      int c2 = blankPos % size;
      int r2 = blankPos / size;
 
      // we convert in the 1D coord
      int clickPos = r1 * size + c1;
 
      int dir = 0;
 
      // we search direction for multiple tile moves at once
      if (c1 == c2  &&  Math.abs(r1 - r2) > 0)
        dir = (r1 - r2) > 0 ? size : -size;
      else if (r1 == r2 && Math.abs(c1 - c2) > 0)
        dir = (c1 - c2) > 0 ? 1 : -1;
 
      if (dir != 0) {
        // we move tiles in the direction
        do {
          int newBlankPos = blankPos + dir;
          tiles[blankPos] = tiles[newBlankPos];
          blankPos = newBlankPos;
        } while(blankPos != clickPos);
 
        tiles[blankPos] = 0;
      }
 
      // we check if game is solved
      gameOver = isSolved();
    }
 
    // we repaint panel
    repaint();
  }
});

Код размещаем в конструкторе класса GameOfFifteen. В самом конце вызываем метод newGame для начала новой игры.

Полный код игры

Последний шаг, прежде чем увидеть игру в действии, — нужно собрать все элементы кода вместе. Вот что получится:

import java.awt.BorderLayout;
import java.awt.Color;
import java.awt.Dimension;
import java.awt.Font;
import java.awt.FontMetrics;
import java.awt.Graphics;
import java.awt.Graphics2D;
import java.awt.RenderingHints;
import java.awt.event.MouseAdapter;
import java.awt.event.MouseEvent;
import java.util.Random;
 
import javax.swing.JFrame;
import javax.swing.JPanel;
import javax.swing.SwingUtilities;
 
// We are going to create a Game of 15 Puzzle with Java 8 and Swing
// If you have some questions, feel free to read comments ;)
public class GameOfFifteen extends JPanel { // our grid will be drawn in a dedicated Panel
 
  // Size of our Game of Fifteen instance
  private int size;
  // Number of tiles
  private int nbTiles;
  // Grid UI Dimension
  private int dimension;
  // Foreground Color
  private static final Color FOREGROUND_COLOR = new Color(239, 83, 80); // we use arbitrary color
  // Random object to shuffle tiles
  private static final Random RANDOM = new Random();
  // Storing the tiles in a 1D Array of integers
  private int[] tiles;
  // Size of tile on UI
  private int tileSize;
  // Position of the blank tile
  private int blankPos;
  // Margin for the grid on the frame
  private int margin;
  // Grid UI Size
  private int gridSize;
  private boolean gameOver; // true if game over, false otherwise
 
  public GameOfFifteen(int size, int dim, int mar) {
    this.size = size;
    dimension = dim;
    margin = mar;
    
    // init tiles
    nbTiles = size * size - 1; // -1 because we don't count blank tile
    tiles = new int[size * size];
    
    // calculate grid size and tile size
    gridSize = (dim - 2 * margin);
    tileSize = gridSize / size;
    
    setPreferredSize(new Dimension(dimension, dimension + margin));
    setBackground(Color.WHITE);
    setForeground(FOREGROUND_COLOR);
    setFont(new Font("SansSerif", Font.BOLD, 60));
    
    gameOver = true;
    
    addMouseListener(new MouseAdapter() {
      @Override
      public void mousePressed(MouseEvent e) {
        // used to let users to interact on the grid by clicking
        // it's time to implement interaction with users to move tiles to solve the game !
        if (gameOver) {
          newGame();
        } else {
          // get position of the click
          int ex = e.getX() - margin;
          int ey = e.getY() - margin;
          
          // click in the grid ?
          if (ex < 0 || ex > gridSize  || ey < 0  || ey > gridSize)
            return;
          
          // get position in the grid
          int c1 = ex / tileSize;
          int r1 = ey / tileSize;
          
          // get position of the blank cell
          int c2 = blankPos % size;
          int r2 = blankPos / size;
          
          // we convert in the 1D coord
          int clickPos = r1 * size + c1;
          
          int dir = 0;
          
          // we search direction for multiple tile moves at once
          if (c1 == c2  &&  Math.abs(r1 - r2) > 0)
            dir = (r1 - r2) > 0 ? size : -size;
          else if (r1 == r2 && Math.abs(c1 - c2) > 0)
            dir = (c1 - c2) > 0 ? 1 : -1;
            
          if (dir != 0) {
            // we move tiles in the direction
            do {
              int newBlankPos = blankPos + dir;
              tiles[blankPos] = tiles[newBlankPos];
              blankPos = newBlankPos;
            } while(blankPos != clickPos);
            
            tiles[blankPos] = 0;
          }
          
          // we check if game is solved
          gameOver = isSolved();
        }
        
        // we repaint panel
        repaint();
      }
    });
    
    newGame();
  }
 
  private void newGame() {
    do {
      reset(); // reset in intial state
      shuffle(); // shuffle
    } while(!isSolvable()); // make it until grid be solvable
    
    gameOver = false;
  }
 
  private void reset() {
    for (int i = 0; i < tiles.length; i++) {
      tiles[i] = (i + 1) % tiles.length;
    }
    
    // we set blank cell at the last
    blankPos = tiles.length - 1;
  }
 
  private void shuffle() {
    // don't include the blank tile in the shuffle, leave in the solved position
    int n = nbTiles;
    
    while (n > 1) {
      int r = RANDOM.nextInt(n--);
      int tmp = tiles[r];
      tiles[r] = tiles[n];
      tiles[n] = tmp;
    }
  }
 
  // Only half permutations of the puzzle are solvable.
  // Whenever a tile is preceded by a tile with higher value it counts
  // as an inversion. In our case, with the blank tile in the solved position,
  // the number of inversions must be even for the puzzle to be solvable
  private boolean isSolvable() {
    int countInversions = 0;
    
    for (int i = 0; i < nbTiles; i++) {
      for (int j = 0; j < i; j++) {
        if (tiles[j] > tiles[i])
          countInversions++;
      }
    }
    
    return countInversions % 2 == 0;
  }
 
  private boolean isSolved() {
    if (tiles[tiles.length - 1] != 0) // if blank tile is not in the solved position ==> not solved
      return false;
    
    for (int i = nbTiles - 1; i >= 0; i--) {
      if (tiles[i] != i + 1)
        return false;      
    }
    
    return true;
  }
 
  private void drawGrid(Graphics2D g) {
    for (int i = 0; i < tiles.length; i++) {
      // we convert 1D coords to 2D coords given the size of the 2D Array
      int r = i / size;
      int c = i % size;
      // we convert in coords on the UI
      int x = margin + c * tileSize;
      int y = margin + r * tileSize;
      
      // check special case for blank tile
      if(tiles[i] == 0) {
        if (gameOver) {
          g.setColor(FOREGROUND_COLOR);
          drawCenteredString(g, "u2713", x, y);
        }
        
        continue;
      }
      
      // for other tiles
      g.setColor(getForeground());
      g.fillRoundRect(x, y, tileSize, tileSize, 25, 25);
      g.setColor(Color.BLACK);
      g.drawRoundRect(x, y, tileSize, tileSize, 25, 25);
      g.setColor(Color.WHITE);
      
      drawCenteredString(g, String.valueOf(tiles[i]), x , y);
    }
  }
 
  private void drawStartMessage(Graphics2D g) {
    if (gameOver) {
      g.setFont(getFont().deriveFont(Font.BOLD, 18));
      g.setColor(FOREGROUND_COLOR);
      String s = "Click to start new game";
      g.drawString(s, (getWidth() - g.getFontMetrics().stringWidth(s)) / 2,
          getHeight() - margin);
    }
  }
 
  private void drawCenteredString(Graphics2D g, String s, int x, int y) {
    // center string s for the given tile (x,y)
    FontMetrics fm = g.getFontMetrics();
    int asc = fm.getAscent();
    int desc = fm.getDescent();
    g.drawString(s,  x + (tileSize - fm.stringWidth(s)) / 2,
        y + (asc + (tileSize - (asc + desc)) / 2));
  }
 
  @Override
  protected void paintComponent(Graphics g) {
    super.paintComponent(g);
    Graphics2D g2D = (Graphics2D) g;
    g2D.setRenderingHint(RenderingHints.KEY_ANTIALIASING, RenderingHints.VALUE_ANTIALIAS_ON);
    drawGrid(g2D);
    drawStartMessage(g2D);
  }
 
  public static void main(String[] args) {
    SwingUtilities.invokeLater(() -> {
      JFrame frame = new JFrame();
      frame.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE);
      frame.setTitle("Game of Fifteen");
      frame.setResizable(false);
      frame.add(new GameOfFifteen(4, 550, 30), BorderLayout.CENTER);
      frame.pack();
      // center on the screen
      frame.setLocationRelativeTo(null);
      frame.setVisible(true);
    });
  }
 
 
}

Наконец, играем!

Самое время запустить игру и проверить ее в действии. Поле должно выглядеть следующим образом:

Пробуем решить головоломку. Если все прошло успешно, получаем вот что:

Вот и всё. А вы ожидали большего?

Skillbox рекомендует:

• Практический курс «Мобильный разработчик PRO».
• Прикладной онлайн-курс «Аналитик данных Python».
• Двухлетний практический курс «Я — веб-разработчик PRO».

В качестве задачки для разминки мозгов, я предлагаю попытаться научить компьютер собирать известную головоломку «Пятнашки».

Пятна́шки — популярная головоломка, придуманная в 1878 году Ноем Чепмэном. Представляет собой набор одинаковых квадратных костяшек с нанесёнными числами, заключённых в квадратную коробку. Длина стороны коробки в четыре раза больше длины стороны костяшек для набора из 15 элементов (и в три раза больше для набора в 8 элементов), соответственно в коробке остаётся незаполненным одно квадратное поле. Цель игры — перемещая костяшки по коробке добиться упорядочивания их по номерам, желательно сделав как можно меньше перемещений.

Ключом, к решению поставленной задачи, станет известный алгоритм поиска по первому наилучшему совпадению на графе А*. Чтобы несколько упростить изложение задачи, я буду рассматривать головоломку с полем размером 3 х 3.

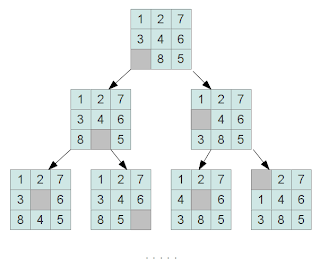
Весь процесс поиска решения в «Пятнашках» можно представить как задачу поиска на графе. Вершинами такого графа будут состояния поля головоломки, полученные в результате перемещения костяшек:

Поиск решения можно свести к поиску терминального состояния игрового поля (обычно, в качестве терминальной, выбирается расстановка костяшек, упорядоченных по возрастанию слева направо, сверху вниз).

Для решения задачи поиска терминальной вершины на графе можно использовать алгоритмы полного перебора (поиск в глубину или ширину), но количество возможных решений(возможных перестановок) скорее всего окажется на столько велико, что результат полного перебора не удастся увидеть до пенсии.

Алгоритм A* позволяет существенно сократить количество состояний для перебора, путем применения некоторой дополнительной информации, эвристики. В качестве такой информации предлагается брать предполагаемое количество перестановок, необходимых для получения терминального состояния.

Чтобы разобраться, как именно A* позволяет выполнять поиск на графе, рекомендую прочитать статью Алгоритм A* для новичков. Материала на тему этого алгоритма написано так много, что у меня нет желания останавливаться на изложении деталей его реализации, но тем не менее, для дальнейшего понимания происходящего понимание алгоритма A* необходимо. Поэтому, вкратце, я все таки изложу последовательность действий, предпринимаемых алгоритмом, для поиска терминального состояния на примере решения выбранной головоломки.

Алгоритм A* предполагает наличие двух списков вершин графа: открытого и закрытого. В первом находятся вершины, еще не проверенные алгоритмом, а во втором те вершины, которые уже встречались в ходе поиска решения.

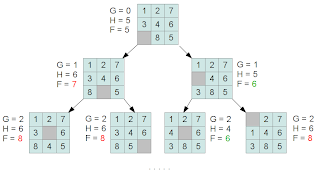
На каждом новом шаге, из списка открытых вершин выбирается вершина с наименьшим весом. Вес (F) каждой вершины вычисляется как сумма расстояния от начальной вершины до текущей (G) и эвристическое предположение о расстоянии от текущей вершины, до терминальной (H).  Fi = Gi + Hi, где i — текущая вершина (состояние игрового поля).

Для «Пятнашек» можно сделать предположение, что для достижения терминальной вершины, необходимо выполнить перемещений не меньше, чем количество костяшек, находящихся не на своих местах, а расстояние от начальной вершины до текущей рассчитывать как количество сделанных перестановок:

Далее, для выбранной вершины порождаются дочерние вершины(состояния, которые могут быть получены перемещением костяшек на пустую клетку). Каждая вершина имеет ссылку на родительскую, т.е. «помнит» из какого состояния в нее перешли.

Выполняется перебор дочерних вершин. Каждая дочерняя вершина проверяется на предмет наличия в списке закрытых. Если вершина не встречалась ранее, она перемещается в список открытых вершин. Для нее рассчитывается эвристическое расстояние до терминальной вершины и пересчитывается расстояние от начальной вершины, ведь есть вероятность, что текущий путь к этой вершине окажется короче, чем найденный ранее (текущая вершина могла уже находится в списке открытых). Если путь оказался короче, ссылка на родительскую вершину изменяется.

Последовательность действий повторяется, пока в списке открытых вершин есть хотя бы одна вершина или пока в ходе выполнения алгоритма не встретится терминальная вершина.

Решение на Java.

Алгоритм А* применим для решения большого числа задач. Мне бы не хотелось ограничивать его реализацию решением только «Пятнашек». Поэтому я предлагаю абстрагироваться от решаемой задачи с помощью интерфейсов, абстрактных классов и наследования.

В первую очередь, задачи, решаемые алгоритмом А*, отличаются определением вершин графа(или состояниями). Введем абстрактный класс, инкапсулирующий общее, для любых вершин, поведение:

Так же, задачи различаются правилами порождения дочерних вершин, алгоритмом расчета расстояния от начальной вершины и эвристической оценкой расстояния до терминальной вершины. Выделим эти особенности в интерфейс:

Основываясь на подобных абстракциях, можно реализовать алгоритм А* следующим образом:

package ru.dokwork.algorithms.astar;

import java.util.*;

/**
 * Реализует алгоритм поиска решения А*.
 */
public class Astar <TState extends State, TRules extends Rules<TState>> {

    /**
     * Применяет алгоритм А* для поиска крадчайшего пути до терминального
     * состояния от указанного.
     *
     * @param startState - начальное состояние.
     * @return последовательность состояний от заданного до терминального.
     */
    public Collection<State> search(TState startState) {
        LinkedList<TState> close = new LinkedList<TState>();
        LinkedList<TState> open = new LinkedList<TState>();
        open.add(startState);
        startState.setG(0);
        startState.setH(rules.getH(startState));

        while (!open.isEmpty()) {
            TState x = getStateWithMinF(open);
            if (rules.isTerminate(x)) {
                closedStates = close.size();
                return completeSolution(x);
            }
            open.remove(x);
            close.add(x);
            List<TState> neighbors = rules.getNeighbors(x);
            for (TState neighbor : neighbors) {
                if (close.contains(neighbor)) {
                    continue;
                }
                int g = x.getG() + rules.getDistance(x, neighbor);
                boolean isGBetter;
                if (!open.contains(neighbor)) {
                    neighbor.setH(rules.getH(neighbor));
                    open.add(neighbor);
                    isGBetter = true;
                } else {
                    isGBetter = g < neighbor.getG();
                }
                if (isGBetter) {
                    neighbor.setParent(x);
                    neighbor.setG(g);
                }
            }
        }
        return null;
    }

    /**
     * Создает объект для поиска терминального состояния по указанным правилам.
     *
     * @param rules правила, в соответствии с которыми будет производиться поиск
     *              терминального состояния.
     */
    public Astar(TRules rules) {
        if (rules == null) {
            throw new IllegalArgumentException("Rules can`t be null.");
        }
        this.rules = rules;
    }

    /**
     * Находит вершину в списке open с наименьшим значением веса.
     *
     * @param open список открытых вершин.
     * @return вершину с наименьшим весом.
     */
    private TState getStateWithMinF(Collection<TState> open) {
        TState res = null;
        int min = Integer.MAX_VALUE;
        for (TState state : open) {
            if (state.getF() < min) {
                min = state.getF();
                res = state;
            }
        }
        return res;
    }

    /**
     * Составляет последовательность состояний пройденных от начального
     * состояния до конечного.
     *
     * @param terminate найденное конечное состояние.
     * @return последовательность состояний пройденных от начального
     * состояния до конечного.
     */
    private Collection<State> completeSolution(TState terminate) {
        Deque<TSate> path = new LinkedList<TState>();
        State c = terminate;
        while (c != null) {
            path.addFirst(c);
            c = c.getParent();
        }
        return path;
    }

    private TRules rules;
}

Данное решение несколько не оптимально. Наверняка вы заметили, что информация в списке закрытых вершин избыточна: нас никогда не интересуют детали вершин из этого списка, а только факт принадлежности некоторой вершины к нему. Для этого достаточно хранить не сами вершины, а значения их хеш функций.

Теперь, что касается реализации непосредственно пятнашек. Я не стану приводить здесь весь исходный код, его вы можете посмотреть в репозитории на bitbucket. Остановлюсь только на интересных, на мой взгляд, вещах.

Во первых, само игровое поле удобно представить одномерным массивом, это позволит избежать лишних вложенных циклов и в целом упростит решение. Алгоритм раскрытия вершины (получение ее потомков), в таком случае, получается достаточно прост. Вначале находится индекс пустой клетки, затем вычисляется индекс кости, которая будет перемещена на пустую клетку. Ее индекс вычисляется как сумма индекса пустой клетки и индекса одного из ее соседей. Индексы соседних клеток элементарны: для соседа слева это -1, для соседа справа +1, для соседа сверху -(размер поля), для соседа снизу +(размер поля):

actions = new int[]{-sideSize, sideSize, -1, 1};

/* Выполняется поиск пустой клетки */
int zero = 0;
for (; zero < field.length; zero++) {
    if (field[zero] == 0) {
        break;
    }
    if (zero >= field.length) {
        return null;
    }
}
/* Вычисляется индекс перемещаемой клетки */
int number = zero + action;
/* Проверяется допустимость хода */
if (number < 0 || number >= field.length) {
    return null;
}
if ((action == 1) && ((zero + 1) % sideSize == 0)) {
    return null;
}
if ((action == -1) && ((zero + 1) % sideSize == 1)) {
    return null;
}
/*
 * Создается новый экземпляр поля, на котором меняются местами пустая и
 * перемещаемая клетки
 */
byte[] newField = Arrays.copyOf(field, field.length);
byte temp = newField[zero];
newField[zero] = newField[number];
newField[number] = temp;

return newField;

Во вторых, для генерирования начального состояния, первое, что обычно приходит на ум — это случайное расположение клеток на игровом поле. Но у этого подхода есть существенный недостаток. Если вы уже заглядывали на вики, то знаете, что ровно половину из всех возможных начальных положений пятнашек невозможно привести к собранному виду. То есть, при таком подходе, вы рискуете сгенерировать такое начальное состояние, решение для которого не существует вообще, или поиск решения затянется на неприлично длительное время. Чтобы не портить себе впечатление от проделанной работы, можно пойти другим путем: можно выполнять N случайных, корректных перестановок костяшек, начиная с терминального состояния. Такой подход гарантировано предоставит начальное состояние, обладающее решением и позволит регулировать сложность его поиска:

byte[] generateStartState(FifteenRules rules, int swapCount) {
    int stepCount = swapCount;
    byte[] startState = rules.getTerminateState();

    int[] actions = rules.getActions();
    Random r = new Random();
    while (stepCount > 0) {
        int j = r.nextInt(actions.length);
        byte[] state = rules.doAction(startState, actions[j]);
        if (state != null) {
            startState = state;
            stepCount--;
        }
    }
    return startState;
} 

UPD:  По настоятельной просьбе анонимного читателя, я опишу второй, казалось бы очевидный, способ генерирования начального состояния.

Чтож, остальные детали реализации не должны вызывать трудностей. Однако, хочу заметить, что предложенная эвристика далека от совершенства. Ее можно усовершенствовать, что позволит сократить количество раскрываемых алгоритмом вершин и, соответственно, ускорить его работу. Буду рад увидеть ваши предложения по развитию эвристической оценки в комментариях.

Опробовать решение в действии: FifteenPuzzle.jar.

$ java -jar FifteenPuzzle.jar -h

По мотивам лекций по курсу «Интеллектуальные системы».

                                                    Выражаю личную благодарность Копылову Андрею Валерьевичу, за интересное изложение курса.

package game;
 
import javax.swing.*;
import java.awt.event.*;
import java.awt.*;
import java.util.Random;  
 
public class VoronCalc extends JFrame implements MouseMotionListener, MouseListener
{
   static int win_width, win_height;
   
   pct[] pt;
   pct t_swap;
   int loc[];
   int n=16;
   int edge = n/4;
   int it_size = 35;
   int x_min = 10, x_max = 115, y_min = 31, y_max = 136;
   
   public void SwapA(int a[], int i, int j){
       int t = a[i]; a[i] = a [j]; a[j] = t;
   }
   
   public void swap_obj(pct a[], int i, int j){
       t_swap = a[i]; a[i] = a[j]; a[j] = t_swap;
       move_order();
   }
      
   public VoronCalc() 
   {
     super("15");
     win_width = 165; 
     win_height = 185;
     
     this.addMouseMotionListener(this);
     this.addMouseListener(this);
     
     loc = new int[n];
     for (int i=0; i<n; i++) 
         loc[i]=i;
        
     Random rand = new Random();
     for (int i=0; i<n; i++) 
         SwapA(loc, i, Math.abs(rand.nextInt() % n));
         
     pt = new pct[n];
     for (int i=0; i<n; i++) 
         pt[i] = new pct(loc[i]);
     
     move_order();
   }
   
   public void move_order()
   {
       pt[0].move(10, 31);
       pt[1].move(45, 31);
       pt[2].move(80, 31);
       pt[3].move(115, 31);
        
       pt[4].move(10, 66);
       pt[5].move(45, 66);
       pt[6].move(80, 66);
       pt[7].move(115, 66);
        
       pt[8].move(10, 101);
       pt[9].move(45, 101);
       pt[10].move(80, 101);
       pt[11].move(115, 101);
        
       pt[12].move(10, 136);
       pt[13].move(45, 136);
       pt[14].move(80, 136);
       pt[15].move(115, 136);
   }
   
   public void paint(Graphics g)
   {
       g.clearRect(0, 0, win_width, win_height);
       for (int i=0; i<n; i++) 
               pt[i].draw_pct(g);  
   }
   
   public void mouseReleased(MouseEvent e)
   {
       int vec_x = 0, vec_y = 0;
       
       for (int i=0; i<n; i++)
       {
           if (pt[i].bBeginDrag)
           {
               vec_x = e.getX() - pt[i].x1;
               vec_y = e.getY() - pt[i].y1;
               
               if (Math.abs(vec_x) > Math.abs(vec_y))
               {
                   if ( (pt[i].imX < x_max) && ((vec_x > 0)&&(pt[i+1].label==0)) )
                       swap_obj(pt, i, i+1);
                   
                   if ( (pt[i].imX > x_min) && ((vec_x < 0)&&(pt[i-1].label==0)) )
                       swap_obj(pt, i, i-1);
               }
               
               else if (Math.abs(vec_y) > Math.abs(vec_x))
               {
                   if ( (pt[i].imY < y_max) && ((vec_y > 0)&&(pt[i+edge].label==0)) ) 
                       swap_obj(pt, i, i+edge);
                   
                   if ( (pt[i].imY > y_min) && ((vec_y < 0)&&(pt[i-edge].label==0)) ) 
                       swap_obj(pt, i, i-edge);
               }
               
               pt[i].bBeginDrag = false;
               repaint();
           }         
       }
   }
   
   public void mousePressed(MouseEvent e)
   {
       for (int i=0; i<n; i++)
           pt[i].is_dragged(e.getX(), e.getY());
   }
   
   public void mouseDragged(MouseEvent e) {}
   public void mouseMoved(MouseEvent e) {}
   public void mouseClicked(MouseEvent e) {}
   public void mouseEntered(MouseEvent e) {}
   public void mouseExited(MouseEvent e) {}
   
   
   public static void main(String[] args) 
   {
     VoronCalc app = new VoronCalc();
     app.setVisible(true);
     app.setSize(win_width, win_height);  
   }
   
   public class pct extends JFrame
   {
       Rectangle rcImage;
       boolean bBeginDrag = false;
       
       int imX = 0;
       int imY = 0; 
       int label;
       int x1, y1;
       
       public pct(int cname) 
       {
           label = cname; 
           rcImage = new Rectangle(imX, imY, it_size, it_size);
       }
       
       public void is_dragged(int X, int Y)
       {
           bBeginDrag = rcImage.contains(X, Y);
           if(bBeginDrag)
           {
               x1 = X; y1 = Y;
           } 
       }
       
       public void draw_pct(Graphics g)
       { 
           if (label !=0){
               rcImage = new Rectangle(imX, imY, it_size, it_size);
               g.drawString(String.valueOf(label), imX + (it_size/2), imY + (it_size/2));
               g.drawRoundRect(imX, imY, it_size, it_size, 10, 10);
           }
       }
       
       public void move(int X, int Y)
       { 
           imX = X; imY = Y;
       }
   }
 }