На чтение 4 мин. Опубликовано 06.07.2020
Рандом в Паскале — это опция с помощью, которой программа может генерировать и получать для своей деятельности случайные числа. Чаще всего данную функцию используют в Паскале для работы с массивами. При этом диапазон заданного числа можно отрегулировать, самостоятельно посчитав разницу между диапазоном и обязательно добавив к результату 1.
Также в Pascal используют randomize, зачастую происходит это совместно с рандом. Так как отдельно опция randomize будет давать постоянно одинаковое число. Данный процесс позволяет нам провести инициализацию датчика.
Цикл for уместно использовать, когда будете заполнять массив. Так как мы уже знаем, сколько в нем элементов. Индексом элементов может стать счетчик цикла.
В Паскале используют вообще два типа массивов одномерные и двумерные. Одномерные массивы, о которых и пойдет речь несут, в себе информацию о разных элементах, которые будут иметь отношение к одному типу данных. Random Pascal необходим, чтобы не приходилось постоянно задавать значение массиву.
Генератор псевдослучайных чисел не дает нам возможности проследить за алгоритмом, по которому подбираются числа. Это крайне важно, поскольку если бы тут имелась какая-то закономерность, работа программы была-бы выполнена не совсем корректно. Числа не зависят друг от друга, и мы не сможем предугадать результат, который выдаст нам такая опция.
Работа генератора случайных чисел
Для того чтобы рандом в Паскале работал программисту необходимо задать промежуток из чисел, который будет актуальным при его работе. Перед началом работы программы, необходимо описать программе функцию рандом. Random и randomize в Паскале всегда работают в совокупности, как и было это указано выше в статье. Randomize в описание вставляют сразу после begin, делают это для того, чтобы упростить считываемость кодов.
Теперь перейдем сразу к самому интересному и разберемся, как запустить генератор случайных чисел в Паскале. Примеры прописанных программ можно просмотреть в интернете и потренироваться на задачах. Нужно быть внимательным и не забыть описать randomize для генерации поистине случайного числа.
Простой пример:
var
n, i, x: integer;
begin
randomize;
n := random (7) + 5;
for i := 1 to n do
begin
x := random (100) — 50;
write (x:5) end;
readln
end.
Иначе просто от функции рандом число, полученное по итогу, будет совсем неслучайным. Часто новички прописывают команду randomize при каждой вставке random, а это является грубейшей ошибкой.
Задавать эту опцию необходимо 1 раз в самом начале написания программы.
С одномерными массивами производят сортировку. Есть три способа, как это выполнить. Рассмотрим каждый детально.
«Пузырек»:
- Работает это по принципу – массив это вода, а его элементы пузырьки. Чем легче элемент, тем быстрее поднимается на поверхность.
- Парные примерно одинаковые по размеру элементы сравниваются между собой. Тот который больше производит замену над напарником.
- Так происходит в работе всего цикла, до его конца.
Метод выбора – следующий способ:
- Элементы выстраиваются по принципу от большего к меньшему.
- Далее минимальный элемент становиться на второе место после самого большого.
- Так происходит и дальше с оставшимися элементами.
Последний способ – быстрая сортировка:
- Находим средний элемент массива;
- Добавляем к L и находим первый элемент (он должен быть больше).
- Делаем R меньше и находим последний элемент ( он должен быть меньше).
- Если пункт 2 меньше или равен пункту 3, то меняем их местами.
Завершение работы с рандом в Паскале
В программе Pascal есть такое понятие числа фибоначчи, подразумевает это ряд последовательности цифр, по принципу следующее число состоит из суммы двух чисел перед ним. Формулу фибоначчи необходимо применять в цикле for, в самом начале, когда прописываем элементы массива.
Функция рандом помогает нам сгенерировать ряд чисел в диапазоне от 0 до 1. Для того чтобы задать свой диапазон, нужно в скобках, сразу после 0 прописать эти значения цифр. Без данной опции у вас наверняка не выйдет сгенерировать число случайным способом, и точно так же каждое последующее. Потому программа Паскаль не может работать без возможности генерации незапланированных чисел.
Объявление массива несет в себе некий синтаксис. Это помогает определить число элементов в массиве. Для многомерного массива может быть использована только начальная размерность.
Получить многомерный массив можно с помощью определенной последовательности константных выражений, которые указаны в программе в квадратных скобках.
Для того чтобы работать с программой Pascal, нужно понимать значение и принцип работы рандом. На первый взгляд, выучить это достаточно легко. Но поскольку случайные числа это очень важно, нужно быть внимательным, дабы не допустить ошибку в написании программы. Генерация чисел очень увлекательна и непредсказуема, в правильно написанной программе вы никогда не сможете предугадать результат.
│
Deutsch (de) │
English (en) │
suomi (fi) │
français (fr) │
polski (pl) │
русский (ru) │
Random numbers are important resources for a diverse field of applications, including scientific analysis, technology, medicine, economy, education, game development and visualization. They play a key role in numeric simulation.
Algorithm-generated random numbers are pseudo-random numbers. They belong to a (large) set of repeating numbers, whose sequence is impossible or at least difficult to predict. Unlike Delphi, that uses a linear congruential generator.(See Delphi compatible LCG Random), Free Pascal uses a MersenneTwister algorithm for its standard random function as defined in RTL. Before its first use, FPC’s random number generator has to be initialized with a single call of the randomize function, which sets the seed of the generator. Preferably this is done in the launch phase of the program.
Alternatively, on Unix- and Linux-based systems, the virtual devices /dev/random and /dev/urandom are available. They generate (pseudo) random numbers based on hardware.
A third option is to use random numbers from external sources, either from specialised hardware devices or from public sources, e.g. based on radioactive decay data.
Uniform Distribution
The continuous uniform distribution (also referred to as rectangular distribution) represents a family of symmetric probability distributions. Here, for each member of the family all intervals of the same length on the distribution’s support are equally probable.
The standard RTL function random generates random numbers that fulfill a uniform distribution. If called without parameter random delivers a floating point pseudorandom number in the interval [0, 1), i.e. 0 <= result < 1. if random is called with a longint argument L it delivers a longint random in the interval [0, L).
A further set of uniformly distributed random number generators is presented in Marsaglia's pseudo random number generators.
Uniformly distributed random numbers are not useful for every application. In order to create random numbers of other distributions special algorithms are necessary:
Normal (Gaussian) Distribution
One of the more common algorithms to produce normally distributed random numbers from uniformly distributed random numbers is the Box-Müller approach. The following function calculates Gaussian-distributed random numbers:
function rnorm (mean, sd: real): real; {Calculates Gaussian random numbers according to the Box-Müller approach} var u1, u2: real; begin u1 := random; u2 := random; rnorm := mean * abs(1 + sqrt(-2 * (ln(u1))) * cos(2 * pi * u2) * sd); end;
The same algorithm is used by the randg randg function from the RTL math unit:
function randg(mean,stddev: float): float;
Exponential Distribution
An exponential distribution occurs frequently in real-world problems. A classical example is the distribution of waiting times between independent Poisson-random events, e.g. the radioactive decay of nuclei [Press et al. 1989].
The following function delivers a single real random number out of an exponential distribution. Rate is the inverse of the mean, and the constant RESOLUTION determines the granularity of generated random numbers.
function randomExp(a, rate: real): real; const RESOLUTION = 1000; var unif: real; begin if rate = 0 then randomExp := NaN else begin repeat unif := random(RESOLUTION) / RESOLUTION; until unif <> 0; randomExp := a - rate * ln(unif); end; end;
Gamma Distribution
The gamma distribution is a two-parameter family of continuous random distributions. It is a generalization of both the exponential distribution and the Erlang distribution. Possible applications of the gamma distribution include modelling and simulation of waiting lines, or queues, and actuarial science.
The following function delivers a single real random number out of a gamma distribution. The shape of the distribution is defined by the parameters a, b and c. The function makes use of the function randomExp as defined above.
function randomGamma(a, b, c: real): real; const RESOLUTION = 1000; T = 4.5; D = 1 + ln(T); var unif: real; A2, B2, C2, Q, p, y: real; p1, p2, v, w, z: real; found: boolean; begin A2 := 1 / sqrt(2 * c - 1); B2 := c - ln(4); Q := c + 1 / A2; C2 := 1 + c / exp(1); found := False; if c < 1 then begin repeat repeat unif := random(RESOLUTION) / RESOLUTION; until unif > 0; p := C2 * unif; if p > 1 then begin repeat unif := random(RESOLUTION) / RESOLUTION; until unif > 0; y := -ln((C2 - p) / c); if unif <= power(y, c - 1) then begin randomGamma := a + b * y; found := True; end; end else begin y := power(p, 1 / c); if unif <= exp(-y) then begin randomGamma := a + b * y; found := True; end; end; until found; end else if c = 1 then { Gamma distribution becomes exponential distribution, if c = 1 } begin randomGamma := randomExp(a, b); end else begin repeat repeat p1 := random(RESOLUTION) / RESOLUTION; until p1 > 0; repeat p2 := random(RESOLUTION) / RESOLUTION; until p2 > 0; v := A2 * ln(p1 / (1 - p1)); y := c * exp(v); z := p1 * p1 * p2; w := B2 + Q * v - y; if (w + D - T * z >= 0) or (w >= ln(z)) then begin randomGamma := a + b * y; found := True; end; until found; end; end;
Erlang Distribution
The Erlang distribution is a two parameter family of continuous probability distributions. It is a generalization of the exponential distribution and a special case of the gamma distribution, where c is an integer. The Erlang distribution has been first described by Agner Krarup Erlang in order to model the time interval between telephone calls. It is used for queuing theory and for simulating waiting lines.
function randomErlang(mean: real; k: integer): real; const RESOLUTION = 1000; var i: integer; unif, prod: real; begin if (mean <= 0) or (k < 1) then randomErlang := NaN else begin prod := 1; for i := 1 to k do begin repeat unif := random(RESOLUTION) / RESOLUTION; until unif <> 0; prod := prod * unif; end; randomErlang := -mean * ln(prod); end; end;
Poisson Distribution
The Poisson distribution applies to integer values. It represents the probability of k successes, when the probability of a success in each trial is small and the rate of occurrence (the mean value) is constant.
function randomPoisson(mean: integer): integer; { Generator for Poisson distribution (Donald Knuth's algorithm) } const RESOLUTION = 1000; var k: integer; b, l: real; begin assert(mean > 0, 'mean < 1'); k := 0; b := 1; l := exp(-mean); while b > l do begin k := k + 1; b := b * random(RESOLUTION) / RESOLUTION; end; randomPoisson := k - 1; end;
t Distribution
The t distribution (also referred to a Student’s t distribution, since it was published by William Sealy Gosset in 1908 under the pseudonym Student) is a continuous probability distribution. Its shape is defined by one parameter, the degrees of freedom (df). In statistics, many estimators are t distributed. Therefore, Student’s t-distribution plays a major role in a number of widely used statistical analyses, including Student’s t-test for assessing the statistical significance of the difference between two sample means, the construction of confidence intervals for the difference between two population means, and in linear regression analysis. The t-distribution also arises in Bayesian analysis of data from a normal family.
The following algorithm depends on the RTL function random and on the randomChisq function
function randomT(df: integer): real; { Generator for Student's t distribution } begin if df < 1 then randomT := NaN else begin randomT := randg(0, 1) / sqrt(randomChisq(df) / df); end; end;
Chi Squared Distribution
The chi squared distribution is a continuous distribution of random numbers with df degrees of freedom. It is the distribution of a sum of the squares of df independent standard normal random variables. The chi squared distribution has numerous applications in inferential statistics, e.g. in estimating variances and for chi-squared tests. It is a special gamma distribution with c = df/ 2 and b = 2. Therefore the following function depends on the function randomGamma.
function randomChisq(df: integer): real; begin if df < 1 then randomChisq := NaN else randomChisq := randomGamma(0, 2, 0.5 * df); end;
F Distribution
The F distribution, also referred to as Fisher-Snedecor distribution, is a continuous probability distribution. It is used for F Test and ANOVA. It has two degrees of freedom that serve as shape parameters v and w and that are positive integers. The following function randomF makes use of randomChisq.
function randomF(v, w: integer): real; begin if (v < 1) or (w < 1) then randomF := NaN else randomF := randomChisq(v) / v / (randomChisq(w) / w); end;
See also
- Dev random
- Functions for descriptive statistics
- Samples and permutations
- Marsaglia’s pseudo random number generators
- A simple implementation of the Mersenne twister
- Delphi compatible LCG Random
- EverettRandom
References
- G. E. P. Box and Mervin E. Muller, A Note on the Generation of Random Normal Deviates, The Annals of Mathematical Statistics (1958), Vol. 29, No. 2 pp. 610–611
- Dietrich, J. W. (2002). Der Hypophysen-Schilddrüsen-Regelkreis. Berlin, Germany: Logos-Verlag Berlin. ISBN 978-3-89722-850-4. OCLC 50451543.
- Press, W. H., B. P. Flannery, S. A. Teukolsky, W. T. Vetterling (1989). Numerical Recipes in Pascal. The Art of Scientific Computing, Cambridge University Press, ISBN 0-521-37516-9.
- Richard Saucier, Computer Generation of Statistical Distributions, ARL-TR-2168, US Army Research Laboratory, Aberdeen Proving Ground, MD, 21005-5068, March 2000.
- R.U. Seydel, Generating Random Numbers with Specified Distributions. In: Tools for Computational Finance, Universitext, DOI 10.1007/978-1-4471-2993-6_2, © Springer-Verlag London Limited 2012
- Christian Walck, Hand-book on STATISTICAL DISTRIBUTIONS for experimentalists, Internal Report SUF–PFY/96–01, University of Stockholm 2007
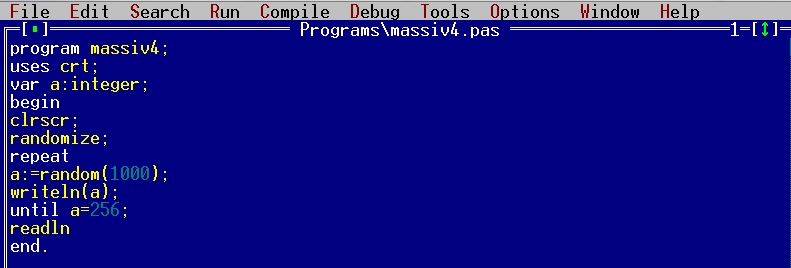
Процедура Randomize используется в Паскаль для включения генератора случайных чисел. Функция Random определяет диапазон случайных чисел. Процедура Randomize и функция Random очень часто используются для демонстрации работы массивов в Паскаль.
Randomize и Random в Паскаль.
program massiv4; uses crt; var a:integer; begin clrscr; randomize; repeat a:=random(1000); writeln(a); until a=256; readln end.
Строка №6. Инициализируем (включаем) генератор случайных чисел с помощью процедуры Randomize.
Строка №8. Присваиваем переменной «a» случайные числа в диапазоне от 0 до 999 (т.е. от 0 до 1000, но, не включая число 1000) с помощью функции Random. Т.е. запись (1000) означает, что все сгенерированные числа будут не меньше 0 и не больше 999. Предположим, что нам необходимо записать другой диапазон чисел, например от -1000 до 1000. В этом случае строка №8 будет иметь вид: a:= -1000 random(2001). Т.е. сначала записываем минимальное число диапазона (-1000), а в функции Random записываем сумму модуля минимального и максимального числа и прибавляем к ней 1. |-1000|+|1000|+1=2001. Таким образом, переменной «a» будут присвоены случайные числа в диапазоне от -1000 до 1000.
В строке №9 выводим сгенерированные числа на экран.
Строки №8 и №9 включены в цикл (строка №7 и №10). Случайные числа будут генерироваться и выводиться на экран до тех пор пока не выполнится условие цикла (строка №10), т.е. когда очередное сгенерированное число окажется числом 256.
Дополнение к материалу.
- Если бы мы записали функцию Random без цикла (т.е. если убрать строки №7 и №10), то у нас будет сгенерировано только одно число и только оно будет выведено на экран.
- Если убрать из программы процедуру Randomize (т.е. строку №6), то каждый раз при запуске программы у нас будут генерироваться одни и те же числа. Например, при первом запуске программы у нас сгенерировалось 50 случайных чисел. Последним числом оказалось число 256. Программа остановилась. Если закрыть программу, и запустить ее по новой, то у нас сгенерируются те же самые 50 чисел.
- Строку «a:= -1000 random(2001)» можно записать и таким способом: «a:= random(2001) — 1000».
- Если для функции Random не указывать диапазон (т.е. строку №8 записать как: a:=random, то переменной «a» будут присвоены случайные значения от 0 до 1, но не включая 1 (например, 0.3, 0.5, 0.9 и т.д.). В этом случае переменная «a» должна иметь не целый тип (integer), а вещественный тип (например, real).
Предыдущая статья : Использование массивов (продолжение).
Оглавление : Уроки Паскаль. Массивы.
Следующая статья : Нахождение максимального элемента массива.
I want to get a random number in pascal from between a range. Basically something like this:
r = random(100,200);
The above code would then have a random number between 100 and 200.
Any ideas?
The built in pascal function only lets you get a number from between 0-your range, while i need to specify the minimum number to return
asked Feb 11, 2011 at 5:16
2
Just get a random number with the correct range (ie 100 to 200 would be range 100) then add the starting value to it
So: random(100) + 100 for your example
answered Feb 11, 2011 at 5:20
RalphRalph
4386 silver badges17 bronze badges
3
As already pointed out, you should use
myrandomnumber := random(span) + basenumber;
However, to get better quality random numbers, you should call
randomize();
once, on start of your application, to initialize the random number generator.
answered Sep 13, 2012 at 13:01
Couldn’t you just declare a starting variable and an end variable and pass random those? e.g.
var
varMyRandomNumber, x, y := extended;
begin
x := 100;
y := 200;
varMyRandomNumber := random(x,y);
ShowMessage(IntToStr(varMyRandomNumber));
end;
?
There’s a good example here of using a for loop to set starting and end values : http://www.freepascal.org/docs-html/rtl/system/random.html
answered Apr 13, 2011 at 19:57
Use RandomRange or RandomFrom:
function RandomRange(const aFrom: Integer; const aTo: Integer): Integer;
RandomFrom returns a random element from the array AValues. The return value has the same type as the type of the array elements.
Robert
1,20814 silver badges25 bronze badges
answered Jan 10, 2022 at 12:39
first of all, i recommend you to use Randomize at the beginning of the program (it changes the algorithm of selecting the number).
To get a random number between some two numbers you need this:
Result:=Min+random(10000)mod max + 1;
I don’t remember the maximum value for random, so you can change it (it don’t changes anything).
By using ‘mod’ you get module from division Random and max. +1 is needed, because you never get the number that = max, only the number that =max-1, so you need to write +1.
Good luck!
answered Jul 14, 2013 at 9:02
1
You can make it like
Int:=Random(100);
it give’s 100 random numbers.
then when you display it or use it just add 101 to that integer so its between 100 and 200
answered Jun 1, 2015 at 21:21
1
На занятии объясняется, как работать с одномерными массивами в Паскале, как использовать генератор случайных чисел — функцию random в Паскале. Рассматривается пример того, как вывести числа Фибоначчи
Материалы сайта labs-org.ru направлены на практическое освоение языка программирования Pascal. Краткие теоретические сведения не претендуют на полное освещение материала по теме; необходимую информацию можно найти в сети Интернет в большом количестве. В наши же задачи входит предоставление возможности получения практических навыков программирования на Паскале. Решенные наглядные примеры и задания изложены по мере увеличения их сложности, что позволит с легкостью изучить материал с нуля.
Одномерные массивы в Паскале
Объявление массива
Массивы в Паскале используются двух типов: одномерные и двумерные.
Определение одномерного массива в Паскале звучит так: одномерный массив — это определенное количество элементов, относящихся к одному и тому же типу данных, которые имеют одно имя, и каждый элемент имеет свой индекс — порядковый номер.
Описание массива в Паскале (объявление) и обращение к его элементам происходит следующим образом:
Объявление массива
var dlina: array [1..3] of integer; begin dlina[1]:=500; dlina[2]:=400; dlina[3]:=150; ...
dlina — идентификатор (имя) массива;Array (в переводе с англ. «массив» или «набор»);[1..3] — в квадратных скобках ставится номер (индекс) первого элемента, затем две точки и индекс последнего элемента массива, т.е. по сути, указывается количество элементов; количество элементов массива называется размерностью массиваof integer (с англ. «из целых чисел») — указывает, к какому типу относится массив, of здесь — служебное слово.Объявить размер можно через константу:
Инициализация массива
Кроме того, массив может быть сам константным, т.е. все его элементы в программе заранее определены. Описание такого массива выглядит следующим образом:
const a:array[1..4] of integer = (1, 3, 2, 5);
Заполнение последовательными числами:
Результат: A[1] = 8, A[2] = 9, A[3] = 10, ..., A[N] = A[N-1] + 1
Ввод с клавиатуры:
Пример: Рассмотрим, как происходит ввод массива в Паскале:
writeln ('введите кол-во элементов: '); readln(n); {если кол-во заранее не известно, - запрашиваем его} for i := 1 to n do begin write('a[', i, ']='); read(a[i]); ... end; ...
✍ Пример результата:
введите кол-во элементов: 3 a[1]=5 a[2]=7 a[3]=4
Вывод элементов массива
Пример: Рассмотрим, как вывести массив в Паскале:
1 2 3 4 5 6 7 8 9 10 11 12 13 |
var a: array[1..5] of integer; {массив из пяти элементов} i: integer; begin a[1]:=2; a[2]:=4; a[3]:=8; a[4]:=6; a[5]:=3; writeln('Массив A:'); for i := 1 to 5 do write(a[i]:2); {вывод элементов массива} end. |
✍ Пример результата:
Для работы с массивами чаще всего используется в Паскале цикл for с параметром, так как обычно известно, сколько элементов в массиве, и можно использовать счетчик цикла в качестве индексов элементов.
Задача Array 0. Необходимо задать вещественный массив размерностью 6 (т.е. из шести элементов); заполнить массив вводимыми значениями и вывести элементы на экран. Использовать два цикла: первый — для ввода элементов, второй — для вывода.
Пример результата:
введите элемент массива: 3.0 введите элемент массива: 0.8 введите элемент массива: 0.56 введите элемент массива: 4.3 введите элемент массива: 23.8 введите элемент массива: 0.7 Массив = 3, 0.8, 0.56, 4.3, 23.8, 0.7
[Название файла: taskArray0.pas]
В данном примере работы с одномерным массивом есть явное неудобство: присваивание значений элементам.
Обработка массивов в Паскале, так же как и заполнение массива, происходит обычно с использованием цикла for.
Динамические массивы (pascalAbc.Net)
Основным недостатком статических массивов является то, что их размер нельзя задать с учетом текущих обрабатываемых данных. Приходится описывать массивы с максимально возможным значением количества элементов, выделяя для них столько памяти, сколько может потребоваться для хранения самой большого из возможных наборов исходных данных.
Объявление:
var a: array of integer; var n:=readInteger; a:=new integer[n]; // инициализация, выделение памяти для элементов массива
или:
var a: array of integer; var n:=readInteger; SetLength(a,n); // устанавливаем размер
Аналогичным образом массивы могут описываться в качестве параметров подпрограмм, например:
procedure p(a: array of integer);
Созданные элементы сразу получают начальное значение, равное нулевому значению соответствующего типа: для чисел это целый или вещественный нуль, для символов — символ с кодом 0, для строк и других ссылочных типов данных — нулевая ссылка nil
Объявление и инициализация массива:
Пример:
begin var a: array of integer; a := new integer[3]; a[0] := 5; a[1] := 2; a[2] := 3; end.
или в одну строку:
begin var a: array of integer; a := new integer[3](5,2,3); print(a) end.
или короткая запись:
var a:=Arr(1,2,3);// по правой части - integer
Элементы динамического массива всегда индексируются от 0.
Ввод элементов:
Пример:
var a:=ReadArrInteger(5); // ввод пяти целых var a:=ReadArrReal(5); // ввод пяти вещественных
Функции генерации массивов:
1. ArrFill :
var a := ArrFill(10, 1); // массив из 10 целых чисел, равных 1
2. ArrGen :
var a := ArrGen(ReadInteger, 1, e -> e + 2); // массив, состоящий из n первых положительных нечетных чисел a.Print;
Проход по элементам массива:
Пример:
for var i:=0 to a.Length-1 do a[i] += 1;
или:
for var i := 0 to a.High do a[i] += 1;
Проход по элементам (только для чтения):
Пример:
foreach var x in a do Print(x)
LengthLow и High, определяющие соответственно нижнюю и верхнюю границу диапазона изменения индекса. Свойство a.Low всегда возвращает 0, а свойство a.High определяется как a.High = a.Length – 1Простой вывод элементов:
Writeln(a); // пример вывода: [1,5,3,13,20]
или метод массива Print:
a.Print; // пример вывода: 1 5 3 13 20 a.PrintLines; // каждый элемент с новой строки
Функция Random в Pascal
Для того чтобы постоянно не запрашивать значения элементов массива используется генератор случайных чисел в Паскаль, который реализуется функцией Random. На самом деле генерируются псевдослучайные числа, но суть не в этом.
Для генерации чисел от 0 до n (не включая само значение n, целые числа в интервале [0,N)) используется запись random (n).
Перед использованием функции необходимо инициализировать датчик случайных чисел с помощью процедуры randomize.
Диапазон в Паскале тех самых случайных чисел от a до b задается формулой:
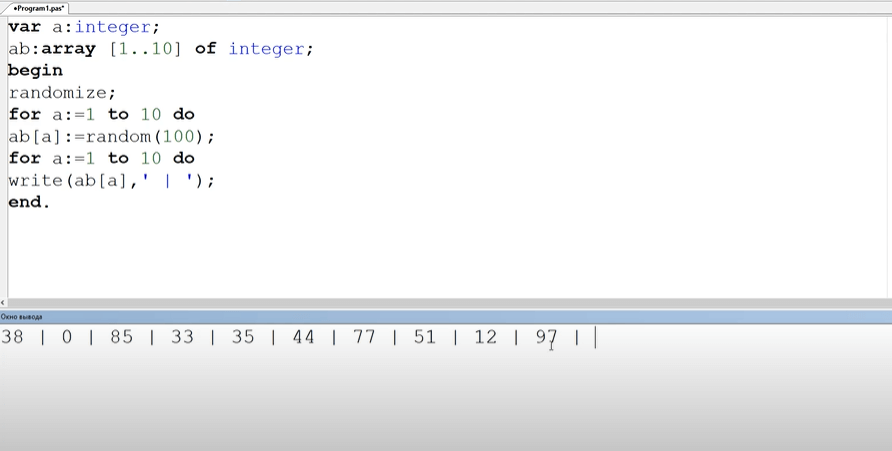
Пример: Заполнение массива случайными числами в Pascal:
1 2 3 4 5 6 7 8 9 10 |
var f: array[1..10] of integer; i:integer; begin randomize; for i:=1 to 10 do begin f[i]:=random(10); { интервал [0,9] } write(f[i],' '); end; end. |
✍ Пример результата:
Для вещественных чисел в интервале [0,1):
var x: real; ... x := random(0.0,1.0);; { интервал [0,1), т.е. единица не включена }
PascalABC.NET:
var (a, b, c) := Random3(10.0, 20.0); // диапазон [10, 20) write(a:0:2,' ',b:0:2,' ', c:0:2) // 14.73 18.63 19.72
Пример:
var a:=arrRandomInteger(10);
или с дополнительными параметрами (диапазон [5;15]):
var a:=arrRandomInteger(10,5,15);
Задача Array 1. Необходимо задать массив размерностью 5, заполнить массив случайными числами в интервале [-1,1] и вывести элементы на экран: определить три позиции для вывода каждого элемента, с двумя знаками после запятой.
Пример результата:
Массив = 0.22 0.00 -0.69 -0.35 -0.11
[Название файла: taskArray1.pas]
Числа Фибоначчи в Паскале
Наиболее распространенным примером работы с массивом является вывод ряда чисел Фибоначчи в Паскаль. Рассмотрим его.
Пример: Ряд чисел Фибоначчи: 1 1 2 3 5 8 13…
f[0]:=1; f[1]:=1; f[2]:=2; …или
f[2]:=f[0]+f[1]; f[3]:=f[1]+f[2];или
Получили формулу элементов ряда.
Пример: Вычислить и распечатать первые 20 чисел Фибоначчи.
1 2 3 4 5 6 7 8 9 10 11 |
var i:integer; f:array[0..19]of integer; begin f[0]:=1; f[1]:=1; for i:=2 to 19 do begin f[i]:=f[i-1]+f[i-2]; writeln(f[i]) end; end. |
На данном примере, становится понятен принцип работы с числовыми рядами. Обычно, для вывода числового ряда находится формула определения каждого элемента данного ряда. Так, в случае с числами Фибоначчи, эта формула-правило выглядит как f[i]:=f[i-1]+f[i-2]. Поэтому ее необходимо использовать в цикле for при формировании элементов массива.
Задача Array 2. Дан ряд из 10 произвольных чисел: a[1], a[2], ... , a[10] (использовать функцию random()). Подсчитать и напечатать суммы троек стоящих рядом чисел: a[1]+a[2]+a[3], a[2]+a[3]+a[4], a[3]+a[4]+a[5], …… , a[8]+a[9]+a[10]
Пример результата:
Массив = 2 0 4 29 3 11 26 11 9 4 mas[1] + mas[2] + mas[3] = 6 mas[2] + mas[3] + mas[4] = 33 mas[3] + mas[4] + mas[5] = 36 mas[4] + mas[5] + mas[6] = 43 mas[5] + mas[6] + mas[7] = 40 mas[6] + mas[7] + mas[8] = 48 mas[7] + mas[8] + mas[9] = 46 mas[8] + mas[9] + mas[10] = 24
[Название файла: taskArray2.pas]
Задача Array 3. Написать программу решения задачи о печати ряда чисел 2 4 8 16 32 ... 512; для заполнения массива использовать цикл Repeat
[Название файла: taskArray3.pas]
Максимальный (минимальный) элемент массива
Псевдокод:
Поиск максимального элемента по его индексу:
PascalABC.NET:
Минимальный элемент и его индекс:
Решение 1:
// … var (min, minind) := (a[0], 0); for var i:=1 to a.Length-1 do if a[i]<min then (min, minind) := (a[i], i); Result := (min, minind);
Решение 2:
// … var (min, minind) := (real.MaxValue, 0); for var i:=0 to a.Length-1 do if a[i]<min then (min, minind) := (a[i], i); Result := (min, minind);
Решение 3:
begin var a := new integer[5]; a := arrRandomInteger(5); // [86,37,41,45,76] print(a.Min,a.IndexMin); // 37 1 end.
Задача Array_min: Найдите минимальный элемент массива. Выведите элемент и его индекс.
Пример результата:
9 5 4 22 23 7 3 16 16 8 Минимальный элемент массива A[7]=3
[Название файла: taskArray_min.pas]
Задача Array 4. Дан массив из 10 целочисленных элементов. Найти количество отрицательных и вывести количество на экран.
Пример результата:
3 4 6 -1 6 -2 1 5 0 1 Количество отрицательных элементов: 2
[Название файла: taskArray4.pas]
Задача Array 5. Найти минимальное и максимальное из n введенных чисел (массива). Определить расстояние между этими элементами.
3 2 6 1 3 4 7 2 >>> min=1, max=7, distance=3
[Название файла: taskArray5.pas]
Задача Array 6. Дан целочисленный массив размера N. Вывести все содержащиеся в данном массиве четные числа в порядке убывания их индексов, а также их количество K.
N=4 mas: 8 9 2 5 >>> 2 8 количество= 2
[Название файла: taskArray6.pas]
Задача Array 7. Ввести с клавиатуры массив из 5 элементов, найти в нем два максимальных элемента и их номера.
Пример:
Исходный массив: 4 -5 10 -10 5 максимальные A[3]=10, A[5]=5
[Название файла: taskArray7.pas]
Поиск в массиве
Рассмотрим сложный пример работы с одномерными массивами:
Пример: Дан массив из 10 чисел. Определить, есть ли в массиве число, введенное пользователем. Если есть – выводить «найдено», если нет – «не найдено».
Сложность задания заключается в том, что выводить слова «найдено» или «не найдено» необходимо один раз.
Для решения поставленной задачи понадобится оператор break — выход из цикла.
Решение Вариант 1. Цикл for:
PascalABC.NET:
Cтандартные методы a.IndexOf(x) и a.LastIndexOf(x):
begin var a := new integer[10]; a := arrRandomInteger(5,0,5); //[1,3,5,4,5] print(a.IndexOf(3)) // 1 end.
или метод a.Contains(x) наравне с x in a:
begin var a := new integer[10]; a := arrRandomInteger(5,0,5); //[1,3,5,4,5] print(a.Contains(3)); // True print(3 in a)// True end.
Рассмотрим эффективное решение:
Задача: найти в массиве элемент, равный X, или установить, что его нет.
Алгоритм:
- начать с 1-го элемента (
i:=1); - если очередной элемент (
A[i]) равенX, то закончить поиск иначе перейти к следующему элементу.
решение на Паскале Вариант 2. Цикл While:
Поиск элемента в массиве
Предлагаем посмотреть подробный видео разбор поиска элемента в массиве (эффективный алгоритм):
Задача Array 8. Заполнить массив из 10 элементов случайными числами в интервале [0..4] и вывести номера всех элементов, равных X.
Пример:
Исходный массив: 4 0 1 2 0 1 3 4 1 0 Что ищем? 0 A[2], A[5], A[10]
[Название файла: taskArray8.pas]
Циклический сдвиг
Пример: сдвинуть элементы массива влево на 1 позицию, первый элемент становится на место последнего.

Решение:
Алгоритм:
A[1]:=A[2]; A[2]:=A[3];… A[N-1]:=A[N];
Программа:

PascalABC.NET:
Циклический сдвиг влево:
// … var v := a[0]; for var i:=0 to a.Length-2 do a[i] := a[i+1]; a[a.Length-1] := v;
Циклический сдвиг вправо:
// … var v := a[a.Length-1]; for var i:=a.Length-1 downto 1 do a[i] := a[i-1]; a[0] := v;
Задача Array 9. Заполнить массив из 10 элементов случайными числами в интервале [-10..10] и выполнить циклический сдвиг влево без первого элемента.
Пример:
Исходный массив: 4 -5 3 10 -4 -6 8 -10 1 0 Результат: 4 3 10 -4 -6 8 -10 1 0 -5
[Название файла: taskArray9.pas]
Перестановка элементов в массиве
Рассмотрим, как происходит перестановка или реверс массива.
Пример: переставить элементы массива в обратном порядке

Решение:
Алгоритм:
Псевдокод:
Программа:

PascalABC.NET:
Перестановка (ревёрс):
Решение 1:
begin var a: array of integer := (1,3,5,7); var n := a.Length; for var i:=0 to n div 2 - 1 do Swap(a[i],a[n-i-1]); End.
Решение 2 (стандартная процедура Reverse()):
begin var a:=new integer[10]; a:=arrRandomInteger(10); print(a);// [41,81,84,63,12,26,88,25,36,72] Reverse(a); print(a) //[72,36,25,88,26,12,63,84,81,41] end.
Задача Array 10. Заполнить массив из 10 элементов случайными числами в интервале [-10..10] и сделать реверс всех элементов, кроме последнего.
Пример:
Исходный массив: -5 3 10 -4 -6 8 -10 1 0 4 Результат: 0 1 -10 8 -6 -4 10 3 -5 4
[Название файла: taskArray10.pas]
Выбор элементов и сохранение в другой массив
Пример: найти в массиве элементы, удовлетворяющие некоторому условию (например, отрицательные), и скопировать их в другой массив

Решение:
Решение: подсчитывать количество найденных элементов с помощью счетчика count, очередной элемент устанавливать на место B[count]. Переменой count необходимо присвоить 1.
Вывод массива B:
writeln('Выбранные элементы'); for i:=1 to count-1 do write(B[i], ' ')
PascalABC.NET:
Процедура SetLength():
// ... for var i := 0 to a.length - 1 do if a[i] < 0 then begin b[j] := a[i]; j += 1; end; SetLength(b, j);
Задача Array 11. Заполнить массив случайными числами в интервале [20,100] и записать в другой массив все числа, которые оканчиваются на 0.
Пример:
Исходный массив: 40 57 30 71 84 Заканчиваются на 0: 40 30
[Название файла: taskArray11.pas]
Сортировка элементов массива
Сортировка методом «Пузырька»
- В таком типе сортировок массив представляется в виде воды, маленькие элементы — пузырьки в воде, которые всплывают наверх (самые легкие).
- При первой итерации цикла элементы массива попарно сравниваются между собой:предпоследний с последним, пред предпоследний с предпоследним и т.д. Если предшествующий элемент оказывается больше последующего, то производится их обмен.
- При второй итерации цикла нет надобности сравнивать последний элемент с предпоследним. Последний элемент уже стоит на своем месте, он самый большой. Значит, число сравнений будет на одно меньше. То же самое касается каждой последующей итерации.
| Pascal | PascalABC.NET | ||||
|
|
Задача Array 12. Заполнить массив из 10 элементов случайными числами в интервале [0..100] и отсортировать первую половину массива по возрастанию, а вторую – по убыванию (методом ‘Пузырька’).
Пример: Исходный массив: 14 25 13 30 76 58 32 11 41 97 Результат: 13 14 25 30 76 97 58 41 32 11
[Название файла: taskArray12.pas]
Сортировка методом выбора
- в массиве ищется минимальный элемент и ставится на первое место (меняется местами с A[1]);
- среди оставшихся элементов также производится поиск минимального, который ставится на второе место (меняется местами с A[2]) и т.д.
| Pascal | PascalABC.NET | ||||
|
|
Задача Array 13: Заполнить массив из 10 элементов случайными числами в интервале [0..50] и отсортировать его по возрастанию суммы цифр
Пример: Исходный массив: 14 25 13 12 76 58 21 87 10 98 Результат: 10 21 12 13 14 25 76 58 87 98
[Название файла: taskArray13.pas]
PascalABC.NET:
Стандартная процедура sort():
Sort(a); SortByDescending(a);
Быстрая сортировка или quick sort
Алгоритм:
- Выбирается и запоминается средний элемент массива (присвоим X):
- Инициализируем две переменные (будущие индексы массива): L:=1, R:=N (N — количество элементов).
- Увеличиваем L и ищем первый элемент A[L], который больше либо равен X (в итоге он должен находиться справа).
- Уменьшаем R и ищем элемент A[R], который меньше либо равен X (в итоге он должен находиться слева).
- Смотрим, если L<=R, то меняем местами A[L] и A[R], возвращаемся к пункту 3.
Выполнение на Паскале:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
procedure QSort ( first, last: integer); var L, R, c, X: integer; begin if first < last then begin X:= A[(first + last) div 2]; L:= first; R:= last; while L <= R do begin while A[L] < X do L:= L + 1; while A[R] > X do R:= R - 1; if L <= R then begin c:= A[L]; A[L]:= A[R]; A[R]:= c; L:= L + 1; R:= R - 1; end; end; QSort(first, R); QSort(L, last); end; end. |
Задача Array 14:
Заполнить массив из 10 элементов случайными числами в интервале [-50..50] и отсортировать его с помощью алгоритма быстрой сортировки.
[Название файла: taskArray14.pas]
Раздел: Стандартные функции Паскаля
|
|
Основы программирования Каждый профессионал когда-то был чайником. Наверняка вам знакомо состояние, когда “не знаешь как начать думать, чтобы до такого додуматься”. Наверняка вы сталкивались с ситуацией, когда вы просто не знаете, с чего начать. Эта книга ориентирована как раз на таких людей, кто хотел бы стать программистом, но совершенно не знает, как начать этот путь. Подробнее… |
Функция Random генерирует и возвращает случайное число. Синтаксис функции следующий:
function Random(L: LongInt) : LongInt; function Random(L: Int64) : Int64; function Random : extended;
Функция возвращает случайное число большее или равное 0 и строго меньше L (то есть L не входит в диапазон возвращаемых значений). Если параметр опущен (последний вариант из трёх приведённых выше), то возвращается вещественное число между 0 и 1 (0 включительно, 1 не входит в диапазон возвращаемых значений).
Математически это можно записать так:
0 <= Random < L, если L передаётся 0 <= Random < 1, если L опущен
ПРИМЕЧАНИЕ
FreePascal использует в процедуре Random имитацию случайностей Мерсенна Твистера. Эта реализация имеет большее статистическое распределение, чем, например, алгоритм Линейного Конгруэнтного генератора, но работает значительно медленнее, чем последний. Если скорость выполнения программы критична, то должны быть рассмотрены альтернативные генераторы случайных чисел.
Процедура Randomize в Паскале запускает генератор случайных чисел. Синтаксис:
procedure Randomize;
Процедура Randomize инициализирует генератор случайных чисел FreePascal, задавая
значение переменной Randseed, вычисленное с помощью системных часов.
Как запустить генератор случайных чисел в Паскале
Пример программы, где используются разные варианты получения случайных чисел, приведён ниже:
program funcrand;
var x : integer;
z : real;
begin
Randomize; //Запустить генератор случайных чисел
x := Random(100); //х - случайное число от 0 до 99
WriteLn(x);
z := Random(100); //х - случайное число от 0 до 99
WriteLn(z:0:4);
z := Random; //х - случайное число от 0 до 0,9999...
WriteLn(z:0:4);
ReadLn;
end.
ВАЖНО!
Перед использованием функции Random надо обязательно
вызвать процедуру Randomize, чтобы запустить генератор случайных чисел. Иначе функция Random будет возвращать НЕ случайное число.
Процедура Randomize вызывается ТОЛЬКО ОДИН РАЗ в начале программы. Типичная ошибка новичков заключается в том, что они вызывают Randomize перед каждым вызовом Random. Этого делать не надо.
Что такое Randseed
Давайте сначала попробуем не использовать процедуру Randomize. Например, так:
x := Random(100); WriteLn(x); z := Random(100); WriteLn(z:0:4);
В этом примере функция Random будет возвращать какое-то значение, но оно НЕ будет случайным числом. Сколько бы раз вы не запускали программу, она всегда будет выводить одинаковые числа.
В моём случае это были числа 54 и 59. В вашем случае это могут быть другие числа, но суть не в этом, а в том, что они будут всегда одинаковыми.
Теперь попробуем сделать так:
Randseed := 500; x := Random(100); //х - случайное число от 0 до 99 WriteLn(x); z := Random(100); //х - случайное число от 0 до 99 WriteLn(z:0:4);
Теперь числа будут другими. В моём случае 69 и 7. Правда, они тоже не будут изменяться, то есть не будут случайными.
Однако эти числа изменились. Потому что мы изменили значение глобальной переменной Randseed.
Переменная Randseed — это глобальная предопределённая переменная в FreePascal.
Она также есть и в Делфи. Так что всё сказанное будет справедливо и для Делфи.
Эта переменная задаёт начальное значение для генератора случайных чисел. Опираясь на это значение функция Random генерирует случайное число. Но, если значение переменной Randseed будет всегда одинаковым, то никаких случайных чисел мы не получим.
Поэтому при запуске программы надо хотя бы один раз вызвать процедуру Randomize, которая устанавливает начальное значение переменной Randseed, получая системное время и из этих данных формируя значение для переменной Randseed.
Так как программа запускается в какое-то случайное время, то и значение переменной Randseed будет случайным. А, следовательно, и функция Random будет возвращать случайные значения.
Давайте попробуем написать свою процедуру Randomize. Она может быть, например, такой:
//************************************** // Процедура, которая имитирует работу // стандартной процедуры Randomize //*************************************** procedure MyRandomize; var h, m, s, ms : Word; begin DecodeTime(Now, h, m, s, ms); Randseed := ms; end;
Я не буду в подробностях разъяснять работу процедуры DecodeTime. Скажу только, то она возвращает, час, минуту, секунду и миллисекунду текущего времени компьютера. Мы используем миллисекунду, значение которой и присваиваем переменной Randseed.
Можете попробовать использовать эту процедуру вместо стандартной процедуры Randomize и
убедиться, что функция Random возвращает случайные значения. Не забудьте подключить к
программе модуль SysUtils, в котором объявлена процедура DecodeTime, иначе программа не откомпилируется.
ПРИМЕЧАНИЕ
Исходя из того, что процедура Randomize задаёт начальное значение переменной Randseed на основе текущего времени компьютера, можно предположить, что, например, если запустить программу сегодня в 12:00:00 и завтра в это же время, то функция Random вернёт одинаковые числа.
К сожалению, проверить это очень трудно, так как запустить программу в одно и то же время с точностью до миллисекунды будет практически невозможно.
|
|
Как стать программистом 2.0
Эта книга для тех, кто хочет стать программистом. На самом деле хочет, а не просто мечтает. И хочет именно стать программистом с большой буквы, а не просто научиться кулебякать какие-то примитивные программки… |
|
|
Помощь в технических вопросах
Помощь студентам. Курсовые, дипломы, чертежи (КОМПАС), задачи по программированию: Pascal/Delphi/Lazarus; С/С++; Ассемблер; языки программирования ПЛК; JavaScript; VBScript; Fortran; Python и др. Разработка (доработка) ПО ПЛК (предпочтение — ОВЕН, CoDeSys 2 и 3), а также программирование панелей оператора, программируемых реле и других приборов систем автоматизации. |
| Description | |||||||||
|
The Random function generates random numbers. They can be floating point numbers in the range :0 <= Number < 1.0
0 <= Number <
|
|||||||||
| Related commands | |||||||||
|
|||||||||
|
Example code : Generate sets of floating point and integer numbers |
|
var float : single; int : Integer; i : Integer; begin // Get ShowMessage(»); // Get an |
| Show full unit code |
|
float = 2.3283064365387E-10 float = 0.031379981256104 float = 0.861048460006714 float = 0.202580958604813 float = 0.2729212641716
|