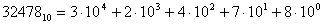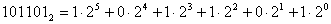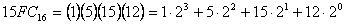Как написать развернутую запись числа

Об этой статье

Была ли эта статья полезной?

Из курса математики известно, что цифры
десятичной записи числа – это коэффициенты
при представлении числа в виде суммы
степеней основания системы счисления.
Например:

246079 = 2*100000 + 4*10000 + 6*1000 + 0*100 + 7*10 + 9*1 =

= 2*10⁵ + 4*10⁴ +
6*10³ + 0*10² + 7*10¹ + 9*10⁰

При записи чисел значение каждой цифры
зависит от ее положения. Место для цифры
в числе называется разрядом, а
количество цифр в числе – разрядностью.
Числа можно записывать как сумму степеней
не только числа 10, но и любого другого
положительного натурального числа –
основания системы счисления.

Развернутой формой записи числа называется запись:

а_n…а₃а₂а₁а₀
= а_n*qⁿ
+…+ a₃*q³ +
a₂*q² + a₁*q¹
+ a₀*q⁰,

где а_n,_…,а₃,а₂,а₁,а₀
–цифры числа, q –основание степени.

Пример 1.

Записать в развернутой форме число
97512₁₀.

Решение: а₄ = 9, а₃ = 7, а₂
= 5, а₁ = 1, а₀ = 2, q=10

_{4 3 2 1 0}

97512₁₀
= 9*10⁴ + 7*10³ + 5*10² + 1*10¹
+ 2*10⁰

Пример2.

Записать в развернутой форме число
112₃.

Решение: _{2 1 0}

112₃ = 1*3² + 1*3¹ +2*3⁰

2. Перевод чисел из одной системы счисления в другую

2.1. Перевод целых чисел из десятичной системы счисления в другие системы счисления

Порядок перевода целых чисел из десятичной системы счисления в систему с основанием q:

1. Последовательно выполнять деление
исходного числа и получаемых частных
на q до тех пор, пока
не получим частное, меньшее делителя.

2. Полученные при таком делении остатки
– цифры числа в системе счисления q
– записать в обратном порядке (снизу
вверх).

Пример1.

Перевести 26₁₀ в двоичную систему
счисления (Х₁₀→Х₂).

Решение:

Ответ:
26₁₀=11010₂

Пример2.

Перевести 19₁₀ в троичную систему
счисления (Х₁₀→Х₃).

19

18

1

3

Р

6

6

0

3

ешение:

2

Ответ: 19₁₀=201₃

Пример3.

Перевести 241₁₀ в восьмеричную
систему счисления (Х₁₀→Х₈).

Решение:

Ответ: 241₁₀=361₈

Пример4.

Перевести 3627₁₀ в шестнадцатеричную
систему счисления (Х₁₀→Х₁₆).

Решение:

В шестнадцатеричной системе счисления
14₁₀ – Е, а 11₁₀ – В, получаем
ответ Е2В₁₆.

Ответ: 3627₁₀=E2B₁₆

Задание для самостоятельной работы .

Перевести
числа из десятичной системы счисления
в указанную:

1)
245₁₀→Х₂

5) 404₁₀→Х₈

2)
1987₁₀→Х₂
6) 673₁₀→Х₁₆

3)
161₁₀→Х₃

7) 45348₁₀→Х₁₆

4)
333₁₀→Х₅

444₁₀→Х₇

2.2. Перевод дробных чисел, у которых целая часть равна нулю, из десятичной системы счисления в другие системы счисления

Порядок перевода дробных чисел из десятичной системы счисления в систему с основанием q:

1. Последовательно выполнять умножение
   исходного числа и получаемых дробные
   части на q до тех пор,
   пока дробная часть не станет равна
   нулю или не будет достигнута требуемая
   точность.

2. Полученные при таком умножении целые
   части — числа в системе счисления q
   – записать в прямом порядке (сверху
   вниз).

Пример1.

Перевести 0,5625₁₀ в двоичную систему
счисления (Х₁₀→Х₂).

Решение:

Ответ: 0,5625₁₀=0,1001₂

Пример2.

Перевести 0,5625₁₀ в восьмеричную
систему счисления (Х₁₀→Х₈).

Решение:

Ответ: 0,5625₁₀=0,52₈

Пример3.

Перевести 0,665₁₀ в двоичную систему
счисления (Х₁₀→Х₂).

Р

0,
665

*
2

1
330

*
2

0
660

*
2

1
320

*
2

0
640

*
2

1
280

…………..

*
2

0
5000

*
2

1
0000

ешение:

Процесс
умножения может продолжаться до
бесконечности. Его прерывают, когда
получена требуемая точность представления
числа.

Ответ: 0,665₁₀=0,10101₂

Задание
для самостоятельной работы.

Переведите
числа из десятичной системы счисления
в указанную:

1)
0, 65625₁₀→Х₁₆

2)
0,7₁₀→Х₂
с точностью до 4 знаков после запятой

3)
0,4125₁₀→Х₈
 с
точностью до 6 знаков после запятой

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

When we write a number as a sum of place value of its
digits, the number is said to be in expended form and when we write a number
using digits, the number is said to be in short form.

Expanded Form of a Number:

When we write 3476, the number really means 3000 + 400 + 70
+ 6. This means we have expanded the number to show the value of each of its
digit.

The expanded form of a number is the method of expressing
the number as the sum of the place value of all its digits.

For example,

Consider the number 2815

2815 = 2000 + 800 + 10 + 5

There are 3 ways to write the expanded form. There are 3 ways to write the expanded form for a given number.

Examples on Expanded Form of a Number:

1. Write the expanded form for 43,257.

Solution:

1^st way: 4 ten thousands + 3 thousands + 2 hundreds + 5 tens + 7 ones

2^nd way: 4 × 10000 + 3 × 1000 + 2 × 100 + 5 × 10 + 7 × 1

3^rd way: 40000 + 3000 + 200 + 50 + 7

2. Write the expanded form for 14,080.

Solution:

14,080 = 1 ten thousand + 4 thousands + 8 tens   [Note: We do not write the place value for
hundreds and ones as these places are filled with zero.]

or, 1 × 10000 + 4 × 1000 + 8 × 10

or, 10000 + 4000 + 80

Standard Form of a Number / Short Form of a Number:

The standard form of a number is a way of expressing the
expanded form in figures.

For example, the standard form of 7000 + 400 + 10 + 1
= 7411

Examples on Expanded Form and Short Form of a Number:

3. Write the short form for the given expanded forms.

(i) 8 ten thousands + 6 hundreds + 6 tens + 3 ones

(ii) 9  × 10000 + 7 ×
1000 + 4 × 10 + 2

(iii) 40000 + 3000 + 900 + 70 + 8

Solution:

Questions and Answers on Expanded Form and Standard Form of a Number:

I. Write in the expanded form:

(i) 5896

(ii) 3817

(iii) 6399

(iv) 1357

(v) 3434

(vi) 5690

Answer:

I. (i) 5000 + 800 + 90 + 6

(ii) 3000 + 800 + 10 + 7

(iii) 6000 + 300 + 90 + 9

(iv) 1000 + 300 + 50 + 7

(v) 3000 + 400 + 30 + 4

(vi) 5000 + 600 + 90 + 0

II. Write in the standard form:

(i) 2000 + 900 + 90 + 9

(ii) 8000 + 200 + 50 + 3

(iii) 1000 + 400 + 50 + 2

(iv) 4000 + 300 + 9

(v) 6000 + 900 + 80 + 4

Answer:

II. (i) 2999

(ii) 8253

(iii) 1452

(iv) 4309

(v) 6984

3rd Grade Math Lessons

From Expanded Form and Short Form of a Number to HOME PAGE

When we write a number as a sum of place value of its
digits, the number is said to be in expended form and when we write a number
using digits, the number is said to be in short form.

Expanded Form of a Number:

When we write 3476, the number really means 3000 + 400 + 70
+ 6. This means we have expanded the number to show the value of each of its
digit.

The expanded form of a number is the method of expressing
the number as the sum of the place value of all its digits.

For example,

Consider the number 2815

2815 = 2000 + 800 + 10 + 5

There are 3 ways to write the expanded form. There are 3 ways to write the expanded form for a given number.

Examples on Expanded Form of a Number:

1. Write the expanded form for 43,257.

Solution:

1^st way: 4 ten thousands + 3 thousands + 2 hundreds + 5 tens + 7 ones

2^nd way: 4 × 10000 + 3 × 1000 + 2 × 100 + 5 × 10 + 7 × 1

3^rd way: 40000 + 3000 + 200 + 50 + 7

2. Write the expanded form for 14,080.

Solution:

14,080 = 1 ten thousand + 4 thousands + 8 tens   [Note: We do not write the place value for
hundreds and ones as these places are filled with zero.]

or, 1 × 10000 + 4 × 1000 + 8 × 10

or, 10000 + 4000 + 80

Standard Form of a Number / Short Form of a Number:

The standard form of a number is a way of expressing the
expanded form in figures.

For example, the standard form of 7000 + 400 + 10 + 1
= 7411

Examples on Expanded Form and Short Form of a Number:

3. Write the short form for the given expanded forms.

(i) 8 ten thousands + 6 hundreds + 6 tens + 3 ones

(ii) 9  × 10000 + 7 ×
1000 + 4 × 10 + 2

(iii) 40000 + 3000 + 900 + 70 + 8

Solution:

Questions and Answers on Expanded Form and Standard Form of a Number:

I. Write in the expanded form:

(i) 5896

(ii) 3817

(iii) 6399

(iv) 1357

(v) 3434

(vi) 5690

Answer:

I. (i) 5000 + 800 + 90 + 6

(ii) 3000 + 800 + 10 + 7

(iii) 6000 + 300 + 90 + 9

(iv) 1000 + 300 + 50 + 7

(v) 3000 + 400 + 30 + 4

(vi) 5000 + 600 + 90 + 0

II. Write in the standard form:

(i) 2000 + 900 + 90 + 9

(ii) 8000 + 200 + 50 + 3

(iii) 1000 + 400 + 50 + 2

(iv) 4000 + 300 + 9

(v) 6000 + 900 + 80 + 4

Answer:

II. (i) 2999

(ii) 8253

(iii) 1452

(iv) 4309

(v) 6984

3rd Grade Math Lessons

From Expanded Form and Short Form of a Number to HOME PAGE

2.5. РАЗВЕРНУТАЯ ФОРМА ЧИСЛА

Развернутая форма записи числа – это запись в виде разрядных слагаемых, записанных с помощью степени соответствующего разряда и основания степени (основание счета).

1. Десятичная система:

Пронумеруем разряды, начиная с младшего:

Теперь запишем выражение:

2. Двоичная система:

Пронумеруем разряды, начиная с младшего:

3. Шестнадцатеричная система:

Пронумеруем разряды, начиная с младшего:

Другие системы счисления записываются аналогично вышеприведенным системам с тем лишь исключением, что основание степени будет соответствовать основанию счета.

В позиционной системе счисления число можно представить в развернутой форме (в виде суммы разрядных слагаемых) и в свернутой форме. Именно такой формой записи чисел мы и пользуемся в повседневной жизни. Иначе свернутую форму записи называют естественной или цифровой.

Десятичное число А₁₀= 4718,63 в развернутой форме будет имеет вид:

А₁₀ = 4718,63₁₀ = 4*10 3 + 7*10 2 + 1*10 1 + 8*10 0 + 6*10 -1 + 3*10 -2 .

Рассмотрим еще примеры записи чисел в развернутом виде

589₁₀ → 500 + 80 + 9 = 5*100 + 8*10 + 9*1 = 5*10 2 +8*10 1 + 9*10 0

₁₀ = 5*10 2 + 8*10 1 + 9*10 0

= 4*10 5 + 8*10 4 + 5*10 3 + 7*10 2 + 6*10 1 + 3*10 0

= 1*2 4 + 1*2 3 + 1*2 2 + 0*2 1 + 0*2 0

= 7*8 2 + 6*8 1 + 4*8 0

= 7*16 2 + 6*16 1 + 4*16 0

= 5*10 1 + 4*10 0 + 3*10 -1 + 2*10 -2

= 5*8 1 + 4*8 0 + 3*8 -1 + 2*8 -2

= 5*16 1 + 4*16 0 + 3*16 -1 + 2*16 -2

= 1*2 2 + 0*2 1 + 1*2 0 + 0*2 -1 + 0*2 -2 + 1*2 3

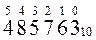
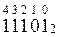
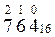
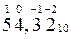
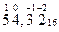
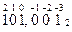
Задания для самостоятельной работы

Задание 1. Запишите числа в развернутой форме

1)	11110102	6)	111101,0012	11)	1110,112	16)	100011102
2)	2174,55	7)	5771,0015	12)	89784515	17)	514763175
3)	6479118		1622,848	13)	1114878	18)	113874,3348
4)	1214710	9)	512001410	14)	1874,59610	19)	1554,01410
5)	1247,032116	10)	15789416	15)	163201,9816	20)	88541216

Перевод чисел в десятичную систему счисления

1. Записать число в развернутом виде

2. Выполнить вычисления как в десятичной системе счисления

→ 1*2 4 + 0*2 3 + 1*2 2 + 0*2 1 + 0*2 0 = 1*16 + 0*8 + 1*4 + 0*2 + 1*1 = 16 + 0 + 4 + 0 + 1 = 21₁₀

→ 3*8 2 + 4*8 1 + 7*8 0 = 3*64 + 4*8 + 7*1 = 192 + 32 + 7 = 231₁₀

→ 10*16 1 + 1*16 0 + 11*16 -1 = 10*16 + 1*1 + 0,6875 = 160 + 1 + 0,6875 = 161,6875

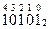
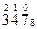
Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Студент – человек, постоянно откладывающий неизбежность. 10571 – | 7330 – или читать все.

78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Сайт учителя информатики. Технологические карты уроков, Подготовка к ОГЭ и ЕГЭ, программирование, полезный материал и многое другое.

Как от свёрнутой формы записи десятичного числа перейти к его развёрнутой форме?

Ответ

Рассмотрим десятичное число 14351,1. Его свёрнутая форма записи настолько привычна, что мы не замечаем, как в уме переходим к развёрнутой записи, умножая цифры числа на «веса» разрядов и складывая полученные произведения:

1 · 10 4 + 4 · 10 3 + 3 · 10 2 + 5 · 10 1 + 1 · 10 0 + 1 · 10 -1 .

Переход от свернутой формы к развернутой

1. Посмотрите на данное вам число и определите количество его цифр.

Пример:
Напишите 5827 в развернутом виде.

Прочитайте число вслух: пять тысяч восемьсот двадцать семь.

Обратите внимание, что в этом числе есть четыре цифры. В результате развернутая форма будет содержать четыре слагаемых.

2. Перепишите число в виде суммы его цифр, оставив между ними некоторое расстояние, чтобы умножить каждую цифру на некоторую цифру (об этом далее).

Пример:
5827 перепишите так:

3. Цифры числа расположены в определенных позициях, которые соответствуют (справа налево) единицам, десяткам, сотням, тысячам и так далее. Определите название позиции и ее значение для каждой цифры (справа налево).

Пример:
Так как в данном числе четыре цифры, то вам нужно определить названия четырех позиций (справа налево).

7 соответствует единицам (значение = 1 = 10 0 ).
2 соответствует десяткам (значение = 10 = 10 1 ).
8 соответствует сотням (значение = 100 = 10 2 ).
5 соответствует тысячам (значение = 1000 = 10 3 ).

4. Умножьте каждую цифру данного числа на значение соответствующей ей позиции.

Пример:
5 · 10 3 + 8 · 10 2 + 2 · 10 1 + 7 · 10 0

Основание: (8).

Алфавит: (0), (1), (2), (3), (4), (5), (6), (7).

Переведём восьмеричное число (4517) в десятичную систему счисления.

435211708=4×83+5×82+1×81+7×80=4×512+5×64+1×8+7×1==2048+320+8+7=238310.

Переведём десятичное число (2383) в восьмеричную систему счисления.

Рис. (2). Восьмеричная система счисления

Основание: (16).

Алфавит: (1), (2), (3), (4), (5), (6), (7), (8), (9), (A (10)), (B (11)), (C (12)), (D (13)), (E (14)), (F (15)).

В системах счисления, которые содержат больше (10) знаков, после цифры (9) начинаются латинские буквы. (10), (11), (12) использовать мы не можем, т. к. это уже числа, а для продолжения алфавита нужны ещё цифры, поэтому было принято использовать латинские буквы.

Переведём шестнадцатеричное число (17AC) в десятичную систему счисления.

1372A1C016=1×163+7×162+10×161+12×160==4096+1792+160+12=606010.

Переведём десятичное число (6060) в шестнадцатеричную систему счисления.

Рис. (3). Шестнадцатеричная система счисления

It is tempting to say that the digits in a number are what define its value, but if you write 25 and 52 – using the same digits but in different places – you get two different values. Learning to write numbers in expanded form is an easy way to remember the importance of each digit’s placement, or its place value, in a number.

Understanding Place Values

Try counting up from zero: 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9 are all pretty straightforward, but once you get to 10, something changes. You now have two digits in the number – the 1 and the 0. Each digit occupies a «slot» or place in the final number, and each place has a different value. The slot on the left represents tens, and the digit 1 in that slot tells you that you have one 10. The slot on the right represents ones – the same numbers you started counting with – and the zero in that slot tells you that you don’t have any extra 1s.

Place Value Examples

If you keep counting, you’ll notice that the digits in the ones column change first. The next number is 11. If you take it apart to its component place values, which is known as decomposing the number, you’ll see that there is a 1 in the tens slot and a 1 in the ones slots. So you have one 10 and one 1. The next number is 12, which still has a 1 in the tens slot, but now there’s a 2 in the ones slot. Keep counting for long enough, and you’ll reach 19, then 20. Notice that now the number in the tens slot has increased to 2, but the ones slot has reset to zero. This pattern continues as you count up. The number in the ones slot keeps increasing until it hits 9; then the tens value goes up, and the ones value resets to zero.

The Hundreds Place

You can decompose any number at all, even large ones. Consider the number 392. It has three digits, so you have a new slot or place value to deal with in a larger number. You’re already familiar with the ones place, which remains on the far right of the number; in this case, you have two 1s. The tens place is still the next column to the left. There’s a 9 there, so you have nine 10s. The next column to the left is called the hundreds column, and there’s a 3 there, so you have three 100s.

Writing Numbers in Expanded Form

Expanded form is a specific way of writing the digits of a number that you’ve broken into each of its component place values. To write numbers in expanded form, you link each digit in the number to its place value with a multiplication sign. Consider the example of 392. Reading the numbers from left to right, you start with the biggest slot, the hundreds place, which has a 3 in it. You have

3 × 100 = 300

The next slot to the right is the tens place, and there’s a 9 in it. You have

9 × 10 = 90

There’s a 2 in the ones place, so you have

2 × 1 = 2

There are three pieces to this number: 300, 90 and 2. Connect those pieces with addition signs, and you have the number in expanded form:

300 + 90 + 2 = 392

The Pattern of Place Values

There’s no limit to how big or small a number you can write in expanded form. You just have to know the value of each place or slot in the number. Perhaps you’ve already noticed this pattern: The place values start with ones on the right, then for each slot you move to the left, the value is multiplied by 10. The next slot on the left is tens is hundreds, and the place after that is thousands, followed by 10 thousands and so on.

You can even write decimals in expanded form, as long as you understand how those place values work. When you have a decimal point, the slot just to the right of the decimal is the tenths slot, the slot to the right of that is the hundredths slot and so on. If you have the number 0.231, there’s a 2 in the tenths slot, a 3 in the hundredths slot and a 1 in the thousandths slot. You can write that number in expanded form by multiplying each digit by its place value, then adding them together:

2 × 0.1 = 0.2, ,3 × 0.01 = 0.03 text{ and }1 × 0.001 = 0.001

The final step is to connect the results with addition signs:

0.2 + 0.03 + 0.001

Another Example of Expanded Form

Let’s write another number in expanded form. Consider 457.2. When you multiply each digit by its place value, you have

4 × 100 = 400, , 5 × 10 = 50, , 7 × 1 = 7 text{ and }2 × 0.1 = 0.2

Put an addition sign between each component, and you have the number in expanded form:

400 + 50 + 7 + 0.2

You can always check your work by adding the components of the number together, which is called composing the number or writing it in standard form. When you do the addition and add

400 + 50 + 7 + 0.2 = 457.2

you end up with the original number.