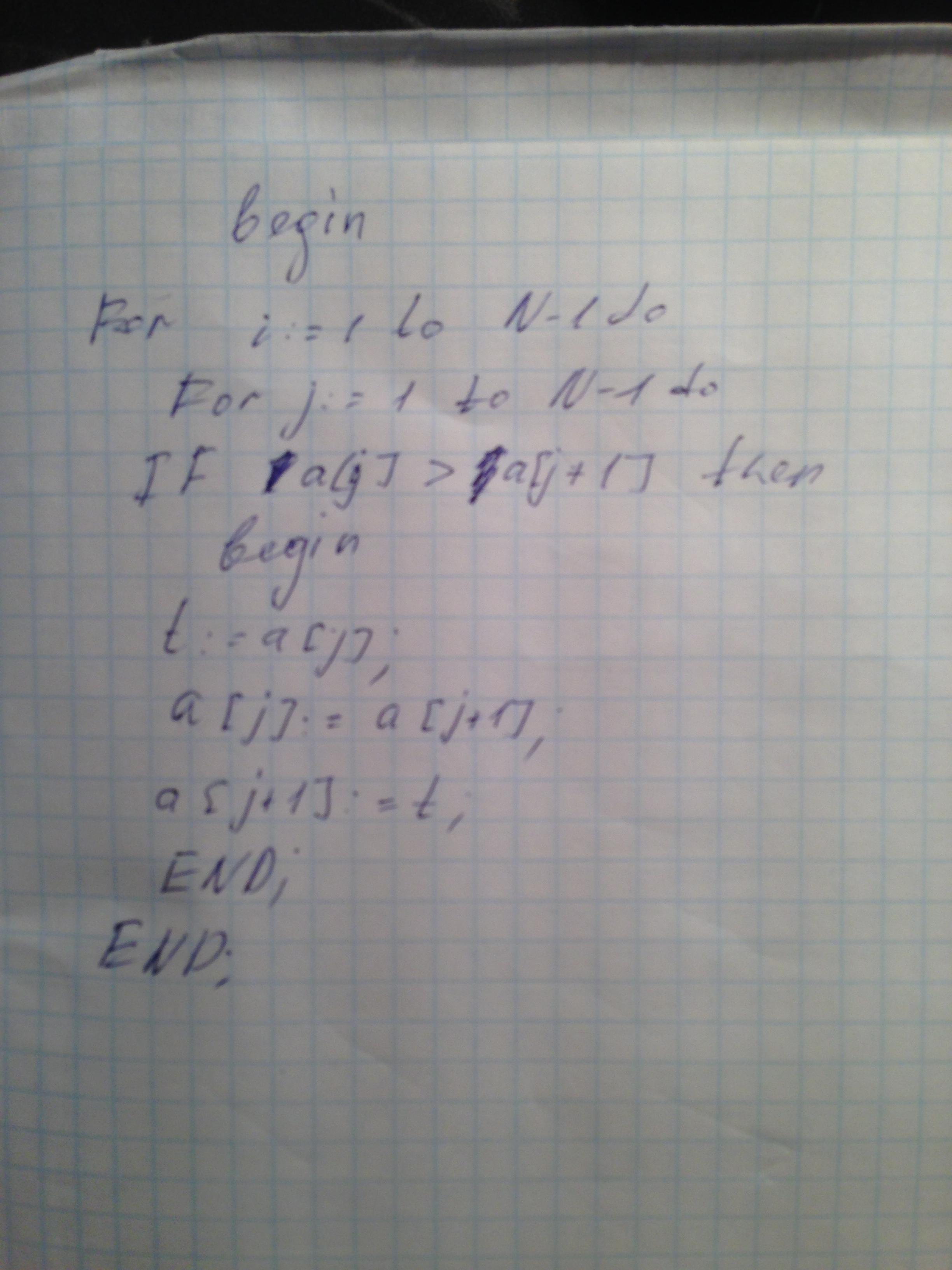Как написать разветвляющийся алгоритм

Статья рассказывает про алгоритмы с разветвлённой структурой. Читатель узнает, чем их решение отличается от решения линейных алгоритмов, как выглядит программный способ записи таких алгоритмов, а также какова будет блок-схема.

В предыдущей статье шла речь об алгоритмах, их особенностях и свойствах. Особое внимание было уделено линейной структуре как самому простому способу реализации. Сегодня поговорим о более сложных алгоритмах, обладающих разветвлённой структурой. Но прежде чем продолжать, следует кое-что вспомнить.

Алгоритм – это ясный перечень действий, который направлен на решение какой-либо задачи. Одно из свойств алгоритма — дискретность. Дискретность связана с наличием в алгоритмической последовательности ряда операций (этапов, действий), выполняемых пошагово, то есть дискретно. Алгоритм обладает свойством дискретности, так как он представляет собой процесс решения задачи в виде последовательного выполнения простых шагов. И каждое действие исполняется лишь после окончания исполнения предыдущего. Также предполагается наличие определённых исходных данных и результата выполнения.

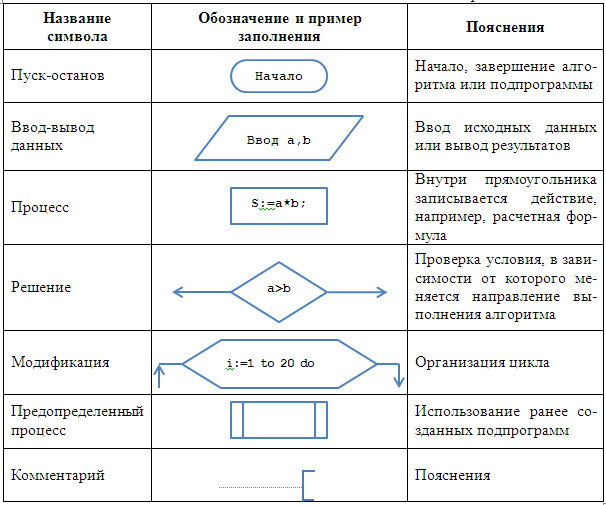
Блок-схема — графический способ описания алгоритмов. Графическое представление обеспечивает наглядность и упрощает запись, делая последовательность более понятной. При использовании схемы каждому действию соответствует определённая геометрическая фигура (эти фигуры называют блоками). Вот наиболее часто употребляемые:

Ещё раз о линейности

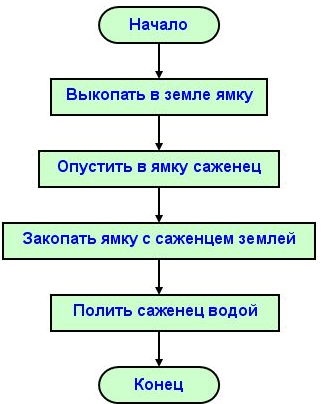
Линейная последовательность — самая простая из возможных структур. При наличии линейности команды выполняются в чёткой последовательности и в порядке их записи, то есть друг за другом. Вот линейная алгоритмическая последовательность посадки дерева:
1) выкапывание ямки в земле;
2) размещение в ямке саженца;
3) закапывание ямки;
4) поливание места посадки водой.

Такой линейный алгоритм имеет следующую блок-схему:

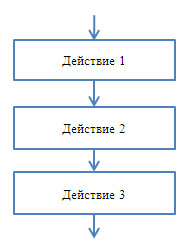
А вот и общая схема линейного алгоритма:

Ветвление в алгоритмических последовательностях

На практике очень редко встречается, чтобы последовательность всех требуемых действий была известна заранее. Если на минуту покинуть мир алгоритмизации и программирования, можно спроецировать ветвление на многие жизненные ситуации. Если на улице дождь, человек берёт зонт, если очень жарко, будет выбрана одежда полегче и т. д. Всё зависит от условия выбора. Как тут не вспомнить рыцаря на распутье из русских народных сказок?

«Направо пойдёшь — жену найдёшь, налево пойдешь — богатым будешь, прямо пойдёшь — смерть найдёшь».

Подобная ситуация заставляет принимать решения с учётом определённого условия. Если нужна жена, то витязь идёт направо, если богатство, то налево, если жизнь не мила, то прямо. Условия, которые влияют на решение, располагаются между словами «если» и «то».

От значения условий зависит дальнейшее поведение. Когда условие выполняется, оно принимает значение «истина», когда нет — «ложь». Иногда анализ ситуации и выбор не вызывают особых затруднений, а иногда принять решение очень трудно. А всё потому, что принимающий решение пытается продумать каждый из вариантов и предугадать последствия выбора. Нельзя не вспомнить гроссмейстера, который анализирует позицию на ходы вперёд, прежде чем передвинуть фигуру на шахматной доске.

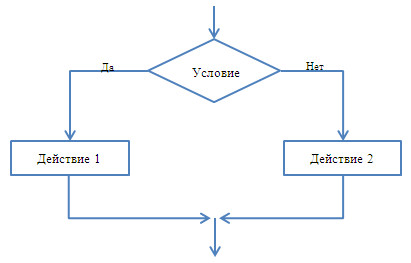
Компьютерные программы и игры тоже построены на выборе действий. А блок-схема при наличии ветвления приобретает иной вид:

Логика разветвляющих алгоритмов

Логику можно описать следующим образом:

ЕСЛИ <условие истинно> ТО <действие 1> ИНАЧЕ <действие 2>


Ветвление — метод и форма организации действий, когда в зависимости от выполнения определённого условия совершается та либо иная последовательность шагов.

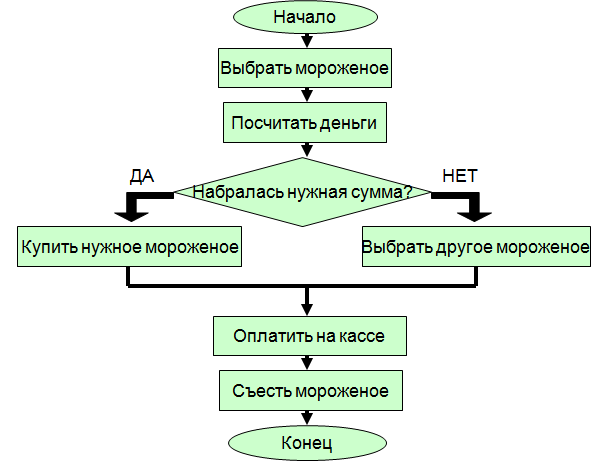
В результате совсем несложно составить алгоритм покупки мороженого с учётом наличия необходимой суммы денег. Описать эту алгоритмическую последовательность с помощью схемы и блоков тоже не составит труда:

Для закрепления можно решить задачу.
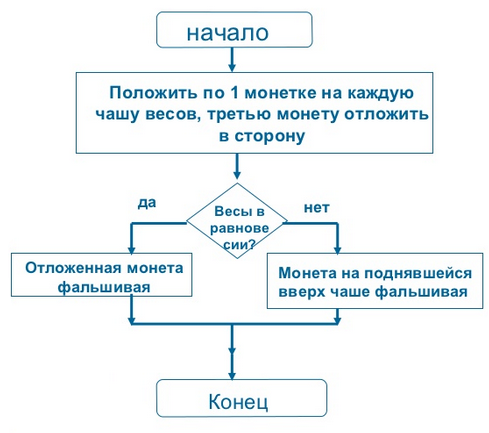
Есть 3 монеты одинакового достоинства. Одна из монет фальшивая (известно, что она имеет меньший вес). Найдите фальшивую монету на чашечных весах без гирь с помощью только одного взвешивания.
Решение легко описывается посредством схематических блоков: 



  


                       
  





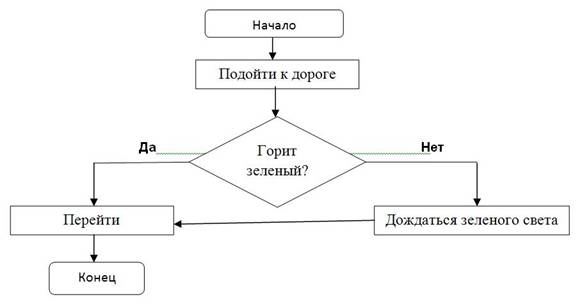
Следующий пример легко экстраполируется в жизнь. Речь идёт об алгоритме для перехода дороги при наличии светофора. Он имеет следующий вид:

1. Подходим к светофору.

2. Смотрим, какой горит свет.

3. Если зелёный, переходим дорогу.

4. Если красный, ждём, пока загорится зелёный, а потом переходим дорогу.
Соответствующая блок-схема:

Программный способ записи
Чтобы алгоритм было понятен компьютеру, машине и любой другой цифровой системе, следует оформить его в таком виде, который эта система способна воспринимать. То есть надо написать программу, используя для этого команды из СКИ. СКИ — это список команд исполнителя — перечень команд, ему понятных. А любой исполнитель способен исполнить лишь те команды, которые включены в его СКИ, а если говорить человеческим языком — входят в набор его компетенций. 
Для примера можно реализовать алгоритм на языке программирования Pascal. Исходя из вышесказанного, следует использовать команды, входящие в терминологию Pascal. 
Простейший пример описания алгоритма с разветвляющейся структурой — условный оператор IF. Полная конструкция этого условного оператора имеет следующий вид:
if<логическое выражение>then<оператор 1>else<оператор 2>


Здесь if — это «если», then — это «то», else — «иначе». 
Условный оператор работает просто:

— вычисляется значение логического выражения, которое расположено после служебного слова IF;

— если результат — истина, выполняется оператор 1, который размещён после THEN, причём действие после ELSE пропускается;

— если результат — ложь, пропускается уже действие после THEN, а действие после ELSE выполняется с помощью оператора 2.
Теперь можно вспомнить пресловутого витязя на распутье и написать простую программу, реализующую этот алгоритм с помощью соответствующих условных операторов.



  


                       
  




program Algoritm_vetvlenia;
Var x :string;
Begin
WriteLn ('Витязь, куда путь держишь?');
ReadLn (x);
If x='Направо'  then  writeLn ('Направо пойдёшь — жену найдёшь');
If x='Налево'  then  writeLn ('Налево пойдешь — богатым будешь');
If x='Прямо'  then  writeLn ('Прямо пойдёшь — смерть найдёшь');
ReadLn;
End.


Попробовать этот алгоритм в работе можно на любом онлайн-компиляторе, поддерживающим Pascal. Но не стоит на этом останавливаться — лучше всего написать собственную программу, что позволит получить максимальную пользу от урока. 

Источники:

• http://informatic.hop.ru/p33.htm;

• https://interneturok.ru/lesson/informatika/6-klass/algoritm-i-ispolniteli/prakticheskaya-rabota-2-sostavlenie-algoritmov;

• https://www.turbopro.ru/index.php/algoritmizatsiya-i-ispolniteli/5210-algoritmy-ponyatie-i-vidy-algoritma-blok-skhemy;

• https://www.yaklass.ru/p/informatika/6-klass/algoritmy-14002/tipy-algoritmov-13610/re-61ead1ff-bc77-453f-ac99-e46da267f3f3.

План урока:

Программирование разветвляющихся алгоритмов

Определение разветвляющегося алгоритма

Условный оператор

Формы записи условного оператора if

Составной условный оператор if

Циклический оператор while

Программирование разветвляющихся алгоритмов

Не все алгоритмы можно представить в виде списка действий. Бывают случаи, когда на выполнение чего-либо влияют определённые факторы. Например, если погода будет хорошей, то Настя пойдёт гулять и есть мороженое, однако, если погода будет плохой – она будет сидеть дома и делать уроки. В данном случае, окончательное действие зависело от того, какой будет погода. Это и есть условие выполнения.

Определение разветвляющегося алгоритма

Разветвляющиеся алгоритмы – это алгоритмы, имеющие несколько альтернативных путей, выбор которых зависит от выполнения некоторых условий. Ветвление — алгоритмическая конструкция, при выполнении которой, в зависимости от результата проверки условия («да» или «нет»), выполняется одна из двух последовательностей команд, называемых ветвями. Способ записи ветвления зависит от выбранного для выполнения определённой задачи оператора.

В линейных разветвляющихся алгоритмах можно выделить два типа условий: простые и составные.

Простые условия содержат одно логическое (булево) выражение, то есть такое утверждение, которое является либо истинным, либо ложным.

Логическое выражение может быть представлено как одним идентификатором логического типа, так и двумя идентификаторами или выражениями, между которыми стоит знак логической операции отношения, позволяющей сравнить их между собой. К операциям отношения относятся:

• > (больше);
• < (меньше);
• >= (больше или равно);
• <= (меньше или равно);
• <> (не равно);
• = (равно).

Примеры простых логических выражений:

• Value (идентификатор Value должен иметь логический тип данных);
• a — b <> 5 (истинно, если a — b не равно 5);
• c >= 10 + 11 (истинно, если c имеет значение 21 или больше);
• 7 > 8 (это выражение всегда ложно);
• ‘бабушка’ <> ‘дедушка’ (это выражение всегда истинно).

Первые три выражения имеют в своём составе переменные или константы, следовательно, об истинности всего выражения можно говорить только когда эти идентификаторы будут иметь какие-то определённые значения:

• Если a = 5, b = 3, то второе выражение является истинным. Однако, если a = 5, b = 0, то результатом их разности будет число 5, которое делает это выражение ложным.
• Если c = 9, то третье выражение будет ложным, при этом, если с имеет значение 21 и более, то выражение будет истинным.

Составные условия представляют выражения, составленные из нескольких логических выражений, соединённых при помощи служебных слов and («И», логическое умножение) или or («ИЛИ», логическое сложение), например:

• p and q (истинно, если истинны обе логические переменные — p И q);
• a > b or x < 7 (истинно, если a > b, ИЛИ если x < 7);
• c < 3 or d > 5 and x <> 2 (истинно, если c < 3, ИЛИ если d > 5 И x <> 2).

В третьем примере сначала определяется истинность выражения d > 5 and x <> 2, а затем выполняется операция or, поскольку логическое умножение, как и арифметическое, имеет приоритет над сложением.

Вложенные ветвления представляют собой условие внутри условия. Когда «условие 1» будет принимать истинное значение, программа перейдёт на проверку «условия 2», иначе – выполнится «ветвь 1». Если «условие 2» окажется истинным, то выполнится «ветвь 3», иначе – «ветвь 2». Таким образом, «условие 2» является вложенным в «условие 1».

Какие условные операторы языка Паскаль позволяют описывать подобные разветвленные алгоритмы?  На этом уроке мы продолжим разбор условного оператора if и рассмотрим различные его формы.

Условный оператор

Условный оператор в Паскале позволяет выбрать ветвь выполнения программы в зависимости от истинности или ложности логического выражения, записанного в условии.  

Формы записи условного оператора if

Неполный условный оператор if включает в себя служебное слово if («если»), за которым следует условие – простое либо составное логическое выражение, после которого пишется слово then («то»). Далее указывается оператор, выполняемый тогда, когда заданное условие является истинным. В конце оператора ставится точка с запятой:

if <условие> then <оператор 1>;

Полный условный оператор if, в дополнение к «оператору 1», выполняющемуся при истинности условия, добавляет «оператор 2», который выполняется если условие ложно. При этом после «оператора 1» пишется служебное слово else («иначе»), за которым следует «оператор 2», а разделитель точка с запятой переносится в конец оператора:

if <условие> then <оператор 1> else <оператор 2>;

Поскольку для транслятора языка Паскаль разделителем между операторами является символ точки с запятой, а не перевод строки, для повышения читабельности программы, условный оператор принято записывать в несколько строк, выделяя отдельные ветви отступом от левого края:

if <условие> then

    <оператор 1>

else

    <оператор 2>;

Составной условный оператор

Составной оператор в Паскале применяется тогда, когда в одной из ветвей нужно выполнить более одного оператора. Составной оператор начинается со служебного слова begin и завершается служебным словом end. В промежутке между этими двумя словами находятся операторы, выполнение которых происходит в том порядке, в котором они записаны. Составные операторы могут применяться везде, где применяются простые операторы, и также как простые операторы, они должны отделяться точкой с запятой по тем же правилам. Пример использования составного оператора в конструкции if..then..else:

if <условие> then

    begin

        <оператор 1>;

        <оператор 2>;

    end

else

    begin

        <оператор 3>;

        <оператор 4>;

    end;

В данном примере, в случае истинности условия будут выполняться операторы 1 и 2, в случае ложности – операторы 3 и 4.

Вложенный условный оператор

Так как «оператор 1» в примерах выше может быть любым допустимым оператором языка Паскаль, никто не запрещает использовать вместо него еще один оператор if, создавая таким образом вложенные условные операторы:

if <условие 1> then

    if <условие 2> then

        <оператор 1>

     else

    <оператор 2>

else

    <оператор 3>;

Таким образом, для множества алгоритмов разветвляющейся структуры существует множество простых и составных операторов.

Однако, на этом многообразие операторов ветвления не заканчивается. Так, для разветвляющихся циклических алгоритмов применяется оператор while.

Циклический оператор while

Если нужно создать цикл, то циклический оператор while отлично подходит для этой задачи. Он используется тогда, когда неизвестно точное число повторений одних и тех же действий. Однако, эти действия могут не выполниться ни разу. Оператор while записывается следующим образом:

While <условие> do

    <оператор 1>;

Выполнение действий, заключённых в операторе 1, продолжается до тех пор, пока логическое выражение в условии принимает истинное значение. Когда условие станет ложным, программа выйдет из цикла и перейдёт к выполнению последующих команд.

Задачи

Для закрепления полученных знаний необходимо решить несколько задач на условные операторы и рассмотреть примеры разветвляющихся алгоритмов.

Задача 1. Необходимо создать программу, которая на вход будет получать 2 числа, а выводить наибольшее из них. Если числа одинаковы, то нужно вывести любое из них.

Решение.

Шаг 1. Необходимо ввести наименование программы. В данном случае это будет решение первой задачи.

Шаг 2. Учитывая, что числа, которые получит программа и запишет в переменные a и b, будут относиться к численному типу данных, необходимо указать тип integer.

Шаг 3. После записи слова begin, обозначающего начало командного блока, нужно записать текст, который программа будет выводить изначально. Так как на вход должны подаваться два числа, так и записывается: «Введите два числа: ».

Шаг 4. Необходимо записать оператора, благодаря которому будет происходить принятие входных данных и закрепление их за определёнными переменными.

Шаг 5. Появление условного оператора if. В данной задаче необходимо вывести наибольшее число, поэтому условием будет сравнение чисел.

Шаг 6. Проверка написанного кода программы и правильности выводящихся данных. Если значение a больше значения b, то программа выводит значение, закреплённое за переменной a. В противном случае, программа выведет число b. Если числа одинаковы, то программа автоматически перейдёт к выполнению оператора, записанного после слова else, так как числа одинаковы, нет разницы в том, какое из них выводить.

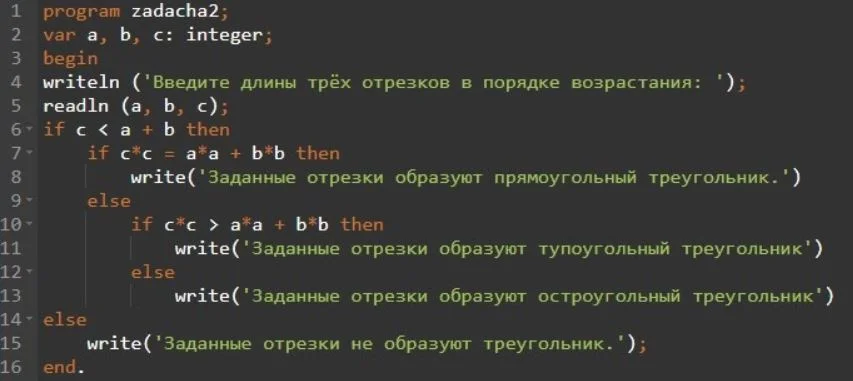
Задача 2. На вход программа получает 3 числа, которые обозначают длины различных отрезков. Необходимо выяснить, можно ли построить с помощью этих отрезков треугольник. Если да, то каким он будет: тупоугольным, прямоугольным или остроугольным.

Решение.

Шаг 1. Для решения этой задачи понадобятся минимальные знания в области математики. Изначально необходимо помнить, что в прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы, в тупоугольном треугольнике сумма квадратов двух наименьших сторон меньше квадрата наибольшей, а в остроугольном то же самое, но наоборот: сумма квадратов двух наименьших сторон больше квадрата наибольшей.

Шаг 2. Построение кода программы. Для начала необходимо дать ей название.

Шаг 3. Указывается тип данных. Поскольку данные, которые получает программа, относятся к численному типу данных, то после названий переменных нужно написать integer.

Шаг 4. После этого пишется запрос программы, в случае со второй задачей текст будет выглядеть так: «Введите длины трёх отрезков в порядке возрастания: ».

Шаг 5. Запись оператора, который поможет программе получить данные.

Шаг 6. Запись и представление примерной работы всех необходимых условий. Изначально нужно понять, образуют ли отрезки какой-либо треугольник, для этого записывается условие, дословно переводящееся как «если c< a+b тогда». Если его значение будет истинным, то программа перейдёт к дальнейшим условиям, таким как «если квадрат c равен сумме квадратов a и b» и так далее.

Шаг 7. Проверка написанного кода программы и правильности выводящихся данных. В зависимости от того, какое из условий окажется верным, программа выведет создают ли эти отрезки треугольник и если да, то его тип. В случае, когда все условия будут ложными, программа выдаст, что «Заданные отрезки не образуют треугольник.».

Задача 3. Нужно найти минимальное целое число a, при котором равенство 3a > n является истинным. На вход подаётся число n, большее чем единица.

Решение.

Шаг 1. Для начала необходимо дать программе название.

Шаг 2. Учитывая, что на вход подаётся целое число, указать тип данных, в данном случае – integer.

Шаг 3. Запись командного блока. Нужно написать слово, обозначающее начало, begin.

Шаг 4. Первоначальный вывод программы. Необходимо написать то, что программа будет выдавать в первую очередь. В данном случае, она будет запрашивать число, запрос так и пишется: «Введите число: » .

Шаг 5. Запись необходимых операторов. Используя оператор readln программа считывает данные и переводит курсор на новую строку. Далее она производит операции над поступившими данными.

Шаг 6. Запись цикла. «Пока 3*а меньше или равно n» она будет прибавлять к a по единице. После того, как цикл закончится, программа выведет итоговое значение a, которое и будет ответом к задаче.

Шаг 7. Проверка правильности записи алгоритма. В конце программного блока, после слова end нельзя забывать точку, её обязательно нужно поставить.

Задача 4. На вход подаётся натуральное число, из которого необходимо удалить заданную пользователем цифру.

Решение.

Шаг 1. Для решения данной задачи понадобится вспомнить операции mod и div в Паскале. Div возвращает целую часть при делении какого-то числа на какое-то число. К примеру, если 5 поделить на 3, то в остатке будет 2. При записи 5 div 3 программа выдаст значение 1, тк 5 делится на 3 ровно 1 раз. Mod возвращает остаток от деления. При записи 5 mod 3 программа выдаст значение 2, поскольку остаток от деления 5 на 3 равен 2. Как же решать эту задачу?

Шаг 2. Записать название программы. В данном случае будет «Задача 4».

Шаг 3. Указание типа вводимых данных. Longint представляет тип данных с длинными целыми числами, к нему можно отнести подающееся на вход число (а) и цифру, которую нужно удалить (b). Следующим типом будет byte, он представляет целый беззнаковый тип.

Шаг 4. После этого следует командный блок. Вписываются 2 оператора readln, позволяющие программе считать необходимые данные.

Шаг 5. Запись цикла. В данной программе лучше всего использовать цикл «Пока a больше 0». Здесь идёт пример составного оператора. После присвоения переменной m нового значения программа переходит к условию «Если m не равно n, тогда», при истинности которого присваивает переменной b новое значение. Из выполненного условия программа переходит к присвоению переменной a нового значения, равному целой части от деления числа, заключённого в a, на 10. После выполнения всех действий и условий в первом цикле, программа переходит ко второму циклу «Пока b больше 0». В нём она присваивает переменным a и b новые значения.

Шаг 6. Проверка кода программы. После окончания всех циклов она должна вывести итоговое число и завершить свою работу.

Вопросы занятия:

·                  
Ветвление;

·                  
Разветвляющиеся
алгоритмы;

·                  
Составление
разветвляющихся алгоритмов.

В
повседневной жизни таких ситуаций, в которых заранее известен алгоритм действий
и результат, очень мало. Практически постоянно нам приходится принимать решения
от которых будут зависеть дальнейшие действия.

Ветвление
–
это алгоритмическая конструкция, в которой в зависимости от выполнения условия
(да или нет) предусмотрен выбор одной из двух последовательностей команд
(ветвей).

А
алгоритмы в которых применяется только «ветвление», называются разветвляющимися.

Рассмотрим
пример. На уроке русского языка для того чтобы применить правило правописания
приставок на «з-» и «с-» вы будете действовать по
алгоритму:

Для
принятия решения ход рассуждений может быть таким:

Полная
форма ветвления:

Графически,
полная форма структуры ветвление представляется следующим образом:

Как
вы помните Проверка условия изображается с помощью блока «Принятие решения»,
который условно обозначается ромбом, внутри его записывается условие.

В
данный блок входит одна линяя связи, а выходят две линии, возле которых
записываются результаты проверки условия да или нет. Далее, в зависимости от
выполнения или невыполнения некоторого условия приводится к исполнению либо
одна, либо другая последовательность команд.

Иногда,
встречаются ситуации, когда вторая последовательность команд отсутствует, то
есть сокращённая форма записи.

Например:

Графически,
неполная форма структуры ветвление представляется следующим образом:

Изображаем
блок «Принятие решения», который условно обозначается ромбом, внутри его
записывается условие.

В
данный блок входит одна линяя связи, а выходят две линии, возле которых
записываются результаты проверки условия да или нет. Здесь, в зависимости от
выполнения или невыполнения некоторого условия приводится к исполнению только
одна последовательность команд, либо алгоритм будет завершён.

Операции
сравнения на алгоритмическом языке можно записать при помощи следующих знаков:
меньше; меньше или равно; равно; больше; больше или равно; не равно.

С
помощью этих знаков можно сравнивать любые переменные, числа и арифметические
выражения, символьные переменные.

Рассмотрим
блок-схему алгоритма, по которому большее число из двух будет удвоено.

Обратите
внимание на второй блок данной блок-схемы. Здесь записаны имена и типы величин
(данных), которые обрабатываются в алгоритме.

В
данном примере, в условии, используется одна операция сравнения. Такие условия
называются простыми.

То
есть простыми называются условия, состоящие из одной операции сравнения.

При
решении различных задач иногда возникает необходимость проверять выполнение
двух (как например, 0 < а < 5) и более условий. Такие условия называют составными.

Составные
условия – это условия которые создаются из
нескольких простых, соединённых друг с другом логическими операциями.

Для
записи составных условий в алгоритмическом языке используют следующие
логические операции: логическое «и» and; логическое «или» оr;
логическое отрицание not.

Так
с помощью логических операций простые условия объединяют в составные. Простые
условия при этом обязательно заключаются в скобки, так как логические операции
имеют более высокий приоритет, чем операции сравнения.

Составное
условие, состоящее из двух простых условий, соединённых операцией И, верно
(истинно) только тогда, когда верны оба простых условия.

Составное
условие, состоящее из двух простых условий, соединённых операцией ИЛИ, верно
тогда, когда верно хотя бы одно из простых условий.

Составное
условие НЕ верно только тогда, когда простое условие ложно.

Рассмотрим
пример: Необходимо с помощью блок-схемы изобразить алгоритм, определяющий,
является ли данное число двузначным.

Математически,
необходимо выполнить сравнение данного числа с числами десять и девяносто
девять.

Если
данное число n больше либо равно 10 и
меньше, либо равно 99, то можно сделать вывод, что данное число двухзначное.

Однако
при решении задач часто приходится выбирать не из двух, а из трёх и более
вариантов. Существуют разные способы построения соответствующих алгоритмов.
Один из них — составить комбинацию из нескольких ветвлений.

Рассмотрим
пример: Задан угол. необходимо определить его вид: острый, прямой, тупой,
развёрнутый или плоский. Представим решение данной задачи в виде блок-схемы.

Выполним
следующее задание. Составим разветвляющийся алгоритм для исполнителя Робот. Дан
горизонтальный коридор длиной в шесть клеток и шириной в три клетки, необходимо
перевести робота в конец коридора и закрасить все клетки над или под которыми
есть выход.

Итак,
робот находится в начале коридора, нужно перевести робота в конец коридора и
закрасить все необходимые клетки.

В
зависимости от выполнения простых или составных условий Робот может выполнять
ту или иную последовательность действий.

Простыми
условиями для Робота будут:

справа
свободно – справа стена, слева свободно – слева стена, сверху свободно – сверху
стена, снизу свободно – снизу стена, клетка чистая – клетка закрашена.

Итак,
начинаем выполнение алгоритма с команды – «использовать робот». Далее
записываем имя алгоритма – «коридор».

Начало

Вправо

Если сверху свободно

То закрасить.

Всё

Если
снизу свободно

То
закрасить

 Всё

Обратите
внимание, мы с вами написали алгоритм, который позволит роботу выполнить один
шаг в лабиринте. Всего в лабиринте шесть шагов, поэтому для оставшихся пяти
достаточно пять раз скопировать данные команды.

Также,
для составления данного алгоритма мы использовали сокращённую форму записи. То
есть

ЕСЛИ
<условие>

ТО
<действия 1>

Так
как разветвляющийся алгоритм должен работать для различных обстановок, давайте
проверим его. Для этого загрузим обстановку Коридор 2 и запустим на выполнение
наш алгоритм. Как мы можем видеть, алгоритм написан правильно, так как все
необходимые клетки закрашены и робот оказался в конце коридора.

Рассмотрим
следующее задание: Из ряда чисел 15, 16, 17 и 18 выписать значения х,
удовлетворяющие условию из блок-схемы.

Перед
нами блок схема. Для определения результата построим таблицу.

Подведем
итоги.

Ветвление
– это алгоритмическая конструкция, в которой в зависимости от выполнения
условия (да или нет) предусмотрен выбор одной из двух последовательностей
команд (ветвей).

А
алгоритмы в которых применяется только «ветвление», называются разветвляющимися.

Линейный
алгоритм —
это такой, в котором все операции
выполняются последовательно одна за
другой (рис. 11.1).

1.4. Алгоритмы разветвленной структуры

Алгоритмы разветвленной структуры
применяются, когда в зависимости от
некоторого условия необходимо выполнить
либо одно, либо другое действие. В
блок-схемах разветвленные алгоритмы
изображаются так, как показано на рис.
11.2 — 11.3.

Рис. 11.2 Фрагмент алгоритма	Рис. 11.3 Пример разветвления

1. Разветвляющиеся
   алгоритмы. Условные операторы.

Определение.
Разветвляющимся называется такой
алгоритм, в котором выбирается один из
нескольких возможных вариантов
вычислительного процесса. Каждый
подобный путь называется ветвью
алгоритма.

Признаком
разветвляющегося алгоритма является
наличие операций проверки условия.
Различают два вида условий — простые и
составные.

Простым условием
(отношением) называется выражение,
составленное из двух арифметических
выражений или двух текстовых величин
(иначе их еще называют операндами),
связанных одним из знаков:

  < — меньше,
чем…
  > — больше, чем…
  <= —
меньше, чем… или равно
  >= — больше,
чем… или равно
  <> — не равно
 
= — равно

Условные операторы Pascal-Паскаль

Условные
операторы позволяют
выбирать для выполнения те или иные
части программы в зависимости от
некоторых условий. Если, например, в
программе используются вещественные
переменные x и z, и на каком-то этапе
решения задачи требуется вычислить
z=max(x, y), то желаемый результат получается
в результате выполнения либо оператора
присваивания z:=x, либо оператора
присваивания z:=y. Поскольку значения
переменных x и y заранее неизвестны, а
определяются в процессе вычислений, то
в программе необходимо предусмотреть
оба эти оператора присваивания. Однако
на самом деле должен выполниться один
из них. Поэтому в программе должно
содержаться указание о том, в каком
случае надо выбирать для исполнения
тот или иной оператор присваивания.

Это указание
естественно сформулировать с использованием
отношения x>y. Если это отношение при
текущих значениях x и y справедливо
(принимает значение true), то для исполнения
должен выбираться оператор z:=x; в противном
случае для исполнения должен выбираться
оператор z:=y (при x=y безразлично, какой
оператор выполнять, так что выполнение
оператора z:=y в этом случае даст правильный
результат).

Для
задания подобного рода разветвляющихся
вычислительных процессов в языках
программирования существуют условные
операторы.
Рассмотрим полный условный
оператор Паскаля:

if B then S1 else S2

Здесь if (если), then (то)
и else (иначе)
являются служебными словами, В –
логическое выражение, а S1 и S2 –
операторы.

Выполнение такого
условного оператора в Паскале сводится
к выполнению одного из входящих в него
операторов S1 или S2: если заданное в
операторе условие выполняется (логическое
выражение В принимает значение true), то
выполняется оператор S1, в противном
случае выполняется оператор S2.

Алгоритм
решения упомянутой выше задачи вычисления
z= max( x, y) можно задать в виде условного
оператора Паскаля

if x>y then z:=
x else z:=
y

При формулировании
алгоритмов весьма типичной является
такая ситуация, когда на определенном
этапе вычислительного процесса какие-либо
действия надо выполнить только при
выполнении некоторого условия, а если
это условие не выполняется, то на данном
этапе вообще не нужно выполнять никаких
действий. Простейшим примером такой
ситуации является замена текущего
значения переменной х на абсолютную
величину этого значения: если x<0, то
необходимо выполнить оператор присваивания
x:= — x; если же x>=0, то текущее значение
х должно остаться без изменений, т.е. на
данном этапе вообще не надо выполнять
каких-либо действий.

В подобных ситуациях
удобна сокращенная форма записи условного
оператора в Паскале:

if B then S

Правило
выполнения сокращенного условного
оператора Паскаля достаточно
очевидно: если значение
логического выражения В есть
true, то выполняется
оператор S; в противном
случае никаких
иных действий не производится.

В языке
программирования Паскаль в условном
операторе между then и else,
а также после else по
синтаксису может стоять только один
оператор. Если же при выполнении (или
невыполнении) заданного условия надо
выполнить некоторую последовательность
действий, то их надо объединить в единый,
составной оператор, т.е. заключить эту
последовательность действий в операторные
скобки begin…
end(это
важно!).

1. Разработка
   алгоритмов циклической структуры.
   Варианты построения циклической
   структуры.

Пусть
требуется ввести и обработать
последовательность чисел. Если чисел
всего пять, можно составить линейный
алгоритм. Если их тысяча, записать
линейный алгоритм можно, но очень
утомительно и нерационально. Если
количество чисел к моменту разработки
алгоритма неизвестно, то линейный
алгоритм принципиально невозможен.

Другой
пример. Чтобы найти фамилию человека в
списке, надо проверить первую фамилию
списка, затем вторую, третью и т.д. до
тех пор, пока не будет найдена нужная
или не будет достигнут конец списка.
Преодолеть подобные трудности можно с
помощью циклов.

Циклом
называется многократно исполняемый
участок алгоритма (программы).
Соответственно циклический алгоритм
— это алгоритм, содержащий циклы.

Различают
два типа циклов: с известным числом
повторений и с неизвестным числом
повторений. При этом в обоих случаях
имеется в виду число повторений на
стадии разработки алгоритма.

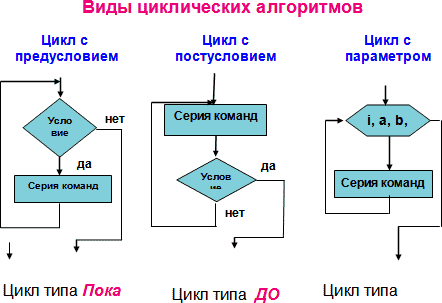
Существует
3 типа циклических структур:

• Цикл
  с предусловием;

• Цикл
  с послеусловием;

• Цикл
  с параметром;

Иначе
данные структуры называют циклами типа
«Пока», «До», «Для».

Графическая
форма записи данных алгоритмических
структур:

Цикл
с предусловием (иначе цикл пока)
имеет вид:

Форматы записи операторов алгоритма	Блок-схема	Форматы записи операторов на Паскале
Пока (условие) нц серия команд кц		while условие do begin             серия команд; end;

где

условие –
выражение логического типа.

Цикл
может не выполняться ни разу, если
значение логического выражения сразу
же оказывается ложь.

Серия
команд, находящихся между begin и end,
выполняются до тех пор, пока
условие истинно.

Для
того чтобы
цикл завершился,
необходимо, чтобы последовательность
инструкций между BEGIN и END изменяла
значение переменных, входящих в условие.

Цикл
с постусловием (иначе цикл до)
имеет вид:

Форматы записи операторов алгоритма	Блок-схема	Форматы записи операторов на Паскале
В алгоритмическом языке нет команды которая могла бы описать данную структуру, но ее можно выразить с помощью других команд (Например, ветвления).		repeat серия команд until условие

где

условие –
выражение логического типа.

Обратите
внимание:

Последовательность
инструкций между repeat и until всегда
будет выполнено хотя
бы один раз;

Для
того чтобы цикл завершился, необходимо,
чтобы последовательность операторов
между repeat и until изменяла
значения переменных, входящих в выражение
условие.

Инструкция
repeat, как и инструкция while, используется
в программе, если надо провести некоторые
повторяющиеся вычисления (цикл), однако
число повторов заранее не известно и
определяется самим ходом вычисления.

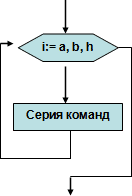
Цикл
с параметром (иначе цикл для) имеет
вид:

Форматы записи операторов алгоритма	Блок-схема	Форматы записи операторов на Паскале
Для i от а до b шаг h  делай       Нц            Серия команд       кц		h = +1 for i:= a to b do      begin        серия команд      end; h = -1 for i:= b downto a do      begin        Cерия команд;      end;

где

i
– параметр цикла;
a – начальное значение
цикла;
b – конечное значение цикла;
h
– шаг изменения параметра.

Структура
данного цикла иначе называют циклом
i раз.

Эта
команда выполняется таким образом:
параметру i присваивается начальное
значение а, сравнивается с конечным
значением b и, если оно меньше или равно
конечному значению b, выполняется серия
команд. Параметру присваивается значение
предыдущего, увеличенного на величинуh –
шага изменения параметра и вновь
сравнивается с конечным значением b.

На
языке программирования Паскаль шаг
изменения параметра может быть равным
одному или минус одному.

Если
между begin и end находится только один
оператор, то операторные скобки можно
не писать. Это правило работает для
цикла типа «Пока» и «Для».

1. Константы и
   переменные. Типы переменных в Turbo
   Pascal
   7.0.

Переменной называют
элемент программы, который предназначен
для хранения, коррекции и передачи
данных внутри программы. Все переменные
программы в Турбо Паскаль должны быть
объявлены в разделе описания переменных
(см. далее).

Наряду
с переменными в пограммах используются
и константы.
Константа — это идентификатор, обозначающий
некоторую неизменную величину
определенного типа. Константы, как и
переменные, должны объявляться в
соответствующем разделе программы.

В Турбо Паскаль
применяется несколько стандартных
видов констант:

• Целочисленные константы.
  Могут быть определены посредством
  чисел, записанных в десятичном или
  шестнадцатиричном формате данных. Это
  число не должно содержать десятичной
  точки.

• Вещественные константы.
  Могут быть определены числами, записанными
  в десятичном формате данных с
  использованием десятичной точки.

• Символьные константы.
  Могут быть определены посредством
  некоторого символа (заключенного в
  апострофы).

• Строковые константы.
  Могут быть определены последовательностью
  произвольных символов (заключенных в
  апострофы).

• Типизированные константы.
  Представляют собой инициализиованные
  переменные, которые могут использоваться
  в программах наравне с обычными
  переменными. Каждой типизированной
  константе ставится в соответствие имя,
  тип и начальное значение. Например:

• year:
  integer = 2001;

• symb:
  char = ‘?’;

• money:
  real = 57.23;

1. Табулирование
   функций. Разработка алгоритмов со
   структурой вложенных циклов.

Задача
табулирования функции предполагает
получение таблицы значений функции при
изменении аргумента с фиксированным
шагом. В качестве исходной информации
должны быть заданы: Х₀,
Х_n –
начало и конец промежутка табулирования,
при этом (Х0< Х_n);
n – число шагов разбиения промежутка
[Х₀,
X_n];
F(X) – описание табулируемой функции.

При
составлении алгоритма предполагается,
что X – текущее значение аргумента; h –
шаг изменения аргумента (иногда его
называют шагом табуляции функции); i –
текущий номер точки, в которой вычисляются
функция (i = 0 .. n).
Количество интервалов
n, шаг табуляции h и величины Х₀,
Х_n связаны
между собой фор-мулой:

Интерпретация
переменных (т. е. их обозначение в
математической постановке задачи, смысл
и тип, обозначения в блок-схеме и
программе) приведена в таблице имен.

Пример.
Табулировать функцию F(X) в N равноотстоящих
точках, заданную на промежутке [Х₀,
X_n],
где

Пример вложенного цикла

1. Поиск минимума
   и максимума функций.

Алгоритм
в общем виде:

1. описать
   для каждого максимума и минимума по
   одной переменной того же типа, что
   анализируемые данные;

2. до
   цикла максимуму присваивается либо
   заведомо малое для анализируемых данных
   значение, либо первый элемент данных;
   минимуму присваивается либо заведомо
   большое для анализируемых данных
   значение, либо первый элемент данных;

3. в теле
   цикла каждый подходящий для поиска
   элемент данных t обрабатывается
   операторами вида:

if
t>max then max:=t;         — для
максимума;
if
t<min then min:=t;         — для
минимума,

где max и min –
переменные для максимума и минимума
соответственно.
Шаг 2 этого алгоритма
требует комментариев, которые мы сделаем
на примере поиска максимума. Очевидно,
что сам алгоритм несложен – каждый
элемент данных t последовательно
сравнивается с ячейкой памяти max и, если
обнаружено значение t, большее текущего
значения max, оно заносится в max
оператором max:=t;.
Как мы помним, после описания на шаге 1
переменной max, ее значение еще не
определено, и может оказаться любым –
откуда следует необходимость задания
начального значения. Представим, что
после выбора начального значения max,
равного нулю, при анализе встретились
только отрицательные значения элементов
t. В этом случае условие t>max не
выполнится ни разу и ответом будет max,
равное нулю, что неправильно! Выбор
заведомо малого начального значения
max (например, значение -1E30, т.е. -1030, вряд
ли встретится в любых реальных данных)
гарантирует, что условие t>max выполнится
хотя бы раз и максимум будет найден.
Альтернативный способ – присвоить max
значение отдельно вычисленного первого
элемента последовательности данных. В
этом случае ответ либо уже найден, если
первый элемент и есть максимальный,
либо будет найден в цикле.
Аналогичные
рассуждения помогают понять, почему
минимуму следует присваивать в качестве
начального значения заведомо большое
число.

Пример. Для
функции y(x)=sin2(x),  
найти минимальное среди положительных
и максимальное значения.
Обозначив
искомые значения min и max соответственно,
составим следующую программу:

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

var x,y,max,min:real; begin  x:=-pi/3;  max:=-2;  min:=2; {эти начальные значения — заведомо малое и большое для синуса}  while x<=pi/3+1e-6 do begin   y:=sqr(sin(x));   ify>0then{ищем min только среди положительных!}    if y<min then min:=y;   if y>max then max:=y;   x:=x+pi/24;  end;  writeln (‘Минимум =’,min:8:2);  writeln (‘Максимум=’,max:8:2);  reset (input); readln; end.

1. Массивы.
   Образование одномерных массивов.
   Обработка одномерных массивов.

Предположим, что
программа работает с большим количеством
однотипных данных. Скажем около ста
разных целых чисел нужно обработать,
выполнив над ними те или иные вычисления.
Как вы себе представляете 100 переменных
в программе? И для каждой переменной
нужно написать одно и тоже выражение
вычисления значения? Это очень
неэффективно.

Есть
более простое решение. Это использование
такой структуры (типа) данных как массив.
Массив представляет собой последовательность
ячеек памяти, в которых хранятся
однотипные данные. При этом существует
всего одно имя переменной связанной с
массивом, а обращение к конкретной
ячейке происходит по ее индексу (номеру)
в массиве.

Нужно четко
понимать, что индекс ячейки массива не
является ее содержимым. Содержимым
являются хранимые в ячейках данные, а
индексы только указывают на них. Действия
в программе над массивом осуществляются
путем использования имени переменной,
связанной с областью данных, отведенной
под массив.

Итак, массив
– это именованная группа однотипных
данных, хранящихся в последовательных
ячейках памяти.
Каждая ячейка содержит элемент массива.
Элементы нумеруются по порядку, но
необязательно начиная с единицы (хотя
в языке программирования Pascal чаще всего
именно с нее). Порядковый номер элемента
массива называется индексом этого
элемента.

Помним, все
элементы определенного массива имеют
один и тот же тип.
У разных массивов типы данных могут
различаться. Например, один массив может
состоять из чисел типа integer,
а другой – из чисел типаreal.

Индексы элементов
массива обычно целые числа, однако могут
быть и символами, а также описываться
другими порядковыми типами. Т.е. для
индекса можно использовать тип, в котором
определена дискретная последовательность
значений, и все эти значения можно
пересчитать по порядку. Индексировать
можно как константами и переменными,
так и выражениями, результат вычисления
которых дает значение перечислимого
типа.

Если индекс массива
может приобретать все допустимые
значения определенного перечислимого
типа, то при описании массива возможно
задание имени типа вместо границ
изменения индекса. При этом границами
индекса будут первое и последнее значения
в описании типа индекса. Границы изменения
индексов могут задаваться с помощью
ранее объявленных констант. Рекомендуется
предварительно объявлять тип массива
в разделе описания типов.

Массив можно
создать несколькими способами.

…

const
n =
200;

type

months
=
(jan,
feb,
mar,
apr,
may,
jun,
jul,
aug,
sep,
oct,
nov,
dec);

years
=
1900..2100;

people
=
array[years]
of
longint;

var

growth:
array[months]
of
real;

hum:
people;

notes:
array[1..n]
of
string;

Обращение к
определенному элементу массива
осуществляется путем указания имени
переменной массива и в квадратных
скобках индекса элемента.

Простой
массив является одномерным.
Он представляет собой линейную структуру.

var
ch:
array
[1..11]
of
char;

h:
char;

i:
integer;

begin

for
i :=
1 to
11 do
read
(ch[i]);

for
i :=
1 to
11 do
write
(ch[i]:3);

readln

end.

В
примере выделяется область памяти под
массив из 11 символов. Их индексы от 1 до
11. В процессе выполнения программы
пользователь вводит 11 любых символов
(например, ‘q’, ’w’, ’e’, ’2’, ’t’, ’9’,
’u’, ’I’, ’I’, ’o’, ’p’), которые
записываются в ячейки массива. Текущее
значение переменной i в цикле for используется
в качестве индекса массива. Второй
цикл for отвечает
за вывод элементов массива на экран.

Функция sizeof,
примененная к имени массива или имени
массивного типа, возвращает количество
байтов, отводимое под массив.

1. Двумерные
   массивы. Обработка двумерных массивов.

Массивы,
положение элементов в которых описывается
двумя индексами, называются двумерными.
Их можно представить в виде прямоугольной
таблицы или матрицы.

Рассмотрим
матрицу А размерностью 2*3, то есть в ней
будет две строки, а в каждой строке по
три элемента:

Каждый
элемент имеет свой номер, как у одномерных
массивов, но сейчас номер уже состоит
из двух чисел — номера строки, в которой
находится элемент, и номера столбца.
Таким образом, номер элемента определяется
пересечением строки и столбца. Например,
a₁₂ —
это элемент, стоящий в первой строке и
во втором столбце.

Существуют
несколько способов объявления двумерного
массива.

Способ
1.
В Паскале двумерный массив можно описать
как одномерный, элементами которого
являются одномерные массивы. Например,
для матрицы А, приведённой выше:

Const n
= 2; m = 3;
Type omyarray
= Array[1..m] Of <тип элементов >;
dmyarray =
Array[1..n] Of omyarray;
Var v
: omyarray;
a : dmyarray;

В
данном случае переменная v объявлена
как одномерный массив из трёх элементов
вещественного типа. Переменная а описана
как двумерный массив из двух строк,
каждую из которых включено по три
элемента.

Способ
2.
Описание массива А можно сократить,
исключив определение типа omyarray в
определении типа dmyarray:

Const n
= 2; m = 3;
Type dmyarray
= Array[1..n, 1..m] Of <тип
элементов>;
Var a
: dmyarray.

Способ
3.
Ещё более краткое описание массива А
можно получить, указывая имя массива и
диапазоны изменения индексов для каждой
размерности массива:

Const n
= 2; m = 3;
Type dmyarray
= Array[1..n, 1..m] Of <тип
элементов
>;

Var a
: dmyarray.

Если
указанный тип используется для определения
одного массива в программе, то удобно
объявление массива в разделе описания
переменных:

Var a:
Array [1..n, 1..m] Of < тип
элементов
>.

Рассмотренные
выше методы решения задач обработки
одномерных массивов могут применяться
для обработки двумерных массивов.
Поскольку положение элемента в двумерном
массиве описывается двумя индексами
[первый — номер строки, второй — номер
столбца], программы большинства матричных
задач строятся на основе вложенных
циклов. Обычно внешний цикл работает
по строкам матрицы, то есть с его помощью
выбирается требуемая строка матрицы,
а внутренний цикл — по столбцам матрицы,
то есть здесь выбирается нужный элемент
из выбранной уже строки. Для задания
значений элементам массива могут быть
использованы операторы присваивания
и операторы ввода данных.

Пример

В
приведённом ниже примере осуществляется
ввод и вывод двумерного массива А
размерностью 10*15. Формирование и вывод
массива описаны в виде двух процедур,
которые вызываются последовательно из
основной программы. Надо заметить, что
формирование двумерного массива можно
осуществлять всеми тремя способами,
описанными для одномерных массивов, то
есть: ввод с клавиатуры, через генератор
случайных чисел или с помощью файла.
Пусть в нашем примере элементы задаются
генератором случайных чисел.

Program
Example_45;
Const
n = 2; m = 15;
Type
dmyarray = Array[1..n., 1..m] Of Integer;
Var
A : dmyarray;

Procedure
Init(Var x: dmyarray);
{процедура
формирования
массива}
Var
i, j : Integer;
Begin
For
i:=1 To n Do
For
j:=1 To m Do
x[i,j]:=-25+Random(51);
End;

Procedure
Print(x: dmyarray);
{процедура
вывода
массива
на
экран}
Var
i, j : Integer;
Begin
For
i:=1 To n Do
Begin
{ввод
i-ой
строки
массива}
For
j:=1 To n Do Write(x[i,j]:5);
Writeln;
{переход
на
начало
следующей
строки}
End;

Begin{основная
программа}
Init(A);
{вызов
процедуры
формирования
массива}
Writeln(‘Массив
А:’);
Print(A);
{вызов
процедуры
вывода}
Readln;
End.

1. Сортировка
   массивов. Методы сортировки (общие
   сведения).

При
решении задачи сортировки обычно
выдвигается требование минимального
использования дополнительной памяти,
из которого вытекает недопустимость
применения дополнительных массивов.
Для
оценки быстродействия алгоритмов
различных методов сортировки, как
правило, используют два показателя:
—
количество присваиваний;
—
количество сравнений.
Все
методы сортировки можно разделить на
две большие группы:
—
прямые методы сортировки;
—
улучшенные методы сортировки.
Прямые
методы сортировки по принципу, лежащему
в основе метода, в свою очередь разделяются
на три подгруппы:
1. сортировка вставкой
(включением);
2. сортировка выбором
(выделением);

Сортировка
вставкой.
Массив
разделяется на две части: отсортированную
и неотсортированную. Элементы из
неотсортированной части поочередно
выбираются и вставляются в отсортированную
часть так, чтобы не нарушить в ней
упорядоченность элементов. В начале
работы алгоритма в качестве отсортированной
части массива принимают только один
первый элемент, а в качестве неотсортированной
части – все остальные.
Сортировка
выбором.
Находим
(выбираем) в массиве элемент с минимальным
значением на интервале от 1-го до n-го
(последнего) элемента и меняем его
местами с первым элементом. На втором
шаге находим элемент с минимальным
значением на интервале от 2-го до n-го
элемента и меняем его местами со вторым
элементом.
И так далее для всех элементов
до n-1-го.
Сортировка
обменом («пузырьковая сортировка»).
Слева
направо поочередно сравниваются два
соседних элемента, и если их
взаиморасположение не соответствует
заданному условию упорядоченности, то
они меняются местами. Далее берутся два
следующих и так далее до конца
массива.
После одного такого прохода
на последней n-ой позиции массива будет
стоять максимальный элемент, поэтому
второй проход обменов выполняется до
n-1-го элемента. И так далее.

Теоретические
и практические исследования алгоритмов
прямых методов сортировки показали,
что как по числу сравнений, так и по
числу присваиваний они имеют квадратичную
зависимость от длины массива п. Исключение
составляет метод выбора, который имеет
число присваиваний порядка n*ln(n).
Это свойство алгоритма выбора полезно
использовать в задачах сортировки в
сложных структурах данных, когда на
одно сравнение выполняется большое
число присваиваний. В таких задачах
метод выбора успешно конкурирует с
самыми быстрыми улучшенными методами
сортировки.
Если сравнить рассмотренные
прямые методы между собой, то в среднем
методы вставки и выбора оказываются
приблизительно эквивалентными и в
несколько раз (в зависимости от длины
массива) лучше, чем метод обмена
(«пузырька»).

Улучшенные
методы сортировки
Ни
один из представленных выше методов
сортировки не является оптимальным.
Обычно алгоритм оптимизируют под
конкретную задачу, например, мы знаем,
что на входе имеется массив, в котором
первые k элементов
упорядочены. Тогда лишено смысла тупо
использовать алгоритм сортировки, так
как имеется возможность его улучшить,
убрав несколько действий. Для нашего
примера используем метод сортировки
выбором. Для наглядности поставим
конкретные условия задачи.
Задан
массив чисел. Первые элементы упорядочены,
последние – нет. Упорядочить весь
массив.

То
есть мы упростили алгоритм, уменьшив
колличество циклов и действий в
нем.
Однако есть и такая оптимизация,
которая подойдет почти
для всех программ.

Например, оптимизируем метод сортировки «пузырьком». Теоритически усовершенствовать алгоритм можно, введя дополнитнльно переменную булевского типа (переменная Iter на рисунке снизу), которая будет показывать, были ли произведены изменения после n-ного прохода. Если нет, то массив уже отсортирован. Если да, то запоминается место последней перестановки (переменная J на рисунке снизу), определяющее границы счетчика (переменная I) при следующем прогоне. Следует заметить, что повторный вход в цикл со счетчиком произойдет только если за предыдущий проход цикла были произведены какие-либо изменения. Таким образом, исключаются дальнейшие бесполезные проходы.

1. Сортировка
   массивов. Метод прямого выбора: общая
   схема алгоритм программа.

Схема

Блок-схема

Текст программы

1. Метод прямого
   обмена: общая схема, алгоритм, программа.

Схема и блок-схема

Текст программы

1. Обработка
   текстовой информации.

В
Паскале при работе с текстовой информацией
существует возможность обработки
одиночных символов типа Char и
последовательности символов — строк
типа String.
Символьный тип. Тип Char — это
один из базовых типов языка, предназначен
для хранения и обработки одного символа.

Множеством
его значений есть отдельные символы
(буквы, цифры, знаки), упорядоченные в
соответствии с расширенным набором
символов ASCII-кода. Переменная этого типа
занимает 1 байт памяти. Благодаря тому
что в памяти машины символы сохраняются
в виде кодов (большим считается тот
символ, чей код больше), их можно
сравнивать. Для символов допустимы все
операции сравнения: <, <=, =,>,> =,
<>.
Описание данных символьного
типа:
Const Name1 = ‘v’; — описание символьной
константы,
Var Name2: CHAR; — описание символьной
переменной.
Как правило, значение для
символьных переменных и констант
задаются в кавычках, например, «f»,
‘1 ‘,’ + ‘. Также можно задать значение,
указав непосредственно числовое значение
ASCII-кода, поставив перед этим числовым
кодом знак #, например, # 35, # 102.
В Паскале
для работы с символьной информацией
реализованы функции преобразования:
CHR (N) — символ с кодом N, ORD (S) — код символа
S. Также применяются функции, определяющие
SUCC (S) — следующий символ, PRED (S) — предыдущий
символ. Для этих функций выполняются
следующие зависимости:
SUCC (S) = CHR (ORD (S)
+1);
PRED (S) = CHR (ORD (S) -1).
Для латинских
букв ‘a’ .. ‘z’ выполняется функция UPCASE (S),
которая переводит эти литеры в верхний
регистр ‘A’ .. ‘Z’.
Строковый тип. Тип
String — тип данных, предназначенный для
хранения и обработки последовательности
символов. Строку можно рассматривать
как особую форму одномерного символьного
массива.
Описание данных строчного
типа:
Const Name1 = ‘computer’; — описание строчной
константы,
Var Name2: STRING; — описание строчной
переменной,
Name3: STRING [20]; — описание
строчной переменной заданной длины,
По
умолчанию длина строчной переменной
равна 255 символам, но можно ограничить
длину строки с помощью явного указания
длины строки.
В Паскале реализовано
обработки строк двумя путями: проработка
строки как единого целого и как объекта,
который создается из отдельных
символов.
Первый путь позволяет:
•
присвоение строчной переменной за одну
операцию целой строки символов, например,
Name2: = ‘computer’; Name3: = ‘science’;
• объединение
строк в произвольном порядке с помощью
операции «+» (операции связывания,
объединения), например,
Name3: = ‘computer’ +
‘science’;
Name3: = Name2 + Name3;
• сравнение строк
с помощью операций сравнения: <, <=,
=,>,> =, <>, например,
If Name3 <> Name2
then write (‘no’);
Второй путь позволяет в
каждый символа строки обращаться за
его номером позиции как к элементу
массива по индексу, например,
Name3: =
Name2 [6] + Name2 [2] + Name2 [4];
Элемент с нулевым
индексом содержит символ, код которого
указывает на действительную длину
данной строки.
В Паскале реализованы
процедуры и функции для обработки строк.
Текущую длину строки S можно узнать с
помощью функции LENGTH (S).
Группа функций
и процедур, направленная на проработку
фрагментов строки:
• функция COPY (S, N,
M) — копирование фрагмента строки S длиной
M, начинается с позиции N;
• функция
POS (S1, S) — поиск фрагмента S1 в строке S
(получаем позицию, с которой начинается
фрагмент S1 в строке S);
• функция CONCAT
(S1, S2, …) — объединение строк S1, S2, …;
•
процедура INSERT (S1, S2, M) — вставка фрагмента
S1 в строку S2 с позиции M;
• процедура
DELETE (S1, N, M) — изъятие части строки S1 длиной
M, начиная с позиции N;
• процедура VAL
(S, N, Code) — преобразование строки цифровых
символов S в число N (параметр Code = 0, если
строка S образован не из цифровых
символов)
• процедура STR (N, S) —
преобразование числа N в строку цифровых
символов S.
Для сортировки символьных
строк (например, по алфавиту) целесообразно
создать массив символьных строк (массив
типа String), что с учетом возможности
использования операций сравнения для
строк, позволит простым способом
применять основные алгоритмы сортировки

1. Записи.

Записи –
это средство описания сложных
структурированных типов данных. В
записях могут содержаться данные
нескольких более простых типов. Хорошим
наглядным примером записи является
информация о контакте в мобильном
телефоне. Каждый контакт имеет такие
поля, как имя, фамилия, номер телефона,
email, фотографию профиля и т.д. Все они
относятся к разным типам, но объединены
в единую структуру.

Формат
описания записей:

TYPE
[имя_записи]
= RECORD
[поле1] : [тип1];
[поле2] :
[тип2];
….
END;
VAR
[экземпляр_записи_1],
[экземпляр_записи_2], …. : [имя_записи];

Обратите
внимание, что записи описываются в
разделе TYPE,
а уже конкретные экземпляры записи
задаются в разделе VAR.

Обращение
к элементам записи в теле программы
происходит путём указания имени
экземпляра записи и через точку –
нужного поля, например:

MyRecord.X
:= 10; { присвоить значение 10 полю X экземпляра
записи MyRecord}

Когда
в программе имеется множество обращений
к одному и тому же экземпляру записи,
существует возможность упростить
обращение в таком виде:

WITH
MyRecord DO BEGIN
{ некоторые
операции
}
END;

Если
операция только одна, то пара BEGIN — END не
нужна.

Пример
описания записи в записной книжке и
обращения к ней в теле программы.

TYPE
ContactRec = RECORD { описываем запись }
Name,
Surname : string[10]; { имя и фамилия, строковый
тип }
HomePhone, MobilePhone : real; { домашний и
мобильный телефоны, вещественный тип
}
Email : string [20]; { email, строковый тип
}
END;

VAR
Contact : ContactRec; { описываем
экземпляр записи }
BEGIN
{…. некоторый
код … }

Write (‘Введите имя контакта:
‘); 
ReadLn(Contact.Name);
{ читаем с клавиатуры значение в поле
ContactName }

{…. некоторый код …}

WITH
Contact DO BEGIN { далее идёт обращение к полям
записи Contact }
if Name = Surname then Write (‘Имя и
фамилия совпадают!’);
if HomePhone = MobilePhone
then Write (‘Домашний и мобильный телефоны
совпадают!);
END;

{…. некоторый код
….}

END.

1. Подпрограммы.
   Процедуры. Функции.

Подпрограмма —
это отдельная функционально независимая
часть программы. Любая подпрограмма
обладает той же структурой, которой
обладает и вся программа. Подпрограммы
решают три важные задачи:

• избавляют
  от необходимости многократно повторять
  в тексте программы аналогичные фрагменты;

• улучшают
  структуру программы, облегчая ее
  понимание;

• повышают
  устойчивость к ошибкам программирования
  и непредвиденным последствиям при
  модификациях программы.

Очень
важно понимать, что в подпрограммы
выделяется любой законченный фрагмент
программы. В качестве ориентиров
просмотрите следующие рекомендации:

1. Когда
   Вы несколько раз перепишите в программе
   одни и те же последовательности команд,
   необходимость введения подпрограммы
   приобретает характер острой внутренней
   потребности.

2. Иногда
   слишком много мелочей закрывают главное.
   Полезно убрать в подпрограмму подробности,
   заслоняющие смысл основной программы.
   Полезно разбить длинную программу на
   составные части — просто как книгу
   разбивают на главы. При этом основная
   программа становится похожей на
   оглавление.

3. Бывают
   сложные частные алгоритмы. Полезно
   отладить их отдельно в небольших
   тестирующих программах. Включение
   программ с отлаженными алгоритмами в
   основную программу будет легким, если
   они оформлены как подпрограммы.

4. Все,
   что Вы сделали хорошо в одной программе,
   Вам захочется перенести в новые. Для
   повторного использования таких частей
   лучше сразу выделять в программе
   полезные алгоритмы в отдельные
   подпрограммы.

Подпрограммы
могут быть стандартными, т.е. определенными
системой, и собственными, т.е. определенными
программистом.

Стандартная
подпрограмма (процедура или функция) —
подпрограмма, включенная в библиотеку
программ ЭВМ, доступ к которой
обеспечивается средствами языка
программирования. Вызывается она по
имени с заданием фактических параметров
с типом описанным при описании данной
процедуры в библиотечке процедур и
функций.

Из
набора стандартных процедур и функций
по обработке одного типа информации
составляются модули. Каждый модуль
имеет своё имя (мы уже хорошо знакомы с
модулями Crt, Graph). Доступ к процедурам и
функциям модуля осуществляется при
подключении этого модуля (Uses Crt, Graph).

Help
содержит подробные описания предусмотренных
средой программирования процедур и
функций. Для вызова помощи при работе
со стандартными процедурами и функциями
нужно поставить на имя подпрограммы
курсор и нажать клавиши .
Описание процедур и функций в Help строится
по стандартному принципу.