Рекурсию не очень просто понять при первом знакомстве, но без ее понимания в разработке будет тяжело. В этом материале рассмотрим:
- Рекурсивную функцию поиска факториала.
- Как рекурсивные функции работают в коде.
- Действительно ли рекурсивные функции выполняют свои задачи лучше итеративных?
Рекурсивные функции
Рекурсивная функция — это та, которая вызывает сама себя.
В качестве простейшего примера рассмотрите следующий код:
def factorial_recursive(n):
if n == 1:
return n
else:
return n*factorial_recursive(n-1)
Вызывая рекурсивную функцию здесь и передавая ей целое число, вы получаете факториал этого числа (n!).
Вкратце о факториалах
Факториал числа — это число, умноженное на каждое предыдущее число вплоть до 1.
Например, факториал числа 7:
7! = 7*6*5*4*3*2*1 = 5040
Вывести факториал числа можно с помощью функции:
num = 3
print(f"Факториал {num} это {factorial_recursive(num)}")
Эта функция выведет: «Факториал 3 это 6». Еще раз рассмотрим эту рекурсивную функцию:
def factorial_recursive(n):
...По аналогии с обычной функцией имя рекурсивной указывается после def, а в скобках обозначается параметр n:
def factorial_recursive(n):
if n == 1:
return n
else:
return n*factorial_recursive(n-1)Благодаря условной конструкции переменная n вернется только в том случае, если ее значение будет равно 1. Это еще называют условием завершения. Рекурсия останавливается в момент удовлетворения условиям.
def factorial_recursive(n):
if n == 1:
return n
else:
return n*factorial_recursive(n-1)В коде выше выделен фрагмент самой рекурсии. В блоке else условной конструкции возвращается произведение n и значения этой же функции с параметром n-1.
Это и есть рекурсия. В нашем примере это так сработало:
3 * (3-1) * ((3-1)-1) # так как 3-1-1 равно 1, рекурсия остановиласьДетали работы рекурсивной функции
Чтобы еще лучше понять, как это работает, разобьем на этапы процесс выполнения функции с параметром 3.
Для этого ниже представим каждый экземпляр с реальными числами. Это поможет «отследить», что происходит при вызове одной функции со значением 3 в качестве аргумента:
# Первый вызов
factorial_recursive(3):
if 3 == 1:
return 3
else:
return 3*factorial_recursive(3-1)
# Второй вызов
factorial_recursive(2):
if 2 == 1:
return 2
else:
return 2*factorial_recursive(2-1)
# Третий вызов
factorial_recursive(1):
if 1 == 1:
return 1
else:
return 1*factorial_recursive(1-1)
Рекурсивная функция не знает ответа для выражения 3*factorial_recursive(3–1), поэтому она добавляет в стек еще один вызов.
Как работает рекурсия
/ factorial_recursive(1) - последний вызов || factorial_recursive(2) - второй вызов || factorial_recursive(3) - первый вызов
Выше показывается, как генерируется стек. Это происходит благодаря процессу LIFO (last in, first out, «последним пришел — первым ушел»). Как вы помните, первые вызовы функции не знают ответа, поэтому они добавляются в стек.
Но как только в стек добавляется вызов factorial_recursive(1), для которого ответ имеется, стек начинает «разворачиваться» в обратном порядке, выполняя все вычисления с реальными значениями. В процессе каждый из слоев выпадает в процессе.
- factorial_recursive(1) завершается, отправляет 1 в
- factorial_recursive(2) и выпадает из стека.
- factorial_recursive(2) завершается, отправляет 2*1 в
- factorial_recursive(3) и выпадает из стека. Наконец, инструкция else здесь завершается, возвращается 3 * 2 = 6, и из стека выпадает последний слой.
Рекурсия в Python имеет ограничение в 3000 слоев.
>>> import sys
>>> sys.getrecursionlimit()
3000
Рекурсивно или итеративно?
Каковы же преимущества рекурсивных функций? Можно ли с помощью итеративных получить тот же результат? Когда лучше использовать одни, а когда — другие?
Важно учитывать временную и пространственную сложности. Рекурсивные функции занимают больше места в памяти по сравнению с итеративными из-за постоянного добавления новых слоев в стек в памяти. Однако их производительность куда выше.
Рекурсия может быть медленной, если реализована неправильно
Тем не менее рекурсия может быть медленной, если ее неправильно реализовать. Из-за этого вычисления будут происходить чаще, чем требуется.
Написание итеративных функций зачастую требуется большего количества кода. Например, дальше пример функции для вычисления факториала, но с итеративным подходом. Выглядит не так изящно, не правда ли?
def factorial_iterative(num):
factorial = 1
if num < 0:
print("Факториал не вычисляется для отрицательных чисел")
else:
for i in range (1, num + 1):
factorial = factorial*i
print(f"Факториал {num} это {factorial}")
В этом руководстве мы поговорим о различных аспектах рекурсивных функций и реализуем рекурсивные функции в Python с нуля.
Будучи профессиональным программистом, вы должны отлично разбираться в таких базовых вещах, как переменные, условные операторы, типы данных, спецификаторы доступа, вызовы функций, области видимости и т.д. Эти знания нужны как тем, кто пишет промежуточное ПО, так и веб-разработчикам. Это основы, которые должен знать каждый.
Одной из таких фундаментальных концепций является рекурсия, и ее невероятно важно знать при написании функций определенного типа.
Возможно, вы уже знаете, что «рекурсия — это когда функция вызывает сама себя». Но что происходит под капотом? Как рекурсия влияет на физическую память? Можете ли вы превратить любую другую функцию в рекурсивную? В нашей статье вы найдете ответы на эти фундаментальные вопросы.
В частности, мы рассмотрим следующие темы:
- Базовая анатомия рекурсивной функции
- Представление памяти рекурсивной функции:
- Дерево
- Стек
- Отслеживание рекурсии
- Пространственно-временной анализ рекурсивной функции
- Реализация простой рекурсивной функции в Python
Анатомия рекурсивной функции
Вероятно, сам термин «рекурсия» вам уже знаком. Сейчас мы рассмотрим эту концепцию еще раз, но более увлекательно, чем в учебнике.
Вернемся к определению рекурсии: «Рекурсия – это функция, которая вызывает сама себя». Давайте рассмотрим пример, подтверждающий это определение:
void A(n){
if(n>=1){
A(n-1);
print(n);
}
}
Вы можете видеть, что функция A() вызывает сама себя. Это пример рекурсии, где A() — рекурсивная функция.
Давайте теперь изучим некоторые основные совйства рекурсивной функции.
Основные принципы работы рекурсивной функции
Рекурсивная функция должна иметь следующие два свойства:
- Рекуррентное отношение
- Условие прекращения
Рассмотрим приведенный выше фрагмент кода, чтобы понять эти моменты. Ясно, что функция представляет собой конкретное рекуррентное соотношение:
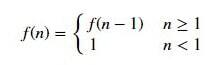
n ≤ 1 — условие завершения, или условие привязки, или базовое условие. Когда оно выполняется, рекурсия останавливается. Указание этого условия является обязательным. В противном случае функция попадет в бесконечный цикл и будет выполняться непрерывно, чего нам не очень хочется.
Обратите внимание, что приведенный выше фрагмент кода не соответствует какому-либо конкретному языку программирования. Основная цель здесь — показать пример рекурсивной функции.
Вы, должно быть, сейчас думаете, зачем вообще писать рекурсивную функцию, если есть лучшие альтернативы? Да, отследить рекурсию иногда бывает сложно, но, освоив эту тему, вы обнаружите, что рекурсия прекрасна с точки зрения читабельности программы и переменных.
Для выполнения рекурсии не нужны дополнительные переменные, однако для остановки требуется правильное условие завершения. Найти его часто бывает непросто. Опять же, здесь вам поможет только практика!
Далее в этом руководстве мы посмотрим, насколько красивой и маленькой может быть программа, если она реализована с помощью рекурсии. Теперь давайте перейдем к представлению памяти рекурсивной функции.
Представление памяти рекурсивной функции
В этом разделе мы изучим, как рекурсивные функции представляются в памяти с помощью деревьев и стеков.
Рассмотрим уже знакомую нам рекурсивную функцию A():
void A(n){
if(n>=1){
A(n-1);
print(n);
}
}
Итак, давайте начнем с представления памяти с помощью деревьев. Это может показаться немного сложным, но на самом деле нужно просто разобраться. Если бы вы записывали каждый вызов функции в виде дерева, как бы это выглядело?
Дерево

Здесь следует отметить пару моментов:
- Функция вызывается с параметром
A(3)и поэтому здесь выполняются 4 (= 3 + 1) вызова функций. Если обобщить, то при вызовеA(n)потребуется всего(n+1)вызовов функции. - Вызовы
P()— это выводы, созданные функциейprint(n). - Функция
A(0)приведет к невыполнению условияif, так как мы получимn < 1, что, в свою очередь, приведет к завершению работы рекурсивной функции.
Мы начали именно с древовидного представления, потому что оно необходимо для представления рекурсивной функции в стеке. Вы увидите это сейчас.
Стек
Стек — структура данных, организованных по принципу LIFO (англ. last in — first out, «последним пришел — первым ушел»).
От редакции Pythonist. О стеке можно почитать в статье «Реализация стека на Python».
Для представления стека вам придется пройти по дереву сверху вниз и слева направо. Следующее изображение прояснит это.
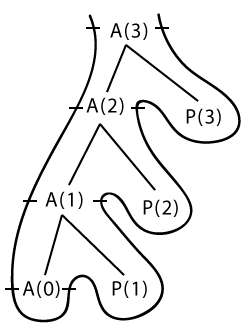
Интерпретация этого странного дерева
Имейте в виду, что стек состоит из двух операций:
- push используется для вставки элемента в стек
- pop — для извлечения элемента из стека.
Мы начинаем обход дерева в порядке сверху вниз и слева направо:
- встречая вызов функции, вы помещаете его в стек
- встречая вызов
print()(т.е.P()), вы просто печатаете соответствующий элемент
Результатом обхода дерева от A(3) до A(0) будут следующие элементы стека (в перевернутом виде):
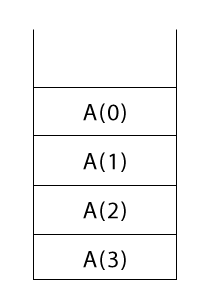
Теперь вы начинаете вторую половину обхода дерева, т. е. слева направо. Встречая вызов функции во второй раз, вы его удаляете (pop). Удивительно, но первым будет удален тот элемент стека, который последним попал в стек (LIFO, помните?).
Также на своем пути вы столкнетесь с тремя вызовами P(): P(1), P(2) и P(3). Вы выведете их на экран в том порядке, в котором они появляются на пути вашего обхода:
1 2 3
Наконец, когда вы закончите процесс обхода, стек будет полностью пуст.

Вы увидели, как представить простую рекурсивную функцию в памяти, используя дерево и стек. Теперь давайте посмотрим, как отслеживать рекурсию.
Отслеживание рекурсии
В этом разделе мы прежде всего рассмотрим, как методично отслеживать рекурсию. Возьмем в качестве примера следующую рекурсивную функцию:
void A(n){
if(n>=1){
A(n-1);
print(n);
}
}
Важный момент: при каждом вызове функции в памяти создается запись активации, содержащая локальные переменные этой функции и указатель инструкции. Указатель обозначает следующую задачу, которая должна быть выполнена, когда вызов возвращается к этой функции.
К примеру, функция с именем main() вызвала указанную выше функцию A() как A(3). Давайте пронумеруем строки A() из оператора if для лучшего понимания:
void A(n){
1. if(n>0)
2. {
3. print(n-1);
4. A(n-1);
5. }
}
Записи активации будут выглядеть следующим образом:
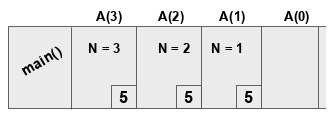
Как упоминалось ранее, функции имеют свои копии локальных переменных и указатели инструкций (в данном случае — номера строк). После того, как A(0) завершит работу, функция произведет выталкивание (pop). Обратите внимание, что здесь используется горизонтальный стек — точно такой же, как те, которые вы видели ранее в уроке. Кроме того, пока записи помещаются в стек, также будет выполняться печать, и будут напечатаны следующие элементы:
2 1 0
Здесь важно отметить указатели инструкций, потому что часто в рекурсивной функции управление переходит к той же функции, но с другим значением переменной. Указатели помогают поддерживать синхронизацию. Вы можете следовать этому же процессу, чтобы отследить рекурсию, используя представление в виде дерева.
Итак, а теперь давайте разберем, как выполнять пространственно-временной анализ рекурсивной функции.
Пространственно-временной анализ рекурсивной функции
Давайте быстро вспомним, что подразумевается под пространственным и временным анализом функции (также известными как пространственная и временная сложность).
Предполагается, что для заданного ввода функция должна производить некоторый вывод. Однако сколько времени для этого потребуется функции? Временная сложность — показатель приблизительного времени (также употребляется термин «время выполнения» функции). Аналогично, пространственная сложность — приблизительные требования к пространству (памяти) для функции (при заданных входных данных). Но зачем вообще нужны эти показатели?
Зная временную и пространственную сложность функции, вы можете легко прикинуть, как она может вести себя при входных данных разного размера. Вам не придется проверять это вручную.
Если у вас есть две функции, выполняющие одну и ту же задачу, какую из них выбрать? Какие метрики вы рассмотрите, чтобы принять решение? Да, вы правильно угадали. Вы сравните эти функции, проанализировав их пространственно-временную сложность, и выберете ту, которая работает лучше и эффективнее.
Давайте теперь возьмем простую рекурсивную функцию и проанализируем ее пространственную и временную сложность.
void A(n){
if(n>1) // Anchor condition
{
return A(n-1);
}
}
Временная сложность
Прежде всего проведем анализ временной сложности. Предположим, что общее время, затраченное на вышеуказанную функцию A(), равно T(n).
T(n) представляет собой сумму времени, затраченного на сравнение, действительно ли n больше 1, и времени, затраченного на выполнение A(n-1).
T(n) можно выразить так:
Т (n) = 1 + Т (n-1),
где 1 — время, затраченное на сравнение (туда можно поставить любую константу).
Каково будет время (T(n)) для выполнения A(n-1)?
Т(n−1) = 1 + T(n−2)
Аналогично,
T(n−2) = 1 + T(n−3) и так далее.
Если внимательно отнестись к уравнениям, то можно заметить, что все они связаны. Не так ли? Если вы подставите их друг в друга, вы получите
T(n) = 1 + (1 + T(n−2)) = 2 + T(n−2) = 3 + T(n−3) = .... = k + T(n−k) ( после запуска функции k раз)
Теперь вам нужно определить, в какой момент функция остановится. В соответствии с заданным условием мы можем написать:

Предположим, что после выполнения k раз функция перестает выполняться. Если так, то должно быть:
n − k = 1 => k = n − 1
Теперь подставим значение k (= n-1) в нашу формулу T(n) = k + T(n−k):
Т(n) = (n-1) + Т(n-(n-1))
=> Т (n) = (n-1) + T(1)
=> T(n) = n−1 + 1 = n // Для T(1) требуется только сравнение.
По правилу асимптотического анализа T(n) = n можно переписать как T(n) = O(n). Это означает, что временная сложность функции (при наихудшем случае) равна O(n).
Здесь вы можете немного притормозить и внимательно понаблюдать за каждым шагом этого процесса. Настоятельно рекомендуется делать это на бумаге, чтобы понять все до мельчайших деталей.
Пространственная сложность
Анализ пространственной сложности функции прост. Эта функция находится в памяти и не использует никаких дополнительных переменных. Поэтому можно сделать вывод, что пространственная сложность функции O(n).
Теперь давайте соберем все это вместе и реализуем простую рекурсивную функцию на Python.
Сейчас мы напишем рекурсивную функцию для нахождения факториала заданного числа. Затем мы напишем итеративную версию той же функции. Итак, давайте начинать:
# Рекурсивная функция factorial_recursion()
def factorial_recursion(n):
if n == 1:
return n
else:
return n*factorial_recursion(n-1)
# Вызов функции
num = 7
print("The factorial of ",num," is ",factorial_recursion(num))
# Output:
# The factorial of 7 is 5040
Помните два ключевых момента для написания рекурсивной функции?
- Рекуррентное отношение
- Условие прекращения
В этом случае рекуррентное соотношение может быть следующим:
f(n) = n!
f(n) = n ∗ f(n−1) и так далее.
Условие завершения — когда n равно 1.
Просто, верно?
Теперь давайте реализуем итеративную версию той же функции.
def factorial_iterative(num):
factorial = 1
if num < 0:
print("Sorry, factorial does not exist for negative numbers")
elif num == 0:
print("The factorial of 0 is 1")
else:
for i in range(1,num + 1):
factorial = factorial*i
print("The factorial of",num,"is",factorial)
factorial_iterative(7)
# Output:
# The factorial of 7 is 5040
Вы можете четко заметить разницу между двумя версиями. Рекурсивная намного красивее итеративной, не так ли?
Заключение
Вы дошли до конца. Поздравляем! В этом руководстве мы подробно разрбрали рекурсивные функции в Python. Начиная с абсолютных основ и заканчивая анализом пространственной и временной сложностей рекурсивной функции, мы охватили все. Более того, мы увидели, как рекурсия может быть полезна для решения определенных задач. Теперь вы должны быть в состоянии решать задачи, используя рекурсию. Возможно, вам будет интересно решить задачу поиска чисел Фибоначчи в заданном диапазоне.
Кроме того, стоит обратить внимание на решение некоторых распространенных задач, таких как двоичный поиск, сортировка слиянием, Ханойская башня и т.д. при помощи рекурсии. Это, безусловно, сделает вас более подкованным программистом.
Надеемся, данная статья была вам полезна! Успехов в написании кода!
Перевод статьи «Understanding Recursive Functions in Python».
Рассмотрим задачу получения факториала числа. В математике он обозначается «!» и функция факториала описывается так:
- 0! = 1.
- n! = 1 * 2 * … * n, n > 0.
Напишем функцию, вычисляющую факториал числа n.
def fact(n):
factorial = 1
for i in range(2, n + 1):
factorial *= i
return factorial
print(fact(5))
Давайте немного перепишем определение факториала:
- 0! = 1.
- n! = (1 * 2 * … * (n — 1)) *n = (n — 1)! * n
Мы видим, что для вычисления n! нам нужно найти (n - 1)! и умножить результат на n. Таким образом, мы используем функцию для вычисления нового значения функции. Функции, в которых происходит вызов самих этих функций называют рекурсивными.
Давайте напишем рекурсивную функцию для вычисления факториала. При создании рекурсивных функций необходимо:
- Написать, что вернёт функция при начальном значении аргумента.
- Написать правило получения нового значения на основе уже вычисленных на предыдущих шагах.
def fact(n):
if n == 0: # 0! = 1
return 1
return fact(n - 1) * n # n! = (n - 1)! * n
print(fact(5))
Вывод программы:
120
Обратите внимание, что рекурсивный вариант функции выполняет действия, которые описаны правилом вычисления факториала. Такой стиль программирования называется декларативным. Данный подход описывает сам результат. Функции, которые мы писали ранее, основаны на императивном стиле, и отвечают на вопрос о способе получения результата.
Рассмотрим применение рекурсивной функции для вычисления n-го числа последовательности Фибоначчи. Числа Фибоначчи — последовательность чисел, вычисляемых по следующему правилу:
- Первые два числа последовательности равны 1.
- n-ое число Фибоначчи равно сумме двух предыдущих, то есть fib(n) = fib(n — 1) + fib(n — 2).
Программа с рекурсивной функцией вычисления n-го числа Фибоначчи запишется так:
def fib(n):
if n in (0, 1):
return 1
return fib(n - 1) + fib(n - 2)
print(fib(35))
Вывод программы:
14930352
При запуске программы, можно заметить, что вычисление 35-го числа последовательности происходит с небольшой задержкой. Проверим, сколько времени занимают вычисления. Выполним вычисления 10 раз и выведем среднее время вычисления с точностью 1 мс. В тестировании скорости работы кода нам помогает стандартный модуль timeit.
from timeit import timeit
def fib(n):
if n in (0, 1):
return 1
return fib(n - 1) + fib(n - 2)
print(f"Среднее время вычисления: "
f"{round(timeit('fib(35)', number=10, globals=globals()) / 10, 3)} с.")
Вывод программы:
Среднее время вычисления: 2.924 с.
Проверим, сколько времени займут те же вычисления у императивной версии функции.
from timeit import timeit
def fib(n):
f_1, f = 1, 1
for i in range(n - 1):
f_1, f = f, f_1 + f
return f
print(f"Среднее время вычисления: "
f"{round(timeit('fib(35)', number=10, globals=globals()) / 10, 3)} с.")
Вывод программы:
Среднее время вычисления: 2e-06 с.
Получили результат 2 микросекунды у императивной функции против почти 3 секунд у рекурсивной. В чём же причина?
Проблема рекурсивной функции заключается в том, что внутри неё происходит два вызова самой себя для каждого значения. И так до тех пор, пока не функция не дойдет до начальных значений аргументов (1 и 1). В итоге появляется несколько рекурсивных веток, которые образуют рекурсивное дерево. Покажем его часть на рисунке.
Числа на схеме показывают номер числа Фибоначчи. Цветом показаны числа с одинаковым номером. Из схемы дерева становится понятно, что рекурсивная реализация функции выполняет много одинаковых вычислений. Давайте добавим счётчик количества вызовов нашей рекурсивной функции:
def fib(n):
global count
count += 1
if n in (0, 1):
return 1
return fib(n - 1) + fib(n - 2)
count = 0
print(f"35-ое число Фибоначчи равно: {fib(35)}.")
print(f"Количество вызовов рекурсивной функции равно: {count}.")
Вывод программы:
35-ое число Фибоначчи равно: 14930352. Количество вызовов рекурсивной функции равно: 29860703.
Для ускорения вычислений нужно запоминать уже посчитанные числа последовательности, а затем использовать их при необходимости. Такой подход называют кэшированием или мемоизацией.
Напишем рекурсивную функцию с кэшированием, использовав для сохранения вычисленных значений словарь, в котором ключами будут номера чисел последовательности, а значения — сами числа.
def fib(n):
global count
count += 1
if n not in cash:
cash[n] = fib(n - 1) + fib(n - 2)
return cash[n]
count = 0
cash = {0: 1, 1: 1}
print(f"35-ое число Фибоначчи равно: {fib(35)}.")
print(f"Количество вызовов рекурсивной функции равно: {count}.")
Вывод программы:
35-ое число Фибоначчи равно: 14930352. Количество вызовов рекурсивной функции равно: 69.
За счет кэширования количество вызовов рекурсивной функции существенно сократилось. Проверим скорость работы нашей функции.
from timeit import timeit
def fib(n):
global count
count += 1
if n not in cash:
cash[n] = fib(n - 1) + fib(n - 2)
return cash[n]
count = 0
cash = {0: 1, 1: 1}
print(f"Среднее время вычисления: "
f"{round(timeit('fib(35)', number=10, globals=globals()) / 10, 6)} с.")
Вывод программы:
Среднее время вычисления: 2e-06 с.
Скорость работы также существенно увеличилась. Попробуем вычислить число Фибоначчи с номером 1000:
from timeit import timeit
def fib(n):
if n not in cash:
cash[n] = fib(n - 1) + fib(n - 2)
return cash[n]
cash = {0: 1, 1: 1}
print(f"Среднее время вычисления: "
f"{round(timeit('fib(1000)', number=10, globals=globals()) / 10, 6)} с.")
Вывод программы:
RecursionError: maximum recursion depth exceeded
Программа выдала ошибку по превышению глубины рекурсии. В Python по умолчанию максимальный размер глубины рекурсии равен 1000. Для изменения глубины рекурсии для вашей программы нужно вызвать функцию setrecursionlimit() из стандартного модуля sys и передать новое значение для предела глубины.
from timeit import timeit
from sys import setrecursionlimit
def fib(n):
if n not in cash:
cash[n] = fib(n - 1) + fib(n - 2)
return cash[n]
setrecursionlimit(2000)
cash = {0: 1, 1: 1}
print(f"Среднее время вычисления: "
f"{round(timeit('fib(1000)', number=10, globals=globals()) / 10, 6)} с.")
Вывод программы:
Среднее время вычисления: 0.000132 с.
Обратите внимание: максимально возможное значение глубины рекурсии зависит от операционной системы. Поэтому бесконечно его увеличивать не получится.
Итак, наша рекурсивная функция с кэшированием стала работать быстро. Однако есть и недостаток: её код стал читаться сложнее. Поручим процесс запоминания промежуточных значений функции интерпретатору. Для этого в Python в стандартном модуле functools есть функция lru_cache. Её следует использовать так, как показано в следующем примере:
from timeit import timeit
from functools import lru_cache
@lru_cache(maxsize=1000)
def fib(n):
if n in (0, 1):
return 1
return fib(n - 1) + fib(n - 2)
print(f"Среднее время вычисления: "
f"{round(timeit('fib(35)', number=10, globals=globals()) / 10, 6)} с.")
Вывод программы:
Среднее время вычисления: 2e-06 с.
Благодаря автоматическому кэшированию, наша функция снова приобрела «декларативный» вид и при этом работает быстро.
Ещё по теме
Функция lru_cache в примере используется как декоратор. Подробнее о них можно почитать в этом материале
If you’re familiar with functions in Python, then you know that it’s quite common for one function to call another. In Python, it’s also possible for a function to call itself! A function that calls itself is said to be recursive, and the technique of employing a recursive function is called recursion.
It may seem peculiar for a function to call itself, but many types of programming problems are best expressed recursively. When you bump up against such a problem, recursion is an indispensable tool for you to have in your toolkit.
By the end of this tutorial, you’ll understand:
- What it means for a function to call itself recursively
- How the design of Python functions supports recursion
- What factors to consider when choosing whether or not to solve a problem recursively
- How to implement a recursive function in Python
Then you’ll study several Python programming problems that use recursion and contrast the recursive solution with a comparable non-recursive one.
What Is Recursion?
The word recursion comes from the Latin word recurrere, meaning to run or hasten back, return, revert, or recur. Here are some online definitions of recursion:
- Dictionary.com: The act or process of returning or running back
- Wiktionary: The act of defining an object (usually a function) in terms of that object itself
- The Free Dictionary: A method of defining a sequence of objects, such as an expression, function, or set, where some number of initial objects are given and each successive object is defined in terms of the preceding objects
A recursive definition is one in which the defined term appears in the definition itself. Self-referential situations often crop up in real life, even if they aren’t immediately recognizable as such. For example, suppose you wanted to describe the set of people that make up your ancestors. You could describe them this way:
Notice how the concept that is being defined, ancestors, shows up in its own definition. This is a recursive definition.
In programming, recursion has a very precise meaning. It refers to a coding technique in which a function calls itself.
Why Use Recursion?
Most programming problems are solvable without recursion. So, strictly speaking, recursion usually isn’t necessary.
However, some situations particularly lend themselves to a self-referential definition—for example, the definition of ancestors shown above. If you were devising an algorithm to handle such a case programmatically, a recursive solution would likely be cleaner and more concise.
Traversal of tree-like data structures is another good example. Because these are nested structures, they readily fit a recursive definition. A non-recursive algorithm to walk through a nested structure is likely to be somewhat clunky, while a recursive solution will be relatively elegant. An example of this appears later in this tutorial.
On the other hand, recursion isn’t for every situation. Here are some other factors to consider:
- For some problems, a recursive solution, though possible, will be awkward rather than elegant.
- Recursive implementations often consume more memory than non-recursive ones.
- In some cases, using recursion may result in slower execution time.
Typically, the readability of the code will be the biggest determining factor. But it depends on the circumstances. The examples presented below should help you get a feel for when you should choose recursion.
Recursion in Python
When you call a function in Python, the interpreter creates a new local namespace so that names defined within that function don’t collide with identical names defined elsewhere. One function can call another, and even if they both define objects with the same name, it all works out fine because those objects exist in separate namespaces.
The same holds true if multiple instances of the same function are running concurrently. For example, consider the following definition:
def function():
x = 10
function()
When function() executes the first time, Python creates a namespace and assigns x the value 10 in that namespace. Then function() calls itself recursively. The second time function() runs, the interpreter creates a second namespace and assigns 10 to x there as well. These two instances of the name x are distinct from each another and can coexist without clashing because they are in separate namespaces.
Unfortunately, running function() as it stands produces a result that is less than inspiring, as the following traceback shows:
>>>
>>> function()
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
File "<stdin>", line 3, in function
File "<stdin>", line 3, in function
File "<stdin>", line 3, in function
[Previous line repeated 996 more times]
RecursionError: maximum recursion depth exceeded
As written, function() would in theory go on forever, calling itself over and over without any of the calls ever returning. In practice, of course, nothing is truly forever. Your computer only has so much memory, and it would run out eventually.
Python doesn’t allow that to happen. The interpreter limits the maximum number of times a function can call itself recursively, and when it reaches that limit, it raises a RecursionError exception, as you see above.
There isn’t much use for a function to indiscriminately call itself recursively without end. It’s reminiscent of the instructions that you sometimes find on shampoo bottles: “Lather, rinse, repeat.” If you were to follow these instructions literally, you’d shampoo your hair forever!
This logical flaw has evidently occurred to some shampoo manufacturers, because some shampoo bottles instead say “Lather, rinse, repeat as necessary.” That provides a termination condition to the instructions. Presumably, you’ll eventually feel your hair is sufficiently clean to consider additional repetitions unnecessary. Shampooing can then stop.
Similarly, a function that calls itself recursively must have a plan to eventually stop. Recursive functions typically follow this pattern:
- There are one or more base cases that are directly solvable without the need for further recursion.
- Each recursive call moves the solution progressively closer to a base case.
You’re now ready to see how this works with some examples.
Get Started: Count Down to Zero
The first example is a function called countdown(), which takes a positive number as an argument and prints the numbers from the specified argument down to zero:
>>>
>>> def countdown(n):
... print(n)
... if n == 0:
... return # Terminate recursion
... else:
... countdown(n - 1) # Recursive call
...
>>> countdown(5)
5
4
3
2
1
0
Notice how countdown() fits the paradigm for a recursive algorithm described above:
- The base case occurs when
nis zero, at which point recursion stops. - In the recursive call, the argument is one less than the current value of
n, so each recursion moves closer to the base case.
The version of countdown() shown above clearly highlights the base case and the recursive call, but there’s a more concise way to express it:
def countdown(n):
print(n)
if n > 0:
countdown(n - 1)
Here’s one possible non-recursive implementation for comparison:
>>>
>>> def countdown(n):
... while n >= 0:
... print(n)
... n -= 1
...
>>> countdown(5)
5
4
3
2
1
0
This is a case where the non-recursive solution is at least as clear and intuitive as the recursive one, and probably more so.
Calculate Factorial
The next example involves the mathematical concept of factorial. The factorial of a positive integer n, denoted as n!, is defined as follows:
In other words, n! is the product of all integers from 1 to n, inclusive.
Factorial so lends itself to recursive definition that programming texts nearly always include it as one of the first examples. You can express the definition of n! recursively like this:
As with the example shown above, there are base cases that are solvable without recursion. The more complicated cases are reductive, meaning that they reduce to one of the base cases:
- The base cases (n = 0 or n = 1) are solvable without recursion.
- For values of n greater than 1, n! is defined in terms of (n — 1)!, so the recursive solution progressively approaches the base case.
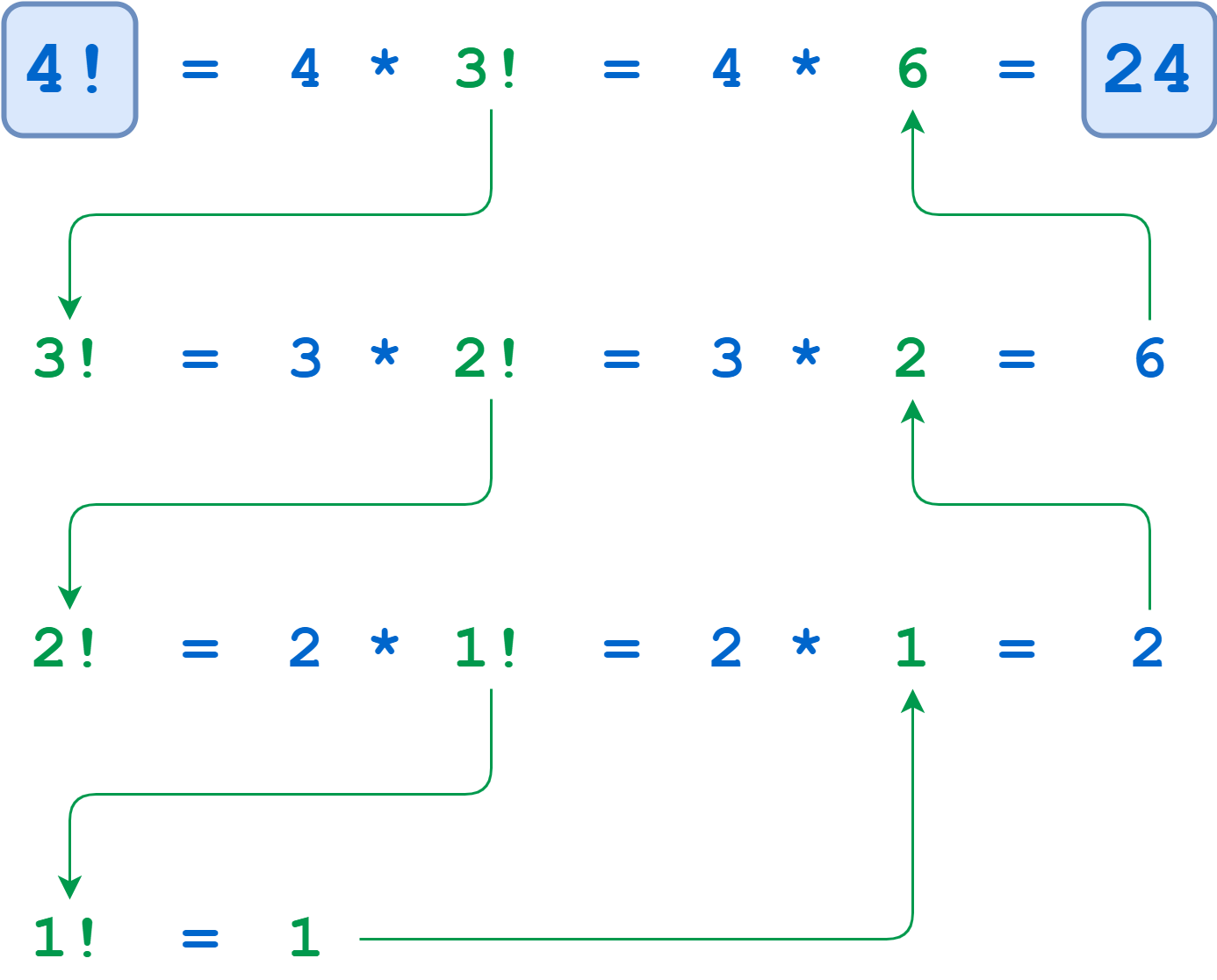
For example, recursive computation of 4! looks like this:
The calculations of 4!, 3!, and 2! suspend until the algorithm reaches the base case where n = 1. At that point, 1! is computable without further recursion, and the deferred calculations run to completion.
Define a Python Factorial Function
Here’s a recursive Python function to calculate factorial. Note how concise it is and how well it mirrors the definition shown above:
>>>
>>> def factorial(n):
... return 1 if n <= 1 else n * factorial(n - 1)
...
>>> factorial(4)
24
A little embellishment of this function with some print() statements gives a clearer idea of the call and return sequence:
>>>
>>> def factorial(n):
... print(f"factorial() called with n = {n}")
... return_value = 1 if n <= 1 else n * factorial(n -1)
... print(f"-> factorial({n}) returns {return_value}")
... return return_value
...
>>> factorial(4)
factorial() called with n = 4
factorial() called with n = 3
factorial() called with n = 2
factorial() called with n = 1
-> factorial(1) returns 1
-> factorial(2) returns 2
-> factorial(3) returns 6
-> factorial(4) returns 24
24
Notice how all the recursive calls stack up. The function gets called with n = 4, 3, 2, and 1 in succession before any of the calls return. Finally, when n is 1, the problem can be solved without any more recursion. Then each of the stacked-up recursive calls unwinds back out, returning 1, 2, 6, and finally 24 from the outermost call.
Recursion isn’t necessary here. You could implement factorial() iteratively using a for loop:
>>>
>>> def factorial(n):
... return_value = 1
... for i in range(2, n + 1):
... return_value *= i
... return return_value
...
>>> factorial(4)
24
You can also implement factorial using Python’s reduce(), which you can import from the functools module:
>>>
>>> from functools import reduce
>>> def factorial(n):
... return reduce(lambda x, y: x * y, range(1, n + 1) or [1])
...
>>> factorial(4)
24
Again, this shows that if a problem is solvable with recursion, there will also likely be several viable non-recursive solutions as well. You’ll typically choose based on which one results in the most readable and intuitive code.
Another factor to take into consideration is execution speed. There can be significant performance differences between recursive and non-recursive solutions. In the next section, you’ll explore these differences a little further.
Speed Comparison of Factorial Implementations
To evaluate execution time, you can use a function called timeit() from a module that is also called timeit. This function supports a number of different formats, but you’ll use the following format in this tutorial:
timeit(<command>, setup=<setup_string>, number=<iterations>)
timeit() first executes the commands contained in the specified <setup_string>. Then it executes <command> the given number of <iterations> and reports the cumulative execution time in seconds:
>>>
>>> from timeit import timeit
>>> timeit("print(string)", setup="string='foobar'", number=100)
foobar
foobar
foobar
.
. [100 repetitions]
.
foobar
0.03347089999988384
Here, the setup parameter assigns string the value 'foobar'. Then timeit() prints string one hundred times. The total execution time is just over 3/100 of a second.
The examples shown below use timeit() to compare the recursive, iterative, and reduce() implementations of factorial from above. In each case, setup_string contains a setup string that defines the relevant factorial() function. timeit() then executes factorial(4) a total of ten million times and reports the aggregate execution.
First, here’s the recursive version:
>>>
>>> setup_string = """
... print("Recursive:")
... def factorial(n):
... return 1 if n <= 1 else n * factorial(n - 1)
... """
>>> from timeit import timeit
>>> timeit("factorial(4)", setup=setup_string, number=10000000)
Recursive:
4.957105500000125
Next up is the iterative implementation:
>>>
>>> setup_string = """
... print("Iterative:")
... def factorial(n):
... return_value = 1
... for i in range(2, n + 1):
... return_value *= i
... return return_value
... """
>>> from timeit import timeit
>>> timeit("factorial(4)", setup=setup_string, number=10000000)
Iterative:
3.733752099999947
Last, here’s the version that uses reduce():
>>>
>>> setup_string = """
... from functools import reduce
... print("reduce():")
... def factorial(n):
... return reduce(lambda x, y: x * y, range(1, n + 1) or [1])
... """
>>> from timeit import timeit
>>> timeit("factorial(4)", setup=setup_string, number=10000000)
reduce():
8.101526299999932
In this case, the iterative implementation is the fastest, although the recursive solution isn’t far behind. The method using reduce() is the slowest. Your mileage will probably vary if you try these examples on your own machine. You certainly won’t get the same times, and you may not even get the same ranking.
Does it matter? There’s a difference of almost four seconds in execution time between the iterative implementation and the one that uses reduce(), but it took ten million calls to see it.
If you’ll be calling a function many times, you might need to take execution speed into account when choosing an implementation. On the other hand, if the function will run relatively infrequently, then the difference in execution times will probably be negligible. In that case, you’d be better off choosing the implementation that seems to express the solution to the problem most clearly.
For factorial, the timings recorded above suggest a recursive implementation is a reasonable choice.
Frankly, if you’re coding in Python, you don’t need to implement a factorial function at all. It’s already available in the standard math module:
>>>
>>> from math import factorial
>>> factorial(4)
24
Perhaps it might interest you to know how this performs in the timing test:
>>>
>>> setup_string = "from math import factorial"
>>> from timeit import timeit
>>> timeit("factorial(4)", setup=setup_string, number=10000000)
0.3724050999999946
Wow! math.factorial() performs better than the best of the other three implementations shown above by roughly a factor of 10.
A function implemented in C will virtually always be faster than a corresponding function implemented in pure Python.
Traverse a Nested List
The next example involves visiting each item in a nested list structure. Consider the following Python list:
names = [
"Adam",
[
"Bob",
[
"Chet",
"Cat",
],
"Barb",
"Bert"
],
"Alex",
[
"Bea",
"Bill"
],
"Ann"
]
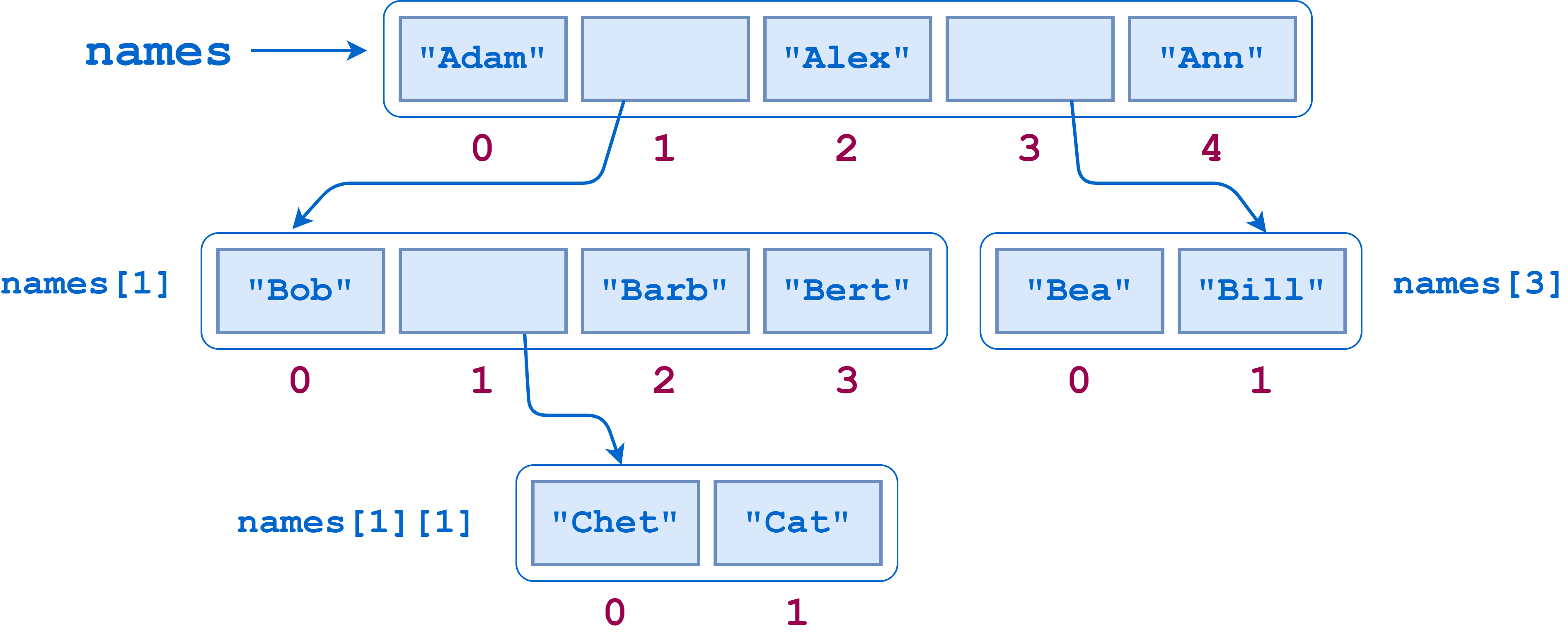
As the following diagram shows, names contains two sublists. The first of these sublists itself contains another sublist:
Suppose you wanted to count the number of leaf elements in this list—the lowest-level str objects—as though you’d flattened out the list. The leaf elements are "Adam", "Bob", "Chet", "Cat", "Barb", "Bert", "Alex", "Bea", "Bill", and "Ann", so the answer should be 10.
Just calling len() on the list doesn’t give the correct answer:
len() counts the objects at the top level of names, which are the three leaf elements "Adam", "Alex", and "Ann" and two sublists ["Bob", ["Chet", "Cat"], "Barb", "Bert"] and ["Bea", "Bill"]:
>>>
>>> for index, item in enumerate(names):
... print(index, item)
...
0 Adam
1 ['Bob', ['Chet', 'Cat'], 'Barb', 'Bert']
2 Alex
3 ['Bea', 'Bill']
4 Ann
What you need here is a function that traverses the entire list structure, sublists included. The algorithm goes something like this:
- Walk through the list, examining each item in turn.
- If you find a leaf element, then add it to the accumulated count.
- If you encounter a sublist, then do the following:
- Drop down into that sublist and similarly walk through it.
- Once you’ve exhausted the sublist, go back up, add the elements from the sublist to the accumulated count, and resume the walk through the parent list where you left off.
Note the self-referential nature of this description: Walk through the list. If you encounter a sublist, then similarly walk through that list. This situation begs for recursion!
Traverse a Nested List Recursively
Recursion fits this problem very nicely. To solve it, you need to be able to determine whether a given list item is leaf item or not. For that, you can use the built-in Python function isinstance().
In the case of the names list, if an item is an instance of type list, then it’s a sublist. Otherwise, it’s a leaf item:
>>>
>>> names
['Adam', ['Bob', ['Chet', 'Cat'], 'Barb', 'Bert'], 'Alex', ['Bea', 'Bill'], 'Ann']
>>> names[0]
'Adam'
>>> isinstance(names[0], list)
False
>>> names[1]
['Bob', ['Chet', 'Cat'], 'Barb', 'Bert']
>>> isinstance(names[1], list)
True
>>> names[1][1]
['Chet', 'Cat']
>>> isinstance(names[1][1], list)
True
>>> names[1][1][0]
'Chet'
>>> isinstance(names[1][1][0], list)
False
Now you have the tools in place to implement a function that counts leaf elements in a list, accounting for sublists recursively:
def count_leaf_items(item_list):
"""Recursively counts and returns the
number of leaf items in a (potentially
nested) list.
"""
count = 0
for item in item_list:
if isinstance(item, list):
count += count_leaf_items(item)
else:
count += 1
return count
If you run count_leaf_items() on several lists, including the names list defined above, you get this:
>>>
>>> count_leaf_items([1, 2, 3, 4])
4
>>> count_leaf_items([1, [2.1, 2.2], 3])
4
>>> count_leaf_items([])
0
>>> count_leaf_items(names)
10
>>> # Success!
As with the factorial example, adding some print() statements helps to demonstrate the sequence of recursive calls and return values:
1def count_leaf_items(item_list):
2 """Recursively counts and returns the
3 number of leaf items in a (potentially
4 nested) list.
5 """
6 print(f"List: {item_list}")
7 count = 0
8 for item in item_list:
9 if isinstance(item, list):
10 print("Encountered sublist")
11 count += count_leaf_items(item)
12 else:
13 print(f"Counted leaf item "{item}"")
14 count += 1
15
16 print(f"-> Returning count {count}")
17 return count
Here’s a synopsis of what’s happening in the example above:
- Line 9:
isinstance(item, list)isTrue, socount_leaf_items()has found a sublist. - Line 11: The function calls itself recursively to count the items in the sublist, then adds the result to the accumulating total.
- Line 12:
isinstance(item, list)isFalse, socount_leaf_items()has encountered a leaf item. - Line 14: The function increments the accumulating total by one to account for the leaf item.
The output from count_leaf_items() when it’s executed on the names list now looks like this:
>>>
>>> count_leaf_items(names)
List: ['Adam', ['Bob', ['Chet', 'Cat'], 'Barb', 'Bert'], 'Alex', ['Bea', 'Bill'], 'Ann']
Counted leaf item "Adam"
Encountered sublist
List: ['Bob', ['Chet', 'Cat'], 'Barb', 'Bert']
Counted leaf item "Bob"
Encountered sublist
List: ['Chet', 'Cat']
Counted leaf item "Chet"
Counted leaf item "Cat"
-> Returning count 2
Counted leaf item "Barb"
Counted leaf item "Bert"
-> Returning count 5
Counted leaf item "Alex"
Encountered sublist
List: ['Bea', 'Bill']
Counted leaf item "Bea"
Counted leaf item "Bill"
-> Returning count 2
Counted leaf item "Ann"
-> Returning count 10
10
Each time a call to count_leaf_items() terminates, it returns the count of leaf elements it tallied in the list passed to it. The top-level call returns 10, as it should.
Traverse a Nested List Non-Recursively
Like the other examples shown so far, this list traversal doesn’t require recursion. You can also accomplish it iteratively. Here’s one possibility:
def count_leaf_items(item_list):
"""Non-recursively counts and returns the
number of leaf items in a (potentially
nested) list.
"""
count = 0
stack = []
current_list = item_list
i = 0
while True:
if i == len(current_list):
if current_list == item_list:
return count
else:
current_list, i = stack.pop()
i += 1
continue
if isinstance(current_list[i], list):
stack.append([current_list, i])
current_list = current_list[i]
i = 0
else:
count += 1
i += 1
If you run this non-recursive version of count_leaf_items() on the same lists as shown previously, you get the same results:
>>>
>>> count_leaf_items([1, 2, 3, 4])
4
>>> count_leaf_items([1, [2.1, 2.2], 3])
4
>>> count_leaf_items([])
0
>>> count_leaf_items(names)
10
>>> # Success!
The strategy employed here uses a stack to handle the nested sublists. When this version of count_leaf_items() encounters a sublist, it pushes the list that is currently in progress and the current index in that list onto a stack. Once it has counted the sublist, the function pops the parent list and index from the stack so it can resume counting where it left off.
In fact, essentially the same thing happens in the recursive implementation as well. When you call a function recursively, Python saves the state of the executing instance on a stack so the recursive call can run. When the recursive call finishes, the state is popped from the stack so that the interrupted instance can resume. It’s the same concept, but with the recursive solution, Python is doing the state-saving work for you.
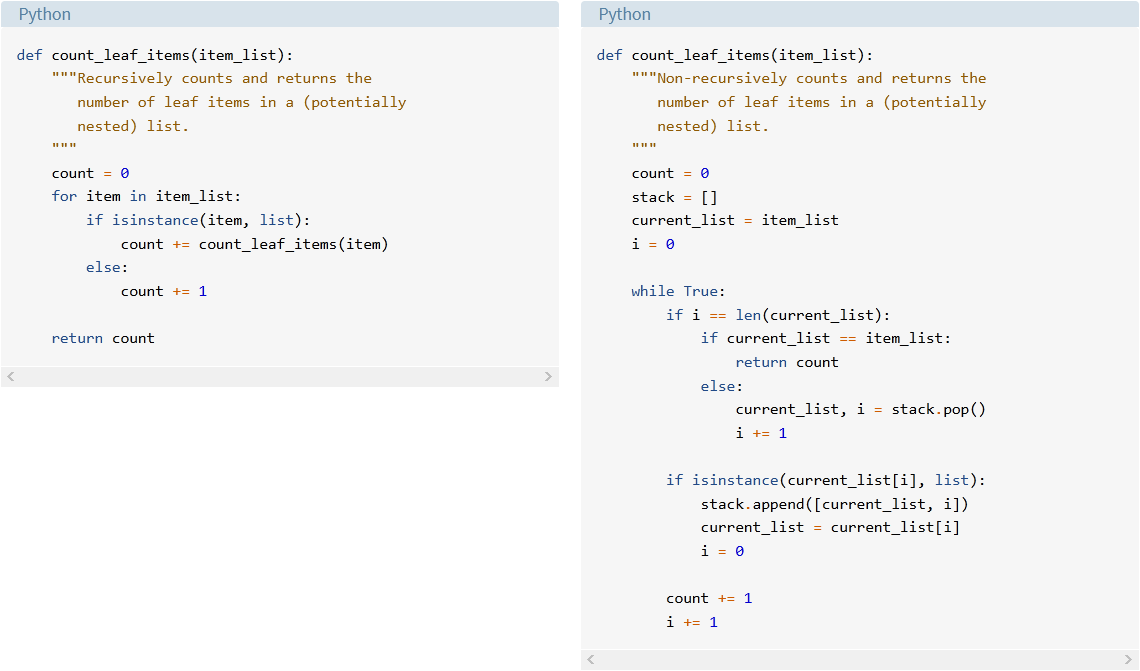
Notice how concise and readable the recursive code is when compared to the non-recursive version:
This is a case where using recursion is definitely an advantage.
Detect Palindromes
The choice of whether to use recursion to solve a problem depends in large part on the nature of the problem. Factorial, for example, naturally translates to a recursive implementation, but the iterative solution is quite straightforward as well. In that case, it’s arguably a toss-up.
The list traversal problem is a different story. In that case, the recursive solution is very elegant, while the non-recursive one is cumbersome at best.
For the next problem, using recursion is arguably silly.
A palindrome is a word that reads the same backward as it does forward. Examples include the following words:
- Racecar
- Level
- Kayak
- Reviver
- Civic
If asked to devise an algorithm to determine whether a string is palindromic, you would probably come up with something like “Reverse the string and see if it’s the same as the original.” You can’t get much plainer than that.
Even more helpfully, Python’s [::-1] slicing syntax for reversing a string provides a convenient way to code it:
>>>
>>> def is_palindrome(word):
... """Return True if word is a palindrome, False if not."""
... return word == word[::-1]
...
>>> is_palindrome("foo")
False
>>> is_palindrome("racecar")
True
>>> is_palindrome("troglodyte")
False
>>> is_palindrome("civic")
True
This is clear and concise. There’s hardly any need to look for an alternative. But just for fun, consider this recursive definition of a palindrome:
- Base cases: An empty string and a string consisting of a single character are inherently palindromic.
- Reductive recursion: A string of length two or greater is a palindrome if it satisfies both of these criteria:
- The first and last characters are the same.
- The substring between the first and last characters is a palindrome.
Slicing is your friend here as well. For a string word, indexing and slicing give the following substrings:
- The first character is
word[0]. - The last character is
word[-1]. - The substring between the first and last characters is
word[1:-1].
So you can define is_palindrome() recursively like this:
>>>
>>> def is_palindrome(word):
... """Return True if word is a palindrome, False if not."""
... if len(word) <= 1:
... return True
... else:
... return word[0] == word[-1] and is_palindrome(word[1:-1])
...
>>> # Base cases
>>> is_palindrome("")
True
>>> is_palindrome("a")
True
>>> # Recursive cases
>>> is_palindrome("foo")
False
>>> is_palindrome("racecar")
True
>>> is_palindrome("troglodyte")
False
>>> is_palindrome("civic")
True
It’s an interesting exercise to think recursively, even when it isn’t especially necessary.
Sort With Quicksort
The final example presented, like the nested list traversal, is a good example of a problem that very naturally suggests a recursive approach. The Quicksort algorithm is an efficient sorting algorithm developed by British computer scientist Tony Hoare in 1959.
Quicksort is a divide-and-conquer algorithm. Suppose you have a list of objects to sort. You start by choosing an item in the list, called the pivot item. This can be any item in the list. You then partition the list into two sublists based on the pivot item and recursively sort the sublists.
The steps of the algorithm are as follows:
- Choose the pivot item.
- Partition the list into two sublists:
- Those items that are less than the pivot item
- Those items that are greater than the pivot item
- Quicksort the sublists recursively.
Each partitioning produces smaller sublists, so the algorithm is reductive. The base cases occur when the sublists are either empty or have one element, as these are inherently sorted.
Choosing the Pivot Item
The Quicksort algorithm will work no matter what item in the list is the pivot item. But some choices are better than others. Remember that when partitioning, two sublists that are created: one with items that are less than the pivot item and one with items that are greater than the pivot item. Ideally, the two sublists are of roughly equal length.
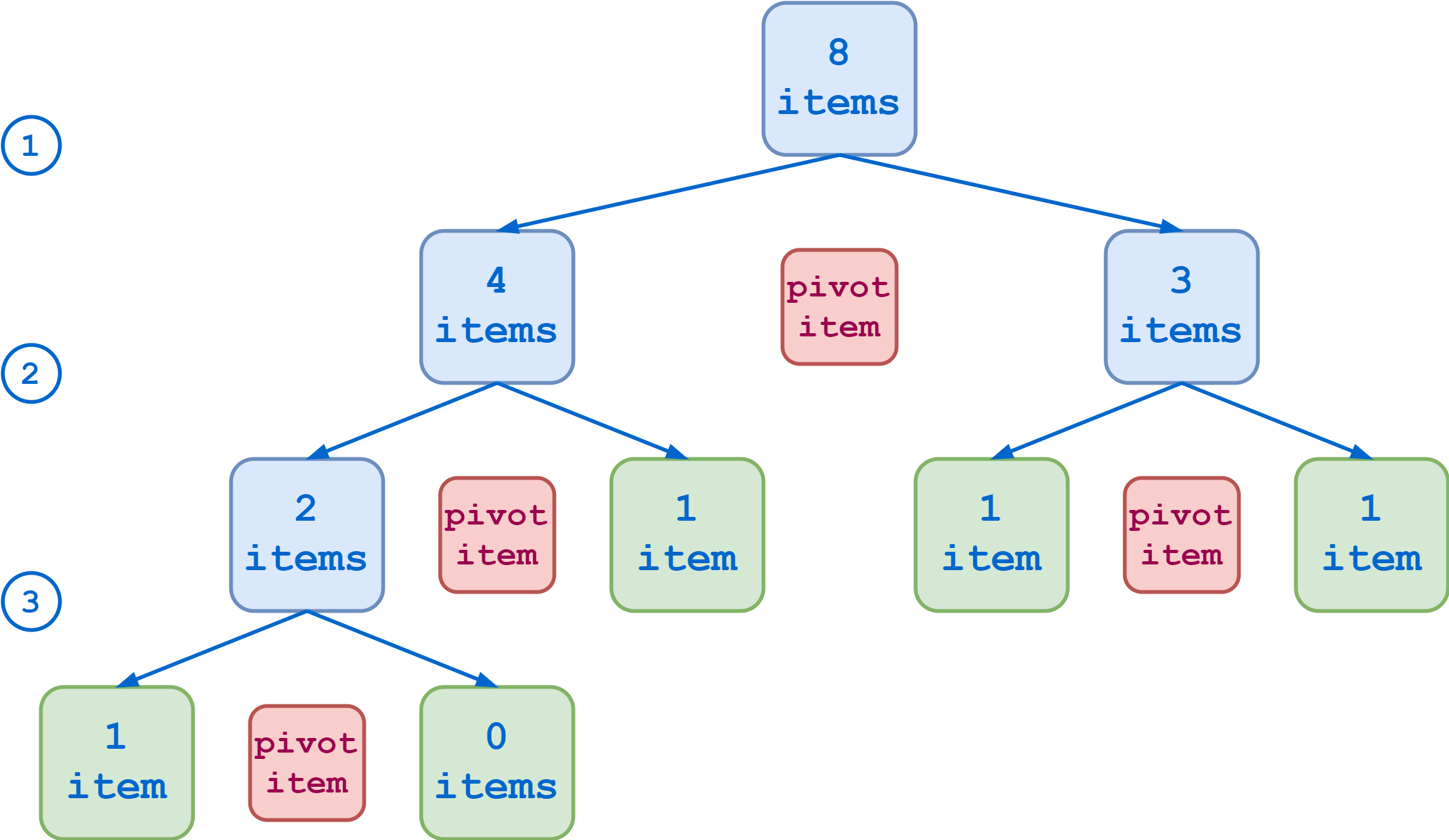
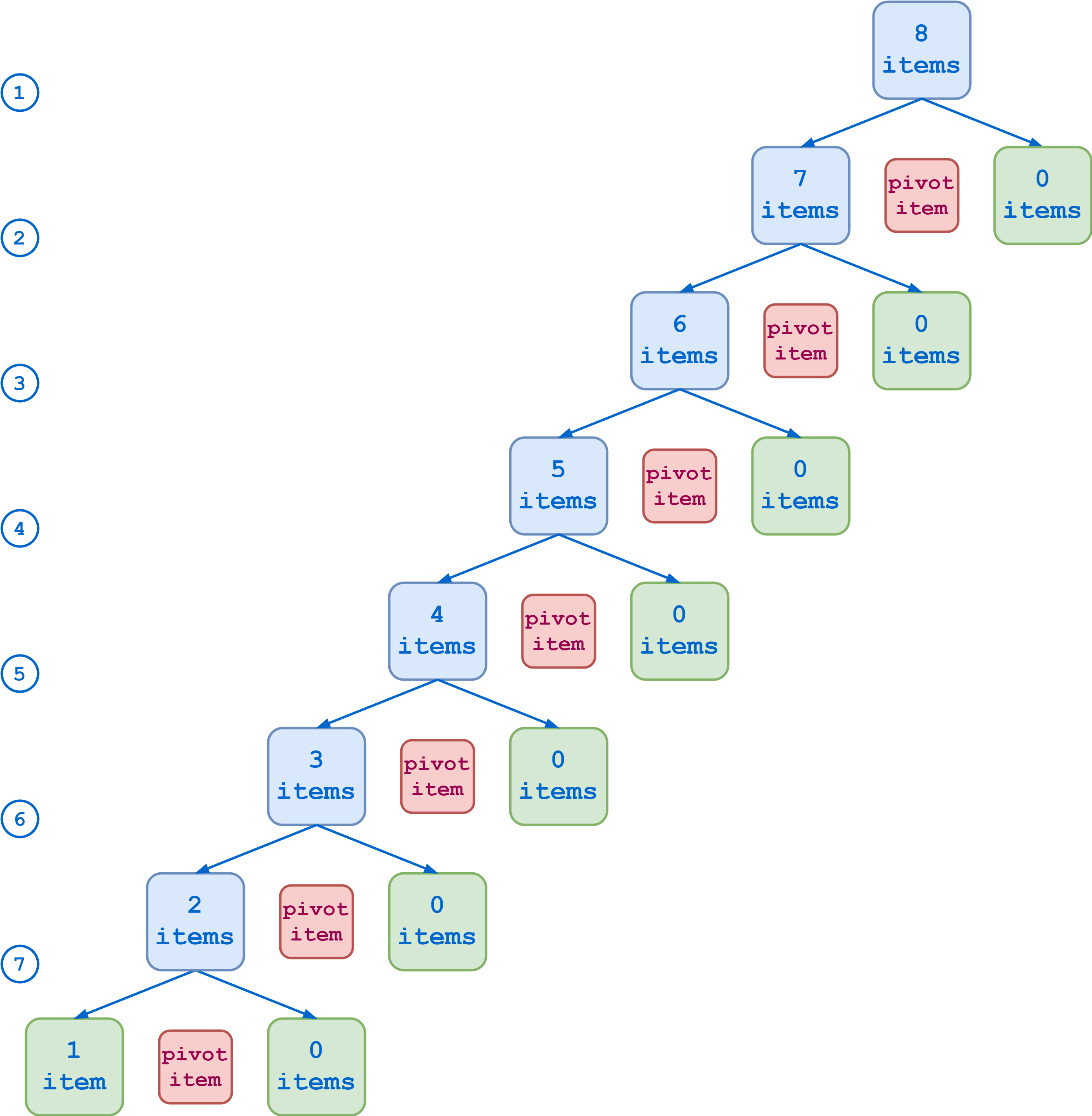
Imagine that your initial list to sort contains eight items. If each partitioning results in sublists of roughly equal length, then you can reach the base cases in three steps:
At the other end of the spectrum, if your choice of pivot item is especially unlucky, each partition results in one sublist that contains all the original items except the pivot item and another sublist that is empty. In that case, it takes seven steps to reduce the list to the base cases:
The Quicksort algorithm will be more efficient in the first case. But you’d need to know something in advance about the nature of the data you’re sorting in order to systematically choose optimal pivot items. In any case, there isn’t any one choice that will be the best for all cases. So if you’re writing a Quicksort function to handle the general case, the choice of pivot item is somewhat arbitrary.
The first item in the list is a common choice, as is the last item. These will work fine if the data in the list is fairly randomly distributed. However, if the data is already sorted, or even nearly so, then these will result in suboptimal partitioning like that shown above. To avoid this, some Quicksort algorithms choose the middle item in the list as the pivot item.
Another option is to find the median of the first, last, and middle items in the list and use that as the pivot item. This is the strategy used in the sample code below.
Implementing the Partitioning
Once you’ve chosen the pivot item, the next step is to partition the list. Again, the goal is to create two sublists, one containing the items that are less than the pivot item and the other containing those that are greater.
You could accomplish this directly in place. In other words, by swapping items, you could shuffle the items in the list around until the pivot item is in the middle, all the lesser items are to its left, and all the greater items are to its right. Then, when you Quicksort the sublists recursively, you’d pass the slices of the list to the left and right of the pivot item.
Alternately, you can use Python’s list manipulation capability to create new lists instead of operating on the original list in place. This is the approach taken in the code below. The algorithm is as follows:
- Choose the pivot item using the median-of-three method described above.
- Using the pivot item, create three sublists:
- The items in the original list that are less than the pivot item
- The pivot item itself
- The items in the original list that are greater than the pivot item
- Recursively Quicksort lists 1 and 3.
- Concatenate all three lists back together.
Note that this involves creating a third sublist that contains the pivot item itself. One advantage to this approach is that it smoothly handles the case where the pivot item appears in the list more than once. In that case, list 2 will have more than one element.
Using the Quicksort Implementation
Now that the groundwork is in place, you are ready to move on to the Quicksort algorithm. Here’s the Python code:
1import statistics
2
3def quicksort(numbers):
4 if len(numbers) <= 1:
5 return numbers
6 else:
7 pivot = statistics.median(
8 [
9 numbers[0],
10 numbers[len(numbers) // 2],
11 numbers[-1]
12 ]
13 )
14 items_less, pivot_items, items_greater = (
15 [n for n in numbers if n < pivot],
16 [n for n in numbers if n == pivot],
17 [n for n in numbers if n > pivot]
18 )
19
20 return (
21 quicksort(items_less) +
22 pivot_items +
23 quicksort(items_greater)
24 )
This is what each section of quicksort() is doing:
- Line 4: The base cases where the list is either empty or has only a single element
- Lines 7 to 13: Calculation of the pivot item by the median-of-three method
- Lines 14 to 18: Creation of the three partition lists
- Lines 20 to 24: Recursive sorting and reassembly of the partition lists
Here are some examples of quicksort() in action:
>>>
>>> # Base cases
>>> quicksort([])
[]
>>> quicksort([42])
[42]
>>> # Recursive cases
>>> quicksort([5, 2, 6, 3])
[2, 3, 5, 6]
>>> quicksort([10, -3, 21, 6, -8])
[-8, -3, 6, 10, 21]
For testing purposes, you can define a short function that generates a list of random numbers between 1 and 100:
import random
def get_random_numbers(length, minimum=1, maximum=100):
numbers = []
for _ in range(length):
numbers.append(random.randint(minimum, maximum))
return numbers
Now you can use get_random_numbers() to test quicksort():
>>>
>>> numbers = get_random_numbers(20)
>>> numbers
[24, 4, 67, 71, 84, 63, 100, 94, 53, 64, 19, 89, 48, 7, 31, 3, 32, 76, 91, 78]
>>> quicksort(numbers)
[3, 4, 7, 19, 24, 31, 32, 48, 53, 63, 64, 67, 71, 76, 78, 84, 89, 91, 94, 100]
>>> numbers = get_random_numbers(15, -50, 50)
>>> numbers
[-2, 14, 48, 42, -48, 38, 44, -25, 14, -14, 41, -30, -35, 36, -5]
>>> quicksort(numbers)
[-48, -35, -30, -25, -14, -5, -2, 14, 14, 36, 38, 41, 42, 44, 48]
>>> quicksort(get_random_numbers(10, maximum=500))
[49, 94, 99, 124, 235, 287, 292, 333, 455, 464]
>>> quicksort(get_random_numbers(10, 1000, 2000))
[1038, 1321, 1530, 1630, 1835, 1873, 1900, 1931, 1936, 1943]
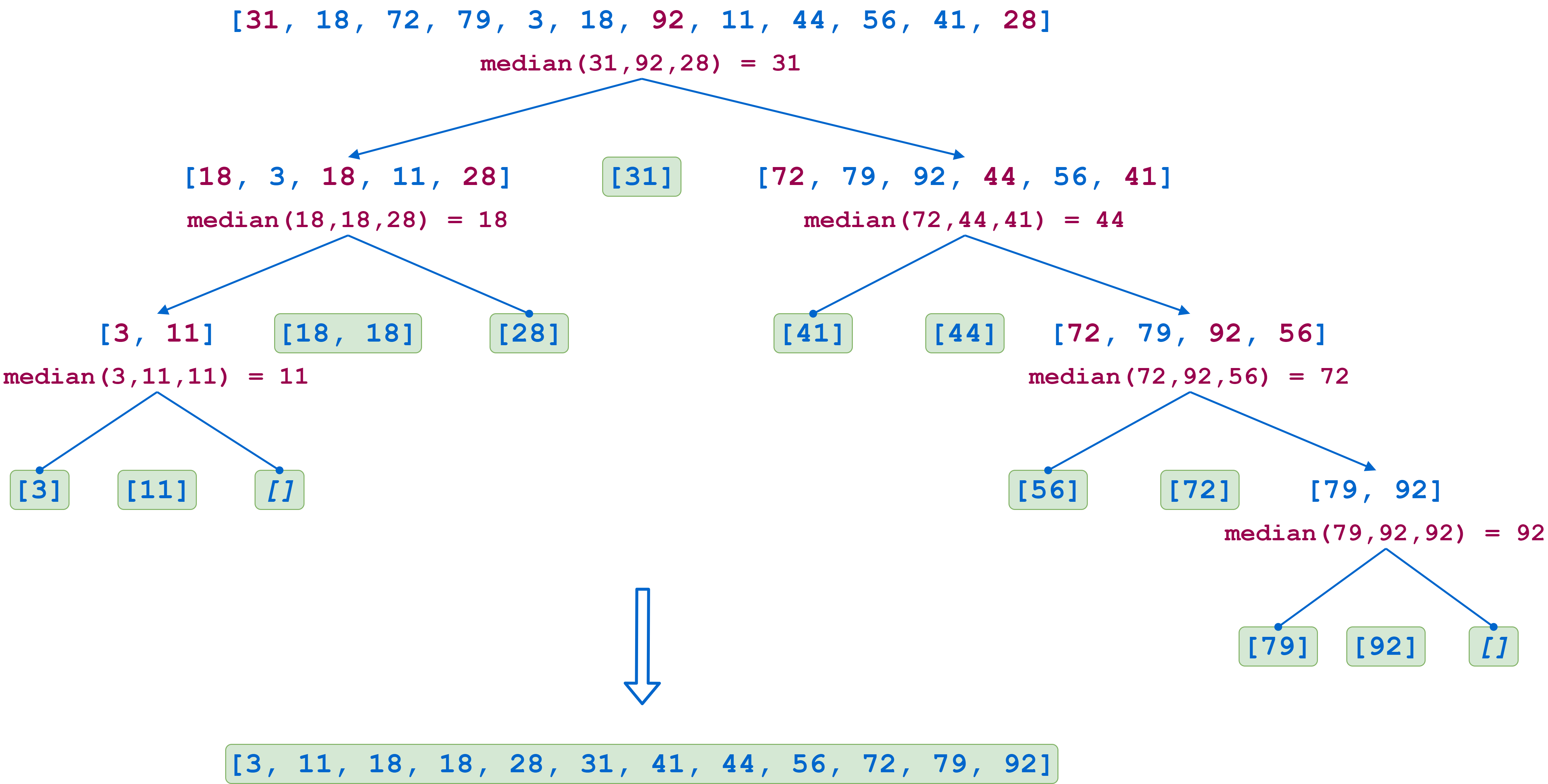
To further understand how quicksort() works, see the diagram below. This shows the recursion sequence when sorting a twelve-element list:
In the first step, the first, middle, and last list values are 31, 92, and 28, respectively. The median is 31, so that becomes the pivot item. The first partition then consists of the following sublists:
| Sublist | Items |
|---|---|
[18, 3, 18, 11, 28] |
The items less than the pivot item |
[31] |
The pivot item itself |
[72, 79, 92, 44, 56, 41] |
The items greater than the pivot item |
Each sublist is subsequently partitioned recursively in the same manner until all the sublists either contain a single element or are empty. As the recursive calls return, the lists are reassembled in sorted order. Note that in the second-to-last step on the left, the pivot item 18 appears in the list twice, so the pivot item list has two elements.
Conclusion
That concludes your journey through recursion, a programming technique in which a function calls itself. Recursion isn’t by any means appropriate for every task. But some programming problems virtually cry out for it. In those situations, it’s a great technique to have at your disposal.
In this tutorial, you learned:
- What it means for a function to call itself recursively
- How the design of Python functions supports recursion
- What factors to consider when choosing whether or not to solve a problem recursively
- How to implement a recursive function in Python
You also saw several examples of recursive algorithms and compared them to corresponding non-recursive solutions.
You should now be in a good position to recognize when recursion is called for and be ready to use it confidently when it’s needed! If you want to explore more about recursion in Python, then check out Thinking Recursively in Python.
Сумма чисел от 1 до n
Если бы я хотел узнать сумму чисел от 1 до n, где n — натуральное число, я мог бы посчитать вручную 1 + 2 + 3 + 4 + … + (несколько часов спустя) + n. А можно просто написать цикл for:
n = 0
for i in range (1, n+1):
n += iИли использовать рекурсию:
def recursion(n):
if n == 1:
return 1
return n + recursion(n - 1)У рекурсии есть несколько преимуществ в сравнении с первыми двумя методами. Рекурсия занимает меньше времени, чем выписывание 1 + 2 + 3 на сумму от 1 до 3.
Для recusion(4) рекурсия может работать в обратную сторону:
Вызов функций: (4 -> 4 + 3 -> 4 + 3 + 2 -> 4 + 3 + 2 + 1 -> 10)
Принимая во внимание, что цикл [for] работает строго вперед: (1 -> 1 + 2 -> 1 + 2 + 3 -> 1 + 2 + 3 + 4 -> 10). Иногда рекурсивное решение проще, чем итеративное решение. Это очевидно при реализации обращения связанного списка.
Как и когда происходит рекурсия
Рекурсия появляется когда вызов функции повторно вызывает ту же функцию до завершения первоначального вызова функции. Например, рассмотрим известное математическое выражение x! (т.е. факториал). Факториал определяется для всех неотрицательных целых чисел следующим образом:
Если число равно 0, то будет 1.
В противном случае ответом будет то, что число умножается на факториал на единицу меньше этого числа.
В Python наивная реализация факториала может быть определена как функция следующим образом:
def factorial(n):
if n == 0:
return 1
else:
return n * factorial(n - 1)Иногда функции рекурсии трудно понять, поэтому давайте рассмотрим поэтапно.
Рассмотрим выражение factorial(3). Эта и все остальные вызовы функций создают
новую
среду. Среда представляет собой таблицу, которая сопоставляет идентификаторы (например, n, factorial, print и т.д.) с их соответствующими значениями.
В любой момент времени вы можете получить доступ к текущей среде с помощью locals(). В первом вызове функции единственная локальная переменная, которая определяется n = 3.Поэтому locals() будет показывать {"n": 3}. Так как n == 3, возвращаемое значение становится n * factorial(n - 1).
На следующем этапе ситуация может немного запутаться. Глядя на наше новое выражение, мы уже знаем, что такое n. Однако мы еще не знаем, что такое factorial(n - 1).
Во-первых, n - 1 принимает значение 2.Затем 2 передаётся factorial как значение для n. Поскольку это новый вызов функции, создаётся вторая среда для хранения нового n.
Пусть A — первое окружение, а B — второе окружение. A всё ещё существует и равен {"n": 3} , однако B (что равно {"n": 2}) является текущей средой. Если посмотреть на тело функции, возвращаемое значение, опять же, n * factorial(n - 1).
Не определяя это выражение, заменим его на исходное выражение return. Делая это, мы мысленно отбрасываем B, поэтому не забудьте заменить n соответственно (т.е. ссылки на B n заменены на n - 1) который использует A n ). Теперь исходное обратное выражение становится n * ((n - 1) * factorial((n - 1) - 1)). Подумайте, почему так?
Теперь давайте определим factorial((n - 1) - 1)). Так как A n == 3, мы пропускаем 1 через factorial. Поэтому мы создаем новую среду C, которая равна {"n": 1}. Мы снова возвращаем значение n * factorial(n - 1). Итак, заменим исходный factorial((n - 1) - 1)) выражения return аналогично тому, как раньше мы скорректировали исходное выражение return. Исходное выражение теперь n * ((n - 1) * ((n - 2) * factorial((n - 2) - 1))).
Почти закончили. Теперь нам нужно оценить factorial((n - 2) - 1). На этот раз мы пропустим через 0. Следовательно, должно получиться 1.
Теперь давайте проведём нашу последнюю замену. Исходное выражение return теперь n * ((n - 1) * ((n - 2) * 1)). Напомню, что исходное выражение возврата оценивается под A , выражение становится 3 * ((3 - 1) * ((3 - 2) * 1)). Здесь получается 6.
Чтобы убедиться, что это правильный ответ, вспомните, что 3! == 3 * 2 * 1 == 6. Прежде чем читать дальше, убедитесь, что вы полностью понимаете концепцию среды и то, как они применяются к рекурсии.
Утверждение, if n == 0: return 1, называется базовым случаем. Потому что это не рекурсия. Базовый случай необходим, без него вы столкнетесь с бесконечной рекурсией. С учетом сказанного, если у вас есть хотя бы один базовый случай, у вас может быть столько случаев, сколько вы хотите. Например, можно записать факториал таким образом:
def factorial(n):
if n == 0:
return 1
elif n == 1:
return 1
else:
return n * factorial(n - 1)У вас может также быть несколько случаев рекурсии, но мы не будем вдаваться в подробности, потому что это редкий случай, и его трудно мысленно обрабатывать.
Вы также можете иметь «параллельные» рекурсивные вызовы функций. Например, рассмотрим последовательность Фибоначчи, которая определяется следующим образом:
- Если число равно 0, то ответ равен 0.
- Если число равно 1, то ответ равен 1.
В противном случае ответ представляет собой сумму двух предыдущих чисел Фибоначчи.
Мы можем определить это следующим образом:
def fib(n):
if n == 0 or n == 1:
return n
else:
return fib(n - 2) + fib(n - 1)
Я не буду разбирать эту функцию также тщательно, как и с factorial(3), но окончательное значение возврата fib(5) эквивалентно следующему (синтаксически недействительному) выражению:
(
fib((n - 2) - 2)
+
(
fib(((n - 2) - 1) - 2)
+
fib(((n - 2) - 1) - 1)
)
)
+
(
(
fib(((n - 1) - 2) - 2)
+
fib(((n - 1) - 2) - 1)
)
+
(
fib(((n - 1) - 1) - 2)
+
(
fib((((n - 1) - 1) - 1) - 2)
+
fib((((n - 1) - 1) - 1) - 1)
)
)
)Решением (1 + (0 + 1)) + ((0 + 1) + (1 + (0 + 1))) будет 5.
Теперь давайте рассмотрим еще несколько терминов:
Tail call — это просто вызов рекурсивной функции, который является последней операцией и должна быть выполнена перед возвратом значения. Чтобы было понятно, return foo(n - 1) — это хвост вызова, но return foo(n - 1) + 1 не является (поскольку операция сложения будет последней операцией).
Оптимизация хвоста вызова (TCO или tail cost optimization) — это способ автоматического сокращения рекурсии в рекурсивных функциях.
Устранение хвоста вызова (TCE или tail cost elimination) — это сокращение хвостового вызова до выражения, которое может быть оценено без рекурсии. TCE — это тип TCO.
Оптимизация хвоста вызова может пригодиться по нескольким причинам:
Интерпретатор может снизить объём памяти, занятый средами. Поскольку ни у кого нет неограниченной памяти, чрезмерные рекурсивные вызовы функций приведут к переполнению стека.
Интерпретатор может уменьшить количество переключателей кадров стека.
В Python нет TCO по нескольким причинам, поэтому для обхода этого ограничения можно использовать другие методы. Выбор используемого метода зависит от варианта использования. Интуитивно понятно, что factorial и fib можно относительно легко преобразовать в итеративный код следующим образом:
def factorial(n):
product = 1
while n > 1:
product *= n
n -= 1
return product
def fib(n):
a, b = 0, 1
while n > 0:
a, b = b, a + b
n -= 1
return aОбычно это самый эффективный способ устранения рекурсии вручную, но для более сложных функций может быть трудно.
Другим полезным инструментом является декодер lru_cache, который можно использовать для уменьшения количества лишних вычислений.
Теперь вы знаете, как избежать рекурсии в Python, но когда её нужно использовать? Ответ «не часто». Все рекурсивные функции могут быть реализованы итеративно. Это просто вопрос, как именно сделать. Однако есть редкие случаи, когда можно использовать рекурсию. Рекурсия распространена в Python, когда ожидаемые вводы не вызовут значительного количества вызовов рекурсивных функций.
Если вы интересуетесь рекурсией, стоит изучить функциональные языки, такие как Scheme или Haskell. На таких языках рекурсия намного полезней.
Хотя приведённый выше пример последовательности Фибоначчи, хорошо показывает, как применять определение в python и позже использовать кэш lru, при этом он имеет неэффективное время работы, из-за того, что выполняет 2 рекурсивных вызова. Количество вызовов функции растет экспоненциально до n.
В таком случае лучше использовать линейную рекурсию:
def fib(n):
if n <= 1:
return (n,0)
else:
(a, b) = fib(n - 1)
return (a + b, a)Но у этого примера есть проблема в возвращении пары числе вместо одного. Это показывает, что не всегда стоит использовать рекурсию.
Исследование дерева с рекурсией
Допустим, у нас есть такое дерево:
root
- A
- AA
- AB
- B
- BA
- BB
- BBAЕсли мы хотим перечислить все имена элементов, мы можем сделать это с помощью простого цикла for. У нас есть функция get_name(), которая возвращает строку с именем узла, функция get_children(), которая возвращает список всех подузлов данного узла в дереве, и функция get_root() для получить корневой узел.
root = get_root(tree)
for node in get_children(root):
print(get_name(node))
for child in get_children(node):
print(get_name(child))
for grand_child in get_children(child):
print(get_name(grand_child))
# Выводит: A, AA, AB, B, BA, BB, BBAЭтот код работает хорошо и быстро, но что если под-узлы получили свои под-узлы? И эти под-узлы могут иметь больше под-узлов … Что если вы не знаете заранее, сколько их будет? Решением этой проблемы будет использование рекурсии.
def list_tree_names(node):
for child in get_children(node):
print(get_name(child))
list_tree_names(node=child)
list_tree_names(node=get_root(tree))
# Выводит: A, AA, AB, B, BA, BB, BBAВозможно, вы не хотите вывести, а вернуть список всех имён узлов. Это можно сделать с помощью передачи прокручиваемого списка в качестве параметра.
def list_tree_names(node, lst=[]):
for child in get_children(node):
lst.append(get_name(child))
list_tree_names(node=child, lst=lst)
return lst
list_tree_names(node=get_root(tree))
# returns ['A', 'AA', 'AB', 'B', 'BA', 'BB', 'BBA']Увеличение максимальной глубины рекурсии
Существует предел глубины возможной рекурсии, который зависит от реализации Python. Когда предел достигнут, возникает исключение RuntimeError:
RuntimeError: Maximum Recursion Depth Exceeded
Пример программы, которая может вызвать такую ошибку:
def cursing(depth):
try:
cursing(depth + 1) # actually, re-cursing
except RuntimeError as RE:
print('I recursed {} times!'.format(depth))
cursing(0)
# Out: I recursed 1083 times!Можно изменить предел глубины рекурсии с помощью
sys.setrecursionlimit(limit)Чтобы проверить текущие параметры лимита, нужно запустить:
sys.getrecursionlimit()Если запустить тот же метод выше с новым пределом, мы получаем
sys.setrecursionlimit(2000)
cursing(0)
# Out: I recursed 1997 times!В Python 3.5 ошибка стала называться RecursionError, которая является производной от RuntimeError.
Хвостовая рекурсия — как не надо делать
Хвостовая рекурсия — частный случай рекурсии, при котором любой рекурсивный вызов является последней операцией перед возвратом из функции.
Вот пример обратного отсчета, написанного с использованием хвостовой рекурсии:
def countdown(n):
if n == 0:
print("Blastoff!")
else:
print(n)
countdown(n-1)Любое вычисление, которое может быть выполнено с использованием итерации, также может быть выполнено с использованием рекурсии. Вот версия find_max, написанная с использованием хвостовой рекурсии:
def find_max(seq, max_so_far):
if not seq:
return max_so_far
if max_so_far < seq[0]:
return find_max(seq[1:], seq[0])
else:
return find_max(seq[1:], max_so_far)Хвостовую рекурсию лучше не использовать, поскольку компилятор Python не обрабатывает оптимизацию для хвостовых рекурсивных вызовов. В таких случаях рекурсивное решение использует больше системных ресурсов, чем итеративное.
Оптимизация хвостовой рекурсии с помощью интроспекции стека
По умолчанию рекурсивный стек Python не превышает 1000 кадров. Это ограничение можно изменить, установив sys.setrecursionlimit(15000) который быстрее, однако этот метод потребляет больше памяти. Вместо этого мы также можем решить проблему рекурсии хвоста, используя интроспекцию стека.
#!/usr/bin/env python2.4
# Эта программа показыает работу декоратора, который производит оптимизацию хвостового вызова. Он делает это, вызывая исключение, если оно является его прародителем, и перехватывает исключения, чтобы вызвать стек.
import sys
class TailRecurseException:
def __init__(self, args, kwargs):
self.args = args
self.kwargs = kwargs
# Эта программа показыает работу декоратора, который производит
# оптимизацию хвостового вызова. Он делает это, вызывая исключение, если
# оно является его прародителем, и перехватывает исключения, чтобы
# подделать оптимизацию хвоста Эта функция не работает, если функция
# декоратора возвращается без хвоста.
def tail_call_optimized(g):
def func(*args, **kwargs):
f = sys._getframe()
if f.f_back and f.f_back.f_back
and f.f_back.f_back.f_code == f.f_code:
raise TailRecurseException(args, kwargs)
else:
while 1:
try:
return g(*args, **kwargs)
except TailRecurseException as e:
args = e.args
kwargs = e.kwargs
func.__doc__ = g.__doc__
return funcЧтобы оптимизировать рекурсивные функции, мы можем использовать декоратор @tail_call_optimized для вызова нашей функции. Вот несколько примеров общей рекурсии с использованием декоратора, описанного выше:
Факториальный пример:
# "calculate a factorial"
@tail_call_optimized
def factorial(n, acc=1):
if n == 0:
return acc
return factorial(n-1, n*acc)
print(factorial(10000))
# печатает очень большое число
# и не достигает лимита рекурсии.
Пример Фибоначчи:
@tail_call_optimized
def fib(i, current = 0, next = 1):
if i == 0:
return current
else:
return fib(i - 1, next, current + next)
print(fib(10000))
# также выводит большое число,
# но не доходит до лимита рекурсииЧтобы выйти из рекурсии, нужно ввести команду stopCondition.
Исходная переменная должна быть передана рекурсивной функции, чтобы сохранить её.
Когда функция вызывает сама себя, она называется рекурсивной функцией. В этом руководстве мы узнаем, как написать функцию рекурсии Python.
Когда функция определена таким образом, что она вызывает сама себя, она называется рекурсивной функцией. Это явление называется рекурсией. Python поддерживает рекурсивные функции.
Рекурсия очень похожа на цикл, в котором функция вызывается на каждой итерации. Вот почему мы всегда можем использовать циклы как замену функции рекурсии Python.
Но некоторые программисты предпочитают рекурсию циклам. В основном это вопрос выбора, и вы можете использовать циклы или рекурсию.
Примеры
Следующий код возвращает сумму первых n натуральных чисел, используя рекурсивную функцию python.
def sum_n(n): if n== 0: return 0 else: return n + sum_n(n-1)
Это печатает сумму первых 100 натуральных чисел и первых 500 натуральных чисел
print(sum_n(100)) print(sum_n(500))
Вывод
C:/Users/TutorialsPoint1/~.py 5050 125250
1. Факториал целого числа
Факториал целого числа вычисляется путем умножения целых чисел от 1 до этого числа. Например, факториал 10 будет 1 * 2 * 3…. * 10.
Давайте посмотрим, как мы можем написать факториальную функцию с помощью цикла for.
def factorial(n):
result = 1
for i in range(1, n + 1):
result = result * i
return result
print(f'Factorial of 10 = {factorial(10)}')
print(f'Factorial of 5 = {factorial(5)}')
Давайте посмотрим, как мы можем изменить функцию factorial() для использования рекурсии.
def factorial(n):
if n == 1:
return 1
else:
return n * factorial(n - 1)
print(f'Factorial of 10 = {factorial(10)}')
print(f'Factorial of 5 = {factorial(5)}')
На изображении ниже показано выполнение рекурсивной функции.
2. Ряд Фибоначчи
Ряд Фибоначчи — это последовательность чисел, каждое из которых представляет собой сумму двух предыдущих чисел. Например — 1, 1, 2, 3, 5, 8, 13, 21 и так далее.
Давайте посмотрим на функцию для возврата чисел ряда Фибоначчи с помощью циклов.
def fibonacci(n):
""" Returns Fibonacci Number at nth position using loop"""
if n == 0:
return 0
if n == 1:
return 1
i1 = 0
i2 = 1
num = 1
for x in range(1, n):
num = i1 + i2
i1 = i2
i2 = num
return num
for i in range(10):
print(fibonacci(i), end=" ")
# Output: 0 1 1 2 3 5 8 13 21 34
Вот реализация функции fibonacci() с использованием рекурсии.
def fibonacci(n):
""" Returns Fibonacci Number at nth position using recursion"""
if n == 0:
return 0
elif n == 1:
return 1
else:
return fibonacci(n - 1) + fibonacci(n - 2)
for i in range(10):
print(fibonacci(i), end=" ")
# Output: 0 1 1 2 3 5 8 13 21 34
Здесь рекурсивный код функции меньше и прост для понимания. Так что использование рекурсии в этом случае имеет смысл.
Базовый случай
При определении рекурсивной функции должен быть хотя бы один базовый случай, для которого нам известен результат. Затем каждый последующий вызов рекурсивной функции должен приближать ее к базовому случаю.
Это необходимо для того, чтобы в конечном итоге рекурсивные вызовы прекратились. В противном случае функция никогда не завершится и мы получим ошибку нехватки памяти.
Вы можете проверить это поведение в обоих приведенных выше примерах. Аргументы вызова рекурсивной функции становятся все ближе к базовому случаю.
Преимущества
- Иногда рекурсия уменьшает количество строк кода.
- Код выглядит просто.
- Если мы знаем базовый случай, тогда использовать в функции проще.
Недостатки
- Если не реализовано должным образом, функция никогда не завершится.
- Понимание рекурсии вызывает большую путаницу по сравнению с циклами.
Recursion in Python works just as recursion in an other language, with the recursive construct defined in terms of itself:
For example a recursive class could be a binary tree (or any tree):
class tree():
def __init__(self):
'''Initialise the tree'''
self.Data = None
self.Count = 0
self.LeftSubtree = None
self.RightSubtree = None
def Insert(self, data):
'''Add an item of data to the tree'''
if self.Data == None:
self.Data = data
self.Count += 1
elif data < self.Data:
if self.LeftSubtree == None:
# tree is a recurive class definition
self.LeftSubtree = tree()
# Insert is a recursive function
self.LeftSubtree.Insert(data)
elif data == self.Data:
self.Count += 1
elif data > self.Data:
if self.RightSubtree == None:
self.RightSubtree = tree()
self.RightSubtree.Insert(data)
if __name__ == '__main__':
T = tree()
# The root node
T.Insert('b')
# Will be put into the left subtree
T.Insert('a')
# Will be put into the right subtree
T.Insert('c')
As already mentioned a recursive structure must have a termination condition. In this class, it is not so obvious because it only recurses if new elements are added, and only does it a single time extra.
Also worth noting, python by default has a limit to the depth of recursion available, to avoid absorbing all of the computer’s memory. On my computer this is 1000. I don’t know if this changes depending on hardware, etc. To see yours :
import sys
sys.getrecursionlimit()
and to set it :
import sys #(if you haven't already)
sys.setrecursionlimit()
edit: I can’t guarentee that my binary tree is the most efficient design ever. If anyone can improve it, I’d be happy to hear how