Как написать шахматный движок

Разработка шахматной программы

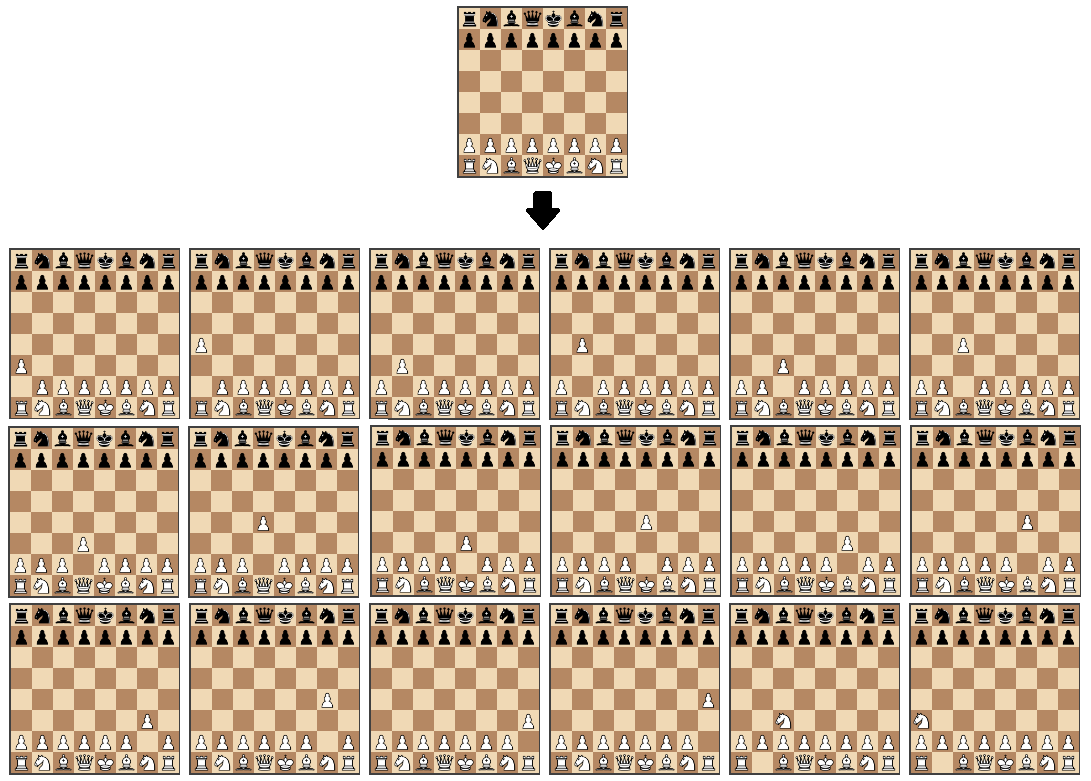
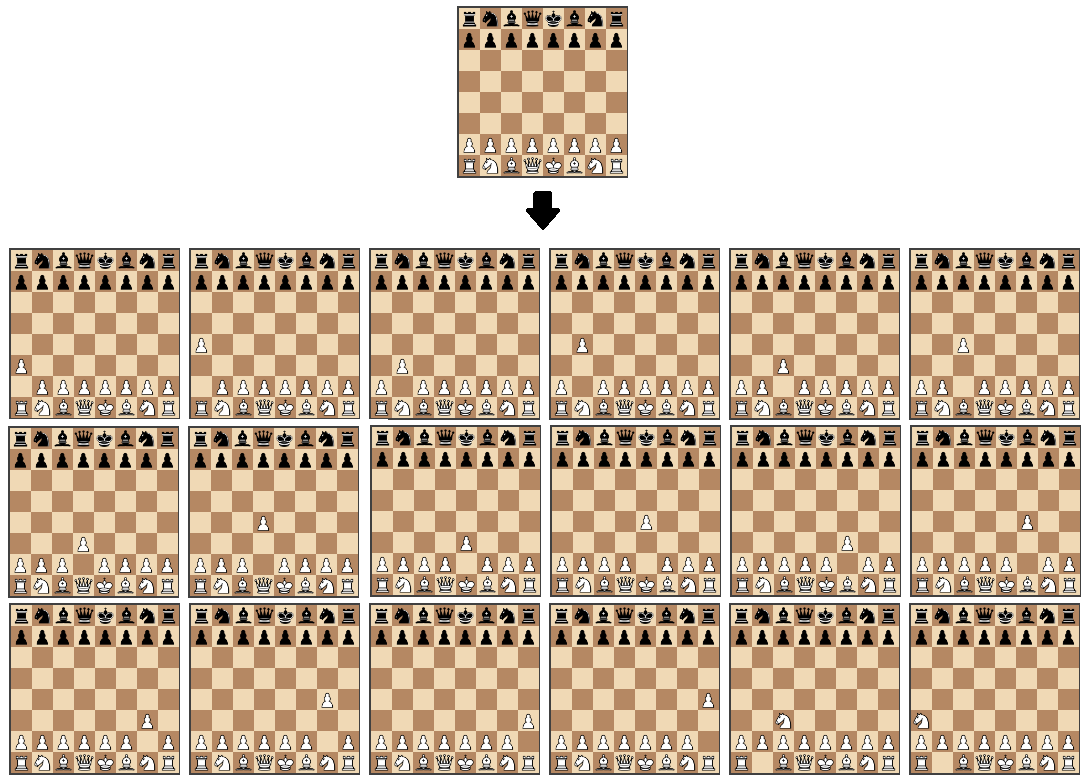
Было ли вам когда-либо интересно написать свою шахматную программу? Настраивать и развивать её, проверять её на знакомых любителях шахмат и радоваться её победам. Но как написать такую программу? Об этом я и расскажу в этой статье.

Сначала я хотел дать полное описание своей реализации шахматного движка (я назвал его Centurion). Но тут я вдруг понял, что на эту тему пишут книжки, а не статьи. В формате статьи просто невозможно описать детально все компоненты шахматной программы с подробностями реализаций. Поэтому я решил ограничиться общим описанием моего шахматного движка и дать ссылку на его исходный код и саму программу. Выглядит программа для Windows так:

Программа для Windows.
Ходить можно как вводом хода в поле (E2-E4), так и мышкой — левая кнопка откуда, правая — куда.

Итак, начнём.
Для начала, стоит поискать специальную литературу о том, как же писать шахматные программы. Я из таковых использовал книжку Корнилова “Программирование шахмат и других логических задач” 2005 года. Одной этой книжки оказалось мало – автор не акцентировал внимание на кое-чём важном, а кое-что просто не рассказал. А это кое-что, между прочим, сильно сокращает дерево перебора. Сразу же предупреждаю, что в моём движке не используется генератор ходов на базе битовых массивов. Этот уровень мне пока недоступен. Впрочем, я особо и не пытался разобраться с ними, предпочитая написать как можно более прозрачный (для меня) механизм работы с ходами фигур, пусть даже в ущерб быстродействию (движок получился не очень быстрый, но вполне работоспособный).

Первое, о чём нам нужно подумать, так это о том, как мы будем представлять игровое поле. Оказывается, очень удобно каждую клетку представлять целым числом, отдельные биты которого отвечают за параметры этой клетки. Я для клеток задал макрос

#define CELL long 

А сама клетка у меня представлена битами как AHIIIIEWB0MFFF, где:

W-фигура белая
B-фигура чёрная
F-тип фигуры (0-фигуры нет)
M-ходила ли фигура
E-край доски
I-индекс фигуры в массиве для поиска фигур (0-15)
H-была короткая рокировка (флаг ставится только у короля и ладьи)
A-была длинная рокировка (флаг ставится только у короля и ладьи)

Чем удобно представление с помощью битов? Наложение маски позволяет быстро определять, что это за клетка. Специально для этого у меня были заданы маски:

#define BYTE8(b7,b6,b5,b4,b3,b2,b1,b0) ((CELL)((b7<<7)|(b6<<6)|(b5<<5)|(b4<<4)|(b3<<3)|(b2<<2)|(b1<<1)|(b0<<0)))

//----------------------------------------------------------------------------------------------------
//Типы фигур
//----------------------------------------------------------------------------------------------------
//король
#define FIGURE_TYPE_KING   1
//ферзь
#define FIGURE_TYPE_QUEEN  2
//ладья
#define FIGURE_TYPE_ROOK   3
//слон
#define FIGURE_TYPE_BISHOP 4
//конь
#define FIGURE_TYPE_KNIGHT 5
//пешка
#define FIGURE_TYPE_PAWN   6

//цвета фигур
#define BLACK BYTE8(0,0,1,0,0,0,0,0)
#define WHITE BYTE8(0,1,0,0,0,0,0,0)
//флаг короткой рокировки
#define CASTLING_O_O (BYTE8(0,0,0,1,0,0,0,0)<<8)
//флаг длинной рокировки
#define CASTLING_O_O_O (BYTE8(0,1,0,0,0,0,0,0)<<8)
//сдвиг индекса
#define INDEX_SHIFT 8
//маска белых
#define MASK_WHITE      WHITE
//маска чёрных
#define MASK_BLACK      BLACK
//маска цвета
#define MASK_COLOR      (MASK_WHITE|MASK_BLACK)
//маска типа
#define MASK_TYPE       BYTE8(0,0,0,0,0,1,1,1)
//маска границы
#define MASK_BORDER     BYTE8(1,0,0,0,0,0,0,0)
//маска,ходила ли фигура
#define MASK_IS_MOVED   BYTE8(0,0,0,0,1,0,0,0)
//маска индекса фигуры в массиве
#define MASK_INDEX      ((BYTE8(0,0,0,0,1,1,1,1))<<INDEX_SHIFT)
//маска рокировки
#define MASK_CASTLING (BYTE8(0,0,1,1,0,0,0,0)<<8)
//пустая клетка
#define CELL_EMPTY 0

Дальше следует решить, какого размера будет доска. 8×8 неудобно для анализа выхода за пределы доски. Гораздо удобнее задать массив 16×16 с доской посередине, задав для всех тех клеток, которые не являются доской, флаг границы. В этом случае изменение координаты по X происходит изменением координаты X на нужный шаг, а по Y на шаг*16. Доска задаётся как

CELL Board[256];//шахматная доска с полем посередине (16x16).

Некоторые параметры в дальнейшем будет удобно задавать для поля 8×8, для этой цели стоит завести массив перекодировки координат из поля 16×16 в поле 8×8.

Кстати, чтобы не пришлось сканировать всю доску, стоит помнить, где на доске находятся фигуры. Например, так:

#define COORD long
COORD FigureWhiteCoord256[16];//позиции белых фигур на доске (для быстрого доступа к фигурам. 0- фигуры нет)
COORD FigureBlackCoord256[16];//позиции чёрных фигур на доске (для быстрого доступа к фигурам. 0- фигуры нет)
COORD *KingWhitePointer;//указатель на короля в массиве позиций белых
COORD *KingBlackPointer;//указатель на короля в массиве позиций чёрных

Теперь определимся с тем, как мы будем задавать ходы. Очень удобно сделать так:

long KingMove[9]={16,-16,1,-1,17,-17,15,-15,0};//ходы короля
long QueenMove[9]={16,-16,1,-1,17,-17,15,-15,0};//ходы ферзя
long RookMove[5]={16,-16,1,-1,0};//ходы ладьи
long BishopMove[5]={17,-17,15,-15,0};//ходы слона
long KnightMove[9]={32+1,32-1,16+2,16-2,-(32+1),-(32-1),-(16+2),-(16-2),0};//ходы коня

Здесь в массивах заданы изменения координат в пространстве нашей доски 16×16 для одного шага фигуры. Ходы пешки удобно рассматривать отдельно, так как у неё ходы простые, но есть специфическое взятие на проходе.
Как таким массивом пользоваться? Ну вот, например, составление всех ходов ферзя:

 long n; 
 CELL cell=Board[coord256]; 
 FIGURE_COLOR color=cell&MASK_COLOR;
 FIGURE_COLOR opponent_color=color^(WHITE|BLACK);
 FIGURE_TYPE type=cell&MASK_TYPE;
//--------------------------------------------------
 //ферзь
 //--------------------------------------------------
 if (type==FIGURE_TYPE_QUEEN)
 {
  n=0;
  while(QueenMove[n]!=0)
  {
   COORD c256=coord256+QueenMove[n];    
   while(Board[c256]==CELL_EMPTY)//пока можно ходить
   {     
    Move_AddMove(coord256,c256,FIGURE_TYPE_QUEEN,MOVE_TYPE_SIMPLY,sMove_Ptr,move,sMove_FirstPtr,sMoveKitPtr);//клетка пустая, добавляем ход в список
    c256+=QueenMove[n];
   }
   cell=Board[c256];
   if ((cell&MASK_COLOR)==opponent_color)//фигура противника
   {
    Move_AddEatMove(coord256,c256,FIGURE_TYPE_QUEEN,MOVE_TYPE_SIMPLY,sMove_EatPtr,move_eat,sMove_FirstEatPtr,sMoveKitPtr);//добавляем ход взятия в список ходов взятия
   }
   n++;
  }
  return;
 }

Как видите, всё просто. Для хранения ходов я создал структуру

//Типы ходов
enum MOVE_TYPE
{
 MOVE_TYPE_EMPTY=-1,//хода нет
 MOVE_TYPE_SIMPLY=0,//простой ход
 MOVE_TYPE_CASTLING=1,//рокировка
 MOVE_TYPE_WHITE_PASSED_PAWN_EAT=2,//взятие проходной пешки
 MOVE_TYPE_BLACK_PASSED_PAWN_EAT=3,//взятие проходной пешки
 MOVE_TYPE_CONVERSION=4,//превращение пешки
};
 
//ход фигурой
struct SMove
{
 //начальная позиция
 COORD Coord256_1;
 //конечная позиция
 COORD Coord256_2;  
 MOVE_TYPE MoveType;//тип хода
 FIGURE_TYPE NewFigureType;//новый тип фигуры, если она получилась из пешки
 COORD Coord256_PassedPawn;//ход проходной пешкой (если он есть. 0- проходной пешки нет)
 ENGINE_BOOL IsEat;//ход-взятие
 //изменение веса хода (используем для сортировки ходов)
 long Score;
 //указатель на следующий элемент
 SMove *sMove_NextPtr;
};

Хоть массив ходов и задаётся как

SMove sMove_Level[MAX_PLY+5][200];//ходы фигурой
SMove sMove_EatLevel[MAX_PLY+5][200];//ходы фигурой со взятием

, где MAX_PLY – максимальная глубина анализа (а 200 – максимальное число ходов любой фигуры (с запасом)), но указатель на следующий элемент sMove_NextPtr позволяет удобно сортировать ходы (а сортировать их придётся). std::list (или ещё что из stl) я тут не стал использовать – у нас крайне критично быстродействие (да и я не скажу, что мастер в stl и современном Си++, скорее наоборот). Впрочем, вы можете сделать и с помощью stl и сравнить скорость работы программы – я же этого не проверял.

Ну, в целом, с ходами закончили, перейдём к алгоритмам.

Во-первых, нам нужна функция оценки позиции. Тут возможностей просто море. У меня в движке в engine_score.cpp вполне читаемо описано всё то, что я использую для оценки позиции. Там представлены массивы очков за нахождение фигуры в данной клетке поля (для поля 8×8 – так просто удобно задавать).

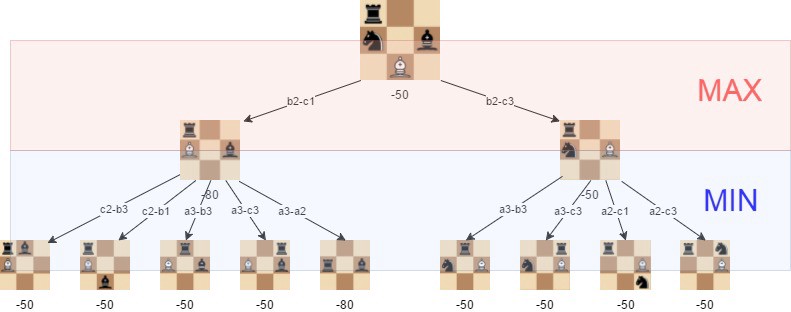
Во-вторых, нам нужен альфа-бета с амортизацией отказов. Думаю, рассматривать сам альфа-бета алгоритм бессмысленно — на эту тему написано множество статей и книг. Да и в общем, он (или его модификации) в основе множества шахматных программ. Самое интересное в шахматных программах, как сократить число ходов для этого алгоритма.

В-третьих, нам нужна хэш-таблица. Дело в том, что в шахматах позиция при переборе часто повторяется – зачем нам заново анализировать то, что уже мы смотрели? Выявить такую позицию и позволяет хэш-таблица. В ней хранятся “уникальные” значения, отличающие одну позицию от другой. Стоятся эти “уникальные” значения просто выполняя операцию xor для ключей элементов, описывающих позицию. Поэтому нам нужны будут массивы уникальных 64 битных чисел (вы можете и любую другую размерность взять, весь вопрос только в том, как часто будут одинаковым значениям позиции соответствовать разные позиции – ошибки хэша). У меня таблица описана так:

//----------------------------------------------------------------------------------------------------
//Зобрист-ключи
//----------------------------------------------------------------------------------------------------
//Хэш-ключи [тип фигуры][цвет фигуры][позиция фигуры на доске 16x16]
unsigned __int64 ZobristKey[FIGURE_TYPE_PAWN+1][2][256]=

Ещё понадобятся ключи смены хода (так как позиции могут быть и одинаковыми, а вот цвет фигур, которые должны ходить разный). И специальный ключ так называемого нулевого хода (о самом нулевом ходе я расскажу ниже). Насколько я помню, вот об этих последних двух ключах Корнилов в своей книжке умолчал.

unsigned __int64 ZobristKeyMove=0x54ca3eb5b5f3cb5b;//ключ смены хода
unsigned __int64 ZobristKeyNullMove=0x08d9bc25bebf91b1;//ключ нулевого хода

Все эти ключи я задал жёстко в программе, чтобы не генерировать каждый раз с проверкой уникальности.

Теперь смотрите какая штука выходит: если мы изначально позицию получим, выполнив xor всех ключей фигур на доске

//----------------------------------------------------------------------------------------------------
//получить хэш-ключ позиции
//----------------------------------------------------------------------------------------------------
unsigned __int64 Hash_GetHKey(void)
{
 unsigned __int64 key=0;
 COORD coord256=4*16+4;
 for(long y=0;y<8;y++,coord256+=16)
 {
  COORD coord256_local=coord256;
  for(long x=0;x<8;x++,coord256_local++)
  {
   CELL cell=Board[coord256_local];
   FIGURE_COLOR color=cell&MASK_COLOR;
   FIGURE_TYPE type=cell&MASK_TYPE;
   if (type==0) continue;
   if (color==WHITE) key^=ZobristKey[type][ZOBRIST_WHITE][coord256_local];
   if (color==BLACK) key^=ZobristKey[type][ZOBRIST_BLACK][coord256_local];
  }
 }
 return(key);
}

, то при выполнении хода, как можно заметить, нам достаточно делать с текущим значением хэша позиции xor ключа фигуры на старом месте, а потом xor ключа фигуры на новом месте. Так же и со взятиями. Это позволяет очень быстро в процессе перебора позиций вычислять значение хэша.

В-четвертых, нам нужна такая штука, как статистика истории. Что это такое? Во время игры можно заметить, что какие-то ходы улучшают оценку позиции. Стоит этот факт отмечать, запоминать и в дальнейшем использовать при сортировке ходов. Как это сделать? Просто завести массив [64][64] ([начальная позиция фигуры на поле 8×8][конечная позиция фигуры на поле 8×8]), обнулить в начале оценки выбора лучшего хода и в дальнейшем просто увеличивать счётчик на 1 в случае хода, улучшающего для нас оценку позиции.

В-пятых, нам нужна сортировка ходов. Самыми первыми должны быть ходы с максимальной выгодой по оценке позиции. Понятно, что ходы взятия приоритетнее обычных “тихих” ходов. Ходы взятия сортируются по принципу MVV/LVA (наиболее ценная жертва – наименее ценный нападающий). При этом стоит продвигать все необычные ходы со взятием (любой ход, который не имеет тип MOVE_TYPE_SIMPLY). Так же вперёд стоит продвинуть и взятие последней ходившей фигуры противника (если взятие будет). Обычные ходы сортируются по возрастанию оценки позиции с учётом эвристики истории. Вся эта сортировка очень важна! Она и сама по себе позволяет сократить обход дерева игры, но более того, на нижних уровнях дерева можно в принципе выбрасывать почти все “тихие” ходы (и если король не под шахом) из рассмотрения без ущерба для качества игры программы! Я увидел такое в коде шахматной программы Ифрит (Ifrit) и, конечно же, применил. Это называется Late Move Reduction, насколько я понимаю.
Для этого используется следующий массив:

static const long FutilityMoveCount[9]={19,19,19,19,19,35,67,131,259};

Здесь числа означают то, сколько “тихих” ходов анализируется в зависимости от уровня дерева (массив задан в обратном порядке). То есть, на последних для анализа 9 уровнях дерева в рассмотрении будет сначала 259 ходов, потом 131, потом 67 и так далее до 19. Это сильно ускоряет работу программы (а также об этом Корнилов вроде как тоже не рассказал в своей книжке). Разумеется, без сортировки ходов такое отсечение не заработает.

В-шестых, нам нужно обязательно продлевать анализ взятий и шахов. Это позволит увеличить точность оценки позиции.

В-седьмых, нам нужна будет эвристика убийцы. Заключается она в том, чтобы при анализе веток дерева пробовать первым ход, вызвавший отсечение на предыдущей ветке. Такой приём также позволяет сократить перебор. Следует помнить, что такой ход может быть только “тихий”: взятия и необычные ходы использовать для таких проверок нельзя.

В-восьмых, есть такая штука, как нулевой ход. Смысл в том, что можно сделать пропуск хода и посмотреть, насколько всё станет плохо. При этом можно сократить глубину анализа дерева (сделать редукцию) – всё равно оценка предварительная. Главное, не забывать пометить хэш позиции ключом этого самого нулевого хода

В-девятых, есть ещё Futility Prunning. Что это такое? На последних двух полуходах дерева оценка позиции не точна и в ряде случаев (если мы не в нулевом ходе, если ход не является шахом, взятием и ход не продление анализа ветки), а также если разность оценки позиции была больше некоторой небольшой величины, то можно просто вернуть эту оценку и не анализировать глубже. Этот приём также ускоряет работу программы.

В-десятых, для сокращения вариантов придуман ещё и Razoring. Это почти то же самое, что и Futility Prunning, но относится к последним четырём полуходам и граница оценки задаётся в некоторую стоимость допустимых потерь фигур.

В-одиннадцатых, некоторые ходы стоит продлевать в анализе. К ним относятся ходы взятия, шахов, приближения фигур противника к королю. Продлевать лучше отдельной функцией анализа, в которой только для шахов стоит запускать полный перебор. Для остальных ходов достаточно анализировать только ходы взятия. Это называется статический поиск.

В-двенадцатых, есть ещё такая штука, как Principal Variation (главное изменение). Это та линия игры, которую программа считает лучшей в данный момент. Эта линия постоянно корректируется во время перебора позиций. Ход из главной линии при сортировке стоит продвигать вперёд.

Ну вот вроде бы и всё из того набора, который использует мой шахматный движок. Надеюсь, я ничего нигде не напутал, так как движку уже два года и я столько же его не касался и вполне мог что-либо забыть.

В архиве лежит сам движок (он поддерживает UCI, так что можете подключить его к Arena), программа под Windows для игры с ним (на скорую руку), шахматы для QNX 6.3. Уровень игры я точно оценить не могу (я не шахматист, как ни странно), но вроде как играет достаточно неплохо.

Добавил ссылку на github:
Шахматы

Всем, кто сейчас смотрит нашумевший сериал «Ход королевы» (The Queen’s Gambit), посвящается. Еще больше шахматных терминов в нашем новом переводе.

В данной статье мы постараемся разобраться, как работают шахматные движки путем портирования шахматного движка sunfish на Go. Sunfish примечателен своей простотой и небольшим размером, но при этом он все-таки способен сыграть достойную шахматную партию. Go в свою очередь известен как простой и хорошо читаемый язык программирования, поэтому я надеюсь, что вместе они составят отличную пару.

Чтобы создать шахматный движок, для начала необходимо определиться с тремя важными моментами:

• Каким образом изобразить шахматную доску (клетки, фигуры, допустимые ходы)?
• Как оценивать доску (кто выиграет с большей вероятностью)?
• Как выполнять поиск оптимального хода?

Фрагменты кода в этом посте упрощены и содержат только самые важные части. Вы можете найти полный код движка по ссылке github.com/zserge/carnatus (carnatus — латинское название морского окуня, вид Sebastes carnatus).

Клетки и фигуры

Важно найти удобное изображение доски, не занимающее много места, так как во время поиска оптимального хода в памяти будут храниться тысячи вариантов досок.

Обычно доска представляет собой набор клеток. Мы добавим отступы вокруг стандартной доски 8×8, чтобы недопустимые ходы фигур попадали в эту область. Это позволит нам избежать проверки границ и значительно упростит код.

Мы будем использовать линейный массив. Самое большое расстояние, на которое может переместиться шахматная фигура, — это ход коня на 2 клетки. Конечно, другие скользящие фигуры могут перемещаться на большие расстояния, но такие ходы будут последовательно оцениваться по мере преодоления каждой клетки, а значит границы доски будут обнаружены раньше, чем фигура сможет выйти за них.

Таким образом, нам необходим отступ по краям доски в две клетки. Мы могли бы создать доску 12×12, но так как мы представляем ее в виде линейного массива, нам нужна доска 12×10, потому что крайний правый квадрат отступа в предыдущей строке может использоваться в качестве крайнего левого квадрата отступа в следующей строке (× = отступ):

××××××××××
××××××××××
×........×
×........×
×........×
×........×
×........×
×........×
×........×
×........×
××××××××××
××××××××××

В нашем обозначении “a1” выглядела бы как 9×10+1=91, а “a8” — как “2×10+1″=21.

Каждая ячейка в массиве доски представляла бы шахматную фигуру, пустую клетку или зону отступа. Мы могли бы использовать числовые константы для этих значений, но, чтобы упростить отладку, используем символы, понятные человеку. Прописными и строчными буквами будут обозначаться фигуры, пробелом — зоны отступа, а точками — пустые клетки:

          |
          |
 RNBQKBNR |
 PPPPPPPP |
 ........ |
 ........ |
 ........ | <- выглядит как настоящая шахматная доска
 ........ |
 ........ |
 ........ |
 pppppppp |
 rnbkqbnr |
          |
          |

Наконец мы можем начать писать код:

type Piece byte
func (p Piece) Value() int { ... }
func (p Piece) Ours() bool { ... }
func (p Piece) Flip() Piece { ... }

type Board [120]piece
func (b Board) Flip() Board { ... }

type Square int
func (s Square) Flip() Square { ... }

Фигуры имеют определенную ценность. Эти значения нужны, чтобы оценивать позиции на доске и понимать, кто выигрывает. Обычно пешка = 100, конь = 280, слон = 320, ладья = 479, ферзь = 929, а король имеет настолько высокую ценность, что она превосходит 8 ферзей (пешки, превратившиеся в ферзей) в совокупности с парами коней, слонов и ладей. Если мы обладаем всем этим богатством, но теряем короля, подсчет все равно покажет, что мы проиграем.

Каждый тип имеет метод переворота (Flip() method), который возвращает то же самое значение после переворота доски перед ходом противника. У фигур он меняет регистр символа фигуры. У клеток он возвращает 119 клеток (считая с другого конца доски). Что касается доски, он копирует все фигуры с клеток в обратном порядке, меняя их регистр.

Генератор ходов

Итак, у нас уже есть «кирпичики» для движка, и теперь мы можем подумать об игровых позициях. Позиция — это доска с фигурами и дополнительные состояния в игре, такие как квадрат прохода, блуждающий квадрат и возможности рокировки. Если бы мы хотели упростить игру, мы бы могли повторно использовать тип доски (Board type), но мы создадим отдельный тип позиции (Position type), отвечающий за ходы и оценку доски.

Что такое ход? Это комбинация двух клеток — клетка, на которой фигура находилась до совершения хода, и клетка, куда переместились фигура. Позиция — это шахматная доска со счетом, правилами рокировки для каждого игрока и квадратами прохода / блуждающими квадратами. Оба типа также имеют метод переворота (Flip() method) для ходов соперника.

type Move struct {
  from Square
  to   Square
}
func (m Move) Flip() Move { ... }

type Position struct {
  board Board   // текущая доска
  score int     // очки по доске — чем их больше, тем лучше
  wc    [2]bool // возможности рокировки для белых
  bc    [2]bool // возможности рокировки для черных
  ep    Square  // битое поле, где пешка может быть взята на проходе
  kp    Square  // поле во время рокировки, где король может быть взят
}
func (p Position) Flip() Position { ... }

Теперь мы можем написать первый большой метод — генератор допустимых ходов. Нам важны только белые фигуры, так как для игры черными мы будем переворачивать доску и снова ходить белыми.

Чтобы сгенерировать все допустимые ходы, нам нужно:

• составить список всех одношаговых ходов в каждом направлении для каждой фигуры;
• выполнить то же самое для всех клеток, игнорируя не белые фигуры;
• обозначить ход в каждом возможном направлении для каждой белой фигуры;
• если длина хода фигуры не ограничена (ладья, слон, ферзь), продолжайте двигать ее, пока на пути не встретится препятствие: фигура соперника или отступ за краем доски.

Это упрощенный код, который не учитывает взятие на проходе и рокировку. Полную реализацию вы можете найти на Github, она не сильно отличается.

Чтобы сделать арифметику направлений более читаемой, мы будем использовать константы направления N/E/S/W:

const N, E, S, W = -10, 1, 10, -1

var directions = map[Piece][]Square{
  'P': {N, N + N, N + W, N + E},
  'N': {N + N + E, E + N + E, E + S + E, S + S + E, S + S + W, W + S + W, W + N + W, N + N + W},
  'B': {N + E, S + E, S + W, N + W},
  'R': {N, E, S, W},
  'Q': {N, E, S, W, N + E, S + E, S + W, N + W},
  'K': {N, E, S, W, N + E, S + E, S + W, N + W},
}

func (pos Position) Moves() (moves []Move) {
  for index, p := range pos.board {
    if !p.ours() {
      continue
    }
    i := Square(index)
    for _, d := range directions[p] {
      for j := i + d; ; j = j + d {
        q := pos.board[j]
        if q == ' ' || (q != '.' && q.ours()) {
          break
        }
        if p == 'P' {
          if (d == N || d == N+N) && q != '.' {
            break
          }
          if d == N+N && (i < A1+N || pos.board[i+N] != '.') {
            break
          }
        }
        moves = append(moves, Move{from: i, to: j})
        if p == 'P' || p == 'N' || p == 'K' || (q != ' ' && q != '.' && !q.ours()) {
          break
        }
      }
    }
  }
  return moves
}

Вот и все правила игры в шахматы, которые нам нужно учитывать, чтобы делать допустимые ходы. Следующим шагом будет применение хода к позиции для создания новой игровой позиции. Без учета взятия на проходе, превращения пешки и рокировки метод будет выглядеть следующим образом:

func (pos Position) Move(m Move) (np Position) {
  np = pos
  np.board[m.to] = pos.board[m.from]
  np.board[m.from] = '.'
  return np.Flip()
}

Он просто передвигает фигуру, помечает клетку, на которой она находилась ранее, как пустую и переворачивает доску. Полную реализацию метода можно найти на Github, он правильно обрабатывает все специальные ходы пешки и короля.

На этом этапе можно играть в шахматы «человек против человека», контролируя процесс и делая только допустимые ходы. Или же можно создать примитивный шахматный движок, который делает случайные ходы пока не проиграет.

Но как понять, что мы проигрываем?

Оценка доски

За каждую позицию на доске начисляются очки. Изначально счет равняется нулю, так как оба игрока начинают в равных условиях. После выполнения хода счет меняется в зависимости от того, какие фигуры были взяты и как фигуры поменяли положение на доске.

В самом простом случае мы можем сосчитать фигуры на доске и сложить их ценность (за вычетом фигур противника). Такой подсчет покажет, если королю будет объявлен шах и мат. Но это очень слабая система оценки.

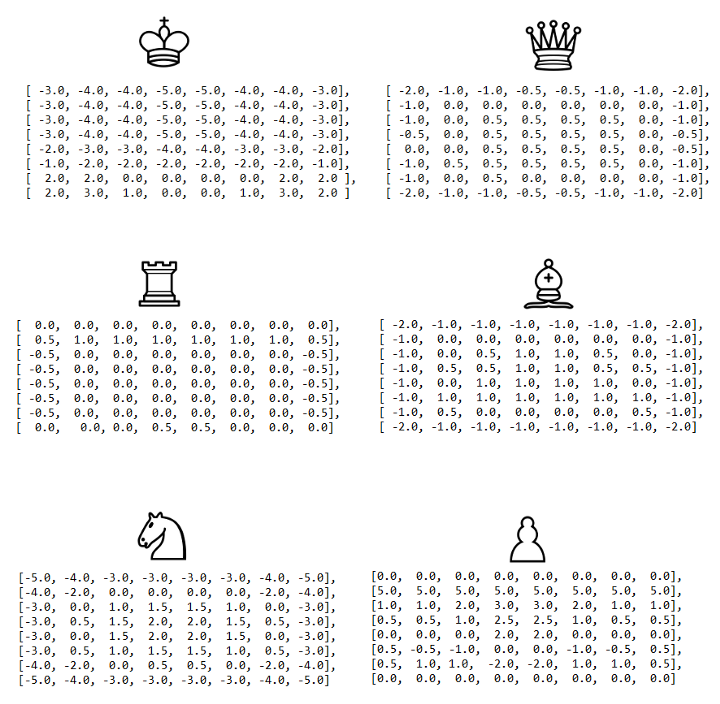
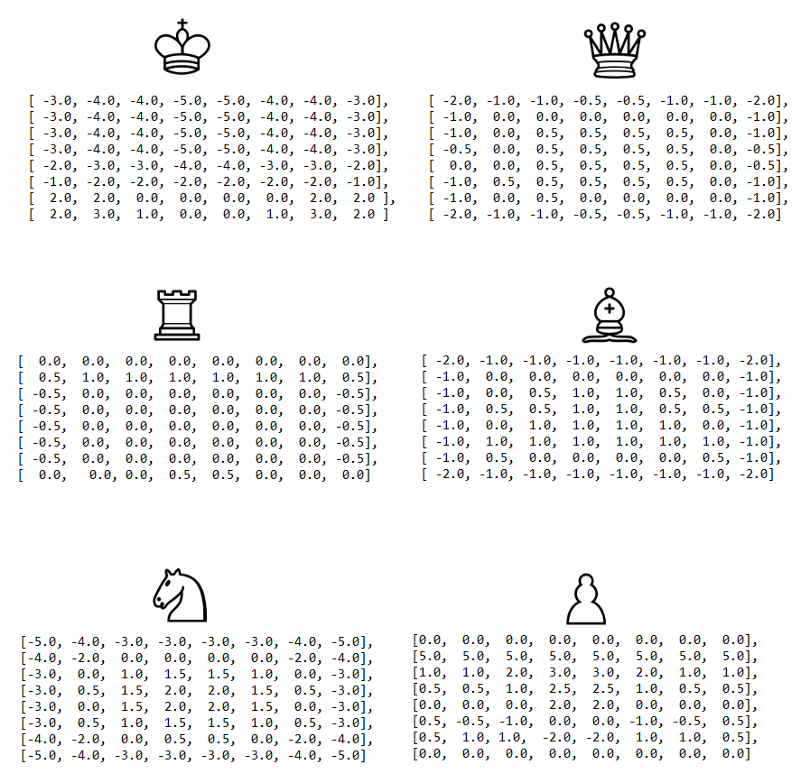
Гораздо более точный и удивительно простой подход — это таблицы соотношения фигур и клеток (PST — Piece-Square Tables). Для каждой фигуры создается таблица такого же размера, как шахматная доска, где для каждой клетки назначается соответствующая ценность. Эти значения являются эмпирическими, поэтому я просто взял их из движка Sunfish.

На самом деле, более продвинутые шахматные движки обновляют PST-таблицы во время игры, потому что ценность фигур меняется (т. е. пешки становятся более ценными к концу игры). Но у нас будет простой движок.

Чтобы оценить позицию после хода, нам нужно:

• определить рейтинг текущей позиции,
• вычесть ценность передвигаемой фигуры,
• прибавить новую ценность фигуры в соответствии с таблицей PTS,
• прибавить ценность захваченной фигуры, если такие имеются.

Дополнительно нам нужно отрегулировать в PST-таблице ценность ладьи во время рокировки и ценность пешки во время превращения или взятия на проходе. Но в здесь мы не будем это рассматривать:

var pst = map[Piece][120]int{
  'P': { ... },
  'N': { ... },
  'B': { ... },
  'R': { ... },
  'Q': { ... },
  'K': { .... },
}

func (pos Position) value(m Move) int {
  i, j := m.from, m.to
  p, q := Piece(pos.board[i]), Piece(pos.board[j])
  // Настроить значение передвигаемой фигуры в PST-таблице
  score := pst[p][j] - pst[p][i]
  if q != '.' && q != ' ' && !q.ours() {
    // Настроить значение захваченной фигуры в PST-таблице
    score += pst[q.Flip()][j.Flip()]
  }
  return score
}

Теперь мы можем сделать немного более продвинутый движок, который будет выбирать наилучший возможный ход, а не любой из допустимых.

Но настоящие шахматные движки проводят более глубокую аналитику и перебирают ветви возможных ходов с каждой стороны, чтобы найти наилучший возможный ход в долгосрочной перспективе.

Алгоритм поиска

Наиболее распространенный алгоритм поиска в шахматных движках попроще — поиск в глубину, который начинается с корня и спускается до заданного предела глубины, повторяя все возможные ходы перед возвратом. Для каждого хода вычисляется ценность позиции с использованием алгоритма минимакс (minimax) c альфа-бета отсечением (alpha-beta pruning).

Минимакс — это правило, используемое для минимизации возможных потерь при наихудшем раскладе: игрок рассматривает все лучшие ходы противника и выбирает такой ход, чтобы лучшая стратегия противника приносила как можно больше очков.

Простой алгоритм минимакс будет слишком медленным для шахмат, он потребует повторения слишком большого количества ходов, чтобы найти хороший.

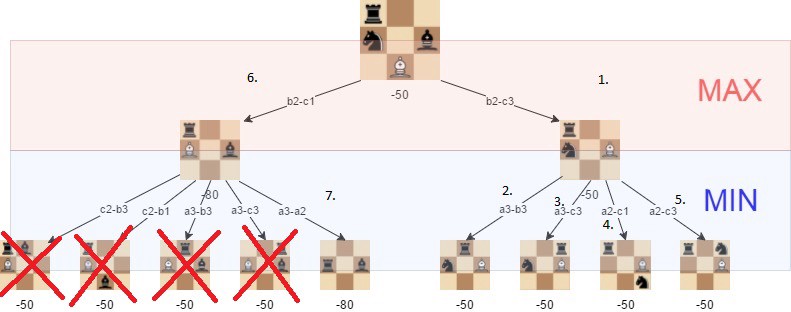
Альфа-бета отсечение (alpha-beta pruning) используется для ускорения алгоритма минимакс путем удаления узлов, которые не стоит рассматривать. В основе альфа-бета отсечения лежит следующая логика: представьте, что вы играете в шахматы и обнаруживаете очень хороший ход А. Вы продолжаете смотреть на доску и находите еще более удачный ход B. Но затем вы анализируете ситуацию глубже и понимаете, что в случае выбора хода B противник объявит вам шах и мат через несколько ходов. Теперь вы отбросите ход B и не будете тратить время на анализ других возможных комбинаций после хода B.

Как минимакс, так и альфа-бета отсечение важны для понимания принципа работы шахматного движка. Движок Sunfish использует усовершенствованный алгоритм поиска MDF(f), который также является вариантом алгоритма минимакс, совмещенного с отсечением.

В нашем движке мы будем постепенно увеличивать глубину поиска и вызывать алгоритм MDF(f) для поиска нижних и верхних границ оптимального результата. Алгоритм MDF (f) будет использовать итерации альфа-бета отсечения с кэшем транспозиции.

Кэш транспозиции — это кэш, где для каждой позиции на доске мы запоминаем глубину, счет и ход, который привел нас к этой позиции. Затем при рассмотрении новой позиции она сначала проверяется по таблице транспозиции.

Я не буду публиковать здесь код алгоритма поиска, так как он представляет собой всего лишь несколько строк рекурсивного поиска, но вы всегда можете найти полные исходники шахматного движка на GitHub.

Что дальше?

Если вам интересны простые шахматные движки, настоятельно рекомендую сыграть с Sunfish. Кстати, основой для Sunfish послужил движок Micromax, к нему прилагается замечательная документация от автора, которую определенно стоит прочитать.

Что касается нашего движка в Go, я добавил небольшую реализацию протокола UCI, чтобы его можно было использовать с пользовательским интерфейсом PyChess. Скорее всего, в нем еще куча ошибок и большой потенциал для улучшений, но это был интересный путь: от идеи о разработке шахматного движка до готовой, работающей компьютерной шахматной программы.

Да, он слабенький, но он играет настоящие шахматные партии!

Надеюсь, вам понравилась эта статья. Вы можете подписаться на меня в Github, Twitter или подписаться через rss.

Введение

Не так давно я захотел написать свой шахматный движок. На удивление в Интернете нашлось не так много хороших статей на эту тему. Были статьи с довольно слабыми программами, многие из которых даже умудрялись пропускать некоторые важные правила. А были статьи с хорошими программами (некоторые из них были даже чуть лучше чем получилось у меня в итоге), но там авторы рассказывали лишь основные идеи, пропуская подробности, из-за чего написать что-то свое по таким статьям было проблематично. Поэтому после написания своей программы, я решил написать статью, дабы облегчить жизнь интересующимся в данной теме. Я не претендую на лучшую шахматную программу или на чистейший код, но эта статья будет хорошим и легким началом для тех, кто хочет написать что-то свое.

Битборды или битовые доски

Существует довольно удобная система представления доски, называемая битбордами или битовыми досками, если по-русски. Идея битбордов строится на замечательном совпадении: шахматная доска содержит 64 клетки, когда как современные компьютеры умеют невероятно быстро работать с 64 битовыми числами. Таким образом мы можем использовать 12 таких битбордов для хранения всех фигур. Каждый такой битборд будет хранить какую-то фигуру (или пешку), например — один битборд отвечает за черных коней, другой — за белые пешки, третий — за черного короля.

Основная причина выбора битбордов, а не массива на 64 клетки — высокая скорость и, как, это не странно, удобность. Например, нам надо проверить является ли пешка проходной. Проходная пешка, согласно Википедии, это

пешка, на одной вертикали перед которой отсутствуют пешки противника, а на
соседних вертикалях или нет пешек противника или они не держат под боем
поля, через которые пешка должна пройти до поля превращения.

Используя массив из 64 клеток, нам надо было бы проверять, в худшем случае, целых 18 клеток для каждой пешки, чтобы сказать какие являются проходными, а какие нет. Используя битборды, мы можем заранее рассчитать на каких клетках не должны стоять пешки противника, чтобы пешка называлась проходной, а затем использовать эти данные чтобы узнать является ли пешка проходной за одну операцию побитового «и».

Предлагаю перейти к реализации наших битбордов. На самом деле, реализовывать их не надо, ведь битборд — просто красивое название для 64 битного числа. Так что объявление битборда будет выглядеть так:

typedef uint64_t Bitboard;

Обращаю внимание, что используется именно беззнаковое число, так как в процессе программирования будут использоваться битовые сдвиги, а битовые сдвиги со знаковыми переменными работают не так как нам надо будет (ведь 1 бит из 64 при использовании знаковых переменных отвечает за знак числа и его компьютер трогать не будет).

Но с одним объявлением жить довольно грустно, нужно реализовать несколько дополнительных операций, чтобы облегчить жизнь.

static constexpr void set_1(Bitboard &bb, uint8_t square) {
        bb = bb | (1ull << square);
}
static constexpr void set_0(Bitboard &bb, uint8_t square) {
     bb = bb & (~(1ull << square));
}


static constexpr bool get_bit(Bitboard bb, uint8_t square) {
    return (bb & (1ull << square));
}

Перед вами примитивные операции для обращения к битбордам по индексу. Нужно пытаться их избегать, так как они довольно медленные, но совсем без них никуда.

Еще нам понадобится считать количество единичных битов. Это знание нужно, например, при оценке позиции. Чтобы узнать насколько хороша позиция надо, как минимум, узнать сколько фигур у белых и сколько фигур у черных, а для этого надо их посчитать.

Но как это сделать? Самое наивное что можно придумать — пройти по всем 64 битам и посчитать, но думаю, что прекрасно понятно, что это очень не эффективно. На эту тему есть отличная статья на хабре, но подобное уже было реализовано в стандартной библиотеке, а именно в заголовке bit, так что просто воспользуемся готовой функцией:

static constexpr uint8_t count_1(Bitboard bb) {
        return std::popcount(bb);
}

Помимо этого нам нужны еще две функции: поиск первого единичного бита и поиск последнего. Для этих операций придумали даже специальные инструкции в процессорах. Но я ими решил не пользоваться, так как они плохо влияют на переносимость проекта. К тому же разница в скорости между этими инструкциями и оптимизированным подходом оказалась на уровне погрешности (по крайней мере, в практических условиях). Поэтому было решено использовать оптимизированный алгоритм. Объяснять его я не буду, так как на объяснение, вероятно, уйдет столько же времени, сколько и на весь остальной движок, а это явно не то зачем сюда пришли люди, так что просто посмотрите на эту замечательную реализацию, взятую с chessprogrammingwiki:

static constexpr std::array<uint8_t, 64> BitScanTable = {
            0, 47,  1, 56, 48, 27,  2, 60,
            57, 49, 41, 37, 28, 16,  3, 61,
            54, 58, 35, 52, 50, 42, 21, 44,
            38, 32, 29, 23, 17, 11,  4, 62,
            46, 55, 26, 59, 40, 36, 15, 53,
            34, 51, 20, 43, 31, 22, 10, 45,
            25, 39, 14, 33, 19, 30,  9, 24,
            13, 18,  8, 12,  7,  6,  5, 63
};


static constexpr uint8_t bsf(Bitboard bb) {
    return BitboardOperations::BitScanTable[((bb ^ (bb - 1)) * 0x03f79d71b4cb0a89) >> 58];
}
static constexpr uint8_t bsr(Bitboard bb) {
    bb = bb | (bb >> 1);
    bb = bb | (bb >> 2);
    bb = bb | (bb >> 4);
    bb = bb | (bb >> 8);
    bb = bb | (bb >> 16);
    bb = bb | (bb >> 32);

    return BitboardOperations::BitScanTable[(bb * 0x03f79d71b4cb0a89) >> 58];
}

Еще нам нужно заготовить битборды с заранее вычисленными столбцами и строками, поэтому напишем еще этот кусок кода:

namespace BitboardRows {
    static consteval std::array<Bitboard, 8> calc_rows() {
        std::array<Bitboard, 8> rows{};

        for (uint8_t y = 0; y < 8; y = y + 1) {
            for (uint8_t x = 0; x < 8; x = x + 1) BitboardOperations::set_1(rows[y], y * 8 + x);
        }

        return rows;
    }


    static constexpr std::array<Bitboard, 8> Rows = BitboardRows::calc_rows();


    static consteval std::array<Bitboard, 8> calc_inversion_rows() {
        std::array<Bitboard, 8> inversion_rows{};

        for (uint8_t i = 0; i < 8; i = i + 1) inversion_rows[i] = ~Rows[i];

        return inversion_rows;
    }


    static constexpr std::array<Bitboard, 8> InversionRows = BitboardRows::calc_inversion_rows();
}


namespace BitboardColumns {
    static consteval std::array<Bitboard, 8> calc_columns() {
        std::array<Bitboard, 8> columns{};

        for (uint8_t x = 0; x < 8; x = x + 1) {
            for (uint8_t y = 0; y < 8; y = y + 1) BitboardOperations::set_1(columns[x], y * 8 + x);
        }

        return columns;
    }


    static constexpr std::array<Bitboard, 8> Columns = BitboardColumns::calc_columns();


    static consteval std::array<Bitboard, 8> calc_inversion_columns() {
        std::array<Bitboard, 8> inversion_columns{};

        for (uint8_t i = 0; i < 8; i = i + 1) inversion_columns[i] = ~Columns[i];

        return inversion_columns;
    }


    static constexpr std::array<Bitboard, 8> InversionColumns = BitboardColumns::calc_inversion_columns();
}

Он супер медленный по сравнению с тем, что, вероятно, можно сделать при помощи битовых сдвигов, но это не критично, так как вычисления происходят все равно на этапе компиляции.

Хранение фигур

Из чего складывается позиция в шахматах? Из прав на рокировку, сложных правил про троекратное повторение позиции, счетчика 50 ходов и так далее, но база — это фигуры и пешки. Сейчас нужно написать структуру, которая будет хранить все фигуры и пешки. Но какие именно типы будет хранить структура? Разумеется, 12 битбордов о которых был разговор в предыдущем разделе, но этого мало. Так же стоит хранить битборды всех белых и всех черных фигур, всех фигур вообще, и битборды, обратные этим битбордам. Такие битборды могут быть составлены на основе базовых 12 битбордов и будут обновляться после обновления базовых битбордов. Но зачем они нам нужны? Например, при генерации ходов. Когда мы будем генерируем ходы, например, коня, нам нужно будет проверять содержится ли в клетке фигура того же цвета, что и конь, и если содержится — то такой ход не может быть выполнен.

Когда известно, что должна хранить структура, можно написать это в коде. Вот так это выглядит:

std::array<std::array<Bitboard, 6>, 2> _piece_bitboards{};
std::array<Bitboard, 2> _side_bitboards{};
std::array<Bitboard, 2> _inversion_side_bitboards{};
Bitboard _all;
Bitboard _empty;

Для индексации по массивам битбордов нужно использовать константы. Вот они:

static constexpr uint8_t Pawn = 0;
static constexpr uint8_t Knight = 1;
static constexpr uint8_t Bishop = 2;
static constexpr uint8_t Rook = 3;
static constexpr uint8_t Queen = 4;
static constexpr uint8_t King = 5;

static constexpr uint8_t White = 0;
static constexpr uint8_t Black = 1;

Так же стоит написать функцию, превращающую белое в черное, а черное в белое. Так как белое и черное у нас отмечено как 0 и 1, то для изменения цвета достаточно вызвать логическое отрицание:

uint8_t Pieces::inverse(uint8_t side) {
    return !side;
}

Еще нам понадобится возможность сравнивать наши структуры:

bool operator ==(Pieces left, Pieces right) {
    for (uint8_t i = 0; i < 2; i = i + 1) {
        for (uint8_t j = 0; j < 6; j = j + 1) {
            if (left._piece_bitboards[i][j] != right._piece_bitboards[i][j]) return false;
        }
    }

    return true;
}

Уже было много сказано про хранение фигур, но еще не был создан конструктор, то есть пока неизвестно как инициализировать битборды.

Если говорить о второстепенных битбордах, то их можно легко инициализировать на основе основных, но это не помогает инициализировать основные:

void Pieces::update_bitboards() {
    this->_side_bitboards[Pieces::White] = this->_piece_bitboards[Pieces::White][Pieces::Pawn] |
                                           this->_piece_bitboards[Pieces::White][Pieces::Knight] |
                                           this->_piece_bitboards[Pieces::White][Pieces::Bishop] |
                                           this->_piece_bitboards[Pieces::White][Pieces::Rook] |
                                           this->_piece_bitboards[Pieces::White][Pieces::Queen] |
                                           this->_piece_bitboards[Pieces::White][Pieces::King];

    this->_side_bitboards[Pieces::Black] = this->_piece_bitboards[Pieces::Black][Pieces::Pawn] |
                                           this->_piece_bitboards[Pieces::Black][Pieces::Knight] |
                                           this->_piece_bitboards[Pieces::Black][Pieces::Bishop] |
                                           this->_piece_bitboards[Pieces::Black][Pieces::Rook] |
                                           this->_piece_bitboards[Pieces::Black][Pieces::Queen] |
                                           this->_piece_bitboards[Pieces::Black][Pieces::King];

    this->_inversion_side_bitboards[Pieces::White] = ~this->_side_bitboards[Pieces::White];
    this->_inversion_side_bitboards[Pieces::Black] = ~this->_side_bitboards[Pieces::Black];

    this->_all = this->_side_bitboards[Pieces::White] | this->_side_bitboards[Pieces::Black];
    this->_empty = ~this->_all;
}

На самом деле инициализировать основные можно довольно легко при помощи операции установки единичного бита, которая был реализована в предыдущем разделе. Мы просто проходим по доске и, согласно шахматным правилам, расставляем фигуры. Производительность тут особо неважна, так как подобный конструктор вызывается крайне редко, но существует более хороший способ сделать это, а именно сделать поддержку нотации шотландского шахматиста, Форсайта Эдвардса, или FEN нотации (англ. Forsyth–Edwards Notation).

Идея очень проста. Сначала идет описания фигур на последней строке (та, на которой стоят фигуры черных в обычной расстановке). Каждой фигура обозначается первой буквой из ее английской записи, за исключением коня: он обозначается второй буквой, так как буква k уже занята королем. Причем если фигура черная, то она стоит в маленьком регистре, а если белая — то в большом. Если клетка пуста, то ставится единичка. Если несколько клеток подряд пусты, то цифра, отражающая сколько клеток пусто подряд. После того как последняя строка была описана ставится разделитель / и идет информация о строке ниже. Так происходит пока все строки не будут описаны. Ниже есть пару примеров, чтобы было понятнее.

Все очень просто. Я немного обманул и это не все про FEN нотацию, там есть еще часть показывающая номер хода, права на рокировку, битое поле и так далее, но нам это не понадобится.

Зная это, можно написать такой вот код инициализирующий все битборды при помощи FEN строки:

Pieces::Pieces(const std::string& short_fen) {
    uint8_t x = 0;
    uint8_t y = 7;

    uint8_t side;

    for (auto buff : short_fen) {
        if (buff == '/') {
            x = 0;
            y = y - 1;
        }
        else if (std::isdigit(buff)) {
            x = x + buff - '0';
        }
        else {
            if (std::isupper(buff)) {
                buff = std::tolower(buff);
                side = Pieces::White;
            }
            else side = Pieces::Black;

            switch (buff) {
                case 'p': BitboardOperations::set_1(this->_piece_bitboards[side][Pieces::Pawn], y * 8 + x); break;
                case 'n': BitboardOperations::set_1(this->_piece_bitboards[side][Pieces::Knight], y * 8 + x); break;
                case 'b': BitboardOperations::set_1(this->_piece_bitboards[side][Pieces::Bishop], y * 8 + x); break;
                case 'r': BitboardOperations::set_1(this->_piece_bitboards[side][Pieces::Rook], y * 8 + x); break;
                case 'q': BitboardOperations::set_1(this->_piece_bitboards[side][Pieces::Queen], y * 8 + x); break;
                case 'k': BitboardOperations::set_1(this->_piece_bitboards[side][Pieces::King], y * 8 + x); break;
            }

            x = x + 1;
        }
    }

    this->update_bitboards();
}

Чтобы проверить, что все правильно можно написать такой вот оператор вывода:

std::ostream &operator<<(std::ostream &ostream, Pieces pieces) {
    for (int8_t y = 7; y >= 0; y = y - 1) {
        for (uint8_t x = 0; x < 8; x = x + 1) {
            ostream << "|  ";

            if (BitboardOperations::get_bit(pieces._piece_bitboards[Pieces::White][Pieces::Pawn], y * 8 + x)) ostream << "♙";
            else if (BitboardOperations::get_bit(pieces._piece_bitboards[Pieces::White][Pieces::Knight], y * 8 + x)) ostream << "♘";
            else if (BitboardOperations::get_bit(pieces._piece_bitboards[Pieces::White][Pieces::Bishop], y * 8 + x)) ostream << "♗";
            else if (BitboardOperations::get_bit(pieces._piece_bitboards[Pieces::White][Pieces::Rook], y * 8 + x)) ostream << "♖";
            else if (BitboardOperations::get_bit(pieces._piece_bitboards[Pieces::White][Pieces::Queen], y * 8 + x)) ostream << "♕";
            else if (BitboardOperations::get_bit(pieces._piece_bitboards[Pieces::White][Pieces::King], y * 8 + x)) ostream << "♔";

            else if (BitboardOperations::get_bit(pieces._piece_bitboards[Pieces::Black][Pieces::Pawn], y * 8 + x)) ostream << "♟";
            else if (BitboardOperations::get_bit(pieces._piece_bitboards[Pieces::Black][Pieces::Knight], y * 8 + x)) ostream << "♞";
            else if (BitboardOperations::get_bit(pieces._piece_bitboards[Pieces::Black][Pieces::Bishop], y * 8 + x)) ostream << "♝";
            else if (BitboardOperations::get_bit(pieces._piece_bitboards[Pieces::Black][Pieces::Rook], y * 8 + x)) ostream << "♜";
            else if (BitboardOperations::get_bit(pieces._piece_bitboards[Pieces::Black][Pieces::Queen], y * 8 + x)) ostream << "♛";
            else if (BitboardOperations::get_bit(pieces._piece_bitboards[Pieces::Black][Pieces::King], y * 8 + x)) ostream << "♚";

            else ostream << " ";

            ostream << "  ";
        }
        ostream << "|n";
    }

    return ostream;
}

Zobrist хеширование

Часто нужно проверять одинаковы ли позиции (самое очевидно — правило троекратного повторения позиции, в будущем это понадобится нам еще для одной вещи). Это можно сделать используя структуру из предыдущего раздела, но для этого потребуется 12 операций сравнения, что дорого. Вместо этого можно хешировать позицию и хранить ее не в 12 64 битных числах, а в 1 и сравнивать не за 12 операций сравнения, а за 1. Разумеется нельзя сжать битборды в 12 раз, даже учитывая факт, что по памяти они не самые оптимальные, но мы можем это сделать если согласится с некоторыми рисками.

Итак, что нам нужно. Нам нужна функция, позволяющая сжимать позицию в одно число. Такая функция есть и называется она Zobrist хешированием, в честь Альберт Линдси Зобриста.

Идея в следующем. Нам надо заготовить константу для каждой фигуры, находящейся в каждой клетке доски. Итоге нам понадобится 12 * 64 = 768 констант, плюс несколько специальных констант для прав на рокировку и право хода (чтобы позиции с одинаковыми фигурами на доске, но с разными правами на ход или на рокировку давали разный хеш).

Это я и сделал. Я написал небольшой ГПСЧ работающий во времени компиляции для генерации случайных констант. Получилось вот что:

#include <cstdint>
#include <array>


#pragma once


namespace ZobristHashConsteval {
    namespace PRNG {
        static constexpr uint64_t Seed = 0x98f107;
        static constexpr uint64_t Multiplier = 0x71abc9;
        static constexpr uint64_t Summand = 0xff1b3f;
    }


    static consteval uint64_t next_random(uint64_t previous) {
        return ZobristHashConsteval::PRNG::Multiplier * previous + ZobristHashConsteval::PRNG::Summand;
    }
    static consteval std::array<std::array<std::array<uint64_t, 6>, 2>, 64> calc_constants() {
        std::array<std::array<std::array<uint64_t, 6>, 2>, 64> constants{};

        uint64_t previous = ZobristHashConsteval::PRNG::Seed;

        for (uint8_t square = 0; square < 64; square = square + 1) {
            for (uint8_t side = 0; side < 2; side = side + 1) {
                for (uint8_t type = 0; type < 6; type = type + 1) {
                    previous = ZobristHashConsteval::next_random(previous);
                    constants[square][side][type] = previous;
                }
            }
        }

        return constants;
    }


    static constexpr std::array<std::array<std::array<uint64_t, 6>, 2>, 64> Constants = calc_constants();
    static constexpr uint64_t BlackMove = ZobristHashConsteval::next_random(ZobristHashConsteval::Constants[63][1][5]);
    static constexpr uint64_t WhiteLongCastling = ZobristHashConsteval::next_random(ZobristHashConsteval::BlackMove);
    static constexpr uint64_t WhiteShortCastling = ZobristHashConsteval::next_random(ZobristHashConsteval::WhiteLongCastling);
    static constexpr uint64_t BlackLongCastling = ZobristHashConsteval::next_random(ZobristHashConsteval::WhiteShortCastling);
    static constexpr uint64_t BlackShortCastling = ZobristHashConsteval::next_random(ZobristHashConsteval::BlackLongCastling);
}

Используя эти константы, можно посчитать хеш текущей позиции при помощи применения XOR между всеми константами и нулем. Википедия дает такой псевдокод:

function hash(board):
    h := 0
    if is_black_turn(board):
        h := h XOR table.black_to_move
    for i from 1 to 64:      # loop over the board positions
        if board[i] ≠ empty:
            j := the piece at board[i], as listed in the constant indices, above
            h := h XOR table[i][j]
    return h

Получается чтобы проверить равны ли позиции нам надо пройтись по всем клеткам, посчитать хеш и сравнить хеши, вместо того чтобы при проходе по всем клеткам сравнивать две позиции напрямую? Звучит как бред. И если бы это работало так на самом деле, то это действительно было бы бредом, но у такого хеширования есть замечательно свойство, делающее его очень эффективным.

Например, у нас есть позиция с двумя королями и пешкой. У нас известен ее хеш. Он получился так:

0 ^ WhiteKingOnD1 ^ BlackKingOnE7 ^ WhitePawnOnC4

Теперь мы хотим добавить к этой позиции белого коня, стоящего на клетке C5. И если мы выполним XOR с текущим хешом и константой для белого коня на C5, то получится тот же самый хеш, что получился бы если бы мы посчитали его заново после добавления коня.

Другой пример. Мы хотим убрать белую пешку, стоящую на C4 из нашего хеша. Если мы выполним XOR с текущим хешом и константой этой белой пешки, стоящей на C4, то получится это:

0 ^ WhiteKingOnD1 ^ BlackKingOnE7 ^ WhitePawnOnC4 ^ WhitePawnOnC4

После чего константы для белых пешек на C4 сократятся, так как XOR обладает самообратимостью, то есть

a ^ a = 0

Получается, и чтобы добавить фигуру, и чтобы ее удалить из хеша, надо просто сделать XOR с текущим хешом и ключом этой фигуры на нужной позиции.

С флагами рокировки и хода все аналогично, для инверсии флага просто нужно выполнять XOR с существующим ключом и флагом.

Используя это знание и созданные константы можно легко реализовать структуру Zobrist хеша:

#include "ZobristHash.hpp"


ZobristHash::ZobristHash() = default;
ZobristHash::ZobristHash(Pieces pieces, bool black_move, bool w_l_castling, bool w_s_castling, bool b_l_castling, bool b_s_castling) {
    this->_hash = 0;

    if (black_move) this->invert_move();
    if (w_l_castling) this->invert_w_l_castling();
    if (w_s_castling) this->invert_w_s_castling();
    if (b_l_castling) this->invert_b_l_castling();
    if (b_s_castling) this->invert_b_s_castling();

    uint8_t side;
    for (uint8_t square = 0; square < 64; square = square + 1) {
        if (BitboardOperations::get_bit(pieces._side_bitboards[Pieces::White], square)) side = Pieces::White;
        else if (BitboardOperations::get_bit(pieces._side_bitboards[Pieces::Black], square)) side = Pieces::Black;
        else continue;

        for (uint8_t type = 0; type < 6; type = type + 1) {
            if (BitboardOperations::get_bit(pieces._piece_bitboards[side][type], square)) {
                this->invert_piece(square, type, side);
                break;
            }
        }
    }
}
bool operator ==(ZobristHash left, ZobristHash right) {
    return (left._hash == right._hash);
}
bool operator <(ZobristHash left, ZobristHash right) {
    return (left._hash < right._hash);
}
void ZobristHash::invert_piece(uint8_t square, uint8_t type, uint8_t side) {
    this->_hash = this->_hash ^ ZobristHashConsteval::Constants[square][side][type];
}
void ZobristHash::invert_move() {
    this->_hash = this->_hash ^ ZobristHashConsteval::BlackMove;
}
void ZobristHash::invert_w_l_castling() {
    this->_hash = this->_hash ^ ZobristHashConsteval::WhiteLongCastling;
}
void ZobristHash::invert_w_s_castling() {
    this->_hash = this->_hash ^ ZobristHashConsteval::WhiteShortCastling;
}
void ZobristHash::invert_b_l_castling() {
    this->_hash = this->_hash ^ ZobristHashConsteval::BlackLongCastling;
}
void ZobristHash::invert_b_s_castling() {
    this->_hash = this->_hash ^ ZobristHashConsteval::BlackShortCastling;
}

Троекратное повторение позиции

В шахматах существует правило, называемое троекратным повторением позиции. Правило заключается в том, что если одна и та же позиция встречается трижды, то фиксируется ничья. Используя хеш функцию из предыдущей части, можно легко реализовать это правило.

Мы будем хранить вектор из Zobrist хешей, пополняющихся после каждого хода, а при запросе на количество повторений считать сколько есть копий последнего добавленного хеша. Это звучит очень не эффективно, но на самом деле в процессе игры можно очень часто очищать вектор, так как есть необратимые ходы. Если произошло движение пешки или взятие, то это уже нельзя отменить. Соответственно не может возникнуть никаких совпадений с позициями до продвижения пешки или взятия. Так что если происходит продвижение пешки или взятие можно полностью очистить весь вектор.

Вот полностью класс:

#include <vector>
#include "ZobristHash.hpp"


#pragma once


class RepetitionHistory {
public:
    RepetitionHistory();

    void add_position(ZobristHash hash);

    void clear();

    uint8_t get_repetition_number(ZobristHash hash);
private:
    std::vector<ZobristHash> _hashes;
};

#include "RepetitionHistory.hpp"


RepetitionHistory::RepetitionHistory() = default;
void RepetitionHistory::add_position(ZobristHash hash) {
    this->_hashes.push_back(hash);
}
void RepetitionHistory::clear() {
    this->_hashes.clear();
}
uint8_t RepetitionHistory::get_repetition_number(ZobristHash hash) {
    uint8_t ctr = 0;

    for (auto hash1 : this->_hashes) if (hash == hash1) ctr = ctr + 1;

    return ctr;
}

Хранение хода

Нам нужна структура, позволяющая хранить ход. Минимальное требование к такой структуре: она должна хранить информацию из какой клетки и куда, а также флаг хода со специальной информацией (например — информация о рокировках или в какую фигуру превращается пешка после продвижения). Я решил пойти дальше и хранить еще информацию о том какая фигура двигалась и какая фигура были съедена (если была). Это нужно для того, чтобы при применении хода не нужно было искать на каком битборде нужно убирать фигуру, а на какой ставить. Кто-то может возразить, что в любом случае это придется искать, просто не в функции применения хода, а в генераторе ходов, но он будет не совсем прав. При генерации ходов мы всегда знаем какая фигура двигалась, а иногда — какую съели. Таким образом мы меньше времени тратим на бессмысленный поиск по битбордам.

Вот заголовок структуры (саму реализацию показывать нет смысла). Обращу внимание только на то, что если защитника нет (то есть того, кого съели), то в переменную мы будем класть максимальное значение uint8_t, то есть 255.

#include <cstdint>


#pragma once


struct Move {
    Move();
    Move(uint8_t from, uint8_t to, uint8_t attacker_type, uint8_t attacker_side, uint8_t defender_type, uint8_t defender_side, uint8_t flag = Move::Flag::Default);

    friend bool operator ==(Move left, Move right);

    uint8_t _from;
    uint8_t _to;

    uint8_t _attacker_type;
    uint8_t _attacker_side;

    uint8_t _defender_type;
    uint8_t _defender_side;

    uint8_t _flag;

    struct Flag {
        static constexpr uint8_t Default = 0;

        static constexpr uint8_t PawnLongMove = 1;
        static constexpr uint8_t EnPassantCapture = 2;

        static constexpr uint8_t WhiteLongCastling = 3;
        static constexpr uint8_t WhiteShortCastling = 4;
        static constexpr uint8_t BlackLongCastling = 5;
        static constexpr uint8_t BlackShortCastling = 6;

        static constexpr uint8_t PromoteToKnight = 7;
        static constexpr uint8_t PromoteToBishop = 8;
        static constexpr uint8_t PromoteToRook = 9;
        static constexpr uint8_t PromoteToQueen = 10;
    };
};

Хранение позиции

После всего этого можно создать класс позиции. Это последний этап в представлении доски.

Что должна хранить позиция?

Во-первых, фигуры. Для них мы уже написали структуру, так что об этом беспокоится не нужно.

Во-вторых, битую клетку. Это нужно для реализации правила взятия на проходе. Если такой клетки нет, то в переменной будет лежать 255. как и в случае со структурой хода.

В-третьих, права на рокировку. Без комментариев.

В-четвертых, переменные, отражающие была ли сделана рокировка. Это не совсем то, что предыдущий пункт, так как права на рокировку можно потерять не сделав ее, а тут мы храним информацию о том была ли она сделана. Это знание поможет в разработке ИИ.

В-пятых, счетчик ходов. Это просто float переменная, добавляющая по 0.5 за каждый ход. Если переменная круглая, то ход белых. Если у нее есть дробная часть, то ход черных.

В-шестых, Zobrist хеш позиции. Структуру Zobrist хеша мы уже написали, об этом беспокоится не нужно. Главное, не забывать обновлять его после изменений в позиции.

В-седьмых, счетчик 50 ходов. Он будет такой же float переменной как и счетчик ходов, только будет обнуляться после продвижения пешки или взятия.

В-восьмых, история повторений для реализации правило троекратного повторения позиции. Класс для этого правила мы уже реализовали, остается только очищать его после продвижения пешки или взятия.

Этого достаточно. Вот как в коде выглядит все то, что я написал сверху:

Pieces _pieces;
uint8_t _en_passant;

bool _w_l_castling;
bool _w_s_castling;
bool _b_l_castling;
bool _b_s_castling;

bool _white_castling_happened;
bool _black_castling_happened;

float _move_ctr;
ZobristHash _hash;
float _fifty_moves_ctr;
RepetitionHistory _repetition_history;

Теперь нам надо научится заполнять все это многообразие при помощи той же FEN строки и пары специальных переменных, отражающих права на рокировку. Выглядит это вот так:

Position::Position(const std::string& short_fen, uint8_t en_passant, bool w_l_castling, bool w_s_castling, bool b_l_castling, bool b_s_castling, float move_ctr) {
    this->_pieces = {short_fen};
    this->_en_passant = en_passant;

    this->_w_l_castling = w_l_castling;
    this->_w_s_castling = w_s_castling;
    this->_b_l_castling = b_l_castling;
    this->_b_s_castling = b_s_castling;

    this->_white_castling_happened = false;
    this->_black_castling_happened = false;

    this->_move_ctr = move_ctr;
    this->_hash = {this->_pieces, (this->_move_ctr - std::floor(this->_move_ctr) > 1e-4), this->_w_l_castling, this->_w_s_castling, this->_b_l_castling, this->_b_s_castling};
    this->_repetition_history.add_position(this->_hash);
    this->_fifty_moves_ctr = 0;
}

Когда мы умеем хранить позиции, нам надо научится применять ходы. Однако просто взять и написать функцию нельзя, так как почти каждое действие требует обновление Zobrist хеша. В связи с этим было решено написать маленькие приватные методы, обновляющие переменные внутри позиции и, при необходимости, Zobrist хеш. Вот они все:

void Position::_add_piece(uint8_t square, uint8_t type, uint8_t side) {
    if (!BitboardOperations::get_bit(this->_pieces._piece_bitboards[side][type], square)) {
        BitboardOperations::set_1(this->_pieces._piece_bitboards[side][type], square);
        this->_hash.invert_piece(square, type, side);
    }
}
void Position::_remove_piece(uint8_t square, uint8_t type, uint8_t side) {
    if (BitboardOperations::get_bit(this->_pieces._piece_bitboards[side][type], square)) {
        BitboardOperations::set_0(this->_pieces._piece_bitboards[side][type], square);
        this->_hash.invert_piece(square, type, side);
    }
}
void Position::_change_en_passant(uint8_t en_passant) {
    this->_en_passant = en_passant;
}
void Position::_remove_w_l_castling() {
    if (this->_w_l_castling) {
        this->_w_l_castling = false;
        this->_hash.invert_w_l_castling();
    }
}
void Position::_remove_w_s_castling() {
    if (this->_w_s_castling) {
        this->_w_s_castling = false;
        this->_hash.invert_w_s_castling();
    }
}
void Position::_remove_b_l_castling() {
    if (this->_b_l_castling) {
        this->_b_l_castling = false;
        this->_hash.invert_b_l_castling();
    }
}
void Position::_remove_b_s_castling() {
    if (this->_b_s_castling) {
        this->_b_s_castling = false;
        this->_hash.invert_b_s_castling();
    }
}
void Position::_update_move_ctr() {
    this->_move_ctr = this->_move_ctr + 0.5f;
    this->_hash.invert_move();
}
void Position::_update_fifty_moves_ctr(bool break_event) {
    if (break_event) this->_fifty_moves_ctr = 0;
    else this->_fifty_moves_ctr = this->_fifty_moves_ctr + 0.5f;
}

Методы очень простые и используют все созданное в структуре Zobrist хеширования. Прокомментирую только 44 строчку, где break_event — обозначает именно взятие или продвижение пешки.

Когда у нас есть такой богатый набор можно приступать к функции применения хода. Несмотря на то, что я всеми силами пытался разбить ее на мелкие куски, получилось она довольно большая, так что показывать ее буду по кускам.

Самая основа — переместить фигуру и удалить взятую, если таковая была. Выглядит это все так:

this->_remove_piece(move._from, move._attacker_type, move._attacker_side);
this->_add_piece(move._to, move._attacker_type, move._attacker_side);
if (move._defender_type != 255) this->_remove_piece(move._to, move._defender_type, move._defender_side);

После нам надо обработать все специальные флаги, объявленные в структуре Move:

switch (move._flag) {
        case Move::Flag::Default:
            break;

        case Move::Flag::PawnLongMove:
            this->_change_en_passant((move._from + move._to) / 2);
            break;
        case Move::Flag::EnPassantCapture:
            if (move._attacker_side == Pieces::White) this->_remove_piece(move._to - 8, Pieces::Pawn, Pieces::Black);
            else this->_remove_piece(move._to + 8, Pieces::Pawn, Pieces::White);
            break;

        case Move::Flag::WhiteLongCastling:
            this->_remove_piece(0, Pieces::Rook, Pieces::White);
            this->_add_piece(3, Pieces::Rook, Pieces::White);
            this->_white_castling_happened = true;
            break;
        case Move::Flag::WhiteShortCastling:
            this->_remove_piece(7, Pieces::Rook, Pieces::White);
            this->_add_piece(5, Pieces::Rook, Pieces::White);
            this->_white_castling_happened = true;
            break;
        case Move::Flag::BlackLongCastling:
            this->_remove_piece(56, Pieces::Rook, Pieces::Black);
            this->_add_piece(59, Pieces::Rook, Pieces::Black);
            this->_black_castling_happened = true;
            break;
        case Move::Flag::BlackShortCastling:
            this->_remove_piece(63, Pieces::Rook, Pieces::Black);
            this->_add_piece(61, Pieces::Rook, Pieces::Black);
            this->_black_castling_happened = true;
            break;

        case Move::Flag::PromoteToKnight:
            this->_remove_piece(move._to, Pieces::Pawn, move._attacker_side);
            this->_add_piece(move._to, Pieces::Knight, move._attacker_side);
            break;
        case Move::Flag::PromoteToBishop:
            this->_remove_piece(move._to, Pieces::Pawn, move._attacker_side);
            this->_add_piece(move._to, Pieces::Bishop, move._attacker_side);
            break;
        case Move::Flag::PromoteToRook:
            this->_remove_piece(move._to, Pieces::Pawn, move._attacker_side);
            this->_add_piece(move._to, Pieces::Rook, move._attacker_side);
            break;
        case Move::Flag::PromoteToQueen:
            this->_remove_piece(move._to, Pieces::Pawn, move._attacker_side);
            this->_add_piece(move._to, Pieces::Queen, move._attacker_side);
            break;
}

Это все что касается изменений с фигурами, так что можно обновить второстепенные битборды о которых было рассказано в самом начале статьи:

this->_pieces.update_bitboards();

Если флаг перемещения не был длинным ходом пешки, то надо сбросить битое поле, так как взятие на проходе возможно только ответным ходом:

if (move._flag != Move::Flag::PawnLongMove) this->_change_en_passant(255);

Еще нужно сбросить права на рокировку, если перемещались короли или ладьи. Фишка в том, что нам неважно какая фигура перемещалась (как это странно и не звучит), а важно перемещалась ли фигура с места на котором должны стоять короли и ладьи. Если да, то сбрасываем рокировку. Это может быть не совсем очевидно, так что давайте рассмотрим два случая. Первый — когда на клетке где должна стоять фигура она действительно стоит. После ее движения рокировка будет, естественно, невозможна. Второй — когда на клетке где должна стоять фигура ее нет. После ее движения права на рокировку не должны меняться, но раз на месте ладьи или короля стоит другая фигура, то это значит, что рокировка уже невозможно и от ее сброса ничего не изменится. Вот код:

switch (move._from) {
        case 0:
            this->_remove_w_l_castling();
            break;
        case 4:
            this->_remove_w_l_castling();
            this->_remove_w_s_castling();
            break;
        case 7:
            this->_remove_w_s_castling();
            break;
        case 56:
            this->_remove_b_l_castling();
            break;
        case 60:
            this->_remove_b_l_castling();
            this->_remove_b_s_castling();
            break;
        case 63:
            this->_remove_b_s_castling();
            break;
}

После этого обновляем счетчик ходов:

this->_update_move_ctr();

Обновляем счетчик 50 ходов:

this->_update_fifty_moves_ctr(move._attacker_type == Pieces::Pawn or move._defender_type != 255);

Обновляем историю троекратного повторения позиции и, если произошел необратимый ход, очищаем (разумеется до добавления позиции):

if (move._attacker_type == Pieces::Pawn or move._defender_type != 255) this->_repetition_history.clear();
this->_repetition_history.add_position(this->_hash);

Разделение ходов на псевдолегальные и легальные

Перед генерацией ходов нужно узнать разницу между псевдолегальными и легальными ходами.

Псевдолегальные ходы — это ходы без учета шахов. То есть все фигуры подчиняются своим правилам, конь ходит буквой «Г», слон не может перепрыгивать через фигуры и так далее, но шахи не учитываются. Это значит, что король может пойти на клетку битую вражеской фигурой, а шах просто проигнорировать.

Что такое легальные ходы объяснять не нужно. За них говорит их название.

В итоге нам нужно генерировать именно легальные ходы, но проблема в том, что без псевдолегальных сгенерировать легальные не получится. Именно поэтому следующие три части будут посвящены генерации псевдолегальных ходов.

Генерация псевдолегальных ходов коней и королей

Сгенерировать все псевдолегальные ходы коней и королей можно очень быстро. Всего за одну примитивную операцию процессора умноженную на количество коней и королей. Но для такой скорости необходимо заранее вычислить маски их перемещений для каждой клетки.

Производительность при вычислении масок неважна, поэтому я вычислил их максимально долгим, но читаемым алгоритмом:

#include "../PositionRepresentation/Bitboard.hpp"


#pragma once


namespace KnightMasks {
    static consteval uint8_t abs_subtract(uint8_t left, uint8_t right) {
        if (left >= right) return left - right;
        return right - left;
    }
    static consteval std::array<Bitboard, 64> calc_masks() {
        std::array<Bitboard, 64> masks{};

        uint8_t dx;
        uint8_t dy;

        for (uint8_t x0 = 0; x0 < 8; x0 = x0 + 1) {
            for (uint8_t y0 = 0; y0 < 8; y0 = y0 + 1) {

                for (uint8_t x1 = 0; x1 < 8; x1 = x1 + 1) {
                    for (uint8_t y1 = 0; y1 < 8; y1 = y1 + 1) {

                        dx = KnightMasks::abs_subtract(x0, x1);
                        dy = KnightMasks::abs_subtract(y0, y1);

                        if ((dx == 2 and dy == 1) or (dx == 1 and dy == 2)) BitboardOperations::set_1(masks[y0 * 8 + x0], y1 * 8 + x1);
                    }
                }
            }
        }

        return masks;
    }


    static constexpr std::array<Bitboard, 64> Masks = KnightMasks::calc_masks();
}

#include "../PositionRepresentation/Bitboard.hpp"


#pragma once


namespace KingMasks {
    static consteval uint8_t abs_subtract(uint8_t left, uint8_t right) {
        if (left >= right) return left - right;
        return right - left;
    }
    static consteval std::array<Bitboard, 64> calc_masks() {
        std::array<Bitboard, 64> masks{};

        uint8_t dx;
        uint8_t dy;

        for (uint8_t x0 = 0; x0 < 8; x0 = x0 + 1) {
            for (uint8_t y0 = 0; y0 < 8; y0 = y0 + 1) {

                for (uint8_t x1 = 0; x1 < 8; x1 = x1 + 1) {
                    for (uint8_t y1 = 0; y1 < 8; y1 = y1 + 1) {

                        dx = KingMasks::abs_subtract(x0, x1);
                        dy = KingMasks::abs_subtract(y0, y1);

                        if (dx <= 1 and dy <= 1) BitboardOperations::set_1(masks[y0 * 8 + x0], y1 * 8 + x1);
                    }
                }
            }
        }

        return masks;
    }


    static constexpr std::array<Bitboard, 64> Masks = KingMasks::calc_masks();
}

Теперь при генерации псевдолегальных ходов коней и короля достаточно одной операции:

Bitboard PsLegalMoveMaskGen::generate_knight_mask(Pieces pieces, uint8_t p, uint8_t side, bool only_captures) {
    if (only_captures) {
        return KnightMasks::Masks[p] & pieces._side_bitboards[Pieces::inverse(side)];
    }
    return KnightMasks::Masks[p] & pieces._inversion_side_bitboards[side];
}

Bitboard PsLegalMoveMaskGen::generate_king_mask(Pieces pieces, uint8_t p, uint8_t side, bool only_captures) {
    if (only_captures) {
        return KingMasks::Masks[p] & pieces._side_bitboards[Pieces::inverse(side)];
    }
    return KingMasks::Masks[p] & pieces._inversion_side_bitboards[side];
}

Обратите внимание на флаг only_captures. Если он включен, то будут сгенерированы только взятия. Может быть не сразу понятно зачем это надо, но оно нам пригодится, причем не один раз.

Генерация псевдолегальных ходов скользящих фигур

Сгенерировать похожим образом псевдолегальных ходы слонов, ферзей и ладей, к сожалению, нельзя, так как они подчиняются другим правилами. Существует, как минимум, два способа это сделать быстро, а именно — вращаемые битборды и магические. Идея последних заключается в том, чтобы закешировать результаты для всех расстановок блокирующих фигур.

К сожалению, меня не хватило на один из этих оптимизированных подходов, поэтому пришлось делать довольно медленным алгоритмом.

Сначала генерируются маски перемещений во всех направлениях со всех клеток. Выглядит этот вот так:

#include "../PositionRepresentation/Bitboard.hpp"


#pragma once


namespace SlidersMasks {
    struct Direction {
        static constexpr int8_t North = 0;
        static constexpr int8_t South = 1;
        static constexpr int8_t West = 2;
        static constexpr int8_t East = 3;

        static constexpr int8_t NorthWest = 4;
        static constexpr int8_t NorthEast = 5;
        static constexpr int8_t SouthWest = 6;
        static constexpr int8_t SouthEast = 7;
    };


    static consteval Bitboard calc_mask(uint8_t p, int8_t direction) {
        Bitboard mask = 0;

        int8_t x = p % 8;
        int8_t y = p / 8;

        for (; ;) {
            switch (direction) {
                case SlidersMasks::Direction::North: y = y + 1; break;
                case SlidersMasks::Direction::South: y = y - 1; break;
                case SlidersMasks::Direction::West: x = x - 1; break;
                case SlidersMasks::Direction::East: x = x + 1; break;

                case SlidersMasks::Direction::NorthWest: y = y + 1; x = x - 1; break;
                case SlidersMasks::Direction::NorthEast: y = y + 1; x = x + 1; break;
                case SlidersMasks::Direction::SouthWest: y = y - 1; x = x - 1; break;
                case SlidersMasks::Direction::SouthEast: y = y - 1; x = x + 1; break;
            }

            if (x > 7 or x < 0 or y > 7 or y < 0) break;

            BitboardOperations::set_1(mask, y * 8 + x);
        }

        return mask;
    }


    static consteval std::array<std::array<Bitboard, 8>, 64> calc_masks() {
        std::array<std::array<Bitboard, 8>, 64> masks{};

        for (uint8_t i = 0; i < 64; i = i + 1) {
            for (uint8_t j = 0; j < 8; j = j + 1) masks[i][j] = SlidersMasks::calc_mask(i, j);
        }

        return masks;
    }


    static constexpr std::array<std::array<Bitboard, 8>, 64> Masks = SlidersMasks::calc_masks();
};

Опять же напомню, что это вычисляется на этапе компиляции, так что читаемость гораздо важнее производительности.

Теперь нам надо написать функцию, генерирующую луч в заданном направлении из заданной точки с учетом блокирующих фигур.

Для начала давайте получим эти блокирующие фигуры. Нам нужно пересечение всех фигур с данным нам лучом.

Bitboard blockers = SlidersMasks::Masks[p][direction] & pieces._all;

После того как мы получили блокирующие фигуры мы обязаны проверить пусты ли они (очень скоро узнаете почему). И если пусты, то со включенным флагом only_captures возвращаем 0, а с выключенным — весь луч:

if (blockers == 0) {
        if (only_captures) return 0;
        return SlidersMasks::Masks[p][direction];
}

Далее нам нужно найти первую клетку на которой стоит блокирующая фигура. Сделать это можно при помощи написанными нами функциями поиска первого бита или поиска последнего бита. Изначально может показаться, что так как мы ищем первый бит, то нам нужна функция поиска первого бита, но это не так. Нам нужен будет как и поиск первого бита, так и поиск последнего, зависит от направления луча. Итак, находим первую блокирующую фигуру:

uint8_t blocking_square;

if (bsr) blocking_square = BitboardOperations::bsr(blockers);
else blocking_square = BitboardOperations::bsf(blockers);

Теперь заводим итоговый битборд:

Bitboard moves;

И со включенным флагом только взятий заполняем его нулями, когда как с выключенным — результатом выполнения XOR’a луча, выпущенного из данной точки с лучом, выпущенным из первой блокирующей фигуры:

if (only_captures) moves = 0;
else moves = SlidersMasks::Masks[p][direction] ^ SlidersMasks::Masks[blocking_square][direction];

Далее надо определить какого цвета первая блокирующая фигура. Если цвета, что и та которой генерируются перемещений, то ее не включаем. Если другого — включаем:

if (BitboardOperations::get_bit(pieces._side_bitboards[side], blocking_square)) BitboardOperations::set_0(moves, blocking_square);
else BitboardOperations::set_1(moves, blocking_square);

Далее просто возвращаем результат:

return moves;

Используя эту замечательную функцию можно легко сгенерировать все перемещения слона:

Bitboard PsLegalMoveMaskGen::generate_bishop_mask(Pieces pieces, uint8_t p, uint8_t side, bool only_captures) {
    Bitboard nw = PsLegalMoveMaskGen::_calc_ray(pieces, p, side, only_captures, SlidersMasks::Direction::NorthWest, false);
    Bitboard ne = PsLegalMoveMaskGen::_calc_ray(pieces, p, side, only_captures, SlidersMasks::Direction::NorthEast, false);
    Bitboard sw = PsLegalMoveMaskGen::_calc_ray(pieces, p, side, only_captures, SlidersMasks::Direction::SouthWest, true);
    Bitboard se = PsLegalMoveMaskGen::_calc_ray(pieces, p, side, only_captures, SlidersMasks::Direction::SouthEast, true);

    return nw | ne | sw | se;
}

Ладьи:

Bitboard PsLegalMoveMaskGen::generate_rook_mask(Pieces pieces, uint8_t p, uint8_t side, bool only_captures) {
    Bitboard n = PsLegalMoveMaskGen::_calc_ray(pieces, p, side, only_captures, SlidersMasks::Direction::North, false);
    Bitboard s = PsLegalMoveMaskGen::_calc_ray(pieces, p, side, only_captures, SlidersMasks::Direction::South, true);
    Bitboard w = PsLegalMoveMaskGen::_calc_ray(pieces, p, side, only_captures, SlidersMasks::Direction::West, true);
    Bitboard e = PsLegalMoveMaskGen::_calc_ray(pieces, p, side, only_captures, SlidersMasks::Direction::East, false);

    return n | s | w | e;
}

И ферзя, на основе предыдущих двух фигур:

Bitboard PsLegalMoveMaskGen::generate_queen_mask(Pieces pieces, uint8_t p, uint8_t side, bool only_captures) {
    Bitboard bishop_mask = PsLegalMoveMaskGen::generate_bishop_mask(pieces, p, side, only_captures);
    Bitboard rook_mask = PsLegalMoveMaskGen::generate_rook_mask(pieces, p, side, only_captures);

    return bishop_mask | rook_mask;
}

Такой подход медленнее вращаемых, а уж тем более магических битбордов, но все же быстрее, чем при простом представлении доски.

Генерация псевдолегальных ходов пешек

Уже было рассказано как генерировать взятия всех фигур, но еще ни слова не было сказано про пешки. А все из-за того, что пешки кардинально отличаются от фигур.

Во-первых, их очень много. Искать все пешки по доске, а потом использовать маскирование с каждой из них было бы, вероятно, даже более затратно, чем генерация ходов скользящих фигур.

Во-вторых, у них есть сложные правила вроде того, что если пешка не двигалась и следующие две клетки свободны, то она может перепрыгнуть через клетку.

В-третьих, у них перемещения не совпадают со взятиями, чего нельзя сказать ни про одну фигуру.

Из-за этих факторов перемещения пешек лучше генерировать совершенно другим способом. А именно — генерировать их всех сразу. Сейчас поясню что я имею ввиду.

У нас будет четыре функции. Одна генерирует все короткие ходы пешек, другая — все длинные, третья — все взятия налево, четвертая — все взятия направо. Но почему мы генерируем их отдельно? Почему нельзя одновременно, например, сгенерировать и взятия налево, и взятия направо? На самом деле я думаю, что можно. Просто я выбрал немного другой путь. Не нужно забывать, что кроме того, чтобы сгенерировать все маски перемещений нам надо сгенерировать ходы (мы писали структуру хода, надеюсь ее еще кто-то помнит). И эти битборды мы, в будущем, будем перебирать для генерации ходов. Проблема в том, что если мы сгенерируем в один битборд и взятия налево, и взятия направо, то мы не будем знать, смотря на битборд, какая из пешек туда может пойти. А если мы взятия генерируем отдельно, то по битборду можно понять, что попасть в такую-то клетку может пешка, находящаяся, например, на 9 индексах ниже.

Итак, приступим. Для начала научимся генерировать обычные ходы пешек. То есть на клетку вперед. Нам надо сдвинуть их на 1 по оси y (что эквивалентно сдвигу на 8 в сторону), после чего сделать объединение с пустыми клетками. Для черных пешек направление сдвига другое. Реализуется очень просто:

Bitboard PsLegalMoveMaskGen::generate_pawn_default_mask(Pieces pieces, uint8_t side) {
    if (side == Pieces::White) {
        return (pieces._piece_bitboards[Pieces::White][Pieces::Pawn] << 8) & pieces._empty;
    }
    return (pieces._piece_bitboards[Pieces::Black][Pieces::Pawn] >> 8) & pieces._empty;
}

Теперь сгенерируем длинные ходы. Я сам долго не мог придумать как это сделать, пока не нашел очень простое решение: мы берем результат предыдущей функции, оставляем только те пешки, которые стояли на начальной строке, после чего, по сути, повторяем операцию. Очень просто:

Bitboard PsLegalMoveMaskGen::generate_pawn_long_mask(Pieces pieces, uint8_t side) {
    Bitboard default_mask = PsLegalMoveMaskGen::generate_pawn_default_mask(pieces, side);

    if (side == Pieces::White) {
        return ((default_mask & BitboardRows::Rows[2]) << 8) & pieces._empty;
    }
    return ((default_mask & BitboardRows::Rows[5]) >> 8) & pieces._empty;
}

Теперь взятия. Но перед тем как их генерировать надо немного подумать наперед. Нам не раз надо будет проверять, например, бьет ли пешка пустую клетку (самый простой пример — проверка битового поля при рокировке). Для этого мы должны добавить в нашу функцию генерации взятий флаг, который при включении будет генерировать не только псевдолегальные взятия, но и взятия всего, включая свои фигуры и пустые клетки. Этот флаг я назвал include_all_possible_captures, не забывайте о нем.

Когда о флаге поговорили, приступим к самой генерации. Нам надо сдвинуть битборд на 1 по оси y и 1 по оси x (эквивалентно сдвигу на 7 или 9 в сторону). Только вот если пешка, например, стоит с левого краю, то после сдвига налево у нее появятся взятия по правому краю, что ошибка. Поэтому после сдвига мы не только выполняем маскирование с фигурами противника (разумеется, если флаг include_all_possible_captures не включен), но и с битбордом, обратному крайнему столбцу (такие битборды мы генерировали в самом начале статьи).

Теперь мы полностью готовы для написания генератора взятий:

Bitboard PsLegalMoveMaskGen::generate_pawn_left_captures_mask(Pieces pieces, uint8_t side, bool include_all_possible_captures) {
    if (side == Pieces::White) {
        Bitboard mask = (pieces._piece_bitboards[Pieces::White][Pieces::Pawn] << 7) & BitboardColumns::InversionColumns[7];
        if (!include_all_possible_captures) mask = mask & pieces._side_bitboards[Pieces::Black];

        return mask;
    }

    Bitboard mask = (pieces._piece_bitboards[Pieces::Black][Pieces::Pawn] >> 9) & BitboardColumns::InversionColumns[7];
    if (!include_all_possible_captures) mask = mask & pieces._side_bitboards[Pieces::White];
    return mask;
}

Bitboard PsLegalMoveMaskGen::generate_pawn_right_captures_mask(Pieces pieces, uint8_t side, bool include_all_possible_captures) {
    if (side == Pieces::White) {
        Bitboard mask = (pieces._piece_bitboards[Pieces::White][Pieces::Pawn] << 9) & BitboardColumns::InversionColumns[0];
        if (!include_all_possible_captures) mask = mask & pieces._side_bitboards[Pieces::Black];

        return mask;
    }

    Bitboard mask = (pieces._piece_bitboards[Pieces::Black][Pieces::Pawn] >> 7) & BitboardColumns::InversionColumns[0];
    if (!include_all_possible_captures) mask = mask & pieces._side_bitboards[Pieces::White];
    return mask;
}

Проверка находится ли клетка под ударом

Нам часто придется проверять находится ли клетка под ударом (например — детектор шахов).

Проверить бьют ли клетку пешки противника можно очень легко из-за особенности генерации ходов пешек:

Bitboard opposite_pawns_left_captures = PsLegalMoveMaskGen::generate_pawn_left_captures_mask(pieces, Pieces::inverse(side), true);
Bitboard opposite_pawns_right_captures = PsLegalMoveMaskGen::generate_pawn_right_captures_mask(pieces, Pieces::inverse(side), true);
Bitboard opposite_pawns_captures = opposite_pawns_left_captures | opposite_pawns_right_captures;

if (BitboardOperations::get_bit(opposite_pawns_captures, p)) return true;

Но что делать с фигурами? Самый наивный вариант — найти все фигуры противника, сгенерировать взятия найденных фигур и поискать в полученных битбордах интересующую нас клетку. Но это плохой вариант, так как можно сделать гораздо быстрее, причем как и по времени выполнения программы, так и по времени написания кода.

Все ходы в шахматах (за исключением ходов пешек, с которыми мы уже разобрались и рокировках о которых речи пока не было) обладают очень интересным свойством, которое очевидно, но мало кто замечает.

Если фигура походила с клетки A на клетку B, то следующим ходом (при отсутствии противника) она всегда может вернуться обратно на клетку А.

Из этого следует, что если фигура, находясь на клетки А, бьет клетку В, то точно такая же фигура, находясь на клетке B, будет бить клетку А.

А из этого следует, что поставив на клетку, которую мы хотим проверить, слона он будет бить вражеского слона тогда и только тогда, когда вражеский слон бьет эту клетку.

Аналогичная логика работает со всеми фигурами. Постарайтесь понять это, а чтобы было легче — снизу есть картинка, где черному королю шах (на картинке мат, но мат в каком-то смысле частный случай шаха).

Используя это знание, можно довольно легко проверить атакуется ли какая-то клетка фигурами:

if (PsLegalMoveMaskGen::generate_knight_mask(pieces, p, side, true) & pieces._piece_bitboards[Pieces::inverse(side)][Pieces::Knight]) return true;
if (PsLegalMoveMaskGen::generate_bishop_mask(pieces, p, side, true) & pieces._piece_bitboards[Pieces::inverse(side)][Pieces::Bishop]) return true;
if (PsLegalMoveMaskGen::generate_rook_mask(pieces, p, side, true) & pieces._piece_bitboards[Pieces::inverse(side)][Pieces::Rook]) return true;
if (PsLegalMoveMaskGen::generate_queen_mask(pieces, p, side, true) & pieces._piece_bitboards[Pieces::inverse(side)][Pieces::Queen]) return true;
if (PsLegalMoveMaskGen::generate_king_mask(pieces, p, side, true) & pieces._piece_bitboards[Pieces::inverse(side)][Pieces::King]) return true;

И если ни пешки, ни фигура не прервали функцию, вернув истину, то надо вернуть ложь:

return false;

Тип для хранения нескольких ходов

Мы уже в шаге от генератора легальных ходов, где надо будет отсеять псевдолегальные и оставить только легальные, после чего их засунуть в тип, содержащий ряд ходов.

Но какой это будет тип? Самое банальное — вектор, но вектор под капотом делает много лишних действий. Менее банальное — список, но он тоже не особо подходит, так как его долго обходить (для обхода нужна прыгать по указателям). В связи с этим надо создать «собственную структуру» на основе статического массива. Это решение показало себя как наиболее производительное.

Данная структура будет содержать в себе большой статический массив и переменную, показывающую размер массива. При добавлении элемента ход будет добавляться в последнюю не занятую ячейку, после чего размер массива будет увеличиваться на 1.

Но как выбрать размер этого большого статического массива? На том же chessprogrammingwiki я нашел, что позиция с наибольшим количеством легальных ходов содержит 218 ходов. Саму позицию я, к сожалению, не нашел (хотя и не очень искал), но все-таки предлагаю поверить chessprogrammingwiki и создать массив размером в 218 ходов.

Вот код этого класса. Он очень простой:

#include <array>
#include "../PositionRepresentation/Move.hpp"
#include "../PositionRepresentation/Pieces.hpp"


#pragma once


class MoveList {
public:
    MoveList();

    Move &operator[](uint8_t index);
    Move operator[](uint8_t index) const;

    void push_back(Move move);
    [[nodiscard]] uint8_t size() const;
private:
    std::array<Move, 218> _moves{};
    uint8_t _size;
};

#include "MoveList.hpp"


MoveList::MoveList() {
    this->_size = 0;
}
Move &MoveList::operator[](uint8_t index) {
    return this->_moves[index];
}
Move MoveList::operator[](uint8_t index) const {
    return this->_moves[index];
}
void MoveList::push_back(Move move) {
    this->_moves[this->_size] = move;
    this->_size = this->_size + 1;
}
uint8_t MoveList::size() const {
    return this->_size;
}

Генерация легальных ходов

У нас есть генератор псевдолегальных ходов, алгоритм, проверяющий находится ли клетка под боем, тип для хранения ходов. Используя этот арсенал, можно сгенерировать все легальные ходы.

Существует два способа это сделать. Первый — делаем ход какой-то облегченной функцией, проверяем есть ли шах, если нет — ход легален. Второй основан на сложных проверках на двойные шахи, определения типа атакующей фигуры, определение связанных фигур и т.д. К сожалению, мне не хватило силы и мужества написать этот восхитительный способ, так что придется пользоваться первым.

Для начала нам надо научиться проверять является ли ход легальным. Простым способом это делается довольно просто, хоть и медленно:

bool LegalMoveGen::_is_legal(Pieces pieces, Move move, bool en_passant_capture) {
    BitboardOperations::set_0(pieces._piece_bitboards[move._attacker_side][move._attacker_type], move._from);
    BitboardOperations::set_1(pieces._piece_bitboards[move._attacker_side][move._attacker_type], move._to);
    if (move._defender_type != 255) BitboardOperations::set_0(pieces._piece_bitboards[move._defender_side][move._defender_type], move._to);
    if (en_passant_capture) {
        if (move._attacker_side == Pieces::White) BitboardOperations::set_0(pieces._piece_bitboards[Pieces::Black][Pieces::Pawn], move._to - 8);
        BitboardOperations::set_0(pieces._piece_bitboards[Pieces::White][Pieces::Pawn], move._to + 8);
    }

    pieces.update_bitboards();

    if (PsLegalMoveMaskGen::in_danger(pieces, BitboardOperations::bsf(pieces._piece_bitboards[move._attacker_side][Pieces::King]), move._attacker_side)) return false;

    return true;
}

Обращаю внимание на то, что обрабатываем мы только флаг взятия на проходе, так как флаги продвижения на легальность ходов не влияют, а рокировка из-за своей необычности будет реализована иначе.

После того как эта функция готова можно начать генерировать ходы. Начнем с пешек, а именно с их взятий.

Сначала генерируем маски:

Bitboard pawn_left_captures_mask = PsLegalMoveMaskGen::generate_pawn_left_captures_mask(position._pieces, side, false);
Bitboard pawn_right_captures_mask = PsLegalMoveMaskGen::generate_pawn_right_captures_mask(position._pieces, side, false);

После при помощи такой вот функции перегоняем их в список ходов:

void LegalMoveGen::_pawn_mask_to_moves(Pieces pieces, Bitboard mask, uint8_t attacker_side, int8_t attacker_index, bool look_for_defender, uint8_t flag, MoveList &moves) {
    uint8_t defender_p;
    uint8_t defender_type = 255;

    Move move;

    while (mask) {
        defender_p = BitboardOperations::bsf(mask);
        BitboardOperations::set_0(mask, defender_p);

        if (look_for_defender) {
            defender_type = 255;
            for (uint8_t i = 0; i < 6; i = i + 1) {
                if (BitboardOperations::get_bit(pieces._piece_bitboards[Pieces::inverse(attacker_side)][i], defender_p)) {
                    defender_type = i;
                    break;
                }
            }
        }

        move = {(uint8_t)(defender_p + attacker_index), defender_p, Pieces::Pawn, attacker_side, defender_type, Pieces::inverse(attacker_side), flag};

        if (LegalMoveGen::_is_legal(pieces, move, false)) {
            if (defender_p < 8 or defender_p > 55) {
                moves.push_back({(uint8_t)(defender_p + attacker_index), defender_p, 0, attacker_side, defender_type, Pieces::inverse(attacker_side), Move::Flag::PromoteToKnight});
                moves.push_back({(uint8_t)(defender_p + attacker_index), defender_p, 0, attacker_side, defender_type, Pieces::inverse(attacker_side), Move::Flag::PromoteToBishop});
                moves.push_back({(uint8_t)(defender_p + attacker_index), defender_p, 0, attacker_side, defender_type, Pieces::inverse(attacker_side), Move::Flag::PromoteToRook});
                moves.push_back({(uint8_t)(defender_p + attacker_index), defender_p, 0, attacker_side, defender_type, Pieces::inverse(attacker_side), Move::Flag::PromoteToQueen});
            }
            else moves.push_back(move);
        }
    }
}

Эта функция находит бит в маске (этот бит обозначает куда может пойти пешка), после, если включен флаг поиска защитника, находит защитника на этой клетке, далее формирует ход при помощи специального индекса по которому можно вычислить координаты атакующий пешки, и если получившийся ход легален, то он добавляется в список. Причем если клетка назначения стоит на последней строке, то генерируются ходы-продвижения.

При помощи этой функции также можно сгенерировать обычные ходы пешек, используя другую маску.

Но что делать с фигурами? Для них надо написать похожую функцию перебирания битбордов. Она гораздо легче:

void LegalMoveGen::_piece_mask_to_moves(Pieces pieces, Bitboard mask, uint8_t attacker_p, uint8_t attacker_type, uint8_t attacker_side, MoveList &moves) {
    uint8_t defender_p;
    uint8_t defender_type;

    Move move;

    while (mask) {
        defender_p = BitboardOperations::bsf(mask);
        BitboardOperations::set_0(mask, defender_p);

        defender_type = 255;
        for (uint8_t i = 0; i < 6; i = i + 1) {
            if (BitboardOperations::get_bit(pieces._piece_bitboards[Pieces::inverse(attacker_side)][i], defender_p)) {
                defender_type = i;
                break;
            }
        }

        move = {attacker_p, defender_p, attacker_type, attacker_side, defender_type, Pieces::inverse(attacker_side)};

        if (LegalMoveGen::_is_legal(pieces, move, false)) moves.push_back(move);
    }
}

Эта функция берет переданный битборд, находит там бит (этот бит отвечает куда может пойти фигура), находит защитника, стоящего на индексе этого бита, после чего формирует ход при помощи переданных координат атакующей фигуры и, если он легален, добавляет его в список.

Вот пример генерации всех ходов коней при помощи этой функции:

Bitboard all_knights = position._pieces._piece_bitboards[side][Pieces::Knight];
uint8_t attacker_p;
Bitboard mask;
while (all_knights) {
    attacker_p = BitboardOperations::bsf(all_knights);
    BitboardOperations::set_0(all_knights, attacker_p);
    mask = PsLegalMoveMaskGen::generate_knight_mask(position._pieces, attacker_p, side, only_captures);
    LegalMoveGen::_piece_mask_to_moves(position._pieces, mask, attacker_p, Pieces::Knight, side, moves);
}

Также нужно сгенерировать все рокировки и взятия на проходе:

void LegalMoveGen::_add_en_passant_captures(Pieces pieces, uint8_t side, uint8_t en_passant, MoveList &moves) {
    if (en_passant == 255) return;

    Move move;

    if (side == Pieces::White) {
        if (en_passant % 8 != 7 and BitboardOperations::get_bit(pieces._piece_bitboards[Pieces::White][Pieces::Pawn], en_passant - 7)) {
            move = {(uint8_t)(en_passant - 7), en_passant, Pieces::Pawn, Pieces::White, 255, 255, Move::Flag::EnPassantCapture};
            if (LegalMoveGen::_is_legal(pieces, move, true)) moves.push_back(move);
        }
        if (en_passant % 8 != 0 and BitboardOperations::get_bit(pieces._piece_bitboards[Pieces::White][Pieces::Pawn], en_passant - 9)) {
            move = {(uint8_t)(en_passant - 9), en_passant, Pieces::Pawn, Pieces::White, 255, 255, Move::Flag::EnPassantCapture};
            if (LegalMoveGen::_is_legal(pieces, move, true)) moves.push_back(move);
        }
    }
    else {
        if (en_passant % 8 != 0 and BitboardOperations::get_bit(pieces._piece_bitboards[Pieces::Black][Pieces::Pawn], en_passant + 7)) {
            move = {(uint8_t)(en_passant + 7), en_passant, Pieces::Pawn, Pieces::Black, 255, 255, Move::Flag::EnPassantCapture};
            if (LegalMoveGen::_is_legal(pieces, move, true)) moves.push_back(move);
        }
        if (en_passant % 8 != 7 and BitboardOperations::get_bit(pieces._piece_bitboards[Pieces::Black][Pieces::Pawn], en_passant + 9)) {
            move = {(uint8_t)(en_passant + 9), en_passant, Pieces::Pawn, Pieces::Black, 255, 255, Move::Flag::EnPassantCapture};
            if (LegalMoveGen::_is_legal(pieces, move, true)) moves.push_back(move);
        }
    }
}
void LegalMoveGen::_add_castling_moves(Pieces pieces, uint8_t side, bool long_castling, bool short_castling, MoveList &moves) {
    uint8_t index;
    uint8_t long_castling_flag;
    uint8_t short_castling_flag;
    if (side == Pieces::White) {
        index = 0;
        long_castling_flag = Move::Flag::WhiteLongCastling;
        short_castling_flag = Move::Flag::WhiteShortCastling;
    }
    else {
        index = 56;
        long_castling_flag = Move::Flag::BlackLongCastling;
        short_castling_flag = Move::Flag::BlackShortCastling;
    }

    if (long_castling and BitboardOperations::get_bit(pieces._piece_bitboards[side][Pieces::Rook], 0 + index) and BitboardOperations::get_bit(pieces._empty, 1 + index) and BitboardOperations::get_bit(pieces._empty, 2 + index) and BitboardOperations::get_bit(pieces._empty, 3 + index)) {
        if (!PsLegalMoveMaskGen::in_danger(pieces, BitboardOperations::bsf(pieces._piece_bitboards[side][Pieces::King]), side) and !PsLegalMoveMaskGen::in_danger(pieces, 2 + index, side) and !PsLegalMoveMaskGen::in_danger(pieces, 3 + index, side)) moves.push_back({(uint8_t)(4 + index), (uint8_t)(2 + index), Pieces::King, side, 255, 255, long_castling_flag});
    }
    if (short_castling and BitboardOperations::get_bit(pieces._piece_bitboards[side][Pieces::Rook], 7 + index) and BitboardOperations::get_bit(pieces._empty, 5 + index) and BitboardOperations::get_bit(pieces._empty, 6 + index)) {
        if (!PsLegalMoveMaskGen::in_danger(pieces, BitboardOperations::bsf(pieces._piece_bitboards[side][Pieces::King]), side) and !PsLegalMoveMaskGen::in_danger(pieces, 5 + index, side) and !PsLegalMoveMaskGen::in_danger(pieces, 6 + index, side)) moves.push_back({(uint8_t)(4 + index), (uint8_t)(6 + index), Pieces::King, side, 255, 255, short_castling_flag});
    }
}

Метод генерации ходов-взятий на проходе выглядит довольно не оптимальным, но он работает довольно редко из-за чего потерь в производительности почти нет.

Поиск ошибок

Было написано очень много кода и хорошо бы было поискать в нем ошибки. Существует способ сделать это довольно просто. Нужно взять какую-то позицию, после чего посчитать к скольким позициям можно прийти из этой спустя n ходов, а затем сверить эту информацию с информацией, полученной другими шахматными программистами.

Но какую позицию выбрать для теста? Самым банальным было бы взять стандартную, но толка от такого тестирования будет мало, ведь многие ошибки могут быть не выявлены на таком раннем этапе игры. Я выбрал эту позицию:

Она особенна тем, что когда-то давно вызвала ошибки во многих движках.

После того как мы определились с позицией можно начать писать тесты. Вот этот небольшой «класс» поможет протестировать наш код:

#include <chrono>
#include <iomanip>
#include "LegalMoveGen.hpp"


#pragma once


class LegalMoveGenTester {
public:
    static void test();
private:
    static uint64_t _get_nodes_number(const Position& position, uint8_t side, uint32_t depth);

    static constexpr std::string_view Fen = "rnbq1k1r/pp1Pbppp/2p5/8/2B5/8/PPP1NnPP/RNBQK2R";
    static constexpr uint8_t EnPassant = 255;
    static constexpr bool WLCastling = true;
    static constexpr bool WSCastling = true;
    static constexpr bool BLCastling = false;
    static constexpr bool BSCastling = false;

    static constexpr std::array<uint64_t, 6> Nodes = {1, 44, 1486, 62379, 2103487, 89941194};
};

#include "LegalMoveGenTester.hpp"


#define nsecs std::chrono::high_resolution_clock::now().time_since_epoch().count()


void LegalMoveGenTester::test() {
    Position position = {(std::string)LegalMoveGenTester::Fen, LegalMoveGenTester::EnPassant, LegalMoveGenTester::WLCastling, LegalMoveGenTester::WSCastling, LegalMoveGenTester::BLCastling, LegalMoveGenTester::BSCastling, 1};

    uint64_t correct;
    uint64_t got;

    uint64_t time_start;
    float speed;

    for (uint32_t i = 0; i < 6; i = i + 1) {
        time_start = nsecs;

        correct = LegalMoveGenTester::Nodes[i];
        got = LegalMoveGenTester::_get_nodes_number(position, Pieces::White, i);

        speed = (float)got / ((float)(nsecs - time_start) / (float)1e+9) / (float)1e+6;

        if (correct == got) std::cout << ANSI::Green << "Depth " << std::setw(4) << i << ". Correct: " << std::setw(18) << correct << ". Got: " << std::setw(18) << got << ". Speed: " << std::setw(10) << speed << " MNPS. OK." << ANSI::End << std::endl;
        else std::cout << ANSI::Red << "Depth " << std::setw(4) << i << ". Correct: " << std::setw(18) << correct << ". Got: " << std::setw(18) << got << ". Speed: " << std::setw(10) << speed << " MNPS. Error." << ANSI::End << std::endl;
    }
}
uint64_t LegalMoveGenTester::_get_nodes_number(const Position& position, uint8_t side, uint32_t depth) {
    if (depth == 0) return 1;

    uint64_t ctr = 0;

    Position copy = position;

    MoveList moves = LegalMoveGen::generate(copy, side);
    Move move;

    for (uint8_t i = 0; i < moves.size(); i = i + 1) {
        move = moves[i];

        copy = position;
        copy.move(move);
        ctr = ctr + LegalMoveGenTester::_get_nodes_number(copy, Pieces::inverse(side), depth - 1);
    }

    return ctr;
}

Сейчас этот тест у меня, разумеется, выдает правильный результат, но получилось это не сразу.

Введение в шахматный ИИ

Спустя столько слов мы добрались до самого, на мой взгляд, интересного — программирование ИИ. Надеюсь, до этого места кто-то дочитал.

Типичный шахматный ИИ состоит из двух частей: статической и динамической оценки.

Статическая оценка извлекает внешние признаки из позиции. Смотрит на количество фигур, считает различные пешечные бонусы и т.д.

Динамическая оценка ищет комбинации и, как правило, использует статическую. Именно она понимает, что после такого хода белые потеряют ферзя, после другого у черных появится проходная пешка, а после этого будет пат.

Статическая оценка

Сейчас нужно разобраться с первой частью шахматного ИИ, а именно — со статической оценкой.

Давайте подумаем о том, что мы хотим получить. А получить мы хотим функцию, принимающую позицию, а возвращающую число. Причем чем больше число, тем лучше позиция для белых, а чем меньше число, тем лучше позиция для черных. Измерять оценку принято в сотых единицах пешки, так что если у белых перевес в две пешки, то оценка будет +200, а если у черных перевес в одну, то -100.

Материал

Первый фактор, самый очевидный и самый важный — материал. Материал показывает количество фигур. Чтобы учитывать материал надо обозначить для каждой фигуры ее стоимость. Я нашел на Википедии вот такую оценку фигур и решил ее использовать:

struct Material {
        static constexpr int32_t Pawn = 100;
        static constexpr int32_t Knight = 305;
        static constexpr int32_t Bishop = 333;
        static constexpr int32_t Rook = 563;
        static constexpr int32_t Queen = 950;
};

Посчитать материал очень просто, особенно при использовании битбордов:

int32_t StaticEvaluator::_material(Pieces pieces) {
    int32_t material = 0;

    material = material + StaticEvaluator::Material::Pawn * (BitboardOperations::count_1(pieces._piece_bitboards[Pieces::White][Pieces::Pawn]) - BitboardOperations::count_1(pieces._piece_bitboards[Pieces::Black][Pieces::Pawn]));
    material = material + StaticEvaluator::Material::Knight * (BitboardOperations::count_1(pieces._piece_bitboards[Pieces::White][Pieces::Knight]) - BitboardOperations::count_1(pieces._piece_bitboards[Pieces::Black][Pieces::Knight]));
    material = material + StaticEvaluator::Material::Bishop * (BitboardOperations::count_1(pieces._piece_bitboards[Pieces::White][Pieces::Bishop]) - BitboardOperations::count_1(pieces._piece_bitboards[Pieces::Black][Pieces::Bishop]));
    material = material + StaticEvaluator::Material::Rook * (BitboardOperations::count_1(pieces._piece_bitboards[Pieces::White][Pieces::Rook]) - BitboardOperations::count_1(pieces._piece_bitboards[Pieces::Black][Pieces::Rook]));
    material = material + StaticEvaluator::Material::Queen * (BitboardOperations::count_1(pieces._piece_bitboards[Pieces::White][Pieces::Queen]) - BitboardOperations::count_1(pieces._piece_bitboards[Pieces::Black][Pieces::Queen]));

    return material;
}

Мобильность

Второй фактор — мобильность. Чем больше развиты фигуры (то есть чем больше полей они бьют), тем лучше. Считать мы будем именно псевдолегальную мобильность (во-первых, генерация легальных ходов у нас значительно медленнее генерации псевдолегальных, во-вторых, легальная мобильность не делает программу значительно сильнее).

После того как стало ясно что это такое, надо подобрать константы для мобильности фигур. Эти значения (как и все дальше) подбирал я своими немного кривыми руками, так что они, вероятно, тоже немного кривые.

struct Mobility {
        static constexpr int32_t Knight = 9;
        static constexpr int32_t Bishop = 4;
        static constexpr int32_t Rook = 3;
        static constexpr int32_t Queen = 3;
};

Реализуется вот так:

int32_t StaticEvaluator::_mobility(Pieces pieces) {
    int32_t mobility = 0;

    std::array<std::array<Bitboard, 6>, 2> iteration_masks = pieces._piece_bitboards;
    uint8_t index;

    int32_t knight_moves = 0;
    int32_t bishop_moves = 0;
    int32_t rook_moves = 0;
    int32_t queen_moves = 0;

    while (iteration_masks[Pieces::White][Pieces::Knight]) {
        index = BitboardOperations::bsf(iteration_masks[Pieces::White][Pieces::Knight]);
        BitboardOperations::set_0(iteration_masks[Pieces::White][Pieces::Knight], index);
        knight_moves = knight_moves + BitboardOperations::count_1(PsLegalMoveMaskGen::generate_knight_mask(pieces, index, Pieces::White, false));
    }
    while (iteration_masks[Pieces::White][Pieces::Bishop]) {
        index = BitboardOperations::bsf(iteration_masks[Pieces::White][Pieces::Bishop]);
        BitboardOperations::set_0(iteration_masks[Pieces::White][Pieces::Bishop], index);
        bishop_moves = bishop_moves + BitboardOperations::count_1(PsLegalMoveMaskGen::generate_bishop_mask(pieces, index, Pieces::White, false));
    }
    while (iteration_masks[Pieces::White][Pieces::Rook]) {
        index = BitboardOperations::bsf(iteration_masks[Pieces::White][Pieces::Rook]);
        BitboardOperations::set_0(iteration_masks[Pieces::White][Pieces::Rook], index);
        rook_moves = rook_moves + BitboardOperations::count_1(PsLegalMoveMaskGen::generate_rook_mask(pieces, index, Pieces::White, false));
    }
    while (iteration_masks[Pieces::White][Pieces::Queen]) {
        index = BitboardOperations::bsf(iteration_masks[Pieces::White][Pieces::Queen]);
        BitboardOperations::set_0(iteration_masks[Pieces::White][Pieces::Queen], index);
        queen_moves = queen_moves + BitboardOperations::count_1(PsLegalMoveMaskGen::generate_queen_mask(pieces, index, Pieces::White, false));
    }

    while (iteration_masks[Pieces::Black][Pieces::Knight]) {
        index = BitboardOperations::bsf(iteration_masks[Pieces::Black][Pieces::Knight]);
        BitboardOperations::set_0(iteration_masks[Pieces::Black][Pieces::Knight], index);
        knight_moves = knight_moves - BitboardOperations::count_1(PsLegalMoveMaskGen::generate_knight_mask(pieces, index, Pieces::Black, false));
    }
    while (iteration_masks[Pieces::Black][Pieces::Bishop]) {
        index = BitboardOperations::bsf(iteration_masks[Pieces::Black][Pieces::Bishop]);
        BitboardOperations::set_0(iteration_masks[Pieces::Black][Pieces::Bishop], index);
        bishop_moves = bishop_moves - BitboardOperations::count_1(PsLegalMoveMaskGen::generate_bishop_mask(pieces, index, Pieces::Black, false));
    }
    while (iteration_masks[Pieces::Black][Pieces::Rook]) {
        index = BitboardOperations::bsf(iteration_masks[Pieces::Black][Pieces::Rook]);
        BitboardOperations::set_0(iteration_masks[Pieces::Black][Pieces::Rook], index);
        rook_moves = rook_moves - BitboardOperations::count_1(PsLegalMoveMaskGen::generate_rook_mask(pieces, index, Pieces::Black, false));
    }
    while (iteration_masks[Pieces::Black][Pieces::Queen]) {
        index = BitboardOperations::bsf(iteration_masks[Pieces::Black][Pieces::Queen]);
        BitboardOperations::set_0(iteration_masks[Pieces::Black][Pieces::Queen], index);
        queen_moves = queen_moves - BitboardOperations::count_1(PsLegalMoveMaskGen::generate_queen_mask(pieces, index, Pieces::Black, false));
    }

    mobility = mobility + StaticEvaluator::Mobility::Knight * knight_moves;
    mobility = mobility + StaticEvaluator::Mobility::Bishop * bishop_moves;
    mobility = mobility + StaticEvaluator::Mobility::Rook * rook_moves;
    mobility = mobility + StaticEvaluator::Mobility::Queen * queen_moves;

    return mobility;
}

Сдвоенные пешки

Третий фактор — сдвоенные пешки. Сдвоенная пешка считается слабостью. В моей программе сдвоенная пешка ухудшает оценку на 25:

static constexpr int32_t DoublePawn = -25;

Реализуется просто:

int32_t StaticEvaluator::_pawn_structure_double_pawn(Pieces pieces) {
    int32_t double_pawn = 0;

    int32_t double_pawn_ctr = 0;

    uint8_t white_pawns;
    uint8_t black_pawns;

    for (uint8_t x = 0; x < 8; x = x + 1) {
        white_pawns = BitboardOperations::count_1(pieces._piece_bitboards[Pieces::White][Pieces::Pawn] & BitboardColumns::Columns[x]);
        black_pawns = BitboardOperations::count_1(pieces._piece_bitboards[Pieces::Black][Pieces::Pawn] & BitboardColumns::Columns[x]);

        double_pawn_ctr = double_pawn_ctr + std::max(0, white_pawns - 1);
        double_pawn_ctr = double_pawn_ctr - std::max(0, black_pawns - 1);
    }

    double_pawn = double_pawn + StaticEvaluator::PawnStructure::DoublePawn * double_pawn_ctr;

    return double_pawn;
}

Соединенные пешки

Четвертый фактор — соединенные пешки. Соединенная пешка — пешка, защищенная другой. Наличие таких пешек является одним из признаков хорошей пешечной структуры. В моей программе соединенные пешки улучшают оценку на 12:

static constexpr int32_t ConnectedPawn = 12;

Реализуется очень просто:

int32_t StaticEvaluator::_pawn_structure_connected_pawn(Pieces pieces) {
    int32_t connected_pawn = 0;

    int32_t connected_pawn_ctr = 0;

    Bitboard white_captures = PsLegalMoveMaskGen::generate_pawn_left_captures_mask(pieces, Pieces::White, true) | PsLegalMoveMaskGen::generate_pawn_right_captures_mask(pieces, Pieces::White, true);
    Bitboard black_captures = PsLegalMoveMaskGen::generate_pawn_left_captures_mask(pieces, Pieces::Black, true) | PsLegalMoveMaskGen::generate_pawn_right_captures_mask(pieces, Pieces::Black, true);

    connected_pawn_ctr = connected_pawn_ctr + BitboardOperations::count_1(white_captures & pieces._piece_bitboards[Pieces::White][Pieces::Pawn]);
    connected_pawn_ctr = connected_pawn_ctr - BitboardOperations::count_1(black_captures & pieces._piece_bitboards[Pieces::Black][Pieces::Pawn]);

    connected_pawn = connected_pawn + StaticEvaluator::PawnStructure::ConnectedPawn * connected_pawn_ctr;

    return connected_pawn;
}

Продвижение пешек

Пятый фактор — продвижение пешек и тут будет кое-что особенное, о чем я упоминал в самом первом разделе. Самым простым способом реализации продвижения пешек было бы добавление всем пешкам бонус за близость к последней для них строке, но это не совсем верно. Проблема (если так можно выразится) заключается в том, что существуют проходные пешки, которых должно значительно сильнее тянуть вперед, чем обычные.

Но как проверить что пешка является проходной? Благодаря битбордам можно заранее рассчитать маски и проверка является ли пешка проходной будет происходить всего за 1-2 операции. Вот код рассчитывающий маски для опознавания проходных пешек:

#include <array>
#include "../Base/PositionRepresentation/Bitboard.hpp"


#pragma once


namespace PassedPawnMasks {
    static consteval std::array<Bitboard, 64> calc_white_passed_pawn_masks() {
        std::array<Bitboard, 64> masks{};

        for (uint8_t x = 0; x < 8; x = x + 1) {
            for (uint8_t y = 0; y < 8; y = y + 1) {

                for (uint8_t y1 = y + 1; y1 < 8; y1 = y1 + 1) {
                    if (x != 0) BitboardOperations::set_1(masks[y * 8 + x], y1 * 8 + x - 1);
                    if (x != 7) BitboardOperations::set_1(masks[y * 8 + x], y1 * 8 + x + 1);
                    BitboardOperations::set_1(masks[y * 8 + x], y1 * 8 + x);
                }
            }
        }

        return masks;
    }


    static consteval std::array<Bitboard, 64> calc_black_passed_pawn_masks() {
        std::array<Bitboard, 64> masks{};

        for (uint8_t x = 0; x < 8; x = x + 1) {
            for (uint8_t y = 0; y < 8; y = y + 1) {

                for (int8_t y1 = y - 1; y1 >= 0; y1 = y1 - 1) {
                    if (x != 0) BitboardOperations::set_1(masks[y * 8 + x], y1 * 8 + x - 1);
                    if (x != 7) BitboardOperations::set_1(masks[y * 8 + x], y1 * 8 + x + 1);
                    BitboardOperations::set_1(masks[y * 8 + x], y1 * 8 + x);
                }
            }
        }

        return masks;
    }


    static constexpr std::array<Bitboard, 64> WhitePassedPawnMasks = PassedPawnMasks::calc_white_passed_pawn_masks();
    static constexpr std::array<Bitboard, 64> BlackPassedPawnMasks = PassedPawnMasks::calc_black_passed_pawn_masks();
}

Используя эти маски, можно легко реализовать этот фактор:

int32_t StaticEvaluator::_pawn_structure_pawn_promotion(Pieces pieces) {
    int32_t pawn_promotion = 0;

    Bitboard white_pawns = pieces._piece_bitboards[Pieces::White][Pieces::Pawn];
    Bitboard black_pawns = pieces._piece_bitboards[Pieces::Black][Pieces::Pawn];

    uint8_t index;

    while (white_pawns) {
        index = BitboardOperations::bsf(white_pawns);
        BitboardOperations::set_0(white_pawns, index);

        if (PassedPawnMasks::WhitePassedPawnMasks[index] & pieces._piece_bitboards[Pieces::Black][Pieces::Pawn]) pawn_promotion = pawn_promotion + StaticEvaluator::PawnStructure::DefaultPawnPromotion[index / 8];
        else pawn_promotion = pawn_promotion + StaticEvaluator::PawnStructure::PassedPawnPromotion[index / 8];
    }
    while (black_pawns) {
        index = BitboardOperations::bsf(black_pawns);
        BitboardOperations::set_0(black_pawns, index);

        if (PassedPawnMasks::BlackPassedPawnMasks[index] & pieces._piece_bitboards[Pieces::White][Pieces::Pawn]) pawn_promotion = pawn_promotion - StaticEvaluator::PawnStructure::DefaultPawnPromotion[7 - index / 8];
        else pawn_promotion = pawn_promotion - StaticEvaluator::PawnStructure::PassedPawnPromotion[7 - index / 8];
    }

    return pawn_promotion;
}

Константы я выбрал следующие:

static constexpr std::array<int32_t, 8> DefaultPawnPromotion = {0, 0, 0, 0, 10, 20, 30, 0};
static constexpr std::array<int32_t, 8> PassedPawnPromotion = {0, 50, 50, 50, 70, 90, 110, 0};

Они показывают, что проходная пешка в 2 раза сильнее хочет дойти до последней строки, чем обычная. Помимо этого любая проходная пешка получает по 50 к оценке просто за то, что она есть.

Потерянная рокировка

Шестой фактор — потерянная рокировка. Если король потерял рокировку не рокировавшись, то это считается серьезной слабостью для безопасности короля. В моей программе сторона ухудшает свою оценку на 50 за каждую потерянную рокировку:

static constexpr int32_t CrashedCastling = -50;

Реализуется предельно просто:

int32_t StaticEvaluator::_king_safety_crashed_castling(bool w_l_castling, bool w_s_castling, bool b_l_castling, bool b_s_castling, bool white_castling_happened, bool black_castling_happened) {
    int32_t crashed_castling = 0;

    if (!white_castling_happened) {
        if (!w_l_castling) crashed_castling = crashed_castling + StaticEvaluator::KingSafety::CrashedCastling;
        if (!w_s_castling) crashed_castling = crashed_castling + StaticEvaluator::KingSafety::CrashedCastling;
    }

    if (!black_castling_happened) {
        if (!b_l_castling) crashed_castling = crashed_castling - StaticEvaluator::KingSafety::CrashedCastling;
        if (!b_s_castling) crashed_castling = crashed_castling - StaticEvaluator::KingSafety::CrashedCastling;
    }

    return crashed_castling;
}

Пешечный щит

Седьмой фактор — пешечный щит. Пешечный щит — один из самых простых способов реализации безопасности короля. Идея заключается в том, что после рокировки важно сохранять пешки на следующих двух строках. В моей программе сторона улучшает свою оценку на 33 за каждую такую пешку:

static constexpr int32_t PawnShield = 33;

Для быстрого вычисления этого фактора имеет смысл рассчитать маски пешечных щитов заранее:

#include <array>
#include "../Base/PositionRepresentation/Bitboard.hpp"


#pragma once


namespace PawnShieldMasks {
    static consteval std::array<Bitboard, 64> calc_white_pawn_shield_masks() {
        std::array<Bitboard, 64> white_pawn_shield_masks{};

        for (uint8_t x = 0; x < 8; x = x + 1) {
            for (uint8_t y = 0; y < 7; y = y + 1) {
                if (x != 0) BitboardOperations::set_1(white_pawn_shield_masks[y * 8 + x], (y + 1) * 8 + x - 1);
                if (x != 7) BitboardOperations::set_1(white_pawn_shield_masks[y * 8 + x], (y + 1) * 8 + x + 1);
                BitboardOperations::set_1(white_pawn_shield_masks[y * 8 + x], (y + 1) * 8 + x);

                if (y != 6) {
                    if (x != 0) BitboardOperations::set_1(white_pawn_shield_masks[y * 8 + x], (y + 2) * 8 + x - 1);
                    if (x != 7) BitboardOperations::set_1(white_pawn_shield_masks[y * 8 + x], (y + 2) * 8 + x + 1);
                    BitboardOperations::set_1(white_pawn_shield_masks[y * 8 + x], (y + 2) * 8 + x);
                }
            }
        }

        return white_pawn_shield_masks;
    }


    static consteval std::array<Bitboard, 64> calc_black_pawn_shield_masks() {
        std::array<Bitboard, 64> black_pawn_shield_masks{};

        for (uint8_t x = 0; x < 8; x = x + 1) {
            for (uint8_t y = 1; y < 8; y = y + 1) {
                if (x != 0) BitboardOperations::set_1(black_pawn_shield_masks[y * 8 + x], (y - 1) * 8 + x - 1);
                if (x != 7) BitboardOperations::set_1(black_pawn_shield_masks[y * 8 + x], (y - 1) * 8 + x + 1);
                BitboardOperations::set_1(black_pawn_shield_masks[y * 8 + x], (y - 1) * 8 + x);

                if (y != 1) {
                    if (x != 0) BitboardOperations::set_1(black_pawn_shield_masks[y * 8 + x], (y - 2) * 8 + x - 1);
                    if (x != 7) BitboardOperations::set_1(black_pawn_shield_masks[y * 8 + x], (y - 2) * 8 + x + 1);
                    BitboardOperations::set_1(black_pawn_shield_masks[y * 8 + x], (y - 2) * 8 + x);
                }
            }
        }

        return black_pawn_shield_masks;
    }


    static constexpr std::array<Bitboard, 64> WhitePawnShieldMasks = PawnShieldMasks::calc_white_pawn_shield_masks();
    static constexpr std::array<Bitboard, 64> BlackPawnShieldMasks = PawnShieldMasks::calc_black_pawn_shield_masks();
}

Далее реализовать этот фактор можно тоже очень просто:

int32_t StaticEvaluator::_king_safety_pawn_shield(Pieces pieces, bool white_castling_happened, bool black_castling_happened) {
    int32_t pawn_shield = 0;

    int32_t pawn_shield_ctr = 0;

    if (white_castling_happened) {
        Bitboard white_pawns = pieces._piece_bitboards[Pieces::White][Pieces::Pawn];
        Bitboard white_pawn_shield = PawnShieldMasks::WhitePawnShieldMasks[BitboardOperations::bsf(pieces._piece_bitboards[Pieces::White][Pieces::King])];
        pawn_shield_ctr = pawn_shield_ctr + BitboardOperations::count_1(white_pawns & white_pawn_shield);
    }

    if (black_castling_happened) {
        Bitboard black_pawns = pieces._piece_bitboards[Pieces::Black][Pieces::Pawn];
        Bitboard black_pawn_shield = PawnShieldMasks::BlackPawnShieldMasks[BitboardOperations::bsf(pieces._piece_bitboards[Pieces::Black][Pieces::King])];
        pawn_shield_ctr = pawn_shield_ctr - BitboardOperations::count_1(black_pawns & black_pawn_shield);
    }

    pawn_shield = pawn_shield + StaticEvaluator::KingSafety::PawnShield * pawn_shield_ctr;

    return pawn_shield;
}

Два слона

Восьмой фактор — два слона. Если игрок смог сохранить двух слонов, то за это стоит улучшить оценку, так как два слона вместе могут отрезать пешки или короля. В моей программе два слона улучшают оценку на 50:

static constexpr int32_t TwoBishops = 50;

Реализуется очень просто:

int32_t StaticEvaluator::_two_bishops(Pieces pieces) {
    int32_t two_bishops = 0;

    if (BitboardOperations::count_1(pieces._piece_bitboards[Pieces::White][Pieces::Bishop]) >= 2) two_bishops = two_bishops + StaticEvaluator::TwoBishops;
    if (BitboardOperations::count_1(pieces._piece_bitboards[Pieces::Black][Pieces::Bishop]) >= 2) two_bishops = two_bishops - StaticEvaluator::TwoBishops;

    return two_bishops;
}

Особая оценка для эндшпиля

В эндшпиле компьютерные программы часто испытывают трудности, так как даже такой примитивный эндшпиль как король с ферзем против короля может содержать мат в 20-30 ходов, что не могут увидеть даже самые оптимизированные движки.

Одним из решений является подключение таблиц Налимова или таблиц syzygy — баз данных где хранятся стратегии для многих эндшпилей. При помощи этих баз ИИ может играть совершенно идеально, но у этих баз есть много недостатков. Один из них — сложность с подключением. Подключить какой-нибудь syzygy будет труднее, чем все, что вы прочитали до этого. Другой, более серьезный, — огромный размер. Эти БД могут весить терабайты, что не очень подходит для подобных движков.

Другим решением является особая оценка для эндшпиля. Она учитывает близость короля побеждающей стороны к королю проигрывающей, а также расстояние проигрывающего короля от центра:

static constexpr int32_t AttackerKingProximityToDefenderKing = 10;
static constexpr int32_t DistanceBetweenDefenderKingAndMiddle = 10;

Но что такое эндшпиль? В моей программе это когда остается менее 9 фигур:

static constexpr int32_t MaximumPiecesForEndgame = 8;

Реализовывается эндшпильная оценка просто:

int32_t StaticEvaluator::_endgame(Pieces pieces, bool white_leading) {
    int32_t endgame = 0;

    if (BitboardOperations::count_1(pieces._all) > StaticEvaluator::Endgame::MaximumPiecesForEndgame) return endgame;

    uint8_t attacker_side;
    uint8_t defender_side;

    if (white_leading) {
        attacker_side = Pieces::White;
        defender_side = Pieces::Black;
    }
    else {
        attacker_side = Pieces::Black;
        defender_side = Pieces::White;
    }

    uint8_t attacker_king_p = BitboardOperations::bsf(pieces._piece_bitboards[attacker_side][Pieces::King]);
    uint8_t attacker_king_x = attacker_king_p % 8;
    uint8_t attacker_king_y = attacker_king_p / 8;

    uint8_t defender_king_p = BitboardOperations::bsf(pieces._piece_bitboards[defender_side][Pieces::King]);
    uint8_t defender_king_x = defender_king_p % 8;
    uint8_t defender_king_y = defender_king_p / 8;

    endgame = endgame + StaticEvaluator::Endgame::AttackerKingProximityToDefenderKing * (16 - std::abs(attacker_king_x - defender_king_x) - std::abs(attacker_king_y - defender_king_y));
    endgame = endgame + StaticEvaluator::Endgame::DistanceBetweenDefenderKingAndMiddle * (std::abs(defender_king_x - 3) + std::abs(defender_king_y - 4));

    if (!white_leading) endgame = -endgame;

    return endgame;
}

Минимакс

Мы закончили писать статическую оценку. Теперь самое время поговорить о динамической. Самой основой является минимакс алгоритм. Его идея очень проста: мы просто ищем наилучший ход для нашей стороны с предположением, что противник тоже будет делать наилучшие ходы. Вот псевдокод такого алгоритма:

int maxi( int depth ) {
    if ( depth == 0 ) return evaluate();
    int max = -oo;
    for ( all moves) {
        score = mini( depth - 1 );
        if( score > max )
            max = score;
    }
    return max;
}

int mini( int depth ) {
    if ( depth == 0 ) return evaluate();
    int min = +oo;
    for ( all moves) {
        score = maxi( depth - 1 );
        if( score < min )
            min = score;
    }
    return min;
}

, где depth — количество полуходов на которое мы хотим искать, а evaluate() — функция статической оценки о которой был разговор выше.

Продление шахов

Улучшить программу можно продлевая шахи. Программа с продлением шахов может находить довольно глубокие матовые комбинации. Идея очень простая — если шах, то глубину не уменьшаем. Это не взрывает дерево поиска, так как шахи встречаются редко и при них доступно мало ходов.

Альфа-бета отсечение

Коэффициент ветвление шахмат — 40. Это значит, что после каждого хода есть в среднем 40 ответных ходов. В дебюте и эндшпиле этот показатель куда ниже, но в середине игры — 40. Теперь, используя эти данные, предлагаю посчитать сколько надо будет оценить позиций после 20 полуходов:

Это огромное число, даже если бы можно было оценивать трилларды позиций в секунду, что в миллионы раз больше вычислительной мощности всей планеты, то мы бы не успели даже за год. Однако, такие топовые движки как Stockfish умудряются считать на такую глубину за секунды. Очевидно, что Stockfish не оценивает все десять в тридцатой степени позиций.

Один из эффективнейших способов пропустить большинство позиций в минимаксе — альфа-бета отсечение. Идея заключается в том, что если мы понимаем, что оценка на текущей ветви по-любому будет хуже оценки на предыдущей, то считать дальше нет смысла. Внизу есть иллюстрация из Википедии, она довольно наглядная:

На картинке видно, что в самом вверху мы ищем максимум трех чисел (3, 6, 5). Эти три числа получаются из минимума других двух чисел, но минимум последней ветви мы считаем не полностью, так как изначально у нас попалась пятерка и независимо от того, что пойдет дальше эта ветвь не подходит, так как результат будет не больше 5, а для изменения максимума с 6 на что-то другое нужно 7 или больше.

Вот псевдокод:

int alphaBetaMax( int alpha, int beta, int depthleft ) {
   if ( depthleft == 0 ) return evaluate();
   for ( all moves) {
      score = alphaBetaMin( alpha, beta, depthleft - 1 );
      if( score >= beta )
         return beta;   // fail hard beta-cutoff
      if( score > alpha )
         alpha = score; // alpha acts like max in MiniMax
   }
   return alpha;
}

int alphaBetaMin( int alpha, int beta, int depthleft ) {
   if ( depthleft == 0 ) return evaluate();
   for ( all moves) {
      score = alphaBetaMax( alpha, beta, depthleft - 1 );
      if( score <= alpha )
         return alpha; // fail hard alpha-cutoff
      if( score < beta )
         beta = score; // beta acts like min in MiniMax
   }
   return beta;
}

Для запуска поиска надо вызвать одну из этих функций (зависит от цвета стороны) с alpha равной отрицательной бесконечности и beta равной положительной бесконечности.

Продление взятий

Представим следующую ситуацию. Происходит анализ позиции с глубиной 8. Особо выделяется одна ветка и одна группа веток. Ветка интересно тем, что на 8 глубине мы забираем ферзя, а группа веток интересна тем, что на 2 глубине мы выигрываем коня. ИИ, естественно, выберет ветку с выигрышем ферзя, а не что-то из группы веток где мы выигрываем коня. Но это будет неправильная оценка, так как коня мы реально выигрывали, а на 9 глубине ветки с выигрышем ферзя забирали нашего ферзя, то есть никакого выигрыша не было.

Такой эффект называется эффектом горизонта. Казалось бы, что мы можем сделать, нашему ИИ просто не хватило глубины, но в этом суждении сразу две ошибки: увеличение глубины тут не поможет (подобные конфузы просто станут происходить на более глубокой глубине), а сделать с этим как раз есть что.

Идея в том, что после завершения основного поиска не возвращать статическую оценку, а запускать новый без лимита по глубине, но с рассмотрением только взятий. Разумеется, если взятия не улучшают оценку, то надо прерывать такой просмотр, а не возвращать оценку после всех взятий.

Сортировка ходов

Эффективность альфа-бета отсечения зависит от порядка ходов. Если ходы отсортированы от лучшего к худшему, то можно оценить только чуть больше корня от общего числа комбинаций, а это очень мало. С другой стороны, если ходы будут отсортированы от худшего к лучшему, то мы вообще не получим никакого профита от альфа-бета отсечения.

Зная это, надо постараться отсортировать ходы от лучшего к худшему. Это, естественно, вряд-ли получится, но приличное преимущество можно получить.

Для сортировки ходов можно воспользоваться принципом наиболее ценная жертва — наименее ценный нападающий. Идея в том, что съесть пешкой ферзя, как правило, гораздо выгоднее, чем наоборот. Согласно этому принципу, все взятия помещаются вперед и сортируются при помощи этого принципа, а тихие ходы остаются в конце.

Но как сортировать тихие ходы? Существует один способ. Он не такой эффективный как сортировка взятий, но тоже позволяет отсечь часть ходов. Идея в том, что двигать фигуру под пешку противника обычно плохая идея.

Зная все это, можно написать простую сортировку пузырьком. Она работает за квадрат, но ходов не так много из-за чего сортировка даже с плохой асимптотикой работает быстро:

#include "MoveSorter.hpp"


MoveList MoveSorter::sort(Pieces pieces, MoveList moves) {
    for (uint8_t i = 0; i < moves.size() - 1; i = i + 1) {
        for (uint8_t j = 0; j < moves.size() - i - 1; j = j + 1) {
            if (MoveSorter::_evaluate_move(pieces, moves[j]) < MoveSorter::_evaluate_move(pieces, moves[j + 1])) std::swap(moves[j], moves[j + 1]);
        }
    }

    return moves;
}
int32_t MoveSorter::_evaluate_move(Pieces pieces, Move move) {
    int32_t evaluation = 0;

    if (move._attacker_type != Pieces::Pawn) {
        Bitboard opponent_pawn_attacks = PsLegalMoveMaskGen::generate_pawn_left_captures_mask(pieces, Pieces::inverse(move._attacker_side), true) | PsLegalMoveMaskGen::generate_pawn_right_captures_mask(pieces, Pieces::inverse(move._attacker_side), true);
        if (BitboardOperations::get_bit(opponent_pawn_attacks, move._to)) {
            switch (move._attacker_type) {
                case Pieces::Knight: evaluation = evaluation - StaticEvaluator::Material::Knight; break;
                case Pieces::Bishop: evaluation = evaluation - StaticEvaluator::Material::Bishop; break;
                case Pieces::Rook: evaluation = evaluation - StaticEvaluator::Material::Rook; break;
                case Pieces::Queen: evaluation = evaluation - StaticEvaluator::Material::Queen; break;
                // Король не может быть на поле, битое пешкой противника.
            }
        }
    }

    if (move._defender_type != 255) {
        switch (move._defender_type) {
            case Pieces::Pawn: evaluation = evaluation + 1000 * StaticEvaluator::Material::Pawn; break;
            case Pieces::Knight: evaluation = evaluation + 1000 * StaticEvaluator::Material::Knight; break;
            case Pieces::Bishop: evaluation = evaluation + 1000 * StaticEvaluator::Material::Bishop; break;
            case Pieces::Rook: evaluation = evaluation + 1000 * StaticEvaluator::Material::Rook; break;
            case Pieces::Queen: evaluation = evaluation + 1000 * StaticEvaluator::Material::Queen; break;
            // Короля нельзя съесть.
        }
        switch (move._attacker_type) {
            case Pieces::Pawn: evaluation = evaluation - StaticEvaluator::Material::Pawn; break;
            case Pieces::Knight: evaluation = evaluation - StaticEvaluator::Material::Knight; break;
            case Pieces::Bishop: evaluation = evaluation - StaticEvaluator::Material::Bishop; break;
            case Pieces::Rook: evaluation = evaluation - StaticEvaluator::Material::Rook; break;
            case Pieces::Queen: evaluation = evaluation - StaticEvaluator::Material::Queen; break;
            // Если съедает король, то ничего не вычитаем, ведь короля нельзя съесть, следовательно, никакого ответного взятия, вероятно, не будет.
        }
    }

    return evaluation;
}

Теперь перед началом альфа-бета поиска нужно отсортировать ходы, что даст прибавку к скорости.

Хеш таблица

Помните начало статьи? Там был разговор про Zobrist хеширование. Тогда я упомянул, что оно нам пригодится для троекратного повторения позиции и еще кое-чего. Так вот: это кое-чего как раз хеш таблица.

Идея в том, что дерево игры — не совсем дерево, а, скорее, граф. Многие позиции постоянно повторяются и считать их каждый раз по-новому довольно не разумно. Вместо этого стоит пробовать использовать результаты предыдущих поисков.

Создадим структуру записи:

#include "../Base/PositionRepresentation/ZobristHash.hpp"


#pragma once


struct Entry {
    Entry();
    Entry(ZobristHash hash, int32_t depth, uint8_t best_move_index);

    friend bool operator <(Entry left, Entry right);

    ZobristHash _hash;
    int32_t _depth;
    uint8_t _best_move_index;
};

Оператор меньше показывает меньше ли хеш:

bool operator <(Entry left, Entry right) {
    return (left._hash < right._hash);
}

Эта структура содержит сам хеш (для возможности сравнивать текущую позицию с позицией из записи), глубину поиска на которой получен результат (чтобы оставлять в таблице только наиболее просчитанные результаты) и индекс лучшего хода.

При поиске мы будем добавлять в некоторое хранилище такие записи, а перед началом поиска искать запись с совпадающим хешом и пробовать ход по лучшему индексу в надежде, что он вызовет отсечку дерева.

Но в каком хранилище мы будем хранить эти записи? Я предлагаю в множестве, то есть в std::set. Множество — список, но не простой, ведь при вставке он бинарным поиском вставляет в список элемент так, чтобы сохранялась сортировка, что позволяет находить там элементы тоже за логарифм благодаря тому же бинарному поиску.

Вот так выглядит полный код хеш таблицы:

#include <set>
#include "Entry.hpp"


#pragma one


class TranspositionTable {
public:
    TranspositionTable();

    void add_entry(Entry entry);
    uint8_t try_to_find_best_move_index(ZobristHash hash);
private:
    std::set<Entry> _set;
};

#include "TranspositionTable.hpp"


TranspositionTable::TranspositionTable() = default;
void TranspositionTable::add_entry(Entry entry) {
    auto hash_copy = this->_set.find(entry);
    if (hash_copy == this->_set.end() or hash_copy->_depth < entry._depth) this->_set.insert(entry);
}
uint8_t TranspositionTable::try_to_find_best_move_index(ZobristHash hash) {
    auto entry = this->_set.find({hash, 0, 0});

    if (entry == this->_set.end()) return 255;
    return entry->_best_move_index;
}

Итеративное углубление

Цель итеративного углубления позволить контролировать время выполнения альфа-бета отсечения. Проблема в том, что мы не можем просто так прервать поиск, так как его результат будет бессмысленным в этом случае.

Вместо этого мы сначала выполняем поиск на глубину 1, потом на глубину 2, потом на глубину 3 и т.д. Благодаря этому поиск всегда можно прервать и вернуть результат предыдущего. Это звучит не эффективно, так как результат каждого нового поиска переделывает все предыдущие, но при использования хеш таблицы он может быть выполнен еще быстрее, чем обычный поиск из-за большого числа отсечений.

База дебютов

Если взять все что было сверху и написать это, то получится довольно хороший алгоритм за исключением одной детали. Он будет абсолютно детерминированным и все партии будут 1 в 1. Играть против такого противника довольно скучно, поэтому стоит добавить базу дебютов из которой будут выбираться случайные ходы.

В качестве базы дебютов я буду использовать первые 6 ходов (или 12 полуходов) из заранее скаченных тысяч игр гроссмейстеров. Вот первые несколько строк из базы:

e2e4 e7e5 g1f3 b8c6 f1c4 f8c5 c2c3 g8f6 d2d3 d7d6 b2b4 c5b6 
d2d4 g8f6 c2c4 g7g6 f2f3 d7d5 c4d5 f6d5 e2e4 d5b6 b1c3 f8g7 
c2c4 e7e6 b1c3 d7d5 d2d4 g8f6 c4d5 e6d5 c1g5 c7c6 d1c2 f8e7 
e2e4 e7e6 d2d4 d7d5 b1d2 c7c5 g1f3 c5d4 f3d4 g8f6 e4d5 d8d5 
e2e4 e7e5 g1f3 b8c6 f1b5 g8f6 d2d3 f8c5 b5c6 d7c6 b1d2 e8g8 
c2c4 e7e5 b1c3 g8f6 g1f3 b8c6 g2g3 f8b4 c3d5 b4c5 f1g2 d7d6 
d2d4 g8f6 c2c4 e7e6 g1f3 d7d5 b1c3 c7c5 c4d5 f6d5 e2e4 d5c3 
d2d4 g8f6 c2c4 g7g6 f2f3 d7d6 e2e4 f8g7 g1e2 e8g8 c1e3 c7c5 
e2e4 e7e5 g1f3 b8c6 f1b5 a7a6 b5a4 g8f6 e1g1 f8e7 d2d3 d7d6 
d2d4 g8f6 c2c4 e7e6 b1c3 f8b4 d1c2 e8g8 c1g5 c7c5 d4c5 d8a5 
e2e4 g7g6 d2d4 f8g7 b1c3 d7d6 c1e3 a7a6 a2a4 g8f6 h2h3 e8g8 
e2e4 e7e5 g1f3 b8c6 f1b5 g8f6 e1g1 f6e4 d2d4 e4d6 b5c6 d7c6 
c2c4 c7c5 g2g3 b8c6 f1g2 g7g6 g1f3 f8g7 e1g1 d7d6 b1c3 f7f5 
d2d4 d7d5 c2c4 c7c6 g1f3 g8f6 d1b3 d5c4 b3c4 c8g4 b1d2 e7e6 

При инициализации базы ходы будут загружаться в вектор, причем эти ходы будут трансформироваться в нашу специальную структуру хода, а также проверяться на легальность (вдруг в базе ошибка). При поиске будет искаться ответ. Вот полный код:

#include <fstream>
#include <sstream>
#include <tuple>
#include "../Base/MoveGeneration/LegalMoveGen.hpp"


#pragma once


class OpeningBook {
public:
    OpeningBook();
    OpeningBook(const std::string& path);

    std::tuple<Move, int32_t> try_to_find_move(const Position& position);
private:
    std::vector<std::vector<Move>> _moves;
};

#include "OpeningBook.hpp"


OpeningBook::OpeningBook() = default;
OpeningBook::OpeningBook(const std::string& path) {
    std::ifstream file(path);
    if (!file.is_open()) {
        std::cout << ANSI::Red << "Could not find the opening book." << ANSI::End << std::endl;
        std::exit(255);
    }

    std::string game;
    std::stringstream game_thread;

    std::string string_move;
    uint8_t from;
    uint8_t to;

    MoveList possible_moves;
    bool move_found;

    Position buff;

    while (std::getline(file, game)) {
        game_thread = std::stringstream(game);
        this->_moves.resize(this->_moves.size() + 1);

        buff = {"rnbqkbnr/pppppppp/8/8/8/8/PPPPPPPP/RNBQKBNR", 255, true, true, true, true, 1};

        while (game_thread >> string_move and game_thread.good()) {
            from = (string_move[1] - '1') * 8 + string_move[0] - 'a';
            to = (string_move[3] - '1') * 8 + string_move[2] - 'a';

            possible_moves = LegalMoveGen::generate(buff, buff._move_ctr - std::floor(buff._move_ctr) > 1e-7);
            move_found = false;
            for (uint8_t i = 0; i < possible_moves.size(); i = i + 1) {
                if (possible_moves[i]._from == from and possible_moves[i]._to == to) {
                    this->_moves.back().push_back(possible_moves[i]);
                    buff.move(possible_moves[i]);
                    move_found = true;
                    break;
                }
            }
            if (!move_found) {
                std::cout << ANSI::Red << "Error in the opening book." << ANSI::End << std::endl;
                std::exit(255);
            }
        }
    }

    file.close();
}
std::tuple<Move, int32_t> OpeningBook::try_to_find_move(const Position& position) {
    Position buff;

    std::vector<Move> possible_moves;
    bool move_exist;

    for (int32_t game = 0; game < this->_moves.size(); game = game + 1) {
        buff = {"rnbqkbnr/pppppppp/8/8/8/8/PPPPPPPP/RNBQKBNR", 255, true, true, true, true, 1};

        if (buff._pieces == position._pieces) {
            move_exist = false;
            for (auto added_move : possible_moves) {
                if (added_move == this->_moves[game][0]) {
                    move_exist = true;
                    break;
                }
            }

            if (!move_exist) possible_moves.push_back(this->_moves[game][0]);
            continue;
        }

        for (int32_t move = 0; move < this->_moves[game].size() - 1; move = move + 1) {
            buff.move(this->_moves[game][move]);

            if (buff._pieces == position._pieces) {
                move_exist = false;
                for (auto added_move : possible_moves) {
                    if (added_move == this->_moves[game][move + 1]) {
                        move_exist = true;
                        break;
                    }
                }

                if (!move_exist) possible_moves.push_back(this->_moves[game][move + 1]);
            }
        }
    }

    if (possible_moves.empty()) {
        return std::make_tuple(Move(), 0);
    }

    return std::make_tuple(possible_moves[time(nullptr) % possible_moves.size()], possible_moves.size());
}

ИИ. Финал

Настало время написать итоговый класс. Комментировать его не вижу смысла, так как он делает все то же самое о чем я говорил последнее время. Вот код:

#include <chrono>
#include <future>
#include <unistd.h>
#include <iomanip>
#include "../Base/MoveGeneration/LegalMoveGen.hpp"
#include "MoveSorter.hpp"
#include "TranspositionTable.hpp"
#include "OpeningBook.hpp"


#pragma once


class AI {
public:
    AI();
    AI(const std::string& opening_book_path);

    Move best_move(const Position& position, uint8_t side, int32_t min_ms, int32_t max_ms);
private:
    OpeningBook _opening_book;

    static std::tuple<int32_t, Move> _best_move(const Position& position, uint8_t side, int32_t depth, TranspositionTable &tt);

    static std::tuple<int32_t, Move> _alpha_beta_min(Position position, int32_t alpha, int32_t beta, int32_t depth_left, int32_t depth_current, TranspositionTable &tt);
    static std::tuple<int32_t, Move> _alpha_beta_max(Position position, int32_t alpha, int32_t beta, int32_t depth_left, int32_t depth_current, TranspositionTable &tt);

    static int32_t _alpha_beta_min_only_captures(const Position& position, int32_t alpha, int32_t beta, int32_t depth_current);
    static int32_t _alpha_beta_max_only_captures(const Position& position, int32_t alpha, int32_t beta, int32_t depth_current);

    struct Infinity {
        static constexpr int32_t Negative = -1e+9;
        static constexpr int32_t Positive = 1e+9;
    };
};

#include "AI.hpp"


#define nsecs std::chrono::high_resolution_clock::now().time_since_epoch().count()


static std::atomic<bool> stop_search;


static int64_t evaluated;
static int32_t maximal_depth;
static int32_t tt_cutoffs;


AI::AI() = default;
AI::AI(const std::string& opening_book_path) {
    this->_opening_book = {opening_book_path};
}
Move AI::best_move(const Position& position, uint8_t side, int32_t min_ms, int32_t max_ms) {
    std::cout << std::endl;
    StaticEvaluator::evaluate(position._pieces, position._w_l_castling, position._w_s_castling, position._b_l_castling, position._b_s_castling, position._white_castling_happened, position._black_castling_happened, true);

    int64_t time_start = nsecs;
    stop_search = false;
    TranspositionTable tt;

    std::tuple<Move, int32_t> opening_book_result = this->_opening_book.try_to_find_move(position);
    std::cout << ANSI::Green << "Number of available moves in the opening book: " << std::get<1>(opening_book_result) << "." << ANSI::End << std::endl;
    if (std::get<1>(opening_book_result)) {
        usleep(std::max((int64_t)0, (min_ms - (nsecs - time_start) / (int64_t)1e+6) * (int64_t)1e+3));
        return std::get<0>(opening_book_result);
    }

    std::cout << ANSI::Green << "Search started." << std::endl;

    int32_t best_move_evaluation;
    Move best_move;
    std::future<std::tuple<int32_t, Move>> best_move_thread;

    bool update_best_move;

    for (int32_t i = 1; i < 1e+3; i = i + 1) {
        evaluated = 0;
        maximal_depth = 0;
        tt_cutoffs = 0;

        best_move_thread = std::async(AI::_best_move, position, side, i, std::ref(tt));

        update_best_move = true;
        while (best_move_thread.wait_for(std::chrono::seconds(0)) != std::future_status::ready) {
            if ((nsecs - time_start) / (int32_t)1e+6 >= max_ms) {
                update_best_move = false;
                break;
            }
            usleep(20000);
        }

        if (update_best_move or i == 1) std::tie(best_move_evaluation, best_move) = best_move_thread.get();
        else {
            stop_search = true;
            break;
        }

        std::cout << "Base depth: " << std::setw(4) << i << ". Maximal depth: " << std::setw(4) << maximal_depth << ". Evaluation: " << std::setw(6) << (float)best_move_evaluation / 100.0f << " pawns. Evaluated (this iteration): " << std::setw(10) << evaluated << ". TT cutoffs (this iteration): " << std::setw(10) << tt_cutoffs << ". Time (full search): " << std::setw(10) << (nsecs - time_start) / (int32_t)1e+6 << " ms." << std::endl;

        if (best_move_evaluation > AI::Infinity::Positive - 2000 or best_move_evaluation < AI::Infinity::Negative + 2000) break;
    }

    usleep(std::max((int64_t)0, (min_ms - (nsecs - time_start) / (int64_t)1e+6) * (int64_t)1e+3));

    std::cout << "Search finished." << std::endl << ANSI::End;

    return best_move;
}
std::tuple<int32_t, Move> AI::_best_move(const Position& position, uint8_t side, int32_t depth, TranspositionTable &tt) {
    if (side == Pieces::White) return AI::_alpha_beta_max(position, AI::Infinity::Negative, AI::Infinity::Positive, depth, 0, tt);
    return AI::_alpha_beta_min(position, AI::Infinity::Negative, AI::Infinity::Positive, depth, 0, tt);
}
std::tuple<int32_t, Move> AI::_alpha_beta_min(Position position, int32_t alpha, int32_t beta, int32_t depth_left, int32_t depth_current, TranspositionTable &tt) {
    if (stop_search) return std::make_tuple(0, Move());
    if (depth_current > maximal_depth) maximal_depth = depth_current;

    if (depth_left == 0) return std::make_tuple(AI::_alpha_beta_min_only_captures(position, alpha, beta, depth_current), Move());

    if (position._fifty_moves_ctr >= 50 or position._repetition_history.get_repetition_number(position._hash) >= 3) return std::make_tuple(0, Move());

    MoveList moves = LegalMoveGen::generate(position, Pieces::Black);
    moves = MoveSorter::sort(position._pieces, moves);
    Move move;
    Move best_move;
    uint8_t best_move_index;

    bool in_check = PsLegalMoveMaskGen::in_danger(position._pieces, BitboardOperations::bsf(position._pieces._piece_bitboards[Pieces::Black][Pieces::King]), Pieces::Black);

    if (moves.size() == 0) {
        if (in_check) return std::make_tuple(AI::Infinity::Positive - depth_current, Move());
        return std::make_tuple(0, Move());
    }

    int32_t evaluation;

    Position copy;

    uint8_t tt_result = tt.try_to_find_best_move_index(position._hash);

    for (uint8_t i = 0; i < moves.size(); i = i + 1) {
        if (tt_result >= moves.size()) move = moves[i];
        else {
            if (i == 0) move = moves[tt_result];
            else {
                if (i == tt_result) move = moves[0];
                else move = moves[i];
            }
        }

        copy = position;
        copy.move(move);
        evaluation = std::get<0>(AI::_alpha_beta_max(copy, alpha, beta, depth_left - !in_check, depth_current + 1, tt));

        if (evaluation <= alpha) {
            if (tt_result >= moves.size() or i != 0) tt.add_entry({position._hash, depth_left, best_move_index});
            else tt_cutoffs = tt_cutoffs + 1;
            return std::make_tuple(alpha, best_move);
        }
        if (evaluation < beta) {
            best_move = move;
            best_move_index = i;
            beta = evaluation;
        }
    }

    tt.add_entry({position._hash, depth_left, best_move_index});
    return std::make_tuple(beta, best_move);
}
std::tuple<int32_t, Move> AI::_alpha_beta_max(Position position, int32_t alpha, int32_t beta, int32_t depth_left, int32_t depth_current, TranspositionTable &tt) {
    if (stop_search) return std::make_tuple(0, Move());
    if (depth_current > maximal_depth) maximal_depth = depth_current;

    if (depth_left == 0) return std::make_tuple(AI::_alpha_beta_max_only_captures(position, alpha, beta, depth_current), Move());

    if (position._fifty_moves_ctr >= 50 or position._repetition_history.get_repetition_number(position._hash) >= 3) return std::make_tuple(0, Move());

    MoveList moves = LegalMoveGen::generate(position, Pieces::White);
    moves = MoveSorter::sort(position._pieces, moves);
    Move move;
    Move best_move;
    uint8_t best_move_index;

    bool in_check = PsLegalMoveMaskGen::in_danger(position._pieces, BitboardOperations::bsf(position._pieces._piece_bitboards[Pieces::White][Pieces::King]), Pieces::White);

    if (moves.size() == 0) {
        if (in_check) return std::make_tuple(AI::Infinity::Negative + depth_current, Move());
        return std::make_tuple(0, Move());
    }

    int32_t evaluation;

    Position copy;

    uint8_t tt_result = tt.try_to_find_best_move_index(position._hash);

    for (uint8_t i = 0; i < moves.size(); i = i + 1) {
        if (tt_result >= moves.size()) move = moves[i];
        else {
            if (i == 0) move = moves[tt_result];
            else {
                if (i == tt_result) move = moves[0];
                else move = moves[i];
            }
        }

        copy = position;
        copy.move(move);
        evaluation = std::get<0>(AI::_alpha_beta_min(copy, alpha, beta, depth_left - !in_check, depth_current + 1, tt));

        if (evaluation >= beta) {
            if (tt_result >= moves.size() or i != 0) tt.add_entry({position._hash, depth_left, best_move_index});
            else tt_cutoffs = tt_cutoffs + 1;
            return std::make_tuple(beta, best_move);
        }
        if (evaluation > alpha) {
            best_move = move;
            best_move_index = i;
            alpha = evaluation;
        }
    }

    tt.add_entry({position._hash, depth_left, best_move_index});
    return std::make_tuple(alpha, best_move);
}
int32_t AI::_alpha_beta_min_only_captures(const Position& position, int32_t alpha, int32_t beta, int32_t depth_current) {
    if (stop_search) return 0;
    if (depth_current > maximal_depth) maximal_depth = depth_current;

    int32_t evaluation = StaticEvaluator::evaluate(position._pieces, position._w_l_castling, position._w_s_castling, position._b_l_castling, position._b_s_castling, position._white_castling_happened, position._black_castling_happened);
    evaluated = evaluated + 1;

    if (evaluation <= alpha) return alpha;
    if (evaluation < beta) beta = evaluation;

    MoveList moves = LegalMoveGen::generate(position, Pieces::Black, true);
    moves = MoveSorter::sort(position._pieces, moves);
    Move move;

    Position copy;

    for (uint8_t i = 0; i < moves.size(); i = i + 1) {
        move = moves[i];

        copy = position;
        copy.move(move);
        evaluation = AI::_alpha_beta_max_only_captures(copy, alpha, beta, depth_current + 1);

        if (evaluation <= alpha) return alpha;
        if (evaluation < beta) beta = evaluation;
    }

    return beta;
}
int32_t AI::_alpha_beta_max_only_captures(const Position& position, int32_t alpha, int32_t beta, int32_t depth_current) {
    if (stop_search) return 0;
    if (depth_current > maximal_depth) maximal_depth = depth_current;

    int32_t evaluation = StaticEvaluator::evaluate(position._pieces, position._w_l_castling, position._w_s_castling, position._b_l_castling, position._b_s_castling, position._white_castling_happened, position._black_castling_happened);
    evaluated = evaluated + 1;

    if (evaluation >= beta) return beta;
    if (evaluation > alpha) alpha = evaluation;

    MoveList moves = LegalMoveGen::generate(position, Pieces::White, true);
    moves = MoveSorter::sort(position._pieces, moves);
    Move move;

    Position copy;

    for (uint8_t i = 0; i < moves.size(); i = i + 1) {
        move = moves[i];

        copy = position;
        copy.move(move);
        evaluation = AI::_alpha_beta_min_only_captures(copy, alpha, beta, depth_current + 1);

        if (evaluation >= beta) return beta;
        if (evaluation > alpha) alpha = evaluation;
    }

    return alpha;
}

Итог

Я написал небольшой интерфейс на SDL2 для этого движка. Для счастливых пользователей deb дистрибутивов Linux я подготовил deb пакет. Тем не менее, SDL2 полностью кроссплатформенный, так что никаких проблем с компилированием под Windows или MacOS быть не должно.

Играет довольно неплохо, меня с треском обыгрывает. На одном очень популярном шахматном сайте (подсказка: он заблокирован в РФ) я нашел ботов и уровень их игры измеренный в Эло. Сыграв с ними при помощи своего движка, я примерно вычислил количество Эло этого движка, получилось около 2000, по крайней мере в рамках этой платформы.

Спасибо за чтение. Код и deb пакет есть тут.

upd. Если будете компилировать сами, то крайне желательно включить оптимизацию (в gcc -O3), а также link-time оптимизацию, дабы компилятор мог заинлайнить код многих легких функций (в gcc -flto).

Рассмотрим некоторые базовые концепции, которые помогут нам создать простой искусственный интеллект, умеющий играть в шахматы:

• перемещение;
• оценка шахматной доски;
• минимакс;
• альфа-бета-отсечение.

На каждом шаге мы будем улучшать наш алгоритм с помощью одного из этих проверенных временем методов шахматного программирования. Вы увидите, как каждый из них влияет на стиль игры алгоритма.

Готовый алгоритм можно найти на GitHub.

Шаг 1. Генерация ходов и визуализация шахматной доски

Мы будем использовать библиотеки chess.js для генерации ходов и chessboard.js для визуализации доски. Библиотека для генерации ходов реализует все правила шахмат. Исходя из этого, мы можем рассчитать все ходы для данного состояния доски.

Визуализация функции генерации движения. Исходное положение используется как вход, а на выходе — все возможные ходы из этой позиции.

Использование этих библиотек поможет нам сосредоточиться только на самой интересной задаче — создании алгоритма, который находит лучший ход. Мы начнем с написания функции, которая возвращает случайный ход из всех возможных ходов:

var calculateBestMove = function(game) {
    //Генерация всех ходов для данной позиции
    var newGameMoves = game.ugly_moves();
    return newGameMoves[Math.floor(Math.random() * newGameMoves.length)];
};

Хотя этот алгоритм не очень солидный шахматист, но это хорошая отправная точка, поскольку его уровня достаточно, чтобы сыграть с нами:

Черные играют случайными ходами

Посмотреть, что получилось на данном этапе, вы можете на JSFiddle.

Шаг 2. Оценка доски

Теперь попробуем понять, какая из сторон сильнее в определенном положении. Самый простой способ добиться этого — посчитать относительную силу фигур на доске, используя следующую таблицу:

С помощью функции оценки мы можем создать алгоритм, который выбирает ход с наивысшей оценкой:

var calculateBestMove = function (game) {

    var newGameMoves = game.ugly_moves();
    var bestMove = null;
    //Используйте любое отрицательное число
    var bestValue = -9999;

    for (var i = 0; i < newGameMoves.length; i++) {
        var newGameMove = newGameMoves[i];
        game.ugly_move(newGameMove);

        //Возьмите отрицательное число, поскольку ИИ играет черными
        var boardValue = -evaluateBoard(game.board())
        game.undo();
        if (boardValue > bestValue) {
            bestValue = boardValue;
            bestMove = newGameMove
        }
    }

    return bestMove;

};

Единственным ощутимым улучшением является то, что теперь наш алгоритм съест фигуру, если это возможно:

Черные играют с помощью простой функции оценки

Посмотреть, что получилось на данном этапе, вы можете на JSFiddle.

Шаг 3. Дерево поиска и минимакс

Затем мы создадим дерево поиска, из которого алгоритм может выбрать лучший ход. Это делается с помощью алгоритма «минимакс».

Прим. перев. В одной из наших статей мы уже имели дело с минимаксом — учились создавать ИИ, который невозможно обыграть в крестики-нолики.

В этом алгоритме рекурсивное дерево всех возможных ходов исследуется до заданной глубины, а позиция оценивается на «листьях» дерева.

После этого мы возвращаем либо наименьшее, либо наибольшее значение потомка в родительский узел, в зависимости от того, чей просчитывается ход (то есть мы стараемся минимизировать или максимизировать результат на каждом уровне).

Визуализация минимакса в искусственном положении. Лучший ход для белых — b2-c3, так мы можем гарантировать, что доберемся до позиции, где оценка равна -50

var minimax = function (depth, game, isMaximisingPlayer) {
    if (depth === 0) {
        return -evaluateBoard(game.board());
    }
    var newGameMoves = game.ugly_moves();
    if (isMaximisingPlayer) {
        var bestMove = -9999;
        for (var i = 0; i < newGameMoves.length; i++) {
            game.ugly_move(newGameMoves[i]);
            bestMove = Math.max(bestMove, minimax(depth - 1, game, !isMaximisingPlayer));
            game.undo();
        }
        return bestMove;
    } else {
        var bestMove = 9999;
        for (var i = 0; i < newGameMoves.length; i++) {
            game.ugly_move(newGameMoves[i]);
            bestMove = Math.min(bestMove, minimax(depth - 1, game, !isMaximisingPlayer));
            game.undo();
        }
        return bestMove;
    }
};

С минимаксом наш алгоритм начинает понимать основную тактику шахмат:

Минимакс с уровнем глубины 2

Посмотреть, что получилось на данном этапе, вы можете на JSFiddle.

Эффективность минимакса в значительной степени зависит от достижимой глубины поиска. Именно это мы улучшим на следующем шаге.

Шаг 4. Альфа-бета-отсечение

Альфа-бета-отсечение — это метод оптимизации алгоритма «минимакс», который позволяет игнорировать некоторые ветви в дереве поиска. Это позволяет нам намного глубже оценить дерево поиска, используя те же ресурсы.

Альфа-бета-отсечение основано на ситуации, когда мы можем прекратить оценивать часть дерева поиска, если найдем шаг, который приведет к худшей ситуации, чем та, к которой приводил ранее обнаруженный шаг.

Альфа-бета-отсечение не влияет на результат минимакса, оно только ускоряет его.

Этот алгоритм будет более эффективным, если мы сначала проверим те пути, которые ведут к хорошим ходам:

Позиции, которые нам не нужны, если используется альфа-бета-отсечение. Дерево посещается в описанном порядке.

С альфа-бета-отсечением мы получаем значительное улучшение минимакса, как показано в следующем примере:

Количество позиций, которые нужно оценить в случае поиска с глубиной 4 и начальной позицией, изображённой на картинке.

Посмотреть, что получилось на данном этапе, вы можете на JSFiddle.

Шаг 5. Улучшенная функция оценки

Первоначальная функция оценки довольно наивна, поскольку мы просто подсчитываем очки фигур, которые находятся на доске. Чтобы улучшить её, мы начнём учитывать положение фигур. Например, конь в центре доски «дороже», потому что он имеет больше доступных ходов и, следовательно, более активен, чем конь на краю доски.

Мы будем использовать слегка скорректированную версию квадратных таблиц, первоначально описанных в вики Chess Programming.

Визуализация квадратных таблиц. Мы можем уменьшить или увеличить оценку в зависимости от местоположения фигуры.

Применив это улучшение, мы получим алгоритм, который неплохо играет в шахматы, по крайней мере, с точки зрения простого игрока:

Улучшенная оценка и альфа-бета-отсечение с глубиной поиска 3

Посмотреть, что получилось на данном этапе, вы можете на JSFiddle.

Заключение

Сила даже простого шахматного алгоритма состоит в том, что он не совершает глупых ошибок. Тем не менее, ему по-прежнему не хватает стратегического взгляда на ситуацию.

С помощью методов, которые представлены здесь, мы смогли запрограммировать шахматный алгоритм, который может неплохо играть в шахматы. В финальном алгоритме реализация ИИ занимает всего 200 строк кода — это означает, что базовые принципы довольно просты. Вы можете посмотреть окончательную версию программы на GitHub.

Вот некоторые дополнительные улучшения, которые мы могли бы внести в алгоритм:

• упорядочивание ходов;
• ускорение генерации ходов;
• оценка эндшпиля.

Если вы хотите узнать о шахматных алгоритмах больше, зайдите на Chess Programming Wiki.

Перевод статьи «A step-by-step guide to building a simple chess AI»

В предыдущей статье я разработал программу игры в шахматы за один день, используя Python.

Теперь я решил поэкспериментировать, чтобы значительно сократить это время, используя chatGPT для генерации кода. ChatGPT — это чат-бот, основанный на GPT3 от OpenAI, о котором сейчас говорят все.

Цель этого эксперимента — проверить способности написания кода chatGPT.

Давайте посмотрим на диалог, который у меня был с chatGPT

Вопрос: Давай вместе напишем программу шахмат на Python

Ответ: Конечно, это звучит очень интересно! Прежде чем мы начнём, я должен упомянуть, что написание полнофункциональной шахматной программы является нетривиальной задачей и, вероятно, потребует значительного количества времени и усилий. Однако мы, безусловно, можем начать с обсуждения некоторых основных концепций и идей, которые были бы задействованы в таком проекте.

Для начала нам нужно было бы представить состояние шахматной доски в нашей программе. Это можно было бы сделать с помощью двумерного массива, где каждый элемент массива представляет собой один квадрат на шахматной доске. Нам нужно было бы сохранить тип фигуры, которая занимает каждый квадрат, а также любую другую соответствующую информацию, такую как переместилась ли фигура, угрожают ли ей какие-либо другие фигуры и т.д.

Как только у нас появится способ представить состояние шахматной доски, нам нужно будет внедрить правила шахмат. Это включало бы такие вещи, как обеспечение того, чтобы фигуры двигались только теми способами, которые им разрешены (например, слон может двигаться только по диагонали), предотвращение совершения игроками незаконных ходов (таких как перемещение фигуры на квадрат, который занят одной из их собственных фигур), и обработка специальных ходов, таких как рокировка и взятие на проходе.

Далее нам нужно было бы реализовать логику игры, которая включала бы отслеживание того, чья очередь, проверку окончания игры (например, когда игрок ставит мат) и обработку других аспектов игры, таких как продвижение пешки и захват фигур.

Наконец, нам нужно было бы реализовать какой-то пользовательский интерфейс, такой как интерфейс командной строки или графический пользовательский интерфейс, чтобы позволить игрокам взаимодействовать с программой и делать свои ходы.

В целом, при написании шахматной программы необходимо учитывать множество различных аспектов, и для её правильного выполнения потребуется хорошее понимание правил шахмат и тщательное планирование. Тем не менее, я думаю, что это был бы сложный и полезный проект для работы, и я с нетерпением жду возможности услышать больше о ваших идеях о том, как подойти к нему!

Вопрос: Начни с генерации кода шахматной доски

Ответ: Конечно, мы можем начать с внедрения шахматной доски. Как я упоминал ранее, одним из способов сделать это было бы использование двумерного массива, где каждый элемент массива представляет собой один квадрат на шахматной доске. Вот один из возможных способов сделать это:

Этот код создаёт массив 8×8 под названием board и заполняет его начальными позициями фигур. Затем он выводит получившуюся доску, которая должна выглядеть примерно так:

Конечно, это всего лишь один из возможных способов представления шахматной доски, и есть много других способов, которыми мы могли бы это сделать. Например, вместо того, чтобы использовать строки для представления типов фрагментов, мы могли бы использовать целые числа или другие типы данных для представления различных типов фрагментов. Кроме того, мы могли бы хранить дополнительную информацию о каждой детали, такую как её цвет, перемещалась ли она и так далее.

Как только у нас будет способ представить шахматную доску, мы сможем перейти к реализации шахматных правил. Это будет включать в себя написание кода для обработки таких вещей, как перемещение фигур, проверка на наличие незаконных ходов и обработка специальных ходов, таких как рокировка и взятие на проходе.

Вопрос: напиши функцию, которая генерирует все возможные для передвижения позиции

Ответ: Конечно, мы можем написать функцию, которая генерирует все возможные ходы для данной позиции на шахматной доске. Чтобы сделать это, нам нужно будет рассмотреть правила шахмат, которые диктуют, как может двигаться фигура каждого типа. Вот один из возможных способов реализации этой функции:

Вопрос: что с остальными фигурами?

Ответ: В коде, который я предоставил ранее, я включил только правила перемещения пешек, ладей и коней. Правила для других фигур (слона, ферзя и короля) аналогичны, но немного отличаются. Вот как может выглядеть остальная часть кода:

Вопрос: пожалуйста, продолжай

Ответ: Конечно! Вот остальная часть кода для функции get_possible_moves():

Этот код обрабатывает правила перемещения фигур каждого типа и генерирует список возможных ходов для данной позиции. Например, если мы вызовем get_possible_moves(board, 0, 1), функция вернёт список возможных ходов для коня, который изначально расположен на квадрате (0,1) на шахматной доске. Она должно включать все квадраты, на которые конь может переместиться за один ход, такие как (2,0), (2,2), (1,3), и так далее.

Конечно, это всего лишь один из способов реализации функции get_possible_moves(), и есть много других способов, которыми мы могли бы это сделать. Например, мы могли бы использовать различные структуры данных для представления шахматной доски и возможных ходов, или мы могли бы включить дополнительную информацию в список возможных ходов. Однако я надеюсь, что это даёт вам общее представление о том, как мы могли бы подойти к этой проблеме. Дайте мне знать, если у вас возникнут какие-либо другие вопросы!

Вопрос: можешь ли ты написать функцию, которая генерирует следующий наилучший ход?

Ответ: Можно написать функцию, которая генерирует следующий “лучший” ход для данной позиции на шахматной доске, но важно отметить, что это очень сложная задача для решения, и универсального варианта не существует. На самом деле, даже самые продвинутые шахматные программы в мире не способны последовательно находить абсолютный “лучший” ход в каждой ситуации.

Одним из возможных способов решения этой проблемы было бы использование метода, называемого “minimax” поиском, который является распространенным методом, используемым в игровых программах искусственного интеллекта. Основная его идея заключается в том, чтобы рассмотреть все возможные ходы, которые могут быть сделаны из текущей позиции, а затем для каждого из этих ходов рассмотреть все возможные контрдвижения, которые мог бы сделать противник. Затем этот алгоритм “минимизирует” значение лучшего хода противника, одновременно “максимизируя” значение хода исходного игрока, чтобы найти ход, который с наибольшей вероятностью приведёт к победе (или, по крайней мере, не к проигрышу).

Чтобы реализовать это, нам нужно было бы определить функцию “value”, которая присваивает числовой счёт каждой позиции на шахматной доске. Эта функция учитывала бы такие факторы, как относительная сила фигур каждого игрока, мобильность фигур каждого игрока и так далее. Затем алгоритм minimax будет использовать эту функцию значений для оценки каждого возможного хода и контрдвижения и выбора хода, который приводит к наибольшему общему баллу.

Однако, как я упоминал ранее, это очень сложная для решения проблема, и даже самые продвинутые шахматные программы не всегда способны найти абсолютный “лучший” ход. Кроме того, производительность алгоритма minimax может быть очень низкой, поскольку он должен учитывать каждый возможный ход и контрдвижение, чтобы найти наилучший ход. По этим причинам часто необходимо использовать различные методы оптимизации, такие как альфа-бета-обрезка и таблицы транспозиции, чтобы сделать этот алгоритм более эффективным.

В целом, хотя возможно написать функцию, которая генерирует следующий “лучший” ход для данной позиции на шахматной доске, это сложная задача, которая потребует хорошего понимания игровых методов искусственного интеллекта и тщательного планирования и реализации. Я надеюсь, что это даёт вам общее представление о том, как можно было бы подойти к этой проблеме, но дайте мне знать, если у вас возникнут какие-либо другие вопросы!

Вопрос: можешь ли ты сгенерировать код на python?

Ответ: Конечно, вот пример того, как алгоритм minimax может быть реализован на Python. Имейте в виду, что это всего лишь один из возможных способов реализации алгоритма, и есть много других способов, которыми мы могли бы это сделать. Кроме того, этот код не включает в себя все оптимизации, которые обычно используются в реальных шахматных программах, поэтому он будет не очень эффективен для больших шахматных позиций.

Вопрос: пожалуйста, продолжай

Ответ: Конечно, вот остальная часть функции minimax():

Этот код использует алгоритм minimax для поиска в пространстве возможных ходов и контр-движений, чтобы найти ход, который с наибольшей вероятностью приведёт к победе (или, по крайней мере, не к проигрышу). Функция evaluate() используется для присвоения числового значения каждой позиции на доске, а функции get_possible_moves() и make_move() используются для генерации и применения возможных ходов.

Опять же, имейте в виду, что это всего лишь один из возможных способов реализации минимаксного алгоритма, и есть много других способов, которыми мы могли бы это сделать. Кроме того, этот код не включает в себя все оптимизации, которые обычно используются в реальных шахматных программах, поэтому он будет не очень эффективен для больших шахматных позиций. Я надеюсь, что это даст вам общее представление о том, как работает алгоритм minimax и как он может быть реализован на Python, но дайте мне знать, если у вас возникнут какие-либо другие вопросы!

Вопрос: можете ли вы сгенерировать для меня функцию оценки?

Ответ: Конечно, вот пример того, как мы могли бы реализовать функцию оценки для шахматной программы на Python:

Этот код использует два фактора для оценки текущего положения на шахматной доске: материальное преимущество каждого игрока (т.е. относительная сила их фигур) и мобильность фигур каждого игрока (т.е. на сколько квадратов они могут переместиться). Эти два фактора объединяются для вычисления общего балла за позицию, который возвращается функцией evaluate().

Конечно, это всего лишь один из возможных способов реализации функции оценки для шахматной программы, и есть много других факторов, которые мы могли бы включить в оценку (таких как структура пешки, безопасность короля и так далее). Кроме того, точные значения, которые мы присваиваем каждому фактору (например, значения для каждого типа шахматной фигуры), могут оказать большое влияние на производительность шахматной программы, поэтому важно тщательно учитывать эти значения и корректировать их по мере необходимости. Я надеюсь, что это даёт вам общее представление о том, как может работать функция оценки, но дайте мне знать, если у вас возникнут какие-либо другие вопросы!

Вопрос: теперь мне нужна функция make_move()

Ответ: Конечно, вот пример того, как мы могли бы реализовать функцию make_move() для шахматной программы на Python:

Этот код использует функцию copy.deepcopy() для создания глубокой копии оригинальной шахматной доски, чтобы мы могли изменять копию, не затрагивая оригинал. Затем он использует исходные и конечные координаты выполняемого хода для обновления доски, перемещая фигуру из исходного квадрата в конечный квадрат.

Заключение

Я нахожу результаты впечатляющими. Непростая задача была не только решена с помощью выходных данных кода, но и объяснена соответствующими и корректными текстами. Также были указаны ограничения и возможные расширения.

Что не сработало:

Однако все эти недостатки также могли быть вызваны тем, что я не задавал достаточно точных вопросов в диалоге. Я думаю, что для эффективного использования этого инструмента нам всем нужно больше практики!

Статья была взята из этого источника:

14-minute read

Jump to heading

Introduction

For a university course this semester we had to write a chess engine in C++. I’m not a chess player and was only familiar
with the most basic chess rules so this was quite a challenge. Below is a video of my engine winning a game during a chess tournament (playing as white).

Jump to heading

Board representation

In my chess engine, a board gets represented using bitboards. A bitboard is basically just 64 bits. By having this simple representation, the computer is able to very rapidly perform certain operations on it. Having just 1 bitboard representation for the whole board is not enough since 1 bit is not enough to store what is going on at a specific square. That is why in total, 12 bitboards are defined. The starting position of a chess board is shown below. The board has 64 squares, 6 types of pieces and 2 colors. In total, I use 12 bitboards to represent this because there are 12 piece types if you take into account the color of a piece.

In C++, I use the uint64_t type for representing bitboards. I also define several operations in order to work with them more easily. For some of these operation, you can use so called built-in functions like __builtin_ctzll which will return the total number of trailing 0-bits. Because we store a bitboard as 64 bits, it is very easy to represent things like the ‘A file’ or the ‘5th rank’ in just a single line.

typedef uint64_t U64;
const U64 FILE_A = 0x8080808080808080ULL;
const U64 RANK_5 = 0xff00000000ULL;
#define set_bit(b, i) ((b) |= (1ULL << i))
#define get_bit(b, i) ((b) & (1ULL << i))  
#define clear_bit(b, i) ((b) &= ~(1ULL << i)) 
#define get_LSB(b) (__builtin_ctzll(b))
inline int pop_LSB(U64 &b) {
    int i = get_LSB(b);
    b &= b - 1;
    return i;
}

Once you have your bitboards, you can work with them by using bitwise operations. As an example let’s say we want to get all the possible promotions of the white pawns. All of the possible promotions are shown in the image below.

In code, the following steps are performed.

// only look at the pawns on the 7th rank 
U64 promotions = (bitboards[P] & RANK_7)
// promote north if the square is empty
U64 north_promotions = north(promotions) & empties;
// promote west/east if there is an enemy piece there that we may capture
U64 west_promotions = north_west(promotions) & blacks;
U64 east_promotions = north_east(promotions) & blacks;

This is a good example of why we use bitboards. We just need to use some bitwise operations and we’re done. The north/west/etc. are helper functions to perform bit-shift operations.

constexpr U64 west(U64 b) { return (b & ~FILE_A) << 1; }
constexpr U64 east(U64 b) { return (b & ~FILE_H) >> 1; }
constexpr U64 north_west(U64 b) { return (b & ~FILE_A) << 9; }
constexpr U64 north_east(U64 b) { return (b & ~FILE_H) << 7; }
// ... etc

When performing the bit-shift operations, I also do out-of-bounds checks which makes these helper functions useful.

Jump to heading

Attack tables

In a chess game there are 2 kind of pieces:

🐇 Leaping pieces: pawns, knights, kings

⛸️ Sliding pieces: bishop, rook, queen

Leaping pieces can just immediately jump to their target square and do not need to take into account any blocking pieces. Sliding pieces are pieces that cannot jump over other pieces. Instead, they slide towards their target and may be blocked by other pieces during the process.

Jump to heading

Leaping pieces

For leaping pieces, all of the attacks are pre-calculated and put in a simple lookup table. During the game when we want to find the possible attacks for a piece, we query the lookup table by index using the position of the piece and in return we get a bitboard that has 1-bits wherever the possible attacks of the piece are located. These attack tables are pre-calculated before the game which saves on runtime-performance. For example the knight attack table is generated as follows.

U64 attacks, knights = 0ULL;
// place knight on board
set_bit(knights, square);
// add attacks
attacks = (((knights >> 6)  | (knights << 10)) & ~FILE_GH) |
          (((knights >> 10) | (knights << 6))  & ~FILE_AB) |
          (((knights >> 15) | (knights << 17)) & ~FILE_H)  |
          (((knights >> 17) | (knights << 15)) & ~FILE_A);

Again, bitwise operations are used to easily generate these, but it doesn’t really matter whether this attack generation is fast or not since it’s precalculated anyway.

The image below shows the possible attacks for a given knight piece. All of these attacks can be generated using straightforward bit-shift operations (>>, <<). Each attack is added together using a bitwise-OR operation (|) and finally it is checked if the attack ends up out of bounds of the board.

At runtime, the potential moves can easily be queried. For example, querying the potential moves for a king is shown below. We perform a bitwise-AND operation to get the actual possible moves since the king can not move to a square where there already is a piece with the same color.

U64 attacks = KING_ATTACKS[from] & targets;

Jump to heading

Sliding pieces

For the sliding pieces, generating the attacks is a bit more complicated since possible attacks depend on possible blocking pieces that are placed on the board. The image below shows how the attack pattern of a queen is influenced by blocking pieces on the board.

I won’t go too much into detail but essentially we use magic bitboards which is a hashing technique. The idea is that for each sliding piece, for each square, for each possible blocking pattern, we generate the possible attacks.

The sentence above has a lot of ‘for each’ in it and so as expected, storing all these combinations take up a significant amount of space. The pre-calculation involves generating all of the possible attack patterns and storing them, indexable by a key. The payoff is worth it. We end up with an easy lookup of possible attacks, given a square and blocker pattern. The attack patterns are stored in a 2D array where the square of the piece is used as a first index, and then a key is generated based on the blocker pattern and the square.

U64 ROOK_ATTACKS[64][4096];
U64 Board::getRookAttacks(int square, U64 blockers) const {
  return ROOK_ATTACKS[square][getRookKey(blockers, square)];
}

If you want to know more about magic bitboards, I put some links at the bottom.

💬 Disclaimer: magic bitboards are not actually magic :/

Now that we have handled both board representation and pre-calculating attack tables, we can get to actually generating the moves.

Jump to heading

Move generation

For a given board position, we want to be able to calculate all the possible moves so that the engine can pick one of them to perform. The main function looks like this:

Board::MoveVec Board::generateMoves<LEGAL>(MoveVec &moves) const {
  // if the king is in check then the legal moves can only be evasions
  isKingInCheck(boardTurn) ? generateMoves<EVASIONS>(moves) : generateMoves<PSEUDO_LEGAL>(moves);
  // extract legal moves from pseudo-legal moves
  std::vector<Move> legal_moves;
  legal_moves.reserve(MOVES_RESERVE_SIZE);
  for (auto &move: moves) {
    if (isMoveLegal(move)) legal_moves.push_back(move);
  }
  return legal_moves;
}

I do a test to see if the king is in check, because then we only need to generate a subset of all the possible moves since the only legal move is to resolve the check. If the king is not in check, we generate pseudo-legal moves (moves that could leave the king in check) and then we filter out the non-legal moves.

Jump to heading

Pseudo-legal moves

Generating pseudo-legal moves is fairly straightforward for most pieces since we have the attack tables pre-calculated. For example for the queen moves are generated as follows:

MoveVec &moves;
generateQueenMoves(moves, friendly_queens, ~friendlies);
void Board::generateQueenMoves(MoveVec &moves, U64 queens, U64 targets) const {
  // for each of our queens
  while (queens) {
    // get the position of the queen
    int from = pop_LSB(queens);
    // get the (pre-calculated) attacks of the queen
    // we limit the attacks to contain enemy squares (captures) and
    // empty squares (regular moves), moving to a friendly square is not possible
    U64 attacks = getQueenAttacks(from, all) & targets;
    // add a move for each attack
    while (attacks) addMove(Move(getSquare(from), getSquare(pop_LSB(attacks))), moves);
  }
}

The generated moves are pseudo-legal since they might leave the king in check. For example in the image below, the white bishop has 4 moves generated for it but none of them are legal since they all would leave the king in check. It is easier and faster to generate pseudo-legal moves, and then check if they are legal, compared to generating only legal moves in the first place, so that is why we do it this way.

Jump to heading

Pawn moves

Pawn moves are more complicated because pawns can move in more complex ways. For example in the image below, the pawn on rank 2 is in its starting position so it could move 1 or 2 squares upwards. The pawn on rank 5 could move either 1 square upwards or do an en-passant capture since black did a double pawn-push in the previous move. The pawn on rank 7 could go for a promotion by moving upwards or by capturing the black rook.

Luckily, our bitboard-approach makes this relatively easy to do. The code below shows how pawn moves are generated. Some of the code is left out since the original code is quite long and contains additional things that need to happen based on whether we’re generating captures, evasions or general moves, but you should get the idea.

// promotion-eligible pawns are on rank 7
U64 promotions = pawns & RANK_7;
U64 non_promotions = pawns & ~RANK_7;
// pawns can be pushed if there is an empty space
U64 singles = north(non_promotions) & empties;
U64 doubles = north(singles & RANK_3) & empties;
if (promotions) {
  // north promotions are regular pushes and need an empty square
  U64 north_promotions = north(promotions) & empties;
  // west/east promotions can only be captures
  U64 west_promotions = north_west(promotions) & blacks; 
  U64 east_promotions = north_east(promotions) & blacks;
}
// captures can happen left/right and need an enemy piece
U64 west_captures = north_west(non_promotions) & blacks;
U64 east_captures = north_east(non_promotions) & blacks;
if (enpassant) {
  U64 enpassants = non_promotions & PAWN_ATTACKS[0][get_LSB(enpassant)];
}

Jump to heading

Castling

Castling is a special move involving the king and the rook. Before you can perform the move, several criteria need to be met.

The conditions are checked using the following code.

if (turn == WHITE && hasCastlingRights(CastlingRights::WhiteKingside)) {
  if (!get_bit(all, f1) && !get_bit(all, g1) &&
    !isSquareAttackedBy(e1, BLACK) &&
    !isSquareAttackedBy(f1, BLACK))
    addMove(Move(Square::E1, Square::G1), moves);
}

The castling rights (whether or not we can castle) are updated after a move (that has an effect on the castling rules) is performed. The code above checks if the necessary preconditions like squares being empty/not attacked are met.

Jump to heading

Check evasions

When our king is in check, we need to resolve the check. In the board setup below, the black king is attacked and check evasion can be done by either moving the king to one of the marked spots, or alternatively we can use the black queen to capture the white knight, which would also resolve the check.

I will not go into detail of how the evasion code works, but it involves finding out the attackers of the king and figuring out the attack lines between the attackers and the king. The possible moves for pieces to resolve the check then include:

1. king moves that resolve the check
2. moves that capture the attacker (if the attacker is a sliding or leaping piece)
3. moves that block the attack line between enemy attacker and king (if the attacker is a sliding piece)

Jump to heading

Testing for correctness

Now that our move generation is done, we want to know if it actually is correct. The easiest way to test if your move generation code is correct is by using perft tests. Basically, given a initial board position, you generate all the possible moves. For each generated move, you perform the move and recursively call the perft function again. Then you undo the move which restores the board to its previous position.

The perft function will essentially count all possible moves up to a specified depth, given an intial board setup. This is useful because if you try this function up to a depth of 5 or 6 and the result is the same as what some established chess engines get as a result, you can be fairly certain that your move generation is correct. The perft function is shown below.

uint64_t perft(Board &board, int depth) {
  std::vector<Move> moves;
  moves.reserve(MOVES_RESERVE_SIZE);
  moves = board.generateMoves<LEGAL>(moves);
  uint64_t nodes = 0;
  if (depth == 1) return moves.size();
  for (const auto &move: moves) {
    Position position = board.copyBoard(board);
    board.makeMove(move);
    nodes += perft(board, depth - 1);
    board.restorePosition(board, position);
  }
  return nodes;
}

I wrote some unit tests where around 10 board positions are evaluated up until a depth of 6. This is very useful to make sure that a change to your engine does not mess up move generation. If your perft result does not match the expected result, you can compare the amount of moves branch-by-branch using another chess engine that you ‘know’ is correct, and track down where your move generation goes wrong.

Jump to heading

Move selection and search

Jump to heading

Board evaluation

Now that we can correctly generate moves, we can write an algorithm that picks the best move for us, given a board position. At the core of this, there is an evaluation function that evaluates whether or not a position is ‘good’. At this stage, it probably helps if you are a good chess player so that you can come up with some good heuristics. I evaluate boards based on 2 criteria:

1. material
2. positional

Material means that some pieces are worth more than others. Positional means that a piece on some square, is better than that piece being on a different square. In code, this looks like this.

const int PIECE_SCORES_MATERIAL[6] = {
    // pawn, knight, bishop, rook, queen, king
    100, 300, 300, 500, 900, 12000
};
const int KNIGHT_SCORES_POSITIONAL[64] = {
  // a score for each square on the board
  -58, -38, -13, -28, -31, -27, -63, -99,
  -25,  -8, -25,  -2,  -9, -25, -24, -52,
  -24, -20,  10,   9,  -1,  -9, -19, -41,
  -17,   3,  22,  22,  22,  11,   8, -18,
  -18,  -6,  16,  25,  16,  17,   4, -18,
  -23,  -3,  -1,  15,  10,  -3, -20, -22,
  -42, -20, -10,  -5,  -2, -20, -23, -44,
  -29, -51, -23, -15, -22, -18, -50, -64,
};

The material scores are pretty straightforward, the king is worth the most, a pawn the least. For the positional scores, I found some tables online that seemed to work well. A good example is the knight: it has a better evaluation if the knight is positioned in the center of the board since that means that it can reach more squares and thus has a larger influence. If the knight is put in the corner of the board, many of its usual attacks fall out of bounds of the board.

I have defined these scores for 3 stages of the game: start, middle and end and depending on the stage of the game, a linear interpolation occurs between them.

Jump to heading

Finding the best move

My chess engine uses an alpha-beta pruning search algorithm. In short, it goes over the game tree (all possible moves up to a certain depth) and finds the best move. The pruning part is useful because by encountering certain good positions, it can remove huge chunks of the tree that are guaranteed not to give a better result.

In order to help the algorithm, moves are sorted because the earlier the search algorithm encounters a good move, the more branches can be pruned and less board positions have to be evaluated. The move ordering uses some heuristics to estimate whether or not a move will be good. I use a scoring system that among other things considers capturing moves and promotion moves to be good.

Captures are evaluated using the most valuable victim, least valuable attacked principle where a pawn capturing a queen is seen as the best, and a queen capturing a pawn is seen as the worst. Promotions to more valuable pieces are considered better.

for (auto &move: moves) {
  int score = 0;
  // capture moves (10010 - 10055)
  if (captured.has_value()) {
    score = 10000 + MVV_LVA[moved.value().toInt() - 6 * (moved.value().toInt() >= 6)][captured.value().toInt()
        - 6 * (captured.value().toInt() >= 6)];
  }
  // promotion moves (9300 - 9900)
  if (promotion.has_value()) {
    score = 9000 + PIECE_SCORES[static_cast<int>(promotion.value())];
  }
  move.setScore(score);
}

This move ordering results in a significant reduction in nodes of the tree that need to be evaluated. Lastly, the search algorithm uses an iterative-deepening approach which allows the engine to keep search depth-by-depth, until the time for searching is up. This allows the engine to use up all the time that is allocated for a search, without using up too much time.

Jump to heading

Conclusion

Writing a chess engine is complex, and frustrating. I can highly recommend it.

Jump to heading

Additional resources

Jump to heading

Magic Bitboards

https://www.chessprogramming.org/Magic_Bitboards

Jump to heading

Chess engines

Sebastian Lague chess engine

March 2022

Python очень обширый язык программирования, на котором можно создать бесконечное множество разнообразных проектов. Свой первый проект я решил посвятить шахматам – одной из древнейших настольных игр с достаточно простыми правилами но в то же время заставляющей человека думать и планировать.

Актуальность выбранной темы проекта связана с актуальностью профессионального изучения информатики и программирования в современном мире.

Новизна проекта заключается в сочетании теории и практики, использовании различных ресурсов для написания кода.

Цель проекта – Создать графический интерфейс на основе PyQt для игры в шахматы для 2 игроков

1. Реализовать классы фигур, механики передвижения.
2. Создать поле для игры, механику атаки
3. Реализовать таймер, обработку событий мыши.
4. С помощью PyQt создаем графический интерфейс

Все фигуры имеют некоторые одинаковые механики, поэтому для начала создадим базовый класс, от которого будем наследовать другие.

Если представить доску в виде матрицы, то можно определять местоположение фигур с помощью координат х и у.

Пешка может двигаться на 1 клетку по вертикали (вверх если белая и вниз если черная), а также на 2 клетки, если её ещё ни разу не двигали. Исходя из этих данных создаем класс:

def can_move ( self , board , row , col , row1 , col1):
# Пешка может ходить только по вертикали
# «взятие на проходе» не реализовано
if col != col1:
return False

if not self .is_path_clear(board , row , col , row1 , col1):
return False

# Пешка может сделать из начального положения ход на 2 клетки
# вперёд, поэтому поместим индекс начального ряда в start_row.
if self .color == WHITE:
direction = 1
start_row = 1
else :
direction = — 1
start_row = 6

# ход на 1 клетку
if row + direction == row1:
return True

# ход на 2 клетки из начального положения
if row == start_row and row + 2 * direction == row1:
return True

def can_attack ( self , board , row , col , row1 , col1):
direction = 1 if ( self .color == WHITE) else — 1
return (row + direction == row1
and (col + 1 == col1 or col — 1 == col1))

Эта фигура может двигаться только по вертикали и горизонтали, т.е. должны совпадать координаты до передвижения и после лтбо по вертикали либо по горизонтали. Зная это, реализуем класс:

def can_move ( self , board , row , col , row1 , col1):
# Невозможно сделать ход в клетку, которая не лежит в том же ряду
# или столбце клеток.
if row != row1 and col != col1:
return False
if not self .is_path_clear(board , row , col , row1 , col1):
return False

Конь двигается буквой «Г», т.е. на 2 по вертикали и 1 по горизонтали и наоборот. При этом направление не важно, значит нужно использовать ф-цию abs(), т.е. модуль.

class Knight(Piece):
ch = ‘N’

def can_move ( self , board , row , col , row1 , col1):
# Конь двигается буквой Г (2 вертикально, 1 горизонтально)
if abs (row — row1) == 2 and abs (col — col1) == 1 :
return True
# Конь двигается буквой Г (1 вертикально, 2 горизонтально)
if abs (row — row1) == 1 and abs (col — col1) == 2 :
return True

Слон двигается по диагонали т.е. его смещение по вертикали должно быть равно смещению по горизонтали:

class Bishop(Piece):
ch = ‘B’

def can_move ( self , board , row , col , row1 , col1):

if not self .is_path_clear(board , row , col , row1 , col1):
return False

# Слон двигается по диагонали
# Смещение по строка должно равняться смещению по столбцам
if abs (row — row1) == abs (col — col1):
return True

Королева двигается по всем сторонам (по горизонтали, вертикали, диагонали). Копируем эти механики из слона и ладьи и получаем:

class Queen(Piece):
ch = ‘Q’

def can_move ( self , board , row , col , row1 , col1):

if not self .is_path_clear(board , row , col , row1 , col1):
return False

# Ферзь двигается вертикально
if col == col1:
return True

# Ферзь двигается горизонтально
if row == row1:
return True

# Ферзь двигается по диагонали
# Смещение по строка должно равняться смещению по столбцам
if abs (row — row1) == abs (col — col1):
return True

Король двигается в любую сторону на расстояние 1:

def can_move ( self , board , row , col , row1 , col1):

if not self .is_path_clear(board , row , col , row1 , col1):
return False

# Король двигается в любую клетку с рассотоянием равным 1
if max ( abs (row — row1) , abs (col — col1)) == 1 :
return True

А теперь необходимо реализовать некоторые особые механики игры, например «Превращение пешки» и «Рокировка».

Когда пешка доходит до противоположного конца доски она может стать Ферзем, Ладьей, Слоном или Конем. Для этого мы можем просто изменить класс фигуры, в том месте, где стоит пешка.

Для рокировки нам нужно знать: двигались ли король и ладья, есть ли между ними фигуры, приведет ли рокировка к шаху короля. От этого будет зависеть успешность рокировки или её невозможность.

Представим доску в виде матрицы на координатной оси. Тогда расположение фигур на доске будет записано в двухмерном списке. Записыаем стартовые значения матрицы:

self .field = [[ None ] * 8 for _ in range ( 8 )]
self .field[ 0 ] = [
Rook(WHITE) , Knight(WHITE) , Bishop(WHITE) , Queen(WHITE) ,
King(WHITE) , Bishop(WHITE) , Knight(WHITE) , Rook(WHITE)
]
self .field[ 1 ] = [
Pawn(WHITE) , Pawn(WHITE) , Pawn(WHITE) , Pawn(WHITE) ,
Pawn(WHITE) , Pawn(WHITE) , Pawn(WHITE) , Pawn(WHITE)
]
self .field[ 6 ] = [
Pawn(BLACK) , Pawn(BLACK) , Pawn(BLACK) , Pawn(BLACK) ,
Pawn(BLACK) , Pawn(BLACK) , Pawn(BLACK) , Pawn(BLACK)
]
self .field[ 7 ] = [
Rook(BLACK) , Knight(BLACK) , Bishop(BLACK) , Queen(BLACK) ,
King(BLACK) , Bishop(BLACK) , Knight(BLACK) , Rook(BLACK)
]

Цвет фигуры определяют константы WHITE и BLACK.

Каждая клетка имеет свое значение, так белая пешка обозначена как «wP». В дальнейшем это обозначение определит графическую модель фигурки на доске.

В этом классе создаем ф-цию проверки возможности движения:

def check_move ( self , row: int , col: int , row1: int , col1: int ):
«»»Проверка перемещения фигуру из точки (row, col) в точку (row1, col1).
Если перемещение возможно, метод выполнит его и вернет True.
Если нет — вернет False»»»
check = self .check() # Есть ли шах к перед ходом
if not correct_coords(row , col) or not correct_coords(row1 , col1):
return False
if row == row1 and col == col1:
return False # нельзя пойти в ту же клетку
piece = self .field[row][col]
target = self .field[row1][col1]
if piece is None :
return False
if piece.get_color() != self .color:
return False

if isinstance (piece , King) and self .is_under_attack(row1 , col1 , opponent( self .current_player_color())):
return False

if not (piece.can_move( self .field , row , col , row1 , col1) and target is None ) and
not (piece.can_attack( self .field , row , col , row1 , col1) and
(target is not None and not isinstance (target , King)
and target.get_color() == opponent( self .current_player_color()))):
return False

old_field = [x.copy() for x in self .field] # Сохранить поле
self .field[row][col] = None # Снять фигуру.
self .field[row1][col1] = piece # Поставить на новое место.
if check and self .check(): # В результате хода избежать шаха не удалось
# Возвращаемся в исходное состояние
self .field = old_field
return False
# Возвращаемся в исходное состояние
self .field = old_field
return True

Ф-ция проверяет сразу все факторы: выход за пределы доски, походила ли фигурка на свое же место, приведет ли ход короля к его шаху или мату и т.д.

Реализуем ф-цию движения в которой используется ф-ция проверки:

def move_piece ( self , row , col , row1 , col1):
«»»Переместить фигуру из точки (row, col) в точку (row1, col1).
Если перемещение возможно, метод выполнит его и вернет True.
Если нет — вернет False»»»
if self .check_move(row , col , row1 , col1):
piece = self .field[row][col]
self .field[row][col] = None # Снять фигуру.
piece.moved()
self .field[row1][col1] = piece # Поставить на новое место.
if self .check_promotion(piece , row1):
self .promotion = True
self .color = opponent( self .color)
self .change = True
return True
return False

Также здесь реализуем механику атаки:

def is_under_attack ( self , row , col , color):
for row1 in range ( 8 ):
for col1 in range ( 8 ):
if self .field[row1][col1] is not None :
if self .field[row1][col1].get_color() == color and
self .field[row1][col1].can_attack( self .field , row1 , col1 , row , col):
return True
return False

Для короля мы должны реализовать «Шах» и «Мат». Это довольно таки сложно из-за того, что у короля пропадает много возможностей, например «Рокировка». Поэтому я все ещё не полностью смог воссоздать эту механику из шахмат. Но все же в случае шаха игроку будут недоступны ходы, которые приведут к мату.

Таймер и обработка событий мыши

С помощью класса QtTimer от PyQt реализуем таймер для каждого игрока с механикой смены после окончания хода. Также с помощью механизма слотов и сигналов PyQt мы сможем обрабатывать события мыши для удобного взаимодействия с графическим интерфейсом.

Реализация графического интерфейса, пожалуй, одна из самых сложных задач проекта, так как PyQt я знаю ещё очень поверхностно. Но что есть – то есть. Создаем модели фигурок, а также модели иконок и изображение поля. Настраиваем механику обработки мыши под границы моделей клеток и иконок.

Дополняем последние детали в виде кнопок «Новая игра» и «Выйти».

Проект завершен, создан рабочий вариант шахмат.

Во время разработки проекта я узнал о многих механиках программирования, получил знания о классах объектов, познакомился с QT. Этот проект ждет ещё множество новых механик и нововведений: добавление ИИ, реализация более сложных механик, которыми пользуются проффесиональные игроки(прим.: «Взятие на проходе»). В дальнейшем я не собираюсь останавливаться на этом проекте, так как меня ждет ещё множество нереализованных идей, ждущих своего часа.

Machine Learning and Chess

In late 2020, Netflix released the Queen’s Gambit, a TV show taking place in the 1950’s where we follow the journey of a young women thriving to become the best chess player.

However, unlike the protagonist Beth Harmon, chess isn’t really my strongest suit. So I did the next best thing by building my own python chess engine to compensate my poor chess skills.

Episode I: Strategies

When it comes to building any board game engine, there are multiple strategies:

• Reinforcement Learning
• Minimax
• ML model trained on human knowledge
• …

I opted for an hybrid of the second and third strategies: As a Data scientist, I am fond of working with large datasets and machine learning models. Also, despite being a little slower, Minimax is a quite reliable algorithm and does a good job at capturing enemy pieces. Reinforcement learning is simply too complex.

My strategy is simple:

• First of all, using the machine learning model, the engine will dismiss 50% of the possible moves given a board. It does so by finding the probability of a move being a ‘good move’. All the moves are sorted according to this probability and only the 50th percentile remains.
• Secondly, the engine will perform the Minimax algorithm on the remaining moves. Depending on the complexity of the board, the search tree will go to a certain depth.

Episode II: Data

In order to make accurate predictions, we need a lot of data. For this project, I will be using a dataset that I found on Kaggle. This dataset is a collection of thousands of games played by chess grand masters in the .pgn format (portable game notation).

The next step is to extract all the moves from all the games and label them as good or bad.

In my opinion, a ‘good move’ is a move that the winner played at some point during the game. A ‘bad move’ is a legal move that the winner chose not to play.

This python script got the job done leaving me with a brand new .csv dataset.

Создаем несложный шахматный ИИ: 5 простых этапов

Перевели для вас статью Лори Хартикка (Lauri Hartikka) о создании простейшего ИИ для шахмат. Она написана еще в 2017 году, но базовые принципы остались теми же. Все файлы, которые использовал Лори, тоже доступны.

Простой искусственный интеллект, который умеет играть в шахматы, можно создать на базе четырех концепций:

1. 1. Перемещение;
2. 2. Оценка доски; ; . На каждом этапе работы с алгоритмом будет использоваться одна из них, это позволит постепенно совершенствовать игровые способности ИИ.

Напоминаем: для всех читателей «Хабра» — скидка 10 000 рублей при записи на любой курс Skillbox по промокоду «Хабр».

Готовый исходный код можно найти на GitHub.

I’m having trouble beating a chess program I wrote.

Not sure if I’m a bad player or the algorithm is decent.

— Lauri Hartikka (@lhartikk) March 28, 2017

Этап 1. Визуализация шахматной доски с генерацией ходов

На этом этапе мы будем использовать библиотеки chess.js для генерации ходов и chessboard.js для визуализации доски. Библиотека, которая отвечает за генерацию ходов, позволяет применять все шахматные правила, так что мы можем рассчитывать каждое действие для конкретного расположения фигур.

При клике на картинке она откроется в полном разрешении.

Работа с этими библиотеками позволяет сконцентрироваться на главной задаче — поиске и создании алгоритма, который позволяет найти оптимальный ход. Работу начинаем с написания функции, которая возвращает случайный ход из списка всех возможных.

Несмотря на то, что алгоритм не является идеальным игроком в шахматы, для большинства игроков его уровня этого будет вполне достаточно.

Этап 2. Оценка позиции

Теперь давайте разберемся, у какой стороны преимущество в том или ином положении. Самый простой путь — подсчитать относительную силу фигур на доске, это можно сделать при помощи таблицы.

Используя функцию оценки, мы получаем возможность создать алгоритм, который выбирает ход с максимальной оценкой.

В принципе, уровень прежний, но алгоритм уже может взять чужую фигуру, когда такая возможность есть.

Черные получили возможность брать белые фигуры. (Исходники и игра здесь).

Этап 3. Дерево поиска с минимакс

После этого мы создаем дерево поиска. Теперь программа может выбрать из него лучший ход. Это делается при помощи минимакс-алгоритма.

Здесь рекурсивное дерево с отображением всех возможных ходов анализируется до заданной глубины. Позиция же оценивается по листьям нашего дерева.

Далее мы возвращаем минимальное или максимальное значение потомка в родительский узел. Все зависит от того, ход какой стороны сейчас просчитывается. Другими словами, результат максимизируется или минимизируется на каждом из уровней.

Здесь лучшим ходом для белых является b2-c3, поскольку он гарантирует, что игрок доберется до позиции с оценкой -50.

С минимакс-алгоритмом наш ИИ уже стал понимать базовую тактику шахмат.

Минимакс с глубиной 2 (Исходники и игра здесь)

Стоит отметить, что эффективность минимакс-алгоритма увеличивается с глубиной поиска. За это отвечает следующий этап.

Этап 4. Альфа-бета-отсечения

Это метод оптимизации минимакс-алгоритма, дающий возможность игнорировать некоторые ветви в дереве поиска. А это позволяет увеличить глубину поиска, затрачивая прежний объем ресурсов.

Альфа-бета-отсечение основано на ситуации, когда мы можем остановить оценку определенной ветви, если обнаруживается, что новый ход приведет к худшей ситуации, чем та, которую мы видели при оценке предыдущего.

На результат минимакса оптимизация не влияет, но все начинает работать быстрее.

Этот алгоритм гораздо более эффективен в том случае, если сначала проверить пути, ведущие к хорошим ходам.

Изображение демонстрирует ходы, которые становятся ненужными в процессе использования альфа-бета-отсечения.

Как видите, с альфа-бета-отсечением минимакс оптимизируется, и весьма значительно.

Количество позиций, которые требуется оценить в случае поиска с глубиной 4 и начальной позицией, которая изображена выше. (исходники и игра доступны здесь)

Этап 5. Улучшенная функция оценки

Изначальная функция оценки достаточно простая, поскольку она просто считает очки фигур, находящихся на доске. Для ее оптимизации можно учитывать положение фигур. К примеру, если разместить коня в центре доски, то он становится дороже — спектр доступных ходов для этой фигуры расширится.

На этом этапе мы будем работать с несколько видоизмененной версией квадратных таблиц, изначально описанной в вики Chess Programming.

И теперь наш алгоритм играет уже весьма неплохо, конечно, по сравнению со средним игроком.

Исходники и игра доступны здесь

Заключение

Достоинством предложенного алгоритма является то, что он не делает совсем уж глупых ошибок. Конечно, стратегию здесь сложно назвать совершенной, но тем не менее.