This article will will put forth an interesting and an important topic that is Sorting Algorithms In C.Following pointers will be covered in this article,
- Bubble Sort
- Insertion Sort
- Selection Sort
- Quick Sort
- Merge Sort
In simple word, sorting means arranging the given elements or data in an ordered sequence. The main purpose of sorting is to easily & quickly locate an element in a sorted list & design an efficient algorithm around it. In this blog we will understand different sorting algorithms & how to implement them in C.
So let us get started then,
Bubble Sort
Bubble Sort is a simple sorting algorithm which repeatedly compares the adjacent elements of the given array & swaps them if they are in wrong order.
Suppose we have an array X which contains n elements which needs to be sorted using Bubble Sort. The sorting works as:
Pass 1:
- X[0] & X[1] are compared, and swapped if X[0] > X[1]
- X[1] & X[2] are compared, and swapped if X[1] > X[2]
- X[2] & X[3] are compared, and swapped if X[2] > X[3] and so on…
At the end of pass 1, the largest element of the list is placed at the highest index of the list.
Pass 2:
- X[0] & X[1] are compared, and swapped if X[0] > X[1]
- X[1] & X[2] are compared, and swapped if X[1] > X[2]
- X[2] & X[3] are compared, and swapped if X[2] > X[3] and so on…
At the end of Pass 2 the second largest element of the list is placed at the second highest index of the list.
Pass n-1:
- X[0] & X[1] are compared, and swapped if X[0] > X[1]
- X[1] & X[2] are compared, and swapped if X[1] > X[2]
- X[2] & X[3] are compared, and swapped if X[2] > X[3] and so on…
At the end of this pass. The smallest element of the list is placed at the first index of the list.
Moving on with this article on Sorting Algorithms In C,
Bubble Sort Program in C
#include <stdio.h>
// Function to swap elements
void swap(int *a, int *b)
{
int temp = *a;
*a = *b;
*b = temp;
}
// bubble sort function
void bubbleSort(int array[], int n)
{
int i, j;
for (i = 0; i < n-1; i++)
for (j = 0; j < n-i-1; j++) if (array[j] > array[j+1])
swap(&array[j], &array[j+1]);
}
// Function to print the elements of an array
void printArray(int array[], int size)
{
int i;
for (i=0; i < size; i++)
printf("%d ", array[i]);
printf("n");
}
// Main Function
int main()
{
int array[] = {89, 32, 20, 113, -15};
int size = sizeof(array)/sizeof(array[0]);
bubbleSort(array, size);
printf("Sorted array: n");
printArray(array, size);
return 0;
}
Output:
Moving on with this article on Sorting Algorithms In C,
Insertion Sort
Insertion Sort is a sorting algorithm where the array is sorted by taking one element at a time. The principle behind insertion sort is to take one element, iterate through the sorted array & find its correct position in the sorted array.
Step 1 − If the element is the first one, it is already sorted.
Step 2 – Move to next element
Step 3 − Compare the current element with all elements in the sorted array
Step 4 – If the element in the sorted array is smaller than the current element, iterate to the next element. Otherwise, shift all the greater element in the array by one position towards right
Step 5 − Insert the value at the correct position
Step 6 − Repeat until the complete list is sorted
Insertion Sort Program in C
#include <math.h>
#include <stdio.h>
// Insertion Sort Function
void insertionSort(int array[], int n)
{
int i, element, j;
for (i = 1; i < n; i++) { element = array[i]; j = i - 1; while (j >= 0 && array[j] > element) {
array[j + 1] = array[j];
j = j - 1;
}
array[j + 1] = element;
}
}
// Function to print the elements of an array
void printArray(int array[], int n)
{
int i;
for (i = 0; i < n; i++)
printf("%d ", array[i]);
printf("n");
}
// Main Function
int main()
{
int array[] = { 122, 17, 93, 3, 56 };
int n = sizeof(array) / sizeof(array[0]);
insertionSort(array, n);
printArray(array, n);
return 0;
}
Output
Moving on with this article on Sorting Algorithms In C,
Selection Sort
Selection Sort repeatedly searches for the smallest element from the unsorted part of the array and places it at the end of sorted part of the array. Selection sort first finds the smallest element in the unsorted array and swaps it with the first element. Then it finds the second smallest element in the unsorted array and swaps it with the second element, and the algorithm keeps doing this until the entire array is sorted.
Selection Sort Program in C
#include <stdio.h>
// Function to swap elements
void swap(int *a, int *b)
{
int temp = *a;
*a = *b;
*b = temp;
}
// Selection Sort
void selectionSort(int array[], int n)
{
int i, j, min_element;
for (i = 0; i < n-1; i++)
{
min_element = i;
for (j = i+1; j < n; j++)
if (array[j] < array[min_element])
min_element = j;
swap(&array[min_element], &array[i]);
}
}
// Function to print the elements of an array
void printArray(int array[], int size)
{
int i;
for (i=0; i < size; i++)
printf("%d ", array[i]);
printf("n");
}
// Main Function
int main()
{
int array[] = {15, 10, 99, 53, 36};
int size = sizeof(array)/sizeof(array[0]);
selectionSort(array, size);
printf("Sorted array: n");
printArray(array, size);
return 0;
}
Output
Moving on with this article on Sorting Algorithms In C,
Quick Sort
QuickSort is a divide & conquer algorithm. QuickSort algorithm partitions the complete array around the pivot element. Pivot element can be picked in mulitple ways:
- First element as pivot
- Last element as pivot
- Median element as pivot
- Random element as pivot
In this blog we will be picking the last element as pivot element.
partition() is the key process behind the QuickSort algorithm. In partitioning, the pivot element plays an important role. Pivot is placed at its correct position in the sorted array, all the elements smaller than pivot is placed before it, and all the elements greater than pivot is placed after it. All this operation is completed in linear time.
Then the array is divided in two parts from the pivot element (i.e. elements less than pivot & elements greater than pivot) & both the arrays are recursively sorted using Quicksort algorithm.
Moving on with this article on Sorting Algorithms In C,
Quicksort Program in C
#include<stdio.h>
// Function to swap two elements
void swapElements(int* x, int* y)
{
int temp = *x;
*x = *y;
*y = temp;
}
// Partition function
int partition (int arr[], int lowIndex, int highIndex)
{
int pivotElement = arr[highIndex];
int i = (lowIndex - 1);
for (int j = lowIndex; j <= highIndex- 1; j++)
{
if (arr[j] <= pivotElement)
{
i++;
swapElements(&arr[i], &arr[j]);
}
}
swapElements(&arr[i + 1], &arr[highIndex]);
return (i + 1);
}
// QuickSort Function
void quickSort(int arr[], int lowIndex, int highIndex)
{
if (lowIndex < highIndex)
{
int pivot = partition(arr, lowIndex, highIndex);
// Separately sort elements before & after partition
quickSort(arr, lowIndex, pivot - 1);
quickSort(arr, pivot + 1, highIndex);
}
}
// Function to print array
void printArray(int arr[], int size)
{
int i;
for (i=0; i < size; i++)
printf("%d ", arr[i]);
}
// Main Function
int main()
{
int arr[] = {81, 27, 38, 99, 51, 5};
int n = sizeof(arr)/sizeof(arr[0]);
quickSort(arr, 0, n-1);
printf("Sorted array: ");
printArray(arr, n);
return 0;
}
Output:
Moving on with this article on Sorting Algorithms In C,
Merge Sort
Merge Sort is one of the best examples of Divide & Conquer algorithm. In Merge sort, we divide the array recursively in two halves, until each sub-array contains a single element, and then we merge the sub-array in a way that it results into a sorted array. merge() function merges two sorted sub-arrays into one, wherein it assumes that array[l .. n] and arr[n+1 .. r] are sorted.
Merge Sort Program in C
#include<stdlib.h>
#include<stdio.h>
// Merge Function
void merge(int arr[], int l, int m, int r)
{
int i, j, k;
int n1 = m - l + 1;
int n2 = r - m;
int L[n1], R[n2];
for (i = 0; i < n1; i++)
L[i] = arr[l + i];
for (j = 0; j < n2; j++)
R[j] = arr[m + 1+ j];
i = 0;
j = 0;
k = l;
while (i < n1 && j < n2)
{
if (L[i] <= R[j])
{
arr[k] = L[i];
i++;
}
else
{
arr[k] = R[j];
j++;
}
k++;
}
while (i < n1)
{
arr[k] = L[i];
i++;
k++;
}
while (j < n2)
{
arr[k] = R[j];
j++;
k++;
}
}
// Merge Sort Function in C
void mergeSort(int arr[], int l, int r)
{
if (l < r)
{
int m = l+(r-l)/2;
mergeSort(arr, l, m);
mergeSort(arr, m+1, r);
merge(arr, l, m, r);
}
}
// Functions to Print Elements of Array
void printArray(int A[], int size)
{
int i;
for (i=0; i < size; i++)
printf("%d ", A[i]);
printf("n");
}
// Main Method
int main()
{
int arr[] = {85, 24, 63, 45, 17, 31, 96, 50};
int arr_size = sizeof(arr)/sizeof(arr[0]);
printf("Given array is n");
printArray(arr, arr_size);
mergeSort(arr, 0, arr_size - 1);
printf("nSorted array is n");
printArray(arr, arr_size);
return 0;
}
Output:
Now after going through the above sorting programs you would have understood various sorting algorithms and how to implement them in C language. I hope this blog is informative and added value to you.
Now after executing the above program you would have understood the Sorting Algorithms In C. Thus we have come to an end of this article on ‘Quicksort in Java’. If you wish to learn more, check out the Java Training by Edureka, a trusted online learning company. Edureka’s Java J2EE and SOA training and certification course is designed to train you for both core and advanced Java concepts along with various Java frameworks like Hibernate & Spring.
Got a question for us? Please mention it in the comments section of this blog and we will get back to you as soon as possible.
This article will will put forth an interesting and an important topic that is Sorting Algorithms In C.Following pointers will be covered in this article,
- Bubble Sort
- Insertion Sort
- Selection Sort
- Quick Sort
- Merge Sort
In simple word, sorting means arranging the given elements or data in an ordered sequence. The main purpose of sorting is to easily & quickly locate an element in a sorted list & design an efficient algorithm around it. In this blog we will understand different sorting algorithms & how to implement them in C.
So let us get started then,
Bubble Sort
Bubble Sort is a simple sorting algorithm which repeatedly compares the adjacent elements of the given array & swaps them if they are in wrong order.
Suppose we have an array X which contains n elements which needs to be sorted using Bubble Sort. The sorting works as:
Pass 1:
- X[0] & X[1] are compared, and swapped if X[0] > X[1]
- X[1] & X[2] are compared, and swapped if X[1] > X[2]
- X[2] & X[3] are compared, and swapped if X[2] > X[3] and so on…
At the end of pass 1, the largest element of the list is placed at the highest index of the list.
Pass 2:
- X[0] & X[1] are compared, and swapped if X[0] > X[1]
- X[1] & X[2] are compared, and swapped if X[1] > X[2]
- X[2] & X[3] are compared, and swapped if X[2] > X[3] and so on…
At the end of Pass 2 the second largest element of the list is placed at the second highest index of the list.
Pass n-1:
- X[0] & X[1] are compared, and swapped if X[0] > X[1]
- X[1] & X[2] are compared, and swapped if X[1] > X[2]
- X[2] & X[3] are compared, and swapped if X[2] > X[3] and so on…
At the end of this pass. The smallest element of the list is placed at the first index of the list.
Moving on with this article on Sorting Algorithms In C,
Bubble Sort Program in C
#include <stdio.h>
// Function to swap elements
void swap(int *a, int *b)
{
int temp = *a;
*a = *b;
*b = temp;
}
// bubble sort function
void bubbleSort(int array[], int n)
{
int i, j;
for (i = 0; i < n-1; i++)
for (j = 0; j < n-i-1; j++) if (array[j] > array[j+1])
swap(&array[j], &array[j+1]);
}
// Function to print the elements of an array
void printArray(int array[], int size)
{
int i;
for (i=0; i < size; i++)
printf("%d ", array[i]);
printf("n");
}
// Main Function
int main()
{
int array[] = {89, 32, 20, 113, -15};
int size = sizeof(array)/sizeof(array[0]);
bubbleSort(array, size);
printf("Sorted array: n");
printArray(array, size);
return 0;
}
Output:
Moving on with this article on Sorting Algorithms In C,
Insertion Sort
Insertion Sort is a sorting algorithm where the array is sorted by taking one element at a time. The principle behind insertion sort is to take one element, iterate through the sorted array & find its correct position in the sorted array.
Step 1 − If the element is the first one, it is already sorted.
Step 2 – Move to next element
Step 3 − Compare the current element with all elements in the sorted array
Step 4 – If the element in the sorted array is smaller than the current element, iterate to the next element. Otherwise, shift all the greater element in the array by one position towards right
Step 5 − Insert the value at the correct position
Step 6 − Repeat until the complete list is sorted
Insertion Sort Program in C
#include <math.h>
#include <stdio.h>
// Insertion Sort Function
void insertionSort(int array[], int n)
{
int i, element, j;
for (i = 1; i < n; i++) { element = array[i]; j = i - 1; while (j >= 0 && array[j] > element) {
array[j + 1] = array[j];
j = j - 1;
}
array[j + 1] = element;
}
}
// Function to print the elements of an array
void printArray(int array[], int n)
{
int i;
for (i = 0; i < n; i++)
printf("%d ", array[i]);
printf("n");
}
// Main Function
int main()
{
int array[] = { 122, 17, 93, 3, 56 };
int n = sizeof(array) / sizeof(array[0]);
insertionSort(array, n);
printArray(array, n);
return 0;
}
Output
Moving on with this article on Sorting Algorithms In C,
Selection Sort
Selection Sort repeatedly searches for the smallest element from the unsorted part of the array and places it at the end of sorted part of the array. Selection sort first finds the smallest element in the unsorted array and swaps it with the first element. Then it finds the second smallest element in the unsorted array and swaps it with the second element, and the algorithm keeps doing this until the entire array is sorted.
Selection Sort Program in C
#include <stdio.h>
// Function to swap elements
void swap(int *a, int *b)
{
int temp = *a;
*a = *b;
*b = temp;
}
// Selection Sort
void selectionSort(int array[], int n)
{
int i, j, min_element;
for (i = 0; i < n-1; i++)
{
min_element = i;
for (j = i+1; j < n; j++)
if (array[j] < array[min_element])
min_element = j;
swap(&array[min_element], &array[i]);
}
}
// Function to print the elements of an array
void printArray(int array[], int size)
{
int i;
for (i=0; i < size; i++)
printf("%d ", array[i]);
printf("n");
}
// Main Function
int main()
{
int array[] = {15, 10, 99, 53, 36};
int size = sizeof(array)/sizeof(array[0]);
selectionSort(array, size);
printf("Sorted array: n");
printArray(array, size);
return 0;
}
Output
Moving on with this article on Sorting Algorithms In C,
Quick Sort
QuickSort is a divide & conquer algorithm. QuickSort algorithm partitions the complete array around the pivot element. Pivot element can be picked in mulitple ways:
- First element as pivot
- Last element as pivot
- Median element as pivot
- Random element as pivot
In this blog we will be picking the last element as pivot element.
partition() is the key process behind the QuickSort algorithm. In partitioning, the pivot element plays an important role. Pivot is placed at its correct position in the sorted array, all the elements smaller than pivot is placed before it, and all the elements greater than pivot is placed after it. All this operation is completed in linear time.
Then the array is divided in two parts from the pivot element (i.e. elements less than pivot & elements greater than pivot) & both the arrays are recursively sorted using Quicksort algorithm.
Moving on with this article on Sorting Algorithms In C,
Quicksort Program in C
#include<stdio.h>
// Function to swap two elements
void swapElements(int* x, int* y)
{
int temp = *x;
*x = *y;
*y = temp;
}
// Partition function
int partition (int arr[], int lowIndex, int highIndex)
{
int pivotElement = arr[highIndex];
int i = (lowIndex - 1);
for (int j = lowIndex; j <= highIndex- 1; j++)
{
if (arr[j] <= pivotElement)
{
i++;
swapElements(&arr[i], &arr[j]);
}
}
swapElements(&arr[i + 1], &arr[highIndex]);
return (i + 1);
}
// QuickSort Function
void quickSort(int arr[], int lowIndex, int highIndex)
{
if (lowIndex < highIndex)
{
int pivot = partition(arr, lowIndex, highIndex);
// Separately sort elements before & after partition
quickSort(arr, lowIndex, pivot - 1);
quickSort(arr, pivot + 1, highIndex);
}
}
// Function to print array
void printArray(int arr[], int size)
{
int i;
for (i=0; i < size; i++)
printf("%d ", arr[i]);
}
// Main Function
int main()
{
int arr[] = {81, 27, 38, 99, 51, 5};
int n = sizeof(arr)/sizeof(arr[0]);
quickSort(arr, 0, n-1);
printf("Sorted array: ");
printArray(arr, n);
return 0;
}
Output:
Moving on with this article on Sorting Algorithms In C,
Merge Sort
Merge Sort is one of the best examples of Divide & Conquer algorithm. In Merge sort, we divide the array recursively in two halves, until each sub-array contains a single element, and then we merge the sub-array in a way that it results into a sorted array. merge() function merges two sorted sub-arrays into one, wherein it assumes that array[l .. n] and arr[n+1 .. r] are sorted.
Merge Sort Program in C
#include<stdlib.h>
#include<stdio.h>
// Merge Function
void merge(int arr[], int l, int m, int r)
{
int i, j, k;
int n1 = m - l + 1;
int n2 = r - m;
int L[n1], R[n2];
for (i = 0; i < n1; i++)
L[i] = arr[l + i];
for (j = 0; j < n2; j++)
R[j] = arr[m + 1+ j];
i = 0;
j = 0;
k = l;
while (i < n1 && j < n2)
{
if (L[i] <= R[j])
{
arr[k] = L[i];
i++;
}
else
{
arr[k] = R[j];
j++;
}
k++;
}
while (i < n1)
{
arr[k] = L[i];
i++;
k++;
}
while (j < n2)
{
arr[k] = R[j];
j++;
k++;
}
}
// Merge Sort Function in C
void mergeSort(int arr[], int l, int r)
{
if (l < r)
{
int m = l+(r-l)/2;
mergeSort(arr, l, m);
mergeSort(arr, m+1, r);
merge(arr, l, m, r);
}
}
// Functions to Print Elements of Array
void printArray(int A[], int size)
{
int i;
for (i=0; i < size; i++)
printf("%d ", A[i]);
printf("n");
}
// Main Method
int main()
{
int arr[] = {85, 24, 63, 45, 17, 31, 96, 50};
int arr_size = sizeof(arr)/sizeof(arr[0]);
printf("Given array is n");
printArray(arr, arr_size);
mergeSort(arr, 0, arr_size - 1);
printf("nSorted array is n");
printArray(arr, arr_size);
return 0;
}
Output:
Now after going through the above sorting programs you would have understood various sorting algorithms and how to implement them in C language. I hope this blog is informative and added value to you.
Now after executing the above program you would have understood the Sorting Algorithms In C. Thus we have come to an end of this article on ‘Quicksort in Java’. If you wish to learn more, check out the Java Training by Edureka, a trusted online learning company. Edureka’s Java J2EE and SOA training and certification course is designed to train you for both core and advanced Java concepts along with various Java frameworks like Hibernate & Spring.
Got a question for us? Please mention it in the comments section of this blog and we will get back to you as soon as possible.
Что такое сортировка и зачем она нужна
Сортировка распределяет элементы в порядке, удобном для работы. Если отсортировать массив чисел в порядке убывания, то первый элемент всегда будет наибольшим, а последний наименьшим. Поэтому желательно хранить информацию упорядочено, чтобы было проще проводить над ней операции.
В данной статье вы научитесь разным техникам сортировок на языке С++. Мы затронем 7 видов:
- Пузырьковая сортировка (Bubble sort);
- Сортировка выбором (Selection sort);
- Сортировка вставками (Insertion sort);
- Быстрая сортировка (Quick sort);
- Сортировка слиянием (Merge sort);
- Сортировка Шелла (Shell sort);
- Сортировка кучей (Heap sort).
Знание этих техник поможет получить работу. На площадке LeetCode содержится более 200 задач, связанных с сортировками. 19 из них входят в топ частых вопросов на собеседованиях по алгоритмам.
1. Пузырьковая сортировка
В пузырьковой сортировке каждый элемент сравнивается со следующим. Если два таких элемента не стоят в нужном порядке, то они меняются между собой местами. В конце каждой итерации (далее называем их проходами) наибольший/наименьший элемент ставится в конец списка.
Прежде чем писать код, разберем сортировку визуально на примере массива из пяти элементов. Отсортируем его в порядке возрастания.
Проход №1
Оранжевым отмечаются элементы, которые нужно
поменять местами. Зеленые уже стоят в нужном порядке.
Наибольший элемент — число 48 — оказался в конце
списка.
Проход №2
Наибольший элемент уже занимает место в конце
массива. Чтобы поставить следующее число по убыванию, можно пройтись лишь до 4-й позиции, а не пятой.
Проход №3
Проход №4
После четвертого прохода получаем
отсортированный массив.
Функция сортировки в качестве параметров будет принимать указатель на массив и его размер. Функцией swap() элементы
меняются местами друг с другом:
#include <iostream>
using namespace std;
void bubbleSort(int list[], int listLength)
{
while(listLength--)
{
bool swapped = false;
for(int i = 0; i < listLength; i++)
{
if(list[i] > list[i + 1])
{
swap(list[i], list[i + 1]);
swapped = true;
}
}
if(swapped == false)
break;
}
}
int main()
{
int list[5] = {3,19,8,0,48};
cout << "Input array ..." << endl;
for(int i = 0; i < 5; i++)
cout << list[i] << 't';
cout << endl;
bubbleSort(list, 5);
cout << "Sorted array ..." << endl;
for(int i = 0; i < 5; i++)
cout << list[i] << 't';
cout << endl;
}
Сложность в лучшем случае: O(n).
Сложность в среднем случае: O(n2).
Сложность в худшем случае: O(n2).
2. Сортировка выбором
Ищем наименьшее значение в массиве и ставим
его на позицию, откуда начали проход. Потом двигаемся на следующую позицию.
Возьмем тот же массив из пяти элементов и отсортируем его.
Проход №1
Зеленым отмечается наименьший элемент в
подмассиве — он ставится в начало списка.
Проход №2
Число 4 — наименьшее в оставшейся части массива.
Перемещаем четверку на вторую позицию после числа 0.
Проход №3
Проход №4
Напишем функцию поиска наименьшего элемента и
используем ее в сортировке:
int findSmallestPosition(int list[], int startPosition, int listLength)
{
int smallestPosition = startPosition;
for(int i = startPosition; i < listLength; i++)
{
if(list[i] < list[smallestPosition])
smallestPosition = i;
}
return smallestPosition;
}
#include <iostream>
using namespace std;
int findSmallestPosition(int list[], int startPosition, int listLength)
{
int smallestPosition = startPosition;
for(int i = startPosition; i < listLength; i++)
{
if(list[i] < list[smallestPosition])
smallestPosition = i;
}
return smallestPosition;
}
void selectionSort(int list[], int listLength)
{
for(int i = 0; i < listLength; i++)
{
int smallestPosition = findSmallestPosition(list, i, listLength);
swap(list[i], list[smallestPosition]);
}
return;
}
int main ()
{
int list[5] = {12, 5, 48, 0, 4};
cout << "Input array ..." << endl;
for(int i = 0; i < 5; i++)
cout << list[i] << 't';
cout << endl;
selectionSort(list, 5);
cout << "Sorted array ..." << endl;
for(int i = 0; i < 5; i++)
cout << list[i] << 't';
cout << endl;
}
Сложность в любом случае: O(n2).
3. Сортировка вставками
В сортировке вставками начинаем со второго
элемента. Проверяем между собой второй элемент с первым и, если надо, меняем местами.
Сравниваем следующую пару элементов и проверяем все пары до нее.
Проход №1. Начинаем со второй позиции.
Число 12 больше 5 — элементы меняются местами.
Проход №2. Начинаем с третьей позиции.
Проверяем вторую и третью позиции. Затем
первую и вторую.
Проход №3. Начинаем с четвертой позиции.
Произошло три смены местами.
Проход №4. Начинаем с последней позиции.
Получаем отсортированный массив на выходе.
#include <iostream>
using namespace std;
void insertionSort(int list[], int listLength)
{
for(int i = 1; i < listLength; i++)
{
int j = i - 1;
while(j >= 0 && list[j] > list[j + 1])
{
swap(list[j], list[j + 1]);
cout<<"ndid";
j--;
}
}
}
int main()
{
int list[8]={3,19,8,0,48,4,5,12};
cout<<"Input array ...n";
for (int i = 0; i < 8; i++)
{
cout<<list[i]<<"t";
}
insertionSort(list, 8);
cout<<"nnSorted array ... n";
for (int i = 0; i < 8; i++)
{
cout<<list[i]<<"t";
}
return 0;
}
Сложность в лучшем случае: O(n).
Сложность в худшем случае: O(n2).
4. Быстрая сортировка
В основе быстрой сортировки лежит стратегия
«разделяй и властвуй». Задача разделяется на более мелкие подзадачи. Подзадачи
решаются отдельно, а потом решения объединяют. Точно так же, массив разделяется
на подмассивы, которые сортируются и затем сливаются в один.
В первую очередь выбираем опорный элемент.
Отметим его синим. Все значения больше опорного элемента ставятся после него,
остальные — перед.
На иллюстрации массив разделяется по опорному
элементу. В полученных массивах также выбираем опорный элемент и разделяем по
нему.
Опорным может быть любой элемент. Мы выбираем
последний в списке.
Чтобы расположить элементы большие — справа от
опорного элемента, а меньшие — слева, будем двигаться от начала списка. Если
число будет больше опорного, то оно ставится на его место, а сам опорный на
место перед ним.
Напишем функцию разделения partition(),
которая возвращает индекс опорного элемента, и используем ее в сортировке.
int partition(int list[], int start, int pivot)
{
int i = start;
while(i < pivot)
{
if(list[i] > list[pivot] && i == pivot-1)
{
swap(list[i], list[pivot]);
pivot--;
}
else if(list[i] > list[pivot])
{
swap(list[pivot - 1], list[pivot]);
swap(list[i], list[pivot]);
pivot--;
}
else i++;
}
return pivot;
}
#include <iostream>
using namespace std;
int partition(int list[], int start, int pivot)
{
int i = start;
while(i < pivot)
{
if(list[i] > list[pivot] && i == pivot-1)
{
swap(list[i], list[pivot]);
pivot--;
}
else if(list[i] > list[pivot])
{
swap(list[pivot - 1], list[pivot]);
swap(list[i], list[pivot]);
pivot--;
}
else i++;
}
return pivot;
}
void quickSort(int list[], int start, int end)
{
if(start < end)
{
int pivot = partition(list, start, end);
quickSort(list, start, pivot - 1);
quickSort(list, pivot + 1, end);
}
}
int main()
{
int list[6]={2, 12, 5, 48, 0, 4};
cout<<"Input array ...n";
for (int i = 0; i < 6; i++)
{
cout<<list[i]<<"t";
}
quickSort(list, 0, 6);
cout<<"nnSorted array ... n";
for (int i = 0; i < 6; i++)
{
cout<<list[i]<<"t";
}
return 0;
}
Сложность в лучшем случае: O(n*logn).
Сложность в худшем случае: O(n2).
5. Сортировка слиянием
Сортировка слиянием также следует стратегии
«разделяй и властвуй». Разделяем исходный массив на два равных подмассива.
Повторяем сортировку слиянием для этих двух подмассивов и объединяем обратно.
Цикл деления повторяется, пока не останется по
одному элементу в массиве. Затем объединяем, пока не образуем полный список.
Алгоритм сортировки состоит из четырех этапов:
- Найти середину массива.
- Сортировать массив от
начала до середины. - Сортировать массив от
середины до конца. - Объединить массив.
void merge(int list[],int start, int end, int mid);
void mergeSort(int list[], int start, int end)
{
int mid;
if (start < end){
mid=(start+end)/2;
mergeSort(list, start, mid);
mergeSort(list, mid+1, end);
merge(list,start,end,mid);
}
}
Для объединения напишем отдельную функцию
merge().
Алгоритм объединения массивов:
- Циклично проходим по
двум массивам.. - В объединяемый ставим тот элемент, что меньше.
- Двигаемся дальше, пока не дойдем до конца
обоих массивов.
#include <iostream>
using namespace std;
void merge(int list[],int start, int end, int mid);
void mergeSort(int list[], int start, int end)
{
int mid;
if (start < end){
mid=(start+end)/2;
mergeSort(list, start, mid);
mergeSort(list, mid+1, end);
merge(list,start,end,mid);
}
}
void merge(int list[],int start, int end, int mid)
{
int mergedList[8];
int i, j, k;
i = start;
k = start;
j = mid + 1;
while (i <= mid && j <= end) {
if (list[i] < list[j]) {
mergedList[k] = list[i];
k++;
i++;
}
else {
mergedList[k] = list[j];
k++;
j++;
}
}
while (i <= mid) {
mergedList[k] = list[i];
k++;
i++;
}
while (j <= end) {
mergedList[k] = list[j];
k++;
j++;
}
for (i = start; i < k; i++) {
list[i] = mergedList[i];
}
}
int main()
{
int list[8]={3,19,8,0,48,4,5,12};
cout<<"Input array ...n";
for (int i = 0; i < 8; i++)
{
cout<<list[i]<<"t";
}
mergeSort(list, 0, 7);
cout<<"nnSorted array ... n";
for (int i = 0; i < 8; i++)
{
cout<<list[i]<<"t";
}
}
Сложность в любом случае: O(n*logn).
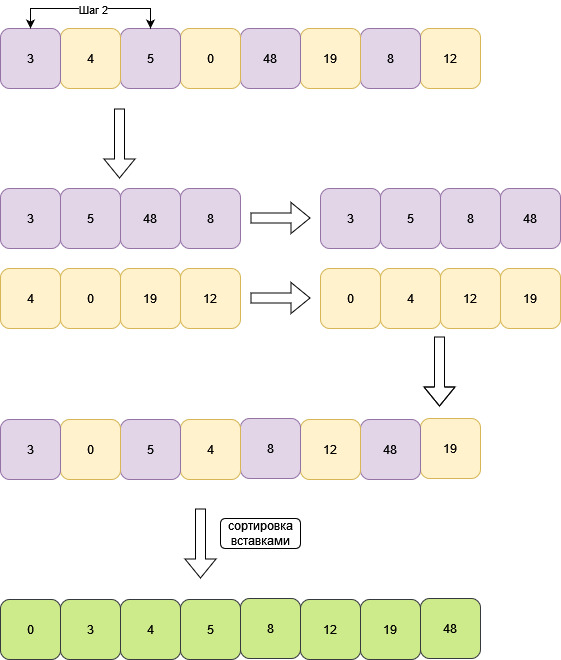
6. Сортировка Шелла
Алгоритм включает в себя сортировку вставками.
Исходный массив размером N разбивается на подмассивы с шагом N/2. Подмассивы
сортируются вставками. Затем вновь разбиваются, но уже с шагом равным N/4. Цикл
повторяется. Производим целочисленное деление шага на два каждую итерацию.
Когда шаг становится равен 1, массив просто сортируется вставками.
У массива размером с 8, первый шаг будет равен 4.
Уменьшаем шаг в два раза. Шаг равен 2.
#include <iostream>
using namespace std;
void shellSort(int list[], int listLength)
{
for(int step = listLength/2; step > 0; step /= 2)
{
for (int i = step; i < listLength; i += 1)
{
int j = i;
while(j >= step && list[j - step] > list[i])
{
swap(list[j], list[j - step]);
j-=step;
cout<<"ndid";
}
}
}
}
int main()
{
int list[8]={3,19,8,0,48,4,5,12};
cout<<"Input array ...n";
for (int i = 0; i < 8; i++)
{
cout<<list[i]<<"t";
}
shellSort(list, 8);
cout<<"nnSorted array ... n";
for (int i = 0; i < 8; i++)
{
cout<<list[i]<<"t";
}
}
Сложность в лучшем и среднем случае:
O(n*logn).
Сложность в худшем случае: O(n2).
Исходный массив представляем в виде структуры
данных кучи. Куча – это один из
типов бинарного дерева.
У кучи есть следующие свойства:
- Родительский узел
всегда больше дочерних; - На i-ом слое 2i
узлов, начиная с нуля. То есть на нулевом слое 1 узел, на первом – 2 узла, на
втором – 4, и т. д. Правило для всех слоев, кроме последнего; - Слои заполняются слева направо.
После формирования кучи будем извлекать самый
старший узел и ставить на конец массива.
Алгоритм сортировки кучей:
- Формируем бинарное
дерево из массива. - Расставляем узлы в
дереве так, чтобы получилась куча (методheapify()). - Верхний элемент
помещаем в конец массива. - Возвращаемся на шаг 2, пока куча не опустеет.
Обращаться к дочерним узлам можно, зная, что
дочерние элементы i-го элемента находятся на позициях 2*i + 1 (левый узел) и
2*i + 2 (правый узел).
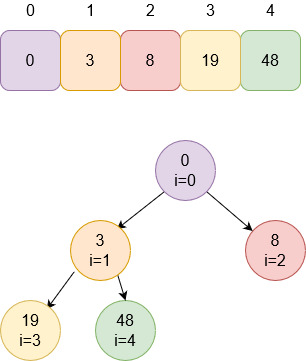
Изначальная куча:
Индекс с нижним левым узлом определим по
формуле n/2-1, где n – длина массива. Получается 5/2 – 1 = 2 – 1 = 1. С этого
индекса и начинаем операцию heapify(). Сравним дочерние узлы 1-й позиции.
Дочерний узел оказался больше. Меняем местами
с родителем.
Теперь проверяем родительский узел от позиции
1.
48 больше 3. Меняем местами.
После смены проверяем все дочерние узлы
элемента, который опустили. То есть для числа 3 проводим heapify(). Так как 3
меньше 19, меняем местами.
Наибольший элемент оказался наверху кучи.
Осталось поставить его в конце массива на позицию 4.
Теперь продолжаем сортировать кучу, но последний элемент игнорируем. Для
этого просто будем считать, что длина массива уменьшилась на 1.
Повторяем алгоритм сортировки, пока куча не
опустеет, и получаем отсортированный массив.
void heapify(int list[], int listLength, int root)
{
int largest = root;
int l = 2*root + 1;
int r = 2*root + 2;
if (l < listLength && list[l] > list[largest])
largest = l;
if (r < listLength && list[r] > list[largest])
largest = r;
if (largest != root)
{
swap(list[root], list[largest]);
heapify(list, listLength, largest);
}
}
#include <iostream>
using namespace std;
void heapify(int list[], int listLength, int root)
{
int largest = root;
int l = 2*root + 1;
int r = 2*root + 2;
if (l < listLength && list[l] > list[largest])
largest = l;
if (r < listLength && list[r] > list[largest])
largest = r;
if (largest != root)
{
swap(list[root], list[largest]);
heapify(list, listLength, largest);
}
}
void heapSort(int list[], int listLength)
{
for(int i = listLength / 2 - 1; i >= 0; i--)
heapify(list, listLength, i);
for(int i = listLength - 1; i >= 0; i--)
{
swap(list[0], list[i]);
heapify(list, i, 0);
}
}
int main()
{
int list[5] = {3,19,8,0,48};
cout<<"Input array ..."<<endl;
for(int i = 0; i < 5; i++)
cout << list[i] << 't';
cout << endl;
heapSort(list, 5);
cout << "Sorted array"<<endl;
for(int i = 0; i < 5; i++)
cout << list[i] << 't';
cout << endl;
}
Сложность алгоритма в любом случае: O(n*logn).
***
В этой статье мы познакомились с семью видами
сортировок, рассмотрели их выполнение и написание на С++. Попробуйте применить
новые знания в решении задачек на LeetCode или Codeforces. Понимание подобных
алгоритмов поможет в будущем пройти собеседование.
Источники:
- https://www.softwaretestinghelp.com/sorting-techniques-in-cpp/
- https://medium.com/@ssbothwell/sorting-algorithms-and-big-o-analysis-332ce7b8e3a1
- https://www.programiz.com/dsa/shell-sort
- https://www.happycoders.eu/algorithms/sorting-algorithms/
***
Материалы по теме
- Какая сортировка самая быстрая? Тестируем алгоритмы
- Пузырьковая сортировка на JavaScript
- Вводный курс по алгоритмам: от сортировок до машины Тьюринга
***
Мне сложно разобраться самостоятельно, что делать?
Алгоритмы и структуры данных действительно непростая тема для самостоятельного изучения: не у кого спросить и что-то уточнить. Поэтому мы запустили курс «Алгоритмы и структуры данных», на котором в формате еженедельных вебинаров вы:
- изучите сленг, на котором говорят все разработчики независимо от языка программирования: язык алгоритмов и структур данных;
- научитесь применять алгоритмы и структуры данных при разработке программ;
- подготовитесь к техническому собеседованию и продвинутой разработке.
Курс подходит как junior, так и middle-разработчикам.
Язык Си в примерах
- Компиляция программ
- Простейшая программа «Hello World»
- Учимся складывать
- Максимум
- Таблица умножения
- ASCII-коды символов
- Верхний регистр
- Скобочки
- Факториал
- Степень числа
- Треугольник Паскаля
- Корень уравнения
- Система счисления
- Сортировка
- Библиотека complex
- Сортировка на основе qsort
- RPN-калькулятор
- RPN-калькулятор на Bison
- Простая грамматика
- Задача «Расчёт сопротивления схемы»
- Простая реализация конечного автомата
- Использование аргументов командной строки
- Чтение и печать без использования stdio
- Декодирование звукозаписи в формате ADX
- Другие примеры
Задача «сортировки» (упорядочения) — одна из первых интересных и сложных задач теории алгоритмов. Общие принципы освещает статья «Алгоритмы сортировки», здесь же мы рассматриваем способы упорядочения посредством языка Си.
Метод «пузырька»[править]
Один из простейших алгоритмов решения — метод «пузырька».
#include <stdio.h> int main() { int n, i, j; scanf_s("%d", &n); int a[n]; // считываем количество чисел n // формируем массив n чисел for(i = 0 ; i < n; i++) { scanf_s("%d", &a[i]); } for(i = 0 ; i < n - 1; i++) { // сравниваем два соседних элемента. for(j = 0 ; j < n - i - 1 ; j++) { if(a[j] > a[j+1]) { // если они идут в неправильном порядке, то // меняем их местами. int tmp = a[j]; a[j] = a[j+1] ; a[j+1] = tmp; } } } }
Понятно, что после первого «пробега» самый большой элемент массива окажется на последнем месте.
После второго пробега мы будем уверены, что второй по величине элемент
находится на предпоследнем месте.
Задача: Докажите, что достаточно 
Решив эту задачу, вы докажете, что метод «пузырька» решает задачу сортировки.
Функция qsort из библиотеки stdlib[править]
Два оператора for, в которых происходит сортировка, можно заменить на одну строку:
qsort(a, n, sizeof(int), cmp );
Это функция, описанная в стандартной библиотеке ANSI C и объявлена в заголовочном файле stdlib.h.
Поэтому в начале программы нужно добавить
Функцией qsort можно упорядочивать объекты любой природы. По сути, она предназначена упорядочивать множества блоков байтов равной длины.
Второй аргумент функции — это число таких блоков, третий аргумент — длина каждого блока.
Первый аргумент — это адрес, где находится начало первого блока (предполагается, что блоки в памяти расположены друг за другом подряд).
Четвёртый аргумент функции qsort — это имя функции, которая умеет сравнивать
два элемента массива. В нашем случае это
int cmp(const void *a, const void *b) { return *(int*)a - *(int*)b; }
В силу указанной универсальности функции сортировки, функция сравнения получает в качества аргумента адреса двух блоков, которые нужно сравнить и возвращает 1, 0 или -1:
- положительное значение, если a > b
- 0, если a == b
- отрицательное значение, если a < b
Поскольку у нас блоки байт — это целые числа (в 32-битной архитектуре это четырёхбайтовые блоки), то
необходимо привести данные указатели типа (const void*) к типу (int *) и осуществляется это с помощью дописывания
перед указателем выражения «(const int*)». Затем нужно получить значение переменной типа int, которая лежит по этому адресу.
Это делается с помощью дописывания спереди звездочки.
Таким образом, мы получили следующую программу
#include <stdio.h> #include <stdlib.h> #define N 1000 int cmp(const void *a, const void *b) { return *(int*)a - *(int*)b; } int main() { int n, i,j; int a[N]; scanf("%d", &n); for(i = 0 ; i < n; i++) { // ЧИТАЕМ ВХОД scanf("%d", &a[i]); } qsort(a, n, sizeof(int), cmp ); // СОРТИРУЕМ for(i = 0 ; i < n; i++) { // ВЫВОДИМ РЕЗУЛЬТАТ printf("%d ", a[i]); } return 0; }
Динамическое выделение памяти[править]
Ниже приведена программа, где память под массив выделяется динамически:
#include <stdio.h> #include <stdlib.h> #include <malloc.h> int cmp(const void *a, const void *b) { return *(int*)a - *(int*)b; } int main() { int n, i; int *a; scanf("%d", &n); a = (int*) malloc(sizeof(int)*n); for(i = 0 ; i < n; i++) { scanf("%d", &a[i]); } qsort(a, n, sizeof(int), cmp ); for(i = 0 ; i < n; i++) { printf("%d ", a[i]); } free(a); return 0; }
Функция malloc (от англ. memory allocation — выделение памяти) делает запрос к ядру операционной системы по выделению заданного количества байт. Единственный аргумент этой функции — число байт, которое вам нужно. В качестве результата функция возвращает указатель на начало выделенной памяти. Указатель на начало выделенной памяти &mbsah — это адрес ячейки памяти, начиная с которого идут N байт, которые вы можете использовать под любые свои нужды. Всю память, которая была выделена с помощью функции malloc, нужно освобождать с помощью функции free. Аргумент функции free — это указатель на начало выделенной когда-то памяти.
Программа упорядочения строк в алфавитном порядке[править]
#include <stdlib.h> #include <string.h> #include <stdio.h> #define N 100 #define M 30 int main(int argc, char* argv[]) { char a[N][M]; int n, i; scanf("%d", &n); for (i=0; i<n; i++) scanf("%s", &a[i]); qsort(a, n, sizeof(char[M]), (int (*)(const void *,const void *)) strcmp); for (i=0; i<n; i++) printf("%sn", a[i]); return 0; }
Обратите внимание на сложное приведение типов.
Функция strcmp, объявленная в файле string.h имеет следующий прототип:
int strcmp(const char*, const char*);
То есть функция получает два аргумента — указатели на кусочки памяти, где хранятся элементы типа char,
то есть два массива символов, которые не могут быть изменены внутри функции strcmp (запрет на изменение задается с помощью модификатора const)[1].
В то же время в качестве четвертого элемента функция qsort хотела бы иметь функцию типа
int cmp(const void*, const void*);
В языке Си можно осуществлять приведение типов являющихся типами функции. В данном примере тип
int (*)(const char*, const char*); // функция, получающая два элемента типа 'const char *' и возвращающая элемент типа 'int'
приводится к типу
int (*)(const void*, const void*); // функция, получающая два элемента типа 'const void *' и возвращающая элемент типа 'int'
Примечания[править]
- ^ Функция strcmp в соответствии с описанием, выдаваемым командой man 3 strcmp, осуществляет сравнение двух строк и определяет, какая из двух строк идёт первой в алфавитном порядке (сравнивает две строки в лексикографическом порядке), а именно: она возвращает значение больше нуля, если первая строка «больше» второй (идёт после второй в алфавитном порядке), 0 – если они совпадают, и значение меньше нуля– если первая строка «меньше» второй.
Привет, дорогие читатели! Этот урок посвящен встроенной сортировке C++ и ее учителю — компаратору.
- sort для вектора
- sort для списка
- sort для массива
- Что такое компаратор
Что такое функция sort
Это функция, которая может сортировать указанный контейнер или обычный массив. По умолчанию она сортирует по неубыванию, но это можно изменить путем применения компаратора, об этом поговорим позже.
Принцип работы построен на алгоритме быстрой сортировки (quicksort), так что за быстроту можно не волноваться.
Также в C++ имеется другая сортировка — qsort, но она работает значительно медленнее текущей.
Чтобы нам оперировать данной функцией понадобится для начала подключить библиотеку — <algorithm>.
Многие языки не могут похвастаться такой гибкостью. Например, Pascal, там придется самостоятельно писать алгоритм сортировки (который составляет несколько десятков строк !).
Функция sort для вектора
Вот как выглядит конструкция вызова:
|
sort (<начало>, <конец>, <компаратор>); |
<начало>— здесь мы должны указать стартовую точку сортировки, необязательно это должно быть начало.<конец>— тут аналогично, только уже указываем конец.<компаратор>— его использовать в аргументах функции не обязательно. Подробнее о нем мы поговорим ниже.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 |
#include <iostream> #include <vector> // vector #include <algorithm> // sort using namespace std; int main () { setlocale(0, «»); int n; vector <int> vec; cout << «Введите количество элементов последовательности: «; cin >> n; int a; for (int i = 0; i < n; i++) { cout << i + 1 << «) «; cin >> a; vec.push_back(a); } cout << «Вот как выглядит последовательность до: «; for (int i = 0; i < n; i++) { cout << vec[i] << » «; } sort (vec.begin(), vec.end()); // сортировка cout << endl << «После сортировки: «; for (int i = 0; i < n; i++) { cout << vec[i] << » «; } sort(vec.begin() + n / 2, vec.end(), comp); cout << endl << «А вот еще раз: «; for (int i = 0; i < n; i++) { cout << vec[i] << » «; } system(«pause»); return 0; } |
- В строках 14 — 17: добавляем элементы в вектор
vec. - В строке 25: сортируем последовательность.
- В строке 32: нашей стартовой точкой стала
n / 2, а также мы применили компаратор, из-за которого смогли поменять сторону сортировки (по не возрастанию).vec.begin() + n / 2— так прибавлять к итератору можно только для вектора и массива, для других контейнеров нельзя. Подробнее почитайте про итераторы здесь.
Вот как выглядит пример запуска программы:
Введите количество элементов последовательности: 10
1) 1
2) 4
3) 2
4) 8
5) 9
6) 5
7) 3

9) 10
10) 6
Вот как выглядит последовательность до: 1 4 2 8 9 5 3 7 10 6
А вот как после: 1 2 3 4 5 6 7 8 9 10
А вот еще раз: 1 2 3 4 5 10 9 8 7 6
Process returned 0 (0x0) execution time : 0.010 s
Press any key to continue.
Функция sort для списка
Для списка list, функция sort() превращается в префиксный метод:
|
<имя списка>.sort(<компаратор>); |
Функция sort для массива (array)
Чтобы отсортировать массив нам нужно использовать схему ниже:
|
sort(<имя массива>, <имя массива> + <размер массива>, компаратор); |
Имя массива указывает на первую ячейку —
[0].
- В первый аргумент записываем имя массива.
- Далее также записываем имя массива, но уже через плюс указываем сколько ячеек надо отсортировать.
Так, например можно:
- Отсортировать только первую половину массива, если укажем
(... , <имя массива> + n / 2)(n— размер массива). - Или начать сортировку со второй ячейки
(<имя массива> + 2, ...).
Что такое компаратор
Компаратор — это функция, которая как бы учит сортировать sort. Так например можно сортировать по:
- Кратности на 3.
- Четности или нечетности.
- Изменить сторону сортировки на — по убыванию.
sort передает элементы компаратору, а компаратор проверяет их по вашему алгоритму и передает true или false.
Обычно его используют когда имеется например — vector < vector <pair <int, int> > > vec и нужно отсортировать вектора по второму элементу первой ячейки (vec[i][0].second).
Как создать компаратор
Самого начала создаём функцию, которая и будет компаратором.
|
bool comp (<первый элемент>, <второй элемент>) { return <первый элемент> <условный оператор> <второй аргумент>; } |
<первый и второй аргумент>— здесь нужно быть аккуратным, потому что если мы укажем неправильно аргументы — никакая сортировка не произойдет.return— эта строчка является основной в этом коде, так как именно она изменяет сортировку.
В аргументах нужно всего лишь указать имя компаратора.
|
sort (vec.begin(), vec.end(), comp); |
Как правильно создавать компаратор чтобы он работал
Чтобы правильно создать компаратор нужно знать это:
- Когда вызывается компаратор ему передается тип сортируемого объекта.
Давайте разберем пример, который был выше — vector < vector < pair <int, int> > >. Для него этим типом будет — vector < pair <int, int> >.
|
bool comp (vector < pair <int, int> > a, vector <pair <int, int> > b) { return a[0].second < b[0].second; } |
Этот компаратор будет сортировать вектора по второму элементу первой ячейки (по неубыванию).
Для массивов «типом сортируемого объекта» и будет тип массива. Например
pair <int, int> p[20]->... (pair <int, int> a, ...) {
По неубыванию означает, что элемент arr[i] может быть равным arr[i — 1] (а по убыванию означает что каждый последующий элемент будет меньше предыдущего). Тоже самое с сортировкой по невозрастанию.
Надеемся вы нашли в этой статье то что искали. Если есть вопрос задайте его в комментариях. Удачи!
Время на прочтение
16 мин
Количество просмотров 67K
Задача сортировки — это классическая задача, которую должен знать любой программист. Именно поэтому эта статья посвящена данной теме — реализации сортировки на платформе .NET. Я хочу рассказать о том, как устроена сортировка массивов в .NET, поговорить о ее особенностях, реализации, а также провести небольшое сравнение с Java.
Итак, начнем с того, что первые версии .NET используют алгоритм быстрой сортировки по умолчанию. Поэтому небольшой экскурс в быструю сортировку:
Достоинства:
- Один из самых быстродействующих (на практике) из алгоритмов внутренней сортировки общего назначения;
- Прост в реализации;
- Требует лишь O(logn) дополнительной памяти для своей работы (не улучшенный рекурсивный алгоритм в худшем случае O(n) памяти);
- Хорошо сочетается с механизмами кэширования и виртуальной памяти.
Недостатки:
- Сильно деградирует по скорости до O(n2) при неудачных выборах опорных элементов, что может случиться при неудачных входных данных. Этого можно избежать, выбирая опорный элемент случайно, а не фиксированным образом;
- Наивная реализация алгоритма может привести к ошибке переполнения стека, так как ей может потребоваться сделать O(n) вложенных рекурсивных вызовов. В улучшенных реализациях, в которых рекурсивный вызов происходит только для сортировки меньшей из двух частей массива, глубина рекурсии гарантированно не превысит O(logn);
- Неустойчив — если требуется устойчивость, приходится расширять ключ.
Наивная реализация алгоритма быстрой сортировки может выглядеть примерно так:
Наивный QuickSort
public void QuickSort(int left, int right)
{
int l = left;
int r = right;
int avg = array[(l + r) / 2)];
do
{
while (array[l] < avg)
++l;
while (array[r] > avg)
--r;
if (l <= r)
{
if (l < r)
{
int temp = array[l];
array[l] = array[r];
array[r] = temp;
}
++l;
--r;
}
}
while (l <= r);
if (left < r)
QuickSort(left, r);
if (l < right)
QuickSort(l, right);
}
Вышеописанный алгоритм сортировки имеет следующие недостатки:
- Поскольку опорный элемент выбирается как середина массива, то возможен случай, когда это будет всегда максимум, в результате чего массив будет разбиваться на две части длинною n — 1 и 1 и скорость алгоритма деградирует до O(n2);
- При вышеописанных условиях глубина рекурсии достигает O(n), в результате чего при больших n может произойти переполнение программного стека;
- Алгоритм неустойчив, то есть он меняет элементы с одинаковыми значениями. На примере сортировки чисел это ни как не сказывается, но если мы сортируем массив объектов по какому-либо свойству то это существенно, так как в результате нескольких вызовов метода Sort будем получать массив элементы которого отличаются порядком.
Переходим к рассмотрению реализации в .NET.
.NET 1.0
Итак, рассмотрим, что происходит в .NET 1.0. Забегая, вперед скажу, что ничего хорошего мы здесь не увидим, особенно для пользовательских значимых типов… (из-за отсутствия обобщений в частности)
public static void Sort(Array array)
{
Array.Sort(array, (Array) null, array.GetLowerBound(0), array.Length, (IComparer) null);
}
public static void Sort(Array keys, Array items, int index, int length, IComparer comparer)
{
if (length > 1) {
if (comparer == Comparer.Default || comparer == null) {
if(TrySZSort(array, null, index, index + length - 1)) {
return;
}
}
object[] keys1 = keys as object[];
object[] items1 = (object[]) null;
if (keys1 != null)
items1 = items as object[];
if (keys1 != null && (items == null || items1 != null))
new Array.SorterObjectArray(keys1, items1, comparer).QuickSort(index, index + length - 1);
else
new Array.SorterGenericArray(keys, items, comparer).QuickSort(index, index + length - 1);
}
А теперь собственно классы SorterObjectArray и SorterGenericArray:
SorterObjectArray
private class SorterObjectArray
{
private object[] keys;
private object[] items;
private IComparer comparer;
public SorterObjectArray(object[] keys, object[] items, IComparer comparer)
{
if (comparer == null)
comparer = (IComparer)Comparer.Default;
this.keys = keys;
this.items = items;
this.comparer = comparer;
}
public virtual void QuickSort(int left, int right)
{
do
{
int left1 = left;
int right1 = right;
object obj1 = this.keys[left1 + right1 >> 1];
do
{
while (this.comparer.Compare(this.keys[left1], obj1) < 0)
++left1;
while (this.comparer.Compare(obj1, this.keys[right1]) < 0)
--right1;
if (left1 <= right1)
{
if (left1 < right1)
{
object obj2 = this.keys[left1];
this.keys[left1] = this.keys[right1];
this.keys[right1] = obj2;
if (this.items != null)
{
object obj3 = this.items[left1];
this.items[left1] = this.items[right1];
this.items[right1] = obj3;
}
}
++left1;
--right1;
}
else
break;
}
while (left1 <= right1);
if (right1 - left <= right - left1)
{
if (left < right1)
this.QuickSort(left, right1);
left = left1;
}
else
{
if (left1 < right)
this.QuickSort(left1, right);
right = right1;
}
}
while (left < right);
}
}
SorterGenericArray
private class SorterGenericArray
{
private Array keys;
private Array items;
private IComparer comparer;
public SorterGenericArray(Array keys, Array items, IComparer comparer)
{
if (comparer == null)
comparer = (IComparer)Comparer.Default;
this.keys = keys;
this.items = items;
this.comparer = comparer;
}
public virtual void QuickSort(int left, int right)
{
do
{
int num1 = left;
int num2 = right;
object obj1 = this.keys.GetValue(num1 + num2 >> 1);
do
{
while (this.comparer.Compare(this.keys.GetValue(num1), obj1) < 0)
++num1;
while (this.comparer.Compare(obj1, this.keys.GetValue(num2)) < 0)
--num2;
if (num1 <= num2)
{
if (num1 < num2)
{
object obj2 = this.keys.GetValue(num1);
this.keys.SetValue(this.keys.GetValue(num2), num1);
this.keys.SetValue(obj2, num2);
if (this.items != null)
{
object obj3 = this.items.GetValue(num1);
this.items.SetValue(this.items.GetValue(num2), num1);
this.items.SetValue(obj3, num2);
}
}
++num1;
--num2;
}
else
break;
}
while (num1 <= num2);
if (num2 - left <= right - num1)
{
if (left < num2)
this.QuickSort(left, num2);
left = num1;
}
else
{
if (num1 < right)
this.QuickSort(num1, right);
right = num2;
}
}
while (left < right);
}
}
Так что же тут происходит? Следующий код
object[] keys1 = keys as object[];
object[] items1 = (object[]) null;
if (keys1 != null)
items1 = items as object[];
это не что иное, как попытка использовать ковариацию массивов, которая, как известно, работает только для ссылочных типов. Получается, для ссылочных типов используется класс SorterObjectArray, а для значимых типов используется SorterGenericArray. Но подождите, чем отличаются данные классы? Как вы можете заметить, они отличаются только способом доступа к элементам массива. Для значимых типов используются методы GetValue и SetValue, которые как вы знаете, являются очень медленными… Получается, что массив целых чисел будет сортироваться очень долго (ведь целое число является значимым типом)? Нет! Массив целых чисел сортируется быстро, причем очень быстро. Все дело в следующем коде
if (length > 1) {
if (comparer == Comparer.Default || comparer == null) {
if(TrySZSort(array, null, index, index + length - 1))
return;
} }
Интерес представляет метод Array.TrySZSort. Этот метод вызывает нативную реализацию сортировки реализованную на С++ в самой CLR. Причем работает он для примитивных типов, когда мы используем стандартную логику сравнения элементов, то есть когда comparer == Comparer.Default || comparer == null.
А вот и нативная реализация:
Нативный TrySZSort
FCIMPL4(INT32, ArrayHelper::TrySZSort, ArrayBase * keys, ArrayBase * items, UINT32 left, UINT32 right)
//если массив не является одномерным с начальным индексом ноль не сортируем
if (keys->GetRank() != 1 || keys->GetLowerBoundsPtr()[0] != 0)
return FALSE;
// Получаем тип элементов массива
TypeHandle keysTH = keys->GetElementTypeHandle();
// Если он не является встроенным примитивным
const CorElementType keysElType = keysTH.GetSigCorElementType();
if (!CorTypeInfo::IsPrimitiveType(keysElType))
return FALSE;
if (items != NULL) {
TypeHandle itemsTH = items->GetElementTypeHandle();
if (keysTH != itemsTH)
return FALSE; // Can't currently handle sorting different types of arrays.
}
// Оптимизация для массива из одного элемента
if (left == right || right == 0xffffffff)
return TRUE;
//Далее вызывается специализированная версия сортировки написанная на шаблонах С++.
switch(keysElType) {
case ELEMENT_TYPE_I1: // 1-байтовое знаковое целое число (sbyte)
ArrayHelpers<I1>::QuickSort((I1*) keys->GetDataPtr(), (I1*) (items == NULL ? NULL : items->GetDataPtr()), left, right);
break;
case ELEMENT_TYPE_U1: // 1-байтовое целое число без знака (byte)
case ELEMENT_TYPE_BOOLEAN: // Логический тип (bool)
ArrayHelpers<U1>::QuickSort((U1*) keys->GetDataPtr(), (U1*) (items == NULL ? NULL : items->GetDataPtr()), left, right);
break;
case ELEMENT_TYPE_I2: // 2-байтовое знаковое целое число (short)
ArrayHelpers<I2>::QuickSort((I2*) keys->GetDataPtr(), (I2*) (items == NULL ? NULL : items->GetDataPtr()), left, right);
break;
case ELEMENT_TYPE_U2: // 2-байтовое целое число без знака (ushort)
case ELEMENT_TYPE_CHAR: // Символьный тип (char)
ArrayHelpers<U2>::QuickSort((U2*) keys->GetDataPtr(), (U2*) (items == NULL ? NULL : items->GetDataPtr()), left, right);
break;
case ELEMENT_TYPE_I4: // 4-байтовое знаковое целое число (int)
ArrayHelpers<I4>::QuickSort((I4*) keys->GetDataPtr(), (I4*) (items == NULL ? NULL : items->GetDataPtr()), left, right);
break;
case ELEMENT_TYPE_U4: // 4-байтовое целое число без знака (uint)
ArrayHelpers<U4>::QuickSort((U4*) keys->GetDataPtr(), (U4*) (items == NULL ? NULL : items->GetDataPtr()), left, right);
break;
case ELEMENT_TYPE_R4: // 4-байтовое число с плавающей запятой (float)
ArrayHelpers<R4>::QuickSort((R4*) keys->GetDataPtr(), (R4*) (items == NULL ? NULL : items->GetDataPtr()), left, right);
break;
case ELEMENT_TYPE_I8: // 8-байтовое знаковое целое число (long)
ArrayHelpers<I8>::QuickSort((I8*) keys->GetDataPtr(), (I8*) (items == NULL ? NULL : items->GetDataPtr()), left, right);
break;
case ELEMENT_TYPE_U8: // 8-байтовое целое число без знака (ulong)
ArrayHelpers<U8>::QuickSort((U8*) keys->GetDataPtr(), (U8*) (items == NULL ? NULL : items->GetDataPtr()), left, right);
break;
case ELEMENT_TYPE_R8: // 8-байтовое число с плавающей запятой (double)
ArrayHelpers<R8>::QuickSort((R8*) keys->GetDataPtr(), (R8*) (items == NULL ? NULL : items->GetDataPtr()), left, right);
break;
case ELEMENT_TYPE_I: // Размер целого числа в машинном коде (IntPtr)
case ELEMENT_TYPE_U: // Размер целого числа без знака в машинном коде (UIntPtr)
// In V1.0, IntPtr & UIntPtr are not fully supported types. They do
// not implement IComparable, so searching & sorting for them should
// fail. In V1.1 or V2.0, this should change.
return FALSE;
default:
return FALSE;
}
return TRUE;
}
Нативный QuickSort
// Шаблонный-класс непосредственно занимающийся сортировкой
template <class KIND>
class ArrayHelpers
{
static void QuickSort(KIND keys[], KIND items[], int left, int right) {
do {
int i = left;
int j = right;
KIND x = keys[(i + j) >> 1];
do {
while (Compare(keys[i], x) < 0) i++;
while (Compare(x, keys[j]) < 0) j--;
if (i > j) break;
if (i < j) {
KIND key = keys[i];
keys[i] = keys[j];
keys[j] = key;
if (items != NULL) {
KIND item = items[i];
items[i] = items[j];
items[j] = item;
}
}
i++;
j--;
}
while (i <= j);
if (j - left <= right - i)
{
if (left < j) QuickSort(keys, items, left, j);
left = i;
}
else
{
if (i < right) QuickSort(keys, items, i, right);
right = j;
}
}
while (left < right);
}
};
Как видите, нативная сортировка работает только для примитивных типов. К ним относятся все числовые типы + логический + символьный. А для значимых пользовательских типов все будет работать плачевно медленно.
Переходим к рассмотрению реализации именно самого алгоритма сортировки. Будем рассматривать реализацию в классе SorterObjectArray, так как и нативная реализация и реализация для значимых типов аналогична.
1. В качестве опорного элемента всегда берется середина массива:
object obj1 = this.keys[left1 + right1 >> 1];
Это не хорошо, так как при плохих входных данных время выполнения алгоритма может стать квадратичным. К тому же середина берется по формуле num1 + num2 >> 1, что может привести к переполнению типа int. Такая же ошибка была сделана в алгоритме бинарного поиска и сортировки в Java (ссылка на баг).
Как увидите в следующих версиях .NET этот недостаток будет исправлен.
2. Для того, чтобы избежать переполнения стека в данной реализация предусмотрена оптимизация, устраняющая одну ветвь рекурсии: вместо того, чтобы после разделения массива вызывать рекурсивно процедуру разделения для обоих найденных подмассивов, рекурсивный вызов делается только для меньшего подмассива, а больший обрабатывается в цикле в пределах этого же вызова процедуры. С точки зрения эффективности в среднем случае разницы практически нет: накладные расходы на дополнительный рекурсивный вызов и на организацию сравнения длин подмассивов и цикла — примерно одного порядка. Зато глубина рекурсии, ни при каких обстоятельствах не превысит log2n, а в худшем случае вырожденного разделения она вообще будет не более 2 — вся обработка пройдёт в цикле первого уровня рекурсии.
.NET 2.0
Новая реализация претерпела незначительные изменения. Поскольку в .NET 2.0 появились обобщения, то я буду приводить обобщенный вариант сортировки.
public static void Sort<T>(T[] array, int index, int length, IComparer<T> comparer)
{
// TrySZSort все еще быстрее чем обобщенная реализация.
// Причина заключается в том что вызов метода Int32.CompareTo выполняется медленнее чем "<" или ">".
if (length <= 1 || (comparer == null || comparer == Comparer<T>.Default) &&
Array.TrySZSort((Array) array, (Array) null, index, index + length - 1))
return;
ArraySortHelper<T>.Default.Sort(array, index, length, comparer);
}
А вот собственно метод, который сортирует
QuickSort
private static void SwapIfGreaterWithItems(T[] keys, IComparer<T> comparer, int a, int b)
{
if (a == b || comparer.Compare(keys[a], keys[b]) <= 0)
return;
T obj = keys[a];
keys[a] = keys[b];
keys[b] = obj;
}
internal static void QuickSort(T[] keys, int left, int right, IComparer<T> comparer)
{
do
{
int index1 = left;
int index2 = right;
int index3 = index1 + (index2 - index1 >> 1);
ArraySortHelper<T>.SwapIfGreaterWithItems(keys, comparer, index1, index3);
ArraySortHelper<T>.SwapIfGreaterWithItems(keys, comparer, index1, index2);
ArraySortHelper<T>.SwapIfGreaterWithItems(keys, comparer, index3, index2);
T obj1 = keys[index3];
do
{
while (comparer.Compare(keys[index1], obj1) < 0)
++index1;
while (comparer.Compare(obj1, keys[index2]) < 0)
--index2;
if (index1 <= index2)
{
if (index1 < index2)
{
T obj2 = keys[index1];
keys[index1] = keys[index2];
keys[index2] = obj2;
}
++index1;
--index2;
}
else
break;
}
while (index1 <= index2);
if (index2 - left <= right - index1)
{
if (left < index2)
ArraySortHelper<T>.QuickSort(keys, left, index2, comparer);
left = index1;
}
else
{
if (index1 < right)
ArraySortHelper<T>.QuickSort(keys, index1, right, comparer);
right = index2;
}
}
while (left < right);
}
Следует сказать, что оптимизация для встроенных примитивных типов все еще есть, не смотря на наличие обобщений (смотри комментарий разработчиков). То есть примитивные типы по-прежнему используют нативную сортировку.
В качестве опорного элемента теперь берется не середина массива, а медиана из первого, серединного и последнего элементов массива.
int index3 = index1 + (index2 - index1 >> 1); //середина
ArraySortHelper<T>.SwapIfGreaterWithItems(keys, comparer, index1, index3);
ArraySortHelper<T>.SwapIfGreaterWithItems(keys, comparer, index1, index2);
ArraySortHelper<T>.SwapIfGreaterWithItems(keys, comparer, index3, index2);
T obj1 = keys[index3];
К тому же теперь середина вычисляется по формуле index1 + (index2 — index1 >> 1), что исключает ошибок связанных с переполнением.
В остальном все по-прежнему без изменений.
Теперь маленькое отступление: пусть нам надо отсортировать по убыванию массив целых чисел. Как вы будете это делать?
Учитывая все вышесказанное, следующий код
Array.Sort(a);
Array.Reverse(a);
на моем компьютере работает примерно в 3 раза быстрее, чем
Array.Sort(a, (x, y) => -x.CompareTo(y))
Вас может смутить тот факт, что метод Array.Reverse не обобщен, а значит, со значимыми типами будет работать медленно (упаковка и методы GetValue, SetValue), но если взглянуть на его реализацию мы опять увидим оптимизацию для встроенных значимых типов, а именно он вызывает нативный метод Array.TrySZReverse, который выглядит так:
Reverse
template <class KIND>
static void Reverse(KIND array[], UINT32 index, UINT32 count) {
if (count == 0) {
return;
}
UINT32 i = index;
UINT32 j = index + count - 1;
while(i < j) {
KIND temp = array[i];
array[i] = array[j];
array[j] = temp;
i++;
j--;
}
}
};
В общем оптимизации в стандартной библиотеке нас поджидают за каждым углом.
Кстати весьма странно, что нет обобщенной версии данного метода. Есть метод Reverse как метод расширение у Enumerable, но его недостаток в том, что он это делает не на месте. Получается, что вызов Array.Reverse на массиве пользовательских значимых типов всегда приводит к автобоксингу.
.NET 3.0 — .NET 4.0
Алгоритм не претерпел изменений.
.NET 4.5
Самое интересное начинается здесь!
Но прежде чем переходить к рассмотрению алгоритма, надо сказать пару слов о разворачивании .NET 4.5. Для полного понимания ситуации советую прочитать эту статью (к сожалению, на английском). При установке VS 2012, то есть при установки .NET 4.5 она заменяет сборки 4 фреймворка. Фактически это значит, что даже когда вы теперь пишете на .NET 4 вы использует сборки .NET 4.5. Получается интересная вещь: до установки 4.5 вы используете один алгоритм сортировки, после установки вы используете другой алгоритм, причем все происходит без вашего ведома.
Чтобы понять, что собственно происходит, взглянем на код из .NET 4.5:
public void Sort(T[] keys, int index, int length, IComparer<T> comparer)
{
if (BinaryCompatibility.TargetsAtLeast_Desktop_V4_5)
ArraySortHelper<T>.IntrospectiveSort(keys, index, length, comparer);
else
ArraySortHelper<T>.DepthLimitedQuickSort(keys, index, length + index - 1, comparer, 32);
}
Как вы видите, в методе стоит проверка на то, в каком .NET мы работаем: если это 4.5, то мы используем IntrospectiveSort если это 4.0 то DepthLimitedQuickSort.
Давайте выясним чем отличается DepthLimitedQuickSort от сортировки, которая использовалась в .NET 4.0 до установки VS 2012. Взглянем на код этого метода:
DepthLimitedQuickSort
internal static void DepthLimitedQuickSort(T[] keys, int left, int right, IComparer<T> comparer, int depthLimit)
{
while (depthLimit != 0)
{
int index1 = left;
int index2 = right;
int index3 = index1 + (index2 - index1 >> 1);
ArraySortHelper<T>.SwapIfGreater(keys, comparer, index1, index3);
ArraySortHelper<T>.SwapIfGreater(keys, comparer, index1, index2);
ArraySortHelper<T>.SwapIfGreater(keys, comparer, index3, index2);
T obj1 = keys[index3];
do
{
while (comparer.Compare(keys[index1], obj1) < 0)
++index1;
while (comparer.Compare(obj1, keys[index2]) < 0)
--index2;
if (index1 <= index2)
{
if (index1 < index2)
{
T obj2 = keys[index1];
keys[index1] = keys[index2];
keys[index2] = obj2;
}
++index1;
--index2;
}
else
break;
}
while (index1 <= index2);
--depthLimit;
if (index2 - left <= right - index1)
{
if (left < index2)
ArraySortHelper<T>.DepthLimitedQuickSort(keys, left, index2, comparer, depthLimit);
left = index1;
}
else
{
if (index1 < right)
ArraySortHelper<T>.DepthLimitedQuickSort(keys, index1, right, comparer, depthLimit);
right = index2;
}
if (left >= right)
return;
}
ArraySortHelper<T>.Heapsort(keys, left, right, comparer);
}
Как видите это та же быстрая сортировка за исключением одного: алгоритм переключается на пирамидальную сортировку, если мы исчерпаем глубину рекурсии, которая по умолчанию равна 32.
А вот собственно и пирамидальная сортировка:
Heapsort
private static void Heapsort(T[] keys, int lo, int hi, IComparer<T> comparer)
{
int n = hi - lo + 1;
for (int i = n / 2; i >= 1; --i)
ArraySortHelper<T>.DownHeap(keys, i, n, lo, comparer);
for (int index = n; index > 1; --index)
{
ArraySortHelper<T>.Swap(keys, lo, lo + index - 1);
ArraySortHelper<T>.DownHeap(keys, 1, index - 1, lo, comparer);
}
}
private static void DownHeap(T[] keys, int i, int n, int lo, IComparer<T> comparer)
{
T x = keys[lo + i - 1];
for (; i <= n / 2; { int num; i = num;})
{
num = 2 * i;
if (num < n && comparer.Compare(keys[lo + num - 1], keys[lo + num]) < 0)
++num;
if (comparer.Compare(x, keys[lo + num - 1]) < 0)
keys[lo + i - 1] = keys[lo + num - 1];
else
break;
}
keys[lo + i - 1] = x;
}
Алгоритм DepthLimitedQuickSort есть ни что иное как IntroSort.
Introsort или интроспективная сортировка — алгоритм сортировки, предложенный Дэвидом Мюссером в 1997 году. Он использует быструю сортировку и переключается на пирамидальную сортировку, когда глубина рекурсии превысит некоторый заранее установленный уровень. Этот подход сочетает в себе достоинства обоих методов с худшим случаем O(n log n) и быстродействием, сравнимым с быстрой сортировкой. Так как оба алгоритма используют сравнения, этот алгоритм также принадлежит классу сортировок на основе сравнений.
Теперь посмотрим на то, что происходит в IntrospectiveSort. Фактически это та же интроспективная сортировка только более оптимизированная. Кстати, MSDN по-прежнему говорит, что использует быструю сортировку.
IntroSort
private static void IntroSort(T[] keys, int lo, int hi, int depthLimit, IComparer<T> comparer)
{
for (; hi > lo; {int num; hi = num - 1;})
{
int num = hi - lo + 1;
if (num <= 16) //если элементов меньше 16 используем сортировку вставками
{
if (num == 1) //если один элемент
break;
if (num == 2) //если два элемента
{
ArraySortHelper<T>.SwapIfGreater(keys, comparer, lo, hi);
break;
}
else if (num == 3) //если три элемента
{
ArraySortHelper<T>.SwapIfGreater(keys, comparer, lo, hi - 1);
ArraySortHelper<T>.SwapIfGreater(keys, comparer, lo, hi);
ArraySortHelper<T>.SwapIfGreater(keys, comparer, hi - 1, hi);
break;
}
else
{
ArraySortHelper<T>.InsertionSort(keys, lo, hi, comparer); //сортировка вставками
break;
}
}
else if (depthLimit == 0) //если исчерпали глубину рекурсии
{
ArraySortHelper<T>.Heapsort(keys, lo, hi, comparer); //используем пирамидальную сортировку
break;
}
else // иначе используем разбиение быстрой сортировки
{
--depthLimit;
num = ArraySortHelper<T>.PickPivotAndPartition(keys, lo, hi, comparer);
ArraySortHelper<T>.IntroSort(keys, num + 1, hi, depthLimit, comparer);
}
}
}
PickPivotAndPartition
//разбиение массива алгоритмом быстрой сортировки
private static int PickPivotAndPartition(T[] keys, int lo, int hi, IComparer<T> comparer)
{
int index = lo + (hi - lo) / 2;
ArraySortHelper<T>.SwapIfGreater(keys, comparer, lo, index);
ArraySortHelper<T>.SwapIfGreater(keys, comparer, lo, hi);
ArraySortHelper<T>.SwapIfGreater(keys, comparer, index, hi);
T obj = keys[index];
ArraySortHelper<T>.Swap(keys, index, hi - 1);
int i = lo;
int j = hi - 1;
while (i < j)
{
do
;
while (comparer.Compare(keys[++i], obj) < 0);
do
;
while (comparer.Compare(obj, keys[--j]) < 0);
if (i < j)
ArraySortHelper<T>.Swap(keys, i, j);
else
break;
}
ArraySortHelper<T>.Swap(keys, i, hi - 1);
return i;
}
InsertionSort
//сортировка вставками
private static void InsertionSort(T[] keys, int lo, int hi, IComparer<T> comparer)
{
for (int index1 = lo; index1 < hi; ++index1)
{
int index2 = index1;
T x;
for (x = keys[index1 + 1]; index2 >= lo && comparer.Compare(x, keys[index2]) < 0; --index2)
keys[index2 + 1] = keys[index2];
keys[index2 + 1] = x;
}
}
Теперь сортировка в массивах представляет собой смесь сортировок: сортировку вставками, быструю сортировку и пирамидальную сортировку.
Использование Introsort положительно влияет на производительность, поскольку в реальных задачах данные бывают частично упорядочены, а на таких данных, как известно сортировка вставками работает очень быстро.
Сравнение производительности
Сравнение с Java
В плане сортировки Java достаточно сильно отличается от .NET. Однако, как и в .NET в Java алгоритм так же менялся.
Как известно быстрая сортировка является неустойчивой, что является недостатком при сортировке ссылочных типов. Поскольку в Java «всё как бы объекты», то эта проблема усиливается, поэтому для сортировки ссылочных типов используется сортировка слиянием. Данная сортировка является устойчивой и гарантирует O(n logn) времени выполнения в худшем случае, однако и требует O(n) дополнительной памяти.
Поскольку проблема устойчивости касается только ссылочных типов, для примитивов не имеет значения, меняем ли мы элементы с одним ключом или нет. Поэтому для сортировки примитивов Java использует улучшенный алгоритм быстрой сортировки — DualPivotQuicksort. Обычный Quicksort делит массив на два отрезка, выбрав случайный элемент P. Потом сортирует массив так, чтобы все элементы меньше P попали в первый отрезок, а остальные — во второй. Затем алгоритм рекурсивно повторяется на первом и на втором отрезках. DualPivotQuicksort делит массив на три отрезка, вместо двух. В результате количество операций перемещения элементов массива существенно сокращается.
В Java 7 алгоритм сортировки ссылочных типов поменялся на TimSort.
Timsort — гибридный алгоритм сортировки, сочетающий сортировку вставками и сортировку слиянием, опубликованный в 2002 году Тимом Петерсом. В настоящее время Timsort является стандартным алгоритмом сортировки в Python, OpenJDK 7 и реализован в Android JDK 1.5. Основная идея алгоритма в том, что в реальном мире сортируемые массивы данных часто содержат в себе упорядоченные подмассивы. На таких данных Timsort существенно быстрее многих алгоритмов сортировки.
Timsort — быстр, однако на случайных данных уступает примерно на 30 процентов быстрой сортировке.
Что вы думаете об этом различии в реализации сортировки в двух фреймворках? Так ли нам нужна устойчивость в реальных задачах, на которую нужно потратить память, и время как это сделано в Java? Или же можно обойтись без устойчивости, взамен на скорость и экономию памяти как это сделано в .NET? Лично я отдаю свой выбор .NET, потому что думаю, что устойчивость нужна лишь в определенных задачах, которые возникают, не так часто, по крайней мере, у меня за 4 года не возникла ни раз, ну, а если и возникнет то решение таких проблем можно положить на плечи программиста, думаю, его не затруднит реализовать алгоритм устойчивой сортировки.
Заключение
Быть может такие подробности о .NET нужны не каждому программисту, но думаю, их знание не повредит никому. К тому же, изощренные интервьюеры могут задать вопросы о сортировке на собеседовании. В общем, спасибо за прочтение. Надеюсь, статья оказалась полезной.
Приветствую всех, сегодня хочу поговорить о алгоритме сортировки. Сегодня в программировании применяются множество готовых решений метод в этой задачи. Но рассмотреть я хотел бы сами алгоритмы сортировки.
Сортировка пузырьковым методом:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
private static void BubbleSort(int[] array) { for (int i = 0; i < array.Length; i++) for (int j = 0; j < array.Length — 1; j++) if (array[j] > array[j + 1]) { int t = array[j + 1]; array[j + 1] = array[j]; array[j] = t; } } public static void Main() { int[] array = {5,3,4,9,7,2,1,8,6 }; BubbleSort(array); foreach (int e in array) Console.WriteLine(e); Console.ReadKey(); } |
Решил не углубляться в разбор метода, а показать наглядно что происходит внутри метода сортировки. Для этого посмотрим анимацию:
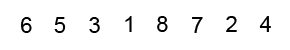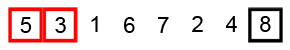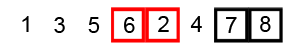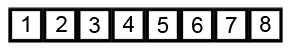
Сортировка слиянием:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 |
static int[] temporaryArray; static void Merge(int[] array, int start, int middle, int end) { var leftPtr = start; var rightPtr = middle + 1; var length = end — start + 1; for (int i = 0; i < length; i++) { if (rightPtr > end || (leftPtr <= middle && array[leftPtr] < array[rightPtr])) { temporaryArray[i] = array[leftPtr]; leftPtr++; } else { temporaryArray[i] = array[rightPtr]; rightPtr++; } } for (int i = 0; i < length; i++) array[i + start] = temporaryArray[i]; } static void MergeSort(int[] array, int start, int end) { if (start == end) return; var middle = (start + end) / 2; MergeSort(array, start, middle); MergeSort(array, middle + 1, end); Merge(array, start, middle, end); } static void MergeSort(int[] array) { temporaryArray = new int[array.Length]; MergeSort(array, 0, array.Length — 1); } public static void Main() { int [] array = {3,2,5,7,8,1,9 }; MergeSort(array); foreach (var e in array) Console.WriteLine(e); Console.ReadKey(); } |
Принцип работы сортировки слияние так же можете увидеть на анимации ниже:
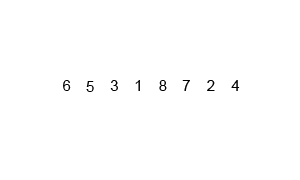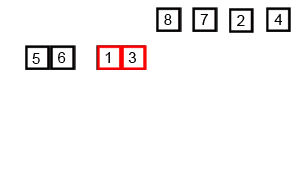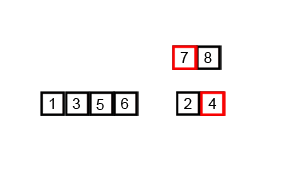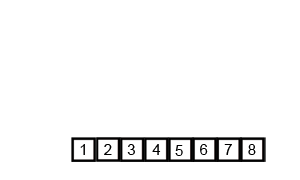
Сортировка Quick-Sort и сортировка Hoare-Sort:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 |
static void HoareSort(int[] array, int start, int end) { if (end == start) return; var pivot = array[end]; var storeIndex = start; for (int i = start; i <= end — 1; i++) if (array[i] <= pivot) { var t = array[i]; array[i] = array[storeIndex]; array[storeIndex] = t; storeIndex++; } var n = array[storeIndex]; array[storeIndex] = array[end]; array[end] = n; if (storeIndex > start) HoareSort(array, start, storeIndex — 1); if (storeIndex < end) HoareSort(array, storeIndex + 1, end); } static void HoareSort(int[] array) { HoareSort(array, 0, array.Length — 1); } static Random random = new Random(); public static void Main() { int [] array = {3,2,5,7,8,1,9 }; HoareSort(array); foreach (var e in array) Console.WriteLine(e); Console.ReadKey(); } |
Еще один пример быстрой сортировки:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 |
class Program { static void Main(string[] args) { int[] i = {4,3,7,23,6,8,123,6,32 }; QuickSort(i,0,8); foreach(int w in i) { Console.WriteLine(w); } Console.ReadKey(); } private static int[] QuickSort(int[] a, int i, int j) { if (i < j) { int q = Partition(a, i, j); a = QuickSort(a, i, q); a = QuickSort(a, q + 1, j); } return a; } private static int Partition(int[] a, int p, int r) { int x = a[p]; int i = p — 1; int j = r + 1; while (true) { do { j—; } while (a[j] > x); do { i++; } while (a[i] < x); if (i < j) { int tmp = a[i]; a[i] = a[j]; a[j] = tmp; } else { return j; } } } } |
Принцип работы сортировки Quick-Sort и сортировка Hoare-Sort так же можете увидеть на анимации ниже:

Существуют:
- алгоритмы сортировки O(n2) вроде сортировки вставками, пузырьком и выбором, которые используются в особых случаях;
- быстрая сортировка (общего назначения): в среднем O(n log n) обменов, но худшее время – O(n2), если массив уже отсортирован, или элементы равны;
- алгоритмы O(n log n), такие как сортировка слиянием и кучей (пирамидальная сортировка), которые также являются хорошими алгоритмами сортировки общего назначения;
- O(n) или линейные алгоритмы сортировки (выбор, выбор с обменом, выбор с подсчетом) для списков целых чисел, которые могут быть подходящими в зависимости от характера целых чисел в ваших списках.
Алгоритм сортировка подсчетом O(n ) C#
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
private static void CountingSort(int[] arr) { int max = arr.Max(); int min = arr.Min(); int[] count = new int[max — min + 1]; int z = 0; for (int i = 0; i < count.Length; i++) { count[i] = 0; } for (int i = 0; i < arr.Length; i++) { count[arr[i] — min]++; } for (int i = min; i <= max; i++) { while (count[i — min]— > 0) { arr[z] = i; z++; } } foreach (var x in arr) { Console.Write(x + » «); } } |
Алгоритм сортировки методом отбора О(n)
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
public static void Sort(int [] a) { int tmp, min_key; for (int j = 0; j < a.Length — 1; j++) { min_key = j; for (int k = j + 1; k < a.Length; k++) { if (a[k] < a[min_key]) { min_key = k; } } tmp = a[min_key]; a[min_key] = a[j]; a[j] = tmp; } for (int i = 0; i < a.Length; i++) { Console.Write(a[i] + » «); } } |
Это конечно не все алгоритмы сортировки описаны мною, их куда больше, однако основные алгоритмы я вам показал. И в конце статьи хочу показать вам последнюю анимацию, которая визуально продемонстрирует принцип всех сортировок, а так же время работы методов по отношению друг к другу.