Как написать свой физический движок - Правописание и грамматика

Время на прочтение
14 мин

Количество просмотров 57K

Приступить к созданию собственного физического движка можно по разными причинам: во-первых, для освоения и усвоения новых знаний в математике, физике и программировании; во-вторых, собственный физический движок может обрабатывать любые технические эффекты, которые сможет создать его автор. В этой вводной статье я расскажу, как создать собственный физический движок с нуля.

Физика даёт игроку потрясающие возможности для погружения в игру. Думаю, что освоение физического движка будет очень полезным умением для любого программиста. Для более глубокого понимания внутренней работы движка можно в любой момент вносить любые оптимизации и специализированные особенности.

В этой части туториала мы рассмотрим следующие темы:

Простое распознавание коллизий
Генерирование простого многообразия
Разрешение импульсов силы

Вот небольшое демо:

Примечание: хоть этот туториал написан на C++, вы сможете использовать те же техники и концепции почти в любой среде разработки игр.

Необходимые знания

Для понимания этой статьи требуется неплохое знание математики и геометрии, и в гораздо меньшей степени — непосредственно программирования. В частности, вам потребуется следующее:

Базовое понимание основ векторной математики
Умение выполнять алгебраические вычисления

Распознавание коллизий

В Интернете достаточно статей и туториалов о распознавании коллизий, поэтому я не буду подробно рассматривать эту тему.

Ограничивающий прямоугольник, выровненный по координатным осям

Ограничивающий прямоугольник, выровненный по координатным осям (Axis Aligned Bounding Box, AABB) — это прямоугольник, четыре оси которого выровнены относительно системы координат, в которой он находится. Это значит, что прямоугольник не может вращаться и всегда находится под углом в 90 градусов (обычно выровнен относительно экрана). Обычно его называют «ограничивающим прямоугольником», потому что AABB используются для ограничения других, более сложных форм.

Пример AABB.

AABB сложной формы можно использовать как простую проверку того, могут ли пересекаться более сложные формы внутри AABB. Однако в случае большинства игр AABB используется как фундаментальная форма и на самом деле ничего не ограничивает. Структура AABB очень важна. Есть несколько способов задания AABB, вот моя любимая:

struct AABB
{
  Vec2 min;
  Vec2 max;
};

Эта форма позволяет задать AABB двумя точками. Точка min обозначает нижние границы по осям x и y, а max обозначает верхние границы — иными словами, они обозначают верхний левый и нижний правый углы. Чтобы определить, пересекаются ли два AABB, необходимо базовое понимание теоремы о разделяющей оси (Separating Axis Theorem, SAT).

Вот быстрая проверка, взятая с сайта Real-Time Collision Detection Кристера Эриксона, в которой используется SAT:

bool AABBvsAABB( AABB a, AABB b )
{
  // Выходим без пересечения, потому что найдена разделяющая ось
  if(a.max.x < b.min.x or a.min.x > b.max.x) return false
  if(a.max.y < b.min.y or a.min.y > b.max.y) return false

  // Разделяющая ось не найдена, поэтому существует по крайней мере одна пересекающая ось
  return true
}

Окружности

Окружность задаётся радиусом и точкой. Вот как может выглядеть структура окружности:

struct Circle
{
  float radius
  Vec position
};

Проверка пересечения двух окружностей очень проста: берём радиусы двух окружностей и складываем их, затем проверяем, больше ли эта сумма расстояния между двумя центрами окружностей.

Важная оптимизация, позволяющая избавиться от оператора квадратного корня:

float Distance( Vec2 a, Vec2 b )
{
  return sqrt( (a.x - b.x)^2 + (a.y - b.y)^2 )
}

bool CirclevsCircleUnoptimized( Circle a, Circle b )
{
  float r = a.radius + b.radius
  return r < Distance( a.position, b.position )
}

bool CirclevsCircleOptimized( Circle a, Circle b )
{
  float r = a.radius + b.radius
  r *= r
  return r < (a.x + b.x)^2 + (a.y + b.y)^2
}

В общем случае умножение — это гораздо менее затратная операция, чем получение квадратного корня значения.

Разрешение импульсов силы

Разрешение импульсов силы — это определённый тип стратегии разрешения коллизий. Разрешение коллизий — это действие, при котором берутся два пересекающихся объекта и изменяются таким образом, чтобы они больше не пересекались.

В общем случае объект в физическом движке имеет три основные степени свободы (в двух измерениях): движение в плоскости xy и вращение. В этой статье мы намеренно ограничили вращение и используем только AABB с окружностями, поэтому единственная степень свободы, которую нам нужно будет рассматривать — это движение в плоскости xy.

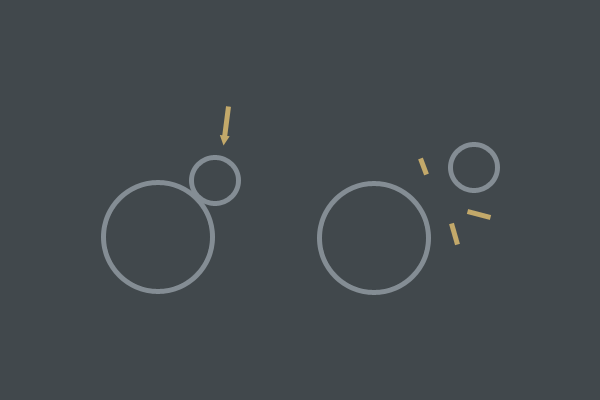
В процессе разрешения обнаруженных коллизий, мы накладываем такие ограничения на движение, чтобы объекты не могли пересекать друг друга. Основная идея разрешения импульсов силы заключается в том, чтобы использовать импульс силы (мгновенное изменение скорости) для разделения объектов, у которых распознаны коллизии. Для этого каким-то образом нужно учитывать положение и скорость каждого из объектов: мы хотим, чтобы большие объекты, пересекающиеся с мелкими, при коллизии перемещались немного, а мелкие объекты отлетали от них. Также мы хотим, чтобы объекты с бесконечной массой не двигались вообще.

Простой пример того, чего можно достичь с помощью разрешения импульсов силы.

Чтобы достигнуть такого эффекта и при этом следовать интуитивному пониманию того, как должны вести себя объекты, мы используем твёрдые тела и немного математики. Твёрдое тело — это просто форма, задаваемая пользователем (то есть вами, разработчиком), которая явно определяется как недеформируемая. И AABB, и окружности в этой статье недеформируемы, и всегда будут являться либо AABB, либо окружностью. Все сжатия и растяжения запрещены.

Работа с твёрдыми телами позволяет очень упростить кучу вычислений. Именно поэтому твёрдые тела часто используют в играх, и поэтому мы используем их в этой статье.

Объекты столкнулись — что дальше?

Предположим, что мы обнаружили столкновение двух тел. Как их разделить? Будем считать, что распознавание коллизий предоставляет нам две важные характеристики:

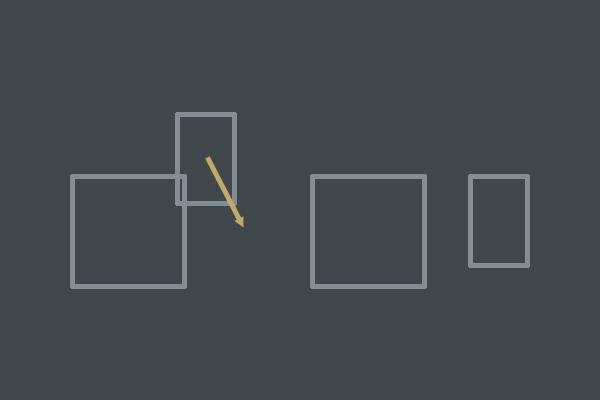
Нормаль коллизии
Глубина проникновения

Чтобы применить импульс силы к обоим объектам и оттолкнуть их друг от друга, нам нужно знать, в каком направлении и насколько их отталкивать. Нормаль коллизии — это направление, в котором будет приложен импульс силы. Глубина проникновения (вместе с некоторыми другими параметрами) определяет, насколько большим будет используемый импульс силы. Это значит, что единственное значение, которое нам нужно вычислить — это величина импульса силы.

Теперь давайте подробно рассмотрим, как же вычислить величину импульса силы. Начнём с двух объектов, для которых обнаружено пересечение:

Уравнение 1

$V^{AB} = V^B - V^A$

Заметьте, что для создания вектора из положения A в положение B необходимо выполнить: endpoint - startpoint. $V^{AB}$ — это относительная скорость из A в B. Это уравнение можно выразить относительно нормали коллизии $n$ , то есть мы хотим узнать относительную скорость из A в B вдоль направления нормали коллизии:

Уравнение 2

$V^{AB} cdot n = (V^B - V^A) cdot n$

Теперь мы используем скалярное произведение. Скалярное произведение — это просто сумма покомпонентных произведений:

Уравнение 3

$V_1 = begin{bmatrix}x_1 \y_1end{bmatrix}, V_2 = begin{bmatrix}x_2 \y_2end{bmatrix} \ V_1 cdot V_2 = x_1 * x_2 + y_2 * y_2$

Следующим шагом будет введение понятия коэффициент упругости. Упругость — это понятие, означающее эластичность. Каждый объект в физическом движке будет иметь упругость, представленное в виде десятичного значения. Однако при вычислении импульса силы будет использоваться только одно десятичное значение.

Чтобы выбрать нужную упругость (обозначаемую как $e$ , «эпсилон»), отвечающую интуитивно ожидаемым результатам, нам следует использовать наименьшую задействованную упругость:

// Два заданных объекта A и B
e = min( A.restitution, B.restitution )

Получив $e$ , мы можем подставить его в уравнение вычисления величины импульса силы.

Ньютоновский закон восстановления гласит следующее:

Уравнение 4

Всё, о чём оно говорит — что скорость после коллизии равна скорости до неё, умноженной на некую константу. Эта константа представляет собой «коэффициент отталкивания». Зная это, легко подставить упругость в наше текущее уравнение:

Уравнение 5

$V^{AB} cdot n = -e * (V^B - V^A) cdot n$

Заметьте, что здесь появилось отрицательное значение. Notice how we introduced a negative sign here. По ньютоновскому закону восстановления $V'$ , результирующий вектор после отталкивания, действительно направляется в обратную сторону от V. Так как же представить противоположные направления в нашем уравнении? Ввести знак «минус».

Теперь нам нужно выразить эти скорости под воздействием импульса силы. Вот простое уравнение для изменения вектора на скаляр импульса силы $j$ в определённом направлении $n$ :

Уравнение 6

Надеюсь, это уравнение вам понятно, потому что оно очень важно. У нас есть единичный вектор $n$ , обозначающий направление. Также у нас есть скаляр $j$ , обозначающий длину вектора $n$ . При суммировании отмасштабированного вектора $n$ с $V$ мы получаем $V'$ . Это просто сложение двух векторов, и мы можем использовать это небольшое уравнение для приложения импульса силы одного вектора к другому.

Здесь нам ещё предстоит проделать небольшую работу. Формально импульс силы определяется как изменение импульса. Импульс — это масса * скорость. Зная это, мы можем выразить импульс в соответствии с формальным определением так:

Уравнение 7

$Impulse = mass * Velocity \ Velocity = frac{Impulse}{mass} therefore V' = V + frac{j * n}{mass}$

Три точки в форме треугольника () можно прочитать как «следовательно». Это обозначение используется для того, чтобы из предшествующего ему вывести истинность последующего.

Мы неплохо двигаемся! Однако нам нужно выразить импульс силы с помощью $j$ относительно двух разных объектов. Во время коллизии объектов A и B объект A отталкивается в противоположном от B направлении:

Уравнение 8

$V'^A = V^A + frac{j * n}{mass^A} \ V'^B = V^B - frac{j * n}{mass^B}$

Эти два уравнения отталкивают A от B вдоль единичного вектора направления $n$ на скаляр импульса силы (величины $n$ ) $j$ .

Всё это нужно для объединения уравнений 8 и 5. Конечное уравнение будет выглядеть примерно так:

Уравнение 9

$(V^A - V^V + frac{j * n}{mass^A} + frac{j * n}{mass^B}) * n = -e * (V^B - V^A) cdot n \ therefore \ (V^A - V^V + frac{j * n}{mass^A} + frac{j * n}{mass^B}) * n + e * (V^B - V^A) cdot n = 0$

Если помните, нашей исходной целью было изолировать величину, потому что мы знаем направление, в котором нужно разрешать коллизию (оно задаётся распознаванием коллизий), и нам осталось только определить величину в этом направлении. В нашем случае неизвестна величина $j$ ; нам нужно выделить $j$ и решить уравнение для неё.

Уравнение 10

$(V^B - V^A) cdot n + j * (frac{j * n}{mass^A} + frac{j * n}{mass^B}) * n + e * (V^B - V^A) cdot n = 0 \ therefore \ (1 + e)((V^B - V^A) cdot n) + j * (frac{j * n}{mass^A} + frac{j * n}{mass^B}) * n = 0 \ therefore \ j = frac{-(1 + e)((V^B - V^A) cdot n)}{frac{1}{mass^A} + frac{1}{mass^B}}$

Ого, довольно много вычислений! Но на этом всё. Важно понимать, что в окончательной форме уравнения 10 слева у нас $j$ (величина), а всё справа нам уже известно. Это значит, что мы можем написать пару строк кода для вычисления скаляра импульса силы $j$ . И этот код гораздо более читаем, чем математическая запись!

void ResolveCollision( Object A, Object B )
{
  // Вычисляем относительную скорость
  Vec2 rv = B.velocity - A.velocity

  // Вычисляем относительную скорость относительно направления нормали
  float velAlongNormal = DotProduct( rv, normal )

  // Не выполняем вычислений, если скорости разделены
  if(velAlongNormal > 0)
    return;

  // Вычисляем упругость
  float e = min( A.restitution, B.restitution)

  // Вычисляем скаляр импульса силы
  float j = -(1 + e) * velAlongNormal
  j /= 1 / A.mass + 1 / B.mass

  // Прикладываем импульс силы
  Vec2 impulse = j * normal
  A.velocity -= 1 / A.mass * impulse
  B.velocity += 1 / B.mass * impulse
}

В этом примере кода нужно заметить два важных аспекта. Во-первых, посмотрите на строку 10, if(VelAlongNormal > 0). Эта проверка очень важна, она гарантирует, что мы разрешаем коллизию, только если объекты движутся друг к другу.

У двух объектов возникла коллизия, но скорость разделит их в следующем кадре. Не разрешаем этот тип коллизии.

Если объекты движутся в противоположные друг от друга стороны, мы ничего не делаем. Благодаря этому мы не будем разрешать коллизии тех объектов, которые на самом деле не сталкиваются. Это важно для создания симуляции, соответствующей интуитивным ожиданиям о том, что должно происходить при взаимодействии объектов.

Во-вторых, стоит заметить, что обратная масса безо всяких причин вычисляется несколько раз. Лучше всего просто сохранить обратную массу внутри каждого объекта и заранее вычислять её одновременно:

A.inv_mass = 1 / A.mass

Во многих физических движках необработанная масса на самом деле не хранится. Часто физические движки хранят только величину, обратную массе. Просто так бывает, что в большинстве математических расчётов используется масса в виде 1/масса.

И последнее, что нужно заметить, что мы должны с умом распределить наш скаляр импульса силы $j$ на два объекта. Мы хотим, чтобы мелкие объекты отлетали от крупных с большей долей $j$ , а скорости больших объектов изменялись на очень небольшую долю $j$ .

Для этого можно сделать следующее:

float mass_sum = A.mass + B.mass
float ratio = A.mass / mass_sum
A.velocity -= ratio * impulse

ratio = B.mass / mass_sum
B.velocity += ratio * impulse

Важно осознавать, что этот код аналогичен приведённому выше примеру функции ResolveCollision(). Как объяснялось выше, обратные массы довольно полезны в физическом движке.

Тонущие объекты

Если мы воспользуемся уже написанным кодом, то объекты будут сталкиваться и отлетать друг от друга. Это отлично, но что случится, если один из объектов имеет бесконечную массу? Нам потребуется удобный способ задания в нашей симуляции бесконечной массы.

Я предлагаю использовать в качестве бесконечной массы ноль — однако если мы попробуем вычислить обратную массу объекта с нулевой массой, мы получим деление на ноль. Решить эту проблему при вычислении обратной массы можно следующим образом:

if(A.mass == 0)
  A.inv_mass = 0
else
  A.inv_mass = 1 / A.mass

Значение «ноль» приведёт к верным вычислениям при разрешении импульсов силы. Это нас устраивает. Проблема тонущих объектов возникает, когда какой-нибудь объект начинает «тонуть» в другом из-за гравитации. Иногда объект с низкой упругостью ударяется о стену с бесконечной массой и начинает тонуть.

Такое утопание возникает из-за ошибок вычислений с плавающей запятой. Во время каждого вычисления с плавающей запятой добавляется небольшая ошибка из-за ограничений оборудования. (Подробнее см. [Floating point error IEEE754] в Google.) Со временем эта ошибка накапливается в ошибку позиционирования, что приводит к утоплению объектов друг в друге.

Для исправления этой ошибки позиционирования необходимо её учитывать, поэтому я покажу вам способ, называемый «линейным проецированием». Линейное проецирование на небольшой процент снижает проникновение двух объектов друг в друга. Оно выполняется после приложения импульса силы. Исправление положения выполняется очень просто: перемещаем каждый объект вдоль нормали коллизии $n$ на процент глубины проникновения:

void PositionalCorrection( Object A, Object B )
{
  const float percent = 0.2 // обычно от 20% до 80%
  Vec2 correction = penetrationDepth / (A.inv_mass + B.inv_mass)) * percent * n
  A.position -= A.inv_mass * correction
  B.position += B.inv_mass * correction
}

Учтите, что мы масштабируем penetrationDepth на общую массу системы. Это даст нам коррекцию положения, пропорциональную величине массы. Мелкие объекты отталкиваются быстрее, чем тяжёлые.

Однако в этой реализации есть небольшая проблема: если мы всегда разрешаем ошибку позиционирования, то объекты всегда будут дрожать, пока они находятся друг на друге. Чтобы устранить дрожание, нужно задать небольшой допуск. Мы будем выполнять корректировку положения только если проникновение выше определённого произвольного порога, который мы назовём «погружением» («slop»):

void PositionalCorrection( Object A, Object B )
{
  const float percent = 0.2 // обычно от 20% до 80%
  const float slop = 0.01 // обычно от 0.01 до 0.1
  Vec2 correction = max( penetration - k_slop, 0.0f ) / (A.inv_mass + B.inv_mass)) * percent * n
  A.position -= A.inv_mass * correction
  B.position += B.inv_mass * correction
}

Это позволит объектам немного проникать друг в друга без задействования коррекции положения.

Генерирование простого многообразия

Последнее, что мы рассмотрим в этой части статьи — генерирование простого многообразия. Многообразие в математике — это что-то вроде «коллекции точек, представляющих собой область пространства». Однако здесь под «многообразнием» я буду понимать небольшой объект, содержащий информацию о коллизии между двумя объектами.

Вот как выглядит объявление стандартного многообразия:

struct Manifold
{
  Object *A;
  Object *B;
  float penetration;
  Vec2 normal;
};

Во время распознавания коллизий необходимо вычислять проникновение и нормаль коллизии. Для определения этой информации необходимо расширить исходные алгоритмы распознавания коллизий из начала статьи.

Окружность-окружность

Давайте начнём с простейшего алгоритма коллизии: коллизия окружность-окружность. Эта проверка в большей степени тривиальна. Можете ли вы представить, каким будет направление разрешения коллизии? Это вектор от окружности A к окружности B. Его можно получить вычитанием положения B из положения A.

Глубина проникновения связана с радиусами окружностей и расстоянием между ними. Наложение окружностей можно вычислить вычитанием из суммы радиусов расстояния до каждого из объектов.

Вот полный пример алгоритма генерирования многообразия коллизии окружность-окружность:

bool CirclevsCircle( Manifold *m )
{
  // Объявление пары указателей на каждый объект
  Object *A = m->A;
  Object *B = m->B;

  // Вектор от A к B
  Vec2 n = B->pos - A->pos

  float r = A->radius + B->radius
  r *= r

  if(n.LengthSquared( ) > r)
    return false

  // У окружностей распознана коллизия, вычисляем многообразие
  float d = n.Length( ) // вычисляем sqrt

  // Если расстояние между окружностями не равно нулю
  if(d != 0)
  {
    // Расстояние - это разность между радиусом и расстоянием
    m->penetration = r - d

    // Используем d, потому что мы уже вычислили sqrt в Length( )
    // Направлен из A в B, и это единичный вектор
    c->normal = t / d
    return true
  }

  // Окружности имеют одинаковое положение
  else
  {
    // Выбираем случайные (но согласованные) значения
    c->penetration = A->radius
    c->normal = Vec( 1, 0 )
    return true
  }
}

Здесь стоит заметить следующее: мы не выполняем вычислений квадратного корня, пока без этого можно обойтись (если у объектов нет коллизии), и мы проверяем, не находятся ли окружности в одной точке. Если они находятся в одной точке, то расстояние будет равно нулю и нужно избежать деления на ноль при вычислении t / d.

AABB-AABB

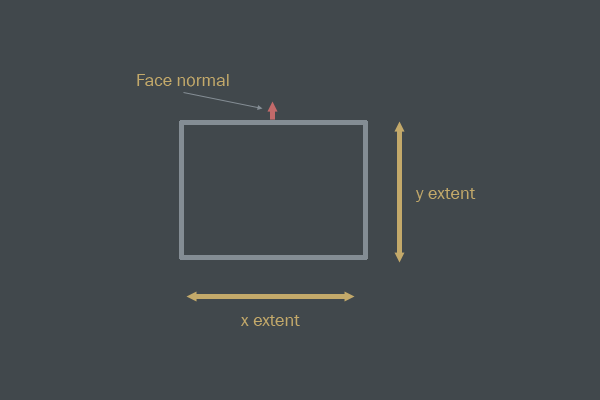
Проверка AABB-AABB немного более сложна, чем окружность-окружность. Нормаль коллизии не будет вектором из A в B, а будет нормалью к ребру. AABB — это прямоугольник с четырьмя рёбрами. Каждое ребро имеет нормаль. Эта нормаль обозначает единичный вектор, перпендикулярный к ребру.

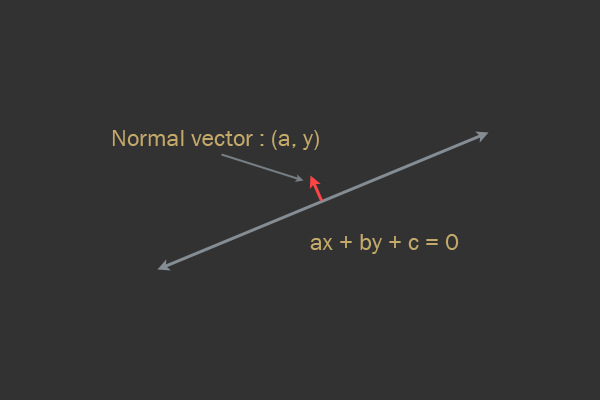
Исследуем общее уравнение прямой в 2D:

$ax + by + c = 0 \ normal = begin{bmatrix}a \bend{bmatrix}$

В уравнении выше a и b — это вектор нормали к прямой, а вектор (a, b) считается нормализованным (длина вектора равна нулю). Нормаль коллизии (направление разрешения коллизии) будет направлена в сторону одной из нормалей рёбер.

Знаете ли вы, что обозначает c в общем уравнении прямой? c — это расстояния до начала координат. Как мы увидим в следующей части статьи, это очень полезно для проверки того, на какой стороне от прямой находится точка.

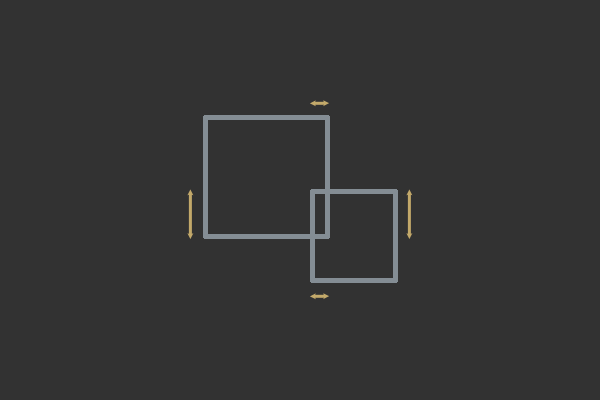
Всё, что теперь нужно — определить, какое из рёбер одного объекта сталкивается с другим объектом, после чего мы получим нормаль. Однако иногда могут пересекаться несколько рёбер двух AABB, например, при пересечении двух углов. Это значит, что нам нужно определить ось наименьшего проникновения.

Две оси проникновения; горизонтальная ось X — ось наименьшего проникновения, поэтому эту коллизию нужно разрешать вдоль оси X.

Вот полный алгоритм генерирования многообразия AABB-AABB и распознавания коллизий:

bool AABBvsAABB( Manifold *m )
{
  // Задание пары указателей для каждого из объектов
  Object *A = m->A
  Object *B = m->B
 
  // Вектор из A в B
  Vec2 n = B->pos - A->pos
 
  AABB abox = A->aabb
  AABB bbox = B->aabb
 
  // Вычисление половины ширины вдоль оси x для каждого объекта
  float a_extent = (abox.max.x - abox.min.x) / 2
  float b_extent = (bbox.max.x - bbox.min.x) / 2
 
  // Вычисление наложения по оси x
  float x_overlap = a_extent + b_extent - abs( n.x )
 
  // Проверка SAT по оси x
  if(x_overlap > 0)
  {
    // Вычисление половины ширины вдоль оси y для каждого объекта
    float a_extent = (abox.max.y - abox.min.y) / 2
    float b_extent = (bbox.max.y - bbox.min.y) / 2
 
    // Вычисление наложения по оси y
    float y_overlap = a_extent + b_extent - abs( n.y )
 
    // Проверка SAT по оси y
    if(y_overlap > 0)
    {
      // Определяем, по какой из осей проникновение наименьшее
      if(x_overlap > y_overlap)
      {
        // Указываем в направлении B, зная, что n указывает в направлении от A к B
        if(n.x < 0)
          m->normal = Vec2( -1, 0 )
        else
          m->normal = Vec2( 0, 0 )
        m->penetration = x_overlap
        return true
      }
      else
      {
        // Указываем в направлении B, зная, что n указывает в направлении от A к B
        if(n.y < 0)
          m->normal = Vec2( 0, -1 )
        else
          m->normal = Vec2( 0, 1 )
        m->penetration = y_overlap
        return true
      }
    }
  }
}

Окружность-AABB

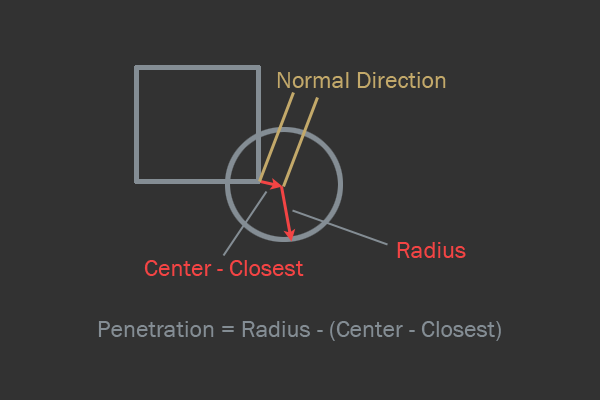
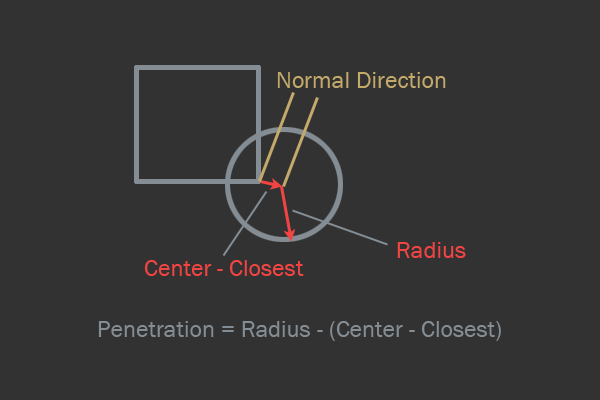
Последняя проверка, которую я рассмотрю — проверка окружность-AABB. Идея здесь заключается в том, чтобы вычислить ближайшую к окружности точку AABB; после этого проверка упрощается до чего-то вроде проверки окружность-окружность. После вычисления ближайшей точки и распознавания коллизий нормаль будет направлением к ближайшей точке из центра окружности. Глубина проникновения — это разность между расстояниями до ближайшей к окружности точки и радиусом окружности.

Схема пересечения AABB-окружность.

Есть один хитрый особый случай — если центр окружности находится внутри AABB, то нужно центр окружности отсечь до ближайшего ребра AABB, а нормаль отразить.

bool AABBvsCircle( Manifold *m )
{
  // Задание пары указателей для каждого из объектов
  Object *A = m->A
  Object *B = m->B

  // Вектор от A к B
  Vec2 n = B->pos - A->pos

  // Ближайшая к центру B точка A
  Vec2 closest = n

  // Вычисление половины ширины вдоль каждой оси
  float x_extent = (A->aabb.max.x - A->aabb.min.x) / 2
  float y_extent = (A->aabb.max.y - A->aabb.min.y) / 2

  // Ограничиваем точку ребром AABB
  closest.x = Clamp( -x_extent, x_extent, closest.x )
  closest.y = Clamp( -y_extent, y_extent, closest.y )

  bool inside = false

  // Окружность внутри AABB, поэтому нам нужно ограничить центр окружности
  // до ближайшего ребра
  if(n == closest)
  {
    inside = true

    // Находим ближайшую ось
    if(abs( n.x ) > abs( n.y ))
    {
      // Отсекаем до ближайшей ширины
      if(closest.x > 0)
        closest.x = x_extent
      else
        closest.x = -x_extent
    }

    // ось y короче
    else
    {
      // Отсекаем до ближайшей ширины
      if(closest.y > 0)
        closest.y = y_extent
      else
        closest.y = -y_extent
    }
  }

  Vec2 normal = n - closest
  real d = normal.LengthSquared( )
  real r = B->radius

  // Если радиус меньше, чем расстояние до ближайшей точки и
  // Окружность не находится внутри AABB
  if(d > r * r && !inside)
    return false

  // Избегаем sqrt, пока он нам не понадобится
  d = sqrt( d )

  // Если окружность была внутри AABB, то нормаль коллизии нужно отобразить
  // в точку снаружи
  if(inside)
  {
    m->normal = -n
    m->penetration = r - d
  }
  else
  {
    m->normal = n
    m->penetration = r - d
  }

  return true
}

Заключение

Надеюсь, теперь вы понимаете немного больше о симуляции физики. Этого туториала будет достаточно, чтобы вы смогли самостоятельно начать создание с нуля собственного физического движка. В следующей части мы рассмотрим все необходимые расширения, необходимые физическому движку, а именно:

Сортировка и отсечение контактных пар
Широкая фаза
Расслоение
Интеграция
Такты
Пересечение полупространств
Модульность (материалы, масса и силы)

Источник

Создаём собственный физический 2D-движок. Часть 1: основы и разрешение импульсов силы +40

Алгоритмы, Математика, Разработка игр

Рекомендация: подборка платных и бесплатных курсов Unity — https://katalog-kursov.ru/

В этой части туториала мы рассмотрим следующие темы:

Простое распознавание коллизий
Генерирование простого многообразия
Разрешение импульсов силы

Вот небольшое демо:

Необходимые знания

Базовое понимание основ векторной математики
Умение выполнять алгебраические вычисления

Распознавание коллизий

Ограничивающий прямоугольник, выровненный по координатным осям

Пример AABB.

struct AABB
{
  Vec2 min;
  Vec2 max;
};

Вот быстрая проверка, взятая с сайта Real-Time Collision Detection Кристера Эриксона, в которой используется SAT:

bool AABBvsAABB( AABB a, AABB b )
{
  // Выходим без пересечения, потому что найдена разделяющая ось
  if(a.max.x < b.min.x or a.min.x > b.max.x) return false
  if(a.max.y < b.min.y or a.min.y > b.max.y) return false

  // Разделяющая ось не найдена, поэтому существует по крайней мере одна пересекающая ось
  return true
}

Окружности

Окружность задаётся радиусом и точкой. Вот как может выглядеть структура окружности:

struct Circle
{
  float radius
  Vec position
};

Важная оптимизация, позволяющая избавиться от оператора квадратного корня:

float Distance( Vec2 a, Vec2 b )
{
  return sqrt( (a.x - b.x)^2 + (a.y - b.y)^2 )
}

bool CirclevsCircleUnoptimized( Circle a, Circle b )
{
  float r = a.radius + b.radius
  return r < Distance( a.position, b.position )
}

bool CirclevsCircleOptimized( Circle a, Circle b )
{
  float r = a.radius + b.radius
  r *= r
  return r < (a.x + b.x)^2 + (a.y + b.y)^2
}

В общем случае умножение — это гораздо менее затратная операция, чем получение квадратного корня значения.

Разрешение импульсов силы

Простой пример того, чего можно достичь с помощью разрешения импульсов силы.

Объекты столкнулись — что дальше?

Нормаль коллизии
Глубина проникновения

Уравнение 1

$V^{AB} = V^B - V^A$

Заметьте, что для создания вектора из положения A в положение B необходимо выполнить: endpoint - startpoint.

$V^{AB}$ — это относительная скорость из A в B. Это уравнение можно выразить относительно нормали коллизии

$n$ , то есть мы хотим узнать относительную скорость из A в B вдоль направления нормали коллизии:

Уравнение 2

$V^{AB} cdot n = (V^B - V^A) cdot n$

Уравнение 3

$V_1 = begin{bmatrix}x_1 \y_1end{bmatrix}, V_2 = begin{bmatrix}x_2 \y_2end{bmatrix} \ V_1 cdot V_2 = x_1 * x_2 + y_2 * y_2$

Чтобы выбрать нужную упругость (обозначаемую как

$e$ , «эпсилон»), отвечающую интуитивно ожидаемым результатам, нам следует использовать наименьшую задействованную упругость:

// Два заданных объекта A и B
e = min( A.restitution, B.restitution )

Получив

$e$ , мы можем подставить его в уравнение вычисления величины импульса силы.

Ньютоновский закон восстановления гласит следующее:

Уравнение 4

Уравнение 5

$V^{AB} cdot n = -e * (V^B - V^A) cdot n$

Заметьте, что здесь появилось отрицательное значение. Notice how we introduced a negative sign here. По ньютоновскому закону восстановления

$V'$ , результирующий вектор после отталкивания, действительно направляется в обратную сторону от V. Так как же представить противоположные направления в нашем уравнении? Ввести знак «минус».

Теперь нам нужно выразить эти скорости под воздействием импульса силы. Вот простое уравнение для изменения вектора на скаляр импульса силы

$j$ в определённом направлении

$n$ :

Уравнение 6

Надеюсь, это уравнение вам понятно, потому что оно очень важно. У нас есть единичный вектор

$n$ , обозначающий направление. Также у нас есть скаляр

$j$ , обозначающий длину вектора

$n$ . При суммировании отмасштабированного вектора

$n$ с

$V$ мы получаем

$V'$ . Это просто сложение двух векторов, и мы можем использовать это небольшое уравнение для приложения импульса силы одного вектора к другому.

Уравнение 7

$Impulse = mass * Velocity \ Velocity = frac{Impulse}{mass} therefore V' = V + frac{j * n}{mass}$

Три точки в форме треугольника (

) можно прочитать как «следовательно». Это обозначение используется для того, чтобы из предшествующего ему вывести истинность последующего.

Мы неплохо двигаемся! Однако нам нужно выразить импульс силы с помощью

$j$ относительно двух разных объектов. Во время коллизии объектов A и B объект A отталкивается в противоположном от B направлении:

Уравнение 8

$V'^A = V^A + frac{j * n}{mass^A} \ V'^B = V^B - frac{j * n}{mass^B}$

Эти два уравнения отталкивают A от B вдоль единичного вектора направления

$n$ на скаляр импульса силы (величины

$n$ )

$j$ .

Всё это нужно для объединения уравнений 8 и 5. Конечное уравнение будет выглядеть примерно так:

Уравнение 9

$(V^A - V^V + frac{j * n}{mass^A} + frac{j * n}{mass^B}) * n = -e * (V^B - V^A) cdot n \ therefore \ (V^A - V^V + frac{j * n}{mass^A} + frac{j * n}{mass^B}) * n + e * (V^B - V^A) cdot n = 0$

$j$ ; нам нужно выделить

$j$ и решить уравнение для неё.

Уравнение 10

Ого, довольно много вычислений! Но на этом всё. Важно понимать, что в окончательной форме уравнения 10 слева у нас

$j$ (величина), а всё справа нам уже известно. Это значит, что мы можем написать пару строк кода для вычисления скаляра импульса силы

$j$ . И этот код гораздо более читаем, чем математическая запись!

void ResolveCollision( Object A, Object B )
{
  // Вычисляем относительную скорость
  Vec2 rv = B.velocity - A.velocity

  // Вычисляем относительную скорость относительно направления нормали
  float velAlongNormal = DotProduct( rv, normal )

  // Не выполняем вычислений, если скорости разделены
  if(velAlongNormal > 0)
    return;

  // Вычисляем упругость
  float e = min( A.restitution, B.restitution)

  // Вычисляем скаляр импульса силы
  float j = -(1 + e) * velAlongNormal
  j /= 1 / A.mass + 1 / B.mass

  // Прикладываем импульс силы
  Vec2 impulse = j * normal
  A.velocity -= 1 / A.mass * impulse
  B.velocity += 1 / B.mass * impulse
}

A.inv_mass = 1 / A.mass

И последнее, что нужно заметить, что мы должны с умом распределить наш скаляр импульса силы

$j$ на два объекта. Мы хотим, чтобы мелкие объекты отлетали от крупных с большей долей

$j$ , а скорости больших объектов изменялись на очень небольшую долю

$j$ .

Для этого можно сделать следующее:

float mass_sum = A.mass + B.mass
float ratio = A.mass / mass_sum
A.velocity -= ratio * impulse

ratio = B.mass / mass_sum
B.velocity += ratio * impulse

Тонущие объекты

if(A.mass == 0)
  A.inv_mass = 0
else
  A.inv_mass = 1 / A.mass

$n$ на процент глубины проникновения:

void PositionalCorrection( Object A, Object B )
{
  const float percent = 0.2 // обычно от 20% до 80%
  Vec2 correction = penetrationDepth / (A.inv_mass + B.inv_mass)) * percent * n
  A.position -= A.inv_mass * correction
  B.position += B.inv_mass * correction
}

void PositionalCorrection( Object A, Object B )
{
  const float percent = 0.2 // обычно от 20% до 80%
  const float slop = 0.01 // обычно от 0.01 до 0.1
  Vec2 correction = max( penetration - k_slop, 0.0f ) / (A.inv_mass + B.inv_mass)) * percent * n
  A.position -= A.inv_mass * correction
  B.position += B.inv_mass * correction
}

Это позволит объектам немного проникать друг в друга без задействования коррекции положения.

Генерирование простого многообразия

Вот как выглядит объявление стандартного многообразия:

struct Manifold
{
  Object *A;
  Object *B;
  float penetration;
  Vec2 normal;
};

Окружность-окружность

Вот полный пример алгоритма генерирования многообразия коллизии окружность-окружность:

bool CirclevsCircle( Manifold *m )
{
  // Объявление пары указателей на каждый объект
  Object *A = m->A;
  Object *B = m->B;

  // Вектор от A к B
  Vec2 n = B->pos - A->pos

  float r = A->radius + B->radius
  r *= r

  if(n.LengthSquared( ) > r)
    return false

  // У окружностей распознана коллизия, вычисляем многообразие
  float d = n.Length( ) // вычисляем sqrt

  // Если расстояние между окружностями не равно нулю
  if(d != 0)
  {
    // Расстояние - это разность между радиусом и расстоянием
    m->penetration = r - d

    // Используем d, потому что мы уже вычислили sqrt в Length( )
    // Направлен из A в B, и это единичный вектор
    c->normal = t / d
    return true
  }

  // Окружности имеют одинаковое положение
  else
  {
    // Выбираем случайные (но согласованные) значения
    c->penetration = A->radius
    c->normal = Vec( 1, 0 )
    return true
  }
}

AABB-AABB

Исследуем общее уравнение прямой в 2D:

$ax + by + c = 0 \ normal = begin{bmatrix}a \bend{bmatrix}$

Вот полный алгоритм генерирования многообразия AABB-AABB и распознавания коллизий:

bool AABBvsAABB( Manifold *m )
{
  // Задание пары указателей для каждого из объектов
  Object *A = m->A
  Object *B = m->B
 
  // Вектор из A в B
  Vec2 n = B->pos - A->pos
 
  AABB abox = A->aabb
  AABB bbox = B->aabb
 
  // Вычисление половины ширины вдоль оси x для каждого объекта
  float a_extent = (abox.max.x - abox.min.x) / 2
  float b_extent = (bbox.max.x - bbox.min.x) / 2
 
  // Вычисление наложения по оси x
  float x_overlap = a_extent + b_extent - abs( n.x )
 
  // Проверка SAT по оси x
  if(x_overlap > 0)
  {
    // Вычисление половины ширины вдоль оси y для каждого объекта
    float a_extent = (abox.max.y - abox.min.y) / 2
    float b_extent = (bbox.max.y - bbox.min.y) / 2
 
    // Вычисление наложения по оси y
    float y_overlap = a_extent + b_extent - abs( n.y )
 
    // Проверка SAT по оси y
    if(y_overlap > 0)
    {
      // Определяем, по какой из осей проникновение наименьшее
      if(x_overlap > y_overlap)
      {
        // Указываем в направлении B, зная, что n указывает в направлении от A к B
        if(n.x < 0)
          m->normal = Vec2( -1, 0 )
        else
          m->normal = Vec2( 0, 0 )
        m->penetration = x_overlap
        return true
      }
      else
      {
        // Указываем в направлении B, зная, что n указывает в направлении от A к B
        if(n.y < 0)
          m->normal = Vec2( 0, -1 )
        else
          m->normal = Vec2( 0, 1 )
        m->penetration = y_overlap
        return true
      }
    }
  }
}

Окружность-AABB

Схема пересечения AABB-окружность.

bool AABBvsCircle( Manifold *m )
{
  // Задание пары указателей для каждого из объектов
  Object *A = m->A
  Object *B = m->B

  // Вектор от A к B
  Vec2 n = B->pos - A->pos

  // Ближайшая к центру B точка A
  Vec2 closest = n

  // Вычисление половины ширины вдоль каждой оси
  float x_extent = (A->aabb.max.x - A->aabb.min.x) / 2
  float y_extent = (A->aabb.max.y - A->aabb.min.y) / 2

  // Ограничиваем точку ребром AABB
  closest.x = Clamp( -x_extent, x_extent, closest.x )
  closest.y = Clamp( -y_extent, y_extent, closest.y )

  bool inside = false

  // Окружность внутри AABB, поэтому нам нужно ограничить центр окружности
  // до ближайшего ребра
  if(n == closest)
  {
    inside = true

    // Находим ближайшую ось
    if(abs( n.x ) > abs( n.y ))
    {
      // Отсекаем до ближайшей ширины
      if(closest.x > 0)
        closest.x = x_extent
      else
        closest.x = -x_extent
    }

    // ось y короче
    else
    {
      // Отсекаем до ближайшей ширины
      if(closest.y > 0)
        closest.y = y_extent
      else
        closest.y = -y_extent
    }
  }

  Vec2 normal = n - closest
  real d = normal.LengthSquared( )
  real r = B->radius

  // Если радиус меньше, чем расстояние до ближайшей точки и
  // Окружность не находится внутри AABB
  if(d > r * r && !inside)
    return false

  // Избегаем sqrt, пока он нам не понадобится
  d = sqrt( d )

  // Если окружность была внутри AABB, то нормаль коллизии нужно отобразить
  // в точку снаружи
  if(inside)
  {
    m->normal = -n
    m->penetration = r - d
  }
  else
  {
    m->normal = n
    m->penetration = r - d
  }

  return true
}

Заключение

Сортировка и отсечение контактных пар
Широкая фаза
Расслоение
Интеграция
Такты
Пересечение полупространств
Модульность (материалы, масса и силы)

Источник

Привет дорогой друг! В прошлой статье я говорил, что больше не буду затрагивать тему 2D игр на XNA. Пожалуй, я вас обманул, но не совсем. Многие начинающие геймдевелоперы используют в своих физических головоломках — физический движок Box2D, о нем довольно много писали на хабре. Да что уж там новички, многие довольно опытные геймдевелоперы — его используют. Но вот мало кто знает, как на самом деле он работает. Остальное под хабракатом.

В этой статье я постараюсь подробно описать процесс создания каркаса физического движка. Конечно, получиться не совсем Box2D: различные хеш оптимизации, отсечения не будут описываться в данной статье, но будет понятно, как он работает.

Общие принципы. Как это вообще работает?

Обычное игровое приложение каждый кадр выполняет примерно такую последовательность действий:

Воздействуем на физический мир
Обновляем физический мир
Отрисовываем его новое состояние
Повторяем

Самый интересный для нас шаг в этой схеме — второй. Именно здесь и происходит вся магия физического движка — он определяет, в какое состояние перейдёт физическая система в следующий момент времени, спустя dt (короткий промежуток времени). Этот шаг, в свою очередь, уже внутри движка разбивается ещё на три подшага:

Обнаружение столкновений
Разрешение столкновений
Интегририрование

И вот именно их мы и будем реализовывать. Эти действия в существенной степени независимы и, реализовав их, мы получаем нехитрый физический движок.

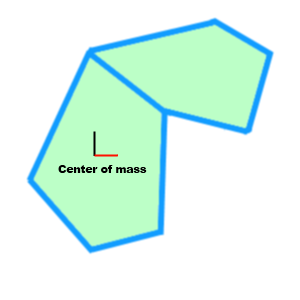
Начнем с устройства физического движка, который мы будем писать. Наша цель — написать физику твердых тел на основе импульсов. В идеале нам хотелось бы, чтоб тело могло быть любой формы, т.е., например, такой:

На самом деле описать такую форму довольно сложно, и движки, работающие на «невыпуклых» формах, найти очень сложно, не говоря уже о 3D. Поэтому мы создадим такую систему, что тело можно будет представить любой сложной формой с помощью простых форм.

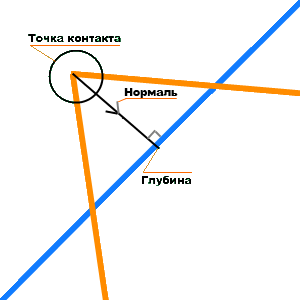
Теперь разъясню составляющие физического тела. Само «тело» в нашем движке будет просто точка, имеющая центр масс. Эта точка будет перемещаться под действием различных сил, например, гравитации. Вокруг нее (точки) могут быть «навешаны» формы. В данной статье будут рассмотрены формы выпуклых полилиний (полигонов). После прочтения статьи — вы можете добавить и свои шейпы (формы), например, различные квадратики и кружечки. При процессинге (обработке физических тел в Update) мы будем искать шейпы, которые пересеклись, т.е. «сколизились» (collision — англ., пересечение), затем искать три основных необходимых для минимального импульсного физического движка величины, это — нормаль, вдоль которой произошла коллизия, глубину проникновения одного объекта в другой и точку контакта тел.

Допустим, имеем контакт:

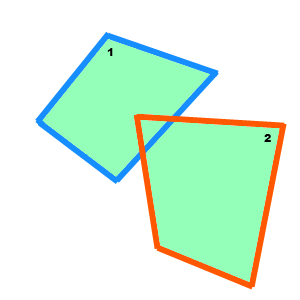
А вот коллизия двух выпуклых полилиний:

Выпуклость полилиний упрощает нам задачу поиска коллизии. Тело должно иметь массу, момент инерции, линейную и угловую скорости, линейное и угловое ускорение, позицию в мировом пространстве (координаты центра масс), коэффициенты трения и упругости, а также текущий угол поворота.

С теорией пока все, начнем реализовывать. Сразу оговорюсь, что я покажу три основных класса и дам максимально развернутую информацию по ним в виде комментариев.

Т.к. в XNA многие операции над векторами у нас уже есть — мы его просто расширим, листинг расширяющегося класса:

namespace phys.V2Math
{
    public static class V2Extend
    {
        public static float PerpDot(this Vector2 self, Vector2 vector) // перпендикуляр с скалярным произведением
        {
            return self.X * vector.Y - self.Y * vector.X;
        }

        public static Vector2 Perp(this Vector2 self) // перпендикуляр
        {
            return new Vector2(-self.Y, self.X);
        }

        public static float Dot(this Vector2 self, Vector2 vector) // скалярное произведение
        {
            return self.X * vector.X + self.Y * vector.Y;
        }

        public static Vector2 Negative(this Vector2 self) // отрицательный вектор
        {
            return new Vector2(-self.X, -self.Y);
        }

        public static Vector2 Rotate(this Vector2 self, Vector2 vector) // вращение вектора
        {
            return new Vector2(self.X * vector.X - self.Y * vector.Y, self.X * vector.Y + self.Y * vector.X);
        }

        public static Vector2 Normalize2(this Vector2 self) // нормирование вектора
        {
            Vector2 vector = self;
            vector.Normalize();
            return vector;
        }
    }
}

Теперь нам нужен класс, который будет отвечать за сами объекты тел, создадим его:

namespace phys
{
    public class Body
    {
        public Vector2 position; // позиция
        public Vector2 velocity; // ускорение
        public float angle;   // текущий угол в радианах
        public float w;   // угловое ускорение в радианах
        public float m;   // масса
        public float f;   // трение
        public float e;   // упругость
        public bool isStatic;  // статичный ли объект

        internal float i;   // момент инерции

        public List<Poly> shapes; // формы данного тела

        // функция накладывает импульс на тело
        // j - импульс (вектор)
        // r - точка приложения импульса в локальных координатах
        public void ApplyImpulse(Vector2 j, Vector2 r)
        {
            if (isStatic)
                return;

            velocity += j / m;
            w += r.PerpDot(j) / i;
        }

        
    }
}

Саму интерацию (движения тела, поворот тела, etc) мы будем просчитывать в другом классе, который будет ответственен за физику в целом, назовем этот класс: «World«.

Этот класс в себе будет хранить список тел, будет содержать метод step, который и будет у нас за все отвечать. Рассмотрим класс:

namespace phys
{
    public class World
    {
        public static float c_Depth = 0.1f;
       
        public Vector2 gravity;
        public List<Body> bodies;

        public World(Vector2 gravity)
        {
            this.gravity = gravity;
            bodies = new List<Body>();
        }

        public void CreateDemo() // создаем демо-сцену
        {
            ...
        }

        public Body Body2;
        public Body sBody;

        //Обновляем позицию, ускорение и угол тела за промежуток
        // времени dt и гравитацией gravity, действующей на тело
        // в нормальной среде (вакум)
 
        public void Step(float delta, int interations)
        {
            float dt = delta / (float)interations;

            for (int interation = 0; interation < interations; interation++)
            {
                
                foreach (Body body in bodies)
                {
                    if (!body.isStatic)
                        body.velocity += gravity * dt;        // добавляем гравитацию

                    body.angle += body.w * dt;            // обновляем угол поворота
                    body.position += body.velocity * dt;  // обновляем позицию тела

                    foreach (Poly poly in body.shapes)
                    {
                        // вычисляем кос и син угла поворота тела
                        poly.rot = new Vector2((float)Math.Cos(poly.body.angle), (float)Math.Sin(poly.body.angle));

                        for (int i = 0; i < poly.VertexsCount; i++)
                        {
                            // находим координаты вершин (мировые)
                            poly.v[i] = poly.body.position + poly.v_base[i].Rotate(poly.rot);

                            // нормаль и скаляр для ребер
                            poly.ed[i].n = poly.ed_base[i].n.Rotate(poly.rot);
                            poly.ed[i].d = poly.body.position.Dot(poly.ed[i].n) + poly.ed_base[i].d;
                        }

                        poly.broadphase = Poly.GetBroadphase(poly);
                    }
                }

                foreach (Body body1 in bodies)
                    foreach (Body body2 in bodies)
                    {
                        if (body1 != body2)
                        {
                            bool collided = false;

                            foreach (Poly poly1 in body1.shapes)
                            {
                                foreach (Poly poly2 in body2.shapes)
                                    if (Broadphase.Collided(poly1.broadphase, poly2.broadphase))
                                    {
                                        Collide(body1, body2);
                                        collided = true;
                                        break;
                                    }

                                if (collided)
                                    break;

                            }
                            
                        }
                    }
            }
        }

        public bool Collide(Body b1, Body b2)
        {
            foreach (Poly poly1 in b1.shapes)
                foreach (Poly poly2 in b2.shapes)
                    if (Poly.FindCollision(poly1, poly2))
                        return true;

            return false;
        }

        public IEnumerable<DebugLine> getDebugLines() // получем линии для отрисовки объектов
        {
		...
        }
}

Теперь рассмотрим код шейпа (Poly):

namespace phys
{
    public class Poly
    {
        public Vector2[] v;           // мировые координаты вершин
        public Vector2[] v_base;       // локальные координаты вершин

        public Edge[] ed;          // мировые данные о гранях
        public Edge[] ed_base;      // локальные данные о гранях
        public Broadphase broadphase;

        public int VertexsCount
        {
            get { return v_base.Length; }   
        }

        public Vector2 rot;    // коссин для поворота вершин
        public Body body;

        public Poly(Body body, Vector2[] vertexs)
        {
            Vector2 a, b;
            
            this.body = body;

            // копируем вершины
            this.v_base = vertexs;
            this.v = new Vector2[VertexsCount];
            this.ed = new Edge[VertexsCount];
            this.ed_base = new Edge[VertexsCount];

            // подсчитываем нормаль и скаляр к ребрам (возможно тут нужен фикс)
            for(int i = 0; i < this.VertexsCount; i++)
            {
                a = this.v_base[i];
                b = this.v_base[((i+1) % VertexsCount)];

                Vector2 someRENAME = ((Vector2)(b - a)).Perp();

                this.ed_base[i].n = someRENAME.Normalize2();
                this.ed_base[i].d = this.ed_base[i].n.Dot(a);
            }


            // присоединяем форму к телу
       
            body.shapes.Add(this);

            Poly poly = this;

            // вычисляем кос и син угла поворота тела
            poly.rot = new Vector2((float)Math.Cos(poly.body.angle), (float)Math.Sin(poly.body.angle));


            for (int i = 0; i < poly.VertexsCount; i++)
            {
                // находим координаты вершин (мировые)
                poly.v[i] = poly.body.position + poly.v_base[i].Rotate(poly.rot);

                // нормаль и скаляр для ребер
                poly.ed[i].n = poly.ed_base[i].n.Rotate(poly.rot);
                poly.ed[i].d = poly.body.position.Dot(poly.ed[i].n) + poly.ed_base[i].d;
            }

            broadphase = Poly.GetBroadphase(this);
        }

        /*
         * Вычисление момента инерции полигона.
         * m-масса тела, verts-вершины полигона, nVerts-их количество
         * Момент инерции всего тела равен сумме моментов инерции всех его форм.
         */

        public float IMoment()
        {
            float sum1, a, b, sum2;
            Vector2 v1, v2;

            sum1 = 0;
            sum2 = 0;

            for (int i = 0; i < VertexsCount; i++)
            {
                v1 = v_base[i];
                v2 = v_base[(i + 1) % VertexsCount];

                a = (v2.X * v1.Y) - (v2.Y * v1.X);
                b = v1.Dot(v1) + v1.Dot(v2) + v2.Dot(v2);

                sum1 += a * b;
                sum2 += a;
            }

            return (body.m * sum1) / (6.0f * sum2);
        }

        /* Суть метода такова: есть процесс, мы его сначала просчитываем от первого полигона в отношении второго,
         * затем наоборот - от второго в отношении первого.
         * Суть процесса заключается в поиске точек одного полигона (суть видно на рисунке в начале статьи, где иллюстрирован контакт двух полигонов),
         * которые лежат внутри второго полигона, если такие точки есть - полилинии пересеклись,
         * причем эта точка и будет точкой контакта.
         * Далее ищем ближайшее к данной точке ребро второго полигона, нормаль к этому ребру и будет нормаль контакта,
         * а расстояние от данной точки до данного ребра и есть глубина проникновения.
         * Таким образом, все три необходимых данных у нас есть,
         * заносим их в структуру контакта и передаем обработчику импульсов тел.
         * А затем выталкиваем тела по нормали, в противоположные стороны для каждого тела, на расстояние,
         * равное половине глубины проникновения.
         * Допустим, мы нашли пересечение полилиний, т.е. одна из точек первого полигона зашла внутрь второго. Напишем функции поиска ближайшего к данной точке ребра.
         * Скалярное произведение векторов хранит их длины, этим и воспользуемся: чем меньше величина скалярного произведения от ребра до точки,
         * тем ближе последняя к нему находится.
         * Функция ищет ближайшее ребро к данной точке.
         */

        public static float EdgeDist(Poly poly, Vector2 n, float d)
        {
            float _m = n.Dot(poly.v[0]);

            for (int i = 1; i < poly.VertexsCount; i++)
                _m = Math.Min(_m, n.Dot(poly.v[i]));

            return _m - d;
        }

        // Находим минимальное расстояние между ребром и точкой полигона
        public static int FindEdgeMinDist(Poly poly, Edge[] ed, int num, ref float _m)
        {
            int _mi = 0;
            float __m, dist;

            __m = Poly.EdgeDist(poly, ed[0].n, ed[0].d);
            if (__m > 0f)
                return -1;

            for (int i = 0; i < num; i++)
            {
                dist = Poly.EdgeDist(poly, ed[i].n, ed[i].d);
                if (dist > 0f)
                    return -1;
                else if (dist > __m)
                {
                    __m = dist;
                    _mi = i;
                }
            }
            _m = __m;
            return _mi;
        }

        // находим какая точка лежит внутри полика
        public static bool PointIn(Poly poly, Vector2 p)
        {
            float dist;

            for (int i = 0; i < poly.VertexsCount; i++)
            {
                dist = poly.ed[i].n.Dot(p) - poly.ed[i].d;
                if (dist > 0f)
                    return false;
            }

            return true;
        }

        /* Ищем точки взаимопроникновения, самая главная функция нашего движка, в ней мы ищем,
         * какими точками полигоны проникли друг в друга, и если проникли,
         * то ищем все необходимые данные для контакта и отправляем на обработку.
         */
        public static void VertsProc(Poly p1, Poly p2, Vector2 n, float d)
        {
            float k;
            // используем абсолютное значение глубины
            d = Math.Abs(d);

            // сначала ищем точки первого полигона внутри второго
            for (int i = 0; i < p1.VertexsCount; i++)
                if (Poly.PointIn(p2, p1.v[i])) // если нашли, то заполняем данные контакта:
                {

                    Contact contact = new Contact();
                    contact.p = p1.v[i];        // точка контакта и есть данная вершина
                    contact.n = n;              // нормаль мы получили из вызывающей функции
                    contact.depth = d * World.c_Depth;  // глубину получили таким ж способом
                    contact.r1 = contact.p - p1.body.position;  // вспомогательные вектора, направлены из // точки контакта в центр масс каждого тела
                    contact.r2 = contact.p - p2.body.position;

                    // далее считаем коэффициент выталкивания тел,
                    // в зависимости от их состояния(статичный или нет)
                    if (p1.body.isStatic)
                        k = 0f;
                    else if (p2.body.isStatic)
                        k = 1f;
                    else k = 0.5f;

                    // расталкиваем тела по нормали в разные стороны на глубину проникновения
                    // учитывая что нормаль направлена относительно 1 тела ко 2
                    p1.body.position -= contact.n * (k * contact.depth);
                    p2.body.position += contact.n * ((1 - k) * contact.depth);

                    // после того, как нашли все данные отправляем их на обработку
                    contact.Solve(p1.body, p2.body);
                }
        }

        /* Далее - функция, которая ищет факт пересечения полигонов (на основе предыдущей функции)
         * и в случае успеха будет вызывать нашу главную функцию поиска точек контакта
         * и передавать ей в качестве параметров найденное ближайшее ребро (а следовательно, и все его данные).
         */
        public static bool FindCollision(Poly p1, Poly p2)
        {
            float min1 = 0f;
            float min2 = 0f;

            int min1_idx, min2_idx;

            min1_idx = Poly.FindEdgeMinDist(p2, p1.ed, p1.VertexsCount, ref min1);
	        if (min1_idx == -1)
                return false;

	        min2_idx = Poly.FindEdgeMinDist(p1, p2.ed, p2.VertexsCount, ref min2);
            if (min2_idx == -1)
	            return false;
            
             if (min1 > min2)
                Poly.VertsProc(p1, p2, p1.ed[min1_idx].n, min1);
                    else
                        Poly.VertsProc(p1, p2, p2.ed[min2_idx].n.Negative(), min2);

            return true;
        }

        public static Broadphase GetBroadphase(Poly poly)
        {
            ...
        }
    }
}

Теперь нужно решить проблему просчета контактов, реализуем класс Contact и метод Solve:

namespace phys
{
    public class Contact
    {
        public Vector2 p;  // координаты точки пересечения 
        public Vector2 n;  // нормаль относительно 1 тела к 2
        public Vector2 r1;  // вектор из 1 тела в точку контакта
        public Vector2 r2;  // вектор из 2 тела в точку контакта
        public float depth; // глубина проникновения 

        // Решаем контакт
        public void Solve(Body c1, Body c2)
        {
            Vector2 v1, v2, vr, t, j;
            float vrn, jn, jnOld, bounce, e, u, mass_sum,
            r1cn, r2cn, vrt, kn, nMass, jtMax, jt, jtOld,
            r1ct, r2ct, kt, tMass, jnAcc, jtAcc;

	     // у статических тел — масса и инерция бесконечны
            float m1 = c1.isStatic ? float.PositiveInfinity : c1.m;
            float m2 = c2.isStatic ? float.PositiveInfinity : c2.m;
            float i1 = c1.isStatic ? float.PositiveInfinity : c1.i;
            float i2 = c2.isStatic ? float.PositiveInfinity : c2.i;

            e = c1.e * c2.e;    // вычисляем общий коэффициент трения поверхностей
            u = c1.f * c2.f;  // и общий коэффициент эластичности

            // {расчет общих коэффициентов может быть другой, например средний арифметический (c1^.f+c2^.f)/2.0}
            jtAcc = 0.0f;
            jnAcc = 0.0f;

            v1 = c1.velocity + (r1.Perp() * c1.w);
            v2 = c2.velocity + (r2.Perp() * c2.w);

            vr = v2 - v1;
            vrn = vr.Dot(n);

            bounce = n.Dot(v2 - v1) * e;
            mass_sum = (1f / m1) + (1f / m2);
            r1cn = r1.PerpDot(n);
            r2cn = r2.PerpDot(n);

            kn = mass_sum + ((r1cn * r1cn) / i1) + ((r2cn * r2cn) / i2);
            nMass = 1.0f / kn;

            jn = -(bounce + vrn) * nMass;

            jnOld = jnAcc;
            jnAcc = Math.Max(jnOld + jn, 0.0f);

            jn = jnAcc - jnOld;
            t = n.Perp();

            vrt = vr.Dot(t); // (0,0)
            t = n.Perp();

            r1ct = r1.PerpDot(t);
            r2ct = r2.PerpDot(t);

            kt = mass_sum + ((r1cn * r1cn) / i1) + ((r2cn * r2cn) / i2);
            tMass = 1.0f / kt;

            // трение
            jtMax = u * jnAcc;
            jt = -vrt * tMass;
            jtOld = jtAcc;
            jtAcc = Math.Min(Math.Max(jtOld + jt, -jtMax), jtMax);
            jt = jtAcc - jtOld;
            j = (n * jn) + (t * jt);

            // накладываем импульсы
            c1.ApplyImpulse(j.Negative(), r1);
            c2.ApplyImpulse(j, r2);
        }
    }
}

Кодом я старался описать основные принципы работы импульсных движков, более разверенуто можно посмотреть все исходном коде.

Итак, подведем итоги. Очевидно, что написать физический движок на основе импульсов в 2D не так сложно, как может показаться на первый взгляд. Удачи в начинаниях!

Исходный код можно скачать тут, а exe-демо тут.

P.S. огромная просьба, об очепятках/ошибках писать мне личным сообщением, не стоит писать комментарии без полезной смысловой нагрузки.

P.S.S. правильность и скорость кода не претендует на что-либо, код изложен только в обучающих целях.

P.S.S.S. если вы хотите, чтобы я осветил одну из тем, связанных с геймдевом — рад видеть вас в личных сообщениях.

Автор: ForhaxeD

Источник

Есть много причин, вы, возможно, захотите, чтобы создать настраиваемый физический движок: во-первых, изучая и оттачивая свои навыки в области математики, физики и программирования больших причин для попыток такого проекта; во-вторых, настраиваемый физический движок может решить какой-либо технический эффект творец обладает умением создать. В этой статье я хотел бы обеспечить наилучшее представление о том, как создать пользовательский полностью физический движок с нуля.

Физика служит прекрасным средством, который позволяет игроку полностью окунуться в игру. Это имеет смысл, что овладение физический движок будет мощным активом для любого программиста, чтобы иметь в своем распоряжении. Оптимизации и специализации могут быть сделаны в любое время за счет глубокого понимания внутренней работы физического движка.

К концу этого учебника в следующих разделах будут покрыты, в двух измерениях:

Простое обнаружение столкновений
Простой коллектор поколения
Разрешение импульс

Вот краткий демо:

Примечание: хотя этот учебник написан на C++, вы должны быть в состоянии использовать те же методы и концепции практически в любой среде разработки.

Предпосылки

Эта статья включает достаточно большое количество математики и геометрии, и в гораздо меньшей степени фактического кодирования. Пару предпосылок для этой статьи являются:

Базовое понимание простой векторной математики
Умение выполнять алгебраические математика

Обнаружение Столкновений

Есть немало статей и руководств по всему интернету, в том числе и здесь на Tuts+, которые охватывают обнаружения столкновений. Зная это, я хотел бы пробежаться по теме очень быстро, так как этот участок не является темой этой статьи.

Оси Выровнены Ограничивающих Прямоугольников

Оси выровнены прямоугольника (ААВВ) — это окно, которое имеет четыре оси совмещена с системой координат, в которой он проживает. Это означает, что это поле, которое не может вращаться, и всегда квадрат на 90 градусов (обычно выравнивается с экрана). В целом это называется «прямоугольник», потому что AABBs используются для связаны другие, более сложные формы.

Пример ААВВ.

ААВВ сложной формы можно использовать как простой тест, чтобы увидеть, если более сложные формы внутри AABBs может быть пересекающимися. Однако в случае большинства игр ААВВ используется в качестве фундаментальной формы, и на самом деле не связаны что-либо другое. Структура ААВВ важно. Есть несколько различных способов, чтобы представлять ААВВ, однако это мое любимое:

struct AABB
{
  Vec2 min;
  Vec2 max;
};

Эта форма позволяет ААВВ быть представлены две точки. Минимальная точка представляет собой нижнюю границы X и оси Y, и Макс представляет собой верхние пределы — иными словами, они представляют собой верхний левый и нижний правый углы. Для того, чтобы сказать, являются ли два ААВВ формы пересекающихся необходимо иметь базовое понимание разделения Теорема оси (СБ).

Вот быстрый тест, взятый из реального времени обнаружение столкновений Кристер Эриксон, которая позволяет использовать в сб.:

bool AABBvsAABB( AABB a, AABB b )
{
  // Exit with no intersection if found separated along an axis
  if(a.max.x < b.min.x or a.min.x > b.max.x) return false
  if(a.max.y < b.min.y or a.min.y > b.max.y) return false

  // No separating axis found, therefor there is at least one overlapping axis
  return true
}

Круги

Круг представляет собой радиус и точка. Вот то, что ваша структура круг должен выглядеть так:

struct Circle
{
  float radius
  Vec position
};

Тестирование на Ли две окружности пересекаются очень просто: взять радиусы двух окружностей и добавить их вместе, а затем проверить, чтобы увидеть, если эта сумма больше, чем расстояние между двумя кругами.

Важным оптимизации, чтобы сделать здесь, это избавиться от необходимости использования оператора квадратного корня:

float Distance( Vec2 a, Vec2 b )
{
  return sqrt( (a.x - b.x)^2 + (a.y - b.y)^2 )
}

bool CirclevsCircleUnoptimized( Circle a, Circle b )
{
  float r = a.radius + b.radius
  return r < Distance( a.position, b.position )
}

bool CirclevsCircleOptimized( Circle a, Circle b )
{
  float r = a.radius + b.radius
  r *= r
  return r < (a.x + b.x)^2 + (a.y + b.y)^2
}

В целом размножение-это намного дешевле, чем операция взятия квадратного корня из значения.

Разрешение Импульс

Разрешение Импульс является особый тип стратегии разрешения коллизий. Разрешения коллизий является акт принятия двух объектов, которые оказываются пересекающимися и модифицируя их таким образом, чтобы не позволить им оставаться пересекающихся.

В целом объект в физический движок имеет три степени свободы (в двух измерениях): движение в плоскости XY и вращения. В этой статье мы неявно ограничить вращение и использовать только AABBs и круги, так что единственная степень свободы, мы действительно должны рассмотреть движение вдоль плоскости XY.

Путем устранения выявленных коллизий мы устанавливаем ограничение на перемещение таких объектов не может оставаться пересекаются. Идея резолюции импульс, чтобы использовать импульс (мгновенное изменение скорости) в объекты столкновения. Для этого масса, положение и скорость каждого объекта должны быть приняты во внимание, как-то: мы хотим, чтобы крупные объекты сталкиваются с мелкими немного двигаться во время столкновения, и чтобы отправить мелкие предметы улетают. Мы также хотим, чтобы объекты с бесконечной массой, чтобы не двигаться вообще.

Простой пример того, что разрешение импульс может достичь.

Для достижения таких эффектов и следите за наряду с природной интуицией, как ведут себя объекты мы будем использовать твердые тела и немного математики. Твердое тело-это просто форма, определенных пользователем (то есть вами, застройщика), который неявно определенными, чтобы не деформироваться. Оба AABBs и круги в этой статье, недеформируемой, и всегда будет либо ААВВ или круг. Никакого сдавливания или растяжения допускается.

Работа с твердыми телами позволяет много математики и деривации должны быть сильно упрощена. Именно поэтому твердые тела широко используются в игровых симуляторах, и поэтому мы будем их использовать в этой статье.

Наши Объекты Столкнулся — Теперь Что?

Предположим, что мы имеем две фигуры оказываются пересекающимися, как на самом деле отделить два? Предположим, что наш обнаружение столкновений дал нам две важные части.

Столкновение нормально
Глубина проникновения

Для того, чтобы применить импульс к объектам, но и перемещать их друг от друга, мы должны знать, в каком направлении толкать их и на сколько. Нормальное столкновение направление, в котором импульс будет применяться. Глубина проникновения (вместе с некоторыми другими вещами) определить, как большие импульса будет использоваться. Это означает, что единственная ценность, которую нужно решить для масштабов нашего импульса.

Теперь давайте вернемся в далекий поход, чтобы узнать, как мы можем решить для этой величины импульса. Мы начнем с наших двух объектов, которые были найдены, чтобы быть пересекающиеся:

Уравнение 1

[ В^{АВ} = V и^Б — В^А ] заметим, что для того, чтобы создать вектор из позиции a в позицию B, вы должны сделать: конечная точка — Исходная позиция. (В^{АВ}) — относительная скорость из А в Б. Это уравнение должно быть выражено в терминах столкновения нормальный (н) — то есть, мы хотели бы знать относительную скорость от А до Б вдоль линии столкновения нормального направления:

Уравнение 2

[ В^{АВ} cDOT на Н = (В^Б — В^А) cDOT на п ]

Мы сейчас используем скалярное произведение. Скалярное произведение простых; это сумма покомпонентно продуктов:

Уравнение 3

[ В_1 = всегда begin{bmatrix}x_1 места \y_1конец{bmatrix}, В_2 = всегда begin{bmatrix}x_2 \y_2конец{bmatrix} \ В_1 cDOT на В_2 = x_1 места * x_2 + y_2 * y_2 ]

Следующий шаг-ввести так называемый коэффициент реституции. Реституция-это термин, который означает эластичность, или bounciness. Каждый объект в свой физический движок будет реституции представляется как десятичное значение. Однако только одно десятичное значение будет использоваться при расчете импульса.

Чтобы решить, что реституция использовать (обозначается (Е) для Эпсилон), вы должны всегда использовать самой низкой реституции, вовлеченные в конфликт, для интуитивного результаты:

// Given two objects A and B
e = min( A.restitution, B.restitution )

После того как (Е) является приобретенным, мы можем разместить его в нашем решая уравнение для величины импульса.

Закон Ньютона о реституции говорится следующее:

Уравнение 4

[В’ = Е * в]

Все это говорит, что скорость после столкновения равна скорости перед ним, умноженной на некоторую константу. Эта константа представляет собой «коэффициент отскока». Зная это, он становится достаточно простой для интеграции реституции в нашей нынешней деривации:

Уравнение 5

[ В^{АВ} cDOT на Н = -Е * (В^Б — В^А) cDOT на п ]

Обратите внимание, как мы ввели здесь отрицательный знак. В закон Ньютона о реституции, (в), получим результирующий вектор после отказов, на самом деле происходит в направлении, противоположном В. Так как мы представляем противоположных направлениях в нашем деривации? Ввести отрицательный знак.

До сих пор так хорошо. Теперь мы должны быть в состоянии выразить эти скорости в то время как под влиянием импульса. Вот простое уравнение для изменения вектора каким-импульса скалярного (к) вдоль определенной направление(Н):

Уравнение 6

[ В’ = в + J В * Н ]

Надеюсь, что приведенное выше уравнение имеет смысл, так как это очень важно понимать. У нас есть единичный вектор (Н), который представляет собой направление. У нас есть скаляр (К), которая представляет как долго наши (Н) вектор будет. Затем мы добавляем наш масштабируется (Н) вектор (v), чтобы привести в (в). Это просто добавление одного вектора на другой, и мы можем использовать этот небольшой уравнение, чтобы применить импульс от одного вектора к другому.

Есть немного больше работы, чтобы быть сделано здесь. Формально, импульс определяется как изменение импульса. Импульс-это масса * скорость. Зная это, мы можем представить импульс как формально определяется так:

Уравнение 7

[ Импульс = масса * скорость \ скорость = фрац{импульс}{масса} следовательно, в’ = в + фрац{Дж * Н}{масса}]

Три точки в маленький треугольник ((поэтому)) можно читать Как «поэтому». Он используется, чтобы показать, что дело заранее может быть использован, чтобы сделать вывод, что все, что дальше верно.

Хороший прогресс был достигнут до сих пор! Однако мы должны быть в состоянии выразить импульс через (К) в отношении двух разных объектов. При столкновении с объектом A и B, а сдвигаются в противоположном направлении Б:

Уравнение 8

[ В’^В = В^А + фрац{Дж * Н}{масс^а} в’^В = В^Б — фрац{Дж * Н}{масса^Б} ]

Эти два уравнения будут толкать от Б вдоль направления единичного вектора (н) с импульсным скаляр (величина (н)) (к).

Все, что сейчас требуется, это объединить уравнения 8 и 5. Наши полученное уравнение будет выглядеть так:

Уравнение 9

[ (В^А — В^В + фрац{Дж * Н}{масс^а} + фрац{Дж * Н}{масса^б}) * н = -е * (В^Б — В^А) cDOT на п \ Поэтому \ (В^А — В^В + фрац{Дж * Н}{масс^а} + фрац{Дж * Н}{масса^Б}) * П + Е * (В^Б — В^А) cDOT на н = 0 ]

Если вы помните, первоначальная цель заключалась в том, чтобы изолировать наши масштабы. Это потому, что мы знаем в каком направлении разрешения конфликта в (предполагается, данное обнаружение столкновений), и осталось только решить масштабы этого направления. Величина, которая является неизвестной в нашем случае (к), мы должны изолировать (К) и удалите его.

Уравнение 10

[ (П^Б — В^А) cDOT на н + з * (фрац{Дж * Н}{масс^а} + фрац{Дж * Н}{масса^б}) * н + е * (В^Б — В^А) cDOT на н = 0 \ поэтому \ (1 + е)((В^Б — В^А) cDOT на н) + з * (фрац{Дж * Н}{масс^а} + фрац{Дж * Н}{масса^Б}) * П = 0 \ поэтому \ Дж = фрац{-(1 + е)((В^Б — В^А) cDOT на Н)}{ГРП{1}{масс^а} + ГРП{1}{масса^Б}} ]

Ух! Это было немного математики! Это сейчас, хотя во всем. Важно заметить, что в окончательном варианте уравнение 10 мы имеем (к) слева (наши масштабы) и все, что справа-это все известно. Это означает, что мы можем написать несколько строк кода, чтобы решить для нашего импульса скалярного (к). И мальчик-это код намного более читабельным, чем математической нотации!

void ResolveCollision( Object A, Object B )
{
  // Calculate relative velocity
  Vec2 rv = B.velocity - A.velocity

  // Calculate relative velocity in terms of the normal direction
  float velAlongNormal = DotProduct( rv, normal )

  // Do not resolve if velocities are separating
  if(velAlongNormal > 0)
    return;

  // Calculate restitution
  float e = min( A.restitution, B.restitution)

  // Calculate impulse scalar
  float j = -(1 + e) * velAlongNormal
  j /= 1 / A.mass + 1 / B.mass

  // Apply impulse
  Vec2 impulse = j * normal
  A.velocity -= 1 / A.mass * impulse
  B.velocity += 1 / B.mass * impulse
}

Есть несколько ключевых вещей, чтобы отметить в приведенном выше примере кода. Первым делом проверка в строке 10, если(VelAlongNormal > 0). Эта проверка очень важна, она гарантирует, что вы только разрешать коллизию, если объекты движутся навстречу друг другу.

Два объекта сталкиваются, но скорость их будет отделять следующий кадр. Не разрешать подобные коллизии.

Если объекты разлетаются друг от друга, мы хотим ничего не делать. Это позволит исключить объекты, которые не должны быть рассмотрены, сталкиваясь с разрешения друг от друга. Это важно для создания моделирования, которые следует человеческую интуицию на том, что должно произойти в процессе взаимодействия объектов.

Второе замечание заключается в том, что обратная массы вычисляется несколько раз без причины. Лучше всего хранить ваши обратных масс в пределах каждого объекта и предварительно вычислить его один раз:

A.inv_mass = 1 / A.mass

Многие физики двигатели на самом деле не хранить сырой массы. Физика двигатели часто магазин обратная массы и один инверсный массы. Просто так получилось, что большинство математических участием масс в виде 1/масса.

Последняя вещь, чтобы отметить, что мы грамотно распределить наши импульса скалярного (к) на два объекта. Мы хотим, чтобы небольшие объекты отскакивают на большие объекты с большой долей (К), и большие объекты, чтобы их скоростей изменяются очень небольшую часть (к).

Для того чтобы сделать это, вы могли бы сделать:

float mass_sum = A.mass + B.mass
float ratio = A.mass / mass_sum
A.velocity -= ratio * impulse

ratio = B.mass / mass_sum
B.velocity += ratio * impulse

Важно понимать, что приведенный выше код эквивалентен ResolveCollision() пример функции раньше. Как уже говорилось, обратная масс весьма полезны в физический движок.

Тонуть Объектов

Если мы идем дальше и использовать код, который мы до сих пор, объекты будут столкнуться друг с другом и отскакивают. Это здорово, хотя что произойдет, если один из объектов имеет бесконечную массу? Ну нам нужен хороший способ, чтобы представить бесконечную массу в нашей модели.

Я предлагаю использовать ноль как бесконечную массу — Хотя, если мы попытаемся вычислить обратную масса объекта с нуля у нас будет деление на ноль. Обходной путь для этого это сделать следующее при вычислении обратных масс:

if(A.mass == 0)
  A.inv_mass = 0
else
  A.inv_mass = 1 / A.mass

Нулевое значение приведет к правильной выкладки при разрешении импульсов. Это еще ладно. Проблема затопления объектов возникает тогда, когда что-то начинает тонуть в другой объект из-за тяжести. Возможно, что-то с низким реституцию попадает в стену с бесконечной массой и начинает тонуть.

Это тонет из-за плавающей ошибки точек. Во время каждого расчета плавающей точкой небольшой плавающей ошибки вводится из-за аппаратных. (Для получения дополнительной информации, компания Google [ошибка плавающей точкой IEEE754].) С течением времени эта ошибка накапливается в позиционную ошибку, заставляя объекты погружаться в друг друга.

Для того, чтобы исправить эту ошибку она должна быть учтена. Чтобы исправить эту позиционную ошибку я покажу вам метод, называемый линейной проекции. Линейная проекция уменьшает проникновение двух объектов на небольшой процент, и это происходит после применения импульса. Позиционная коррекция очень проста: перемещение каждого объекта вдоль линии столкновения нормальный (н) в процентах от глубины проникновения:

void PositionalCorrection( Object A, Object B )
{
  const float percent = 0.2 // usually 20% to 80%
  Vec2 correction = penetrationDepth / (A.inv_mass + B.inv_mass)) * percent * n
  A.position -= A.inv_mass * correction
  B.position += B.inv_mass * correction
}

Обратите внимание, что мы масштаб penetrationDepth общая масса системы. Это даст позиционной коррекции пропорционально тому, сколько масс Мы имеем дело. Мелкие предметы отталкивают быстрее, чем более тяжелые предметы.

Есть небольшая проблема с этой реализации: если мы всегда решаем наши позиционные ошибки, то объекты будут джиттера взад и вперед, пока они отдыхают друг с другом. Для того, чтобы предотвратить эту поблажку надо дать. Мы выполняем только позиционной коррекции, если проникновение превышает некоторый произвольный порог, называется «помои»:

void PositionalCorrection( Object A, Object B )
{
  const float percent = 0.2 // usually 20% to 80%
  const float slop = 0.01 // usually 0.01 to 0.1
  Vec2 correction = max( penetration - k_slop, 0.0f ) / (A.inv_mass + B.inv_mass)) * percent * n
  A.position -= A.inv_mass * correction
  B.position += B.inv_mass * correction
}

Это позволяет объектам проникнуть очень немного без коррекции положения в ногами.

Простой Коллектор Поколения

Последние темы в данной статье, является простой коллектор поколения. Коллектор в математическом плане-это что-то вдоль линий «коллекцию очков, которая представляет собой область в пространстве». Однако, когда я ссылаюсь на этот термин коллектор я имею в виду небольшой объект, который содержит информацию о столкновении между двумя объектами.

Вот типичный коллектор установки:

struct Manifold
{
  Object *A;
  Object *B;
  float penetration;
  Vec2 normal;
};

Во время обнаружения столкновения оба проникновения и нормальный столкновения должны быть вычислены. Для того, чтобы найти эту информацию, оригинальные алгоритмы определения столкновений с вершины этой статье должен быть продлен.

Круг против круга

Давайте начнем с алгоритма простейшей столкновения: круг против круга. Этот тест в основном тривиальными. Можете ли вы представить, что в направлении разрешения конфликта будет? Это вектор от точки А в точку Б. Этот круг может быть получен путем вычитания установки Б У в.

Глубина проникновения связана с окружностей радиусов и расстояния друг от друга. Перекрытия кругов может быть вычислено путем вычитания сумма радиусов на расстояние от каждого объекта.

Вот полный пример алгоритма для генерации коллектор круга против столкновения кругу:

bool CirclevsCircle( Manifold *m )
{
  // Setup a couple pointers to each object
  Object *A = m->A;
  Object *B = m->B;

  // Vector from A to B
  Vec2 n = B->pos - A->pos

  float r = A->radius + B->radius
  r *= r

  if(n.LengthSquared( ) > r)
    return false

  // Circles have collided, now compute manifold
  float d = n.Length( ) // perform actual sqrt

  // If distance between circles is not zero
  if(d != 0)
  {
    // Distance is difference between radius and distance
    m->penetration = r - d

    // Utilize our d since we performed sqrt on it already within Length( )
    // Points from A to B, and is a unit vector
    c->normal = t / d
    return true
  }

  // Circles are on same position
  else
  {
    // Choose random (but consistent) values
    c->penetration = A->radius
    c->normal = Vec( 1, 0 )
    return true
  }
}

Наиболее заметные вещи здесь: мы не выполняете какие-либо квадратные корни, пока это необходимо (предметы оказываются столкновения), и мы проверяем, чтобы убедиться, что круги не в том же положении. Если они находятся на той же позиции, наша дистанция будет равна нулю, и мы должны избежать деления на ноль при вычислении т / сут.

ААВВ В. ААВВ

ААВВ в ААВВ тест является немного более сложным, чем круг против круга. Столкновение нормального не будет вектор из A в B, но будет лицо нормальное. В ААВВ-это коробка с четырьмя лицами. Каждое лицо имеет нормальный. Это нормально представляет собой единичный вектор, который перпендикулярен к лицу.

Изучить общее уравнение линии в 2D:

[ ах + ьу + с = 0 \ нормальный = всегда begin{bmatrix} абконец{bmatrix} ]

В приведенном выше уравнении, A и B-вектор нормали к линии, а вектор (А, B) предполагается нормированной (длина вектора равна нулю). Опять же, наши столкновения нормальное (направление разрешения конфликта) будет в направлении одного из нормалей к граням.

Вы знаете, что c представляет собой в общее уравнение линии? c — расстояние от начала координат. с-расстояние от источника. Это очень полезно для тестирования, чтобы увидеть, если точка находится на одной стороне линии или другой, как вы увидите в следующей статье.

Теперь все, что необходимо, чтобы выяснить, какие лица встречных на одном из объектов с другим объектом, и у нас нормальные. Однако иногда несколько граней двух AABBs могут пересекаться, например, двух углов пересекаются друг с другом. Это означает, что мы должны найти ось наименьшего проникновения.

Две оси проходки; горизонтальная ось X является осью крайней мере проникновение и эта коллизия должна разрешаться вдоль оси X.

Вот полный алгоритм ААВВ в ААВВ коллектор поколение и обнаружение столкновений:

bool AABBvsAABB( Manifold *m )
{
  // Setup a couple pointers to each object
  Object *A = m->A
  Object *B = m->B
 
  // Vector from A to B
  Vec2 n = B->pos - A->pos
 
  AABB abox = A->aabb
  AABB bbox = B->aabb
 
  // Calculate half extents along x axis for each object
  float a_extent = (abox.max.x - abox.min.x) / 2
  float b_extent = (bbox.max.x - bbox.min.x) / 2
 
  // Calculate overlap on x axis
  float x_overlap = a_extent + b_extent - abs( n.x )
 
  // SAT test on x axis
  if(x_overlap > 0)
  {
    // Calculate half extents along x axis for each object
    float a_extent = (abox.max.y - abox.min.y) / 2
    float b_extent = (bbox.max.y - bbox.min.y) / 2
 
    // Calculate overlap on y axis
    float y_overlap = a_extent + b_extent - abs( n.y )
 
    // SAT test on y axis
    if(y_overlap > 0)
    {
      // Find out which axis is axis of least penetration
      if(x_overlap > y_overlap)
      {
        // Point towards B knowing that n points from A to B
        if(n.x < 0)
          m->normal = Vec2( -1, 0 )
        else
          m->normal = Vec2( 0, 0 )
        m->penetration = x_overlap
        return true
      }
      else
      {
        // Point toward B knowing that n points from A to B
        if(n.y < 0)
          m->normal = Vec2( 0, -1 )
        else
          m->normal = Vec2( 0, 1 )
        m->penetration = y_overlap
        return true
      }
    }
  }
}

Круг против ААВВ

Последний тест я закрою тест круг против ААВВ. Идея здесь состоит в том, чтобы вычислить ближайшую точку на ААВВ круга; оттуда тест переходит в нечто похожее на круг против теста круг. Как только ближайшая точка вычисляется и столкновения обнаруживается нормальный направлении ближайшей точки до центра окружности. Глубина проникновения-это разница между расстоянием от ближайшей точки на окружности и радиус окружности.

ААВВ с круговой диаграммой пересечения.

Есть один хитрый особый случай; если центр окружности находится в пределах ААВВ затем в центр круга должен быть закреплен к ближайшей кромке ААВВ, а нормальная должна быть перевернута.

bool AABBvsCircle( Manifold *m )
{
  // Setup a couple pointers to each object
  Object *A = m->A
  Object *B = m->B

  // Vector from A to B
  Vec2 n = B->pos - A->pos

  // Closest point on A to center of B
  Vec2 closest = n

  // Calculate half extents along each axis
  float x_extent = (A->aabb.max.x - A->aabb.min.x) / 2
  float y_extent = (A->aabb.max.y - A->aabb.min.y) / 2

  // Clamp point to edges of the AABB
  closest.x = Clamp( -x_extent, x_extent, closest.x )
  closest.y = Clamp( -y_extent, y_extent, closest.y )

  bool inside = false

  // Circle is inside the AABB, so we need to clamp the circle's center
  // to the closest edge
  if(n == closest)
  {
    inside = true

    // Find closest axis
    if(abs( n.x ) > abs( n.y ))
    {
      // Clamp to closest extent
      if(closest.x > 0)
        closest.x = x_extent
      else
        closest.x = -x_extent
    }

    // y axis is shorter
    else
    {
      // Clamp to closest extent
      if(closest.y > 0)
        closest.y = y_extent
      else
        closest.y = -y_extent
    }
  }

  Vec2 normal = n - closest
  real d = normal.LengthSquared( )
  real r = B->radius

  // Early out of the radius is shorter than distance to closest point and
  // Circle not inside the AABB
  if(d > r * r && !inside)
    return false

  // Avoided sqrt until we needed
  d = sqrt( d )

  // Collision normal needs to be flipped to point outside if circle was
  // inside the AABB
  if(inside)
  {
    m->normal = -n
    m->penetration = r - d
  }
  else
  {
    m->normal = n
    m->penetration = r - d
  }

  return true
}

Заключение

Надеюсь, что теперь вы узнали кое-что о симуляции физики. В этом учебнике достаточно, чтобы позволить вам создать простой настраиваемый физический движок сделан полностью с нуля. В следующей части мы будем рассматривать все необходимые расширения, что все физики двигатели требуют, в том числе:

Контактной пары сортировки и выбраковки
Broadphase
Наслаивать
Интеграция
Timestepping
Пересечение полупространство
Модульная конструкция (материалы, массы и силы)

Я надеюсь, вам понравилась эта статья и я с нетерпением жду ответов на вопросы в комментариях.

Источник

Making a 2D Physics Engine: The Series

This is the first article in the Making a 2D Physics Engine Series.

Making a 2D Physics Engine: The Math
Making a 2D Physics Engine: Spaces and Bodies
Making a 2D Physics Engine: Shapes, Worlds and Integration
Making a 2D Physics Engine: Mass, Inertia and Forces

Introduction

Why do we need physics in games?

Physics in games helps us simulate a semi-realistic world with which gamers can easily relate to. From the first Donkey Kong game to the latest The Last Of Us, physics help materialize a world. Physics can be realistic or unrealistic depending on the type of game you’re developing. This series of articles will hopefully give you an idea along with the algorithms of how physics engines work and give you enough knowledge to implement your own version of Box2D from scratch!

What do I need to know to simulate physics in my games?

You can always choose to code your own physics engine (which is the main focus of this series of articles) or you can use some commercially or freely available engines like NVIDIA’s PhysX Engine and Havok Physics that you can use in your projects. All game engines come with a physics engine bundled with them, though you still will have to implement game-specific physical entities/simulations such as a vehicle engine, boat, buoyancy, air resistance, and so on. All of these require knowledge in vectors and matrices in both 2D and 3D. This article will go through some of the more important concepts of vectors and matrices required for implementing 2D physics in your games.

Vectors

Let’s start with the most basic concept of points and direction in ‘n’ dimensions: Vectors.

What are Vectors?

A vector is a geometric object used to «carry» point A to point B. It has a magnitude as well as a direction. It is commonly used to represent «vector» quantities like forces, velocities which were talked about in high school physics.

Representing a Vector

A Vector in the ‘n’th dimension has ‘n’ components. 2D, 3D and 4D vectors are commonly used. A vector can be represented as a column matrix, i.e. an nD vector is represented as an n*1 matrix. It can also be represented as an ordered set, like so: ((a_1, a_2, ldots a_{n-1}, a_n))

The components of any vector of 2D or 3D vectors are generally represented by the x, y and z alphabets which also represent the corresponding cartesian coordinates of that vector.

The contents below are targeted towards 2D vectors, but can easily be extended to 3D vectors.

Vector Operations

Length of a Vector

The length (or magnitude) of a vector is equal to the Pythagorean distance between it and the origin (zero vector). It can be represented as follows: (mathbf{||A||} = sqrt{a_1^2 + a_2^2 + ldots + a_n^2})

In code, it can be defined as follows:

float length(Vec2 vec)
    return sqrt(vec.x * vec.x + vec.y * vec.y)

In many cases which require comparision of distances, the expensive sqrt operation is avoided and the square of the length of the vector is used instead.

float sqrLength(Vec2 vec)
    return vec.x * vec.x + vec.y * vec.y

Normalization of Vector (Unit Vector)

A unit vector is a vector whose length is 1. It is commonly used to represent directions like normals and tangents. To get the unit vector (direction) for a specific vector, that vector is divided by it’s length. This process is called normalization.

Vec2 normalized(Vec2 vec)
    return vec * (1 / length(vec))

Multiplication of Vectors

Vectors can be multiplied by a scalar as well as another vector of the same dimensions.

Multiplication of a Vector with a scalar

Vectors can be scaled by a scalar, i.e. each of its components will be multiplied by the scalar.

$mathbf{A}*s=(a_1*s, a_2*s, ldots, a_n*s)$

Multiplication of a Vector with another vector

Two vectors can be multiplied using the Dot (Scalar) Product or Cross (Vector) Product.

Dot Product

The dot product is the sum of the component-wise product of two vectors. It returns a scalar.

$mathbf{A cdotp B} = a_1*b_1 + a_2*b_2 + ldots + a_n*b_n)$

The dot product is one of the most used vector operations as it is closely related to the cosine of the angle between the two vectors.

cos theta = A dot B / (length(A) * length(B))

cos theta = normalized(a) dot normalized(b)

One important thing to remember is that if two vectors are perpendicular to each other, their dot product will be equal to zero (as cos theta = 0).

Cross Product

The cross product is a popular operation in 3D. The cross product, denoted a × b, is a vector perpendicular to both a and b and is defined as

Where n is the vector perpendicular to both a and b.

The cross product is properly defined only for 3D vectors. But since 2D vectors can be considered as 3D vectors lying on the XY plane, the cross product of any two 2D vectors can be defined as the cross product of their 3D planar representations, resulting in a vector along the Z axis which can be represented as a scalar (representing the magnitude of the Z axis vector).

Similarly, a 2D vector crossed with a scalar will result in another 2D vector perpendicular to the original 2D vector.

The cross product for 2D vectors looks as follows:

float cross(Vector2 a, Vec2 b)
  return a.x * b.y - a.y * b.x;
 

Vector2 cross(Vector2 a, float s)
  return Vec2(s * a.y, -s * a.x);
 
Vector2 cross(float s, Vector2 a)
  return Vec2(-s * a.y, s * a.x);

Vector2 Struct Pseudocode

In the programming language of your choice, the Vector2 structure should look as follows. You can change the names according to your choice.

struct Vector2 {
    float x, y;

    float length() {
        return sqrt(x * x + y * y);
    }
    float sqrLength() {
        return x * x + y * y;
    }
    
    Vector2 operator *(Vector2 v, float s) {
        return Vector2(v.x * s, v.y * s);
    }
    
    void normalize() {
        float inv_len = 1 / length();
        x *= inv_len; y *= inv_len;
    }
    
    float dot(Vector2 a, Vector2 b) {
        return a.x * b.x + a.y * b.y;
    }
    
        float cross(Vector2 a, Vec2 b) {
        return a.x * b.y - a.y * b.x;
    }
        Vector2 cross(Vector2 a, float s) {
        return Vec2(s * a.y, -s * a.x);
    }
    Vector2 cross(float s, Vector2 a) {
        return Vec2(-s * a.y, s * a.x);
    }
}

Note that all instances the Vector2 structure, like all primitives in most languages, should be copied by value and not by reference, unless explicitly required. Reference copying of vectors will lead to unnecessary problems and invisible bugs.

Matrices

A matrix is a rectangular array—of numbers, symbols, or expressions, arranged in rows and columns—that is treated in certain prescribed ways. Matrices are generally used in Computer Graphics and physics to transform a point from one basis to another, which includes rotation, translation and scaling.

In this article I will only be covering 2×2 matrices which are used to rotate 2D vectors.

Why Matrices?

If you remember high school mathematics, multiplication of a (l times m) matrix by a (m times n) matrix results in a (l times n) matrix. In this case, a 2×2 matrix multiplied by a vector represented as a 2×1 matrix gives another 2×1 matrix (2D vector). This makes it mathematically easier and computationally efficient to transform a vector. An important transformation, rotation, will be covered in the next few sub-sections.

Rotation in 2D

Each object has an orientation. In terms of rotation, orientation is synonymous with position (i.e the rotation of the object at an instant), angular velocity (the rate of change of orientation) is synonymous with velocity and torque with force. Since objects in 2D can only rotate about the imaginary z-axis, the orientation of a 2D body is a scalar which represents the rotation about the z-axis in radians. Since the distance of the point from the origin must stay constant (by the definition of rotation in angular kinematics), a rotating point will always lie on the circumference of a circle with center as the origin and radius equal to the distance from the origin.

Rotating a Vector by some angle

In a 2D Cartesian plane, for some vector P(x, y), where the angle through which P should be rotated is «theta» then

$begin{bmatrix} x’ \ y’ end{bmatrix} = begin{bmatrix} x cos theta — y sin theta \ x sin theta + y cos theta end{bmatrix} $

This comes directly from the trigonometric compound angle formulae after converting the vectors into polar form.

Using Matrices to Rotate a Vector

Look at the above equation again. I’ve presented it in matrix form so that it’s easier to obtaining the rotation matrix after creating a matrix equation. Try and find the rotation matrix yourself before moving ahead.

The formula for matrix-matrix multiplication for a 2×2 and 2×1 matrix will look somewhat like this:

$begin{bmatrix} A & B\ C & D end{bmatrix} begin{bmatrix} x \ y end{bmatrix} = begin{bmatrix} Ax + By \ Cx + Dy end{bmatrix}$

Now compare this result to the result of the previous equation.

$begin{bmatrix} Ax + By \ Cx + By end{bmatrix} = begin{bmatrix} x cos theta — y sin theta \ x sin theta + y cos theta end{bmatrix}$

From the above relation, we can conclude that

$begin{bmatrix} A & B\ C & D end{bmatrix} = begin{bmatrix}cos theta & -sin theta \ sin theta & cos theta end{bmatrix}$

Matrix2 Structure Pseudocode

A 2*2 matrix structure would look as follows:

struct Matrix2
{
    float m00, m01
    float m10, m11;
    
        void set(real radians) {
        real c = cos(radians);
        real s = sin(radians);

        m00 = c; m01 = -s;
        m10 = s; m11 =  c;
    }
    
    Matrix2 transpose() {
        return Matrix2(m00, m10,
                       m01, m11);
    }
    
    Vector2 operator*(Vector2 rhs) {
        return Vec2(m00 * rhs.x + m01 * rhs.y, m10 * rhs.x + m11 * rhs.y);
    }

    Matrix2 operator*(Matrix2 rhs ) {
    return Mat2(
      m00 * rhs.m00 + m01 * rhs.m10, m00 * rhs.m01 + m01 * rhs.m11,
      m10 * rhs.m00 + m11 * rhs.m10, m10 * rhs.m01 + m11 * rhs.m11);
    }
}

Just like the Vector2 structure, the instances of the Matrix2 structure must also be copied by value.

What Next?

The next article will get you started on making a very basic physics engine with the code. It will include concepts such as shapes, bodies and integration of velocities and forces. I hope to cover collision detection, collision resolution, concave shapes, broad phasing, raycasting, extending to 3D and other such concepts in future articles. I will try to split it into as many articles as I can because it can be a lot to take in!

If you have any comments/suggestions please do let me know!

History

13 Sep 2015: Initially posted

5 Nov 2017: Language and content improvements

Teen programmer with a great zeal for programming, and interested work on Assets for Unity3D, games in Unity3D and small tools and applications for Windows, Linux and Android under Evudio.

Источник

Making a 2D Physics Engine: The Series

This is the first article in the Making a 2D Physics Engine Series.

Making a 2D Physics Engine: The Math
Making a 2D Physics Engine: Spaces and Bodies
Making a 2D Physics Engine: Shapes, Worlds and Integration
Making a 2D Physics Engine: Mass, Inertia and Forces

Introduction

Why do we need physics in games?

What do I need to know to simulate physics in my games?

Vectors

Let’s start with the most basic concept of points and direction in ‘n’ dimensions: Vectors.

What are Vectors?

Representing a Vector

The components of any vector of 2D or 3D vectors are generally represented by the x, y and z alphabets which also represent the corresponding cartesian coordinates of that vector.

The contents below are targeted towards 2D vectors, but can easily be extended to 3D vectors.

Vector Operations

Length of a Vector

In code, it can be defined as follows:

float length(Vec2 vec)
    return sqrt(vec.x * vec.x + vec.y * vec.y)

In many cases which require comparision of distances, the expensive sqrt operation is avoided and the square of the length of the vector is used instead.

float sqrLength(Vec2 vec)
    return vec.x * vec.x + vec.y * vec.y

Normalization of Vector (Unit Vector)

Vec2 normalized(Vec2 vec)
    return vec * (1 / length(vec))

Multiplication of Vectors

Vectors can be multiplied by a scalar as well as another vector of the same dimensions.

Multiplication of a Vector with a scalar

Vectors can be scaled by a scalar, i.e. each of its components will be multiplied by the scalar.

$mathbf{A}*s=(a_1*s, a_2*s, ldots, a_n*s)$

Multiplication of a Vector with another vector

Two vectors can be multiplied using the Dot (Scalar) Product or Cross (Vector) Product.

Dot Product

The dot product is the sum of the component-wise product of two vectors. It returns a scalar.

$mathbf{A cdotp B} = a_1*b_1 + a_2*b_2 + ldots + a_n*b_n)$

The dot product is one of the most used vector operations as it is closely related to the cosine of the angle between the two vectors.

cos theta = A dot B / (length(A) * length(B))

cos theta = normalized(a) dot normalized(b)

One important thing to remember is that if two vectors are perpendicular to each other, their dot product will be equal to zero (as cos theta = 0).

Cross Product

The cross product is a popular operation in 3D. The cross product, denoted a × b, is a vector perpendicular to both a and b and is defined as

Where n is the vector perpendicular to both a and b.

Similarly, a 2D vector crossed with a scalar will result in another 2D vector perpendicular to the original 2D vector.

The cross product for 2D vectors looks as follows:

float cross(Vector2 a, Vec2 b)
  return a.x * b.y - a.y * b.x;
 

Vector2 cross(Vector2 a, float s)
  return Vec2(s * a.y, -s * a.x);
 
Vector2 cross(float s, Vector2 a)
  return Vec2(-s * a.y, s * a.x);

Vector2 Struct Pseudocode

In the programming language of your choice, the Vector2 structure should look as follows. You can change the names according to your choice.

struct Vector2 {
    float x, y;

    float length() {
        return sqrt(x * x + y * y);
    }
    float sqrLength() {
        return x * x + y * y;
    }
    
    Vector2 operator *(Vector2 v, float s) {
        return Vector2(v.x * s, v.y * s);
    }
    
    void normalize() {
        float inv_len = 1 / length();
        x *= inv_len; y *= inv_len;
    }
    
    float dot(Vector2 a, Vector2 b) {
        return a.x * b.x + a.y * b.y;
    }
    
        float cross(Vector2 a, Vec2 b) {
        return a.x * b.y - a.y * b.x;
    }
        Vector2 cross(Vector2 a, float s) {
        return Vec2(s * a.y, -s * a.x);
    }
    Vector2 cross(float s, Vector2 a) {
        return Vec2(-s * a.y, s * a.x);
    }
}

Matrices

In this article I will only be covering 2×2 matrices which are used to rotate 2D vectors.

Why Matrices?

Rotation in 2D

Rotating a Vector by some angle

In a 2D Cartesian plane, for some vector P(x, y), where the angle through which P should be rotated is «theta» then

$begin{bmatrix} x’ \ y’ end{bmatrix} = begin{bmatrix} x cos theta — y sin theta \ x sin theta + y cos theta end{bmatrix} $

This comes directly from the trigonometric compound angle formulae after converting the vectors into polar form.

Using Matrices to Rotate a Vector

The formula for matrix-matrix multiplication for a 2×2 and 2×1 matrix will look somewhat like this:

$begin{bmatrix} A & B\ C & D end{bmatrix} begin{bmatrix} x \ y end{bmatrix} = begin{bmatrix} Ax + By \ Cx + Dy end{bmatrix}$

Now compare this result to the result of the previous equation.

$begin{bmatrix} Ax + By \ Cx + By end{bmatrix} = begin{bmatrix} x cos theta — y sin theta \ x sin theta + y cos theta end{bmatrix}$

From the above relation, we can conclude that

$begin{bmatrix} A & B\ C & D end{bmatrix} = begin{bmatrix}cos theta & -sin theta \ sin theta & cos theta end{bmatrix}$

Matrix2 Structure Pseudocode

A 2*2 matrix structure would look as follows:

struct Matrix2
{
    float m00, m01
    float m10, m11;
    
        void set(real radians) {
        real c = cos(radians);
        real s = sin(radians);

        m00 = c; m01 = -s;
        m10 = s; m11 =  c;
    }
    
    Matrix2 transpose() {
        return Matrix2(m00, m10,
                       m01, m11);
    }
    
    Vector2 operator*(Vector2 rhs) {
        return Vec2(m00 * rhs.x + m01 * rhs.y, m10 * rhs.x + m11 * rhs.y);
    }

    Matrix2 operator*(Matrix2 rhs ) {
    return Mat2(
      m00 * rhs.m00 + m01 * rhs.m10, m00 * rhs.m01 + m01 * rhs.m11,
      m10 * rhs.m00 + m11 * rhs.m10, m10 * rhs.m01 + m11 * rhs.m11);
    }
}

Just like the Vector2 structure, the instances of the Matrix2 structure must also be copied by value.

What Next?

If you have any comments/suggestions please do let me know!

History

13 Sep 2015: Initially posted

5 Nov 2017: Language and content improvements

Teen programmer with a great zeal for programming, and interested work on Assets for Unity3D, games in Unity3D and small tools and applications for Windows, Linux and Android under Evudio.

Источник