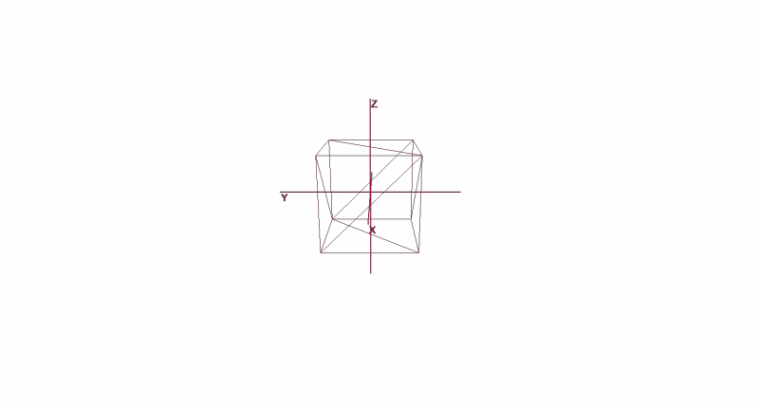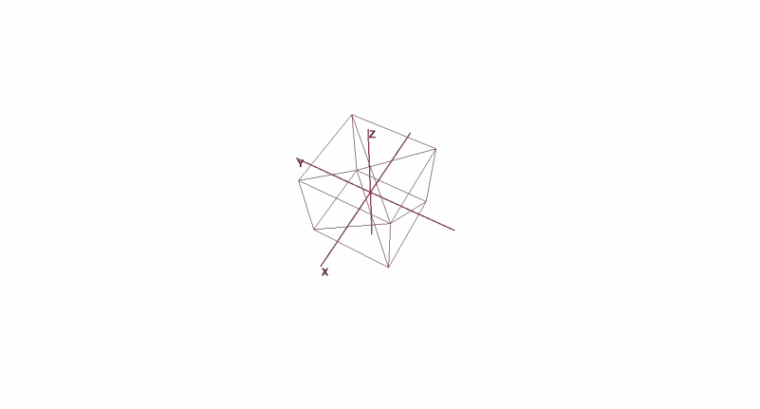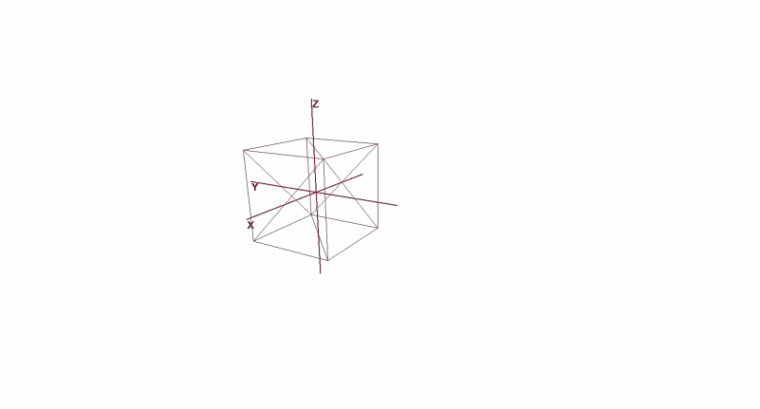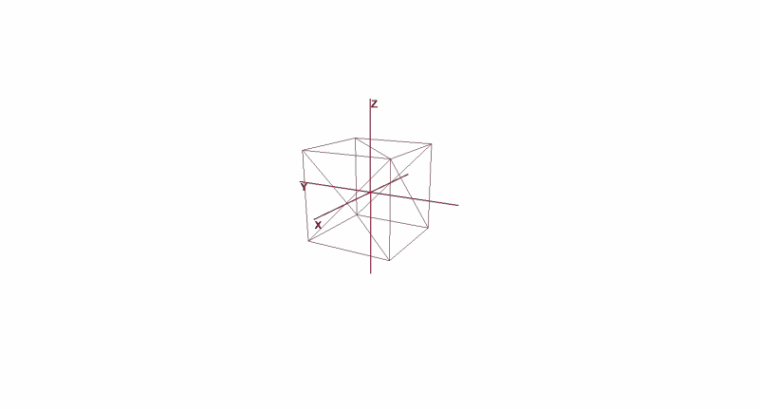
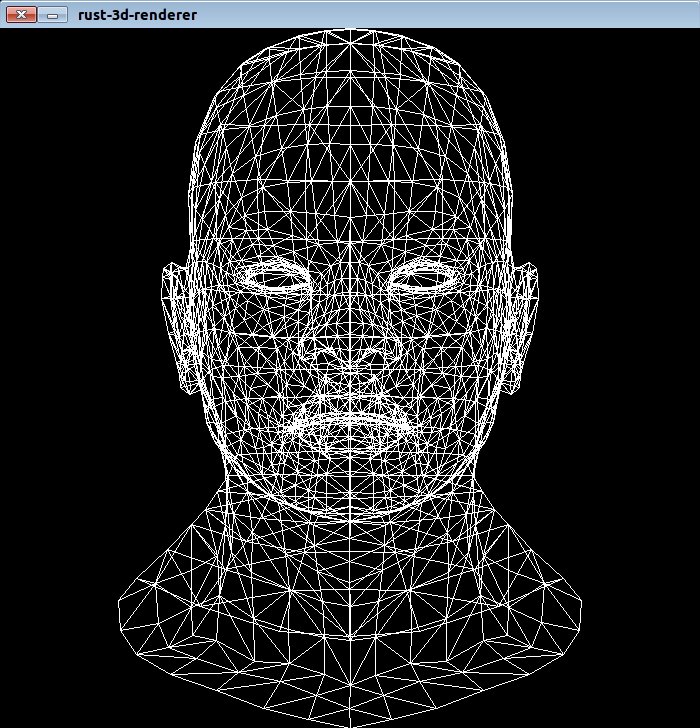
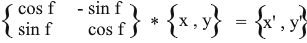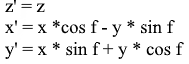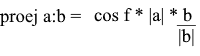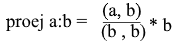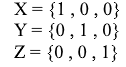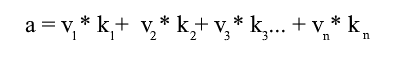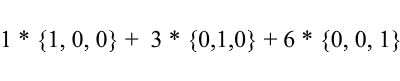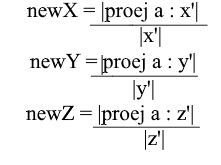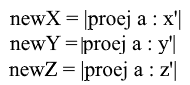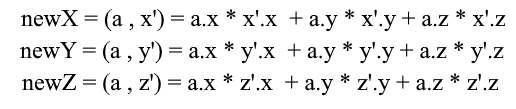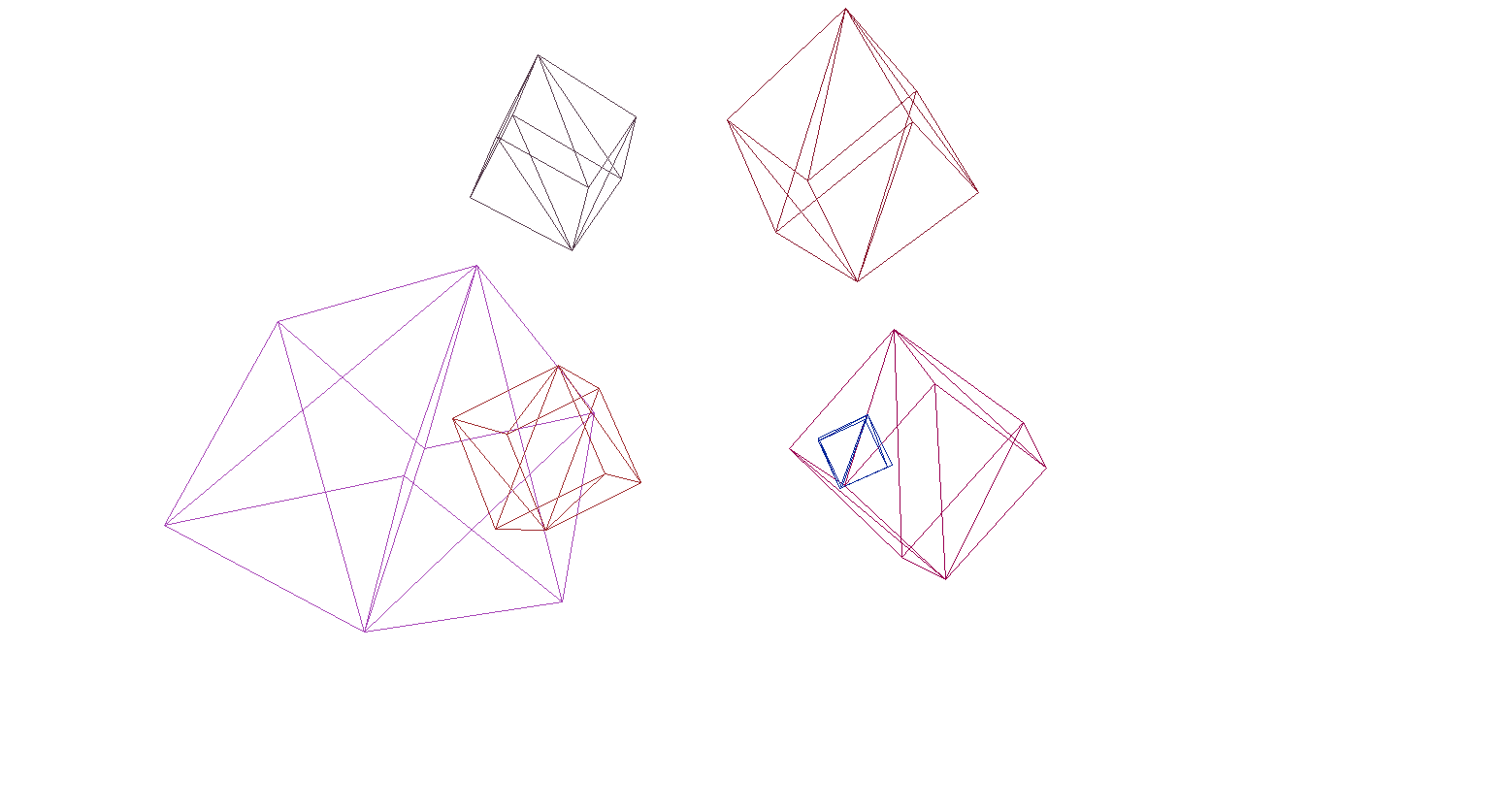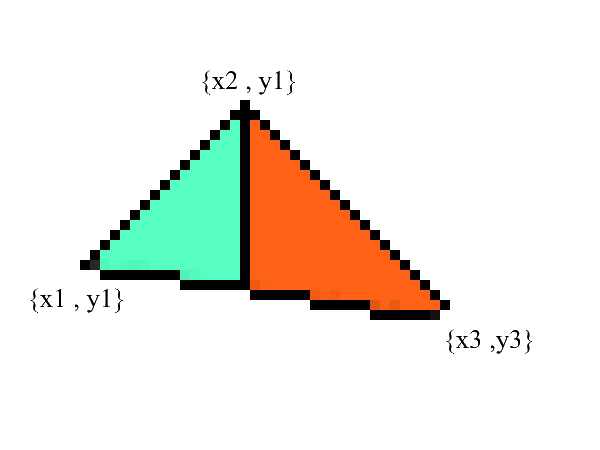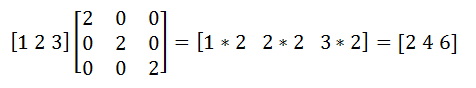Привет меня зовут Давид, а вот я собственной персоной отрендеренный своим самописным рендером:
К сожалению я не смог найти более качественную бесплатную модель, но все равно выражаю благодарность заморскому скульптору запечатлевшему меня в цифре! И как вы уже догадались, речь пойдет о написании CPU — рендера.
Идея
С развитием шейдерных языков и увеличением мощностей GPU все больше людей заинтересовались программированием графики. Появились новые направления, такие как например Ray marching со стремительным ростом своей популярности.
В преддверии выхода нового монстра от NVidia я решил написать свою (ламповую и олдскульную) статью про основы рендеринга на CPU. Она является отражением моего личного опыта написания рендера, и в ней я попытаюсь довести понятия и алгоритмы с которыми я столкнулся в процессе кодинга. Стоит понимать, что производительность данного софта будет весьма низкая в силу непригодности процессора для выполнения подобных задач.
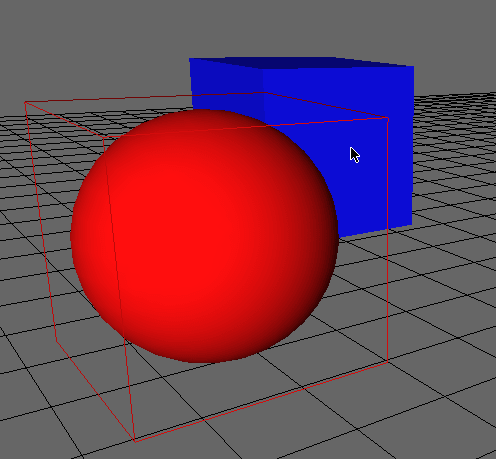
Выбор языка изначально падал на c++ или rust, но я остановился на c# из-за простоты написания кода и широких возможностей для оптимизации. Итоговым продуктом данной статьи будет рендер, способный выдавать подобные картинки:
Все модели, использованные мной здесь, распространяются в открытом доступе, не занимайтесь пиратством и уважайте труд художников!
Математика
Само собой куда же писать рендеры без понимания их математических основ. В этом разделе я изложу только те концепции, которые я использовал в коде. Тем кто не уверен в своих знаниях пропускать данный раздел не советую, без понимания этих основ трудно будет понять дальнейшее изложение. Так же я рассчитываю, что тот кто решил изучать computation geometry будет иметь базовые знания в линейной алгебре, геометрии, а так же тригонометрии(углы, вектора, матрицы, скалярное произведение). Для тех кто хочет понять вычислительную геометрию глубже, могу порекомендовать книгу Е. Никулина «Компьютерная геометрия и алгоритмы машинной графики».
Повороты вектора. Матрица поворота
Поворот — это одно из основных линейных преобразований векторного пространства. Так же оно является еще и ортогональным преобразованием, так как сохраняет длины преобразованных векторов. В двумерном пространстве существует два типа поворотов:
- Поворот относительно начала координат
- Поворот относительно некоторой точки
Здесь я рассмотрю только первый тип, т.к. второй является производным от первого и отличается лишь сменой системы координат вращения (системы координат мы разберем далее).
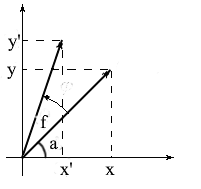
Давайте выведем формулы для вращения вектора в двумерном пространстве. Обозначим координаты исходного вектора — {x, y}. Координаты нового вектора, повернутого на угол f, обозначим как {x’ y’}.
Мы знаем, что длина у этих векторов общая и поэтому можем использовать понятия косинуса и синуса для того, чтобы выразить эти вектора через длину и угол относительно оси OX:
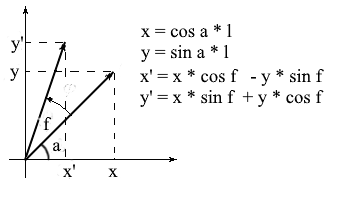
Заметьте, что мы можем использовать формулы косинуса и синуса суммы для того, чтобы разложить значения x’ и y’. Для тех, кто подзабыл я напомню эти формулы:
Разложив координаты повернутого вектора через них получим:
Здесь нетрудно заметить, что множители l * cos a и l * sin a – это координаты исходного вектора: x = l * cos a, y = l * sin a. Заменим их на x и y:
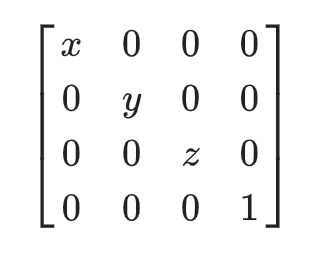
Таким образом мы выразили повернутый вектор через координаты исходного вектора и угол его поворота. В виде матрицы это выражение будет выглядеть так:
Умножьте и проверьте что результат эквивалентен тому, что мы вывели.
Поворот в трехмерном пространстве
Мы рассмотрели поворот в двумерном пространстве, а так же вывели матрицу для него. Теперь возникает вопрос, а как получить подобные преобразования для трех измерений? В двумерном случае мы вращали вектора на плоскости, здесь же бесконечное количество плоскостей относительно которых мы можем это сделать. Однако существует три базовых типа вращений, при помощи которых можно выразить любой поворот вектора в трехмерном пространстве — это XY, XZ, YZ вращения.
XY вращение.
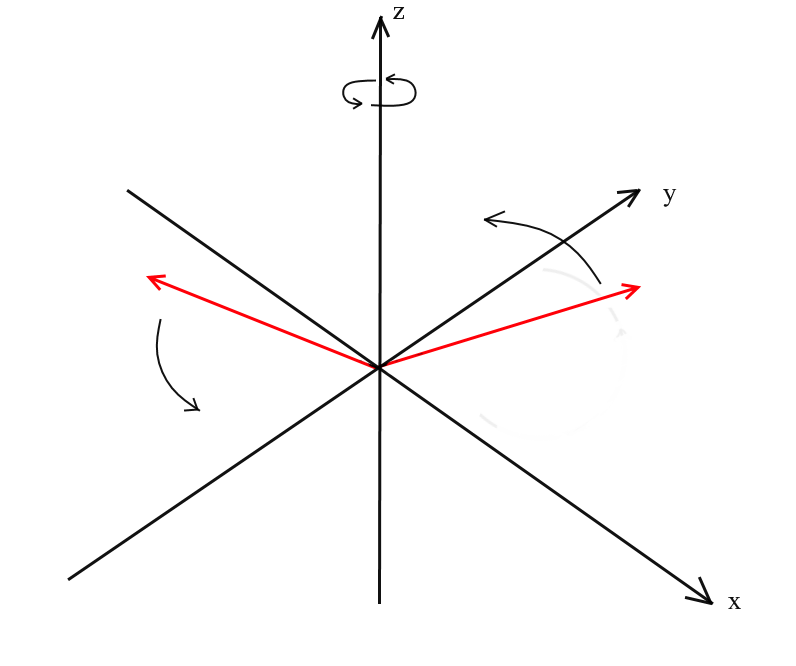
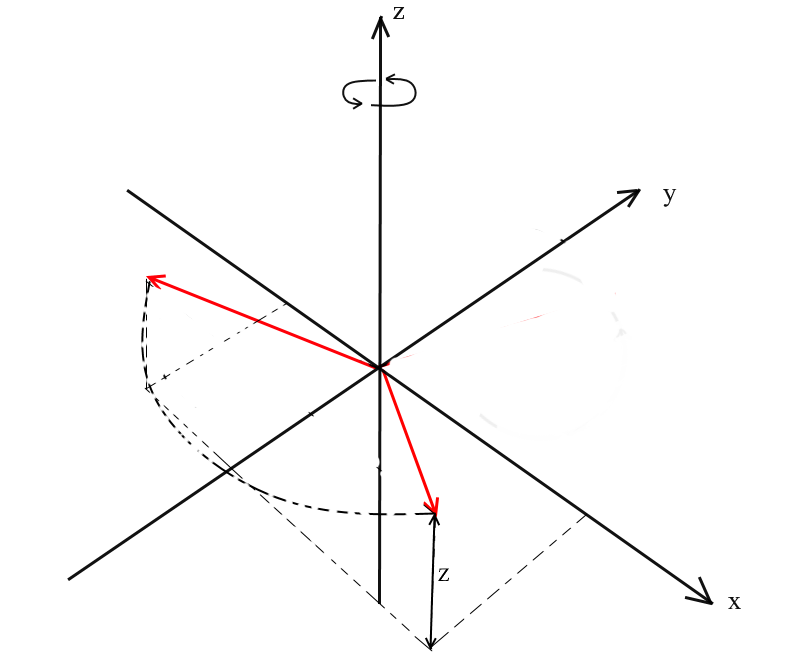
При таком повороте мы вращаем вектор относительно оси OZ координатной системы. Представьте, что вектора — это вертолётные лопасти, а ось OZ — это мачта на которой они держаться. При XY вращении вектора будут поворачиваться относительно оси OZ, как лопасти вертолета относительно мачты.
Заметьте, что при таком вращении z координаты векторов не меняются, а меняются x и x координаты — поэтому это и называется XY вращением.
Нетрудно вывести и формулы для такого вращения: z — координата остается прежней, а x и y изменяются по тем же принципам, что и в 2д вращении.
То же в виде матрицы:
Для XZ и YZ вращений все аналогично:
Проекция
Понятие проекции может варьироваться в зависимости от контекста в котором его используют. Многие, наверное, слышали про такие понятия, как проекция на плоскость или проекция на координатную ось.
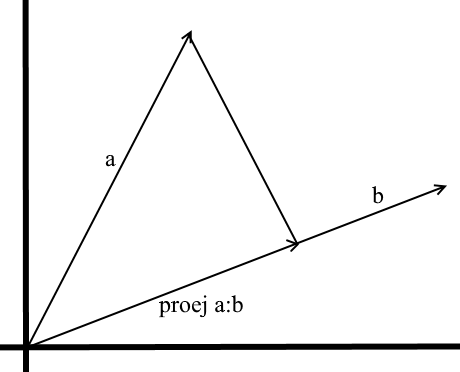
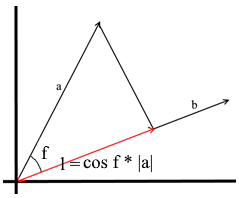
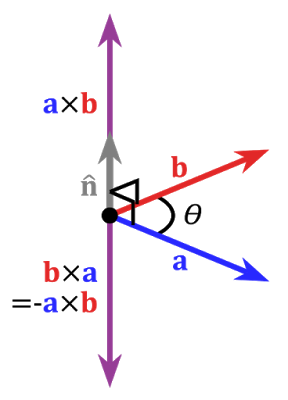
В том понимании которое мы используем здесь проекция на вектор — это тоже вектор. Его координаты – точка пересечения перпендикуляра опущенного из вектора a на b с вектором b.
Для задания такого вектора нам нужно знать его длину и направление. Как мы знаем прилегающий катет и гипотенуза в прямоугольном треугольнике связаны отношением косинуса, поэтому используем его, чтобы выразить длину вектора проекции:
Направление вектора проекции по определению совпадает с вектором b, значит проекция определяется формулой:
Здесь мы получаем направление проекции в виде единичного вектора и умножаем его на длину проекции. Несложно понять, что результатом будет как раз-таки то, что мы ищем.
Теперь представим все через скалярное произведение:
Получаем удобную формулу для нахождения проекции:
Системы координат. Базисы
Многие привыкли работать в стандартной системе координат XYZ, в ней любые 2 оси будут перпендикулярны друг другу, а координатные оси можно представить в виде единичных векторов:
На деле же систем координат бесконечное множество, каждая из них является базисом. Базис n-мерного пространства является набором векторов {v1, v2 …… vn} через которые представляются все вектора этого пространства. При этом ни один вектор из базиса нельзя представить через другие его вектора. По сути каждый базис является отдельной системой координат, в которой вектора будут иметь свои, уникальные координаты.
Давайте разберем, что из себя представляет базис для двумерного пространства. Возьмём для примера всем знакомую декартову систему координат из векторов X {1, 0}, Y {0, 1}, которая является одним из базисов для двумерного пространства:
Любой вектор на плоскости можно представить в виде суммы векторов этого базиса с некими коэффициентами или же в виде линейной комбинации. Вспомните, что вы делаете когда записываете координаты вектора — вы пишете x — координату, а далее — y. Таким образом вы на самом деле определяете коэффициенты разложения по векторам базиса.
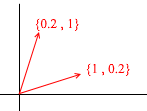
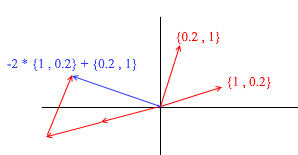
Теперь возьмём другой базис:
Через его вектора также можно представить любой 2д вектор:
А вот такой набор векторов не является базисом двухмерного пространства:
В нем два вектора {1,1} и {2,2} лежат на одной прямой. Какие бы их комбинации вы не брали получать будете только вектора, лежащие на общей прямой y = x. Для наших целей такие дефектные не пригодятся, однако, понимать разницу, я считаю, стоит. По определению все базисы объединяет одно свойство – ни один из векторов базиса нельзя представить в виде суммы других векторов базиса с коэффициентами или же ни один вектор базиса не является линейной комбинацией других. Вот пример набора из 3-х векторов который так же не является базисом:
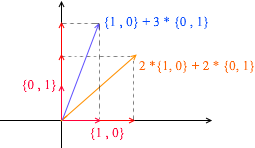
Через него можно выразить любой вектор двумерной плоскости, однако вектор {1, 1} в нем является лишним так как сам может быть выражен через вектора {1, 0} и {0,1} как {1,0} + {0,1}.
Вообще любой базис n-мерного пространства будет содержать ровно n векторов, для 2д это n соответственно равно 2.
Перейдем к 3д. Трехмерный базис будет содержать в себе 3 вектора:
Если для двумерного базиса достаточно было двух векторов не лежащих на одной прямой, то в трехмерном пространстве набор векторов будет базисом если:
- 1)2 вектора не лежат на одной прямой
- 2)3-й не лежит на плоскости образованной двумя другими.
С данного момента базисы, с которыми мы работаем будут ортогональными (любые их вектора перпендикулярны) и нормированными (длина любого вектора базиса — 1). Другие нам просто не понадобятся. К примеру стандартный базис
удовлетворяет этим критериям.
Переход в другой базис
До сих пор мы записывали разложение вектора как сумму векторов базиса с коэффициентами:
Снова рассмотрим стандартный базис – вектор {1, 3, 6} в нем можно записать так:
Как видите коэффициенты разложения вектора в базисе являются его координатами в этом базисе. Разберем следующий пример:
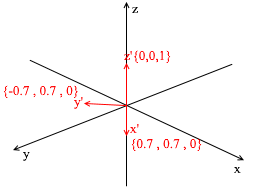
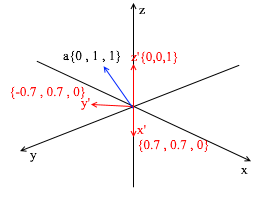
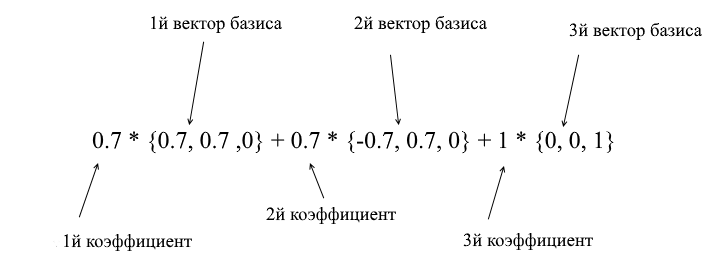
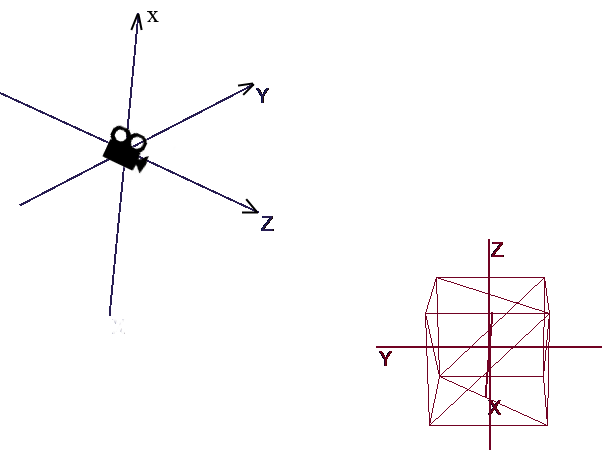
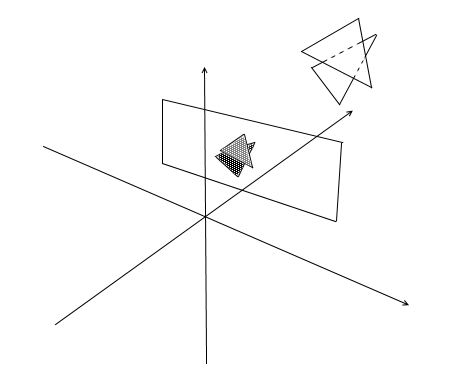
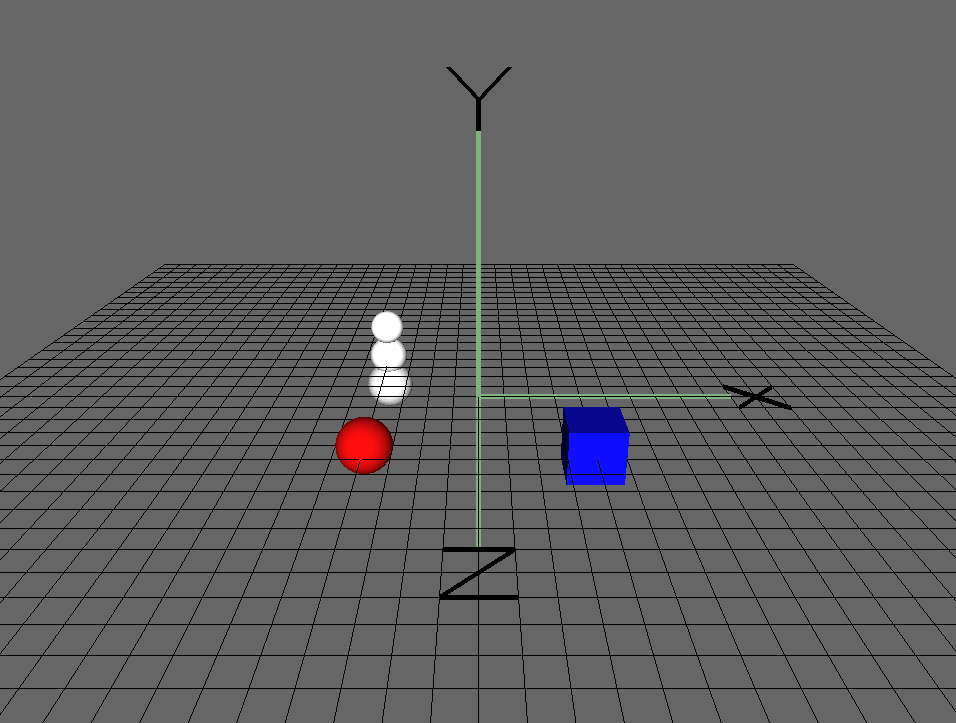
Этот базис получен из стандартного применением к нему XY вращения на 45 градусов. Возьмем вектор a в стандартной системе имеющий координаты {0 ,1, 1}
Через вектора нового базиса его можно разложить таким образом:
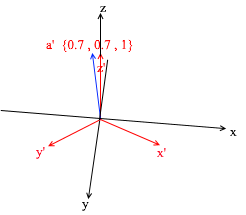
Если вы посчитаете эту сумму, то получите {0, 1, 1} – вектор а в стандартном базисе. Исходя из этого выражения в новом базисе вектор а имеет координаты {0.7, 0.7, 1} – коэффициенты разложения. Это будет виднее если взглянуть с другого ракурса:
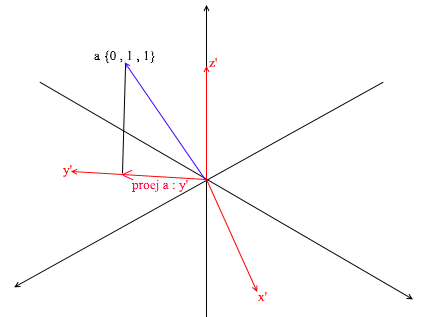
Но как находить эти коэффициенты? Вообще универсальный метод — это решение довольно сложной системы линейных уравнений. Однако как я сказал ранее использовать мы будем только ортогональные и нормированные базисы, а для них есть весьма читерский способ. Заключается он в нахождении проекций на вектора базиса. Давайте с его помощью найдем разложение вектора a в базисе X{0.7, 0.7, 0} Y{-0.7, 0.7, 0} Z{0, 0, 1}
Для начала найдем коэффициент для y’. Первым шагом мы находим проекцию вектора a на вектор y’ (как это делать я разбирал выше):
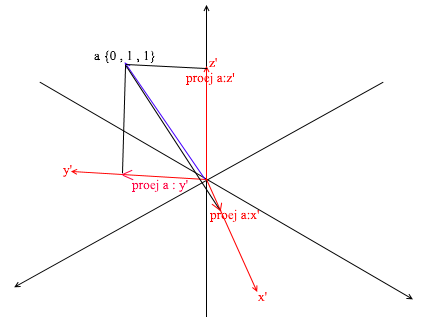
Второй шаг: делим длину найденной проекции на длину вектора y’, тем самым мы узнаем “сколько векторов y’ помещается в векторе проекции” – это число и будет коэффициентом для y’, а также y — координатой вектора a в новом базисе! Для x’ и z’ повторим аналогичные операции:
Теперь мы имеем формулы для перехода из стандартного базиса в новый:
Ну а так как мы используем только нормированные базисы и длины их векторов равны 1 отпадет необходимость делить на длину вектора в формуле перехода:
Раскроем x-координату через формулу проекции:
Заметьте, что знаменатель (x’, x’) и вектор x’ в случае нормированного базиса так же равен 1 и их можно отбросить. Получим:
Мы видим, что координата x базисе выражается как скалярное произведение (a, x’), координата y соответственно – как (a, y’), координата z – (a, z’). Теперь можно составить матрицу перехода к новым координатам:
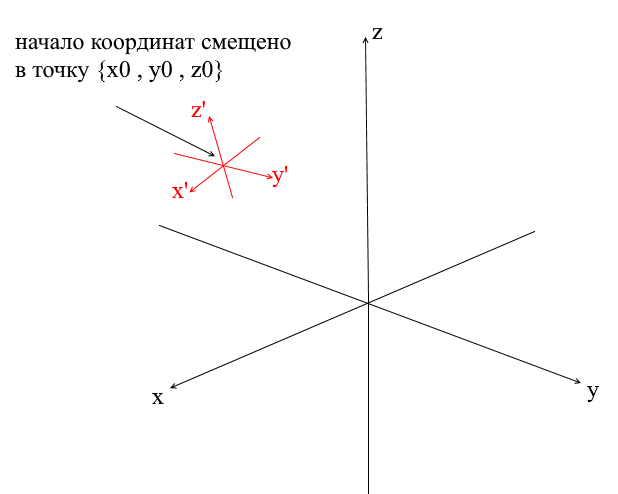
Системы координат со смещенным центром
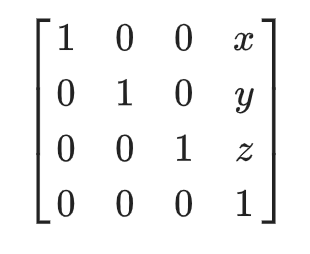
У всех систем координат которые мы рассмотрели выше началом координат была точка {0,0,0}. Помимо этого существуют еще системы со смещенной точкой начала координат:
Для того, чтобы перевести вектор в такую систему нужно сначала выразить его относительно нового центра координат. Сделать это просто — вычесть из вектора этот центр. Таким образом вы как бы «передвигаете» саму систему координат к новому центу, при этом вектор остается на месте. Далее можно использовать уже знакомую нам матрицу перехода.
Пишем геометрический движок. Создание проволочного рендера.
Ну вот, думаю тому кто прошел раздел с математикой и не закрыл статью можно промывать мозги более интересными вещами! В этом разделе мы начнем писать основы 3д движка и рендеринга. Вообще рендеринг — это довольно сложная процедура, которая включает в себя много разных операций: отсечение невидимых граней, растеризация, расчет света, обработку различных эффектов, материалов(иногда даже физику). Все это мы частично разберем в дальнейшем, а сейчас мы займемся более простыми вещами — напишем проволочный рендер. Суть его в том, что он рисует объект в виде линий, соединяющих его вершины, поэтому результат выглядит похожим на сеть из проволок:
Полигональная графика
Традиционно в компьютерной графике используется полигональное представление данных трехмерных объектов. Таким образом представляются данные в форматах OBJ, 3DS, FBX и многих других. В компьютере такие данные хранятся в виде двух множеств: множество вершин и множество граней(полигонов). Каждая вершина объекта представлена своей позицией в пространстве — вектором, а каждая грань(полигон) представлена тройкой целых чисел которые являются индексами вершин данного объекта. Простейшие объекты(кубы, сферы и т.д.) состоят из таких полигонов и называются примитивами.
В нашем движке примитив будет основным объектом трехмерной геометрии — все остальные объекты будут наследоваться от него. Опишем класс примитива:
abstract class Primitive
{
public Vector3[] Vertices { get; protected set; }
public int[] Indexes { get; protected set; }
}
Пока все просто — есть вершины примитива и есть индексы для формирования полигонов. Теперь можно использовать этот класс чтобы создать куб:
public class Cube : Primitive
{
public Cube(Vector3 center, float sideLen)
{
var d = sideLen / 2;
Vertices = new Vector3[]
{
new Vector3(center.X - d , center.Y - d, center.Z - d) ,
new Vector3(center.X - d , center.Y - d, center.Z) ,
new Vector3(center.X - d , center.Y , center.Z - d) ,
new Vector3(center.X - d , center.Y , center.Z) ,
new Vector3(center.X + d , center.Y - d, center.Z - d) ,
new Vector3(center.X + d , center.Y - d, center.Z) ,
new Vector3(center.X + d , center.Y + d, center.Z - d) ,
new Vector3(center.X + d , center.Y + d, center.Z + d) ,
};
Indexes = new int[]
{
1,2,4 ,
1,3,4 ,
1,2,6 ,
1,5,6 ,
5,6,8 ,
5,7,8 ,
8,4,3 ,
8,7,3 ,
4,2,8 ,
2,8,6 ,
3,1,7 ,
1,7,5
};
}
}
int Main()
{
var cube = new Cube(new Vector3(0, 0, 0), 2);
}
Реализуем системы координат
Мало задать объект набором полигонов, для планирования и создания сложных сцен необходимо расположить объекты в разных местах, поворачивать их, уменьшать или увеличивать их в размере. Для удобства этих операций используются так называемые локальные и глобальная системы координат. Каждый объект на сцене имеет свои свою собственную систему координат — локальную, а так же собственную точку центра.
Представление объекта в локальных координатах позволяет легко производить любые операции с ним. Например, для перемещения объекта на вектор a достаточно будет сдвинуть центр его системы координат на этот вектор, для вращения объекта — повернуть его локальные координаты.
При работе с объектом мы будем производить операции с его вершинами в локальной системе координат, при рендеринге будем предварительно переводить все объекты сцены в единую систему координат — глобальную. Добавим системы координат в код. Для этого создадим объект класса Pivot (стержень, точка опоры) который будет представлять локальный базис объекта и его центральную точку. Перевод точки в систему координат представленную Pivot будет производиться в 2 шага:
- 1)Представление точки относительно центра новых координат
- 2)Разложение по векторам нового базиса
Наоборот же, чтобы представить локальную вершину объекта в глобальных координатах необходимо выполнить эти действия в обратном порядке:
- 1)Разложение по векторам глобального базиса
- 2)Представление относительно глобального центра
Напишем класс для представления систем координат:
public class Pivot
{
//точка центра
public Vector3 Center { get; private set; }
//вектора локального базиса - локальные координатные оси
public Vector3 XAxis { get; private set; }
public Vector3 YAxis { get; private set; }
public Vector3 ZAxis { get; private set; }
//Матрица перевода в локальные координаты
public Matrix3x3 LocalCoordsMatrix => new Matrix3x3
(
XAxis.X, YAxis.X, ZAxis.X,
XAxis.Y, YAxis.Y, ZAxis.Y,
XAxis.Z, YAxis.Z, ZAxis.Z
);
//Матрица перевода в глобальные координаты
public Matrix3x3 GlobalCoordsMatrix => new Matrix3x3
(
XAxis.X , XAxis.Y , XAxis.Z,
YAxis.X , YAxis.Y , YAxis.Z,
ZAxis.X , ZAxis.Y , ZAxis.Z
);
public Vector3 ToLocalCoords(Vector3 global)
{
//Находим позицию вектора относительно точки центра и раскладываем в локальном базисе
return LocalCoordsMatrix * (global - Center);
}
public Vector3 ToGlobalCoords(Vector3 local)
{
//В точности да наоборот - раскладываем локальный вектор в глобальном базисе и находим позицию относительно глобального центра
return (GlobalCoordsMatrix * local) + Center;
}
public void Move(Vector3 v)
{
Center += v;
}
public void Rotate(float angle, Axis axis)
{
XAxis = XAxis.Rotate(angle, axis);
YAxis = YAxis.Rotate(angle, axis);
ZAxis = ZAxis.Rotate(angle, axis);
}
}
Теперь используя данный класс добавим в примитивы функции вращения, передвижения и увеличения:
public abstract class Primitive
{
//Локальный базис объекта
public Pivot Pivot { get; protected set; }
//Локальные вершины
public Vector3[] LocalVertices { get; protected set; }
//Глобальные вершины
public Vector3[] GlobalVertices { get; protected set; }
//Индексы вершин
public int[] Indexes { get; protected set; }
public void Move(Vector3 v)
{
Pivot.Move(v);
for (int i = 0; i < LocalVertices.Length; i++)
GlobalVertices[i] += v;
}
public void Rotate(float angle, Axis axis)
{
Pivot.Rotate(angle , axis);
for (int i = 0; i < LocalVertices.Length; i++)
GlobalVertices[i] = Pivot.ToGlobalCoords(LocalVertices[i]);
}
public void Scale(float k)
{
for (int i = 0; i < LocalVertices.Length; i++)
LocalVertices[i] *= k;
for (int i = 0; i < LocalVertices.Length; i++)
GlobalVertices[i] = Pivot.ToGlobalCoords(LocalVertices[i]);
}
}
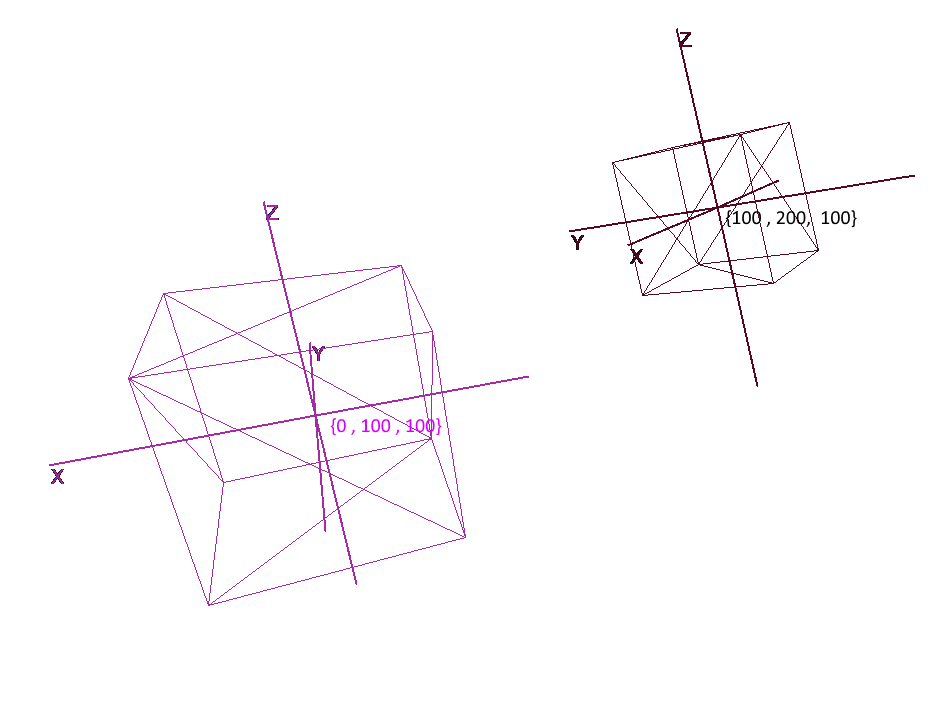
Вращение и перемещение объекта с помощью локальных координат
Рисование полигонов. Камера
Основным объектом сцены будет камера — с помощью нее объекты будут рисоваться на экране. Камера, как и все объекты сцены, будет иметь локальные координаты в виде объекта класса Pivot — через него мы будем двигать и вращать камеру:
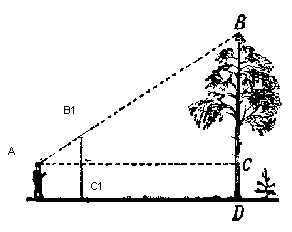
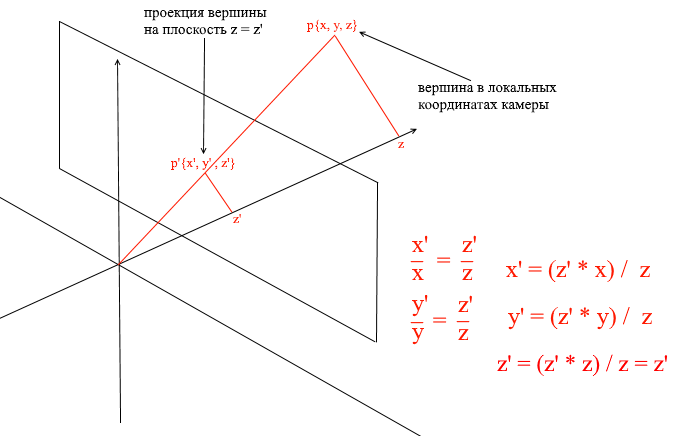
Для отображения объекта на экране будем использовать немудреный способ перспективной проекции. Принцип на котором основан этом метод заключается в том, что чем дальше от нас расположен объект тем меньше он будет казаться. Наверное многие решали когда-то в школе задачу про измерение высоты дерева находящимся на некотором расстоянии от наблюдателя:
Представьте, что луч от верхней точки дерева падает на некую проекционную плоскость находящуюся на расстоянии C1 от наблюдателя и рисует на ней точку. Наблюдатель видит эту точку и хочет по ней определить высоту дерева. Как вы могли заметить высота дерева и высота точки на проекционной плоскости связанны отношением подобных треугольников. Тогда наблюдатель может определить высоту точки используя это отношение:
Наоборот же, зная высоту дерева он может найти высоту точки на проекционной плоскости:
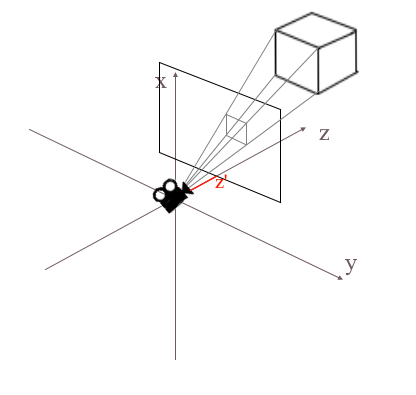
Теперь вернемся к нашей камере. Представьте, что к оси z координат камеры прикреплена проекционная плоскость на расстоянии z’ от начала координат. Формула такой плоскости z = z’, ее можно задать одним числом — z’. На эту плоскость падают лучи от вершин различных объектов. Попадая на плоскость луч будет оставлять на ней точку. Соединяя такие точки можно нарисовать объект.
Такая плоскость будет представлять экран. Координату проекции вершины объекта на экран будем находить в 2 этапа:
- 1)Переводим вершину в локальные координаты камеры
- 2)Находим проекцию точки через отношение подобных треугольников
Проекция будет 2-мерным вектором, ее координаты x’ и y’ и будут определять позицию точки на экране компьютера.
Класс камеры 1
public class Camera
{
//локальные координаты камеры
public Pivot Pivot { get; private set; }
//расстояние до проекционной плоскости
public float ScreenDist { get; private set; }
public Camera(Vector3 center, float screenDist)
{
Pivot = new Pivot(center);
ScreenDist = screenDist;
}
public void Move(Vector3 v)
{
Pivot.Move(v);
}
public void Rotate(float angle, Axis axis)
{
Pivot.Rotate(angle, axis);
}
public Vector2 ScreenProection(Vector3 v)
{
var local = Pivot.ToLocalCoords(v);
//через подобные треугольники находим проекцию
var delta = ScreenDist / local.Z;
var proection = new Vector2(local.X, local.Y) * delta;
return proection;
}
}
Данный код имеет несколько ошибок, о исправлении которых мы поговорим далее.
Отсекаем невидимые полигоны
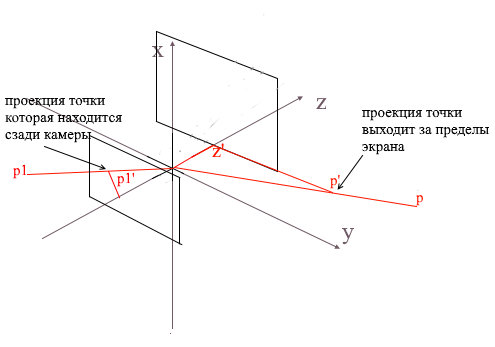
Спроецировав таким образом на экран три точки полигона мы получим координаты треугольника который соответствует отображению полигона на экране. Но таким образом камера будет обрабатывать любые вершины, включая те, чьи проекции выходят за область экрана, если попытаться нарисовать такую вершину велика вероятность словить ошибок. Камера так же будет обрабатывать полигоны которые находятся позади нее (координаты z их точек в локальном базисе камеры меньше z’) — такое «затылковое» зрение нам тоже ни к чему.
Для отсечения невидимых вершин в open gl используются метод усекающей пирамиды. Заключается он в задании двух плоскостей — ближней(near plane) и дальней(far plane). Все, что лежит между этими двумя плоскостями будет подлежать дальнейшей обработке. Я же использую упрощенный вариант с одной усекающей плоскостью — z’. Все вершины, лежащие позади нее будут невидимыми.
Добавим в камеру два новых поля — ширину и высоту экрана.
Теперь каждую спроецированную точку будем проверять на попадание в область экрана. Так же отсечем точки позади камеры. Если точка лежит сзади или ее проекция не попадает на экран то метод вернет точку {float.NaN, float.NaN}.
Код камеры 2
public Vector2 ScreenProection(Vector3 v)
{
var local = Pivot.ToLocalCoords(v);
//игнорируем точки сзади камеры
if (local.Z < ScreenDist)
{
return new Vector2(float.NaN, float.NaN);
}
//через подобные треугольники находим проекцию
var delta = ScreenDist / local.Z;
var proection = new Vector2(local.X, local.Y) * delta;
//если точка принадлежит экранной области - вернем ее
if (proection.X >= 0 && proection.X < ScreenWidth && proection.Y >= 0 && proection.Y < ScreenHeight)
{
return proection;
}
return new Vector2(float.NaN, float.NaN);
}
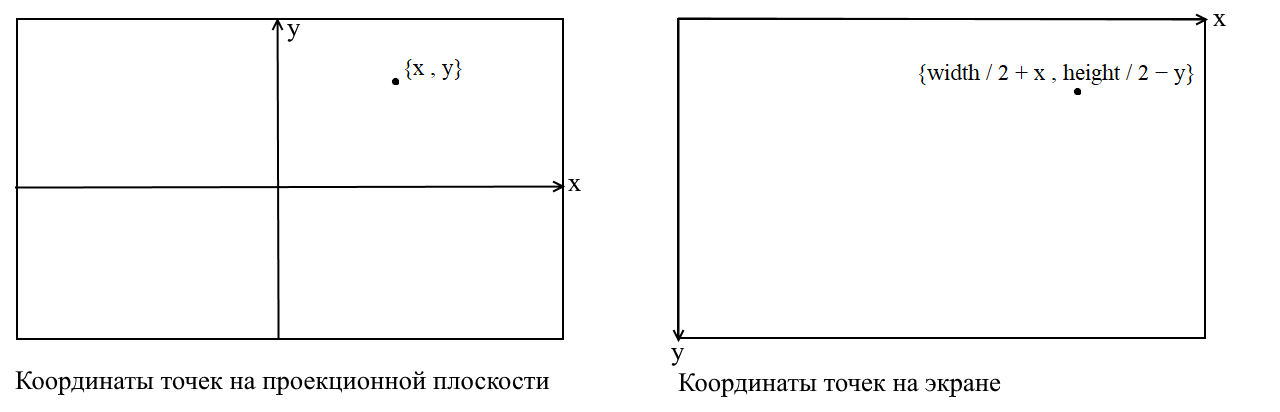
Переводим в экранные координаты
Здесь я разъясню некоторый момент. Cвязан он с тем, что во многих графических библиотеках рисование происходит в экранной системе координат, в таких координатах начало — это верхняя левая точка экрана, x увеличивается при движении вправо, а y — при движении вниз. В нашей проекционной плоскости точки представлены в обычных декартовых координатах и перед отрисовкой необходимо переводить эти координаты в экранные. Сделать это нетрудно, нужно только сместить начало координат в верхний левый угол и инвертировать y:
Код камеры 3
public Vector2 ScreenProection(Vector3 v)
{
var local = Pivot.ToLocalCoords(v);
//игнорируем точки сзади камеры
if (local.Z < ScreenDist)
{
return new Vector2(float.NaN, float.NaN);
}
//через подобные треугольники находим проекцию
var delta = ScreenDist / local.Z;
var proection = new Vector2(local.X, local.Y) * delta;
//этот код нужен для перевода проекции в экранные координаты
var screen = proection + new Vector2(ScreenWidth / 2, -ScreenHeight / 2);
var screenCoords = new Vector2(screen.X, -screen.Y);
//если точка принадлежит экранной области - вернем ее
if (screenCoords.X >= 0 && screenCoords.X < ScreenWidth && screenCoords.Y >= 0 && screenCoords.Y < ScreenHeight)
{
return screenCoords;
}
return new Vector2(float.NaN, float.NaN);
}
Корректируем размер спроецированного изображения
Если вы используете предыдущий код для того, чтобы нарисовать объект то получите что-то вроде этого:
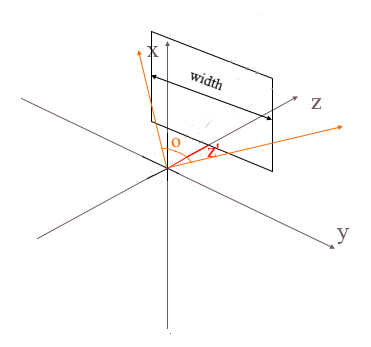
Почему — то все объекты рисуются очень маленькими. Для того, чтобы понять причину вспомните как мы вычисляли проекцию — умножали x и y координаты на дельту отношения z’ / z. Это значит, что размер объекта на экране зависит от расстояния до проекционной плоскости z’. А ведь z’ мы можем задать сколь угодно маленьким значением. Значит нам нужно корректировать размер проекции в зависимости от текущего значения z’. Для этого добавим в камеру еще одно поле — угол ее обзора.
Он нам нужен для сопоставления углового размера экрана с его шириной. Угол будет сопоставлен с шириной экрана таким образом: максимальный угол в пределах которого смотрит камера — это левый или правый край экрана. Тогда максимальный угол от оси z камеры составляет o / 2. Проекция, которая попала на правый край экрана должна иметь координату x = width / 2, а на левый: x = -width / 2. Зная это выведем формулу для нахождения коэффициента растяжения проекции:
Код камеры 4
public float ObserveRange { get; private set; }
public float Scale => ScreenWidth / (float)(2 * ScreenDist * Math.Tan(ObserveRange / 2));
public Vector2 ScreenProection(Vector3 v)
{
var local = Pivot.ToLocalCoords(v);
//игнорируем точки сзади камеры
if (local.Z < ScreenDist)
{
return new Vector2(float.NaN, float.NaN);
}
//через подобные треугольники находим проекцию и умножаем ее на коэффициент растяжения
var delta = ScreenDist / local.Z * Scale;
var proection = new Vector2(local.X, local.Y) * delta;
//этот код нужен для перевода проекции в экранные координаты
var screen = proection + new Vector2(ScreenWidth / 2, -ScreenHeight / 2);
var screenCoords = new Vector2(screen.X, -screen.Y);
//если точка принадлежит экранной области - вернем ее
if (screenCoords.X >= 0 && screenCoords.X < ScreenWidth && screenCoords.Y >= 0 && screenCoords.Y < ScreenHeight)
{
return screenCoords;
}
return new Vector2(float.NaN, float.NaN);
}
Вот такой простой код отрисовки я использовал для теста:
Код рисования объектов
public DrawObject(Primitive primitive , Camera camera)
{
for (int i = 0; i < primitive.Indexes.Length; i+=3)
{
var color = randomColor();
// индексы вершин полигона
var i1 = primitive.Indexes[i];
var i2 = primitive.Indexes[i+ 1];
var i3 = primitive.Indexes[i+ 2];
// вершины полигона
var v1 = primitive.GlobalVertices[i1];
var v2 = primitive.GlobalVertices[i2];
var v3 = primitive.GlobalVertices[i3];
// рисуем полигон
DrawPolygon(v1,v2,v3 , camera , color);
}
}
public void DrawPolygon(Vector3 v1, Vector3 v2, Vector3 v3, Camera camera , color)
{
//проекции вершин
var p1 = camera.ScreenProection(v1);
var p2 = camera.ScreenProection(v2);
var p3 = camera.ScreenProection(v3);
//рисуем полигон
DrawLine(p1, p2 , color);
DrawLine(p2, p3 , color);
DrawLine(p3, p2 , color);
}
Давайте проверим рендер на сцене и кубов:
И да, все прекрасно работает. Для тех, кому разноцветные кубики не кажутся пафосными я написал функцию парсинга моделей формата OBJ в объекты типа Primitive, залил фон черным и отрисовал несколько моделей:
Результат работы рендера
Растеризация полигонов. Наводим красоту.
В прошлом разделе мы написали проволочный рендер. Теперь мы займемся его модернизацией — реализуем растеризацию полигонов.
По простому растеризировать полигон — это значит закрасить его. Казалось бы зачем писать велосипед, когда есть уже готовые функции растеризации треугольника. Вот что будет если нарисовать все дефолтными инструментами:
Современное искусство, полигоны сзади нарисовались поверх передних, одним словом — каша. К тому же как таким образом текстурировать объекты? Да, никак. Значит нам нужно написать свой имба-растерайзер, который будет уметь в отсечение невидимых точек, текстуры и даже в шейдеры! Но для того чтобы это сделать стоит понять как вообще красить треугольники.
Алгоритм Брезенхема для рисования линии.
Начнем с линий. Если кто не знал алгоритм Брезенхема — это основной алгоритм рисования прямых в компьютерной графике. Он или его модификации используется буквально везде: рисование прямых, отрезков, окружностей и т.п. Кому интересно более подробное описание — читайте вики. Алгоритм Брезенхема
Имеется отрезок соединяющий точки {x1, y1} и {x2, y2}. Чтобы нарисовать отрезок между ними нужно закрасить все пиксели которые попадают на него. Для двух точек отрезка можно найти x-координаты пикселей в которых они лежат: нужно лишь взять целые части от координат x1 и x2. Чтобы закрасить пиксели на отрезке запускаем цикл от x1 до x2 и на каждой итерации вычисляем y — координату пикселя который попадает на прямую. Вот код:
void Brezenkhem(Vector2 p1 , Vector2 p2)
{
int x1 = Floor(p1.X);
int x2 = Floor(p2.X);
if (x1 > x2) {Swap(x1, x2); Swap(p1 , p2);}
float d = (p2.Y - p1.Y) / (x2 - x1);
float y = p1.Y;
for (int i = x1; i <= x2; i++)
{
int pixelY = Floor(y);
FillPixel(i , pixelY);
y += d;
}
}
Картинка из вики
Растеризация треугольника. Алгоритм заливки
Линии рисовать мы умеем, а вот с треугольниками будет чуть посложнее(не намного)! Задача рисования треугольника сводится к нескольким задачам рисования линий. Для начала разобьем треугольник на две части предварительно отсортировав точки в порядке возрастания x:
Заметьте — теперь у нас есть две части в которых явно выражены нижняя и верхняя границы. все что осталось — это залить все пиксели находящиеся между ними! Сделать это можно в 2 цикла: от x1 до x2 и от x3 до x2.
void Triangle(Vector2 v1 , Vector2 v2 , Vector2 v3)
{
//хардкодим BubbleSort для упорядочивания по x
if (v1.X > v2.X) { Swap(v1, v2); }
if (v2.X > v3.X) { Swap(v2, v3); }
if (v1.X > v2.X) { Swap(v1, v2); }
//узнаем на сколько увеличивается y границ при увеличении x
//избегаем деления на 0: если x1 == x2 значит эта часть треугольника - линия
var steps12 = max(v2.X - v1.X , 1);
var steps13 = max(v3.X - v1.X , 1);
var upDelta = (v2.Y - v1.Y) / steps12;
var downDelta = (v3.Y - v1.Y) / steps13;
//верхняя граница должна быть выше нижней
if (upDelta < downDelta) Swap(upDelta , downDelta);
//изначально у координаты границ равны y1
var up = v1.Y;
var down = v1.Y;
for (int i = (int)v1.X; i <= (int)v2.X; i++)
{
for (int g = (int)down; g <= (int)up; g++)
{
FillPixel(i , g);
}
up += upDelta;
down += downDelta;
}
//все то же самое для другой части треугольника
var steps32 = max(v2.X - v3.X , 1);
var steps31 = max(v1.X - v3.X , 1);
upDelta = (v2.Y - v3.Y) / steps32;
downDelta = (v1.Y - v3.Y) / steps31;
if (upDelta < downDelta) Swap(upDelta, downDelta);
up = v3.Y;
down = v3.Y;
for (int i = (int)v3.X; i >=(int)v2.X; i--)
{
for (int g = (int)down; g <= (int)up; g++)
{
FillPixel(i, g);
}
up += upDelta;
down += downDelta;
}
}
Несомненно этот код можно отрефакторить и не дублировать цикл:
void Triangle(Vector2 v1 , Vector2 v2 , Vector2 v3)
{
if (v1.X > v2.X) { Swap(v1, v2); }
if (v2.X > v3.X) { Swap(v2, v3); }
if (v1.X > v2.X) { Swap(v1, v2); }
var steps12 = max(v2.X - v1.X , 1);
var steps13 = max(v3.X - v1.X , 1);
var steps32 = max(v2.X - v3.X , 1);
var steps31 = max(v1.X - v3.X , 1);
var upDelta = (v2.Y - v1.Y) / steps12;
var downDelta = (v3.Y - v1.Y) / steps13;
if (upDelta < downDelta) Swap(upDelta , downDelta);
TrianglePart(v1.X , v2.X , v1.Y , upDelta , downDelta);
upDelta = (v2.Y - v3.Y) / steps32;
downDelta = (v1.Y - v3.Y) / steps31;
if (upDelta < downDelta) Swap(upDelta, downDelta);
TrianglePart(v3.X, v2.X, v3.Y, upDelta, downDelta);
}
void TrianglePart(float x1 , float x2 , float y1 , float upDelta , float downDelta)
{
float up = y1, down = y1;
for (int i = (int)x1; i <= (int)x2; i++)
{
for (int g = (int)down; g <= (int)up; g++)
{
FillPixel(i , g);
}
up += upDelta; down += downDelta;
}
}
Отсечение невидимых точек.
Для начала подумайте каким образом вы видите. Сейчас перед вами экран, а то что находится позади него скрыто от ваших глаз. В рендеринге работает примерно такой же механизм — если один полигон перекрывает другой рендер нарисует его поверх перекрытого. Наоборот же, закрытую часть полигона рисовать он не будет:
Для того, чтобы понять видима точки или нет, в рендеринге применяют механизм zbuffer-а(буфера глубины). zbuffer можно представить как двумерный массив (можно сжать в одномерный) с размерностью width * height. Для каждого пикселя на экране он хранит значение z — координаты на исходном полигоне откуда эта точка была спроецирована. Соответственно чем ближе точка к наблюдателю, тем меньше ее z — координата. В конечном итоге если проекции нескольких точек совпадают растеризировать нужно точку с минимальной z — координатой:
Теперь возникает вопрос — как находить z-координаты точек на исходном полигоне? Это можно сделать несколькими способами. Например можно пускать луч из начала координат камеры, проходящий через точку на проекционной плоскости {x, y, z’}, и находить его пересечение с полигоном. Но искать пересечения крайне затратная операция, поэтому будем использовать другой способ. Для рисования треугольника мы интерполировали координаты его проекций, теперь, помимо этого, мы будем интерполировать также и координаты исходного полигона. Для отсечения невидимых точек будем использовать в методе растеризации состояние zbuffer-а для текущего фрейма.
Мой zbuffer будет иметь вид Vector3[] — он будет содержать не только z — координаты, но и интерполированные значения точек полигона(фрагменты) для каждого пикселя экрана. Это сделано в целях экономии памяти так как в дальнейшем нам все равно пригодятся эти значения для написания шейдеров! А пока что имеем следующий код для определения видимых вершин(фрагментов):
Код
public void ComputePoly(Vector3 v1, Vector3 v2, Vector3 v3 , Vector3[] zbuffer)
{
//находим проекцию полигона
var v1p = Camera.ScreenProection(v1);
var v2p = Camera.ScreenProection(v2);
var v3p = Camera.ScreenProection(v3);
//упорядочиваем точки по x - координате
//Заметьте, также меняем исходные точки - они должны соответствовать проекциям
if (v1p.X > v2p.X) { Swap(v1p, v2p); Swap(v1p, v2p); }
if (v2p.X > v3p.X) { Swap(v2p, v3p); Swap(v2p, v3p); }
if (v1p.X > v2p.X) { Swap(v1p, v2p); Swap(v1p, v2p); }
//считаем количество шагов для построения линии алгоритмом Брезенхема
int x12 = Math.Max((int)v2p.X - (int)v1p.X, 1);
int x13 = Math.Max((int)v3p.X - (int)v1p.X, 1);
//теперь помимо проекций будем интерполировать и исходные точки
float dy12 = (v2p.Y - v1p.Y) / x12; var dr12 = (v2 - v1) / x12;
float dy13 = (v3p.Y - v1p.Y) / x13; var dr13 = (v3 - v1) / x13;
Vector3 deltaUp, deltaDown; float deltaUpY, deltaDownY;
if (dy12 > dy13) { deltaUp = dr12; deltaDown = dr13; deltaUpY = dy12; deltaDownY = dy13;}
else { deltaUp = dr13; deltaDown = dr12; deltaUpY = dy13; deltaDownY = dy12;}
TrianglePart(v1 , deltaUp , deltaDown , x12 , 1 , v1p , deltaUpY , deltaDownY , zbuffer);
//вторую часть треугольника аналогично - думаю вы поняли
}
public void ComputePolyPart(Vector3 start, Vector3 deltaUp, Vector3 deltaDown,
int xSteps, int xDir, Vector2 pixelStart, float deltaUpPixel, float deltaDownPixel , Vector3[] zbuffer)
{
int pixelStartX = (int)pixelStart.X;
Vector3 up = start - deltaUp, down = start - deltaDown;
float pixelUp = pixelStart.Y - deltaUpPixel, pixelDown = pixelStart.Y - deltaDownPixel;
for (int i = 0; i <= xSteps; i++)
{
up += deltaUp; pixelUp += deltaUpPixel;
down += deltaDown; pixelDown += deltaDownPixel;
int steps = ((int)pixelUp - (int)pixelDown);
var delta = steps == 0 ? Vector3.Zero : (up - down) / steps;
Vector3 position = down - delta;
for (int g = 0; g <= steps; g++)
{
position += delta;
var proection = new Point(pixelStartX + i * xDir, (int)pixelDown + g);
int index = proection.Y * Width + proection.X;
//проверка на глубину
if (zbuffer[index].Z == 0 || zbuffer[index].Z > position.Z)
{
zbuffer[index] = position;
}
}
}
}
Анимация шагов растеризатора(при перезаписи глубины в zbuffer-е пиксель выделяется красным):
Для удобства я вынес весь код в отдельный модуль Rasterizer:
Класс растеризатора
public class Rasterizer
{
public Vertex[] ZBuffer;
public int[] VisibleIndexes;
public int VisibleCount;
public int Width;
public int Height;
public Camera Camera;
public Rasterizer(Camera camera)
{
Shaders = shaders;
Width = camera.ScreenWidth;
Height = camera.ScreenHeight;
Camera = camera;
}
public Bitmap Rasterize(IEnumerable<Primitive> primitives)
{
var buffer = new Bitmap(Width , Height);
ComputeVisibleVertices(primitives);
for (int i = 0; i < VisibleCount; i++)
{
var vec = ZBuffer[index];
var proec = Camera.ScreenProection(vec);
buffer.SetPixel(proec.X , proec.Y);
}
return buffer.Bitmap;
}
public void ComputeVisibleVertices(IEnumerable<Primitive> primitives)
{
VisibleCount = 0;
VisibleIndexes = new int[Width * Height];
ZBuffer = new Vertex[Width * Height];
foreach (var prim in primitives)
{
foreach (var poly in prim.GetPolys())
{
MakeLocal(poly);
ComputePoly(poly.Item1, poly.Item2, poly.Item3);
}
}
}
public void MakeLocal(Poly poly)
{
poly.Item1.Position = Camera.Pivot.ToLocalCoords(poly.Item1.Position);
poly.Item2.Position = Camera.Pivot.ToLocalCoords(poly.Item2.Position);
poly.Item3.Position = Camera.Pivot.ToLocalCoords(poly.Item3.Position);
}
}
Теперь проверим работу рендера. Для этого я использую модель Сильваны из известной RPG «WOW»:
Не очень понятно, правда? А все потому что здесь нет ни текстур ни освещения. Но вскоре мы это исправим.
Текстуры! Нормали! Освещение! Мотор!
Почему я объединил все это в один раздел? А потому что по своей сути текстуризация и расчет нормалей абсолютно идентичны и скоро вы это поймете.
Для начала рассмотрим задачу текстуризации для одного полигона. Теперь помимо обычных координат вершин полигона мы будем хранить еще и его текстурные координаты. Текстурная координата вершины представляется двумерным вектором и указывает на пиксель изображения текстуры. В интернете я нашел хорошую картинку чтобы показать это:
Заметьте, что начало текстуры (левый нижний пиксель) в текстурных координатах имеет значение {0, 0}, конец (правый верхний пиксель) — {1, 1}. Учитывайте систему координат текстуры и возможность выхода за границы картинки когда текстурная координата равна 1.
Сразу создадим класс для представления данных вершины:
public class Vertex
{
public Vector3 Position { get; set; }
public Color Color { get; set; }
public Vector2 TextureCoord { get; set; }
public Vector3 Normal { get; set; }
public Vertex(Vector3 pos , Color color , Vector2 texCoord , Vector3 normal)
{
Position = pos;
Color = color;
TextureCoord = texCoord;
Normal = normal;
}
}
Зачем нужны нормали я объясню позже, пока что просто будем знать, что у вершин они могут быть. Теперь для текстуризации полигона нам необходимо каким-то образом сопоставить значение цвета из текстуры конкретному пикселю. Помните как мы интерполировали вершины? Здесь нужно сделать то же самое! Я не буду еще раз переписывать код растеризации, а предлагаю вам самим реализовать текстурирование в вашем рендере. Результатом должно быть корректное отображение текстур на модели. Вот, что получилось у меня:
текстурированная модель
Вся информация о текстурных координатах модели находятся в файле OBJ. Для того, чтобы использовать это изучите формат: Формат OBJ.
Освещение
С текстурами все стало гораздо веселее, но по настоящему весело будет когда мы реализуем освещение для сцены. Для имитации «дешевого» освещения я буду использовать модель Фонга.
Модель Фонга
В общем случае этот метод имитирует наличие 3х составляющих освещения: фоновая(ambient), рассеянная(diffuse) и зеркальная(reflect). Сумма этих трех компонент в итоге даст имитацию физического поведения света.
Модель Фонга
Для расчета освещения по Фонгу нам будут нужны нормали к поверхностям, для этого я и добавил их в классе Vertex. Где же брать значения этих нормалей? Нет, ничего вычислять нам не нужно. Дело в том, что великодушные 3д редакторы часто сами считают их и предоставляют вместе с данными модели в контексте формата OBJ. Распарсив файл модели мы получаем значение нормалей для 3х вершин каждого полигона.
Картинка из вики
Для того, чтобы посчитать нормаль в каждой точке на полигоне нужно интерполировать эти значения, мы уже умеем делать это. Теперь разберем все составляющие для вычисления освещения Фонга.
Фоновый свет (Ambient)
Изначально мы задаем постоянное фоновое освещение, для нетекстурированных объектов можно выбрать любой цвет, для объектов с текстурами я делю каждую из компонент RGB на некий коэффициент базового затенения (baseShading).
Рассеянный свет (Diffuse)
Когда свет падает на поверхность полигона он равномерно рассеивается. Для расчета diffuse значения на конкретном пикселе учитывается угол под которым свет падает на поверхность. Чтобы рассчитать этот угол можно применить скалярное произведение падающего луча и нормали(само собой вектора перед этим нужно нормализировать). Этот угол будет умножаться на некий коэффициент интенсивности света. Если скалярное произведение отрицательно — это значит, что угол между векторами больше 90 градусов. В этом случае мы начнем рассчитывать уже не осветление, а, наоборот, затенение. Стоит избегать этого момента, сделать это можно с помощью функции max.
Код
public interface IShader
{
void ComputeShader(Vertex vertex, Camera camera);
}
public struct Light
{
public Vector3 Pos;
public float Intensivity;
}
public class PhongModelShader : IShader
{
public static float DiffuseCoef = 0.1f;
public Light[] Lights { get; set; }
public PhongModelShader(params Light[] lights)
{
Lights = lights;
}
public void ComputeShader(Vertex vertex, Camera camera)
{
if (vertex.Normal.X == 0 && vertex.Normal.Y == 0 && vertex.Normal.Z == 0)
{
return;
}
var gPos = camera.Pivot.ToGlobalCoords(vertex.Position);
foreach (var light in Lights)
{
var ldir = Vector3.Normalize(light.Pos - gPos);
var diffuseVal = Math.Max(VectorMath.Cross(ldir, vertex.Normal), 0) * light.Intensivity;
vertex.Color = Color.FromArgb(vertex.Color.A,
(int)Math.Min(255, vertex.Color.R * diffuseVal * DiffuseCoef),
(int)Math.Min(255, vertex.Color.G * diffuseVal * DiffuseCoef,
(int)Math.Min(255, vertex.Color.B * diffuseVal * DiffuseCoef));
}
}
}
Давайте применим рассеянный свет и рассеем тьму:
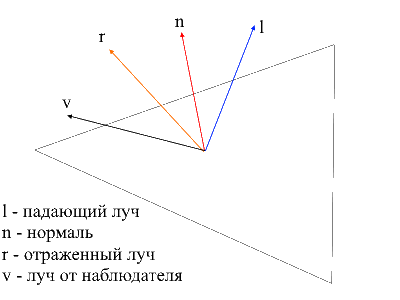
Зеркальный свет (Reflect)
Для расчета зеркальной компоненты нужно учитывать точку из которой мы смотрим на объект. Теперь мы будем брать скалярное произведение луча от наблюдателя и отраженного от поверхности луча умноженное на коэффициент интенсивности света.
Найти луч от наблюдателя к поверхности легко — это будет просто позиция обрабатываемой вершины в локальных координатах. Для того, чтобы найти отраженный луч я использовал следующий способ. Падающий луч можно разложить на 2 вектора: его проекцию на нормаль и второй вектор который можно найти вычитанием из падающего луча этой проекции. Чтобы найти отраженный луч нужно из проекции на нормаль вычесть значение второго вектора.
код
public class PhongModelShader : IShader
{
public static float DiffuseCoef = 0.1f;
public static float ReflectCoef = 0.2f;
public Light[] Lights { get; set; }
public PhongModelShader(params Light[] lights)
{
Lights = lights;
}
public void ComputeShader(Vertex vertex, Camera camera)
{
if (vertex.Normal.X == 0 && vertex.Normal.Y == 0 && vertex.Normal.Z == 0)
{
return;
}
var gPos = camera.Pivot.ToGlobalCoords(vertex.Position);
foreach (var light in Lights)
{
var ldir = Vector3.Normalize(light.Pos - gPos);
//Следующие три строчки нужны чтобы найти отраженный от поверхности луч
var proection = VectorMath.Proection(ldir, -vertex.Normal);
var d = ldir - proection;
var reflect = proection - d;
var diffuseVal = Math.Max(VectorMath.Cross(ldir, -vertex.Normal), 0) * light.Intensivity;
//луч от наблюдателя
var eye = Vector3.Normalize(-vertex.Position);
var reflectVal = Math.Max(VectorMath.Cross(reflect, eye), 0) * light.Intensivity;
var total = diffuseVal * DiffuseCoef + reflectVal * ReflectCoef;
vertex.Color = Color.FromArgb(vertex.Color.A,
(int)Math.Min(255, vertex.Color.R * total),
(int)Math.Min(255, vertex.Color.G * total),
(int)Math.Min(255, vertex.Color.B * total));
}
}
}
Теперь картинка выглядит следующим образом:
Тени
Конечной точкой моего изложения будет реализация теней для рендера. Первая тупиковая идея которая зародилась у меня в черепушке — для каждой точки проверять не лежит ли между ней и светом какой-нибудь полигон. Если лежит — значит не нужно освещать пиксель. Модель Сильваны содержит 220к с лихвой полигонов. Если так для каждой точки проверять пересечение со всеми этими полигонами, то нужно сделать максимум 220000 * 1920 * 1080 * 219999 вызовов метода пересечения! За 10 минут мой компьютер смог осилить 10-у часть всех вычислений (2600 полигонов из 220000), после чего у меня случился сдвиг и я отправился на поиски нового метода.
В интернете мне попался очень простой и красивый способ, который выполняет те же вычисления в тысячи раз быстрее. Называется он Shadow mapping(построение карты теней). Вспомните как мы определяли видимые наблюдателю точки — использовали zbuffer. Shadow mapping делает тоже самое! В первом проходе наша камера будет находиться в позиции света и смотреть на объект. Таким образом мы сформируем карту глубин для источника света. Карта глубин — это знакомый нам zbuffer. Во втором проходе мы используем эту карту, чтобы определять вершины которые должны освещаться. Сейчас я нарушу правила хорошего кода и пойду читерским путем — просто передам шейдеру новый объект растеризатора и он используя его создаст нам карту глубин.
Код
public class ShadowMappingShader : IShader
{
public Enviroment Enviroment { get; set; }
public Rasterizer Rasterizer { get; set; }
public Camera Camera => Rasterizer.Camera;
public Pivot Pivot => Camera.Pivot;
public Vertex[] ZBuffer => Rasterizer.ZBuffer;
public float LightIntensivity { get; set; }
public ShadowMappingShader(Enviroment enviroment, Rasterizer rasterizer, float lightIntensivity)
{
Enviroment = enviroment;
LightIntensivity = lightIntensivity;
Rasterizer = rasterizer;
//я добвил события в объекты рендера, привязав к ним перерасчет карты теней
//теперь при вращении/движении камеры либо при изменение сцены шейдер будет перезаписывать глубину
Camera.OnRotate += () => UpdateDepthMap(Enviroment.Primitives);
Camera.OnMove += () => UpdateDepthMap(Enviroment.Primitives);
Enviroment.OnChange += () => UpdateDepthMap(Enviroment.Primitives);
UpdateVisible(Enviroment.Primitives);
}
public void ComputeShader(Vertex vertex, Camera camera)
{
//вычисляем глобальные координаты вершины
var gPos = camera.Pivot.ToGlobalCoords(vertex.Position);
//дистанция до света
var lghDir = Pivot.Center - gPos;
var distance = lghDir.Length();
var local = Pivot.ToLocalCoords(gPos);
var proectToLight = Camera.ScreenProection(local).ToPoint();
if (proectToLight.X >= 0 && proectToLight.X < Camera.ScreenWidth && proectToLight.Y >= 0
&& proectToLight.Y < Camera.ScreenHeight)
{
int index = proectToLight.Y * Camera.ScreenWidth + proectToLight.X;
if (ZBuffer[index] == null || ZBuffer[index].Position.Z >= local.Z)
{
vertex.Color = Color.FromArgb(vertex.Color.A,
(int)Math.Min(255, vertex.Color.R + LightIntensivity / distance),
(int)Math.Min(255, vertex.Color.G + LightIntensivity / distance),
(int)Math.Min(255, vertex.Color.B + LightIntensivity / distance));
}
}
else
{
vertex.Color = Color.FromArgb(vertex.Color.A,
(int)Math.Min(255, vertex.Color.R + (LightIntensivity / distance) / 15),
(int)Math.Min(255, vertex.Color.G + (LightIntensivity / distance) / 15),
(int)Math.Min(255, vertex.Color.B + (LightIntensivity / distance) / 15));
}
}
public void UpdateDepthMap(IEnumerable<Primitive> primitives)
{
Rasterizer.ComputeVisibleVertices(primitives);
}
}
Для статичной сцены достаточно будет один раз вызвать построение карты глубин, после во всех фреймах использовать ее. В качестве тестовой я использую менее полигональную модель пушки. Вот такое изображение получается на выходе:
Многие из вас наверное заметили артефакты данного шейдера(необработанные светом черные точки). Опять же обратившись в всезнающую сеть я нашел описание этого эффекта с противным названием «shadow acne»(да простят меня люди с комплексом внешности). Суть таких «зазоров» заключается в том, что для определения тени мы используем ограниченное разрешение карты глубин. Это значит, что несколько вершин при рендеринге получают одно значение из карты глубин. Такому артефакту наиболее подвержены поверхности на которые свет падает под пологим углом. Эффект можно исправить, увеличив разрешение рендера для света, однако существует более элегантный способ. Заключается он в том, чтобы добавлять определенный сдвиг для глубины в зависимости от угла между лучом света и поверхностью. Это можно сделать при помощи скалярного произведения.
Улучшенные тени
public class ShadowMappingShader : IShader
{
public Enviroment Enviroment { get; set; }
public Rasterizer Rasterizer { get; set; }
public Camera Camera => Rasterizer.Camera;
public Pivot Pivot => Camera.Pivot;
public Vertex[] ZBuffer => Rasterizer.ZBuffer;
public float LightIntensivity { get; set; }
public ShadowMappingShader(Enviroment enviroment, Rasterizer rasterizer, float lightIntensivity)
{
Enviroment = enviroment;
LightIntensivity = lightIntensivity;
Rasterizer = rasterizer;
//я добвил события в объекты рендера, привязав к ним перерасчет карты теней
//теперь при вращении/движении камеры либо при изменение сцены шейдер будет перезаписывать глубину
Camera.OnRotate += () => UpdateDepthMap(Enviroment.Primitives);
Camera.OnMove += () => UpdateDepthMap(Enviroment.Primitives);
Enviroment.OnChange += () => UpdateDepthMap(Enviroment.Primitives);
UpdateVisible(Enviroment.Primitives);
}
public void ComputeShader(Vertex vertex, Camera camera)
{
//вычисляем глобальные координаты вершины
var gPos = camera.Pivot.ToGlobalCoords(vertex.Position);
//дистанция до света
var lghDir = Pivot.Center - gPos;
var distance = lghDir.Length();
var local = Pivot.ToLocalCoords(gPos);
var proectToLight = Camera.ScreenProection(local).ToPoint();
if (proectToLight.X >= 0 && proectToLight.X < Camera.ScreenWidth && proectToLight.Y >= 0
&& proectToLight.Y < Camera.ScreenHeight)
{
int index = proectToLight.Y * Camera.ScreenWidth + proectToLight.X;
var n = Vector3.Normalize(vertex.Normal);
var ld = Vector3.Normalize(lghDir);
//вычисляем сдвиг глубины
float bias = (float)Math.Max(10 * (1.0 - VectorMath.Cross(n, ld)), 0.05);
if (ZBuffer[index] == null || ZBuffer[index].Position.Z + bias >= local.Z)
{
vertex.Color = Color.FromArgb(vertex.Color.A,
(int)Math.Min(255, vertex.Color.R + LightIntensivity / distance),
(int)Math.Min(255, vertex.Color.G + LightIntensivity / distance),
(int)Math.Min(255, vertex.Color.B + LightIntensivity / distance));
}
}
else
{
vertex.Color = Color.FromArgb(vertex.Color.A,
(int)Math.Min(255, vertex.Color.R + (LightIntensivity / distance) / 15),
(int)Math.Min(255, vertex.Color.G + (LightIntensivity / distance) / 15),
(int)Math.Min(255, vertex.Color.B + (LightIntensivity / distance) / 15));
}
}
public void UpdateDepthMap(IEnumerable<Primitive> primitives)
{
Rasterizer.ComputeVisibleVertices(primitives);
}
}
Бонус
Играем с нормалями
Я подумал, стоит ли интерполировать значения нормалей, если можно посчитать среднее между 3мя нормалями полигона и использовать для каждой его точки. Оказывается, что интерполяция дает куда более естественный и гладкий материал картинки.
Двигаем свет
Реализовав простой цикл получим набор отрендеренных картинок с разными позициями света на сцене:
float angle = (float)Math.PI / 90;
var shader = (preparer.Shaders[0] as PhongModelShader);
for (int i = 0; i < 180; i+=2)
{
shader.Lights[0] = = new Light()
{
Pos = shader.Lights[0].Pos.Rotate(angle , Axis.X) ,
Intensivity = shader.Lights[0].Intensivity
};
Draw();
}
Производительность
Для теста использовалась следующие конфигурации:
- Модель Сильваны: 220к полигонов.
- Разрешение экрана: 1920×1080.
- Шейдеры: Phong model shader
- Конфигурация компьютера: cpu — core i7 4790, 8 gb ram
FPS рендеринга составлял 1-2 кадр/сек. Это далеко не realtime. Однако стоит все же учитывать, что вся обработка происходила без использования многопоточности, т.е. на одном ядре cpu.
Заключение
Я считаю себя новичком в 3д графике не исключаю ошибок допущенных мною в ходе изложения. Единственное на что я опираюсь — это практический результат, полученный в процессе создания. Все поправки и оптимизации(если таковые будут) вы можете оставить в комментариях, я с радостью их прочту. Ссылка на репозиторий проекта.
Работа с анимацией и 3D-графикой, Программирование, Rust
Рекомендация: подборка платных и бесплатных курсов Python — https://katalog-kursov.ru/
Итак, в продолжение предыдущей статьи пишу 2-ю часть, где мы попробуем добраться до того, чтобы написать проволочный рендер. Напоминаю, что цель этого цикла статей — написать сильно упрощенный аналог OpenGL на Rust. В качестве основы используется «Краткий курс компьютерной графики» от haqreu, в своих же статьях я сосредоточиваюсь больше не на графике как таковой, а на особенностях реализации при помощи Rust: возникающие проблемы и их решения, личные впечатления, полезные ресурсы для изучающих Rust. Сама получившаяся программа не имеет особенной ценности, польза от этого дела в изучении нового перспективного ЯП и основ трехмерной графики. Наконец, это занятие довольно таки увлекательно.
Напоминаю также, что поскольку я не являюсь профессионалом ни в Rust ни в 3D-графике, а изучаю эти вещи прямо по ходу написания статьи, то в ней могут быть грубые ошибки и упущения, которые я, впрочем, рад исправить, если мне на них укажут в комментариях.
Машинка, которую мы получим в конце статьи
Приводим линию в порядок
Что ж, давайте начнем с того, чтобы переписать нашу кошмарную handmade-функцию line на нормальную реализацию алгоритма Брезенхэма из статьи haqreu. Во-первых она более быстрая, во-вторых более каноничная, в-третьих мы сможем сравнить код на Rust с кодом на C++.
pub fn line(&mut self, mut x0: i32, mut y0: i32, mut x1: i32, mut y1: i32, color: u32) {
let mut steep = false;
if (x0-x1).abs() < (y0-y1).abs() {
mem::swap(&mut x0, &mut y0);
mem::swap(&mut x1, &mut y1);
steep = true;
}
if x0>x1 {
mem::swap(&mut x0, &mut x1);
mem::swap(&mut y0, &mut y1);
}
let dx = x1-x0;
let dy = y1-y0;
let derror2 = dy.abs()*2;
let mut error2 = 0;
let mut y = y0;
for x in x0..x1+1 {
if steep {
self.set(y, x, color);
} else {
self.set(x, y, color);
}
error2 += derror2;
if error2 > dx {
y += if y1>y0 { 1 } else { -1 };
error2 -= dx*2;
}
}
}
Как видите отличия минимальны, а количество строк относительно оригинала осталось без изменений. Никаких особых затруднений на этом этапе не возникло.
Делаем тест
После того, как с реализацией линии было покончено, я решил не удалять сослуживший мне столь хорошую службу в деле тестирования код, который рисовал 3 наших тестовых линии:
let mut canvas = canvas::Canvas::new(100, 100);
canvas.line(13, 20, 80, 40, WHITE);
canvas.line(20, 13, 40, 80, RED);
canvas.line(80, 40, 13, 20, BLUE);
Уж не знаю, какой опыт у автора оригинальной статьи, но оказывается как раз эти 3 вызова неплохо прокрывают почти весь спектр ошибок, которые можно допустить при реализации линии. И которые я, конечно же, допускал.
Вынос кода в неиспользуемую функцию заставит Rust выдавать warning при каждой компиляции (компилятор ругается на каждую неиспользуемую функцию, или переменную). Конечно, warning можно и подавить, дав функции имя, начинающееся с нижнего прочерка _test_line() , но это как-то плохо пахнет. А хранить потенциально полезный но сейчас ненужный код в комментариях вообще, на мой взгляд, дурной тон программирования. Гораздо более разумное решение — создать тест! Так что, за информацией обращаемся к соответствующей статье про функциональность тестирования в Rust, чтобы сделать свой первый тест на этом языке.
Это делается элементарно. Достаточно написать #[test] строчкой выше сигнатуры функции. Это превращает ее в тест. На такие функции Rust не выводит warning’ов как на неиспользуемые, а запуск cargo test приводит к тому, что Cargo выводит нам статистику по прогону всех таких функций в проекте:
Running target/debug/rust_project-2d87cd565073580b
running 1 test
test test_line ... ok
test result: ok. 1 passed; 0 failed; 0 ignored; 0 measured
Что интересно он также выводит warning’и по всем неиспользуемым функциям и переменным исходя из того, что входная точка проекта — функции, помеченные как тест. В перспективе это помогает определить покрытие тестами функций проекта. Понятное дело, что пока наш тест толком ничего не тестирует, потому-что окошко с результатами рисования просто появляется и сразу исчезает. По-хорошему должен быть mock-объект, заменяющий наш Canvas, который позволяет проверить последовательность вызовов функции set(x, y, color); на соответствие заданному. Тогда это будет автоматический юнит-тест. Пока же мы просто поигрались с соответствующей функциональностью компилятора. Вот снимок репозитория после этих изменений.
Векторы и чтение файлов
Что ж, самое время приступить к реализации проволочного рендера. Первое препятствие на этом пути — нам понадобится читать файл модели (который хранится в формате «Wavefront .obj file»). haqreu в своей статье дает готовый парсер для своих студентов, который при работе использует классы 2-хмерного и 3-хмерного векторов, также представленные haqreu. Поскольку его реализация на C++, нам все это надо будет переписать на Rust. Начнем, естественно с векторов. Вот отрывок кода оригинального вектора (двухмерный вариант):
template <class t> struct Vec2 {
union {
struct {t u, v;};
struct {t x, y;};
t raw[2];
};
Vec2() : u(0), v(0) {}
Vec2(t _u, t _v) : u(_u),v(_v) {}
inline Vec2<t> operator +(const Vec2<t> &V) const { return Vec2<t>(u+V.u, v+V.v); }
inline Vec2<t> operator -(const Vec2<t> &V) const { return Vec2<t>(u-V.u, v-V.v); }
inline Vec2<t> operator *(float f) const { return Vec2<t>(u*f, v*f); }
template <class > friend std::ostream& operator<<(std::ostream& s, Vec2<t>& v);
};
В реализации векторов на C++ используются шаблоны. В Rust их аналогом выступают обобщенные типы (Generics), про которое можно почитать соответствующую статью, а также посмотреть примеры их использования на сайте rustbyexample.com. Вообще этот сайт является очень полезным ресурсом при изучении Rust. На каждую возможность языка там есть пример использования с подробными комментариями и возможностью редактировать и запускать примеры прямо в окне браузера (код исполняется на удаленном сервере).
Когда я попытался сделать конструктор, не принимающий аргументов, а создающий нулевой вектор (0, 0), я столкнулся с еще одной проблемой. Насколько я понял систему типов раста, такой создать нельзя, потому-что мы не сможем инициализировать структуру значениями по умолчанию из-за отсутствия неявного приведения типов. Подобную функциональность можно реализовать через типажи (Traits), но для этого придется писать немало кода или использовать стандартный типаж std::num::Zero , который является unstable. Оба варианта мне не понравились, поэтому я решил, что проще писать new(0, 0) в коде.
На разборки с обобщенными типами, типажами и перегрузкой операторов ушло несколько часов. Когда я понял, что для реализации аналога оригинальных классов векторов мне понадобится еще вникать, как делать перегрузку операторов (которая сама устроена при помощи типажей) для обобщенного типа, я решил зайти с другого бока. Похоже то, что в C++ делается несколькими строчками кода и, в Rust порой реализуется в разы более сложным и длинным кодом. Возможно это из-за того, что я пытаюсь дословно перевести C++-код на Rust, вместо того, чтобы осмыслить алгоритм и написать его аналог на языке с существенно другой идеологией. В общем я остановился на том, чтобы сделать свой вектор с только теми возможностями, которые, насколько я могу судить, точно мне понадобятся для хранения информации из файла модели согласно моим собственным суждениям об этом. Получился вот такой вот нехитрый класс, которого вполне достаточно на текущем этапе задачи:
pub struct Vector3D {
pub x: f32,
pub y: f32,
pub z: f32,
}
impl Vector3D {
pub fn new(x: f32, y: f32, z: f32) -> Vector3D {
Vector3D {
x: x,
y: y,
z: z,
}
}
}
impl fmt::Display for Vector3D {
fn fmt(&self, f: &mut fmt::Formatter) -> fmt::Result {
write!(f, "({},{},{})", self.x, self.y, self.z)
}
}
Теперь можно взяться за парсер, но работу с файлами в Rust мы еще не изучали. Тут на выручку пришел StackOverflow, где был ответ с простым для понимания примером кода. На основе него был получен следующий код:
pub struct Model {
pub vertices: Vec<Vector3D>,
pub faces : Vec<[i32; 3]>,
}
impl Model {
pub fn new(file_path: &str) -> Model {
let path = Path::new(file_path);
let file = BufReader::new(File::open(&path).unwrap());
let mut vertices = Vec::new();
let mut faces = Vec::new();
for line in file.lines() {
let line = line.unwrap();
if line.starts_with("v ") {
let words: Vec<&str> = line.split_whitespace().collect();
vertices.push(Vector3D::new(words[1].parse().unwrap(),
words[2].parse().unwrap(),
words[3].parse().unwrap()));
debug!("readed vertex: {}", vertices.last().unwrap());
} else if line.starts_with("f ") {
let mut face: [i32; 3] = [-1, -1, -1];
let words: Vec<&str> = line.split_whitespace().collect();
for i in 0..3 {
face[i] = words[i+1].split("/").next().unwrap().parse().unwrap();
face[i] -= 1;
debug!("face[{}] = {}", i, face[i]);
}
faces.push(face);
}
}
Model {
vertices: vertices,
faces: faces,
}
}
}
Особых сложностей с ним не было. Просто чтение файла и обработка строк. Разве что только поиск информации, как сделать ту или иную штуку в расте осложняется тем, что
язык быстро меняется
в интернете много информации для старых версий Rust < 1.0. (спасибо stepik777 за то, что конструктивно поправил) Подчас находишь какие-то ответы, пробуешь их, а они не работают, потому-что оказывается этот метод переименовали, удалили и т. п. Столкнулся с этим на примере метода from_str() .
Поначалу я допустил в этом коде ошибку, забыв написать строчку faces.push(face); и долго не мог понять, почему мой рендер даже и не входит в цикл, пробегающий по всем faces. Только после того, как я методом тыка выяснил, в чем проблема, я обнаружил интересную строчку в выводе компилятора warning: variable does not need to be mutable, #[warn(unused_mut)] on by default относительно строчки объявления переменной face. А не заметил я этого warning’а потому, что у меня была еще пачка предупреждений относительно неиспользуемых переменных, так что я забил просматривать их. После этого я закомментировал все неиспользуемые переменные, так что теперь любой warning бросится в глаза. В Rust предупреждения компилятора весьма полезны в поиске ошибок и не стоит ими пренебрегать.
Стоит также отметить, что код выглядит достаточно простым и понятным в отличии от оригинала на C++. Примерно также он мог бы быть написан на каком-нибудь Python или Java. Интересно еще, насколько он производителен по сравнению с оригинальным. Планирую сделать замеры производительности, когда весь рендер от начала до конца будет готов.
Проволочный рендер
Наконец, вот он проволочный рендер. Большая часть работы была сделана на предыдущих этапах, так что код простейший:
fn main() {
env_logger::init().unwrap();
info!("starting up");
let model = Model::new("african_head.obj");
let mut canvas = canvas::Canvas::new(WIDTH, HEIGHT);
debug!("drawing wireframe");
for face in model.faces {
debug!("processing face:");
debug!("({}, {}, {})", face[0], face[1], face[2]);
for j in 0..3 {
let v0 = &model.vertices[face[j] as usize];
let v1 = &model.vertices[face[(j+1)%3] as usize];
let x0 = ((v0.x+1.)*WIDTH as f32/2.) as i32;
let y0 = ((v0.y+1.)*HEIGHT as f32/2.) as i32;
let x1 = ((v1.x+1.)*WIDTH as f32/2.) as i32;
let y1 = ((v1.y+1.)*HEIGHT as f32/2.) as i32;
debug!("drawing line ({}, {}) - ({}, {})", x0, y0, x1, y1);
canvas.line(x0, y0, x1, y1, WHITE);
}
}
info!("waiting for ESC");
canvas.wait_for_esc();
}
Если не считать мелких отличий в синтаксисе, то от C++ он отличается главным образом большим количеством преобразований типов. Ну и логгированием, которое я везде понатыкал, когда искал ошибки. Вот, какую картинку мы получаем в итоге (снапшот кода в репозитории):
Это уже довольно неплохо, но во-первых если скормить моей программе в ее текущем виде модель машинки, которую я планирую нарисовать, она ее просто не покажет. Во-вторых рисуются все эти красоты жутко долго (запустил программу и можно идти пить кофе). Первая проблема из-за того, что в модели машинки вершины записаны совсем в других масштабах. Код выше подогнан под масштабы модели головы. Чтобы он стал универсальным с ним еще надо поработать. Вторая проблема пока не знаю из-за чего, но если подумать, то варианта всего 2: или используется неэффективный алгоритм, или написана на данном конкретном стеке технологий неэффективная реализация этого алгоритма. В любом случае возникнет еще вопрос, какой конкретно кусок алгоритма (реализации) неэффективен.
В общем, как вы уже поняли, я решил начать с вопроса скорости.
Меряемся производительностью
Поскольку у меня все равно в планах было сравнение производительности оригинального проекта и моей реализации на Rust, я решил просто сделать это пораньше. Однако принцип работы оригинала и моей реализации существенно отличаются. Оригинал рисует во временном буфере и только под конец записывает TGA-файл, в то время как мое приложение выполняет команды отрисовки SDL прямо по ходу обработки треугольников.
Решение простое — переделать наш Canvas, чтобы метод рисования точки set(x, y, color) только лишь сохранял данные во внутренний массив, а непосредственно рисование средствами SDL уже выполнялось в конце работы программы, после отработки всех вычислений. Этим мы убиваем 3-х зайцев:
- Получаем возможность сравнить скорость реализаций до отрисовки/сохранения в файл, т. е. там где они по сути еще делают идентичные вещи.
- Получаем заготовки на будущее для двойной буферизации.
- Отделяем свои вычисления от рисования, что позволяет нам оценить оверхэд, накладываемый вызовами SDL.
По-быстрому переписав Canvas, я увидел, что сам расчет линий происходил очень быстро. А вот отрисовка при помощи SDL выполнялась с черепашьей скоростью. Тут есть простор для оптимизации. Оказалось, что функция рисования точки в Rust-SDL2 отнюдь не была такой быстрой, как я ожидал. Проблему удалось решить при помощи сохранения всего изображения в текстуру и последующего вывода этой текстуры вот таким вот кодом:
pub fn show(&mut self) {
let mut texture = self.renderer.create_texture_streaming(PixelFormatEnum::RGB24,
(self.xsize as u32, self.ysize as u32)).unwrap();
texture.with_lock(None, |buffer: &mut [u8], pitch: usize| {
for y in (0..self.ysize) {
for x in (0..self.xsize) {
let offset = y*pitch + x*3;
let color = self.canvas[x][self.ysize - y - 1];
buffer[offset + 0] = (color >> (8*2)) as u8;
buffer[offset + 1] = (color >> (8*1)) as u8;
buffer[offset + 2] = color as u8;
}
}
}).unwrap();
self.renderer.clear();
self.renderer.copy(&texture, None, Some(Rect::new_unwrap(0, 0,
self.xsize as u32, self.ysize as u32)));
self.renderer.present();
}
Вообще в переписывании Canvas не возникло ничего нового с точки зрения программирования на Rust, так что рассказывать особо не о чем. Код на этом этапе в соответствующем снимке репозитория. После этих изменений программа стала летать. Прорисовка занимала доли секунды. Тут уже интерес к тому, чтобы померяться производительностью исчез. Поскольку выполнение программы занимало очень мало времени, простая погрешность измерений из-за случайных процессов в ОС могла увеличить это время в 2 раза или же наоборот уменьшить его. Чтобы как-то с этим побороться заключил основное тело программы (чтение .obj-файла и вычисление двумерной проекции) в цикл, который выполнялся 100 раз. Теперь можно было что-то мерить. То же самое сделал и с C++ реализацией от haqreu.
Собственно вот цифры Rust-реализации:
cepreu@cepreu-P5K:~/Загрузки/rust-3d-renderer-70de52d8e8c82854c460a41d1b8d8decb0c2e5c1$ time ./rust_project
real 0m0.769s
user 0m0.630s
sys 0m0.137s
А вот цифры реализации на C++:
cepreu@cepreu-P5K:~/Загрузки/tinyrenderer-f6fecb7ad493264ecd15e230411bfb1cca539a12$ time ./a.out
real 0m1.492s
user 0m1.483s
sys 0m0.008s
Каждую из программ я запускал 10 раз, а потом выбирал лучшее время (real). Его я вам и привел. В свою реализацию я внес модификации, чтобы выпилить все упоминания SDL, чтобы внешние обращения не влияли на результирующее время. Собственно можете увидеть в снимке репозитория.
Вот модификации, которые я внес в C++-реализацию:
int main(int argc, char** argv) {
for (int cycle=0; cycle<100; cycle++){
if (2==argc) {
model = new Model(argv[1]);
} else {
model = new Model("obj/african_head.obj");
}
TGAImage image(width, height, TGAImage::RGB);
for (int i=0; i<model->nfaces(); i++) {
std::vector<int> face = model->face(i);
for (int j=0; j<3; j++) {
Vec3f v0 = model->vert(face[j]);
Vec3f v1 = model->vert(face[(j+1)%3]);
int x0 = (v0.x+1.)*width/2.;
int y0 = (v0.y+1.)*height/2.;
int x1 = (v1.x+1.)*width/2.;
int y1 = (v1.y+1.)*height/2.;
line(x0, y0, x1, y1, image, white);
}
}
delete model;
}
//image.flip_vertically(); // i want to have the origin at the left bottom corner of the image
//image.write_tga_file("output.tga");
return 0;
}
Ну и еще удалил отладочную печать в model.cpp. Вообще, конечно, результат меня удивил. Мне казалось, что компилятор Rust еще не должен быть так же хорошо оптимизирован как gcc, а я по незнанию наверняка нагородил неоптимального кода… Я как-то даже и не понимаю толком, почему это мой код оказался быстрее. Или это Rust такой супербыстрый. Или в C++-реализации что-то неоптимально. В общем желающие это обсудить — добро пожаловать в комментарии.
Итоги
Наконец путем нехитрой подгонки коэффициентов (смотрите снимок репозитория) я получил картинку с машиной, оптимально занимающую пространство окна. Ее вы и наблюдали в начале статьи.
Немного впечатлений:
- Писать на Rust становится все проще. Первые дни были непрестанной борьбой с компилятором. Сейчас же я просто сажусь и пишу код, время от времени подсматривая в интернете, как сделать ту или иную штуку. Вобщем по большей части язык уже воспринимается знакомым. Как видите, это не заняло много времени.
- По-прежнему радуют warning’и раста. То, что в других языках подсказывет только очень продвинутая IDE (типа IntelliJ IDEA в Java), в Rust говорит сам компилятор. Помогает поддерживать хороший стиль, бережет от ошибок.
- То, что Rust оказался быстрее — шок. Видимо компилятор уже далеко не такой сырой, как я думал.
Заключительная — 3-я часть цикла: Пишем свой упрощенный OpenGL на Rust — часть 3 (растеризатор)
Современные движки для 3D-рендеринга, использующиеся в играх и мультимедиа, поражают своей сложностью в плане математики и программирования. Соответственно, результат их работы превосходен.
Многие разработчики ошибочно полагают, что создание даже простейшего 3D-приложения с нуля требует нечеловеческих знаний и усилий. К счастью, это не совсем так. Более того, при наличии компьютера и свободного времени, можно создать нечто подобное самостоятельно. Давайте взглянем на процесс разработки нашего собственного движка для 3D-рендеринга.
Итак, для чего же это всё нужно? Во-первых, создание движка для 3D-рендеринга поможет понять, как же работают современные движки изнутри. Во-вторых, сам движок при желании можно использовать и в своём собственном приложении, не прибегая к вызову внешних зависимостей. В случае с Java это значит, что вы можете создать своё собственное приложение для просмотра 3D-изображений без зависимостей (далёких от API Java), которое будет работать практически везде и уместится в 50 КБ!
Само собой, если вы хотите создать какое-нибудь большое 3D-приложение с плавной анимацией, вам лучше использовать OpenGL/WebGL. Однако, имея базовое представление о том, как устроены подобные движки, работа с более сложными движками будет казаться в разы проще.
В этой статье я постараюсь объяснить базовый 3D-рендеринг с ортографической проекцией, простую треугольную растеризацию (процесс, обратный векторизации), Z-буферизацию и плоское затенение. Я не буду заострять своё внимание на таких вещах, как оптимизация, текстуры и разные настройки освещения — если вам это нужно, попробуйте использовать более подходящие для этого инструменты, вроде OpenGL (существует множество библиотек, позволяющих вам работать с OpenGL, даже используя Java).
Примеры кода будут на Java, но сами идеи могут, разумеется, быть применены для любого другого языка по вашему выбору.
Довольно болтать — давайте приступим к делу!
GUI
Для начала, давайте поместим хоть что-нибудь на экран. Для этого, я буду использовать простое приложение, в котором будет отображаться наше отрендеренное изображение и два скроллера для вращения.
import javax.swing.*;
import java.awt.*;
public class DemoViewer {
public static void main(String[] args) {
JFrame frame = new JFrame();
Container pane = frame.getContentPane();
pane.setLayout(new BorderLayout());
// slider to control horizontal rotation
JSlider headingSlider = new JSlider(0, 360, 180);
pane.add(headingSlider, BorderLayout.SOUTH);
// slider to control vertical rotation
JSlider pitchSlider = new JSlider(SwingConstants.VERTICAL, -90, 90, 0);
pane.add(pitchSlider, BorderLayout.EAST);
// panel to display render results
JPanel renderPanel = new JPanel() {
public void paintComponent(Graphics g) {
Graphics2D g2 = (Graphics2D) g;
g2.setColor(Color.BLACK);
g2.fillRect(0, 0, getWidth(), getHeight());
// rendering magic will happen here
}
};
pane.add(renderPanel, BorderLayout.CENTER);
frame.setSize(400, 400);
frame.setVisible(true);
}
}Результат должен выглядеть вот так:
Теперь давайте добавим некоторые модели — вершины и треугольники. Вершина — это просто структура для хранения наших трёх координат (X, Y и Z), а треугольник соединяет вместе три вершины и содержит их цвет.
class Vertex {
double x;
double y;
double z;
Vertex(double x, double y, double z) {
this.x = x;
this.y = y;
this.z = z;
}
}
class Triangle {
Vertex v1;
Vertex v2;
Vertex v3;
Color color;
Triangle(Vertex v1, Vertex v2, Vertex v3, Color color) {
this.v1 = v1;
this.v2 = v2;
this.v3 = v3;
this.color = color;
}
}Здесь я буду считать, что X означает перемещение влево-вправо, Y — вверх-вниз, а Z будет глубиной (так, что ось Z перпендикулярна вашему экрану). Положительная Z будет означать «ближе к пользователю».
В качестве примера я выбрал тетраэдр как простейшую фигуру, о которой вспомнил — нужно всего 4 треугольника, чтобы описать её.
Код также будет достаточно простым — мы просто создаём 4 треугольника и добавляем их в ArrayList:
List tris = new ArrayList<>();
tris.add(new Triangle(new Vertex(100, 100, 100),
new Vertex(-100, -100, 100),
new Vertex(-100, 100, -100),
Color.WHITE));
tris.add(new Triangle(new Vertex(100, 100, 100),
new Vertex(-100, -100, 100),
new Vertex(100, -100, -100),
Color.RED));
tris.add(new Triangle(new Vertex(-100, 100, -100),
new Vertex(100, -100, -100),
new Vertex(100, 100, 100),
Color.GREEN));
tris.add(new Triangle(new Vertex(-100, 100, -100),
new Vertex(100, -100, -100),
new Vertex(-100, -100, 100),
Color.BLUE));В результате мы получим фигуру, центр которой находится в начале координат (0, 0, 0), что довольно удобно, так как мы будем вращать фигуру относительно этой точки.
Теперь давайте добавим всё это на экран. Сперва мы не будем добавлять возможность вращения и просто отрисуем каркасное представление фигуры. Так как мы используем ортографическую проекцию, это довольно просто — достаточно убрать координату Z и нарисовать наши треугольники.
g2.translate(getWidth() / 2, getHeight() / 2);
g2.setColor(Color.WHITE);
for (Triangle t : tris) {
Path2D path = new Path2D.Double();
path.moveTo(t.v1.x, t.v1.y);
path.lineTo(t.v2.x, t.v2.y);
path.lineTo(t.v3.x, t.v3.y);
path.closePath();
g2.draw(path);
}Заметьте, что сейчас я совершил все преобразования до отрисовки треугольников. Это сделано, чтобы для того, что бы поместить наш центр (0, 0, 0) в центр экрана — по умолчанию начало координат находится в левом верхнем углу экрана. После компиляции вы должны получить:
Вы можете не поверить, но это наш тетраэдр в ортогональной проекции, честно!
Теперь нам нужно добавить вращение. Для этого мне нужно будет немного отойти от темы и поговорить об использовании матриц и о том, как с их помощью достичь трёхмерной трансформации 3D-точек.
Существует много путей манипулировать 3D-точками, но самый гибкий из них — это использование матричного умножения. Идея заключается в том, чтобы показать точки в виде вектора размера 3×1, а переход — это, собственно, домножение на матрицу размера 3×3.
Возьмём наш входной вектор A:
И умножим его на так называемую матрицу трансформации T, чтобы получить в итоге выходной вектор B:
Например, вот как будет выглядеть трансформация, если мы умножим на 2:
Вы не можете описать любую возможную трансформацию, используя матрицы размера 3×3 — например, если переход происходит за пределы пространства. Вы можете использовать матрицы размера 4×4, делая перекос в 4D-пространство, но об этом не в этой статье.
Трансформации, которые нам пригодятся здесь — масштабирование и вращение.
Любое вращение в 3D-пространстве может быть выражено в 3 примитивных вращениях: вращение в плоскости XY, вращение в плоскости YZ и вращение в плоскости XZ. Мы можем записать матрицы трансформации для каждого из данных вращений следующим путём:
- Матрица вращения XY:
- Матрица вращения YZ:
- Матрица вращения XZ:
И вот здесь начинается магия: если вам нужно сначала совершить вращение точки в плоскости XY, используя матрицу трансформации T1, и затем совершить вращение этой точки в плоскости YZ, используя матрицу трансформации T2, то вы можете просто умножить T1 на T2 и получить одну матрицу, которая опишет всё вращение:
Это очень полезная оптимизация — вместо того, чтобы постоянно считать вращения на каждой точке, мы заранее считаем одну матрицу и затем используем её.
Что ж, довольно страшной математики, давайте вернёмся к коду. Создадим служебный класс Matrix3, который будет обрабатывать перемножения типа «матрица-матрица» и «вектор-матрица»:
class Matrix3 {
double[] values;
Matrix3(double[] values) {
this.values = values;
}
Matrix3 multiply(Matrix3 other) {
double[] result = new double[9];
for (int row = 0; row < 3; row++) {
for (int col = 0; col < 3; col++) {
for (int i = 0; i < 3; i++) {
result[row * 3 + col] += this.values[row * 3 + i] * other.values[i * 3 + col];
}
}
}
return new Matrix3(result);
}
Vertex transform(Vertex in) {
return new Vertex(in.x * values[0] + in.y * values[3] + in.z * values[6],
in.x * values[1] + in.y * values[4] + in.z * values[7],
in.x * values[2] + in.y * values[5] + in.z * values[8]);
}
}Теперь можно и оживить наши скроллеры вращения. Горизонтальный скроллер будет контролировать вращение влево-вправо (XZ), а вертикальный скроллер будет контролировать вращение вверх-вниз (YZ).
Давайте создадим нашу матрицу вращения:
double heading = Math.toRadians(headingSlider.getValue());
Matrix3 transform = new Matrix3(new double[] {Math.cos(heading), 0, -Math.sin(heading),
0, 1, 0,
Math.sin(heading), 0, Math.cos(heading)});
g2.translate(getWidth() / 2, getHeight() / 2);
g2.setColor(Color.WHITE);
for (Triangle t : tris) {
Vertex v1 = transform.transform(t.v1);
Vertex v2 = transform.transform(t.v2);
Vertex v3 = transform.transform(t.v3);
Path2D path = new Path2D.Double();
path.moveTo(v1.x, v1.y);
path.lineTo(v2.x, v2.y);
path.lineTo(v3.x, v3.y);
path.closePath();
g2.draw(path);
}Вам также будет нужно добавить слушателей на скроллеры, чтобы обеспечить обновление изображения, когда вы будете тянуть их вверх-вниз или вправо-влево.
headingSlider.addChangeListener(e -> renderPanel.repaint());
pitchSlider.addChangeListener(e -> renderPanel.repaint());Как вы, наверное, уже заметили, вращение вверх-вниз ещё не работает. Добавим эти строки в код:
Matrix3 headingTransform = new Matrix3(new double[] {Math.cos(heading), 0, Math.sin(heading),
0, 1, 0,
-Math.sin(heading), 0, Math.cos(heading)});
double pitch = Math.toRadians(pitchSlider.getValue());
Matrix3 pitchTransform = new Matrix3(new double[] {1, 0, 0,
0, Math.cos(pitch), Math.sin(pitch),
0, -Math.sin(pitch), Math.cos(pitch)});
Matrix3 transform = headingTransform.multiply(pitchTransform);До сих пор мы отрисовывали только каркасное представление нашей фигуры. Теперь давайте заполним его чем-нибудь. Для этого нам нужно сначала растеризовать треугольник — представить его в виде пикселей на экране.
Я буду использовать очень простой, но крайне неэффективный метод — растеризация через барицентрические координаты. Настоящие 3D-движки используют растеризацию, задействуя железо компьютера, что очень быстро и эффективно, но мы не можем использовать нашу видеокарту, так что будем делать всё вручную, через код.
Идея заключается в том, чтобы посчитать барицентрическую координату для каждого пикселя, который может лежать внутри нашего треугольника и исключить те, что вне его пределов. Следующий фрагмент содержит алгоритм. Обратите внимание на то, как мы стали напрямую обращаться к пикселям изображения.
BufferedImage img = new BufferedImage(getWidth(), getHeight(), BufferedImage.TYPE_INT_ARGB);
for (Triangle t : tris) {
Vertex v1 = transform.transform(t.v1);
Vertex v2 = transform.transform(t.v2);
Vertex v3 = transform.transform(t.v3);
// since we are not using Graphics2D anymore, we have to do translation manually
v1.x += getWidth() / 2;
v1.y += getHeight() / 2;
v2.x += getWidth() / 2;
v2.y += getHeight() / 2;
v3.x += getWidth() / 2;
v3.y += getHeight() / 2;
// compute rectangular bounds for triangle
int minX = (int) Math.max(0, Math.ceil(Math.min(v1.x, Math.min(v2.x, v3.x))));
int maxX = (int) Math.min(img.getWidth() - 1, Math.floor(Math.max(v1.x, Math.max(v2.x, v3.x))));
int minY = (int) Math.max(0, Math.ceil(Math.min(v1.y, Math.min(v2.y, v3.y))));
int maxY = (int) Math.min(img.getHeight() - 1, Math.floor(Math.max(v1.y, Math.max(v2.y, v3.y))));
double triangleArea = (v1.y - v3.y) * (v2.x - v3.x) + (v2.y - v3.y) * (v3.x - v1.x);
for (int y = minY; y <= maxY; y++) {
for (int x = minX; x <= maxX; x++) {
double b1 = ((y - v3.y) * (v2.x - v3.x) + (v2.y - v3.y) * (v3.x - x)) / triangleArea;
double b2 = ((y - v1.y) * (v3.x - v1.x) + (v3.y - v1.y) * (v1.x - x)) / triangleArea;
double b3 = ((y - v2.y) * (v1.x - v2.x) + (v1.y - v2.y) * (v2.x - x)) / triangleArea;
if (b1 >= 0 && b1 <= 1 && b2 >= 0 && b2 <= 1 && b3 >= 0 && b3 <= 1) {
img.setRGB(x, y, t.color.getRGB());
}
}
}
}
g2.drawImage(img, 0, 0, null);Довольно много кода, но теперь у нас есть цветной тетраэдр на экране.
Если вы поиграетесь с демкой, то вы заметите, что не всё сделано идеально — например, синий треугольник всегда выше других. Так происходит потому, что мы отрисовываем наши треугольники один за другим. Синий здесь — последний, поэтому он отрисовывается поверх других.
Чтобы исправить это, давайте рассмотрим Z-буферизацию. Идея состоит в том, чтобы в процессе растеризации создать промежуточный массив, который будет хранить в себе расстояние до последнего видимого элемента на каждом из пикселей. Делая растеризацию треугольников, мы будем проверять, меньше ли расстояние до пикселя, чем расстояние до предыдущего, и закрашивать его только в том случае, если он находится поверх других.
double[] zBuffer = new double[img.getWidth() * img.getHeight()];
// initialize array with extremely far away depths
for (int q = 0; q < zBuffer.length; q++) {
zBuffer[q] = Double.NEGATIVE_INFINITY;
}
for (Triangle t : tris) {
// handle rasterization...
// for each rasterized pixel:
double depth = b1 * v1.z + b2 * v2.z + b3 * v3.z;
int zIndex = y * img.getWidth() + x;
if (zBuffer[zIndex] < depth) {
img.setRGB(x, y, t.color.getRGB());
zBuffer[zIndex] = depth;
}
}Теперь видно, что у нашего тетраэдра есть одна белая сторона:
Вот мы и получили работающий движок для 3D-рендеринга!
Но и это ещё не конец. В реальном мире восприятие какого-либо цвета меняется в зависимости от положения источников света — если на поверхность падает лишь небольшое количество света, то она видится более темной.
В компьютерной графике мы можем достичь подобного эффекта с помощью так называемого «затенения» — изменения цвета поверхности в зависимости от угла наклона и расстояния относительно источника света.
Простейшая форма затенения — это плоское затенение. Этот способ учитывает только угол между поверхностью, нормаль и направление источника света. Вам всего лишь нужно найти косинус угла между двумя векторами и умножить цвет на получившееся значение. Такой подход очень прост и эффективен, поэтому он часто используется для высокоскоростного рендеринга, когда наиболее продвинутые технологии затенения слишком неэффективны.
Для начала нам нужно посчитать вектор нормали для нашего треугольника. Если у нас есть треугольник ABC, мы можем посчитать его вектор нормали, рассчитав векторное произведение векторов AB и AC и поделив получившийся вектор на его длину.
Векторное произведение — это бинарная операция на двух векторах, которые определены в 3D пространстве вот так:
Вот так выглядит визуальное представление того, что делает наше векторное произведение:
for (Triangle t : tris) {
// transform vertices before calculating normal...
Vertex norm = new Vertex(ab.y * ac.z - ab.z * ac.y,
ab.z * ac.x - ab.x * ac.z,
ab.x * ac.y - ab.y * ac.x);
double normalLength = Math.sqrt(norm.x * norm.x + norm.y * norm.y + norm.z * norm.z);
norm.x /= normalLength;
norm.y /= normalLength;
norm.z /= normalLength;
}Теперь нам нужно посчитать косинус между нормалью треугольника и направлением света. Для упрощения будем считать, что наш источник света расположен прямо за камерой на каком-либо расстоянии (такая конфигурация называется «направленный свет») — таким образом, наш источник света будет находиться в точке (0, 0, 1).
Косинус угла между векторами можно посчитать по формуле:
Где ||A|| — длина вектора, а числитель — скалярное произведение векторов A и B:
Обратите внимание на то, что длина вектора направления света равна 1, так же, как и длина нормали треугольника (мы уже нормализовали это). Таким образом, формула просто превращается в это:
Заметьте, что только Z компонент направления света не равен нулю, так что мы можем просто всё упростить:
В коде это всё выглядит тривиально:
double angleCos = Math.abs(norm.z);Мы опускаем знак результата, потому что для наших целей нам не важно, какая сторона треугольника смотрит на камеру. В реальном приложении вам нужно будет отслеживать это и применять затенение соответственно.
Теперь, получив наш коэффициент затенения, мы можем применить его к цвету нашего треугольника. Простой вариант будет выглядеть как-то так:
public static Color getShade(Color color, double shade) {
int red = (int) (color.getRed() * shade);
int green = (int) (color.getGreen() * shade);
int blue = (int) (color.getBlue() * shade);
return new Color(red, green, blue);
}Код будет давать нам некоторые эффекты затенения, но спадать они будут куда быстрее, чем нам нужно. Так происходит, потому что в Java используется спектр цветов sRGB.
Так что нам нужно конвертировать каждый цвет в линейный формат, применить затенение и затем конвертировать обратно. Реальный переход из sRGB к линейному RGB — довольно трудоёмкий процесс, так что я не буду выполнять полный перечень задач здесь. Вместо этого, я сделаю нечто приближенное к этому.
public static Color getShade(Color color, double shade) {
double redLinear = Math.pow(color.getRed(), 2.4) * shade;
double greenLinear = Math.pow(color.getGreen(), 2.4) * shade;
double blueLinear = Math.pow(color.getBlue(), 2.4) * shade;
int red = (int) Math.pow(redLinear, 1/2.4);
int green = (int) Math.pow(greenLinear, 1/2.4);
int blue = (int) Math.pow(blueLinear, 1/2.4);
return new Color(red, green, blue);
}И теперь мы видим, как наш тетраэдр оживляется. У нас есть работающий движок для 3D рендеринга с цветами, освещением, затенением, и заняло это около 200 строк кода — неплохо!
Вот небольшой бонус для вас — вы можете быстро создать фигуру, приближенную к сфере из своего тетраэдра. Этого можно достичь путём разбивания каждого треугольника на 4 маленьких и «надувая».
public static List inflate(List tris) {
List result = new ArrayList<>();
for (Triangle t : tris) {
Vertex m1 = new Vertex((t.v1.x + t.v2.x)/2, (t.v1.y + t.v2.y)/2, (t.v1.z + t.v2.z)/2);
Vertex m2 = new Vertex((t.v2.x + t.v3.x)/2, (t.v2.y + t.v3.y)/2, (t.v2.z + t.v3.z)/2);
Vertex m3 = new Vertex((t.v1.x + t.v3.x)/2, (t.v1.y + t.v3.y)/2, (t.v1.z + t.v3.z)/2);
result.add(new Triangle(t.v1, m1, m3, t.color));
result.add(new Triangle(t.v2, m1, m2, t.color));
result.add(new Triangle(t.v3, m2, m3, t.color));
result.add(new Triangle(m1, m2, m3, t.color));
}
for (Triangle t : result) {
for (Vertex v : new Vertex[] { t.v1, t.v2, t.v3 }) {
double l = Math.sqrt(v.x * v.x + v.y * v.y + v.z * v.z) / Math.sqrt(30000);
v.x /= l;
v.y /= l;
v.z /= l;
}
}
return result;
}Вот что должно у вас получиться:
Я бы закончил эту статью, порекомендовав одну занимательную книгу: «Основы 3D-математики для графики и разработки игр». В ней вы можете найти детальное объяснение процесса рендеринга и математики в этом процессе. Её стоит прочитать, если вам интересны движки для рендеринга.
Источник: blog.rogach.org
Дисклеймер: несмотря на многие ограничения и практически отсутствующий инструментарий, этот проект все-таки является 3д-движком, т. к. позволяет в режиме реального времени визуализировать трехмерную сцену. Unity3d используется исключительно как способ доступа к нужным мне технологиям. Штатный рендер Unity не используется.
Немного теории
Рендер трехмерного мира являет собой чрезвычайно сложную задачу, как с точки зрения объема работы, так и с используемого математического аппарата. В связи с этим проще и эффективнее доработать старое двигло с учетом новых технологий, чем писать с нуля движок. Даже самые новые игровые движки, типа CryEngeich, Unity 2015-2020, EU4-5 содержат в своей основе год бородатых годов. А может и не содержат, свечку не держал, исходники не видел. Итак, позволить себе создание нового 3д движка могут или крупные компании или, напротив, инди-студии, которым нечего терять можно и можно пуститься во все тяжкие
Самый распространенным способ описание трехмерной модели объекта является полигональная модель. Модель задается в виде массива вершин и отношений между ними:
- пара вершин образует ребро
- три ребра образуют треугольник
- множество треугольников образуют трехмерную поверхность
Этот способ позволяет описывать объекты любой сложности и размеров, но полностью игнорирует внутренне устройство объектов — потому что полигональная модель описывает только форму поверхности. Так же реализация динамического изменения модели очень сложна, неочевидна и имеет ограничения.
Другой способ задание трехмерной сцены — это использование так называемых вокселей — трехмерных писелей. В этом случае трехмерная сцена задается как трехмерный массив цветов. Это решение кажется довольно интуитивным, но из-за многих проблем не получило должного распространения. Основным ограничениями являются:
- затраты видеопамяти при рендере пропорциональны размеру сцены
- фундаментальная угловатость мира, связанная с тем, что сцена задается в виде «кубиков»
- невозможность текстурирования объектов
- сохраненное на диске состояние сцены занимает большой объем памяти
Однако, воксели имеют уникальные положительные стороны:
- возможность легко изменять объекты на сцене
- физически корректная реализация распространения света в полупрозрачных телах
- полный контроль за процессом рендеринга из-за его простоты
- возможность создания физической симуляции мира на уровне поведения отдельных частиц
Как я дошел до жизни такой
Предистория разработки этого движка началась ещё в 2003 году, когда в журнале Game. exe была выпущена статья о разработке компьютерной игры «Периметр: Геометрия войны». В моей памяти навсегда остались описание деформируемого в реальном времени ландшафта, по которому медленно ползут танки, которые обстреливают гаубицы на искусственных насыпях. »Периметр» навеки стал для меня эталоном стратегии, пускай даже сама игра была не столько хороша, как в моих мечтах. Идея использовать ландшафт в качестве основного элемента игрового процесса крепко поселилась в голове. И, когда я в 2019 году узрел на Хабре статьи, посвященные использованию вычислительных шейдеров я понял — настало то самое время. Идея создать свой воксельный движок не имела конкретной цели (вроде создания игры), но начав я уже не мог остановится.
Базовый принцип работы
Сцена для рендера представляет собой Texture3D, т. е. трехмерный массив, где индекс обозначает положение вокселя в трехмерном пространстве, а хранится в нем его цвет в формате RGBA (Red, Green, Blue, Alpha). Размер сцены составляет 256x256x256 вокселей. Для каждого пикселя экрана из точки положения наблюдателя (камеры) выпускается луч, в направлении данного пикселя. Далее в цикле происходит «шагание» по лучу, где читается цвет из трехмерной текстуры, где индекс — это округленные координаты текущей точки. Если прозрачность цвета близка к нулю — то цикл продолжается дальше. Если прозрачность цвета больше нуля — то пиксель закрашивается в этот цвет и цикл прерывается. Вот такой простой алгоритм, дающий, тем не менее рендер в реальном времени. На самом деле я его позаимствовал его из этой статьи.
Так как я статью не понял, у меня получился свой собственный рабочий алгоритм.
Первые шаги
Что бы не тянуть интригу — мне удалось сделать с нуля рабочий рендер 3d сцены на Юнити, собрав при этом чуть ли не все возможные проблемы.
Самого старого варианта, с белым шаром в пустом пространстве, не сохранилось. Однако, и на этом скриншоте видны характерные черты воксельного рендера — угловатость пейзажа и его низкое разрешение. Но картинка есть! Я не знаю, кто будет читать эту статью и настолько мой читатель будет грамотен в вопросах компьютерной графики. Поэтому, я должен сказать, что сделанное мной даже на этапе скриншота — значительный успех. На каждом шагу меня подстерегали неразрешимые проблемы, любая из которых могла меня навсегда остановить, а хитроумным решениям для обхода глюков несть числа. Результатом является стабильный рендер картинки с частотой 30 герц и смутные перспективы на будущее технологии. Останавливаться на достигнутом было слишком просто, к тому же такой результат не годился для практического применения.
Реализация
Иметь алгоритм — это хорошо, но иметь конкретную реализацию — несравнимо лучше. Для простоты я использовал игровой движок Unity. Мой движок состоит из двух основных компонентов — скрипты для управления процессом рендера и compute shader (вычислительный шейдер) для самого процесса рендера. Вычислительный шейдер — это очень полезная и оригинальная технология, которая позволяет запускать на видеокарте любой выполнимый код и возвращать результат обратно на сторону процессора. В отличии от процессора, видеокарта при помощи compute shader может параллельно обрабатывать миллионы потоков, что идеально подходит под задачу. Однако, сложность заключается в том, что вычислительными шейдерами трудно управлять и ещё сложнее отлаживать.
Просто рендера непрозрачных тел не хватает для красивой и убедительной картинки, поэтому следующий логический шаг — это добавление к рендеру освещения. Собственно, освещение — это и есть основная задача 3д-движков. Все графические технологии направлены на улучшение освещения и приближения его к реальной физике распространения света. Для моего случая вполне допустимо использовать простые законы геометрической оптики. Алгоритм:
- из источника света выпускается луч для каждого вокселя, каждый воксель обрабатывается параллельно
- в цикле происходит шагание по лучу и проверяется наличие препятствий для распространения света. В случае их отсутствия воксель считается освещенным. В противном случае он будет неосвещенным
- данные о освещенности записываются в специальную текстуру, называемую картой теней. Она имеет такое же разрешение, что и текстура изображения.
- цвет пре-рендера сцены умножается на карту теней.
На самом деле этот алгоритм имеет оптимизацию, позволяющую его выполнять в экранном пространстве. Это означает, что для каждого пикселя сцены берется воксель, который виден в этом пикселе и вычисляется его освещенность. В этом случае затраты вычислений на видеокарте будут пропорциональны разрешению экрана, дальности обзора и дальности действия источников света. Для большой сцены этот метод будет значительно снижать количество вычислений.
Однако, данный метод можно улучшить, добавив отображение нескольких источников света.
На скриншоте видно две цветные тени от источников света. В общем случае такой эффект некорректен с точки зрения оптики, поскольку тени должны быть черными, а цвет должно иметь освещенное пространство. Дальнейшая работа над освещением — это использование более сложной модели освещения. Прошлая модель не учитывала расстояние от источника света и угол его падения. Новая учитывает это, что позволяет получить более красивую картинку. Для пояснения принципа работы следует рассказать, что такое нормаль. Нормалью называется вектор, который перпендикулярен поверхности и имеет длину, равную единице. По закона оптики, интенсивность освещения поверхности тела пропорциональна скалярному произведению нормали поверхности и луча света. Для создания этого механизма я для каждого вокселя вычислял его нормаль путем проверки его соседей на прозрачность. В итоге я получал карту нормалей всей сцены, которую использовал для дальнейших расчетов. В итоге, лучи света, падающие полого к поверхности, хуже освещают поверхность, чем те, которые падают перпендикулярно. Это создает более правдоподобную картинку и визуально скругляет острые грани.
На рендер на последнем скриншоте — это, пожалуй, предел того, что можно вытащить из расчет освещения в экранным пространстве. Этот метод очень производителен и дает красивую картинку. К моей великой печали, он не позволяет работать с полупрозрачными объектами, а это одно из главных потенциальных достоинств воксельной технологии. Я испробовал много СПОБСобов обойти это ограничение, но лишь доказал, что это невозможно. печальный результат можно увидеть на картинке ниже.
Объемное освещение
Когда я понял фундаментальные ограничения старой системы, то было сложно справится с печалью. Требовалось радикально отойти от старого алгоритма, что бы продвинутся дальше. Мой новый алгоритм (названный «Accumulation de perte de lumière» или «Pertalum») имитирует реальное распространение света. Суть этого алгоритма заключается в использовании особой трехмерной текстуры, названной картой светопотерь. При расчете лучей в эту текстуру сохраняется цвет, который равен потери яркости луча при прохождении через данный воксель. Эти вычисления применяются для всех вокселей сцены. Да, для всех 16 миллионов. Результатом была довольно красивая картинка ценой чудовищных вычислительных затрат.
При запуска получилась приятная картинка и неприятное явление в лице загрузки видеокарты на 100%. Я долго думал как уменьшить загрузку, пока не придумал поистине гениальный план.
Я купил новую видеокарту! RTX2060 (на то время она была весьма мощной).
Однако, христианское милосердие не давало мне забыть о несчастных, которые не имели мощной видюшеньки и я решил продолжить оптимизацию расчета освещения. Самым очевидным вариантом было бросать лучи из источника света во все стороны и для каждого затронутого ими вокселя производить расчет освещения. Это дало небольшой прирост производительности, за счет отбрасывание многократной обработки одного и того же вокселя. Картинку смотрите ниже.
Можно видеть так называемыелучи Бога— безо всяких дополнителньных махинаций, которые нужны в обычном движке.
На данном этапе движок выполняет максимум того, что можно выжать с существующих технологий. Дальнейшее развитие требует совершенно новых решений. Для оптимизации воксельной сцены используется так называемое восьмидрево — древовидная структура данных, в которой сцена разбивается на 8 элементов. Каждый элемент, если он не пустой, так же разбивается на восемь элементов и так до тех пор, пока не будет достигнут некий минимальный размер элемента. Если элемент оказывается пустым (содержит только прозрачные воксели) то он обрабатывается как один воксель и на нем разбиение прекращается. Как вы можете догадаться, до полноценной реализации этого у меня руки не дошли.
Реализация и беды с ней
Создание и отладка двигла — это отдельное сказание, по эпичности сравнимое с Махабарахтой и Рагнарёком. За каждым скриншотом скрывается драма
Разработка движка началась с Unity3d. Звучит немного абсурдно, но этой самый простой способ получить доступ к необходимым мне технологиям. Разумеется, я изучил возможности главного конкурента Unity — Unreal Ingeich (ну ладно, Engine) 4. В Анрыле написание, компиляция и запуск compute shader занимают гораздо больше усилий и сомнительных плюсах. Работа с вычислительными шейдерами в Юнити укладывается в простую последовательность:
- написать шейдер
- сохранить его в папке Resources
- в скрипте загрузить его из этой папки
- назначить переменные загруженному шейдеру
- запустить его
В Анрыле для этого надо выполнить множество сложных и неочевидных операций и написать уйму кода, который делает неизвестно что (во всяком случае для меня) и неизвестно как (аналогично). Возможно, подход Анрыла имеет свой плюс. Или даже два плюса (++).
Как я уже писал в прошлой части, Compute Shader — это технология, которая позволяет выполнять на видеокарте любой произвольный код и даже возвращать его на сторону центрального процессора. При обычной работе видеокарта обрабатывает 3д-сцену, формирует картинку и отправляет её в кадровый буффер, после чего она оправляется на монитор. Использование вычислительных шейдеров превращает видеокарту в отдельное вычислительное устройство. Видеокарта из-за особенностей архитектуры идеально приспособлена для параллельного выполнения множества однотипных операций над данными. Например, обработка текстуры (фильтрация, наложение эффектов и т. д.). Возьмем текстуру размером 1024х1024. В этом случае ComputeShader (далее — CS) позволяет параллельно обрабатывать все пиксели, благодаря чему этот процесс завершается за считанные миллисекунды. Центральный процессор может обрабатывать текстуру в 5-10 потоков и завершит работу за несколько секунд, чего недостаточно для создания эффектов в режиме реального времени. Однако, даже CS будет тормозить при слишком большом количестве потоков.
Сам CS представляет собой код, написанный на языке HLSL (англ. высокоуровневый язык шейдеров). Это один из диалектов си, с вырезанной работой с памятью и добавленной векторной арифметикой. CS состоит из глобальных переменных и ядер (kernel). Кернель — это обычная функция, которая имеет параметр id, который имеет уникальное значение для каждого потока. Шейдер запускается на стороне скрипта с указанным количеством потоков. Подробная информация о этой технологии тайной не является и доступна по первым ссылкам в гугле.
Беды
Если бы у меня CS и другие технологии работали точно так же, как и в руководстве — я бы добился бы такого же результата за две недели, а не за три месяца. Среди самых неожиданных проблем:
- Нельзя в скрипте создать трехмерную текстуру (Texture3D) размером больше чем 256х256х170. В противном случае движок будет выдавать черный экран вместо рендера, даже если эта текстура НИГДЕ не используется. При этом никаких ошибок и предупреждений Unity не выдает и посему решить эту проблему не удалось, лишь обойти.
- Для использования трехмерной текстуры необходимо дополнительно указать, что она именно трехмерная, причем в руководстве это нигде не указано. В противном случае шейдер будет выдавать ошибку, что нет третьего измерения у текстуры.
- В CS в текстуру нельзя сохранять отрицательные значения цвета.
- Полностью отсутствуют средства отладки шейдера, поэтому для определения проблем приходится создавать свои инструменты
- Юнити последних версий имеет дурную привычку обновлятся, что приводит к крушению всего проекта. Решилось переходом на старую версию.
- На ноль делить нельзя. Даже если очень хочется.
Физическая симуляция
Воспоминания о разрушаемом ландшафте не давали мне покоя и я решил воплотить физическую симуляцию мира на уровне отдельных частиц. Я знал что задача была решаема и с головой пустился в разработку. Для этого пришлось отказаться от представления мира в виде обычной трехмерной текстуры. Вместо сцену я представил в виде списка частиц длиной 256х256х256. Частица представляет собой структуру, которая содержит в себе:
- Цвет (куда уж без него?)
- Позицию в пространстве
- Текущую скорость
- Массу
Для визуализации оравы частиц я использовал дополнительный кернель, в котором их копировал их в другую текстуру по индексу, соответсвующую их пространственным координатам. Далее кернели рендера отсисовывают эту промежуточную текстуру. Для того, что бы можно было найти частицу по её положению, я завел ещё одну текстуру, в котором по индексу хранил номер частицы в общем списке. Фактически я реализовал указатель в языке, который их не поддерживал.
Принцип работы физической симуляции был таков:
- в отдельном кернеле каждая частица меняет свою позицию на величину, равную своей скорости
- Частица передает импульс другим частицам, которые она могла задеть.
Я смело предположил, что это должно работать. А на самом деле — нет. Все, что у меня получилось — это сделать падение под действием гравитации и обнаружение столкновений.
Редактор
В процессе работы я сталкивался с тем, что мне надо прямо во время работы добавить или удалить объекты на сцене. Это значит, что пришло время создать 3д-редактор на основе моего движка! На этот раз дело шло безо всяких эпических превозмоганий, некоторую сложность составило создание отката рисования (undo-redo, как в любом редакторе). Захват всей сцены требовам большого объема памяти и на несколько секунд тормозил рендер. Я решил эту проблему сохраняя в памяти только измененный фрагмент сцены.
Сейчас редактор имеет следующие функции:
- Рисование на сцене/добавление новых вокселей.
- Изменение режимов рисования (глобальное/экранное, непрерывное/дискретное).
- Отмена изменений
- Сохранение в файл (расширение. tempete) и загрузка из файла сцены.
Ну наверное, все. На этой ноте я прекратил работу над проектом, что бы заняться другим, более важным для себя. Если кому-нибудь нужны исходники — пишите.
И главное: время танков, ползущих по динамически изменяемому ландшафту к гаубицам на искусственных насыпях, обязательно придет.
#лонгрид #движок #воксели #разработка
В рамках мероприятия Blender Conference 2017 известный белорусский 3D-художник и активный представитель комьюнити Blender Глеб Александров прочитал доклад о секретах успешного рендера, которые известны лучшим художникам ArtStation. Делимся основными тезисами выступления.
Просматривая работы на ArtStation, многие начинающие художники наверняка замечали, что одни рендеры собирают множество лайков и комментариев, а другие остаются незамеченными. Причём последние словно попадают в серую зону: их никто не хвалит, но никто и не критикует. Почему так происходит?
После создания модели или рендера 3D-художники порой сталкиваются с тем, что итоговый результат их не впечатляет. Но сами они не могут понять, в чём заключается проблема, поэтому обращаются к коллегам или спрашивают совета у друзей в соцсетях. В результате им приходит огромное количество противоречивого фидбэка: «не хватает деталей», «минимализм был бы лучше», «неудачная цветовая гамма», «нужны другие референсы» и, наконец, всеми любимое «пересмотри композицию». У начинающих художников действительно часто хромает композиция, но что именно нужно исправить, поймёт далеко не каждый.
Существует одна из теорий композиции, зная которую, художник может понять, почему его работа неудачна и как в дальнейшем избежать подобных ошибок. Это своего рода секрет, который, по мнению Глеба, знают профессионалы из крупных студий, таких как Activision Blizzard, Dreamworks, Industrial Light & Magic и Pixar, а также специалисты и известные в CG-индустрии личности — например, Дэниел Бистедт, Джерри Перкинс, Виталий Булгаров и Нил Блевинс.
Стоит сказать пару слов о Ниле Блевинсе. Он профессиональный 3D-художник с многолетним опытом, центральная тема его творчества — роботы, внеземные существа и пейзажи в стиле sci-fi. Нил сотрудничает с такими студиями, как Pixar, Blur Studio и Monolith, а также ведёт блог, в котором выкладывает массу полезных уроков для художников, в частности по работе с композицией. Один из таких туториалов привлёк внимание Глеба. Художник провёл небольшое исследование и понял, что способ Блевинса действительно работает. Речь идёт о первичных, вторичных и третичных формах композиции. Идея в том, что при грамотном размещении больших, средних и малых деталей на рендере итоговый результат выходит более приятным для глаз.
Если отобрать самые рейтинговые арты и пометить разными цветами скопления форм, можно увидеть определённые закономерности. В докладе Глеба эти участки обозначены следующими цветами:
Кадр: презентация Глеба Антонова на Blender Conference 2017
- первичные формы (крупные детали) — красный;
- вторичные формы (средние детали) — синий;
- третичные формы (малые детали) — жёлтый.
Первичные формы — крупные детали рендера. Как правило, из них состоит основа модели, и они легко считываются на изображении. Первичные формы определяют расположение остальных форм.
Вторичные формы — детали среднего размера. Расположены поверх первичных форм. Обеспечивают плавный переход между крупными и малыми деталями.
Третичные формы — самые мелкие детали. С их помощью художник расставляет правильные акценты в работе.
Вышеперечисленные градации форм присутствуют во всех успешных работах. Самое важное, что при этом они сбалансированы между собой. Баланс в рендере можно сравнить с музыкой: если в любимой песне выборочно отключить отдельные частоты — звучание уже не будет таким гармоничным.
Выходит, что самая распространённая ошибка в рендерах возникает из-за нарушения баланса либо отсутствия тех или иных деталей в рендере. Неудачные примеры — огромная стена с прорисованными крошечными кирпичами, но без промежуточных вторичных форм, или модель робота без точечных акцентов в дизайне.
Как же художнику определить правильный баланс форм с точки зрения их размеров и существуют ли какие-то общепринятые стандарты по аналогии с золотым сечением? Однозначного ответа на этот вопрос не существует из-за специфики самой профессии. Во многом это зависит от подхода самого художника: стиль, масштабы проекта, референсы и другие аспекты могут влиять на результат. Тем не менее в лучших работах ArtStation прослеживаются определённые закономерности. Согласно личным подсчётам Глеба, примерное соотношение между размерами трёх типов форм варьируется от 1:5 до 1:10. То есть вторичные формы в 5–10 раз меньше, чем первичные, и в 5–10 раз больше, чем третичные.
Важно отметить, что приведённую выше рекомендацию нельзя считать эталоном. Это всего лишь примерный диапазон соотношений, который Глеб определил на основе собственного исследования чужих работ.
Примерно понимая, как работает баланс форм, необходимо грамотно распределить все детали внутри композиции.
Кадр: презентация Глеба Антонова на Blender Conference 2017
Изображение выше демонстрирует распределение форм в работе Джеймса Миллера. Если обратить внимание на схему справа, то можно заметить, что расположение деталей кажется более естественным и в каком-то плане непредсказуемым. Всё дело в том, что взгляд подсознательно задерживается на интересной композиции форм, а не на однородной и быстро узнаваемой. В этом можно убедиться на следующем примере.
На схеме видно, что поверх первичной формы камня равномерно распределены три вторичные формы, на которых, в свою очередь, так же ровно раскиданы третичные формы. В итоге результат становится слишком тяжёлым для восприятия. Расположение деталей не даёт сфокусироваться на каких-то акцентах и недостаточно вариативно, чтобы заинтересовать зрителя. Совсем иное впечатление производит следующий рендер.
Кадр: презентация Глеба Антонова на Blender Conference 2017
Визуально такое распределение форм смотрится намного приятнее. Здесь нет обилия малых блоков, выстроенных в ряд, но есть области с высокой детализацией и, наоборот, пустые участки. В совокупности такая вариативность добавляет рендеру динамики и притягивает взгляд. Это также можно сравнить с музыкой. Выбирая между треками с однородным и оригинальным ритмическим рисунком, человек вероятнее остановится на втором варианте, ведь гораздо интереснее услышать какой-то мотив, чем монотонное звучание.
Ещё одна вещь, на которую стоит обратить внимание, — распределение пустого пространства. Опытные художники используют его, чтобы выгодно подчеркнуть более мелкие детали или убрать излишнюю «плотность» отдельных элементов. К тому же чередование пустых участков с высокодетализированными облегчает восприятие и не перегружает внимание зрителя.
Кадр: презентация Глеба Антонова на Blender Conference 2017
Это очень важный момент: если у каждого участка изображения одинаковая интенсивность, то общий вид рендера превратится в месиво. Это как если музыканты из одного оркестра станут одновременно исполнять свои партии на максимальной громкости — выйдет какофония.
Кадр: презентация Глеба Антонова на Blender Conference 2017
Совет эксперта
«Представленный выше рендер динозавра смотрится неудачно не столько из-за одинаковой интенсивности форм, сколько из-за того, что в модели не хватает крупных деталей. Средние детали, отмеченные на схеме, сливаются со средними деталями окружения, в данном случае с машинами на заднем плане. Из-за этого итоговая картинка „рассыпается“ по композиции. Это говорит о том, что в рендере важен не только баланс форм, но и окружение. Оно должно оттенять персонажа. Это достигается за счёт размытия заднего плана, ракурса либо освещения».
Кирилл Резниченко,
CEO RainStyle Games
Из трёх предыдущих пунктов можно сделать вывод, что на рендере получаются своеобразные скопления деталей разного размера. Это ведёт к последней отличительной особенности качественного рендера — слиянию групп форм. Данное явление универсально и охватывает весь спектр визуальных искусств, начиная от пиксель-арта и заканчивая фотографией. Здесь важно помнить о двух вещах:
- точки интереса улучшат композицию;
- группирование по 3, 5, 7, 9 элементов или объектов помогает эффективнее организовать пространство и способствует лучшему восприятию.
Кадр: презентация Глеба Антонова на Blender Conference 2017
Человеческое зрение устроено так, что нам нравится группировать мелкие детали в более крупные объекты. Слияние деталей на рендере лучше воспринимается мозгом, а значит, такой арт покажется зрителю более эстетичным. И если внимательно рассмотреть лучшие работы на ArtStation, то в каждой можно увидеть эту закономерность.
Для создания качественного рендера следует учитывать четыре пункта:
- используйте все три типа форм: большие, средние и малые;
- следите, чтобы эти формы были примерно пропорциональны;
- распределяйте их по композиции неоднородно и непредсказуемо;
- чередуйте области деталей с пустым пространством и разделяйте формы на отдельные группы.
Совет эксперта
«Чтобы рендер оказался в центре внимания, художнику необходимо усвоить три вещи.
- Композиция. Купите книжку по теории фотографии. Если вы научитесь красиво фотографировать, даже на смартфон, этот навык заметно улучшит качество ваших работ. Искусство фотографии тоже изучает распределение и сочетание объёмов больших, средних и малых объектов. Также рекомендую ознакомиться со статьёй «Мастерство визуального рассказа», в которой подробно разбирают основные приёмы композиции на примере анимационного фильма «Суперсемейка» от Pixar.
- Исходя из первого пункта, научитесь работать с освещением. Свет так же важен, как и детализация. Он создаёт настроение и точки внимания.
- Если говорить об ArtStation, мне кажется, что в рамках этой площадки художнику важно выкладывать не только итоговый результат, но и сами модели с разных ракурсов, в том числе детальные снимки текстур. Посетители сайта всегда это оценят».
Кирилл Резниченко,
CEO RainStyle Games
Введение
Люди от природы креативны. Мы постоянно проектируем и создаём новые, полезные и интересные вещи. Сегодня мы пишем ПО, помогающее процессу проектирования и творчества. Программы САПР (Computer-aided design, CAD) позволяют творцам проектировать здания, мосты, графику видеоигр, чудовищ для фильмов, объектов для 3D-печати и множество других вещей перед созданием физической версии проекта.
По своей сути, инструменты CAD являются способом абстрагирования трёхмерного проекта в нечто, что можно просматривать и редактировать на двухмерном экране. Чтобы справляться со своей задачей, инструменты CAD должны обеспечивать три основных элемента функциональности. Во-первых, они должны иметь структуру данных, описывающую проектируемый объект: это то, как компьютер понимает создаваемый пользователем трёхмерный мир. Во-вторых, инструмент CAD должен обеспечивать отображение проекта на экране пользователя. Пользователь проектирует физический объект с тремя измерениями, но экран компьютера имеет всего два измерения. Инструмент CAD должен моделировать способ восприятия нами объектов и отрисовывать их на экране так, чтобы пользователь смог понять все три измерения объекта. В-третьих, CAD должен предоставлять возможность взаимодействия с проектируемым объектом. Пользователь должен быть способен дополнять или модифицировать проект, чтобы создать нужный результат. Кроме того, все инструменты должны иметь возможность сохранения и загрузки проектов с диска, чтобы пользователи могли сотрудничать, обмениваться своей работой и сохранять её.
Специализированные инструменты CAD предоставляют множество дополнительных функций, соответствующих требованиям своей области. Например, в архитектурном CAD есть симуляции физики для тестирования климатических нагрузок на здание, в программе для 3D-печати будут присутствовать функции, проверяющие возможность печати объекта, а пакет для создания кинематографических спецэффектов содержит функции точной симуляции пирокинетики.
Однако во всех инструментах CAD должны присутствовать по крайней мере три описанных выше элемента: структура данных, описывающая проект, возможность отображения на экране и способ взаимодействия с проектом.
Давайте теперь узнаем, как можно описать 3D-проект, отобразить его на экране и взаимодействовать с ним всего в 500 строках на Python.
Рендеринг как ориентир
Движущей силой многих архитектурных решений 3D-редактора является процесс рендеринга. Нам нужна возможность хранения и рендеринга в проекте сложных объектов, но в то же время мы хотим обеспечить низкую сложность кода рендеринга. Давайте изучим процесс рендеринга и исследуем структуру данных для проекта, позволяющую нам хранить и отрисовывать произвольные сложные объекты при помощи простой логики рендеринга.
Управление интерфейсами и основным циклом
Прежде чем мы приступим к рендерингу, нам нужно подготовить некоторые аспекты. Во-первых, нам требуется создать окно для отображения проекта. Во-вторых, мы хотим обмениваться данными с графическими драйверами для рендеринга на экране. Мы бы не хотели обмениваться данными напрямую, поэтому для управления окном воспользуемся кроссплатформенным слоем абстракции под названием OpenGL и библиотекой под названием GLUT (OpenGL Utility Toolkit).
Примечание о OpenGL
OpenGL — это интерфейс программирования графических приложений (API) для кроссплатформенной разработки. Это стандартный API для разработки графических приложений для множества платформ. OpenGL имеет два основных варианта: Legacy OpenGL и Modern OpenGL.
Рендеринг в OpenGL основан на полигонах, задаваемых вершинами и нормалями. Например, для рендеринга одной стороны куба мы задаём 4 вершины и нормаль к стороне.
Legacy OpenGL имеет конвейер с фиксированными функциями (fixed function pipeline). Задавая глобальные переменные, программист может включать и отключать автоматизированные реализации таких функций, как освещение, раскраска, усечение граней и т.д. После чего OpenGL автоматически рендерит сцену со включенной функциональностью. Такая система является устаревшей.
В Modern OpenGL используется программируемый конвейер рендеринга (programmable rendering pipeline), при котором программист пишет небольшие программы, называемые «шейдерами»; они выполняются на специализированном графическом оборудовании (GPU). Программируемый конвейер Modern OpenGL заменил устаревший Legacy OpenGL.
В своём проекте мы будем использовать Legacy OpenGL. Фиксированная функциональность, предоставляемая Legacy OpenGL, очень полезна для обеспечения небольшого размера кода. Она уменьшает количество необходимых знаний линейной алгебры и упрощает наш код.
Что такое GLUT
Библиотека GLUT из комплекта OpenGL позволяет нам создавать окна операционной системы и регистрировать функции обратного вызова интерфейса пользователя. Этой базовой функциональности достаточно для наших целей. Если бы нам была нужна более функциональная библиотека для управления окнами и взаимодействия с пользователем, то мы бы задумались об использовании полноценного тулкита наподобие GTK или Qt.
Средство просмотра
Для управления параметрами GLUT и OpenGL, а также остальной частью программы моделирования мы создадим класс под названием Viewer. Мы будем использовать единственный экземпляр Viewer, управляющий созданием и рендерингом окон, содержащий основной цикл нашей программы. Внутри процесса инициализации Viewer мы создадим окно GUI и инициализируем OpenGL.
Функция init_interface создаёт окно, в которое будет рендериться редактор, и задаёт функцию, котороая должна вызываться для рендеринга проекта. Функция init_opengl задаёт нужное для программы состояние OpenGL. Она задаёт матрицы, включает отсечение задних граней, регистрирует источник света для освещения сцены и сообщает OpenGL, что объекты нужно раскрашивать. Функция init_scene создаёт объекты Scene и располагает начальные узлы, чтобы пользователь мог начать работу. Чуть ниже мы узнаем больше о структуре данных Scene. Наконец, init_interaction регистрирует обратные вызовы функций для взаимодействия с пользователем, что мы обсудим позже.
После инициализации Viewer мы вызываем glutMainLoop, чтобы перенести исполнение программы в GLUT. Эта функция никогда не выполняет возврат. Обратные вызовы функций, зарегистрированные нами для событий GLUT, будут вызываться при выполнении этих событий.
class Viewer(object):
def __init__(self):
""" Initialize the viewer. """
self.init_interface()
self.init_opengl()
self.init_scene()
self.init_interaction()
init_primitives()
def init_interface(self):
""" initialize the window and register the render function """
glutInit()
glutInitWindowSize(640, 480)
glutCreateWindow("3D Modeller")
glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB)
glutDisplayFunc(self.render)
def init_opengl(self):
""" initialize the opengl settings to render the scene """
self.inverseModelView = numpy.identity(4)
self.modelView = numpy.identity(4)
glEnable(GL_CULL_FACE)
glCullFace(GL_BACK)
glEnable(GL_DEPTH_TEST)
glDepthFunc(GL_LESS)
glEnable(GL_LIGHT0)
glLightfv(GL_LIGHT0, GL_POSITION, GLfloat_4(0, 0, 1, 0))
glLightfv(GL_LIGHT0, GL_SPOT_DIRECTION, GLfloat_3(0, 0, -1))
glColorMaterial(GL_FRONT_AND_BACK, GL_AMBIENT_AND_DIFFUSE)
glEnable(GL_COLOR_MATERIAL)
glClearColor(0.4, 0.4, 0.4, 0.0)
def init_scene(self):
""" initialize the scene object and initial scene """
self.scene = Scene()
self.create_sample_scene()
def create_sample_scene(self):
cube_node = Cube()
cube_node.translate(2, 0, 2)
cube_node.color_index = 2
self.scene.add_node(cube_node)
sphere_node = Sphere()
sphere_node.translate(-2, 0, 2)
sphere_node.color_index = 3
self.scene.add_node(sphere_node)
hierarchical_node = SnowFigure()
hierarchical_node.translate(-2, 0, -2)
self.scene.add_node(hierarchical_node)
def init_interaction(self):
""" init user interaction and callbacks """
self.interaction = Interaction()
self.interaction.register_callback('pick', self.pick)
self.interaction.register_callback('move', self.move)
self.interaction.register_callback('place', self.place)
self.interaction.register_callback('rotate_color', self.rotate_color)
self.interaction.register_callback('scale', self.scale)
def main_loop(self):
glutMainLoop()
if __name__ == "__main__":
viewer = Viewer()
viewer.main_loop()Прежде чем разбирать функцию render, мы должны немного поговорить о линейной алгебре.
Координатное пространство
В нашем случае координатное пространство будет представлять собой точку начала координат и набор из трёх базисных векторов, обычно обозначаемых как оси x, y и z.
Точка
Любую точку в трёх измерениях можно представить как смещение в направлениях x, y и z относительно точки начала координат. Описание точки задаётся относительно координатного пространства, в котором находится точка. Одна и та же точка имеет различные описания в разных координатных пространствах. Любая точка в трёх измерениях может быть представлена в любом трёхмерном координатном пространстве.
Вектор
Вектор — это значение из x, y и z, определяющее разницу между двумя точками по осям x, y и z.
Матрица преобразований
В компьютерной графике удобно использовать несколько разных координатных пространств для разных типов точек. Матрицы преобразований преобразуют точки из одного координатного пространства в другое. Чтобы преобразовать вектор v из одного координатного пространства в другое, мы выполняем умножение на матрицу преобразований M: v′=Mv. Примерами распространённых матриц преобразования являются перемещение, масштабирование и поворот.
Координатные пространства модели, мира, окна просмотра и проецирования
Рисунок 1 — Конвейер преобразований
Для отрисовки на экране элемента нам нужно выполнить преобразование между несколькими координатными пространствами.
Все преобразования, показанные в правой части Рисунка 1, в том числе все преобразования из пространства камеры (Eye Space) в пространство окна просмотра (Viewport Space) будет выполнять за нас OpenGL.
Преобразование из пространства камеры в однородное пространство усечения (clip space) выполняется функцией gluPerspective, а преобразование в нормализованное пространство устройства и пространство окна обзора — функцией glViewport. Эти матрицы перемножаются и хранятся как матрица GL_PROJECTION. Для нашего проекта не обязательно знать терминологию или подробности работы этих матриц.
Однако нам самостоятельно придётся заняться левой частью схемы. Мы задаём матрицу, преобразующую точки модели (также называемой мешем) из пространств моделей в мировое пространство, это называется матрицей модели. Также мы задаём матрицу обзора, выполняющую преобразование из мирового пространства в пространство камеры. В этом проекте мы скомбинируем эти две матрицы, чтобы получить матрицу ModelView.
Чтобы узнать больше о полном конвейере рендеринга графики и используемых координатных пространствах, прочитайте главу 2 книги Real Time Rendering или другую книгу о компьютерной графике для начинающих.
Рендеринг при помощи Viewer
Функция render начинается с подготовки любого состояния OpenGL, что необходимо выполнять во время рендеринга. Она инициализирует матрицу проецирования при помощи init_view и использует данные из функции взаимодействия с пользователем для инициализации матрицы ModelView с матрицей преобразований, выполняющей переход из пространства сцены в мировое пространство. Подробнее о классе Interaction будет написано ниже. Она очищает экран при помощи glClear, приказывает сцене отрендериться, а затем рисует сетку единичных квадратов.
Перед рендерингом сетки мы отключаем освещение OpenGL. При отключении освещения OpenGL рендерит объекты сплошным цветом, а не симулирует источники освещения. Благодаря этому сетка визуально отличается от сцены. Далее glFlush подаёт сигнал графическому драйверу, что мы готовы к очистке буфера и отображению на экран.
# class Viewer
def render(self):
""" The render pass for the scene """
self.init_view()
glEnable(GL_LIGHTING)
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT)
# Load the modelview matrix from the current state of the trackball
glMatrixMode(GL_MODELVIEW)
glPushMatrix()
glLoadIdentity()
loc = self.interaction.translation
glTranslated(loc[0], loc[1], loc[2])
glMultMatrixf(self.interaction.trackball.matrix)
# store the inverse of the current modelview.
currentModelView = numpy.array(glGetFloatv(GL_MODELVIEW_MATRIX))
self.modelView = numpy.transpose(currentModelView)
self.inverseModelView = inv(numpy.transpose(currentModelView))
# render the scene. This will call the render function for each object
# in the scene
self.scene.render()
# draw the grid
glDisable(GL_LIGHTING)
glCallList(G_OBJ_PLANE)
glPopMatrix()
# flush the buffers so that the scene can be drawn
glFlush()
def init_view(self):
""" initialize the projection matrix """
xSize, ySize = glutGet(GLUT_WINDOW_WIDTH), glutGet(GLUT_WINDOW_HEIGHT)
aspect_ratio = float(xSize) / float(ySize)
# load the projection matrix. Always the same
glMatrixMode(GL_PROJECTION)
glLoadIdentity()
glViewport(0, 0, xSize, ySize)
gluPerspective(70, aspect_ratio, 0.1, 1000.0)
glTranslated(0, 0, -15)Что рендерить: сцена
После того, как мы инициализировали конвейер рендеринга для выполнения отрисовки в координатном пространстве мира, что мы будем рендерить? Вспомним, что наша цель — создание проекта, состоящего из 3D-моделей. Нам нужна структура данных для хранения этого проекта. а также структура данных для его рендеринга. Обратите внимание на вызов self.scene.render() в цикле рендеринга viewer. Что такое scene?
Класс Scene — это интерфейс со структурой данных, которую мы используем для описания проекта. Он абстрагирует подробности структуры данных и предоставляет функции интерфейса, необходимые для взаимодействия с проектом, в том числе функции для рендеринга, добавления элементов и манипулирования элементами. Существует один объект Scene, которым владеет viewer. Экземпляр Scene хранит список всех элементов сцены, называемый node_list. Также он отслеживает выбранный элемент. Функция render сцены просто вызывает render для каждого пункта списка node_list.
class Scene(object):
# the default depth from the camera to place an object at
PLACE_DEPTH = 15.0
def __init__(self):
# The scene keeps a list of nodes that are displayed
self.node_list = list()
# Keep track of the currently selected node.
# Actions may depend on whether or not something is selected
self.selected_node = None
def add_node(self, node):
""" Add a new node to the scene """
self.node_list.append(node)
def render(self):
""" Render the scene. """
for node in self.node_list:
node.render()Узлы
В функции render класса Scene мы вызываем render для каждого элемента node_list класса Scene. Но что за элементы находятся в этом списке? Мы называем их узлами. Узел может быть всем, что можно поместить в сцену. В объектно-ориентированном ПО мы пишем Node как абстрактный базовый класс. Любые классы, представляющие объекты, размещаемые в Scene, будут наследовать от Node. Этот базовый класс позволяет нам рассуждать о сцене абстрактно. Остальная часть кодовой базы не обязана знать подробностей об отображаемом ею объекте; ей достаточно знать, что они принадлежат к классу Node.
Каждый тип Node определяет собственное поведение для рендеринга самого себя и для любых других взаимодействий. Node отслеживает важные данные о самом себе: матрицу преобразований, матрицу масштабирования, цвет, и т.п. При умножении матрицы преобразований узла на его матрицу масштабирования, мы получаем матрицу преобразований из координатного пространства модели узла в координатное пространство мира. Кроме того, узел также хранит в себе параллельный осям ограничивающий параллелепипед (axis-aligned bounding box, AABB). Подробнее об AABB мы поговорим ниже.
Простейшей конкретной реализацией Node является примитив. Примитив — это единая фигура, которую можно добавить в сцену. В нашей программе примитивами будут куб (Cube) и сфера (Sphere).
class Node(object):
""" Base class for scene elements """
def __init__(self):
self.color_index = random.randint(color.MIN_COLOR, color.MAX_COLOR)
self.aabb = AABB([0.0, 0.0, 0.0], [0.5, 0.5, 0.5])
self.translation_matrix = numpy.identity(4)
self.scaling_matrix = numpy.identity(4)
self.selected = False
def render(self):
""" renders the item to the screen """
glPushMatrix()
glMultMatrixf(numpy.transpose(self.translation_matrix))
glMultMatrixf(self.scaling_matrix)
cur_color = color.COLORS[self.color_index]
glColor3f(cur_color[0], cur_color[1], cur_color[2])
if self.selected: # emit light if the node is selected
glMaterialfv(GL_FRONT, GL_EMISSION, [0.3, 0.3, 0.3])
self.render_self()
if self.selected:
glMaterialfv(GL_FRONT, GL_EMISSION, [0.0, 0.0, 0.0])
glPopMatrix()
def render_self(self):
raise NotImplementedError(
"The Abstract Node Class doesn't define 'render_self'")
class Primitive(Node):
def __init__(self):
super(Primitive, self).__init__()
self.call_list = None
def render_self(self):
glCallList(self.call_list)
class Sphere(Primitive):
""" Sphere primitive """
def __init__(self):
super(Sphere, self).__init__()
self.call_list = G_OBJ_SPHERE
class Cube(Primitive):
""" Cube primitive """
def __init__(self):
super(Cube, self).__init__()
self.call_list = G_OBJ_CUBEРендеринг узлов основан на матрицах преобразований, хранящихся в каждом из узлов. Матрица преобразований узла — это сочетание его матрицы масштабирования и матрицы перемещения. Вне зависимости от типа узла, первым этапом рендеринга является задание матрице ModelView интерфейса OpenGL матрицы преобразований, чтобы выполнить переход от координатного пространства модели к координатному пространству окна просмотра. После обновления матриц OpenGL мы вызываем render_self, чтобы приказать узлу выполнить необходимые вызовы OpenGL для отрисовки себя. Затем мы отменяем все изменения, внесённые в состояние OpenGL этого конкретного узла. Мы используем функции OpenGL glPushMatrix и glPopMatrix для сохранения и восстановления состояния матрицы ModelView до и после рендеринга узла. Обратите внимание, что узел хранит свой цвет, расположение и масштаб, применяя их к состоянию OpenGL перед рендерингом.
Если узел в данный момент выделен, мы заставим его излучать свет. Благодаря этому пользователь будет видеть, какой узел выбран.
Для рендеринга примитивов мы используем функцию OpenGL списков вызовов. Список вызовов OpenGL — это набор вызовов OpenGL, заданных и объединённых под одним названием. Вызовы могут выполняться с помощью glCallList(LIST_NAME). Каждый примитив (Sphere и Cube) определяет список вызовов, необходимый для его рендеринга (не показан).
Например, список вызовов куба отрисовывает 6 граней куба с центром в точке начала координат и с рёбрами длиной ровно 1 единицу.
# Pseudocode Cube definition
# Left face
((-0.5, -0.5, -0.5), (-0.5, -0.5, 0.5), (-0.5, 0.5, 0.5), (-0.5, 0.5, -0.5)),
# Back face
((-0.5, -0.5, -0.5), (-0.5, 0.5, -0.5), (0.5, 0.5, -0.5), (0.5, -0.5, -0.5)),
# Right face
((0.5, -0.5, -0.5), (0.5, 0.5, -0.5), (0.5, 0.5, 0.5), (0.5, -0.5, 0.5)),
# Front face
((-0.5, -0.5, 0.5), (0.5, -0.5, 0.5), (0.5, 0.5, 0.5), (-0.5, 0.5, 0.5)),
# Bottom face
((-0.5, -0.5, 0.5), (-0.5, -0.5, -0.5), (0.5, -0.5, -0.5), (0.5, -0.5, 0.5)),
# Top face
((-0.5, 0.5, -0.5), (-0.5, 0.5, 0.5), (0.5, 0.5, 0.5), (0.5, 0.5, -0.5))Использование исключительно примитивов сильно ограничивает возможности моделирования. 3D-модели обычно состоят из множества примитивов (или треугольных мешей, которые мы здесь рассматривать не будем). К счастью, структура класса Node упрощает создание узлов Scene, составленных из множественных примитивов. На самом деле, мы можем обеспечить поддержку произвольной группировки узлов без повышения сложности кода.
В качестве источника мотивации представим очень простую фигуру: обычного снеговика, составленного из трёх сфер. Даже несмотря на то, что фигура состоит из трёх отдельных примитивов, мы хотели бы иметь возможность работать с ней как с единым объектом.
Мы создадим класс HierarchicalNode, то есть Node, содержащий другие узлы. Он управляет списком «дочерних узлов». Функция render_self для иерархических узлов просто вызывает render_self для каждого из дочерних узлов. При помощи класса HierarchicalNode очень легко добавлять в сцену фигуры. Теперь для задания снеговика достаточно указать составляющие его фигуры, а также их относительные позиции и размеры.
Рисунок 2 — Иерархия подклассов Node
class HierarchicalNode(Node):
def __init__(self):
super(HierarchicalNode, self).__init__()
self.child_nodes = []
def render_self(self):
for child in self.child_nodes:
child.render()class SnowFigure(HierarchicalNode):
def __init__(self):
super(SnowFigure, self).__init__()
self.child_nodes = [Sphere(), Sphere(), Sphere()]
self.child_nodes[0].translate(0, -0.6, 0) # scale 1.0
self.child_nodes[1].translate(0, 0.1, 0)
self.child_nodes[1].scaling_matrix = numpy.dot(
self.scaling_matrix, scaling([0.8, 0.8, 0.8]))
self.child_nodes[2].translate(0, 0.75, 0)
self.child_nodes[2].scaling_matrix = numpy.dot(
self.scaling_matrix, scaling([0.7, 0.7, 0.7]))
for child_node in self.child_nodes:
child_node.color_index = color.MIN_COLOR
self.aabb = AABB([0.0, 0.0, 0.0], [0.5, 1.1, 0.5])Вы могли заметить, что объекты Node образуют древовидную структуру данных. Функция render, проходящая иерархические узлы, выполняет обход в глубину по дереву. При обходе она хранит стек матриц ModelView, используемых для преобразования в мировое пространство. На каждом шаге она записывает в стек текущую матрицу ModelView, а когда завершает рендеринг всех дочерних узлов, она извлекает матрицу из стека, оставляя на вершине стека матрицу ModelView родительского узла.
Благодаря тому, что мы сделали класс Node расширяемым, можно добавлять в сцену новые типы фигур, не меняя весь остальной код манипуляций сценой и рендеринга. Благодаря концепции узлов мы абстрагируемся от того факта, что объект Scene может иметь множество дочерних элементов. Это называется шаблоном проектирования «Компоновщик».
Взаимодействие с пользователем
Теперь, когда наша программа моделирования способна хранить и отображать сцену, нам нужен способ взаимодействия с ней. Нам нужно упростить два вида взаимодействий. Во-первых, нам нужна возможность изменения перспективы обзора сцены. Мы хотим иметь возможность двигать глаз (камеру) по сцене. Во-вторых, нам нужна возможность добавления новых узлов и изменения узлов в сцене.
Для реализации взаимодействия с пользователем нам нужно знать, когда пользователь нажимает клавиши или двигает мышь. К счастью, операционная система знает, когда происходят эти события. GLUT позволяет нам регистрировать функцию, которая будет вызываться при совершении определённого события. Мы напишем функции для интерпретирования нажатий клавиш и движения мыши, а затем прикажем GLUT вызывать эти функции при нажатии соответствующих клавиш. Узнав, какие клавиши нажимает пользователь, мы должны будем интерпретировать ввод и применить к сцене соответствующие действия.
Логика прослушивания событий операционной системы и интерпретации их значения находится в классе Interaction. Написанный нами ранее класс Viewer владеет единственным экземпляром Interaction. Мы используем механизм функций обратного вызова GLUT для регистрации функций, вызываемых при нажатии клавиши мыши (glutMouseFunc), при перемещении мыши (glutMotionFunc), при нажатии клавиши клавиатуры (glutKeyboardFunc) и при нажатии клавиш со стрелками (glutSpecialFunc). Чуть ниже вы увидите функции, обрабатывающие события ввода.
class Interaction(object):
def __init__(self):
""" Handles user interaction """
# currently pressed mouse button
self.pressed = None
# the current location of the camera
self.translation = [0, 0, 0, 0]
# the trackball to calculate rotation
self.trackball = trackball.Trackball(theta = -25, distance=15)
# the current mouse location
self.mouse_loc = None
# Unsophisticated callback mechanism
self.callbacks = defaultdict(list)
self.register()
def register(self):
""" register callbacks with glut """
glutMouseFunc(self.handle_mouse_button)
glutMotionFunc(self.handle_mouse_move)
glutKeyboardFunc(self.handle_keystroke)
glutSpecialFunc(self.handle_keystroke)Функции обратного вызова операционной системы
Для осмысленного интерпретирования пользовательского ввода нам нужно скомбинировать знание о позиции мыши, клавишах мыши и клавиатуре. Поскольку для интерпретирования ввода в осмысленные действия требуется много строк кода, мы инкапсулируем его в отдельный класс, отдалённый от основного пути исполнения кода. Класс Interaction скрывает ненужную сложность от остальной части кодовой базы и преобразует события операционной системы в события уровня приложения.
# class Interaction
def translate(self, x, y, z):
""" translate the camera """
self.translation[0] += x
self.translation[1] += y
self.translation[2] += z
def handle_mouse_button(self, button, mode, x, y):
""" Called when the mouse button is pressed or released """
xSize, ySize = glutGet(GLUT_WINDOW_WIDTH), glutGet(GLUT_WINDOW_HEIGHT)
y = ySize - y # invert the y coordinate because OpenGL is inverted
self.mouse_loc = (x, y)
if mode == GLUT_DOWN:
self.pressed = button
if button == GLUT_RIGHT_BUTTON:
pass
elif button == GLUT_LEFT_BUTTON: # pick
self.trigger('pick', x, y)
elif button == 3: # scroll up
self.translate(0, 0, 1.0)
elif button == 4: # scroll up
self.translate(0, 0, -1.0)
else: # mouse button release
self.pressed = None
glutPostRedisplay()
def handle_mouse_move(self, x, screen_y):
""" Called when the mouse is moved """
xSize, ySize = glutGet(GLUT_WINDOW_WIDTH), glutGet(GLUT_WINDOW_HEIGHT)
y = ySize - screen_y # invert the y coordinate because OpenGL is inverted
if self.pressed is not None:
dx = x - self.mouse_loc[0]
dy = y - self.mouse_loc[1]
if self.pressed == GLUT_RIGHT_BUTTON and self.trackball is not None:
# ignore the updated camera loc because we want to always
# rotate around the origin
self.trackball.drag_to(self.mouse_loc[0], self.mouse_loc[1], dx, dy)
elif self.pressed == GLUT_LEFT_BUTTON:
self.trigger('move', x, y)
elif self.pressed == GLUT_MIDDLE_BUTTON:
self.translate(dx/60.0, dy/60.0, 0)
else:
pass
glutPostRedisplay()
self.mouse_loc = (x, y)
def handle_keystroke(self, key, x, screen_y):
""" Called on keyboard input from the user """
xSize, ySize = glutGet(GLUT_WINDOW_WIDTH), glutGet(GLUT_WINDOW_HEIGHT)
y = ySize - screen_y
if key == 's':
self.trigger('place', 'sphere', x, y)
elif key == 'c':
self.trigger('place', 'cube', x, y)
elif key == GLUT_KEY_UP:
self.trigger('scale', up=True)
elif key == GLUT_KEY_DOWN:
self.trigger('scale', up=False)
elif key == GLUT_KEY_LEFT:
self.trigger('rotate_color', forward=True)
elif key == GLUT_KEY_RIGHT:
self.trigger('rotate_color', forward=False)
glutPostRedisplay()Внутренние функции обратного вызова
В показанном выше фрагменте кода можно заметить, что когда экземпляр Interaction интерпретирует действие пользователя, он вызывает self.trigger со строкой, описывающей тип действия. Функция trigger в классе Interaction — это часть простой системы обратных вызовов, которую мы будем использовать для обработки событий на уровне приложения. Вспомним, что функция init_interaction в классе Viewer регистрирует обратные вызовы в экземпляре Interaction, вызывая register_callback.
# class Interaction
def register_callback(self, name, func):
self.callbacks[name].append(func)Когда коду интерфейса пользователя нужно запустить событие в сцене, класс Interaction вызывает все сохранённые обратные вызовы, имеющиеся для этого события:
# class Interaction
def trigger(self, name, *args, **kwargs):
for func in self.callbacks[name]:
func(*args, **kwargs)Эта система обратных вызовов уровня приложения абстрагирует необходимость остальной части системы знать о вводе в операционной системе. Каждый обратный вызов уровня приложения представляет собой значимый запрос в рамках приложения. Класс Interaction используется как переводчик между событиями операционной системы и событиями уровня приложения. Это означает, что если бы мы решили портировать программу моделирования на другой тулкит, нам бы достаточно было заменить класс Interaction на класс, преобразующий ввод из нового тулкита в тот же набор значимых обратных вызовов уровня приложения. Мы используем обратные вызовы и аргументы в Таблице 1.
Таблица 1 — обратные вызовы и аргументы взаимодействия
Эта простая система обратных вызовов обеспечивает всю функциональность, необходимую для нашей программы. Однако в готовом 3D-редакторе объекты интерфейса пользователя часто создаются и уничтожаются динамически. В таком случае нам потребовалась бы более сложная система прослушивания событий, в которой объекты могут и регистрировать и отменять регистрацию обратных вызовов для событий.
Взаимодействие со сценой
Благодаря механизму обратных вызовов мы можем получать значимую информацию о событиях пользовательского ввода от класса Interaction. Мы готовы к применению этих действий к Scene.
Перемещение сцены
В этой программе мы выполняем движение камеры преобразованием сцены. Другими словами, камера находится на одном месте, а пользовательский ввод двигает сцену, а не камеру. Камера расположена в точке [0, 0, -15] и направлена на точку начала координат мира. (Или же мы можем изменить матрицу перспективы так, чтобы она двигала камеру вместо сцены. Это архитектурное решение очень слабо повлияет на остальную часть программы.) Вернувшись к функции render в Viewer, мы видим, что состояние Interaction используется для преобразования состояния матрицы OpenGL перед рендерингом Scene. Существует два типа взаимодействия со сценой: поворот и перемещение.
Поворот сцены с помощью трекбола
Мы реализуем поворот сцены с помощью алгоритма trackball. Трекбол — это интуитивно-понятный интерфейс для манипуляций со сценой в трёх измерениях. Интерфейс трекбола работает так, как будто сцена находится внутри прозрачного шара. Если положить руку на поверхность шара и толкнуть его, шар повернётся. Аналогично, при зажимании правой клавиши мыши и перемещении курсора по экрану вращает сцену. Подробнее о теории трекбола можно прочитать в OpenGL Wiki. В нашей программе мы используем реализацию трекбола, являющуюся частью Glumpy.
Мы взаимодействуем с трекболом с помощью функции drag_to: текущее положение мыши является начальной точкой, а изменение положения мыши — параметрами функции.
self.trackball.drag_to(self.mouse_loc[0], self.mouse_loc[1], dx, dy)Получившаяся матрица поворота — это trackball.matrix в окне просмотра при рендеринге сцены.
Примечание: кватернионы
Традиционно повороты описываются одним из двух способов. Первый — это значения поворота вокруг каждой из осей; можно хранить их как кортеж из трёх членов, представляющих собой числа с плавающей запятой. Другим распространённым способом задания поворотов является кватернион — элемент, состоящий из вектора с координатами x, y и z, а также поворота w. Использование кватернионов имеет множество преимуществ по сравнению с поворотом по осям; в частности, они более стабильны численно. Благодаря использованию кватернионов можно избежать таких проблем, как «шарнирный замок» (gimbal lock). Недостаток кватернионов в том, что они менее интуитивно-понятны в работе. Если вы не боитесь и хотите узнать больше о кватернионах, то можете изучить это объяснение.
Реализация трекбола избегает gimbal lock благодаря хранению поворота сцены при помощи кватернионов. К счастью, нам не нужно работать с кватернионами напрямую, потому что матричный член трекбола преобразует поворот в матрицу.
Перемещение сцены
Перемещение сцены (например, сдвиг) гораздо проще, чем её поворот. Перемещения сцены выполняются колесом и левой клавишей мыши. Левая клавиша мыши перемещает сцену по координатам x и y. Прокрутка колеса мыши перемещает сцену по координате z (ближе или дальше от камеры). Класс Interaction хранит текущее перемещение сцены и модифицирует его при помощи функции translate. Окно просмотра получает расположение камеры класса Interaction при рендеринге и использует его в вызове glTranslated.
Выбор объектов сцены
Теперь, когда пользователь может перемещать и поворачивать всю сцену для получения нужного обзора, следующим шагом будет обеспечение возможности изменения объектов и манипуляций ими.
Чтобы пользователь мог манипулировать объектами сцены, он должен иметь возможность выбора элементов.
Для выбора элемента мы используем текущую матрицу проецирования для генерации луча, представляющего щелчок мыши, как будто указатель мыши испускает в сцену луч. Выбранным узлом будет ближайший к камере узел, который пересёк луч. Следовательно, задача выбора сводится к задаче нахождения пересечений между лучом и узлами сцены. То есть вопрос заключается в том, как нам узнать, что луч столкнулся с узлом.
Вычисление точного ответа на вопрос, пересёкся ли луч с узлом — это сложная задача, с точки зрения и кода, и производительности. Нам бы потребовалось написать проверку пересечения луча с объектом для каждого типа примитива. Для узлов сцены со сложными геометриями мешей
и множеством граней вычисление точного пересечения луча с объектом потребует проверки луча с каждой гранью, что будет вычислительно затратной задачей.
Для сохранения компактности кода и достаточной производительности мы используем простую и быструю аппроксимацию теста пересечения луча с объектом. В нашей реализации каждый узел хранит параллельный осям ограничивающий параллелепипед (axis-aligned bounding box, AABB), который является аппроксимацией занимаемого узлом пространства. Чтобы проверить, пересекается ли луч с узлом, мы проверим, пересекается ли луч с AABB узла. Такая реализация означает, что все узлы используют один код для тестов пересечения, а вычислительные затраты остаются постоянными и небольшими для всех типов узлов.
# class Viewer
def get_ray(self, x, y):
"""
Generate a ray beginning at the near plane, in the direction that
the x, y coordinates are facing
Consumes: x, y coordinates of mouse on screen
Return: start, direction of the ray
"""
self.init_view()
glMatrixMode(GL_MODELVIEW)
glLoadIdentity()
# get two points on the line.
start = numpy.array(gluUnProject(x, y, 0.001))
end = numpy.array(gluUnProject(x, y, 0.999))
# convert those points into a ray
direction = end - start
direction = direction / norm(direction)
return (start, direction)
def pick(self, x, y):
""" Execute pick of an object. Selects an object in the scene. """
start, direction = self.get_ray(x, y)
self.scene.pick(start, direction, self.modelView)Чтобы определить, какой из узлов щёлкнули мышью, мы обходим сцену, проверяя, пересёкся ли луч с каким-нибудь из узлов. Вы снимаем выбор с текущего узла и выбираем узел, который ближе всего пересекается к точке начала луча.
# class Scene
def pick(self, start, direction, mat):
"""
Execute selection.
start, direction describe a Ray.
mat is the inverse of the current modelview matrix for the scene.
"""
if self.selected_node is not None:
self.selected_node.select(False)
self.selected_node = None
# Keep track of the closest hit.
mindist = sys.maxint
closest_node = None
for node in self.node_list:
hit, distance = node.pick(start, direction, mat)
if hit and distance < mindist:
mindist, closest_node = distance, node
# If we hit something, keep track of it.
if closest_node is not None:
closest_node.select()
closest_node.depth = mindist
closest_node.selected_loc = start + direction * mindist
self.selected_node = closest_nodeВ классе Node функция pick проверяет, пересекается ли луч с AABB Node. Если узел выбран, то функция select переключает состояние выбора узла. Обратите внимание, что в качестве третьего параметра функция ray_hit AABB получает матрицу преобразований между координатным пространством параллелепипеда и координатным пространством луча. Перед вызовом функции ray_hit каждый узел вносит собственные преобразования в матрицу.
# class Node
def pick(self, start, direction, mat):
"""
Return whether or not the ray hits the object
Consume:
start, direction form the ray to check
mat is the modelview matrix to transform the ray by
"""
# transform the modelview matrix by the current translation
newmat = numpy.dot(
numpy.dot(mat, self.translation_matrix),
numpy.linalg.inv(self.scaling_matrix)
)
results = self.aabb.ray_hit(start, direction, newmat)
return results
def select(self, select=None):
""" Toggles or sets selected state """
if select is not None:
self.selected = select
else:
self.selected = not self.selectedСхему выбора на основе пересечения луча и AABB очень легко понять и реализовать. Однако в некоторых ситуациях результаты оказываются ошибочными.
Рисунок 3 — Ошибка AABB
Например, в случае примитива Sphere, сама сфера касается AABB только в центре каждой из граней AABB. Однако если пользователь нажмёт на угол AABB сферы, будет обнаружена коллизия со сферой, даже если пользователь хотел нажать на что-то за ней (Рисунок 3).
Такой компромисс между сложностью, производительностью и точностью очень распространён в компьютерной графике и во многих областях проектирования ПО.
Изменение объектов сцены
Далее мы хотим дать пользователю возможность манипуляций с выбранными узлами. Ему может потребоваться перемещать выбранный узел, изменять его размер или цвет. Когда пользователь вводит команду манипуляции с узлом, класс Interaction преобразует ввод в действие, которое намеревался сделать пользователь, и вызывает соответствующую функцию обратного вызова.
Когда Viewer получает обратный вызов для одного из этих событий, он вызывает соответствующую функцию Scene, которая, в свою очередь, применяет преобразование к текущему выбранному Node.
# class Viewer
def move(self, x, y):
""" Execute a move command on the scene. """
start, direction = self.get_ray(x, y)
self.scene.move_selected(start, direction, self.inverseModelView)
def rotate_color(self, forward):
"""
Rotate the color of the selected Node.
Boolean 'forward' indicates direction of rotation.
"""
self.scene.rotate_selected_color(forward)
def scale(self, up):
""" Scale the selected Node. Boolean up indicates scaling larger."""
self.scene.scale_selected(up)Смена цвета
Манипуляция цветом выполняется через список возможных цветов. Пользователь может перемещаться по списку клавишами со стрелками. Сцена отдаёт команду смены цвета текущему выбранному узлу.
# class Scene
def rotate_selected_color(self, forwards):
""" Rotate the color of the currently selected node """
if self.selected_node is None: return
self.selected_node.rotate_color(forwards)Каждый цвет хранит свой текущий цвет. Функция rotate_color просто изменяет текущий цвет узла. Цвет передаётся OpenGL с помощью glColor при рендеринге узла.
# class Node
def rotate_color(self, forwards):
self.color_index += 1 if forwards else -1
if self.color_index > color.MAX_COLOR:
self.color_index = color.MIN_COLOR
if self.color_index < color.MIN_COLOR:
self.color_index = color.MAX_COLORМасштабирование узлов
Как и в случае с цветом, сцена отдаёт команды изменения масштаба выбранному узлу, если он есть.
# class Scene
def scale_selected(self, up):
""" Scale the current selection """
if self.selected_node is None: return
self.selected_node.scale(up)Каждый узел хранит текущую матрицу, содержащую его масштаб. Матрица, изменяющая масштаб по параметрам x, y и z в соответствующих направлениях, имеет вид:
Когда пользователь изменяет масштаб узла, получившаяся матрица масштабирования умножается на текущую матрицу масштабирования узла.
# class Node
def scale(self, up):
s = 1.1 if up else 0.9
self.scaling_matrix = numpy.dot(self.scaling_matrix, scaling([s, s, s]))
self.aabb.scale(s)Функция scaling возвращает матрицу, соответствующую коэффициентам масштабирования x, y и z.
def scaling(scale):
s = numpy.identity(4)
s[0, 0] = scale[0]
s[1, 1] = scale[1]
s[2, 2] = scale[2]
s[3, 3] = 1
return sПеремещение узлов
Для перемещения узла мы используем то же вычисление луча, что и для выбора. Мы передаём луч, представляющий текущую позицию мыши, в функцию move сцены. Новое местоположение узла должно находится на луче. Чтобы определить, куда луч должен поместить узел, нам нужно знать, расстояние узла от камеры. Так как мы сохранили местоположение узла и расстояние до камеры при его выборе (в функции pick), можно использовать здесь эти данные. Мы находим точку, находящуюся на том же расстоянии от камеры вдоль луча и вычисляем разность векторов между новым и старым местоположением. Затем мы перемещаем узел на получившийся вектор.
# class Scene
def move_selected(self, start, direction, inv_modelview):
"""
Move the selected node, if there is one.
Consume:
start, direction describes the Ray to move to
mat is the modelview matrix for the scene
"""
if self.selected_node is None: return
# Find the current depth and location of the selected node
node = self.selected_node
depth = node.depth
oldloc = node.selected_loc
# The new location of the node is the same depth along the new ray
newloc = (start + direction * depth)
# transform the translation with the modelview matrix
translation = newloc - oldloc
pre_tran = numpy.array([translation[0], translation[1], translation[2], 0])
translation = inv_modelview.dot(pre_tran)
# translate the node and track its location
node.translate(translation[0], translation[1], translation[2])
node.selected_loc = newlocОбратите внимание, что новое и старое местоположения задаются в координатном пространстве камеры. Нам нужно, чтобы перемещение задавалось в координатном пространстве мира. Следовательно, мы преобразуем перемещение в пространстве камеры в перемещение в мировом пространстве, умножив на матрицу, обратную modelview.
Как и в случае с масштабом, каждый узел хранит матрицу, представляющую его перемещение. Матрица перемещения выглядит так:
При перемещении узла мы создаём новую матрицу перемещения для текущего перемещения, и умножаем её на матрицу перемещения узла, чтобы использовать во время рендеринга.
# class Node
def translate(self, x, y, z):
self.translation_matrix = numpy.dot(
self.translation_matrix,
translation([x, y, z]))Функция translation возвращает матрицу перемещения, соответствующую списку расстояний перемещения по x, y и z.
def translation(displacement):
t = numpy.identity(4)
t[0, 3] = displacement[0]
t[1, 3] = displacement[1]
t[2, 3] = displacement[2]
return tРазмещение новых узлов
Для размещения узлов используются методики и из выбора, и из перемещения. Для определения места размещения узла мы используем то же вычисление луча для текущего расположения курсора мыши.
# class Viewer
def place(self, shape, x, y):
""" Execute a placement of a new primitive into the scene. """
start, direction = self.get_ray(x, y)
self.scene.place(shape, start, direction, self.inverseModelView)Для размещения нового узла мы сначала просто создаём новый экземпляр соответствующего типа узла и добавляем его в сцену. Мы хотим разместить узел под курсором пользователя, поэтому находим точку на луче на фиксированном расстоянии от камеры. Луч тоже представлен в пространстве камеры, поэтому мы преобразуем получившийся вектор перемещения в координатное пространство мира, умножив его на матрицу, обратную modelview. Затем мы перемещаем новый узел на вычисленный вектор.
# class Scene
def place(self, shape, start, direction, inv_modelview):
"""
Place a new node.
Consume:
shape the shape to add
start, direction describes the Ray to move to
inv_modelview is the inverse modelview matrix for the scene
"""
new_node = None
if shape == 'sphere': new_node = Sphere()
elif shape == 'cube': new_node = Cube()
elif shape == 'figure': new_node = SnowFigure()
self.add_node(new_node)
# place the node at the cursor in camera-space
translation = (start + direction * self.PLACE_DEPTH)
# convert the translation to world-space
pre_tran = numpy.array([translation[0], translation[1], translation[2], 1])
translation = inv_modelview.dot(pre_tran)
new_node.translate(translation[0], translation[1], translation[2])Итог
Поздравляю! Мы успешно реализовали небольшой 3D-редактор!
Рисунок 4 — Пример сцены
Мы узнали, как разработать расширяемую структуру данных, описывающую модели в сцене. Также мы поняли, что использование шаблона проектирования «Компоновщик» и древовидных структур данных упрощает обход сцены для рендеринга и позволяет добавлять новые типы узлов без повышения сложности кода. Мы использовали эту структуру данных для рендеринга проекта на экран и манипулировали матрицами OpenGL при обходе графа сцены. Мы создали очень простую систему обратных вызовов для событий уровня приложения, и использовали её для инкапсуляции обработки событий операционной системы. Далее мы рассмотрели возможные реализации обнаружения коллизий луча с объектом и компромиссы между точностью, сложностью и производительностью. В конце мы реализовали методы манипуляций с содержимым сцены.
При разработке полнофункционального 3D-приложения вы столкнётесь с этими же базовыми строительными блоками. Структура графа сцены и относительные координатные пространства используются во многих видах приложений для работы с 3D-графикой, от САПР до игровых движков. Сильным упрощением в этом проекте стал интерфейс пользователя. Готовый 3D-редактор должен иметь полный интерфейс пользователя, которому потребуется гораздо более сложная система событий, чем наша простая система обратных вызовов.
Вы можете экспериментировать дальше и попробовать добавить в проект новые функции. Попробуйте реализовать что-нибудь из этого списка:
- Добавить тип
Nodeдля поддержки мешей треугольников произвольной формы. - Добавить стек отмены действий, чтобы можно было отменять/повторять действия пользователя.
- Сохранение/загрузка проекта в трёхмерный формат файлов, например, в DXF.
- Интеграция движка рендеринга: экспорт проекта для использования в фотореалистичном рендерере.
- Улучшить распознавание коллизий точным пересечением луча с объектом.
Дальнейшее исследование
Для дальнейшего изучения реального ПО 3D-моделирования интересно рассмотреть проекты с открытым исходным кодом.
Blender — это полнофункциональный пакет для 3D-анимаций с открытым исходным кодом. В нём есть полный 3D-конвейер для создания спецэффектов в видео или для создания игр. Моделирование — это небольшая часть данного проекта, и оно является хорошим примером интеграции моделирования в большой программный пакет.
OpenSCAD — это инструмент для 3D-моделирования с открытым исходным кодом. Он не интерактивен — программа считывает скрипт, определяющий, как генерировать сцену. Это даёт проектировщику «полный контроль над процессом моделирования».
Подробнее об алгоритмах и техниках компьютерной графики можно узнать из замечательного ресурса Graphics Gems.
Об авторе
Эрик — разработчик ПО и фанат двухмерной и трёхмерной компьютерной графики. Он занимался разработкой видеоигр, ПО для трёхмерных спецэффектов и инструментов САПР. Если дело касается симулирования реальности, то есть вероятность, что ему захочется об этом узнать. Найти его онлайн можно на сайте erickdransch.com.
|
40 / 60 / 8 Регистрация: 16.11.2012 Сообщений: 459 Записей в блоге: 7 |
|
|
1 |
|
Свой рендер на с++22.10.2017, 16:45. Показов 4738. Ответов 15
Вопрос собственно такой: какова должна быть структура рендера для игры? Вообще, эта тема нигде не раскрыта,
__________________
0 |
|
21265 / 8281 / 637 Регистрация: 30.03.2009 Сообщений: 22,638 Записей в блоге: 30 |
|
|
22.10.2017, 18:00 |
2 |
|
Крайне рекомендую для начала изучить матчасть https://habrahabr.ru/post/248153/ А потом уже работать со всякими библиотеками типа OpenGL
0 |
|
40 / 60 / 8 Регистрация: 16.11.2012 Сообщений: 459 Записей в блоге: 7 |
|
|
23.10.2017, 02:23 [ТС] |
3 |
|
Evg, Спасибо конечно, я в свое время уже читал эту статью, с математикой и её спецификой тоже знаком, матрицы, векторы и прочие штуки для меня не новинка. Я имел в виду что хочу написать для своей игры рендер, ту часть программы где сцена (уровень) обрабатывается и выплевывает готовые данные для обработки их DirectX/OpenGL. Смысла то большого нет писать свой растеризатор — аналог директа/опенгла, даже для обучения. Да интересно, но задача другая. Не по теме: P.S. Пишу свой двиг не потому что слабо разобраться с Юнити, и не потому что «когда не знаешь с чего начать игру — начни писать двиг», а потому что меня не удовлетворяют лицензии на продукт/ либо функционал не соответствует моим потребностям.
0 |
|
21265 / 8281 / 637 Регистрация: 30.03.2009 Сообщений: 22,638 Записей в блоге: 30 |
|
|
23.10.2017, 10:37 |
4 |
|
хочу написать для своей игры рендер, ту часть программы где сцена (уровень) обрабатывается и выплевывает готовые данные для обработки их DirectX/OpenGL Хз как остальные, но я не понял Ты имеешь в виду моделирование сцены? Т.е. расстановка набора моделей, чтобы всё это передать в OpenGL или чего?
0 |
|
40 / 60 / 8 Регистрация: 16.11.2012 Сообщений: 459 Записей в блоге: 7 |
|
|
23.10.2017, 22:56 [ТС] |
5 |
|
Evg, Попытаюсь объяснить более внятно. Так вот не могу же я просто взять и передать не обработанные графические данные прямо в графический API? Надеюсь в этот раз я смог изложить мысль более понятно.
0 |
|
21265 / 8281 / 637 Регистрация: 30.03.2009 Сообщений: 22,638 Записей в блоге: 30 |
|
|
24.10.2017, 10:06 |
6 |
|
Да в принципе по сравнению с постом #3 ничего нового не открылось. Суть вопроса я примерно понял. Просто словом «рендер» называют непосредственно процесс формирования изображения, а ты в слово «рендер» включаешь как моделирование (расстановку объектов по сцене), так и рисование Я на твой вопрос ответить не могу, т.к. играми никогда не занимался. Но и проблему толком понять не могу. В том смысле, что конкретно тебе мешает взять и сделать всё то, что ты написал в посте #5
0 |
|
2 / 2 / 1 Регистрация: 23.03.2017 Сообщений: 17 |
|
|
06.11.2017, 00:26 |
7 |
|
Если на пальцах это работает так. По очереди в GPU загружаются слои будущей картинки. Грунт, статик, итемы и мобы Представь белый лист бумаги, сначала наклеиваем на нее траву, потом прям на траву клеим камни вырезные из бумаги, потом кусты… деревья, дома. Дом может заклеить дерево, мы же не можем видеть сквозь дом ) и т.д. Лист бумаги это буфер видеокарты, потом переключаем этот буфер на вывод и лицезреем шедевр на экране. В любой видеокарте минимум 2 буфера. Все делается в GPU, движок игры только загружает данные. CPU никакие сцены не строит(кроме порядка вывода слоев), по этому на чем написан движок фиолетово, хоть бэйсик. Зашитые в движок супер-мупер эффекты получив параметры загрузят в GPU шейдер невероятной сложности который все это и провернет. Скорость оброботки от языка движка не увеличится и не уменьшится.
0 |
|
40 / 60 / 8 Регистрация: 16.11.2012 Сообщений: 459 Записей в блоге: 7 |
|
|
06.11.2017, 00:42 [ТС] |
8 |
|
omi4691, спасибо за ответ, изучаю вопрос более детально. Добавлено через 6 минут
на чем написан движок фиолетово, хоть бэйсик. С этим можно поспорить. Если бы не имело разницы на чем написан движок, то игры уровня ААА мог бы писать любой школьник изучив паскаль/Delphi. Однако в индустрии прижился именно С++, это говорит о многом. Я не могу с ходу привести в пример популярный движок на чем то кроме CPP
0 |
|
2 / 2 / 1 Регистрация: 23.03.2017 Сообщений: 17 |
|
|
06.11.2017, 02:15 |
9 |
|
Представь кубик 3D, видео карта будет рисовать не ту часть что мы видим. А весь кубик, видимые грани просто затрут те что невидимы ). Если брать карту местности, то ЦПУ выберет из нее только то что в зоне видимости по дистанции. Глупо лить в видеокарту бесконечный мир. А вот картинку уже будет собирать ГПУ. Анимация для карты это не мультик, это 1 кадр. А вот какой именно определит ЦПУ, тут мозгов много не требуется. ЦПУ передает в карту текстуры, координаты, только ей фиолетово будет ли это отображаться на экране или нет. Сначала задний план и т.д. Все построение и обрезку сделает видеокарта. А игры класса ААА делают специалисты того же класса, ну никак не движки. На тех же собеседованиях при приеме на работу обязательно попросят реализовать что то что известный тебе движок не может даже в планах, движок это обвертка и набор классов для упрощения создания игры. Необходимость в знаниях GL, DX и прочих АПИ никто не отменял. Движки чаще приобретают фишечки от игр ААА чем игры от них. В обозримом будущем вряд ли появится движок который станет причиной рождения игры шедевра.
0 |
|
129 / 126 / 22 Регистрация: 23.06.2009 Сообщений: 700 |
|
|
08.11.2017, 17:26 |
10 |
|
В обозримом будущем вряд ли появится движок который станет причиной рождения игры шедевра. бессплатно врядли)) но тот же гэтэа сделан на каком то движке?) разве это не шедевр ?
0 |
|
40 / 60 / 8 Регистрация: 16.11.2012 Сообщений: 459 Записей в блоге: 7 |
|
|
08.11.2017, 17:52 [ТС] |
11 |
|
omi4691, Вы говорите очевидные вещи, а кроме того разводите срач. По вашим комментариям можно заметить, что вы не являетесь специалистом по заданному вопросу, но постоянно пытаетесь выдавить из себя что-то умное. У вас не получается. petruchodd,
бессплатно врядли)) Поясняю. Моя цель — реализовать свой инди-проект. Игру. После глубокого анализа, я выяснил что для воплощения особенностей моей игры, мне потребуется собственный игровой движок. Про деньги разговор отдельный, это хобби, и я сотрудничаю с двумя энтузиастами, такими же как я. У нас уже что-то получается, хоть это и малая часть того что требуется. Модераторов прошу закрыть топик, дабы прохожие не флудили.
0 |
|
129 / 126 / 22 Регистрация: 23.06.2009 Сообщений: 700 |
|
|
08.11.2017, 18:00 |
12 |
|
тут уже на форуме был чувак как ты . Верящий в свою идею , Этигибосекью как то так. Его игры были просто божественны , а главное он верил в то, что они классные. Разводил клоунаду такую же как вы в последнем своем посте. Делайте , вам никто не запрещает. У всех есть цель. Но если вы приходите на форум и что-то спрашиваете , а потом так гневно реагируете, может вы не будете тогда спрашивать?) комик блин
0 |
|
40 / 60 / 8 Регистрация: 16.11.2012 Сообщений: 459 Записей в блоге: 7 |
|
|
08.11.2017, 18:06 [ТС] |
13 |
|
petruchodd, По данному вопросу вы ничего сказать не можете, что мотивирует вас здесь флудить? Мне всё равно что было до меня и что будет после меня, я делаю здесь и сейчас. Получаю фан. Собственно, я здесь спрашиваю опытных специалистов, по вполне конкретным вопросам. Вы мне будете указывать где и на каком форуме я должен спрашивать? А не много ли вы на себя берете?
0 |
|
Evg |
|
08.11.2017, 19:32
|
|
Не по теме:
omi4691, Вы говорите очевидные вещи, а кроме того разводите срач На всякий случай поясню. На форуме уже неоднократно светились всякие товарищи, которые планировали реализовать собственный игровой движок или собственную игру, которая порвёт всех и вся, причём в мелкие клочья и на годы вперёд. Твои невнятно поставленные вопросы и рассуждения по внешнему виду не сильно отличаются от тех товарищей, поэтому кто-то начал считать своим долгом начать троллинг
0 |
|
40 / 60 / 8 Регистрация: 16.11.2012 Сообщений: 459 Записей в блоге: 7 |
|
|
09.11.2017, 13:31 [ТС] |
15 |
|
Evg, Не по теме: Тут надо понимать различие. Если те ребята просто хотели написать сначала движок, а потом под него подогнать игру, это один случай. То бишь писать код ради кода. В моем случае, именно игра требует движок, а не иначе.
0 |
|
3226 / 1416 / 233 Регистрация: 26.02.2009 Сообщений: 7,317 Записей в блоге: 5 |
|
|
10.11.2017, 14:15 |
16 |
|
0 |
|
IT_Exp Эксперт 87844 / 49110 / 22898 Регистрация: 17.06.2006 Сообщений: 92,604 |
10.11.2017, 14:15 |
|
Помогаю со студенческими работами здесь Рендер текста Получил файл *.bmp Рендер градиента Рендер изображения 3D рендер на форме Искать еще темы с ответами Или воспользуйтесь поиском по форуму: 16 |