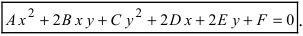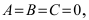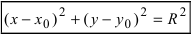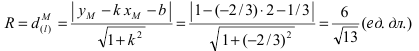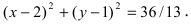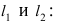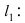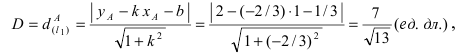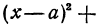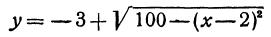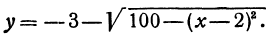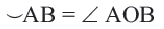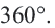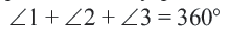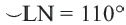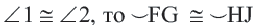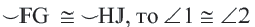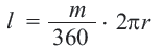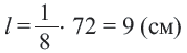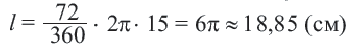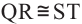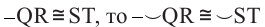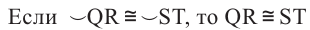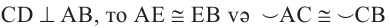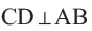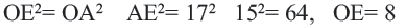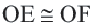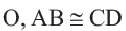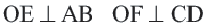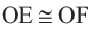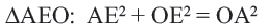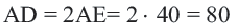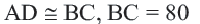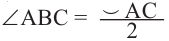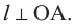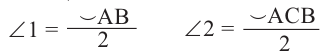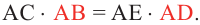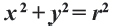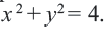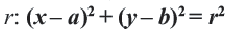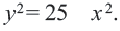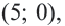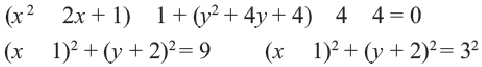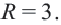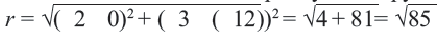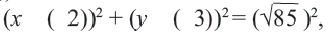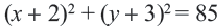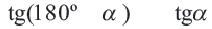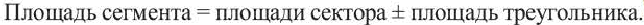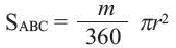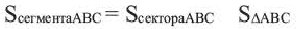Написать уравнение окружности
Рассмотрим некоторые примеры, в которых требуется написать уравнение окружности по заданным условиям.
1) Написать уравнение окружности с центром в точке K(5;-1) и радиусом 7.
Уравнение окружности с центром в точке (a;b) и радиусом R имеет вид:
Так как центр окружности — точка K(5; -1), то a=5, b=-1.Подставляем эти данные в уравнение окружности:
2) Напишите уравнение окружности с центром в точке A (8;-3) проходящей через точку C(3;-6).
Так как центр окружности — точка A(8; -3), то a=8, b=-3.
Остаётся найти радиус. Он равен расстоянию от центра окружности до точки, лежащей на окружности, то есть в данном случае радиус окружности равен расстоянию между точками A и C.
Следовательно, уравнение данной окружности
3) Составить уравнение окружности, диаметром которой является отрезок AB, если A (-4; -9), B(6;5).
Центром окружности является середина диаметра, в нашем случае — середина отрезка AB. По формулам координат середины отрезка
Центр окружности — точка O(1;-2). Значит, a=1, b=-2.
Радиус можно найти как расстояние от центра окружности до любой из точек A или B окружности. Например,
Таким образом, уравнение окружности с диаметром AB —
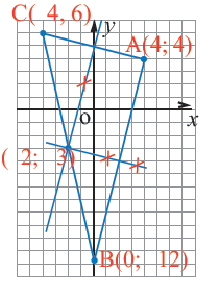
4) Написать уравнение окружности, проходящей через три точки: A(4; -5), B(8; 3) C(-8; 11).
Так как точки A, B C принадлежат окружности, то их координаты удовлетворяют уравнению окружности. Подставив координаты точек в уравнение
получаем систему уравнений:
Поскольку правые части уравнений равны, левые также равны. Приравняв правые части 1-го и 2-го уравнений получим
Приравняем правые части 2-го и 3-го уравнений:
на -1 и сложив результат почленно с уравнением
получаем a=-2, b=3. Подставив этот результат в первое уравнение системы:
Следовательно, уравнение окружности, проходящей через три данные точки —
5) Написать уравнение окружности, описанной около треугольника ABC с вершинами в точках A(2; 6), B(1; 5) C(8; -2).
Решение аналогично решению задания 4. В результате получим уравнение
Уравнение окружности.
Окружностью принято обозначать множество всех точек плоскости, равноудаленных от одной точки – от центра.
В формулировке окружности упоминается расстояние между точкой окружности и центром.
Формула расстояния между двумя точками М1(х1; у1) и М2(х2; у2) имеет вид:
,
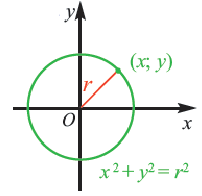
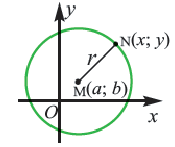
Применив формулу и формулировку окружности, получаем уравнение окружности с центром в точке С (х0; у0) и радиусом r.
Отметим произвольную точку М(х; у) на этой окружности.
.
Предположим, что М принадлежит окружности с центром С и радиусом r, то МС = r.
Следовательно, МС 2 = r 2 и координаты точки М удовлетворяют уравнению окружности (х – х0 ) 2 +(у – у0 ) 2 = r 2 .
Из выше изложенного делаем вывод, что уравнение окружности с центром в точке С (х0; у0) и радиусом r имеет вид:
В случае когда центр окружности совпадает с началом координат, то получаем частный случай уравнения окружности с центром в точке О (0;0):
Уравнение окружности по заданному центру и радиусу в различных формах
Этот онлайн-калькулятор показывает уравнение окружности в стандартной, параметрической и общей формах, по заданному центру и радиусу окружности. Описание и формулы приведены под калькулятором
Уравнение окружности по заданному центру и радиусу в различных формах
Центр окружности
Уравнение окружности
Уравнение окружности — это алгебраический способ описания всех точек, лежащих на некоторой окружности. То есть если координаты точки x и y обращают уравнение окружности в равенство — эта точка принадлежит данной окружности. Существуют разные формы записи уравнения окружности:
- общее уравнение окружности
- стандартное уравнение окружности 1
- параметрическое уравнение окружности
- уравнение окружности в полярных координатах
Общее уравнение окружности
Общее уравнение окружности с центром и радиусом выглядит так:
,
где
В таком виде довольно сложно судить о свойствах заданной этим уравнением окружности, а именно, о координатах центра и радиусе. Но эту форму достаточно легко привести к стандартной форме (ниже), которая гораздо нагляднее.
Стандартное уравнение окружности
Стандартное уравнение окружности с центром и радиусом выглядит так:
Переход от общей формы к стандартной заключается в применении метода выделения полного квадрата. Получив стандартную форму, можно легко узнать координаты центра и радиус. Подробнее можно посмотреть здесь — Метод выделения полного квадрата и здесь — Нахождение центра и радиуса окружности по общему уравнению окружности.
Параметрическое уравнение окружности
Параметрическое уравнение окружности с центром и радиусом выглядит так:
Уравнение называется «параметрическим», потому что и x и y зависят от «параметра» тета. Это переменная, которая может принимать любые значения (но конечно это должно быть одно и то же значение в обоих уравнениях). Для параметрического уравнения используется определение синуса и косинуса в прямоугольном треугольнике построенном на радиусе и перпендикуляров от точки на окружности до координатных осей.
Уравнение окружности в полярных координатах
Для записи уравнения окружности в полярных координатах требуются полярные координаты центра окружности по отношению к началу координат. Если полярные координаты центра окружности — это , то полярные координаты точки окружности должны удовлетворять следующему уравнению:
,
где a — радиус окружности.
Так, во всяком случае, его называют в англоязычной литературе. Насчет русского термина я не уверен, по-моему эту форму рассматривают просто как еще один способ записи общего уравнения окружности, тем более что переход от общего уравнения к стандартному довольно простой. ↩
источники:
http://www.calc.ru/Uravneniye-Okruzhnosti.html
http://planetcalc.ru/8115/
На чтение 3 мин Просмотров 1.9к. Опубликовано 05.10.2020
 |
| План занятий |
 |





Окружность. Центр окружности. Радиус окружности.
Уравнение окружности. Уравнение касательной к окружности.
Условие касания прямой и окружности.
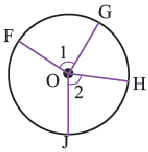
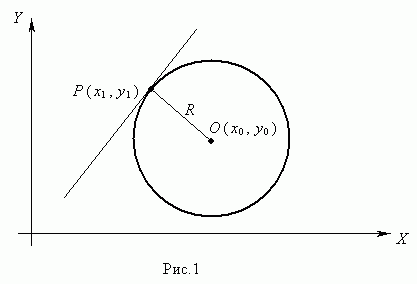
Окружностью ( рис.1 ) называется геометрическое место точек, равноудалённых от данной точки О, называемой центром окружности, на расстояние R . Число R > 0 называется радиусом окружности.
Уравнение окружности радиуса R с центром в точке О ( х , у ) имеет вид:
Если центр окружности совпадает с началом координат, то уравнение окружности упрощается:
Пусть Р ( х 1 , у 1 ) – точка окружности ( рис.1 ), тогда уравнение касательной к окружности в данной точке имеет вид:
Рассмотрим некоторые примеры, в которых требуется написать уравнение окружности по заданным условиям.
1) Написать уравнение окружности с центром в точке K(5;-1) и радиусом 7.
Уравнение окружности с центром в точке (a;b) и радиусом R имеет вид:
Так как центр окружности — точка K(5; -1), то a=5, b=-1.Подставляем эти данные в уравнение окружности:
2) Напишите уравнение окружности с центром в точке A (8;-3) проходящей через точку C(3;-6).
Так как центр окружности — точка A(8; -3), то a=8, b=-3.
Остаётся найти радиус. Он равен расстоянию от центра окружности до точки, лежащей на окружности, то есть в данном случае радиус окружности равен расстоянию между точками A и C.
Следовательно, уравнение данной окружности
3) Составить уравнение окружности, диаметром которой является отрезок AB, если A (-4; -9), B(6;5).
Центром окружности является середина диаметра, в нашем случае — середина отрезка AB. По формулам координат середины отрезка
Центр окружности — точка O(1;-2). Значит, a=1, b=-2.
Радиус можно найти как расстояние от центра окружности до любой из точек A или B окружности. Например,
Таким образом, уравнение окружности с диаметром AB —
4) Написать уравнение окружности, проходящей через три точки: A(4; -5), B(8; 3) C(-8; 11).
Так как точки A, B C принадлежат окружности, то их координаты удовлетворяют уравнению окружности. Подставив координаты точек в уравнение
получаем систему уравнений:
Поскольку правые части уравнений равны, левые также равны. Приравняв правые части 1-го и 2-го уравнений получим
Приравняем правые части 2-го и 3-го уравнений:
на -1 и сложив результат почленно с уравнением
получаем a=-2, b=3. Подставив этот результат в первое уравнение системы:
Следовательно, уравнение окружности, проходящей через три данные точки —
5) Написать уравнение окружности, описанной около треугольника ABC с вершинами в точках A(2; 6), B(1; 5) C(8; -2).
Решение аналогично решению задания 4. В результате получим уравнение
Для расчета уравнения, надо знать определение окружности. Итак, окружность – это множество точек в пространстве, равноудаленных от одной точки, называемой центром. Отрезок, соединяющий две точки окружности и проходящий через точку центра, называется диаметром. Отрезок, соединяющий две точки окружности – хорда. Отрезок, соединяющий центр и любую точку окружности – радиус. Радиус равен половине диаметра.
Рассчитывая уравнение окружности, получаем следующие данные:
• координаты точки центра;
• длину радиуса.
И наоборот, зная длину радиуса и координаты точки центра, можно определить координаты любой точки и начертить окружность.
Для чего необходимо рассчитывать уравнение окружности? Зная длину радиуса, который рассчитывается, исходя из данных уравнения, можно определить длину любой окружности и площадь круга по следующим формулам:
• l=2πr, где l – длина окружности, π=3,14
• S=πr2
Следует помнить, круг – это множество точек на плоскости координат, расположенных внутри окружности. Оптимальный способ рассчитать уравнение окружности – воспользоваться онлайн калькулятором. Это ускорит процесс и позволит быстро решить задачи по соответствующим формулам.
- Распечатать
Оцените статью:
- 5
- 4
- 3
- 2
- 1
(0 голосов, среднее: 0 из 5)
Поделитесь с друзьями!
Рассмотрим некоторые примеры, в которых требуется написать уравнение окружности по заданным условиям.
1) Написать уравнение окружности с центром в точке K(5;-1) и радиусом 7.
Решение:
Уравнение окружности с центром в точке (a;b) и радиусом R имеет вид:
Так как центр окружности — точка K(5; -1), то a=5, b=-1.Подставляем эти данные в уравнение окружности:
2) Напишите уравнение окружности с центром в точке A (8;-3) проходящей через точку C(3;-6).
Решение:
Так как центр окружности — точка A(8; -3), то a=8, b=-3.
Остаётся найти радиус. Он равен расстоянию от центра окружности до точки, лежащей на окружности, то есть в данном случае радиус окружности равен расстоянию между точками A и C.
Следовательно, уравнение данной окружности
3) Составить уравнение окружности, диаметром которой является отрезок AB, если A (-4; -9), B(6;5).
Решение:
Центром окружности является середина диаметра, в нашем случае — середина отрезка AB. По формулам координат середины отрезка
Центр окружности — точка O(1;-2). Значит, a=1, b=-2.
Радиус можно найти как расстояние от центра окружности до любой из точек A или B окружности. Например,
Таким образом, уравнение окружности с диаметром AB —
4) Написать уравнение окружности, проходящей через три точки: A(4; -5), B(8; 3) C(-8; 11).
Решение:
Так как точки A, B C принадлежат окружности, то их координаты удовлетворяют уравнению окружности. Подставив координаты точек в уравнение
получаем систему уравнений:
Поскольку правые части уравнений равны, левые также равны. Приравняв правые части 1-го и 2-го уравнений получим
Приравняем правые части 2-го и 3-го уравнений:
Умножив уравнение
на -1 и сложив результат почленно с уравнением
получаем a=-2, b=3. Подставив этот результат в первое уравнение системы:
получаем R²=100.
Следовательно, уравнение окружности, проходящей через три данные точки —
5) Написать уравнение окружности, описанной около треугольника ABC с вершинами в точках A(2; 6), B(1; 5) C(8; -2).
Решение аналогично решению задания 4. В результате получим уравнение
Используем два уже известных факта и выведем уравнение окружности:
1) все точки окружности находятся на данном расстоянии (радиус) от данной точки (центр);
2) мы имеем формулу для расчёта расстояния между двумя точками, если знаем координаты точек
AB=xA−xB2+yA−yB2
, а если так, то квадрат расстояния
AB2=xA−xB2+yA−yB2
.
Допустим, что центр окружности находится в точке
CxC;yC
, а радиус окружности равен (R).
Любая точка
Px;y
на этой окружности находится на расстоянии (R) от центра (C), значит, справедливо равенство
Это и есть уравнение окружности с центром (C) и радиусом (R). Координаты всех точек, которые находятся на окружности, удовлетворяют уравнению.
Если центр окружности находится в начале координат
0;0
, то уравнение имеет вид
Для выведения уравнения прямой проведём эту прямую как серединный перпендикуляр некоторому отрезку с данными координатами конечных точек отрезка.
Известно, что все точки серединного перпендикуляра находятся на равных расстояниях от концов отрезка.
Координаты концов отрезка
AxA;yA
и
BxB;yB
. Любая точка
Px;y
находится на равных расстояниях от конечных точек
PA=PB
, конечно, равны и квадраты расстояний
PA2=PB2
, значит, справедливо равенство
, которое и есть уравнение прямой.
После возведения выражений в скобках и приведения подобных слагаемых
x2−2⋅x⋅xA+xA2+y2−2⋅y⋅yA+yA2=
=x2−2⋅x⋅xB+xB2+y2−2⋅y⋅yB+yB2;
2⋅x⋅xB−2⋅x⋅xA+2⋅y⋅yB−2⋅y⋅yA+xA2−xB2+yA2−yB2=0;
2xB−2xA⋅x+2yB−2yA⋅y+xA2−xB2+yA2−yB2=0;
уравнение будет в таком виде:
ax+by+c=0;a=2xB−xA;b=2yB−yA;
c=xA2−xB2+yA2−yB2.
Рассмотрим особые прямые.
1. Прямая проходит через некоторую точку на оси (Ox) с координатами
AxA;0
.
Для любой точки на этой прямой
x=xA
, это и есть уравнение прямой.
Так как ось (Oy) проходит через начало координат, то уравнение оси (Oy) есть
x=0
.
2. Прямая проходит через некоторую точку на оси (Oy) с координатами
B0;yB
.
Для любой точки на этой прямой
y=yB
, это и есть уравнение прямой.
Так как ось (Ox) проходит через начало координат, то уравнение оси (Ox) есть
y=0
..
In mathematics, a circle is a shape that contains all the points in the plane and these points are equidistant from the given point. This given point is known as the centre of the circle. Or in other words, it is a curve that is traced by a point that moves in a plane such that its distance from a fixed point in that plane is always constant. The distance between a point on the circle to the centre of the circle is known as the radius of the circle and when a chord passes through the centre of the circle is known as diameter or the circle.
Standard equation of a circle
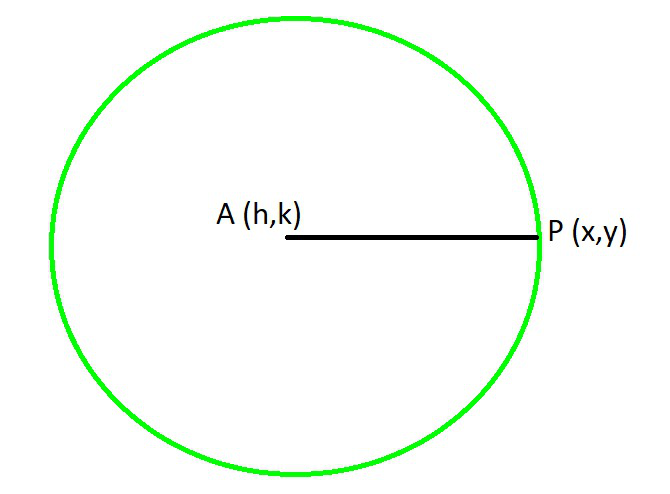
To find the standard form of the circle let us assume that A(h, k) be the centre of the circle and r be the radius of the circle and P(x, y) be any point on the circumference.
Then, AP = r …..(i)
Now using the distance formula we find the value of AP
AP =
Now put the value of AP in eq(i), we get
= r
Or squaring both side we get
(x – h)2 + (y – k)2 = r2
This is the relation between the coordinates of any point on the circumference and hence it is the required equation of the circle having centre at A(h, k) and radius equal to r. Now we will see the variation in the Standard equation of a circle:
Case 1: When centre of the circle is at the origin(0, 0) and radius in r.
h = 0 and k = 0
On substituting in the standard equation of circle, we get
x2 + y2 = r2Case 2: When the circle passes through the origin.
Here, let centre be A(h, k) and O be the origin which passes through circle.
Draw AM⊥OM
In △AMO, OA2 = OM2 + AM2
r2 = h2 + k2
On substituting in the standard equation of circle, we get
(x – h)2 + (y – k)2 = h2 + k2
x2 + y2 – 2hx – 2ky = 0Case 3: When circle touched x-axis
Here, let centre be A(h, k). Since the circle touches the x-axis,
k = r
On substituting in the standard equation of circle, we get
(x – h)2 + (y – r)2 = r2
x2 + y2 – 2hx – 2ry + h2 = 0Case 4: When circle touched x-axis
Here, let centre be A(h, k). Since the circle touches the x-axis,
h = r
On substituting in the standard equation of circle, we get
(x – r)2 + (y – k)2 = r2
x2 + y2 – 2rx – 2ky + k2 = 0Case 5: When the circle touched both the axes.
Here, h = k = r
On substituting in the standard equation of circle, we get
(x – r)2 + (y – r)2 = r2
x2 + y2 – 2rx – 2ry + r2 = 0Case 6: When the circle passes through the origin and centre lies on x-axis.
Here, k = 0 and h = r
On substituting in the standard equation of circle, we get
(x – r)2 + (y – 0)2 = r2
x2 + y2 – 2rx = 0Case 7: When the circle passes through the origin and centre lies on y-axis.
Here, h = 0 and k = r
On substituting in the standard equation of circle, we get
(x – 0)2 + (y – r)2 = r2
x2 + y2 – 2ry = 0
Sample Problems
Question 1. Find centre and radius of the circle from the given equation:
x2 + (y + 2)2 = 9
Solution:
After rearranging, we get
(x – 0)2 + (y – (-2))2 = 32
On comparing with the standard equation of circle, we have
h = 0, k = -2 and r = 3
So the centre of the circle is (0, -2)
and the radius of the circle = 3
Question 2. Find centre and radius of the circle from the given equation:
x2 + y2 + 6x – 4y + 4 = 0
Solution:
We have,
(x2 + 6x) + (y2 – 4y) = – 4
To make it a perfect square identity, add and subtract 9 and 4,
(x2 + 6x + 9) + (y2 – 4y + 4) – 9 – 4 = – 4
(x + 3)2 + (y – 2)2 = – 4 + 4 + 9
(x – (-3))2 + (y – 2)2 = 9
(x – (-3))2 + (y – 2)2 =32
On comparing with the standard equation of circle, we have
h = -3, k = 2 and r = 3
So the centre of the circle is (-3, 2)
and the radius of the circle = 3
Graphing a circle from its standard equation
As we know that the standard equation of the circle is
(x – h)2 + (y – k)2 = r2
Here, the centre of the circle is (h, k) and the radius of the circle is r. Now let us take an example:
The equation of the circle is (x + 2)2 + (y – 6)2 = 4
we can rewrite this equation as
(x – (-2))2 + (y – 6)2 = 22
On comparing with the standard equation of the circle we get
The centre of the circle is (-2, 6) and the radius of the circle is 2.
Now we will draw a circle on the graph.
Step 1: Draw x and y-axis
Step 2: Plot the centre of the circle on the graph that is (-2, 6)
Step 3: Mark any four points in the four directions from the centre of the circles and the distance between the points and the centre is 2.
Step 4: Join all these points to get a circle.
Expanded equation of a Circle
Now we will find the expanded equation of a circle. So, let us assume that A(h, k) be the centre of the circle and r be the radius of the circle and P(x, y) be any point on the circumference.
Then AP = r …(i)
In right-angled △ACP,
AP2 = AC2 + PC2
r2 = (x – h)2 + (y – k)2
Expanding further, we get
(x – h)2 + (y – k)2 = r2
(x2 – 2hx + h2) + (y2 – 2ky + k2) = r2
and if we bring r2 to the left-hand side and rearrange we get
The expanded equation of circle:
x2 – 2hx + h2 + y2 – 2ky + k2 – r2 = 0
Example: Find centre and radius of the circle using the following equation: x2 + y2 – 4x + 6y = 12.
Solution:
Given: x2 + y2 – 4x + 6y = 12
We can write as
(x2 – 4x) + (y2 – 6y) = 12
By manipulating identity, we get
(x2 – 4x + 4) + (y2 – 6y + 9) – 9 – 4 = 12
(x2 – 4x + 4) + (y2 – 6y + 9) = 12 + 9 + 4
(x – 2)2 + (y – 3)2 = 25
(x – 2)2 + (y – 3)2 = 52
On comparing with the standard equation of circle, we have
h = 2, k = 3 and r = 5
General Equation of a Circle
The general equation of a circle is:
x2 + y2 + 2gx + 2fy + c = 0
For all values of g, f and c.
Now, on adding g2 + f2 on both sides of the equation, we get
(x2 + 2gx + g2)+ (y2 + 2fy + f2) = g2 + f2 − c
As, (x + g)2 = x2+ 2gx + g2 and (y + f)2 =y2 + 2fy + f2
(x + g)2 + (y + f)2 = g2 + f2 – c
(x – (-g))2 + (y – (-f))2 = g2 + f2 – c ……….(1)
On comparing eq(1) with the standard equation, we get
h = −g, k = −f
r2 = g2+ f2−c
where (h, k) is the centre and ‘r’ is the radius of the circle.
Hence,
x2 + y2 + 2gx + 2fy + c = 0, represents the circle with centre (−g, −f) and radius (r) equal to r2 = g2 + f2− c.
- If g2 + f2 > c, then the radius of the circle is real.
- If g2 + f2 = c, then the radius of the circle is zero which tells us that the circle is a point which coincides with the centre. Such type of circle is called a point circle
- g2 + f2 <c, then the radius of the circle become imaginary. Therefore, it is a circle having a real centre and imaginary radius.
Some features of the general equation x2 + y2 + 2gx + 2fy + c = 0 of the circle are as follows:
- It is quadratic in both x and y.
- Coefficient of x2 = y2. (It is advisable to keep the coefficient of x2 and y2 unity)
- There is no term containing xy i.e., the coefficient of xy is zero.
- It contains three arbitrary constants viz. g, f and c.
Sample Problems
Question 1. Find the equation of a circle whose centre is (-3, -2) and radius 6.
Solution:
Given: h = -3, k = -2, and, r = 6
Using the standard equation of circle,
(x – h)2 + (y – k)2 = r2
(x – (-3))2 + (y – (-2))2 = 62
(x + 3)2 + (y + 2)2 = 62
x2 + 6x + 9 + y2 + 4y + 4 = 36
Hence, the required equation is
x2 + y2 + 6x + 4y – 23 = 0
Question 2. Find the equation of a circle whose radius is 7 and the centre is at the origin.
Solution:
Given : r = 7 and the centre = (0, 0)
Using the standard equation of circle,
(x – h)2 + (y – k)2 = r2
x2 + y2 = r2
x2 + y2 = 72
Hence, the required equation is
x2 + y2 – 49 = 0
Question 3. Find the radius and centre of the circle given by the equation
2x2 + 2y2 + 8x + 12y – 38 = 0
Solution:
In the given equation the coefficients of x2 and y2 are not unity.
Firstly, lets make them unity by dividing equation by 2,
x2 + y2 + 4x + 6y – 19 = 0
So, the coordinates of the centre are (-2, -3)
and, Radius =
Radius =
Radius = 4√2
Question 4. Find the equation of the circle that passed through the points (1, 0), (-1, 0), and (0, 1).
Solution:
Let the required circle be
x2 + y2 + 2gx + 2fy + c = 0
As, it passes through (1, 0), (-1, 0), and (0, 1). Hence, they will satisfy the equation
By substituting them, we get
1 + 2g + c = 0 ……..(1)
1 – 2g + c = 0 ……..(2)
1 + 2f + c = 0 ……..(3)
From eq(1) and (2), we get
g = 0 and c = -1
Now, putting c = -1 in eq(3), we get
f = 0
Now, substituting the values of g, f and c in the main equation, we get
x2 + y2 = 1
Question 5. Find the equation of the image of the circle x2 + y2 + 16x – 8y + 64 = 0 in the line mirror x = 0.
Solution:
Equation given is:
x2 + y2 + 16x – 8y = – 64
(x2 + 16x) + (y2 – 8y) = – 64
On adding and subtracting 64 and 16, we get
(x2 + 16x + 64) + (y2 – 8y + 16) – 64 – 16 = – 64
(x2 + 16x + 64) + (y2 – 8y + 16) = – 64 + 64 + 16
(x +
2 + (y – 4)2 = 16
(x – (-8))2 + (y – 4)2 = 42
As, the radius of this circle is (-8, 4) and radius = 4.
The image of the circle in the line mirror will have its centre as (8, 4) and radius 4.
So, the equation will be,
(x –
2 + (y – 4)2 = 42
x2 + y2 – 16x – 8y + 64 = 0
In mathematics, a circle is a shape that contains all the points in the plane and these points are equidistant from the given point. This given point is known as the centre of the circle. Or in other words, it is a curve that is traced by a point that moves in a plane such that its distance from a fixed point in that plane is always constant. The distance between a point on the circle to the centre of the circle is known as the radius of the circle and when a chord passes through the centre of the circle is known as diameter or the circle.
Standard equation of a circle
To find the standard form of the circle let us assume that A(h, k) be the centre of the circle and r be the radius of the circle and P(x, y) be any point on the circumference.
Then, AP = r …..(i)
Now using the distance formula we find the value of AP
AP =
Now put the value of AP in eq(i), we get
= r
Or squaring both side we get
(x – h)2 + (y – k)2 = r2
This is the relation between the coordinates of any point on the circumference and hence it is the required equation of the circle having centre at A(h, k) and radius equal to r. Now we will see the variation in the Standard equation of a circle:
Case 1: When centre of the circle is at the origin(0, 0) and radius in r.
h = 0 and k = 0
On substituting in the standard equation of circle, we get
x2 + y2 = r2Case 2: When the circle passes through the origin.
Here, let centre be A(h, k) and O be the origin which passes through circle.
Draw AM⊥OM
In △AMO, OA2 = OM2 + AM2
r2 = h2 + k2
On substituting in the standard equation of circle, we get
(x – h)2 + (y – k)2 = h2 + k2
x2 + y2 – 2hx – 2ky = 0Case 3: When circle touched x-axis
Here, let centre be A(h, k). Since the circle touches the x-axis,
k = r
On substituting in the standard equation of circle, we get
(x – h)2 + (y – r)2 = r2
x2 + y2 – 2hx – 2ry + h2 = 0Case 4: When circle touched x-axis
Here, let centre be A(h, k). Since the circle touches the x-axis,
h = r
On substituting in the standard equation of circle, we get
(x – r)2 + (y – k)2 = r2
x2 + y2 – 2rx – 2ky + k2 = 0Case 5: When the circle touched both the axes.
Here, h = k = r
On substituting in the standard equation of circle, we get
(x – r)2 + (y – r)2 = r2
x2 + y2 – 2rx – 2ry + r2 = 0Case 6: When the circle passes through the origin and centre lies on x-axis.
Here, k = 0 and h = r
On substituting in the standard equation of circle, we get
(x – r)2 + (y – 0)2 = r2
x2 + y2 – 2rx = 0Case 7: When the circle passes through the origin and centre lies on y-axis.
Here, h = 0 and k = r
On substituting in the standard equation of circle, we get
(x – 0)2 + (y – r)2 = r2
x2 + y2 – 2ry = 0
Sample Problems
Question 1. Find centre and radius of the circle from the given equation:
x2 + (y + 2)2 = 9
Solution:
After rearranging, we get
(x – 0)2 + (y – (-2))2 = 32
On comparing with the standard equation of circle, we have
h = 0, k = -2 and r = 3
So the centre of the circle is (0, -2)
and the radius of the circle = 3
Question 2. Find centre and radius of the circle from the given equation:
x2 + y2 + 6x – 4y + 4 = 0
Solution:
We have,
(x2 + 6x) + (y2 – 4y) = – 4
To make it a perfect square identity, add and subtract 9 and 4,
(x2 + 6x + 9) + (y2 – 4y + 4) – 9 – 4 = – 4
(x + 3)2 + (y – 2)2 = – 4 + 4 + 9
(x – (-3))2 + (y – 2)2 = 9
(x – (-3))2 + (y – 2)2 =32
On comparing with the standard equation of circle, we have
h = -3, k = 2 and r = 3
So the centre of the circle is (-3, 2)
and the radius of the circle = 3
Graphing a circle from its standard equation
As we know that the standard equation of the circle is
(x – h)2 + (y – k)2 = r2
Here, the centre of the circle is (h, k) and the radius of the circle is r. Now let us take an example:
The equation of the circle is (x + 2)2 + (y – 6)2 = 4
we can rewrite this equation as
(x – (-2))2 + (y – 6)2 = 22
On comparing with the standard equation of the circle we get
The centre of the circle is (-2, 6) and the radius of the circle is 2.
Now we will draw a circle on the graph.
Step 1: Draw x and y-axis
Step 2: Plot the centre of the circle on the graph that is (-2, 6)
Step 3: Mark any four points in the four directions from the centre of the circles and the distance between the points and the centre is 2.
Step 4: Join all these points to get a circle.
Expanded equation of a Circle
Now we will find the expanded equation of a circle. So, let us assume that A(h, k) be the centre of the circle and r be the radius of the circle and P(x, y) be any point on the circumference.
Then AP = r …(i)
In right-angled △ACP,
AP2 = AC2 + PC2
r2 = (x – h)2 + (y – k)2
Expanding further, we get
(x – h)2 + (y – k)2 = r2
(x2 – 2hx + h2) + (y2 – 2ky + k2) = r2
and if we bring r2 to the left-hand side and rearrange we get
The expanded equation of circle:
x2 – 2hx + h2 + y2 – 2ky + k2 – r2 = 0
Example: Find centre and radius of the circle using the following equation: x2 + y2 – 4x + 6y = 12.
Solution:
Given: x2 + y2 – 4x + 6y = 12
We can write as
(x2 – 4x) + (y2 – 6y) = 12
By manipulating identity, we get
(x2 – 4x + 4) + (y2 – 6y + 9) – 9 – 4 = 12
(x2 – 4x + 4) + (y2 – 6y + 9) = 12 + 9 + 4
(x – 2)2 + (y – 3)2 = 25
(x – 2)2 + (y – 3)2 = 52
On comparing with the standard equation of circle, we have
h = 2, k = 3 and r = 5
General Equation of a Circle
The general equation of a circle is:
x2 + y2 + 2gx + 2fy + c = 0
For all values of g, f and c.
Now, on adding g2 + f2 on both sides of the equation, we get
(x2 + 2gx + g2)+ (y2 + 2fy + f2) = g2 + f2 − c
As, (x + g)2 = x2+ 2gx + g2 and (y + f)2 =y2 + 2fy + f2
(x + g)2 + (y + f)2 = g2 + f2 – c
(x – (-g))2 + (y – (-f))2 = g2 + f2 – c ……….(1)
On comparing eq(1) with the standard equation, we get
h = −g, k = −f
r2 = g2+ f2−c
where (h, k) is the centre and ‘r’ is the radius of the circle.
Hence,
x2 + y2 + 2gx + 2fy + c = 0, represents the circle with centre (−g, −f) and radius (r) equal to r2 = g2 + f2− c.
- If g2 + f2 > c, then the radius of the circle is real.
- If g2 + f2 = c, then the radius of the circle is zero which tells us that the circle is a point which coincides with the centre. Such type of circle is called a point circle
- g2 + f2 <c, then the radius of the circle become imaginary. Therefore, it is a circle having a real centre and imaginary radius.
Some features of the general equation x2 + y2 + 2gx + 2fy + c = 0 of the circle are as follows:
- It is quadratic in both x and y.
- Coefficient of x2 = y2. (It is advisable to keep the coefficient of x2 and y2 unity)
- There is no term containing xy i.e., the coefficient of xy is zero.
- It contains three arbitrary constants viz. g, f and c.
Sample Problems
Question 1. Find the equation of a circle whose centre is (-3, -2) and radius 6.
Solution:
Given: h = -3, k = -2, and, r = 6
Using the standard equation of circle,
(x – h)2 + (y – k)2 = r2
(x – (-3))2 + (y – (-2))2 = 62
(x + 3)2 + (y + 2)2 = 62
x2 + 6x + 9 + y2 + 4y + 4 = 36
Hence, the required equation is
x2 + y2 + 6x + 4y – 23 = 0
Question 2. Find the equation of a circle whose radius is 7 and the centre is at the origin.
Solution:
Given : r = 7 and the centre = (0, 0)
Using the standard equation of circle,
(x – h)2 + (y – k)2 = r2
x2 + y2 = r2
x2 + y2 = 72
Hence, the required equation is
x2 + y2 – 49 = 0
Question 3. Find the radius and centre of the circle given by the equation
2x2 + 2y2 + 8x + 12y – 38 = 0
Solution:
In the given equation the coefficients of x2 and y2 are not unity.
Firstly, lets make them unity by dividing equation by 2,
x2 + y2 + 4x + 6y – 19 = 0
So, the coordinates of the centre are (-2, -3)
and, Radius =
Radius =
Radius = 4√2
Question 4. Find the equation of the circle that passed through the points (1, 0), (-1, 0), and (0, 1).
Solution:
Let the required circle be
x2 + y2 + 2gx + 2fy + c = 0
As, it passes through (1, 0), (-1, 0), and (0, 1). Hence, they will satisfy the equation
By substituting them, we get
1 + 2g + c = 0 ……..(1)
1 – 2g + c = 0 ……..(2)
1 + 2f + c = 0 ……..(3)
From eq(1) and (2), we get
g = 0 and c = -1
Now, putting c = -1 in eq(3), we get
f = 0
Now, substituting the values of g, f and c in the main equation, we get
x2 + y2 = 1
Question 5. Find the equation of the image of the circle x2 + y2 + 16x – 8y + 64 = 0 in the line mirror x = 0.
Solution:
Equation given is:
x2 + y2 + 16x – 8y = – 64
(x2 + 16x) + (y2 – 8y) = – 64
On adding and subtracting 64 and 16, we get
(x2 + 16x + 64) + (y2 – 8y + 16) – 64 – 16 = – 64
(x2 + 16x + 64) + (y2 – 8y + 16) = – 64 + 64 + 16
(x +
2 + (y – 4)2 = 16
(x – (-8))2 + (y – 4)2 = 42
As, the radius of this circle is (-8, 4) and radius = 4.
The image of the circle in the line mirror will have its centre as (8, 4) and radius 4.
So, the equation will be,
(x –
2 + (y – 4)2 = 42
x2 + y2 – 16x – 8y + 64 = 0
Содержание:
Окружность:
Определение: Кривой второго порядка называется линия, описываемая уравнением
Замечание: Если коэффициенты
При определенных значениях параметров, входящих в это уравнение, оно дает канонические у равнения окружности, эллипса (не путать с овалом), гиперболы и параболы. Рассмотрим эти кривые второго порядка в указанной последовательности.
Определение: Окружностью называется геометрическое место точек равноудаленных от выделенной точки 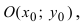
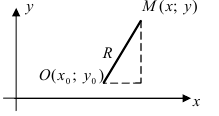
Получим уравнение окружности (Рис. 27). Пусть точка М(х;у) лежит на окружности:
Рис. 27. Вывод уравнения окружности.
Из рисунка видно, что по теореме Пифагора 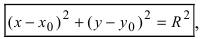
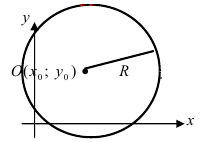
Рис. 28. Окружность.
Если 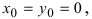
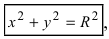
Пример:
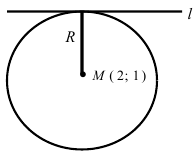
Составить уравнение окружности, центр которой совпадает с точкой М (2; 1), прямая линия 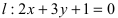
Решение:
Радиус окружности равен расстоянию от центра окружности точки М (2; 1) до прямой l, т.е.
В уравнении окружности 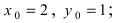
Пример:
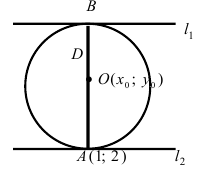
Составить уравнение окружности, касающейся двух параллельных прямых 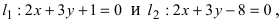
Решение:
Прежде всего определим, на какой из прямых 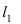
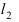
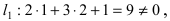
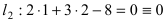
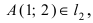
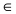
а радиус окружности 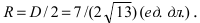
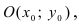
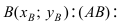
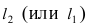
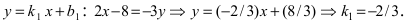
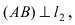
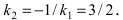
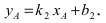
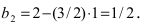
Найдем координаты точки B, которая является пересечением прямых 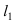
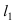
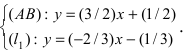
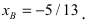
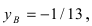
Для вычисления координат точки О применим формулы деления отрезка пополам (О): 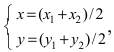
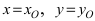
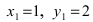
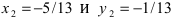
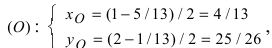
Таким образом, уравнение искомой окружности имеет вид:
Окружность в высшей математике
Рассмотрим уравнение
которое получается из уравнения (I), если положить 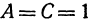
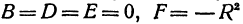
Если в формулу, выражающую расстояние между двумя точками, подставить 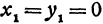
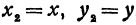
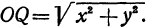
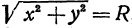
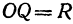
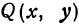
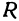

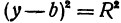

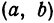
Пример:
Найдем уравнение окружности с центром в точке 
Решение:
Полагая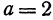
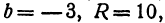
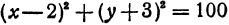
Разрешим это уравнение относительно 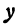
и
Первое из этих уравнений есть уравнение верхней половины окружности, второе—нижней.
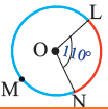
Центральный угол. Градусная мера дуги
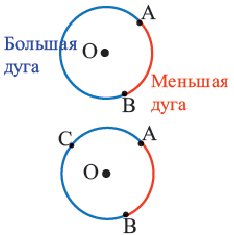
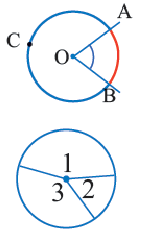
Дуга окружности. Если отметить на окружности точки 

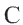
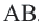
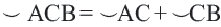


Центральный угол. Угол, вершина которого находится в центре окружности, называется центральным углом. Дугу окружности можно измерять в градусах. Градусная мера дуги равна градусной мере соответствующего центрального угла:
Сумма всех центральных углов окружности, не имеющих общую внутреннюю точку, равна
Дуги окружности и их величины
Пример: 
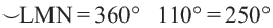
Конгруэнтные дуги
В окружности конгруэнтным центральным углам соответствуют конгруэнтные дуги и наоборот.
Если
Если
Длина дуги
Какую часть составляет центральный угол от всей окружности, такую же часть длина дуги составляет от длины всей окружности.
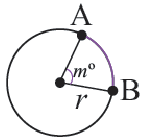
Длина дуги в 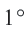
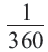
Длина дуги, соответствующей центральному углу с градусной мерой 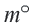
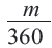
Длина дуги выражается единицами измерения длины (мм, см, м, и т.д.)
Пример №1
Длина окружности равна 72 см. Найдите длину дуги, соответствующей центральному углу 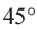
Решение:
Так как центральный угол 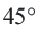
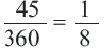
Пример №2
Найдите длину дуги, соответствующей центральному углу 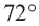
Решение: подставляя значения 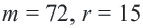
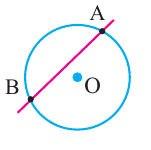
Окружность и хорда
Теорема о конгруэнтных хордах
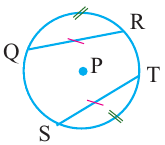
Теорема 1. Хорды, стягивающие конгруэнтные дуги окружности, конгруэнтны.
Обратная теорема 1. Дуги, стягиваемые конгруэнтными хордами окружности, конгруэнтны.
1)Если 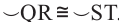
2)Если
Доказательство теоремы 1:
Теорема о серединном перпендикуляре хорд
Теорема 2.
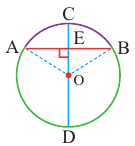
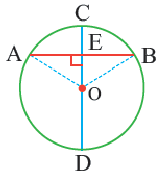
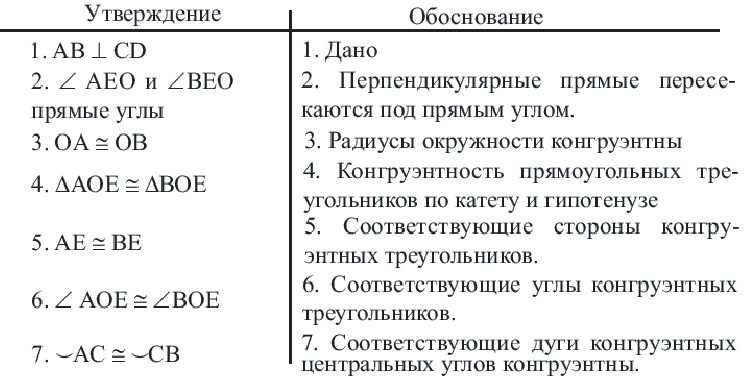
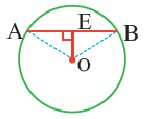
Диаметр, перпендикулярный хорде, делит хорду и соответствующую дугу пополам.
Если
Доказательство теоремы 2.
Дано: 
Докажите:
Начертите радиусы 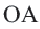
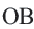
Следствие 1. Прямая, проходящая через центр окружности и перпендикулярная хорде, делит хорду и ее дугу пополам.
Следствие 2. Центр окружности расположен на серединном перпендикуляре хорды. Серединный перпендикуляр хорды проходит через центр окружности.
Пример: Найдите расстояние от центра до хорды длиной 30 единиц в окружности радиусом 17 единиц. Если 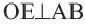
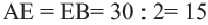
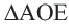
Теорема о хордах, находящихся на одинаковом расстоянии от центра окружности
Теорема 3.
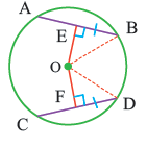
Конгруэнтные хорды окружности находятся на одинаковом расстоянии от центра окружности.
Если 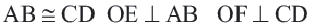
Обратная теорема 3. Хорды, находящиеся на одинаковом расстоянии от центра окружности, конгруэнтны.
Доказательство теоремы 3
Дано: Окружность с центром
Докажите:
Доказательство (текстовое): Прямая, проходящая через центр окружности и перпендикулярная хорде, делит хорду и стягивающую ее дугу пополам. 

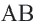
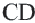

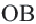
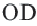
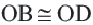
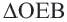
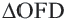


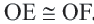
Задача. Хорды 

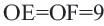
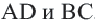
Решение: Так как хорды 

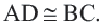
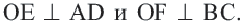
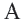
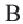
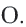
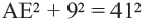
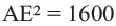
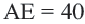
Так как
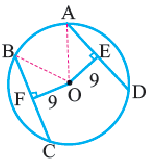
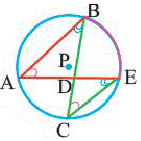
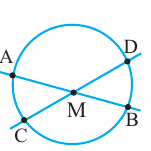
Угол, вписанный в окружность
Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется углом вписанным в окружность. Дуга, соответствующая углу, вписанному в окружность, называется дугой, на которую опирается этот угол.
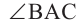
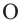
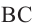
Угол, вписанный в окружность:
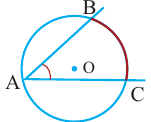
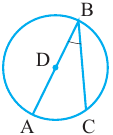
Теорема 1. Градусная мера угла, вписанного в окружность, равна половине градусной меры дуги, на которую он опирается.
Доказательство (текстовое): 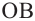
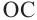
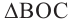
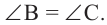
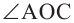
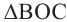
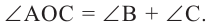
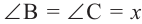
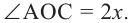
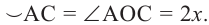
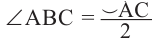
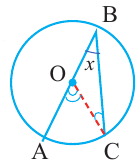
Следствие 1. Угол, вписанный в окружность, равен половине соответствующего центрального угла.
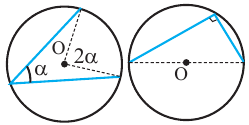
Следствие 2. Угол, вписанный в окружность и опирающийся на диаметр (полуокружность), является прямым углом.
Конгруэнтные углы, вписанные в окружность
Следствие 3. Вписанные углы, опирающиеся на одну и ту же дугу, конгруэнтны. 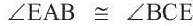
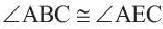
Следствие 4. Вписанные углы, опирающиеся на конгруэнтные дуги, конгруэнтны. Если 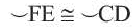
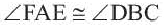
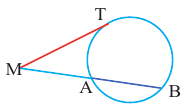
Касательная к окружности
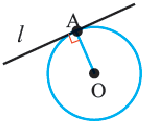
Касательная. Признак касательной
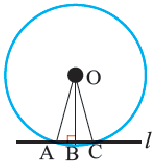
Прямая, имеющая одну общую точку с окружностью, называется касательной. Теорема 1. Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.
Прямая 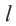
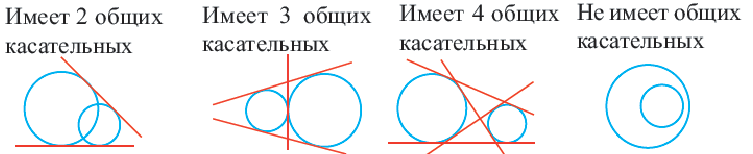
Прямая, касающаяся обеих окружностей, называется общей касательной этих окружностей. Окружности, касаясь друг друга изнутри или извне, могут иметь общую касательную в одной точке. Также окружности могут касаться одной касательной в разных точках.
Две окружности могут иметь несколько общих касательных или вообще не иметь общих касательных.
Доказательство теоремы 1. Если прямая 

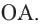
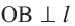

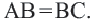
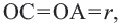
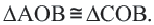
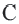

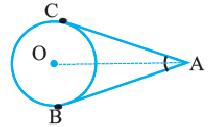
Свойства касательных, проведенных к окружности из одной точки
Теорема 2. Отрезки касательных к окружности, проведенных из одной точки, конгруэнтны, и центр окружности находится на биссектрисе угла, образованного касательными.
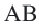
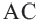
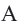
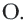
Углы, образованные секущими и касательными
Прямая, имеющая две общие точки с окружностью, называется секущей окружности.
Углы между двумя секущими
Вершина угла находится внутри окружности
Теорема. Если вершина угла, образованного двумя секущими, находится внутри окружности, то градусная мера угла равна полусумме величин дуг на которые опирается этот угол и угол вертикальный данному.
Углы между касательной и секущей
Вершина угла находится на окружности
Теорема. Если вершина угла, образованного касательной и секущей, находится на окружности, то градусная мера угла равна половине градусной меры дуги, на которую он опирается.
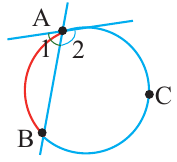
Углы, образованные касательной и секущей
Вершина угла находится вне окружности
Теорема 1.
Градусная мера угла, образованного секущей и касательной, двумя касательными, двумя секущими окружности (если вершина угла находится вне окружности), равна половине разности градусных мер дуг, находящихся между сторонами угла.
Отрезки секущих и касательных
Длина отрезков, секущих окружность
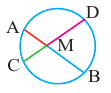
Теорема 1. При пересечении двух хорд, произведение отрезков одной хорды, полученных точкой пересечения, равно произведению отрезков второй хорды.
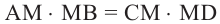
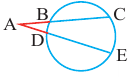
Теорема 2. Если из точки 

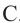
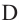
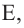
Теорема 3. Если из точки 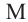


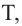
Уравнение окружности
Используя формулу расстояния между двумя точками, можно написать уравнение окружности с радиусом 
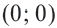
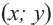

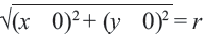
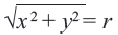
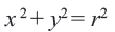
Уравнение окружности с центром в начале координат и радиусом 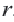
Например, уравнение окружности с центром в начале координат 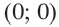
По формуле расстояния между центром окружности 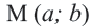
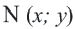
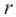
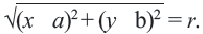
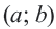
Например, уравнение окружности с центром в точке 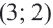
Пример №3
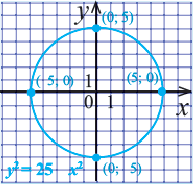
Постройте на координатной плоскости окружность, заданную уравнением
Решение: Напишем уравнение в виде 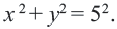
Отметим 4 точки, находящиеся на расстоянии 5 единиц от начала координат. Например, 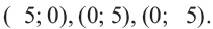
Пример №4
Точка 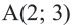
Решение: Записав координаты точки 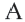
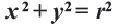
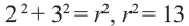
Пример №5
Найдем центр и радиус окружности, заданной уравнением
Решение:
Центр окружности точка 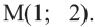
Пример №6
Мобильные телефоны работают с помощью передачи сигналов посредством спутников из одной передающей станции в другую. Компания мобильного оператора старается расположить передающую станцию так, чтобы обслуживать больше пользователей. Представим, что три больших города находятся в точках 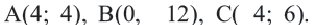
Решение: Сначала соединим эти точки и найдем точку пересечения серединных перпендикуляров сторон полученного треугольника. Эта точка 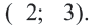
Уравнение окружности:
Заметка. Определив линейные уравнения, соответствующие серединным перпендикулярам, можно найти координаты центра окружности решением системы уравнений.
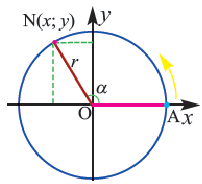
Координаты точек, находящихся на окружности, и тригонометрические отношения
Если точка 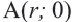
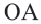
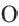
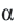
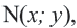
Для координат точки 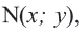

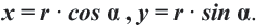

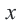
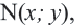
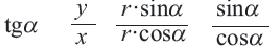
Синусы смежных углов равны, а косинусы взаимно противоположны.
Из этих формул при 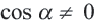
С помощью формул, приведенных выше, вычисление синуса, косинуса, тангенса для тупого угла можно свести к вычислению синуса, косинуса, тангенса острого угла, соответственно.
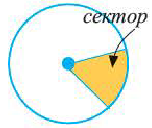
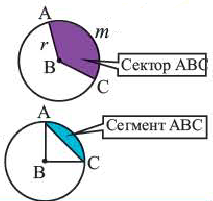
Сектор и сегмент
Сектор часть круга, ограниченная центральным углом, образованным двумя радиусами и соответствующей этому углу дугой. Площадь сектора, соответствующего центральному углу, составляет ту часть площади круга, которую составляет центральный угол от полного угла.
Например, часть круга, соответствующая центральному углу 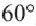
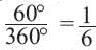
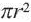

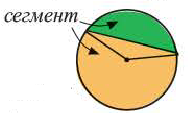
Площадь сектора
Площадь сектора:
Площадь сегмента:
Указание: При нахождении площади сегмента, соответствующего большей дуге, к площади соответствующего сектора прибавляется площадь
- Эллипс
- Гипербола
- Парабола
- Многогранник
- Сфера в геометрии
- Шар в геометрии
- Правильные многогранники в геометрии
- Многогранники

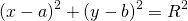
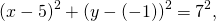
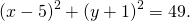
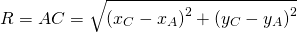
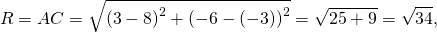
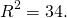
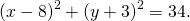
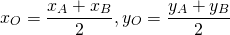
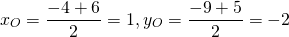
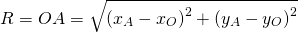
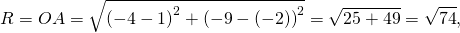
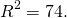
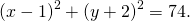
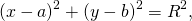
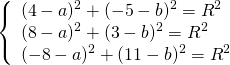
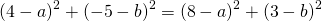
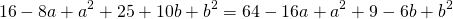
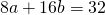
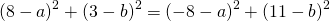
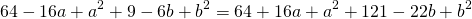
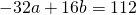
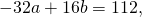
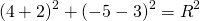
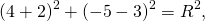
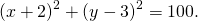


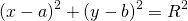
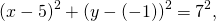
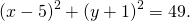
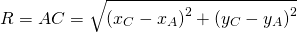
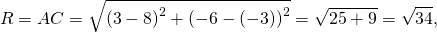
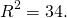
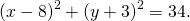
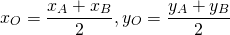
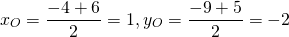
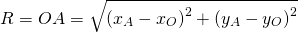
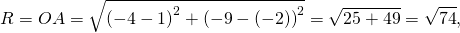
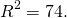
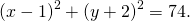
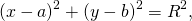
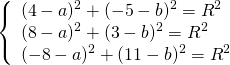
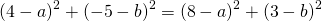
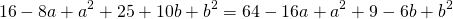
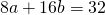
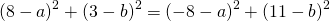
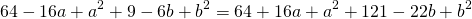
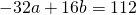
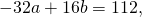
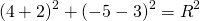
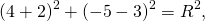
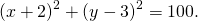





 2 + (y – 4)2 = 16
2 + (y – 4)2 = 16