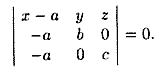Как написать уравнение плоскости проходящей через точку перпендикулярно вектору

ВОПРОСЫ
ПО АЛГЕБРЕ
И ГЕОМЕТРИИ

Уравнение
плоскости в пространстве
Канонические
уравнения эллипса, гиперболы
и
параболы
Векторное
произведение векторов
Скалярное
произведение векторов
Линейные
(векторные )
пространства.
Примеры
Линейная
независимость и базис
Уравнение
прямой в пространстве
Решение
систем линейных
уравнений
методом обратной
матрицы
Решение
систем линейных
уравнений методом Гаусса
Матрицы
и действия над
ними
Классификация
поверхностей второго порядка
Линейные
операторы. Примеры
Задача
на собственные
значения
Обратная
матрица и ее вычисление
Полярные
координаты
Ранг
Матрицы. Теорема Кронекера-Капелли
Уравнение
прямой на
плоскости Определитель
матрицы
Уравнение
гиперплоскости в n-мерном
пространстве Применения
к проблемам ИИ*.
Действия
над векторами Координаты
вектора.

1.Уравнения
плоскости в пространстве

Простейшей
поверхностью является плоскость.
Плоскость в пространстве Oxyz можно задать
разными способами. Каждому из них
соответствует определенный вид ее
уравнения.

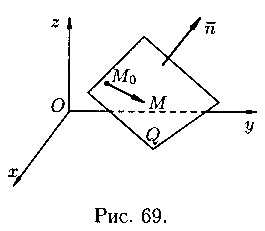
Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору

Пусть
в пространстве Oxyz плоскость Q задана
точкой

и
вектором

,
перпендикулярным этой плоскости (см.
рис. 69). Выведем уравнение плоскости Q.
Возьмем на ней произвольную точку

и
составим вектор

.
При любом расположении точки Μ на
плоскости Q векторы

и

взаимно
перпендикулярны, поэтому их скалярное
произведение равно нулю:

,
т. е.

(12.3)

Координаты
любой точки плоскости Q удовлетворяют
уравнению (12.3), координаты точек, не
лежащих на плоскости Q, этому уравнению
не удовлетворяют (для них

).

Уравнение
(12.3) называется уравнением плоскости,
проходящей через данную точку

перпендикулярно
вектору

.
Оно первой степени относительно текущих
координат x, y, z. Вектор

называется
нормальным вектором плоскости.

Придавая
коэффициентам А, В и С уравнения (12.3)
различные значения, можно получить
уравнение любой плоскости, проходящей
череp точку

.
Совокупность плоскостей, проходящих
через данную точку, называется связкой
плоскостей, а уравнение (12.3) — уравнением
связки плоскостей.

Общее уравнение плоскости

Рассмотрим
общее уравнение первой степени с тремя
переменными х, у и z:

(12.4)

Полагая,
что по крайней мере один из коэффициентов
А, В или С не равен нулю, например

,
перепишем уравнение (12.4) в виде

(12.5)

Сравнивая
уравнение (12.5) с уравнением (12.3), видим,
что уравнения (12.4) и (12.5) являются
уравнением плоскости с нормальным
вектором

,
проходящей через точку

.

Итак,
уравнение (12.4) определяет в системе
координат Oxyz некоторую плоскость.
Уравнение (12.4) называется общим уравнением
плоскости.

Частные
случаи общего уравнения плоскости:

1.
Если D = 0, то оно принимает вид

.
Этому уравнению удовлетворяет точка

.
Следовательно, в этом случае плоскость
проходит через начало координат.

2.
Если С = 0, то имеем уравнение

.
Нормальный вектор

перпендикулярен
оси Οz. Следовательно, плоскость
параллельна оси Οz; если B = 0 — параллельна
оси Оу, А = 0 — параллельна оси Ох.

3.
Если С = D = 0, то плоскость проходит через

параллельно
оси Οz, т. е. плоскость

проходит
через ось Οz. Аналогично, уравнениям

и

отвечают
плоскости, проходящие соответственно
через оси Ох и Оу.

4.
Если А = В = 0, то уравнение (12.4) принимает
вид

,
т. е.

Плоскость
параллельна плоскости Оху. Аналогично,
уравнениям

и

отвечают
плоскости, соответственно параллельные
плоскостям Oyz и Οxz.

5.
Если A = B = D = 0, то уравнение (12.4) примет
вид

,
т. е. z = 0. Это уравнение плоскости Оху.
Аналогично: у = 0 — уравнение плоскости
Οxz; x = О — уравнение плоскости Oyz.

Уравнение
плоскости, проходящей через три данные
точки

Три
точки пространства, не лежащие на одной
прямой, определяют единственную
плоскость. Найдем уравнение плоскости
Q, проходящей через три данные точки
M₁(x₁;y₁;z₁),
М₂(x₂;y₂;z₂) и
М₃(х₃,y₃,z₃), не
лежащие на одной прямой.

Возьмем
на плоскости произвольную точку M(x;y;z)
и составим векторы

,

,

.
Эти векторы лежат на плоскости Q,
следовательно, они компланарны. Используем
условие компланарности трех векторов
(их смешанное произведение равно нулю),
получаем

,
т. е.

(12.6)

Уравнение
(12.6) есть уравнение плоскости, проходящей
через три данные точки.

Уравнение
плоскости в отрезках

Пусть
плоскость отсекает на осях Ох, Оу и Оz
соответственно отрезки a, b и c,
т. е. проходит через три точки A(a;0;0),
B(0;b;0) и C(0;0;c) (см.рис. 70). Подставляя
координаты этих точек в уравнение
(12.6), получаем

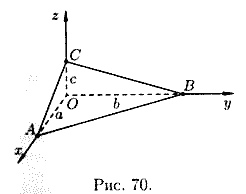
Раскрыв
определитель, имеем

,
т. е.

или

(12.7)

Уравнение
(12.7) называется уравнением плоскости в
отрезках на осях. Им удобно пользоваться
при построении плоскости.

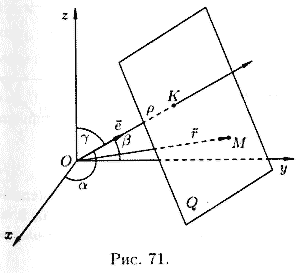
Нормальное
уравнение плоскости

Положение
плоскости Q вполне определяется заданием
единичного вектора

,
имеющего направление перпендикуляра
ОК, опущенного на

плоскость
из начала координат, и длиной p этого
перпендикуляра (см. рис. 71).

П
усть
ОК = p, а α, β,  —
углы, образованные единичным вектором
ё с осями Ох, Оу и Οz. Тогда

.
Возьмем на плоскости произвольную точку
М(х; у; z) и соединим ее с началом координат.
Образуем вектор

.
При любом положении точки Μ на плоскости
Q проекция радиус-вектора

на
направление вектора

всегда
равно р:

,
т. е.

или

(12.8)

Уравнение
(12.8) называется нормальным уравнением
плоскости в векторной форме. Зная
координаты векторов f и e, уравнение
(12.8) перепишем в виде

(12.9)

Уравнение (12.9)
называется нормальным уравнением
плоскости в координатной форме.

Отметим,
что общее уравнение плоскости (12.4) можно
привести к нормальному уравнению (12.9)
так, как это делалось для уравнения
прямой на плоскости. А именно: умножить
обе части уравнения (12.4) на нормирующий
множитель

,
где знак берется противоположным знаку
свободного члена D общего уравнения
плоскости.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
#
#
#
#
#
#
#
#
#
16.02.201641.76 Mб17Гайтон 11_-_Nervnaya_sistema_V_Neyrofiziologia_dvigate.pdf
#
16.02.201630.55 Mб12Гайтон 13_-_Metabolizm_i_termoregulyatsia.pdf

Источник

Уравнения плоскости, проходящей через точку перпендикулярно вектору

Общее уравнение плоскости

Ненулевой вектор vec{n} , перпендикулярный заданной плоскости, называется нормальным вектором (или, короче, нормалью) для этой плоскости.

Пусть в координатном пространстве Oxyz (в прямоугольной системе координат) заданы:

а) точка $M_{0}(x_{0},y_{0},z_{0})$ ;

б) ненулевой вектор vec{n}=Acdotvec{i}+Bcdotvec{j}+Ccdotvec{k} (рис.4.8,а).

Требуется составить уравнение плоскости, проходящей через точку $M_{0}(x_{0},y_{0},z_{0})$ перпендикулярно вектору vec{n}.

Общее уравнение плоскости, проходящей через точку перпендикулярно вектору

Выберем в пространстве произвольную точку M(x,y,z) . Обозначим vec{r}=overrightarrow{OM}=xvec{i}+yvec{j}+zvec{k}, $vec{r}_{0}=overrightarrow{OM_{0}}=x_{0}vec{i}+y_{0}vec{j}+z_{0}vec{k},$ — радиус-векторы точек и $M_{0}(x_{0},y_{0},z_{0})$ Точка принадлежит заданной плоскости тогда и только тогда, когда векторы $overrightarrow{M_{0}M}$ и vec{n} перпендикулярны (рис.4.8,б). Условие ортогональности запишем при помощи скалярного произведения:

$leftlangleoverrightarrow{M_{0}M},,vec{n}rightrangle=0.$

Учитывая, что $overrightarrow{M_{0}M}=vec{r}-vec{r}_{0}$ , получаем векторное уравнение плоскости:

${color{red}boxed{{color{black}langlevec{r}-vec{r}_{0},,vec{n}rangle=0}}}$

(4.12)

Это уравнение можно записать в другой форме. Преобразуем левую часть $langlevec{r}-vec{r}_{0},vec{n}rangle=langlevec{r},vec{n}rangle-langlevec{r}_{0},vec{n}rangle$ используя свойства скалярного произведения. Обозначая $c=langlevec{r}_{0},vec{n}rangle$ получаем уравнение langlevec{r},vec{n}rangle-c=0, или

langlevec{r},,vec{n}rangle=c,

(4.13)

выражающее постоянство проекций на нормаль радиус-векторов точек, принадлежащих плоскости.

Получим координатную форму записи векторного уравнения плоскости (4.12). Так как $vec{r}-vec{r}_{0}=(x-x_{0})vec{i}+(y-y_{0})vec{j}+(z-z_{0})vec{k},$ vec{n}=Avec{i}+Bvec{j}+Cvec{k}, формуле (1.10) находим

$langlevec{r}-vec{r}_{0},vec{n}rangle= (x-x_{0})cdot A+(y-y_{0})cdot B+(z-z_{0})cdot C=0,$

$Acdot(x-x_{0})+ Bcdot(y-y_{0})+ Ccdot(z-z_{0}) =0.$

(4.14)

Полученное соотношение (4.14) позволяет по координатам точки $M_{0}(x_{0},y_{0},z_{0})$ и координатам A,,B,,C нормали vec{n} сразу записать искомое уравнение плоскости.

Обозначив $D=-Acdot x_{0}-Bcdot y_{0}-Ccdot z_{0}$ , получим общее уравнение плоскости

{color{red}boxed{{color{black}Acdot x+Bcdot y+Ccdot z+D=0}}}

(4.15)

Поскольку коэффициенты A,,B,,C не равны нулю одновременно (это координаты ненулевого вектора vec{n} ), уравнение (4.15) является алгебраическим уравнением первой степени, т.е. линейным уравнением с тремя неизвестными. Следовательно, плоскость является алгебраической поверхностью первого порядка.

Проводя рассуждения в обратном порядке, делаем вывод о том, что линейное уравнение (4.15) задает в координатном пространстве плоскость. Полученные выводы сделаны для прямоугольной системы координат, но, учитывая теорему 4.1, они переносятся (без изменений) и на любую аффинную систему координат.

Теорема (4.2) об алгебраической поверхности первого порядка

Всякое уравнение первой степени с тремя неизвестными задает в аффинной системе координат плоскость, и наоборот, всякая плоскость в любой аффинной системе координат может быть задана уравнением первой степени с тремя неизвестными. Другими словами, алгебраическая поверхность первого порядка есть плоскость.

Замечания 4.2.

1. При составлении общего уравнения плоскости нормаль выбирается неоднозначно: можно выбрать любую, отличную от нуля, длину нормали vec{n}, а также одно из двух возможных направлений (противоположный вектор (-vec{n}) также является нормалью). Например, вместо нормали vec{n} можно взять нормаль -7vec{n}, что соответствует умножению обеих частей уравнения (4.15) на число –7.

2. Если в общем уравнении плоскости (4.15) коэффициент при неизвестной равен нулю, то плоскость параллельна координатной оси. Например, если A=0 то плоскость (4.15) параллельна оси абсцисс (рис.4.9,а); если A=B=0 то плоскость (4.15) параллельна координатным осям и Oy, т.е. параллельна координатной плоскости Oxy (рис.4.9,б).

Если в общем уравнении плоскости (4.15) свободный член равен нулю (D=0), то плоскость проходит через начало координат (рис.4.9,в).

Варианты расположения плоскости в пространстве

3. Нормаль vec{n}=Avec{i}+Bvec{j}+Cvec{k} к плоскости Ax+By+Cz+D=0 совпадает с градиентом функции f(x,y,z)=Ax+By+Cz+D:

$begin{aligned} operatorname{grad}f(x,y,z)=nabla f(x,y,z)&= frac{partial f(x,y,z)}{partial x}cdotvec{i}+ frac{partial f(x,y,z)}{partial y}cdotvec{j}+ frac{partial f(x,y,z)}{partial z}cdotvec{k}=\[3pt] &=Acdotvec{i}+Bcdotvec{j}+Ccdotvec{k}=vec{n},. end{aligned}$

В курсе математического анализа доказывается, что градиент направлен в сторону наискорейшего возрастания функции в данной точке.

Положительное и отрицательное полупространства

4. Плоскость Ax+By+Cz+D=0 разбивает пространство на два полупространства (рис.4.10): положительное, координаты всех точек которого удовлетворяют неравенству Ax+By+Cz+Dgeqslant0, и отрицательное, для точек которого Ax+By+Cz+Dleqslant0. Нормаль vec{n}=Avec{i}+Bvec{j}+Cvec{k}, приложенная к произвольной точке плоскости Ax+By+Cz+D=0, указывает на положительное полупространство (рис.4.10).

Это свойство следует из пункта 3.

5. Абсолютное значение |Ax+By+Cz+D| пропорционально расстоянию от точки M(x,y,z) до плоскости Ax+By+Cz+D=0 т.е. отношение расстояний от точек $M_{1}(x_{1},y_{1},z_{1})$ и $M_{2}(x_{2},y_{2},z_{2})$ до плоскости равно отношению $frac{|Ax_{1}+By_{1}+Cz_{1}+D|}{|Ax_{2}+By_{2}+Cz_{2}+D|},.$

Доказательство аналогично доказательству пункта 5 замечаний 3.2.

6. В аффинной системе координат $Ovec{e}_{1}vec{e}_{2}vec{e}_3$ линейное уравнение $a_{1}x_{1}+a_{2}x_{2}+a_3x_3+a_4=0$ задает, согласно теореме 4.2, плоскость. Выводы, полученные в п.2,3,4,5, остаются справедливыми с тем лишь исключением, что вектор $vec{n}=a_{1}vec{e}_{1}+a_{2}vec{e}_{2}+a_3vec{e}_3$ не является нормалью.

Пример 4.5. В координатном пространстве Oxyz (в прямоугольной системе координат) заданы точки K(1;2;3) и L(5;0;1). Составить уравнение плоскости, перпендикулярной отрезку и проходящей через его середину (рис.4.11).

Уравнение плоскости, перпендикулярной отрезку и проходящей через его середину

Решение. Находим координаты середины отрезка $Kcolon,M!left(frac{1+5}{2};frac{2+0}{2};frac{3+1}{2}right)!,$ т.е. M(3;1;2). Вектор overrightarrow{KL} можно взять в качестве нормали к плоскости. Находим координаты этого вектора, вычитая из координат его конца соответствующие координаты его начала:

overrightarrow{KL}= (5-1)cdotvec{i}+(0-2)cdotvec{j}+(1-3)cdotvec{k}= 4cdotvec{i}-2cdotvec{j}-2cdotvec{k}=vec{n},.

Следовательно, уравнение (4.15) искомой плоскости имеет вид 4x-2y-2z+D=0.

Осталось найти величину свободного члена . Поскольку точка M(3;1;2) принадлежит плоскости, то ее координаты x=3, y=1, z=2 должны удовлетворять уравнению этой плоскости, следовательно, 4cdot3-2cdot1-2cdot2+D=0, отсюда В=-6 Таким образом, искомая плоскость задается уравнением

4cdot x-2cdot y-2cdot z-6=0 quad Leftrightarrow quad 2cdot x-y-z-3=0.

Уравнение этой прямой можно было получить в виде (4.14), подставляя координаты нормали vec{n}=4vec{i}-2vec{j}-2vec{k} и точки M(3;1;2): 4(x-3)-2(y-1)-2(z-1)=0.

Расстояние от точки до плоскости

Расстояние от точки до плоскости и ортогональная проекция вектора

Пусть заданы:

а) плоскость, описываемая общим уравнением (4.15): Acdot x+Bcdot y+Ccdot z+D=0 ;

б) точка $M^{ast}(x^{ast},y^{ast},z^{ast})$ в пространстве.

Требуется найти расстояние от точки до плоскости.

Искомое расстояние равняется длине ортогональной проекции вектора $overrightarrow{M_{0}M^{ast}}$ на направление нормали vec{n} (рис.4.12) и находится по формуле:

$d=left|overrightarrow{operatorname{pr}}_{vec{n}}overrightarrow{M_{0}M^{ast}}right|= frac{Bigl|Bigllanglevec{n}, overrightarrow{M_{0}M^{ast}} BiglrangleBigr|}{|vec{n}|}$ ,

где $M_{0}(x_{0},y_{0},z_{0})$ — любая точка на заданной плоскости.

Запишем правую часть в координатной форме, выражая скалярное произведение и длину через координаты векторов

$begin{gathered} vec{n}=Acdotvec{i}+Bcdotvec{j}+Ccdotvec{k}, quad overrightarrow{M_{0}M^{ast}}=(x^{ast}-x_{0})cdotvec{i}+(y^{ast}-y_{0})cdotvec{j}+(z^{ast}-z_{0})cdotvec{k},colon\[5pt] d=frac{|A(x^{ast}-x_{0})+B(y^{ast}-y_{0})+C(z^{ast}-z_{0})|}{sqrt{A^2+B^2+C^2}}= frac{|Ax^{ast}+By^{ast}+Cz^{ast}-(Ax_{0}+By_{0}+Cz_{0})|}{sqrt{A^2+B^2+C^2}},. end{gathered}$

Поскольку координаты точки $M_{0}(x_{0},y_{0},z_{0})$ удовлетворяют уравнению (4.15), то $Ax_{0}+By_{0}+Cz_{0}=-D.$ Подставляя это выражение, получаем формулу расстояния от точки до плоскости

${color{red}boxed{{color{black}d=frac{|Acdot x^{ast}+Bcdot y^{ast}+Ccdot z^{ast}+D|}{sqrt{A^2+B^2+C^2}}}}}$

(4.16)

Пример 4.6. В координатном пространстве Oxyz (в прямоугольной системе координат) заданы точки K(1;2;3) и L(5;0;1). Требуется найти, в каком отношении плоскость rhocolon3x-4y+z-13=0 делит отрезок (рис.4.13).

Решение. Найдем значения линейного четырехчлена p(x,y,z)=3x-5y+z-13 в точках K(1;2;3) и L(5;0;1):

Найти, в каком отношении плоскость p делит отрезок KL

p(1;2;3)=3cdot1-4cdot2+1cdot3-13=-15phantom{H} и phantom{H}p(5;0;1)=3cdot5-4cdot0+1cdot1-13=3.

Получили значения разных знаков. Следовательно, точки и лежат по разные стороны от плоскости я (согласно пункту 4 замечаний 4.2, эти точки лежат в разных полупространствах), т.е. плоскость rho действительно пересекает отрезок (в точке на рис.4.13). Так как эти значения по абсолютной величине пропорциональны расстояниям от точек и до плоскости rho , то

$frac{KM}{ML}=frac{|p(1;2;3)|}{|p(5;0;1)|}=frac{|-15|}{|3|}=frac{5}{1}=5:1,.$

Этот же результат можно получить по формуле (4.16). Находим расстояния $d_{K}$ и $d_{L}$ от точек и до плоскости rho:

$d_{K}=frac{|3cdot1-4cdot2+3-13|}{sqrt{3^2+(-4)^2+1^2}}=frac{15}{sqrt{26}}; quad d_{L}=frac{|3cdot5-4cdot0+1-13|}{sqrt{3^2+(-4)^2+1^2}}=frac{3}{sqrt{26}},.$

Следовательно, $frac{KL}{ML}=frac{d_{K}}{d_{L}}=frac{5}{1}=5:1.$

Нормированное уравнение плоскости

Преобразуем общее уравнение плоскости Ax+By+Cz+D=0 следующим образом. Если свободный член D<0, то разделим обе части на длину нормали $|vec{n}|=sqrt{A^2+B^2+C^2},,$ а если Dgeqslant0, то разделим на $-|vec{n}|=-sqrt{A^2+B^2+C^2},,$ Коэффициенты при неизвестных при этом станут равными направляющим косинусам нормали:

$cosalpha=frac{A}{pmsqrt{A^2+B^2+C^2}}, quad cosbeta=frac{B}{pmsqrt{A^2+B^2+C^2}}, quad cosgamma=frac{C}{pmsqrt{A^2+B^2+C^2}},,$

а свободный член $frac{D}{pmsqrt{A^2+B^2+C^2}}$ , в силу описанного выбора знака, будет неположительным. Обозначим его через $-rho=frac{D}{pmsqrt{A^2+B^2+C^2}}.$ Тогда получим нормированное уравнение плоскости

{color{red}boxed{{color{black}xcdotcosalpha+ycdotcosbeta+zcdotcosgamma-rho=0,~rhogeqslant0}}}

(4.17)

Нормированное уравнение плоскости

Замечания 4.3.

1. Свободный член rho нормированного уравнения (4.17) равен расстоянию от начала координат до плоскости. Это следует из формулы (4.16).

2. Нормированное уравнение плоскости (4.17) можно записать в виде (4.13): langlevec{r},vec{n}rangle=rho, если в качестве нормали vec{n} вы брать единичный вектор vec{n}=vec{i}cosalpha+vec{j}cosbeta+vec{k}cosgamma,, так как xcosalpha+ycosbeta+zcosgamma=langlevec{r},vec{n}rangle. Из двух возможных единичных нормалей условию rho>0 отвечает нормаль vec{n}, направленная к плоскости (рис.4.14), если вектор vec{n} приложить к началу координат. При выборе противоположного вектора (-vec{n}) получилось бы отрицательное значение rho, которое не допускается в уравнении (4.17).

3. Коэффициенты общего уравнения плоскости (4.15) определяются неоднозначно в силу неоднозначного выбора нормали (см. пункт 1 замечаний 4.2). При составлении нормированного уравнения (4.17) плоскости такого произвола нет. Здесь все коэффициенты определены однозначно (при rho>0 ) или с точностью до знака (при rho=0).

4. Нормированное уравнение плоскости имеет смысл только в прямоугольной системе координат.

Пример 4.7. В координатном пространстве Oxyz (в прямоугольной системе координат) заданы точки K(1;2;3) и L(5;0;1) (см. рис.4.11). Требуется:

а) составить нормированное уравнение плоскости, перпендикулярной отрезку и проходящей через его середину;

б) найти расстояние от начала координат до этой плоскости.

Решение. а) Общее уравнение искомой плоскости было получено в примере 4.5: 2x-y-z-3=0. Найдем длину нормали

$vec{n}=2cdotvec{i}-1cdotvec{j}-1cdotvec{k} quad Rightarrow quad |vec{n}|=sqrt{2^2+(-1)^2+(-1)^2}=sqrt{6},.$

Так как свободный член отрицательный, разделим уравнение на sqrt{6}: $frac{2x}{sqrt{6}}-frac{y}{sqrt{6}}-frac{z}{sqrt{6}}-frac{3}{sqrt{6}}=0.$ Нормированное уравнение плоскости получено.

б) По нормированному уравнению определяем расстояние $rho=frac{3}{sqrt{6}}$ от начала координат до плоскости (см. пункт 1 замечаний 4.3).

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Уравнение плоскости.

Навигация по странице:

Плоскость — определение
Общее уравнение плоскости
Уравнение плоскости в отрезках
Уравнение плоскости, проходящей через точку, перпендикулярно вектору нормали
Уравнение плоскости, проходящей через три заданные точки, не лежащие на одной прямой

Определение. Плоскость — есть поверхность, полностью содержащая, каждую прямую, соединяющую любые её точки.

Общее уравнение плоскости

Любую плоскость можно задать уравнением плоскости первой степени вида

A x + B y + C z + D = 0

где A, B и C не могут быть одновременно равны нулю.

Уравнение плоскости в отрезках

Если плоскость пересекает оси OX, OY и OZ в точках с координатами (a, 0, 0), (0, b, 0) и (0, 0, с), то она может быть найдена, используя формулу уравнения плоскости в отрезках

x	+	y	+	z	= 1
a	b	c

Уравнение плоскости, проходящей через точку, перпендикулярно вектору нормали

Чтобы составить уравнение плоскости, зная координаты точки плоскости M(x₀, y₀, z₀) и вектора нормали плоскости n = {A; B; C} можно использовать следующую формулу.

A(x — x₀) + B(y — y₀) + C(z — z₀) = 0

Уравнение плоскости, проходящей через три заданные точки, не лежащие на одной прямой

Если заданы координаты трех точек A(x₁, y₁, z₁), B(x₂, y₂, z₂) и C(x₃, y₃, z₃), лежащих на плоскости, то уравнение плоскости можно найти по следующей формуле

x — x₁	y — y₁	z — z₁	= 0
x₂ — x₁	y₂ — y₁	z₂ — z₁
x₃ — x₁	y₃ — y₁	z₃ — z₁

Источник