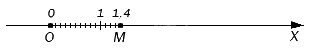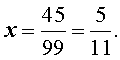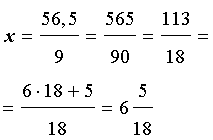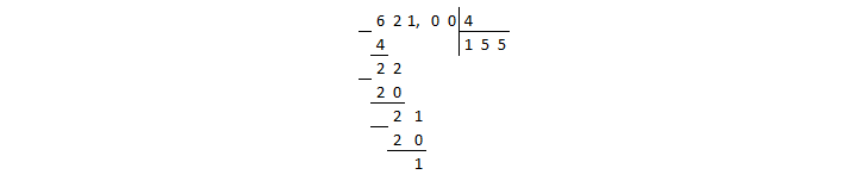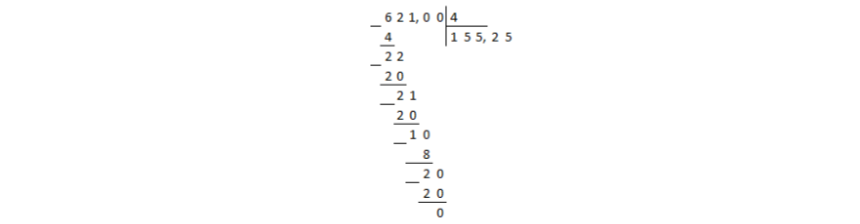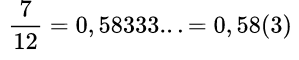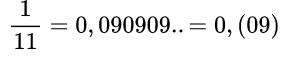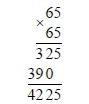Как пишется бесконечная дробь

Данный материал мы посвятим такой важной теме, как десятичные дроби. Сначала определимся с основными определениями, приведем примеры и остановимся на правилах десятичной записи, а также на том, что из себя представляют разряды десятичных дробей. Далее выделим основные виды: конечные и бесконечные, периодические и непериодические дроби. В финальной части мы покажем, как точки, соответствующие дробным числам, расположены на оси координат.

Что такое десятичная запись дробных чисел

Так называемая десятичная запись дробных чисел может быть использована как для натуральных, так и для дробных чисел. Она выглядит как набор из двух и более цифр, между которыми есть запятая.

Десятичная запятая нужна для того, чтобы отделять целую часть от дробной. Как правило, последняя цифра десятичной дроби не бывает нулем, за исключением случаев, когда десятичная запятая стоит сразу после первого же нуля.

Какие можно привести примеры дробных чисел в десятичной записи? Это может быть 34,21, 0,35035044, 0,0001, 11 231 552,9 и др.

В некоторых учебниках можно встретить использование точки вместо запятой (5.67, 6789.1011 и др.) Это вариант считается равнозначным, но он более характерен для англоязычных источников.

Определение десятичных дробей

Основываясь на указанном выше понятии десятичной записи, мы можем сформулировать следующее определение десятичных дробей:

Десятичные дроби представляют собой дробные числа в десятичной записи.

Для чего нам нужна запись дробей в такой форме? Она дает нам некоторые преимущества перед обыкновенными, например, более компактную запись, особенно в тех случаях, когда в знаменателе стоят 1000, 100, 10 и др. или смешанное число. Например, вместо 610 мы можем указать 0,6, вместо 2510000 – 0, 0023, вместо 5123100 –  512,03.

О том, как правильно представить в десятичном виде обыкновенные дроби с десятками, сотнями, тысячами в знаменателе, будет рассказано в рамках отдельного материала.

Как правильно читать десятичные дроби

Существуют некоторые правила чтения записей десятичных дробей. Так, те десятичные дроби, которым соответствуют их правильные обыкновенные эквиваленты, читаются почти так же, но с добавлением слов «ноль десятых» в начале. Так, запись 0,14, которой соответствует 14100, читается как «ноль целых четырнадцать сотых».

Если же десятичной дроби можно поставить в соответствие смешанное число, то она читается тем же образом, как и это число. Так, если у нас есть дробь 56,002, которой соответствует 5621000, мы читаем такую запись как «пятьдесят шесть целых две тысячных».

Что такое разряды в десятичных дробях

Значение цифры в записи десятичной дроби зависит от того, на каком месте она расположена (так же, как и в случае с натуральными числами). Так, в десятичной дроби 0,7 семерка – это десятые доли, в 0,0007 – десятитысячные, а в дроби 70 000,345 она означает семь десятков тысяч целых единиц. Таким образом, в десятичных дробях тоже существует понятие разряда числа.

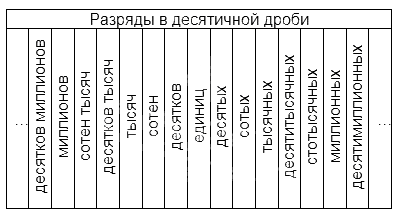
Названия разрядов, расположенных до запятой, аналогичны тем, что существуют в натуральных числах. Названия тех, что расположены после, наглядно представлены в таблице:

Разберем пример.

У нас есть десятичная дробь 43,098. У нее в разряде десятков находится четверка, в разряде единиц тройка, в разряде десятых – ноль, сотых – 9, тысячных – 8.

Принято различать разряды десятичных дробей по старшинству. Если мы движемся по цифрам слева направо, то мы будем идти от старших разрядов к младшим. Получается, что сотни старше десятков, а миллионные доли младше, чем сотые. Если взять ту конечную десятичную дробь, которую мы приводили в качестве примера выше, то в ней старшим, или высшим будет разряд сотен, а младшим, или низшим – разряд 10-тысячных.

Любую десятичную дробь можно разложить по отдельным разрядам, то есть представить в виде суммы. Это действие выполняется так же, как и для натуральных чисел.

Если мы вспомним свойства сложения, то сможем представить эту дробь и в других видах, например, как сумму 56+0,0455, или 56,0055+0,4 и др.

Что такое конечные десятичные дроби

Все дроби, о которых мы говорили выше, являются конечными десятичными дробями. Это означает, что количество цифр, расположенное у них после запятой, является конечным. Выведем определение:

Конечные десятичные дроби представляют собой вид десятичных дробей, у которых после знака запятой стоит конечное число знаков.

Примерами таких дробей могут быть 0,367, 3,7, 55,102567958, 231 032,49 и др.

Любую из этих дробей можно перевести либо в смешанное число (если значение их дробной части отличается от нуля), либо в обыкновенную дробь (при нулевой целой части). Тому, как это делается, мы посвятили отдельный материал. Здесь просто укажем пару примеров: так, конечную десятичную дробь 5,63 мы можем привести к виду 563100, а 0,2 соответствует 210 (или любая другая равная ей дробь, например, 420 или 15.)

Но обратный процесс, т.е. запись обыкновенной дроби в десятичном виде, может быть выполнен не всегда. Так, 513 нельзя заменить на равную дробь с знаменателем 100, 10 и др., значит, конечная десятичная дробь из нее не получится.

Основные виды бесконечных десятичных дробей: периодические и непериодические дроби

Мы указывали выше, что конечные дроби называются так потому, что после запятой у них стоит конечное число цифр. Однако оно вполне может быть и бесконечным, и в этом случае сами дроби также будут называться бесконечными.

Бесконечными десятичными дробями называются такие, у которых после запятой стоит бесконечное количество цифр.

Очевидно, что полностью такие числа записаны быть просто не могут, поэтому мы указываем лишь часть из них и дальше ставим многоточие. Это знак говорит о бесконечном продолжении последовательности знаков после запятой. Примерами бесконечных десятичных дробей могут быть 0,143346732…, 3,1415989032…, 153,0245005…, 2,66666666666…, 69,748768152…. и т.д.

В «хвосте» такой дроби могут стоять не только случайные на первый взгляд последовательности цифр, но постоянное повторение одного и того же знака или группы знаков. Дроби с чередованием после десятичной запятой называются периодическими.

Периодическими десятичными дробями называются такие бесконечные десятичные дроби, у которых после запятой повторяется одна цифра или группа из нескольких цифр. Повторяющаяся часть называется периодом дроби.

К примеру, для дроби 3,444444…. периодом будет цифра 4, а для 76, 134134134134… – группа 134.

Какое же минимальное количество знаков допустимо оставить в записи периодической дроби? Для периодических дробей достаточно будет записать весь период один раз в круглых скобках. Так, дробь 3,444444…. правильно будет записать как 3,(4), а 76, 134134134134…– как 76,(134).

В целом записи с несколькими периодами в скобках будут иметь точно такой же смысл: к примеру, периодическая дробь 0,677777 – это то же самое, что 0,6(7) и 0,6(77) и т.д. Также допустимы записи вида 0,67777(7), 0,67(7777) и др.

Во избежание ошибок введем однообразие обозначений. Условимся записывать только один период (максимально короткую последовательность цифр), который стоит ближе всего к десятичной запятой, и заключать его в круглые скобки.

То есть для указанной выше дроби основной будем считать запись 0,6(7), а, например, в случае с дробью 8,9134343434 будем писать 8,91(34).

Если знаменатель обыкновенной дроби содержит простые множители, не равные 5 и 2, то при переводе в десятичную запись из них получатся бесконечные дроби.

В принципе, любую конечную дробь мы можем записать в виде периодической. Для этого нам просто нужно добавить справа бесконечно много нулей. Как это выглядит в записи? Допустим, у нас есть конечная дробь 45,32. В периодическом виде она будет выглядеть как 45,32(0). Это действие возможно потому, что добавление нулей справа в любую десятичную дробь дает нам в результате равную ей дробь.

Отдельно следует остановиться на периодических дробях с периодом 9, например, 4,89 (9), 31,6(9). Они являются альтернативной записью схожих дробей с периодом 0, поэтому их часто заменяют при письме именно дробями с нулевым периодом. При этом к значению следующего разряда добавляют единицу, а в круглых скобках указывают (0). Равенство получившихся чисел легко проверить, представив их в виде обыкновенных дробей.

К примеру, дробь 8,31(9) можно заменить на соответствующую ей дробь 8,32(0). Или 4,(9)=5,(0)=5.

Бесконечные десятичные периодические дроби относятся к рациональным числам. Иначе говоря, любую периодическую дробь можно представить в виде обыкновенной, и наоборот.

Существуют и дроби, у которых после запятой бесконечно повторяющаяся последовательность отсутствует. В таком случае их называют непериодическими дробями.

К непериодическим десятичным дробям относятся те бесконечные десятичные дроби, в которых после запятой не содержится периода, т.е. повторяющейся группы цифр.

Иногда непериодические дроби выглядят очень похожими на периодические. Например, 9,03003000300003… на первый взгляд кажется имеющей период, однако подробный анализ знаков после запятой подтверждает, что это все же непериодическая дробь. С такими числами надо быть очень внимательным.

Непериодические дроби относятся к иррациональным числам. В обыкновенные дроби их не переводят.

Основные действия с десятичными дробями

С десятичными дробями можно производить следующие действия: сравнение, вычитание, сложение, деление и умножение. Разберем каждое из них отдельно.

Сравнение десятичных дробей может быть сведено к сравнению обыкновенных дробей, которые соответствуют исходным десятичным. Но бесконечные непериодические дроби свести к такому виду нельзя, а перевод десятичных дробей в обыкновенные зачастую является трудоемкой задачей. Как же быстро произвести действие сравнения, если нам нужно сделать это по ходу решения задачи? Удобно сравнивать десятичные дроби по разрядам таким же образом, как мы сравниваем натуральные числа. Этому методу мы посвятим отдельную статью.

Чтобы складывать одни десятичные дроби с другими, удобно использовать метод сложения столбиком, как для натуральных чисел. Чтобы складывать периодические десятичные дроби, необходимо предварительно заменить их обыкновенными и считать по стандартной схеме. Если же по условиям задачи нам надо сложить бесконечные непериодические дроби, то нужно перед этим округлить их до некоторого разряда, а потом уже складывать. Чем меньше разряд, до которого мы округляем, тем выше будет точность вычисления. Для вычитания, умножения и деления бесконечных дробей предварительное округление также необходимо.

Нахождение разности десятичных дробей обратно действию сложения. По сути, с помощью вычитания мы можем найти такое число, сумма которого с вычитаемой дробью даст нам уменьшаемую. Подробнее об этом расскажем в рамках отдельного материала.

Умножение десятичных дробей производится так же, как и для натуральных чисел. Для этого тоже подходит метод вычисления столбиком. Это действие с периодическими дробями мы опять же сводим к умножению обыкновенных дробей по уже изученным правилам. Бесконечные дроби, как мы помним, надо округлить перед подсчетами.

Процесс деления десятичных дробей является обратным процессу умножения. При решении задач мы также пользуемся подсчетами в столбик.

Положение десятичных дробей на оси координат

Можно установить точное соответствие между конечной десятичной дробью и точкой на оси координат. Выясним, как отметить точку на оси, которая будет точно соответствовать необходимой десятичной дроби.

Мы уже изучали, как построить точки, соответствующие обыкновенным дробям, а ведь десятичные дроби можно привести к такому виду. Например, обыкновенная дробь 1410 – это то же самое, что и 1,4, поэтому соответствующая ей точка будет удалена от начала отсчета в положительном направлении ровно на такое же расстояние:

Можно обойтись без замены десятичной дроби на обыкновенную, а взять на основу метод разложения по разрядам. Так, если нам надо отметить точку, координата которой будет равна 15,4008, то мы предварительно представим это число в виде суммы 15+0,4+,0008. Для начала отложим от начала отсчета 15 целых единичных отрезков в положительном направлении, потом 4 десятых доли одного отрезка, а потом 8 десятитысячных долей одного отрезка. В итоге мы получим точку координат, которой соответствует дробь 15,4008.

Для бесконечной десятичной дроби лучше пользоваться именно этим способом, поскольку он позволяет приблизиться к нужной точке сколь угодно близко. В некоторых случаях можно построить и точное соответствие бесконечной дроби на оси координат: так, 2=1,41421…, и с этой дробью может быть соотнесена точка на координатном луче, удаленная от 0 на длину диагонали квадрата, сторона которого будет равна одному единичному отрезку.

Если мы находим не точку на оси, а десятичную дробь, соответствующую ей, то это действие называется десятичным измерением отрезка. Посмотрим, как правильно это сделать.

Допустим, нам нужно попасть от нуля в заданную точку на оси координат (или максимально приблизиться в случае с бесконечной дробью). Для этого мы постепенно откладываем единичные отрезки от начала координат, пока не попадем в нужную точку. После целых отрезков при необходимости отмеряем десятые, сотые и более мелкие доли, чтобы соответствие было максимально точным. В итоге мы получили десятичную дробь, которая соответствует заданной точке на оси координат.

Выше мы приводили рисунок с точкой M. Посмотрите на него еще раз: чтобы попасть в эту точку, нужно отмерить от нуля один единичный отрезок и четыре десятых доли от его, поскольку этой точке соответствует десятичная дробь 1,4.

Если мы не можем попасть в точку в процессе десятичного измерения, то значит, что ей соответствует бесконечная десятичная дробь.

Бесконечные периодические и непериодические десятичные дроби

Содержание

Бесконечные периодические и непериодические десятичные дроби

В десятичной записи конечной десятичной дроби после запятой стоит конечное число десятичных знаков.

В десятичной записи бесконечной десятичной дроби после запятой стоит бесконечное число десятичных знаков.

Бесконечные десятичные дроби бывают периодическими и непериодическими.

Бесконечной периодической десятичной дробью называют такую дробь, десятичные знаки которой, начиная с некоторого, представляют собой повторение одной и той же группы цифр, состоящей или из одной цифры, отличной от   0   и   9 ,   или из нескольких цифр, причем последовательность цифр при повторении в этой группе не изменяется.

Повторяющаяся группа цифр называется периодом бесконечной периодической десятичной дроби.

Для обозначения периода десятичной дроби используют круглые скобки.

Например,

2,616161… = 2,(61) ;      
53222222… = 5,3(2) .      

ЗАМЕЧАНИЕ. Еще раз подчеркнем, что период бесконечной десятичной дроби не может состоять из одной или нескольких цифр   0   и не может состоять из одной или нескольких цифр   9 . 

Бесконечная десятичная дробь, не являющаяся периодической, называется непериодической.

Алгоритм обращения бесконечной периодической десятичной дроби в простую дробь

Разберем алгоритм обращения бесконечной периодической десятичной дроби в простую дробь на примере решений следующих задач.

ЗАДАЧА 1. Обратить периодическую дробь

0,(45)

в простую дробь.

РЕШЕНИЕ. Если ввести обозначение

x = 0,(45) = 0,4545… ,

то, умножив это соотношение на   100 ,   получим:

100x = 45,4545… .

При этом

100x – x = 99 x =
= 45,0000… = 45.

Следовательно,

ОТВЕТ:       .

ЗАДАЧА 2. Обратить периодическую дробь

6,2(7)

в простую дробь.

РЕШЕНИЕ. Если ввести обозначение

x = 6,2(7) = 6,2777… ,

то, умножив это соотношение на   10 , получим:

10x = 62,7777… .

При этом

10x – x = 9x =
= 62,7777… – 6,2777… =
= 56,5.

Следовательно,

      ОТВЕТ:       .

Бесконечные десятичные дроби

Десятичные дроби после запятой могут содержать бесконечное количество цифр.

Бесконечные десятичные дроби — это десятичные дроби, в записи которых находится бесконечное число цифр.

Бесконечную десятичную дробь практически невозможно записать полностью, поэтому при их записи ограничиваются только некоторым конечным количеством цифр после запятой, после чего ставят многоточие, которое указывает на бесконечно продолжающуюся последовательность цифр.

Рассмотрим последние две бесконечные десятичные дроби. В дроби $4,33333333333dots$ бесконечно повторяется цифра $3$, а в дроби $676,68349349dots$ с третьего знака после запятой повторяется группа цифр $3$, $4$ и $9$. Подобные бесконечные десятичные дроби называются периодическими.

Онлайн-репетитор для вашего ребенка

Подтянем знания школьной программы, подготовим к ЕГЭ и ОГЭ по индивидуальному плану

Выбрать программу

Периодические десятичные дроби

Периодические десятичные дроби (или периодические дроби) — это бесконечные десятичные дроби, в записи которых с некоторого знака после запятой бесконечно повторяется какая-нибудь цифра или их группа, которая называется периодом дроби}.

Для краткости записи бесконечных периодических десятичных дробей принято период записывать один раз, заключив его в круглые скобки. Например, периодическую дробь $4,33333333333dots$ записывают $4,(3)$, а периодическую дробь $676,68349349dots$ записывают $676,68(349)$.

Бесконечные десятичные периодические дроби получают при переводе обыкновенных дробей, знаменатели которых содержат простые множители, кроме $2$ и $5$, в десятичные дроби.

Любая конечная десятичная дробь (и целое число) может быть записана в виде периодической дроби, для чего достаточно справа дописать бесконечное количество цифр $0$.

«Периодические десятичные дроби» 👇

В случае периодических дробей, которые имеют период 9, используют переход к другой записи периодической дроби с периодом $0$. Только для этого период 9заменяют периодом $0$, при этом значение следующего по старшинству разряда увеличивается на $1$.

Бесконечные десятичные периодические дроби представляются рациональными числами. Другими словами, любая периодическая дробь может быть переведена в обыкновенную дробь, а любая обыкновенная дробь может быть представлена в виде периодической дроби.

Перевод обыкновенных дробей в конечные и бесконечные периодические десятичные дроби

В десятичную дробь можно перевести не только обыкновенные дроби со знаменателями $10, 100, dots$.

В некоторых случаях исходную обыкновенную дробь можно легко привести к знаменателю $10$, $100$ или $1 000$, после чего можно полученную дробь представить в виде десятичной дроби.

Для остальных случаев используется другой способ перевода обыкновенной дроби в десятичную}:

• числитель нужно заменить десятичной дробью с любым числом нулей после десятичной запятой;

• разделить числитель дроби на знаменатель (деление выполняется как деление натуральных чисел в столбик, а в частном ставят десятичную запятую после окончания деления целой части делимого).

Возможен случай, когда при делении числителя и знаменателя обыкновенной дроби в остатке $0$ так и не получается. В этом случае деление можно продолжать бесконечно. Начиная с определенного момента остатки от деления периодически повторяются, а значит повторяются и цифры в частном. Из этого можно сделать вывод, что данная обыкновенная дробь переведется в бесконечную периодическую десятичную дробь.

Общий вывод о переводе обыкновенных дробей в десятичные:

• если знаменатель можно разложить на простые множители, среди которых будут присутствовать только числа $2$ и $5$, то такую дробь можно перевести в конечную десятичную дробь;

• если кроме чисел $2$ и $5$ в разложении знаменателя присутствуют другие простые числа, то такая дробь переводится в бесконечную десятичную периодическую дробь.

Бесконечные периодические десятичные дроби – это дроби, у которых одна цифра или группа цифр повторяются.
Примеры: 0,66666666666666…; 0,33333333333333…; 0,68181818181818…

Повторяющаяся группа цифр называется периодом и записывается в скобках.
Примеры: 0,(6); 0,(3); 0,6(81).

Получить периодическую дробь можно тогда, когда при делении числителя на знаменатель получаются повторяющиеся остатки. Именно повторяющиеся остатки делают процесс деления бесконечным, что приводит к появлению бесконечной периодической дроби.

Пример 1.  Разделить 1 на 3: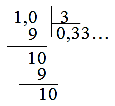
При делении мы постоянно получаем остаток 1, затем приписываем к нему 0 и делим 10 на 3. Эта операция повторяется снова и снова. В результате мы каждый раз получаем повторяющиеся остатки. Поэтому деление 1 на 3 будет выполняться бесконечно. В результате этого образуется бесконечная десятичная дробь.

• Записывается. Обычно бесконечные периодические дроби записывают сокращенно: сначала записывают целую часть, затем ставят запятую и в скобках указывают период (цифру, которая повторяется).
• Читается. Бесконечные периодические дроби читаются так:  «ноль целых и три в периоде»

Пример 2.  Разделить 5 на 11:
При делении мы постоянно получаем остаток 5 или 6. Затем приписываем к остатку 0 и делим 50 или 60 на 11. В результате мы получаем повторяющиеся остатки, поэтому деление 5 на 11 будет выполняться бесконечно. 

• Записывается: 0,(45).
• Читается:  «ноль целых и сорок пять в периоде»

Виды периодических дробей

Периодические дроби бывают двух видов: чистые и смешанные.

• Чистые — дроби, у которых период начинается сразу после запятой.
  Примеры: 0,(3); 0,(5); 0,(6).
• Смешанные — дроби, у которых период начинается после некоторого количества не повторяющихся цифр.
  Примеры: 0,52(3); 0,16(5); 0,31(6)

Чтобы  записать периодическую дробь в виде десятичной дроби, нужно округлить эту дробь до нужного разряда. Как округлять, можно прочитать в статье «Правила округления чисел«

Примеры округления:
Округлить 0,(3) до сотых. Получаем 0,333333…≈ 0,33.
Округлить 6,31(6) до тысячных. Получаем 6,31666666… ≈ 6,317

Перевод периодической дроби в обыкновенную

✅  Для чистой периодической дроби

Чтобы перевести чистую периодическую дробь в обыкновенную дробь, нужно
➤  в числитель обыкновенной дроби записать период периодической дроби, 
➤  в знаменатель обыкновенной дроби записать некоторое количество девяток, при этом, количество девяток должно быть равно количеству цифр в периоде периодической дроби.

Пример 1: перевести 0,(3) в обыкновенную дробь.
В периодической дроби 0,(3) период состоит из одной цифры 3, поэтому в числителе записываем одну тройку, а в знаменателе — одну девятку.  Полученную дробь  можно сократить на 3, тогда получим обыкновенную дробь 1/3.

Пример 2. Перевести  0,(45) в обыкновенную дробь.
В периодической дроби 0,(45) период состоит из двух цифр, поэтому в числителе записываем 45, а в знаменателе — 99.  Полученную дробь  можно сократить на 9, тогда получим обыкновенную дробь 5/11.

✅  Для смешанной периодической дроби

 Чтобы перевести смешанную периодическую дробь в обыкновенную дробь, нужно

• в числителе записать разность:
  • уменьшаемое — все цифры, стоящие после запятой, в том числе в периоде,
  • вычитаемое — цифры, стоящие между запятой и первым периодом периодической дроби.
• в знаменателе записать некоторое количество девяток и нулей.
  • количество девяток должно быть равно количеству цифр в периоде периодической дроби,
  • количество нулей должно быть равно количеству цифр между запятой и периодом периодической дроби.

Пример 3: перевести 0,31(6) в обыкновенную дробь.
➤  В числителе запишем разность разность:
уменьшаемое —  все цифры, стоящие после запятой, включая и период = 316
вычитаемое — цифры, стоящие между запятой и периодом = 31
получаем числитель = (316-31).
➤  В знаменателе запишем некоторое количество девяток и нулей.
количество девяток равно количеству цифр в периоде периодической дроби 0,31(6) — одна девятка
количество нулей равно количеству цифр между запятой и периодом — два нуля.
получаем знаменатель = 900. Получили дробь, которую можно сократить.

316-31 900

=

285 900

=

285:15 900:15

=

19 60

Пример 4. перевести 0,72(62) в обыкновенную дробь.
➤  В числителе: уменьшаемое = 7262, вычитаемое = 72, получаем числитель = (7262-72).
➤  В знаменателе:  2 цифры в периоде (99), две цифры между запятой и периодом (00), получаем 9900.
Получили дробь, которую можно сократить.

7262-72 9900

=

7190 9900

=

7190:10 9900:10

=

719 990

При переводе обыкновенной дроби в десятичную можно получить конечную периодическую или бесконечную десятичные дроби (кроме простой десятичной, разумеется).

Конечная десятичная дробь

Конечная десятичная дробь – десятичная дробь с конечным числом знаков после запятой, то есть когда у аналога обыкновенной дроби числитель без остатка делится на знаменатель.

Пример №1. ¾ – делим 3 на 4 и получаем 0,75.

Пример №2. ³¹/₅₀  делим 31 на 50 и получаем 0,62.

Пример №3. ³/₂₅ делим 3 на 25 и получаем 0,12.

Периодическая десятичная дробь

Периодическая десятичная дробь – дробь, у которой после запятой (в дробной части) присутствует бесконечный повтор одной цифры или сочетания нескольких одинаковых цифр.

Пример №4. ⁷/₁₂ При делении 7 на 12 получается 0,5833333…, где постоянно повторяется цифра 3, запись делают следующим образом: 0,58(3); читается эта дробь следующим образом: нуль целых пятьдесят восемь сотых и три в периоде.

Пример №5. ¹/₁₁ При делении 1 на 11 получается 0,090909… и так до бесконечности повторяются цифры 0 и 9. Данную дробь записывают в виде 0,(09) и читают как нуль целых и нуль десять в периоде.

Иррациональные числа

 Иррациональные числа – числа, которые не могут быть представлены в виде обыкновенной дроби.

В школьной программе такие числа встречаются чаще всего в виде так называемых “неизвлекаемых корней”, чисел  π, e , а в 10-11 классах и логарифмов (так как они связаны со степенями).

Пример №6. √15=3,8729833….

Пример №7. π = 3,1415926535…

Задание OM0805o

Значение какого из выражений является рациональным числом?

1. √6-3
2. √3•√5
3. (√5)²
4. (√6-3)²

---

В данном задании у нас проверяют навыки операций с иррациональными числами.

Разберем каждый вариант ответа в решении:

1) √6-3

√6 само по себе является иррациональным числом, для решения подобных задач достаточно помнить, что рационально извлечь корень можно из квадратов натуральных чисел, например, 4, 9, 16, 25…

При вычитании из иррационального числа любого другого, кроме его же самого, приведет вновь к иррациональному числу, таким образом, в этом варианте получается иррациональное число.

2) √3•√5

При умножении корней, мы можем извлечь корень из произведения подкоренных выражений, то есть:

√3•√5 = √(3•5) = √15

Но √15 является иррациональным, поэтому данный вариант ответа не подходит.

3) (√5)²

При возведении квадратного корня в квадрат, мы получаем просто подкоренное выражение (если уж быть точнее, то подкоренное выражение по модулю, но в случае числа, как в данном варианте, это не имеет значения), поэтому:

(√5)² = 5

Данный вариант ответа нам подходит.

4) (√6-3)²

Данное выражение представляет продолжение 1 пункта, но если √6-3 иррациональное число, то никакими известными нам операциями перевести в рациональное его нельзя.

Ответ: 3

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM0803o

Какое из данных чисел является рациональным?

1. √810
2. √8,1
3. √0,81
4. все эти числа иррациональны

---

Для решения этой задачи нужно действовать следующим образом:

Сначала разберемся, степень какого числа рассмотрена в данном примере — это число 9, так как его квадрат 81, и это уже чем-то похоже на выражения в ответах. Далее рассмотрим формы числа 9 — это могут быть:

0,9

90

Рассмотри каждое из них:

0,9 = √(0,9)² = √0,81

90 = √(90²) = √8100

Следовательно, число √0,81 является рациональным, остальные же числа

• √810
• √8,1

хотя и похожи на форму 9 в квадрате, не являются рациональными.

Таким образом, правильный ответ третий.

Ответ: √0,81

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM0802o

Значение какого из данных ниже выражений является наибольшим?

1. 3√5
2. 2√11
3. 2√10
4. 6,5

---

Для решения данного задания нужно привести все выражения к общему виду — представить выражения в виде подкоренных выражений:

• 3√5

Переносим 3 под корень:

3√5 =  √(3² •5) = √(9•5) =  √45

• 2√11

Переносим 2 под корень:

2√11 = √(2² • 11) = √(4 • 11) =√44

• 2√10

Переносим 2 под корень:

2√10 = √(2² • 10) = √(4 • 10) =√40

• 6,5

Возводим 6,5 в квадрат:

6,5 = √(6,5²) = √42,25

Посмотрим на все получившиеся варианты:

1. 3√5 =  √45
2. 2√11 = √44
3. 2√10 = √40
4. 6,5 = √42,25

Следовательно, правильный ответ первый.

Ответ: 3√5

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM0702o

Какое из данных чисел принадлежит промежутку [ 6 ; 7 ] ?

1. √6
2. √7
3. √38
4. √50

---

Для решения этого задания достаточно представлять себе значения чисел меньше и больше заданного, корни которых подлежат вычислению.

• Рассмотрим √6. √4 — это 2, √9 — это 3, значит √6 лежит в промежутке между 2 и 3
• Рассмотрим √7. Ситуация аналогична √6. √4 — это 2, √9 — это 3, значит √6 лежит в промежутке между 2 и 3
• Рассмотрим √38. Ближайшее вычисляемое число меньше 38 — 36, √36 = 6, ближайшее вычисляемое число больше 38 — 49, √49 = 7, значит √38 лежит между 6 и 7
• Рассмотрим √50. Ближайшее вычисляемое число меньше 50 — 49, √49 = 7, ближайшее вычисляемое число больше 50 — 64, √64 = 8, значит √50 лежит между 7 и 8

Значит, нам подходит третий вариант ответа —  √38.

Ответ: √38

pазбирался: Даниил Романович | обсудить разбор | оценить

Алла Василевская | Просмотров: 4.4k

Обновлено: 03.03.2023

В данной публикации мы рассмотрим, что из себя представляют бесконечные периодические десятичные дроби, какие бывают виды, и как их можно перевести в обыкновенную дробь. Также разберем примеры для закрепления материала.

Периодические десятичные дроби

Определение

Если в дробной части бесконечной десятичной дроби есть один или несколько цифр, которые повторяются в одной и той же последовательности, такая дробь является периодической.

Примеры периодических десятичных дробей:

Запись

Повторяющаяся цифра/цифры – это период дроби, который пишется в скобке для сокращения длины записи. Например, дроби выше сокращенно следует писать так:

Произношение

• 0,17 (3) – ноль целых, семнадцать сотых и три в периоде;

Чистые периодические дроби – это такие бесконечные десятичные дроби, период которых начинается сразу после запятой.

Смешанные периодические дроби – бесконечные десятичные дроби, у которых между запятой и периодом присутствует одна и более цифр (их количество ограничено).

Перевод периодической десятичной дроби в обыкновенную

Для того, чтобы перевести периодическую дробь в обыкновенную (простую), выполняем следующие шаги:

1. Считаем количество цифр, содержащихся в периоде дроби. Даем ей буквенное обозначение, например, n .

2. Считаем количество цифр в дробной части между запятой и периодом. Пусть это будет буква m .

3. Составляем из дробной части, в т.ч. из периода, обычное натуральное число. Дадим ему названием a . При этом если первая цифра после запятой – это ноль, его не учитываем.

4. Составляем еще одно число из цифр после запятой, но до периода. Пусть это будет b . Ноль в начале, если он есть, также убираем.

5. Целую часть десятичной дроби примем за x .

6. Итак, обыкновенная дробь y , которую требуется найти, вычисляется по формуле:

Пример 1

Действовать будет пошагово согласно инструкции выше:
1. n = 1
2. m = 1
3. a = 83
4. b = 8
5. x = 0
6. Остается только применить формулу:

Пример 2

Представим периодическую дробь 2,64(378) в виде обыкновенной.

1. n = 3
2. m = 2
3. a = 64378
4. b = 64
5. x = 2
6. Подставляем эти значения в формулу нахождения простой дроби и получаем:

Бесконечная периодическая десятичная дробь – это дробь, у которой одна цифра или группа цифр повторяются. Повторяющаяся группа цифр называется периодом и записывается в скобках.

Любое рациональное число p/q можно разложить в периодическую десятичную дробь.

Любая периодическая дробь есть десятичное разложение некоторого рационального числа.

Список литературы

Обязательная литература:

1. Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017, стр. 258.

Дополнительная литература:

1. Чулков П. В. Математика: тематические тесты.5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина – М.: Просвещение, 2009, стр. 142.

2. Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин – М.: Просвещение, 2014, стр. 95.

Теоретический материал для самостоятельного изучения

Обыкновенную дробь можно разложить в конечную десятичную, если в знаменателе нет простых множителей, кроме 2 и 5.

Вы уже знаете, как это сделать.

1. Умножить числитель и знаменатель на одно и то же число, чтобы привести к знаменателю 10, 100, 1000 и т. д.;

2. Выполнить деление числителя на знаменатель.

Пример 1. Умножили числитель и знаменатель на 2.

Пример 2. Сначала сократили дробь.

Пример 3. Выполнили деление 3 на 125.

Рассмотрим примеры, когда привести к знаменателю 10, 100 и т. д. нельзя. Возможно только деление числителя на знаменатель.

Заметим, что при делении получаются повторяющиеся остатки и, соответственно, повторяющиеся цифры в частном. Из-за этого процесс деления бесконечен. Отсюда происходит бесконечная десятичная дробь.

Рассмотрим другие примеры.

Повторяющиеся цифры 3; 27; 6 называют периодом дроби. Бесконечные десятичные дроби 0,333…; 0,2727…; 0,1666… называют периодическими.

Периодическая дробь – это бесконечная десятичная дробь, у которой, начиная с некоторого десятичного знака, повторяется одна и та же цифра или несколько цифр (период дроби).

Отметим, что любое рациональное число p/q разлагается в периодическую десятичную дробь.

Любая периодическая дробь есть десятичное разложение некоторого рационального числа.

Замечание. При делении уголком десятичное разложение с периодом 9 не возникает.

Далее рассмотрим, как выполняются действия с периодическими дробями?

1. Сравните дроби

Запишем дробь 1/3 в виде бесконечной периодической дроби 0,333…

Запишем дробь 0,3 в следующем виде 0,300… Приписывая бесконечно много нулей, мы превращаем конечную дробь в равную ей бесконечную периодическую дробь с периодом 0.

Теперь можем сравнить: 0,333… > 0,300…

2. Разложите обыкновенную дробь в бесконечную периодическую десятичную дробь, округлите до десятых.

Разбор заданий тренировочного модуля

Представьте в виде периодической дроби. В ответе укажите её период.

Используя предыдущие задания, запишите периодическую дробь в виде обыкновенной дроби: 0,(3); 0,(5); 0,(6).

Оказывается, научиться работать с дробями полезно не только для школы, но и чтобы написать музыкальный трек или сверстать сайт. В этой статье разбираемся с теорией и учимся выполнять основные действия с дробями.

О чем эта статья:

5 класс, 6 класс

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Понятие десятичной дроби

Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.

Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи:

• обыкновенный вид — ½ или a/b,
• десятичный вид — 0,5.

В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.

В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:

Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.

Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.

Свойства десятичных дробей

Главное свойство десятичной дроби звучит так: если к десятичной дроби справа приписать один или несколько нулей — ее величина не изменится. Это значит, что если в вашей дроби куча нулей — их можно просто отбросить. Например:

• 0,600 = 0,6
• 21,10200000 = 21,102

1. Дробь не имеет значения, при условии, если делитель равен нулю.
2. Дробь равна нулю, если числитель равен нулю, а знаменатель — нет.
3. Две дроби a/b и c/d называются равными, если a * d = b * c.
4. Если числитель и знаменатель умножить или разделить на одно и то же натуральное число, то получится равная ей дробь

Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:

• Целая часть десятичной дроби равна целой части смешанной дроби. Если числитель меньше знаменателя, то целая часть равна нулю.
• Дробная часть десятичной дроби содержит те же цифры, что и числитель этой же дроби в обыкновенном виде.
• Количество цифр после запятой зависит от количества нулей в знаменателе обыкновенной дроби. То есть 1 цифра — делитель 10, 4 цифры — делитель 10000.

Обучение на курсах по математике — отличный способ закрепить полученные знания на практике и подтянуть сложные темы.

Как записать десятичную дробь

Давайте разберем на примерах, как записывается десятичная дробь. Небольшая напоминалка: сначала пишем целую часть, ставим запятую и после записываем числитель дробной части.

Пример 1. Перевести обыкновенную дробь 16/10 в десятичную.

1. Знаменатель равен 10 — это один ноль.
2. Отсчитываем справа налево в числителе дробной части один знак и ставим запятую.
3. В полученной десятичной дроби цифра 1 — целая часть, цифра 6 — дробная часть.

Пример 2. Перевести 37/1000 в десятичную дробь.

1. Знаменатель равен 1000 — это три нуля.
2. Отсчитываем справа налево в числителе дробной части три знака и ставим запятую.
3. Так как в числителе только две цифры, то на пустующие места пишем нули.
4. В полученной десятичной дроби цифра 0 — целая часть, 037 — дробная часть.

Ответ: 37/1000 = 0,037.

Как читать десятичную дробь

Сколько цифр после запятой?	Читается, как
одна цифра — десятых;	1,3 — одна целая, три десятых;
две цифры — сотых	2,22 — две целых, двадцать две сотых;
три цифры — тысячных;	23,885 — двадцать три целых, восемьсот восемьдесят пять тысячных;
четыре цифры — десятитысячных;	0,5712 — ноль целых пять тысяч семьсот двенадцать десятитысячных;
и т.д.

Сохраняй наглядную картинку, чтобы быстрее запомнить.

Преобразование десятичных дробей

Чтобы ни одна задача не смутила вас своей формулировкой, важно знать, как преобразовывать десятичные дроби в другие виды. Сейчас научимся!

Как перевести десятичную дробь в проценты

Уже в пятом классе задачки по математике намекают, что дроби как-то связаны с процентами. И это правда: процент — это одна сотая часть от любого числа, обозначают его значком %.

Чтобы узнать, как перевести проценты в дробь, нужно убрать знак % и разделить наше число на 100, как в примере выше.

А чтобы перевести десятичную дробь в проценты — умножаем дробь на 100 и добавляем знак %. Давайте на примере:

0,15 = 0,15 · 100% = 15%.

Выразить дробь в процентах просто: сначала превратим её в десятичную дробь, а потом применим предыдущее правило.

2/5 = 0,4
0,4 · 100% = 40%

8/25 = 0,32
0,32 · 100% = 32%

Чтобы разрезать торт на равные кусочки и не обижать гостей, нужно всего-то запомнить соотношения частей и целого. Наглядная табличка — наш друг-помощник:

Преобразование десятичных дробей

Десятичная дробь — это число с остатком, где остаток стоит после целой части и разделяется запятой.

Смешанная дробь — это тоже число с остатком, но остаток записывают в виде простой дроби (с черточкой).

Чтобы переводить десятичные дроби в смешанные, не нужно запоминать особые алгоритмы. Достаточно понимать определения и правильно читать заданную дробь — этим школьники и занимаются в 5 классе. А теперь давайте потренируемся!

Пример 1. Перевести 5,4 в смешанное число.

Пример 2. Перевести 4,005 в смешанное число.

1. Читаем вслух: четыре целых пять тысячных. Значит 5 — идет в числитель, а 1000 — в знаменатель. В смешанном виде получается так: 4 5/1000. После сокращения: 4 1/200.

Ответ: 4,005 = 4 1/200.

Пример 3. Перевести 5,60 в смешанное число.

1. Читаем вслух: пять целых шестьдесят сотых. Отправляем 60 в числитель, а 100 — в знаменатель. В смешанном виде дробь такая: 5 60/100.
2. Сократим дробную часть на 10 и получим 5 6/10. Или можно вспомнить про свойство десятичной дроби и просто отбросить нули в числителе и знаменателе.

Ответ: 5,60 = 5 6/10.

Как перевести десятичную дробь в обыкновенную

Не будем придумывать велосипед и рассмотрим самый простой способ превращения десятичной дроби в обыкновенную. Вот, как это сделать:

1. Перепишем исходную дробь в новый вид: в числитель поставим исходную десятичную дробь, а в знаменатель — единицу. Например:
   • 0,35 = 0,35/1
   • 2,34 = 2,34/1
2. Умножим числитель и знаменатель на 10 столько раз, чтобы в числителе исчезла запятая. При этом после каждого умножения запятая в числителе сдвигается вправо на один знак, а у знаменателя соответственно добавляются нули. На примере легче:
   • 0,35 = 0,35/1 = 3,5/10 = 35/100
   • 2,34 = 2,34/1 = 23,4/10 = 234/100
3. А теперь сокращаем — то есть делим числитель и знаменатель на кратные им числа:
   • 0,35 = 35/100, делим числитель и знаменатель на пять, получаем 6/20, еще раз делим на 2, получаем итоговый ответ 3/10.
   • 2,34 = 234/100 = 117/50 = 2 17/50.

Не забывайте про минус в ответе, если пример был про отрицательное число. Очень обидная ошибка!

Действия с десятичными дробями

С десятичными дробями можно производить те же действия, что и с любыми другими числами. Рассмотрим самые распространенные на простых примерах.

Как разделить десятичную дробь на натуральное число

1. Разделить целую часть десятичной дроби на это число.
2. Поставить запятую в частном и продолжить вычисление, как при обычном делении.

Ответ: 4,8 : 2 = 2,4.

Пример 2. Разделить 183,06 на 45.

1. Записать деление уголком.
2. Разделить целую часть 183 на 45. Записать результат, поставить запятую в частном.
3. Записать результат разницы 183 и 180. Снести 0. Записать 0 в частное, чтобы снести 6.
4. Записать результат разницы 306 и 270. 36 не делится на 45, поэтому добавляем ноль и производим разницу.

Ответ: 183,06 : 45 = 4,068.

Как разделить десятичную дробь на обыкновенную

Чтобы разделить десятичную дробь на обыкновенную или смешанную, нужно представить десятичную дробь в виде обыкновенной, а смешанное число записать, как неправильную дробь.

Пример 1. Разделить 0,25 на 3/4.

Ответ: 0,25 : 3/4 = 1/3.

Пример 2. Разделить 2,55 на 1 1/3.

Ответ: 2,55 : 1 1/3 = 1 73/80.

Как умножить десятичную дробь на обыкновенную

Чтобы умножить десятичную дробь на обыкновенную или смешанную, используют два правила за 6 класс. При первом приводим десятичную дробь к виду обыкновенной и потом умножаем на нужное число. Во втором случае приводим обыкновенную или смешанную дробь в десятичную и потом умножаем.

ГОСТ

Бесконечные десятичные дроби

Десятичные дроби после запятой могут содержать бесконечное количество цифр.

Бесконечные десятичные дроби — это десятичные дроби, в записи которых находится бесконечное число цифр.

Бесконечную десятичную дробь практически невозможно записать полностью, поэтому при их записи ограничиваются только некоторым конечным количеством цифр после запятой, после чего ставят многоточие, которое указывает на бесконечно продолжающуюся последовательность цифр.

Например, $0,443340831dots ; 3,1415935432dots ; 135,126730405dots ; 4,33333333333dots ; 676,68349349dots$.

Рассмотрим последние две бесконечные десятичные дроби. В дроби $4,33333333333dots$ бесконечно повторяется цифра $3$, а в дроби $676,68349349dots$ с третьего знака после запятой повторяется группа цифр $3$, $4$ и $9$. Подобные бесконечные десятичные дроби называются периодическими.

Периодические десятичные дроби

Периодические десятичные дроби (или периодические дроби) — это бесконечные десятичные дроби, в записи которых с некоторого знака после запятой бесконечно повторяется какая-нибудь цифра или их группа, которая называется периодом дроби>.

Например, период периодической дроби $4,33333333333dots$ — цифра $3$, а период дроби $676,68349349dots$ — группа цифр $349$.

Бесконечные десятичные периодические дроби получают при переводе обыкновенных дробей, знаменатели которых содержат простые множители, кроме $2$ и $5$, в десятичные дроби.

Любая конечная десятичная дробь (и целое число) может быть записана в виде периодической дроби, для чего достаточно справа дописать бесконечное количество цифр $0$.

Готовые работы на аналогичную тему

Например, конечная десятичная дробь $45,12$ может быть записана в виде периодической дроби как $45,12(0)$, а целое число $(74)$ в виде бесконечной периодической десятичной дроби будет иметь вид $74(0)$.

В случае периодических дробей, которые имеют период 9, используют переход к другой записи периодической дроби с периодом $0$. Только для этого период 9заменяют периодом $0$, при этом значение следующего по старшинству разряда увеличивается на $1$.

Например, периодическую дробь $7,45(9)$ можно заменить периодической дробью $7,46(0)$ или равной ей десятичной дробью $7,46$.

Бесконечные десятичные периодические дроби представляются рациональными числами. Другими словами, любая периодическая дробь может быть переведена в обыкновенную дробь, а любая обыкновенная дробь может быть представлена в виде периодической дроби.

Перевод обыкновенных дробей в конечные и бесконечные периодические десятичные дроби

В десятичную дробь можно перевести не только обыкновенные дроби со знаменателями $10, 100, dots$.

В некоторых случаях исходную обыкновенную дробь можно легко привести к знаменателю $10$, $100$ или $1 000$, после чего можно полученную дробь представить в виде десятичной дроби.

Чтобы дробь $frac$ >привести к дроби со знаменателем $10$, нужно числитель и знаменатель дроби умножить на $2$, после чего получим $frac$, которую не составит труда перевести в десятичную дробь $0,6$.

Для остальных случаев используется другой способ перевода обыкновенной дроби в десятичную>:

числитель нужно заменить десятичной дробью с любым числом нулей после десятичной запятой;

разделить числитель дроби на знаменатель (деление выполняется как деление натуральных чисел в столбик, а в частном ставят десятичную запятую после окончания деления целой части делимого).

Перевести обыкновенную дробь $frac$ в десятичную дробь.

Решение.

Число $621$ в числителе представим в виде десятичной дроби. Для этого добавим десятичную запятую и для начала два нуля после нее. Далее при необходимости можно буде добавить нули еще. Итак, получили $621,00$.

Выполним деление числа $621,00$ на $4$ в столбик:

Деление дошло до десятичной запятой в делимом, а остаток при этом получили не нулевой. В таком случае в частном ставится десятичная запятая и продолжается деление столбиком, не взирая на запятые:

В остатке получили нуль, значит деление окончено.

Ответ: $155,25$.

Возможен случай, когда при делении числителя и знаменателя обыкновенной дроби в остатке $0$ так и не получается. В этом случае деление можно продолжать бесконечно. Начиная с определенного момента остатки от деления периодически повторяются, а значит повторяются и цифры в частном. Из этого можно сделать вывод, что данная обыкновенная дробь переведется в бесконечную периодическую десятичную дробь.

Перевести обыкновенную дробь $frac$ в десятичную дробь.

Для перевода обыкновенной дроби в десятичную выполним деление в столбик:

При делении повторяются остатки $8$ и $36$, а в частном также повторяются цифры $1$ и $8$. Итак, исходную обыкновенную дробь $frac$ перевели в периодическую дробь $frac=0,43181818dots =0,43(18)$.

Ответ: $0,43(18)$.

Общий вывод о переводе обыкновенных дробей в десятичные:

если знаменатель можно разложить на простые множители, среди которых будут присутствовать только числа $2$ и $5$, то такую дробь можно перевести в конечную десятичную дробь;

если кроме чисел $2$ и $5$ в разложении знаменателя присутствуют другие простые числа, то такая дробь переводится в бесконечную десятичную периодическую дробь.

Читайте также:

  

• Реабилитация жертв политических репрессий доклад

  

• Ливонская война 7 класс доклад

  

• Экология кмв доклад на тему

  

• Доклад дидактические игры как средство всестороннего воспитания детей дошкольного возраста

  

• Федеральная служба по надзору в сфере природопользования доклад

Десятичные дроби – для чайников

Действия с десятичными дробями – деление умножение, сложение, вычитание, сравнение. Разбор примеров.

Все это здесь.

Между прочим, большинство ошибок на экзаменах происходят как раз из-за незнания простейших действий вроде этих.

Так что читай эту статью и отрабатывай скиллы.

Десятичные дроби – коротко о главном

1. Определение

Десятичной дробью называется обыкновенная дробь, знаменателем которой является ( 10) в какой-либо степени.

2. Конечная и бесконечная десятичная дробь

Десятичная дробь может быть:

• конечной, если она содержит конечное число цифр после запятой (( displaystyle frac{8}{10}, frac{13}{100},frac{49}{1000}));
• бесконечной, в том числе периодичной, если конечное число цифр определить не определено (( 0,05882352941…));
• периодической, если её последовательность цифр после запятой, начиная с некоторого места, представляет собой периодически повторяющуюся группу цифр (( displaystyle frac{1}{7}=0,underbrace{142857}_{{период}}underbrace{142857}_{период}142…=0,left( 142857 right)))

3. Свойства десятичных дробей

• Десятичная дробь не меняется, если справа добавить нули ( displaystyle frac{3}{100}=0,03=0,030=0,030000)и т.д.;
• Десятичная дробь не меняется, если удалить нули, расположенные в конце десятичной дроби: ( 0,014330000=0,01433);
• Десятичная дробь возрастает в ( 10), ( 100), ( 1000) и т.д. раз, если перенести десятичную точку на одну, две, три и т.д. позиций вправо: ( 0,0125cdot 100=1,25) (перенесли запятую на ( 2) знака вправо – умножили на ( 100) и дробь возросла в ( 100) раз);
• Десятичная дробь уменьшается в ( 10), ( 100), ( 1000) и т.д. раз, если перенести десятичную точку на одну, две, три и т.д. позиций влево: ( 124,56:100=1,2456) (перенесли запятую на ( 2) знака влево – разделили на ( 100) и дробь уменьшилась в ( 100) раз).

4. Сложение десятичных дробей

Сложение происходит, как и сложение натуральных чисел в столбик, при этом запятая в ответе ставиться четко на том же месте, как и в складываемых числах.

5. Вычитание десятичных дробей

Так же, как и при сложении, при вычитании десятичные дроби записываются «столбиком»:

6. Умножение десятичных дробей

Десятичные дроби также записываются в столбик и умножаются как обыкновенные числа. При умножении нам неважно, стоят ли запятые под запятыми и так далее.

Однако, удобно, когда числа выровнены по правому краю – умножение происходит более упорядочено.

7. Деление десятичных дробей

Деление десятичной дроби на натуральное число

• Делим десятичную дробь на натуральное число по правилам деления в столбик, не обращая внимания на запятую в делимом (то число, которое мы делим на какое-либо другое число)
• Ставим в частном запятую, когда заканчивается деление целой части делимого.

Деление десятичных дробей друг на друга

• Считаем количество знаков справа от запятой в десятичной дроби.
• Умножаем и делимое, и делитель на 10, 100 или 1000 и т.д., в зависимости от того, сколько мы насчитали знаков в первом пункте. Умножать необходимо, чтобы превратить десятичную дробь в целое число.

Десятичные дроби – подробнее

Конечно, ты знаешь, что такое обыкновенная дробь. Например, ( displaystyle frac{1}{3}, frac{1}{4},frac{5}{112}).

Наравне с приведенными выше дробями существуют дроби ( displaystyle frac{8}{10}, frac{13}{100},frac{49}{1000}) и т.д.

Такие дроби можно записать намного удобнее и более кратко, то есть:

( displaystyle frac{8}{10}=0,8)

( displaystyle frac{13}{100}=0,13)

( displaystyle frac{49}{1000}=0,049)

Данного вида дроби называются десятичными. Иными словами:

Десятичной дробью называется обыкновенная дробь, знаменателем которой является ( 10) в какой-либо степени (первый пример – ( 10) в первой степени, второй – ( 10) во второй степени и т.д.).

Ты наверняка знаешь, что каждая цифра после запятой имеет свое название. На всякий случай напомню тебе про них, чтобы в дальнейшем мы говорили на одном языке:

Это огромное число читается по следующему алгоритму:

1. Сначала читается число, стоящее до запятой и добавляется слово «целых»: ««( 46) целых»;
2. Затем читается как обыкновенное число слева после запятой и добавляется слово, обозначающее название самой последней цифры. В нашем случае – «одна тысяча двести тридцать четыре десятитысячные».

А теперь прочитаем все вместе – «( 46) целых одна тысяча двести тридцать четыре десятитысячные». Разобрался? Переходим к визуализации полученных знаний!

Итак, небольшая тренировка на понимание, что такое эта десятичная дробь! Нарисуй квадрат ( 10) на ( 10) и закрась какую-нибудь его часть равную:

• ( 0,05;)
• ( 0,4;)
• ( 0,27;)
• ( 0,245)

Справился? Проверяем, что у тебя получилось.

Во-первых, квадрат ( 10) на ( 10) состоит из ( 100) клеточек. Соответственно, ( 0.05) – ( 5) клеточек из ( 100); ( 0,4) – ( 40) клеточек из ( 100) и так далее.

Наверняка, наибольшее затруднение составило последнее число – ( -0,245). На картинке это необходимо отразить как 24,5 клетки.

В общем, смотри:

С понятиями разобрались, теперь научимся переводить из десятичной дроби в обыкновенную и обратно.

Перевод из десятичной дроби в обыкновенную и обратно

Попробуй перевести:

• ( 0,136)
• ( 0,2436)
• ( 0,0456)
• ( 0,21)

Сравним ответы:

• ( displaystyle 0,136=frac{136}{1000})
• ( displaystyle 0,2436=frac{2436}{10000})
• ( displaystyle 0,0456=frac{456}{10000})
• ( displaystyle 0,21=frac{21}{100})

Уверена, что ты с легкостью справился! А как насчет обратного перевода? Из обыкновенных в десятичные?

Попробуй свои силы на вот этих дробях:

• ( displaystyle frac{2}{10})
• ( displaystyle frac{3}{100})
• ( displaystyle frac{4}{1000})
• ( displaystyle frac{4562}{100})

А вот и ответы:

• ( displaystyle frac{2}{10}=0,2)
• ( displaystyle frac{3}{100}=0,03)
• ( displaystyle frac{4}{1000}=0,004)
• ( displaystyle frac{4562}{100}=45frac{62}{100}=45,62)

Если ты со всем справился, можешь пропускать следующий абзац, а если где-то допустил ошибку, внимательно прочти о том, как легко и 100% правильно переводить дроби из обыкновенных в десятичные.

1. Смотрим на дробь и определяем, есть ли у нее целая часть? Если есть, выделяем целую часть, записываем ее, и ставим запятую.
2. После запятой должно быть столько знаков, сколько нулей стоит в знаменателе. Например, дробь ( displaystyle frac{4}{1000}) – ( 3) нуля в знаменателе, соответственно, мы как бы мысленно выделяем ( 3) ячейки.
3. Затем записываем числитель – ( 4), но выравниваем его по правому краю, а в пустые ячейки вставляем нули.

Разобрался? Посмотри еще раз эту маленькую «инструкцию»:

Я думаю, ты во всем-всем разобрался! Потренируемся? Попробуй поработать еще с вот этими дробями:

• ( displaystyle frac{26}{10})
• ( displaystyle frac{43}{100})
• ( displaystyle frac{99}{1000})
• ( displaystyle frac{3562}{100})

А теперь ответы:

• ( displaystyle frac{26}{10}=2,6)
• ( displaystyle frac{43}{100}=0,43)
• ( displaystyle frac{99}{1000}=0,099)
• ( displaystyle frac{3562}{100}=35,62)

Виды десятичных дробей

Десятичная дробь может быть:

• конечной, если она содержит конечное число цифр после запятой (( displaystyle frac{8}{10}, frac{13}{100},frac{49}{1000}));
• бесконечной, в том числе периодичной, если конечное число цифр определить не определено (( 0,05882352941…));
• периодической, если её последовательность цифр после запятой, начиная с некоторого места, представляет собой периодически повторяющуюся группу цифр (( displaystyle frac{1}{7}=0,underbrace{142857}_{{период}}underbrace{142857}_{период}142…=0,left( 142857 right))).

Поговорим сначала о конечных дробях.

Конечная десятичная дробь

Само собой понятно, что дроби ( displaystyle frac{8}{10}, frac{13}{100},frac{49}{1000}) являются конечными, ведь знаменатель дроби уже представлен как единица с последующими нулями, и поэтому мы сразу можем сказать, что данную обыкновенную дробь можно перевести в конечную десятичную. А что ты скажешь насчет этой дроби: ( displaystyle frac{1}{4})? Ее знаменатель далеко не единица с последующими нулями, но ты четко знаешь, что у нее есть десятичный «аналог»:

( displaystyle frac{1}{4}=frac{1cdot 25}{4cdot 25}=frac{25}{100}=0,25)

То есть, чтобы определить, можно ли перевести дробь в десятичную, необходимо умножить числитель и знаменатель на одно и то же число, такое, чтобы знаменатель стал равен ( 10), ( 100), ( 1000) и так далее.

Усвоил? Постарайся представить в виде конечной десятичной дроби следующие обыкновенные дроби:

• ( displaystyle frac{1}{5})
• ( displaystyle frac{1}{8})
• ( displaystyle frac{3}{5})
• ( displaystyle frac{1}{16})

Сравним наши ответы:

• ( displaystyle frac{1cdot 2}{5cdot 2}=frac{2}{10}=0,2)
• ( displaystyle frac{125}{1000}=0,125)
• ( displaystyle frac{3}{5}=frac{6}{10}=0,6)
• ( displaystyle frac{1}{16}=frac{625}{10000}=0,0625)

Справился? Молодец. Выходим на новый уровень и переходим к бесконечным десятичным дробям.

Бесконечная десятичная дробь

Итак, бери калькулятор и дели ( 1) на ( 17). Поделил? Ты получил ( 0,05882352941) и дальше окошко калькулятора не показывает… Это тоже является десятичной дробью, только данная десятичная дробь является бесконечной. Ты сейчас скажешь, а как же наше определение?

Десятичной дробью называется обыкновенная дробь, знаменателем которой является ( 10) в какой-либо степени (первый пример – ( 10) в первой степени, второй – ( 10) во второй степени и т.д.).

Все очень просто и никаких противоречий с определением нет. В данном случае нам необходимо привести наш знаменатель к ( {{10}^{n}}), с учетом, что ( n) это какое-либо бесконечное число, которое мы не можем «обозреть» взглядом», или иными словами – ( nto +infty )

Таким образом:

Бесконечной десятичной дробью называется обыкновенная дробь, в записи которой после запятой содержится бесконечное количество цифр.

Как правило, в задачах, где встречаются бесконечные десятичные дроби, просят указать ответ либо с округлением (например, до десятых, или до сотых), либо записать в виде обыкновенной дроби, то есть как ( displaystyle frac{1}{17}).

Подумай, какой самый популярный пример можно привести на тему «бесконечная десятичная дробь»? Правильно! Число ( pi ) является бесконечной десятичной дробью. Во всем мире люди договорились, что для решения математических задач принято, что ( pi =3,14), но это далеко не так. Число ( pi ) не имеет определенного завершения. Оно настолько бесконечно, что ежегодно в мире проводятся соревнования по запоминанию числа ( pi ). Мировой рекорд по запоминанию знаков числа ( pi ) после запятой принадлежит китайцу Лю Чао, который в 2006 году в течение 24 часов и 4 минут воспроизвёл 67 890 знаков после запятой без ошибки! Все 67 890 знаков после запятой мы приводить не будем, а приведем несколько сокращенную запись:

( pi =3,1415926535text{ }8979323846text{ }2643383279text{ }5028841971)

Думаю, этого хватит, чтобы оценить «масштабы» данного числа.

Наравне с бесконечными десятичными дробями существуют периодические десятичные дроби. Они так же не имеют конца, но последующие числа в них повторяются, например, попробуй перевести в десятичную дробь ( displaystyle frac{1}{3}). Что у тебя получилось?

( displaystyle frac{1}{3}=0,333333333….)

Чтобы не повторять число ( 3) много много раз, решили говорить «ноль целых и три в периоде», так как тройка будет повторяться после запятой бесконечное число раз. Из этого умозаключения следует определение:

Дробь называется периодической, если её последовательность цифр после запятой, начиная с некоторого места, представляет собой периодически повторяющуюся группу цифр.

Чтобы кратко записать такую дробь, период (повторяющиеся цифры после запятой) пишут в скобках:

( displaystyle frac{1}{3}=0,underbrace{3}_{период}33333333….=0,left( 3 right))

( displaystyle frac{1}{7}=0,underbrace{142857}_{{период}}underbrace{142857}_{период}142…=0,left( 142857 right))

Важно, что период не может начинаться слева от запятой:

( displaystyle frac{100}{7}=underbrace{14,2857}_{не период}1428571428571…=14,left( 285714 right)).

Свойства десятичных дробей

Существует четыре свойства десятичных дробей. Они очень простые, и ты 100% знаешь о всех них, но давай их перечислим и вспомним:

1. Десятичная дробь не меняется, если справа добавить нули

( displaystyle frac{3}{100}=0,03=0,030=0,030000)и т.д.

2. Десятичная дробь не меняется, если удалить нули, расположенные в конце десятичной дроби:

( 0,014330000=0,01433)

ВНИМАНИЕ!!! Нельзя удалять нули, расположенные не в конце десятичной дроби!!!!

( 0,014330000ne 0,1433)

3. Десятичная дробь возрастает в ( 10), ( 100), ( 1000) и т.д. раз, если перенести десятичную точку на одну, две, три и т.д. позиций вправо:

( 0,0125cdot 100=1,25) (перенесли запятую на ( 2) знака вправо – умножили на ( 100) и дробь возросла в ( 100) раз)

4. Десятичная дробь уменьшается в ( 10), ( 100), ( 1000) и т.д. раз, если перенести десятичную точку на одну, две, три и т.д. позиций влево:

( 124,56:100=1,2456) (перенесли запятую на ( 2) знака влево – разделили на ( 100) и дробь уменьшилась в ( 100) раз)

Последние два свойства позволяют быстро умножать и делить десятичные дроби на ( 10), ( 100), ( 1000) и т.д. о чем подробнее мы поговорим чуть ниже.

Действия с десятичными дробями

Десятичные дроби – это обычные числа. Мы можем складывать их, вычитать из одной другую, умножать и делить.

Очень важно уметь правильно производить с ними математические действия, так как зачастую именно от арифметических ошибок зависит твоя оценка на экзамене.

Несомненно, ты знаешь, как все это делать, но на всякий случай, дам тебе краткую инструкцию к применению.

Как складывать десятичные дроби

При сложении десятичные дроби записываются «столбиком», так чтобы одноимённые разряды находились друг под другом без смещения. Соответственно, запятые стоят четко друг под другом.

Разберемся на примере:

Сложение происходит, как и сложение натуральных чисел в столбик, при этом запятая в ответе ставится четко на том же месте, как и в складываемых числах.

Если исходные числа имеют разное количество знаков после запятой, то к дроби с меньшим количеством десятичных знаков нужно приписать необходимое число нулей, чтобы уравнять в дробях количество знаков после запятой.

Если при сложении в сумме мы получаем больше ( 10), то одна единица прибавляется к сумме при сложении цифр следующего разряда.

Решим наш пример, учтя все правила:

Разобрался? Посчитай в столбик самостоятельно:

• ( 0,0125+0,141)
• ( 2,4225+0,34)
• ( 122,4355+1,34)
• ( 2,435+12,3)

Сравним ответы:

• ( 0,0125+0,141=0,1535)
• ( 2,4225+0,34=2,7625)
• ( 122,4355+1,34=123,7755)
• ( 2,435+12,3=14,735)

Как вычитать десятичные дроби

Так же, как и при сложении, при вычитании десятичные дроби записываются «столбиком», так чтобы одноимённые разряды находились друг под другом без смещения.

Соответственно, запятые стоят четко друг под другом.

Вычитание происходит, как и вычитание натуральных чисел в столбик, при этом запятая в ответе ставиться четко на том же месте, как и в числах, с которыми мы работаем.

Если исходные числа имеют разное количество знаков после запятой, то к дроби с меньшим количеством десятичных знаков нужно приписать необходимое число нулей, чтобы уравнять в дробях количество знаков после запятой.

Если при вычитании получается, что мы из меньшего числа вычитаем большее, то мы как бы занимаем десяток у более высокого разряда (при вычитании сотых частей, берем десяток у десятых, при вычитании десятых – у единиц и так далее), не забывая уменьшить вычитаемое число у заимствованного разряда.

Посмотрим подробно на примере:

Думаю, с рисунком тебе стало все понятно. Попробуй посчитать в столбик следующие выражения:

• ( 0,0125-0,141)
• ( 2,4225-0,34)
• ( 122,4355-1,34)
• ( 12,435-12,3)

Сравним полученные ответы:

• ( 0,0125-0,141=-0,1285)
• ( 2,4225-0,34=2,0825)
• ( 122,4355-1,34=121,0955)
• ( 12,435-12,3=0,135)

Как умножать десятичные дроби

Десятичные дроби также записываются в столбик и умножаются как обыкновенные числа. При умножении нам неважно, стоят ли запятые под запятыми и так далее.

Однако, удобно, когда числа выровнены по правому краю – умножение происходит более упорядочено.

Мы начинаем запись числа, получающего при перемножении, под тем разрядом второго числа, на который умножаем. Далее мы суммируем полученные числа и только затем ставим запятую.

Чтобы определить, между какими числами должна стоять запятая, мы должны посмотреть, сколько чисел стоит после знака запятой у первого множителя, сколько у второго, сложить их и отсчитать справа данное количество чисел.

Непонятно? Смотри:

Как ты видишь, при перемножении мы будем складывать столько слагаемых, сколько разрядов содержится во втором множителе, поэтому удобней записывать числа так, чтобы первый множитель был по количеству чисел больше, чем второй.

Таким способом мы значительно снизим вероятность ошибок.

Не веришь? Смотри:

Если при умножении мы получаем число, которое больше ( 9), например ( 12), то единицу мы прибавляем к значению, полученному при умножении последующих чисел следующего десятка.

Соответственно, если получаем, например, ( 24), то прибавляем ( 2).

Проиллюстрируем данное правило:

Разобрался? Дорешай данный пример самостоятельно.

Сколько у тебя получилось? У меня ( 10,33911).

А теперь пора приступить к некоторым очень важным моментам, которые помогут сохранить время на экзамене.

Как делить десятичные дроби

Теперь ты знаешь о десятичных дробях почти все. Осталось только разобраться с тем, как их делить друг на друга.

Если ты отлично это представляешь, смело пропускай данный подраздел. Если нет – смотри инструкцию к применению.

Итак. Мы рассмотрим два вида деления:

• деление десятичной дроби на натуральное число;
• деление десятичной дроби на десятичную дробь.

Начнем с деления десятичной дроби на натуральное число.

Чтобы делить десятичную дробь на натуральное число, необходимо пользоваться следующими правилами:

1. Делим десятичную дробь на натуральное число по правилам деления в столбик, не обращая внимания на запятую в делимом (то число, которое мы делим на какое-либо другое число)
2. Ставим в частном запятую, когда заканчивается деление целой части делимого.

Важно!!!

Если целая часть делимого меньше делителя, то в частном ставим ( 0) целых. Логично, правда?

Рассмотрим на конкретном примере:

Усвоил? Раздели столбиком следующие числа:

• ( 135,2:5)
• ( 16,4:2)
• ( 158,14:4)
• ( 2,456:2)
• ( 0,626:2)

Сравним наши ответы:

• ( 135,2:5=27,04)
• ( 16,4:2=8,2)
• ( 158,14:4=39,535)
• ( 2,456:2=1,228)
• ( 0,626:2=0,313)

Вспомни теперь свойства десятичных дробей, описанные ранее: если нам необходимо разделить дробь на ( 10), ( 100), ( 1000) и так далее, нет необходимости делать это в столбик – мы можем просто перенести запятую на столько цифр влево, сколько нулей у нас в делителе.

Например: ( 135,2:10=13,52).

А теперь попробуй самостоятельно:

• ( 135,2:100)
• ( 16,4:10)
• ( 158,14:1000)
• ( 2,456:10)

Перенес? Смотри, что у меня получилось:

• ( 135,2:100=1,352)
• ( 16,4:10=1,64)
• ( 158,14:1000=0,15814)
• ( 2,456:10=0,2456)

Молодец! Переходим к делению десятичных дробей друг на друга.

Деление десятичных дробей друг на друга

Итак, для того чтобы это делать существует три правила:

1. Считаем количество знаков справа от запятой в десятичной дроби.
2. Умножаем и делимое, и делитель на ( 10), ( 100) или ( 1000) и т.д., в зависимости от того, сколько мы насчитали знаков в первом пункте. Умножать необходимо, чтобы превратить десятичную дробь в целое число.
3. Делим числа как натуральные.

ВАЖНО!!! При умножении мы смотрим, в каком из чисел, участвующих в делении, присутствует наибольшее количество знаков после запятой? Ориентируясь именно на это число мы умножаем на ( 10), ( 100), ( 1000) и так далее.

Рассмотрим на примере ( 16,4:0,02)

В каком числе у нас стоит наибольшее количество знаков после запятой? Правильно, во втором, то есть в делителе: после нуля стоит два знака. Что из этого следует? Что мы умножаем и делимое и делитель на ( 100)!

Что дальше? Мы получаем следующий пример: ( 1640:2) Посчитай, сколько это будет самостоятельно. У меня получилось ( 820).

Рассмотрим примерчик посложнее: ( 5,31:0,3)

Самое большое количество знаков после запятой содержится в первом числе – их два, соответственно, умножаем оба числа, участвующего в делении на ( 100). Получаем: ( 531:30).

А теперь делим в столбик:

Ты видишь, что нацело разделить не получилось, мы «снесли» еще один ноль, и только тогда пришли к ответу, поэтому сразу после окончания деления нашего делимого, мы ставим запятую.

Теперь ты полностью готов совершать любые действия с десятичными дробями. Молодец! Рассмотрим только, как их сравнивать, хотя я думаю, ты уже и сам с этим справишься!

Как сравнивать десятичные дроби

Мы можем сравнивать десятичные дроби двумя способами.

Способ первый – поразрядно.

Допустим, нам необходимо сравнить ( 5,365 V 5,36)

1. Смотрим, одинаковое ли количество знаков после запятой стоит у каждой дроби? Нет? Значит дописываем справа необходимое количество нулей (ты же помнишь, что от дописывания нулей дробь неизменна, правда?)

Что у нас получилось? Верно: ( 5,365 V 5,360)

2. Начинаем сравнивать слева направо: целую часть с целой, десятые части с десятыми и так далее. Когда одна из частей дроби оказывается больше аналогичной части другой, эта дробь и больше.

Перейдем к нашему примеру: целые части у нас одинаковы – их значение ( 5). Десятые тоже – ( 3). Сотые – ( 6), а вот тысячные у первой дроби ( 5), а у второй ( 0). Что больше: ( 5) или ( 0)? Верно, ( 5), соответственно:

( 5,365 > 5,360)

Способ второй – с помощью умножения.

Внимательно смотрим на дроби. На сколько нам нужно умножить два числа, чтобы сравнивать целые числа? Смотрим на ту дробь, у которой знаков после запятой больше, то есть на первую. У нее после запятой ( 3) знака, соответственно, чтобы сделать из нее целое число, необходимо умножить на ( 1000) Умножаем обе дроби на это значение:

( 5,365cdot 1000 V 5,36cdot 1000)

( 5365 V 5360)

Эти числа ты сравнишь без проблем:

( 5365 > 5360)

Заметь, результат получился одинаковый. Теперь попробуй сравнить дроби самостоятельно любым наиболее удобным для тебя способом:

• ( 21,34 V 20,34)
• ( 0,34 V 0,341)
• ( 120,15 V 1210,16)
• ( 10,565 V 10,465)

Справился? Смотри что вышло:

• ( 21,34 > 20,34)
• ( 0,34 < 0,341)
• ( 120,15 < 1210,16)
• ( 10,565 > 10,465)

Вот теперь ты усвоил дроби полностью!

Самые бюджетные курсы по подготовке к ЕГЭ на 90+

Алексей Шевчук – ведущий мини-групп

математика, информатика, физика

+7 (905) 541-39-06 – WhatsApp/Телеграм для записи

alexei.shevchuk@youclever.org – email для записи

• тысячи учеников, поступивших в лучшие ВУЗы страны
• автор понятного всем учебника по математике ЮКлэва (с сотнями благодарных отзывов);
• закончил МФТИ, преподавал на малом физтехе;
• репетиторский стаж – c 2003 года;
• в 2021 году сдал ЕГЭ (математика 100 баллов, физика 100 баллов, информатика 98 баллов – как обычно дурацкая ошибка:);
• отзыв на Профи.ру: “Рейтинг: 4,87 из 5. Очень хвалят. Такую отметку получают опытные специалисты с лучшими отзывами”.