Единицы измерений, переводные таблицы и формулы
Units, Conversion Tables, and Formulas
Единицы измерения давления / Pressure
|
Па, паскаль |
кПа, килопаскаль |
МПа, мегапаскаль |
кгс/см², ат, техническая атмосфера |
атм, физическая атмосфера |
|
Pa, pascal |
kPa, kilopascal |
MPa, megapascal |
kgf/cm² или kp/cm², at, technical atmosphere |
аtm, atmosphere |
|
бар |
PSI или psi (фунт/кв. дюйм), фунт-сила на квадратный дюйм |
мм рт. ст., миллиметр ртутного столба |
мм вод. ст., миллиметр водяного столба |
|
bar |
PSI или psi (pounds/square inch или lbf/in²), pound-force per square inch |
1 mm Hg |
1 mm of water |
Паскаль (Па, Pa)
Паскаль (Па, Pa) – единица измерения давления в Международной системе единиц измерения (система СИ). Единица названа в честь французского физика и математика Блеза Паскаля.
Паскаль равен давлению, вызываемому силой, равной одному ньютону (Н), равномерно распределённой по нормальной к ней поверхности площадью один квадратный метр:
1 паскаль (Па) ≡ 1 Н/м²
Кратные единицы образуют с помощью стандартных приставок СИ:
1 МПа (1 мегапаскаль) = 1000 кПа (1000 килопаскалей)
Атмосфера (физическая, техническая)
Атмосфера — внесистемная единица измерения давления, приблизительно равная атмосферному давлению на поверхности Земли на уровне Мирового океана.
Существуют две примерно равные друг другу единицы с таким названием:
- Физическая, нормальная или стандартная атмосфера (атм, atm) — в точности равна 101 325 Па или 760 миллиметрам ртутного столба.
-
Техническая атмосфера (ат, at, кгс/см²) — равна давлению, производимому силой 1 кгс, направленной перпендикулярно и равномерно распределённой по плоской поверхности площадью 1 см² (98 066,5 Па).
1 техническая атмосфера = 1 кгс/см² («килограмм-сила на сантиметр квадратный»). // 1 кгс = 9,80665 ньютонов (точно) ≈ 10 Н; 1 Н ≈ 0,10197162 кгс ≈ 0,1 кгс
На английском языке килограмм-сила обозначается как kgf (kilogram-force) или kp (kilopond) – килопонд, от латинского pondus, означающего вес.
Заметьте разницу: не pound (по-английски «фунт»), а pondus.
На практике приближенно принимают: 1 МПа = 10 атмосфер, 1 атмосфера = 0,1 МПа.
Бар
Бар (от греческого βάρος — тяжесть) — внесистемная единица измерения давления, примерно равная одной атмосфере. Один бар равен 105 Н/м² (или 0,1 МПа).
Соотношения между единицами давления
1 МПа = 10 бар = 10,19716 кгс/см² = 145,0377 PSI = 9,869233 (физ. атм.) =7500,7 мм рт.ст.
1 бар = 0,1 МПа = 1,019716 кгс/см² = 14,50377 PSI = 0,986923 (физ. атм.) =750,07 мм рт.ст.
1 ат (техническая атмосфера) = 1 кгс/см² (1 kp/cm², 1 kilopond/cm²) = 0,0980665 МПа = 0,98066 бар = 14,223
1 атм (физическая атмосфера) = 760 мм рт.ст.= 0,101325 МПа = 1,01325 бар = 1,0333 кгс/см²
1 мм ртутного столба = 133,32 Па =13,5951 мм водяного столба
Объемы жидкостей и газов / Volume
|
л (литр) |
куб.м (кубический метр) |
куб.см (кубический сантиметр) |
кубический фут |
кубический дюйм |
галлон (США) |
галлон (Англия) |
|
l (liter) |
cubic meter или cbm |
cc или ccm |
cubic feet или cu ft |
cubic inch, cubic in, cu inch, cu in |
gl или gallon (US) |
gl или gallon (UK, Imperial) |
1 gl (US) = 3,785 л
1 gl (Imperial) = 4,546 л
1 cu ft = 28,32 л = 0,0283 куб.м
1 cu in = 16,387 куб.см
Скорость потока / Flow
|
л/с (литр в секунду) |
л/мин (литр в минуту) |
куб.м/час (кубический метр в час) |
кубический фут в минуту |
|
l/s (liter/second) |
l/min (liter/minute) |
cbm/h (cubic meter/hour) |
CFM или cfm (cubic feet/minute) |
1 л/с = 60 л/мин = 3,6 куб.м/час = 2,119 cfm
1 л/мин = 0,0167 л/с = 0,06 куб.м/час = 0,0353 cfm
1 куб.м/час = 16,667 л/мин = 0,2777 л/с = 0,5885 cfm
1 cfm (кубический фут в минуту) = 0,47195 л/с = 28,31685 л/мин = 1,699011 куб.м/час
Пропускная способность / Valve flow characteristics
Коэффициент (фактор) расхода Kv
Flow Factor – Kv
Основным параметром запорного и регулирующего органа является коэффициент расхода Kv. Коэффициент расхода Kv показывает объем воды в куб.м/час (cbm/h) при температуре 5-30ºC, проходящей через затвор с потерей напора в 1 бар.
Коэффициент расхода Cv
Flow Coefficient – Cv
В странах с дюймовой системой измерений используется коэффициент Cv. Он показывает, какой расход воды в галлон/мин (gallon/minute, gpm) при температуре 60ºF проходит через арматуру при перепаде давления на арматуре в 1 psi.
Cv = 1,16 Kv
Kv = 0,853 Cv
Кинематическая вязкость / Viscosity
|
сСт (сантистокс) |
м²/с (квадратный метр в секунду) |
|
cSt |
m²/s |
м²/с – единица кинематической вязкости в системе СИ
Стокс – единица кинематической вязкости в системе СГС
1 сСт = 1 мм²/с = 0,000001 м²/с
1 м²/с = 1000000 сСт
Единицы длины / Length
|
м (метр) |
мм (миллиметр) |
фут |
дюйм |
|
m |
mm |
ft (feet) |
in (inch) |
1 ft = 12 in = 0,3048 м
1 in = 0,0833 ft = 0,0254 м = 25,4 мм
1 м = 3,28083 ft = 39,3699 in
Единицы силы / Force
|
Н (ньютон) |
кгс (килограмм-сила) |
фунт-сила |
|
N (newton) |
kp (kilogram force) |
lbf (pound force) |
1 Н = 0,102 кгс = 0,2248 lbf
1 lbf = 0,454 кгс = 4,448 Н
1 кгс = 9,80665 Н (точно) ≈ 10 Н; 1 Н ≈ 0,10197162 кгс ≈ 0,1 кгс
На английском языке килограмм-сила обозначается как kgf (kilogram-force) или kp (kilopond) – килопонд, от латинского pondus, означающего вес. Обратите внимание: не pound (по-английски «фунт»), а pondus.
Единицы массы / Mass
|
г (грамм) |
кг (килограмм) |
фунт |
унция |
|
g |
kg |
lb (pound) |
oz (ounce) |
1 фунт = 16 унций = 453,59 г
Момент силы (крутящий момент) / Torque
|
1 Нм (ньютон-метр) |
1 кгсм (килограмм-сила-метр) |
фунт-сила-фут |
|
N * m |
kp * m или kgf * m |
lbf * ft |
1 кгс . м = 9,81 Н . м = 7,233 фунт-сила-фут (lbf * ft)
Единицы измерения мощности / Power
Некоторые величины:
Ватт (Вт, W, 1 Вт = 1 Дж/с), лошадиная сила (л.с. – рус., hp или HP – англ., CV – франц., PS – нем.)
Соотношение единиц:
В России и некоторых других странах 1 л.с. (1 PS, 1 CV) = 75 кгс* м/с = 735,4988 Вт
В США, Великобритании и других странах 1 hp = 550 фут*фунт/с = 745,6999 Вт
Температура / Temperature
|
°C |
K |
°F |
|
Градус Цельсия Celsius |
Градус Кельвина Kelvin |
Градус Фаренгейта Fahrenheit |
Температура по шкале Фаренгейта:
[°F] = [°C] × 9⁄5 + 32
[°F] = [K] × 9⁄5 − 459,67
Температура по шкале Цельсия:
[°C] = [K] − 273,15
[°C] = ([°F] − 32) × 5⁄9
Температура по шкале Кельвина:
[K] = [°C] + 273.15
[K] = ([°F] + 459,67) × 5⁄9
Эта информация в формате doc.
Ниже представлена таблица с единицами измерения давления, включающая их названия, обозначения на английском (международном) и русском языках. Также отдельно приведено соотношение между перечисленными единицами.
- Единицы измерения давления
- Соотношение единиц измерения давления
Единицы измерения давления
| Единица | Обозначение | Выражение через другие единицы | ||
| рус. | англ. | рус. | англ. | |
| Паскаль | Pascal | Па | Pa | 1 Па = 1 Н/м2 (или 1 Н · м-2) |
| Бар | Bar | бар | bar | 1 бар = 105 Па = 1 ⋅ 106 дин/см2 |
| Миллиметр ртутного столба | Millimetre of mercury | мм рт. ст. / торр |
mm Hg / Torr |
1 мм рт. ст. ≈ 133,3223684 Па |
| Физическая атмосфера | Standard atmosphere | атм | atm | 1 атм = 101 325 Па |
| Техническая атмосфера | Technical atmosphere | ат | at | 1 ат = 1 кгс/см2 = 98 066,5 Па |
| Метр водяного столба | Meter of water | м вод. ст. / м H2O |
m H2O | 1 м вод. ст. = 9806,65 Па |
| Фунт-сила на квадратный дюйм | Pound per square inch | psi / lb.p.sq.in. |
1 psi = 1 lbf/in2 = 6894,75729 Па |
Примечания:
- Из указанных единиц только Паскаль относится к международной системе СИ, поэтому все остальные единицы выражены через нее.
- Атмосферное давление, принятое за стандарт, равняется примерно 760 мм рт. ст. или 101 325 Па.
- psi (фунт-сила на квадратный дюйм) – внесистемная единица, которая в основном используется в США и Великобритании.
Соотношение единиц измерения давления
| Единица | Па | бар | мм рт. ст. | атм | ат | м вод. ст. | psi |
| 1 Па | 1 | 10-5 | 7,5006 ⋅ 10-3 | 9,8692 ⋅ 10-6 | 10,197 ⋅ 10-6 | 1,0197 ⋅ 10-4 | 145,04 ⋅ 10-6 |
| 1 бар | 105 | 1 | 750,06 | 0,98692 | 1,0197 | 10,197 | 14,504 |
| 1 мм рт. ст. | 133,322 | 1,3332 ⋅ 10-3 | 1 | 1,3158 ⋅ 10-3 | 1,3595 ⋅ 10-3 | 13,595 ⋅ 10-3 | 19,337 ⋅ 10-3 |
| 1 атм | 101325 | 1,01325 | 760 | 1 | 1,033 | 10,33 | 14,696 |
| 1 ат | 98066,5 | 0,980665 | 735,56 | 0,96784 | 1 | 10 | 14,223 |
| 1 м вод. ст. | 9806,65 | 9,80665 ⋅ 10-2 | 73,556 | 0,096784 | 0,1 | 1 | 1,4223 |
| 1 psi | 6894,76 | 68,948 ⋅ 10-3 | 51,715 | 68,046 ⋅ 10-3 | 70,307 ⋅ 10-3 | 0,70307 | 1 |
|
Проект Карла III Ребане и хорошей компании |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Техническая информация тут Поиск на сайте DPVA Поставщики оборудования Полезные ссылки О проекте Обратная связь Ответы на вопросы. Оглавление
|
|
Перевод единиц давления. Единицы величин давления и их соотношение. Таблица перевода единиц измерения давления. Па; МПа; бар; атм; мм рт.ст. = торр = тор; мм в.ст.; м в.ст., кг/см2; кгс/см2; psf; psi; дюймы рт.ст.; дюймы в.ст. Версия для печати.
Подробный список единиц давления, один паскаль это:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Поиск в инженерном справочнике DPVA. Введите свой запрос: |
Поиск в инженерном справочнике DPVA. Введите свой запрос:
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста.
Вложите в письмо ссылку на страницу с ошибкой, пожалуйста.
Коды баннеров проекта DPVA.ru
Начинка: KJR Publisiers
Консультации и техническая
поддержка сайта: Zavarka Team
Free xml sitemap generator
Давление – важная физическая величина, часто использующаяся в автомобильной технике. Тут и самые простые случаи, например, всем известные требования к давлению в шинах и более скрытые, давление топлива, масла в двигателе и трансмиссии, многочисленные узлы гидравлики. При указании и измерении численных значений потребуется система единиц, которая различается в технических традициях разных стран и школ.
Что такое онлайн конвертер величин и как им пользоваться
Для перевода одних величин давления в другие можно использовать специально написанные скрипты (программы) с удобным пользовательским интерфейсом (пример ниже).
Калькулятор перевода давления в бар на давление в мегапаскалях, килограмм силы, фунт силы и атмосферах
=
1 MPa равен 9.8692 физическая атмосфера, 10.197 кгс/см², 145.04 фунт/дюйм², 10.19716 техническая атмосфера
Достаточно ввести в одно из полей формы нужное значение, как тут же во всех остальных появляются числа, рассчитанные по известным формулам перевода одних единиц в другие.
При наличии доступа в интернет переводить величины через такую онлайн-конвертацию очень удобно, не надо искать коэффициенты пересчёта, вспоминать формулы и пользоваться калькулятором.
Единицы
Для начала выясним, какие единицы измерения давления воды в водопроводе используются в настоящее время.
Атмосфера
Эта единица соответствует атмосферному давлению на уровне моря. Здесь, однако, есть небольшая тонкость: речь идет об избыточном давлении относительно атмосферного. Его значение в водопроводе в 0,2 атмосферы, показанное манометром, соответствует абсолютному значению в 1,2 атмосферы.
Полезно: вместо слова “атмосфера” часто используется равноценное понятие – кгс/см2. Физический смысл единицы – усилие, с которым масса в 1 кг при земном ускорении свободного падения будет давить на площадь в 1 см2.
Бар
Устаревшая единица измерения, заимствованная из использовавшейся до СИ системы измерений СГС. О ней достаточно знать, что бар приблизительно (с точностью около 2%) равен атмосфере. Довольно часто манометр для измерения давления воды в водопроводе имеет две шкалы – в барах и мегапаскалях.
Мегапаскаль
Паскаль соответствует одному ньютону на квадратный метр поверхности. Поскольку масса в один килограмм давит на основание с силой в 9,8 ньютонов, 1 мегапаскаль примерно соответствует 9,8 кгс/см2. Иногда это значение округляют до 10.
Напор
Под понятием напора, измеряемого в метрах, понимается высота водяного столба, соответствующая определенному избыточному давлению. Как узнать напор при известных показаниях манометра в кгс/см2? Достаточно просто умножить их на 10: одна избыточная атмосфера способно поднять водяной столб на 10 метров.
Таблица перевода некоторых единиц измерения.
Таблица перевода единиц измерения давления
Помимо конвертеров, существуют и таблицы перевода, где по вертикали выбирается одна величина, а по горизонтали другая. На пересечении строки и столбца обнаруживается искомое значение.
Ниже самые популярные переводы:
бар = 100 кПа бар = 1 техн. атм (at) бар = 750 мм рт. столба бар = 0,1 МПа бар = 1,0197 кГс/см 2
Таблицы могут быть двух видов:
Мультисистемные служат для определения соотношения между разными единицами измерения в любом сочетании. В этом случае таблица заполняется коэффициентами пересчёта.
Например, если выбрать строку «фунт на квадратный дюйм» (psi) и столбец «килопаскаль» (кПА), то на пересечении можно увидеть, что одному psi соответствует 6,895 кПА. Для дальнейших вычислений придётся воспользоваться операциями умножения или деления на калькуляторе.
Таблицы для выражения конкретных значений в одних единицах через другие. Обычно там числа располагаются парами, в определённом диапазоне от минимального давления до максимального, на который рассчитана данная таблица.
Результат получается с некоторой погрешностью, поскольку при выборе нужного числа приходится применять округление до ближайшего табличного значения. Чем больше в таблице пар чисел, тем точность выше. Практически высокая точность и не требуется.
Табличный метод излишне громоздок, поэтому устарел, расчёт с помощью конвертеров величин куда точнее и быстрее, а форма занимает меньше места на экране. Но при отсутствии электронных средств остаются только таблицы, они могут иметь бумажное исполнение, а считать на логарифмической линейке или в уме сейчас мало кто умеет и желает.
Давление. Перевод единиц измерения давления. Таблица соотношения единиц давления.
Давление
относится к числу распространенных измеряемых физических величин. Контроль за протеканием большинства технологических процессов в тепловой и атомной энергетике, металлургии, химии связан с
измерением давления
или разности давлений газовых и жидких сред.
Давление — широкое понятие, характеризующее нормально распределенную силу, действующую со стороны одного тела на единицу поверхности другого. Если действующая среда — жидкость или газ, то давление, характеризуя внутреннюю энергию среды, является одним из основных параметров состояния. Единица измерения давления
в системе СИ — Паскаль (Па), равный давлению, создаваемому силой в один ньютон, действующей на площадь в один квадратный метр (Н/м2). Широко применяются кратные единицы кПа и МПа. Допускается использование таких единиц, как
килограмм-сила на квадратный сантиметр
(кгс/см2) и
квадратный метр
(кгс/м2), последняя численно равна
миллиметру водяного столба
(мм вод. ст.). В таблице 1 приведены перечисленные единицы давления и соотношения между ними, перевод и соотношение единиц измерения давления. В зарубежной литературе встречаются следующие единицы измерения давления: 1 inch = 25,4 мм вод. ст., 1 psi = 0,06895 бар.
Таблица 1. Единицы измерения давления. Перевод, преобразование единиц измерения давления.
| Единицы измерения | Па | Бар | кгс/см2 | кгс/м2 (мм вод. ст.) | мм рт. ст. |
| 1 Па | 1 | 10-5 | 1,0197*10-5 | 0,10197 | 7,5006*10-3 |
| 1 Бар | 105 | 1 | 1,0197 | 1,0197*104 | 750,06 |
| 1 кгс/см2 | 9,8066*104 | 0,98066 | 1 | 104 | 735,56 |
| 1 кгс/м2 (мм вод. ст.) | 9,8066 | 0,98066*10-4 | 10-4 | 1 | 7,3556*10-2 |
| 1 мм рт. ст. | 133,32 | 1,3332*10-3 | 1,3595*10-3 | 13,595 | 1 |
Воспроизведение единицы измерения давления с наивысшей точностью в области избыточных давлений 106…2,5 * 108 Па осуществляется первичным эталоном, включающим грузопоршневые манометры, специальный набор мер массы и установку для поддержания давления. Для воспроизведения единицы давления вне указанного диапазона от 10-8 до 4 * 105 Па и от 109 до 4 * 106, а также разности давлений до 4 * 106 Па используются специальные эталоны. Передача единицы измерения давления от эталонов рабочим средствам измерения выполняется многоступенчато. Последовательность и точность передачи единицы измерения давления к рабочим средствам с указанием способов поверки и сравнения показаний определяются общегосударственными поверочными схемами (ГОСТ 8.017-79, 8.094-73, 8.107-81, 8.187-76, 8.223-76). Поскольку на каждой ступени передачи единицы измерения погрешности возрастают в 2,5—5 раз, то соотношение между погрешностями рабочих средств измерения давления и первичного эталона составляют 1022… 103.
При измерениях различают абсолютное, избыточное и вакуумметрическое давление. Под абсолютным давлением
P, понимают полное давление, которое равно сумме атмосферного давления Pат и избыточного Ри:
Ра = Ри + Рат
Понятие вакуумметрического давления
вводится при измерении давления ниже атмосферного: Рв = Рат — Ра. Средства измерения, предназначенные для измерения давления и разности давлений, называются
манометрами
. Последние подразделяются на барометры, манометры избыточного давления, вакуумметры и манометры абсолютного давления в зависимости от измеряемого ими соответственно атмосферного давления, избыточного давления, вакуумметрического давления и абсолютного давлений. Манометры, предназначенные для измерения давления или разрежения в диапазоне до 40 кПа (0,4 кгс/см2), называются напоромерами и тягомерами. Тягонапоромеры имеют двустороннюю шкалу с пределами измерения до ± 20 кПа (± 0,2 кгс/см2). Дифференциальные манометры применяются для измерения разности давлений.
Какие единицы давления переводят чаще всего
При работе с автомобилями импортного производства приходится иметь дело с единицами совершенно непривычными, особенно это касается фунтов на квадратный дюйм (psi). Тут быстро сообразить в уме сколько это будет в привычных барах (bar) или атмосферах (атм) неподготовленному человеку затруднительно.
Даже если ему всё понятно с фунтом и дюймом, то с их сочетанием попадают в тупик. Приходится заглядывать в таблицы или специализированные калькуляторы. С прочими единицами ситуация не лучше.
Сколько бар в 1 МПа
Бар – единица внесистемная, но поскольку он примерно равен одной атмосфере, то сложностей не возникает, а незначительные погрешности почти всегда ни на что не влияют. Но если точно, то бар – это десять ньютон на квадратный сантиметр, то есть 0,1 мегапаскаля (МПа).
Поскольку паскаль – это один ньютон на квадратный метр, чисто системная единица в международной системе СИ. Значит в одном МПа точно 10 бар.
Сколько бар в 1 атмосфере
Строго говоря, атмосфера, как единица измерения давления, может быть технической или физической. Техническая точно равна одной килограмм-силе на квадратный сантиметр (кгс/см2), физическая чуть больше за счёт неравенства между килограмм-силой и десятком ньютон.
Разница получается из-за того, что связь между ньютоном и килограмм-силой выводится через ускорение свободного падения на уровне моря, а это не ровно 10, а примерно 9,87. То есть в 1 технической атмосфере (1 at) примерно 0,98 бар, а в физической (1 атм) – 1,013 бар. Такими ошибками всегда можно пренебречь, как и разницей между обеими атмосферными единицами.
Единицы измерения давления
Единица измерения давления в СИ- паскаль (русское обозначение: Па; международное: Pa) = Н/м2
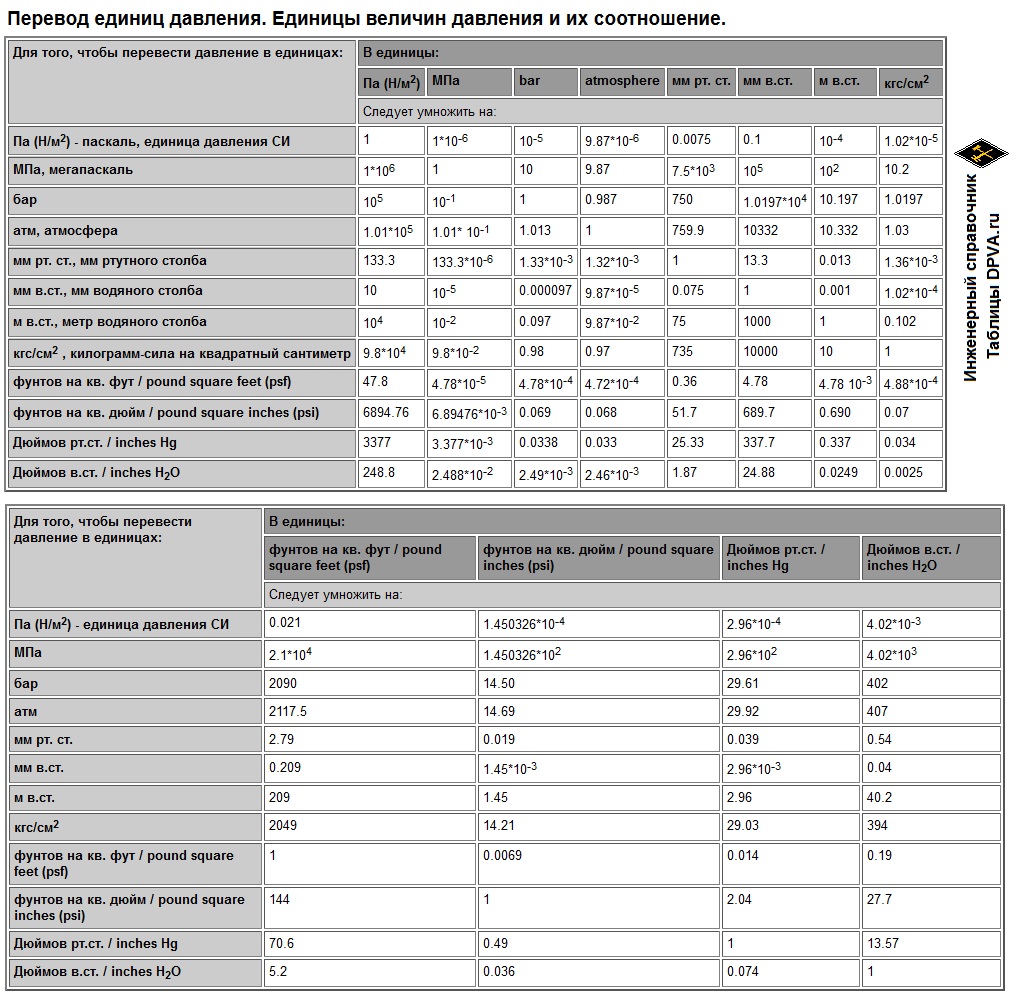
| Таблица перевода единиц измерения давления. Па; МПа; бар; атм; мм рт.ст.; мм в.ст.; м в.ст., кг/см 2; psf; psi; дюймы рт.ст.; дюймы в.ст. | ||||||||
| Для того, чтобы перевести давление в единицах: | В единицы: | |||||||
| Па (Н/м2) | МПа | bar | atmosphere | мм рт. ст. | мм в.ст. | м в.ст. | кгс/см2 | |
| Следует умножить на: | ||||||||
| Па (Н/м2) — единица давления СИ | 1 | 1*10-6 | 10-5 | 9.87*10-6 | 0.0075 | 0.1 | 10-4 | 1.02*10-5 |
| МПа | 1*106 | 1 | 10 | 9.87 | 7.5*103 | 105 | 102 | 10.2 |
| бар | 105 | 10-1 | 1 | 0.987 | 750 | 1.0197*104 | 10.197 | 1.0197 |
| атм | 1.01*105 | 1.01* 10-1 | 1.013 | 1 | 759.9 | 10332 | 10.332 | 1.03 |
| мм рт. ст. | 133.3 | 133.3*10-6 | 1.33*10-3 | 1.32*10-3 | 1 | 13.3 | 0.013 | 1.36*10-3 |
| мм в.ст. | 10 | 10-5 | 0.000097 | 9.87*10-5 | 0.075 | 1 | 0.001 | 1.02*10-4 |
| м в.ст. | 104 | 10-2 | 0.097 | 9.87*10-2 | 75 | 1000 | 1 | 0.102 |
| кгс/см2 | 9.8*104 | 9.8*10-2 | 0.98 | 0.97 | 735 | 10000 | 10 | 1 |
| фунтов на кв. фут / pound square feet (psf) | 47.8 | 4.78*10-5 | 4.78*10-4 | 4.72*10-4 | 0.36 | 4.78 | 4.78 10-3 | 4.88*10-4 |
| фунтов на кв. дюйм / pound square inches (psi) | 6894.76 | 6.89476*10-3 | 0.069 | 0.068 | 51.7 | 689.7 | 0.690 | 0.07 |
| Дюймов рт.ст. / inches Hg | 3377 | 3.377*10-3 | 0.0338 | 0.033 | 25.33 | 337.7 | 0.337 | 0.034 |
| Дюймов в.ст. / inches H2O |
248.8 | 2.488*10-2 | 2.49*10-3 | 2.46*10-3 | 1.87 | 24.88 | 0.0249 | 0.0025 |
| Таблица перевода единиц измерения давления. Па; МПа; бар; атм; мм рт.ст.; мм в.ст.; м в.ст., кг/см 2; psf; psi; дюймы рт.ст.; дюймы в.ст | ||||
| Для того, чтобы перевести давление в единицах: | В единицы: | |||
| фунтов накв.фут/ pound square feet (psf) |
фунтов накв.дюйм/ pound square inches (psi) |
Дюймов рт.ст. / inches Hg |
Дюймов в.ст. / inches H2O |
|
| Следует умножить на: | ||||
| Па (Н/м2) — единица давления СИ | 0.021 | 1.450326*10-4 | 2.96*10-4 | 4.02*10-3 |
| МПа | 2.1*104 | 1.450326*102 | 2.96*102 | 4.02*103 |
| бар | 2090 | 14.50 | 29.61 | 402 |
| атм | 2117.5 | 14.69 | 29.92 | 407 |
| мм рт. ст. | 2.79 | 0.019 | 0.039 | 0.54 |
| мм в.ст. | 0.209 | 1.45*10-3 | 2.96*10-3 | 0.04 |
| м в.ст. | 209 | 1.45 | 2.96 | 40.2 |
| кгс/см2 | 2049 | 14.21 | 29.03 | 394 |
| фунтов на кв. фут / pound square feet (psf) | 1 | 0.0069 | 0.014 | 0.19 |
| фунтов на кв. дюйм / pound square inches (psi) | 144 | 1 | 2.04 | 27.7 |
| Дюймов рт.ст. / inches Hg | 70.6 | 0.49 | 1 | 13.57 |
| Дюймов в.ст. / inches H2O | 5.2 | 0.036 | 0.074 | 1 |
Подробный список единиц давления:
- 1 Па (Н/м2) = 0.0000102 А / Atmosphere (metric)
- 1 Па (Н/м2) = 0.0000099 Атмосфера стандартная Atmosphere (standard) = Standard atmosphere
- 1 Па (Н/м2) = 0.00001 Бар / Bar
- 1 Па (Н/м2) = 10 Барад / Barad
- 1 Па (Н/м2) = 0.0007501 Сантиметров рт. ст. (0 °C)
- 1 Па (Н/м2) = 0.0101974 Сантиметров во. ст. (4 °C)
- 1 Па (Н/м2) = 10 Дин/квадратный сантиметр
- 1 Па (Н/м2) = 0.0003346 Футов водяного столба / Foot of water (4 °C)
- 1 Па (Н/м2) = 10-9 Гигапаскалей
- 1 Па (Н/м2) = 0.01 Гектопаскалей
- 1 Па (Н/м2) = 0.0002953 Дюмов рт.ст. / Inch of mercury (0 °C)
- 1 Па (Н/м2) = 0.0002961 Дюймов рт. ст. / Inch of mercury (15.56 °C)
- 1 Па (Н/м2) = 0.0040186 Дюмов в.ст. / Inch of water (15.56 °C)
- 1 Па (Н/м2) = 0.0040147 Дюмов в.ст. / Inch of water (4 °C)
- 1 Па (Н/м2) = 0.0000102 кгс/см2 / Kilogram force/centimetre2
- 1 Па (Н/м2) = 0.0010197 кгс/дм2 / Kilogram force/decimetre2
- 1 Па (Н/м2) = 0.101972 кгс/м2 / Kilogram force/meter2
- 1 Па (Н/м2) = 10-7 кгс/мм2 / Kilogram force/millimeter2
- 1 Па (Н/м2) = 10-3 кПа
- 1 Па (Н/м2) = 10-7 Килофунтов силы/ квадратный дюйм / Kilopound force/square inch
- 1 Па (Н/м2) = 10-6 МПа
- 1 Па (Н/м2) = 0.000102 Метров в.ст. / Meter of water (4 °C)
- 1 Па (Н/м2) = 10 Микробар / Microbar (barye, barrie)
- 1 Па (Н/м2) = 7.50062 Микронов рт.ст. / Micron of mercury (millitorr)
- 1 Па (Н/м2) = 0.01 Милибар / Millibar
- 1 Па (Н/м2) = 0.0075006 Миллиметров рт.ст / Millimeter of mercury (0 °C)
- 1 Па (Н/м2) = 0.10207 Миллиметров в.ст. / Millimeter of water (15.56 °C)
- 1 Па (Н/м2) = 0.10197 Миллиметров в.ст. / Millimeter of water (4 °C)
- 1 Па (Н/м2) =7.5006 Миллиторр / Millitorr
- 1 Па (Н/м2) = 1Н/м2/ Newton/square meter
- 1 Па (Н/м2) = 32.1507 Повседневных унций / кв. дюйм / Ounce force (avdp)/square inch
- 1 Па (Н/м2) = 0.0208854 Фунтов силы на кв. фут / Pound force/square foot
- 1 Па (Н/м2) = 0.000145 Фунтов силы на кв. дюйм / Pound force/square inch
- 1 Па (Н/м2) = 0.671969 Паундалов на кв. фут / Poundal/square foot
- 1 Па (Н/м2) = 0.0046665 Паундалов на кв. дюйм / Poundal/square inch
- 1 Па (Н/м2) = 0.0000093 Длинных тонн на кв. фут / Ton (long)/foot2
- 1 Па (Н/м2) = 10-7 Длинных тонн на кв. дюйм / Ton (long)/inch2
- 1 Па (Н/м2) = 0.0000104 Коротких тонн на кв. фут / Ton (short)/foot2
- 1 Па (Н/м2) = 10-7 Тонн на кв. дюйм / Ton/inch2
- 1 Па (Н/м2) = 0.0075006 Торр / Torr
- Давление —
- физическая величина, численно равная силе, действующей на единицу площади поверхности перпендикулярно этой поверхности.
Перевод единиц измерения давления онлайн.
Калькулятор давления. Перевод единиц измерения давления (Па, даПa, ГПa, кПa, МПa, кгc/cм2, кгc/м2, aт, мм вод. cт., м вод. cт., мм рт. cт., бaр, мбaр и т.д.)
Результат перевода единиц измерения давления (pp)
Результаты работы калькулятора давления при переводе в другие единицы измерения давления:
Примеры результатов работы калькулятора давления:
Поделится ссылкой на расчет:
Единицы измерения.
- Паскаль — единица измерения давления в СИ. Обозначение в России: Па; международное: Pa. Единицы измерения Па определяются выражением (P=F/S, Н/м2). Данная единица измерения широко применяется при инженерных расчетах, в современной справочной литературе, в обозначение параметров оборудования, технических устройств, при разработке проектной и рабочей документации;
- бар — внесистемные единицы измерения. Обозначение в России: бар; международное: bar. Один бар равен 105 Па. Данная единица измерения широко применяется при обозначение и выборе параметров оборудования, технических устройств;
- миллибар — внесистемные единицы измерения. Обозначение на сайте: мбар. Данная единица измерения широко применяется при обозначение и выборе параметров оборудования, технических устройств (встречает в документации на оборудование иностранного образца);
- мм рт. ст. — внесистемная единица измерения давления. Обозначение в России: мм рт. ст.; международное: mm Hg. Миллиметр рту́тного столба́ равен 101 325 / 760 ≈ 133,3223684 Па;
- мм вод. ст. — внесистемная единица измерения давления. Обозначение в России: мм вод. ст., мм H2O; международное: mm H2O. Миллиметр водяного столба́ равен гидростатическому давлению столба воды высотой 1 мм, оказываемому на плоское основание при температуре воды 4 °С. В Российской Федерации допущен к использованию в качестве внесистемной единицы измерения давления без ограничения срока с областью использования «все области»;
- атмосфера — внесистемная единица измерения давления, приблизительно равная атмосферному давлению на поверхности Земли на уровне Мирового океана. Различают техническую и физическую (нормальная, стандартная) атмосферу. В Российской Федерации к использованию в качестве внесистемной единицы допущена только техническая атмосфера с областью применения «все области». Обозначение в России: ат; международное: at. Существовавшее ранее ограничение срока действия допуска 2016 годом отменено в августе 2015 года. Техническая атмосфера равна давлению, производимому силой в 1 кгс, равномерно распределённой по перпендикулярной к ней плоской поверхности площадью 1 см². В справочной литературе и старой документации встречаются так же (на данный момент не используются):
- ати — избыточной давление;
- ата — абсолютное давление;
- килограмм-силы на см2 — единица давления в системе единиц МКГСС (система единиц измерения, в которой основными единицами являются метр, килограмм-сила и секунд). Обозначение в России: кгс/см2. В Российской Федерации допущена к использованию в качестве внесистемных единиц без ограничения срока действия с областью применения «все области». Килограмм-сила равна силе, сообщающей телу массой один килограмм ускорение 9,80665 м/с².
Перевод единиц измерения давления (в табличном виде).
| Переводимые единицы давления | Перевод давления в единицы: | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Пa | кПа | МПа | бар | мбар | мм рт. ст. | мм вод. ст. | м вод. ст. | ат | кгс/см2 | |
| Па | 1 | 10-3 | 10-6 | 10-5 | 10-2 | 0.0075 | 0.1 | 10-4 | 9.87*10-5 | 1.02*10-5 |
| кПа | 103 | 1 | 10—3 | 10-2 | 10 | 7.5 | 103 | 10-1 | 9.87*10-2 | 1.02*10-3 |
| МПа | 106 | 103 | 1 | 10 | 104 | 7.5*103 | 105 | 102 | 9.87 | 10.2 |
| бар | 105 | 102 | 10-1 | 1 | 103 | 750 | 1.0197*104 | 10.197 | 0.987 | 1.0197 |
| мбар | 102 | 0.1 | 10-4 | 0.001 | 1 | 0.750 | 10.197 | 10.197*10-2 | 0.987*10-3 | 1.0197*10-3 |
| мм рт. ст. | 133.3 | 133.3*10-3 | 133.3*10-6 | 1.33*10-3 | 1.33 | 1 | 13.3 | 0.013 | 1.32*10-3 | 1.36*10-3 |
| мм вод. ст. | 10 | 10-2 | 10-5 | 9.7*10-5 | 0.097 | 0.075 | 1 | 0.001 | 9.87*10-5 | 1.02*10-4 |
| м вод. ст. | 104 | 10 | 10-2 | 0.097 | 97 | 75 | 1000 | 1 | 9.87*10-2 | 0.102 |
| ат | 1.01*105 | 1.01*102 | 1.01* 10-1 | 1.013 | 1013 | 759.9 | 10332 | 10.332 | 1 | 1.03 |
| кгс/см2 | 9.8*104 | 9.8*10 | 9.8*10-2 | 0.98 | 980 | 735 | 10000 | 10 | 0.9708 | 1 |
Порядки единиц измерения давления.
| Порядок единиц измерения | Единицы измерения |
||||||
| Па | ат | мм рт. ст. | мм вод. ст. | кгс/м2 | бар | мбар | |
| 10 | даПa | — | см рт. cт. | см вод. cт. | — | — | — |
| 1 00 | ГПa | — | — | — | — | — | — |
| 1 000 | кПa | — | м рт. cт. | м вод. cт. | — | — | бар |
| 10 000 | — | — | — | — | кгc/cм2 | ||
| 1 000 000 | МПa | — | — | — | — | — |
Виды давления.
Различают три основных вида давления:
- вакуумметрическое давление;
- избыточной давление;
- абсолютное давление.
Вид давления непосредственно связан со сравнением его относительно атмосферного давления (Рат). или с использованием атмосферного давления.
Избыточное давление (Ризб) это величина показывающие на сколько давление в оборудовании или трубопроводе выше атмосферного давления. Т.е. если давление измеряют относительно атмосферного давления, то такое давление называется избыточным. Избыточное давление измеряется с помощью манометров.
Избыточное давление широко применяется в эксплуатации, в том числе:
-
- при выборе и подборе оборудования по паспортным данным;
- при различных классификациях оборудования и трубопроводов на стадиях проектирования и монтажа;
- при нанесении маркировки на оборудование и трубопроводы.
Абсолютное давление (Рабс) это величина давления с учетом действующего атмосферного давления, т.е.:
Рабс=Ризб + Рат;
Другим словами, если давление определяют относительно давления равного 0, то измеренное давление называют абсолютным.
Абсолютное давление применяется в основном инженерно-техническим персоналом (ИТР) при инженерных расчетах и в расчетах при выборе оборудования (основных на применении абсолютного давления). Ярким примером использования абсолютного давления в расчетах служит уравнение состояния идеального газа.
Примером использования абсолютного давления являются:
-
- подбор счетчиков на трубопроводах с газовыми средами (в том числе водяного пара);
- гидравлические расчеты трубопроводов газов (в том числе водяного пара);
- расчеты на прочность оборудования и трубопроводов с газовыми средами (в том числе водяной пар);
- и т.д.
В случаях когда атмосферное давления больше абсолютного давления речь идет о вакуумметрическом давлении (Рвак). Т.е. вакуумметрическое давление это величина давления показывающая на сколько атмосферное давления больше абсолютного давления.
Рвак=Рат — Рабс;
Вакуум широко применяется в технологических процессах на промышленных предприятиях. На всех этих объектах применяется вакуумметрическое давление на стадиях проектирования, монтажа и эксплуатации.
Дополнительная классификация давления в инженерных расчетах.
-
- гидростатическое давление (Pg) — давление столба жидкости (газа) над условным уровнем;
Это давление создаваемое собственным весом жидкости (газа) в определенном сечении, то есть:
Pg=Fg/S, где Fg — вес столба жидкости (газа), S — площадь сечения.
Другая наиболее распространения форма записи гидростатического давления (после преобразования) представляет из себя формулу:
Pg=ρgh, где ρ — плотность жидкости (газа), g — ускорение свободного падения, h — высота столба жидкости (газа).
Гидростатического давления учитывается при расчет открытых систем (связанных с атмосферой). В открытых системах низкого давления учитывать необходимо обязательно (например: вентиляция, системы дымоудаления, газопроводы низкого давления и т.д.).
Примерами гидростатического давления могут служить атмосферное давление, различные гидравлические затворы (например гидрозатвор на деаэраторе), использующие вес водяного столба для предохранения от повышения давления в системы выше допустимого.
Рассчитать гидростатическое давление можно в отдельной теме.
-
- естественное давление (Pe) — вызывается разностью гидростатических давлений двух столбов жидкости (газов) высотой h, имеющей различную среднюю плотность. При расчетах естественное давление обычно учитывают в системах низкого давления (например: естественная вытяжная вентиляция);
Естественное давление обычно рассчитывают по формуле (выведенной из разности гидростатических давлений в двух сечения с разной плотностью):
Pe =( ρ1 — ρ2)ghe,
где ρ1 — плотность жидкости (газа) в 1-ом сечении, ρ2 — плотность жидкости (газа) в 1-ом сечении, he — разность высотных отметок двух сечений.
Рассчитать естественное давление можно в отдельной теме.
-
- парциальное давление (Pp) — называют давление, которое оказывает отдельно взятый компонент из газовой смеси (например, на колбу, баллон или границу атмосферы) исходя из того, что он один займет весь объем смеси при той же температуре. Понятие парциального давления широко используется в химии. Возможно определение парциального давления по уравнению состояния идеального газа при заданном общем объеме смеси и той же температуре. Общее давление смеси газов определяется, как суммам парциальных давлений отдельных компонентов смеси.
- потери давления (ΔP) — называют давление, равное разности давлений в двух сечениях системы. Разность давления обуславливается в основном потерями на преодоления сопротивления при движении вещества в системе (возможно участие естественного и гидростатического давления). Различают сопротивления: путевые и местные. Путевые сопротивления связанны с преодолением трения в системе. Местные сопротивления связаны с изменением скорости движения или направления потока. Потери давления определяются расчетным методом в процессе выполнения гидравлического или аэродинамического расчета системы. Например: гидравлический расчет газопроводов природного газа.
- разряжение (или тяга) — снижение давления в системе, способствующее притоку среды в область пониженного давления. Может быть естественное или принудительное. Примерами использования разряжения (тяги) служат:
- системы естественной вентиляции;
- системы механического дымоудаления (перед дымососам);
- различные системы инжекции (элеваторы в системах отопления, инжекционные газовые горелки и т.д. ), основанные на уменьшении давления в сечении за счет уменьшения площади сечения и увеличении скорости истечения в нем.
Видеоматериал по теме давление и виды давления:
Приборы измерения давления.
Для измерения давления используются измерительные приборы под общим названием — манометры (согласно ГОСТ 8.271-77 манометр это измерительный прибор или измерительная установка для измерения давления или разности давлений). Но в практике сложилось ассоциировать манометры с измерением избыточного давления.
Общая классификация манометров.
-
- по типу измеряемого давления;
- по принципу действия;
- по классу точности;
- по назначению.
По типу измеряемого давления.
Основные виды измеряемого давления разобраны выше. Типы измеряемых давлений шире и содержит производные типы от основных:
-
- манометр абсолютного давления;
- барометр (манометр абсолютного давления для измерения давления околоземной атмосферы), в том числе барограф (барометр с непрерывной записью);
- манометр избыточного давления (обычно просто манометр), в том числе напоромер (манометр избыточного давления в газовых средах с верхним пределом измерения не более 40000 Па /4000 кгс/м2 );
- вакуумметр (манометр для измерения давления разреженного газа) , в том числе тягомер (вакуумметр для измерения давления разреженного газа с верхним пределом измерения не более 40000 Па/4000 кгс/м2);
- мановакуумметр (манометр, для измерения избыточного давления и давления разреженного газа), в том числе тягонапоромер (мановакуумметр для газовых сред с верхним пределом измерения не более 20000 Па/2000 кгс/м2);
- дифференциальный манометр (манометр для измерения разности двух давлений), в том числе микроманометр (дифманометр с верхним пределом измерения не более 40000 Па/4000 кгс/м2);
- измеритель парциальных давлений (манометр для измерения давления, которое оказывал бы один из газов, входящих в газовую смесь, если бы из нее были удалены остальные газы, при условии сохранения первоначальных объема и температуры).
По принципу действия.
По принципу действия манометров общий список классификации включает:
-
- жидкостный манометр;
- U-образный манометр;
- компрессионный манометр;
- колокольный манометр;
- кольцевой манометр;
- грузопоршневой манометр;
- деформационный манометр;
- мембранный манометр;
- сильфонный манометр;
- трубчато-пружинный манометр;
- манометр с вялой мембраной;
- электрический манометр;
- пьезоэлектрический манометр;
- манометр сопротивления;
- ионизационный манометр;
- электронный ионизационный манометр;
- магнитный электроразрядный манометр;
- радиоизотопный манометр;
- тепловой манометр;
- термопарный манометр;
- вязкостный манометр.
В промышленности широко применяются следующие типы манометров:
-
- жидкостные манометры.
- грузопоршневые манометры.
- трубчато-пружинный манометры.
Жидкостные манометров — манометр, принцип действия которого основан на уравновешивании измеряемого давления, или разности давлений, давлением столба жидкости.
Грузопоршневые манометры — манометр, принцип действия которого основан на уравновешивании измеряемого давления давлением, создаваемым весом поршня с грузоприемным устройством, и грузов с учетом сил жидкостного трения.
Трубчато-пружинный манометры- деформационный манометр, в котором чувствительным элементом является трубчатая пружина.
Видеоматериал по теме типы манометров:
По классу точности.
Манометры точности измерения согласно ГОСТ 8.271-77 «Манометры, вакуумметры, мановакуумметры, напоромеры, тягомеры и тягонапоромеры. Общие технические условия» классифицируются на несколько классов точности:
-
- 0,4*;
- 0,6;
- 1,0;
- 1,5;
- 2,5;
- 4,0*.
Примечание: * Устанавливается по заказу потребителя.
Класс точности манометра отражает пределы допустимой основной погрешности в % от диапазона показания шкалы.
Нормы (ГОСТ) устанавливает зависимость диаметра или размера лицевой панели корпуса манометру классу точности:
| Диаметр или размер лицевой панели корпуса, мм, не более | Класс точности | |||||
| 0,4* | 0,6 | 1,0 | 1,5 | 2,5 | 4,0* | |
| 40, 50 | — | — | — | — | + | + |
| 60**, 63 | — | — | + | + | + | + |
| 100 | — | — | + | + | + | — |
| 160 | — | + | + | + | + | — |
| 250 | + | + | + | + | — | — |
| * Устанавливается по заказу потребителя. ** В новых разработках не применять. |
По назначению.
Манометры в зависимости от области применения и рабочей среду по назначению классифицируются:
-
- общетехнические, общепромышленные;
- специальные манометры;
- судовые манометры;
- железнодорожные манометры.
Манометры в зависимости от способа фиксации давления классифицируются:
-
- показывающие;
- самопишущие манометры;
- электроконтактные манометры.
В зависимости от метрологического назначения манометры делятся:
-
- на образцовые (эталонные);
- рабочие;
Калькуляторы давления.
Расчет давления (классическая формула).
Результат расчета давления (Pf)
Формула расчета давления :
Скачать результат расчета давления :

Поделится ссылкой на расчет давления:
Расчет абсолютного давления.
Введите давление (избыточное) (P1)
Введите давление (атмосферное) (Pat)
Результат расчета давления (абсолютного) (Pa)
Формула расчета давления (абсолютного):
Скачать результат расчета давления (абсолютного):

Поделится ссылкой на расчет давления:
Поделиться ссылкой:
This article is about pressure in the physical sciences. For other uses, see Pressure (disambiguation).
| Pressure | |
|---|---|
|
Common symbols |
p, P |
| SI unit | pascal [Pa] |
| In SI base units | 1 N/m2, 1 kg/(m·s2), or 1 J/m3 |
|
Derivations from |
p = F / A |
| Dimension | M L−1 T−2 |
Pressure as exerted by particle collisions inside a closed container
Pressure (symbol: p or P) is the force applied perpendicular to the surface of an object per unit area over which that force is distributed.[1]: 445 Gauge pressure (also spelled gage pressure)[a] is the pressure relative to the ambient pressure.
Various units are used to express pressure. Some of these derive from a unit of force divided by a unit of area; the SI unit of pressure, the pascal (Pa), for example, is one newton per square metre (N/m2); similarly, the pound-force per square inch (psi, symbol lbf/in2) is the traditional unit of pressure in the imperial and U.S. customary systems. Pressure may also be expressed in terms of standard atmospheric pressure; the atmosphere (atm) is equal to this pressure, and the torr is defined as 1⁄760 of this. Manometric units such as the centimetre of water, millimetre of mercury, and inch of mercury are used to express pressures in terms of the height of column of a particular fluid in a manometer.
Definition[edit]
Pressure is the amount of force applied perpendicular to the surface of an object per unit area. The symbol for it is «p» or P.[2]
The IUPAC recommendation for pressure is a lower-case p.[3]
However, upper-case P is widely used. The usage of P vs p depends upon the field in which one is working, on the nearby presence of other symbols for quantities such as power and momentum, and on writing style.
Formula[edit]
Mathematically:
[4]
where:
is the pressure,
is the magnitude of the normal force,
is the area of the surface on contact.
Pressure is a scalar quantity. It relates the vector area element (a vector normal to the surface) with the normal force acting on it. The pressure is the scalar proportionality constant that relates the two normal vectors:
The minus sign comes from the convention that the force is considered towards the surface element, while the normal vector points outward. The equation has meaning in that, for any surface S in contact with the fluid, the total force exerted by the fluid on that surface is the surface integral over S of the right-hand side of the above equation.
It is incorrect (although rather usual) to say «the pressure is directed in such or such direction». The pressure, as a scalar, has no direction. The force given by the previous relationship to the quantity has a direction, but the pressure does not. If we change the orientation of the surface element, the direction of the normal force changes accordingly, but the pressure remains the same.[citation needed]
Pressure is distributed to solid boundaries or across arbitrary sections of fluid normal to these boundaries or sections at every point. It is a fundamental parameter in thermodynamics, and it is conjugate to volume.[5]
Units[edit]
The SI unit for pressure is the pascal (Pa), equal to one newton per square metre (N/m2, or kg·m−1·s−2). This name for the unit was added in 1971;[6] before that, pressure in SI was expressed simply in newtons per square metre.
Other units of pressure, such as pounds per square inch (lbf/in2) and bar, are also in common use. The CGS unit of pressure is the barye (Ba), equal to 1 dyn·cm−2, or 0.1 Pa. Pressure is sometimes expressed in grams-force or kilograms-force per square centimetre (g/cm2 or kg/cm2) and the like without properly identifying the force units. But using the names kilogram, gram, kilogram-force, or gram-force (or their symbols) as units of force is expressly forbidden in SI. The technical atmosphere (symbol: at) is 1 kgf/cm2 (98.0665 kPa, or 14.223 psi).
Pressure is related to energy density and may be expressed in units such as joules per cubic metre (J/m3, which is equal to Pa).
Mathematically:
Some meteorologists prefer the hectopascal (hPa) for atmospheric air pressure, which is equivalent to the older unit millibar (mbar). Similar pressures are given in kilopascals (kPa) in most other fields, except aviation where the hecto- prefix is commonly used. The inch of mercury is still used in the United States. Oceanographers usually measure underwater pressure in decibars (dbar) because pressure in the ocean increases by approximately one decibar per metre depth.
The standard atmosphere (atm) is an established constant. It is approximately equal to typical air pressure at Earth mean sea level and is defined as 101325 Pa.
Because pressure is commonly measured by its ability to displace a column of liquid in a manometer, pressures are often expressed as a depth of a particular fluid (e.g., centimetres of water, millimetres of mercury or inches of mercury). The most common choices are mercury (Hg) and water; water is nontoxic and readily available, while mercury’s high density allows a shorter column (and so a smaller manometer) to be used to measure a given pressure. The pressure exerted by a column of liquid of height h and density ρ is given by the hydrostatic pressure equation p = ρgh, where g is the gravitational acceleration. Fluid density and local gravity can vary from one reading to another depending on local factors, so the height of a fluid column does not define pressure precisely. When millimetres of mercury (or inches of mercury) are quoted today, these units are not based on a physical column of mercury; rather, they have been given precise definitions that can be expressed in terms of SI units.[7] One millimetre of mercury is approximately equal to one torr. The water-based units still depend on the density of water, a measured, rather than defined, quantity. These manometric units are still encountered in many fields. Blood pressure is measured in millimetres of mercury in most of the world, and lung pressures in centimetres of water are still common.[citation needed]
Underwater divers use the metre sea water (msw or MSW) and foot sea water (fsw or FSW) units of pressure, and these are the standard units for pressure gauges used to measure pressure exposure in diving chambers and personal decompression computers. A msw is defined as 0.1 bar (= 100000 Pa = 10000 Pa), is not the same as a linear metre of depth. 33.066 fsw = 1 atm[citation needed] (1 atm = 101325 Pa / 33.066 = 3064.326 Pa). Note that the pressure conversion from msw to fsw is different from the length conversion: 10 msw = 32.6336 fsw, while 10 m = 32.8083 ft.[citation needed]
Gauge pressure is often given in units with «g» appended, e.g. «kPag», «barg» or «psig», and units for measurements of absolute pressure are sometimes given a suffix of «a», to avoid confusion, for example «kPaa», «psia». However, the US National Institute of Standards and Technology recommends that, to avoid confusion, any modifiers be instead applied to the quantity being measured rather than the unit of measure.[8] For example, «pg = 100 psi» rather than «p = 100 psig».
Differential pressure is expressed in units with «d» appended; this type of measurement is useful when considering sealing performance or whether a valve will open or close.
Presently or formerly popular pressure units include the following:
- atmosphere (atm)
- manometric units:
- centimetre, inch, millimetre (torr) and micrometre (mTorr, micron) of mercury,
- height of equivalent column of water, including millimetre (mm H
2O), centimetre (cm H
2O), metre, inch, and foot of water;
- imperial and customary units:
- kip, short ton-force, long ton-force, pound-force, ounce-force, and poundal per square inch,
- short ton-force and long ton-force per square inch,
- fsw (feet sea water) used in underwater diving, particularly in connection with diving pressure exposure and decompression;
- non-SI metric units:
- bar, decibar, millibar,
- msw (metres sea water), used in underwater diving, particularly in connection with diving pressure exposure and decompression,
- kilogram-force, or kilopond, per square centimetre (technical atmosphere),
- gram-force and tonne-force (metric ton-force) per square centimetre,
- barye (dyne per square centimetre),
- kilogram-force and tonne-force per square metre,
- sthene per square metre (pieze).
- bar, decibar, millibar,
Examples[edit]
The effects of an external pressure of 700 bar on an aluminum cylinder with 5 mm (0.197 in) wall thickness
As an example of varying pressures, a finger can be pressed against a wall without making any lasting impression; however, the same finger pushing a thumbtack can easily damage the wall. Although the force applied to the surface is the same, the thumbtack applies more pressure because the point concentrates that force into a smaller area. Pressure is transmitted to solid boundaries or across arbitrary sections of fluid normal to these boundaries or sections at every point. Unlike stress, pressure is defined as a scalar quantity. The negative gradient of pressure is called the force density.[9]
Another example is a knife. If we try to cut with the flat edge, force is distributed over a larger surface area resulting in less pressure, and it will not cut. Whereas using the sharp edge, which has less surface area, results in greater pressure, and so the knife cuts smoothly. This is one example of a practical application of pressure[10]
For gases, pressure is sometimes measured not as an absolute pressure, but relative to atmospheric pressure; such measurements are called gauge pressure. An example of this is the air pressure in an automobile tire, which might be said to be «220 kPa (32 psi)», but is actually 220 kPa (32 psi) above atmospheric pressure. Since atmospheric pressure at sea level is about 100 kPa (14.7 psi), the absolute pressure in the tire is therefore about 320 kPa (46 psi). In technical work, this is written «a gauge pressure of 220 kPa (32 psi)». Where space is limited, such as on pressure gauges, name plates, graph labels, and table headings, the use of a modifier in parentheses, such as «kPa (gauge)» or «kPa (absolute)», is permitted. In non-SI technical work, a gauge pressure of 32 psi (220 kPa) is sometimes written as «32 psig», and an absolute pressure as «32 psia», though the other methods explained above that avoid attaching characters to the unit of pressure are preferred.[8]
Gauge pressure is the relevant measure of pressure wherever one is interested in the stress on storage vessels and the plumbing components of fluidics systems. However, whenever equation-of-state properties, such as densities or changes in densities, must be calculated, pressures must be expressed in terms of their absolute values. For instance, if the atmospheric pressure is 100 kPa (15 psi), a gas (such as helium) at 200 kPa (29 psi) (gauge) (300 kPa or 44 psi [absolute]) is 50% denser than the same gas at 100 kPa (15 psi) (gauge) (200 kPa or 29 psi [absolute]). Focusing on gauge values, one might erroneously conclude the first sample had twice the density of the second one.[citation needed]
Scalar nature[edit]
In a static gas, the gas as a whole does not appear to move. The individual molecules of the gas, however, are in constant random motion. Because we are dealing with an extremely large number of molecules and because the motion of the individual molecules is random in every direction, we do not detect any motion. When the gas is at least partially confined (that is, not free to expand rapidly), the gas will exhibit a static pressure. This confinement can be achieved with either a physical container of some sort, or in a gravitational well such as a planet, otherwise known as atmospheric pressure. In a physical container, the pressure of the gas originates from the molecules colliding with the walls of the container. We can put the walls of our container anywhere inside the gas, and the force per unit area (the pressure) is the same. We can shrink the size of our «container» down to a very small point (becoming less true as we approach the atomic scale), and the pressure will still have a single value at that point. Therefore, pressure is a scalar quantity, not a vector quantity. It has magnitude but no direction sense associated with it. Pressure force acts in all directions at a point inside a gas. At the surface of a gas, the pressure force acts perpendicular (at right angle) to the surface.[citation needed]
A closely related quantity is the stress tensor σ, which relates the vector force 
vector area 

This tensor may be expressed as the sum of the viscous stress tensor minus the hydrostatic pressure. The negative of the stress tensor is sometimes called the pressure tensor, but in the following, the term «pressure» will refer only to the scalar pressure.[citation needed]
According to the theory of general relativity, pressure increases the strength of a gravitational field (see stress–energy tensor) and so adds to the mass-energy cause of gravity. This effect is unnoticeable at everyday pressures but is significant in neutron stars, although it has not been experimentally tested.[11]
Types[edit]
Fluid pressure[edit]
Fluid pressure is most often the compressive stress at some point within a fluid. (The term fluid refers to both liquids and gases – for more information specifically about liquid pressure, see section below.)
Water escapes at high speed from a damaged hydrant that contains water at high pressure
Fluid pressure occurs in one of two situations:
- An open condition, called «open channel flow», e.g. the ocean, a swimming pool, or the atmosphere.
- A closed condition, called «closed conduit», e.g. a water line or gas line.
Pressure in open conditions usually can be approximated as the pressure in «static» or non-moving conditions (even in the ocean where there are waves and currents), because the motions create only negligible changes in the pressure. Such conditions conform with principles of fluid statics. The pressure at any given point of a non-moving (static) fluid is called the hydrostatic pressure.
Closed bodies of fluid are either «static», when the fluid is not moving, or «dynamic», when the fluid can move as in either a pipe or by compressing an air gap in a closed container. The pressure in closed conditions conforms with the principles of fluid dynamics.
The concepts of fluid pressure are predominantly attributed to the discoveries of Blaise Pascal and Daniel Bernoulli. Bernoulli’s equation can be used in almost any situation to determine the pressure at any point in a fluid. The equation makes some assumptions about the fluid, such as the fluid being ideal[12] and incompressible.[12] An ideal fluid is a fluid in which there is no friction, it is inviscid[12] (zero viscosity).[12] The equation for all points of a system filled with a constant-density fluid is[13]
where:
- p, pressure of the fluid,
= ρg, density × acceleration of gravity is the (volume-) specific weight of the fluid,[12]
- v, velocity of the fluid,
- g, acceleration of gravity,
- z, elevation,
, pressure head,
, velocity head.
Applications[edit]
- Hydraulic brakes
- Artesian well
- Blood pressure
- Hydraulic head
- Plant cell turgidity
- Pythagorean cup
- Pressure washing
Explosion or deflagration pressures[edit]
Explosion or deflagration pressures are the result of the ignition of explosive gases, mists, dust/air suspensions, in unconfined and confined spaces.
Negative pressures[edit]
While pressures are, in general, positive, there are several situations in which negative pressures may be encountered:
- When dealing in relative (gauge) pressures. For instance, an absolute pressure of 80 kPa may be described as a gauge pressure of −21 kPa (i.e., 21 kPa below an atmospheric pressure of 101 kPa). For example, abdominal decompression is an obstetric procedure during which negative gauge pressure is applied intermittently to a pregnant woman’s abdomen.
- Negative absolute pressures are possible. They are effectively tension, and both bulk solids and bulk liquids can be put under negative absolute pressure by pulling on them.[14] Microscopically, the molecules in solids and liquids have attractive interactions that overpower the thermal kinetic energy, so some tension can be sustained. Thermodynamically, however, a bulk material under negative pressure is in a metastable state, and it is especially fragile in the case of liquids where the negative pressure state is similar to superheating and is easily susceptible to cavitation.[15] In certain situations, the cavitation can be avoided and negative pressures sustained indefinitely,[15] for example, liquid mercury has been observed to sustain up to −425 atm in clean glass containers.[16] Negative liquid pressures are thought to be involved in the ascent of sap in plants taller than 10 m (the atmospheric pressure head of water).[17]
- The Casimir effect can create a small attractive force due to interactions with vacuum energy; this force is sometimes termed «vacuum pressure» (not to be confused with the negative gauge pressure of a vacuum).
- For non-isotropic stresses in rigid bodies, depending on how the orientation of a surface is chosen, the same distribution of forces may have a component of positive pressure along one surface normal, with a component of negative pressure acting along another surface normal.
- The stresses in an electromagnetic field are generally non-isotropic, with the pressure normal to one surface element (the normal stress) being negative, and positive for surface elements perpendicular to this.
- In cosmology, dark energy creates a very small yet cosmically significant amount of negative pressure, which accelerates the expansion of the universe.
Stagnation pressure[edit]
Stagnation pressure is the pressure a fluid exerts when it is forced to stop moving. Consequently, although a fluid moving at higher speed will have a lower static pressure, it may have a higher stagnation pressure when forced to a standstill. Static pressure and stagnation pressure are related by:
where
is the stagnation pressure,
is the density,
is the flow velocity,
is the static pressure.
The pressure of a moving fluid can be measured using a Pitot tube, or one of its variations such as a Kiel probe or Cobra probe, connected to a manometer. Depending on where the inlet holes are located on the probe, it can measure static pressures or stagnation pressures.
Surface pressure and surface tension[edit]
There is a two-dimensional analog of pressure – the lateral force per unit length applied on a line perpendicular to the force.
Surface pressure is denoted by π:
and shares many similar properties with three-dimensional pressure. Properties of surface chemicals can be investigated by measuring pressure/area isotherms, as the two-dimensional analog of Boyle’s law, πA = k, at constant temperature.
Surface tension is another example of surface pressure, but with a reversed sign, because «tension» is the opposite to «pressure».
Pressure of an ideal gas[edit]
In an ideal gas, molecules have no volume and do not interact. According to the ideal gas law, pressure varies linearly with temperature and quantity, and inversely with volume:
where:
- p is the absolute pressure of the gas,
- n is the amount of substance,
- T is the absolute temperature,
- V is the volume,
- R is the ideal gas constant.
Real gases exhibit a more complex dependence on the variables of state.[18]
Vapour pressure[edit]
Vapour pressure is the pressure of a vapour in thermodynamic equilibrium with its condensed phases in a closed system. All liquids and solids have a tendency to evaporate into a gaseous form, and all gases have a tendency to condense back to their liquid or solid form.
The atmospheric pressure boiling point of a liquid (also known as the normal boiling point) is the temperature at which the vapor pressure equals the ambient atmospheric pressure. With any incremental increase in that temperature, the vapor pressure becomes sufficient to overcome atmospheric pressure and lift the liquid to form vapour bubbles inside the bulk of the substance. Bubble formation deeper in the liquid requires a higher pressure, and therefore higher temperature, because the fluid pressure increases above the atmospheric pressure as the depth increases.
The vapor pressure that a single component in a mixture contributes to the total pressure in the system is called partial vapor pressure.
Liquid pressure[edit]
When a person swims under the water, water pressure is felt acting on the person’s eardrums. The deeper that person swims, the greater the pressure. The pressure felt is due to the weight of the water above the person. As someone swims deeper, there is more water above the person and therefore greater pressure. The pressure a liquid exerts depends on its depth.
Liquid pressure also depends on the density of the liquid. If someone was submerged in a liquid more dense than water, the pressure would be correspondingly greater. Thus, we can say that the depth, density and liquid pressure are directly proportionate. The pressure due to a liquid in liquid columns of constant density or at a depth within a substance is represented by the following formula:
where:
- p is liquid pressure,
- g is gravity at the surface of overlaying material,
- ρ is density of liquid,
- h is height of liquid column or depth within a substance.
Another way of saying the same formula is the following:
| Derivation of this equation |
|---|
| This is derived from the definitions of pressure and weight density. Consider an area at the bottom of a vessel of liquid. The weight of the column of liquid directly above this area produces pressure. From the definition
we can express this weight of liquid as where the volume of the column is simply the area multiplied by the depth. Then we have With the «area» in the numerator and the «area» in the denominator canceling each other out, we are left with Written with symbols, this is our original equation: |
The pressure a liquid exerts against the sides and bottom of a container depends on the density and the depth of the liquid. If atmospheric pressure is neglected, liquid pressure against the bottom is twice as great at twice the depth; at three times the depth, the liquid pressure is threefold; etc. Or, if the liquid is two or three times as dense, the liquid pressure is correspondingly two or three times as great for any given depth. Liquids are practically incompressible – that is, their volume can hardly be changed by pressure (water volume decreases by only 50 millionths of its original volume for each atmospheric increase in pressure). Thus, except for small changes produced by temperature, the density of a particular liquid is practically the same at all depths.
Atmospheric pressure pressing on the surface of a liquid must be taken into account when trying to discover the total pressure acting on a liquid. The total pressure of a liquid, then, is ρgh plus the pressure of the atmosphere. When this distinction is important, the term total pressure is used. Otherwise, discussions of liquid pressure refer to pressure without regard to the normally ever-present atmospheric pressure.
The pressure does not depend on the amount of liquid present. Volume is not the important factor – depth is. The average water pressure acting against a dam depends on the average depth of the water and not on the volume of water held back. For example, a wide but shallow lake with a depth of 3 m (10 ft) exerts only half the average pressure that a small 6 m (20 ft) deep pond does. (The total force applied to the longer dam will be greater, due to the greater total surface area for the pressure to act upon. But for a given 5-foot (1.5 m)-wide section of each dam, the 10 ft (3.0 m) deep water will apply one quarter the force of 20 ft (6.1 m) deep water). A person will feel the same pressure whether their head is dunked a metre beneath the surface of the water in a small pool or to the same depth in the middle of a large lake. If four vases contain different amounts of water but are all filled to equal depths, then a fish with its head dunked a few centimetres under the surface will be acted on by water pressure that is the same in any of the vases. If the fish swims a few centimetres deeper, the pressure on the fish will increase with depth and be the same no matter which vase the fish is in. If the fish swims to the bottom, the pressure will be greater, but it makes no difference what vase it is in. All vases are filled to equal depths, so the water pressure is the same at the bottom of each vase, regardless of its shape or volume. If water pressure at the bottom of a vase were greater than water pressure at the bottom of a neighboring vase, the greater pressure would force water sideways and then up the narrower vase to a higher level until the pressures at the bottom were equalized. Pressure is depth dependent, not volume dependent, so there is a reason that water seeks its own level.
Restating this as energy equation, the energy per unit volume in an ideal, incompressible liquid is constant throughout its vessel. At the surface, gravitational potential energy is large but liquid pressure energy is low. At the bottom of the vessel, all the gravitational potential energy is converted to pressure energy. The sum of pressure energy and gravitational potential energy per unit volume is constant throughout the volume of the fluid and the two energy components change linearly with the depth.[19] Mathematically, it is described by Bernoulli’s equation, where velocity head is zero and comparisons per unit volume in the vessel are
Terms have the same meaning as in section Fluid pressure.
Direction of liquid pressure[edit]
An experimentally determined fact about liquid pressure is that it is exerted equally in all directions.[20] If someone is submerged in water, no matter which way that person tilts their head, the person will feel the same amount of water pressure on their ears. Because a liquid can flow, this pressure isn’t only downward. Pressure is seen acting sideways when water spurts sideways from a leak in the side of an upright can. Pressure also acts upward, as demonstrated when someone tries to push a beach ball beneath the surface of the water. The bottom of a boat is pushed upward by water pressure (buoyancy).
When a liquid presses against a surface, there is a net force that is perpendicular to the surface. Although pressure doesn’t have a specific direction, force does. A submerged triangular block has water forced against each point from many directions, but components of the force that are not perpendicular to the surface cancel each other out, leaving only a net perpendicular point.[20] This is why water spurting from a hole in a bucket initially exits the bucket in a direction at right angles to the surface of the bucket in which the hole is located. Then it curves downward due to gravity. If there are three holes in a bucket (top, bottom, and middle), then the force vectors perpendicular to the inner container surface will increase with increasing depth – that is, a greater pressure at the bottom makes it so that the bottom hole will shoot water out the farthest. The force exerted by a fluid on a smooth surface is always at right angles to the surface. The speed of liquid out of the hole is 
Kinematic pressure[edit]
is the kinematic pressure, where 



- Navier–Stokes equation with kinematic quantities
See also[edit]
- Atmospheric pressure – Static pressure exerted by the weight of the atmosphere
- Blood pressure – Pressure exerted by circulating blood upon the walls of arteries
- Boyle’s law – Relationship between pressure and volume in a gas at constant temperature
- Combined gas law – Combination of Charles’, Boyle’s and Gay-Lussac’s gas laws
- Conversion of units – Comparison of various scales
- Critical point (thermodynamics) – Temperature and pressure point where phase boundaries disappear
- Dimensional analysis – Analysis of the relationships between different physical quantities
- Dynamic pressure – Kinetic energy per unit volume of a fluid
- Electric potential – Line integral of the electric field
- Electron degeneracy pressure – Repulsive force in quantum mechanics
- High pressure – Great force distributed over a small area
- Hydraulics – Fluid engineering and fluid mechanics
- Internal pressure – measure of how the internal energy of a system changes when it expands or contracts at constant temperature
- Kinetic theory – Historical physical model of gases
- Microphone – Device that converts sound into an electrical signal
- Orders of magnitude (pressure) – Range of exerted pressure from vacuums to black holes.
- Partial pressure – Pressure attributed to a component gas in a mixture
- Pressure measurement – Analysis of force applied by a fluid on a surface
- Pressure sensor – Pressure measurement device
- Sound pressure – Local pressure deviation caused by a sound wave
- Static pressure – Term in fluid dynamics; how «heavy» a stagnant fluid is
- Timeline of temperature and pressure measurement technology
- Torricelli’s law – theorem in fluid dynamics
- Vacuum – Space that is empty of matter
- Vacuum pump – Equipment generating a relative vacuum
- Vertical pressure variation – Variation in pressure as a function of elevation
Notes[edit]
- ^ The preferred spelling varies by country and even by industry. Further, both spellings are often used within a particular industry or country. Industries in British English-speaking countries typically use the «gauge» spelling.
References[edit]
- ^ Knight, PhD, Randall D. (2007). «Fluid Mechanics». Physics for Scientists and Engineers: A Strategic Approach (google books) (2nd ed.). San Francisco: Pearson Addison Wesley. p. 1183. ISBN 978-0-321-51671-8. Retrieved 6 April 2020.
Pressure itself is not a Force, even though we sometimes talk «informally» about the «force exerted by the pressure. The correct statement is that the Fluid exerts a force on a surface. In addition, Pressure is a scalar, not a vector.
- ^
Giancoli, Douglas G. (2004). Physics: principles with applications. Upper Saddle River, N.J.: Pearson Education. ISBN 978-0-13-060620-4. - ^
McNaught, A. D.; Wilkinson, A.; Nic, M.; Jirat, J.; Kosata, B.; Jenkins, A. (2014). IUPAC. Compendium of Chemical Terminology, 2nd ed. (the «Gold Book»). 2.3.3. Oxford: Blackwell Scientific Publications. doi:10.1351/goldbook.P04819. ISBN 978-0-9678550-9-7. Archived from the original on 2016-03-04. - ^ R Nave. «Pressure». Hyperphysics. Georgia State University, Dept. of Physics and Astronomy. Retrieved 2022-03-05.
- ^ Alberty, Robert A. (2001). «USE OF LEGENDRE TRANSFORMS IN CHEMICAL THERMODYNAMICS (IUPAC Technical Report)» (PDF). Pure Appl. Chem. 73 (8): 1349–1380. doi:10.1351/pac200173081349. S2CID 98264934. Retrieved 1 November 2021.
See Table 1 Conjugate pairs of variables … (p.1357)
- ^ «14th Conference of the International Bureau of Weights and Measures». Bipm.fr. Archived from the original on 2007-06-30. Retrieved 2012-03-27.
- ^ International Bureau of Weights and Measures (2006), The International System of Units (SI) (PDF) (8th ed.), p. 127, ISBN 92-822-2213-6, archived (PDF) from the original on 2021-06-04, retrieved 2021-12-16
- ^ a b «Rules and Style Conventions for Expressing Values of Quantities». NIST. 2 July 2009. Archived from the original on 2009-07-10. Retrieved 2009-07-07.
- ^ Lautrup, Benny (2005). Physics of continuous matter : exotic and everyday phenomena in the macroscopic world. Bristol: Institute of Physics. p. 50. ISBN 9780750307529.
- ^ Breithaupt, Jim (2015). Physics (Fourth ed.). Basingstoke. p. 106. ISBN 9781137443243.
- ^ Vishwakarma, Ram Gopal (2009). «Einstein’s gravity under pressure». Astrophysics and Space Science. 321 (2): 151–156. arXiv:0705.0825. Bibcode:2009Ap&SS.321..151V. doi:10.1007/s10509-009-0016-8. S2CID 218673952.
- ^ a b c d e Finnemore, John, E. and Joseph B. Franzini (2002). Fluid Mechanics: With Engineering Applications. New York: McGraw Hill, Inc. pp. 14–29. ISBN 978-0-07-243202-2.
{{cite book}}: CS1 maint: multiple names: authors list (link) - ^ NCEES (2011). Fundamentals of Engineering: Supplied Reference Handbook. Clemson, South Carolina: NCEES. p. 64. ISBN 978-1-932613-59-9.
- ^ Imre, A. R. (2007). «How to generate and measure negative pressure in liquids?». Soft Matter under Exogenic Impacts. NATO Science Series II: Mathematics, Physics and Chemistry. Vol. 242. pp. 379–388. doi:10.1007/978-1-4020-5872-1_24. ISBN 978-1-4020-5871-4. ISSN 1568-2609.
- ^ a b Imre, A. R; Maris, H. J; Williams, P. R, eds. (2002). Liquids Under Negative Pressure (Nato Science Series II). Springer. doi:10.1007/978-94-010-0498-5. ISBN 978-1-4020-0895-5.
- ^ Briggs, Lyman J. (1953). «The Limiting Negative Pressure of Mercury in Pyrex Glass». Journal of Applied Physics. 24 (4): 488–490. Bibcode:1953JAP….24..488B. doi:10.1063/1.1721307. ISSN 0021-8979.
- ^ Karen Wright (March 2003). «The Physics of Negative Pressure». Discover. Archived from the original on 8 January 2015. Retrieved 31 January 2015.
- ^ P. Atkins, J. de Paula Elements of Physical Chemistry, 4th Ed, W. H. Freeman, 2006. ISBN 0-7167-7329-5.
- ^ Streeter, V. L., Fluid Mechanics, Example 3.5, McGraw–Hill Inc. (1966), New York.
- ^ a b c Hewitt 251 (2006)[full citation needed]
External links[edit]
- Introduction to Fluid Statics and Dynamics on Project PHYSNET
- Pressure being a scalar quantity
- wikiUnits.org — Convert units of pressure
This article is about pressure in the physical sciences. For other uses, see Pressure (disambiguation).
| Pressure | |
|---|---|
|
Common symbols |
p, P |
| SI unit | pascal [Pa] |
| In SI base units | 1 N/m2, 1 kg/(m·s2), or 1 J/m3 |
|
Derivations from |
p = F / A |
| Dimension | M L−1 T−2 |
Pressure as exerted by particle collisions inside a closed container
Pressure (symbol: p or P) is the force applied perpendicular to the surface of an object per unit area over which that force is distributed.[1]: 445 Gauge pressure (also spelled gage pressure)[a] is the pressure relative to the ambient pressure.
Various units are used to express pressure. Some of these derive from a unit of force divided by a unit of area; the SI unit of pressure, the pascal (Pa), for example, is one newton per square metre (N/m2); similarly, the pound-force per square inch (psi, symbol lbf/in2) is the traditional unit of pressure in the imperial and U.S. customary systems. Pressure may also be expressed in terms of standard atmospheric pressure; the atmosphere (atm) is equal to this pressure, and the torr is defined as 1⁄760 of this. Manometric units such as the centimetre of water, millimetre of mercury, and inch of mercury are used to express pressures in terms of the height of column of a particular fluid in a manometer.
Definition[edit]
Pressure is the amount of force applied perpendicular to the surface of an object per unit area. The symbol for it is «p» or P.[2]
The IUPAC recommendation for pressure is a lower-case p.[3]
However, upper-case P is widely used. The usage of P vs p depends upon the field in which one is working, on the nearby presence of other symbols for quantities such as power and momentum, and on writing style.
Formula[edit]
Mathematically:
[4]
where:
is the pressure,
is the magnitude of the normal force,
is the area of the surface on contact.
Pressure is a scalar quantity. It relates the vector area element (a vector normal to the surface) with the normal force acting on it. The pressure is the scalar proportionality constant that relates the two normal vectors:
The minus sign comes from the convention that the force is considered towards the surface element, while the normal vector points outward. The equation has meaning in that, for any surface S in contact with the fluid, the total force exerted by the fluid on that surface is the surface integral over S of the right-hand side of the above equation.
It is incorrect (although rather usual) to say «the pressure is directed in such or such direction». The pressure, as a scalar, has no direction. The force given by the previous relationship to the quantity has a direction, but the pressure does not. If we change the orientation of the surface element, the direction of the normal force changes accordingly, but the pressure remains the same.[citation needed]
Pressure is distributed to solid boundaries or across arbitrary sections of fluid normal to these boundaries or sections at every point. It is a fundamental parameter in thermodynamics, and it is conjugate to volume.[5]
Units[edit]
The SI unit for pressure is the pascal (Pa), equal to one newton per square metre (N/m2, or kg·m−1·s−2). This name for the unit was added in 1971;[6] before that, pressure in SI was expressed simply in newtons per square metre.
Other units of pressure, such as pounds per square inch (lbf/in2) and bar, are also in common use. The CGS unit of pressure is the barye (Ba), equal to 1 dyn·cm−2, or 0.1 Pa. Pressure is sometimes expressed in grams-force or kilograms-force per square centimetre (g/cm2 or kg/cm2) and the like without properly identifying the force units. But using the names kilogram, gram, kilogram-force, or gram-force (or their symbols) as units of force is expressly forbidden in SI. The technical atmosphere (symbol: at) is 1 kgf/cm2 (98.0665 kPa, or 14.223 psi).
Pressure is related to energy density and may be expressed in units such as joules per cubic metre (J/m3, which is equal to Pa).
Mathematically:
Some meteorologists prefer the hectopascal (hPa) for atmospheric air pressure, which is equivalent to the older unit millibar (mbar). Similar pressures are given in kilopascals (kPa) in most other fields, except aviation where the hecto- prefix is commonly used. The inch of mercury is still used in the United States. Oceanographers usually measure underwater pressure in decibars (dbar) because pressure in the ocean increases by approximately one decibar per metre depth.
The standard atmosphere (atm) is an established constant. It is approximately equal to typical air pressure at Earth mean sea level and is defined as 101325 Pa.
Because pressure is commonly measured by its ability to displace a column of liquid in a manometer, pressures are often expressed as a depth of a particular fluid (e.g., centimetres of water, millimetres of mercury or inches of mercury). The most common choices are mercury (Hg) and water; water is nontoxic and readily available, while mercury’s high density allows a shorter column (and so a smaller manometer) to be used to measure a given pressure. The pressure exerted by a column of liquid of height h and density ρ is given by the hydrostatic pressure equation p = ρgh, where g is the gravitational acceleration. Fluid density and local gravity can vary from one reading to another depending on local factors, so the height of a fluid column does not define pressure precisely. When millimetres of mercury (or inches of mercury) are quoted today, these units are not based on a physical column of mercury; rather, they have been given precise definitions that can be expressed in terms of SI units.[7] One millimetre of mercury is approximately equal to one torr. The water-based units still depend on the density of water, a measured, rather than defined, quantity. These manometric units are still encountered in many fields. Blood pressure is measured in millimetres of mercury in most of the world, and lung pressures in centimetres of water are still common.[citation needed]
Underwater divers use the metre sea water (msw or MSW) and foot sea water (fsw or FSW) units of pressure, and these are the standard units for pressure gauges used to measure pressure exposure in diving chambers and personal decompression computers. A msw is defined as 0.1 bar (= 100000 Pa = 10000 Pa), is not the same as a linear metre of depth. 33.066 fsw = 1 atm[citation needed] (1 atm = 101325 Pa / 33.066 = 3064.326 Pa). Note that the pressure conversion from msw to fsw is different from the length conversion: 10 msw = 32.6336 fsw, while 10 m = 32.8083 ft.[citation needed]
Gauge pressure is often given in units with «g» appended, e.g. «kPag», «barg» or «psig», and units for measurements of absolute pressure are sometimes given a suffix of «a», to avoid confusion, for example «kPaa», «psia». However, the US National Institute of Standards and Technology recommends that, to avoid confusion, any modifiers be instead applied to the quantity being measured rather than the unit of measure.[8] For example, «pg = 100 psi» rather than «p = 100 psig».
Differential pressure is expressed in units with «d» appended; this type of measurement is useful when considering sealing performance or whether a valve will open or close.
Presently or formerly popular pressure units include the following:
- atmosphere (atm)
- manometric units:
- centimetre, inch, millimetre (torr) and micrometre (mTorr, micron) of mercury,
- height of equivalent column of water, including millimetre (mm H
2O), centimetre (cm H
2O), metre, inch, and foot of water;
- imperial and customary units:
- kip, short ton-force, long ton-force, pound-force, ounce-force, and poundal per square inch,
- short ton-force and long ton-force per square inch,
- fsw (feet sea water) used in underwater diving, particularly in connection with diving pressure exposure and decompression;
- non-SI metric units:
- bar, decibar, millibar,
- msw (metres sea water), used in underwater diving, particularly in connection with diving pressure exposure and decompression,
- kilogram-force, or kilopond, per square centimetre (technical atmosphere),
- gram-force and tonne-force (metric ton-force) per square centimetre,
- barye (dyne per square centimetre),
- kilogram-force and tonne-force per square metre,
- sthene per square metre (pieze).
- bar, decibar, millibar,
Examples[edit]
The effects of an external pressure of 700 bar on an aluminum cylinder with 5 mm (0.197 in) wall thickness
As an example of varying pressures, a finger can be pressed against a wall without making any lasting impression; however, the same finger pushing a thumbtack can easily damage the wall. Although the force applied to the surface is the same, the thumbtack applies more pressure because the point concentrates that force into a smaller area. Pressure is transmitted to solid boundaries or across arbitrary sections of fluid normal to these boundaries or sections at every point. Unlike stress, pressure is defined as a scalar quantity. The negative gradient of pressure is called the force density.[9]
Another example is a knife. If we try to cut with the flat edge, force is distributed over a larger surface area resulting in less pressure, and it will not cut. Whereas using the sharp edge, which has less surface area, results in greater pressure, and so the knife cuts smoothly. This is one example of a practical application of pressure[10]
For gases, pressure is sometimes measured not as an absolute pressure, but relative to atmospheric pressure; such measurements are called gauge pressure. An example of this is the air pressure in an automobile tire, which might be said to be «220 kPa (32 psi)», but is actually 220 kPa (32 psi) above atmospheric pressure. Since atmospheric pressure at sea level is about 100 kPa (14.7 psi), the absolute pressure in the tire is therefore about 320 kPa (46 psi). In technical work, this is written «a gauge pressure of 220 kPa (32 psi)». Where space is limited, such as on pressure gauges, name plates, graph labels, and table headings, the use of a modifier in parentheses, such as «kPa (gauge)» or «kPa (absolute)», is permitted. In non-SI technical work, a gauge pressure of 32 psi (220 kPa) is sometimes written as «32 psig», and an absolute pressure as «32 psia», though the other methods explained above that avoid attaching characters to the unit of pressure are preferred.[8]
Gauge pressure is the relevant measure of pressure wherever one is interested in the stress on storage vessels and the plumbing components of fluidics systems. However, whenever equation-of-state properties, such as densities or changes in densities, must be calculated, pressures must be expressed in terms of their absolute values. For instance, if the atmospheric pressure is 100 kPa (15 psi), a gas (such as helium) at 200 kPa (29 psi) (gauge) (300 kPa or 44 psi [absolute]) is 50% denser than the same gas at 100 kPa (15 psi) (gauge) (200 kPa or 29 psi [absolute]). Focusing on gauge values, one might erroneously conclude the first sample had twice the density of the second one.[citation needed]
Scalar nature[edit]
In a static gas, the gas as a whole does not appear to move. The individual molecules of the gas, however, are in constant random motion. Because we are dealing with an extremely large number of molecules and because the motion of the individual molecules is random in every direction, we do not detect any motion. When the gas is at least partially confined (that is, not free to expand rapidly), the gas will exhibit a static pressure. This confinement can be achieved with either a physical container of some sort, or in a gravitational well such as a planet, otherwise known as atmospheric pressure. In a physical container, the pressure of the gas originates from the molecules colliding with the walls of the container. We can put the walls of our container anywhere inside the gas, and the force per unit area (the pressure) is the same. We can shrink the size of our «container» down to a very small point (becoming less true as we approach the atomic scale), and the pressure will still have a single value at that point. Therefore, pressure is a scalar quantity, not a vector quantity. It has magnitude but no direction sense associated with it. Pressure force acts in all directions at a point inside a gas. At the surface of a gas, the pressure force acts perpendicular (at right angle) to the surface.[citation needed]
A closely related quantity is the stress tensor σ, which relates the vector force 
vector area 

This tensor may be expressed as the sum of the viscous stress tensor minus the hydrostatic pressure. The negative of the stress tensor is sometimes called the pressure tensor, but in the following, the term «pressure» will refer only to the scalar pressure.[citation needed]
According to the theory of general relativity, pressure increases the strength of a gravitational field (see stress–energy tensor) and so adds to the mass-energy cause of gravity. This effect is unnoticeable at everyday pressures but is significant in neutron stars, although it has not been experimentally tested.[11]
Types[edit]
Fluid pressure[edit]
Fluid pressure is most often the compressive stress at some point within a fluid. (The term fluid refers to both liquids and gases – for more information specifically about liquid pressure, see section below.)
Water escapes at high speed from a damaged hydrant that contains water at high pressure
Fluid pressure occurs in one of two situations:
- An open condition, called «open channel flow», e.g. the ocean, a swimming pool, or the atmosphere.
- A closed condition, called «closed conduit», e.g. a water line or gas line.
Pressure in open conditions usually can be approximated as the pressure in «static» or non-moving conditions (even in the ocean where there are waves and currents), because the motions create only negligible changes in the pressure. Such conditions conform with principles of fluid statics. The pressure at any given point of a non-moving (static) fluid is called the hydrostatic pressure.
Closed bodies of fluid are either «static», when the fluid is not moving, or «dynamic», when the fluid can move as in either a pipe or by compressing an air gap in a closed container. The pressure in closed conditions conforms with the principles of fluid dynamics.
The concepts of fluid pressure are predominantly attributed to the discoveries of Blaise Pascal and Daniel Bernoulli. Bernoulli’s equation can be used in almost any situation to determine the pressure at any point in a fluid. The equation makes some assumptions about the fluid, such as the fluid being ideal[12] and incompressible.[12] An ideal fluid is a fluid in which there is no friction, it is inviscid[12] (zero viscosity).[12] The equation for all points of a system filled with a constant-density fluid is[13]
where:
- p, pressure of the fluid,
= ρg, density × acceleration of gravity is the (volume-) specific weight of the fluid,[12]
- v, velocity of the fluid,
- g, acceleration of gravity,
- z, elevation,
, pressure head,
, velocity head.
Applications[edit]
- Hydraulic brakes
- Artesian well
- Blood pressure
- Hydraulic head
- Plant cell turgidity
- Pythagorean cup
- Pressure washing
Explosion or deflagration pressures[edit]
Explosion or deflagration pressures are the result of the ignition of explosive gases, mists, dust/air suspensions, in unconfined and confined spaces.
Negative pressures[edit]
While pressures are, in general, positive, there are several situations in which negative pressures may be encountered:
- When dealing in relative (gauge) pressures. For instance, an absolute pressure of 80 kPa may be described as a gauge pressure of −21 kPa (i.e., 21 kPa below an atmospheric pressure of 101 kPa). For example, abdominal decompression is an obstetric procedure during which negative gauge pressure is applied intermittently to a pregnant woman’s abdomen.
- Negative absolute pressures are possible. They are effectively tension, and both bulk solids and bulk liquids can be put under negative absolute pressure by pulling on them.[14] Microscopically, the molecules in solids and liquids have attractive interactions that overpower the thermal kinetic energy, so some tension can be sustained. Thermodynamically, however, a bulk material under negative pressure is in a metastable state, and it is especially fragile in the case of liquids where the negative pressure state is similar to superheating and is easily susceptible to cavitation.[15] In certain situations, the cavitation can be avoided and negative pressures sustained indefinitely,[15] for example, liquid mercury has been observed to sustain up to −425 atm in clean glass containers.[16] Negative liquid pressures are thought to be involved in the ascent of sap in plants taller than 10 m (the atmospheric pressure head of water).[17]
- The Casimir effect can create a small attractive force due to interactions with vacuum energy; this force is sometimes termed «vacuum pressure» (not to be confused with the negative gauge pressure of a vacuum).
- For non-isotropic stresses in rigid bodies, depending on how the orientation of a surface is chosen, the same distribution of forces may have a component of positive pressure along one surface normal, with a component of negative pressure acting along another surface normal.
- The stresses in an electromagnetic field are generally non-isotropic, with the pressure normal to one surface element (the normal stress) being negative, and positive for surface elements perpendicular to this.
- In cosmology, dark energy creates a very small yet cosmically significant amount of negative pressure, which accelerates the expansion of the universe.
Stagnation pressure[edit]
Stagnation pressure is the pressure a fluid exerts when it is forced to stop moving. Consequently, although a fluid moving at higher speed will have a lower static pressure, it may have a higher stagnation pressure when forced to a standstill. Static pressure and stagnation pressure are related by:
where
is the stagnation pressure,
is the density,
is the flow velocity,
is the static pressure.
The pressure of a moving fluid can be measured using a Pitot tube, or one of its variations such as a Kiel probe or Cobra probe, connected to a manometer. Depending on where the inlet holes are located on the probe, it can measure static pressures or stagnation pressures.
Surface pressure and surface tension[edit]
There is a two-dimensional analog of pressure – the lateral force per unit length applied on a line perpendicular to the force.
Surface pressure is denoted by π:
and shares many similar properties with three-dimensional pressure. Properties of surface chemicals can be investigated by measuring pressure/area isotherms, as the two-dimensional analog of Boyle’s law, πA = k, at constant temperature.
Surface tension is another example of surface pressure, but with a reversed sign, because «tension» is the opposite to «pressure».
Pressure of an ideal gas[edit]
In an ideal gas, molecules have no volume and do not interact. According to the ideal gas law, pressure varies linearly with temperature and quantity, and inversely with volume:
where:
- p is the absolute pressure of the gas,
- n is the amount of substance,
- T is the absolute temperature,
- V is the volume,
- R is the ideal gas constant.
Real gases exhibit a more complex dependence on the variables of state.[18]
Vapour pressure[edit]
Vapour pressure is the pressure of a vapour in thermodynamic equilibrium with its condensed phases in a closed system. All liquids and solids have a tendency to evaporate into a gaseous form, and all gases have a tendency to condense back to their liquid or solid form.
The atmospheric pressure boiling point of a liquid (also known as the normal boiling point) is the temperature at which the vapor pressure equals the ambient atmospheric pressure. With any incremental increase in that temperature, the vapor pressure becomes sufficient to overcome atmospheric pressure and lift the liquid to form vapour bubbles inside the bulk of the substance. Bubble formation deeper in the liquid requires a higher pressure, and therefore higher temperature, because the fluid pressure increases above the atmospheric pressure as the depth increases.
The vapor pressure that a single component in a mixture contributes to the total pressure in the system is called partial vapor pressure.
Liquid pressure[edit]
When a person swims under the water, water pressure is felt acting on the person’s eardrums. The deeper that person swims, the greater the pressure. The pressure felt is due to the weight of the water above the person. As someone swims deeper, there is more water above the person and therefore greater pressure. The pressure a liquid exerts depends on its depth.
Liquid pressure also depends on the density of the liquid. If someone was submerged in a liquid more dense than water, the pressure would be correspondingly greater. Thus, we can say that the depth, density and liquid pressure are directly proportionate. The pressure due to a liquid in liquid columns of constant density or at a depth within a substance is represented by the following formula:
where:
- p is liquid pressure,
- g is gravity at the surface of overlaying material,
- ρ is density of liquid,
- h is height of liquid column or depth within a substance.
Another way of saying the same formula is the following:
| Derivation of this equation |
|---|
| This is derived from the definitions of pressure and weight density. Consider an area at the bottom of a vessel of liquid. The weight of the column of liquid directly above this area produces pressure. From the definition
we can express this weight of liquid as where the volume of the column is simply the area multiplied by the depth. Then we have With the «area» in the numerator and the «area» in the denominator canceling each other out, we are left with Written with symbols, this is our original equation: |
The pressure a liquid exerts against the sides and bottom of a container depends on the density and the depth of the liquid. If atmospheric pressure is neglected, liquid pressure against the bottom is twice as great at twice the depth; at three times the depth, the liquid pressure is threefold; etc. Or, if the liquid is two or three times as dense, the liquid pressure is correspondingly two or three times as great for any given depth. Liquids are practically incompressible – that is, their volume can hardly be changed by pressure (water volume decreases by only 50 millionths of its original volume for each atmospheric increase in pressure). Thus, except for small changes produced by temperature, the density of a particular liquid is practically the same at all depths.
Atmospheric pressure pressing on the surface of a liquid must be taken into account when trying to discover the total pressure acting on a liquid. The total pressure of a liquid, then, is ρgh plus the pressure of the atmosphere. When this distinction is important, the term total pressure is used. Otherwise, discussions of liquid pressure refer to pressure without regard to the normally ever-present atmospheric pressure.
The pressure does not depend on the amount of liquid present. Volume is not the important factor – depth is. The average water pressure acting against a dam depends on the average depth of the water and not on the volume of water held back. For example, a wide but shallow lake with a depth of 3 m (10 ft) exerts only half the average pressure that a small 6 m (20 ft) deep pond does. (The total force applied to the longer dam will be greater, due to the greater total surface area for the pressure to act upon. But for a given 5-foot (1.5 m)-wide section of each dam, the 10 ft (3.0 m) deep water will apply one quarter the force of 20 ft (6.1 m) deep water). A person will feel the same pressure whether their head is dunked a metre beneath the surface of the water in a small pool or to the same depth in the middle of a large lake. If four vases contain different amounts of water but are all filled to equal depths, then a fish with its head dunked a few centimetres under the surface will be acted on by water pressure that is the same in any of the vases. If the fish swims a few centimetres deeper, the pressure on the fish will increase with depth and be the same no matter which vase the fish is in. If the fish swims to the bottom, the pressure will be greater, but it makes no difference what vase it is in. All vases are filled to equal depths, so the water pressure is the same at the bottom of each vase, regardless of its shape or volume. If water pressure at the bottom of a vase were greater than water pressure at the bottom of a neighboring vase, the greater pressure would force water sideways and then up the narrower vase to a higher level until the pressures at the bottom were equalized. Pressure is depth dependent, not volume dependent, so there is a reason that water seeks its own level.
Restating this as energy equation, the energy per unit volume in an ideal, incompressible liquid is constant throughout its vessel. At the surface, gravitational potential energy is large but liquid pressure energy is low. At the bottom of the vessel, all the gravitational potential energy is converted to pressure energy. The sum of pressure energy and gravitational potential energy per unit volume is constant throughout the volume of the fluid and the two energy components change linearly with the depth.[19] Mathematically, it is described by Bernoulli’s equation, where velocity head is zero and comparisons per unit volume in the vessel are
Terms have the same meaning as in section Fluid pressure.
Direction of liquid pressure[edit]
An experimentally determined fact about liquid pressure is that it is exerted equally in all directions.[20] If someone is submerged in water, no matter which way that person tilts their head, the person will feel the same amount of water pressure on their ears. Because a liquid can flow, this pressure isn’t only downward. Pressure is seen acting sideways when water spurts sideways from a leak in the side of an upright can. Pressure also acts upward, as demonstrated when someone tries to push a beach ball beneath the surface of the water. The bottom of a boat is pushed upward by water pressure (buoyancy).
When a liquid presses against a surface, there is a net force that is perpendicular to the surface. Although pressure doesn’t have a specific direction, force does. A submerged triangular block has water forced against each point from many directions, but components of the force that are not perpendicular to the surface cancel each other out, leaving only a net perpendicular point.[20] This is why water spurting from a hole in a bucket initially exits the bucket in a direction at right angles to the surface of the bucket in which the hole is located. Then it curves downward due to gravity. If there are three holes in a bucket (top, bottom, and middle), then the force vectors perpendicular to the inner container surface will increase with increasing depth – that is, a greater pressure at the bottom makes it so that the bottom hole will shoot water out the farthest. The force exerted by a fluid on a smooth surface is always at right angles to the surface. The speed of liquid out of the hole is 
Kinematic pressure[edit]
is the kinematic pressure, where 



- Navier–Stokes equation with kinematic quantities
See also[edit]
- Atmospheric pressure – Static pressure exerted by the weight of the atmosphere
- Blood pressure – Pressure exerted by circulating blood upon the walls of arteries
- Boyle’s law – Relationship between pressure and volume in a gas at constant temperature
- Combined gas law – Combination of Charles’, Boyle’s and Gay-Lussac’s gas laws
- Conversion of units – Comparison of various scales
- Critical point (thermodynamics) – Temperature and pressure point where phase boundaries disappear
- Dimensional analysis – Analysis of the relationships between different physical quantities
- Dynamic pressure – Kinetic energy per unit volume of a fluid
- Electric potential – Line integral of the electric field
- Electron degeneracy pressure – Repulsive force in quantum mechanics
- High pressure – Great force distributed over a small area
- Hydraulics – Fluid engineering and fluid mechanics
- Internal pressure – measure of how the internal energy of a system changes when it expands or contracts at constant temperature
- Kinetic theory – Historical physical model of gases
- Microphone – Device that converts sound into an electrical signal
- Orders of magnitude (pressure) – Range of exerted pressure from vacuums to black holes.
- Partial pressure – Pressure attributed to a component gas in a mixture
- Pressure measurement – Analysis of force applied by a fluid on a surface
- Pressure sensor – Pressure measurement device
- Sound pressure – Local pressure deviation caused by a sound wave
- Static pressure – Term in fluid dynamics; how «heavy» a stagnant fluid is
- Timeline of temperature and pressure measurement technology
- Torricelli’s law – theorem in fluid dynamics
- Vacuum – Space that is empty of matter
- Vacuum pump – Equipment generating a relative vacuum
- Vertical pressure variation – Variation in pressure as a function of elevation
Notes[edit]
- ^ The preferred spelling varies by country and even by industry. Further, both spellings are often used within a particular industry or country. Industries in British English-speaking countries typically use the «gauge» spelling.
References[edit]
- ^ Knight, PhD, Randall D. (2007). «Fluid Mechanics». Physics for Scientists and Engineers: A Strategic Approach (google books) (2nd ed.). San Francisco: Pearson Addison Wesley. p. 1183. ISBN 978-0-321-51671-8. Retrieved 6 April 2020.
Pressure itself is not a Force, even though we sometimes talk «informally» about the «force exerted by the pressure. The correct statement is that the Fluid exerts a force on a surface. In addition, Pressure is a scalar, not a vector.
- ^
Giancoli, Douglas G. (2004). Physics: principles with applications. Upper Saddle River, N.J.: Pearson Education. ISBN 978-0-13-060620-4. - ^
McNaught, A. D.; Wilkinson, A.; Nic, M.; Jirat, J.; Kosata, B.; Jenkins, A. (2014). IUPAC. Compendium of Chemical Terminology, 2nd ed. (the «Gold Book»). 2.3.3. Oxford: Blackwell Scientific Publications. doi:10.1351/goldbook.P04819. ISBN 978-0-9678550-9-7. Archived from the original on 2016-03-04. - ^ R Nave. «Pressure». Hyperphysics. Georgia State University, Dept. of Physics and Astronomy. Retrieved 2022-03-05.
- ^ Alberty, Robert A. (2001). «USE OF LEGENDRE TRANSFORMS IN CHEMICAL THERMODYNAMICS (IUPAC Technical Report)» (PDF). Pure Appl. Chem. 73 (8): 1349–1380. doi:10.1351/pac200173081349. S2CID 98264934. Retrieved 1 November 2021.
See Table 1 Conjugate pairs of variables … (p.1357)
- ^ «14th Conference of the International Bureau of Weights and Measures». Bipm.fr. Archived from the original on 2007-06-30. Retrieved 2012-03-27.
- ^ International Bureau of Weights and Measures (2006), The International System of Units (SI) (PDF) (8th ed.), p. 127, ISBN 92-822-2213-6, archived (PDF) from the original on 2021-06-04, retrieved 2021-12-16
- ^ a b «Rules and Style Conventions for Expressing Values of Quantities». NIST. 2 July 2009. Archived from the original on 2009-07-10. Retrieved 2009-07-07.
- ^ Lautrup, Benny (2005). Physics of continuous matter : exotic and everyday phenomena in the macroscopic world. Bristol: Institute of Physics. p. 50. ISBN 9780750307529.
- ^ Breithaupt, Jim (2015). Physics (Fourth ed.). Basingstoke. p. 106. ISBN 9781137443243.
- ^ Vishwakarma, Ram Gopal (2009). «Einstein’s gravity under pressure». Astrophysics and Space Science. 321 (2): 151–156. arXiv:0705.0825. Bibcode:2009Ap&SS.321..151V. doi:10.1007/s10509-009-0016-8. S2CID 218673952.
- ^ a b c d e Finnemore, John, E. and Joseph B. Franzini (2002). Fluid Mechanics: With Engineering Applications. New York: McGraw Hill, Inc. pp. 14–29. ISBN 978-0-07-243202-2.
{{cite book}}: CS1 maint: multiple names: authors list (link) - ^ NCEES (2011). Fundamentals of Engineering: Supplied Reference Handbook. Clemson, South Carolina: NCEES. p. 64. ISBN 978-1-932613-59-9.
- ^ Imre, A. R. (2007). «How to generate and measure negative pressure in liquids?». Soft Matter under Exogenic Impacts. NATO Science Series II: Mathematics, Physics and Chemistry. Vol. 242. pp. 379–388. doi:10.1007/978-1-4020-5872-1_24. ISBN 978-1-4020-5871-4. ISSN 1568-2609.
- ^ a b Imre, A. R; Maris, H. J; Williams, P. R, eds. (2002). Liquids Under Negative Pressure (Nato Science Series II). Springer. doi:10.1007/978-94-010-0498-5. ISBN 978-1-4020-0895-5.
- ^ Briggs, Lyman J. (1953). «The Limiting Negative Pressure of Mercury in Pyrex Glass». Journal of Applied Physics. 24 (4): 488–490. Bibcode:1953JAP….24..488B. doi:10.1063/1.1721307. ISSN 0021-8979.
- ^ Karen Wright (March 2003). «The Physics of Negative Pressure». Discover. Archived from the original on 8 January 2015. Retrieved 31 January 2015.
- ^ P. Atkins, J. de Paula Elements of Physical Chemistry, 4th Ed, W. H. Freeman, 2006. ISBN 0-7167-7329-5.
- ^ Streeter, V. L., Fluid Mechanics, Example 3.5, McGraw–Hill Inc. (1966), New York.
- ^ a b c Hewitt 251 (2006)[full citation needed]
External links[edit]
- Introduction to Fluid Statics and Dynamics on Project PHYSNET
- Pressure being a scalar quantity
- wikiUnits.org — Convert units of pressure




 главная страница / / Техническая информация / / Алфавиты, номиналы, единицы / / Перевод единиц измерения величин. Перевод единиц измерения физических величин. Таблицы перевода единиц величин. Перевод химических и технических единиц измерения величин. Величины измерения. Таблицы соответствия величин. / / Перевод единиц измерения Давления и вакуума. Единицы давления. Единицы вакуума. / / Единицы измерения давления. Таблица перевода единиц измерения давления. Единицы давления. Единицы вакуума.Па; МПа; бар; атм; мм рт.ст. = торр = тор; мм в.ст.; м в.ст., кг/см2; кгс/см2; psf; psi; дюймы рт.ст.; дюймы в.ст…
главная страница / / Техническая информация / / Алфавиты, номиналы, единицы / / Перевод единиц измерения величин. Перевод единиц измерения физических величин. Таблицы перевода единиц величин. Перевод химических и технических единиц измерения величин. Величины измерения. Таблицы соответствия величин. / / Перевод единиц измерения Давления и вакуума. Единицы давления. Единицы вакуума. / / Единицы измерения давления. Таблица перевода единиц измерения давления. Единицы давления. Единицы вакуума.Па; МПа; бар; атм; мм рт.ст. = торр = тор; мм в.ст.; м в.ст., кг/см2; кгс/см2; psf; psi; дюймы рт.ст.; дюймы в.ст…