Как правильно пишется слово «интерпретатор»
интерпрета́тор
интерпрета́тор, -а
Источник: Орфографический
академический ресурс «Академос» Института русского языка им. В.В. Виноградова РАН (словарная база
2020)
Делаем Карту слов лучше вместе
Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать
Карту слов. Я отлично
умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!
Спасибо! Я стал чуточку лучше понимать мир эмоций.
Вопрос: подсека — это что-то нейтральное, положительное или отрицательное?
Синонимы к слову «интерпретатор»
Предложения со словом «интерпретатор»
- Мы думаем, что нормировать рецепцию, как это предполагает позиция интерпретатора, необязательно.
- Специалист в литературоведении – это издатель сочинений, собиратель архива, при этом дотошный интерпретатор текстов.
- Вы станете первыми и главными интерпретаторами поведения детей из других социальных групп.
- (все предложения)
Значение слова «интерпретатор»
-
ИНТЕРПРЕТА́ТОР, -а, м. Книжн. Тот, кто интерпретирует что-л.; истолкователь. (Малый академический словарь, МАС)
Все значения слова ИНТЕРПРЕТАТОР
Отправить комментарий
Дополнительно
- Download source — 2.9 KB
Writing Interpreters and Compilers
Writing an interpreter or a compiler is one of the most educational tasks in programming because you can become familiarized with the details of the code interpretation and evaluation process. You can obtain much deeper knowledge of what sorts of things are going on behind the scenes and gain some insights into the decisions behind language design.
This article will perform a basic overview of this process by showing how to write an interpreter for a simple language that we can use for a calculator application.
This article assumes that you have intermediate programming experience and basic familiarity with JavaScript.
Some Background
The Difference Between Interpreters, Compilers and Transpilers
In this article, we will be creating an interpreter, as opposed to a compiler. Our program will take some code as input and immediately execute it.
If we were writing a compiler, we would instead transform the inputted code in the source language into code in some lower-level target language, such as MSIL, or an assembly language, or even machine code.
A transpiler is similar to a compiler, except that the source language and target language are about the same level of abstraction. The canonical example of this in the client side web programming world is CoffeeScript, which transcompiles into JavaScript.
The Traditional Language Code Interpretation Process
Most compilers will interpret code in a multi-step process that involves processes that include lexical analysis, preprocessing, parsing, optimization, and finally code generation, or, in the case of an interpreter, evaluation.
In this article, we will only focus on lexing, parsing, and evaluation.
Lexing
A lexer takes a input a string of characters, and outputs a list of tokens. For example, if we had some code like this…
(12 + 4) / 6
…the lexer would divide it up into the individual parts, called tokens, and output a list that might look something like this
[ ["operator", "("], ["number", 12], ["operator", "+"], ["number", 4], ["operator", ")"], ["operator", "/"], ["number", 6] ]
This process is usually relatively simple. Somebody with a little bit of experience with string manipulation can work their way through building a lexer fairly quickly.
Parsing
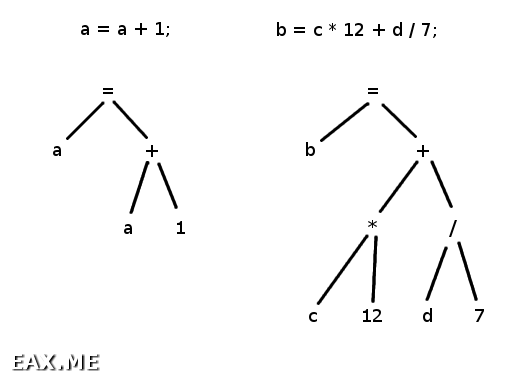
The parser takes the list of tokens produced by the lexer as input, parses it according to some syntax rules, and outputs a representation of the syntactic structure called a parse tree.
{
operation: "/",
left: {
operation: "+",
left: 12,
right: 4
}
right: 6
}
This tends to be the most difficult part of the process.
Evaluation
The evaluator takes the parse tree produced by the parser and evaluates it. Evaluators usually traverse the parse tree recursively. Given the syntax tree above, the evaluator might first evaluate the left operand of the top-level / operation, then the right operand, and then return the result of the division.
Evaluating the left operand would simplify the syntax tree to this:
{
operation: "/",
left: 16,
right: 6
}
which in turn will evaluate to the final result:
2.6666666666666665
AEL: The Calculator Language
Before we can start writing our interpreter, we need to understand the language that we will be interpreting, which I just made up and will refer to as AEL, short for Arithmetic Expression Language.
The language is written as a series of arithmetic expressions composed of numbers and the arithmetic operators + (addition), - (subtraction and negation), * (multiplication), / (division), % (modulo), ^ (exponentiation), as well as parentheses () for grouping.
The interpreter will evaluate each expression and print the result of each in the order that they were presented. For example, given the following input…
3 2 ^ 8 (12 % 7) * (3 + 2) 19 / -9
…the interpreter will output:
3 256 25 -2.111111111111111
AEL also will allow you to define variable assignments using the = operator. The left hand side will be some identifier, and the right hand side will be an arithmetic expression. A statement with an assignment has no return value, so the interpreter will not print out a corresponding line.
For example:
hoursPerDay = 24 minutesPerHour = 60 minutesPerDay = minutesPerHour * hoursPerDay minutesPerDay minutesPerDay * 60
outputs:
1440 86400
AEL will have two pre-defined variables: pi and e, which will correspond to the values 3.141592653589793 and 2.718281828459045, respectively.
Finally, AEL will allow you to define functions. A function assignment also uses the = operator, but the left hand argument must be an identifier followed by parentheses, which will contain zero or more argument names separated by commas. Once defined, a function can be called by writing an identifier name followed by parentheses containing zero or more arithmetic expressions separated by commas.
For example:
toDegrees(radians) = radians * 180 / pi toDegrees(2 * pi) cylinderVolume(r, h) = pi * r ^ 2 * h cylinderVolume(2, 4)
outputs:
360 50.26548245743669
Now that we know what the language is like, we can start writing the interpreter.
For reference, I have put an implementation of an AEL interpreter online.
Step 1: The Lexer
The lexer takes text input and returns a list of tokens. The skeleton of our lex function thus should look like this:
var lex = function (input) { var tokens = []; return tokens; };
We have several different types of tokens. There are operators, which are defined by the set of characters +-*/^%=(), there are numbers composed of numeral digits, there is whitespace, which our lexer will ignore, and there are identifiers, which will be defined as any string of characters that does not contain operators, digits, or whitespace.
var isOperator = function (c) { return /[+-*/^%=(),]/.test(c); }, isDigit = function (c) { return /[0-9]/.test(c); }, isWhiteSpace = function (c) { return /s/.test(c); }, isIdentifier = function (c) { return typeof c === "string" && !isOperator(c) && !isDigit(c) && !isWhiteSpace(c); };
We will create a simple loop to scan the input text. We will have a variable c which corresponds to the current character, create a function called advance to step forward one character in the input and return the next character, and a function called addToken which appends a token to the list of tokens.
var tokens = [], c, i = 0; var advance = function () { return c = input[++i]; }; var addToken = function (type, value) { tokens.push({ type: type, value: value }); }; while (i < input.length) { c = input[i]; }
If c is whitespace, we just ignore it and move on. If c is an operator, add an operator token to the list and move on.
if (isWhiteSpace(c)) advance(); else if (isOperator(c)) { addToken(c); advance(); }
For simplicity, we will define a number as a series of digits, optionally followed by a decimal point and another series of digits.
else if (isDigit(c)) { var num = c; while (isDigit(advance())) num += c; if (c === ".") { do num += c; while (isDigit(advance())); } num = parseFloat(num); if (!isFinite(num)) throw "Number is too large or too small for a 64-bit double."; addToken("number", num); }
Every other character is an identifier.
else if (isIdentifier(c)) { var idn = c; while (isIdentifier(advance())) idn += c; addToken("identifier", idn); }
And, just in case something weird gets thrown at us:
else throw "Unrecognized token.";
After we’re done scanning the input, we’ll add a token to demarcate the end. Then we’re done.
addToken("(end)"); return tokens;
Step 2: The Parser
There are lots of different strategies for writing a parser. One of the most common is writing a Backus-Naur grammar and using recursive descent. In this article, we will be using a somewhat less common strategy called operator-precedence parsing, using techniques described Douglas Crockford’s Top Down Operator Precedence article.
Operator precedence parsing begins with the following process:
- Associate every operational token with a left binding power, and an operational function.
- If the operator manipulates tokens to its left (such as
+), associate it with a left denotative function (hereafter abbreviated asled). If the operator does not manipulate the tokens on its left (such as the unary-), associate it with anulldenotative function (hereafter abbreviated asnud). Identifiers and numbers also have anudfunction associated with them.
After this is done, it can start to generate the parse tree. To show how this works, I’ll use the arithmetic expression below as an example.
12 + 4 / 6
The parser function starts by executing the nud of the first token (12), which returns itself.
{ type: "number", value: 12 }
This become the left hand side that we pass into the led of the next token (+), which will recursively call the parser function to parse the remaining tokens.
{
type: "+",
left: { type: "number", value: 12 },
right:
}
We start over by calling the nud of the first of the remaining tokens (4), which will return itself.
{ type: "number", value: 4 }
This becomes the left hand side that we pass into the led of the next token (/), which will recursively call the parser function to parse the remaining tokens.
{
type: "+",
left: { type: "number", value: 12 },
right: {
type: "/"
left: { type: "number", value: 4 },
right:
}
}
We call the nud of the first of the remaining tokens (6), which will return itself. This is the end of the list of tokens, so the parse tree is complete.
{
type: "+",
left: { type: "number", value: 12 },
right: {
type: "/"
left: { type: "number", value: 4 },
right: { type: "number", value: 6 }
}
}
If we now switch the + and /, we will see how binding power comes into play. / has a higher binding power than +, so it will bind more tightly to the operands around it.
12 / 4 + 6
We start out the same way as before:
{
type: "/",
left: { type: "number", value: 12 },
right:
}
But this time, after we call the nud of the 4, we will look ahead one token, and see that + has lower precedence than the /. This means that we will stick the 4 in the right hand side, and then pass the entire current tree into the led of +, which makes us end up with this parse tree:
{
type: "+",
left: {
type: "/",
left: { type: "number", value: 12 },
right: { type: "number", value: 4 }
},
right: { type: "number", value: 6 },
}
Now that we have some understanding of the parsing process, we can begin writing our parser. The parser accepts the tokens that the lexer produced, and returns a parse tree, so the skeleton of our parse function will look like this:
var parse = function (tokens) { var parseTree = []; return parseTree; };
We need to have some sort of symbol table that associates symbol with a binding power, nud or led, and we need a function that will associate a token with the corresponding symbol.
var symbols = {}, symbol = function (id, nud, lbp, led) { var sym = symbols[id] || {}; symbols[id] = { lbp: sym.lbp || lbp, nud: sym.nud || nud, led: sym.led || led }; }; var interpretToken = function (token) { var sym = Object.create(symbols[token.type]); sym.type = token.type; sym.value = token.value; return sym; };
We need some way to see what the current token is and a way to advance to the next token.
var i = 0, token = function () { return interpretToken(tokens[i]); }; var advance = function () { i++; return token(); };
Now we can write an expression function which will generate the parse tree of an expression according to the way it was described above:
var expression = function (rbp) { var left, t = token(); advance(); if (!t.nud) throw "Unexpected token: " + t.type; left = t.nud(t); while (rbp < token().lbp) { t = token(); advance(); if (!t.led) throw "Unexpected token: " + t.type; left = t.led(left); } return left; };
We can now create the infix and prefix functions, which we will be able to use to define operators:
var infix = function (id, lbp, rbp, led) { rbp = rbp || lbp; symbol(id, null, lbp, led || function (left) { return { type: id, left: left, right: expression(rbp) }; }); }, prefix = function (id, rbp) { symbol(id, function () { return { type: id, right: expression(rbp) }; }); };
Now we can define all of arithmetic operators declaratively. Note that the exponentiation operator (^) has a right binding power that is smaller than its left binding power. This is because exponentiation is right associative.
prefix("-", 7); infix("^", 6, 5); infix("*", 4); infix("/", 4); infix("%", 4); infix("+", 3); infix("-", 3);
There are some operators that just exist as separation or end demarcation. They are not prefixes or infixes so it is sufficient to add them to the symbol table.
symbol(","); symbol(")"); symbol("(end)");
The parentheses nud just returns what is inside of it, and the number nud just returns itself.
symbol("(", function () { value = expression(2); if (token().type !== ")") throw "Expected closing parenthesis ')'"; advance(); return value; }); symbol("number", function (number) { return number; });
The identifier nud and the = operator’s nud are more complicated because they have context-dependent behaviour.
symbol("identifier", function (name) { if (token().type === "(") { var args = []; if (tokens[i + 1].type === ")") advance(); else { do { advance(); args.push(expression(2)); } while (token().type === ","); if (token().type !== ")") throw "Expected closing parenthesis ')'"; } advance(); return { type: "call", args: args, name: name.value }; } return name; }); infix("=", 1, 2, function (left) { if (left.type === "call") { for (var i = 0; i < left.args.length; i++) { if (left.args[i].type !== "identifier") throw "Invalid argument name"; } return { type: "function", name: left.name, args: left.args, value: expression(2) }; } else if (left.type === "identifier") { return { type: "assign", name: left.value, value: expression(2) }; } else throw "Invalid lvalue"; });
Now that all the hard stuff is out of the way, we can just put on the finishing glue.
var parseTree = []; while (token().type !== "(end)") { parseTree.push(expression(0)); } return parseTree;
Step 3: The Evaluator
The evaluator accepts the parse tree generated by the parser, evaluates each item, and produces the evaluated output. The skeleton of our evaluate function will look like this:
var evaluate = function (parseTree) { var parseNode = function (node) { }; var output = ""; for (var i = 0; i < parseTree.length; i++) { var value = parseNode(parseTree[i]); if (typeof value !== "undefined") output += value + "n"; } return output; };
It is straightforward to define the behavior of the operators and all of the predefined variables and functions:
var operators = { "+": function(a, b) { return a + b; }, "-": function(a, b) { if (typeof b === "undefined") return -a; return a - b; }, "*": function(a, b) { return a * b; }, "/": function(a, b) { return a / b; }, "%": function(a, b) { return a % b; }, "^": function(a, b) { return Math.pow(a, b); } }; var variables = { pi: Math.PI, e: Math.E }; var functions = { sin: Math.sin, cos: Math.cos, tan: Math.cos, asin: Math.asin, acos: Math.acos, atan: Math.atan, abs: Math.abs, round: Math.round, ceil: Math.ceil, floor: Math.floor, log: Math.log, exp: Math.exp, sqrt: Math.sqrt, max: Math.max, min: Math.min, random: Math.random }; var args = {};
Now we can put in the meat of our evaluator, and we’re done. The parseNode function recursively traverses and evaluates the parse tree.
var parseNode = function (node) { if (node.type === "number") return node.value; else if (operators[node.type]) { if (node.left) return operators[node.type](parseNode(node.left), parseNode(node.right)); return operators[node.type](parseNode(node.right)); } else if (node.type === "identifier") { var value = args.hasOwnProperty(node.value) ? args[node.value] : variables[node.value]; if (typeof value === "undefined") throw node.value + " is undefined"; return value; } else if (node.type === "assign") { variables[node.name] = parseNode(node.value); } else if (node.type === "call") { for (var i = 0; i < node.args.length; i++) node.args[i] = parseNode(node.args[i]); return functions[node.name].apply(null, node.args); } else if (node.type === "function") { functions[node.name] = function () { for (var i = 0; i < node.args.length; i++) { args[node.args[i].value] = arguments[i]; } var ret = parseNode(node.value); args = {}; return ret; }; } };
Putting It All Together
Now we can wrap it all up and put the thee pieces together in one single calculate function.
var calculate = function (input) { try { var tokens = lex(input); var parseTree = parse(tokens); var output = evaluate(parseTree); return output; } catch (e) { return e; } };
What To Do Next
There are many things you could add to the language to make it more useful or just to see how things work. Some additions would be fairly easy, some could be very hard.
Easy Stuff
- Play around with adding your own predefined functions.
- Fiddle with the binding power numbers to see how that changes the way expressions are evaluated.
- Allow scientific notation in number literals or make it possible to use binary or hexidecimal number literals.
Intermediate Stuff
- Allow manipulation of more types of data, such as strings, booleans and arrays.
- Allow functions to have multiple statements and conditionally return values.
- Replace the evaluator with a compiler or transpiler that takes the parse tree and outputs code in another language.
- Make a package manager that allows you to import code from other files.
Harder Stuff
- Implement optimizations to allow calculations to be performed more quickly.
- Make function first-class citizens and allow closures.
- Make it so that all the data is evaluated lazily.
If you know how to do some of this stuff, you are prepared to start making interpreters and compilers for your own domain specific languages.
That’s All, Folks!
If there is an error in this article or you see some way to make either the code or the explanations of the code easier to understand, let me know, and I can update it accordingly.
History
- 30th October, 2014: Initial version
- Download source — 2.9 KB
Writing Interpreters and Compilers
Writing an interpreter or a compiler is one of the most educational tasks in programming because you can become familiarized with the details of the code interpretation and evaluation process. You can obtain much deeper knowledge of what sorts of things are going on behind the scenes and gain some insights into the decisions behind language design.
This article will perform a basic overview of this process by showing how to write an interpreter for a simple language that we can use for a calculator application.
This article assumes that you have intermediate programming experience and basic familiarity with JavaScript.
Some Background
The Difference Between Interpreters, Compilers and Transpilers
In this article, we will be creating an interpreter, as opposed to a compiler. Our program will take some code as input and immediately execute it.
If we were writing a compiler, we would instead transform the inputted code in the source language into code in some lower-level target language, such as MSIL, or an assembly language, or even machine code.
A transpiler is similar to a compiler, except that the source language and target language are about the same level of abstraction. The canonical example of this in the client side web programming world is CoffeeScript, which transcompiles into JavaScript.
The Traditional Language Code Interpretation Process
Most compilers will interpret code in a multi-step process that involves processes that include lexical analysis, preprocessing, parsing, optimization, and finally code generation, or, in the case of an interpreter, evaluation.
In this article, we will only focus on lexing, parsing, and evaluation.
Lexing
A lexer takes a input a string of characters, and outputs a list of tokens. For example, if we had some code like this…
(12 + 4) / 6
…the lexer would divide it up into the individual parts, called tokens, and output a list that might look something like this
[ ["operator", "("], ["number", 12], ["operator", "+"], ["number", 4], ["operator", ")"], ["operator", "/"], ["number", 6] ]
This process is usually relatively simple. Somebody with a little bit of experience with string manipulation can work their way through building a lexer fairly quickly.
Parsing
The parser takes the list of tokens produced by the lexer as input, parses it according to some syntax rules, and outputs a representation of the syntactic structure called a parse tree.
{
operation: "/",
left: {
operation: "+",
left: 12,
right: 4
}
right: 6
}
This tends to be the most difficult part of the process.
Evaluation
The evaluator takes the parse tree produced by the parser and evaluates it. Evaluators usually traverse the parse tree recursively. Given the syntax tree above, the evaluator might first evaluate the left operand of the top-level / operation, then the right operand, and then return the result of the division.
Evaluating the left operand would simplify the syntax tree to this:
{
operation: "/",
left: 16,
right: 6
}
which in turn will evaluate to the final result:
2.6666666666666665
AEL: The Calculator Language
Before we can start writing our interpreter, we need to understand the language that we will be interpreting, which I just made up and will refer to as AEL, short for Arithmetic Expression Language.
The language is written as a series of arithmetic expressions composed of numbers and the arithmetic operators + (addition), - (subtraction and negation), * (multiplication), / (division), % (modulo), ^ (exponentiation), as well as parentheses () for grouping.
The interpreter will evaluate each expression and print the result of each in the order that they were presented. For example, given the following input…
3 2 ^ 8 (12 % 7) * (3 + 2) 19 / -9
…the interpreter will output:
3 256 25 -2.111111111111111
AEL also will allow you to define variable assignments using the = operator. The left hand side will be some identifier, and the right hand side will be an arithmetic expression. A statement with an assignment has no return value, so the interpreter will not print out a corresponding line.
For example:
hoursPerDay = 24 minutesPerHour = 60 minutesPerDay = minutesPerHour * hoursPerDay minutesPerDay minutesPerDay * 60
outputs:
1440 86400
AEL will have two pre-defined variables: pi and e, which will correspond to the values 3.141592653589793 and 2.718281828459045, respectively.
Finally, AEL will allow you to define functions. A function assignment also uses the = operator, but the left hand argument must be an identifier followed by parentheses, which will contain zero or more argument names separated by commas. Once defined, a function can be called by writing an identifier name followed by parentheses containing zero or more arithmetic expressions separated by commas.
For example:
toDegrees(radians) = radians * 180 / pi toDegrees(2 * pi) cylinderVolume(r, h) = pi * r ^ 2 * h cylinderVolume(2, 4)
outputs:
360 50.26548245743669
Now that we know what the language is like, we can start writing the interpreter.
For reference, I have put an implementation of an AEL interpreter online.
Step 1: The Lexer
The lexer takes text input and returns a list of tokens. The skeleton of our lex function thus should look like this:
var lex = function (input) { var tokens = []; return tokens; };
We have several different types of tokens. There are operators, which are defined by the set of characters +-*/^%=(), there are numbers composed of numeral digits, there is whitespace, which our lexer will ignore, and there are identifiers, which will be defined as any string of characters that does not contain operators, digits, or whitespace.
var isOperator = function (c) { return /[+-*/^%=(),]/.test(c); }, isDigit = function (c) { return /[0-9]/.test(c); }, isWhiteSpace = function (c) { return /s/.test(c); }, isIdentifier = function (c) { return typeof c === "string" && !isOperator(c) && !isDigit(c) && !isWhiteSpace(c); };
We will create a simple loop to scan the input text. We will have a variable c which corresponds to the current character, create a function called advance to step forward one character in the input and return the next character, and a function called addToken which appends a token to the list of tokens.
var tokens = [], c, i = 0; var advance = function () { return c = input[++i]; }; var addToken = function (type, value) { tokens.push({ type: type, value: value }); }; while (i < input.length) { c = input[i]; }
If c is whitespace, we just ignore it and move on. If c is an operator, add an operator token to the list and move on.
if (isWhiteSpace(c)) advance(); else if (isOperator(c)) { addToken(c); advance(); }
For simplicity, we will define a number as a series of digits, optionally followed by a decimal point and another series of digits.
else if (isDigit(c)) { var num = c; while (isDigit(advance())) num += c; if (c === ".") { do num += c; while (isDigit(advance())); } num = parseFloat(num); if (!isFinite(num)) throw "Number is too large or too small for a 64-bit double."; addToken("number", num); }
Every other character is an identifier.
else if (isIdentifier(c)) { var idn = c; while (isIdentifier(advance())) idn += c; addToken("identifier", idn); }
And, just in case something weird gets thrown at us:
else throw "Unrecognized token.";
After we’re done scanning the input, we’ll add a token to demarcate the end. Then we’re done.
addToken("(end)"); return tokens;
Step 2: The Parser
There are lots of different strategies for writing a parser. One of the most common is writing a Backus-Naur grammar and using recursive descent. In this article, we will be using a somewhat less common strategy called operator-precedence parsing, using techniques described Douglas Crockford’s Top Down Operator Precedence article.
Operator precedence parsing begins with the following process:
- Associate every operational token with a left binding power, and an operational function.
- If the operator manipulates tokens to its left (such as
+), associate it with a left denotative function (hereafter abbreviated asled). If the operator does not manipulate the tokens on its left (such as the unary-), associate it with anulldenotative function (hereafter abbreviated asnud). Identifiers and numbers also have anudfunction associated with them.
After this is done, it can start to generate the parse tree. To show how this works, I’ll use the arithmetic expression below as an example.
12 + 4 / 6
The parser function starts by executing the nud of the first token (12), which returns itself.
{ type: "number", value: 12 }
This become the left hand side that we pass into the led of the next token (+), which will recursively call the parser function to parse the remaining tokens.
{
type: "+",
left: { type: "number", value: 12 },
right:
}
We start over by calling the nud of the first of the remaining tokens (4), which will return itself.
{ type: "number", value: 4 }
This becomes the left hand side that we pass into the led of the next token (/), which will recursively call the parser function to parse the remaining tokens.
{
type: "+",
left: { type: "number", value: 12 },
right: {
type: "/"
left: { type: "number", value: 4 },
right:
}
}
We call the nud of the first of the remaining tokens (6), which will return itself. This is the end of the list of tokens, so the parse tree is complete.
{
type: "+",
left: { type: "number", value: 12 },
right: {
type: "/"
left: { type: "number", value: 4 },
right: { type: "number", value: 6 }
}
}
If we now switch the + and /, we will see how binding power comes into play. / has a higher binding power than +, so it will bind more tightly to the operands around it.
12 / 4 + 6
We start out the same way as before:
{
type: "/",
left: { type: "number", value: 12 },
right:
}
But this time, after we call the nud of the 4, we will look ahead one token, and see that + has lower precedence than the /. This means that we will stick the 4 in the right hand side, and then pass the entire current tree into the led of +, which makes us end up with this parse tree:
{
type: "+",
left: {
type: "/",
left: { type: "number", value: 12 },
right: { type: "number", value: 4 }
},
right: { type: "number", value: 6 },
}
Now that we have some understanding of the parsing process, we can begin writing our parser. The parser accepts the tokens that the lexer produced, and returns a parse tree, so the skeleton of our parse function will look like this:
var parse = function (tokens) { var parseTree = []; return parseTree; };
We need to have some sort of symbol table that associates symbol with a binding power, nud or led, and we need a function that will associate a token with the corresponding symbol.
var symbols = {}, symbol = function (id, nud, lbp, led) { var sym = symbols[id] || {}; symbols[id] = { lbp: sym.lbp || lbp, nud: sym.nud || nud, led: sym.led || led }; }; var interpretToken = function (token) { var sym = Object.create(symbols[token.type]); sym.type = token.type; sym.value = token.value; return sym; };
We need some way to see what the current token is and a way to advance to the next token.
var i = 0, token = function () { return interpretToken(tokens[i]); }; var advance = function () { i++; return token(); };
Now we can write an expression function which will generate the parse tree of an expression according to the way it was described above:
var expression = function (rbp) { var left, t = token(); advance(); if (!t.nud) throw "Unexpected token: " + t.type; left = t.nud(t); while (rbp < token().lbp) { t = token(); advance(); if (!t.led) throw "Unexpected token: " + t.type; left = t.led(left); } return left; };
We can now create the infix and prefix functions, which we will be able to use to define operators:
var infix = function (id, lbp, rbp, led) { rbp = rbp || lbp; symbol(id, null, lbp, led || function (left) { return { type: id, left: left, right: expression(rbp) }; }); }, prefix = function (id, rbp) { symbol(id, function () { return { type: id, right: expression(rbp) }; }); };
Now we can define all of arithmetic operators declaratively. Note that the exponentiation operator (^) has a right binding power that is smaller than its left binding power. This is because exponentiation is right associative.
prefix("-", 7); infix("^", 6, 5); infix("*", 4); infix("/", 4); infix("%", 4); infix("+", 3); infix("-", 3);
There are some operators that just exist as separation or end demarcation. They are not prefixes or infixes so it is sufficient to add them to the symbol table.
symbol(","); symbol(")"); symbol("(end)");
The parentheses nud just returns what is inside of it, and the number nud just returns itself.
symbol("(", function () { value = expression(2); if (token().type !== ")") throw "Expected closing parenthesis ')'"; advance(); return value; }); symbol("number", function (number) { return number; });
The identifier nud and the = operator’s nud are more complicated because they have context-dependent behaviour.
symbol("identifier", function (name) { if (token().type === "(") { var args = []; if (tokens[i + 1].type === ")") advance(); else { do { advance(); args.push(expression(2)); } while (token().type === ","); if (token().type !== ")") throw "Expected closing parenthesis ')'"; } advance(); return { type: "call", args: args, name: name.value }; } return name; }); infix("=", 1, 2, function (left) { if (left.type === "call") { for (var i = 0; i < left.args.length; i++) { if (left.args[i].type !== "identifier") throw "Invalid argument name"; } return { type: "function", name: left.name, args: left.args, value: expression(2) }; } else if (left.type === "identifier") { return { type: "assign", name: left.value, value: expression(2) }; } else throw "Invalid lvalue"; });
Now that all the hard stuff is out of the way, we can just put on the finishing glue.
var parseTree = []; while (token().type !== "(end)") { parseTree.push(expression(0)); } return parseTree;
Step 3: The Evaluator
The evaluator accepts the parse tree generated by the parser, evaluates each item, and produces the evaluated output. The skeleton of our evaluate function will look like this:
var evaluate = function (parseTree) { var parseNode = function (node) { }; var output = ""; for (var i = 0; i < parseTree.length; i++) { var value = parseNode(parseTree[i]); if (typeof value !== "undefined") output += value + "n"; } return output; };
It is straightforward to define the behavior of the operators and all of the predefined variables and functions:
var operators = { "+": function(a, b) { return a + b; }, "-": function(a, b) { if (typeof b === "undefined") return -a; return a - b; }, "*": function(a, b) { return a * b; }, "/": function(a, b) { return a / b; }, "%": function(a, b) { return a % b; }, "^": function(a, b) { return Math.pow(a, b); } }; var variables = { pi: Math.PI, e: Math.E }; var functions = { sin: Math.sin, cos: Math.cos, tan: Math.cos, asin: Math.asin, acos: Math.acos, atan: Math.atan, abs: Math.abs, round: Math.round, ceil: Math.ceil, floor: Math.floor, log: Math.log, exp: Math.exp, sqrt: Math.sqrt, max: Math.max, min: Math.min, random: Math.random }; var args = {};
Now we can put in the meat of our evaluator, and we’re done. The parseNode function recursively traverses and evaluates the parse tree.
var parseNode = function (node) { if (node.type === "number") return node.value; else if (operators[node.type]) { if (node.left) return operators[node.type](parseNode(node.left), parseNode(node.right)); return operators[node.type](parseNode(node.right)); } else if (node.type === "identifier") { var value = args.hasOwnProperty(node.value) ? args[node.value] : variables[node.value]; if (typeof value === "undefined") throw node.value + " is undefined"; return value; } else if (node.type === "assign") { variables[node.name] = parseNode(node.value); } else if (node.type === "call") { for (var i = 0; i < node.args.length; i++) node.args[i] = parseNode(node.args[i]); return functions[node.name].apply(null, node.args); } else if (node.type === "function") { functions[node.name] = function () { for (var i = 0; i < node.args.length; i++) { args[node.args[i].value] = arguments[i]; } var ret = parseNode(node.value); args = {}; return ret; }; } };
Putting It All Together
Now we can wrap it all up and put the thee pieces together in one single calculate function.
var calculate = function (input) { try { var tokens = lex(input); var parseTree = parse(tokens); var output = evaluate(parseTree); return output; } catch (e) { return e; } };
What To Do Next
There are many things you could add to the language to make it more useful or just to see how things work. Some additions would be fairly easy, some could be very hard.
Easy Stuff
- Play around with adding your own predefined functions.
- Fiddle with the binding power numbers to see how that changes the way expressions are evaluated.
- Allow scientific notation in number literals or make it possible to use binary or hexidecimal number literals.
Intermediate Stuff
- Allow manipulation of more types of data, such as strings, booleans and arrays.
- Allow functions to have multiple statements and conditionally return values.
- Replace the evaluator with a compiler or transpiler that takes the parse tree and outputs code in another language.
- Make a package manager that allows you to import code from other files.
Harder Stuff
- Implement optimizations to allow calculations to be performed more quickly.
- Make function first-class citizens and allow closures.
- Make it so that all the data is evaluated lazily.
If you know how to do some of this stuff, you are prepared to start making interpreters and compilers for your own domain specific languages.
That’s All, Folks!
If there is an error in this article or you see some way to make either the code or the explanations of the code easier to understand, let me know, and I can update it accordingly.
History
- 30th October, 2014: Initial version
В течение нескольких лет я работала над личным проектом создания (а на самом деле исследования) «фальшивого эмулятора», то есть написанного на JavaScript эмулятора никогда не существовавшего компьютера. Эта машина должна была стать данью памяти восьми- и шестнадцатибитным компьютерам 1980-х и 90-х.
Однако мне нравятся сложности: в этой машине ещё и использовался новый набор инструкций. Он похож на наборы, применявшиеся в ту эпоху, но немного проще в работе. Так родился Retroputer. В течение нескольких лет эмулятор расширял свои возможности и совершенствовался, но, скорее всего, он никогда не будет «закончен» (в конце концов, это ведь личный проект-исследование).
Когда появился @bbcmicrobot, я захотела создать нечто подобное для Retroputer. Мои навыки разработки на JS в основном ограничивались фронтендом, поэтому это будет отличным поводом получить опыт бэкенда. Только есть одна проблема: Retroputer может понимать только собственный язык ассемблера. Пока у него нет поддержки BASIC.
Так я и пришла к созданию интерпретатора BASIC в стиле 80-х, то есть полностью на языке ассемблера, как его тогда и писали. Я решила, что стоит поделиться своей работой, потому что нам не часто приходится погружаться в области, столь далёкие от привычных абстракций. Мой повседневный инструмент (JavaScript) делает многие аспекты тривиальными, и иногда это даже кажется магией. Понимание самого нижнего уровня процессов часто помогает в понимании этих абстракций.
Итак, давайте приступим.
Характеристики Retroputer
- 16КБ ROM (KERNEL) c 1КБ для временного хранения (scratch space)
- 512КБ ОЗУ, из которых 64КБ можно использовать для исполняемых инструкций
- 16-битный процессор 6516, способный выполнять адресацию 512КБ ОЗУ в 4 банках по 64КБ каждый
- Генератор видеосигналов 4025, способный генерировать дисплей, спрайты и произвольные шрифты
- Генератор звука 1125
- Интерфейс жёсткого диска 9800 для устройства постоянного хранения
Парсинг на низкоуровневом языке ассемблера
Когда я писала ассемблер для Retroputer, то могла использовать очень удобный инструмент Pegjs. Он обеспечивал быструю работу собственного синтаксиса ассемблера, но, к сожалению, ничего подобного для Retroputer ASM не существует. То есть нам придётся идти трудным путём.
Сам парсинг выполняется в несколько этапов. Язык, использующий компилятор, парсит код в абстрактное синтаксическое дерево (AST) (или в иное представление), а затем может использовать это дерево для генерации готового нативного кода. Следовательно, для успешной компиляции программа должна быть синтаксически корректной.
У некоторых современных интерпретаторов тоже имеется эта концепция, потому что часто полезно бывает генерировать промежуточное AST и исполнять его, а не исходный код.
Но для интерпретатора BASIC на машине с ограниченными ресурсами наиболее эффективно будет выполнять парсинг в несколько этапов, часть из которых происходит во время выполнения. Однако это означает, что синтаксические ошибки невозможно будет обнаружить до запуска программы и перехода к области кода с ошибкой.
Парсинг Retroputer BASIC состоит из трёх этапов:
- Преобразование строк
- Токенизация
- Проверка синтаксиса во время выполнения
Первые два этапа происходят в процессе ввода пользователем программы (или её загрузки). Последний происходит при выполнении программы. По сути, первые два создают фюзеляж самолёта, но не гарантируют, что он взлетит. Последний этап является лётчиком-испытателем — мы надеемся, что он взлетит, но не уверены в этом, пока он не попробует.
Примечание: исходный код Retroputer BASIC (в процессе разработки) доступен на GitHub.
Преобразование строк
Это простейшая часть всего процесса. Вводимая пользователем строка преобразуется в верхний регистр, чтобы упростить (и ускорить) последующие процессы. BASIC не учитывает регистр символов, поэтому мы можем этим воспользоваться.
<pre>print 2+2
' becomes:
PRINT 2+2</pre>Выполнить подобное на JavaScript очень легко, правда?
theLine = theLine.toUpperCase();Но на языке ассемблера этот процесс более детализирован. Нам нужно считать символ, преобразовать его в верхний регистр, а затем куда-то сохранить.
ld y, 0 # y is our index
_loop: ld al, [d, x, y] # [d,x] is pointer to string
cmp al, 97 # is al (char) in range?
brs n _continue # Not a lowercase char; continue
cmp al, 123 # high portion
brs !n _continue # not a lowercase char; continue
and al, 0b1101_1111 # uppercase!
st [d, x, y], al # store back (we modify the original)
_continue: inc y # move our index along
cmp al, 0 # check for NULL
brs !z _loop # No? Go back for more.Приведённый выше код не совсем соответствует семантике версии кода на JavaScript. Важное отличие заключается в том, что сегодня для работы с текстом мы используем Unicode, поэтому преобразование ввода из нижнего в верхний регистр часто может оказываться более сложным, а иногда и невозможным (это зависит от языка). Retroputer живёт в мире ASCII (точнее, в мире собственной вариации ASCII под названием RetSCII), то есть все поддерживаемые символы кодируются восемью битами. Для многих языков этого совершенно недостаточно, зато отвечает реалиям того времени.
Это также означает, что для преобразования из нижнего в верхний регистр мы можем использовать милую особенность ASCII. «A» в верхнем регистре представлена в ASCII кодом 65, а буква «a» в нижнем регистре представлена кодом 97. Если вам знакомы степени двойки, то вы должны были заметить эту разницу.
Итак, оказывается, буквы в нижнем регистре задаются числом, которое ровно на 32 больше, чем число буквы в нижнем регистре. Если мы знаем, что значение находится в нужном интервале, нам достаточно всего лишь вычесть 32!
Такой подход сработает, но мы можем и просто немного модифицировать биты. В случае Retroputer это не будет быстрее, чем вычитание, однако при отсутствии вычитания нам не придётся во время выполнения вычислений обращать внимание на флаг переноса/заимствования. Оказывается, мы можем использовать побитовое and, чтобы отключить бит в месте значения 32.
and al, 0b1101_1111 # turn off bit in 32-place
# versus
clr c # clear carry
sub al, 32 # subtract 32Но тут есть одна тонкость: не всё можно преобразовать в верхний регистр. Например, если пользователь добавил строковый литерал, то нам нужно быть более внимательными, ведь мы не хотим, чтобы Retroputer BASIC постоянно кричал на пользователя капсом. (Хотя у многих компьютеров той эпохи не было нижнего регистра, у Retroputer такого ограничения нет.)
Например:
print "Hello, World!"
' should become:
PRINT "Hello, World!"
' and not
PRINT "HELLO, WORLD!"Это означает, что нам нужно отслеживать, не находимся ли мы посередине строкового литерала. В BASIC есть только одно обозначение этого: двойные кавычки. Если символ является двойной кавычкой, мы можем установить флаг и в зависимости от значения флага выполнять преобразование в верхний регистр или оставить всё как есть.
Оказывается, в JavaScript для этого нет встроенной функциональности, но мы можем создать её сами:
const len = theLine.length;
let insideString = false;
for (let i = 0; i < len; i++) {
const ch = theLine[i];
if (ch === `"`) insideString = !insideString;
if (!insideString) {
const newCh = ch.toUpperCase();
if (ch !== newCh) theLine[i] = newCh;
}
}Теперь логика на JS более точно соответствует ассемблерной версии, хотя мы снова немного используем возможности поддержки Unicode в JS.
Версия на ассемблере выглядит так:
ld y, 0 # y is our index
ld bl, 0 # === insideString (false)
_loop: ld al, [d, x, y] # [d,x] is pointer to string
cmp al, 34 # is al a double quote?
brs !z check_char # no? should we uppercase it?
xor bl, 0xFF # yes? toggle insideString
_check_char:
cmp bl, 0xFF # inside a string?
brs z _continue # yes? don't modify it
cmp al, 97 # is al (char) in range? "a"
brs n _continue # Not a lowercase char; continue
cmp al, 123 # high portion "z"
brs !n _continue # not a lowercase char; continue
and al, 0b1101_1111 # uppercase!
st [d, x, y], al # store back (we modify the original)
_continue: inc y # move our index along
cmp al, 0 # check for NULL
brs !z _loop # No? Go back for more.Пока мы выполнили только преобразование вводимого текста в верхний регистр, но можно использовать определение строкового литерала ещё для другой возможности. Мы можем выполнить ещё одну проверку синтаксиса!
Если в конце процесса мы выясним, что inString по-прежнему истинно (bl = 0xFF), то можем вернуть ошибку, потому что это означает что где-то в строке есть незавершённый строковый литерал.
Примечание: оказалось, что многие версии BASIC довольно снисходительно относятся к отсутствию закрывающих кавычек у строк. Это я выяснила при создании собственного интерпретатора. Хоть это и так, мне не кажется такое правильным, поэтому Retroputer BASIC не позволяет этого.
Токенизация
Следующий этап парсинга заключается в преобразовании введённой строки в нечто более эффективное для выполнения интерпретатором Retroputer BASIC. Мы стремимся максимально близко подойти к концепции абстрактного дерева синтаксиса, но результат всё равно не будет деревом. Но это будет нечто, что мы сможем быстро обрабатывать во время выполнения.
Общей чертой первых микрокомпьютеров была очень ограниченная память. Retroputer имеет больше памяти, чем большинство стандартных машин того времени, но её всё равно намного меньше, чем у современных компьютеров. Поэтому длинные программы на BASIC запросто могут занять слишком много памяти, если они сохраняются в процессе ввода пользователем.
Для экономии места ключевые слова в процессе ввода программы в память токенизируются. Этот процесс преобразует ключевые слова в однобайтовые токены. Ключевые слова всегда имеют длину не менее двух байтов, так что при вводе экономия становится больше. Также это означает, что мы можем использовать во время выполнения таблицу поиска для вызова соответствующих процедур языка ассемблера.
Однако Retroputer BASIC заходит немного дальше, чем большинство версий BASIC того времени. Сверх того он преобразует числа в двоичный вид, помечает строки, вычисляет ссылки на переменные, и многое другое. Если честно, из-за этого тратится больше места, но преимущества скорости (и простоты выполнения) перевешивают этот недостаток.
Итак, здесь используются следующие этапы:
- Токенизация чисел
Числа преобразуются в двоичный вид, чтобы не преобразовывать их каждый раз, когда они встречаются в программе. Если числа встречаются только один раз, то рост производительности оказывается не таким большим, но в цикле с большим количеством вычислений это выгодно, потому что число уже представлено в виде, который может понять компьютер.
- Пометка строк
Так как память ограничена, если в коде есть строка, которую можно использовать без изменений, то логично будет так и поступить. Например,
PRINT "Hello, World"может выводить «Hello, World» непосредственно из строки программы вместо выделения нового пространства, копирования строки и её вывода.Чтобы упростить пропуск строк во время выполнения программы, мы также храним длину самой строки.
- Поиск в таблице ключевых слов
Всё, что не является числом или строкой, может быть ключевым словом, поэтому нам нужно выполнять поиск по списку ключевых слов. Это тривиально на JavaScript, но совсем непросто на ассемблере!
После нахождения ключевого слова связанный с ним токен сохраняется в памяти программы (вместо всего ключевого слова целиком). В результате этого мы можем сэкономить много пространства, особенно когда команду типа
PRINTможно сократить до одного байта! - Вычисление указателей на переменные
Имена переменных Retroputer BASIC значимы только до первых двух символов (на данный момент). Благодаря этому можно тривиальным образом искать переменную в массиве при помощи довольно простого математического выражения. Но даже в таком случае вычисления занимают время, поэтому было бы здорово, если бы нам не приходилось этого делать при встрече с переменной.
Retroputer BASIC будет вычислять индекс и хранить его вместе с именем переменной. Кроме имени переменной он также хранит длину переменной, чтобы ускорить выполнение программы. Это занимает большое количество пространства и не было бы хорошим решением для компьютеров с ограниченной памятью, но подходит для Retroputer BASIC.
В посте я не буду подробно рассказывать о реализации этого этапа на языке ассемблера, оставлю его на будущее. Но не волнуйтесь, кода там много.
Проверка синтаксиса во время выполнения программы
Последним, но не менее важным этапом является проверка синтаксиса во время выполнения. После преобразования кода в токенизированный вид реализовать его довольно легко.
Во-первых, на этапе выполнения BASIC проверяет, обрабатывает ли он в данный момент токен. У всех токенов включен старший бит (то есть они имеют значение от 128 и выше). Если обнаружен токен, то мы можем определить, какую подпроцедуру нужно вызвать, найдя её в таблице векторов. Кроме того, это делает тривиальным отображение ошибок синтаксиса — некоторые ключевые слова не имеют смысла в качестве операторов, поэтому таблица векторов просто указывает на процедуру, генерирующую синтаксическую ошибку.
После вызова обработчика токена оператора обработчик берёт на себя всю дополнительную работу по парсингу. Для получения токенов и перехода между ними он может использовать gettok, gettok-raw, peektok и т.д. Если токен представляет собой нечто, не ожидаемое процедурой, то процедура просто возвращает код ошибки. Именно на этом этапе отлавливаются и синтаксические ошибки, и ошибки согласования типов.
В случае, если оператор должен вычислить выражение, то выполняется другой этап парсинга. Во время парсинга выражения используется ещё одна таблица поиска векторов, то есть мы можем перехватывать ключевые слова, не относящиеся к математическому выражению, и возвращать соответствующие ошибки. Например, если попробовать ввести PRINT 2+CLS, то мы получим синтаксическую ошибку на CLS (CLS — это ключевое слово-сокращение от «clear screen»).
Примечание: из этой таблицы мы также можем определять приоритет математических операторов и количество необходимых параметров. Это важно для самого вычисления выражения, но это можно также использовать для перехватывания случаев, когда пользователь не указал достаточное количество аргументов.
Так как токен напрямую сопоставляется с элементом таблицы поиска векторов, выполнение программы может выполняться довольно быстро и с минимальными усилиями. Задача парсинга каждого типа операторов поручается самому обработчику, и в общем случае это не вызывает особых проблем. Наверно, самыми сложными для парсинга являются PRINT и INPUT, но на каждом шаге за раз берётся по одному токену.
Поскольку многие проверки не выполняются до времени выполнения программы, это означает, что до возникновения ошибки у нас могут быть частичные результаты. Например:
PRINT "Hello";CLS
Hello
?Syntax ErrorКроме того, это означает, что если программа оставляет экран в состоянии, в котором мы не можем видеть текст, то у нас могут возникнуть проблемы с устранением ошибок. Если выводится синтаксическая ошибка, но мы её не видим, то что нам делать?
У такого способа проверки синтаксиса определённо есть свои недостатки, однако он позволяет реализовать довольно простой интерпретатор.
Токенизация пользовательского ввода
Как упоминалось ранее, обычно версии BASIC той эпохи использовали тактику токенизации. Для экономии пространства и повышения скорости выполнения ключевые слова «ужимались» в однобайтные токены (или двухбайтные, если нужно больше ключевых слов).
Давайте представим, что у нас есть простая строка кода, очищающая экран и печатающая стандартное приветствие:
CLS: PRINT "Hello, World"Хотя само по себе это не занимает особо много памяти, если писать длинную программу, то множество слов в этой программе будет ключевыми словами. Если сжать их (токенизировать), то можно сэкономить солидную долю пространства. Например, после токенизации показанной выше строки в памяти будет находиться примерно такое:
8A E3 B5 FC Hello, World 00 00Не составит особого труда преобразовать это обратно в исходную конструкцию:
Возможно, вам покажется, что это большой объём работы, зато и экономия пространства может быть значительной. В примере это не особо заметно, но даже по нему можно представить, как быстро может накапливаться сэкономленное пространство. В данном случае сжатый результат имеет размер 19 байт. Исходный текст состоит из 26 байт (с учётом завершающего нулевого байта).
Экономия пространства становится важной, если речь идёт об интерпретаторе BASIC, работающем на машине с очень малым количеством ОЗУ под пользовательские программы. Поэтому такое сжатие очень важно и привлекательно, даже если бы оно не имело дополнительных преимуществ.
Итак, как же нам токенизировать нечто подобное? Поначалу кажется, что на JavaScript это делается достаточно тривиально. Имея массив строк, можно быстро заменить каждое ключевое слово соответствующим токеном. Правда?
Кажется, это работа для String#replace? При наивном подходе можно попробовать нечто подобное:
const tokens = ["CLS", "PRINT", ":" ];
function tokenize (inStr) {
const newStr = inStr;
tokens.forEach((token, idx) => newStr = newStr.replace(
new RegExp(token, "g"), String.fromCharCode(128+idx)
);
return newStr;
}К сожалению, вскоре мы осознаем, что не можем заменять токенами строковые литералы. Это значит, что нужно выполнять обработку посимвольно, с учётом контекста, чтобы не сжимать элементы, не являющиеся ключевыми словами.
Этот новый алгоритм более близок к коду на языке ассемблера в Retroputer, но JS всё равно сильно упрощает работу. Вот начало кода на JS (в этом посте мы постепенно будем его дополнять):
const tokens = ["CLS", "PRINT", ":" ];
function tokenize(inStr) {
let out = []; // return value is "crunched" array
let idx = 0; // index into inStr
let ch = ""; // current character
while (idx < inStr.length) {
ch = inStr.charCodeAt(idx); // get the current character code
// our logic is going to go here
out.push(ch); // for now push the character
idx++; // and keep going (next char)
}
out.push(0); // we end with NUL
return out;
}Мы начинаем с очень упрощённого списка токенов, потому что никому не захочется видеть всю таблицу в таком формате (она длинная, а таблицы токенов Retroputer на самом деле создаёт из файла JS!), но для наших целей этого будет достаточно. Принцип здесь заключается в том, что когда мы видим токен, то записываем его индекс в выходной массив.
На этом этапе у нас есть функция, которая пока просто преобразует строку в эквивалентные ей коды символов. Пока она не особо полезна, но может служить удобным каркасом.
Версия на языке ассемблера довольно похожа на показанную выше.
do {
call _get-source-index # get next character index (in y)
dl := <BP+source>,y # read next char from our source string (ch)
call _adv-source-index # advance our source index
call _get-target-index # get position in target ("out" in JS)
<BP+target>,y := dl # store to target (out[y] = ch)
call _adv-target-index # move it along
cmp dl, 0 # was char 0? if so, break
} while !z
Я не включил в пример выше _get-source-index или другие функции, потому что их задачи понятны из названия: они просто получают, задают исходный и целевой индексы, а также перемещаются по ним. Стоит заметить что в отличие от JS, в языке ассемблера нет динамически выделяемых массивов, поэтому этот алгоритм выделяет буфер достаточного размера. При перемещении по входной строке мы должны знать, куда записывать следующий токен в целевом буфере, и что целевой индекс делает выше. Каждая из вызываемых выше функций возвращает индекс в Y. Например, функция _adv-target-index увеличивает целевой индекс на единицу (эквивалент y++).
Аккуратнее с литералами
Нам нужно быть внимательными: строковые литералы могут сбить с толку токенизатор — мы не можем просто заменить каждую соответствующую ключевому слову строку символов значением токена. Если мы видим строковый литерал, в котором есть «CLS», то не должны стремиться токенизировать его. Он не должен быть исполняемым, и если мы выведем его… то вместо него выведем соответствующий токену байт. Скорее всего, разработчик подразумевал не это.
С другой стороны, численные литералы не должны иметь подобной проблемы, потому что в BASIC нет ключевых слов в виде чисел. Но даже в таком случае, нет никакого смысла, столкнувшись с числом, выполнять поиск ключевого слова — зачем зря тратить время?
Токенизация строковых литералов
Итак, давайте для начала проверим, начинается ли строка — в JS это сделать не особо сложно:
if (ch === 34) {
out.push (0xFB); // string-in-code token
idx++;
ch = inStr.charCodeAt(idx); // get next character after the quote
while (ch !== 34 && idx < inStr.length) {
out.push(ch);
idx++;
ch = inStr.charCodeAt(idx);
};
idx++; // go past the quote
out.push(0); // end of string
continue;
}Двойная кавычка представлена кодом символа 34. Другие языки программирования могут распознавать намного больше стилей кавычек (например, JS или C), но с BASIC всё просто: или двойные кавычки, или ничего.
Когда мы видим, что начинается строка, то можем просто брать оставшиеся символы и добавлять в выходной массив, пока не встретим ещё одну кавычку.
После считывания всей строки нужно добавить нулевой байт, потому что Retroputer BASIC использует строки в стиле C. Если бы мы хотели использовать строки в стиле Pascal, то могли бы хранить счётчик и вставлять длину строкового литерала. В любом случае, это не вызывает особых проблем. Единственная причина, по которой я использовала строки, завершающиеся нулевым байтом, заключается в том, что с ними очень просто работать на языке ассемблера — нам достаточно просто сравнивать с нулевым байтом, а не хранить счётчик.
Итак, JavaScript был не особо сложным. Думаю, большинство из вас решило бы использовать нечто более абстрактное, например, регулярное выражение. Мне кажется, этот код сделает наши намерения более очевидными.
if (ch === 34) {
out.push (0xFB); // string-in-code token
const stringLiteral = inStr.substr(idx+1).match(/^[^"]*/)[0];
idx += stringLiteral.length+1;
out.push(...Array.from(stringLiteral, ch => ch.charCodeAt(0)));
idx++; // go past the quote
out.push(0); // end of string
continue;
}
Приведённый выше код примерно такой же, но вместо посимвольной проверки мы позволяем JS просто выполнить match. Мы знаем, что получим совпадение (мы ведь находимся в строке), поэтому нам даже не нужно проверять, было ли совпадение удачным. Затем мы выполняем инкремент индекса на длину строки и копируем символы в выходной массив. По моему мнению, такой код гораздо легче понять (однако он подразумевает понимание регулярных выражений, а также особенностей синтаксиса ES6, например, … и стрелочных функций).
Разумеется, на языке ассемблера нам придётся вручную проделывать всю работу, которую выполняет JS. Результат оказывается очень похожим на нашу первую попытку создания кода на JS:
cmp dl, constants.QUOTE # is dl a quote?
brs !Z not-a-string # nope; not a string
call _get-target-index # get next position in crunch target
dl := brodata.TOK_CODE_STRING # "String" token
<bp+target>,y := dl # Store it into the crunch target
call _adv-target-index
still-a-string:
call _get-source-index
dl := <bp+source>,y # get string character
call _adv-source-index
cmp dl, constants.QUOTE # if it's a quote, we can zero it
if Z {
dl := 0
}
call _get-target-index
<bp+target>,y := dl # write to target
call _adv-target-index
cmp dl, 0 # are we done?
brs !Z still-a-string # no, keep going
continue # next!
not-a-string:
Стоит добавить замечание о парсере языка ассемблера Retroputer — он имеет базовую поддержку высокоуровневых конструкций, например, блоков и циклов. Поэтому if Z {…} будет выполнять содержимое внутри блока при установленном нулевом флаге, а continue можно использовать для ветвления обратно к началу блока (break также используется для выхода из блока). Ассемблер преобразует это в различные инструкции сравнения и ветвления, поэтому CPU не видит высокоуровневых частей кода, но это немного упрощает написание кода.
Токенизация чисел
Кроме того, не имеет смысла пытаться искать в списке ключевых слов числа, поэтому мы можем просто их пропускать. Большинство версий BASIC делают нечто похожее на показанную выше процедуру обработки строк — если считанный символ является цифрой, он будет конкатенирован с выходными данными, после чего за дело примется сжиматель.
Retroputer BASIC (и некоторые другие версии BASIC, например, Atari BASIC) делает ещё один шаг вперёд: он преобразует число в соответствующий двоичный формат. Это сделать очень легко — если мы встречаем цифру, то умножаем накопитель на 10 и прибавляем цифру, продолжая так, пока продолжают встречаться цифры. (Однако стоит заметить, что пока Retroputer BASIC работает только с целочисленными значениями, добавление чисел с плавающей запятой уже в моём списке todo.)
(Надо сказать, что в настоящее время Retroputer BASIC ничего не делает, когда происходит целочисленное переполнение, знаковое или беззнаковое. Когда я добавлю числа с плавающей запятой, Retroputer будет преобразовывать и в вид с плавающей запятой.)
Retroputer BASIC делает и ещё один шаг вперёд: он также распознаёт шестнадцатеричные числа и преобразует их в двоичный эквивалент. В качестве обозначения таких чисел используется 0x (как и в JS), а сам язык имеет дополнительную логику, обеспечивающую возврат ошибки, если указано несколько символов x.
На языке ассемблера проверка того, является ли символ цифрой, не так уж сложна, но для этого требуется пара сравнений: нужно убедиться, что код символа находится между 0x30 и 0x39. (Это коды символов «0» и «9».)
Получив символ-цифру, мы можем воспользоваться ещё одним удобным свойством набора символов. 0x30 — это код символа «0», 0x31 — код «1», и так далее. При желании мы могли бы вычесть 0x30, но есть способ попроще: достаточно отбросить четыре старших бита:
and dl, 0b0000_1111К сожалению, это не сработает, если нам нужно обрабатывать шестнадцатеричные числа. В этом случае можно выполнить вычитание, а затем сравнить с 10, а потом снова уменьшить на 7, если код больше 10 (учитывая, что шестнадцатеричные числа — это «A»-«Z» в верхнем регистре).
В JS можно снова использовать регулярные выражения, а затем, когда получим совпадение числа, можно вызвать Number(), что даёт нам ещё одно преимущество: шестнадцатеричные числа тоже преобразуются тривиально, потому что Number() делает это автоматически, если число начинается с 0x.
Как же это будет выглядеть на JavaScript?
if (ch >= 48 && ch <= 57) {
out.push (0xFD); // number token
const numberLiteralStr = inStr.substr(idx).match(/^[d|A-F|a-f|x|X]+/)[0];
idx += numberLiteralStr.length;
const numberLiteral = Number(numberLiteralStr);
const bytes = new Uint8Array(new Uint16Array([numberLiteral]).buffer);
out.push(...bytes)
continue;
}
Регулярное выражение позволяет использовать любые сочетания цифр или шестнадцатеричных цифр (плюс x для перехода в шестнадцатеричный режим). Выражение неидеально, например, оно позволяет использовать несколько x, но пока этого вполне достаточно.
В приведённом выше коде может вызывать вопросы преобразование числа в байты. Number() выполнила всю сложную работу по превращению строки цифр в число, с которым может работать JavaScript, но теперь нам нужно представить его в виде последовательности байтов. Для такого преобразования можно использовать математику:
const hiByte = (numberLiteral & 0xFF00) >> 8;
const loByte = (numberLiteral & 0x00FF);
… и для целого числа это сделать легко. Но благодаря использованию типизированных массивов JS можно не заниматься всеми этими вычислениями, а заодно подготовиться к обработке чисел с плавающей запятой в будущем (мы просто заменим Uint16Array на Float64Array).
Код для выполнения этой задачи на языке ассемблера немного длиннее, зато он и делает немного больше. Retroputer использует ещё одну оптимизацию: если число мало, то оно сохраняется в меньшем формате. Это означает, что 0-255 можно хранить в одном байте, а более длинные числа занимают два.
Поиск ключевых слов
Итак мы проделали довольно много работы, но пока так и не сжали ни одного ключевого слова. Разобравшись с числами и строковыми литералами, мы можем быть уверенными, что всё остальное является или ключевым словом, или именем переменной. (Или же пробелом, но это легко проверить.)
В BASIC ключевые слова не всегда начинаются с алфавитного символа, токенами также считаются операторы и разделители. Но переменные тоже начинаются с алфавитного символа. Так что мы не можем сразу определить, что будем сжимать — ключевое слово или переменную. Это нас устраивает — если мы не найдём совпадения в списке токенов, то будем считать, что это переменная.
Как же нам проверить, что потенциальное ключевое слово действительно им является? Если бы мы писали на JavaScript, то могли бы использовать метод Array#findIndex.
const tokenMatch = tokens.findIndex(token =>
inStr.substr(idx).startsWith(token));
if (tokenMatch > -1) {
out.push(tokenMatch + 128);
idx += tokens[tokenMatch].length;
continue;
}
Метод Array#findIndex итеративно обходит массив tokens и мы можем проверить, начинается ли inStr (по текущему idx) с проверяемого нами токена. Работая с нашим упрощённым списком токенов, мы сделаем нечто подобное (предположим, что inStr.substr(idx)===”PRINT”):
Примечание: как и в случае indexOf в JS, если ничего не найдено, мы получаем -1.
Если совпадение найдено, можно сохранить его индекс в возвращаемом массиве. Но как нам позже отличить токен от символа? Легко: включим старший бит, а это можно сделать, прибавив к значению токена 128.
(Примечание: если нам нужно больше токенов, чем 128, то для некоторых токенов пришлось бы использовать два байта. Это немного всё усложняет, но не так сильно. В некоторых версиях BASIC это реализовано, например, в различных Microsoft BASIC.)
Мы закончили работу на JavaScript, но как нам это сделать на языке ассемблера?
Оказывается, почти так же, но код будет намного длиннее.
search-keywords:
bl := [d, x] # get first character of current token
cmp bl, constants.NUL # if it's NUL, we've exhausted the list
brs Z exit-keyword-search # so we're clearly not a keyword
clr Z # compare strings, but with partial equality
call [vectors.STRCMP] # so that our source doesn't need NUL between
# tokens; c will now be how many chars got
# compared
if !Z {
do { # no match; advance past our token in the list
inc x # character by character
bl := [d, x] # tokens are terminated with NULs
cmp bl, constants.NUL # so if we see it, we can stop
} while !z
inc x # go past the token #
inc x # in the lookup table
brs search-keywords # and keep looking for a match
}
clr c # found the match!
add x, c # c is the length of the match
inc x # past the NUL
bl := [d, x] # bl is now the token #
call _get-target-index
<bp+target>,y := bl # write the token #
call _adv-target-index
call _get-source-index # advance past the token in the source
clr c
add y, c # by adding the character count
dec y # back off by one (we'll advance again later)
call _set-source-index
continueНу всё выглядит не так уж плохо. Алгоритм почти такой же, только таблица токенов на языке ассемблера структурирована немного иначе. Она выглядит примерно так:
CLS 00 80
PRINT 00 81
: 00 82Каждое ключевое слово завершается нулевым байтом, за которым следует номер токена.
Однако мы упускаем здесь нечто важное — как же вообще выполняется это сравнение строк? В ядре Retroputer есть процедура STRCMP, которой мы можем воспользоваться, но как она выглядит?
strcmp: {
enter 0x00
push a
push b
push d
push y
pushf
if Z {
bl := 0x00 # Checking for full equality
} else {
bl := 0x01 # only checking for partial equality
}
_main:
y := 0 # start of string
top:
cl := [d, x, y] # character in string A
al := <bp+4>,y # character in string B
cmp bl, 0x01 # check if we're doing full equality
if Z {
cmp cl, 0 # we're not, so check for an early nul
# in string b
brs Z strings-are-equal # if it's NUL, we calling them equal
}
cmp cl, al # check character
if Z {
cmp cl, 0 # equal, but check for NUL
brs Z strings-are-equal # NUL reached, strings are equal
inc y # next character
brs top # not NUL, so keep going...
}
# if here, the strings aren't equal
if N {
popf # string is less than
set N
clr Z
brs _out
} else {
popf # string is greater than
clr N
clr Z
brs _out
}
strings-are-equal:
popf
clr N # Not less than
set Z # but Equal
_out:
c := y # make sure we know how many chars
# were compared
pop y
pop d
pop b
pop a
exit 0x00
ret
}
Не знаю как вы, а я всё больше и больше начинаю любить метод String#startsWith из JS. Да, он делает то же самое, но нам не приходится писать всю внутреннюю логику!
Обработка переменных
Работа над сжатием ключевых завершена, так что мы можем закончить. Но Retroputer BASIC делает ещё один шаг вперёд — токенизирует переменные. Мне кажется, так поступали только немногие версии BASIC из 80-х и 90-х, потому что в условиях ограниченной памяти это может вредить. Но если памяти много, то токенизация переменных помогает повысить производительность.
Вот что делает Retroputer BASIC:
- Он считывает до двух первых символов имени переменной. (Это было стандартным неудобством версий BASIC той эпохи из-за ограничений памяти.)
- По этим двум символам он определяет индекс переменной. «A» — это переменная 0, «A0» — переменная 53, и т.д. Уравнение довольно простое, но сейчас оно нас не интересует.
- BASIC продолжает сканирование в поисках символа типа переменной. Например,
$в BASIC обозначает строковую переменную. Тип переменной хранится парой битов выше в индексе переменной. - Затем BASIC записывает тип и индекс в выходные данные, а потом вместе с самим именем переменной записывает длину этого имени. Именно на этом мы теряем экономию пространства!
(Примечание: когда Retroputer BASIC научится динамически выделять память под переменные, мы заменим индекс указателем на переменную. Ещё один пункт в списке todo!)
Благодаря этому поиск переменных во время выполнения становится невероятно быстрым: нам не нужно парсить имя переменной и вычислять индекс каждый раз, когда мы встречаем переменную. В сплошных циклах экономия может быть солидной. Но за это приходится платить большую цену: нам нужно хранить указатель и имя переменной вместе, поэтому для каждой встреченной переменной нам нужно добавлять в выходные данные по четыре лишних байта.
Вам решать, стоит ли оно того.
Как бы то ни было, на JavaScript тоже легко определять, является ли оставшееся в потоке символов переменной:
const variableMatch = inStr.substr(idx).match(/^[A-Z]+[A-Z0-9]*[$]*/);
if (variableMatch) {
const variableName = variableMatch[0];
idx += variableName.length;
// tokenize it (omitted; nothing new here)
continue;
}Я не буду подробно описывать код, который сейчас Retroputer использует для токенизации переменных, он слишком многословен. Мы вернёмся к нему, когда я добавлю динамическое выделение памяти под переменные.
Токенизация завершена
Если теперь протестировать наш код на JS, то мы получим массив байтов, похожий на тот, который Retroputer BASIC использует внутри:
console.log(toHex(tokenize(`CLS: PRINT "Hello, World"`)));
// 80 82 20 81 20 FB 48 65 6C 6C 6F 2C 20 57 6F 72 6C 64 00 00 Ого, какой объём работы для экономии нескольких байтов. Но когда свободной памяти всего пара килобайтов, оно того стоит! Но это не единственное преимущество сжимания вводимого пользователем текста, мы ещё и ускоряем выполнение программы.
Чтобы объяснить, почему так получается, нам нужно понять, как Retroputer исполняет код. Пока я не буду вдаваться в подробности, но вкратце для исполнения кода требуется следующее:
- Получаем байт из памяти
- Если у байта включен старший бит, то это токен, а в противном случае это синтаксическая ошибка (или NUL; в любом случае, на этом мы заканчиваем работу со строкой программы)
- Ищем обработчик токена в массиве — этот массив содержит указатели на сами функции, которые обрабатывают токен
- Вызываем обработчик (он отвечает за получение аргументов и тому подобное)
- Повторяем всё заново
Это ещё одна причина токенизации ключевых слов — выполнение логики ключевого слова становится тривиальным, достаточно найти адрес в массиве и вызвать его.
Хотелось бы подчеркнуть, что несмотря на важность токенизации для экономии пространства, она также повышает скорость выполнения.
Например, цикл выполнения на JS может выглядеть примерно так:
const handlers = [ cls, print, endOfStmt ];
bytes.forEach(byte => handlers[byte] && handlers[byte]());Разумеется, на самом деле всё не так просто, он гораздо больше, но это уже тема для другого поста!
Ресурсы
- Полный код этого поста на JavaScript
- Исходный код Retroputer (на текущем этапе развития)
- Список ресурсов, использованных для этого проекта
На правах рекламы
Мощные VPS с защитой от DDoS-атак и новейшим железом. Всё это про наши эпичные серверы. Максимальная конфигурация — 128 ядер CPU, 512 ГБ RAM, 4000 ГБ NVMe.
На чтение 1 мин.
Значение слова «Интерпретатор»
— тот, кто занимается интерпретацией чего-либо
Содержание
- Транскрипция слова
- MFA Международная транскрипция
- Цветовая схема слова
Транскрипция слова
[и́нтэрпрэтатар]
В данном слове имеется буква е, перед которой произносится твёрдый парный согласный звук или которая произносится без йотации
MFA Международная транскрипция
[ɪntɛrprʲɪˈtatər]
| и | [́и] | гласный, ударный |
| н | [н] | согласный, звонкий непарный (сонорный), твердый парный |
| т | [т] | согласный, глухой парный, твердый парный |
| е | [э] | гласный, безударный |
| р | [р] | согласный, звонкий непарный (сонорный), твердый парный |
| п | [п] | согласный, глухой парный, твердый парный |
| р | [р] | согласный, звонкий непарный (сонорный), твердый парный |
| е | [э] | гласный, безударный |
| т | [т] | согласный, глухой парный, твердый парный |
| а | [а] | гласный, безударный |
| т | [т] | согласный, глухой парный, твердый парный |
| о | [а] | гласный, безударный |
| р | [р] | согласный, звонкий непарный (сонорный), твердый парный |
Букв: 13 Звуков: 13
Цветовая схема слова
интерпретатор
Как произносится слово «Интерпретатор»
Тег audio не поддерживается вашим браузером.
Как правильно пишется «Интерпретатор»
интерпрета́тор
интерпрета́тор, -а
Как правильно перенести «Интерпретатор»
ин—тер—пре—та́—тор
Часть речи
Часть речи слова «интерпретатор» — Имя существительное
Морфологические признаки.
интерпретатор (именительный падеж, единственного числа)
Постоянные признаки:
- нарицательное
- одушевлённое
- мужской
- 2-e склонение
Непостоянные признаки:
- именительный падеж
- единственного числа
Может относится к разным членам предложения.
Склонение слова «Интерпретатор»
| Падеж | Единственное число | Множественное число |
|---|---|---|
| Именительный Кто? Что? |
интерпрета́тор | интерпрета́торы |
| Родительный Кого? Чего? |
интерпрета́тора | интерпрета́торов |
| Дательный Кому? Чему? |
интерпрета́тору | интерпрета́торам |
| Винительный (одуш.) Кого? Что? |
интерпрета́тора | интерпрета́торов |
| Творительный Кем? Чем? |
интерпрета́тором | интерпрета́торами |
| Предложный О ком? О чём? |
интерпрета́торе | интерпрета́торах |
Разбор по составу слова «Интерпретатор»
Состав слова «интерпретатор»:
корень — [интерпрет], суффикс — [атор], нулевое окончание — [ ]
Проверьте свои знания русского языка
Категория: Русский язык
Русский язык
Тест на тему “Мягкие согласные”
1 / 5
Укажите верное утверждение.
В русском языкознании нет термина «мягкие согласные буквы»
В русском языкознании нет термина «мягкие согласные звуки»
Термин «мягкие согласные буквы» равнозначен термину «мягкие согласные звуки»
В русском языкознании есть только термин «мягкие согласные»
2 / 5
Какие буквы не выражают мягкость согласных звуков?
3 / 5
Что можно сказать про буквы б, в, г, д, з, к, л, м, н, п, р, с, т, ф, х?
Обозначают всегда мягкие звуки
Обозначают всегда твердые звуки
Обозначают и мягкие, и твердые звуки
Не обозначают звуки
4 / 5
Какие буквы всегда обозначают мягкие согласные звуки?
ж, ц, ш
б, в, г
й, ч, щ
с, т, ф
5 / 5
Почему согласные звуки называются мягкими?
Потому что после согласных звуков стоят гласные буквы я, е, ё, и, ю
Потому что после согласных звуков стоит мягкий знак (ь)
Потому что после согласных звуков стоят гласные буквы а, э, о, ы, у
Потому что при произношении таких согласных средняя спинка языка поднята к твердому нёбу
Синонимы к слову «интерпретатор»
Предложения со словом «интерпретатор»
- Мы думаем, что нормировать рецепцию, как это предполагает позиция интерпретатора, необязательно.
Павел Успенский, К русской речи: Идиоматика и семантика поэтического языка О. Мандельштама
- Специалист в литературоведении – это издатель сочинений, собиратель архива, при этом дотошный интерпретатор текстов.
Иоганн Петер Эккерман, Разговоры с Гете
- Рис. 2.7. Окно командного интерпретатора после выполнения команды.
Владимир Волков, Программирование для карманных компьютеров
Происхождение слова «Интерпретатор»
Из лат. interpretator «толкователь, истолкователь», далее из interpretari «толковать, объяснять; преводить», далее из interpres «посредник, переводчик», далее из inter- «между» (из праиндоевр. *enter «между», сравн. степень от *en- «в») + -pres (происхождение этого компонента неясно).
Сегодня совместными усилиями мы с вами создадим простенький скриптовый язык программирования. В нем не будет массивов или условных операторов, зато будут целочисленные переменные и множество операций над ними. Писать, как вы уже поняли, будем на замечательном языке Haskell. Также мы познакомимся с «компиляторами компиляторов» Alex и Happy.
Вспоминаем теоретическую часть
Каким образом исходный код программы преобразуется в исполняемый файл? Это происходит в несколько шагов/этапов. Выходные данные, полученные на шаге N, служат входными данными для шага N+1. На вход такому «конвейеру» байт за байтом подается исходный код, а на выходе получается программа. Что же это за этапы?
Первый этап — это лексический анализ. На этом шаге код программы, скажем:
разбивается на лексемы (строки «foo», «=», «+», …), их которых затем получается последовательность токенов:
[ ИДЕНТ «foo», РАВНО, ИДЕНТ «foo», ПЛЮС, 1, ТОЧКА_С_ЗАПЯТОЙ ]
То есть, лексический анализатор разбивает программу на элементарные составные части — операторы, ключевые слова, имена переменных и тп. Также на этапе лексического анализа опционально удаляются комментарии, а запись 0b1101 преобразуется в число 13.
Выход лексического анализатора подается на вход синтаксическому анализатору (или парсеру), задача которого заключается в проверке синтаксиса (такой штуки, которая не позволяет писать десять знаков равенства подряд) и преобразовании последовательности токенов в дерево синтаксического разбора. На этом этапе мы уже не беспокоимся о том, что в коде программы есть табуляции или переносы строк. Также мы точно знаем, что программа не содержит лексическую ошибку, то есть в ней нет несуществующих операторов или переменной, имя которой начинается с цифры.
Дерево разбора представляет собой структуру наподобие следующих:
Рассмотрим левое дерево. Читая его снизу вверх, получим «взять значение переменной a и число 1, сложить их, а затем присвоить результат переменной a», что в точности описывает поведение программы. Правое дерево наглядно демонстрирует, что при его построении были учтены приоритеты операторов, то есть сначала производятся умножение и деление и только потом сложение.
Также вы можете заметить, что ни одно из деревьев не содержит токена «точка с запятой». Вообще-то, узлы дерева могут содержать не токены, а какие-то другие типы данных. Или токены, но не те, что пришли от лексического анализатора. Скажем, инкремент (оператор ++) может быть преобразован в дерево, представленное слева.
Происходящее за лексическим и синтаксическим анализом зависит от решаемой задачи, реализации компилятора, пестрости рубашек его автора и тп. За ними может следовать (или не следовать) семантический анализ, цель которого состоит в обнаружении обращений к несуществующим переменным, вызовов функций с неверным числом аргументов и тп. Если мы пишем оптимизирующий компилятор, то за семантическим анализом последует оптимизация кода, затем — непосредственно генерация кода и, возможно, его оптимизация на уровне машинных команд.
Наш интерпретатор не будет генерировать никакого кода, работая напрямую с синтаксическим деревом. Семантика будет проверяться прямо во время интерпретации. Оптимизация производиться не будет.
Поскольку редкий компилятор (интерпретатор, транслятор, …) обходится без лексического и синтаксического анализатора, была написана масса генераторов этих самых анализаторов. «Компиляторы компиляторов» экономят время и силы, а также существенно сокращают количество багов в создаваемых с их помощью компиляторах. Мы воспользуемся генераторами Alex и Happy. Устанавливаются они, как и следовало ожидать, с помощью утилиты cabal.
Лексический анализатор
Все исходники к этой заметке вы найдете в этом архиве.
Код лексического анализатора находится в файле Lex.x. Он слишком объемен, чтобы приводить его здесь целиком, но при этом не содержит какой-то особой магии. Мы просто определяем тип данных «токен»:
data Token = TInt Int | TIdent String
| TPlus | TMinus | TMul | TDiv | TMod
| …
instance Show Token where
show x = case x of
TInt i -> show i
TIdent s -> s
TModifSet -> «=»
TPlus -> «+»
TMinus -> «-«
TMul -> «*»
TDiv -> «/»
TMod -> «%»
…
… и задаем старые добрые регулярные выражения, определяющие, какой лексеме (последовательности символов) какой токен соответствует:
$alpha = [a-zA-Z]
$digit = [0-9]
$hex = [0-9a-fA-F]
$bin = [0-1]
tokens :-
$white+ ;
$digit+ { (p,_,_,s) len -> return $ TInt (read $ take len s) }
«+» { (p,_,_,s) len -> return $ TPlus }
«-» { (p,_,_,s) len -> return $ TMinus }
«*» { (p,_,_,s) len -> return $ TMul }
«/» { (p,_,_,s) len -> return $ TDiv }
«%» { (p,_,_,s) len -> return $ TMod }
…
На самом деле, это не сам код лексического анализатора, а что-то вроде его заготовки. А вот если выполнить команду:
… то будет сгенерирован файл Lex.hs, содержащий непосредственно код. Убедиться, что он действительно работает, можно с помощью следующей программы:
module Main where
import Lex
main = do
s <- getContents
putStrLn $ case alexScanTokens s of
Right lst -> concatMap (t -> «‘» ++ show t ++ «‘ «) lst
Left err -> «ERROR: « ++ err
Проверяем:
$ alex Lex.x
$ ghc LexMain.hs
[1 of 2] Compiling Lex ( Lex.hs, Lex.o )
[2 of 2] Compiling Main ( LexMain.hs, LexMain.o )
Linking LexMain …
$ echo ‘a = a + 1; a—;’ | ./LexMain
‘a’ ‘=’ ‘a’ ‘+’ ‘1’ ‘;’ ‘a’ ‘—‘ ‘;’ ‘(EOF)’
Согласитесь, ничего сложного.
Синтаксический анализатор
Синтаксис языка программирования обычно задается с помощью контекстно-свободной грамматики, для описания которой в свою очередь используется BNF. Откроем файл Synt.y и найдем в нем описание грамматики нашего языка программирования:
Program:
ExprList { Program $1 }
ExprList:
Expr ‘;’ ExprList { ExprList $1 $3 }
| ‘EOF’ { ExprEnd }
Expr:
ident ‘=’ RVal { Expr $1 $3 }
…
RVal:
RVal ‘+’ RVal { BinOp Add $1 $3 }
| RVal ‘-‘ RVal { BinOp Sub $1 $3 }
| RVal ‘*’ RVal { BinOp Mul $1 $3 }
| RVal ‘/’ RVal { BinOp Div $1 $3 }
…
| RVal ‘?’ RVal ‘:’ RVal { IfElse $1 $3 $5 }
| ‘(‘ RVal ‘)’ { $2 }
| int { IntVal $1 }
| ident { IdentVal $1 }
Символы в кавычках, а также int и ident — это просто другие обозначения токенов:
%token
int { TInt $$ }
ident { TIdent $$ }
‘+’ { TPlus }
‘-‘ { TMinus }
‘*’ { TMul }
‘/’ { TDiv }
‘%’ { TMod }
…
Также Synt.y содержит описание типа «синтаксическое дерево»:
data Program = Program ExprList
deriving (Show, Eq)
data ExprList = ExprList Expr ExprList | ExprEnd
deriving (Show, Eq)
data Expr = Expr String RVal
deriving (Show, Eq)
data BinOpType = Add | Sub | Mul | Div | Mod | LogOr | LogXor
| LogAnd | BinAnd | BinOr | BinXor
| Eq | Lt | Le | Shl | Rol
deriving (Show, Eq)
data UnOpType = LogNot | BinNot | Neg
deriving (Show, Eq)
data RVal = IntVal Int | IdentVal String
| BinOp BinOpType RVal RVal | UnOp UnOpType RVal
| IfElse RVal RVal RVal
deriving (Show, Eq)
Некоторые грамматики, включая нашу, содержат неоднозначности. Это приводит к конфликтам — ситуациям, когда по заданной грамматике и заданной последовательности токенов можно построить несколько различных деревьев синтаксического разбора. Если грамматика содержит конфликты, Happy сообщит об их наличии при генерации кода синтаксического анализатора. Есть два типа конфликтов.
Наличие reduce/reduce конфликтов означает, что некой последовательности токенов может соответствовать более одного нетерминального символа. Другими словами, при некоторых условиях может оказаться неясно, то ли в программе объявляется функция, то ли происходит деление на десять. Избавиться от reduce/reduce конфликтов можно только изменив грамматику. Наша грамматика таких конфликтов не содержит.
Конфликты типа shift/reduce возникают, когда некая последовательность токенов может быть представлена только одним нетерминалом, но, тем не менее, несколькими деревьями разбора. Например, 1 + 2 * 3 — это (1 + 2) * 3 или 1 + (2 * 3)? Очевидно, наша грамматика в изобилии содержит такого рода конфликты. Разрешаются они с помощью приоритетов и ассоциативности операторов:
%right ‘=’ ‘+=’ ‘-=’ ‘*=’ ‘/=’ ‘%=’ …
%right ‘?’ ‘:’
%left ‘||’
%left ‘^^’
%left ‘&&’
%left ‘|’
%left ‘^’
%left ‘&’
%left ‘==’ ‘<>’
%left ‘<‘ ‘<=’ ‘>’ ‘>=’
%left ‘>>’ ‘<<‘ ‘<<<‘ ‘>>>’
%left ‘+’ ‘-‘
%left ‘*’ ‘/’ ‘%’
%right ‘!’ ‘~’
%right NEG
%%
Чем ниже оператор в этом списке, тем выше его приоритет. Чтобы не накосячить, я подсмотрел приоритеты и ассоциативность у Кернигана и Ритчи. Что такое NEG, будет показано немного ниже.
Теперь о shift/reduce конфликтах можно не волноваться — если операторы имеют разный приоритет, дерево синтаксического разбора будет строиться в соответствии с их приоритетами, а если одинаковый, в ход вступит ассоциативность. Например, оператор сложения является левоассоциативным, потому выражение 1 + 2 + 3 + 4 — это на самом деле ((1 + 2) + 3) + 4.
Оператор может быть безассоциативным (%nonassoc). Если два таких оператора находятся в непосредственной близости, это означает синтаксическую ошибку. Также оператор может менять свой приоритет в зависимости от контекста. Классический пример — унарный минус:
RVal:
RVal ‘+’ RVal { BinOp Add $1 $3 }
| RVal ‘-‘ RVal { BinOp Sub $1 $3 }
| RVal ‘*’ RVal { BinOp Mul $1 $3 }
| RVal ‘/’ RVal { BinOp Div $1 $3 }
…
| ‘-‘ RVal %prec NEG { UnOp Neg $2 }
…
Все, с матчастью покончено! Теперь попробуем синтаксический анализатор в действии:
$ happy Synt.y
$ ghc SyntMain.hs
[2 of 3] Compiling Synt ( Synt.hs, Synt.o )
[3 of 3] Compiling Main ( SyntMain.hs, SyntMain.o )
Linking SyntMain …
$ echo ‘a = 0xFF; b = a << 3; b |= 0b10;’ | ./SyntMain
Program (ExprList (Expr «a» (IntVal 255)) (ExprList (Expr «b»
(BinOp Shl (IdentVal «a») (IntVal 3))) (ExprList (Expr «b»
(BinOp BinOr (IdentVal «b») (IntVal 2))) ExprEnd)))
Обратите внимание на то, какое синтаксическое дерево было построено для последнего выражения. Наш синтаксический анализатор производит очень много подобный преобразований.
Интерпретатор (наконец-то!)
Исходный код интерпретатора вы найдете в файле Interpret.hs. Этот код прост и очевиден, так что оставляю его вам для самостоятельного изучения. А вот как это работает:
$ ghc InterpretMain.hs
[3 of 4] Compiling Interpret ( Interpret.hs, Interpret.o )
[4 of 4] Compiling Main ( InterpretMain.hs, InterpretMain.o )
Linking InterpretMain …
$ ./InterpretMain
a = 1 * 2 + 3 * 4;
a = 14
b = 1 * (2 + 3) * 4;
a = 14
b = 20
c = a > b ? a / b : b / a;
a = 14
b = 20
c = 1
d = 1 $ 2;
lexical error
d + + + +
syntax error
e = a + b + c + d;
undefined variable ‘d’
a %= 0;
divide by zero
Ну разве это не прекрасно? Теперь мы можем пачками штамповать компиляторы, трансляторы и интерпретаторы, а также парсеры различных форматов, статические анализаторы кода типа lint и perlcritic, обфускаторы и деобфускаторы, программы для подсветки синтаксиса и тп. Как я уже когда-то писал, это целый новый мир!
Заключение
В качестве источника дополнительной информации настоятельно рекомендую драконью книгу. Сей труд — библия разработчика компиляторов. Вы просто обязаны прочитать его от и до, если серьезно намерены создать свой Единственный Правильный Язык Программирования.
Ваше домашнее задание, если вы примите его, заключается в доработке интерпретатора таким образом, чтобы он поддерживал строки, массивы, хеши, условные операторы, циклы и функции. Для выполнения миссии вы можете выбрать любых напарников. В случае успеха, вы должны послать мне пулл реквест с соответствующими изменениями. Вы нужны нам, мистер Хант.
Как всегда, я с нетерпением жду ваших вопросов, дополнений и прочего рода комментариев.
Метки: Haskell, Функциональное программирование, Языки программирования.