- До 7 класса: Алгоритмика, Кодланд, Реботика.
- 8-11 класс: Умскул, Годограф, Знанио.
- Английский: Инглекс, Puzzle, Novakid.
- Взрослым: Skillbox, Нетология, Geekbrains, Яндекс, Otus, SkillFactory.
Как пишется: «измерение» или «измирение»?
Правило
Нарицательное, неодушевлённое существительное «измерение» отвечает на вопрос «что?». Это номинатив среднего рода, единственного числа, 2-го склонения.
В составе лексемы выделяется приставка «из», корень «мер», суффикс «ени», окончание «е». Безударная гласная в корне проверяется с помощью однокоренных слов «мера», «измерить», «примерка». В них корневая «е» находится в сильной позиции.
Значение
Измерение — определение величины чего-либо с помощью какой-либо единицы.
Примеры
- Ежедневное измерение скорости ветра — обязанность метеорологов.
- Килограмм — единица измерения веса.
- Ежедневное утреннее измерение артериального давления подтвердило, что его нижняя граница не соответствует норме.
- До 7 класса: Алгоритмика, Кодланд, Реботика.
- 8-11 класс: Умскул, Годограф, Знанио.
- Английский: Инглекс, Puzzle, Novakid.
- Взрослым: Skillbox, Нетология, Geekbrains, Яндекс, Otus, SkillFactory.
Как правильно пишется словосочетание «измерить скорость»
- Как правильно пишется слово «измерить»
- Как правильно пишется слово «скорость»
Делаем Карту слов лучше вместе
Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать
Карту слов. Я отлично
умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!
Спасибо! Я стал чуточку лучше понимать мир эмоций.
Вопрос: сопель — это что-то нейтральное, положительное или отрицательное?
Ассоциации к слову «измерить»
Ассоциации к слову «скорость»
Синонимы к словосочетанию «измерить скорость»
Предложения со словосочетанием «измерить скорость»
- Итак, мы нашли крайне неординарный способ определения секунды – но как это поможет измерить скорость света?
- На самом деле способов измерить скорость чтения может быть много.
- Например, можно измерить скорость чтения, учитывая количество слов, прочитанных за год.
- (все предложения)
Сочетаемость слова «скорость»
- на полной скорости
с бешеной скоростью
с огромной скоростью - скорость света
скорость движения
скорость передвижения - превышение скорости
увеличение скорости
переключение скоростей - скорость увеличилась
скорость упала
скорость возросла - набирать скорость
сбавить скорость
снизить скорость - (полная таблица сочетаемости)
Значение слова «измерить»
-
ИЗМЕ́РИТЬ, —рю, —ришь; сов., перех. (несов. мерить). 1. (несов. также измерять). Определить какой-л. мерой величину чего-л. Измерить силу тока. (Малый академический словарь, МАС)
Все значения слова ИЗМЕРИТЬ
Значение слова «скорость»
-
СКО́РОСТЬ, -и, род. мн. —е́й, ж. 1. Степень быстроты движения кого-, чего-л. или распространения чего-л. Скорость полета. Скорость бега. Скорость течения. Скорость света. Скорость звука. (Малый академический словарь, МАС)
Все значения слова СКОРОСТЬ
Афоризмы русских писателей со словом «измерить»
- Но ты, художник, твердо веруй
В начала и концы. Ты знай,
Где стерегут нас ад и рай.
Тебе дано бесстрастной мерой
Измерить все, что видишь ты. - Мы уходим, в дорогу веря,
Далекие звезды любя,
Планету свою измерив,
Мы хотим измерить себя. - Неверно рассуждает математик, если хочет циркулем измерить Божью волю, но не прав и богослов, если он думает, что на Псалтирье можно научиться астрономии или химии.
- (все афоризмы русских писателей)
Отправить комментарий
Дополнительно
Смотрите также
ИЗМЕ́РИТЬ, —рю, —ришь; сов., перех. (несов. мерить). 1. (несов. также измерять). Определить какой-л. мерой величину чего-л. Измерить силу тока.
Все значения слова «измерить»
СКО́РОСТЬ, -и, род. мн. —е́й, ж. 1. Степень быстроты движения кого-, чего-л. или распространения чего-л. Скорость полета. Скорость бега. Скорость течения. Скорость света. Скорость звука.
Все значения слова «скорость»
-
Итак, мы нашли крайне неординарный способ определения секунды – но как это поможет измерить скорость света?
-
На самом деле способов измерить скорость чтения может быть много.
-
Например, можно измерить скорость чтения, учитывая количество слов, прочитанных за год.
- (все предложения)
- конечная скорость
- скорость частицы
- изменение скорости
- относительная скорость
- приближаться к скорости света
- (ещё синонимы…)
- радиус
- периметр
- параметр
- мера
- размер
- (ещё ассоциации…)
- радар
- машина
- интенсивность
- автобан
- мотоциклист
- (ещё ассоциации…)
- измерить давление
- измерить температуру
- измерить расстояние
- (полная таблица сочетаемости…)
- на полной скорости
- скорость света
- превышение скорости
- скорость увеличилась
- набирать скорость
- (полная таблица сочетаемости…)
- Разбор по составу слова «измерить»
- Разбор по составу слова «скорость»
- Как правильно пишется слово «измерить»
- Как правильно пишется слово «скорость»
Морфемный разбор слова:
Однокоренные слова к слову:
Формула скорости — обозначение, единицы измерения и примеры нахождения
Довольно часто в точных науках приходится сталкиваться с понятием скорость. Формула, дающаяся в школе на уроке математики, справедлива лишь для частного случая, при котором перемещение остаётся всегда постоянным. По сути, термин обозначает быстроту изменения чего-либо. Существует несколько видов движения и методов расчета.
Понятие и основные термины
Под скоростью понимается величина, определяющая быстроту и направление перемещения материальной точки в выбранной системе отсчёта. Термин широко применяется в математике, физике, химии. Так, с его помощью описывают реакции, изменения температуры, передвижение тел, используют как производную рассматриваемой величины.
Слово «скорость» произошло от латинского «velocitas», обозначающее движение. В качестве единицы измерения, согласно Международной системе единиц (СИ), для неё выбран метр, делённый на секунду (м/с). Обозначается скорость буквой V, вне зависимости от науки, в которой её применяют. Простейшая формула, с помощью которой определяют величину, выглядит следующим образом: V = S: t. Где:
Это обобщённое уравнение, но в то же время позволяющее получить представление о понятии. Часто это неравенство называют уравнением пути. Формула используется для вычисления только в том случае, если движение не изменяется на всём исследуемом участке.
Впервые с выражением знакомят учащихся на уроках математики в пятом классе. Учитель предлагает научиться решать простые задачи на нахождение характеристики при известной длине пройденного пути и потраченного на это времени. Например, автомобиль за четыре часа проехал 16 километров. Необходимо найти, с какой скоростью он двигался. Решение задачи сводится к двум действиям. В первом все заданные величины переводятся в систему СИ: 4 часа = 240 минут = 10240 секунд; 16 километров = 16000 метров. Во втором действии данные подставляют в формулу и вычисляют ответ: V = 16000/10240 = 1,6 м/с.
Но, помимо равномерного движения, то есть при котором скорость является константой, есть ещё и другие виды перемещений. Использовать обобщённое уравнение для них нельзя. Для каждого вида движения применяется своя формула. Существующую скорость разделяют на следующие виды:
Равноускоренное движение
Если в течение времени положение тела изменяется относительно предметов, находящихся в покое, то считается, что оно движется. При этом в качестве основного параметра, описывающего перемещение, используется скорость. Движение тела или точки можно представить в виде линии, повторяющей путь прохождения. Называется она траекторией. Если линия прямая, то движение считается прямолинейным.
Неравномерное движение характеризуется перемещением по различной траектории с непостоянной величиной скорости. При этом изменение положения может быть равноускоренным, то есть параметр на одинаковых промежутках увеличивается или уменьшается на одно и то же значение. В качестве примера можно привести падение камня.
В произвольно взятой точке скорость перемещения равна ускорению свободного падения.
Таким образом, если векторы V и ускорения A лежат вдоль прямой, то в проекциях такое направление можно рассматривать как алгебраические величины. При равноускоренном движении по прямой траектории скорость точки вычисляется по формуле: V = V0 + A*t. Где:
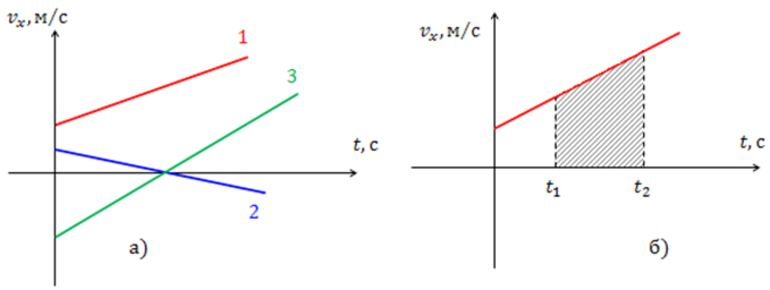
Это основная формула в физике. На графике она изображается как прямая линия v (t). По оси ординат откладывается время, а абсцисс — скорость. Построив график, по наклону прямой можно определить ускорение точки A. Для этого используется формула нахождения сторон треугольника: A = (v-v0) / t.
Среднее значение
В кинематике для нахождения характеристики используется усреднённый параметр. Используют его при изучении движения материальной точки или любого физического тела. Для определения средней скорости используют две величины: скалярную и векторную. Первой обозначают путевое движение, а второй — перемещение.
Путевая скорость определяется как отношение расстояния пройденного тела ко времени, затраченному на его прохождение: V = Σs / Σt.
По сути, среднее значение находится как среднеарифметическое от всех скоростей, если рассматриваемая точка передвигалась одинаковые отрезки времени. В ином же случае найденная величина будет взвешенной среднеарифметической величиной.
Математически формулу средней скорости записывают так: V (t + Δ t) = Δ s/ Δ t = (s (t + Δ t) — s (t)) / Δ t. Учитывая, что Δs зависит от длины пути, которую преодолела точка за время Δt, верной будет запись: Δ s = s (t + Δt) — s (t). Если же затраченное время стремится к нулю, получится формула, совпадающая с выражением для нахождения мгновенной скорости.
Вектор материальной точки находится из отношения положения тела к отрезку времени: V (t + Δt) = Δr / Δt = (r (t + Δt) — r (t)) / Δt, где r — радиус-вектор. Когда тело выполняет равномерно-прямолинейное перемещение, то справедливым будет равенство: = V.
Например, мяч первую половину пути длиной 100 метров катился с одной скоростью в течение двадцати секунд, а вторую с другой и одну минуту. Необходимо вычислить среднюю скорость. Согласно формулам, интервал движения на первом участке пути будет равен: t1 = s/2*V1, а на втором t2 = s/2*V2. Решением задачи будет: Vср = s/(t1+t2) = s/(s/2*v1 + s/2*v2) = 2*V1*V2/(V1+V2) = 100/(20 +60) = 1,25 м/с.
Угловая скорость
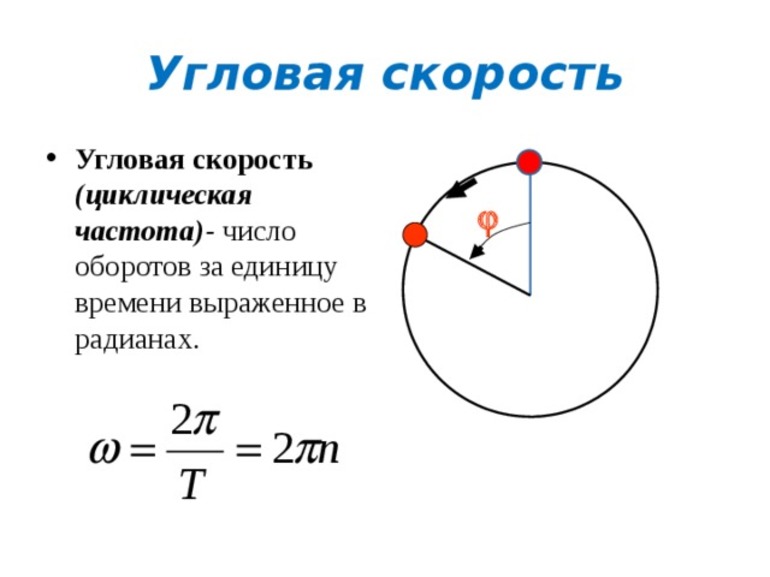
Проявляется этот вид при вращении тела вокруг оси. Траектория представляет собой круговое движение. Основным параметром, учитывающимся при его нахождении, является угол поворота (f). Все элементарные угловые движения являются векторами. Обычный поворот равен углу вращения тела df за небольшой отрезок времени dt в противоположную сторону от хода часовой стрелки.
В математике формулу для нахождения углового параметра записывают как w = df/dt. Угловая скорость — аксиальная величина, располагающаяся вдоль мгновенной оси и совпадающая с поступательным вращением правого винта. Равномерное вращение, то есть движение, при котором происходит поворот на один и тот же угол, называют равномерным. Модуль угловой скорости определяют по формуле: w = f/t, где f — угол поворота, t — время, в течение которого происходило вращение. Учитывая, что Δf = 2p, формулу можно переписать до вида: w = 2p/T, то есть с использованием периода.
Существует связь между угловой скоростью и числом оборотов: w = 2*p*v. Это понятие используется для решения заданий при описании неравномерного вращения. Есть также выражение, связывающее линейную скорость с угловой: v = [w*R], где R — компонента, проведённая перпендикулярно к радиус-вектору. В качестве единицы измерения параметра используется радиан, делённый на секунду (рад/с).
Например, необходимо определить угловую скорость вариатора в тот момент, когда подвешенная масса пройдёт расстояние, равное 10 метрам. Радиус плеча составляет 40 сантиметров. В начальный момент подвес находится в состоянии покоя, а затем начинает опускаться с ускорением A = 0,04 м/с2.
Учитывая, что линейная скорость вариатора совпадает с движением груза по прямой, можно записать: V = (2*a*S)½. Должен получится ответ: V = (4*0,04*10)½ = 1,26 м/с. Угловую же скорость находят по формуле: w = v/R, так как R = 40 см = 0,4 м, то W = 1,26/0,4 = 3,15 рад/с.
Закон сложения
Для разных систем отсчёта движения материальных точек существует закон, связывающий их между собой. Согласно ему, скорость чего-либо относительно системы, находящейся в покое, определяется суммой силы перемещения скоростей в подвижной области и более быстрой системы отсчёта по отношению к неподвижной.
Чтобы понять суть закона, лучше всего рассмотреть простой пример. Пусть по железной дороге движется вагон со скоростью 80 км/ч. В этом вагоне перемещается пассажир со скоростью 3 км/ч. Приняв за систему отсчёта неподвижный железнодорожный путь, можно утверждать, что скорость пассажира относительно неё равна сумме скорости вагона и человека.
Если движение вагона и пассажира происходит в одном направлении, то значения просто складываются, V = 80+3 = 83 км/ч, в противоположном — вычитаются V = 80−3 = 77 км/ч. Но это правило будет верным лишь тогда, когда перемещение происходит по одной линии. Поэтому, если человек будет передвигаться в вагоне под углом, следует учитывать и этот фактор, так как по своей сути искомый параметр — величина векторная. Фактически рассчитываются две скорости: сближения и удаления.
Рассматриваемое событие происходит за время Δt. За этот промежуток человек преодолеет расстояние ΔS1, вагон же сможет проехать путь ΔS2. Используя закон, перемещение пассажира будет определяться по формуле: ΔS = ΔS1 + ΔS2. Собственное движение человека относительно железнодорожного пути будет равно V = ΔS1 / Δ t. Выразив значение из формулы нахождения ΔS, можно найти скорость вагона относительно железной дороги: V2 = ΔS2 / Δt.
Использование онлайн-калькулятора
В интернете существуют сервисы, позволяющие находить параметр даже тем, кто не знает формулы или слабо ориентируется в теме. С их помощью можно решать довольно сложные задания, которые требуют скрупулёзного расчёта и немалой затраты времени. Онлайн-вычисление обычно занимает не более нескольких секунд, а за достоверность результата можно не беспокоиться.
Воспользоваться сайтами-калькуляторами сможет любой пользователь, имеющий подключение к интернету и установленный веб-браузер с поддержкой Flash-технологии. Никакой регистрации или указания личных данных сервисы, предлагающие такого рода услуги, не требуют. Система автоматически рассчитает ответ.
Из множества сайтов можно выделить три наиболее популярных среди потребителей:
Все они имеют интуитивно понятный интерфейс и, что примечательно, на своих страницах содержат таблицы всех формул, используемых для решения заданий, правильные условные обозначения и описания процессов вычисления.
Расчёт скорости любого тела несложен. Главное, знать формулы и правильно определить вид перемещения. При этом всегда можно воспользоваться услугами онлайн-калькуляторов. Через них решить поставленную задачу или проверить свои расчёты.
Источник
Понятие и основные термины
Под скоростью понимается величина, определяющая быстроту и направление перемещения материальной точки в выбранной системе отсчёта. Термин широко применяется в математике, физике, химии. Так, с его помощью описывают реакции, изменения температуры, передвижение тел, используют как производную рассматриваемой величины.
Слово «скорость» произошло от латинского «velocitas», обозначающее движение. В качестве единицы измерения, согласно Международной системе единиц (СИ), для неё выбран метр, делённый на секунду (м/с). Обозначается скорость буквой V, вне зависимости от науки, в которой её применяют. Простейшая формула, с помощью которой определяют величину, выглядит следующим образом: V = S: t. Где:
Это обобщённое уравнение, но в то же время позволяющее получить представление о понятии. Часто это неравенство называют уравнением пути. Формула используется для вычисления только в том случае, если движение не изменяется на всём исследуемом участке.
Впервые с выражением знакомят учащихся на уроках математики в пятом классе. Учитель предлагает научиться решать простые задачи на нахождение характеристики при известной длине пройденного пути и потраченного на это времени. Например, автомобиль за четыре часа проехал 16 километров. Необходимо найти, с какой скоростью он двигался. Решение задачи сводится к двум действиям. В первом все заданные величины переводятся в систему СИ: 4 часа = 240 минут = 10240 секунд; 16 километров = 16000 метров. Во втором действии данные подставляют в формулу и вычисляют ответ: V = 16000/10240 = 1,6 м/с.
Но, помимо равномерного движения, то есть при котором скорость является константой, есть ещё и другие виды перемещений. Использовать обобщённое уравнение для них нельзя. Для каждого вида движения применяется своя формула. Существующую скорость разделяют на следующие виды:
Равноускоренное движение
Если в течение времени положение тела изменяется относительно предметов, находящихся в покое, то считается, что оно движется. При этом в качестве основного параметра, описывающего перемещение, используется скорость. Движение тела или точки можно представить в виде линии, повторяющей путь прохождения. Называется она траекторией. Если линия прямая, то движение считается прямолинейным.
Неравномерное движение характеризуется перемещением по различной траектории с непостоянной величиной скорости. При этом изменение положения может быть равноускоренным, то есть параметр на одинаковых промежутках увеличивается или уменьшается на одно и то же значение. В качестве примера можно привести падение камня.
В произвольно взятой точке скорость перемещения равна ускорению свободного падения.
Таким образом, если векторы V и ускорения A лежат вдоль прямой, то в проекциях такое направление можно рассматривать как алгебраические величины. При равноускоренном движении по прямой траектории скорость точки вычисляется по формуле: V = V0 + A*t. Где:
Это основная формула в физике. На графике она изображается как прямая линия v (t). По оси ординат откладывается время, а абсцисс — скорость. Построив график, по наклону прямой можно определить ускорение точки A. Для этого используется формула нахождения сторон треугольника: A = (v-v0) / t.
Среднее значение
В кинематике для нахождения характеристики используется усреднённый параметр. Используют его при изучении движения материальной точки или любого физического тела. Для определения средней скорости используют две величины: скалярную и векторную. Первой обозначают путевое движение, а второй — перемещение.
Путевая скорость определяется как отношение расстояния пройденного тела ко времени, затраченному на его прохождение: V = Σs / Σt.
По сути, среднее значение находится как среднеарифметическое от всех скоростей, если рассматриваемая точка передвигалась одинаковые отрезки времени. В ином же случае найденная величина будет взвешенной среднеарифметической величиной.
Математически формулу средней скорости записывают так: V (t + Δ t) = Δ s/ Δ t = (s (t + Δ t) — s (t)) / Δ t. Учитывая, что Δs зависит от длины пути, которую преодолела точка за время Δt, верной будет запись: Δ s = s (t + Δt) — s (t). Если же затраченное время стремится к нулю, получится формула, совпадающая с выражением для нахождения мгновенной скорости.
Вектор материальной точки находится из отношения положения тела к отрезку времени: V (t + Δt) = Δr / Δt = (r (t + Δt) — r (t)) / Δt, где r — радиус-вектор. Когда тело выполняет равномерно-прямолинейное перемещение, то справедливым будет равенство: = V.
Например, мяч первую половину пути длиной 100 метров катился с одной скоростью в течение двадцати секунд, а вторую с другой и одну минуту. Необходимо вычислить среднюю скорость. Согласно формулам, интервал движения на первом участке пути будет равен: t1 = s/2*V1, а на втором t2 = s/2*V2. Решением задачи будет: Vср = s/(t1+t2) = s/(s/2*v1 + s/2*v2) = 2*V1*V2/(V1+V2) = 100/(20 +60) = 1,25 м/с.
Угловая скорость
Проявляется этот вид при вращении тела вокруг оси. Траектория представляет собой круговое движение. Основным параметром, учитывающимся при его нахождении, является угол поворота (f). Все элементарные угловые движения являются векторами. Обычный поворот равен углу вращения тела df за небольшой отрезок времени dt в противоположную сторону от хода часовой стрелки.
В математике формулу для нахождения углового параметра записывают как w = df/dt. Угловая скорость — аксиальная величина, располагающаяся вдоль мгновенной оси и совпадающая с поступательным вращением правого винта. Равномерное вращение, то есть движение, при котором происходит поворот на один и тот же угол, называют равномерным. Модуль угловой скорости определяют по формуле: w = f/t, где f — угол поворота, t — время, в течение которого происходило вращение. Учитывая, что Δf = 2p, формулу можно переписать до вида: w = 2p/T, то есть с использованием периода.
Существует связь между угловой скоростью и числом оборотов: w = 2*p*v. Это понятие используется для решения заданий при описании неравномерного вращения. Есть также выражение, связывающее линейную скорость с угловой: v = [w*R], где R — компонента, проведённая перпендикулярно к радиус-вектору. В качестве единицы измерения параметра используется радиан, делённый на секунду (рад/с).
Например, необходимо определить угловую скорость вариатора в тот момент, когда подвешенная масса пройдёт расстояние, равное 10 метрам. Радиус плеча составляет 40 сантиметров. В начальный момент подвес находится в состоянии покоя, а затем начинает опускаться с ускорением A = 0,04 м/с2.
Учитывая, что линейная скорость вариатора совпадает с движением груза по прямой, можно записать: V = (2*a*S)½. Должен получится ответ: V = (4*0,04*10)½ = 1,26 м/с. Угловую же скорость находят по формуле: w = v/R, так как R = 40 см = 0,4 м, то W = 1,26/0,4 = 3,15 рад/с.
Закон сложения
Для разных систем отсчёта движения материальных точек существует закон, связывающий их между собой. Согласно ему, скорость чего-либо относительно системы, находящейся в покое, определяется суммой силы перемещения скоростей в подвижной области и более быстрой системы отсчёта по отношению к неподвижной.
Чтобы понять суть закона, лучше всего рассмотреть простой пример. Пусть по железной дороге движется вагон со скоростью 80 км/ч. В этом вагоне перемещается пассажир со скоростью 3 км/ч. Приняв за систему отсчёта неподвижный железнодорожный путь, можно утверждать, что скорость пассажира относительно неё равна сумме скорости вагона и человека.
Если движение вагона и пассажира происходит в одном направлении, то значения просто складываются, V = 80+3 = 83 км/ч, в противоположном — вычитаются V = 80−3 = 77 км/ч. Но это правило будет верным лишь тогда, когда перемещение происходит по одной линии. Поэтому, если человек будет передвигаться в вагоне под углом, следует учитывать и этот фактор, так как по своей сути искомый параметр — величина векторная. Фактически рассчитываются две скорости: сближения и удаления.
Рассматриваемое событие происходит за время Δt. За этот промежуток человек преодолеет расстояние ΔS1, вагон же сможет проехать путь ΔS2. Используя закон, перемещение пассажира будет определяться по формуле: ΔS = ΔS1 + ΔS2. Собственное движение человека относительно железнодорожного пути будет равно V = ΔS1 / Δ t. Выразив значение из формулы нахождения ΔS, можно найти скорость вагона относительно железной дороги: V2 = ΔS2 / Δt.
Использование онлайн-калькулятора
В интернете существуют сервисы, позволяющие находить параметр даже тем, кто не знает формулы или слабо ориентируется в теме. С их помощью можно решать довольно сложные задания, которые требуют скрупулёзного расчёта и немалой затраты времени. Онлайн-вычисление обычно занимает не более нескольких секунд, а за достоверность результата можно не беспокоиться.
Воспользоваться сайтами-калькуляторами сможет любой пользователь, имеющий подключение к интернету и установленный веб-браузер с поддержкой Flash-технологии. Никакой регистрации или указания личных данных сервисы, предлагающие такого рода услуги, не требуют. Система автоматически рассчитает ответ.
Из множества сайтов можно выделить три наиболее популярных среди потребителей:
Все они имеют интуитивно понятный интерфейс и, что примечательно, на своих страницах содержат таблицы всех формул, используемых для решения заданий, правильные условные обозначения и описания процессов вычисления.
Расчёт скорости любого тела несложен. Главное, знать формулы и правильно определить вид перемещения. При этом всегда можно воспользоваться услугами онлайн-калькуляторов. Через них решить поставленную задачу или проверить свои расчёты.
Источник
Основная особенность используемых в настоящее время систем единиц состоит в том, что между единицами разных величин имеются определенные соотношения. Эти соотношения установлены теми физическими законами (определениями), которыми связываются между собой измеряемые величины. Так, единица скорости выбрана таким образом, что она выражается через единицы расстояния и времени. При выборе единиц скорости используется определение скорости. Единицу силы, например, устанавливают при помощи второго закона Ньютона.
При построении определенной системы единиц, выбирают несколько физических величин, единицы которых устанавливают независимо друг от друга. Единицы таких величин называют основными. Единицы остальных величин выражают через основные, их называют производными.
Таблица единиц измерения «Пространство и время»
Физическая величина
Символ
Единица измерения физической величины
Ед. изм. физ. вел.
Описание
Примечания
l, s, d
Протяжённость объекта в одном измерении.
Протяженность объекта в двух измерениях.
Протяжённость объекта в трёх измерениях.
α, φ
Величина изменения направления.
α, β, γ
Быстрота изменения координат тела.
метр в секунду в квадрате
м/с 2
Быстрота изменения скорости объекта.
рад/с =
Скорость изменения угла.
радиан на секунду в квадрате
рад/с 2 =
Быстрота изменения угловой скорости
Таблица единиц измерения «Механика»
Физическая величина
Символ
Единица измерения физической величины
Ед. изм. физ. вел.
Описание
Примечания
Величина, определяющая инерционные и гравитационные свойства тел.
килограмм на кубический метр
кг/м 3
Масса на единицу объёма.
Масса на единицу площади.
кг/м 2
Отношение массы тела к площади его поверхности
Масса на единицу длины.
Отношение массы тела к его линейному параметру
кубический метр на килограмм
м 3 /кг
Объём, занимаемый единицей массы вещества
килограмм в секунду
Масса вещества, которая проходит через заданную площадь поперечного сечения потока за единицу времени
кубический метр в секунду
м 3 /с
Объёмный расход жидкости или газа
килограмм-метр в секунду
кг•м/с
Произведение массы и скорости тела.
экстенсивная, сохраняющаяся величина
килограмм-метр в квадрате в секунду
кг•м 2 /с
Мера вращения объекта.
килограмм-метр в квадрате
кг•м 2
Мера инертности объекта при вращении.
Действующая на объект внешняя причина ускорения.
Произведение силы на длину перпендикуляра, опущенного из точки на линию действия силы.
Произведение силы на время её действия
Давление, механическое напряжение
Па = (кг/(м·с 2 ))
Сила, приходящаяся на единицу площади.
Дж = (кг·м 2 /с 2 )
Скалярное произведение силы и перемещения.
Дж = (кг·м 2 /с 2 )
Способность тела или системы совершать работу.
экстенсивная, сохраняющаяся величина, скаляр
Вт = (кг·м 2 /с 3 )
Скорость изменения энергии.
Таблица единиц измерения «Периодические явления, колебания и волны»
Физическая величина
Символ
Единица измерения физической величины
Ед. изм. физ. вел.
Описание
Примечания
Промежуток времени, за который система совершает одно полное колебание
Частота периодического процесса
Число повторений события за единицу времени.
Циклическая (круговая) частота
рад/с
Циклическая частота электромагнитных колебаний в колебательном контуре.
секунда в минус первой степени
Периодический процесс, равный числу полных циклов, совершённых за единицу времени.
Расстояние между двумя ближайшими друг к другу точками в пространстве, в которых колебания происходят в одинаковой фазе.
метр в минус первой степени
Пространственная частота волны
Таблица единиц измерения «Тепловые явления»
Физическая величина
Символ
Единица измерения физической величины
Ед. изм. физ. вел.
Описание
Примечания
Средняя кинетическая энергия частиц объекта.
кельвин в минус первой степени
Зависимость электрического сопротивления от температуры
gradT
Изменение температуры на единицу длины в направлении распространения теплоты.
Теплота (количество теплоты)
Дж = (кг·м 2 /с 2 )
Энергия, передаваемая от одного тела к другому немеханическим путём
джоуль на килограмм
Дж/кг
Кол-во теплоты, которое необходимо подвести к веществу, взятому при температуре плавления, чтобы расплавить его.
Кол-во теплоты, поглощаемой (выделяемой) телом в процессе нагревания.
джоуль на килограмм-кельвин
Дж/(кг•К)
Теплоёмкость единичной массы вещества.
джоуль на килограмм
Дж/кг
Мера необратимого рассеивания энергии или бесполезности энергии.
Таблица единиц измерения «Молекулярная физика»
Физическая величина
Символ
Единица измерения физической величины
Описание
Примечания
моль
Количество однотипных структурных единиц, из которых состоит вещество.
M, μ
кг/моль
Отношение массы вещества к количеству молей этого вещества.
Дж/моль
Энергия термодинамической системы.
джоуль на моль-кельвин
Дж/(моль•К)
Теплоёмкость одного моля вещества.
метр в минус третьей степени
Число молекул, содержащихся в единице объема.
килограмм на кубический метр
кг/м 3
Отношение массы компонента, содержащегося в смеси, к объёму смеси.
моль на кубический метр
моль/м 3
Содержание компонента относительно всей смеси.
В, μ
квадратный метр на вольт-секунду
м 2 /(В•с)
Коэффициент пропорциональности между дрейфовой скоростью носителей и приложенным внешним электрическим полем.
Таблица единиц измерения «Электричество и магнетизм»
Физическая величина
Символ
Единица измерения физической величины
Ед. изм. физ. вел.
Описание
Примечания
Протекающий в единицу времени заряд.
ампер на квадратный метр
А/м 2
Сила электрического тока, протекающего через элемент поверхности единичной площади.
Кл = (А·с)
Способность тел быть источником электромагнитных полей и принимать участие в электромагнитном взаимодействии.
экстенсивная, сохраняющаяся величина
Электрический дипольный момент
Электрические свойства системы заряженных частиц в смысле создаваемого ею поля и действия на неё внешних полей.
кулон на квадратный метр
Кл/м 2
Процессы и состояния, связанные с разделением каких-либо объектов, преимущественно в пространстве.
Изменение потенциальной энергии, приходящееся на единицу заряда.
Работа сторонних сил (некулоновских) по перемещению заряда.
Отношение силы F, действующей на неподвижный точечный заряд, помещённый в данную точку поля, к величине этого заряда q
Мера способности проводника накапливать электрический заряд
Ом = (м 2 ·кг/(с 3 ·А 2 ))
сопротивление объекта прохождению электрического тока
Удельное электрическое сопротивление
Способность материала препятствовать прохождению электрического тока
Способность тела (среды) проводить электрический ток
Векторная величина, являющаяся силовой характеристикой магнитного поля
Величина, учитывающая интенсивность магнитного поля и занимаемую им область.
Напряженность магнитного поля
Разность вектора магнитной индукции B и вектора намагниченности M
А•м 2
Величина, характеризующая магнитные свойства вещества
Величина, характеризующая магнитное состояние макроскопического физического тела.
Коэффициент пропорциональности между электрическим током, текущим в каком-либо замкнутом контуре, и полным магнитным потоком
Дж = (кг·м 2 /с 2 )
Энергия, заключенная в электромагнитном поле
Объемная плотность энергии
джоуль на кубический метр
Дж/м 3
Энергия электрического поля конденсатора
Мощность в цепи переменного тока
Величина, характеризующая нагрузки, создаваемые в электротехнических устройствах колебаниями энергии электромагнитного поля в цепи переменного тока
Суммарная мощность с учетом активной и реактивной ее составляющих, а также отклонения формы тока и напряжения от гармонической
Таблица единиц измерения «Оптика, электромагнитное излучение»
Физическая величина
Символ
Единица измерения физической величины
Ед. изм. физ. вел.
Описание
Примечания
Количество световой энергии, излучаемой в заданном направлении в единицу времени.
Световая, экстенсивная величина
Физическая величина, характеризующая количество «световой» мощности в соответствующем потоке излучения
Физическая величина, характеризует способность энергии, переносимой светом, вызывать у человека зрительные ощущения
Отношение светового потока, падающего на малый участок поверхности, к его площади.
люмен на квадратный метр
лм/м 2
Световая величина, представляющая собой световой поток
кандела на квадратный метр
кд/м 2
Сила света, излучаемая единицей площади поверхности в определенном направлении
Дж = (кг·м 2 /с 2 )
Энергия, переносимая оптическим излучением
Таблица единиц измерения «Акустика»
Физическая величина
Символ
Единица измерения физической величины
Ед. изм. физ. вел.
Описание
Примечания
Переменное избыточное давление, возникающее в упругой среде при прохождении через неё звуковой волны
кубический метр в секунду
м 3 /с
Отношение объема сырья, подаваемого в реактор в час к объему катализатора
Скорость распространения упругих волн в среде
ватт на квадратный метр
Вт/м 2
Величина, характеризующая мощность, переносимую звуковой волной в направлении распространения
скалярная физическая величина
паскаль-секунда на кубический метр
Па•с/м 3
Отношение амплитуды звукового давления в среде к колебательной скорости её частиц при прохождении через среду звуковой волны
ньютон-секунда на метр
Указывает силу, необходимую для движения тела при каждой частоте
Физическая величина
Символ
Единица измерения физической величины
Ед. изм. физ. вел.
Описание
Примечания
Масса объекта, находящегося в состоянии покоя.
Величина, выражающая влияние внутренних взаимодействий на массу составной частицы
Элементарный электрический заряд
Минимальная порция (квант) электрического заряда, наблюдающегося в природе у свободных долгоживущих частиц
Дж = (кг·м 2 /с 2 )
Разность между энергией состояния, в котором составляющие части системы бесконечно удалены
Период полураспада, среднее время жизни
Время, в течение которого система распадается в примерном отношении 1/2
Величина, характеризующая вероятность взаимодействия элементарной частицы с атомным ядром или другой частицей
Величина, равная отношению общего числа распадов радиоактивных ядер нуклида в источнике ко времени распада
Энергия ионизирующего излучения
Дж = (кг·м 2 /с 2 )
Вид энергии, высвобождаемой атомами в форме электромагнитных волн (гамма- или рентгеновское излучение) или частиц
Поглощенная доза ионизирующего излучения
Доза, при которой массе 1 кг передаётся энергия ионизирующего излучения в 1 джоул
Эквивалентная доза ионизирующего излучения
Поглощенная доза любого ионизирующего излучения, равная 100 эрг на 1 грамм облученного вещества
Экспозиционная доза рентгеновского и гамма-излучения
кулон на килограмм
Кл/кг
отношение суммарного электрического заряда ионов одного знака от внешнего гамма-излучения
Обозначения в физике с несколькими буквами
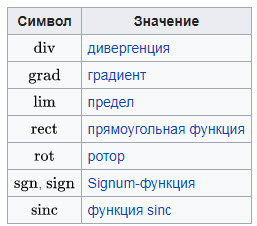
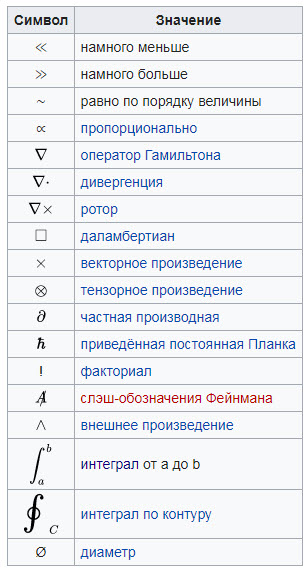
Специальные символы
Для удобства написания и чтения в среде ученых физиков принято использовать специальные символы, характеризующие те или иные явления и свойства.
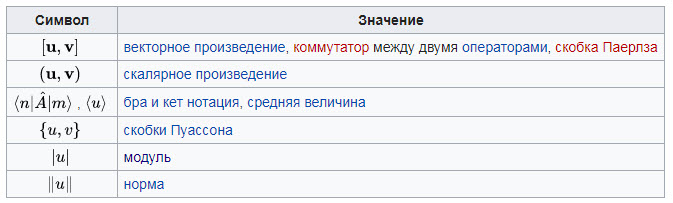
Скобки
В физике принято использовать не только формулы, которые применяют в математике, но и специализированные скобки.
Диакритические знаки
Диакритические знаки добавляются к символу физической величины для обозначения определённых различий. Ниже диакритические знаки добавлены для примера к букве x.
Источник
Теперь вы знаете какие однокоренные слова подходят к слову Как пишется и читается символ скорости принятый в физике, а так же какой у него корень, приставка, суффикс и окончание. Вы можете дополнить список однокоренных слов к слову «Как пишется и читается символ скорости принятый в физике», предложив свой вариант в комментариях ниже, а также выразить свое несогласие проведенным с морфемным разбором.
Расстояние
Мы постоянно ходим пешком и ездим на транспорте из одной точки в другую. Давайте узнаем, как можно посчитать это пройденное расстояние.
Расстояние — это длина от одного пункта до другого.
- Например: расстояние от дома до школы 3 км, от Москвы до Петербурга 705 км.
Расстояние обозначается латинской буквой s.
Единицы расстояния чаще всего выражаются в метрах (м), километрах (км).
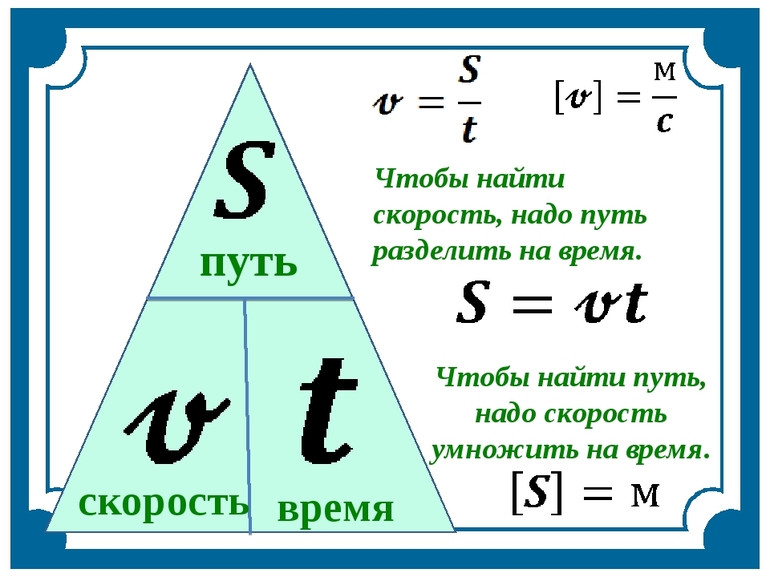
Формула пути
Чтобы найти расстояние, нужно умножить скорость на время движения:
s = v × t
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Реши домашку по математике на 5.
Подробные решения помогут разобраться в самой сложной теме.
Скорость
Двигаться со скоростью черепахи — значит медленно, а со скоростью света — значит очень быстро. Сейчас узнаем, как пишется скорость в математике и как ее найти по формуле.
Скорость определяет путь, который преодолеет объект за единицу времени. Скорость обозначается латинской буквой v.
Проще говоря, скоростью называют расстояние, пройденное телом за единицу времени.
Впервые формулу скорости проходят на математике в 5 классе. Сейчас мы ее сформулируем и покажем, как ее использовать.
Формула скорости
Чтобы найти скорость, нужно разделить путь на время:
v = s : t
Показатели скорости чаще всего выражаются в м/сек или км/час.
Скорость сближения — это расстояние, на которое сблизились два объекта за единицу времени. Чтобы найти скорость сближения двух объектов, которые движутся навстречу друг другу, надо сложить скорости этих объектов.
Скорость удаления — расстояние, на которое отдалились друг от друга два объекта за единицу времени.
Чтобы найти скорость удаления объектов, которые движутся в противоположных направлениях, нужно сложить скорости этих объектов.
Чтобы найти скорость удаления при движении с отставанием или скорость сближения при движении вдогонку, нужно из большей скорости вычесть меньшую.
Онлайн-курсы по математике для детей — отличный способ разобраться в сложных темах под руководством внимательного преподавателя.
Время
Время — самое дорогое, что у нас есть. Но кроме философии, у времени есть важная роль и в математике.
Время — это продолжительность каких-то действий, событий.
- Например: от метро до дома — 10 минут, от дома до дачи — 2 часа.
Время движения обозначается латинской буквой t.
Чаще всего вам будут встречаться такие единицы времени, как секунды, минуты и часы.
Формула времени
Чтобы найти время, нужно разделить расстояние на скорость:
t = s : v
Эта формула пригодится, если нужно узнать, за какое время тело преодолеет то или иное расстояние.
Взаимосвязь скорости, времени, расстояния
Скорость, время и расстояние связаны между собой очень крепко. Одно без другого даже сложно представить.
Если известны скорость и время движения, то можно найти расстояние. Оно равно скорости, умноженной на время: s = v × t.
Задачка 1. Мы вышли из дома и направились в гости в соседний двор. Мы дошли до соседнего двора за 15 минут. Фитнес-браслет показал, что наша скорость была 50 метров в минуту. Какое расстояние мы прошли?
Как рассуждаем:
Если за одну минуту мы прошли 50 метров, то сколько таких пятьдесят метров мы пройдем за 10 минут? Умножив 50 метров в минуту на 15 минут, мы определим расстояние от дома до магазина:
v = 50 м/мин
t = 15 мин
s = v × t = 50 × 15 = 750 (м)
Ответ: мы прошли 750 метров.
Если известно время и расстояние, то можно найти скорость: v = s : t.
Задачка 2. Двое школьников решили проверить, кто быстрее добежит от двора до спортплощадки. Расстояние между двором и площадкой — 100 метров. Первый школьник добежал за 25 секунд, второй за 50 секунд. Кто добежал быстрее?
Как рассуждаем:
Быстрее добежал тот, кто за 1 секунду пробежал большее расстояние. Говорят, что у него скорость движения больше. В этой задаче скорость школьников — это расстояние, которое они пробегают за 1 секунду.
Чтобы найти скорость, нужно расстояние разделить на время движения. Найдем скорость первого школьника: для этого разделим 100 метров на время движения первого школьника, то есть на 25 секунд:
100 : 25 = 4
Если расстояние дано в метрах, а время движения в секундах, то скорость измеряется в метрах в секунду (м/с). Если расстояние дано в километрах, а время движения в часах, скорость измеряется в километрах в час (км/ч).
В нашей задаче расстояние дано в метрах, а время в секундах. Значит, будем измерять скорость в метрах в секунду (м/с).
100 м : 25 с = 4 м/с
Так мы узнали, что скорость движения первого школьника 4 метра в секунду.
Теперь найдем скорость движения второго школьника. Для этого разделим расстояние на время движения второго школьника, то есть на 50 секунд:
100 : 50 = 2
Значит, скорость движения второго школьника составляет 2 метра в секунду.
Сейчас можно сравнить скорости движения каждого школьника и узнать, кто добежал быстрее.
4 (м/с) > 2 (м/с)
Скорость первого школьника больше. Значит, он добежал до спортивной площадки быстрее.
Ответ: первый школьник добежал быстрее.
Если известны скорость и расстояние, то можно найти время: t = s : v.
Задачка 3. От школы до стадиона 500 метров. Мы должны дойти до него пешком. Наша скорость будет 100 метров в минуту. За какое время мы дойдем до стадиона из школы?
Как рассуждаем:
Если за одну минуту мы будем проходить 100 метров, то сколько таких минут со ста метрами будет в 500 метрах?
Чтобы ответить на этот вопрос, нужно 500 метров разделить на расстояние, которое мы будем проходить за одну минуту, то есть на 100. Тогда мы получим время, за которое дойдем до стадиона:
s = 500 м
v = 100 м/мин
t = s : v = 500 : 100 = 5 (мин)
Ответ: от школы до стадиона мы дойдем за 5 минут.
Специально для уроков математики можно распечатать или нарисовать самостоятельно такую таблицу, чтобы быстрее запомнить и применять формулы скорости, времени, расстояния.
Содержание материала
- Формула времени. Решение задач
- Видео
- Формулы для расчета пути и времени движения при неравномерном движении тела
- Скорость
- График пути равномерного движения
- Единицы измерения времени
- Первые часы
- Как люди измеряли время?
- Способы вычисления расстояния и времени
Формула времени. Решение задач
Скорость, время и расстояние — физические величины, взаимосвязаны процессом движения. Виды движений: 1) равномерное (прямолинейное, криволинейное и по окружности), 2) равноускоренное (с постоянным ускорением), 3) гармоническое. Для каждого вида движения своя формула времени.
Время обозначается как t. Единица измерения времени – с (секунды).
Самая простая формула при равномерном прямолинейном движении. Время, необходимое для прохождения пути равняется частному от деления пути на скорость равномерного прямолинейного движения: t = S / v.
При равноускоренном движении время равняется частному от деления разницы конечной и начальной скорости на ускорение: t = (v — v) / a или частному от деления пути на разность конечной и начальной скорости: t = S / (v — v).
Видео
Формулы для расчета пути и времени движения при неравномерном движении тела
При неравномерном движении мы используем определение средней скорости, которую можем найти по формуле
$$upsilon_{ср} = frac{S}{t}$$
Чтобы определить путь при неравномерном движении, нужно среднюю скорость движения умножить на время:
$$large S = upsilon_{ср} t$$
Также мы можем рассчитать время, разделив путь, пройденный телом, на среднюю скорость его движения:
$$t = frac{s}{upsilon_{ср}}$$
Скорость
Двигаться со скоростью черепахи — значит медленно, а со скоростью света — значит очень быстро. Сейчас узнаем, как пишется скорость в математике и как ее найти по формуле.
Скорость определяет путь, который преодолеет объект за единицу времени. Скорость обозначается латинской буквой v.
Проще говоря, скоростью называют расстояние, пройденное телом за единицу времени.
Впервые формулу скорости проходят на математике в 5 классе. Сейчас мы ее сформулируем и покажем, как ее использовать.
Формула скорости
Чтобы найти скорость, нужно разделить путь на время:
v = s : t
Показатели скорости чаще всего выражаются в м/сек или км/час.
Скорость сближения — это расстояние, на которое сблизились два объекта за единицу времени. Чтобы найти скорость сближения двух объектов, которые движутся навстречу друг другу, надо сложить скорости этих объектов.
Скорость удаления — расстояние, на которое отдалились друг от друга два объекта за единицу времени.
Чтобы найти скорость удаления объектов, которые движутся в противоположных направлениях, нужно сложить скорости этих объектов.
Чтобы найти скорость удаления при движении с отставанием или скорость сближения при движении вдогонку, нужно из большей скорости вычесть меньшую.
Онлайн-курсы по математике для детей — отличный способ разобраться в сложных темах под руководством внимательного преподавателя.
График пути равномерного движения
Пример графика зависимости пути равномерного движения представлен на рисунке 3.
Здесь $S$ — ось пройденных путей, $t$ — ось времени. По этому графику мы можем найти путь, пройденный телом за определенный промежуток времени. Например, за 1 с тело проходит путь длиной 2 м, за 2 с – 4 м, за 3 с – 6 м.
Зная путь и время, мы можем рассчитать скорость. Для удобства расчета возьмем самый первый отрезок пути: $t = 1 с, s = 2 м$. Тогда,
$upsilon = frac{s}{t} = frac{2 м}{1 с} = 2 frac{м}{с}$.
Единицы измерения времени
Основной единицей измерения момента силы в системах СИ и СГС является: [t]=c
Единицы измерения времени основываются на периоде вращения Земли около своей оси и вокруг Солнца, Луни вокруг Земли. Внесистемные единицы измерения времени: час, минута, сутки и т.д.
Первые часы
Сначала было достаточно палочки, на которой каменным топором можно делать зарубки и тем самым отсчитывать прошедшие дни. Но это скорее был календарь, а не часы.
Первые и самые древние часы – солнечные. Их действие основано на изменении длины тени предметов по мере того, как солнце движется по небосводу. Такие часы представляли собой гномон – длинный шест, воткнутый в землю. Солнечные часы применялись в Древнем Египте и Китае. О них было доподлинно известно уже в 1200 году до нашей эры.
Затем появились водяные, песочные и огненные часы. Работа этих механизмов не была привязана к движению небесных светил. Долгое время водяные часы были главным инструментом для измерения времени.
Первые механические часы были изготовлены китайскими мастерами в 725 году нашей эры. Однако широкое распространение они получили относительно недавно.
В средневековой Европе механические часы устанавливались в башнях соборов и имели только одну стрелку – часовую. Карманные часы появились только в 1675 году (изобретение запатентовал Гюйгенс), а наручные – намного позже.
Как люди измеряли время?
Для измерения времени нужны какие-либо повторяющиеся с одинаковым периодом события. Например, смена дня и ночи. Солнце каждый день встает на востоке и садится на западе, а Луна каждый синодический месяц проходит весь цикл фаз освещенности солнцем — от тоненького серпа полумесяца до полнолуния.
Древним людям ничего не оставалось, как привязать отсчет времени к движению небесных тел и событиям, связанным с ним. А именно – к смене дней, ночей и сезонов года.
В году 4 сезона и 12 месяцев. Именно столько раз за весну, лето, осень и зиму Луна меняет свои фазы.
По мере развития прогресса методы измерения времени совершенствовались, появились солнечные, водяные, песочные, огненные, механические, электронные и, наконец, молекулярные часы.
Способы вычисления расстояния и времени
Можно и наоборот, зная скорость, найти значение расстояния или времени. Например:
S=v*t, где v — понятно что такое,
S — расстояние, которое требуется найти,
t — время, за которое объект прошел это расстояние.
Таким образом вычисляется значение расстояния.
Или вычисляем значение времени, за которое пройдено расстояние:
t=S/v, где v — все та же скорость,
S — расстояние, пройденный путь,
t — время, значение которого в данном случае нужно найти.
Для нахождения средних значений этих параметров существует довольно много представлений как данной формулы, так и всех остальных. Главное, знать основные правила перестановок и вычислений. А еще главнее знать сами формулы и лучше наизусть. Если же запомнить не получается, тогда лучше записывать. Это поможет, не сомневайтесь.
Пользуясь такими перестановками можно с легкостью найти время, расстояние и другие параметры, используя нужные, правильные способы их вычисления.
И это еще не предел!
Теги
Download Article
Download Article
Speed is an expression of how fast an object moves. An object’s speed is the total distance it travels in a certain amount of time. Units of speed include miles per hour (mph), centimeters per second (cm/sec or cm/s), meters per second (m/sec or m/s), or kilometers per hour (kph or km/hr). Measuring speed involves observing the distance an object travels and the amount of time elapsed and then calculating the speed from those observations by dividing distance by time.
-
1
Determine the distance the runner is to run. This can be done on a running track of a known length, such as 100 m (328 ft), or by staking out the distance on an open field.
- Use a measuring tape or a meter stick to measure the distance if you’re in a field.
- Mark the starting and ending points with a piece of string or a cone.
-
2
Set-up the experiment. In order to determine the runner’s speed you need to know the amount of time it takes the runner to travel the set distance. Tell the runner to wait until you say “Go!” to get an accurate reading on the stopwatch. Make sure your stopwatch is set to zero, then have the runner get in position at the start of the measured distance.
- You can also use a watch to time the runner, but it will be less accurate.
Advertisement
-
3
Start the runner and your watch at the same time. To sync up the timing as best as possible, yell “Go!” and start the watch at the same time. If you realize that the timing was off, have the runner reset and try again.
-
4
Stop your watch when the runner crosses the finish line. Watch closely to see when the runner crosses the point designated as the finish line. Be sure to stop the watch as close to the exact moment he crosses as possible.
-
5
Divide the distance the runner traveled by the number of seconds elapsed. This division is the calculation to determine the runner’s speed. The equation for speed is distance traveled/time to travel that distance.[1]
Using the example length of 100 m (328 ft), if the runner took 10 seconds to run that distance, the runner’s speed would be 100 m (328 ft) divided by 10, or 10 m/sec (32.8 feet per second).- Multiplying 10 m/sec by 3,600 (the number of seconds in an hour), the runner traveled 36,000 meters per hour, or 36 kilometers per hour (1 kilometer equals 1,000 m).
- Multiplying 32.8 feet per second by 3,600, the runner traveled 118,080 feet per hour, or 22.4 miles per hour (5,280 feet equals 1 mile).
Advertisement
-
1
Find a wall that reflects sound. A large brick or concrete wall will work well for this experiment. You can test the wall by clapping your hands or yelling and listening for an echo. If you hear a strong echo, it’s a good wall to use.[2]
-
2
Measure a distance of at least 50 m (54.5 yards) from the wall. A 50 m (54.5 yd) distance is suggested because it should give you enough time to make accurate measurements. Because you are taking into account the distance the sound will travel from you to the wall and back to you, you are actually measuring a distance of 100 m (109 yd).
- Measure the distance with a tape measure. Try to be as accurate as possible with your measurements.
-
3
Clap your hands in time to the echo from the wall. Stand in front of the wall at the measured distance and clap your hands slowly. You should be able to hear the echo as you do it. Speed up or slow down your clapping rhythm until your clap coincides with the echo from the previous clap.[3]
- If you are perfectly in sync, you shouldn’t hear the echo, just your clap.
-
4
Clap your hands 11 times while recording time with the stopwatch. Have your friend start the watch on the first clap and stop on the last clap. By clapping 11 times you will have timed 10 distance intervals for the sound of the clap to reverberate off the wall. In essence, the sound has traveled 10 times the initial 100 m distance.[4]
- Clapping 11 times also gives your friend enough time to start and stop the watch accurately.
- Perform this step multiple times and average the times together to get a more accurate measurement. To average the trials, add up all the times and divide by the number of trials.
-
5
Multiply the distance by 10. Because you clapped 11 times, the sound actually traveled 10 times the distance. 100 meters multiplied by 10 is 1000 meters.
-
6
Divide the distance the sound traveled by the amount of time it took to clap. This will measure the speed of the sound of the clap from your hands to the wall and back to your ears.
- For example, let’s say it took 2.89 seconds for the 11 claps. To find speed we take the distance, 1000 meters, and divide by the time, 2.89 seconds to get a speed of sound of 346 m/sec.
- The speed of sound at sea level is 340.29 m/sec (1,116 feet per second or 761.2 mph).[5]
Your calculations should come close to this figure, but may not match it exactly, especially if you aren’t at sea level. At higher altitudes, the air gets thinner and the speed of sound is slower. - Sound travels faster through liquids and solids than it does through air because sounds moves more quickly through materials of higher density.[6]
Advertisement
-
1
Obtain an anemometer. An anemometer is a device that measures wind speed.[7]
It consists of 3 or 4 cups mounted on wires attached to a central rotating shaft. Wind catches the cups and makes them spin. The faster the wind blows, the faster the cups spin around their axis.- You can either buy an anemometer or make your own.
- To make your own, get five three-ounce paper cups, two straws, a sharpened pencil with an eraser, a stapler, a small sharp pin, and a ruler.[8]
Color the sides of one of the cups to make it distinct from the others. - Punch a hole in the side of four of the cups about 1 inch from the rim. In the fifth cup, punch four holes equally spaced around the cup about 1 inch from the rim. Also, punch one hole in the bottom of this cup.
- Push one straw through the side of one of the cups leaving about 1 inch of straw inside the cup. Staple the straw to the side of the cup. Feed the rest of the straw through the fifth cup with 4 holes in one side and out the other. Place a second cup on the end of this straw and staple it in place. Make sure all of the cups face the same direction.
- Repeat the above step with the other two cups, feeding the straw through the remaining two holes in the middle cup. Again, make sure all cups are facing the same direction.
- Carefully, place a pin through the intersection point of the straws in the middle cup.
- Feed the pencil through the bottom hole of the fifth cup and push the pin through the eraser. Make sure your anemometer can spin freely. If so, it is now ready to use. If not, adjust the pencil so the eraser is not directly up against the straws.
-
2
Calculate the circumference of the anemometer. When one of the cups completes a full rotation, the distance it travels is the circumference of the circle. To calculate the circumference you need to measure the diameter of the circle.
- Measure the distance from the center of the anemometer to the center of one of the cups. This is the radius of the anemometer. Doubling this distance is the diameter.
- The circumference of a circle is equal to the diameter times the constant pi or 2 times the radius times pi.
- For example, if the distance between the center of the cup and the center of the anemometer is 30 cm (1 foot), the distance the cup travels in a single rotation is 2 x 30 x 3.14 (rounding pi to 2 decimal places), or 188.4 cm (74.2 inches).
-
3
Place the anemometer where the wind will catch its cups. You want enough wind to spin the anemometer, but not blow it over. You may need to anchor it to the ground or a post to keep it upright.
-
4
Count the number of times the anemometer spins for a fixed length of time. Stand at a fixed point and count the number of times the colored cup rotates around the circle. Possible intervals are 5, 10, 15, 20, 30 seconds, or even a full minute. Set a timer to go off at your specific time interval to ensure accuracy in the count.
- If you don’t have a timer, have a friend watch the clock, while you count the rotations.
- If you purchased an anemometer, mark one of the cups in some way to allow you count properly.
-
5
Multiply the number of rotations by the distance the anemometer travels in a single rotation. This will give you the total distance the anemometer traveled in the time you were watching it.
- For example, your anemometer has a radius of 30 cm (.98 ft), therefore it travels 188.4 cm (6.18 ft) in a single rotation. If it rotated 50 times during your count, then the total distance is 50 x 188.4 = 9420 cm.
-
6
Divide the total distance over the elapsed time. The equation for speed is total distance divided by the amount of time it takes to travel that distance. Taking the total distance the anemometer spun and dividing it by the amount of time you counted for will give you the current wind speed.
- For example, if you counted the number of rotations in 10 seconds you would divide the distance traveled by 10 seconds. Speed = (9420 cm/10 sec) = 942 cm/sec (30.9 ft/sec).
- Multiplying 942 cm/sec by 3600 gives 3,391,200 cm/hr, divided by 100,000 (the number of centimeters in a kilometer) or 33.9 km/hr.
- Multiplying 30.9 feet per second by 3,600 gives 111,240 feet per hour, divided by 5,280 gives 21.1 miles per hour.
Advertisement
Add New Question
-
Question
Speed is just how far one travels divided by the time it takes to get there, while________ adds the element of direction and _________. What goes in the blanks?
Speed is just how far one travels divided by the time it takes to get there, while velocity adds the element of direction and change in speed over time.
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
-
Related to speed is velocity, which is both the speed and the direction the object travels. A simple way to distinguish the two is that because an anemometer spins in a circle it can only measures wind speed, not velocity. A windsock measures wind velocity because it points in the direction the wind is blowing as it fills with air.
Thanks for submitting a tip for review!
Advertisement
Things You’ll Need
- Stopwatch
- An assistant
- Running track (for measuring a runner’s speed)
- Sound-reflecting wall (for measuring the speed of sound)
- Measuring tape (for measuring the speed of sound)
- Anemometer (for measuring wind speed)
References
About This Article
Article SummaryX
To measure speed, use the formula “Speed = Distance ÷ Time.” You can do this by determining the distance that something is going to cover and marking it with a piece of string or a cone. Then, time the object or person using a stopwatch and record how long it took to travel that distance. Finally, divide the distance by the time it took the object to get to the finishing point. For example, if a runner ran 100 meters in 10 seconds, his speed would be 10 meters per second. To learn how to measure the speed of things that aren’t objects, like wind or sound, read on!
Did this summary help you?
Thanks to all authors for creating a page that has been read 199,143 times.
Did this article help you?
Download Article
Download Article
Speed is an expression of how fast an object moves. An object’s speed is the total distance it travels in a certain amount of time. Units of speed include miles per hour (mph), centimeters per second (cm/sec or cm/s), meters per second (m/sec or m/s), or kilometers per hour (kph or km/hr). Measuring speed involves observing the distance an object travels and the amount of time elapsed and then calculating the speed from those observations by dividing distance by time.
-
1
Determine the distance the runner is to run. This can be done on a running track of a known length, such as 100 m (328 ft), or by staking out the distance on an open field.
- Use a measuring tape or a meter stick to measure the distance if you’re in a field.
- Mark the starting and ending points with a piece of string or a cone.
-
2
Set-up the experiment. In order to determine the runner’s speed you need to know the amount of time it takes the runner to travel the set distance. Tell the runner to wait until you say “Go!” to get an accurate reading on the stopwatch. Make sure your stopwatch is set to zero, then have the runner get in position at the start of the measured distance.
- You can also use a watch to time the runner, but it will be less accurate.
Advertisement
-
3
Start the runner and your watch at the same time. To sync up the timing as best as possible, yell “Go!” and start the watch at the same time. If you realize that the timing was off, have the runner reset and try again.
-
4
Stop your watch when the runner crosses the finish line. Watch closely to see when the runner crosses the point designated as the finish line. Be sure to stop the watch as close to the exact moment he crosses as possible.
-
5
Divide the distance the runner traveled by the number of seconds elapsed. This division is the calculation to determine the runner’s speed. The equation for speed is distance traveled/time to travel that distance.[1]
Using the example length of 100 m (328 ft), if the runner took 10 seconds to run that distance, the runner’s speed would be 100 m (328 ft) divided by 10, or 10 m/sec (32.8 feet per second).- Multiplying 10 m/sec by 3,600 (the number of seconds in an hour), the runner traveled 36,000 meters per hour, or 36 kilometers per hour (1 kilometer equals 1,000 m).
- Multiplying 32.8 feet per second by 3,600, the runner traveled 118,080 feet per hour, or 22.4 miles per hour (5,280 feet equals 1 mile).
Advertisement
-
1
Find a wall that reflects sound. A large brick or concrete wall will work well for this experiment. You can test the wall by clapping your hands or yelling and listening for an echo. If you hear a strong echo, it’s a good wall to use.[2]
-
2
Measure a distance of at least 50 m (54.5 yards) from the wall. A 50 m (54.5 yd) distance is suggested because it should give you enough time to make accurate measurements. Because you are taking into account the distance the sound will travel from you to the wall and back to you, you are actually measuring a distance of 100 m (109 yd).
- Measure the distance with a tape measure. Try to be as accurate as possible with your measurements.
-
3
Clap your hands in time to the echo from the wall. Stand in front of the wall at the measured distance and clap your hands slowly. You should be able to hear the echo as you do it. Speed up or slow down your clapping rhythm until your clap coincides with the echo from the previous clap.[3]
- If you are perfectly in sync, you shouldn’t hear the echo, just your clap.
-
4
Clap your hands 11 times while recording time with the stopwatch. Have your friend start the watch on the first clap and stop on the last clap. By clapping 11 times you will have timed 10 distance intervals for the sound of the clap to reverberate off the wall. In essence, the sound has traveled 10 times the initial 100 m distance.[4]
- Clapping 11 times also gives your friend enough time to start and stop the watch accurately.
- Perform this step multiple times and average the times together to get a more accurate measurement. To average the trials, add up all the times and divide by the number of trials.
-
5
Multiply the distance by 10. Because you clapped 11 times, the sound actually traveled 10 times the distance. 100 meters multiplied by 10 is 1000 meters.
-
6
Divide the distance the sound traveled by the amount of time it took to clap. This will measure the speed of the sound of the clap from your hands to the wall and back to your ears.
- For example, let’s say it took 2.89 seconds for the 11 claps. To find speed we take the distance, 1000 meters, and divide by the time, 2.89 seconds to get a speed of sound of 346 m/sec.
- The speed of sound at sea level is 340.29 m/sec (1,116 feet per second or 761.2 mph).[5]
Your calculations should come close to this figure, but may not match it exactly, especially if you aren’t at sea level. At higher altitudes, the air gets thinner and the speed of sound is slower. - Sound travels faster through liquids and solids than it does through air because sounds moves more quickly through materials of higher density.[6]
Advertisement
-
1
Obtain an anemometer. An anemometer is a device that measures wind speed.[7]
It consists of 3 or 4 cups mounted on wires attached to a central rotating shaft. Wind catches the cups and makes them spin. The faster the wind blows, the faster the cups spin around their axis.- You can either buy an anemometer or make your own.
- To make your own, get five three-ounce paper cups, two straws, a sharpened pencil with an eraser, a stapler, a small sharp pin, and a ruler.[8]
Color the sides of one of the cups to make it distinct from the others. - Punch a hole in the side of four of the cups about 1 inch from the rim. In the fifth cup, punch four holes equally spaced around the cup about 1 inch from the rim. Also, punch one hole in the bottom of this cup.
- Push one straw through the side of one of the cups leaving about 1 inch of straw inside the cup. Staple the straw to the side of the cup. Feed the rest of the straw through the fifth cup with 4 holes in one side and out the other. Place a second cup on the end of this straw and staple it in place. Make sure all of the cups face the same direction.
- Repeat the above step with the other two cups, feeding the straw through the remaining two holes in the middle cup. Again, make sure all cups are facing the same direction.
- Carefully, place a pin through the intersection point of the straws in the middle cup.
- Feed the pencil through the bottom hole of the fifth cup and push the pin through the eraser. Make sure your anemometer can spin freely. If so, it is now ready to use. If not, adjust the pencil so the eraser is not directly up against the straws.
-
2
Calculate the circumference of the anemometer. When one of the cups completes a full rotation, the distance it travels is the circumference of the circle. To calculate the circumference you need to measure the diameter of the circle.
- Measure the distance from the center of the anemometer to the center of one of the cups. This is the radius of the anemometer. Doubling this distance is the diameter.
- The circumference of a circle is equal to the diameter times the constant pi or 2 times the radius times pi.
- For example, if the distance between the center of the cup and the center of the anemometer is 30 cm (1 foot), the distance the cup travels in a single rotation is 2 x 30 x 3.14 (rounding pi to 2 decimal places), or 188.4 cm (74.2 inches).
-
3
Place the anemometer where the wind will catch its cups. You want enough wind to spin the anemometer, but not blow it over. You may need to anchor it to the ground or a post to keep it upright.
-
4
Count the number of times the anemometer spins for a fixed length of time. Stand at a fixed point and count the number of times the colored cup rotates around the circle. Possible intervals are 5, 10, 15, 20, 30 seconds, or even a full minute. Set a timer to go off at your specific time interval to ensure accuracy in the count.
- If you don’t have a timer, have a friend watch the clock, while you count the rotations.
- If you purchased an anemometer, mark one of the cups in some way to allow you count properly.
-
5
Multiply the number of rotations by the distance the anemometer travels in a single rotation. This will give you the total distance the anemometer traveled in the time you were watching it.
- For example, your anemometer has a radius of 30 cm (.98 ft), therefore it travels 188.4 cm (6.18 ft) in a single rotation. If it rotated 50 times during your count, then the total distance is 50 x 188.4 = 9420 cm.
-
6
Divide the total distance over the elapsed time. The equation for speed is total distance divided by the amount of time it takes to travel that distance. Taking the total distance the anemometer spun and dividing it by the amount of time you counted for will give you the current wind speed.
- For example, if you counted the number of rotations in 10 seconds you would divide the distance traveled by 10 seconds. Speed = (9420 cm/10 sec) = 942 cm/sec (30.9 ft/sec).
- Multiplying 942 cm/sec by 3600 gives 3,391,200 cm/hr, divided by 100,000 (the number of centimeters in a kilometer) or 33.9 km/hr.
- Multiplying 30.9 feet per second by 3,600 gives 111,240 feet per hour, divided by 5,280 gives 21.1 miles per hour.
Advertisement
Add New Question
-
Question
Speed is just how far one travels divided by the time it takes to get there, while________ adds the element of direction and _________. What goes in the blanks?
Speed is just how far one travels divided by the time it takes to get there, while velocity adds the element of direction and change in speed over time.
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
-
Related to speed is velocity, which is both the speed and the direction the object travels. A simple way to distinguish the two is that because an anemometer spins in a circle it can only measures wind speed, not velocity. A windsock measures wind velocity because it points in the direction the wind is blowing as it fills with air.
Thanks for submitting a tip for review!
Advertisement
Things You’ll Need
- Stopwatch
- An assistant
- Running track (for measuring a runner’s speed)
- Sound-reflecting wall (for measuring the speed of sound)
- Measuring tape (for measuring the speed of sound)
- Anemometer (for measuring wind speed)
References
About This Article
Article SummaryX
To measure speed, use the formula “Speed = Distance ÷ Time.” You can do this by determining the distance that something is going to cover and marking it with a piece of string or a cone. Then, time the object or person using a stopwatch and record how long it took to travel that distance. Finally, divide the distance by the time it took the object to get to the finishing point. For example, if a runner ran 100 meters in 10 seconds, his speed would be 10 meters per second. To learn how to measure the speed of things that aren’t objects, like wind or sound, read on!
Did this summary help you?
Thanks to all authors for creating a page that has been read 199,143 times.