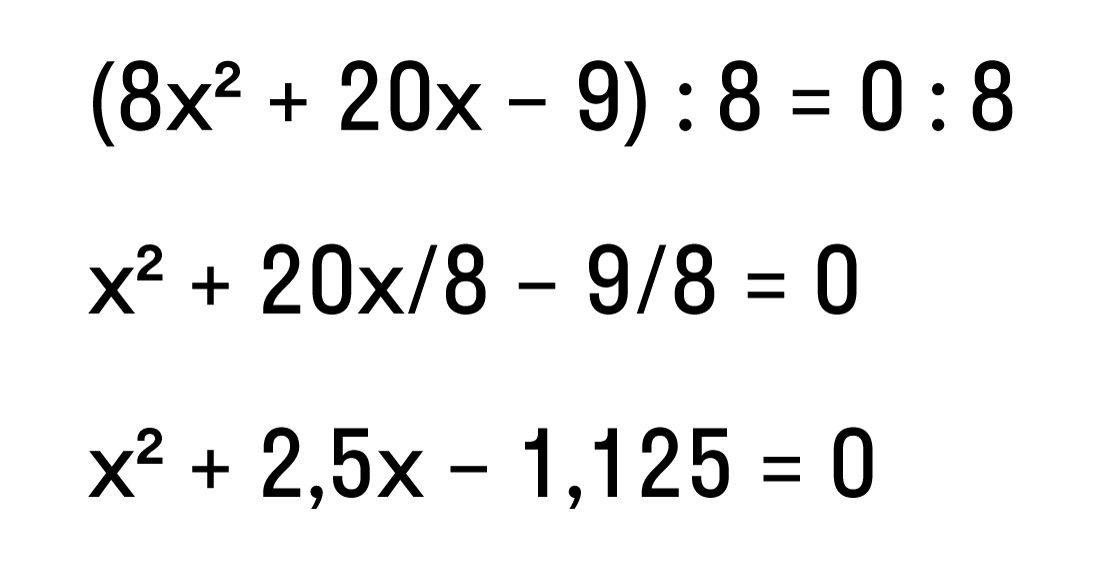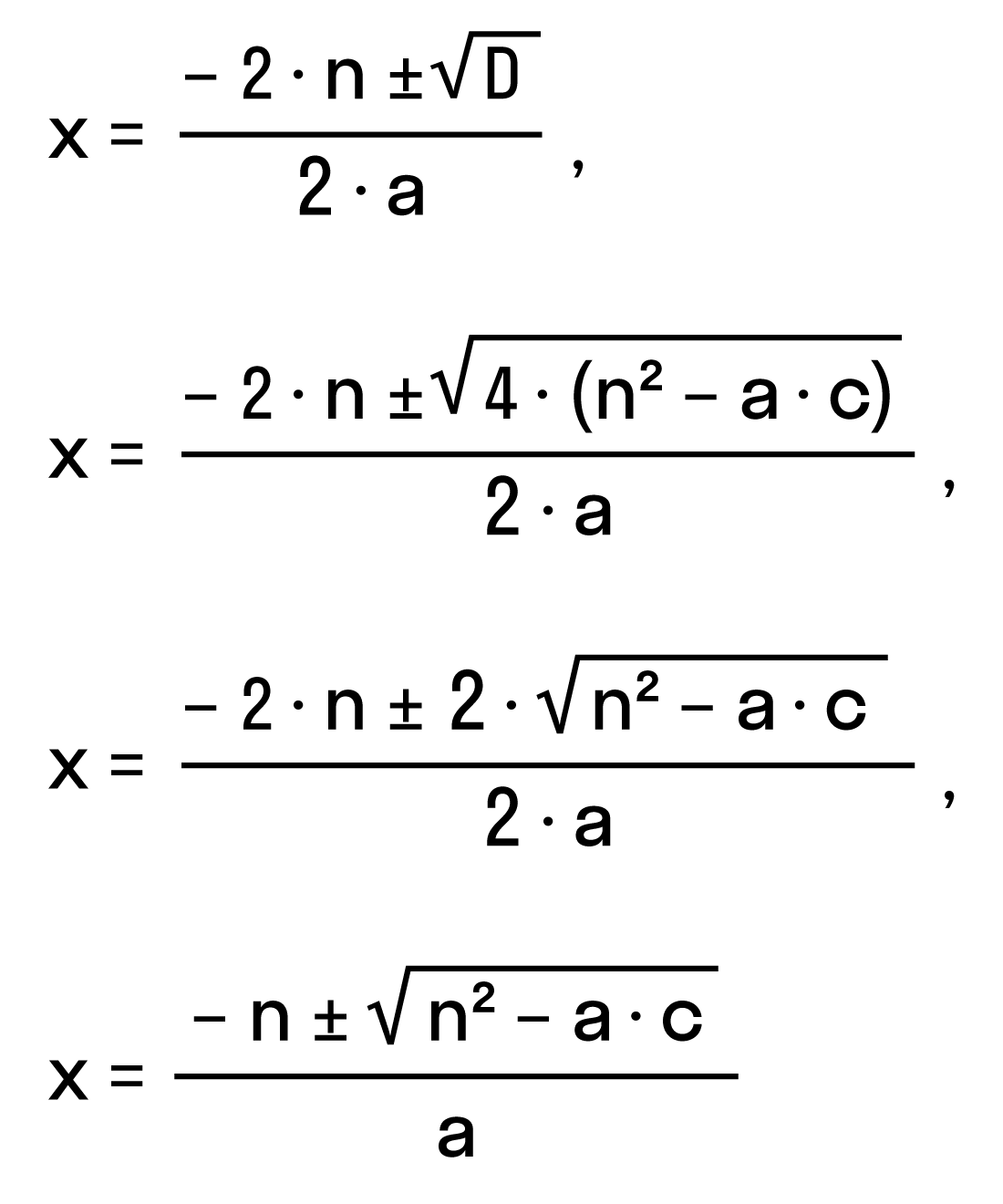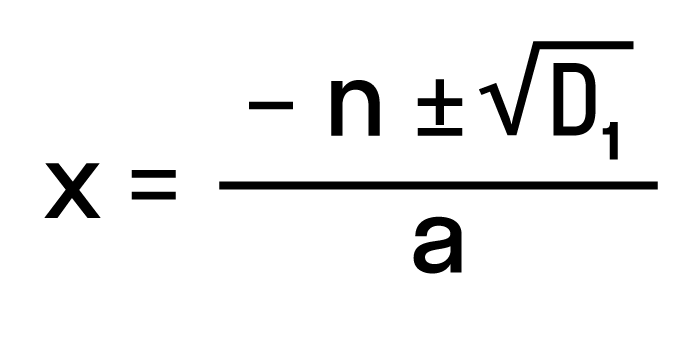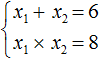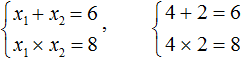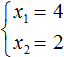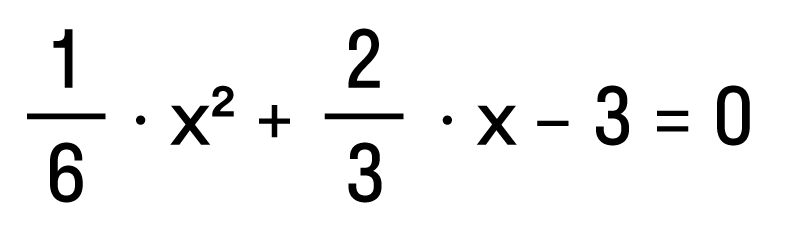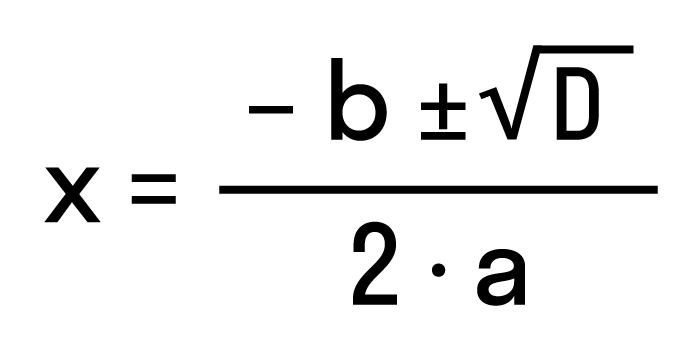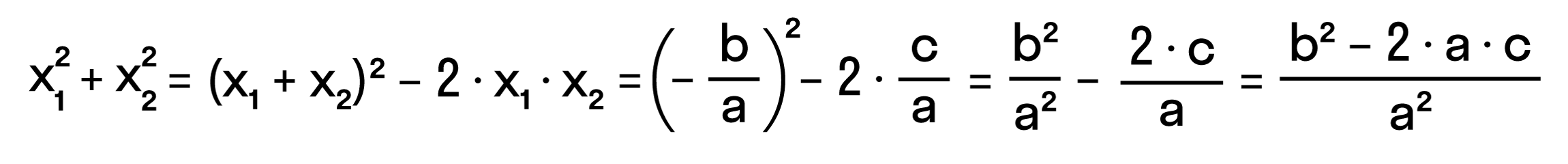Как пишется квадратное уравнение

Понятие квадратного уравнения

Уравнение — это равенство, содержащее переменную, значение которой нужно найти.

Например, х + 8 = 12 — это уравнение, которое содержит переменную х.

Корень уравнения — это такое значение переменной, которое при подстановке в уравнение обращает его в верное числовое равенство.

Например, если х = 5, то при подстановке в уравнение мы получим 5 + 8 = 12. 13 = 12 — противоречие. Значит, х = 5 не является корнем уравнения.

А вот если х = 4, то при подстановке в уравнение мы получим 4 + 8 = 12. 12 = 12 — верное равенство. Значит, х = 4 является корнем уравнения.

Решить уравнение — значит найти все его корни или доказать, что их не существует.

Квадратное уравнение — это уравнение вида ax² + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.

Чтобы запомнить месторасположение коэффициентов, давайте потренируемся определять их.

Квадратные уравнения могут иметь два корня, один корень или не иметь корней.

Чтобы определить, сколько корней имеет уравнение, нужно обратить внимание на дискриминант. Чтобы его найти, берем формулу: D = b² − 4ac. А вот свойства дискриминанта:

• если D < 0, корней нет;
• если D = 0, есть один корень;
• если D > 0, есть два различных корня.

С этим разобрались. А сейчас посмотрим подробнее на различные виды квадратных уравнений.

Разобраться в теме еще быстрее с помощью опытного преподавателя можно
на курсах по математике в онлайн-школе Skysmart.

Приведенные и неприведенные квадратные уравнения

Квадратное уравнение может быть приведенным или неприведенным — все зависит от от значения первого коэффициента.

Приведенное квадратное уравнение — это уравнение, где старший коэффициент, тот который стоит при одночлене высшей степени, равен единице.

Неприведенным называют квадратное уравнение, где старший коэффициент отличается от единицы.

Давайте-ка на примерах — вот у нас есть два уравнения:

• x² — 2x + 6 = 0
• x² — x — 1/4 = 0

В каждом из них старший коэффициент равен единице (которую мы мысленно представляем при x² ), а значит уравнение называется приведенным.

• 2x² − 4x — 12 = 0 — первый коэффициент отличен от единицы (2), значит это неприведенное квадратное уравнение.

Каждое неприведенное квадратное уравнение можно преобразовать в приведенное, если произвести равносильное преобразование — разделить обе его части на первый коэффициент.

Пример 1. Превратим неприведенное уравнение: 8x² + 20x — 9 = 0 — в приведенное.

Для этого разделим обе части исходного уравнения на старший коэффициент 8:

Ответ: равносильное данному приведенное уравнение x² + 2,5x — 1,125 = 0.

Пройдите тест и узнайте, какие темы отделяют от пятёрки по математике

Полные и неполные квадратные уравнения

В определении квадратного уравнения есть условие: a ≠ 0. Оно нужно, чтобы уравнение ax² + bx + c = 0 было именно квадратным. Если a = 0, то уравнение обретет вид линейного: bx + c = 0.

Что касается коэффициентов b и c, то они могут быть равны нулю, как по отдельности, так и вместе. В таком случае квадратное уравнение принято называть неполным.

Неполное квадратное уравнение —— это квадратное уравнение вида ax² + bx + c = 0, где оба или хотя бы один из коэффициентов b и c равен нулю.

Полное квадратное уравнение — это уравнение, у которого все коэффициенты отличны от нуля.

Решение неполных квадратных уравнений

Как мы уже знаем, есть три вида неполных квадратных уравнений:

• ax² = 0, ему отвечают коэффициенты b = 0 и c = 0;
• ax² + c = 0, при b = 0;
• ax² + bx = 0, при c = 0.

Давайте рассмотрим по шагам, как решать неполные квадратные уравнения по видам.

Как решить уравнение ax² = 0

Начнем с решения неполных квадратных уравнений, в которых b и c равны нулю, то есть, с уравнений вида ax² = 0.

Уравнение ax² = 0 равносильно x² = 0. Такое преобразование возможно, когда мы разделили обе части на некое число a, которое не равно нулю. Корнем уравнения x² = 0 является нуль, так как 0² = 0. Других корней у этого уравнения нет, что подтверждают свойства степеней.

Таким образом, неполное квадратное уравнение ax² = 0 имеет единственный корень x = 0.

Пример 1. Решить −6x² = 0.

Как решаем:

1. Замечаем, что данному уравнению равносильно x² = 0, значит исходное уравнение имеет единственный корень — нуль.
2. По шагам решение выглядит так:

   −6x² = 0

   x² = 0

   x = √0

   x = 0

Ответ: 0.

Как решить уравнение ax² + с = 0

Обратим внимание на неполные квадратные уравнения вида ax² + c = 0, в которых b = 0, c ≠ 0. Мы давно знаем, что слагаемые в уравнениях носят двусторонние куртки: когда мы переносим их из одной части уравнения в другую, они надевает куртку на другую сторону — меняют знак на противоположный.

Еще мы знаем, что если обе части уравнения поделить на одно и то же число (кроме нуля) — у нас получится равносильное уравнение. Ну есть одно и то же, только с другими цифрами.

Держим все это в голове и колдуем над неполным квадратным уравнением (производим «равносильные преобразования»): ax² + c = 0:

• перенесем c в правую часть: ax² = — c,
• разделим обе части на a: x² = — c/а.

Ну все, теперь мы готовы к выводам о корнях неполного квадратного уравнения. В зависимости от значений a и c, выражение — c/а может быть отрицательным или положительным. Разберем конкретные случаи.

Если — c/а < 0, то уравнение x² = — c/а не имеет корней. Все потому, что квадрат любого числа всегда равен неотрицательному числу. Из этого следует, что при — c/а < 0 ни для какого числа p равенство р2 = — c/а не является верным.

Если — c/а > 0, то корни уравнения x² = — c/а будут другими. Например, можно использовать правило квадратного корня и тогда корень уравнения равен числу √- c/а, так как (√- c/а)² = — c/а. Кроме того, корнем уравнения может стать -√- c/а, так как (-√- c/а)² = — c/а. Ура, больше у этого уравнения нет корней.

Пример 1. Найти решение уравнения 8x² + 5 = 0.

Как решать:

1. Перенесем свободный член в правую часть:

   8x² = — 5

2. Разделим обе части на 8:

   x² = — 5/8

3. В правой части осталось число со знаком минус, значит у данного уравнения нет корней.

Ответ: уравнение 8x² + 5 = 0 не имеет корней.

Как решить уравнение ax² + bx = 0

Осталось разобрать третий вид неполных квадратных уравнений, когда c = 0.

Неполное квадратное уравнение ax² + bx = 0 можно решить методом разложения на множители. Как разложить квадратное уравнение:

1. Разложим на множители многочлен, который расположен в левой части уравнения — вынесем за скобки общий множитель x.

2. Теперь можем перейти от исходного уравнения к равносильному x * (ax + b) = 0. А это уравнение равносильно совокупности двух уравнений x = 0 и ax + b = 0, последнее — линейное, его корень x = −b/a.

Таким образом, неполное квадратное уравнение ax² + bx = 0 имеет два корня:

• x = 0;
• x = −b/a.

Пример 1. Решить уравнение 0,5x² + 0,125x = 0

Как решать:

1. Вынести х за скобки

   х(0,5x + 0,125) = 0

2. Это уравнение равносильно х = 0 и 0,5x + 0,125 = 0.
3. Решить линейное уравнение:

   0,5x = −0,125,
   х = −0,125/0,5

4. Разделить:

   х = −0,25

5. Значит корни исходного уравнения — 0 и −0,25.

Ответ: х = 0 и х = −0,25.

Как разложить квадратное уравнение

С помощью теоремы Виета можно получить формулу разложения квадратного трехчлена на множители. Выглядит она так:

Дискриминант: формула корней квадратного уравнения

Чтобы найти результат квадратного уравнения, придумали формулу корней. Выглядит она так:

где D = b² − 4ac — дискриминант квадратного уравнения.

Эта запись означает:

,

.

Чтобы легко применять эту формулу, нужно понять, как она получилась. Давайте разбираться.

Алгоритм решения квадратных уравнений по формулам корней

Теперь мы знаем, что при решении квадратных уравнения можно использовать универсальную формулу корней — это помогает находить комплексные корни.

В 8 классе на алгебре можно встретить задачу по поиску действительных корней квадратного уравнения. Для этого важно перед использованием формул найти дискриминант и убедиться, что он неотрицательный, и только после этого вычислять значения корней. Если дискриминант отрицательный, значит уравнение не имеет действительных корней.

Алгоритм решения квадратного уравнения ax² + bx + c = 0:

• вычислить его значение дискриминанта по формуле D = b²−4ac;
• если дискриминант отрицательный, зафиксировать, что действительных корней нет;
• если дискриминант равен нулю, вычислить единственный корень уравнения по формуле х = −b/2a;
• если дискриминант положительный, найти два действительных корня квадратного уравнения по формуле корней

Чтобы запомнить алгоритм решения квадратных уравнений и с легкостью его использовать, давайте тренироваться!

Примеры решения квадратных уравнений

Как решать квадратные уравнения мы уже знаем, осталось закрепить знания на практике.

Пример 1. Решить уравнение −4x² + 28x — 49 = 0.

Как решаем:

1. Найдем дискриминант: D = 28² — 4(-4)(-49) = 784 — 784 = 0
2. Так как дискриминант равен нулю, значит это квадратное уравнение имеет единственный корень
3. Найдем корень

   х = — 28/2(-4)

   х = 3,5

Ответ: единственный корень 3,5.

Пример 2. Решить уравнение 54 — 6x² = 0.

Как решаем:

1. Произведем равносильные преобразования. Умножим обе части на −1

   54 — 6x² = 0 | *(-1)

   6x² — 54 = 0

2. Оставим неизвестное в одной части, остальное перенесем с противоположным знаком в другую

   6x² = 54

   х² = 9

   х = ±√9

   х₁ = 3, х₂ = — 3

Ответ: два корня 3 и — 3.

Пример 3. Решить уравнение x²— х = 0.

Как решаем:

1. Преобразуем уравнение так, чтобы появились множители

   х(х — 1) = 0

   х₁ = 0, х₂ = 1

Ответ: два корня 0 и 1.

Пример 4. Решить уравнение x²— 10 = 39.

Как решаем:

1. Оставим неизвестное в одной части, остальное перенесем с противоположным знаком в другую

   x²— 10 = 39

   x²= 39 + 10

   x²= 49

   х = ±√49

   х₁ = 7, х₂ = −7

Ответ: два корня 7 и −7.

Пример 5. Решить уравнение 3x²— 4x+94 = 0.

Как решаем:

1. Найдем дискриминант по формуле

   D = (-4)² — 4 * 3 * 94 = 16 — 1128 = −1112

2. Дискриминант отрицательный, поэтому корней нет.

Ответ: корней нет.

В школьной программе за 8 класс нет обязательного требования искать комплексные корни, но такой подход может ускорить ход решения. Если дискриминант отрицательный — сразу пишем ответ, что действительных корней нет и не мучаемся.

Формула корней для четных вторых коэффициентов

Рассмотрим частный случай. Формула решения корней квадратного уравнения 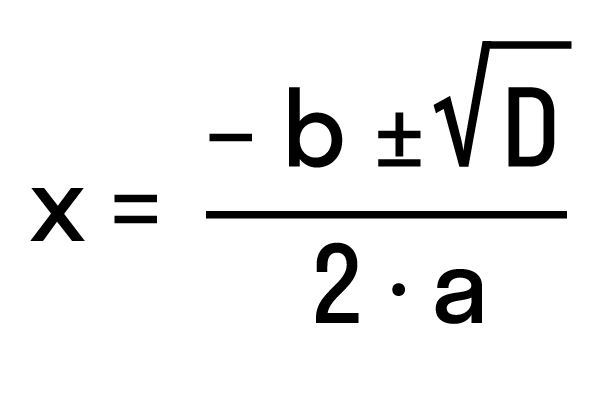, где D = b² — 4ac, помогает получить еще одну формулу, более компактную, при помощи которой можно решать квадратные уравнения с четным коэффициентом при x. Рассмотрим, как появилась эта формула.

Например, нам нужно решить квадратное уравнение ax² + 2nx + c = 0. Сначала найдем его корни по известной нам формуле. Вычислим дискриминант D = (2n)²— 4ac = 4n² — 4ac = 4(n²— ac) и подставим в формулу корней:

Для удобства вычислений обозначим выражение n² -ac как D₁. Тогда формула корней квадратного уравнения со вторым коэффициентом 2·n примет вид:

где D₁ = n²— ac.

Самые внимательные уже заметили, что D = 4D₁, или D₁= D/4. Проще говоря, D₁ — это четверть дискриминанта. И получается, что знак D1 является индикатором наличия или отсутствия корней квадратного уравнения.

Сформулируем правило. Чтобы найти решение квадратного уравнения со вторым коэффициентом 2n, нужно:

• вычислить D₁= n²— ac;
• если D₁< 0, значит действительных корней нет;
• если D₁= 0, значит можно вычислить единственный корень уравнения по формуле x = -n/a;
• если же D₁> 0, значит можно найти два действительных корня по формуле

Формула Виета

---

Если в школьной геометрии чаще всего используется теорема Пифагора, то в школьной алгебре ведущую роль занимают формулы Виета. Теорема звучит так: 

Если дано x² + bx + c = 0, где x₁ и x₂ являются корнями, то справедливы два равенства:

Знак системы, который принято обозначать фигурной скобкой, означает, что значения x₁ и x₂ удовлетворяют обоим равенствам.

Рассмотрим теорему Виета на примере: x² + 4x + 3 = 0.

Пока неизвестно, какие корни имеет данное уравнение. Но в соответствии с теоремой можно записать, что сумма этих корней равна второму коэффициенту с противоположным знаком. Он равен четырем, значит будем использовать минус четыре:

Произведение корней по теореме соответствует свободному члену. В данном случае свободным членом является число три. Значит:

Необходимо проверить равна ли сумма корней −4, а произведение 3. Для этого найдем корни уравнения x² + 4x + 3 = 0. Воспользуемся формулами для чётного второго коэффициента:

Получилось, что корнями уравнения являются числа −1 и −3. Их сумма равняется второму коэффициенту с противоположным знаком, а значит решение верное.

Произведение корней −1 и −3 по теореме Виета должно равняться свободному члену, то есть числу 3. Это условие также выполняется:

Результат проделанных вычислений в том, что мы убедились в справедливости выражения:

Когда дана сумма и произведение корней квадратного уравнения, принято начинать подбор подходящих корней. Теорема, обратная теореме Виета, при таких условиях может быть главным помощником. Вот она:

Обычно вся суть обратных теорем в том самом выводе, которое дает первая теорема. Так, при доказательстве теоремы Виета стало понятно, что сумма x₁ и x₂ равна −b, а их произведение равно c. В обратной теореме это и есть утверждение.

Пример 1. Решить при помощи теоремы Виета: x² − 6x + 8 = 0.

Как решаем:

1. Для начала запишем сумму и произведение корней уравнения. Сумма будет равна 6, так как второй коэффициент равен −6. А произведение корней равно 8.

   

2. Когда у нас есть эти два равенства, можно подобрать подходящие корни, которые будут удовлетворять обоим равенствам системы.

   Чтобы проще подобрать корни, нужно их перемножить. Число 8 можно получить путем перемножения чисел 4 и 2 либо 1 и 8. Но значения x₁ и x₂ надо подбирать так, чтобы они удовлетворяли и второму равенству тоже.

   Можно сделать вывод, что значения 1 и 8 не подходят, так как они не удовлетворяют равенству x₁ + x₂ = 6. А значения 4 и 2 подходят обоим равенствам:

   

3. Значит числа 4 и 2 — корни уравнения x² − 6x + 8 = 0. p>

Упрощаем вид квадратных уравнений

Если мы ходили в школу всегда одной тропинкой, а потом вдруг обнаружили путь короче — это значит теперь у нас есть выбор: упростить себе задачу и сократить время на дорогу или прогуляться по привычному маршруту.

Так же и при вычислении корней квадратного уравнения. Ведь проще посчитать уравнение 11x² — 4 x — 6 = 0, чем 1100x² — 400x — 600 = 0.

Часто упрощение вида квадратного уравнения можно получить через умножение или деление обеих частей на некоторое число. Например, в предыдущем абзаце мы упростили уравнение 1100x² — 400x — 600 = 0, просто разделив обе части на 100.

Такое преобразование возможно, когда коэффициенты не являются взаимно простыми числами. Тогда принято делить обе части уравнения на наибольший общий делитель абсолютных величин его коэффициентов.

Покажем, как это работает на примере 12x²— 42x + 48 = 0. Найдем наибольший общий делитель абсолютных величин его коэффициентов: НОД (12, 42, 48) = 6. Разделим обе части исходного квадратного уравнения на 6, и придем к равносильному уравнению 2x² — 7x + 8 = 0. Вот так просто.

А умножение обеих частей квадратного уравнения отлично помогает избавиться от дробных коэффициентов. Умножать в данном случае лучше на наименьшее общее кратное знаменателей его коэффициентов. Например, если обе части квадратного уравнения

умножить на НОК (6, 3, 1) = 6, то оно примет более простой вид x² + 4x — 18 = 0.

Также для удобства вычислений можно избавиться от минуса при старшем коэффициенте квадратного уравнения — для этого умножим или разделим обе части на −1. Например, удобно от квадратного уравнения −2x²— 3x + 7 = 0 перейти к решению 2x² + 3x — 7 = 0.

Связь между корнями и коэффициентами

Мы уже запомнили, что формула корней квадратного уравнения выражает корни уравнения через его коэффициенты:

Из этой формулы, можно получить другие зависимости между корнями и коэффициентами.

Например, можно применить формулы из теоремы Виета:

• x₁ + x₂ = — b/a,
• x₁* x₂ = c/a.

Для приведенного квадратного уравнения сумма корней равна второму коэффициенту с противоположным знаком, а произведение корней — свободному члену. Например, по виду уравнения 3x²— 7x + 22 = 0 можно сразу сказать, что сумма его корней равна 7/3, а произведение корней равно 22/3.

Можно активно использовать уже записанные формулы и с их помощью получить ряд других связей между корнями и коэффициентами квадратного уравнения. Таким образом можно выразить сумму квадратов корней квадратного уравнения через его коэффициенты:

Решение квадратных уравнений

6 июля 2011

Квадратные уравнения изучают в 8 классе, поэтому ничего сложного здесь нет. Умение решать их совершенно необходимо.

Квадратное уравнение — это уравнение вида ax² + bx + c = 0, где коэффициенты a, b и c — произвольные числа, причем a ≠ 0.

Прежде, чем изучать конкретные методы решения, заметим, что все квадратные уравнения можно условно разделить на три класса:

1. Не имеют корней;
2. Имеют ровно один корень;
3. Имеют два различных корня.

В этом состоит важное отличие квадратных уравнений от линейных, где корень всегда существует и единственен. Как определить, сколько корней имеет уравнение? Для этого существует замечательная вещь — дискриминант.

Дискриминант

Пусть дано квадратное уравнение ax² + bx + c = 0. Тогда дискриминант — это просто число D = b² − 4ac.

Эту формулу надо знать наизусть. Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение. А именно:

1. Если D < 0, корней нет;
2. Если D = 0, есть ровно один корень;
3. Если D > 0, корней будет два.

Обратите внимание: дискриминант указывает на количество корней, а вовсе не на их знаки, как почему-то многие считают. Взгляните на примеры — и сами все поймете:

Задача. Сколько корней имеют квадратные уравнения:

1. x² − 8x + 12 = 0;
2. 5x² + 3x + 7 = 0;
3. x² − 6x + 9 = 0.

Выпишем коэффициенты для первого уравнения и найдем дискриминант:
a = 1, b = −8, c = 12;
D = (−8)² − 4 · 1 · 12 = 64 − 48 = 16

Итак, дискриминант положительный, поэтому уравнение имеет два различных корня. Аналогично разбираем второе уравнение:
a = 5; b = 3; c = 7;
D = 3² − 4 · 5 · 7 = 9 − 140 = −131.

Дискриминант отрицательный, корней нет. Осталось последнее уравнение:
a = 1; b = −6; c = 9;
D = (−6)² − 4 · 1 · 9 = 36 − 36 = 0.

Дискриминант равен нулю — корень будет один.

Обратите внимание, что для каждого уравнения были выписаны коэффициенты. Да, это долго, да, это нудно — зато вы не перепутаете коэффициенты и не допустите глупых ошибок. Выбирайте сами: скорость или качество.

Кстати, если «набить руку», через некоторое время уже не потребуется выписывать все коэффициенты. Такие операции вы будете выполнять в голове. Большинство людей начинают делать так где-то после 50-70 решенных уравнений — в общем, не так и много.

Корни квадратного уравнения

Теперь перейдем, собственно, к решению. Если дискриминант D > 0, корни можно найти по формулам:

Когда D = 0, можно использовать любую из этих формул — получится одно и то же число, которое и будет ответом. Наконец, если D < 0, корней нет — ничего считать не надо.

Задача. Решить квадратные уравнения:

1. x² − 2x − 3 = 0;
2. 15 − 2x − x² = 0;
3. x² + 12x + 36 = 0.

Первое уравнение:
x² − 2x − 3 = 0 ⇒ a = 1; b = −2; c = −3;
D = (−2)² − 4 · 1 · (−3) = 16.

D > 0 ⇒ уравнение имеет два корня. Найдем их:

Второе уравнение:
15 − 2x − x² = 0 ⇒ a = −1; b = −2; c = 15;
D = (−2)² − 4 · (−1) · 15 = 64.

D > 0 ⇒ уравнение снова имеет два корня. Найдем их

[begin{align} & {{x}_{1}}=frac{2+sqrt{64}}{2cdot left( -1 right)}=-5; \ & {{x}_{2}}=frac{2-sqrt{64}}{2cdot left( -1 right)}=3. \ end{align}]

Наконец, третье уравнение:
x² + 12x + 36 = 0 ⇒ a = 1; b = 12; c = 36;
D = 12² − 4 · 1 · 36 = 0.

D = 0 ⇒ уравнение имеет один корень. Можно использовать любую формулу. Например, первую:

[x=frac{-12+sqrt{0}}{2cdot 1}=-6]

Как видно из примеров, все очень просто. Если знать формулы и уметь считать, проблем не будет. Чаще всего ошибки возникают при подстановке в формулу отрицательных коэффициентов. Здесь опять же поможет прием, описанный выше: смотрите на формулу буквально, расписывайте каждый шаг — и очень скоро избавитесь от ошибок.

Неполные квадратные уравнения

Бывает, что квадратное уравнение несколько отличается от того, что дано в определении. Например:

1. x² + 9x = 0;
2. x² − 16 = 0.

Несложно заметить, что в этих уравнениях отсутствует одно из слагаемых. Такие квадратные уравнения решаются даже легче, чем стандартные: в них даже не потребуется считать дискриминант. Итак, введем новое понятие:

Уравнение ax² + bx + c = 0 называется неполным квадратным уравнением, если b = 0 или c = 0, т.е. коэффициент при переменной x или свободный элемент равен нулю.

Разумеется, возможен совсем тяжелый случай, когда оба этих коэффициента равны нулю: b = c = 0. В этом случае уравнение принимает вид ax² = 0. Очевидно, такое уравнение имеет единственный корень: x = 0.

Рассмотрим остальные случаи. Пусть b = 0, тогда получим неполное квадратное уравнение вида ax² + c = 0. Немного преобразуем его:

Поскольку арифметический квадратный корень существует только из неотрицательного числа, последнее равенство имеет смысл исключительно при (−c/a) ≥ 0. Вывод:

1. Если в неполном квадратном уравнении вида ax² + c = 0 выполнено неравенство (−c/a) ≥ 0, корней будет два. Формула дана выше;
2. Если же (−c/a) < 0, корней нет.

Как видите, дискриминант не потребовался — в неполных квадратных уравнениях вообще нет сложных вычислений. На самом деле даже необязательно помнить неравенство (−c/a) ≥ 0. Достаточно выразить величину x² и посмотреть, что стоит с другой стороны от знака равенства. Если там положительное число — корней будет два. Если отрицательное — корней не будет вообще.

Теперь разберемся с уравнениями вида ax² + bx = 0, в которых свободный элемент равен нулю. Тут все просто: корней всегда будет два. Достаточно разложить многочлен на множители:

Произведение равно нулю, когда хотя бы один из множителей равен нулю. Отсюда находятся корни. В заключение разберем несколько таких уравнений:

Задача. Решить квадратные уравнения:

1. x² − 7x = 0;
2. 5x² + 30 = 0;
3. 4x² − 9 = 0.

x² − 7x = 0 ⇒ x · (x − 7) = 0 ⇒ x₁ = 0; x₂ = −(−7)/1 = 7.

5x² + 30 = 0 ⇒ 5x² = −30 ⇒ x² = −6. Корней нет, т.к. квадрат не может быть равен отрицательному числу.

4x² − 9 = 0 ⇒ 4x² = 9 ⇒ x² = 9/4 ⇒ x₁ = 3/2 = 1,5; x₂ = −1,5.

Смотрите также:

1. Теорема Виета
2. Следствия из теоремы Виета
3. Тест на тему «Значащая часть числа»
4. Метод коэффициентов, часть 1
5. Однородные тригонометрические уравнения: общая схема решения
6. Задача B4: строительные бригады

В продолжение темы «Решение уравнений» материал данной статьи познакомит вас с квадратными уравнениями.

Рассмотрим все подробно: суть и запись квадратного уравнения, зададим сопутствующие термины, разберем схему решения неполных и полных уравнений, познакомимся с формулой корней и дискриминантом, установим связи между корнями и коэффициентами, ну и конечно приведем наглядное решение практических примеров.

Квадратное уравнение, его виды

Квадратное уравнение – это уравнение, записанное как a·x2+b·x+c=0, где x – переменная, a, b и c – некоторые числа, при этом a не есть нуль.

Зачастую квадратные уравнения также носят название уравнений второй степени, поскольку по сути квадратное уравнение есть алгебраическое уравнение второй степени.

Приведем пример для иллюстрации заданного определения: 9·x2+16·x+2=0;  7,5·x2+3,1·x+0,11=0 и т.п. – это квадратные уравнения.

Числа a, b и c – это коэффициенты квадратного уравнения a·x2+b·x+c=0, при этом коэффициент a носит название первого, или старшего, или коэффициента при x2, b – второго коэффициента, или коэффициента при x, а c называют свободным членом.

К примеру, в квадратном уравнении 6·x2−2·x−11=0 старший коэффициент равен 6, второй коэффициент есть −2, а свободный член равен −11. Обратим внимание на тот факт, что, когда коэффициенты b и/или c являются отрицательными, то используется краткая форма записи вида 6·x2−2·x−11=0, а не 6·x2+(−2)·x+(−11)=0.

Уточним также такой аспект: если коэффициенты a и/или b равны 1 или −1, то явного участия в записи квадратного уравнения они могут не принимать, что объясняется особенностями записи указанных числовых коэффициентов. К примеру, в квадратном уравнении y2−y+7=0 старший коэффициент равен 1, а второй коэффициент есть −1.

Приведенные и неприведенные квадратные уравнения

По значению первого коэффициента квадратные уравнения подразделяют на приведенные и неприведенные.

Приведенное квадратное уравнение – это квадратное уравнение, где старший коэффициент равен 1. При иных значениях старшего коэффициента квадратное уравнение является неприведенным.

Приведем примеры: квадратные уравнения x2−4·x+3=0, x2−x−45=0 являются приведенными, в каждом из которых старший коэффициент равен 1.

9·x2−x−2=0 — неприведенное квадратное уравнение, где первый коэффициент отличен от 1.

Любое неприведенное квадратное уравнение возможно преобразовать в приведенное уравнение, если разделить обе его части на первый коэффициент (равносильное преобразование). Преобразованное уравнение будет иметь такие же корни, как и заданное неприведенное уравнение или так же не иметь корней вовсе.

Рассмотрение конкретного примера позволит нам наглядно продемонстрировать выполнение перехода от неприведенного квадратного уравнения к приведенному.

Полные и неполные квадратные уравнения

Обратимся к определению квадратного уравнения. В нем мы уточнили, что a≠0. Подобное условие необходимо, чтобы уравнение a·x2+b·x+c=0 было именно квадратным, поскольку при a=0 оно по сути преобразуется в линейное уравнение b·x+c=0.

В случае же, когда коэффициенты b и c равны нулю (что возможно, как по отдельности, так и совместно), квадратное уравнение носит название неполного.

Порассуждаем, почему типам квадратных уравнений даны именно такие названия.

При b=0 квадратное уравнение примет вид a·x2+0·x+c=0, что то же самое, что a·x2+c=0. При c=0 квадратное уравнение записано как a·x2+b·x+0=0, что равносильно a·x2+b·x=0. При b=0 и c=0 уравнение примет вид a·x2=0. Уравнения, которые мы получили, отличны от полного квадратного уравнения тем, что в их левых частях не содержится либо слагаемого с переменной x, либо свободного члена, либо обоих сразу. Собственно, этот факт и задал название такому типу уравнений – неполное.

Например, x2+3·x+4=0 и −7·x2−2·x+1,3=0 – это полные квадратные уравнения; x2=0, −5·x2=0; 11·x2+2=0, −x2−6·x=0 – неполные квадратные уравнения.

Решение неполных квадратных уравнений

Заданное выше определение дает возможность выделить следующие виды неполных квадратных уравнений:

• a·x2=0, такому уравнению соответствуют коэффициенты b=0 и c=0;
• a·x2+c=0 при b=0;
• a·x2+b·x=0 при c=0.

Рассмотрим последовательно решение каждого вида неполного квадратного уравнения.

Решение уравнения a·x²=0

Как уже было указано выше, такому уравнению отвечают коэффициенты b и c, равные нулю. Уравнение a·x2=0 возможно преобразовать в равносильное ему уравнение x2=0, которое мы получим, поделив обе части исходного уравнения на число a, не равное нулю. Очевидный факт, что корень уравнения x2=0 это нуль, поскольку 02=0. Иных корней это уравнение не имеет, что объяснимо свойствами степени: для любого числа p, не равного нулю, верно неравенство p2>0, из чего следует, что при p≠0 равенство p2=0 никогда не будет достигнуто.

Таким образом, для неполного квадратного уравнение a·x2=0 существует единственный корень x=0.

Решение уравнения a·x2+c=0

На очереди — решение неполных квадратных уравнений, где b=0, c≠0, то есть уравнений вида a·x2+c=0. Преобразуем это уравнение, перенеся слагаемое из одной части уравнения в другую, сменив знак на противоположный и разделив обе части уравнения на число, не равное нулю:

• переносим c в правую часть, что дает уравнение a·x2=−c;
• делим обе части уравнения на a, получаем в итоге x=-ca.

Наши преобразования являются равносильными, соответственно полученное уравнение также равносильно исходному, и этот факт дает возможность делать вывод о корнях уравнения. От того, каковы значения a и c зависит значение выражения  -ca: оно может иметь знак  минус (допустим, если a=1 и c=2, тогда -ca=-21=-2 ) или знак плюс (например, если a=−2 и c=6, то -ca=-6-2=3 ); оно не равно нулю, поскольку c≠0. Подробнее остановимся на ситуациях, когда  -ca<0 и -ca>0.

В случае, когда -ca<0,  уравнение x2=-ca не будет иметь корней. Утверждая это, мы опираемся на то, что квадратом любого числа является число неотрицательное. Из сказанного следует, что при -ca<0  ни для какого числа p равенство p2=-ca  не может быть верным.

Все иначе, когда -ca>0: вспомним о квадратном корне, и станет очевидно, что корнем уравнения x2=-ca будет число -ca, поскольку -ca2=-ca. Нетрудно понять, что число —ca — также корень уравнения x2=-ca: действительно, —ca2=-ca.

Прочих корней уравнение не будет иметь. Мы можем это продемонстрировать, используя метод от противного. Для начала зададим обозначения найденных выше корней как _x1 и _−x1. Выскажем предположение, что уравнение  x2=-ca имеет также корень x2, который отличается от корней _x1 и _−x1. Мы знаем, что, подставив в уравнение вместо x его корни, преобразуем уравнение в справедливое числовое равенство.

Для _x1 и _−x1 запишем: x12=-ca , а для x2 — x22=-ca  . Опираясь на свойства числовых равенств, почленно вычтем одно верное равенство из другого, что даст нам: x12−x22=0. Используем свойства действий с числами, чтобы переписать последнее равенство как (x1−x2)·(x1+x2)=0. Известно, что произведение двух чисел есть нуль тогда и только тогда, когда хотя бы одно из чисел является нулем. Из сказанного следует, что x1−x2=0 и/или x1+x2=0, что то же самое, x2=x1 и/или x2=−x1. Возникло очевидное противоречие, ведь  вначале было условлено, что корень уравнения x2 отличается от _x1 и _−x1. Так, мы доказали, что уравнение  не имеет иных корней, кроме x=-ca и x=—ca.

Резюмируем все рассуждения выше.

Приведем примеры решения уравнений a·x2+c=0.

Решение уравнения a·x²+b·x=0

Разберем третий вид неполных квадратных уравнений, когда c=0. Чтобы найти решение неполного квадратного уравнения a·x2+b·x=0, воспользуемся методом разложения на множители. Разложим на множители многочлен, который находится в левой части уравнения, вынеся за скобки общий множитель x. Этот шаг даст возможность преобразовать исходное неполное квадратное уравнение в равносильное ему x·(a·x+b)=0. А это уравнение, в свою очередь,  равносильно совокупности уравнений x=0 и a·x+b=0. Уравнение a·x+b=0 линейное, и корень его: x=−ba.

Таким образом, неполное квадратное уравнение a·x2+b·x=0 будет иметь  два корня x=0 и x=−ba.

Закрепим материал примером.

Дискриминант, формула корней квадратного уравнения

Для нахождения решения квадратных уравнений существует формула корней:

x=-b±D2·a, где D=b2−4·a·c – так называемый дискриминант квадратного уравнения.

Запись x=-b±D2·a по сути означает, что x1=-b+D2·a, x2=-b-D2·a.

Нелишним будет понимать, как была выведена указанная формула и каким образом ее применять.

Вывод формулы корней квадратного уравнения

Пускай перед нами стоит задача решить квадратное уравнение a·x2+b·x+c=0. Осуществим ряд равносильных преобразований:

• разделим обе части уравнения на число a, отличное от нуля, получим приведенное квадратное уравнение: x2+ba·x+ca=0;
• выделим полный квадрат в левой  части получившегося уравнения:
  x2+ba·x+ca=x2+2·b2·a·x+b2·a2-b2·a2+ca==x+b2·a2-b2·a2+ca
  После этого уравнения примет вид: x+b2·a2-b2·a2+ca=0;
• теперь возможно сделать перенос двух последних слагаемых в правую часть, сменив знак на противоположный, после чего получаем: x+b2·a2=b2·a2-ca;
• наконец, преобразуем выражение, записанное в правой части последнего равенства:
  b2·a2-ca=b24·a2-ca=b24·a2-4·a·c4·a2=b2-4·a·c4·a2.

Таким образом, мы пришли к уравнению x+b2·a2=b2-4·a·c4·a2, равносильному исходному уравнению a·x2+b·x+c=0.

Решение подобных уравнений мы разбирали в предыдущих пунктах (решение неполных квадратных уравнений). Уже полученный опыт дает возможность сделать вывод касательно корней уравнения x+b2·a2=b2-4·a·c4·a2:

• при b2-4·a·c4·a2<0 уравнение не имеет действительных решений;
• при b2-4·a·c4·a2=0 уравнение имеет вид x+b2·a2=0, тогда x+b2·a=0.

Отсюда очевиден единственный корень x=-b2·a;

• при b2-4·a·c4·a2>0 верным будет: x+b2·a=b2-4·a·c4·a2 или x=b2·a-b2-4·a·c4·a2, что то же самое, что x+-b2·a=b2-4·a·c4·a2 или x=-b2·a-b2-4·a·c4·a2,  т.е. уравнение имеет два корня.

Возможно сделать вывод, что наличие или отсутствие корней уравнения x+b2·a2=b2-4·a·c4·a2 (а значит и исходного уравнения) зависит от знака выражения b2-4·a·c4·a2, записанного в правой части. А знак этого выражения задается знаком числителя, (знаменатель 4·a2 всегда будет положителен), то есть, знаком выражения b2−4·a·c. Этому выражению b2−4·a·c дано название — дискриминант квадратного уравнения и определена в качестве его обозначения буква D. Здесь можно записать суть дискриминанта – по его значению и знаку делают вывод, будет ли квадратное уравнение иметь действительные корни, и, если будет, то каково количество корней — один или два.

Вернемся к уравнению x+b2·a2=b2-4·a·c4·a2. Перепишем его, используя обозначение дискриминанта:  x+b2·a2=D4·a2.

Вновь сформулируем выводы:

Так, результатом наших рассуждений стало выведение формулы корней квадратного уравнения:

x=-b+D2·a, x=-b-D2·a, дискриминант D вычисляется по формуле D=b2−4·a·c.

Данные формулы дают возможность при дискриминанте больше нуля определить оба действительных корня. Когда дискриминант равен нулю, применение обеих формул даст один и тот же корень, как единственное решение квадратного уравнения. В случае, когда дискриминант отрицателен, попытавшись использовать формулу корня квадратного уравнения, мы столкнемся с необходимостью извлечь квадратный корень из отрицательного числа, что выведет нас за рамки действительных чисел. При отрицательном дискриминанте у квадратного уравнения не будет действительных корней, но возможна пара комплексно сопряженных корней, определяемых теми же полученными нами формулами корней.

Алгоритм решения квадратных уравнений по формулам корней

Решить квадратное уравнение возможно, сразу задействуя формулу корней, но в основном так поступают при необходимости найти комплексные корни.

В основной же массе случаев обычно подразумевается поиск не комплексных, а действительных корней квадратного уравнения. Тогда оптимально перед тем, как использовать формулы корней квадратного уравнения, сначала определить дискриминант и удостовериться, что он не является отрицательным (в ином случае сделаем вывод, что у уравнения нет действительных корней), а после приступить к вычислению значения корней.

Рассуждения выше дают возможность сформулировать  алгоритм решения квадратного уравнения.

Отметим, что, когда дискриминант есть нуль, можно использовать формулу x=-b±D2·a, она даст тот же результат, что и формула x=-b2·a.

Рассмотрим примеры.

Примеры решения квадратных уравнений

Приведем решение примеров при различных значениях дискриминанта.

В школьной программе стандартно нет требования искать комплексные корни, поэтому, если в ходе решения дискриминант определен как отрицательный, сразу записывается ответ, что действительных корней нет.

Формула корней для четных вторых коэффициентов

Формула корней x=-b±D2·a (D=b2−4·a·c) дает возможность получить еще одну формулу, более компактную, позволяющую находить решения квадратных уравнений с четным коэффициентом при x (либо с коэффициентом вида 2·n, к примеру, 2 · 3 или 14·ln5=2·7·ln5). Покажем, как выводится эта формула.

Пусть перед нами стоит задача найти решение квадратного уравнения a·x2+2·n·x+c=0. Действуем по алгоритму: определяем дискриминантD=(2·n)2−4·a·c=4·n2−4·a·c=4·(n2−a·c), а затем используем формулу корней:

x=-2·n±D2·a,x=-2·n±4·n2-a·c2·a,x=-2·n±2n2-a·c2·a,x=-n±n2-a·ca.

Пусть выражение n2−a·c будет обозначено как D1 (иногда его обозначают D’). Тогда формула корней рассматриваемого квадратного уравнения со вторым коэффициентом 2·n примет вид:

 x=-n±D1a, где D1=n2−a·c.

Легко увидеть, что что D=4·D1, или D1=D4. Иначе говоря, D1 – это четверть дискриминанта. Очевидно, что знак D1 такой же, как знак D, а значит знак D1 также может служить индикатором наличия или отсутствия корней квадратного уравнения.

Упрощение вида квадратных уравнений

Иногда существует возможность оптимизировать вид исходного уравнения, что позволит упростить процесс вычисления корней.

К примеру, квадратное уравнение 12·x2−4·x−7=0 явно удобнее для решения, чем 1200·x2−400·x−700=0.

Чаще упрощение вида квадратного уравнения производится действиями умножения или деления его обеих частей на некое число. К примеру, выше мы показали упрощенную запись уравнения 1200·x2−400·x−700=0, полученную делением обеих его частей на 100.

Такое преобразование возможно, когда коэффициенты квадратного уравнения не являются взаимно простыми числами. Тогда обычно осуществляют деление обеих частей уравнения на наибольший общий делитель абсолютных величин его коэффициентов.

Как пример используем квадратное уравнение 12·x2−42·x+48=0. Определим НОД абсолютных величин его коэффициентов: НОД(12, 42, 48)=НОД(НОД(12, 42), 48)=НОД(6, 48)=6. Произведем деление обеих частей исходного квадратного уравнения на 6 и получим равносильное ему квадратное уравнение 2·x2−7·x+8=0.

Умножением обеих частей квадратного уравнения обычно избавляются от дробных коэффициентов. При этом умножают на наименьшее общее кратное знаменателей его коэффициентов. К примеру, если каждую часть квадратного уравнения 16·x2+23·x-3=0 перемножить с НОК(6, 3, 1)=6, то оно станет записано в более простом виде x2+4·x−18=0.

Напоследок отметим, что почти всегда избавляются от минуса при первом коэффициенте квадратного уравнения, изменяя знаки каждого члена уравнения, что достигается путем умножения (или деления) обеих частей на −1. К примеру, от квадратного уравнения −2·x2−3·x+7=0 можно перейти к упрощенной его версии 2·x2+3·x−7=0.

Связь между корнями и коэффициентами

Уже известная нам формула корней квадратных уравнений x=-b±D2·a выражает корни уравнения через его числовые коэффициенты. Опираясь на данную формулу, мы имеем возможность задать другие зависимости между корнями и коэффициентами.

Самыми известными и применимыми являются формулы теоремы Виета:

x1+x2=-ba и x2=ca.

В частности, для приведенного квадратного уравнения сумма корней есть второй коэффициент с противоположным знаком, а произведение корней равно свободному члену. К примеру, по виду квадратного уравнения 3·x2−7·x+22=0 возможно сразу определить, что сумма его корней равна 73, а произведение корней — 223.

Также можно найти ряд прочих связей между корнями и коэффициентами квадратного уравнения. Например, сумма квадратов корней квадратного уравнения может быть выражена через коэффициенты:

x12+x22=(x1+x2)2-2·x1·x2=-ba2-2·ca=b2a2-2·ca=b2-2·a·ca2.

• Если b = 0, то квадратное уравнение принимает вид ax 2 + 0x+c=0 и оно равносильно ax 2 + c = 0.
• Если c = 0, то квадратное уравнение выглядит так ax 2 + bx + 0 = 0, иначе его можно написать как ax 2 + bx = 0.
• Если b = 0 и c = 0, то квадратное уравнение выглядит так ax 2 = 0.

Такие уравнения отличны от полного квадратного тем, что их левые части не содержат либо слагаемого с неизвестной переменной, либо свободного члена, либо и того и другого. Отсюда и их название — неполные квадратные уравнения.

Решение неполных квадратных уравнений

Как мы уже знаем, есть три вида неполных квадратных уравнений:

• ax 2 = 0, ему отвечают коэффициенты b = 0 и c = 0;
• ax 2 + c = 0, при b = 0;
• ax 2 + bx = 0, при c = 0.

Давайте рассмотрим по шагам, как решать неполные квадратные уравнения по видам.

Как решить уравнение ax 2 = 0

Начнем с решения неполных квадратных уравнений, в которых b и c равны нулю, то есть, с уравнений вида ax 2 = 0.

Уравнение ax 2 = 0 равносильно x 2 = 0. Такое преобразование возможно, когда мы разделили обе части на некое число a, которое не равно нулю. Корнем уравнения x 2 = 0 является нуль, так как 0 2 = 0. Других корней у этого уравнения нет, что подтверждают свойства степеней.

Таким образом, неполное квадратное уравнение ax 2 = 0 имеет единственный корень x = 0.

Пример 1. Решить −6x 2 = 0.

1. Замечаем, что данному уравнению равносильно x 2 = 0, значит исходное уравнение имеет единственный корень — нуль.
2. По шагам решение выглядит так:

Как решить уравнение ax 2 + с = 0

Обратим внимание на неполные квадратные уравнения вида ax 2 + c = 0, в которых b = 0, c ≠ 0. Мы давно знаем, что слагаемые в уравнениях носят двусторонние куртки: когда мы переносим их из одной части уравнения в другую, они надевает куртку на другую сторону — меняют знак на противоположный.

Еще мы знаем, что если обе части уравнения поделить на одно и то же число (кроме нуля) — у нас получится равносильное уравнение. Ну есть одно и то же, только с другими цифрами.

Держим все это в голове и колдуем над неполным квадратным уравнением (производим «равносильные преобразования»): ax 2 + c = 0:

• перенесем c в правую часть: ax 2 = — c,
• разделим обе части на a: x 2 = — c/а.

Ну все, теперь мы готовы к выводам о корнях неполного квадратного уравнения. В зависимости от значений a и c, выражение — c/а может быть отрицательным или положительным. Разберем конкретные случаи.

Если — c/а 2 = — c/а не имеет корней. Все потому, что квадрат любого числа всегда равен неотрицательному числу. Из этого следует, что при — c/а 0, то корни уравнения x 2 = — c/а будут другими. Например, можно использовать правило квадратного корня и тогда корень уравнения равен числу √- c/а, так как (√- c/а) 2 = — c/а. Кроме того, корнем уравнения может стать -√- c/а, так как (-√- c/а) 2 = — c/а. Ура, больше у этого уравнения нет корней.

Неполное квадратное уравнение ax 2 + c = 0 равносильно уравнению х 2 = -c/a, которое:

• не имеет корней при — c/а 0.

В двух словах

Пример 1. Найти решение уравнения 8x 2 + 5 = 0.

Перенесем свободный член в правую часть:

Разделим обе части на 8:

В правой части осталось число со знаком минус, значит у данного уравнения нет корней.

Ответ: уравнение 8x 2 + 5 = 0 не имеет корней.

Как решить уравнение ax 2 + bx = 0

Осталось разобрать третий вид неполных квадратных уравнений, когда c = 0.

Неполное квадратное уравнение ax 2 + bx = 0 можно решить методом разложения на множители. Как разложить квадратное уравнение:

Разложим на множители многочлен, который расположен в левой части уравнения — вынесем за скобки общий множитель x.

Теперь можем перейти от исходного уравнения к равносильному x * (ax + b) = 0. А это уравнение равносильно совокупности двух уравнений x = 0 и ax + b = 0, последнее — линейное, его корень x = −b/a.

Таким образом, неполное квадратное уравнение ax 2 + bx = 0 имеет два корня:

Пример 1. Решить уравнение 0,5x 2 + 0,125x = 0

Это уравнение равносильно х = 0 и 0,5x + 0,125 = 0.

Решить линейное уравнение:

0,5x = 0,125,
х = 0,125/0,5

Значит корни исходного уравнения — 0 и 0,25.

Ответ: х = 0 и х = 0,25.

Как разложить квадратное уравнение

С помощью теоремы Виета можно получить формулу разложения квадратного трехчлена на множители. Выглядит она так:

Формула разложения квадратного трехчлена

Если x₁ и x₂ — корни квадратного трехчлена ax 2 + bx + c, то справедливо равенство ax 2 + bx + c = a (x − x₁) (x − x₂).

Дискриминант: формула корней квадратного уравнения

Чтобы найти результат квадратного уравнения, придумали формулу корней. Выглядит она так:

где D = b 2 − 4ac — дискриминант квадратного уравнения.

Эта запись означает:

Чтобы легко применять эту формулу, нужно понять, как она получилась. Давайте разбираться.

Алгоритм решения квадратных уравнений по формулам корней

Теперь мы знаем, что при решении квадратных уравнения можно использовать универсальную формулу корней — это помогает находить комплексные корни.

В 8 классе на алгебре можно встретить задачу по поиску действительных корней квадратного уравнения. Для этого важно перед использованием формул найти дискриминант и убедиться, что он неотрицательный, и только после этого вычислять значения корней. Если дискриминант отрицательный, значит уравнение не имеет действительных корней.

Алгоритм решения квадратного уравнения ax 2 + bx + c = 0:

• вычислить его значение дискриминанта по формуле D = b 2 −4ac;
• если дискриминант отрицательный, зафиксировать, что действительных корней нет;
• если дискриминант равен нулю, вычислить единственный корень уравнения по формуле х = −b/2a;
• если дискриминант положительный, найти два действительных корня квадратного уравнения по формуле корней

Чтобы запомнить алгоритм решения квадратных уравнений и с легкостью его использовать, давайте тренироваться!

Примеры решения квадратных уравнений

Как решать квадратные уравнения мы уже знаем, осталось закрепить знания на практике.

Пример 1. Решить уравнение −4x 2 + 28x — 49 = 0.

1. Найдем дискриминант: D = 28 2 — 4(-4)(-49) = 784 — 784 = 0
2. Так как дискриминант равен нулю, значит это квадратное уравнение имеет единственный корень
3. Найдем корень

Ответ: единственный корень 3,5.

Пример 2. Решить уравнение 54 — 6x 2 = 0.

Произведем равносильные преобразования. Умножим обе части на −1

Оставим неизвестное в одной части, остальное перенесем с противоположным знаком в другую

Ответ: два корня 3 и — 3.

Пример 3. Решить уравнение x 2 — х = 0.

Преобразуем уравнение так, чтобы появились множители

Ответ: два корня 0 и 1.

Пример 4. Решить уравнение x 2 — 10 = 39.

Оставим неизвестное в одной части, остальное перенесем с противоположным знаком в другую

Ответ: два корня 7 и −7.

Пример 5. Решить уравнение 3x 2 — 4x+94 = 0.

Найдем дискриминант по формуле

D = (-4) 2 — 4 * 3 * 94 = 16 — 1128 = −1112

Дискриминант отрицательный, поэтому корней нет.

Ответ: корней нет.

В школьной программе за 8 класс нет обязательного требования искать комплексные корни, но такой подход может ускорить ход решения. Если дискриминант отрицательный — сразу пишем ответ, что действительных корней нет и не мучаемся.

Формула корней для четных вторых коэффициентов

Рассмотрим частный случай. Формула решения корней квадратного уравнения , где D = b 2 — 4ac, помогает получить еще одну формулу, более компактную, при помощи которой можно решать квадратные уравнения с четным коэффициентом при x. Рассмотрим, как появилась эта формула.

Например, нам нужно решить квадратное уравнение ax 2 + 2nx + c = 0. Сначала найдем его корни по известной нам формуле. Вычислим дискриминант D = (2n) 2 — 4ac = 4n 2 — 4ac = 4(n 2 — ac) и подставим в формулу корней:

2 + 2nx + c = 0″ height=»705″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc11a460e2f8354381151.png» width=»588″>

Для удобства вычислений обозначим выражение n 2 -ac как D₁. Тогда формула корней квадратного уравнения со вторым коэффициентом 2·n примет вид:

где D₁ = n 2 — ac.

Самые внимательные уже заметили, что D = 4D₁, или D₁= D/4. Проще говоря, D₁ — это четверть дискриминанта. И получается, что знак D1 является индикатором наличия или отсутствия корней квадратного уравнения.

Сформулируем правило. Чтобы найти решение квадратного уравнения со вторым коэффициентом 2n, нужно:

• вычислить D₁= n 2 — ac;
• если D₁ 0, значит можно найти два действительных корня по формуле

Формула Виета

Если в школьной геометрии чаще всего используется теорема Пифагора, то в школьной алгебре ведущую роль занимают формулы Виета. Теорема звучит так:

Сумма корней x 2 + bx + c = 0 равна второму коэффициенту с противоположным знаком, а произведение корней равняется свободному члену.

Если дано x 2 + bx + c = 0, где x₁ и x₂ являются корнями, то справедливы два равенства:

Знак системы, который принято обозначать фигурной скобкой, означает, что значения x₁ и x₂ удовлетворяют обоим равенствам.

Рассмотрим теорему Виета на примере: x 2 + 4x + 3 = 0.

Пока неизвестно, какие корни имеет данное уравнение. Но в соответствии с теоремой можно записать, что сумма этих корней равна второму коэффициенту с противоположным знаком. Он равен четырем, значит будем использовать минус четыре:

Произведение корней по теореме соответствует свободному члену. В данном случае свободным членом является число три. Значит:

Необходимо проверить равна ли сумма корней −4, а произведение 3. Для этого найдем корни уравнения x 2 + 4x + 3 = 0. Воспользуемся формулами для чётного второго коэффициента:
2 + 4x + 3 = 0″ height=»215″ src=»https://lh5.googleusercontent.com/E_X403ETh_88EANRWdQN03KRT8yxP2HO4HoCrxj__c8G0DqmNJ1KDRqtLH5Z1p7DtHm-rNMDB2tEs41D7RHpEV5mojDTMMRPuIkcW33jVNDoOe0ylzXdHATLSGzW4NakMkH2zkLE» width=»393″>

Получилось, что корнями уравнения являются числа −1 и −3. Их сумма равняется второму коэффициенту с противоположным знаком, а значит решение верное.
2 + 4x + 3 = 0″ height=»52″ src=»https://lh5.googleusercontent.com/VzGPXO9B0ZYrr9v0DpJfXwuzeZtjYnDxE_ma76PUC8o7jVWwa8kZjTJhq2Lof0TiJXAp_ny3yRwI_OyRzeucv9xUZ63yoozGPP4xd4OxvElVT7Pt-d6xL5w17e_mQNs5qZJQiwfG» width=»125″>

Произведение корней −1 и −3 по теореме Виета должно равняться свободному члену, то есть числу 3. Это условие также выполняется:
2 + 4x + 3 = 0″ height=»52″ src=»https://lh4.googleusercontent.com/Cq-LCFmY3YGNSan1VF3l3CqIeojoJYAvGAiTBWnzyoZu_xJFrF5NfQ3xCe59apJklw6uYbmQ4lAkBTeC-TJmEGicN3rgGtsezhuqdNiOWjZT39NziOB5uOmQr3cr9-5fNnepdZDo» width=»112″>

Результат проделанных вычислений в том, что мы убедились в справедливости выражения:

Когда дана сумма и произведение корней квадратного уравнения, принято начинать подбор подходящих корней. Теорема, обратная теореме Виета, при таких условиях может быть главным помощником. Вот она:

Обратная теорема Виета

Если числа x₁ и x₂ таковы, что их сумма равна второму коэффициенту уравнения x 2 + bx + c = 0, взятому с противоположным знаком, а их произведение равно свободному члену, то эти числа и есть корни x 2 + bx + c = 0.

Обычно вся суть обратных теорем в том самом выводе, которое дает первая теорема. Так, при доказательстве теоремы Виета стало понятно, что сумма x₁ и x₂ равна −b, а их произведение равно c. В обратной теореме это и есть утверждение.

Пример 1. Решить при помощи теоремы Виета: x 2 − 6x + 8 = 0.

Для начала запишем сумму и произведение корней уравнения. Сумма будет равна 6, так как второй коэффициент равен −6. А произведение корней равно 8.

2 − 6x + 8 = 0″ height=»59″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc101ce2e346034751939.png» width=»117″>

Когда у нас есть эти два равенства, можно подобрать подходящие корни, которые будут удовлетворять обоим равенствам системы.

Чтобы проще подобрать корни, нужно их перемножить. Число 8 можно получить путем перемножения чисел 4 и 2 либо 1 и 8. Но значения x₁ и x₂ надо подбирать так, чтобы они удовлетворяли и второму равенству тоже.

Можно сделать вывод, что значения 1 и 8 не подходят, так как они не удовлетворяют равенству x₁ + x₂ = 6. А значения 4 и 2 подходят обоим равенствам:

Значит числа 4 и 2 — корни уравнения x 2 − 6x + 8 = 0. p>

Упрощаем вид квадратных уравнений

Если мы ходили в школу всегда одной тропинкой, а потом вдруг обнаружили путь короче — это значит теперь у нас есть выбор: упростить себе задачу и сократить время на дорогу или прогуляться по привычному маршруту.

Так же и при вычислении корней квадратного уравнения. Ведь проще посчитать уравнение 11x 2 — 4 x — 6 = 0, чем 1100x 2 — 400x — 600 = 0.

Часто упрощение вида квадратного уравнения можно получить через умножение или деление обеих частей на некоторое число. Например, в предыдущем абзаце мы упростили уравнение 1100x 2 — 400x — 600 = 0, просто разделив обе части на 100.

Такое преобразование возможно, когда коэффициенты не являются взаимно простыми числами. Тогда принято делить обе части уравнения на наибольший общий делитель абсолютных величин его коэффициентов.

Покажем, как это работает на примере 12x 2 — 42x + 48 = 0. Найдем наибольший общий делитель абсолютных величин его коэффициентов: НОД (12, 42, 48) = 6. Разделим обе части исходного квадратного уравнения на 6, и придем к равносильному уравнению 2x 2 — 7x + 8 = 0. Вот так просто.

А умножение обеих частей квадратного уравнения отлично помогает избавиться от дробных коэффициентов. Умножать в данном случае лучше на наименьшее общее кратное знаменателей его коэффициентов. Например, если обе части квадратного уравнения

умножить на НОК (6, 3, 1) = 6, то оно примет более простой вид x 2 + 4x — 18 = 0.

Также для удобства вычислений можно избавиться от минуса при старшем коэффициенте квадратного уравнения — для этого умножим или разделим обе части на −1. Например, удобно от квадратного уравнения −2x 2 — 3x + 7 = 0 перейти к решению 2x 2 + 3x — 7 = 0.

Связь между корнями и коэффициентами

Мы уже запомнили, что формула корней квадратного уравнения выражает корни уравнения через его коэффициенты:

Из этой формулы, можно получить другие зависимости между корнями и коэффициентами.

Например, можно применить формулы из теоремы Виета:

Для приведенного квадратного уравнения сумма корней равна второму коэффициенту с противоположным знаком, а произведение корней — свободному члену. Например, по виду уравнения 3x 2 — 7x + 22 = 0 можно сразу сказать, что сумма его корней равна 7/3, а произведение корней равно 22/3.

Можно активно использовать уже записанные формулы и с их помощью получить ряд других связей между корнями и коэффициентами квадратного уравнения. Таким образом можно выразить сумму квадратов корней квадратного уравнения через его коэффициенты:

Решение квадратных уравнений: формула корней, примеры

В продолжение темы «Решение уравнений» материал данной статьи познакомит вас с квадратными уравнениями.

Рассмотрим все подробно: суть и запись квадратного уравнения, зададим сопутствующие термины, разберем схему решения неполных и полных уравнений, познакомимся с формулой корней и дискриминантом, установим связи между корнями и коэффициентами, ну и конечно приведем наглядное решение практических примеров.

Квадратное уравнение, его виды

Квадратное уравнение – это уравнение, записанное как a · x 2 + b · x + c = 0 , где x – переменная, a , b и c – некоторые числа, при этом a не есть нуль.

Зачастую квадратные уравнения также носят название уравнений второй степени, поскольку по сути квадратное уравнение есть алгебраическое уравнение второй степени.

Приведем пример для иллюстрации заданного определения: 9 · x 2 + 16 · x + 2 = 0 ; 7 , 5 · x 2 + 3 , 1 · x + 0 , 11 = 0 и т.п. – это квадратные уравнения.

Числа a , b и c – это коэффициенты квадратного уравнения a · x 2 + b · x + c = 0 , при этом коэффициент a носит название первого, или старшего, или коэффициента при x 2 , b – второго коэффициента, или коэффициента при x , а c называют свободным членом.

К примеру, в квадратном уравнении 6 · x 2 − 2 · x − 11 = 0 старший коэффициент равен 6 , второй коэффициент есть − 2 , а свободный член равен − 11 . Обратим внимание на тот факт, что, когда коэффициенты b и/или c являются отрицательными, то используется краткая форма записи вида 6 · x 2 − 2 · x − 11 = 0 , а не 6 · x 2 + ( − 2 ) · x + ( − 11 ) = 0 .

Уточним также такой аспект: если коэффициенты a и/или b равны 1 или − 1 , то явного участия в записи квадратного уравнения они могут не принимать, что объясняется особенностями записи указанных числовых коэффициентов. К примеру, в квадратном уравнении y 2 − y + 7 = 0 старший коэффициент равен 1 , а второй коэффициент есть − 1 .

Приведенные и неприведенные квадратные уравнения

По значению первого коэффициента квадратные уравнения подразделяют на приведенные и неприведенные.

Приведенное квадратное уравнение – это квадратное уравнение, где старший коэффициент равен 1 . При иных значениях старшего коэффициента квадратное уравнение является неприведенным.

Приведем примеры: квадратные уравнения x 2 − 4 · x + 3 = 0 , x 2 − x − 4 5 = 0 являются приведенными, в каждом из которых старший коэффициент равен 1 .

9 · x 2 − x − 2 = 0 — неприведенное квадратное уравнение, где первый коэффициент отличен от 1 .

Любое неприведенное квадратное уравнение возможно преобразовать в приведенное уравнение, если разделить обе его части на первый коэффициент (равносильное преобразование). Преобразованное уравнение будет иметь такие же корни, как и заданное неприведенное уравнение или так же не иметь корней вовсе.

Рассмотрение конкретного примера позволит нам наглядно продемонстрировать выполнение перехода от неприведенного квадратного уравнения к приведенному.

Задано уравнение 6 · x 2 + 18 · x − 7 = 0 . Необходимо преобразовать исходное уравнение в приведенную форму.

Решение

Cогласно указанной выше схеме разделим обе части исходного уравнения на старший коэффициент 6 . Тогда получим: ( 6 · x 2 + 18 · x − 7 ) : 3 = 0 : 3 , и это то же самое, что: ( 6 · x 2 ) : 3 + ( 18 · x ) : 3 − 7 : 3 = 0 и далее: ( 6 : 6 ) · x 2 + ( 18 : 6 ) · x − 7 : 6 = 0 . Отсюда: x 2 + 3 · x — 1 1 6 = 0 . Таким образом, получено уравнение, равносильное заданному.

Ответ: x 2 + 3 · x — 1 1 6 = 0 .

Полные и неполные квадратные уравнения

Обратимся к определению квадратного уравнения. В нем мы уточнили, что a ≠ 0 . Подобное условие необходимо, чтобы уравнение a · x 2 + b · x + c = 0 было именно квадратным, поскольку при a = 0 оно по сути преобразуется в линейное уравнение b · x + c = 0 .

В случае же, когда коэффициенты b и c равны нулю (что возможно, как по отдельности, так и совместно), квадратное уравнение носит название неполного.

Неполное квадратное уравнение – такое квадратное уравнение a · x 2 + b · x + c = 0 , где хотя бы один из коэффициентов b и c (или оба) равен нулю.

Полное квадратное уравнение – квадратное уравнение, в котором все числовые коэффициенты не равны нулю.

Порассуждаем, почему типам квадратных уравнений даны именно такие названия.

При b = 0 квадратное уравнение примет вид a · x 2 + 0 · x + c = 0 , что то же самое, что a · x 2 + c = 0 . При c = 0 квадратное уравнение записано как a · x 2 + b · x + 0 = 0 , что равносильно a · x 2 + b · x = 0 . При b = 0 и c = 0 уравнение примет вид a · x 2 = 0 . Уравнения, которые мы получили, отличны от полного квадратного уравнения тем, что в их левых частях не содержится либо слагаемого с переменной x , либо свободного члена, либо обоих сразу. Собственно, этот факт и задал название такому типу уравнений – неполное.

Например, x 2 + 3 · x + 4 = 0 и − 7 · x 2 − 2 · x + 1 , 3 = 0 – это полные квадратные уравнения; x 2 = 0 , − 5 · x 2 = 0 ; 11 · x 2 + 2 = 0 , − x 2 − 6 · x = 0 – неполные квадратные уравнения.

Решение неполных квадратных уравнений

Заданное выше определение дает возможность выделить следующие виды неполных квадратных уравнений:

• a · x 2 = 0 , такому уравнению соответствуют коэффициенты b = 0 и c = 0 ;
• a · x 2 + c = 0 при b = 0 ;
• a · x 2 + b · x = 0 при c = 0 .

Рассмотрим последовательно решение каждого вида неполного квадратного уравнения.

Решение уравнения a·x 2 =0

Как уже было указано выше, такому уравнению отвечают коэффициенты b и c , равные нулю. Уравнение a · x 2 = 0 возможно преобразовать в равносильное ему уравнение x 2 = 0 , которое мы получим, поделив обе части исходного уравнения на число a , не равное нулю. Очевидный факт, что корень уравнения x 2 = 0 это нуль, поскольку 0 2 = 0 . Иных корней это уравнение не имеет, что объяснимо свойствами степени: для любого числа p , не равного нулю, верно неравенство p 2 > 0 , из чего следует, что при p ≠ 0 равенство p 2 = 0 никогда не будет достигнуто.

Таким образом, для неполного квадратного уравнение a · x 2 = 0 существует единственный корень x = 0 .

Для примера решим неполное квадратное уравнение − 3 · x 2 = 0 . Ему равносильно уравнение x 2 = 0 , его единственным корнем является x = 0 , тогда и исходное уравнение имеет единственный корень — нуль.

Кратко решение оформляется так:

− 3 · x 2 = 0 , x 2 = 0 , x = 0 .

Решение уравнения a · x 2 + c = 0

На очереди — решение неполных квадратных уравнений, где b = 0 , c ≠ 0 , то есть уравнений вида a · x 2 + c = 0 . Преобразуем это уравнение, перенеся слагаемое из одной части уравнения в другую, сменив знак на противоположный и разделив обе части уравнения на число, не равное нулю:

• переносим c в правую часть, что дает уравнение a · x 2 = − c ;
• делим обе части уравнения на a , получаем в итоге x = — c a .

Наши преобразования являются равносильными, соответственно полученное уравнение также равносильно исходному, и этот факт дает возможность делать вывод о корнях уравнения. От того, каковы значения a и c зависит значение выражения — c a : оно может иметь знак минус (допустим, если a = 1 и c = 2 , тогда — c a = — 2 1 = — 2 ) или знак плюс (например, если a = − 2 и c = 6 , то — c a = — 6 — 2 = 3 ); оно не равно нулю, поскольку c ≠ 0 . Подробнее остановимся на ситуациях, когда — c a 0 и — c a > 0 .

В случае, когда — c a 0 , уравнение x 2 = — c a не будет иметь корней. Утверждая это, мы опираемся на то, что квадратом любого числа является число неотрицательное. Из сказанного следует, что при — c a 0 ни для какого числа p равенство p 2 = — c a не может быть верным.

Все иначе, когда — c a > 0 : вспомним о квадратном корне, и станет очевидно, что корнем уравнения x 2 = — c a будет число — c a , поскольку — c a 2 = — c a . Нетрудно понять, что число — — c a — также корень уравнения x 2 = — c a : действительно, — — c a 2 = — c a .

Прочих корней уравнение не будет иметь. Мы можем это продемонстрировать, используя метод от противного. Для начала зададим обозначения найденных выше корней как _{x 1} и _{− x 1} . Выскажем предположение, что уравнение x 2 = — c a имеет также корень x 2 , который отличается от корней _{x 1} и _{− x 1} . Мы знаем, что, подставив в уравнение вместо x его корни, преобразуем уравнение в справедливое числовое равенство.

Для _{x 1} и _{− x 1} запишем: x 1 2 = — c a , а для x 2 — x 2 2 = — c a . Опираясь на свойства числовых равенств, почленно вычтем одно верное равенство из другого, что даст нам: x 1 2 − x 2 2 = 0 . Используем свойства действий с числами, чтобы переписать последнее равенство как ( x 1 − x 2 ) · ( x 1 + x 2 ) = 0 . Известно, что произведение двух чисел есть нуль тогда и только тогда, когда хотя бы одно из чисел является нулем. Из сказанного следует, что x 1 − x 2 = 0 и/или x 1 + x 2 = 0 , что то же самое, x 2 = x 1 и/или x 2 = − x 1 . Возникло очевидное противоречие, ведь вначале было условлено, что корень уравнения x 2 отличается от _{x 1} и _{− x 1} . Так, мы доказали, что уравнение не имеет иных корней, кроме x = — c a и x = — — c a .

Резюмируем все рассуждения выше.

Неполное квадратное уравнение a · x 2 + c = 0 равносильно уравнению x 2 = — c a , которое:

• не будет иметь корней при — c a 0 ;
• будет иметь два корня x = — c a и x = — — c a при — c a > 0 .

Приведем примеры решения уравнений a · x 2 + c = 0 .

Задано квадратное уравнение 9 · x 2 + 7 = 0 . Необходимо найти его решение.

Решение

Перенесем свободный член в правую часть уравнения, тогда уравнение примет вид 9 · x 2 = − 7 .
Разделим обе части полученного уравнения на 9 , придем к x 2 = — 7 9 . В правой части мы видим число со знаком минус, что означает: у заданного уравнения нет корней. Тогда и исходное неполное квадратное уравнение 9 · x 2 + 7 = 0 не будет иметь корней.

Ответ: уравнение 9 · x 2 + 7 = 0 не имеет корней.

Необходимо решить уравнение − x 2 + 36 = 0 .

Решение

Перенесем 36 в правую часть: − x 2 = − 36 .
Разделим обе части на − 1 , получим x 2 = 36 . В правой части — положительное число, отсюда можно сделать вывод, что x = 36 или x = — 36 .
Извлечем корень и запишем окончательный итог: неполное квадратное уравнение − x 2 + 36 = 0 имеет два корня x = 6 или x = − 6 .

Ответ: x = 6 или x = − 6 .

Решение уравнения a·x 2 +b·x=0

Разберем третий вид неполных квадратных уравнений, когда c = 0 . Чтобы найти решение неполного квадратного уравнения a · x 2 + b · x = 0 , воспользуемся методом разложения на множители. Разложим на множители многочлен, который находится в левой части уравнения, вынеся за скобки общий множитель x . Этот шаг даст возможность преобразовать исходное неполное квадратное уравнение в равносильное ему x · ( a · x + b ) = 0 . А это уравнение, в свою очередь, равносильно совокупности уравнений x = 0 и a · x + b = 0 . Уравнение a · x + b = 0 линейное, и корень его: x = − b a .

Таким образом, неполное квадратное уравнение a · x 2 + b · x = 0 будет иметь два корня x = 0 и x = − b a .

Закрепим материал примером.

Необходимо найти решение уравнения 2 3 · x 2 — 2 2 7 · x = 0 .

Решение

Вынесем x за скобки и получим уравнение x · 2 3 · x — 2 2 7 = 0 . Это уравнение равносильно уравнениям x = 0 и 2 3 · x — 2 2 7 = 0 . Теперь следует решить полученное линейное уравнение: 2 3 · x = 2 2 7 , x = 2 2 7 2 3 .

Далее осуществим деление смешанного числа на обыкновенную дробь и определяем, что x = 3 3 7 . Таким образом, корни исходного уравнения это: x = 0 и x = 3 3 7 .

Кратко решение уравнения запишем так:

2 3 · x 2 — 2 2 7 · x = 0 x · 2 3 · x — 2 2 7 = 0

x = 0 или 2 3 · x — 2 2 7 = 0

x = 0 или x = 3 3 7

Ответ: x = 0 , x = 3 3 7 .

Дискриминант, формула корней квадратного уравнения

Для нахождения решения квадратных уравнений существует формула корней:

x = — b ± D 2 · a , где D = b 2 − 4 · a · c – так называемый дискриминант квадратного уравнения.

Запись x = — b ± D 2 · a по сути означает, что x 1 = — b + D 2 · a , x 2 = — b — D 2 · a .

Нелишним будет понимать, как была выведена указанная формула и каким образом ее применять.

Вывод формулы корней квадратного уравнения

Пускай перед нами стоит задача решить квадратное уравнение a · x 2 + b · x + c = 0 . Осуществим ряд равносильных преобразований:

• разделим обе части уравнения на число a, отличное от нуля, получим приведенное квадратное уравнение: x 2 + b a · x + c a = 0 ;
• выделим полный квадрат в левой части получившегося уравнения:
  x 2 + b a · x + c a = x 2 + 2 · b 2 · a · x + b 2 · a 2 — b 2 · a 2 + c a = = x + b 2 · a 2 — b 2 · a 2 + c a
  После этого уравнения примет вид: x + b 2 · a 2 — b 2 · a 2 + c a = 0 ;
• теперь возможно сделать перенос двух последних слагаемых в правую часть, сменив знак на противоположный, после чего получаем: x + b 2 · a 2 = b 2 · a 2 — c a ;
• наконец, преобразуем выражение, записанное в правой части последнего равенства:
  b 2 · a 2 — c a = b 2 4 · a 2 — c a = b 2 4 · a 2 — 4 · a · c 4 · a 2 = b 2 — 4 · a · c 4 · a 2 .

Таким образом, мы пришли к уравнению x + b 2 · a 2 = b 2 — 4 · a · c 4 · a 2 , равносильному исходному уравнению a · x 2 + b · x + c = 0 .

Решение подобных уравнений мы разбирали в предыдущих пунктах (решение неполных квадратных уравнений). Уже полученный опыт дает возможность сделать вывод касательно корней уравнения x + b 2 · a 2 = b 2 — 4 · a · c 4 · a 2 :

• при b 2 — 4 · a · c 4 · a 2 0 уравнение не имеет действительных решений;
• при b 2 — 4 · a · c 4 · a 2 = 0 уравнение имеет вид x + b 2 · a 2 = 0 , тогда x + b 2 · a = 0 .

Отсюда очевиден единственный корень x = — b 2 · a ;

• при b 2 — 4 · a · c 4 · a 2 > 0 верным будет: x + b 2 · a = b 2 — 4 · a · c 4 · a 2 или x = b 2 · a — b 2 — 4 · a · c 4 · a 2 , что то же самое, что x + — b 2 · a = b 2 — 4 · a · c 4 · a 2 или x = — b 2 · a — b 2 — 4 · a · c 4 · a 2 , т.е. уравнение имеет два корня.

Возможно сделать вывод, что наличие или отсутствие корней уравнения x + b 2 · a 2 = b 2 — 4 · a · c 4 · a 2 (а значит и исходного уравнения) зависит от знака выражения b 2 — 4 · a · c 4 · a 2 , записанного в правой части. А знак этого выражения задается знаком числителя, (знаменатель 4 · a 2 всегда будет положителен), то есть, знаком выражения b 2 − 4 · a · c . Этому выражению b 2 − 4 · a · c дано название — дискриминант квадратного уравнения и определена в качестве его обозначения буква D . Здесь можно записать суть дискриминанта – по его значению и знаку делают вывод, будет ли квадратное уравнение иметь действительные корни, и, если будет, то каково количество корней — один или два.

Вернемся к уравнению x + b 2 · a 2 = b 2 — 4 · a · c 4 · a 2 . Перепишем его, используя обозначение дискриминанта: x + b 2 · a 2 = D 4 · a 2 .

Вновь сформулируем выводы:

• при D 0 уравнение не имеет действительных корней;
• при D = 0 уравнение имеет единственный корень x = — b 2 · a ;
• при D > 0 уравнение имеет два корня: x = — b 2 · a + D 4 · a 2 или x = — b 2 · a — D 4 · a 2 . Эти корни на основе свойства радикалов возможно записать в виде: x = — b 2 · a + D 2 · a или — b 2 · a — D 2 · a . А, когда раскроем модули и приведем дроби к общему знаменателю, получим: x = — b + D 2 · a , x = — b — D 2 · a .

Так, результатом наших рассуждений стало выведение формулы корней квадратного уравнения:

x = — b + D 2 · a , x = — b — D 2 · a , дискриминант D вычисляется по формуле D = b 2 − 4 · a · c .

Данные формулы дают возможность при дискриминанте больше нуля определить оба действительных корня. Когда дискриминант равен нулю, применение обеих формул даст один и тот же корень, как единственное решение квадратного уравнения. В случае, когда дискриминант отрицателен, попытавшись использовать формулу корня квадратного уравнения, мы столкнемся с необходимостью извлечь квадратный корень из отрицательного числа, что выведет нас за рамки действительных чисел. При отрицательном дискриминанте у квадратного уравнения не будет действительных корней, но возможна пара комплексно сопряженных корней, определяемых теми же полученными нами формулами корней.

Алгоритм решения квадратных уравнений по формулам корней

Решить квадратное уравнение возможно, сразу задействуя формулу корней, но в основном так поступают при необходимости найти комплексные корни.

В основной же массе случаев обычно подразумевается поиск не комплексных, а действительных корней квадратного уравнения. Тогда оптимально перед тем, как использовать формулы корней квадратного уравнения, сначала определить дискриминант и удостовериться, что он не является отрицательным (в ином случае сделаем вывод, что у уравнения нет действительных корней), а после приступить к вычислению значения корней.

Рассуждения выше дают возможность сформулировать алгоритм решения квадратного уравнения.

Чтобы решить квадратное уравнение a · x 2 + b · x + c = 0 , необходимо:

• по формуле D = b 2 − 4 · a · c найти значение дискриминанта;
• при D 0 сделать вывод об отсутствии у квадратного уравнения действительных корней;
• при D = 0 найти единственный корень уравнения по формуле x = — b 2 · a ;
• при D > 0 определить два действительных корня квадратного уравнения по формуле x = — b ± D 2 · a .

Отметим, что, когда дискриминант есть нуль, можно использовать формулу x = — b ± D 2 · a , она даст тот же результат, что и формула x = — b 2 · a .

Примеры решения квадратных уравнений

Приведем решение примеров при различных значениях дискриминанта.

Необходимо найти корни уравнения x 2 + 2 · x − 6 = 0 .

Решение

Запишем числовые коэффициенты квадратного уравнения: a = 1 , b = 2 и c = − 6 . Далее действуем по алгоритму, т.е. приступим к вычислению дискриминанта, для чего подставим коэффициенты a , b и c в формулу дискриминанта: D = b 2 − 4 · a · c = 2 2 − 4 · 1 · ( − 6 ) = 4 + 24 = 28 .

Итак, мы получили D > 0 , а это означает, что исходное уравнение будет иметь два действительных корня.
Для их нахождения используем формулу корня x = — b ± D 2 · a и, подставив соответствующие значения, получим: x = — 2 ± 28 2 · 1 . Упростим полученное выражение, вынеся множитель за знак корня с последующим сокращением дроби:

x = — 2 + 2 · 7 2 или x = — 2 — 2 · 7 2

x = — 1 + 7 или x = — 1 — 7

Ответ: x = — 1 + 7 ​​​​​​, x = — 1 — 7 .

Необходимо решить квадратное уравнение − 4 · x 2 + 28 · x − 49 = 0 .

Решение

Определим дискриминант: D = 28 2 − 4 · ( − 4 ) · ( − 49 ) = 784 − 784 = 0 . При таком значении дискриминанта исходное уравнение будет иметь лишь один корень, определяемый по формуле x = — b 2 · a .

x = — 28 2 · ( — 4 ) x = 3 , 5

Ответ: x = 3 , 5 .

Необходимо решить уравнение 5 · y 2 + 6 · y + 2 = 0

Решение

Числовые коэффициенты этого уравнения будут: a = 5 , b = 6 и c = 2 . Используем эти значения для нахождения дискриминанта: D = b 2 − 4 · a · c = 6 2 − 4 · 5 · 2 = 36 − 40 = − 4 . Вычисленный дискриминант отрицателен, таким образом, исходное квадратное уравнение не имеет действительных корней.

В случае, когда стоит задача указать комплексные корни, применим формулу корней, выполняя действия с комплексными числами:

x = — 6 + 2 · i 10 или x = — 6 — 2 · i 10 ,

x = — 3 5 + 1 5 · i или x = — 3 5 — 1 5 · i .

Ответ: действительные корни отсутствуют; комплексные корни следующие: — 3 5 + 1 5 · i , — 3 5 — 1 5 · i .

В школьной программе стандартно нет требования искать комплексные корни, поэтому, если в ходе решения дискриминант определен как отрицательный, сразу записывается ответ, что действительных корней нет.

Формула корней для четных вторых коэффициентов

Формула корней x = — b ± D 2 · a ( D = b 2 − 4 · a · c ) дает возможность получить еще одну формулу, более компактную, позволяющую находить решения квадратных уравнений с четным коэффициентом при x (либо с коэффициентом вида 2 · n , к примеру, 2 · 3 или 14 · ln 5 = 2 · 7 · ln 5 ). Покажем, как выводится эта формула.

Пусть перед нами стоит задача найти решение квадратного уравнения a · x 2 + 2 · n · x + c = 0 . Действуем по алгоритму: определяем дискриминант D = ( 2 · n ) 2 − 4 · a · c = 4 · n 2 − 4 · a · c = 4 · ( n 2 − a · c ) , а затем используем формулу корней:

x = — 2 · n ± D 2 · a , x = — 2 · n ± 4 · n 2 — a · c 2 · a , x = — 2 · n ± 2 n 2 — a · c 2 · a , x = — n ± n 2 — a · c a .

Пусть выражение n 2 − a · c будет обозначено как D 1 (иногда его обозначают D ‘ ). Тогда формула корней рассматриваемого квадратного уравнения со вторым коэффициентом 2 · n примет вид:

x = — n ± D 1 a , где D 1 = n 2 − a · c .

Легко увидеть, что что D = 4 · D 1 , или D 1 = D 4 . Иначе говоря, D 1 – это четверть дискриминанта. Очевидно, что знак D 1 такой же, как знак D , а значит знак D 1 также может служить индикатором наличия или отсутствия корней квадратного уравнения.

Таким образом, чтобы найти решение квадратного уравнения со вторым коэффициентом 2 · n , необходимо:

• найти D 1 = n 2 − a · c ;
• при D 1 0 сделать вывод, что действительных корней нет;
• при D 1 = 0 определить единственный корень уравнения по формуле x = — n a ;
• при D 1 > 0 определить два действительных корня по формуле x = — n ± D 1 a .

Необходимо решить квадратное уравнение 5 · x 2 − 6 · x − 32 = 0 .

Решение

Второй коэффициент заданного уравнения можем представить как 2 · ( − 3 ) . Тогда перепишем заданное квадратное уравнение как 5 · x 2 + 2 · ( − 3 ) · x − 32 = 0 , где a = 5 , n = − 3 и c = − 32 .

Вычислим четвертую часть дискриминанта: D 1 = n 2 − a · c = ( − 3 ) 2 − 5 · ( − 32 ) = 9 + 160 = 169 . Полученное значение положительно, это означает, что уравнение имеет два действительных корня. Определим их по соответствующей формуле корней:

x = — n ± D 1 a , x = — — 3 ± 169 5 , x = 3 ± 13 5 ,

x = 3 + 13 5 или x = 3 — 13 5

x = 3 1 5 или x = — 2

Возможно было бы произвести вычисления и по обычной формуле корней квадратного уравнения, но в таком случае решение было бы более громоздким.

Ответ: x = 3 1 5 или x = — 2 .

Упрощение вида квадратных уравнений

Иногда существует возможность оптимизировать вид исходного уравнения, что позволит упростить процесс вычисления корней.

К примеру, квадратное уравнение 12 · x 2 − 4 · x − 7 = 0 явно удобнее для решения, чем 1200 · x 2 − 400 · x − 700 = 0 .

Чаще упрощение вида квадратного уравнения производится действиями умножения или деления его обеих частей на некое число. К примеру, выше мы показали упрощенную запись уравнения 1200 · x 2 − 400 · x − 700 = 0 , полученную делением обеих его частей на 100 .

Такое преобразование возможно, когда коэффициенты квадратного уравнения не являются взаимно простыми числами. Тогда обычно осуществляют деление обеих частей уравнения на наибольший общий делитель абсолютных величин его коэффициентов.

Как пример используем квадратное уравнение 12 · x 2 − 42 · x + 48 = 0 . Определим НОД абсолютных величин его коэффициентов: НОД ( 12 , 42 , 48 ) = НОД(НОД ( 12 , 42 ) , 48 ) = НОД ( 6 , 48 ) = 6 . Произведем деление обеих частей исходного квадратного уравнения на 6 и получим равносильное ему квадратное уравнение 2 · x 2 − 7 · x + 8 = 0 .

Умножением обеих частей квадратного уравнения обычно избавляются от дробных коэффициентов. При этом умножают на наименьшее общее кратное знаменателей его коэффициентов. К примеру, если каждую часть квадратного уравнения 1 6 · x 2 + 2 3 · x — 3 = 0 перемножить с НОК ( 6 , 3 , 1 ) = 6 , то оно станет записано в более простом виде x 2 + 4 · x − 18 = 0 .

Напоследок отметим, что почти всегда избавляются от минуса при первом коэффициенте квадратного уравнения, изменяя знаки каждого члена уравнения, что достигается путем умножения (или деления) обеих частей на − 1 . К примеру, от квадратного уравнения − 2 · x 2 − 3 · x + 7 = 0 можно перейти к упрощенной его версии 2 · x 2 + 3 · x − 7 = 0 .

Связь между корнями и коэффициентами

Уже известная нам формула корней квадратных уравнений x = — b ± D 2 · a выражает корни уравнения через его числовые коэффициенты. Опираясь на данную формулу, мы имеем возможность задать другие зависимости между корнями и коэффициентами.

Самыми известными и применимыми являются формулы теоремы Виета:

x 1 + x 2 = — b a и x 2 = c a .

В частности, для приведенного квадратного уравнения сумма корней есть второй коэффициент с противоположным знаком, а произведение корней равно свободному члену. К примеру, по виду квадратного уравнения 3 · x 2 − 7 · x + 22 = 0 возможно сразу определить, что сумма его корней равна 7 3 , а произведение корней — 22 3 .

Также можно найти ряд прочих связей между корнями и коэффициентами квадратного уравнения. Например, сумма квадратов корней квадратного уравнения может быть выражена через коэффициенты:

x 1 2 + x 2 2 = ( x 1 + x 2 ) 2 — 2 · x 1 · x 2 = — b a 2 — 2 · c a = b 2 a 2 — 2 · c a = b 2 — 2 · a · c a 2 .

Квадратные уравнения (8 класс)

Уравнение называют квадратным, если его можно записать в виде (ax^2+bx+c=0), где (x) неизвестная, (a), (b) и (с) коэффициенты (то есть, некоторые числа, причем (a≠0)).

В первом примере (a=3), (b=-26), (c=5). В двух других (a),(b) и (c) не выражены явно. Но если эти уравнения преобразовать к виду (ax^2+bx+c=0), они обязательно появятся.

Коэффициент (a) называют первым или старшим коэффициентом, (b) – вторым коэффициентом, (c) – свободным членом уравнения.

Виды квадратных уравнений

Если в квадратном уравнении присутствуют все три его члена, его называют полным. В ином случае уравнение называется неполным.

Как решать квадратные уравнения

В данной статье мы рассмотрим вопрос решения полных квадратных уравнений. Про решение неполных — смотрите здесь .

Итак, стандартный алгоритм решения полного квадратного уравнения:

Преобразовать уравнение к виду (ax^2+bx+c=0).

Выписать значения коэффициентов (a), (b) и (c).
Пока не отработали решение квадратных уравнений до автоматизма, не пропускайте этот этап! Особенно обратите внимание, что знак перед членом берется в коэффициент. То есть, для уравнения (2x^2-3x+5=0), коэффициент (b=-3), а не (3).

Вычислить значение дискриминанта по формуле (D=b^2-4ac).

Решите квадратное уравнение (2x(1+x)=3(x+5))
Решение:

Теперь переносим все слагаемые влево, меняя знак.

Уравнение приняло нужный нам вид. Выпишем коэффициенты.

Найдем дискриминант по формуле (D=b^2-4ac).

Найдем корни уравнения по формулам (x_1=frac<-b + sqrt><2a>) и (x_2=frac<-b — sqrt><2a>).

Решите квадратное уравнение (x^2+9=6x)
Решение:

Тождественными преобразованиями приведем уравнение к виду (ax^2+bx+c=0).

Найдем дискриминант по формуле (D=b^2-4ac).

Найдем корни уравнения по формулам (x_1=frac<-b + sqrt><2a>) и (x_1=frac<-b — sqrt><2a>).

В обоих корнях получилось одинаковое значение. Нет смысла писать его в ответ два раза.

Решите квадратное уравнение (3x^2+x+2=0)
Решение:

Уравнение сразу дано в виде (ax^2+bx+c=0), преобразования не нужны. Выписываем коэффициенты.

Найдем дискриминант по формуле (D=b^2-4ac).

Найдем корни уравнения по формулам (x_1=frac<-b + sqrt><2a>) и (x_1=frac<-b — sqrt><2a>).

Оба корня невычислимы, так как арифметический квадратный корень из отрицательного числа не извлекается.

Обратите внимание, в первом уравнении у нас два корня, во втором – один, а в третьем – вообще нет корней. Это связано со знаком дискриминанта (подробнее смотри тут ).

Также многие квадратные уравнения могут быть решены с помощью обратной теоремы Виета . Это быстрее, но требует определенного навыка.

Пример. Решить уравнение (x^2-7x+6=0).
Решение: Согласно обратной теореме Виета, корнями уравнения будут такие числа, которые в произведении дадут (6), а в сумме (7). Простым подбором получаем, что эти числа: (1) и (6). Это и есть наши корни (можете проверить решением через дискриминант).
Ответ: (x_1=1), (x_2=6).

Данную теорему удобно использовать с приведенными квадратными уравнениями, имеющими целые коэффициенты (b) и (c).

О квадратных уравнениях в правильном порядке

Как вам преподавали квадратные уравнения в школе? Это был 7-8 класс, примерно. Вероятнее всего, вам рассказали что есть формулы корней через дискриминант, что направление ветвей зависит от старшего коэффициента. Через пару занятий дали теорему Виета. Счастливчикам еще рассказали про метод переброски. И на этом решили отпустить.

Вы довольны такой базой? Вам не рассказали ни геометрический смысл, ни как это получить.

Спустя некоторое время обдумывания сей несправедливости, я решил написать эту статью и тем самым закрыть гештальт о фрагментарности знаний.

Вы не найдете здесь ничего нового по факту, но, возможно, это даст посмотреть на такое простое понятие с другой стороны.

Начнем с конца

Когда я перечислял темы, касающиеся квадратных уравнений, я делал это примерно в том же порядке, в котором изучают их в школе. Но такой порядок не оправдан с точки зрения обучения, и вот почему:

• Дискриминант дается просто как данность (за редким исключением, когда показывают вывод этих формул через приведение к полному квадрату)

• Мощнейшая по своей сути теорема Виета дается в конце и только как эвристический способ решения

Гораздо проще начать с теоремы Виета.

Рассмотрим квадратный трехчлен

В силу основной теоремы алгебры (примем её как данность, так как её действительно тяжело доказать), мы знаем, что у этого уравнения должно быть два корня. Допустим, что это некоторые числа . Тогда можно переписать изначальное уравнение как выражение его корней:

Оба эти уравнения эквиваленты, так как они оба зануляются в (первое по определению , второе по построению).

Раскрывая скобки, мы получим следующее:

Откуда приравняв соответствующие коэффициенты с имеющимися, получим знаменитую систему:

Мы только что доказали теорему Виета на случай квадратного трехчлена. Это потрясающий результат: мы начинаем получать некоторую информацию о корнях, которые, как мы предположили, существуют. И этот результат мы будем использовать далее.

Геометрия параболы

Вершина

Здесь можно было бы рассказать весь первый курс алгебры университета: о фокусах, директрисах, о конических сечениях, первой и второй производной…

Но раз мы ограничились школьной программой (7-8 класс, если быть точным), то и рассуждения у нас будут простые.

Самая, на мой субъективный взгляд, интересная точка параболы – это её вершина. Она уникальным образом задает положение параболе и дает понимание о том, как устроены корни.

Но формулу для нее мы не знаем, до первых понятий о производной нам еще 3 года в среднем. Будем выкручиваться.

Парабола – симметричная фигура. До того момента, как мы сдвинули ее относительно оси , ось служит для нее осью симметрии. Когда же мы начинаем ее сдвигать, становится видно, что она продолжает быть симметричной, но уже относительно оси, проходящей через вершину.

Тогда от вершины в обе стороны до корней равные расстояния, а это значит, что вершина параболы лежит ровно между корнями. Тогда координата вершины это среднее между ее корнями

Пока что мы не знаем наши корни. Но благодаря теореме Виета мы знаем, чему равна сумма корней!

Потрясающий результат, который нам пригодится далее.

Ещё немного про корни

Мы знаем, что корни, графически, это те точки, в которых кривая пересекает ось . Очень полезное знание, учитывая, что смотря на параболу, исключительно визуально, мы понимаем что у нас может быть 3 случая:

1. Корней нет, при этом

   1. Либо значение в вершине больше нуля и старший коэффициент больше нуля

   2. Либо значение в вершине меньше нуля и старший коэффициент меньше нуля

2. Корень один, но кратности 2 (не забываем основную теорему алгебры), и значение в вершине равно нулю

3. Корня два

Второй случай тривиален, до третьего мы еще дойдем. Интересно математически взглянуть на первый. Найдем значение квадратного трехчлена в вершине:

И теперь все же рассмотрим первый случай: парабола висит над осью ветвями вверх.

Домножим первое неравенство на . Учитывая, что , знак неравенства сменится на противоположный:

Это условие, при котором корней нет.

Рассмотрим вкратце противоположный случай: парабола висит под осью ветвями вниз.

Какая-то магия. Получается, что это условие инвариантно относительно положения параболы. Но тем оно лучше.

На данном этапе прошу заметить, что это только условие отсутствия действительных корней. Да, это похоже на дискриминант, но давайте представим, что вы этого не знаете.

Понятие дискриминанта

Мы уже многое поняли о корнях: в какой они связи с коэффициентами, когда они не существуют, каким образом они лежат относительно вершины. Все это безумно полезно, но это все до сих пор не способ найти значения алгебраически.

Давайте будем отталкиваться от того, что мы уже знаем: от вершины. Если бы мы каким-то образом знали расстояние между корнями, то могли бы однозначно найти и сами корни.

Таки что мешает нам это сделать? Но как настоящие математики, давайте находить квадрат расстояния между корнями. Не теряя общности, будем считать, что – больший корень. Тогда

Пока что выглядит не очень, но на что-то это очень сильно похоже. Не видите? Давайте выделим полный квадрат, но по сумме, а не по разности: добавим , но чтобы все осталось в точности так же, это же и вычтем.

Все еще не видите? Воспользуемся снова теоремой Виета:

Мы получили квадрат расстояния между корнями с учетом растяжения коэффициентом .

Так мы теперь можем найти корни! Вершина параболы да половину расстояния между корнями в обе стороны:

Или, немного преобразовав

Квадрат расстояния между корнями квадратного трехчлена и есть дискриминант.

В общем случае, дискриминант — более сложное понятие, связанное с кратными корнями. Но для квадратного уравнения в 7 классе этого достаточно.

Теперь, если рассуждать о дискриминанте как о расстоянии, становится логично и понятно, почему если он равен нулю, то корень всего один; а если отрицательный, то действительных корней вообще нет.

Заключение

Заметьте, что единственное, что мы предположили, что корня два и они существуют. Единственное, что приняли на веру, это основную теорему алгебры. До всего остального мы дошли исключительно умозрительными заключениями и простейшей алгеброй.

Как по мне, это именно то, как должны преподавать эту тему в школе.

Квадратное уравнение — это уравнение вида ax² + bx + c, где a, b, c — некоторые числа (причём обязательно a ≠ 0),

В таком уравнении:

• x — переменная, которая присутствует в таком уравнении во второй степени,
• a — первый коэффициент,
• b — второй коэффициент,
• c — свободный член.

Ещё такое уравнение называется квадратный трёхчлен, т.к. самая большая степень в нём квадрат и он состоит из 3 одночленов.

Для решения таких уравнений сначала находится дискриминант по этой формуле:

Если:

• D < 0 <=> корней не существует,
• D = 0 <=> есть один корень,
• D > 0 <=> есть два корня.

Пример: x² – x – 3 = 0; a = 1, b = –1, c = –3, D = (–1)² – 4×1×(–3) = 1 + 12 = 13, D > 0 <=> есть два корня.

Когда уже точно известно, что корни существуют, и известно количество этих корней, можно приступить к их поиску с помощью этой формулы:

Пример: x² – x – 3 = 0; a = 1, b = –1, c = –3, D = 13.

X1,2 = ((–(–1)) ±√13)/(2×1) =>

x1 = (1 + √13)/2 ≈ (1 + 3,60555)/2 ≈ 2,302775

x2 = (1 – √13)/2 ≈ (1 – 3,60555)/2 ≈ -1,302775

Примеры

Пример 1

20x² – 15x – 10 = 0

Лучше сразу выписать так: a = 20, b = – 15, c = – 10.

1. Ищем дискриминант: формула D = b² – 4ac <=> D = (– 15)² – 4 × 20 × (– 10) = 225 + 800 = 1025; D > 0 <=> значит есть два корня.

2. Ищем эти корни: формула корней

2.1. Разбиваем формулу на две части, первый корень:

Уравнение 20x² – 15x – 10 = 0, где a = 20, b = – 15, c = – 10; D =1025.

x1 = ((–(–15)) + √ 1025)/(2×20) = (15 + 32,0156) / 40 ≈ 1,17539

2.2. Второй корень:

Уравнение 20x² – 15x – 10 = 0, где a = 20, b = – 15, c = – 10; D =1025.

x2 = ((–(–15)) – √ 1025)/(2×20) ≈ (15 – 32,0156) / 40 ≈ -0,42539

Пример 2

–x² +6x + 18 = 0

a = –1, b = 6, c = 18

Дискриминант D = b² – 4ac

D = 6² – 4×(–1)×(18) = 36 + 72 = 108, D > 0 <=> есть два корня

Ищем корни:

a = –1, b = 6, c = 18, D = 108

X1,2 = ((–6) ±√108)/(2×(–1)) =>

x1 = ((–6) +√108)/(–2) = ((–6) + 10,3923)/(–2) = – 2,19615

x2 = ((–6) –√108)/(–2) = ((–6) – 10,3923)/(–2) = 8,19615

Как разложить квадратный трёхчлен на множители?

Продолжим с примером уравнения 20x² – 15x – 10 = 0

Мы уже нашли корни

x1 ≈ 1,17539, x2 ≈ -0,42539

Выносим коэффициент x² за скобки, и оба корня ставятся с противоположными знаками таким образом:

20x² – 15x – 10 = 20 (x – 1,17539) (x+0,42539)

Хотите проверить? Открываем скобки и проверяем

20 (x – 1,17539) (x+0,42539) = 20 (x²–1,17539x + 0,42539x–0,42539×1,17539) = 20 (x²–0,75x – 0,4999991521) =

20 x²–15x–9,999983042

Погрешность в 0,000016958 должна быть из-за округления в предыдущих расчётах.

Виды квадратных уравнений

Полное и неполное квадратное уравнение

В полном уравнении присутствуют все три его члена (ax² + bx + c = 0). В противном случае уравнение неполное, например:

–x² – 9 = 0 (отсутствует bx)

x² + 16x = 0 (отсутствует с)

–5x² = 0 (отсутствуют bx и с)

Т.е. это когда коэффициент с = 0 или b = 0 (или оба одновременно равны нулю). Внимание: о том, что «a» может быть равно нулю, не говорится, т.к. таким образом уравнение станет линейным (ax + b = 0).

Как решать неполное квадратное уравнение?

Способ решения, когда b=0

5x² – 5 = 0

5x² = 5, делим всё на 5

x² = 1

x = ± √1 ⇔ x = 1 или x = –1

Первый способ решения, когда c=0 (это быстрый метод)

Пример:

x² + 16x = 0 (выносим x за скобки)

x (x + 16) = 0, таким образом, либо x = 0, либо то, что в скобках, равно нулю,

x = 0 или (x + 16)= 0

(x + 16)= 0 ⇔ x = – 16

Второй способ решения, когда c=0

Неполное уравнение (c=0, b=0 или когда оба равны нулю) можно решить по той же системе, как и полное, правильно выписав коэффициенты (но это долго и нерационально).

Например:

x² + 16x = 0

a = 1, b = 16, c = 0 (здесь отсутствует c, значит он равен нулю)

Дискриминант: D = b² – 4ac = 16² – 4×1×0 = 16² = 256 >0, есть два корня.

Ищем корни X1,2 = ((–b) ±√D)/(2×(a)) =>

X1,2 = ((–16) ± √256)/(2×(1)) =>

x1 = ((–16) + √256)/(2×(1)) = ((–16) + 16)/2 = 0

x2 = ((–16) – √256)/(2×(1)) = ((–16) – 16)/2 = –32/2 = – 16

Способ решения, когда b=0 и c=0

Например:

3x² = 0

Делим всё на 3

x² = 0

x = 0

Приведённое квадратное уравнение

Чтобы получить приведённое квадратное уравнение, нужно лишь разделить обе части уравнения на a:

x² + px + q = 0, где:

p = b/a

q = c/a

Примеры:

3x² – 6x = 0 (делим всё на 3) ⇔ x² – (6/3)x = 0 ⇔ x² – 2x = 0 (неполное приведённое)

2x² – 4x – 2 = 0 (делим всё на 2) ⇔ x² – (4/2)x – (2/2) = 0 ⇔ x² – 2x – 1 = 0 (полное приведённое)

Геометрический смысл решения корней квадратных уравнений

Корни квадратного уравнения ещё являются и нулями функции, т.е. если вы ищете нули функции (в каких точках функция пересекает ось Ox), то вы их найдёте именно через этот процесс: поймёте, если они существуют, рассчитав дискриминант, затем найдёте их, используя формулу корней.

Вспомним наш пример уравнения 20x² – 15x – 10 = 0.

Узнайте также, что такое Теорема Виета и Парабола.