Как пишется неевший

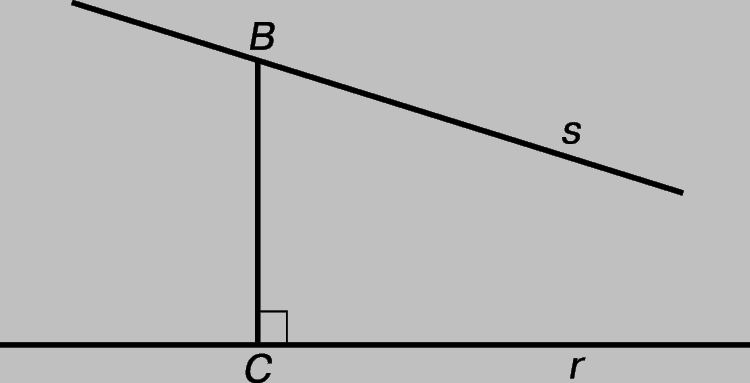
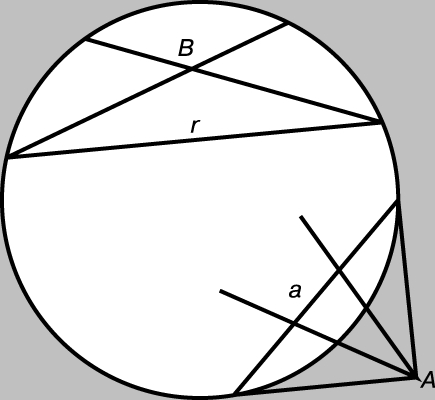
НЕЕВКЛИДОВА ГЕОМЕТРИЯ — геометрия, сходная с геометрией Евклида в том, что в ней определено движение фигур, но отличающаяся от евклидовой геометрии тем, что один из пяти ее постулатов (второй или пятый) заменен его отрицанием. Отрицание одного из евклидовых постулатов (1825) явилось значительным событием в истории мысли, ибо послужило первым шагом на пути к теории относительности. Второй постулат Евклида утверждает, что любой отрезок прямой можно неограниченно продолжить. Евклид, по-видимому, считал, что этот постулат содержит в себе и утверждение, что прямая имеет бесконечную длину. Однако в «эллиптической» геометрии любая прямая конечна и, подобно окружности, замкнута. Пятый постулат утверждает, что если прямая пересекает две данные прямые так, что два внутренних угла по одну сторону от нее в сумме меньше двух прямых углов, то эти две прямые, если продолжить их неограниченно, пересекутся с той стороны, где сумма этих углов меньше суммы двух прямых. Но в «гиперболической» геометрии может существовать прямая CB (рис. 1), перпендикулярная в точке С к заданной прямой r и пересекающая другую прямую s под острым углом в точке B, но, тем не менее бесконечные прямые r и s никогда не пересекутся.

Рис. 1. В ГИПЕРБОЛИЧЕСКОЙ ГЕОМЕТРИИ может существовать прямая CB, перпендикулярная данной прямой r и пересекающая другую данную прямую s под острым углом в точке B так, что бесконечный луч s не пересекает прямую r.

Из этих пересмотренных постулатов следовало, что сумма углов треугольника, равная 180° в евклидовой геометрии, больше 180° в эллиптической геометрии и меньше 180° в гиперболической геометрии.

История. Первым неевклидовым геометром, вероятно, можно считать самого Евклида.

Его нежелание использовать «несамоочевидный» пятый постулат следует хотя бы из того, что свои первые двадцать восемь предложений Евклид доказывает, не прибегая к этому постулату. С первого века до н.э. до 1820 математики пытались вывести пятый постулат из остальных, но преуспели лишь в замене его различными эквивалентными допущениями, такими, как «две параллельные линии всюду равно удалены друг от друга» или «любые три точки, не расположенные на одной прямой, принадлежат окружности». Ближе всех подошел к цели иезуит, логик и математик Дж.Саккери (1667-1733), который начал свои исследования с так называемого четырехугольника Саккери (рис. 2), т.е. с четырехугольника BCED, у которого BC = DE, а углы при вершинах C и E прямые. Заметив, что углы при вершинах B и D обязательно равны, Саккери рассмотрел поочередно три гипотезы: верхние углы четырехугольника тупые, прямые и острые. Он доказал, что любая из этих гипотез, если ее принять для какого-нибудь одного такого четырехугольника, остается в силе для всех таких четырехугольников. Саккери намеревался обосновать гипотезу о том, что верхние углы прямые, доказав, что любая другая гипотеза приводит к противоречию. Вскоре он отверг гипотезу о тупом угле (и тем самым лишил себя возможности открыть эллиптическую геометрию), поскольку, как и все геометры до 1854, рассматривал второй постулат как утверждение о том, что прямая имеет бесконечную длину, и отказываться от этого постулата он не хотел. Точно также Саккери в конце концов отверг и гипотезу об остром угле, но прежде, чем принять это ошибочное решение, он, сам того не ведая, открыл многие теоремы геометрии, получившей впоследствии название гиперболической.

Рис. 2. ЧЕТЫРЕХУГОЛЬНИК САККЕРИ — четырехугольник BCED с BC = ED и прямыми углами при вершинах C и E. Евклидова геометрия требует, чтобы углы B и D также были прямыми. В эллиптической геометрии эти углы — тупые, а в гиперболической — острые.

К. Гаусса (1777-1855) принято считать одним из величайших математиков всех времен. Он первым подошел к проблеме с современной точки зрения, согласно которой геометрию, отрицающую пятый постулат, надлежит развивать ради нее самой, не ожидая, что при этом возникнет какое-то противоречие. Письма Гаусса к друзьям говорят о том, что к 1816 он преодолел традиционный предрассудок относительно неизбежности противоречия и развил «антиевклидову» геометрию, удовлетворяющую гипотезе Саккери об остром угле. Но, опасаясь насмешек, он воздерживался от публикации этих идей и тем самым позволил разделить честь открытия гиперболической геометрии (примерно в 1825) венгру Я. Бойяи (1802-1860) и русскому Н. И. Лобачевскому (1793-1856). Бойяи опубликовал свою работу до того, как услышал о Лобачевском, а последний, судя по всему, так никогда и не узнал об исследованиях Бойяи. В 1854 Б. Риман (1826-1866) заметил, что из неограниченности пространства еще не следует его бесконечная протяженность. Смысл этого утверждения станет яснее, если представить, что в неограниченной, но конечной вселенной астроном в принципе мог бы увидеть в телескоп, обладающий достаточно высокой разрешающей способностью, свой собственный затылок (если отвлечься от небольшой детали, связанной с тем, что свет, отраженный от затылка, достиг бы глаза астронома через тысячи миллионов лет). В своем доказательстве того, что внешний угол при любой вершине треугольника больше внутреннего угла при любой из двух остальных вершин, Евклид неявно использовал бесконечную длину прямой. Из этой теоремы тотчас же следует теорема о том, что сумма любых двух углов треугольника меньше суммы двух прямых углов. Если отказаться от бесконечной длины прямой, то гипотеза Саккери о тупом угле становиться верной и из нее следует, что сумма углов треугольника больше суммы двух прямых. Такое положение дел было давно известно в сферической тригонометрии, где стороны треугольника являются дугами больших кругов. Риман внес эпохальный вклад, распространив представление о конечном, но неограниченном пространстве с двух на три и большее число измерений.

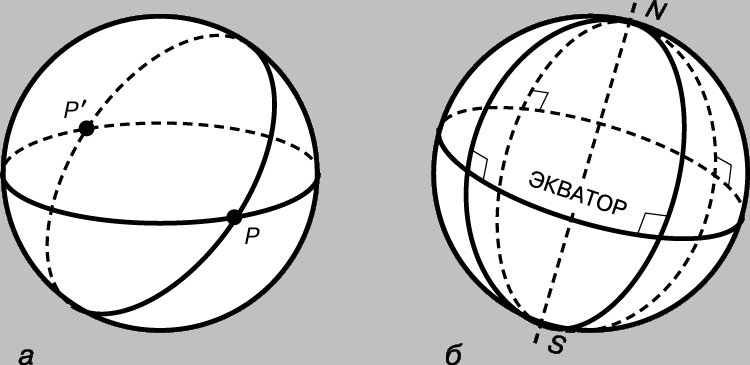
Эллиптическая плоскость. Ф. Клейн (1849-1925) первым увидел, как избавить сферическую геометрию от одного из ее недостатков — того, что две лежащие в одной плоскости «прямые» (два больших круга на сфере) имеют не одну общую точку, а две (рис. 3,а). Так как для каждой точки существует одна-единственная точка-антипод (диаметрально противоположная точка), а для любой фигуры существует ее дубликат из точек-антиподов, мы можем, ничем не жертвуя, но многое приобретая, абстрактно отождествить обе точки такой пары, объединив их в одну. Таким образом можно изменить смысл термина «точка», условившись впредь называть «одной точкой» пару диаметрально противоположных точек. Иначе говоря, точки так называемой «эллиптической» плоскости представлены на единичной сфере парами точек-антиподов или диаметрами, соединяющими точки-антиподы. Вся эллиптическая прямая замкнута, как окружность, но, поскольку каждая из ее точек представлена двумя точками-антиподами на единичной сфере, полная длина эллиптической прямой равна половине длины окружности большого круга, т.е. ее полная длина равна p.

Рис. 3. а — на эллиптической плоскости «точка» представлена двумя точками-антиподами на сфере, например, точками P и P’. б — диаметр, соединяющий северный и южный полюсы сферы, на эллиптической плоскости является «полюсом» экватора.

Такое представление с помощью диаметров и диаметральных плоскостей сферы (при котором диаметр, соединяющий северный и южный полюсы сферы, является «полюсом» экватора), показывает, что все свойства действительной проективной плоскости сохраняются и для эллиптической плоскости.

Геометрия порядка. Один из подходов к построению гиперболической геометрии исходит из некоторых фундаментальных аксиом порядка, справедливых и в евклидовой, но не в эллиптической геометрии. Если считать «точки» исходными понятиями, то запись [[ABC]] означает, что точка B лежит «между» точками A и C (это первичное отношение мы принимаем, не пытаясь его определить). Первые четыре аксиомы порядка утверждают, что 1) существует по крайней мере две точки; 2) если A и B — две различные точки, то существует по крайней мере одна точка C, для которой [[ABC]]; 3) эта точка C отлична от точки A и 4) порядок [[ABC]] влечет за собой [[CBA]], но не [[BCA]]. «Отрезок» AB, по определению, состоит из точек P, для которых [[APB]], а «луч» A/B («исходящий из A в другую сторону, чем B») — из точек Q, для которых [[QAB]]. «Прямая» AB состоит из отрезка AB, точек A, B и двух лучей A/B, B/A. Пятая аксиома утверждает, что если C и D — различные точки на прямой AB, то A лежит на прямой CD (из этой же аксиомы следует, что прямые AB и CD совпадают). Шестая аксиома дает нам точку вне данной прямой, а седьмая, сформулированная М. Пашем (1843-1931), позволяет определить плоскость как множество всех точек, коллинеарных с парами точек на одной или двух сторонах данного треугольника.

Абсолютная геометрия. Большая часть вклада Бойяи связана с теми разделами гиперболической геометрии, которые принадлежат и евклидовой геометрии. Его «абсолютная геометрия» может быть выведена из геометрии порядка, если к последней добавить еще одно фундаментальное отношение, а именно «конгруэнтность». Это отношение определяется пятью аксиомами типа «Если ABC и A’B’C’ — два треугольника, таких, что BC є B’C’, CA є C’A’, AB є A’B’, а D и D’ — еще две точки, такие, что [[BCD]] и [[B’C’D’]] и BD є B’D’, то AD є A’D'». Эти аксиомы служат основой теории длины и позволяют распространить отношение конгруэнтности с пар точек на углы. Определив обычным образом окружность, мы можем рассматривать первые четыре постулата Евклида как теоремы и доказать его первые двадцать восемь предложений, заменив слово «параллельные» на «не пересекающиеся». Однако необходимо тщательно избегать любого обращения к нашему обычному представлению о сумме углов треугольника; например, мы не можем более утверждать, что углы, опирающиеся на один и тот же сегмент окружности, равны, так как доказательство этого предложения зависело бы от суммы углов треугольника. С другой стороны, мы можем доказать, что три высоты остроугольного треугольника пересекаются в одной точке, построить теорию правильных многоугольников и правильных многогранников (с небольшими оговорками). Уточнив понятие параллельности (определив как параллельные лучи, которые просто не пересекаются), мы можем показать, что параллельность — отношение симметричное и транзитивное (т. е. если прямая r параллельна прямой s, то s параллельна r; если r параллельна s, а s параллельна t, то r параллельна t). Множество прямых, параллельных данному лучу, называется «пучком параллельных»; он содержит единственную прямую, проходящую через любую заданную точку. Следуя аналогии с обычным пучком (состоящим из всех прямых, проходящих через точку), мы можем считать, что пучок параллельных определяет «бесконечно удаленную точку», или, по терминологии Д. Гильберта (1862-1943), «конец». Вместо того, чтобы говорить, что два луча (или две прямые) параллельны или что они принадлежат некоторому пучку параллельных M, мы говорим, что два луча имеют общий конец M. Луч, проходящий через точку C и принадлежащий данному пучку параллельных, принято обозначать CM, как если бы это был отрезок; тот же символ CM можно использовать и для обозначения всей прямой. Если BM и CM — параллельные лучи, то фигура MCB называется «асимптотическим треугольником», поскольку она во многом ведет себя, как обычный треугольник. В частности, два асимптотических треугольника конгруэнтны, если у них имеется по конгруэнтной стороне и конгруэнтному углу.

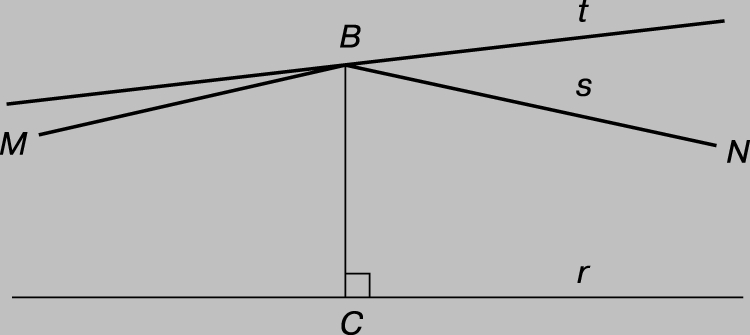
Гиперболическая плоскость. Из абсолютной геометрии Бойяи можно вывести евклидову геометрию, добавив евклидову (или аффинную) аксиому: через точку B, не лежащую на данной прямой r, можно провести не более одной прямой, параллельной данной. Гиперболическую геометрию можно вывести из абсолютной геометрии, добавив гиперболическую аксиому, повторяющую только что приведенную, но без отрицания «не» во втором случае. Таким образом, лучи BM и BN на рис. 4 могут быть оба параллельны r, а если M и N их концы, то r называется «прямой MN». Любая прямая, например t, являющаяся продолжением стороны угла РNBM, образует с r пару «гиперпараллельных», т.е. пару прямых, которые не пересекаются и не параллельны. Две такие прямые имеют единственный общий перпендикуляр. Множество прямых, перпендикулярных данной прямой a, называются «пучком гиперпараллельных» с «осью» a.

Рис. 4. ЛЮБАЯ ПОЛУПРЯМАЯ, например t, являющаяся продолжением стороны угла NBM, образует с r пару «гиперпараллельных», т.е. две прямые, которые не пересекаются и не параллельны.

Отражение относительно BC показывает, что РCBM и РNBC — равные острые углы. Лобачевский назвал каждый из них «углом параллельности» П(a), где a — длина BC. Он показал, что функция П(a) монотонно убывает от p ¤ 2 до 0, когда a возрастает от 0 до беск. Треугольник BMN естественно назвать «дважды асимптотическим треугольником». Два дважды асимптотических треугольника конгруэнтны, если имеют конгруэнтные углы. Если отрезок CB возрастает до тех пор, пока не превратится в луч CL, то BMN превращается в «трижды асимптотический треугольник» LMN, все три вершины которого являются концами (все три стороны такого треугольника бесконечны, а все три угла равны нулю). Все трижды асимптотические треугольники конгруэнтны. Одной из самых прекрасных страниц в литературе по неевклидовой геометрии со времен Лобачевского считается предложенное Г.Либманом доказательство того, что площадь треугольника остается конечной, когда две (или три) его стороны становятся бесконечными. Доказательство сводится к разбиению асимптотического треугольника на бесконечную последовательность конечных треугольников и перекладыванию их с соблюдением одного условия: все они должны умещаться внутри некоторого конечного пятиугольника. Метод Либмана восполняет один из двух недостающих шагов в предложенном Гауссом красивом доказательстве того, что площадь любого треугольника пропорциональна его «угловому дефекту» — величине, показывающей, насколько сумма углов треугольника меньше двух прямых. Аналогия с выражением (A + B + C) — p для площади сферического треугольника (на единичной сфере) наводит на мысль о естественной единице измерения, при которой площадь треугольника ABC просто равна p — (A + B + C). Используя эту единицу, Лобачевский выразил угол параллельности, соответствующий расстоянию x, формулой П(x) = 2arctg e-x.

Кривые, ортогональные обычному пучку прямых, имеют вид концентрических окружностей; кривые, ортогональные пучку параллельных, имеют вид концентрических «орициклов». В действительности орицикл — это предельная форма окружности, центр которой уходит в бесконечность (так, что диаметры окружности становятся параллельными).

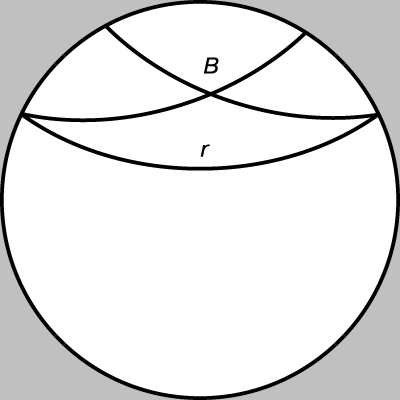
Евклидовы модели неевклидовых геометрий. Ф. Вахтер (1792-1817) за несколько месяцев до безвременной кончины сообщил в письме к Гауссу о своем наблюдении: если пятый постулат Евклида ложен, то сфера, радиус которой стремиться к бесконечности, приближается к предельной поверхности, чья внутренняя геометрия совпадает с геометрией евклидовой плоскости. Тем самым Вахтер предвосхитил появление «орисферы», сыгравшей важную роль в работах Бойяи и Лобачевского. Эта поверхность получается при вращении орицикла вокруг любого из его диаметров. Кривые на орисфере, которые ведут себя, как евклидовы прямые, — орициклы, по которым орисферу пересекают ее диаметральные плоскости. А. Пуанкаре (1854-1912) открыл представление гиперболического пространства с помощью конформной модели, в которой геометрическое место концов имеет вид плоскости W в евклидовом пространстве, а сферам с центрами в W соответствуют плоскости гиперболического пространства. Заменив сферы полусферами, Пуанкаре получил возможность представить все гиперболическое пространство с помощью половины евклидова пространства, а именно всеми точками, лежащими по одну сторону от W. Один пучок концентрических орисфер представлен плоскостями, параллельными W; можно доказать, что евклидовы расстояния в такой плоскости пропорциональны соответствующим геодезическим на орисфере, что полностью согласуется с наблюдением Вахтера. Рассматривая сечение трехмерной модели Пуанкаре плоскостью, перпендикулярной W, мы получим модель аналогичную модели Пуанкаре для гиперболической плоскости. В этой модели геометрическое место концов имеет вид евклидовой прямой. В другой модели геометрическое место концов имеет вид окружности w, а прямые на гиперболической плоскости — дуг окружностей, ортогональных w. Две параллельные дуге r, проходящие через точку B, — просто дуги, проходящие через точку B и касающиеся дуги r в ее концах, как на рис. 5.

Рис. 5. ПАРАЛЛЕЛЬНЫЕ BC и BD к r, проходящие через точку B, — это просто две дуги, проходящие через точку B так, что они касаются r в ее концах. Эта модель «конформна», так как углы сохраняются, хотя расстояния неизбежно искажаются.

Такая модель называется «конформной» потому, что углы сохраняют свою величину, хотя расстояния неизбежно искажаются. Если пойти на искажение углов, то дуги можно заменить хордами, как на рис. 6. Эту более простую модель предложил в 1868 году Э. Бельтрами (1835-1900) для доказательства того, что гиперболическая геометрия так же логически непротиворечива, как и евклидова (хотя и Бойяи и Лобачевский были интуитивно убеждены, что их исследования никогда не приведут к двум противоречащим друг другу утверждениям, ни один из них не дожил до строгого доказательства непротиворечивости гиперболической геометрии). В модели Бельтрами множество прямых, проходящих через точку A, представлено обычным пучком параллельных или гиперпараллельных в зависимости от того, находится ли A внутри w, на w или вне w. В последнем случае (см. нижнюю часть рис. 6) ось пучка гиперпараллельных есть «поляра» точки A, соединяющая точки касания двух касательных, проведенных из точки A. Иначе говоря, две перпендикулярные прямые гиперболической плоскости представлены двумя прямыми, «сопряженными» относительно w. Такого рода идеи относятся к проективной геометрии; действительно, w можно рассматривать как коническое сечение на действительной проективной плоскости; в этом случае мы приходим к модели А.Кэли (1821-1895) и Ф. Клейна. Это коническое сечение w, геометрическое место концов, есть то, что Кэли назвал «абсолютом». (Преисполненный энтузиазмом, он сначала даже писал это слово с прописной буквы «А», но позднее перешел на строчную «а» во избежание упрека в непочтительности). Чтобы быть совершенно точным, следует отметить, что проективная плоскость, на которой работал Кэли, была не действительной, а комплексной: Кэли разрешал w быть коническим сечением, не содержащим действительных точек, отчего геометрия становится не гиперболической, а эллиптической.

Рис. 6. В ЭТОЙ КОНФОРМНОЙ МОДЕЛИ, если мы согласимся, что углы также искажаются, дуги, изображенные на рис. 5, можно заменить их хордами. В нижней части рисунка ось пучка параллельных — «поляра» точки A, соединяющая точки касания двух касательных, проведенных из A.

неевкли́дова геоме́трия, неевкли́довой геоме́трии

не евший

Синонимы:

Морфемный разбор слова:

Однокоренные слова к слову:

Разумеется, в приведённом случае верным будет раздельное написание частицы «не». Слова *неесть не существует в русском языке.

Есть — это глагол. Он может выступать в различных значениях:

1) «есть» — синоним глаголов «кушать», «питаться» или словосочетания «потреблять пищу». В этом случае форма «есть» представляет собой инфинитив.

2) «есть» равносильно глаголу «имеется». Означает наличие, существование чего-то либо в данный момент или же принадлежность, владение предметом, существом или явлением («У меня есть две квартиры»).

3) «есть» служит формой третьего лица единственного числа настоящего времени глагола «быть». Является глаголом-связкой, употребляется в официальном стиле речи (научном или официально-деловом). Например:

В разговорном стиле речи эта связка всегда опускается. Её заменяют на тире.

Независимо от значения, при написании частицы «не» с глаголом «есть» действует правило: «не» с глаголами пиши раздельно. Поэтому при любом значении мы напишем выражение не есть в два слова. Пример:

В школе учили, что Не с глаголами пишется раздельно.

Данное слово является заимствованным, а потому сверяем его правильное написание с орфографическим словарем.

Это слово пишется с одной «л», двумя «м» и безударной гласной «о», то есть:

—килограмм-.

Написание этого словарного слова нужно просто запомнить!

Корректно писать «мезонин». Это слово заимствовано из итальянского языка (mezzanino). Оно обозначает следующее: Надстройка над средней частью жилого дома (обычно небольшого). Например, жить в мезонине.

Это зависит от того, какой частью речи является слово. Заметьте, «насколько» пишется слитно, являясь наречием, в примерах: «Насколько я знаю, он необычайно умен». «На сколько» пишется раздельно тогда, когда это вопросительное слово с предлогом. Пример: «На сколько ее платье короче твоего?».

Слово, о правописании которого задан вопрос, является именем существительным и относится к литературоведческим терминам.

У этого слова есть много определений. Чаще всего, под эл*егией понимают лирическое стихотворение, в котором автор рассказывает о сильных эмоциональных переживаниях, повествование в таком произведении ведется, как правило, от первого лица. Этот термин также используют как название литературного жанра, в котором автор рассуждает о проблемах мироздания с философской точки зрения. Наконец, это стихотворение, написанное определенным размером.

В русский язык термин был позаимствован из немецкого ( Еlеgiе ), куда, очевидно, попал из латинского языка ( elegia ), а в латинский в свою очередь из греческого ( ἐλεγεία ). Несложно заметить, что во всех этих язык буква l и λ одинарные, а не удвоенные. Что получило свое отражение в орфографии данного слова и в русском языке. Правильно пишется элегия.

Слово является словарным, его правописание нужно запомнить, чтобы не делать ошибок.

Источник

Не, ни, не, ни.

Не или ни? Ни или не? Кто только ни задавался этим вопросом, кто (да что уж там, сознаемся!) ни проклинал все на свете, пытаясь вспомнить правило из школьной программы: что же, что именно здесь надо написать, не или ни.

А поскольку ошибки все-таки встречаются, причем и в рекламе, и в журнальных текстах, не говоря уж об Интернете, можно сделать вывод, что вспомнить удается далеко не всегда. Тогда в силу вступает правило, известное всем как «русский авось». Вот исходя из этого правила обычно и выбирают: не или ни.

Итак, ни. Существуют случаи, которые смело можно назвать простыми.

Мы пишем ни, и только ни в устойчивых выражениях (таких, как ни свет ни заря, ни днем ни ночью, ни жив ни мертв, ни рыба ни мясо). Ни с места! Ни шагу назад! Ни один человек не пришел на акцию (то есть никто). Он ни разу мне не позвонил (то есть нисколько). Это запомнить просто.

Но есть и непростые ситуации, куда же без них!

О, это «ни для усиления отрицания». Со школьных времен мы думаем о тебе с содроганием. А напрасно, между прочим. И это можно попробовать запомнить. Итак, в предложениях, где ни используется для усиления отрицания, обычно уже имеется отрицание (нет или не): Нет ни копейки денег. Он не дал мне ни рубля. Иногда отрицание только подразумевается: Ни копеечки (не было) в кармане.

Существует, правда, двойное отрицание с не (ты не мог меня не заметить). Но это двойное отрицание придает предложению смысл утверждения, а вовсе не отрицания! Что такое не мог не заметить? Это значит «заметил». Как сказали бы математики, «минус на минус дает плюс».

Однако вернемся к ни.

Если же речь идет о независимом восклицательном или вопросительном предложении, то пишется не: Кто не восхищался ею! Что он только не передумал!

Ни, и только ни мы напишем в так называемых уступительных придаточных, чтобы усилить утверждение.

Тут будет уместно вспомнить шлягер Аллы Пугачевой: «Я отправлюсь за тобой, что бы путь мне ни пророчил». Да, знаю, сама она поет не пророчил. Но это ошибка, увы. Ни пророчил, и только ни!

Источник

не евший

Смотреть что такое «не евший» в других словарях:

евший — прил., кол во синонимов: 158 • ажлибавший (3) • берлявший (2) • бирлявший (3) • … Словарь синонимов

евший поедом — прил., кол во синонимов: 11 • грызший (45) • евший (158) • плешь грызший (8) • … Словарь синонимов

евший так, что за ушами трещит — прил., кол во синонимов: 1 • евший (158) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов

евший-пивший — прил., кол во синонимов: 1 • евший (158) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов

евший в три горла — прил., кол во синонимов: 4 • обжиравшийся (7) • объедавшийся (15) • переедавший … Словарь синонимов

евший глазами — прил., кол во синонимов: 27 • вперившийся (21) • впившийся (27) • глаза обмозоливший … Словарь синонимов

евший чужой хлеб — прил., кол во синонимов: 7 • был на шее (7) • дармоедничавший (18) • живший з … Словарь синонимов

евший не досыта — прил., кол во синонимов: 1 • недоедавший (6) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов

евший вечером — прил., кол во синонимов: 1 • ужинавший (5) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов

евший до отвала — прил., кол во синонимов: 1 • уплетавший за обе щеки (8) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов

евший икру ложками — прил., кол во синонимов: 3 • жировавший (13) • мажоривший (4) • шиковавший (23) … Словарь синонимов

Источник

«Что нинаесть» или «что ни на есть»?

В русском языке существует группа устойчивых сочетаний слов, правописание которых можно объяснить, но легче просто запомнить. Как правильно написать: «что нинаесть» или «что ни на есть», и на какое правило опираться, если потребуется объяснить выбор?

Как правильно пишется

Данное сочетание пишется в 4 слова: что ни на есть. Это фразеологическое (то есть устойчивое) выражение, где каждое из слов является отдельной частью речи.

Достаточно часто пишут с ошибками: «что нинаесть», «что-нинаесть», «что ни-наесть», «чтони на есть», «чтони наесть». Нужно понимать, что каждое слово, написанное слитно, является отдельным и должно иметь свое лексическое значение. В данном случае стоит задуматься: что означают слова «нинаесть» или «чтони». В русском языке таких слов не существует, и в подобном написании выражение не несет никакого смысла.

Если же разобрать частеречную принадлежность каждого из слов «что ни на есть», то легко можно выделить такую последовательность: «что» – относительное местоимение, «ни» – усилительная частица, «на» – предлог, «есть» – глагол.

Что означает выражение, примеры

Что ни на есть – устойчивое сочетание слов, которое в целом несет свою смысловую нагрузку:

Можно заметить, что практически всегда перед фразеологизмом стоит слово «самый». Подобные выражения используются для выделения какого-либо качества описываемого человека или явления.

Как запомнить написание

Правописание данного сочетания можно подчинить правилу о раздельном написании слов разных частей речи, но не всегда бывает просто их выделить.

Так как выражение относится к фразеологическим, то его написание следует заучить и воспринимать как устоявшееся.

Пишется только так, любое другое написание ошибочно: ЧТО НИ НА ЕСТЬ.

Источник

Правильное написание НЕ и НИ: примеры, правила, разъяснения

Содержание статьи:

Краткий видео-обзор статьи:

В русском языке одними из самых труднозапоминаемых остаются правила правописания «не» и «ни».

Частицы НЕ, НИ в словах, правило их употребления всегда вызывают множество трудностей. И как не запутаться, что и когда писать? В этой статье вам будет предложено на конкретных примерах разобраться с основополагающими моментами и запомнить их.

Чтобы писать грамотно, для начала Вам необходимо хорошо выучить группы слов, которые всегда будут писаться слитно или раздельно с частицей НЕ.

Всегда слитно НЕ пишется с теми словами, которые нельзя употребить без «НЕ».

Например: нехватка (сущ.), невзрачный (прил.), нелепый (прил.), невежда (сущ.), невмоготу (нар.), ненароком (нар.) и другие.

Как видите, эти слова относятся к разным частям речи, и систематизировать как-либо их нельзя. Поэтому их нужно просто запоминать.

Всегда раздельно НЕ пишется:

Отдельное внимание стоит здесь обратить еще на один момент.

Например: недоставать (не хватать), недосыпать (слишком мало спать, не высыпаться), недосмотреть (за ребенком), недоедать (слишком мало есть).

Итак, для того чтобы не ошибиться в постановке правильной частицы в русском языке, необходимо следовать определенному алгоритму.

Частица НЕ с разными частями речи

С существительными и прилагательными

НЕ пишется слитно, если слова без НЕ не употребляются (небрежный, невежда, ненастный и т.п.) или к слову можно подобрать близкое по значению слово – синоним без не.

Примеры: Он говорит неправду (т.е. ложь). Нам предстоит неблизкий (далекий) путь.

НЕ пишется раздельно, если есть противопоставление, выраженное союзом А и нельзя подобрать синоним.

Примеры: Нас постигла не удача, а разочарование. Помещение не большое, а маленькое. К сожалению, я не специалист в этой сфере.

С наречиями

Примеры: Разговаривайте, пожалуйста, негромко (тихо). В этой ситуации я выглядела совершенно нелепо.

Примеры: Мы шли не быстро, а медленно. Ты одета совсем не по-зимнему.

Также НЕ с наречиями пишется раздельно в том случае, когда НЕ употребляется в сочетаниях: вовсе не, ничуть не, совсем не, далеко не, никогда не, отнюдь не, нисколько не.

Примеры: Я чувствую себя совсем не плохо. Он далеко не идеально выполнил эту работу.

С местоимениями

НЕ с местоимениями пишется раздельно.

Примеры: не я, не она, не твой, не сами.

С отрицательными и неопределенными местоимениями (некто, нечто, некого, нечего и т.п.) НЕ пишется слитно. Но если между НЕ и местоимением этих групп есть предлог, то в таком случае НЕ будет писаться раздельно.

Примеры: Некто зашел в комнату и спрятался за занавеской. В сложившейся ситуации мне было не у кого просить помощи. Здесь просто не к чему придраться.

С причастиями

НЕ пишется слитно с причастиями, которые не употребляются без НЕ (ненавидящий, негодующий); причастиями, у которых есть приставка НЕДО- (недооценивавший, недоговоривший и т.п.) и причастиями, у которых нет зависимых слов.

Примеры: Недоумевающий человек выбежал из автобуса со скоростью света. Недолюбливавший кашу, он отодвинул тарелку в сторону. Ненаписанное сочинение не давало мне покоя.

НЕ пишется раздельно с причастиями, у которых есть зависимые слова (т.е. в причастном обороте), со всеми краткими причастиями (не сделана, не прочитана и т.п.) и в предложениях, в которых есть противопоставления с союзами А, НО.

Примеры: Сад наполняли цветы не увядшие, а свежие. В ресторане нам подали овощи не отваренные, а запеченные. Это был спортсмен, не победивший, но участвовавший в соревнованиях. Книга была не прочитана (краткая форма причастия). Отчет, не отправленный начальнику вовремя, будет зафиксирован (зависимое слово: не отправленный кому? – начальнику).

С деепричастиями

НЕ с деепричастиями пишется раздельно. Исключительными являются случаи, когда деепричастие образовано от глагола, который без «НЕ» не употребляется (ненавидя, негодуя и др.).

Примеры: Не отдохнув, он поехал на работу. Ненавидя друг друга, они продолжали совместный проект.

Итак, вы ознакомились с основными правилами написания НЕ с различными частями речи.

По аналогии, давайте рассмотрим особенности правописания с частицей НИ.

Частица НИ с разными частями речи

В остальных же случаях, частица «НИ» пишется раздельно.

Как вы видите, с НИ информации для запоминания в разы меньше. И поэтому теперь, когда усвоено правило НЕ, НИ, слитно или раздельно они пишутся, важно научиться различать случаи, когда необходимо писать частицу НЕ, а когда НИ.

Чем отличаются частицы НЕ и НИ?

Правило написания этих неударяемых частиц зависит, в первую очередь, от их значения. Поэтому рассмотрим разные случаи употребления НЕ, НИ, правило и примеры для более точного понимания.

НЕ, НИ: правило, примеры

Частица «НЕ» используется:

В простых предложениях, если она имеет значение отрицания при глаголе, причастии или деепричастии.

Примеры: Я не хочу читать. Не интересующаяся историей молодежь.

В составном глагольном сказуемом при отрицании частице «НЕ» в первой и второй его части, дает утвердительный смысл.

Примеры: Не могу не сообщить. Не смогу не купить.

В вопросительных и восклицательных предложениях в сочетаниях с местоимениями, наречиями и частицами (только не, как не, чего не, чего только не и т.п.)

Примеры: Кого я только не знаю! Как не порадовать любимого человека?

В придаточной части сложного предложения в сочетании с союзом ПОКА.

Примеры: Стой тут, пока не скажу! Сиди, пока не придут за тобой.

В составе устойчивых сочетаний, которые обозначают предположение (далеко не, ничуть не, отнюдь не, вовсе не, нисколько не) и отрицание (чуть ли не, едва ли не, вряд ли не).

Примеры: Едва ли не каждый был виновен в этом. Им было принято отнюдь не справедливое решение.

В составе сочинительных союзов: не то; не то – не то; не только – но; не то что не – а; не то чтобы не – а.

Примеры: Наверху за потолком кто-то не то стонет, не то смеется (А. П. Чехов). Отдай кольцо и ступай; не то я с тобой сделаю то, чего ты не ожидаешь (А. С. Пушкин).

Частица «НИ» используется:

Для усиления отрицания.

Примеры: Ни кусочка нигде я не могла найти. У нас не было ни одного шанса.

При повторении, приобретая значение союза.

Примеры: Он не мог найти ни книгу, ни тетрадь. Ни он, ни его родители не замечали происходящего.

В придаточных предложениях для усиления утвердительного смысла.

Примеры: Делайте, пожалуйста, все, что ни скажу! Куда ни посмотрю, повсюду беспорядок.

В устойчивых сочетаниях со значением категорического приказания: ни с места, ни слова, ни шагу назад и т.п.

В устойчивых оборотах, представленных сочетанием двух противопоставляемых понятий: ни рыба ни мясо; ни жив ни мертв; ни дать ни взять и т.п.

Теперь, когда мы разобрали все примеры НЕ и НИ в предложениях, правило должно стать более понятным. Главное, постарайтесь попрактиковаться и придумать несколько собственных примеров на каждый пункт правил. Тогда материал лучше закрепится в памяти. Успехов!

Источник

Как правильно пишется «не есть»?

УМК под редакцией Т. А. Ладыженской, 5 класс.

---

Проверить правописание любого слова

Как правильно «не ест» или «неест»

Чтобы узнать как пишется то или иное слово, необходимо определить какой частью речи оно является. Далее найти правило русского языка, которое определяет правописание необходимого слова. С этим мы сейчас вам поможем.

Правильно писать:
«НЕ ЕСТ»

Каким правилом проверить

Не с глаголами

В правилах сказано
Не пишется с глаголами раздельно. Исключения составляют те глаголы, которые не употребляются без не.

НЕВЕРНО!
«НЕЕСТ»