Загрузить PDF
Загрузить PDF
Одной из важнейших составляющих алгебры является понятие обратной функции. Обратная функции обозначается как f^-1(х) и графически представляется как отражение графика исходной функции относительно прямой у=х. В этой статье мы расскажем вам, как найти обратную функцию.
Шаги
-
1
Убедитесь, что данная функция биективна. Только биективные функции имеют обратные функции.
- Функция биективна, если она проходит тест вертикальной и горизонтальной прямыми. Проведите вертикальную прямую через график функции и подсчитайте количество раз, которое прямая пересекает график функции. Потом проведите горизонтальную прямую через график функции и подсчитайте количество раз, которое прямая пересекает график функции. Если каждая прямая пересекает график функции только один раз, то функция биективна.
- Если график не проходит тест вертикальной прямой, то он не задан функцией.
- Для алгебраического определения биективности функции подставьте f(а) и f(b) в данную функцию и определите, выполняется ли равенство a=b. В качестве примера рассмотрим функцию f(x) = 3x+5.
- f(a) = 3a + 5; f(b) = 3b + 5
- 3a + 5 = 3b + 5
- 3a = 3b
- a = b
- Таким образом, данная функция биективна.
- Функция биективна, если она проходит тест вертикальной и горизонтальной прямыми. Проведите вертикальную прямую через график функции и подсчитайте количество раз, которое прямая пересекает график функции. Потом проведите горизонтальную прямую через график функции и подсчитайте количество раз, которое прямая пересекает график функции. Если каждая прямая пересекает график функции только один раз, то функция биективна.
-
2
В данной функции поменяйте местами «х» и «у». Помните, что f(х) — другое написание «у».
- «f(x)» или «y» представляет собой функцию, а «х» — переменную. Чтобы найти обратную функцию, нужно поменять местами функцию и переменную.
- Пример: рассмотрим функцию f(x) = (4x+3)/(2x+5), которая является биективной. Поменяв местами «х» и «у», получите x = (4y + 3)/(2y + 5).
-
3
Найдите «у». Решите новое уравнение и найдите «у».
- Возможно, чтобы найти значение выражения и упростить его, вам понадобятся алгебраические приемы вроде умножения дробей или разложения на множители.
- Решение нашего примера:
- х = (4y + 3)/(2y + 5)
- х(2y + 5) = 4y + 3 — избавьтесь от дроби. Для этого умножьте обе части уравнения на знаменатель дроби (2у + 5).
- 2xy + 5x = 4y + 3 — раскройте скобки.
- 2xy — 4y = 3 — 5x — перенесите все члены с переменной (в данном случае это «у») на одну сторону уравнения.
- у (2x — 4) = 3 — 5x — вынесите «у» за скобку.
- у = (3 — 5x)/(2x — 4) — разделите обе части уравнения на (2х-4), чтобы получить окончательный ответ.
-
4
Замените «у» на f^-1(х). Это есть обратная функция для исходной функции.
- Окончательный ответ: f^-1(x) = (3 — 5x)/(2x — 4). Это обратная функция для f(х) = (4x + 3)/(2x + 5) .
Реклама
Об этой статье
Эту страницу просматривали 210 117 раз.
Была ли эта статья полезной?
Понятие обратной функции и ее определение в алгебре
Допустим, что у нас есть некая функция y=f(x), которая является строго монотонной (убывающей или возрастающей) и непрерывной на области определения x∈a; b; область ее значений y∈c; d, а на интервале c; d при этом у нас будет определена функция x=g(y) с областью значений a; b. Вторая функция также будет называться непрерывной и строго монотонной. По отношению к y=f(x) она будет обратной функцией. То есть мы можем говорить об обратной функции x=g(y) тогда, когда y=f(x) на заданном интервале будет либо убывать, либо возрастать.
Две этих функции, f и g, будут взаимно обратными.
Обратная функция – это что такое? Дадим определение взаимно обратимой функции (что такое обратимая функция — определение).
Для чего вообще нам нужно понятие обратных функций?
Это нужно нам для решения уравнений y=f(x), которые записываются как раз с помощью этих выражений. Также понятие особенностей обратных функций помогают в решении операций по извлечению n-ой степени (она обратна возведению в степень).
На самом деле это не является чем-то сложным. Онлайн, как и в нашем материале, вы можете найти много примеров обратной функции, которые помогут в этом убедиться.
Важно знать, что любая функция y = y (x) – это определенное правило, которое определяет соответствие между двумя значениями: x и y. К примеру, функция y = x² ставит соответственно каждому действительному числу его в квадрат. Можно сделать определенную таблицу, в которой будут располагаться значения этой функции для целых аргументов.
| x | -2 | -1 | 0 | 1 | 2 |
| y = x² | 4 | 1 | 0 | 1 | 4 |
Как найти функцию обратную данной
Как найти обратную функцию?
Допустим, нам нужно найти решение уравнения cos(x)=13. Его решениями будут все точки: x=±arсcos13+2π·k, k∈Z
Обратными по отношению друг к другу будут, например, функции арккосинуса и косинуса.
Разберем несколько задач на нахождение функций, обратных заданным. Вот несколько примеров обратной функции.
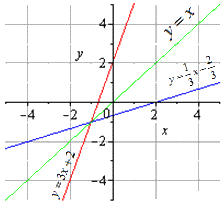
Условие: какая функция будет обратной для y=3x+2?
Решение
Область определений и область значений линейной функции, данной в условии, – это множество всех действительных чисел. Попробуем решить данное уравнение через x, то есть выразив x через y.
Мы получим x=13y-23. Это и есть нужная нам обратная функция, но y здесь будет аргументом, а x — функцией. Переставим их, чтобы получить более привычную форму записи:
y=13x-23
Ответ: функция y=13x-23 будет обратной для y=3x+2.
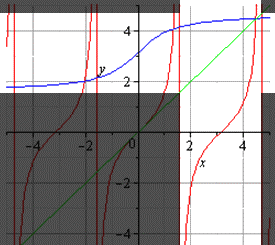
Обе взаимообратные функции можно отобразить на графике следующим образом:
На графике мы находим симметричность обоих графиков относительно y=x (они отображаются симметрично). Эта прямая является биссектрисой первого и третьего квадрантов. Что это позволило нам доказать? Получилось доказательство одного из свойств взаимно обратных функций, о котором мы поговорим далее.
Возьмем онлайн-пример, в котором нужно найти логарифмическую функцию, обратную заданной показательной.
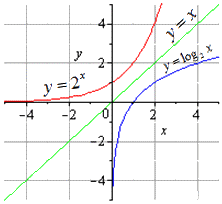
Условие: определите, какая функция будет обратной для y=2x.
Решение
Для заданной функции областью определения являются все действительные числа. Область значений лежит в интервале 0; +∞. Теперь нам нужно выразить x через y, то есть решить указанное уравнение через x. Мы получаем x=log2y. Переставим переменные и получим y=log2x.
В итоге этого примера у нас вышли показательная и логарифмическая функции, которые будут взаимно обратными друг другу на всей области определения.
Ответ: y=log2x.
Графически обе функции будут выглядеть или иметь следующее отображение:
Также взаимно обратные функции можно рассматривать на примере теорем.
Предположим, мы имеем определенную, с возрастающей или убывающей монотонностью, а также непрерывную в определенном промежутке x функцию y = f(x). Значит, в промежутке значений y этой функции существует и обратная функция. Она также монотонно убывает или возрастает. Также ее можно определить как непрерывную (в промежутке y).
Основные свойства взаимно обратных функций
В этом пункте мы перечислим основные свойства обратимых функций y=f(x) и x=g(y). Какими же свойствами обладают взаимообратные функции?
- Первое (исходное) свойство мы уже вывели ранее: y=f(g(y)) и x=g(f(x)).
- Второе свойство вытекает из первоначального (первого) и означает, что область определения y=f(x) будет совпадать с областью значений обратной функции x=g(y), и наоборот.
- Графики обратных функций будут симметричными (находиться в симметрии) относительно y=x.
- Если y=f(x) является возрастающей, то и x=g(y) будет возрастать, а если y=f(x) убывает, то убывает и x=g(y).
Советуем внимательно отнестись к понятиям области определения и области значения функций и никогда их не путать, так как это не одно и тоже даже исходя из названий. Допустим, что у нас есть две взаимно обратные функции y=f(x)=ax и x=g(y)=logay. Согласно первому свойству, y=f(g(y))=alogay. Данное равенство будет верным только в случае положительных значений y, а для отрицательных логарифмов не определен, поэтому не спешите записывать, что alogay=y. Обязательно проверьте и добавьте характеристику, что это верно только при положительном y.
А вот равенство x=f(g(x))=logaax=x будет верным при любых действительных значениях x.
Не забывайте про этот момент, особенно если приходится работать с тригонометрическими и обратными тригонометрическими функциями. Так, arcsinsin7π3≠7π3, потому что область значений арксинуса -π2; π2 и 7π3 в нее не входит. Верной будет запись
arcsinsin7π3=arcsinsin2π+π3==по формуле привидения=arcsinsinπ3=π3
А вот sinarcsin13=13 – верное равенство, т.е. sin(arcsin x)=x при x∈-1; 1 и arcsin(sin x)=x при x∈-π2; π2. Всегда будьте внимательны с областью значений и областью определений обратных функций!
Графики взаимно обратных функций
- Основные взаимно обратные функции: степенные
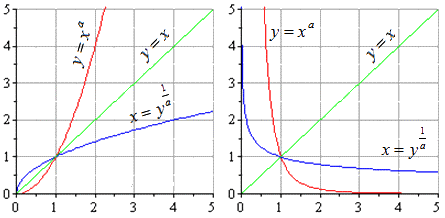
Если у нас есть степенная функция y=xa, то при x>0 степенная функция x=y1a также будет обратной ей. Замена букв будет давать соответственно y=xa и x=y1a.
Сделаем график. На графике они будут выглядеть следующим образом (случаи с положительным и отрицательным коэффициентом a):
- Основные взаимно обратные функции: показательные и логарифмические
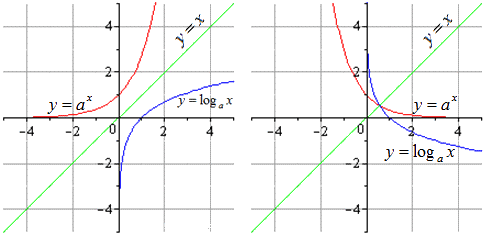
Возьмем a, которое будет положительным числом, не равным 1.
Узнаем, какими будут графики для функций с a>1 и a<1. Они будут выглядеть так:
- Основные взаимно обратные функции: тригонометрические и обратные тригонометрические
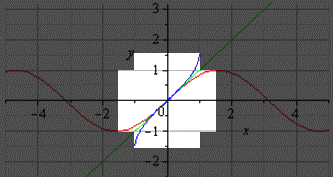
Если нам нужно построить график главной ветви синуса и арксинуса, он будет выглядеть следующим образом (показан выделенной светлой областью):
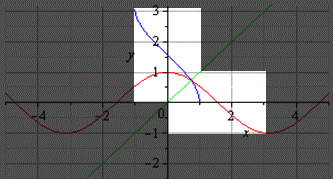
Если построить график главной ветви косинуса и арккосинуса, то он будет выглядеть так:
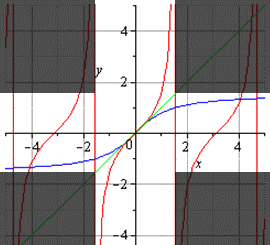
Если строить график главной ветви арктангенса и тангенса, то он будет таким:
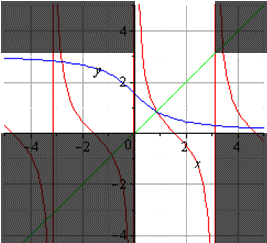
График главной ветви арккотангенса и котангенса будет таким:
В случае построения обратных ветвей, отличные от главных, то обратную тригонометрическую функцию мы сдвигаем вдоль оси Oy на нужное число периодов. Так, если требуется обратная функция для ветви тангенса на π2; 3π2, то мы можем сдвинуть ее на величину π вдоль оси абсцисс. График будет представлять собой ветвь арктангенса, которая сдвинута на π вдоль оси ординат.
Это все свойства обратных функций, о которых мы хотели бы вам рассказать.
Mathematics is a subject with various disciplines and subtopics. Arithmetics, geometry, exponential, percentage are some of these branches of mathematics that deal with the calculation, analysis, and manipulation of numbers as well as symbols. Algebra is also one of the disciplines of mathematics that deals with the manipulation of symbols which represent the unknown value in the equation. The equation of algebra is consists of coefficients, variables, and constants.
Function
The function is a mathematical expression or a relation between the dependent and independent variables. Functions are generally represented f(x). Other than the symbols f(x) use of g(x) or P(x) is also seen in some relations to represent a function. And, the relation between two sets of variables is represented by
y = f(x)
For that relation, y = f(x), for every x, there will be a unique value of y. The relation will give only one value at a time as an output.
Types of algebraic functions
Functions are divided into different types on the basis of variables and their way of representation. These algebraic functions are described below,
- Linear Function: Linear function includes one dependent and one independent variable in the expression. The expression is written in the form of y = mx + c
- Quadratic Function: Quadratic function includes a 2 degree polynomial in its expression. The expression is written in the form of g(x) = ax2 + bx + c.
- Cubic Function: Cubic function includes a 3 degree polynomial in its expression. The expression is written in the form of g(x) = ax3 + bx2 + cx + d.
- Polynomial Function: A polynomial function includes an n-degrees polynomial in the expression. The expression is written in the form of g(x) = cnxn + cn – 1xn – 1 + … + c2x2 + c1x + c0.
- Rational Function: Rational function is written in the form of g(x) = p(x)/q(x), where p(x) and q(x) stands for polynomial functions.
- Radical Function: Radical function is written in the form of g(x) =
, where q(x) is a polynomial function.
What is an inverse function?
Answer:
An inverse function or also widely known as “anti function” is a function that reverses the result of given another function.Such as if an f(x) = 11, then, its inverse function will be f-1(x) = -11.
The inverse functions generally used for common functions,
| Function | Inverse | Descriptions |
|---|---|---|
| + | – | (+) changes to (-) |
| x | ÷ | Should not be divided by 0 |
| 1/x | 1/y | x and y, not zero. |
| x2 | √y | x and y=0 |
| xn | 1/yn | n not to be zero |
| ex | In(y) | y>0 |
| ax | loga(y) | y and a>0 |
| sin(x) | sin-1(y) | -π/2 to +π/2 |
| cos(x) | cos-1(y) | 0 to π |
| tan(x) | tan-1(y) | -π/2 to +π/2 |
Types of Inverse functions:
There are different types of inverse functions. They are Inverse trigonometric functions, Inverse rational functions, and Inverse hyperbolic functions. Let’s take a look at these in more detail,
- Inverse Trigonometric Function
Inverse functions are responsible to give the length of the arc which is required to attain a particular value. The inverse trigonometric function is also widely known as the arc function. There are basically six inverse trigonometric functions.
- arcsine (sin-1)
- arccosine (cos-1)
- arctangent (tan-1)
- arcsecant (sec-1)
- arccotangent (cot-1)
- arccosecant (cosec-1)
- Inverse Rational Function
It is the function represented in the form of f(x) = P(x)/Q(x)
Where Q(x) ≠ 0
- Inverse Hyperbolic Function
Inverse hyperbolic functions are the inverse of hyperbolic functions. The six types of inverse hyperbolic functions are sinh-1, cosh-1, tanh-1, coth-1, sech-1, cosech-1
Sample Problems
Question 1: Find the inverse function of f(x) = y = 3x + 2/x – 1
Solution:
f(x) = y = 3x + 2/x – 1
y(x – 1) = 3x + 2
yx – y = 3x + 2
yx = 3x = y + 2
x(y – 3) = y + 2
x = f-1(y) = y + 2/y – 3
Question 2: check the function f(x) = 5x – 2 if, x = 4. and find the inverse function.
Solution:
f(x) = 5x – 2
f(4) = 5 × 4 – 2
f(4) = 18
Then,
f-1(x) = (18 + 2)/5
f-1(x) = 20/5
f-1(x) = 4
Question 3: Find the inverse of function f(x) = -2x + 7/x
Solution:
f(x) = -2x + 7/x
y = -2x + 7/x
x = -2y + 7/y
xy = -2y + 7
xy + 2y = 7
y(x + 2) = 7
y = 7/x + 2
f-1(x) = 7/x + 2
Mathematics is a subject with various disciplines and subtopics. Arithmetics, geometry, exponential, percentage are some of these branches of mathematics that deal with the calculation, analysis, and manipulation of numbers as well as symbols. Algebra is also one of the disciplines of mathematics that deals with the manipulation of symbols which represent the unknown value in the equation. The equation of algebra is consists of coefficients, variables, and constants.
Function
The function is a mathematical expression or a relation between the dependent and independent variables. Functions are generally represented f(x). Other than the symbols f(x) use of g(x) or P(x) is also seen in some relations to represent a function. And, the relation between two sets of variables is represented by
y = f(x)
For that relation, y = f(x), for every x, there will be a unique value of y. The relation will give only one value at a time as an output.
Types of algebraic functions
Functions are divided into different types on the basis of variables and their way of representation. These algebraic functions are described below,
- Linear Function: Linear function includes one dependent and one independent variable in the expression. The expression is written in the form of y = mx + c
- Quadratic Function: Quadratic function includes a 2 degree polynomial in its expression. The expression is written in the form of g(x) = ax2 + bx + c.
- Cubic Function: Cubic function includes a 3 degree polynomial in its expression. The expression is written in the form of g(x) = ax3 + bx2 + cx + d.
- Polynomial Function: A polynomial function includes an n-degrees polynomial in the expression. The expression is written in the form of g(x) = cnxn + cn – 1xn – 1 + … + c2x2 + c1x + c0.
- Rational Function: Rational function is written in the form of g(x) = p(x)/q(x), where p(x) and q(x) stands for polynomial functions.
- Radical Function: Radical function is written in the form of g(x) =
, where q(x) is a polynomial function.
What is an inverse function?
Answer:
An inverse function or also widely known as “anti function” is a function that reverses the result of given another function.Such as if an f(x) = 11, then, its inverse function will be f-1(x) = -11.
The inverse functions generally used for common functions,
| Function | Inverse | Descriptions |
|---|---|---|
| + | – | (+) changes to (-) |
| x | ÷ | Should not be divided by 0 |
| 1/x | 1/y | x and y, not zero. |
| x2 | √y | x and y=0 |
| xn | 1/yn | n not to be zero |
| ex | In(y) | y>0 |
| ax | loga(y) | y and a>0 |
| sin(x) | sin-1(y) | -π/2 to +π/2 |
| cos(x) | cos-1(y) | 0 to π |
| tan(x) | tan-1(y) | -π/2 to +π/2 |
Types of Inverse functions:
There are different types of inverse functions. They are Inverse trigonometric functions, Inverse rational functions, and Inverse hyperbolic functions. Let’s take a look at these in more detail,
- Inverse Trigonometric Function
Inverse functions are responsible to give the length of the arc which is required to attain a particular value. The inverse trigonometric function is also widely known as the arc function. There are basically six inverse trigonometric functions.
- arcsine (sin-1)
- arccosine (cos-1)
- arctangent (tan-1)
- arcsecant (sec-1)
- arccotangent (cot-1)
- arccosecant (cosec-1)
- Inverse Rational Function
It is the function represented in the form of f(x) = P(x)/Q(x)
Where Q(x) ≠ 0
- Inverse Hyperbolic Function
Inverse hyperbolic functions are the inverse of hyperbolic functions. The six types of inverse hyperbolic functions are sinh-1, cosh-1, tanh-1, coth-1, sech-1, cosech-1
Sample Problems
Question 1: Find the inverse function of f(x) = y = 3x + 2/x – 1
Solution:
f(x) = y = 3x + 2/x – 1
y(x – 1) = 3x + 2
yx – y = 3x + 2
yx = 3x = y + 2
x(y – 3) = y + 2
x = f-1(y) = y + 2/y – 3
Question 2: check the function f(x) = 5x – 2 if, x = 4. and find the inverse function.
Solution:
f(x) = 5x – 2
f(4) = 5 × 4 – 2
f(4) = 18
Then,
f-1(x) = (18 + 2)/5
f-1(x) = 20/5
f-1(x) = 4
Question 3: Find the inverse of function f(x) = -2x + 7/x
Solution:
f(x) = -2x + 7/x
y = -2x + 7/x
x = -2y + 7/y
xy = -2y + 7
xy + 2y = 7
y(x + 2) = 7
y = 7/x + 2
f-1(x) = 7/x + 2
Функция f и ее обратная функция f − 1 . Поскольку f отображает a в 3, обратный f − 1 отображает 3 обратно в a .
В математике обратная функция функции f ( также называемая обратной f ) — это функция , которая отменяет операцию f . Обратное к f существует тогда и только тогда , когда f биективно , и если оно существует, то обозначается
Для функции, его инверсиядопускает явное описание: оно посылает каждый элементк уникальному элементутак что ж ( Икс ) знак равно y .
В качестве примера рассмотрим функцию с действительным знаком действительной переменной, заданную как f ( x ) = 5 x − 7 . Можно думать о f как о функции, которая умножает свои входные данные на 5, а затем вычитает 7 из результата. Чтобы отменить это, к входным данным добавляется 7, а затем результат делится на 5. Следовательно, обратная функция f — это функцияопределяется
Определения
Если f отображает X в Y , то f −1 отображает Y обратно в X .
Пусть f будет функцией, областью определения которой является множество X , а областью определения является множество Y . Тогда f обратима , если существует функция g из Y в X такая, чтодля всеха такжедля всех. [1]
Если f обратима, то существует ровно одна функция g , удовлетворяющая этому свойству. Функция g называется обратной функцией f и обычно обозначается как f − 1 — обозначение, введенное Джоном Фредериком Уильямом Гершелем в 1813 году. [2] [3] [4] [5] [6] [nb 1]
Функция f обратима тогда и только тогда, когда она биективна. Это потому, что условиедля всехследует инъективность f и условиедля всехследует, что f сюръективен .
Функция, обратная f −1 к f , может быть явно описана как функция
- .
Инверсии и композиция
Напомним, что если f — обратимая функция с доменом X и кодоменом Y , то
- , для каждогоа такжедля каждого.
Используя композицию функций , это утверждение можно переписать в виде следующих уравнений между функциями:
- а также
где id X — тождественная функция на множестве X ; то есть функция, которая оставляет свой аргумент неизменным. В теории категорий это утверждение используется как определение обратного морфизма .
Рассмотрение композиции функций помогает понять обозначение f −1 . Многократное составление функции f : X → X с самой собой называется итерацией . Если f применяется n раз, начиная со значения x , то это записывается как fn ( x ) ; поэтому f 2 ( x ) = f ( f ( x )) и т. д. Поскольку f −1 ( f ( x )) = x, составление f −1 и f n дает f n −1 , «отменяя» эффект одного применения f .
Обозначение
Хотя обозначение f −1 ( x ) может быть неправильно понято, [1] ( f ( x )) −1 определенно обозначает мультипликативную обратную функцию f ( x ) и не имеет ничего общего с обратной функцией f . [6]
В соответствии с общими обозначениями, некоторые английские авторы используют такие выражения, как sin − 1 ( x ) , для обозначения обратной функции синуса, применяемой к x (на самом деле частичной обратной , см. ниже). [7] [6] Другие авторы считают, что это может быть перепутано с обозначением для мультипликативного обратного sin ( x ) , которое может быть обозначено как (sin ( x )) −1 . [6] Чтобы избежать путаницы, обратная тригонометрическая функция часто обозначается префиксом « дуга » (от латинского arcus ).[8] [9] Например, функция, обратная синусу, обычно называется функцией арксинуса и записывается как arcsin ( x ) . [8] [9] Аналогично, обратная гиперболическая функция обозначается префиксом « ar » (от латинского ārea ). [9] Например, функция, обратная гиперболическому синусу , обычно записывается как arsinh ( x ) . [9] Обратите внимание, что такие выражения, как sin − 1 ( x )все еще может быть полезно отличить многозначное обратное от частичного обратного:. Другие обратные специальные функции иногда имеют префикс «inv», если следует избегать двусмысленности обозначения f −1 . [10] [9]
Примеры
Функции возведения в квадрат и извлечения квадратного корня
Функция f : R → [0,∞), заданная формулой f ( x ) = x 2 , не является инъективной, посколькудля всех. Следовательно, f необратима.
Если область определения функции ограничена неотрицательными вещественными числами, то есть мы берем функциюпо тому же правилу , что и раньше, то функция биективна и, следовательно, обратима. [11] Обратная функция здесь называется (положительной) функцией квадратного корня и обозначается.
Стандартные обратные функции
В следующей таблице показаны несколько стандартных функций и их обратные функции:
| Функция f ( х ) | Обратное f −1 ( y ) | Заметки |
|---|---|---|
| х + а | у — а | |
| а — х | а — у | |
| МХ | у/м | м ≠ 0 |
| 1/Икс(т.е. х -1 ) |
1/у(т.е. у- 1 ) |
х , у ≠ 0 |
| х 2 | (т.е. у 1/2 ) |
х , только у ≥ 0 |
| х 3 | (т.е. у 1/3 ) |
нет ограничений на x и y |
| х р | (т.е. у 1/ р ) |
x , y ≥ 0 , если p четно; целое число р > 0 |
| 2 х | фунт у | у > 0 |
| е х | в у | у > 0 |
| 10 х | войти у | у > 0 |
| х _ | войти _ _ | у > 0 и а > 0 |
| х е х | Вт ( г ) | x ≥ −1 и y ≥ −1/ e |
| тригонометрические функции | обратные тригонометрические функции | различные ограничения (см. таблицу ниже) |
| гиперболические функции | обратные гиперболические функции | различные ограничения |
Формула обратного
Многие функции, заданные алгебраическими формулами, имеют формулу своей обратной. Это потому, что обратнаяобратимой функцииимеет явное описание как
- .
Это позволяет легко определять обратные функции многих функций, заданных алгебраическими формулами. Например, если f — функция
затем определитьдля действительного числа y нужно найти уникальное действительное число x такое, что (2 x + 
Таким образом, обратная функция f −1 задается формулой
Иногда обратная функция не может быть выражена формулой в закрытой форме . Например, если f — функция
тогда f является биекцией и, следовательно, имеет обратную функцию f − 1 . Формула для этого обратного имеет выражение в виде бесконечной суммы:
Свойства
Поскольку функция представляет собой особый тип бинарного отношения , многие свойства обратной функции соответствуют свойствам обратных отношений .
Уникальность
Если для данной функции f существует обратная функция , то она единственна. [12] Это следует из того, что обратная функция должна быть обратным отношением, которое полностью определяется f .
Симметрия
Существует симметрия между функцией и ее обратной. В частности, если f является обратимой функцией с областью определения X и кодовой областью Y , то ее обратная функция f −1 имеет область определения Y и образ X , а обратная функция f −1 является исходной функцией f . В символах для функций f : X → Y и f − 1 : Y → X [ 12]
- а также
Это утверждение является следствием того, что для того, чтобы f было обратимым, оно должно быть биективным. Инволютивный характер обратного может быть кратко выражен как [ 13]
Обратное к g ∘ f есть f −1 ∘ g −1 .
Обратная композиция функций дается выражением [14]
Обратите внимание, что порядок g и f поменялся местами; чтобы отменить f , за которым следует g , мы должны сначала отменить g , а затем отменить f .
Например, пусть f ( x ) = 3 x и пусть g ( x ) = x + 5 . Тогда композиция g ∘ f — это функция, которая сначала умножает на три, а затем прибавляет пять,
Чтобы обратить этот процесс вспять, мы должны сначала вычесть пять, а затем разделить на три,
Это композиция
( f −1 ∘ g −1 )( x ) .
Самоинверсия
Если X — множество, то тождественная функция на X является обратной самой себе:
В более общем смысле функция f : X → X равна своей обратной тогда и только тогда, когда композиция f ∘ f равна id X . Такая функция называется инволюцией .
График обратного
Графики y = f ( x ) и y = f −1 ( x ) . Пунктирная линия y = x .
Если f обратима, то график функции
совпадает с графиком уравнения
Это идентично уравнению y = f ( x ) , которое определяет график f , за исключением того, что роли x и y поменялись местами. Таким образом, график f − 1 можно получить из графика f , поменяв местами оси x и y . Это эквивалентно отражению графика через линию
y = x . [15] [1]
Обратные и производные
Теорема об обратной функции утверждает, что непрерывная функция f обратима на своем диапазоне (образе) тогда и только тогда, когда она либо строго возрастает, либо убывает (без локальных максимумов или минимумов ). Например, функция
обратим, так как производная
f′ ( x ) = 3 x 2 + 1 всегда положительна.
Если функция f дифференцируема на интервале I и f′ ( x ) ≠ 0 для каждого x ∈ I , то обратная функция f − 1 дифференцируема на f ( I ) . [16] Если y = f ( x ) , производная обратной функции дается теоремой об обратной функции,
Используя обозначения Лейбница, приведенную выше формулу можно записать как
Этот результат следует из цепного правила (см. статью об обратных функциях и дифференцировании ).
Теорему об обратной функции можно обобщить на функции многих переменных. В частности, дифференцируемая функция многих переменных f : Rn → Rn обратима в окрестности точки p до тех пор , пока обратима матрица Якоби функции f в точке p . В этом случае якобиан функции f − 1 в точке f ( p ) является матрицей, обратной якобиану функции f в точке p .
Примеры из жизни
- Пусть f будет функцией, которая переводит температуру в градусах Цельсия в температуру в градусах Фаренгейта ,тогда его обратная функция переводит градусы Фаренгейта в градусы Цельсия,[17] так как
- Предположим , f назначает каждому ребенку в семье его год рождения. Обратная функция будет выводить, какой ребенок родился в данном году. Однако, если в семье есть дети, родившиеся в один год (например, близнецы или тройни и т. д.), то выход не может быть известен, когда входом является общий год рождения. Кроме того, если указан год, в котором не было рождено ни одного ребенка, имя ребенка не может быть названо. Но если каждый ребенок родился в отдельный год и если мы ограничимся тремя годами, в которые родился ребенок, то мы получим обратную функцию. Например,
- Пусть R будет функцией, которая приводит к увеличению некоторой величины на x процентов, а F будет функцией, приводящей к уменьшению x процентов. Применительно к 100 долларам с x = 10% мы обнаруживаем, что применение первой функции, за которой следует вторая, не восстанавливает исходное значение 100 долларов, демонстрируя тот факт, что, несмотря на внешний вид, эти две функции не являются обратными друг другу.
- Формула для расчета pH раствора: pH = -log 10 [H + ] . Во многих случаях нам нужно найти концентрацию кислоты по измерению pH. Используется обратная функция [H + ] = 10 −pH .
Обобщения
Частичные инверсии
Квадратный корень из x является частично обратным к f ( x ) = x 2 .
Даже если функция f не является взаимно однозначной, можно определить частичную обратную функцию f , ограничив область определения. Например, функция
не является взаимно однозначным, так как x 2 = (− x ) 2 . Однако функция становится взаимно однозначной, если мы ограничиваемся областью x ≥ 0 , и в этом случае
(Если вместо этого мы ограничимся областью значений x ≤ 0 , тогда обратная функция будет отрицательным значением квадратного корня из y .) В качестве альтернативы нет необходимости ограничивать область определения, если мы довольствуемся тем, что обратная функция является многозначной :
Иногда этот многозначный обратный называется полным обратным f , а части (такие как √ x и − √ x ) называются ветвями . Самая важная ветвь многозначной функции (например, положительный квадратный корень) называется главной ветвью , а ее значение в точке y называется главным значением f − 1 ( y ) .
Для непрерывной функции на прямой требуется одна ветвь между каждой парой локальных экстремумов . Например, обратная кубическая функция с локальным максимумом и локальным минимумом имеет три ветви (см. рисунок рядом).
Эти соображения особенно важны для определения обратных тригонометрических функций . Например, функция синуса не является взаимно однозначной, поскольку
для каждого реального x (и, в более общем случае, sin( x + 2 π n ) = sin( x ) для каждого целого числа n ). Однако синус взаимно однозначен на интервале
[−π/2, π/2] , а соответствующий частичный обратный называется арксинусом . Это считается основной ветвью обратного синуса, поэтому основное значение обратного синуса всегда находится между —π/2а такжеπ/2. В следующей таблице описаны основные ветви каждой обратной тригонометрической функции: [18]
| функция |
Диапазон обычной основной стоимости |
|---|---|
| арксин | −π/2≤ sin −1 ( x ) ≤π/2 |
| арккос | 0 ≤ cos− 1 ( x ) ≤ π |
| арктический | −π/2< тангенс −1 ( х ) <π/2 |
| арккот | 0 < раскладушка −1 ( x ) < π |
| угловая секунда | 0 ≤ сек −1 ( х ) ≤ π |
| arccsc | −π/2≤ csc −1 ( x ) ≤π/2 |
Инверсия слева и справа
Композиция функций слева и справа может не совпадать. В общем, условия
- «Существует такое g , что g ( f ( x )) = x » и
- «Существует такое g , что f ( g ( x )) = x »
подразумевают различные свойства f . Например, пусть f : R → [0, ∞) обозначает карту возведения в квадрат, такую, что f ( x ) = x 2 для всех x в R , и пусть g : [0, ∞) → R обозначает карту квадратного корня, такой, что г ( Икс ) знак равно √ Икс для всех Икс ≥ 0 . Тогда f ( g ( x )) = x для всех x в [0, ∞); то есть g является правой обратной к f . Однако g не является левым обратным к f , так как, например, g ( f (−1)) = 1 ≠ −1 .
Левые инверсии
Если f : X → Y , левая обратная для f (или ретракция f ) есть функция g : Y → X такая, что составление f с g слева дает тождественную функцию [19]
То есть функция g удовлетворяет правилу
- Если f ( x ) = y , то g ( y ) = x .
Функция g должна быть равна обратной функции f на изображении f , но может принимать любые значения для элементов Y , не находящихся на изображении.
Функция f с непустой областью определения инъективна тогда и только тогда, когда она имеет левую обратную. [20] Элементарное доказательство выглядит следующим образом:
- Если g является левой инверсией f , и f ( x ) = f ( y ) , то g ( f ( x )) = g ( f ( y )) = x = y .
-
Если непустое f : X → Y инъективно, постройте левый обратный g : Y → X следующим образом: для всех y ∈ Y , если y находится в образе f , то существует x ∈ X такой, что f ( x ) = у . Пусть g ( y ) = x ; это определение единственно, потому что f инъективно. В противном случае пусть g ( y ) — произвольный элементХ .
Для всех x ∈ X , f ( x ) находится в образе f . По построению g ( f ( x )) = x , условие для левого обратного.
В классической математике каждая инъективная функция f с непустой областью определения обязательно имеет левую обратную; однако это может потерпеть неудачу в конструктивной математике . Например, левая инверсия включения {0,1} → R двухэлементного множества в вещественные числа нарушает неразложимость , давая ретракцию вещественной линии на множество {0,1} . [21]
Правые инверсии
Пример правой обратной с неинъективной сюръективной функцией
Правая обратная функция для f (или части f ) — это функция h : Y → X такая, что [ необходима ссылка ]
То есть функция h удовлетворяет правилу
- Если, тогда
Таким образом, h ( y ) может быть любым из элементов X , которые отображаются в y при f .
Функция f имеет правую обратную тогда и только тогда, когда она сюръективна (хотя построение такой обратной в общем случае требует аксиомы выбора ).
- Если h правый обратный f , то f сюръективен. Для всех, естьтакой, что.
- Если f сюръективно, f имеет правый обратный h , который можно построить следующим образом: для всех, есть хотя бы одинтакой, что(поскольку f сюръективно), поэтому мы выбираем одно значение h ( y ) . [ нужна ссылка ]
Двусторонние инверсии
Инверсия, которая является как левой, так и правой инверсией ( двусторонняя инверсия ), если она существует, должна быть уникальной. На самом деле, если у функции есть левая обратная и правая обратная, они обе являются одной и той же двусторонней обратной, поэтому ее можно назвать обратной .
- Еслиявляется левым обратным иправая инверсия, для всех,.
Функция имеет двустороннюю обратную тогда и только тогда, когда она биективна.
- Биективная функция f инъективна, поэтому она имеет обратную слева (если f — пустая функция,является своим левым обратным). f сюръективен, поэтому имеет правый обратный. Согласно вышеизложенному, левая и правая обратные одинаковы.
- Если f имеет двусторонний обратный g , то g является левым обратным и правым обратным к f , поэтому f инъективен и сюръективен.
Прообразы
Если f : X → Y — любая функция (не обязательно обратимая), прообраз (или прообраз ) элемента y ∈ Y определяется как множество всех элементов X , которые отображаются в y :
Прообраз y можно рассматривать как образ y при (многозначной) полной обратной функции f .
Точно так же, если S является любым подмножеством Y , прообраз S , обозначаемый, это набор всех элементов X , которые отображаются в S :
Например, возьмем функцию f : R → R ; х ↦ х 2 . Эта функция необратима, поскольку она не является биективной, но прообразы могут быть определены для подмножеств домена кода, например
- .
Прообраз одного элемента y ∈ Y — одноэлементное множество { y } — иногда называют слоем y . Когда Y представляет собой набор действительных чисел, обычно называют f −1 ({ y }) набором уровней .
Смотрите также
- Теорема Лагранжа об обращении дает разложение в ряд Тейлора обратной функции аналитической функции.
- Интеграл обратных функций
- Обратное преобразование Фурье
- Обратимые вычисления
Примечания
- ^ Не путать с числовым возведением в степень, например, с мультипликативной инверсией ненулевого действительного числа.
Ссылки
- ^ a b c Вайсштейн, Эрик В. «Обратная функция» . mathworld.wolfram.com . Проверено 08 сентября 2020 г. .
- ^ Гершель, Джон Фредерик Уильям (1813) [1812-11-12]. «Об одном замечательном применении теоремы Котса» . Философские труды Лондонского королевского общества . Лондон: Лондонское королевское общество , напечатано W. Bulmer and Co., Cleveland-Row, St. James’s, продано G. и W. Nicol, Pall-Mall. 103 (Часть 1): 8–26 [10]. doi : 10.1098/rstl.1813.0005 . JSTOR 107384 . S2CID 118124706 .
- ^ Гершель, Джон Фредерик Уильям (1820). «Часть III. Раздел I. Примеры прямого метода разностей» . Сборник примеров приложений исчисления конечных разностей . Кембридж, Великобритания: напечатано Дж. Смитом, продано Дж. Дейтон и сыновьям. стр. 1–13 [5–6]. Архивировано из оригинала 04.08.2020 . Проверено 4 августа 2020 г. . [1] (NB. Здесь Гершель ссылается на свою работу 1813 года и упоминает более раннюю работу Ганса Генриха Бюрманна .)
- ^ Пирс, Бенджамин (1852 г.). Кривые, функции и силы . Том. Я (новое изд.). Бостон, США. п. 203.
- ^ Пеано, Джузеппе (1903). Formulaire mathématique (на французском языке). Том. IV. п. 229.
- ^ a b c d Каджори, Флориан (1952) [март 1929]. «§472. Степень логарифма / §473. Повторные логарифмы / §533. Обозначения Джона Гершеля для обратных функций / §535. Сохранение конкурирующих обозначений для обратных функций / §537. Полномочия тригонометрических функций». История математических обозначений . Том. 2 (3-й исправленный тираж 1929 г., 2-е изд.). Чикаго, США: Издательство Open Court . стр. 108, 176–179, 336, 346. ISBN . 978-1-60206-714-1. Проверено 18 января 2016 г. .
[…] §473. Повторные логарифмы […] Здесь мы отмечаем символизм, использованный Прингсхеймом и Молком в их совместной статье Encyclopédie : « 2 log b a = log b (log b a ), …, k + 1 log b a = log b ( k log b a )». […] §533. Обозначения Джона Гершеля для обратных функций, sin −1 x , tan −1 xи т. д ., было опубликовано им в лондонских Philosophical Transactions за 1813 год. Он говорит ( стр. 10 ): «Это обозначение cos . обычно записывается так, arc (cos.= e )». Он признает, что некоторые авторы используют cos. m A для (cos. A ) m , но он обосновывает свои собственные обозначения, указывая, что поскольку d 2 x , Δ 3 x , Σ 2 x означает dd x , ΔΔΔ x , ΣΣ x , мы должны написать sin. 2 х за грех. грех. х , лог. 3 х для лог. журнал. журнал. х . Точно так же, как мы пишем d − n V = ∫ n V, мы можем аналогичным образом писать sin. −1 x = дуга (sin.= x ), лог. −1 Икс .= с Икс . Несколько лет спустя Гершель объяснил, что в 1813 году он использовал fn ( x ), f − n ( x ) , sin. −1 x и т. д.», как он тогда впервые предположил. Работа немецкого аналитика, Бурман , однако, в течение этих нескольких месяцев узнал, что то же самое объясняется значительно раньше. Однако он [Бурманн], по-видимому, не заметил удобства применения этой идеи к обратным функциям tan −1 и т. д., а также, по-видимому, совсем не осведомлен об обратном исчислении функций, к которому она приводит». Гершель добавляет: «Симметрия этого обозначения и, прежде всего, новые и наиболее обширные взгляды, которые оно открывает на природу аналитических операций, по-видимому, санкционируют его универсальное принятие » . обратная функция.- […] Использование обозначений Гершеля претерпело небольшое изменение у Бенджамина Пирса .книги, чтобы снять главное возражение против них; Пирс писал: «cos [−1] x », «log [−1] x ». [б] […] §537. Степени тригонометрических функций. — Для обозначения, скажем, квадрата sin x использовались три основных обозначения , а именно (sin x ) 2 , sin x 2 , sin 2 x . В настоящее время преобладающим обозначением является sin 2 x , хотя первое менее вероятно будет неправильно истолковано. В случае sin 2 x напрашиваются две интерпретации; во- первых, грех х · грех х; во-вторых, [c] sin (sin x ). Поскольку функции последнего типа обычно не проявляются, опасность неправильной интерпретации гораздо меньше, чем в случае log 2 x , где log x · log x и log (log x ) часто встречаются в анализе. […] Обозначение sin n x для (sin x ) n широко использовалось и в настоящее время является преобладающим. […]
(xviii+367+1 страница, включая 1 страницу приложений) (NB. ISBN и ссылка для перепечатки 2-го издания Cosimo, Inc., Нью-Йорк, США, 2013 г.) - ↑ Томас 1972 , стр. 304–309.
- ^ б Корн, Грандино Артур ; Корн, Тереза М. (2000) [1961]. «21.2.-4. Обратные тригонометрические функции». Математический справочник для ученых и инженеров: определения, теоремы и формулы для справки и обзора (3-е изд.). Минеола, Нью-Йорк, США: Dover Publications, Inc., с. 811 . ISBN 978-0-486-41147-7.
- ^ a b c d e Олдхэм, Кейт Б .; Миланд, Ян К.; Спаниер, Джером (2009) [1987]. Атлас функций: с Экватором, Калькулятор функций Атласа (2-е изд.). Спрингер Сайенс+Бизнес Медиа, ООО . doi : 10.1007/978-0-387-48807-3 . ISBN 978-0-387-48806-6. LCCN 2008937525 .
- ^ Холл, Артур Грэм; Фринк, Фред Гудрич (1909). «Статья 14: Обратные тригонометрические функции» . Написано в Анн-Арборе, Мичиган, США. Плоская тригонометрия . Нью-Йорк: Генри Холт и компания . стр. 15–16 . Проверено 12 августа 2017 г. .
α = arcsin
m
Это обозначение повсеместно используется в Европе и быстро завоевывает популярность в этой стране.
Менее желательный символ α = sin
-1
m
до сих пор встречается в английских и американских текстах.
Обозначение α = inv sin
m
, возможно, еще лучше ввиду его общей применимости.
[…] Аналогичное символическое отношение верно и для других
тригонометрических функций
. Его часто читают как «арксинус m » или «антисинус m » , так как говорят, что две взаимно обратные функции являются антифункциями друг друга.
- ^ Лей 2006 , с. 69, пример 7.24
- ^ а б Вольф 1998 , с. 208, теорема 7.2.
- ^ Смит, Эгген и Сент-Андре 2006 , стр. 141 Теорема 3.3(а)
- ^ Лей 2006 , с. 71, теорема 7.26
- ↑ Briggs & Cochran 2011 , стр. 28–29.
- ^ Лей 2006 , с. 246, теорема 26.10.
- ^ «Обратные функции» . www.mathsisfun.com . Проверено 08 сентября 2020 г. .
- ↑ Briggs & Cochran 2011 , стр. 39–42.
- ^ Тупица; Фут. Абстрактная алгебра .
- ^ Мак Лейн, Сондерс. Категории для работающего математика .
- ^ Френкель. Абстрактная теория множеств .
Библиография
- Бриггс, Уильям; Кокран, Лайл (2011). Исчисление / Ранние трансцендентальные одинарные переменные . Эддисон-Уэсли . ISBN 978-0-321-66414-3.
- Девлин, Кейт Дж. (2004). Множества, функции и логика / Введение в абстрактную математику (3-е изд.). Чепмен и Холл / CRC Mathematics . ISBN 978-1-58488-449-1.
- Флетчер, Питер; Пэтти, К. Уэйн (1988). Основы высшей математики . PWS-Кент. ISBN 0-87150-164-3.
- Лэй, Стивен Р. (2006). Анализ / С введением в доказательство (4-е изд.). Пирсон / Прентис Холл . ISBN 978-0-13-148101-5.
- Смит, Дуглас; Эгген, Морис; Сент-Андре, Ричард (2006). Переход к высшей математике (6-е изд.). Томпсон Брукс/Коул . ISBN 978-0-534-39900-9.
- Томас-младший, Джордж Бринтон (1972). Исчисление и аналитическая геометрия, часть 1: функции одной переменной и аналитическая геометрия (альтернативный вариант). Эддисон-Уэсли .
- Вольф, Роберт С. (1998). Доказательство, логика и гипотеза / Набор инструментов математика . ISBN WH Freeman and Co. 978-0-7167-3050-7.
Дальнейшее чтение
- Амазиго, Джон С .; Рубенфельд, Лестер А. (1980). «Неявные функции; якобианы; обратные функции». Усовершенствованное исчисление и его приложения к инженерным и физическим наукам . Нью-Йорк: Уайли. стр. 103–120 . ISBN 0-471-04934-4.
- Бинмор, Кен Г. (1983). «Обратные функции». исчисление . Нью-Йорк: Издательство Кембриджского университета . стр. 161–197. ISBN 0-521-28952-1.
- Спивак, Майкл (1994). Исчисление (3-е изд.). Опубликуй или погибни. ISBN 0-914098-89-6.
- Стюарт, Джеймс (2002). Исчисление (5-е изд.). Брукс Коул . ISBN 978-0-534-39339-7.
Внешние ссылки
- «Обратная функция» , Математическая энциклопедия , EMS Press , 2001 [1994]
Нахождение формулы для функции, обратной данной
Пользуясь формулой (y = f(x)), следует выразить (x) через (y), а в полученной формуле (x = g(y)) заменить (x) на (y), а (y) на (x).
Пример:
найти функцию, обратную для функции
y=x2,x∈0;+∞)
.
Функция
y=x2
возрастает на промежутке
0;+∞)
. Делаем вывод, что обратная функция существует. Если значения (x) принадлежат промежутку
0;+∞)
, то
x=y
. Заменим (x) на (y), а (y) на (x), получим обратную функцию
y=x,x∈0;+∞)
. Обратная функция определена на промежутке
0;+∞)
и её график симметричен графику функции
y=x2,x∈0;+∞)
относительно прямой (y=x).
- Функция, обратная данной
- Алгоритм вывода формулы функции, обратной данной
- Свойства взаимно обратных функций
- Примеры
Функция, обратная данной
По определению (см. §34 справочника для 7 класса)
Функция – это соответствие, при котором каждому значению независимой переменной соответствует единственное значение зависимой переменной.
Пусть некоторое соответствие задано таблицей:
|
x |
-4 |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
|
y |
-2 |
-1,5 |
-1 |
-0,5 |
0 |
0,5 |
1 |
1,5 |
2 |
Множество значений X = {-4;-3;…;4} отображается в множество значений Y = {-2;-1,5;…;2}: $X xrightarrow{f} Y$. При этом каждому значению x соответствует единственное значение y, т.е., данное соответствие f является функцией.
С другой стороны, мы можем рассмотреть обратное отображение $Y xrightarrow{g} X$, заданное той же таблицей. При этом каждому значению y соответствует единственное значение x, т.е., обратное соответствие $g = f^{-1}$ также является функцией.
Функцию $f: X xrightarrow{f} Y$ с областью определения X и областью значений Y называют обратимой, если обратное ей соответствие $g: Y xrightarrow{g} g X$ также является фунцией.
Если функция f обратима, то обратное ей соответствие $g = f^{-1}$ называют обратной функцией к f.
Например: аналитическое выражение для функции $X xrightarrow{f} Y$, заданной таблицей $y = f(x) = frac{x}{2}$. Обратное соответствие $Y xrightarrow{g} X$ также является функцией x = g(y) = 2y.
Функция g — обратная функция к f.
В общем случае формулы функций записывают в виде y(x). При такой записи, функции $y = frac{x}{2}$ и y=2x являются взаимно обратными.
Алгоритм вывода формулы функции, обратной данной
На входе: множества X и Y, для которых оба соответствия $X xrightarrow{f} Y$ и $Y xrightarrow{g} X$ являются функциями.
Шаг 1. В формуле для исходной функции заменить обозначения аргумента и значения: $x rightarrow y$, $y rightarrow x$.
Шаг 2. Из полученной формулы выразить y(x). Искомое выражение для обратной функции найдено.
Шаг 3. Учесть ограничения для области определения и области значений исходной и/или обратной функций.
Например:
1) Пусть исходная функция $y = frac{x}{2}$
Шаг 1. Меняем аргумент и значение: $x = frac{y}{2}$
Шаг 2. Находим y из полученной формулы: y = 2x — искомая обратная функция
Шаг 3. Ограничений на x и y нет
2) Пусть исходная функция y = -2x+3
Шаг 1. Меняем аргумент и значение: x = -2y+3
Шаг 2. Находим y из полученной формулы: $y = frac{-x+3}{2}$ — искомая обратная функция
Шаг 3. Ограничений на x и y нет
3) Пусть исходная функция $y = sqrt{x+1}$
Шаг 1. Меняем аргумент и значение: $x = sqrt{y+1}$
Шаг 2. Находим y из полученной формулы: $y = x^2-1$ — искомая обратная функция
Шаг 3. На исходную функцию накладываются ограничения
на $x:x+1 ge 0 Rightarrow x ge -1$, на $y:y ge 0$
Тогда исходная функция определяется на множествах $y ge -1$, $x ge 0$
4) Пусть исходная функция $y = 2x^2+1$
Шаг 1. Меняем аргумент и значение: $x = 2y^2+1$
Шаг 2. Находим y из полученной формулы: $y = sqrt{frac{x-1}{2}}$ — искомая обратная функция
Шаг 3. На обратную функцию накладываются ограничения
на $x:x-1 ge 0 Rightarrow x ge 1$, на $y:y ge 0$
Тогда исходная функция определяется на множествах $y ge 1$, $x ge 0$
Исходная функция — парабола получает ограничения из-за обратной функции; только в этом случаи функции будут взаимно обратными.
Свойства взаимно обратных функций
Пусть f и g — взаимно обратные функции. Тогда:
1. Область определения функции f является областью значений функции g, а область значений функции f является областью определения функции g.
2. Функции f и g либо одновременно возрастающие, либо одновременно убывающие.
3. Если f — нечётная, то и g — нечётная.
4. Графики f и g симметричны относительно биссектрисы 1-й четверти y = x.
5. Справедливы тождества f(g(x) ) = x и g(f(x) ) = x.
Например:
Графики пар взаимно обратных функций, найденных выше:
Примеры
Пример 1. Задайте формулой функцию, обратную данной.
а) y = 5x-4
Меняем аргумент и значение: x = 5y-4
Получаем: $y = frac{x+4}{5}$ — искомая обратная функция
б) y = -3x+2
Меняем аргумент и значение: x = -3y+2
Получаем: $y = frac{-x+2}{3}$ — искомая обратная функция
в) y = 4x+1, где $-1 le x le 5$
Меняем аргумент и значение: x = 4y+1
Получаем: $y = frac{x-1}{4}$
Требуем, чтобы: $-1 le y le 5 Rightarrow -1 le frac{x-1}{4} le 5 Rightarrow -4 le x-1 le 20 Rightarrow -3 le x le 21$
Итак, искомая обратная функция: $y = frac{x-1}{4}$, где -3 $le x le 21$
г) $y=- frac{1}{2} x+7$, где $2 le x le 9$
Меняем аргумент и значение: $x=-frac{1}{2} y+7$
Получаем: y = 2(-x+7) = -2x+14
Требуем, чтобы: $2 le y le 9 Rightarrow 2 le -2x+14 le 9 Rightarrow -12 le -2x le -5 Rightarrow$
$6 ge x ge 2,5 Rightarrow 2,5 le x le 6$
$y = -2x+14,где 2,5 le x le 6$ — искомая обратная функция
Пример 2. Найдите функцию, обратную данной.
Постройте график исходной и обратной функции в одной системе координат.
|
а) $y=x^2,x le 0$ Обратная функция $x = y^2 Rightarrow y = pm sqrt{x}$ При этом $y le 0$ Поэтому выбираем $y = — sqrt{x}$ – искомая обратная функция |
 |
|
б) y = x-3, $-1 le x le 4$ Обратная функция $x = y-3 Rightarrow y = x+3$ При этом $-1 le y le 4 Rightarrow -1 le x+3 le 4$ $Rightarrow -4 le x le 1$ y = x+3, $-4 le x le 1$ — искомая обратная функция |
 |
|
в) $y = frac{1}{x+1} $ Обратная функция $x = frac{1}{y+1} Rightarrow y = frac{1}{x} -1$ |
 |
|
г) $y = 1+ sqrt{x-3}$ Область определения: $x ge 3$ Область значений: $y ge 1$ Обратная функция: $x = 1+ sqrt{y-3} Rightarrow y = (x-1)^2+3$ Область определения: $x ge 1$ Область значений: $y ge 3$ |
 |