Как пишется площадь одной буквой - Правописание и грамматика

В жизни каждого человека по достижении 7-летнего возраста появляется необходимость обучаться в средней общеобразовательной школе. В этом заведении ученик получает базовые знания и навыки. В рамках учебной программы по математике школьники узнают, как обозначается площадь. Необходимо рассмотреть, какой буквой и единицей измерения необходимо это делать.

Общие сведения

Изучение того, как и какой буквой обозначается общая площадь, необходимо начать с определения данного понятия в математике.

Под площадью понимается характеристика, имеющая числовое выражение. Ею описывается геометрическая фигура в двухмерном пространстве.

Объект, по отношению к которому возникает вопрос, как обозначить в письменном выражении площадь, может быть плоским или искривленным.Обозначение площади дает представление о размере и параметрах изучаемой площади.

В отдельных литературных источниках общая площадь встречается под названием квадратуры. Фигура, для которой возможно обозначить площадь, имеет наименование квадрируемой. Геометрические объекты, для которых значение площади в полученном решении оказалось одинаковым, встречаются под названием равновеликих.

Возможность определения площади и обозначения ее буквой появилась благодаря интегральному исчислению в математике. Общее представление о данном понятии было получено в результате формулирования теории меры множества. Постулаты, составляющие данную теорию, являются правдивыми для большинства объектов, изучаемых в геометрии.

Возможность практического измерения данной величины отмечается в результате использования планиметра и специальной палетки.

Важно! Основы геометрии: что это такое биссектриса треугольника

Площадь, обозначение которой становится доступным в результате ее числового выражения, характеризуется следующими параметрами:

Положительная. В числе ее характеристик отсутствует понятие отрицательного значения.
Аддитивная. Данный показатель относительно любого геометрического объекта определяется как суммированное значение объектов, образующих изучаемую фигуру при отсутствии внутренних ограничений.
Инвариантная. Позволяет приравнивать площади фигур, которые в движении переходят друг в друга и полностью совпадают.
Нормированная. Соответствует правилу, согласно которому 1 составляет площадь единичного квадрата.
Монотонная. Параметр площади отдельной части геометрического объекта не превышает общую площадь всей изучаемой фигуры.

Знак площади, используемый в математике, появился в результате присвоения данного параметра для многоугольных геометрических объектов. Впоследствии перечень фигур, в отношении к площади которых использовалось обозначение буквой, увеличился на группу квадрируемых объектов.

Обратите внимание, к категории квадрируемой относится объект, поддающийся вписыванию в пределы многоугольника. Также достоверной является способность заключить многоугольник в данный квадрируемый объект.

Познавательно! Как найти и чему будет равна длина окружности

Общее понимание категории позволяет ее трактовать в качестве числовой характеристики. При этом этот признак используется по отношению только к поверхности двухмерной, находящейся в пространстве трехмерном.

Для данного показателя присуща система измерения. Основными единицами, дающими представление о величине геометрического объекта, являются сантиметры, миллиметры, дециметры, метры, километры. В ряде источников встречается упоминание проведенных измерений в арах, гектарах. Отличительная особенность, свойственная для рассматриваемого показателя, возведение единиц измерения в квадрат.

Важно! Урок геометрии: как найти по формуле периметр треугольника

Варианты обозначения

Понятие используется не только в математике. Оно актуально и для физики.

В связи с разносторонностью применения возникает вопрос, какой буквой обозначается площадь.

В зависимости от дисциплины, в рамках которой применяется изучаемое понятие, становится очевидным ответ, какой буквой алфавита обозначают данную величину. Проститутки в Екатеринбурге intim66.ru

В таких науках, как физика и математика, используется знак латинского алфавита S. Данная буква имеет произношение {эс}.

Обратите внимание! Знаком S обозначают площадь таких фигур, как квадрат, треугольник, ромб, прямоугольник, круг.

Среди вопросов, занимающих умы студентов высших учебных заведений, присутствует тема: как обозначить данную величину нескольких геометрических объектов. В данном случае в письменном варианте применяются нижние индексы. Среди значений, используемых в индексной системе обозначений, присутствуют числа.

Примером выступает обозначение S1, S2, S3. Также считается допустимым применение сокращенных наименований геометрических объектов, по отношению к которым производится числовое измерение. Так, при изучении треугольников для сокращенного названия используются наименования вершин, обозначенные латинскими буквами. В качестве примера могут быть SAOB, SCLE, SOME.

Интересно! Что значит вертикально и как выглядит вертикальная линия

Актуальным для учащихся является вопрос, как пишется в физике площадь. Следует отметить, что данным понятием характеризуется поперечное сечение. Считается допустимым использовать для уточненного обозначения нижний индекс. Сохраняется возможность написания простых чисел в индексной системе.

Вопрос, как пишется в строительной механике и сопромате данная величина, заставляет задуматься студентов. В данных дисциплинах под буквой латинского алфавита S подразумевается обозначение статического момента. Так выражается площадь по отношению к рассматриваемой оси. В качестве символа, обозначающего данный показатель, используется буква латинского алфавита A или F.

Полезное видео

Подведем итоги

Пространственное представление об изучаемом геометрическом объекте становится возможным благодаря площади. Обозначение данного показателя разнится в зависимости от выбранной дисциплины.

Источник

Каким знаком обозначается площадь

Опубликовано 23.06.2022

В математике площадь плоских фигур обозначается определенным знаком. Какой буквой обозначается площадь в математике – она обозначается буквой S.

Запомни!

Площадь плоской фигуры в математике обозначается буквой S.

История обозначения

Почему знак площади в математике – это буква S. Так как буква из латинского алфавита, то и ответ надо искать в словах, которые могут начинаться с этой буквы. Например, слово “square” означает площадь.

Кстати, иностранные школьники используют еще одну букву для обозначения площади плоской фигуры – латинскую букву A, от начальной буквы слова “area” – площадь.

Так или иначе, но во всем мире общепринятым знаком площади является знак S.

Как обозначать

Если нам нужно указать площадь какой-либо фигуры, то мы просто напишем S= и число, которому равна площадь. Например, как записать “площадь прямоугольника ABCD равно 40 квадратных сантиметров”? А вот так: $S_{ABCD}=40$ см².

Аналогично запишем и площадь треугольника, например, если нам известно, что площадь некоторого треугольника ABC равна 45 см². Значок площади поможет нам в записи: $S_{ABC}=45$ см².

Если вы работаете с зарубежными учебниками (не с китайскими – в Китае тоже площадь обозначается знаком S), то площадь надо будет обозначать заглавной буквой A.

В российских школах площадь плоской фигуры (квадрат, треугольник, трапеция и другие) обозначается заглавной буквой латинского алфавита – буквой S. Если дано обозначение фигуры с помощью указания ее вершин, то под буквой S в виде нижнего индекса пишется название фигуры.

Например, площадь квадрата ABCD можно обозначить так $S_{ABCD}$ , а площадь треугольника ABC обозначается так $S_{ABC}$ .

( 2 оценки, среднее 5 из 5 )

Источник

Как обозначается площадь в строительстве?

Какой латинской буквой отмечается площадь?

Мерой протяжённости плоского участка Земли по длине и ширине является площадь. В математике она обычно обозначается латинской буквой S (от англ. «square» — «площадь», «квадрат») или греческой буквой σ (сигма). S обозначает площадь фигуры на плоскости или площадь поверхности тела.

Чем отмечается площадь?

Площадь
, от фр. superficie
Размерность	L²
Единицы измерения
СИ	м²

Какой буквой обозначают ширину?

Как было сказано выше, в математике рассматриваемая величина является одним из трех пространственных измерений любого объекта, при условии что его замеры производятся в поперечном направлении. Так чем знаменита ширина? Обозначение буквой «В» она имеет.

Как обозначается площадь математика?

В таких науках, как физика и математика, используется знак латинского алфавита S. Данная буква имеет произношение . Обратите внимание! Знаком S обозначают площадь таких фигур, как квадрат, треугольник, ромб, прямоугольник, круг.

Как обозначается площадь на чертеже?

В математике и в физике площадь обозначается буквой S заглавной (читается: [эс]). Так, в геометрии этой буквой обозначается площадь любых фигур (треугольника, прямоугольника, квадрата, ромба и т. п.). Если нужно в одной задаче обозначить площадь нескольких фигур, то используются нижние индексы.

Как найти площадь прямоугольника в 3 классе?

Для определения площади прямоугольника необходимо длину прямоугольника умножить на его ширину. Площадь прямоугольника вычисляется умножением длины АК на ширину КМ.

Какая буква обозначает толщину?

Обозначения буквенные (ЕСКД ГОСТ 2.321-68)

Длина	L, l
Высота, глубина	H, h
Толщина (листов, стенок, ребер и т.д.)	s
Диаметр	D, d
Радиус	R, r

Какой буквой обозначается площадь треугольника?

Как обозначается площадь прямоугольника?

Площадь прямоугольника равна произведению его длины и ширины. S = · b, где S — площадь, — длина, b — ширина прямоугольника. Периметр прямоугольника равен удвоенной сумме его длины и ширины. P = ( + b) · 2, где P — периметр, — длина, b — ширина прямоугольника.

Как записать площадь?

S = a · b, где a,b – ширина и длина фигуры. К примеру, если длина прямоугольника 5 см, а ширина 4 см, то площадь будет равна 4*5=20 см2.

Как рассчитать площадь комнаты?

Простая комната прямоугольной или квадратной формы

В помещении, которое представляет собой прямоугольник или квадрат, нужно измерить длину и ширину и умножить значения между собой. Вы получите площадь комнаты в квадратных метрах. Формула по которой можно высчитать площадь: S комнаты = А х B, где A – длина, B – ширина.

Что нужно сделать чтобы найти ширину?

Ширину можно вычислить по длине, если известна еще площадь или периметр прямоугольника. Например, зная площадь и длину, можно найти ширину по формуле а = S/b. А зная периметр и длину, можно вычислить ширину по формуле a = (P — 2b) / 2.

Как пишется ширина и длина?

длину — буквой l, если речь идет об одной прямой линии: маятнике, рычаге, отрезке, прямой. Но если речь идет о геометрической фигуре, например, прямоугольнике, то используется А; высоту или глубину – h; ширину – В.

В каком порядке указываются размеры?

Габаритные размеры изделия длина 1500 мм ширина 1200 мм высота 2500 мм, есть сомнению что может нужно записать 1500×1200×2500, как прописана во многих формулярах изделий, но вот правильности чередования в ГОСТах (длина×ширина×высота или ширина×длина×высота или. )

Формула площади.

Формула площади необходима для определения площадь фигуры, которая является вещественнозначной функцией, определённой на некотором классе фигур евклидовой плоскости и удовлетворяющая 4м условиям:

Положительность — Площадь не может быть меньше нуля;
Нормировка — квадрат со стороной единица имеет площадь 1;
Конгруэнтность — конгруэнтные фигуры имеют равную площадь;
Аддитивность — площадь объединения 2х фигур без общих внутренних точек равна сумме площадей этих фигур.

Результат сложения расстояний между серединами противоположных сторон выпуклого четырехугольника будут равна его полупериметру.

Сектор круга.

Площадь сектора круга равна произведению его дуги на половину радиуса.

Сегмент круга.

Чтобы получить площадь сегмента ASB, достаточно из площади сектора AOB вычесть площадь треугольника AOB.

Площадь эллипса равна произведению длин большой и малой полуосей эллипса на число пи.

Эллипс.

Еще один вариант как вычислить площадь эллипса – через два его радиуса.

Треугольник. Через основание и высоту.

Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты.

Треугольник. Через две стороны и угол.

Площадь треугольника равна половине произведения двух его сторон, умноженного на синус угла между ними.

Треугольник. Формула Герона.

Площадь треугольника можно определить при помощи формулы Герона.

Треугольник. Через радиус вписанной окружности.

Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.

Треугольник. Через радиус описанной окружности.

Площадь треугольника можно определить по радиусу описанной окружности.

Треугольник.

Площадь прямоугольного треугольника.

Треугольник.

Площадь прямоугольного треугольника через вписанную окружность.

Треугольник.

Формула Герона для прямоугольного треугольника.

Треугольник.

Площадь равнобедренного треугольника.

Трапеция.

Площадь трапеции равна произведению полусуммы ее оснований на высоту.

Ромб. По длине стороны и высоте.

Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты.

Ромб. По длине стороны и углу.

Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба.

Ромб.

Формула площади ромба по длинам его диагоналей.

Формула площади круга через его радиус и диаметр.

Квадрат. Через его сторону.

Площадь квадрата равна квадрату длины его стороны.

Квадрат. Через его диагонали.

Площадь квадрата равна половине квадрата длины его диагонали.

Правильный многоугольник.

Для определения площади правильного многоугольника необходимо разбить его на равные треугольники, которые бы имели общую вершину в центре вписанной окружности.

Сфера.

Площадь поверхности сферы равна учетверенной площади большого круга.

Куб.

Площадь поверхности куба равна сумме площадей шести его граней.

Конус.

Боковая площадь поверхности круглого конуса равна произведению половины окружности основания (C) на образующую (l).

S = 1/2 C * l = π r l

Усеченный конус.

Боковая площадь поверхности усеченного конуса.

Цилиндр.

Площадь боковой поверхности круглого цилиндра.

Сегмент шара.

Площадь поверхности шарового сегмента равняется произведению его высоты на окружность большого круга шара.

Поверхность шарового слоя.

Кривая поверхность шарового слоя равна произведению его высоты на окружность большого круга шара.

Каким символом обозначается площадь в геометрии?

Площадь — численная характеристика двумерной (плоской или искривлённой) геометрической фигуры, неформально говоря, показывающая размер этой фигуры. Исторически вычисление площади называлось квадратурой.

Фигура, имеющая площадь, называется квадрируемой. Конкретное значение площади для простых фигур однозначно вытекает из предъявляемых к этому понятию практически важных требований. Фигуры с одинаковой площадью называются равновеликими.

Источник

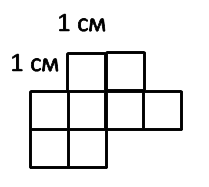
Рассмотрим фигуру ниже:

Вся фигура состоит из 8 квадратов со стороной 1 см каждый.

Площадь одного такого квадрата называют квадратным сантиметром и записывают:
1 см².

Площадь всей фигуры 8 см².

Запомните!

Площадь измеряется только в квадратных единицах длины. Всегда проверяйте свои ответы.

В математике для нахождения площади геометрических фигур используют специальные формулы,
в которых площадь обозначается заглавной латинской буквой «S».

Напоминаем, что площадь квадрата можно найти, умножив длину его стороны на саму себя.

Единицей площади служит площадь единичного квадрата. Например, если длина стороны квадрата,
равна 1 м, то его площадь равна 1
квадратному метру (1 м²); если длина
его стороны равна 1 см, то его площадь
равна 1 квадратному сантиметру
(1 см²).

Для нахождения площади какой-либо фигуры её сравнивают с единичным квадратом.

Как перевести квадратные единицы

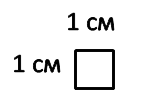
Рассмотрим квадрат со стороной 1 см.

Его площадь равна:

S = 1 см · 1 см = 1см²

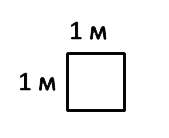
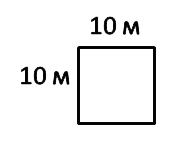
Рассмотрим квадрат со стороной 1 м.

Его площадь равна:

S = 1 м · 1 м = 1 м²

Известно, что: 1 м = 100 см

1 м² = 1 м · 1 м = 100 см · 100 см = 10 000 см²

Увеличим сторону квадрата равную 1 м в
10 раз. Получим квадрат со
стороной 10 м.

Площадь такого квадрата называют ар или сотка.

S = 10 м · 10 м = 100 м²

В одном аре — сто квадратных метров.

Слово «сотка» часто используют в дачном хозяйстве, хотя это тоже самое, что и «ар».

1 ар (сотка) = 100 м²

Чтобы выразить ар в cм², вспомним, что 1 м² = 10 000 см².

Значит: 1 ар (сотка) = 100 м² = 100 · 10 000 см² = 1 000 000 см²

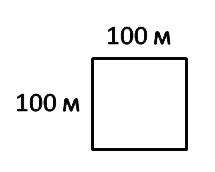
Увеличим сторону квадрата равную 10 м в 10 раз.
Получим квадрат со
стороной 100 м.

Площадь такого квадрата называют гектар. Сокращенно «га». Но при произношении вслух наименование
проговаривается полностью.

Выразим гектар в квадратных метрах.

1 га = 100 м · 100 м = 10 000 м²

Теперь определим, сколько в одном гектаре аров.

1 ар = 100 м²

Значит: 10 000 м² : 100 м² = 100 (ар)

1 га = 100 ар

Для измерения больших площадей, например, территорий государств, материков используют квадратный километр.
То есть квадрат со стороной 1 км и
площадью 1 км².

1 км = 1000 м

1 км² = 1 км · 1 км = 1 000 м · 1 000 м = 1 000 000 м²

Для простоты расчётов предлагаем вам в помощь таблицу переводов квадратных единиц.

Таблица переводов квадратных единиц

Данная таблица поможет перевести гектары в кв. метры, гектары в ары и наоборот.

	га	ар	м²	cм²
1 км²	100 га	10 000 ар	1 000 000 м²	1 000 000 000 cм²
1 га	1 га	100 ар	10 000 м²	100 000 000 cм²
1 ар	0,01 га	1 ар	100 м²	1 000 000cм²
1 м²	0,000 1 га	0,01 ар	1 м²	10 000 cм²

Источник

Содержание

— Какой буквой обозначается площадь фигуры?
— Как обозначается площадь прямоугольника?
— Что такое площадь как пишется?
— Что такое площадь 3 класс?
— Чем обозначается площадь и периметр?
— Какая буква обозначает толщину?
— Как пишется сокращенно площадь?
— Что такое периметр в математике?

Какой буквой обозначается площадь фигуры?

Обозначение площади

S (square) — знак площади. Если параметры фигуры переданы в разных единицах измерения длины, мы не сможем решить ни одну задачу.

Как обозначается площадь прямоугольника?

Для вычисления площади прямоугольника нужно умножить его длину на ширину. Нельзя вычислять периметр или площадь, если длина и ширина выражены в разных единицах длины.

Что такое площадь как пишется?

Слово “площадь” пишется только так – площадь.

Что такое площадь 3 класс?

Площадь – внутренняя часть любой плоской геометрической фигуры. Квадрат – это прямоугольник, у которого все стороны равны. … Квадратный сантиметр – квадрат со стороной 1 сантиметр.

Чем обозначается площадь и периметр?

Периметр прямоугольника – это сумма длин всех сторон прямоугольника или сумма длины и ширины, умноженная на 2. Периметр обозначается латинской буквой P.

Какая буква обозначает толщину?

Обозначения буквенные (ЕСКД ГОСТ 2.321-68)

Длина	L, l
Ширина	B, b
Высота, глубина	H, h
Толщина (листов, стенок, ребер и т.д.)	s
Диаметр	D, d

Как пишется сокращенно площадь?

Сокращенно «га».

Что такое периметр в математике?

Периметром принято называть длину всех сторон многоугольника. Какой буквой обозначается периметр — заглавной латинской P. Под обозначением «P» удобно писать маленькими буквами название фигуры, чтобы не запутаться в задачах по ходу решения.

Интересные материалы:

Как определить прямой угол или нет?
Как определить работающую камеру наблюдения?
Как определить радиус окружности?
Как определить силикон или нет?
Как определить скорый отел у коровы?
Как определить SMD диод?
Как определить SMD стабилитрон?
Как определить толщину акриловой ванны?
Как определить толщину пленки для теплицы?
Как определить цену на землю?

Источник

Практически каждый раз при решении задач по математике, физике или другим дисциплинам приходится выбирать обозначения тех или иных величин. Среди них следует различать обозначения общепринятые (или даже устанавливаемые нормативными документами) и обозначения, выбор которых обычно выполняется самостоятельно, в зависимости от индивидуальных предпочтений. Есть также величины, обозначения которых в разных дисциплинах приняты свои. Есть обозначения международные, а есть – принятые различными в разных странах.

Как обозначается длина, ширина, высота, толщина, глубина

Обозначение длины в математике обычно зависит от того, какой объект в данном случае рассматривается: одномерный, двумерный или трехмерный. Если речь идёт об обозначении длины одномерного объекта (нити, проволоки и т.п.) или обозначении длины куска сортового проката (трубы, швеллера, двутавра и т.п.), то длина обычно обозначается буквой l (написанной курсивом, т.е. с наклоном, чтобы не было похоже на «единицу») или L. Если же речь идёт о двумерном объекте, в котором нужно обозначить не только длину, но и ширину, то обычно принимают одну из таких пар обозначений: a и b (а – длина, b — ширина), l и b (l – длина, b — ширина), l и h (l – длина, h — высота). Для обозначений могут быть использованы и соответствующие заглавные буквы, в литературе часто встречается сочетание L, B, H (L – длина, В – ширина, Н — высота). Эти же буквы приняты и в физике для обозначения длины, ширины, высоты объектов. Если же речь идёт о длине волны, то она обозначается строчной греческой буквой «лямбда».

Высота обозначается обычно буквой h (читается: [аш]). В технической литературе для обозначения высоты также используют букву Н (читается: [аш]). Этими же буквами (h, реже Н) обозначается глубина.

Толщина в физике обозначается либо строчной (маленькой) буквой s, либо греческой строчной буквой «дельта», с использованием (при необходимости) нижних индексов (обычно – числовых, соответствующих номеру слоя, т.е. 1, 2, 3, 4 и т.д.).

Вопросы «как в математике пишется длина», «как в математике пишется периметр», «как в математике пишется площадь» некорректны. Здесь уместно вместо слова «пишется» употребить слово «обозначается».

Как обозначается периметр

При решении задач по геометрии часто возникает необходимость обозначить периметр. Периметр в математике обозначается заглавной (т.е. большой) буквой Р (читается: [пэ]).

Как обозначается площадь

Обозначение площади в научно-технической литературе можно встретить различные. Поэтому и возникают вопросы «Как обозначается площадь в математике», «Как обозначается площадь в физике» и т.п. Ответ на вопрос о том, какой буквой обозначается площадь, зависит от конкретной дисциплины, о которой в данный момент идёт речь. В математике и в физике площадь обозначается буквой S заглавной (читается: [эс]). Так, в геометрии этой буквой обозначается площадь любых фигур (треугольника, прямоугольника, квадрата, ромба и т.п.). Если нужно в одной задаче обозначить площадь нескольких фигур, то используются нижние индексы. В качестве индекса могут быть использованы числа (1, 2, 3 и т.д.), т.е. площади обозначаются как S₁, S₂, S₃ и т.д., а могут быть использованы сокращения от названия фигур (S_тр, S_пр, S_кв, S_р и т.п.). При необходимости обозначения в одной задаче площадей нескольких треугольников чаще в качестве нижнего индекса принимают обозначения этих треугольников (например, S_ABC, S_MNP, S_LPH со значком треугольника перед буквами ABC, MNP, LPH). В физике обозначается площадь поперечного сечения той же буквой S, при необходимости – с добавлением нижнего индекса (например, S₁, S₂, S₃ и т.д.). Однако, в сопромате и в строительной механике буквой S (с добавлением индекса) обозначается не площадь, а статический момент площади относительно оси, а для обозначения площади в этих дисциплинах обычно используются буквы F (читается: [эф]) и A (читается: [а]).

Источники информации:

Справочник по элементарной математике. Геометрия, тригонометрия, векторная алгебра/ Под ред. П.Ф. Фильчакова
Яворский Б.М., Детлаф А.А., Лебедев А.К. Справочник по физике для инженеров и студентов вузов
ru.wikipedia.org – список обозначений в физике

Источник

Единицы измерения
Площадь

Размерность	L²
СИ	м²
СГС	см²
Примечания
скаляр

Площадь — численная характеристика двумерной (плоской или искривлённой) геометрической фигуры^[1], неформально говоря, показывающая размер этой фигуры. Исторически вычисление площади называлось квадратурой. Фигура, имеющая площадь, называется квадрируемой. Конкретное значение площади для простых фигур однозначно вытекает из предъявляемых к этому понятию практически важных требований (см. ниже). Фигуры с одинаковой площадью называются равновеликими.

Общий метод вычисления площади геометрических фигур предоставило интегральное исчисление. Обобщением понятия площади стала теория меры множества, пригодная для более широкого класса геометрических объектов.

Для приближенного вычисления площади на практике используют палетку или специальный измерительный прибор — планиметр.

Содержание

1 Свойства
2 Общий метод определения площади
- 2.1 Площадь плоской фигуры
  - 2.1.1 Декартовы координаты
  - 2.1.2 Полярные координаты
- 2.2 Площадь поверхности
3 Единицы измерения площади
- 3.1 Метрические единицы
- 3.2 Русские устаревшие
- 3.3 Античные
4 Формулы вычисления площадей простейших фигур
- 4.1 Планиметрические фигуры
- 4.2 Формулы для вычисления площади круга, его частей, описанных и вписанных в круг фигур
- 4.3 Формулы для вычисления площади поверхности тел в пространстве
5 См. также
6 Литература
7 Ссылки
8 Примечания

Свойства

Площадь единичного квадрата равна 1.
Площадь аддитивна.
Площадь неотрицательна.
Площади конгруэнтных фигур равны.

Для фигур на плоскости, не состоящих из целого количества единичных квадратов, а также для искривлённых трёхмерных поверхностей, площадь определяется с помощью предельного перехода; при этом требуется, чтобы как фигура, так и её граница были кусочно-гладкими^[2].

Общий метод определения площади

Площадь плоской фигуры

Декартовы координаты

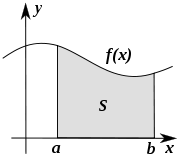
Определённый интеграл как площадь фигуры

Площадь между графиками двух функций равна разности интегралов от этих функций в одинаковых пределах интегрирования

Площадь, заключённая между графиком непрерывной функции на интервале [a, b] и горизонтальной осью, может быть вычислена как определённый интеграл от этой функции:

Площадь, заключённая между графиками двух непрерывных функций на интервале [a, b] находится как разность определённых интегралов от этих функций:

Полярные координаты

В полярных координатах: площадь, ограниченная графиком функции и лучами вычисляется по формуле:

$S = {1 over 2} intlimits_{theta_1}^{theta_2} r^2(theta) , dtheta$

Площадь поверхности

Площадь искривлённой поверхности A, заданной вектор-функцией , даётся двойным интегралом:

$S = iintlimits_A left|frac{partialmathbf{r}}{partial u}timesfrac{partialmathbf{r}}{partial v}right|,du,dv.$

То же в координатах:

$S = iintlimits_A sqrt{left(frac{D(x,y)}{D(u,v)}right)^2+left(frac{D(y,z)}{D(u,v)}right)^2+left(frac{D(z,x)}{D(u,v)}right)^2};mathrm{d},u,mathrm{d},v$

Здесь $frac{D(y,z)}{D(u,v)}=begin{vmatrix}y'_u & y'_v \ z'_u & z'_v end{vmatrix},quadfrac{D(z,x)}{D(u,v)}=begin{vmatrix} z'_u & z'_v\ x'_u & x'_v end{vmatrix},quadfrac{D(x,y)}{D(u,v)}=begin{vmatrix}x'_u & x'_v \ y'_u & y'_v end{vmatrix}$ .

Единицы измерения площади

Метрические единицы

Квадратный километр, 1 км² = 1 000 000 м²
Гектар, 1 га = 10 000 м²
Ар (сотка), 1 а = 100 м²
Квадратный метр, производная единица системы СИ 1 м² = 1 са (сантиар)
Квадратный дециметр, 100 дм² = 1 м²;
Квадратный сантиметр, 10 000 см² = 1 м²;
Квадратный миллиметр, 1 000 000 мм² = 1 м².

Русские устаревшие

Квадратная верста = 1,13806 км²
Десятина = 10925,4 м²
Копна = 0,1 десятины — сенные покосы меряли копнами
Квадратная сажень = 4,55224 м²

Мерами земли при налоговых расчетах были выть, соха, обжа, размеры которых зависели от качества земли и социального положения владельца. Существовали и различные местные меры земли:коробья, веревка, жеребья и др.

Античные

Арура

Формулы вычисления площадей простейших фигур

Планиметрические фигуры

Фигура	Формула	Переменные
Квадрат		— длина стороны квадрата.
Правильный треугольник	$frac{sqrt{3}}{4}s^2,!$	— длина стороны треугольника.
Правильный шестиугольник	$frac{3sqrt{3}}{2}s^2,!$	— длина стороны шестиугольника.
Правильный восьмиугольник	$2(1+sqrt{2})s^2,!$	— длина стороны восьмиугольника.
Правильный многоугольник	$frac{P^2/n} {4 cdot tan(pi/n)},!$	— периметр, а — количество сторон.
Прямоугольный треугольник	$frac{ab}{2},!$	и — катеты треугольника.
Произвольный треугольник	$frac{1}{2}ah,!$	— сторона треугольника, — высота, проведенная к этой стороне.
$frac{1}{2}ab sin alpha,!$	, — любые две стороны, — угол между ними.
(формула Герона)	, , — стороны треугольника, — полупериметр $left(p = frac{a+b+c}{2}right)$ .
$frac{1}{2}begin{vmatrix} x_0 & y_0 & 1 \ x_1 & y_1 & 1 \ x_2 & y_2 & 1 end{vmatrix}$	в случае обхода вершин треугольника по часовой стрелке получим положительный результат, иначе отрицательный.
Прямоугольник		и — длины сторон прямоугольника (его длина и ширина).
Параллелограмм		и — длина стороны и опущенной на неё высоты соответственно.
	и — соседние стороны параллелограмма, — угол между ними.
Ромб	$frac{1}{2}cd$	и — длины диагоналей ромба.
Эллипс		и — длины малой и большой полуосей.
Трапеция	$frac{1}{2}(a+b)h ,!$	та — параллельные стороны, и — расстояние между ними (высота трапеции).

Формулы для вычисления площади круга, его частей, описанных и вписанных в круг фигур

Фигура	Формула	Переменные
Круг	или $frac{pi d^2}{4} ,!$	— радиус, а — диаметр круга.
Сектор круга	$frac{alpha r^2}{2},!$	— радиус круга, — центральный угол сектора (в радианах).
Сегмент	$frac{r^2}{2}(alpha - sin alpha),!$	— радиус круга, — центральный угол сегмента (в радианах).
Треугольник, вписанный в окружность	$frac{abc}{4R}$	, , — стороны треугольника, — радиус описанной окружности.
Произвольный многоугольник, описанный вокруг окружности	$frac{1}{2}Pr,!$	— радиус окружности, вписанной в многоугольник, и — периметр многоугольника.

Формулы для вычисления площади поверхности тел в пространстве

Тело	Формула	Переменные
Полная площадь поверхности цилиндра		и — радиус и высота соответственно.
Площадь боковой поверхности цилиндра		и — радиус и высота соответственно.
Полная площадь конуса		и — радиус и высота боковой поверхности соответственно.
Площадь боковой поверхности конуса		и — радиус и образующая боковой поверхности соответственно.
Площадь поверхности сферы (шара)	или	и радиус и диаметр, соответственно.

См. также

Площадь фигуры — математические аспекты понятия.
Длина кривой
Квадратура (математика)
Объём
Поверхность

Литература

Рашевский П. К. Риманова геометрия и тензорный анализ. Изд. 3-е, М.: Наука, 1967.
Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. — М.: ФИЗМАТЛИТ, 1960. — Т. 2. — 680 с. — ISBN 5-9221-0155-2

Ссылки

Болтянский В. О понятиях площади и объёма. Квант, № 5, 1977.
Рохлин В. А. Площадь и объём. Энциклопедия элементарной математики, Книга 5, Геометрия.

Примечания

↑ Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 4.
↑ Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. — Изд. 6-е. — М.: ФИЗМАТЛИТ, 1966. — Т. 2. — С. 186-224. — 800 с.

Источник