В данной публикации мы рассмотрим, как можно вычислить площадь поверхности прямоугольного параллелепипеда и разберем пример решения задачи для закрепления материала.
- Формула вычисления площади
- Пример задачи
Формула вычисления площади
Площадь (S) поверхности прямоугольного параллелепипеда вычисляется следующим образом:
S = 2 (ab + bc + ac)
Формула получена следующим образом:
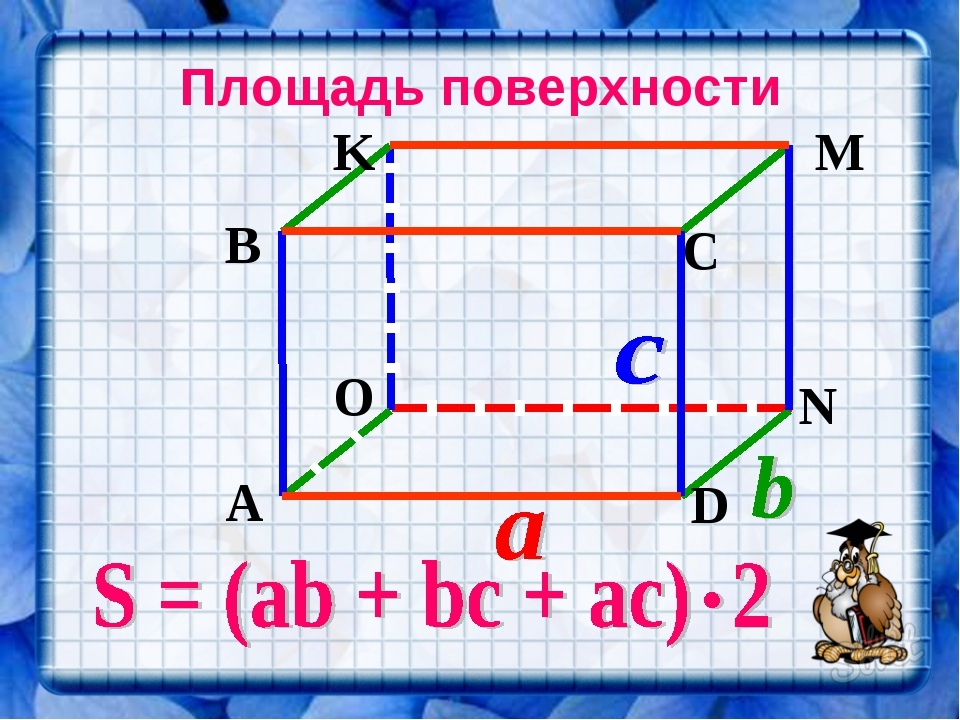
- Гранями прямоугольного параллелепипеда являются прямоугольники, причем противоположные грани равны между собой:
- два основания: со сторонами a и b;
- четыре боковые грани: со стороной a/b и высотой c.
- Сложив площади всех граней, каждая из которых равна произведению сторон разной длины, получаем: S = ab + ab + bc + bc + ac + ac = 2 (ab + bc + ac).
Пример задачи
Вычислите площадь поверхности прямоугольного параллелепипеда, если известно, что его длина равна 6 см, ширина – 4 см, а высота – 7 см.
Решение:
Воспользуемся формулой выше, подставив в нее известные значения:
S = 2 ⋅ (6 см ⋅ 4 см + 6 см ⋅ 7 см + 4 см ⋅ 7 см) = 188 см2.
Прямоугольным параллелепипедом называется трехмерное тело, у которого противоположные грани параллельны и являются прямоугольниками. Проще говоря, прямоугольный параллелепипед представляет собой вытянутый куб.
Онлайн-калькулятор площади поверхности параллелепипеда
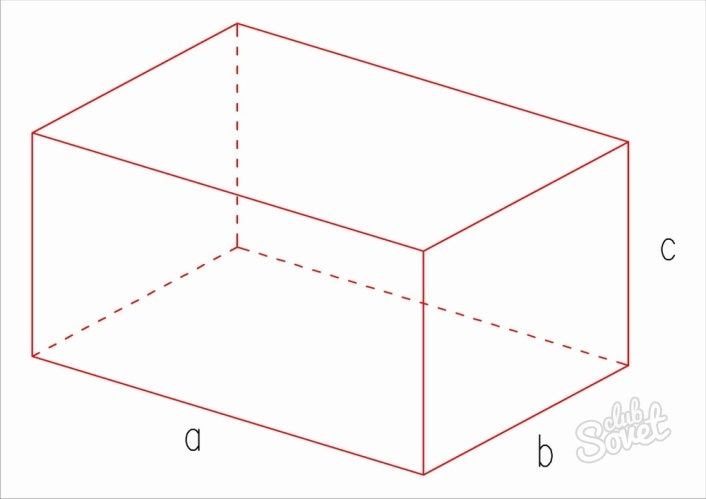
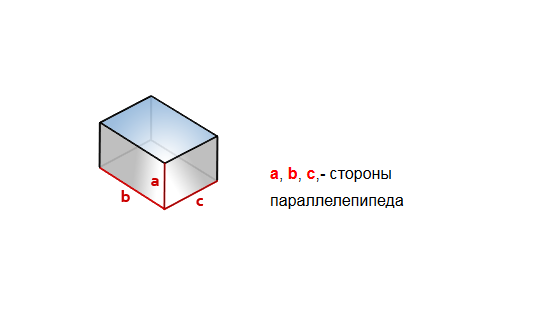
Прямоугольный параллелепипед можно охарактеризовать тремя числами — длинами его сторон: aa, bb, cc.
Формула площади поверхности параллелепипеда
Чтобы найти полную площадь поверхности параллелепипеда, нужно сложить площади всех его граней. Граней у параллелепипеда шесть, поэтому:
S=S1+S2+S3+S4+S5+S6S=S_1+S_2+S_3+S_4+S_5+S_6
Но так как противоположные грани прямоугольного параллелепипеда равны между собой, то: S1=S2S_1=S_2, S3=S4S_3=S_4, S5=S6S_5=S_6.
Поскольку гранями данного параллелепипеда являются прямоугольники, то их площади равны соответственно:
S1=S2=abS_1=S_2=ab
S3=S4=bcS_3=S_4=bc
S5=S6=acS_5=S_6=ac
Итак, полная площадь поверхности параллелепипеда:
S=2(ab+bc+ac)S=2(ab+bc+ac)
Из этой формулы следует, что если a=b=ca=b=c, то получим: S=6a2S=6a^2. Это и есть формула для площади поверхности куба со стороной aa.
Найдите площадь поверхности прямоугольного параллелепипеда со сторонами 2 см.2text{ см.}, 4 см.4text{ см.}, 6 см.6text{ см.}
Решение
a=2a=2
b=4b=4
c=6c=6
S=2(ab+bc+ac)=2(2⋅4+4⋅6+2⋅6)=88 (см. кв.)S=2(ab+bc+ac)=2(2cdot4+4cdot6+2cdot6)=88text{ (см. кв.)}
Ответ: 88 см. кв.88text{ см. кв.}
Найдите площадь поверхности прямоугольного параллелепипеда высотой 3 см.3text{ см.}, в основании которого лежит квадрат со стороной 1 см.1text{ см.}
Решение
a=b=1a=b=1
c=3c=3
S=2(ab+bc+ac)=2(1+3+3)=14 (см. кв.)S=2(ab+bc+ac)=2(1+3+3)=14text{ (см. кв.)}
Ответ: 14 см. кв.14text{ см. кв.}
Не знаете, где заказать задачу по геометрии? Обратитесь к нашим экспертам в данной области!
Тест по теме «Площадь поверхности параллелепипеда»

{S_{полн} = 2(ab+bc+ac)}
Чтобы найти площадь поверхности параллелепипеда необходимо знать длины трех его ребер. Для вычисления площади поверхности прямоугольного параллелепипеда используется формула, в которой сумма попарных произведений ребер параллелепипеда умножается на 2. По другому формулу можно трактовать как произведение площадей трех граней параллелепипеда (так как произведение ребер — это площадь грани). Кроме того на странице вы найдете калькулятор, с помощью которого в режиме онлайн можно найти площадь полной и боковой поверхности прямоугольного параллелепипеда.
В дополнение на сайте можно найти объем параллелепипеда.
Прямоугольный параллелепипед — это параллелепипед, у которого все грани — прямоугольники.
Ребро — сторона прямоугольного параллелепипеда. Длина, ширина и высота — это ребра прямоугольного параллелепипеда.
Содержание:
- калькулятор площади поверхности прямоугольного параллелепипеда
- формула площади поверхности прямоугольного параллелепипеда
- формула площади боковой поверхности прямоугольного параллелепипеда
- примеры задач
Формула площади поверхности прямоугольного параллелепипеда
{S_{полн} = 2(ab+bc+ac)}
a — длина прямоугольного параллелепипеда
b — ширина прямоугольного параллелепипеда
c — высота прямоугольного параллелепипеда
Формула площади боковой поверхности прямоугольного параллелепипеда
{S_{бок} = 2(ac+bc)}
a — длина прямоугольного параллелепипеда
b — ширина прямоугольного параллелепипеда
c — высота прямоугольного параллелепипеда
Примеры задач на нахождение площади поверхности прямоугольного параллелепипеда
Задача 1
Найдите площадь поверхности прямоугольного параллелепипеда измерения которого равны 2 4 и 5.
Решение
Для нахождения площади поверхности воспользуемся первой формулой. Подставим в нее значения длины, ширины и высоты параллелепипеда и произведем вычисления.
S_{полн} = 2(ab+bc+ac) = 2(2 cdot 4 + 4 cdot 5 + 2 cdot 5) = 2(8 + 20 + 10) = 2(38) = 76 : см^2
Ответ: 76 см²
Проверим ответ с помощью калькулятора .
Задача 2
Найдите площадь поверхности прямоугольного параллелепипеда, если его измерения равны 3см 5см и 6см.
Решение
Задача аналогична предыдущей, поэтому повторим действия, подставив новые значения измерений параллелепипеда.
S_{полн} = 2(ab+bc+ac) = 2(3 cdot 5 + 5 cdot 6 + 3 cdot 6) = 2(15 + 30 + 18) = 2(63) = 126 : см^2
Ответ: 126 см²
Для проверки ответа используем калькулятор .
Задача 3
Найдите площадь поверхности прямоугольного параллелепипеда измерения которого равны 9м 24м 11м.
Решение
Еще одна типовая задача. Для ее решения также воспользуемся первой формулой.
S_{полн} = 2(ab+bc+ac) = 2(9 cdot 24 + 24 cdot 11 + 9 cdot 11) = 2(216 + 264 + 99) = 2(579) = 1158 : см^2
Ответ: 1158 см²
Проверка .
Задача 4
Найдите площадь боковой поверхности прямоугольного параллелепипеда у которого a=4см, b=5см, c=7см.
Решение
В этой задаче нам необхожимо найти площадь боковой поверхности. Поэтому мы будем использовать для ее решения вторую формулу.
S_{бок} = 2(ac+bc) = 2(4 cdot 7 + 5 cdot 7) = 2(28 + 35) = 2(63) = 126 : см^2
Ответ: 126 см²
Как всегда ответ можно проверить с помощью калькулятора .
Как найти площадь поверхности параллелепипеда
На данной странице калькулятор поможет рассчитать площадь поверхности параллелепипеда онлайн. Для расчета задайте высоту, ширину и длину.
Прямоугольный параллелепипед – это многогранник, у которого все грани являются прямоугольниками.
Через стороны
a:
b:
c:
Результат
Ответы:
Формула площади поверхности параллелепипеда через его ребра:
a, b, c — ребра параллелепипеда.
Алик Беникович Айрапетян
Эксперт по предмету «Калькуляторы»
Задать вопрос автору статьи
На этой странице вы узнаете, как выглядят формулы для расчёта полной и боковой площади поверхности параллелепипеда. Также на страницу добавлен онлайн-калькулятор для расчёта площади прямоугольного параллелепипеда.
Определение 1
Параллелепипед является разновидностью призмы, основания которой представляют собой параллелограммы. Также параллелепипедами называют призмы, в основании которых лежат многогранники, а все грани являются параллелограммами.
Наиболее знакомый всем вид параллелепипеда — это прямоугольный параллелепипед. Все его грани являются прямоугольниками.
Для расчёта полной площади прямоугольного параллелепипеда введите значение сторон и высоты в поля для ввода.
Площадь поверхности параллелепипеда через стороны
Для прямоугольного параллелепипеда площадь поверхности определяется по формуле:
$S = 2 cdot (a cdot b + b cdot h + a cdot h)$, здесь
$a, b$ — стороны основания параллелепипеда;
$h$ — высота параллелепипеда.

Начни разбираться в искусстве
Обучающие курсы по психологии, маркетингу, нутрициологии и работе в сфере кино
Выбрать программу
Разберём пример на нахождение полной площади параллелепипеда.
Пример 1
Задача
Стороны основания прямоугольного параллелепипеда равны $a = 3$ см и $b = 7$ см, а его высота $h$ равна $4$ см. Чему равна полная площадь поверхности параллелепипеда?
Решение:
Воспользуемся вышеприведённой формулой:
$S = 2 cdot (3 cdot 4 + 7 cdot 4 + 3 cdot 7) = 122$ кв. см.
Результаты совпадают с решением онлайн-калькулятора, а значит, ответ найден верно.
Также используя следующий онлайн-калькулятор, вы сможете рассчитать площадь боковой поверхности прямоугольного параллелепипеда.
Площадь боковой поверхности прямоугольного параллелепипеда через стороны
Площадь боковой поверхности прямоугольного параллелепипеда определяется по формуле:
$S = 2 cdot h cdot (a + b)$, где
$h$ — длина ребра параллелепипеда;
$a, b$ — стороны основания.
Рассчитаем для примера площадь боковой поверхности для параллелепипеда из предыдущей задачи.
Пример 2
Задача
$a = 3$ см, $b = 7$ см, а высота $h = 4$ см. Чему равна боковая площадь поверхности прямоугольного параллелепипеда?
Решение:
$S_б = 2 cdot 4 cdot (3 + 7) = 80$ кв. см.
Решение соответствует решению, полученному с помощью онлайн-калькулятора, а значит, ответ правильный.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Как найти площадь параллелепипеда
С началом изучения геометрии, все дети знакомятся с такими понятиями, как площадь и периметр. Если второе значение они учатся находить быстро, так как там не нужно умножение, то к значению площади младшие классы приходят позднее. Для начала, малышу нужно хорошо понять, что представляет из себя параллелепипед, какие грани он имеет и как выглядит в пространстве. Только потом стоит переходить к непосредственному перемножению и формуле площади. Как понять этот процесс постепенно, вы увидите в данной статье.
1
Как найти площадь параллелепипеда: грани фигуры
Чтобы понять, как именно находится площадь любой фигуры, вам достаточно найти её стороны. У параллелепипеда двенадцать рёбер и шесть граней. Попытайтесь заметить, сколько из них равны? Если вы находили площадь квадрата, то вам понадобилась бы всего одна величина, так как его стороны равны, у параллелепипеда же может быть своё значение высоты, ширины и длины. Вам достаточно знать три этих значения, чтобы найти площадь всей фигуры.
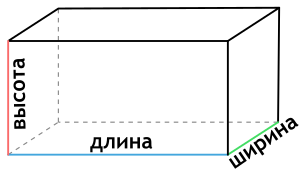
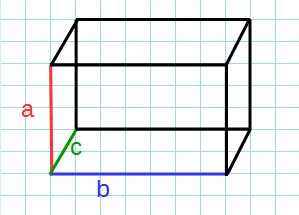
Посмотрите на рисунке, что называется шириной, длинной и высотой фигуры.
- a – высота параллелепипеда;
- b – его длинна. Длинной всегда является сама большая величина;
- с – ширина фигуры.
Заметьте, что, если бы величина “а” стала длиннее b в два раза, то она бы уже была длинной, а не высотой. Точно так же может быть с остальными сторонами. Все величины – сугубо относительное понятие, главное – вам понимать принцип их определения.
2
Как найти площадь параллелепипеда: формула
Когда вы знаете величины, вы без труда можете найти площадь параллелепипеда. Она выглядит так:
- S = ( аb + bc + ac ) х 2
То есть, вам нужно перемножить между собой все известные величины, сложить полученные значения, а потом умножить ещё на два. Умножение вдвое происходит потому, что параллелепипед – объёмная фигура и у неё есть совершенно одинаковые стороны.
Посмотрите на пример:
У параллелепипеда высота равна всего 2 см, его длина аж 22 см, а ширина составляет 5 см. В целом, это длинная фигура, очень сплющенная в высоту, если попытаться ее себе представить в уме. Попробуйте найти площадь данного параллелепипеда.
- Сначала, вы перемножите все известные величины, то есть, 2*22, 2*5 и 5*22. Получаются значения 10 см, 44 см и 110 см соответственно.
- Сложите все полученные решения. 10+44+110 получится 164 см.
- Осталось лишь умножить 164 см на два. Выходит, площадь параллелепипеда 328 см.
Вот так просто можно узнать площадь фигуры. Чуть позднее, можно усложнить задачу и найти одну из сторон при известной площади. Это закрепит знания ребенка и не даст ему забыть о формуле, по которой находится площадь.