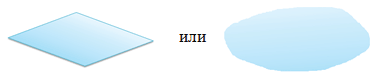А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Э Ю Я
пло́скость, -и, мн. -и, плоскосте́й (поверхность) и -ей (плоская шутка)
Рядом по алфавиту:
плосконо́сый
плоскопане́льный
плоскопаралле́льный
плоскопеча́тный
плоскополяризо́ванный
плоскоре́жущий
плоскоре́з , -а
плоскоре́зный
плоскосемя́нник , -а
плоскосемя́нный
плоскоспира́льный
плоскостно́й , (матем.; то же, что пло́скостный)
пло́скостность , -и
пло́скостный , кр. ф. -тен, -тна (изображенный в одной плоскости, без перспективы)
плоскосто́пие , -я
пло́скость , -и, мн. -и, плоскосте́й (поверхность) и -ей (плоская шутка)
плоскоте́лка , -и, р. мн. -лок
плоскохво́ст , -а
плоскоцилиндри́ческий
плоскочуло́чный
плоскошлифова́льный
плоску́шка , -и, р. мн. -шек
плот , плота́, предл. на плоту́
пло́тбище , -а
плотва́ , -ы́
плотви́ца , -ы, тв. -ей
плотви́чка , -и, р. мн. -чек
пло́тик , -а
плоти́на , -ы
плоти́нка , -и, р. мн. -нок
плоти́нный
Слово плоскостях может употребляться в 2-х разных значениях:
I. плоскостя́х
— предложный падеж, множественное число слова плоскость (в обычн. знач.)
В данном слове ударение должно быть поставлено на слог с буквой Я — плоскостЯх.
II. пло́скостях
— предложный падеж, множественное число слова плоскость (плоская шутка)
В указанном выше варианте ударение следует ставить на слог с первой буквой О — плОскостях.
Примеры предложений, как пишется плоскостях
Вслед «Илье», уносившему на плоскостях, на фюзеляже, на радиаторе куски дерева, обрывки металла и клочья зеленого шинельного сукна, неслись сотни снарядов автоматических пушек.
На текущей странице указано на какой слог правильно ставить ударение в слове плоскостях. Слово «плоскостях» может употребляться в разных значениях, в зависимости от которых ударение может падать на разные слоги. В слове плоскостя́х, предложный падеж, множественное число слова плоскость (в обычн. знач.), ударение должно быть поставлено на слог с буквой Я. В слове пло́скостях, предложный падеж, множественное число слова плоскость (плоская шутка), ударение ставят на слог с первой буквой О. Надеемся, что теперь у вас не будет вопросов, как пишется слово плоскостях, куда ставить ударение, какое ударение, или где должно стоять ударение в слове плоскостях, чтобы верно его произносить.
Как написать слово «плоскость» правильно? Где поставить ударение, сколько в слове ударных и безударных гласных и согласных букв? Как проверить слово «плоскость»?
пло́ско́сть
Правильное написание — плоскость, ударение падает на букву: о, безударными гласными являются: о.
Выделим согласные буквы — плоскость, к согласным относятся: п, л, с, к, т, звонкие согласные: л, глухие согласные: п, с, к, т.
Количество букв и слогов:
- букв — 9,
- слогов — 2,
- гласных — 2,
- согласных — 6.
Формы слова: пло́скость, -и, мн. -и, -е́й (поверхность) и -ей (плоская шутка).
Параллельные прямые a и b лежат в плоскости гамма. Через прямую a проведена плоскость альфа, а через прямую b — плоскость бета так, что плоскости альфа и бета пересекаются по прямой c. Докажите, что c параллельна гамма.
————-
1) Если через каждую из двух параллельных прямых проведена плоскость, причем эти плоскости пересекаются, то линия их пересечения параллельна каждой из данных прямых.
⇒ с || аис || b
2) Если прямая, не лежащая в плоскости, параллельна некоторой прямой, лежащей в этой плоскости, то данная прямая параллельна самой плоскости
Прямая с, по которой пересекаются плоскости α и β, не лежит в плоскости гамма и параллельна а, лежащей в этой плоскости (см.п1). Требуется доказать п.2, т.е. что прямая с параллельна плоскости гамма.
Плоскость α содержит прямые с и а (с || а- см п.1).
Предположим, что прямая с пересекает плоскость гамма в точке М.
Тогда точка М принадлежит и плоскости гамма, и плоскости α, т.е. точка М принадлежит прямой а, содержащей линию, по которой плоскости α и гамма пересекаются. Получается, что прямые с и а пересекаются, что противоречит п.1.
(аналогично требуемое доказывается через прямую b).
Следовательно, с || гамма, ч.т.д.
плоскостно́й
Правильное ударение в этом слове падает на 3-й слог. На букву о
Посмотреть все слова на букву П
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Геометрия
- Плоскость
Понятие плоскости
Стол, окно, школьная доска — знакомые предметы. Все они имеют поверхность:
поверхность стола:
поверхность окна:
поверхность школьной доски:
Эти поверхности ограничены, у них есть края. Но представление о плоскости мы имеем с их помощью.
Только плоскость простирается безгранично (в любом направлении, заданном на этой плоскости).
Понятие плоскость принадлежит к числу основных понятий геометрии.
Обозначение плоскости
Конечно, нарисовать плоскость, у которой нет краев, невозможно. Поэтому, при изображении плоскости, рисуют только ее часть:
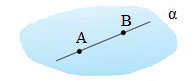
Обозначается плоскость строчными буквами греческого алфавита – α (альфа), β (бета), γ (гамма) и т.д.:
Буквы пишут либо рядом с плоскостью, либо на плоскости.
Определение плоскости
Плоскость — поверхность, содержащая полностью каждую прямую, соединяющую любые её точки. ( то есть, любая прямая, соединяющая две ее точки, целиком принадлежит ей).
Советуем посмотреть:
Отрезок
Ломаная
Четырехугольники
Единицы измерения площадей. Свойства площадей
Прямоугольник, его периметр и площадь. Ось симметрии фигуры
Квадрат. Периметр и площадь квадрата.
Многоугольники. Правильные многоугольники. Равенство фигур.
Прямая
Луч
Шкалы и координаты
Прямоугольный параллелепипед. Пирамида.
Объем прямоугольного параллелепипеда
Куб. Площадь поверхности куба
Куб. Объем куба
Угол. Обозначение углов
Прямой и развернутый угол
Чертежный треугольник
Измерение углов. Транспортир. Виды углов
Треугольник и его виды
Окружность, круг, шар
Цилиндр, конус
Отрезок-xx
Геометрия
Правило встречается в следующих упражнениях:
5 класс
Задание 80,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Номер 102,
Мерзляк, Полонский, Якир, Учебник
Номер 104,
Мерзляк, Полонский, Якир, Учебник
Номер 1,
Мерзляк, Полонский, Якир, Учебник
Номер 7,
Мерзляк, Полонский, Якир, Учебник
Гамма — третья буква греческого алфавита. В ионийской системе счисления обозначала число 3. Произошла от финикийской буквы гамл 𐤂. От самой же гаммы произошли многие другие латинские и кириллические буквы (G, C, Г…).
Строчная греческая буква гамма имеет большое распространение в научной нотации (в математике, физике, астрономии).
В геометрии при указании углов обычно используются по порядку альфа, бета и гамма.
Гамма-излучение (γ-лучи) — электромагнитное излучение в предельно коротковолновом диапазоне.
«Гамма» часто является частью названия звёзд (γ Centauri — Гамма Центавра), обычно указывает на их относительную светимость (альфа — наиболее яркая звезда в созвездии, бета и гамма тусклее).
Символ «Греческая строчная буква гамма» был утвержден как часть Юникода версии 1.1 в 1993 г.
Этот текст также доступен на следующих языках:
English;
Гамма (буква)
- Гамма (буква)
-
Категория:
- Греческие буквы
Wikimedia Foundation.
2010.
Полезное
Смотреть что такое «Гамма (буква)» в других словарях:
-
ГАММА (буква) — ГАММА (g, G), третья буква греческого алфавита … Энциклопедический словарь
-
Гамма (буква) — ГАММА (g, G), третья буква греческого алфавита. … Иллюстрированный энциклопедический словарь
-
гамма- — (буква греческого алфавита γ) первая часть сложных слов, пишется через дефис, но: гаммаг/рамма, гамма/трон (прибор), гамма/графия, гам/маметрия, гам/маскопия … Слитно. Раздельно. Через дефис.
-
Гамма — Гамма: Гамма (буква) третья буква греческого алфавита. Гамма (музыка) музыкальный термин. Цветовая гамма термин в живописи, цветоведении и цветопсихологии. Гамма (единица измерения) единица измерения напряженности… … Википедия
-
ГАММА — (греч. gamma, третья буква греческой азбуки). 1) старинная Гвидонова система звуков, начинавшаяся с греч. буквы гаммы. 2) семь основных музыкальных звуков (do, re, mi, fa, sol, la, si), расположенных в постепенном возвышении. Словарь иностранных… … Словарь иностранных слов русского языка
-
буква — Знак (азбучный), письмена (множ. ч.), иероглиф (гиероглиф), каракуля, руны. Нагородил какие то каракули, и читай. .. Ср. знак… Словарь русских синонимов и сходных по смыслу выражений. под. ред. Н. Абрамова, М.: Русские словари, 1999. буква … Словарь синонимов
-
ГАММА — 1. ГАММА1, гаммы, жен. (греч. gamma название буквы, обозначавшей звук соль в средневековой музыке). Последовательный ряд звуков, повышающийся или понижающийся, обычно в пределах одной или двух октав (муз.). Играть гаммы на рояле. Мажорная,… … Толковый словарь Ушакова
-
ГАММА — 1. ГАММА1, гаммы, жен. (греч. gamma название буквы, обозначавшей звук соль в средневековой музыке). Последовательный ряд звуков, повышающийся или понижающийся, обычно в пределах одной или двух октав (муз.). Играть гаммы на рояле. Мажорная,… … Толковый словарь Ушакова
-
гамма — звукоряд, буква, палитра Словарь русских синонимов. гамма сущ., кол во синонимов: 5 • анабазис (8) • буква … Словарь синонимов
-
Буква Г — Буква кириллицы Г Кириллица А Б В Г Ґ Д … Википедия
Знак гамма и омега в Ворде
Гамма и омега — 3-я и 24-я буква греческого алфавита. Знаки часто встречаются в математике, физике и других науках. Рассмотрим способы их печати в документах Word.
Заглавное и строчное написание:
- Гамма — Γ / γ.
- Омега — Ω / ω.
Шрифт Symbol
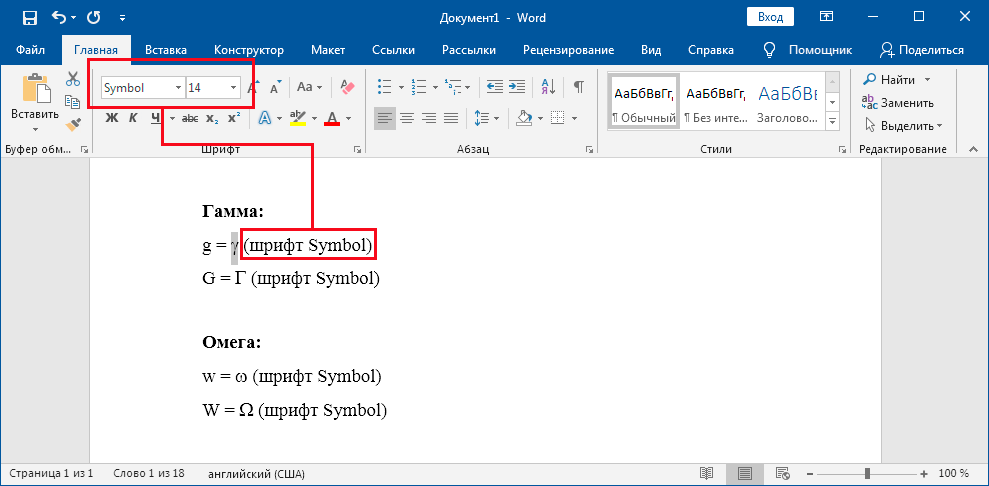
Напечатайте в Word букву «g», выделите её и установите шрифт «Symbol» — получаем знак гаммы. Проделайте тоже самое с буквой «w» для печати омеги.
Для заглавного начертания используем большие «G» и «W».
Alt коды
Вариант предполагает наличие полноценной клавиатуры с цифровым блоком справа.
- Зажимаем клавишу Alt.
-
На правом цифровом блоке вводим нужный код:
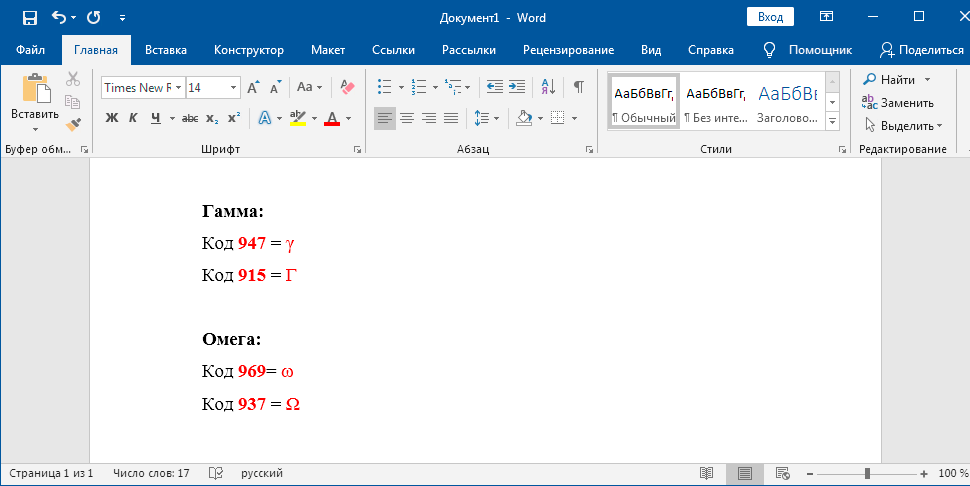
- 947 — γ
- 915 — Γ
- 969 — ω
- 937 — Ω
При отсутствии правого цифрового блока можно воспользоваться «Экранной клавиатурой» Windows. По умолчанию он там отсутствует, но включается через «Параметры». После ввода кода нажмите дополнительно пробел.
- Отпускаем Alt и получаем символ.
Юникод знаков
Универсальный, но более долгий способ — преобразование юникода знаков в буквы.
-
В любом месте документа на английском языке вводим юникод знака:
- 03B3 — γ
- 0393 — Γ
- 03C9 — ω
- 03A9 — Ω
Первой идёт цифра ноль. Буквы только английские.
- Нажимаем одновременно клавиши Alt и X.
- Юникод автоматически преобразуется в букву.
Кроме рассмотренных способов, гамму и омегу в Word можно вставить из верхнего меню. Ищите пункт «Символ» на вкладке «Вставка».
Как написать греческие буквы
Греческие буквы активно используются в различных научных дисциплинах. Например, в астрономии — для обозначения ярких звезд в созвездиях, в математике и физике — в виде констант. Кроме того, с их помощью называют коэффициенты, углы и плоскости и т.п. И, конечно, без них не написать греческую фразу. Всего в греческом алфавите 24 буквы. Каждая имеет свое название.

Вам понадобится
- — ручка;
- — бумага.
Инструкция
Напишите первые четыре буквы греческого алфавита. Заглавная «альфа» имеет вид как обычная А, строчная может иметь вид «а» или горизонтальной петельки — α. Большая «бета» пишется «В», а маленькая – привычная «в» или с хвостиком, опустившемся ниже строки – β. Заглавная «гамма» выглядит как русская «Г», а вот строчная – словно вертикальная петелька (γ). «Дельта» представляет собой равносторонний треугольник – Δ или русскую рукописную «Д» в начале строки, а в ее продолжении больше похожа на «б» с хвостиком из правой части окружности — δ.
Запомните написание следующих четырех букв – «эпсилон», «дзета», «эта» и «тета». Первая в заглавном печатном и рукописном виде неотличима от знакомой «Е», а в строчном является зеркальным отражением «з» — ε. Большая «дзета» — это хорошо известная «Z». Другой вариант написания – ζ. В рукописях может выглядеть как письменная латинская f – вертикальная петля над линией строки и ее зеркальное отражение ниже ее. «Эта» пишется «H» или словно строчная n с хвостиком вниз – η. «Тета» не имеет аналогов ни в латинском алфавите, ни в кириллице: это «О» с черточкой внутри – Θ, θ. На письме ее строчное начертание имеет вид латинской v, у которой правый хвостик поднят вверх и закруглен сначала влево, а потом внутрь. Есть еще один вариант написания – аналогично письменной русской «в», но в зеркальном отображении.
Уточните вид следующих четырех букв – «йота», «каппа», «ламбда», «мю». Написание первой ничем не отличается от латинской I, только у строчной не ставится вверху точка. «Каппа» — вылитая «К», но на письме внутри слова похожа на русское «и». «Ламбда»-заглавная пишется как треугольник без основания — Λ, а строчная имеет дополнительный хвост на верху и игриво загнутую правую ножку – λ. Очень похоже можно сказать про «мю»: в начале строки она выглядит «М», а в середине слова – μ. Ее еще можно написать как длинную вертикальную черту, опустившуюся ниже строки, к которой прилипла «л».
Попробуйте написать «ню», «кси», «омикрон» и «пи». «Ню» отображаем как Ν или как ν. Важно, чтобы при строчном написании был четко выражен угол внизу буквы. «Кси» — это три горизонтальные черты, которые или ничем не соединены или имеют по центру вертикальную линию, Ξ. Строчная буква гораздо изящнее, она пишется как «дзета», но с хвостиками внизу и вверху – ξ. «Омикрон» только называется незнакомо, а выглядит в любом написании как «о». «Пи» в заглавном варианте представляет собой «П» с более широкой верхней перекладиной, чем в русском варианте. Строчная пишется или так же, как прописная — π, или как маленькая «омега» (ω), но с залихватской петлей вверху.
Разберите «ро», «сигму», «тау» и «ипсилон». «Ро» — это печатная «Р» большая и маленькая, да и рукописный вариант выглядит как вертикальная черточка с кружочком — Ρ и ρ. «Сигму» в прописном варианте легче всего описать как печатную букву «М», которую опрокинули налево — Σ. Строчная имеет два варианта написания: кружок с хвостиком вправо (σ) или непропорциональная s, нижняя часть которого свешивается со строки – ς. «Тау»-заглавную пишем как печатную «Т» , а обычную – как крючок с горизонтальной шляпкой или русскую письменную «ч». «Ипсилон» — это латинский «игрек» в прописном варианте: или v на ножке – Υ. Строчная υ должна быть плавной, без угла внизу – это признак гласного.
Обратите внимание на последние четыре буквы. «Фи» пишется как «ф» и в заглавном, и строчном варианте. Правда, последняя может иметь вид «с», у которой есть петелька и хвост ниже строки – φ. «Хи» — это наше «х» и большое и маленькое, только на письме черточка, идущая вниз слева направо имеет плавный изгиб – χ. «Пси» напоминает букву «I», у которой выросли крылья – Ψ, ψ. В рукописи она изображается аналогично русской «у». Отличаются заглавная «омега» печатная и рукописная. В первом случае это незакрытая петля с ножками – Ω. Рукой напишите в середине строки кружок, под ним — черту, которые можно соединить вертикальной линией, а можно не соединять. Строчная буква пишется как сдвоенная «u» — ω.
Видео по теме
Источники:
- Греческий алфавит. Технология письма
- греческая буква из 4 букв
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Для обозначения геометрических фигур и их проекций, для отображения отношения между ними, а также для краткости записей геометрических предложений, алгоритмов решения задач и доказательства теорем в курсе используется геометрический язык, составленный из обозначений и символов, принятых в курсе математики (в частности, в новом курсе геометрии в средней школе).
Все многообразие обозначений и символов, а также связи между ними могут быть подразделены на две группы:
группа I — обозначения геометрических фигур и отношений между ними;
группа II обозначения логических операций, составляющие синтаксическую основу геометрического языка.
Ниже приводится полный список математических символов, используемых в данном курсе. Особое внимание уделяется символам, которые применяются для обозначения проекций геометрических фигур.
Группа I
СИМВОЛЫ, ОБОЗНАЧАЮЩИЕ ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ И ОТНОШЕНИЯ МЕЖДУ НИМИ
А. Обозначение геометрических фигур
1. Геометрическая фигура обозначается — Ф.
2. Точки обозначаются прописными буквами латинского алфавита или арабскими цифрами:
А, В, С, D, … , L, М, N, …
1,2,3,4,…,12,13,14,…
3. Линии, произвольно расположенные по отношению к плоскостям проекций, обозначаются строчными буквами латинского алфавита:
а, b, с, d, … , l, m, n, …
Линии уровня обозначаются: h — горизонталь; f— фронталь.
Для прямых используются также следующие обозначения:
(АВ) — прямая, проходящая через точки А а В;
[АВ) — луч с началом в точке А;
[АВ] — отрезок прямой, ограниченный точками А и В.
4. Поверхности обозначаются строчными буквами греческого алфавита:
α, β, γ, δ,…,ζ,η,ν,…
Чтобы подчеркнуть способ задания поверхности, следует указывать геометрические элементы, которыми она определяется, например:
α(а || b) — плоскость α определяется параллельными прямыми а и b;
β(d1 d2gα) — поверхность β определяется направляющими d1 и d2 , образующей g и плоскостью параллелизма α.
5. Углы обозначаются:
∠ABC — угол с вершиной в точке В, а также ∠α°, ∠β°, … , ∠φ°, …
6. Угловая: величина (градусная мера) обозначается знаком 


Прямой угол отмечается квадратом с точкой внутри
7. Расстояния между геометрическими фигурами обозначаются двумя вертикальными отрезками — ||.
Например:
|АВ| — расстояние между точками А и В (длина отрезка АВ);
|Аа| — расстояние от точки А до линии a;
|Аα| — расстояшие от точки А до поверхности α;
|аb| — расстояние между линиями а и b;
|αβ| расстояние между поверхностями α и β.
8. Для плоскостей проекций приняты обозначения: π1 и π2,
где π1 — горизонтальная плоскость проекций;
π2 —фрюнтальная плоскость проекций.
При замене плоскостей проекций или введении новых плоскостей последние обозначают π3, π4 и т. д.
9. Оси проекций обозначаются: х, у, z, где х — ось абсцисс; у — ось ординат; z — ось аппликат.
Постояшную прямую эпюра Монжа обозначают k.
10. Проекции точек, линий, поверхностей, любой геометрической фигуры обозначаются теми же буквами (или цифрами), что и оригинал, с добавлением верхнего индекса, соответствующего плоскости проекции, на которой они получены:
А’, В’, С’, D’, … , L’, М’, N’, горизонтальные проекции точек; А», В», С», D», … , L», М», N», … фронтальные проекции точек; a’ , b’ , c’ , d’ , … , l’, m’ , n’ , —
горизонтальные проекции линий; а» ,b» , с» , d» , … , l» , m» , n» , … фронтальные проекции линий; α’, β’, γ’, δ’,…,ζ’,η’,ν’,… горизонтальные проекции поверхностей;
α», β», γ», δ»,…,ζ»,η»,ν»,…
фронтальные проекции поверхностей.
11. Следы плоскостей (поверхностей) обозначаются теми же буквами, что и горизонталь или фронталь, с добавлением подстрочного индекса 0α, подчеркивающего, что эти линии лежат в плоскости проекции и принадлежат плоскости (поверхности) α.
Так: h0α — горизонтальный след плоскости (поверхности) α;
f0α — фронтальный след плоскости (поверхности) α.
12. Следы прямых (линий) обозначаются заглавными буквами, с которых начинаются слова, определяющие название (в латинской транскрипции) плоскости проекции, которую пересекает линия, с подстрочным индексом, указывающим принадлежность к линии.
Например: Ha — горизонтальный след прямой (линии) а;
Fa — фронтальный след прямой (линии ) a.
13. Последовательность точек, линий (любой фигуры) отмечается подстрочными индексами 1,2,3,…, n:
А1, А2, А3,…,Аn;
a1, a2, a3,…,an;
α1, α2, α3,…,αn;
Ф1, Ф2, Ф3,…,Фn и т. д.
Вспомогательная проекция точки, полученная в результате преобразования для получения действительной величины геометрической фигуры, обозначается той же буквой с подстрочным индексом 0:
A0, B0, С0, D0, …
Аксонометрические проекции
14. Аксонометрические проекции точек, линий, поверхностей обозначаются теми же буквами, что и натура с добавлением верхнего индекса 0:
А0, В0, С0, D0, …
10, 20, 30, 40, …
a0, b0, c0, d0, …
α0, β0, γ0, δ0, …
15. Вторичные проекции обозначаются путем добавления верхнего индекса 1 :
А1 0, В1 0, С1 0, D1 0, …
11 0, 21 0, 31 0, 41 0, …
a1 0, b1 0, c1 0, d1 0, …
α1 0, β1 0, γ1 0, δ1 0, …
Для облегчения чтения чертежей в учебнике при оформлении иллюстративного материала использованы несколько цветов, каждый из которых имеет определенное смысловое значение: линиями (точками) черного цвета обозначены исходные данные; зеленый цвет использован для линий вспомогательных графических построений; красными линиями (точками) показаны результаты построений или те геометрические элементы, на которые следует обратить особое внимание.
| № по пор. | Обозначение | Содержание | Пример символической записи |
|---|---|---|---|
| 1 | ≡ | Совпадают | (АВ)≡(CD) — прямая, проходящая через точки А и В, совпадает с прямой, проходящей через точки С и D |
| 2 | ≅ | Конгруентны | ∠ABC≅∠MNK — угол АВС конгруентен углу MNK |
| 3 | ∼ | Подобны | ΔАВС∼ΔMNK — треугольники АВС и MNK подобны |
| 4 | || | Параллельны | α||β — плоскость α параллельна плоскости β |
| 5 | ⊥ | Перпендикулярны | а⊥b — прямые а и b перпендикулярны |
| 6 |  |
Скрещиваются | с  d — прямые с и d скрещиваются d — прямые с и d скрещиваются |
| 7 |  |
Касательные | t  l — прямая t является касательной к линии l. l — прямая t является касательной к линии l. β  α — плоскость β касательная к поверхности α α — плоскость β касательная к поверхности α |
| 8 | → | Отображаются | Ф1→Ф2 — фигура Ф1 отображается на фигуру Ф2 |
| 9 | S | Центр проецирования. Если центр проецирования несобственная точка, то его положение обозначается стрелкой, указывающей направление проецирования |
— |
| 10 | s | Направление проецирования | — |
| 11 | P | Параллельное проецирование | рsα Параллельное проецирование — параллельное проецирование на плоскость α в направлении s |
| № по пор. | Обозначение | Содержание | Пример символической записи | Пример символической записи в геометрии |
|---|---|---|---|---|
| 1 | M,N | Множества | — | — |
| 2 | A,B,C,… | Элементы множества |
— | — |
| 3 | { … } | Состоит из … | Ф{A, B, C,… } | Ф{A, B, C,… } — фигура Ф состоит из точек А, В,С, … |
| 4 | ∅ | Пустое множество | L — ∅ — множество L пустое (не содержит элементов ) | — |
| 5 | ∈ | Принадлежит, является элементом | 2∈N (где N — множество натуральных чисел) — число 2 принадлежит множеству N |
А ∈ а — точка А принадлежит прямой а (точка А лежит на прямой а ) |
| 6 | ⊂ | Включает, cодержит | N⊂М — множество N является частью (подмножеством) множества М всех рациональных чисел |
а⊂α — прямая а принадлежит плоскости α (понимается в смысле: множество точек прямой а является подмножеством точек плоскости α) |
| 7 | ∪ | Объединение | С = A U В — множество С есть объединение множеств A и В; {1, 2. 3, 4,5} = {1,2,3}∪{4,5} |
ABCD = [AB] ∪ [ВС] ∪ [CD] — ломаная линия, ABCD есть объединение отрезков [АВ], [ВС], [CD] |
| 8 | ∩ | Пересечение множеств | М=К∩L — множество М есть пересечение множеств К и L (содержит в себе элементы, принадлежащие как множеству К, так и множеству L). М ∩ N = ∅— пересечение множеств М и N есть пустое множество (множества М и N не имеют общих элементов) |
а = α ∩ β — прямая а есть пересечение плоскостей α и β а ∩ b = ∅ — прямые а и b не пересекаются (не имеют общих точек) |
| № по пор. | Обозначение | Содержание | Пример символической записи |
|---|---|---|---|
| 1 | ∧ | Конъюнкция предложений; соответствует союзу «и». Предложение (р∧q) истинно тогда и только тогда,когда р и q оба истинны |
α∩β = { К:K∈α∧K∈β} Пересечение поверхностей α и β есть множество точек (линия), состоящее из всех тех и только тех точек К, которые принадлежат как поверхности α, так и поверхности β |
| 2 | ∨ | Дизъюнкция предложений; соответствует союзу «или». Предложение (p∨q) истинно, когда истинно хотя бы одно из предложений р или q (т. е. или р, или q, или оба). |
— |
| 3 | ⇒ | Импликация — логическое следствие. Предложение р⇒q означает: «если р, то и q» | (а||с∧b||с)⇒a||b. Если две прямые параллельны третьей, то они параллельны между собой |
| 4 | ⇔ | Предложение (р⇔q) понимается в смысле: «если р, то и q; если q, то и р» | А∈α⇔А∈l⊂α. Точка принадлежит плоскости, если она принадлежит некоторой линии, принадлежащей этой плоскости. Справедливо также и обратное утверждение: если точка принадлежит некоторой линии, принадлежащей плоскости, то она принадлежит и самой плоскости |
| 5 | ∀ | Квантор общности, читается: для всякого, для всех, для любого. Выражение ∀(x)P(x) означает: «для всякого x: имеет место свойство Р(х) « |
∀( ΔАВС)(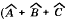 = 180°) Для всякого (для любого) треугольника сумма величин его углов = 180°) Для всякого (для любого) треугольника сумма величин его углов при вершинах равна 180° |
| 6 | ∃ | Квантор существования, читается: существует. Выражение ∃(х)P(х) означает: «существует х, обладающее свойством Р(х)» |
(∀α)(∃a)[a⊄α∧a||α].Для любой плоскости α существует прямая а, не принадлежащая плоскости α и параллельная плоскости α |
| 7 | ∃1 | Квантор единственности существования, читается: существует единственное (-я, -й)… Выражение ∃1(x)(Рх) означает: «существует единственное (только одно) х, обладающее свойством Рх» |
(∀ А, В)(А≠B)(∃1а)(а∋А, В) Для любых двух различных точек А и В существует единственная прямая a, проходящая через эти точки. |
| 8 | (Px) | Отрицание высказывания P(x) | а b(∃α)(α⊃а, Ь).Если прямые а и b скрещиваются, то не существует плоскости а, которая содержит их b(∃α)(α⊃а, Ь).Если прямые а и b скрещиваются, то не существует плоскости а, которая содержит их |
| 9 | Отрицание знака | [AB]≠[CD] —отрезок [АВ] не равен отрезку [CD].а?b — линия а не параллельна линии b |