Как правильно пишется слово «процентиль»
проценти́ль
проценти́ль, -я и перценти́ль, -я
Источник: Орфографический
академический ресурс «Академос» Института русского языка им. В.В. Виноградова РАН (словарная база
2020)
Делаем Карту слов лучше вместе
Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать
Карту слов. Я отлично
умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!
Спасибо! Я стал чуточку лучше понимать мир эмоций.
Вопрос: сквош — это что-то нейтральное, положительное или отрицательное?
Синонимы к слову «процентиль»
Предложения со словом «процентиль»
- Процентиль девяносто девять. Я пытаюсь внутренне найти какие-то признаки этого. Какое должно быть ощущение?
- – Это я знаю, – отвечаю я, думая о другом. – Когда нас в школе тестировали, я попал в процентиль семнадцать.
- Разбирается или не разбирается, но с цифрами мы сталкиваемся ежедневно – в газетных статьях о росте преступности или промышленности, в рекламных брошюрах, обещающих «эффективность больше на 26 %», в брошюрах медицинских, доказывающих «снижение риска заболеваемости на 31 %», в школе, где нам сообщают, что ребёнок попал в такой-то процентиль.
- (все предложения)
Значение слова «процентиль»
-
1. значение, выделяющее одну из 100 частей распределения, выстроенных в ряд по их величине (Викисловарь)
Все значения слова ПРОЦЕНТИЛЬ
Отправить комментарий
Смотрите также
1. значение, выделяющее одну из 100 частей распределения, выстроенных в ряд по их величине
Все значения слова «процентиль»
-
Процентиль девяносто девять. Я пытаюсь внутренне найти какие-то признаки этого. Какое должно быть ощущение?
-
– Это я знаю, – отвечаю я, думая о другом. – Когда нас в школе тестировали, я попал в процентиль семнадцать.
-
Разбирается или не разбирается, но с цифрами мы сталкиваемся ежедневно – в газетных статьях о росте преступности или промышленности, в рекламных брошюрах, обещающих «эффективность больше на 26 %», в брошюрах медицинских, доказывающих «снижение риска заболеваемости на 31 %», в школе, где нам сообщают, что ребёнок попал в такой-то процентиль.
- (все предложения)
- стандартное отклонение
- фиктивная переменная
- фактор общего интеллекта
- состоятельная оценка
- выборочная дисперсия
- (ещё синонимы…)
Русский[править]
Морфологические и синтаксические свойства[править]
процентиль
Существительное, неодушевлённое, мужской род (тип склонения ?? по классификации А. А. Зализняка).
Корень: —.
Произношение[править]
Семантические свойства[править]
Значение[править]
- значение, выделяющее одну из 100 частей распределения, выстроенных в ряд по их величине ◆ Так, в 1995 г. значение его ROA составляло 1,46%, позволяя банку войти в 87-й процентиль своей группы. Джозеф Синки-мл., «Финансовый менеджмент в коммерческом банке и в индустрии финансовых услуг», 2007 г.
Синонимы[править]
- перцентиль, центиль
Антонимы[править]
Гиперонимы[править]
Гипонимы[править]
Родственные слова[править]
| Ближайшее родство | |
|
Этимология[править]
Происходит от ??
Фразеологизмы и устойчивые сочетания[править]
Перевод[править]
| Список переводов | |
Библиография[править]
|
|
Для улучшения этой статьи желательно:
|
Ударение в слове процентиль
В упомянутом выше слове ударение должно быть поставлено на слог с буквой И — процентИль.
А вы знаете, как правильно ставить ударение в слове ?
Примеры предложений, как пишется процентиль
Разбирается или не разбирается, но с цифрами мы сталкиваемся ежедневно – в газетных статьях о росте преступности или промышленности, в рекламных брошюрах, обещающих «эффективность больше на 26 %», в брошюрах медицинских, доказывающих «снижение риска заболеваемости на 31 %», в школе, где нам сообщают, что ребёнок попал в такой-то проценти́ль.
— Smart Reading, Краткое содержание книги: Как лгать при помощи статистики. Дарелл Хафф, 2020
При этом минимальный приемлемый проценти́ль доходов жены для мужчин оказался всего лишь сороковым.
— Дэвид Басс, Эволюция сексуального влечения: Стратегии поиска партнеров, 1994
Он просил мужчин и женщин указать «минимальный проценти́ль» каждой характеристики, который кажется им приемлемым.
— Дэвид Басс, Эволюция сексуального влечения: Стратегии поиска партнеров, 1994
Когда объявили результаты, то выяснилось, что я получил 1400 баллов из 1520 возможных, 96‐й проценти́ль.
— Дэвид Юн, Весь мир Фрэнка Ли, 2019
Студентки американских колледжей указали, что минимальный приемлемый для них проценти́ль доходов мужа – семидесятый, т. е. они предпочитают мужчин, которые зарабатывают более 70 % от доходов других мужчин.
— Дэвид Басс, Эволюция сексуального влечения: Стратегии поиска партнеров, 1994
На данной странице размещена информация о том, на какой слог правильно ставить ударение в слове процентиль. В слове «процентиль» ударение падает на слог с буквой И — проценти́ль. Надеемся, что теперь у вас не возникнет вопросов, как пишется слово процентиль, куда ставить ударение, какое ударение, или где должно стоять ударение в слове процентиль, чтобы грамотно его произносить.
ПРОЦЕНТИЛЬ
- ПРОЦЕНТИЛЬ
-
- ПРОЦЕНТИЛЬ
-
(реrcentile) Значения, выделяющие 100-е части распределения, выстроенные в ряд по их величине. 99-й процентиль распределения дохода, например, представляет собой такой уровень дохода, когда только один процент населения имеет больший доход.
Экономика. Толковый словарь. — М.: «ИНФРА-М», Издательство «Весь Мир».
.
2000.
Экономический словарь.
2000.
Смотреть что такое «ПРОЦЕНТИЛЬ» в других словарях:
-
процентиль — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN percentile … Справочник технического переводчика
-
Процентиль — Квантиль (или процентиль) в математической статистике число, такое что заданная случайная величина не превышает его лишь с фиксированной вероятностью. Содержание 1 Определение 2 Квантили нормального распределения 3 Замечания … Википедия
-
Процентиль — показатель того, какой процент значений находится ниже определённого уровня. Например, значение 50 й процентили указывает, что 50% значений располагается ниже этого уровня … Энциклопедический словарь по психологии и педагогике
-
ПРОЦЕНТИЛЬ — Любая из 99 пронумерованных точек, которые делят упорядоченный набор значений на 100 частей, каждая из которых содержит 1/100 ю от общего значения. Это прямое значение, к сожалению, часто путается; см. центиль и партиль для обсуждения … Толковый словарь по психологии
-
процентиль — Процентили – это величины, делящие выборку данных на сто групп, содержащих (по возможности) равное количество наблюдений. Например, 30% данных имеют значение, меньшее 30 го процентиля. См. тж. квантиль … Словарь социологической статистики
-
SAT — У этого термина существуют и другие значения, см. SAT (значения). SAT Reasoning Test (а также «Scholastic Aptitude Test» и «Scholastic Assessment Test», дословно «Школьный Оценочный Тест») стандартизованный тест для приема в высшие учебные… … Википедия
-
квантиль — 3.32 квантиль (fractile): р квантиль (квантиль уровня р или процентиль) и соответствующее значение квантили хропределяется как: F(xp) = p, (3.1) где F функция распределения для хр. Источник … Словарь-справочник терминов нормативно-технической документации
-
Алкогольный синдром плода (fetal alcohol syndrome) — А. с. п. представляет собой комплекс физ. аномалий и нейроповеденческого дефицита, к рый может серьезно поражать потомство сильно пьющих матерей. Менее серьезные последствия тяжелой алкоголизации матерей обычно обозначаются как алкогольные… … Психологическая энциклопедия
-
Статистика в психологии (statistics in psychology) — Первое применение С. в психологии часто связывают с именем сэра Фрэнсиса Гальтона. В психологии под «статистикой» понимается применение количественных мер и методов для описания и анализа результатов психол. исслед. Психологии как науке С.… … Психологическая энциклопедия
-
Медиана (статистика) — В этой статье не хватает ссылок на источники информации. Информация должна быть проверяема, иначе она может быть поставлена под сомнение и удалена. Вы можете … Википедия
From Wikipedia, the free encyclopedia
In statistics, a k-th percentile, also known as percentile score or centile, is a score below which a given percentage k of scores in its frequency distribution falls («exclusive» definition) or a score at or below which a given percentage falls («inclusive» definition).
Percentiles are expressed in the same unit of measurement as the input scores, not in percent; for example, if the scores refer to human weight, the corresponding percentiles will be expressed in kilograms or pounds.
The 25th percentile is also known as the first quartile (Q1), the 50th percentile as the median or second quartile (Q2), and the 75th percentile as the third quartile (Q3).
For example, the 50th percentile (median) is the score below (or at or below, depending on the definition) which 50% of the scores in the distribution are found.
The percentile score and the percentile rank are related terms. The percentile rank of a score is the percentage of scores in its distribution that are less than it, an exclusive definition, and one that can be expressed with a single, simple formula.
Percentile scores and percentile ranks are often used in the reporting of test scores from norm-referenced tests, but, as just noted, they are not the same. For percentile rank, a score is given and a percentage is computed. Percentile ranks are exclusive. If the percentile rank for a specified score is 90%, then 90% of the scores were lower. In contrast, for percentiles a percentage is given and a corresponding score is determined, which can be either exclusive or inclusive. The score for a specified percentage (e.g., 90th) indicates a score below which (exclusive definition) or at or below which (inclusive definition) other scores in the distribution fall.
Definitions[edit]
There is no standard definition of percentile,[1][2][3]
however all definitions yield similar results when the number of observations is very large and the probability distribution is continuous.[4] In the limit, as the sample size approaches infinity, the 100pth percentile (0<p<1) approximates the inverse of the cumulative distribution function (CDF) thus formed, evaluated at p, as p approximates the CDF. This can be seen as a consequence of the Glivenko–Cantelli theorem. Some methods for calculating the percentiles are given below.
The normal distribution and percentiles[edit]
Representation of the three-sigma rule. The dark blue zone represents observations within one standard deviation (σ) to either side of the mean (μ), which accounts for about 68.3% of the population. Two standard deviations from the mean (dark and medium blue) account for about 95.4%, and three standard deviations (dark, medium, and light blue) for about 99.7%.
The methods given in the definitions section (below) are approximations for use in small-sample statistics. In general terms, for very large populations following a normal distribution, percentiles may often be represented by reference to a normal curve plot. The normal distribution is plotted along an axis scaled to standard deviations, or sigma (
Percentiles represent the area under the normal curve, increasing from left to right. Each standard deviation represents a fixed percentile. Thus, rounding to two decimal places, −3σ is the 0.13th percentile, −2σ the 2.28th percentile, −1σ the 15.87th percentile, 0σ the 50th percentile (both the mean and median of the distribution), +1σ the 84.13th percentile, +2σ the 97.72nd percentile, and +3σ the 99.87th percentile. This is related to the 68–95–99.7 rule or the three-sigma rule. Note that in theory the 0th percentile falls at negative infinity and the 100th percentile at positive infinity, although in many practical applications, such as test results, natural lower and/or upper limits are enforced.
Applications[edit]
When ISPs bill «burstable» internet bandwidth, the 95th or 98th percentile usually cuts off the top 5% or 2% of bandwidth peaks in each month, and then bills at the nearest rate. In this way, infrequent peaks are ignored, and the customer is charged in a fairer way. The reason this statistic is so useful in measuring data throughput is that it gives a very accurate picture of the cost of the bandwidth. The 95th percentile says that 95% of the time, the usage is below this amount: so, the remaining 5% of the time, the usage is above that amount.
Physicians will often use infant and children’s weight and height to assess their growth in comparison to national averages and percentiles which are found in growth charts.
The 85th percentile speed of traffic on a road is often used as a guideline in setting speed limits and assessing whether such a limit is too high or low.[5][6]
In finance, value at risk is a standard measure to assess (in a model-dependent way) the quantity under which the value of the portfolio is not expected to sink within a given period of time and given a confidence value.
Calculation methods[edit]
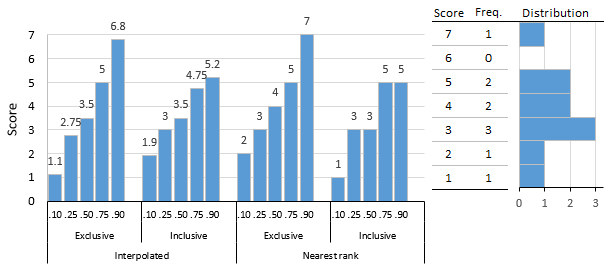
Interpolated and nearest-rank, exclusive and inclusive, percentiles for 10-score distribution
There are many formulas or algorithms[7] for a percentile score. Hyndman and Fan [1] identified nine and most statistical and spreadsheet software use one of the methods they describe.[8] Algorithms either return the value of a score that exists in the set of scores (nearest-rank methods) or interpolate between existing scores and are either exclusive or inclusive.
| PC: percentile specified | 0.10 | 0.25 | 0.50 | 0.75 | 0.90 |
|---|---|---|---|---|---|
| N: Number of scores | 10 | 10 | 10 | 10 | 10 |
| OR: ordinal rank = PC × N | 1 | 2.5 | 5 | 7.5 | 9 |
| Rank: >OR / ≥OR | 2/1 | 3/3 | 6/5 | 8/8 | 10/9 |
| Score at rank (exc/inc) | 2/1 | 3/3 | 4/3 | 5/5 | 7/5 |
The figure shows a 10-score distribution, illustrates the percentile scores that result from these different algorithms, and serves as an introduction to the examples given subsequently. The simplest are nearest-rank methods that return a score from the distribution, although compared to interpolation methods, results can be a bit crude. The Nearest-Rank Methods table shows the computational steps for exclusive and inclusive methods.
| PC: percentile specified | 0.10 | 0.25 | 0.50 | 0.75 | 0.90 |
|---|---|---|---|---|---|
| N: number of scores | 10 | 10 | 10 | 10 | 10 |
| OR: PC×(N+1) / PC×(N−1)+1 | 1.1/1.9 | 2.75/3.25 | 5.5/5.5 | 8.25/7.75 | 9.9/9.1 |
| LoRank: OR truncated | 1/1 | 2/3 | 5/5 | 8/7 | 9/9 |
| HIRank: OR rounded up | 2/2 | 3/4 | 6/6 | 9/8 | 10/10 |
| LoScore: score at LoRank | 1/1 | 2/3 | 3/3 | 5/4 | 5/5 |
| HiScore: score at HiRank | 2/2 | 3/3 | 4/4 | 5/5 | 7/7 |
| Difference: HiScore − LoScore | 1/1 | 1/0 | 1/1 | 0/1 | 2/2 |
| Mod: fractional part of OR | 0.1/0.9 | 0.75/0.25 | 0.5/0.5 | 0.25/0.75 | 0.9/0.1 |
| Interpolated score (exc/inc) = LoScore + Mod × Difference |
1.1/1.9 | 2.75/3 | 3.5/3.5 | 5/4.75 | 6.8/5.2 |
Interpolation methods, as the name implies, can return a score that is between scores in the distribution. Algorithms used by statistical programs typically use interpolation methods, for example, the percentile.exc and percentile.inc functions in Microsoft Excel. The Interpolated Methods table shows the computational steps.
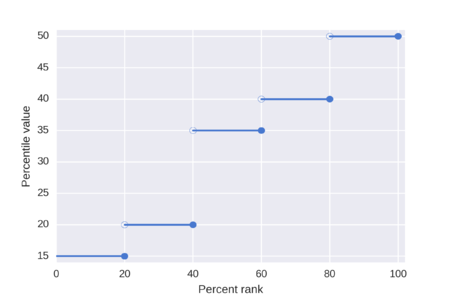
The nearest-rank method[edit]
The percentile values for the ordered list {15, 20, 35, 40, 50}
One definition of percentile, often given in texts, is that the P-th percentile 
- Using the nearest-rank method on lists with fewer than 100 distinct values can result in the same value being used for more than one percentile.
- A percentile calculated using the nearest-rank method will always be a member of the original ordered list.
- The 100th percentile is defined to be the largest value in the ordered list.
The linear interpolation between closest ranks method[edit]
An alternative to rounding used in many applications is to use linear interpolation between adjacent ranks.
All of the following variants have the following in common. Given the order statistics
we seek a linear interpolation function that passes through the points 
where 




There are two ways in which the variant approaches differ. The first is in the linear relationship between the rank x, the percent rank 
There is the additional requirement that the midpoint of the range 

and our revised function now has just one degree of freedom, looking like this:
The second way in which the variants differ is in the definition of the function near the margins of the ![[0,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)

![[1,N]](https://wikimedia.org/api/rest_v1/media/math/render/svg/d6fc7b14276a914ff6cbdf59b806eb601020f473)

First variant, C = 1/2[edit]
The result of using each of the three variants on the ordered list {15, 20, 35, 40, 50}
(Sources: Matlab «prctile» function,[9][10])
where
Furthermore, let
The inverse relationship is restricted to a narrower region:
Second variant, C = 1[edit]
(Source: Some software packages, including NumPy[11] and Microsoft Excel[3] (up to and including version 2013 by means of the PERCENTILE.INC function). Noted as an alternative by NIST[8])
Note that the 
![pin [0,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/33c3a52aa7b2d00227e85c641cca67e85583c43c)
Third variant, C = 0[edit]
(The primary variant recommended by NIST.[8] Adopted by Microsoft Excel since 2010 by means of PERCENTIL.EXC function. However, as the «EXC» suffix indicates, the Excel version excludes both endpoints of the range of p, i.e., 

The inverse is restricted to a narrower region:
The weighted percentile method[edit]
In addition to the percentile function, there is also a weighted percentile, where the percentage in the total weight is counted instead of the total number. There is no standard function for a weighted percentile. One method extends the above approach in a natural way.
Suppose we have positive weights 
the sum of the weights. Then the formulas above are generalized by taking
when
,
or
for general
,
and
The 50% weighted percentile is known as the weighted median.
See also[edit]
- Decile
- Percentile rank
- Quantile
- Summary statistics
References[edit]
- ^ a b Hyndman, Rob J.; Fan, Yanan (November 1996). «Sample Quantiles in Statistical Packages». American Statistician. American Statistical Association. 50 (4): 361–365. doi:10.2307/2684934. JSTOR 2684934.
- ^ Lane, David. «Percentiles». Retrieved 2007-09-15.
- ^ a b Pottel, Hans. «Statistical flaws in Excel» (PDF). Archived from the original (PDF) on 2013-06-04. Retrieved 2013-03-25.
- ^ Schoonjans F, De Bacquer D, Schmid P (2011). «Estimation of population percentiles». Epidemiology. 22 (5): 750–751. doi:10.1097/EDE.0b013e318225c1de. PMC 3171208. PMID 21811118.
- ^ Johnson, Robert; Kuby, Patricia (2007), «Applied Example 2.15, The 85th Percentile Speed Limit: Going With 85% of the Flow», Elementary Statistics (10th ed.), Cengage Learning, p. 102, ISBN 9781111802493.
- ^ «Rational Speed Limits and the 85th Percentile Speed» (PDF). lsp.org. Louisiana State Police. Archived from the original (PDF) on 23 September 2018. Retrieved 28 October 2018.
- ^ Wessa, P (2021). «Percentiles in Free Statistics Software». Office for Research Development and Education. Retrieved 13 November 2021.
- ^ a b c «Engineering Statistics Handbook: Percentile». NIST. Retrieved 2009-02-18.
- ^ «Matlab Statistics Toolbox – Percentiles». Retrieved 2006-09-15., This is equivalent to Method 5 discussed here
- ^ Langford, E. (2006). «Quartiles in Elementary Statistics». Journal of Statistics Education. 14 (3). doi:10.1080/10691898.2006.11910589.
- ^ «NumPy 1.12 documentation». SciPy. Retrieved 2017-03-19.
From Wikipedia, the free encyclopedia
In statistics, a k-th percentile, also known as percentile score or centile, is a score below which a given percentage k of scores in its frequency distribution falls («exclusive» definition) or a score at or below which a given percentage falls («inclusive» definition).
Percentiles are expressed in the same unit of measurement as the input scores, not in percent; for example, if the scores refer to human weight, the corresponding percentiles will be expressed in kilograms or pounds.
The 25th percentile is also known as the first quartile (Q1), the 50th percentile as the median or second quartile (Q2), and the 75th percentile as the third quartile (Q3).
For example, the 50th percentile (median) is the score below (or at or below, depending on the definition) which 50% of the scores in the distribution are found.
The percentile score and the percentile rank are related terms. The percentile rank of a score is the percentage of scores in its distribution that are less than it, an exclusive definition, and one that can be expressed with a single, simple formula.
Percentile scores and percentile ranks are often used in the reporting of test scores from norm-referenced tests, but, as just noted, they are not the same. For percentile rank, a score is given and a percentage is computed. Percentile ranks are exclusive. If the percentile rank for a specified score is 90%, then 90% of the scores were lower. In contrast, for percentiles a percentage is given and a corresponding score is determined, which can be either exclusive or inclusive. The score for a specified percentage (e.g., 90th) indicates a score below which (exclusive definition) or at or below which (inclusive definition) other scores in the distribution fall.
Definitions[edit]
There is no standard definition of percentile,[1][2][3]
however all definitions yield similar results when the number of observations is very large and the probability distribution is continuous.[4] In the limit, as the sample size approaches infinity, the 100pth percentile (0<p<1) approximates the inverse of the cumulative distribution function (CDF) thus formed, evaluated at p, as p approximates the CDF. This can be seen as a consequence of the Glivenko–Cantelli theorem. Some methods for calculating the percentiles are given below.
The normal distribution and percentiles[edit]
Representation of the three-sigma rule. The dark blue zone represents observations within one standard deviation (σ) to either side of the mean (μ), which accounts for about 68.3% of the population. Two standard deviations from the mean (dark and medium blue) account for about 95.4%, and three standard deviations (dark, medium, and light blue) for about 99.7%.
The methods given in the definitions section (below) are approximations for use in small-sample statistics. In general terms, for very large populations following a normal distribution, percentiles may often be represented by reference to a normal curve plot. The normal distribution is plotted along an axis scaled to standard deviations, or sigma (
Percentiles represent the area under the normal curve, increasing from left to right. Each standard deviation represents a fixed percentile. Thus, rounding to two decimal places, −3σ is the 0.13th percentile, −2σ the 2.28th percentile, −1σ the 15.87th percentile, 0σ the 50th percentile (both the mean and median of the distribution), +1σ the 84.13th percentile, +2σ the 97.72nd percentile, and +3σ the 99.87th percentile. This is related to the 68–95–99.7 rule or the three-sigma rule. Note that in theory the 0th percentile falls at negative infinity and the 100th percentile at positive infinity, although in many practical applications, such as test results, natural lower and/or upper limits are enforced.
Applications[edit]
When ISPs bill «burstable» internet bandwidth, the 95th or 98th percentile usually cuts off the top 5% or 2% of bandwidth peaks in each month, and then bills at the nearest rate. In this way, infrequent peaks are ignored, and the customer is charged in a fairer way. The reason this statistic is so useful in measuring data throughput is that it gives a very accurate picture of the cost of the bandwidth. The 95th percentile says that 95% of the time, the usage is below this amount: so, the remaining 5% of the time, the usage is above that amount.
Physicians will often use infant and children’s weight and height to assess their growth in comparison to national averages and percentiles which are found in growth charts.
The 85th percentile speed of traffic on a road is often used as a guideline in setting speed limits and assessing whether such a limit is too high or low.[5][6]
In finance, value at risk is a standard measure to assess (in a model-dependent way) the quantity under which the value of the portfolio is not expected to sink within a given period of time and given a confidence value.
Calculation methods[edit]
Interpolated and nearest-rank, exclusive and inclusive, percentiles for 10-score distribution
There are many formulas or algorithms[7] for a percentile score. Hyndman and Fan [1] identified nine and most statistical and spreadsheet software use one of the methods they describe.[8] Algorithms either return the value of a score that exists in the set of scores (nearest-rank methods) or interpolate between existing scores and are either exclusive or inclusive.
| PC: percentile specified | 0.10 | 0.25 | 0.50 | 0.75 | 0.90 |
|---|---|---|---|---|---|
| N: Number of scores | 10 | 10 | 10 | 10 | 10 |
| OR: ordinal rank = PC × N | 1 | 2.5 | 5 | 7.5 | 9 |
| Rank: >OR / ≥OR | 2/1 | 3/3 | 6/5 | 8/8 | 10/9 |
| Score at rank (exc/inc) | 2/1 | 3/3 | 4/3 | 5/5 | 7/5 |
The figure shows a 10-score distribution, illustrates the percentile scores that result from these different algorithms, and serves as an introduction to the examples given subsequently. The simplest are nearest-rank methods that return a score from the distribution, although compared to interpolation methods, results can be a bit crude. The Nearest-Rank Methods table shows the computational steps for exclusive and inclusive methods.
| PC: percentile specified | 0.10 | 0.25 | 0.50 | 0.75 | 0.90 |
|---|---|---|---|---|---|
| N: number of scores | 10 | 10 | 10 | 10 | 10 |
| OR: PC×(N+1) / PC×(N−1)+1 | 1.1/1.9 | 2.75/3.25 | 5.5/5.5 | 8.25/7.75 | 9.9/9.1 |
| LoRank: OR truncated | 1/1 | 2/3 | 5/5 | 8/7 | 9/9 |
| HIRank: OR rounded up | 2/2 | 3/4 | 6/6 | 9/8 | 10/10 |
| LoScore: score at LoRank | 1/1 | 2/3 | 3/3 | 5/4 | 5/5 |
| HiScore: score at HiRank | 2/2 | 3/3 | 4/4 | 5/5 | 7/7 |
| Difference: HiScore − LoScore | 1/1 | 1/0 | 1/1 | 0/1 | 2/2 |
| Mod: fractional part of OR | 0.1/0.9 | 0.75/0.25 | 0.5/0.5 | 0.25/0.75 | 0.9/0.1 |
| Interpolated score (exc/inc) = LoScore + Mod × Difference |
1.1/1.9 | 2.75/3 | 3.5/3.5 | 5/4.75 | 6.8/5.2 |
Interpolation methods, as the name implies, can return a score that is between scores in the distribution. Algorithms used by statistical programs typically use interpolation methods, for example, the percentile.exc and percentile.inc functions in Microsoft Excel. The Interpolated Methods table shows the computational steps.
The nearest-rank method[edit]
The percentile values for the ordered list {15, 20, 35, 40, 50}
One definition of percentile, often given in texts, is that the P-th percentile 
- Using the nearest-rank method on lists with fewer than 100 distinct values can result in the same value being used for more than one percentile.
- A percentile calculated using the nearest-rank method will always be a member of the original ordered list.
- The 100th percentile is defined to be the largest value in the ordered list.
The linear interpolation between closest ranks method[edit]
An alternative to rounding used in many applications is to use linear interpolation between adjacent ranks.
All of the following variants have the following in common. Given the order statistics
we seek a linear interpolation function that passes through the points 
where 




There are two ways in which the variant approaches differ. The first is in the linear relationship between the rank x, the percent rank 
There is the additional requirement that the midpoint of the range 

and our revised function now has just one degree of freedom, looking like this:
The second way in which the variants differ is in the definition of the function near the margins of the ![[0,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)

![[1,N]](https://wikimedia.org/api/rest_v1/media/math/render/svg/d6fc7b14276a914ff6cbdf59b806eb601020f473)

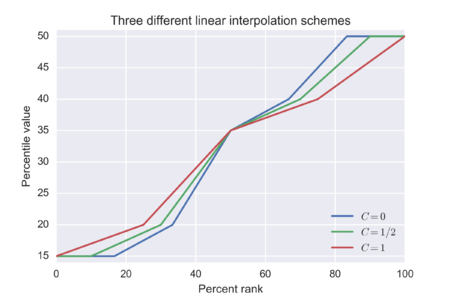
First variant, C = 1/2[edit]
The result of using each of the three variants on the ordered list {15, 20, 35, 40, 50}
(Sources: Matlab «prctile» function,[9][10])
where
Furthermore, let
The inverse relationship is restricted to a narrower region:
Second variant, C = 1[edit]
(Source: Some software packages, including NumPy[11] and Microsoft Excel[3] (up to and including version 2013 by means of the PERCENTILE.INC function). Noted as an alternative by NIST[8])
Note that the 
![pin [0,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/33c3a52aa7b2d00227e85c641cca67e85583c43c)
Third variant, C = 0[edit]
(The primary variant recommended by NIST.[8] Adopted by Microsoft Excel since 2010 by means of PERCENTIL.EXC function. However, as the «EXC» suffix indicates, the Excel version excludes both endpoints of the range of p, i.e., 

The inverse is restricted to a narrower region:
The weighted percentile method[edit]
In addition to the percentile function, there is also a weighted percentile, where the percentage in the total weight is counted instead of the total number. There is no standard function for a weighted percentile. One method extends the above approach in a natural way.
Suppose we have positive weights 
the sum of the weights. Then the formulas above are generalized by taking
when
,
or
for general
,
and
The 50% weighted percentile is known as the weighted median.
See also[edit]
- Decile
- Percentile rank
- Quantile
- Summary statistics
References[edit]
- ^ a b Hyndman, Rob J.; Fan, Yanan (November 1996). «Sample Quantiles in Statistical Packages». American Statistician. American Statistical Association. 50 (4): 361–365. doi:10.2307/2684934. JSTOR 2684934.
- ^ Lane, David. «Percentiles». Retrieved 2007-09-15.
- ^ a b Pottel, Hans. «Statistical flaws in Excel» (PDF). Archived from the original (PDF) on 2013-06-04. Retrieved 2013-03-25.
- ^ Schoonjans F, De Bacquer D, Schmid P (2011). «Estimation of population percentiles». Epidemiology. 22 (5): 750–751. doi:10.1097/EDE.0b013e318225c1de. PMC 3171208. PMID 21811118.
- ^ Johnson, Robert; Kuby, Patricia (2007), «Applied Example 2.15, The 85th Percentile Speed Limit: Going With 85% of the Flow», Elementary Statistics (10th ed.), Cengage Learning, p. 102, ISBN 9781111802493.
- ^ «Rational Speed Limits and the 85th Percentile Speed» (PDF). lsp.org. Louisiana State Police. Archived from the original (PDF) on 23 September 2018. Retrieved 28 October 2018.
- ^ Wessa, P (2021). «Percentiles in Free Statistics Software». Office for Research Development and Education. Retrieved 13 November 2021.
- ^ a b c «Engineering Statistics Handbook: Percentile». NIST. Retrieved 2009-02-18.
- ^ «Matlab Statistics Toolbox – Percentiles». Retrieved 2006-09-15., This is equivalent to Method 5 discussed here
- ^ Langford, E. (2006). «Quartiles in Elementary Statistics». Journal of Statistics Education. 14 (3). doi:10.1080/10691898.2006.11910589.
- ^ «NumPy 1.12 documentation». SciPy. Retrieved 2017-03-19.
Значение слова «ПРОЦЕНТИЛЬ» найдено в 15 источниках
ПРОЦЕНТИЛЬ
- ПРОЦЕНТИЛЬ
-
(реrcentile) Значения, выделяющие 100-е части распределения, выстроенные в ряд по их величине. 99-й процентиль распределения дохода, например, представляет собой такой уровень дохода, когда только один процент населения имеет больший доход.
Экономика. Толковый словарь. — М.: «ИНФРА-М», Издательство «Весь Мир»..2000.
Статистика выборки случайной величины, которая выражает ранг элемента в виде процента — от 0 до 100 процентов, таким образом, что наименьшему значению соответствует нулевой процентиль, наибольшему — 100-й процентиль, медиане — 50-й процентиль и т.д.
Любая из 99 пронумерованных точек, которые делят упорядоченный набор значений на 100 частей, каждая из которых содержит 1/100-ю от общего значения. Это прямое значение, к сожалению, часто путается; см. центиль и партиль для обсуждения.
Процентили – это величины, делящие
выборку данных на сто групп, содержащих (по возможности) равное количество
наблюдений. Например, 30% данных имеют значение, меньшее 30-го процентиля.
См. тж. квантиль.
показатель того, какой процент значений находится ниже определённого уровня. Например, значение 50-й процентили указывает, что 50% значений располагается ниже этого уровня.
(prozentil). Одна сотая часть условной шкалы, делящей распределение на 100 равных частей. Используется для ранжирования испытуемых по результатам теста.
centile, percentile, percentile rank
процент испытуемых из выборки стандартизации, который получили равный или более низкий балл, чем балл данного испытуемого.
percentile
* * *
проценти́ль
ж. стат.
percentile, centile
стат.
(per)centile, centesimal grade
centile, (квантиль порядка n/100, где n = 1, 2, … 99) percentile
1) centile
2) percentile
3) percentile rank





![{displaystyle v(x)=v_{lfloor xrfloor }+(x{bmod {1}})(v_{lfloor xrfloor +1}-v_{lfloor xrfloor }),forall xin [1,N]:v(i)=v_{i}{text{, for }}i=1,2,ldots ,N,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eeae87405f0184fabff114665b843cbb94a3abbc)



![{displaystyle x=f(p)={begin{cases}Np+{frac {1}{2}},forall pin left[p_{1},p_{N}right],\1,forall pin left[0,p_{1}right],\N,forall pin left[p_{N},1right].end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b7800366b8eeac526ee3fc22b45ed5dfd1550e62)
![p_{i}={frac {1}{N}}left(i-{frac {1}{2}}right),iin [1,N]cap mathbb {N}](https://wikimedia.org/api/rest_v1/media/math/render/svg/69e7a4bfdbaf07f8b5e36ccd021ff966f5e540d3)



![x=f(p,N)=p(N-1)+1{text{, }}pin [0,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/e25ef7db919bca75354f8af45d7208a1c5a626b2)
![therefore p={frac {x-1}{N-1}}{text{, }}xin [1,N].](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a4c15310db22c92a626068484739e320bace185)
![{displaystyle x=f(p,N)={begin{cases}1{text{, }}pin left[0,{frac {1}{N+1}}right]\p(N+1){text{, }}pin left({frac {1}{N+1}},{frac {N}{N+1}}right)\N{text{, }}pin left[{frac {N}{N+1}},1right]end{cases}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e7bef62b06df2ee9322c8ac5b1d10b43c07176f6)






