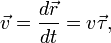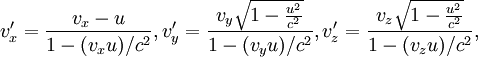Уважаемые форумчане!
Есть учебник по физике, набранный в Word, довольно большой — 300 стр., сотня рисунков и под полтысячи формул. Шрифт основного текста и формул — Times New Roman, формулы набраны в MathType. Редактор доволен, кроме следующего — буква v, обозначающая скорость, у меня в Times New Roman выглядит следующим образом:
В литературе же эту букву принято писать по другому:
Тут еще и z и фи по другому выглядят, но это уже второстепенно.
Вопрос — как с минимальными усилиями мне у себя переделать эту букву, чтобы она выглядела как в литературе (без заострения снизу, с более выраженным изгибом слева вверху)? Наверное, для нее нужен другой шрифт, но какой будет сочетаться с Times New Roman (v встречается как в отдельных формулах, так и посереди текста)?
Как обозначается скорость
Понятие скорости широко используется в науке: математике, физике, механике. Школьники начинают знакомиться с ним уже в третьем классе. Более подробно это происходит в 7-8 классах. В общепринятом смысле скорость — это величина, которая характеризует, насколько быстро предмет перемещается в пространстве за единицу времени. В зависимости от области применения, скорость обозначается разными символами.
1
Как обозначается скорость в математике
В учебниках по математике принято использовать строчную прописную латинскую букву v. Скорость взаимосвязана с пройденным путем и временем, за который оно пройдено.
При равномерном движении величина v=S/t, где:
- S – пройденный телом путь,
- t – время движения.
2
Как обозначается скорость в физике
В разделе физики, именуемом механикой, также изучается скорость. Обозначение скорости зависит от того, векторная это величина или обычная. В первом случае над буквой v ставится стрелочка, направленная вправо →. Если же нет необходимости учитывать направление, то применяют обычный символ v.
3
Единицы измерения скорости
В международной системе единиц измерения принято оперировать метрами в секунду (м/с). В то же время общепризнанными единицами измерения являются километр в час (км/ч), узел (морская миля в час).
4
Как обозначается скорость света и звука
Учеными доказано, что скорость света является абсолютной величиной, с которой могут перемещаться информация и энергия. Этот показатель постоянен и равен 299 792 458 ± 1,2 м/с. Его символом выбрали латинскую букву с.
Скорость звука зависит от плотности и упругости среды, в которой распространяются звуковые волны. Ее измеряют в Махах. Например, сверхзвуковая скорость находится в границах от 1,2 до 5 Махов. А все что выше, называют гиперзвуковой скоростью.
Очевидно, что символ, которым обозначается скорость, зависит от математического или физического смысла, которым наполняется данное понятие.
Со времен возникновения различных наук и математических расчетов ученые начали использовать множество символов и сокращений. Это вполне оправданное решение, ведь длинные формулы, записанные при помощи слов, отнимали бы много времени. По какому принципу выбираются эти обозначения, в частности буквы, указывающие на скорость и расстояние?
Как обозначают физические величины и понятия?
В физике существует общепринятый список обозначений. Он включает латинские и греческие буквы, кириллицу (редко), специальные символы, надстрочные и подстрочные знаки, скобки и др. В качестве самостоятельной науки физика зародилась в 17-м веке во время научной революции, но многие идеи, физические воззрения появились еще в античный период. Отсюда и использование латыни, греческого языка.
Количество физических величин довольно большое – букв в алфавитах недостаточно для обозначения их всех. Поэтому одни и те же буквы могут обозначать разные понятия. Важно различать и стиль написания.
Например, латинские символы обычно пишутся курсивом, греческие – обыкновенным прямым начертанием. Строчными буквами обозначают интенсивные величины (не зависят от размеров системы, например, температура), заглавными – экстенсивные.
Интересный факт: среди всех латинских букв для обозначения понятий из области физики реже всего встречается буква о.
Ввиду исторических причин множество обозначений с использованием латинских букв – это сокращения слов, которые указывают на данные понятия. Чаще всего это латинские, английские, немецкие и французские слова. Во избежание путаницы почти не используются греческие заглавные буквы, если они похожи на латинские по манере написания.
Почему в физике расстояние обозначается буквой s?
Расстояние в физике измеряется единицами длины (метр в международной системе единиц) и имеет два значения:
- степень удаленности объектов друг от друга;
- длина пути, которую прошел объект.
Расстояние – один из тех случаев, когда обозначающая буква является первой в слове-определении. Некоторые источники по-разному объясняют происхождение буквы s:
- От английского слова «space», которое означает расстояние, пространство, площадь.
- От латинского «spatium» – пространство между двумя предметами, протяжение в длину и ширину.
Фактически оба варианта являются правильными. Согласно этимологии слова «space», оно вошло в употребление в 1300-х годах и происходит от французского «espace», а оно, в свою очередь, от латинского «spatium». В значении космического пространства «space» начало употребляться лишь с конца 17-го века, после того как появилось в художественном произведении Джона Мильтона.
Почему в физике скорость обозначается буквой v?
Для обозначения скорости в физике используют строчную букву v тоже не случайно. Это первая буква в латинском слове «velocitas», французском «vitesse» и английском «velocity». Все они означают скорость, быстроту, стремительность.
Возникает другой вопрос: почему именно «velocity» стало определением скорости, а не другие английские слова с похожим значением, например, «speed»? Дело в том, что в физике скорость является векторной величиной, которая отображает быстроту и направление перемещения объекта относительно заданной системы отсчета.
Слово «speed» указывает на скалярную скорость – величину, которая не зависит от системы координат. Например, скорость света – постоянная величина, поэтому на английском данный термин будет выглядеть как «the speed of light».
Кроме того, скорость и расстояние – взаимосвязанные величины наряду со временем. Эта связь в физике выражается формулой. Зная две величины, можно рассчитать и третью. Использование одинаковых букв нецелесообразно.
Если Вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
Цель
: продолжить формировать представление о новой величине «скорость, время, расстояние» и единицах ее измерения.
Задачи
:
- Создать условия для осознания детьми зависимости между величинами, характеризующими движение тел — скоростью, временем и расстоянием.
- Познакомить детей с понятием скорости и единицами её измерения.
- Отрабатывать вычислительные навыки, обучать детей работе с графическими моделями.
- Развивать познавательную активность детей, способности к самооценке и самоконтролю, формировать коммуникативные умения.
Оборудование
: карточки, карточки для работы в парах, интерактивная доска, название единиц времени на карточках, рабочая тетрадь, компьютер, проектор, экран учебник.
Тип урока:
урок закрепления и развития знаний, умений и навыков.
Методы
: формы познавательной деятельности учащихся на уроке, индивидуальная работа, работа в парах.
Планируемые достижения учащихся на уроке:
- знать понятие скорости, времени и расстоянии как новой единицы измерения, уметь решать задачи на нахождение скорости движения по известным расстоянию и времени движения;
- закрепить табличные и внетабличные случаи умножения и деления, знание единиц длины и времени.
Как обозначается скорость света и звука
Учеными доказано, что скорость света является абсолютной величиной, с которой могут перемещаться информация и энергия. Этот показатель постоянен и равен 299 792 458 ± 1,2 м/с. Его символом выбрали латинскую букву с.
Скорость звука зависит от плотности и упругости среды, в которой распространяются звуковые волны. Ее измеряют в Махах. Например, сверхзвуковая скорость находится в границах от 1,2 до 5 Махов. А все что выше, называют гиперзвуковой скоростью.
Очевидно, что символ, которым обозначается скорость, зависит от математического или физического смысла, которым наполняется данное понятие.
Как решать задачи на движение? Формула зависимости между скоростью, временем и расстоянием. Задачи и решения.
Угловая скорость
Проявляется этот вид при вращении тела вокруг оси. Траектория представляет собой круговое движение. Основным параметром, учитывающимся при его нахождении, является угол поворота (f). Все элементарные угловые движения являются векторами. Обычный поворот равен углу вращения тела df за небольшой отрезок времени dt в противоположную сторону от хода часовой стрелки.
В математике формулу для нахождения углового параметра записывают как w = df/dt. Угловая скорость — аксиальная величина, располагающаяся вдоль мгновенной оси и совпадающая с поступательным вращением правого винта. Равномерное вращение, то есть движение, при котором происходит поворот на один и тот же угол, называют равномерным. Модуль угловой скорости определяют по формуле: w = f/t, где f — угол поворота, t — время, в течение которого происходило вращение. Учитывая, что Δf = 2p, формулу можно переписать до вида: w = 2p/T, то есть с использованием периода.
Существует связь между угловой скоростью и числом оборотов: w = 2*p*v. Это понятие используется для решения заданий при описании неравномерного вращения. Есть также выражение, связывающее линейную скорость с угловой: v = [w*R], где R — компонента, проведённая перпендикулярно к радиус-вектору. В качестве единицы измерения параметра используется радиан, делённый на секунду (рад/с).
Например, необходимо определить угловую скорость вариатора в тот момент, когда подвешенная масса пройдёт расстояние, равное 10 метрам. Радиус плеча составляет 40 сантиметров. В начальный момент подвес находится в состоянии покоя, а затем начинает опускаться с ускорением A = 0,04 м/с2.
Учитывая, что линейная скорость вариатора совпадает с движением груза по прямой, можно записать: V = (2*a*S)½. Должен получится ответ: V = (4*0,04*10)½ = 1,26 м/с. Угловую же скорость находят по формуле: w = v/R, так как R = 40 см = 0,4 м, то W = 1,26/0,4 = 3,15 рад/с.
Как найти время, зная скорость и расстояние?
Для того, чтобы найти время, понадобившееся для прохождения пути, нужно знать расстояние и скорость. Если расстояние разделить на скорость — вы узнаете время. Пример такой задачи:
Задача про Зайца.
Заяц убегал от Волка со скоростью 1 километр за минуту. Он пробежал до своей норы 3 километра. За какое время Заяц добежал до норы?
Как легко решать задачи на движение, где нужно найти расстояние, время или скорость?
- Внимательно прочитайте задачу и определите, что известно из условия задачи.
- Напишите на черновике эти данные.
- Также напишите, что неизвестно и что нужно найти
- Воспользуйтесь формулой для задач про расстояние, время и скорость
- Введите в формулу известные данные и решите задачу
Решение для задачи про Зайца и Волка.
- Из условия задачи определяем, что нам известно скорость и расстояние.
- Также из условия задачи определяем, что нам нужно найти время, которое нужно было зайцу, чтобы добежать до норы.
Пишем в черновик эти данные например так:
Время — неизвестно
Теперь запишем то же самое математическими знаками:
S — 3 километра
V — 1 км/мин
t — ?
Вспоминаем и записываем в тетрадь формулу для нахождения времени:
t = S: v
t = 3: 1 = 3 минуты
Среднее значение
В кинематике для нахождения характеристики используется усреднённый параметр. Используют его при изучении движения материальной точки или любого физического тела. Для определения средней скорости используют две величины: скалярную и векторную. Первой обозначают путевое движение, а второй — перемещение.
Путевая скорость определяется как отношение расстояния пройденного тела ко времени, затраченному на его прохождение: V = Σs / Σt.
По сути, среднее значение находится как среднеарифметическое от всех скоростей, если рассматриваемая точка передвигалась одинаковые отрезки времени. В ином же случае найденная величина будет взвешенной среднеарифметической величиной.
Математически формулу средней скорости записывают так: V (t + Δ t) = Δ s/ Δ t = (s (t + Δ t) — s (t)) / Δ t. Учитывая, что Δs зависит от длины пути, которую преодолела точка за время Δt, верной будет запись: Δ s = s (t + Δt) — s (t). Если же затраченное время стремится к нулю, получится формула, совпадающая с выражением для нахождения мгновенной скорости.
Вектор материальной точки находится из отношения положения тела к отрезку времени: V (t + Δt) = Δr / Δt = (r (t + Δt) — r (t)) / Δt, где r — радиус-вектор. Когда тело выполняет равномерно-прямолинейное перемещение, то справедливым будет равенство: {V} = V.
Например, мяч первую половину пути длиной 100 метров катился с одной скоростью в течение двадцати секунд, а вторую с другой и одну минуту. Необходимо вычислить среднюю скорость. Согласно формулам, интервал движения на первом участке пути будет равен: t1 = s/2*V1, а на втором t2 = s/2*V2. Решением задачи будет: Vср = s/(t1+t2) = s/(s/2*v1 + s/2*v2) = 2*V1*V2/(V1+V2) = 100/(20 +60) = 1,25 м/с.
Таблица 4 класс: скорость, время, расстояние
В таблице ниже приведены данные для которых нужно придумать задачи, а потом их решить.
| № | Скорость (км/час) | Время (час) | Расстояние (км) |
| 1 | 5 | 2 | ? |
| 2 | 12 | ? | 12 |
| 3 | 60 | 4 | ? |
| 4 | ? | 3 | 300 |
| 5 | 220 | ? | 440 |
Вы можете пофантазировать и придумать задачи к таблице сами. Ниже наши варианты условия задач:
- Мама отправила Красную Шапочку к бабушке. Девочка постоянно отвлекалась и шла по лесу медленно, со скоростью 5 км/час. На путь она потратила 2 часа. Какое расстояние за это время прошла Красная Шапочка?
- Почтальон Печкин вез на велосипеде посылку со скоростью 12 км/час. Он знает, что расстояние между его домом и домом Дяди Федора 12 км. Помогите Печкину рассчитать, сколько времени понадобится на дорогу?
- Папа Ксюши купил автомобиль и решил отвезти семью на море. Машина ехала со скоростью 60 км/час и на дорогу было потрачено 4 часа. Какое расстояние между домом Ксюши и морским побережьем?
- Утки собрались в клин и полетели в теплые края. Птицы махали крыльями без устали 3 часа и преодолели за это время 300 км. Какой была скорость птиц?
- Самолет АН-2 летит со скоростью 220 км/час. Он вылетел из Москвы и летит в Нижний Новгород, расстояние между этими двумя городами 440 км. Сколько времени самолет будет в пути?
Ответы на приведенные задачи можно найти в таблице ниже:
| № | Скорость (км/час) | Время (час) | Расстояние (км) |
| 1 | 5 | 2 | 10 |
| 2 | 12 | 1 | 12 |
| 3 | 60 | 4 | 240 |
| 4 | 100 | 3 | 300 |
| 5 | 220 | 2 | 440 |
Примеры решения задач на скорость, время, расстояние за 4 класс
Если в одной задаче есть несколько объектов движения, нужно научить ребенка рассматривать движение этих объектов отдельно и только потом вместе. Пример такой задачи:
Двое друзей Вадик и Тема решили прогуляться и вышли из своих домов навстречу друг другу. Вадик ехал на велосипеде, а Тема шел пешком. Вадик ехал со скоростью 10 км/час, а Тема шел со скоростью 5 км в час. Через час они встретились. Какое расстояние между домами Вадика и Темы?
Эту задачу можно решить используя формулу зависимости расстояния от скорости и времени.
S = v ⋅ t
Расстояние, которое проехал Вадик на велосипеде будет равно его скорости умноженной на время в пути.
S = 10 ⋅ 1 = 10 километров
Расстояние, которое прошел Тема считают аналогично:
S = v ⋅ t
Подставляем в формулу цифровые значения его скорости и времени
S = 5 ⋅ 1 = 5 километров
Расстояние, которое проехал Вадик нужно прибавить к расстоянию, которое прошел Тема.
10 + 5 = 15 километров
Как научиться решать сложные задачи, для решения которых требуется логически мыслить?
Развивать логическое мышление ребенка, нужно решая с ним простые, а затем и сложные логические задачи. Эти задачи могут состоять из нескольких этапов. Перейти с одного этапа на другой можно только в том случае, если решен предыдущий. Пример такой задачи:
Антон ехал на велосипеде со скоростью 12 км/час, а Лиза ехала на самокате со скоростью в 2 раза меньше, чем у Антона, а Денис шел пешком со скоростью в 2 раза меньше, чем у Лизы. Какова скорость Дениса?
Чтобы решить эту задачу нужно сначала узнать скорость Лизы и только после этого скорость Дениса.
Кто едет быстрее? Задача про друзей
Иногда в учебниках для 4 класса попадаются непростые задачи. Пример такой задачи:
Два велосипедиста выехали из разных городов навстречу друг другу. Один из них спешил и мчался со скоростью 12 км/час, а второй ехал не спеша со скоростью 8 км/час. Расстояние между городами из которых выехали велосипедисты 60 км. Какое расстояние проедет каждый велосипедист, перед тем как они встретятся? (решение под фото)
Решение:
- 12+8 = 20 (км/час) — это общая скорость двух велосипедистов, или скорость с которой они приближались друг к другу
- 60 :
20 = 3 (часа) — это время через которое велосипедисты встретились - 3 ⋅
8 = 24 (км) — это расстояние, которое проехал первый велосипедист - 12 ⋅ 3
= 36 (км) — это расстояние, которое проехал второй велосипедист - Проверка: 36+24=60 (км) — это расстояние, которое проехали два велосипедиста.
- Ответ: 24 км, 36 км.
Предлагайте детям в форме игры решать такие задачи. Возможно, они сами захотят составить свою задачу про друзей, животных или птиц.
Ход урока
Организационный момент
Психологический настрой
Прозвенел заливистый школьный звонок. Начинается новый урок. Мы готовы считать и задачи решать.
Учитель
: Я улыбнулась вам, и вы улыбнитесь друг другу, и подумайте, как хорошо, что мы сегодня все вместе. Мы спокойны, добры и приветливы. Глубоко вдохните и выдохните. Выдохните вчерашнюю обиду и злость, беспокойство. Забудьте о них. Я желаю вам хорошего настроения.
Сообщение темы и цели урока
Сегодня на уроке мы с вами вспомним о величинах, с которыми познакомились на предыдущих уроках и решали с ними задачи на движение и ставить свои ответы на листах самооценки.
(Ответы учащихся) Верно, это скорость, время, расстояние. Какими латинскими буквами они обозначаются. (s, v, t).
Слайд № 1
Девиз нашего урока: «Один за всех, все за одного»
Работа в парах
На партах карточки с примерами:
Увеличь произведение чисел 805 и 5 на 1025 (5050) Из 10000 вычти частное число 40025 и 5 (1995) Увеличь частное чисел 4025 и 5 в 100 раз (80500) Прибавь к числу 1207 частное чисел 51300 и 9 (6907) Из произведения чисел 480 и 7 вычти число 1406 (1954) Произведение чисел 4070 и 6 уменьши на 4420 (20000) Записать ответы в порядке возрастания (ответ записан на интерактивной доске)
Минутка чистописания
Слайд № 2
2 4 6 8 10 (образец в тетради)
Прочитайте числа. Какие это числа? В каком порядке они расположены? Как они увеличиваются? Прочитайте число целиком. Сколько цифр использовано? В обратном направлении можем прочитать? Прочитайте. Запишите числа в порядке возрастания, через клеточку в порядке убывания. Прочитайте их, сравните. Запишите еще раз в порядке возрастания, найдите сумму этих четных чисел. Как вы это сделали?
Индивидуальная работа по карточкам
(4 ученика решают № 7)
Устная работа с остальными учениками:
В саду растут груши и ивы. На груше росло 69 груш, а на иве на 100 груш больше. Сколько груш росло на иве?
Мама варила одно яйцо 5 минут. Сколько времени будет варить 3 яйца?
Масса 1 мешка сахара 50 кг. Сколько кг в 4 таких мешках?
За 1 с человек делает 2 шага. Сколько шагов он сделает за 5 с.? За 10 с?
Слайд № 3
Физминутка
Слайд № 4
Качу, лечу во весь опор. (Выполняют ходьбу на месте.) Я сам — шофер (Имитируют управление автомобильным рулем.) И сам — мотор. (Круговые движения плечами вперед-назад.) Нажимаю на педаль, (Имитируют нажимание на педаль.) И машина мчится вдаль! (Бег на месте.)
Первичное закрепление
Слайд № 5
Орел летел со скоростью 20 км/ч. За сколько часов он пролетит 80 км?
Cкорость полета космического спутника 8 км/сек. Сколько км он пролетит за 10 сек?
Слайд № 6
Решение задачи № 2
Автобус
S — 90 км 90: 45= 2 часа T — ? V — 45 км/ч
Легковая машина
S — 270 км 270: 90 = 3 часа T — ? V — 90 км/ч
Самостоятельная работа по учебнику
Итог урока
Давайте подведем итог урока
Чем занимались на уроке?
Что запомнили?
Рефлексия
Окрасьте сегодняшний урок (Дети рисуют сердечко своего настроения от урока) Учитель объясняет значении выбранного цвета.
- Красный — радость
- Жёлтый — приятное
- Зелёный — спокойное
- Синий — грустное
- Фиолетовый — тревожный
- Оранжевый — удовлетворение
- Чёрный — неудовлетворение
И на память об уроке солнышко дарит вам частичку своего тепла и хорошего настроения.
Наш закончен урок — Спасибо за внимание, Будем рады новой встрече, Всем Вам до свидания!
Понятие скорости широко используется в науке: математике, физике, механике. Школьники начинают знакомиться с ним уже в третьем классе. Более подробно это происходит в 7-8 классах. В общепринятом смысле скорость — это величина, которая характеризует, насколько быстро предмет перемещается в пространстве за единицу времени. В зависимости от области применения, скорость обозначается разными символами.
ВИДЕО: Задачи на движение
Мы будем учиться решать задачи на нахождение скорости движения по данному расстоянию и времени. Сравните скорость Зелибобы и Кубика. ЗНАКИ МАТЕМАТИЧЕСКИЕ — условные обозначения, служащие для записи математических понятий, предложений и выкладок.
Для некоторых физических величин принято несколько обозначений (например для энергии, скорости, длины и других), чтобы предотвратить путаницу с другими величинами в данном разделе физики. Иногда также для обозначения используется готический шрифт. Интенсивные величины обычно обозначаются строчными, а экстенсивные — заглавными буквами.
Кириллические буквы сейчас очень редко используются для обозначения физических величин, хотя частично применялись в русскоязычной научной традиции. Поскольку скорость света в вакууме – величина постоянная, в расчетах она принимается за константу. Скорость это величина, которая характеризует быстроту перемещения объекта относительно выбранной системы отсчета.
какой буквой в алгебре обозначается время
Самая простая формула скорость, это длина деленная на расстояние. Латинской буквой V. Такое обозначение используется и в математике, и в физике. Начатки буквенного обозначения и исчисления возникают в позднеэллинистич.
В различных странах стихийно появляются 3. м. для нек-рых действий и для степеней неизвестной величины. Кто готов назвать их в порядке возрастания? В единицах длины).
Запись в тетради: 24 ׃ 3 = 8 (м/мин) скорость Зелибобы. Задача 2. Кубик прошёл на лыжах расстояние, равное 24 м за 4 минуты. Вы назвали формулу, по которой находят скорость движения. Этой формулой вы будете пользоваться и в старших классах.
Урок математики в 3-м классе по теме «Скорость. Время. Расстояние»
S ׃ t 24 ׃ 4 = 6 (м/мин) скорость Кубика. Вывод: Скорость – это величина, которую можно измерить и сравнить. Вместе с вами они научились измерять скорость движения. Давайте потренируемся в решении задач на нахождение скорости, выполняя работу самостоятельно. Бусинка вам предлагает найти скорость движения своих друзей в других видах спорта.
Как будете находить скорость движения? Будьте внимательны при обозначении скорости. Ещё 3 ученика – это скорости движения: 800 км/ч; 90 км/ч; 6 км/с. Найдите пару, соотнесите, у кого из вас какая скорость движения? Цель: продолжить формировать представление о новой величине «скорость, время, расстояние» и единицах ее измерения.
Закон сложения
Для разных систем отсчёта движения материальных точек существует закон, связывающий их между собой. Согласно ему, скорость чего-либо относительно системы, находящейся в покое, определяется суммой силы перемещения скоростей в подвижной области и более быстрой системы отсчёта по отношению к неподвижной.
Чтобы понять суть закона, лучше всего рассмотреть простой пример. Пусть по железной дороге движется вагон со скоростью 80 км/ч. В этом вагоне перемещается пассажир со скоростью 3 км/ч. Приняв за систему отсчёта неподвижный железнодорожный путь, можно утверждать, что скорость пассажира относительно неё равна сумме скорости вагона и человека.
Если движение вагона и пассажира происходит в одном направлении, то значения просто складываются, V = 80+3 = 83 км/ч, в противоположном — вычитаются V = 80−3 = 77 км/ч. Но это правило будет верным лишь тогда, когда перемещение происходит по одной линии. Поэтому, если человек будет передвигаться в вагоне под углом, следует учитывать и этот фактор, так как по своей сути искомый параметр — величина векторная. Фактически рассчитываются две скорости: сближения и удаления.
Рассматриваемое событие происходит за время Δt. За этот промежуток человек преодолеет расстояние ΔS1, вагон же сможет проехать путь ΔS2. Используя закон, перемещение пассажира будет определяться по формуле: ΔS = ΔS1 + ΔS2. Собственное движение человека относительно железнодорожного пути будет равно V = ΔS1 / Δ t. Выразив значение из формулы нахождения ΔS, можно найти скорость вагона относительно железной дороги: V2 = ΔS2 / Δt.
Какой буквой обозначается скорость?
В печатном тексте математические обозначения, использующие латиницу, принято писать курсивом. Названия функций, а также цифры и греческие буквы оставляют прямыми. Буквы также могут быть записаны различными шрифтами для того, чтобы различать природу величин или математических операций. В частности принято обозначать жирным шрифтом векторные величины, а тензорные величины — рубленым шрифтом. Когда такая связь существует, это обозначено в скобках.
В круглых скобках указывается одна или несколько переменных, от которых зависит физическая величина. Диакритические знаки добавляются к символу физической величины для обозначения определённых различий.
Дата и время в английском языке
Очень часто люди путают скорость с ускорением, что приводит плохим последствиям. Развитие математической символики было тесно связано с общим развитием понятий и методов математики. Первые 3. м. для произвольных величин появились много позднее (начиная с 5-4 вв. до н. э.) в Греции. Произвольные величины (площади, объемы, углы) изображались в виде отрезков, а произведение двух произвольных величин — в виде прямоугольника, построенного на соответствующих отрезках.
14-17 вв.; оно определялось успехами практич. Проходят многие десятилетия и даже века, прежде чем вырабатывается тот или иной удобный для исчисления символ. Вслед за Леонардо Пизанским (Leonardo Pisano, 1220) многие обозначали (вплоть до 17 в.) квадратный корень знаком (от лат. radix — корень). Весьма различны были 3. м. неизвестной и ее степеней. Значительным шагом вперед в развитии математич.
Дальнейшее развитие 3. м. было тесно связано с созданием анализа бесконечно малых, для разработки символики к-рого основа была уже в большой мере подготовлена в алгебре. Благодаря этому знак годится и для записи формул замены переменных и легко может быть использован для записи кратных и криволинейных интегралов.
Огромная заслуга в создании символики современной математики принадлежит Л. Эйлеру (L. Euler). В 19 в. роль символики еще более возрастает и, наряду с созданием новых 3. м., математики стремятся к стандартизации основных символов. С точки зрения математической логики, среди 3. м. можно наметить следующие основные группы: А) знаки объектов, Б) знаки операций, В) знаки отношений.
Время передачи “Улицы Сезам” истекает. Обычно в физике скорость обозначается латинской буквой v. Иногда эту букву пишут прописной, иногда строчной. Основной его расшифровкой служит определение: Скорость — это отношение пройденного пути (расстояния) за определенный промежуток времени.
Равноускоренное движение
Если в течение времени положение тела изменяется относительно предметов, находящихся в покое, то считается, что оно движется. При этом в качестве основного параметра, описывающего перемещение, используется скорость. Движение тела или точки можно представить в виде линии, повторяющей путь прохождения. Называется она траекторией. Если линия прямая, то движение считается прямолинейным.
Неравномерное движение характеризуется перемещением по различной траектории с непостоянной величиной скорости. При этом изменение положения может быть равноускоренным, то есть параметр на одинаковых промежутках увеличивается или уменьшается на одно и то же значение. В качестве примера можно привести падение камня.
В произвольно взятой точке скорость перемещения равна ускорению свободного падения.
Таким образом, если векторы V и ускорения A лежат вдоль прямой, то в проекциях такое направление можно рассматривать как алгебраические величины. При равноускоренном движении по прямой траектории скорость точки вычисляется по формуле: V = V0 + A*t. Где:
- V0 — начальная скорость;
- A — ускорение (имеет постоянное значение);
- t — время движения.
Это основная формула в физике. На графике она изображается как прямая линия v (t). По оси ординат откладывается время, а абсцисс — скорость. Построив график, по наклону прямой можно определить ускорение точки A. Для этого используется формула нахождения сторон треугольника: A = (v-v0) / t.
Если на оси времени выделить промежуток Δt, то можно предположить, что движение будет равномерным и описываться некоторым параметром, равным мгновенному значению в середине отрезка. Эта моментальная величина является векторной. Она численно равна пределу, который пытается достигнуть скорость за промежуток времени, стремящийся к нулю. В физике это состояние описывается формулой мгновенной скорости: V = lim (Δ s/ Δ t) = r-1(t). То есть, с математической точки зрения, это первая производная.
Исходя из этого можно утверждать, что движение Δs = v*Δt. Так как произведение ускорения на время определяется разницей V -V0, то верной будет запись: S = V0*t + A*t2/2 = (V2 — V20) /2*A.
Из этой формулы можно вывести выражение для нахождения конечной скорости материальной точки: V = (V20 — 2* A * s)½. Если же в начальный момент V0 = 0, то формулу можно упростить до вида: V = (2* A * s)½.
Ско́рость (часто обозначается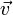 
, от англ. velocity или фр. vitesse) — векторная величина, характеризующая быстроту перемещения и направление движения материальной точки в пространстве относительно выбранной системы отсчёта. Этим же словом может называться скалярная величина, точнее модуль производной радиус-вектора.
В науке повсеместно используется также скорость в широком смысле, то есть как скорость изменения какой-либо величины (не обязательно радиус-вектора). Так, например, говорят об угловой скорости, скорости роста температуры, скорости химической реакции и т. д. Математически находится с помощью производной от данной величины (обычно по времени, либо от другого аргумента).
Содержание
- 1 Скорость тела в механике
- 1.1 Мгновенная и средняя скорость
- 2 Преобразование скорости
- 3 Единицы измерения скорости
- 3.1 Соотношение между единицами скорости
- 4 См. также
Скорость тела в механике
Вектор скорости материальной точки в каждый момент времени определяется производной по времени радиус-вектора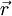 
этой точки:
Здесь v — модуль скорости,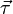 
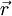
— направленный вдоль скорости единичный вектор касательной к траектории в точке .
Говорят, что тело совершает мгновенно-поступательное движение, если в данный момент времени скорости всех составляющих его точек равны. Так, например, равны скорости всех точек кабинки колеса обозрения (если, конечно, пренебречь колебаниями кабинки).
В общем случае, скорости точек, образующих твёрдое тело, не равны между собой. Так, например, для катящегося без проскальзывания колеса величина скорости точек на ободе относительно дороги принимает значения от нуля (в точке касания с дорогой) до удвоенного значения скорости автомобиля (в точке, диаметрально противоположной точке касания). Распределение скоростей в твёрдом теле определяется с помощью кинематической формулы Эйлера.
Если скорость тела (как векторная величина) не меняется во времени, то движение тела — равномерное (ускорение равно нулю).
Полезно отличать понятие средней скорости перемещения от понятия средней скорости пути, равной отношению пройденного точкой пути ко времени, за которое этот путь был пройден. В отличие от скорости перемещения, средняя скорость пути — скаляр.
Мгновенная и средняя скорость
Когда говорят о средней скорости , для различения, скорость согласно выше приведённому определению называют мгновенной скоростью. Так, хотя мгновенная скорость бегуна, кружащего по стадиону, в каждый момент времени отлична от нуля, его средняя скорость (перемещения) от старта до финиша оказывается равной нулю, если точки старта и финиша совпадают. Заметим, что при этом, средняя путевая скорость остаётся отличной от нуля.
Преобразование скорости
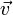
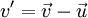
В классической механике Ньютона скорости преобразуются при переходе из одной инерциальной системы отсчёта в другую согласно преобразованиям Галилея. Если скорость тела в системе отсчёта S была равна , а скорость системы отсчёта S’ относительно системы отсчёта S равна 
, то скорость тела в при переходе в систему отсчёта S’ будет равна 
.
Для скоростей, близких к скорости света преобразования Галилея становятся несправедливы. При переходе из системы S в систему S’ необходимо использовать преобразования Лоренца для скоростей:
в предположении, что скорость направлена вдоль оси х системы S. Легко убедиться, что в пределе нерелятивистских скоростей преобразования Лоренца сводятся к преобразованиям Галилея.
Единицы измерения скорости
- Метр в секунду, (м/с), производная единица системы СИ
- Километр в час, (км/ч)
- узел (морская миля в час)
- Мах, 1 Мах равен скорости звука; Max n в n раз быстрее. Как единица, зависящая от конкретных условий, должна дополнительно определяться.
- Скорость света в вакууме (обозначается c)
Соотношение между единицами скорости
- 1 м/с = 3,6 км/ч
- 1 узел = 1,852 км/ч = 0,514 м/c
- Мах 1 ~ 330 м/c ~ 1200 км/ч (зависит от условий, в которых находится воздух)
- c = 299 792 458 м/c
См. также
- Ускорение
- Годограф
- Крейсерская скорость
- Быстрота
- Скорость света
- Скорость звука
- Космическая скорость
- 1-я космическая скорость
- 2-я космическая скорость
- 3-я космическая скорость
- 4-я космическая скорость
- Скорость гравитации
Wikimedia Foundation.
2010.