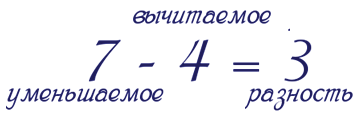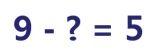Как пишется проверка вычитания

Математика, 2 класс. Урок №27

Проверка сложения. Проверка вычитания.

Перечень вопросов, рассматриваемых в теме:

— Что такое обратные математические действия?

— Как проверить сложение?

— Как проверить вычитание?

Глоссарий по теме:

Сложение – это объединение объектов в одно целое. Результатом сложения чисел является число, называемое суммой чисел (слагаемых).

Вычитание – это такое действие, в котором отнимают меньшее число от большего. Большее число называется уменьшаемым, меньшее – вычитаемым, результат вычитания – разностью.

Обратные действия – действия, приводящие к прежнему, исходному состоянию.

Основная и дополнительная литература по теме урока (точные библиографические данные с указанием страниц):

1. Математика. 2 класс. Учебник для общеобразовательных организаций. В 2 ч. Ч.1/ М. И. Моро, М. А. Бантова, Г. В. Бельтюкова и др. – 8-е изд. – М.: Просвещение, 2017. – с.84-86.
2. Математика. Рабочая тетрадь. 2 класс. Учебное пособие для общеобразовательных организаций. В 2 ч. Ч.1/ М. И. Моро, М. А. Бантова – 6-е изд., дораб. – М.: Просвещение, 2016. – с.60.
3. Математика: переходим в 3-й класс. Учебное пособие для общеобразовательных организаций. А. В. Светин – М.: Просвещение: Уч. Лит, 2017. – с.40.

Теоретический материал для самостоятельного изучения

Используя числа 7, 5, 12 составим все возможные равенства.

7 + 5 = 12 12 – 5 = 7

12 – 7 = 5 5 + 7 = 12

Назовём компоненты и результат действия сложения.

7 + 5 = 12

Слагаемое + слагаемое = сумма

Назовём компоненты и результат действия вычитания.

12 — 7 = 5

Уменьшаемое – вычитаемое = разность

Действия сложение и вычитание связаны друг с другом, являются взаимно обратными действиями.

СЛОЖЕНИЕ ВЫЧИТАНИЕ

Как проверить, верно ли выполнено сложение. Воспользуемся знанием того, как связаны слагаемые и сумма. Если из суммы двух слагаемых вычесть одно из них, то получится другое слагаемое. Это позволяет сложение проверить вычитанием.

Например, надо проверить, верно ли вычислили сумму чисел 28 и 5. Для этого из суммы 33 вычтем одно из слагаемых. Например, 5. Должно получиться другое слагаемое. Получилось 28. Значит, сумма чисел 28 и 5 найдена правильно. Можно вычесть из суммы другое слагаемое.

28 + 5 = 33

33 – 5 = 28

33 – 28 = 5

Сумма чисел 36 и 9 найдена неверно, т.к. после вычитания из суммы 47 слагаемого 9, другое слагаемое, 36 не получается.

36 + 9 = 47

47 – 9 = 38

38 = 36

Вычислим ещё раз сумму чисел 36 и 9 и проверим результат.

36 + 9 = 45

45 – 9 = 36

36 = 36

36 – первое слагаемое

Сформулируем правило проверки сложения: «Для проверки сложения надо из значения суммы вычесть одно из слагаемых. Если в результате вычитания получается другое слагаемое, значит, сложение выполнено верно».

Как проверить вычитание? Воспользуемся знанием того, как связаны между собой уменьшаемое, вычитаемое, разность. Если к разности прибавить вычитаемое, то получится уменьшаемое. Значит, вычитание можно проверить сложением.

Вычислим разность чисел 48 и 30. Она равна 18. Проверим вычитание сложением. К разности 18 прибавим вычитаемое 30, получим 48. Это уменьшаемое.

48 – 30 = 18

18 + 30 = 48

48 = 48

48 — уменьшаемое

Если из уменьшаемого вычесть разность, то получится вычитаемое.

Значит, вычитание можно проверить и вычитанием. Рассмотрим это на примере.

Из уменьшаемого 48 вычтем разность 18, получим 30, т.е. вычитаемое. Значит, разность чисел 48 и 30 вычислена верно.

48 – 30 = 18

48 – 18 = 30

30 = 30

30 — вычитаемое

Сформулируем правила проверки вычитания: «Для проверки вычитания, надо к значению разности прибавить вычитаемое. Если в результате сложения получается уменьшаемое, значит, вычитание выполнено верно», или «Для проверки вычитания, надо из уменьшаемого вычесть разность. Если в результате получается вычитаемое, значит, вычитание выполнено верно».

Вывод: Сложение и вычитание – это обратные действия. Для проверки сложения надо из значения суммы вычесть одно из слагаемых. Если в результате вычитания получается другое слагаемое, значит, сложение выполнено верно. Для того, чтобы выполнить проверку вычитания, надо к значению разности прибавить вычитаемое. Если в результате сложения получается уменьшаемое, значит, вычитание выполнено верно.

Тренировочные задания.

1. Найдите значение первого выражения в каждой рамке, а затем выполни проверку полученного результата двумя способами.

42 + 30 = …..	54 + 6 = …..	65 – 12 = …..	78 – 50 = …..
— 30 = ……. — 30 = …….	— 6 = ……. — 30 = …….	+ 12 =……. — 30 = …….	+ 50 =……. — 30 = …….

Правильные ответы:

42 + 30 = 72.	54 + 6 = 60..	65 – 12 = 53..	78 – 50 = 28.
72 — 30 = 42. 72 — 42 = 30.	60 — 6 = …54. 60 — 54 = …6.	53 + 12 = 65 65 — 53 = 12.	28 + 50 =78. 78 — 28 = 50

2. Распределите все записи с вычислениями и проверкой на верные и неверные.

Правильные ответы:

• До 7 класса: Алгоритмика, Кодланд, Реботика.
• 8-11 класс: Умскул, Годограф, Знанио.
• Английский: Инглекс, Puzzle, Novakid.
• Взрослым: Skillbox, Нетология, Geekbrains, Яндекс, Otus, SkillFactory.

Проверка вычитания

Выполнять самопроверку важно и полезно, поскольку это позволяет удостовериться в правильности решения. Рассмотрим, как следует проводить проверку вычитания.

Вычитание

Вычитание – одно из простейших арифметических действий, обратное сложению. В примерах его обозначают знаком минус («-»). Главными составляющими вычитания являются:

• уменьшаемое (число, из которого вычитают);
• вычитаемое (число, которое вычитают);
• разность (итог математического действия вычитания).

Способы проверки вычитания

Существуют два надёжных способа, которые помогают проверить результат вычитания. Рассмотрим принципы их применения.

Проверка вычитанием

Чтобы осуществить проверку способом вычитания, из уменьшаемого вычитают разность. Если в результате получается число, равное вычитаемому, пример решён верно. Например, мы вычислили, что 59-24=35. Попробуем теперь вычесть из 59 число 35: 59-35=24. Значит, 35 – верный ответ.

Проверка сложением

Чтобы проверить решение способом сложения, к разности прибавляют вычитаемое. Если в результате этого действия получилось равное уменьшаемому число, вычисления были произведены верно. Обратимся к примеру из предыдущего раздела: 59-24=35. Проверим его сложением и прибавим к 35 24. 35+24=59. Значит, 35 – верный ответ.

Вычитание

Познакомимся с вычитанием.

Рассмотрим числовой ряд и вспомним, в каком порядке идут числа.

Числа идут слева направо, по порядку, как при счёте.

0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10

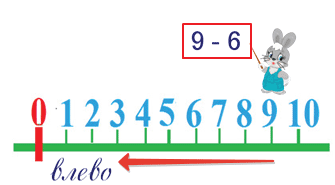
Посмотри на числовой ряд, по которому идёт заяц.

Какое действие выполняет заяц?

Вычитает число 6.

Из какого числа он вычитает число 6?

Из числа 9. Мы поставили зайчика на число 9.

В какую сторону он пойдёт?

Влево, потому что у него на табличке знак минус.

Сколько шагов влево сделает зайчик? 6.

На каком делении он остановится? На числе 3.

Когда вычитаем, становится меньше.

Чем левее, тем числа меньше.

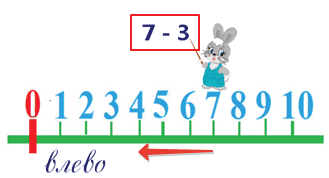
Рассмотрим еще один пример.

Какое действие выполняет заяц?

Вычитает число 3.

Из какого числа он вычитает число 3?

Из числа 7. Мы поставили зайчика на число 7.

В какую сторону он пойдёт?

Влево, потому что у него на табличке знак минус.

Сколько шагов влево сделает зайчик? 3.

На каком делении он остановится? На числе 4.

Когда вычитаем, становится меньше.

Чем левее, тем числа меньше.

Как называются числа при вычитании?

Число, из которого вычитают, становится МЕНЬШЕ, уменьшается, поэтому его называют «уменьшаемое».

Число, которое вычитают, называют «вычитаемое».

Число, которое получается в результате вычитания, называют «разность».

У жонглёра было 9 шариков.

Когда несколько шариков упало, осталось ещё 5 шариков.

Сколько шариков упало?

Каким действием будем находить? Вычитанием.

Как называются числа при вычитании?

Как найти неизвестное вычитаемое

У жонглера было 9 шариков. Когда несколько шариков упало, осталось 5. Упали, значит, убрали.

Решаем вычитанием. Что нужно найти?

Нужно найти вычитаемое.

Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность.

Как найти неизвестное уменьшаемое

Нужно найти уменьшаемое.

Чтобы найти уменьшаемое, нужно к разности прибавить вычитаемое.

5 + 4 = 9

Проверка вычитания

Если к разности прибавить вычитаемое, получится уменьшаемое.

Именно эта связь между разностью, уменьшаемым и вычитаемым используют для проверки вычитания.

Правильно ли произведено вычисление? Можно проверить так:

20 + 15 = 35, мы к разности прибавили вычитаемое и получили уменьшаемое. Значит, вычисление произведено верно и пример решен правильно.

Поделись с друзьями в социальных сетях:

Источник

Проверочное слово к слову «отражать»

Написание бук­вы «о» в пер­вом сло­ге и «а» во вто­ром сло­ге сло­ва «отра­жать» и одно­ко­рен­но­го суще­стви­тель­но­го «отра­же­ние» сле­ду­ет запом­нить или про­ве­рять по орфо­гра­фи­че­ско­му словарю.

Поставив уда­ре­ние, убе­дим­ся, что в сло­ве « о тр а жать» удар­ным явля­ет­ся глас­ный звук суффикса:

В без­удар­ной пози­ции ока­за­лись оба глас­ных кор­ня инте­ре­су­ю­ще­го нас сло­ва. Возникает вопрос: что напи­сать в пер­вом и вто­ром сло­ге, бук­ву «о» или «а»?

«Отражать» или «атрожать»?

В напи­са­нии это­го сло­ва опи­ра­ем­ся на прин­цип рус­ской орфо­гра­фии, что в без­удар­ном поло­же­нии пишет­ся та же глас­ная бук­ва, что в том же сло­ге одно­ко­рен­но­го сло­ва или в грам­ма­ти­че­ской фор­ме исход­но­го сло­ва под уда­ре­ни­ем. Посмотрим, как про­ве­ря­ют­ся без­удар­ные глас­ные в сле­ду­ю­щих словах:

Чтобы пра­виль­но напи­сать гла­гол «отра­жать» с без­удар­ны­ми глас­ны­ми в корне, поищем про­ве­роч­ное сло­во сре­ди одно­ко­рен­ных лек­сем и их форм с целью, что­бы уда­ре­ние про­яс­ни­ло сомни­тель­ные гласные:

Как видим, уда­ре­ние во всех подо­бран­ных сло­вах пада­ет на глас­ные суффиксов.

Следовательно, о напи­са­нии без­удар­ных глас­ных в корне слов «отра­жать», «отра­зить», «отра­же­ние» и про­из­вод­ных форм гла­го­лов справ­ля­ем­ся в орфо­гра­фи­че­ском словаре.

Чтобы понять, поче­му это сло­во пишет­ся имен­но так, ука­жем, что в мор­фем­ном соста­ве гла­го­ла «отра­жать» от- явля­ет­ся эти­мо­ло­ги­че­ской при­став­кой, кото­рая срос­лась с древним кор­нем -раз-/-раж- (чере­до­ва­ние соглас­ных з//ж). Отметим, что в ука­зан­ном корне сохра­ни­лось ста­ро­сла­вян­ское непол­но­гла­сие -ра-, в кото­ром глас­ный [а], как пра­ви­ло, явля­ет­ся без­удар­ным во мно­гих словах:

Примеры предложений

Только такая про­зрач­ная вода озе­ра мог­ла так чет­ко отража́ть при­бреж­ные дере­вья и кусты.

В древ­но­сти горо­жане постро­и­ли это мощ­ное укреп­ле­ние, что­бы отража́ть набе­ги врагов.

Лучший выход из это­го непри­ят­но­го поло­же­ния — это отража́ть напад­ки остро­та­ми и насмешками.

Источник

Поиск ответа

Почему лисица-словарное слово, если проверочное слово лис?

Ответ справочной службы русского языка

Мы бы не стали включать это слово в список словарных слов.

Здравствуйте! Есть ли проверочное слово у слова «разОбрать»?

Ответ справочной службы русского языка

Последнюю гласную приставки разо— можно проверить словом разо́бранный. Но гласные в приставках обычно не проверяют. Так как приставок немного (по сравнению с корнями, например), то их запоминают и воспроизводят по памяти.

Ответ справочной службы русского языка

Вентиль, вентилировать, вентилятор – родственные слова, они восходят к лат. ventilo «развеиваю, проветриваю», в них выделяется корень вентил(ь)-. Родство слов ощущается носителями русского языка. Это дает орфографистам основание считать слово вентиль проверочным для вентилировать и вентилятор. См. здесь.

Однако найти у слов вентиль, вентилировать, вентилятор общий смысловой компонент, который однозначно бы показывал, что они однокоренные, затруднительно. Вентилятор – устройство для проветривания помещений или охлаждения воздуха, двигателей и т.п.; вентилировать – производить вентиляцию. Вентиль – клапан для регулирования расхода жидкости, пара, газа и т.п.

Поэтому в современном русском языке эти слова все же однокоренными признать нельзя, а значит, и проверять слова вентилировать, вентилятор словом вентиль неправильно. Но опереться на слово вентиль, чтобы запомнить, как пишутся родственные слова вполне можно. Эту проверку условно можно назвать этимологической.

Ответ справочной службы русского языка

Добрый вечер! Проверочное слово к слову мур. вьи?

Ответ справочной службы русского языка

Можно проверить уменьшительно-ласкательным мураш.

Здравствуйте. Как правильно: перескОчил или перескАчил? Знаю, что первый вариант, но почему? Ведь проверочное слово «перескАкивать». Спасибо.

Ответ справочной службы русского языка

Какое проверочное слово у НАЦИОНАЛЬНЫЙ, ЧТОБЫ ПРОВЕРИТЬ БУКВУ И

Ответ справочной службы русского языка

Написание проверяется в словарном порядке.

Школьная программа за 3-й класс. Найдите проверочное слово к «молчать». И правильный ответ вроде как «молча». Вопрос в том, а как быть со словами «умалчивать», «замалчивать» и проч.? Они, насколько я понимаю, тоже однокоренные и если проверять ими, то написать я должен «мАлчать».. Получается, проверить это слово нельзя?

Ответ справочной службы русского языка

В справочниках по русскому языку (в том числе у Д. Э. Розенталя) есть правило, которое дает прямой ответ на Ваш вопрос.

Гласные о — а в неударяемых корнях глаголов совершенного вида нельзя проверять формами несовершенного вида на -ывать (-ивать), например: опоздать (по ́ здний, хотя опа ́ здывать), раскроить (кро ́ йка, хотя раскра ́ ивать).

Таких примеров десятки. К сожалению, в школе об этом правиле часто не говорят, поэтому и возникает недопонимание.

Ответ справочной службы русского языка

проверочное слово к слову праздник

Ответ справочной службы русского языка

Добрый день! Подскажите, пожалуйста, как в слове «одинокий» проверить первую букву «о»? Или это словарное слово и именно эта буква не проверяется? Спасибо большое и извините, если повторюсь с вопросом. По поиску проверяла, ответ не смогла найти. С уважением, Ольга.

Ответ справочной службы русского языка

Подобрать проверочное слово для безударной о в слове одинокий нельзя.

Ответ справочной службы русского языка

Согласно «Морфемно-орфографическому словарю русского языка» А. Н. Тихонова, в слове пропускной про- – приставка. Но безударные гласные можно проверять ударением в любой морфеме, не только в корне. Проверочное слово – пропуск (где та же приставка про- под ударением).

Как правильно писать извазюкаться или извозюкаться (в грязи), и какие проверочные слова? Спасибо

Ответ справочной службы русского языка

Правила правописания согласных говорят, что для проверки «. нужно взять другую форму того же слова или подобрать другое слово того же корня. ».
Возможно ли проверить согласную подобрав однокоренное слово с чередующейся согласной?

Например:
Снег — Снежок
Творог — Творожок

Или проверочное слово обязательно должно использовать ту же букву?

Ответ справочной службы русского языка

Это правило не очень удобно для применения, но в целом оно действует.

есть ли проверочное слово у слова праздник?

Ответ справочной службы русского языка

Проверочное слово подобрать затруднительно. Следует запомнить написание непроизносимой согласной.

Источник

Проверочное слово к слову «отражать»

Написание бук­вы «о» в пер­вом сло­ге и «а» во вто­ром сло­ге сло­ва «отра­жать» и одно­ко­рен­но­го суще­стви­тель­но­го «отра­же­ние» сле­ду­ет запом­нить или про­ве­рять по орфо­гра­фи­че­ско­му словарю.

Поставив уда­ре­ние, убе­дим­ся, что в сло­ве « о тр а жать» удар­ным явля­ет­ся глас­ный звук суффикса:

В без­удар­ной пози­ции ока­за­лись оба глас­ных кор­ня инте­ре­су­ю­ще­го нас сло­ва. Возникает вопрос: что напи­сать в пер­вом и вто­ром сло­ге, бук­ву «о» или «а»?

«Отражать» или «атрожать»?

В напи­са­нии это­го сло­ва опи­ра­ем­ся на прин­цип рус­ской орфо­гра­фии, что в без­удар­ном поло­же­нии пишет­ся та же глас­ная бук­ва, что в том же сло­ге одно­ко­рен­но­го сло­ва или в грам­ма­ти­че­ской фор­ме исход­но­го сло­ва под уда­ре­ни­ем. Посмотрим, как про­ве­ря­ют­ся без­удар­ные глас­ные в сле­ду­ю­щих словах:

Чтобы пра­виль­но напи­сать гла­гол «отра­жать» с без­удар­ны­ми глас­ны­ми в корне, поищем про­ве­роч­ное сло­во сре­ди одно­ко­рен­ных лек­сем и их форм с целью, что­бы уда­ре­ние про­яс­ни­ло сомни­тель­ные гласные:

Как видим, уда­ре­ние во всех подо­бран­ных сло­вах пада­ет на глас­ные суффиксов.

Следовательно, о напи­са­нии без­удар­ных глас­ных в корне слов «отра­жать», «отра­зить», «отра­же­ние» и про­из­вод­ных форм гла­го­лов справ­ля­ем­ся в орфо­гра­фи­че­ском словаре.

Чтобы понять, поче­му это сло­во пишет­ся имен­но так, ука­жем, что в мор­фем­ном соста­ве гла­го­ла «отра­жать» от- явля­ет­ся эти­мо­ло­ги­че­ской при­став­кой, кото­рая срос­лась с древним кор­нем -раз-/-раж- (чере­до­ва­ние соглас­ных з//ж). Отметим, что в ука­зан­ном корне сохра­ни­лось ста­ро­сла­вян­ское непол­но­гла­сие -ра-, в кото­ром глас­ный [а], как пра­ви­ло, явля­ет­ся без­удар­ным во мно­гих словах:

Примеры предложений

Только такая про­зрач­ная вода озе­ра мог­ла так чет­ко отража́ть при­бреж­ные дере­вья и кусты.

В древ­но­сти горо­жане постро­и­ли это мощ­ное укреп­ле­ние, что­бы отража́ть набе­ги врагов.

Лучший выход из это­го непри­ят­но­го поло­же­ния — это отража́ть напад­ки остро­та­ми и насмешками.

Источник

Математика. 2 класс

Конспект урока

Математика, 2 класс. Урок №27

Проверка сложения. Проверка вычитания.

Перечень вопросов, рассматриваемых в теме:

— Что такое обратные математические действия?

— Как проверить сложение?

— Как проверить вычитание?

Сложение – это объединение объектов в одно целое. Результатом сложения чисел является число, называемое суммой чисел (слагаемых).

Вычитание – это такое действие, в котором отнимают меньшее число от большего. Большее число называется уменьшаемым, меньшее – вычитаемым, результат вычитания – разностью.

Обратные действия – действия, приводящие к прежнему, исходному состоянию.

Основная и дополнительная литература по теме урока (точные библиографические данные с указанием страниц):

Теоретический материал для самостоятельного изучения

Используя числа 7, 5, 12 составим все возможные равенства.

Назовём компоненты и результат действия сложения.

Слагаемое + слагаемое = сумма

Назовём компоненты и результат действия вычитания.

Уменьшаемое – вычитаемое = разность

Действия сложение и вычитание связаны друг с другом, являются взаимно обратными действиями.

Как проверить, верно ли выполнено сложение. Воспользуемся знанием того, как связаны слагаемые и сумма. Если из суммы двух слагаемых вычесть одно из них, то получится другое слагаемое. Это позволяет сложение проверить вычитанием.

Например, надо проверить, верно ли вычислили сумму чисел 28 и 5. Для этого из суммы 33 вычтем одно из слагаемых. Например, 5. Должно получиться другое слагаемое. Получилось 28. Значит, сумма чисел 28 и 5 найдена правильно. Можно вычесть из суммы другое слагаемое.

Сумма чисел 36 и 9 найдена неверно, т.к. после вычитания из суммы 47 слагаемого 9, другое слагаемое, 36 не получается.

Вычислим ещё раз сумму чисел 36 и 9 и проверим результат.

36 – первое слагаемое

Сформулируем правило проверки сложения: «Для проверки сложения надо из значения суммы вычесть одно из слагаемых. Если в результате вычитания получается другое слагаемое, значит, сложение выполнено верно».

Как проверить вычитание? Воспользуемся знанием того, как связаны между собой уменьшаемое, вычитаемое, разность. Если к разности прибавить вычитаемое, то получится уменьшаемое. Значит, вычитание можно проверить сложением.

Вычислим разность чисел 48 и 30. Она равна 18. Проверим вычитание сложением. К разности 18 прибавим вычитаемое 30, получим 48. Это уменьшаемое.

Если из уменьшаемого вычесть разность, то получится вычитаемое.

Значит, вычитание можно проверить и вычитанием. Рассмотрим это на примере.

Из уменьшаемого 48 вычтем разность 18, получим 30, т.е. вычитаемое. Значит, разность чисел 48 и 30 вычислена верно.

Сформулируем правила проверки вычитания: «Для проверки вычитания, надо к значению разности прибавить вычитаемое. Если в результате сложения получается уменьшаемое, значит, вычитание выполнено верно», или «Для проверки вычитания, надо из уменьшаемого вычесть разность. Если в результате получается вычитаемое, значит, вычитание выполнено верно».

Вывод: Сложение и вычитание – это обратные действия. Для проверки сложения надо из значения суммы вычесть одно из слагаемых. Если в результате вычитания получается другое слагаемое, значит, сложение выполнено верно. Для того, чтобы выполнить проверку вычитания, надо к значению разности прибавить вычитаемое. Если в результате сложения получается уменьшаемое, значит, вычитание выполнено верно.

1. Найдите значение первого выражения в каждой рамке, а затем выполни проверку полученного результата двумя способами.

Источник

Вычитание чисел

• Уменьшаемое, вычитаемое и разность
• Проверка вычитания

Вычитание чисел — это арифметическое действие, с помощью которого от единиц одного числа отнимают столько единиц, сколько их содержится в другом числе.

Вычесть – значит от одного числа отнять столько единиц, сколько их содержится в другом.

Для записи вычитания используется знак  —  (минус),  который ставится между числами. Например:

9 — 5.

Эта запись означает, что от  9  надо отнять пять. Справа от записи вычитания ставится знак  =  (равно),  после которого записывается полученный результат:

9 — 5 = 4.

Уменьшаемое, вычитаемое и разность

Уменьшаемое — это число, из которого вычитают. Вычитаемое — это число, которое вычитают. Например, в записи:

9 — 4,

9  — это уменьшаемое,  4  — вычитаемое.

Разность (остаток) — это число, которое получается в результате вычитания. Например, в записи:

9 — 4 = 5,

5  — это разность. При этом сама запись  9 — 4  тоже называется разностью.

Эту запись можно прочитать так:  разность девяти и четырёх равна пяти,  девять минус четыре равно пяти  или  из девяти вычесть четыре, получится пять.

Вычитание – это арифметическое действие обратное сложению, с помощью которого по сумме и одному слагаемому находится другое слагаемое.

Проверка вычитания

Рассмотрим выражение

15 — 7 = 8,

где  15  — это уменьшаемое,  7  — это вычитаемое, а  8  — разность. Чтобы узнать правильно ли было выполнено вычитание, можно:

1. Вычитаемое сложить с разностью, если получится уменьшаемое, то вычитание было выполнено верно:

   7 + 8 = 15.

2. От уменьшаемого отнять разность, если получится вычитаемое, то вычитание было выполнено верно:

   15 — 8 = 7.

Проверка арифметических действий

Чтобы убедиться, что какое-нибудь арифметическое действие сделано без ошибки, его проверяют.

Проверкой называют совокупность арифметических приемов с целью убедиться, что данное арифметическое действие исполнено верно. Проверка также состоит из арифметических действий, выполненных в другом порядке.

Самый простой способ убедиться, что действие выполнено верно, состоит, конечно, в том, чтобы повторить его снова. Однако, замечено, что уверенность наша увеличивается, если мы убедимся другим путем в верности какого-нибудь результата, поэтому проверяют арифметические действия иначе.

Проверка основана на главных свойствах самих арифметических действий и на зависимости, существующей между данными и искомыми числами.

Основываясь на главных свойствах самих действий, мы можем каждое действие проверять тем же действием, только выполненным в другом порядке. Таким образом, сложение проверяется сложением, вычитание — вычитанием и т. д.

Проверка арифметических действий теми же действиями

Проверка сложения

Сумма не изменяется от перемены порядка слагаемых, следовательно, чтобы проверить сложение, нужно сложить слагаемые в другом порядке; если получится та же самая сумма, сложение сделано верно.

Сложение:

Проверка сложения:

сложение верно.

Обычно при проверке складываются слагаемые в обратном порядке, то есть снизу вверх.

Проверка вычитания

Вычитаемое равно уменьшаемому без разности, следовательно, чтобы проверить вычитание, нужно из уменьшаемого вычесть разность; если в остатке получится вычитаемое, вычитание сделано верно.

Вычитание:

Проверка вычитания:

Вычитание верно.

Проверка умножения

Произведение не изменяется от перемены порядка множителей, следовательно, чтобы проверить умножение, нужно переменить порядок множителей и снова выполнить умножение; если получим то же произведение, умножение выполнено верно.

Умножение:

Проверка умножения:

Умножение верно.

Проверка деления

При делении нацело делитель равен делимому, разделенному на частное, следовательно, чтобы проверить деление, в случае деления нацело, нужно делимое разделить на частное; если в частном получится делитель, деление сделано верно.

Деление верно.