Как пишется прямоугольный треугольник - Правописание и грамматика

Прямоугольный треугольник

Прямоугольный треугольник – треугольник, в котором один угол прямой (то есть равен 90˚).

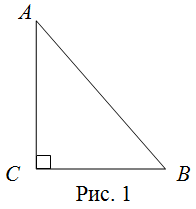
Сторона, противоположная прямому углу, называется гипотенузой прямоугольного треугольника.

Стороны, прилежащие к прямому углу, называются катетами .

Признаки равенства прямоугольных треугольников

Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны ( по двум катетам ).

Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны ( по катету и острому углу ).

Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны ( по гипотенузе и острому углу ).

Если гипотенуза и катет одного прямоугольного треугольника равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны ( по гипотенузе и катету ).

Свойства прямоугольного треугольника

1. Сумма острых углов прямоугольного треугольника равна 90˚.

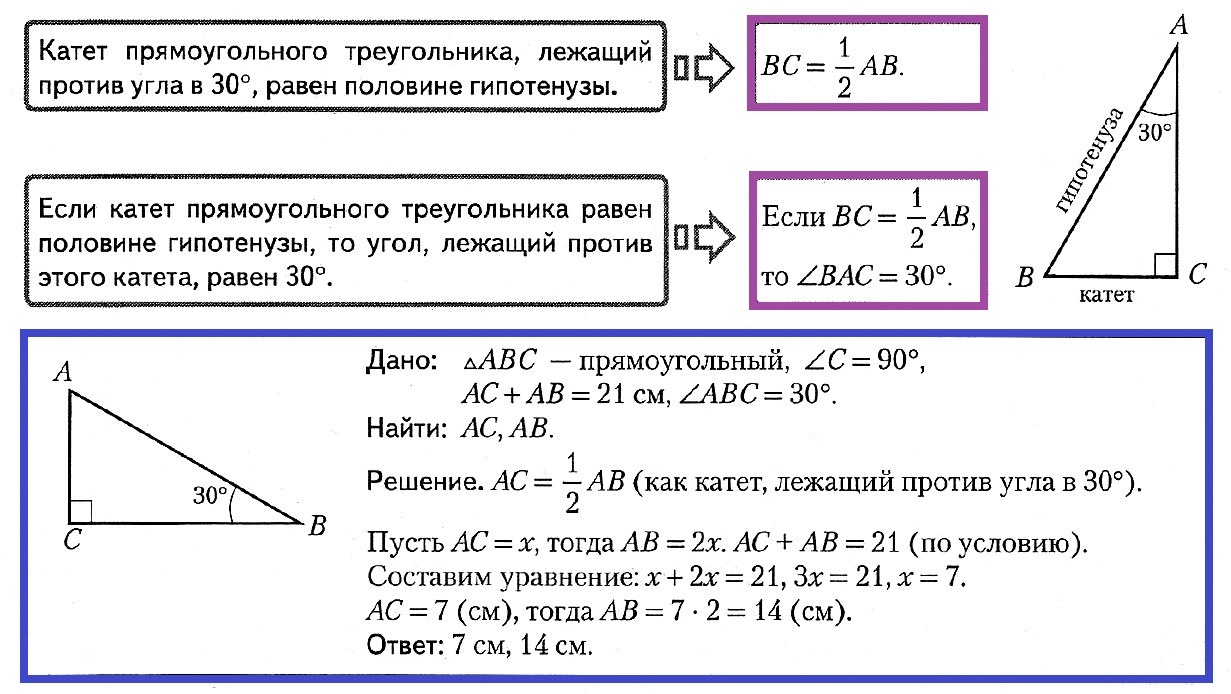
2. Катет, противолежащий углу в 30˚, равен половине гипотенузы.

И обратно, если в треугольнике катет вдвое меньше гипотенузы, то напротив него лежит угол в 30˚.

3. Теорема Пифагора:

, где – катеты, – гипотенуза. Видеодоказательство

4. Площадь прямоугольного треугольника с катетами :

5. Высота прямоугольного треугольника, проведенная к гипотенузе выражается через катеты и гипотенузу следующим образом:

6. Центр описанной окружности – есть середина гипотенузы.

7. Радиус описанной окружности есть половина гипотенузы :

8. Медиана, проведенная к гипотенузе, равна ее половине

9. Радиус вписанной окружности выражается через катеты и гипотенузу следующим образом:

Тригонометрические соотношения в прямоугольном треугольнике смотрите здесь.

Как правильно пишется словосочетание «прямоугольный треугольник»

Делаем Карту слов лучше вместе

Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!

Спасибо! Я стал чуточку лучше понимать мир эмоций.

Вопрос: невестка — это что-то нейтральное, положительное или отрицательное?

Ассоциации к словосочетанию «прямоугольный треугольник&raquo

Синонимы к словосочетанию «прямоугольный треугольник&raquo

Предложения со словосочетанием «прямоугольный треугольник&raquo

Почему стороны прямоугольного треугольника обязаны всегда следовать настолько простому правилу?

Сочетаемость слова «прямоугольный&raquo

Сочетаемость слова «треугольник&raquo

Значение словосочетания «прямоугольный треугольник&raquo

Прямоуго́льный треуго́льник — это треугольник, в котором один угол прямой (то есть 90 градусов). (Википедия)

Отправить комментарий

Дополнительно

Значение словосочетания «прямоугольный треугольник&raquo

Прямоуго́льный треуго́льник — это треугольник, в котором один угол прямой (то есть 90 градусов).

Предложения со словосочетанием «прямоугольный треугольник&raquo

Почему стороны прямоугольного треугольника обязаны всегда следовать настолько простому правилу?

Если рассуждать логически, справедливо было бы прийти к выводу, что в таком мире невозможно построить правильный равнобедренный прямоугольный треугольник.

К примеру, зубья пил по металлу имеют вид прямоугольного треугольника с передней режущей кромкой.

Теорема Пифагора

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Основные понятия

Теорема Пифагора, определение: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

Гипотенуза — сторона, лежащая напротив прямого угла.

Катет — одна из двух сторон, образующих прямой угол.

Формула Теоремы Пифагора выглядит так:

где a, b — катеты, с — гипотенуза.

Из этой формулы можно вывести следующее:

a = √c 2 − b 2
b = √c 2 − a 2
c = √a 2 + b 2

Для треугольника со сторонами a, b и c, где c — большая сторона, действуют следующие правила:

если c 2 2 + b 2 , значит угол, противолежащий стороне c, является острым.
если c 2 = a 2 + b 2 , значит угол, противолежащий стороне c, является прямым.
если c 2 > a 2 +b 2 , значит угол, противолежащий стороне c, является тупым.

Записывайтесь на курсы обучения математике для школьников с 1 по 11 классы!

Теорема Пифагора: доказательство

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Дано: ∆ABC, в котором ∠C = 90º.

Доказать: a 2 + b 2 = c 2 .

Пошаговое доказательство:

Проведём высоту из вершины C на гипотенузу AB, основание обозначим буквой H.
Прямоугольная фигура ∆ACH подобна ∆ABC по двум углам:

Также прямоугольная фигура ∆CBH подобна ∆ABC:

Введем новые обозначения: BC = a, AC = b, AB = c.

Из подобия треугольников получим: a : c = HB : a, b : c = AH : b.

Значит a 2 = c * HB, b 2 = c * AH.
Сложим полученные равенства:

a 2 + b 2 = c * HB + c * AH

a 2 + b 2 = c * (HB + AH)

a 2 + b 2 = c * AB

Обратная теорема Пифагора: доказательство

Если сумма квадратов двух сторон треугольника равна квадрату третьей стороны, то такой треугольник является прямоугольным.

Дано: ∆ABC

Доказать: ∠C = 90º

Пошаговое доказательство:

Построим прямой угол с вершиной в точке C₁.
Отложим на его сторонах отрезки C₁A₁ = CA и C₁B₁ = CB.

Проведём отрезок A₁B₁.
Получилась фигура ∆A₁B₁C₁, в которой ∠C₁=90º.

В этой фигуре ∆A₁B₁C₁ применим теорему Пифагора: A₁B₁ 2 = A₁C₁ 2 + B₁C₁ 2 .
Таким образом получится:

Значит, в фигурах треугольниках ∆ABC и ∆A₁B₁C₁:

C₁A₁ = CA и C₁B₁ = CB по результату построения,
A₁B₁ = AB по доказанному результату.

Поэтому, ∆A₁B₁C₁ = ∆ABC по трем сторонам.
Из равенства фигур следует равенство их углов: ∠C =∠C₁ = 90º.

Обратная теорема доказана.

Решение задач

Задание 1. Дан прямоугольный треугольник ABC. Его катеты равны 6 см и 8 см. Какое значение у гипотенузы?

Как решаем:

Пусть катеты a = 6 и b = 8.

По теореме Пифагора c 2 = a 2 + b 2 .

Подставим значения a и b в формулу:
c 2 = 6 2 + 8 2 = 36 + 64 = 100
c = √100 = 10.

Задание 2. Является ли треугольник со сторонами 8 см, 9 см и 11 см прямоугольным?

Выберем наибольшую сторону и проверим, выполняется ли теорема Пифагора:

Ответ: треугольник не является прямоугольным.

источники:

http://kartaslov.ru/%D0%BA%D0%B0%D0%BA-%D0%BF%D1%80%D0%B0%D0%B2%D0%B8%D0%BB%D1%8C%D0%BD%D0%BE-%D0%BF%D0%B8%D1%88%D0%B5%D1%82%D1%81%D1%8F-%D1%81%D0%BB%D0%BE%D0%B2%D0%BE%D1%81%D0%BE%D1%87%D0%B5%D1%82%D0%B0%D0%BD%D0%B8%D0%B5/%D0%BF%D1%80%D1%8F%D0%BC%D0%BE%D1%83%D0%B3%D0%BE%D0%BB%D1%8C%D0%BD%D1%8B%D0%B9+%D1%82%D1%80%D0%B5%D1%83%D0%B3%D0%BE%D0%BB%D1%8C%D0%BD%D0%B8%D0%BA

http://skysmart.ru/articles/mathematic/teorema-pifagora-formula

Источник

Прямоугольный треугольник

Прямоуго́льный треуго́льник — это треугольник, в котором один угол прямой (то есть составляет 90 градусов).

Соотношения между сторонами и углами прямоугольного треугольника лежат в основе тригонометрии.

Содержание

1 Связанные определения
2 Типы прямоугольных треугольников
3 Свойства
- 3.1 Высота
- 3.2 Характеристики
- 3.3 Тригонометрические соотношения
- 3.4 Специальные прямоугольные треугольники
- 3.5 Теорема Фалеса
- 3.6 Другие свойства
4 Примечания
5 Ссылки

Связанные определения

Сторона, противоположная прямому углу, называется гипотенузой (сторона c на рисунке выше).
Стороны, прилегающие к прямому углу, называются катетами. Сторона a может быть идентифицирована как прилежащая к углу В и противолежащая углу A, а сторона b — как прилежащая к углу A и противолежащая углу В.

Типы прямоугольных треугольников

Если длины всех трёх сторон прямоугольного треугольника являются целыми числами, то треугольник называется пифагоровым треугольником, а длины его сторон образуют так называемую пифагорову тройку.

Свойства

Далее предполагаем, что и длины катетов, а длина гипотенузы

(Теорема Пифагора)

Площадь прямоугольного треугольника равна половине произведения двух его катетов. То есть,

$S=tfrac{1}{2}ab.$

Высота

Высота прямоугольного треугольника.

Если высота проведена из вершины с прямым углом к гипотенузе, то треугольник делится на два меньших треугольника, подобных исходному и подобных друг другу. Из этого следует:

Высота есть среднее геометрическое (среднее пропорциональное) двух сегментов гипотенузы.

Каждый катет треугольника есть среднее пропорциональное гипотенузы и смежных сегментов.

Справедливы соотношения:

(иногда это называют теоремой высоты прямоугольного треугольника)

где a, b, c, d, e, f показаны на диаграмме.^[1] Следовательно:

$f=frac{ab}{c}.$

Высота, опущенная на гипотенузу, связана с катетами прямоугольного треугольника соотношением:^[2]^[3]

$frac{1}{a^2} + frac{1}{b^2} = frac{1}{ f^2}.$

Характеристики

Треугольник ABC со сторонами a, b, c (где c — самая длинная сторона), площади T, с описанной окружностью радиуса R является прямоугольным треугольником тогда и только тогда, когда верно одно из следующих соотношений:^[4]

Тригонометрические соотношения

Тригонометрические функции для острых углов можно определить как отношения сторон прямоугольного треугольника. Для любого данного угла можно построить прямоугольный треугольник, содержащий такой угол, и со сторонами: противолежащим катетом, прилежащим катетом и гипотенузой, связанными с этим углом определёнными выше соотношениями. Эти отношения сторон не зависят от конкретного выбранного прямоугольного треугольника, а зависят только от заданного угла, так как все треугольники, построенные таким образом, являются подобными. Если для заданного угла α, противолежащий катет, прилежащий катет и гипотенузу обозначить a, b и c соответственно, то тригонометрические функции имеют вид:

$sinalpha =frac {a}{c},,cosalpha =frac {b}{c},,operatorname{tg}alpha =frac {a}{b},,operatorname{ctg}alpha =frac {b}{a},secalpha =frac {c}{b},,,cscalpha =frac {c}{a}.$

Специальные прямоугольные треугольники

Значения тригонометрических функций можно точно оценить для определённых углов, используя прямоугольные треугольники с особыми значениями углов. К таким треугольникам относятся треугольник 30-60-90, который можно использовать для оценки тригонометрических функций для любых значений, кратных π/6, и »треугольник 45-45-90, который можно использовать для оценки тригонометрических функций для значений, кратных π/4.

Теорема Фалеса

Медиана прямого угла треугольника

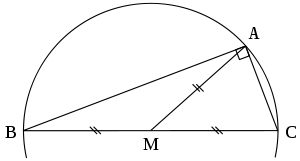
Теорема Фалеса утверждает, что если какая-нибудь точка A лежит на окружности диаметра BC (за исключением самих точек B и C), то △ABC представляет собой прямоугольный треугольник с прямым углом A. Обратное утверждение таково: если прямоугольный треугольник вписан в окружность, то гипотенуза будет её диаметром. Следствием является то, что длина гипотенузы равна удвоенному расстоянию от вершины прямого угла до середины гипотенузы. Верно также, что центр окружности, описывающей прямоугольный треугольник, является серединой гипотенузы, а её радиус равен половине длины гипотенузы.

Другие свойства

Радиус вписанной окружности в прямоугольный треугольник с катетами a и b и гипотенузой c равен:

$r = frac{a+b-c}{2} = frac{ab}{a+b+c}.$

Если отрезки длиной p и q, исходящие из вершины C, делят гипотенузу на три равных отрезка длины c/3, то:^[5]^{:pp. 216-217}

$p^2 + q^2 = 5left(frac{c}{3}right)^2.$

Прямоугольный треугольник является единственным треугольник с двумя, а не тремя, отличными друг от друга вписанными квадратами.^[6]

Пусть h и s (h>s) сторонами двух квадратов, вписанных в прямоугольный треугольник с гипотенузой c. Тогда:

$frac{1}{c^2} + frac{1}{h^2} = frac{1}{s^2}.$

Периметр прямоугольного треугольника равен сумме радиусов вписанной и трёх описанных окружностей.

Примечания

↑ Wentworth p. 156
↑ Voles, Roger, «Integer solutions of $a^{-2}+b^{-2}=d^{-2}$ ,» Mathematical Gazette 83, July 1999, 269—271.
↑ Richinick, Jennifer, «The upside-down Pythagorean Theorem, » Mathematical Gazette 92, July 2008, 313—317.
↑ Andreescu, Titu and Andrica, Dorian, «Complex Numbers from A to…Z», Birkhäuser, 2006, pp. 109—110.
↑ Posamentier, Alfred S., and Salkind, Charles T. Challenging Problems in Geometry, Dover, 1996.
↑ Bailey, Herbert, and DeTemple, Duane, «Squares inscribed in angles and triangles», Mathematics Magazine 71(4), 1998, 278—284.

Ссылки

	Прямоугольный треугольник на Викискладе^?

Calculator for right triangles
Weisstein, Eric W. Right Triangle (англ.) на сайте Wolfram MathWorld.
Wentworth G.A. A Text-Book of Geometry. — Ginn & Co., 1895.

Источник

31
Июл 2013

Категория: Справочные материалы

Прямоугольный треугольник

2013-07-31
2019-09-30

Прямоугольный треугольник – треугольник, в котором один угол прямой (то есть равен 90˚).

Сторона, противоположная прямому углу, называется гипотенузой прямоугольного треугольника.

Стороны, прилежащие к прямому углу, называются катетами.

Признаки равенства прямоугольных треугольников

Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны (по гипотенузе и острому углу).

Свойства прямоугольного треугольника

1. Сумма острых углов прямоугольного треугольника равна 90˚.

2. Катет, противолежащий углу в 30˚, равен половине гипотенузы.

И обратно, если в треугольнике катет вдвое меньше гипотенузы, то напротив него лежит угол в 30˚.

3. Теорема Пифагора:

, где – катеты, – гипотенуза. Видеодоказательство

4. Площадь прямоугольного треугольника с катетами :

$S=frac{1}{2}ab$

$h=frac{ab}{c}$

6. Центр описанной окружности – есть середина гипотенузы.

7. Радиус описанной окружности есть половина гипотенузы :

$R=frac{c}{2}$

8. Медиана, проведенная к гипотенузе, равна ее половине

9. Радиус вписанной окружности выражается через катеты и гипотенузу следующим образом:

$r=frac{a+b-c}{2}$

cvb

Тригонометрические соотношения в прямоугольном треугольнике смотрите здесь.

И, думаю, будет полезна таблица формул для треугольника

Автор: egeMax |

комментария 3

Печать страницы

Источник

Прямоугольный треугольник

Определение и формулы прямоугольного треугольника

ОПРЕДЕЛЕНИЕ

Треугольник называется прямоугольным, если один из его углов прямой.

Стороны, прилежащие к прямому углу называются катетами, а сторона, лежащая против прямого угла, – гипотенузой.

Для прямоугольного треугольника справедливы следующие утверждения:

Прямоугольный треугольник

Теорема Пифагора. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов:

(
A C^{2}+A B^{2}=B C^{2}
)

Сумма острых углов прямоугольного треугольника равна (
90^{circ}
) :

(
angle B+angle C=90^{circ}
)

Гипотенуза прямоугольного треугольника больше каждого их катетов:

(
A C>B C, A B>B C
)

Катет, лежащий против угла (
30^{circ}
) , равен половине гипотенузы.

Две высоты прямоугольного треугольника совпадают с его катетами.

Центр описанной окружности прямоугольного треугольника лежит на середине гипотенузы.

Медиана прямоугольного треугольника, проведенная из вершины прямого угла на гипотенузу, является радиусом описанной около этого треугольника окружности:

(
mathrm{AM}=mathrm{R}
)

Признаки равенства прямоугольных треугольников

По двум катетам: если два катета одного прямоугольного треугольника равны катетам другого прямоугольного треугольника, то такие треугольники равны.

По гипотенузе и катету: если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны.

По стороне и острому углу: Если сторона и прилежащий к ней острый угол одного прямоугольного треугольника соответственно равны стороне и прилежащему к ней острому углу другого прямоугольного треугольника, то такие треугольники равны

Подробнее про признаки равенства треугольников читайте по ссылке.

Тригонометрические соотношения в прямоугольном треугольнике

Площадь прямоугольного треугольника равна половине произведения катетов и вычисляется по формуле

(
S=frac{1}{2} a b
)

Примеры решения задач

ПРИМЕР 1

Задание ]В прямоугольном треугольнике (
mathrm{ABC}
) катет (
mathrm{AC}
) равен 5 см, а (
angle C=60^{circ}
) . Найти гипотенузу (
mathrm{BC}
).

Решение

В прямоугольном треугольнике сумма острых углов равна (
90^{circ}
) значит

(
angle B=90^{circ}-angle C=30^{circ}
)

Также известно, что катет (
mathrm{AC}
) (рис. 1), лежащий против угла (
angle B=30^{circ}
) равен половине гипотенузы, т.е.

(
B C=2 A C=2 cdot 5=10
)

Ответ

(
mathrm{BC}=10 mathrm{см.}
)

ПРИМЕР 2

Задание

В равнобедренном треугольнике (
mathrm{ABC}
) угол (
mathrm{A}
) – прямой, (
mathrm{BC=4 см}
). Найти площадь (
Delta A B C
)

Решение

Запишем для прямоугольного треугольника (
mathrm{ABC}
) теорему Пифагора:

(
B C^{2}=A C^{2}+A B^{2}
)

Так как этот треугольник равнобедренный, то (
A B=A C
). Тогда

(
B C^{2}=4^{2}=2 A C^{2} Rightarrow 2 A C^{2}=16
)

откуда (
A C=sqrt{8}
)

Площадь прямоугольного треугольника равна половине произведения катетов, т.е.

(
S=frac{1}{2} A B cdot A C=frac{1}{2} A C^{2}=4 mathrm{см}^{2}
)

Ответ

(
mathrm{S}=4 mathrm{см} 2
)

Источник

Прямоугольный треугольник

Прямоуго́льный треуго́льник — это треугольник, в котором один угол прямой (то есть 90 градусов).

Соотношения между сторонами и углами прямоугольного треугольника лежат в основе тригонометрии.

Связанные определения

Сторона, противоположная прямому углу, называется гипотенузой (сторона c на рисунке выше).
Стороны, прилегающие к прямому углу, называются катетами. Сторона a может быть идентифицирована как прилежащая к углу В и противолежащая углу A, а сторона b — как прилежащая к углу A и противолежащая углу В.

Типы прямоугольных треугольников

Если катеты равны, то треугольник называется равнобедренным прямоугольным треугольником.
Если длины всех трёх сторон прямоугольного треугольника являются натуральными числами, то треугольник называется пифагоровым треугольником, а длины его сторон образуют так называемую пифагорову тройку.

Признаки равенства прямоугольных треугольников

По двум катетам: если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны.

Этот признак немедленно следует из первого признака равенства треугольников, так как у двух треугольников будут равны по два катета и прямой угол.

По катету и прилежащему острому углу: если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны

Этот признак немедленно следует из второго признака равенства треугольников, так как у двух треугольников будут равен один катет, прилежащий к нему угол и прямой угол.

По гипотенузе и острому углу: если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.

Этот признак следует из второго признака равенства треугольников, так как вторые острые углы будут равны по теореме о сумме углов треугольника и у треугольников будут равны гипотенузы и два прилежащих к ней угла.

По гипотенузе и катету: если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны.

Этот признак докажем так. Наложим два треугольника друг на друга так, чтобы получить равнобедренный треугольник, то есть совместим их равными катетами так, чтобы углы, лежащие при этих катетах, лежали в разных плоскостях. Так как гипотенузы равны, получившийся треугольник — равнобедренный, тогда углы при основании равны. Тогда два прямоугольных треугольника будут равны по гипотенузе и острому углу.

По катету и противолежащему острому углу: если катет и противолежащий острый угол одного прямоугольного треугольника соответственно равны катету и острому углу другого прямоугольного треугольника, то такие треугольники равны.

Этот признак доказывается так: если один из острых углов первого треугольника равен острому углу второго треугольника, то второй острый угол будет известен по теореме о сумме углов треугольника. Так как второй острый угол прилегает к катету, то далее равенство треугольников будет доказываться по предыдущей теореме.

Свойства

Далее предполагаем, что и длины катетов, а длина гипотенузы

(Теорема Пифагора)

$c^{2}=a^{2}+b^{2}$

Площадь прямоугольного треугольника равна половине произведения двух его катетов. То есть,

$S={tfrac {1}{2}}ab.$

Высота

Высота прямоугольного треугольника.

Если высота проведена к гипотенузе, то треугольник делится на два меньших треугольника, подобных исходному и подобных друг другу. Из этого следует, что в обозначениях, показанных на диаграмме:^[1]

Высота есть среднее геометрическое (среднее пропорциональное) двух образованных ею сегментов гипотенузы, то есть

$displaystyle f^{2}=de,$

(иногда это называют теоремой высоты прямоугольного треугольника)

Каждый катет треугольника есть среднее геометрическое гипотенузы и проекции катета на гипотенузу, то есть

$displaystyle b^{2}=ce,$

$displaystyle a^{2}=cd$

В прямоугольном треугольнике высота, опущенная из вершины прямого угла на гипотенузу, делит гипотенузу в таком отношении, в каком находятся квадраты прилежащих катетов, то есть

$displaystyle d:e=a^{2}:b^{2},$

Кроме того высота, опущенная на гипотенузу, связана с катетами прямоугольного треугольника соотношением:^[2]^[3]

${frac {1}{a^{2}}}+{frac {1}{b^{2}}}={frac {1}{f^{2}}}.$

$f={frac {ab}{c}}.$

Также если прямоугольный треугольник является равнобедренным, то высота, опущенная на гипотенузу будет равна:

$f=rdelta _{S} =r(1+{sqrt {2}})$

, где

— это радиус вписанной окружности, а $delta _{S}$

— серебряное сечение.

Характеристики

Треугольник ABC со сторонами a, b, c (где c — самая длинная сторона), с описанной окружностью радиуса R является прямоугольным треугольником тогда и только тогда, когда верно любое из следующих соотношений:^[4]

Тригонометрические соотношения

$sin alpha ={frac {a}{c}},,cos alpha ={frac {b}{c}},,operatorname {tg} alpha ={frac {a}{b}},,operatorname {ctg} alpha ={frac {b}{a}},sec alpha ={frac {c}{b}},,,csc alpha ={frac {c}{a}}.$

И таким образом:

Катет, противолежащий углу, равен произведению гипотенузы на синус этого угла

Катет, прилежащий углу, равен произведению гипотенузы на косинус этого угла

Катет, противолежащий углу, равен произведению второго катета на тангенс угла

a=bcdot operatorname {tg} alpha ,,b=acdot operatorname {tg} beta .

Катет, прилежащий углу, равен произведению второго катета на котангенс угла

a=bcdot operatorname {ctg} beta ,,b=acdot operatorname {ctg} alpha .

Гипотенуза равна отношению катета к синусу противолежащего угла, и/или частному отношению катета и косинуса прилежащего угла (угла между ними)

$c={frac {a}{sin alpha }}={frac {b}{sin beta }}={frac {a}{cos beta }}={frac {b}{cos alpha }}.$

Специальные прямоугольные треугольники

Значения тригонометрических функций можно точно оценить для определённых углов, используя прямоугольные треугольники с особыми значениями углов. К таким треугольникам относятся треугольник 30-60-90, который можно использовать для оценки тригонометрических функций для любых значений, кратных π/6, и треугольник 45-45-90 (равнобедренный прямоугольный), который можно использовать для оценки тригонометрических функций для значений, кратных π/4.
В частности,

Катет, лежащий против острого угла в 30° (и соответственно, прилежащий к углу в 60°), равен половине гипотенузы.

Теорема Фалеса

Медиана прямого угла треугольника

Другие свойства

Радиус вписанной окружности в прямоугольный треугольник с катетами a и b и гипотенузой c равен:

$r={frac {a+b-c}{2}}={frac {ab}{a+b+c}}.$

Если отрезки длиной p и q, исходящие из вершины C, делят гипотенузу на три равных отрезка длины c/3, то:^[5]^{:pp. 216-217}

$p^{2}+q^{2}=5left({frac {c}{3}}right)^{2}.$

Прямоугольный треугольник является единственным треугольником с двумя, а не тремя, отличными друг от друга вписанными квадратами.^[6]

Пусть h и s (h>s) являются сторонами двух квадратов, вписанных в прямоугольный треугольник с гипотенузой c. Тогда:

${frac {1}{c^{2}}}+{frac {1}{h^{2}}}={frac {1}{s^{2}}}.$

Периметр прямоугольного треугольника равен сумме двух радиусов вписанной и четырёх описанных окружностей:

Если заданы S и r, то стороны треугольника находятся по формулам:

${displaystyle a={frac {1}{2}}left(r+{frac {S}{r}}-{sqrt {r^{2}-6S+{frac {S^{2}}{r^{2}}}}}right)}$

${displaystyle b={frac {1}{2}}left(r+{frac {S}{r}}+{sqrt {r^{2}-6S+{frac {S^{2}}{r^{2}}}}}right)}$

${displaystyle c={frac {S}{r}}-r}$

Еще важное соотношение:

${displaystyle a={frac {l_{b}}{4c}},left({l_{b}+{sqrt {8,c^{2}+l_{b}^{2}}}}right),,,}$

, где ${displaystyle l_{b},}$

— длина биссектрисы, исходящей из острого угла B, с — гипотенуза.

Во всех прямоугольных треугольниках медиана, опущенная на гипотенузу, равна половине гипотенузы.

Окружность девяти точек касается описанной окружности того же треугольника в единственном случае, если треугольник прямоугольный. При этом касание двух окружностей идёт в вершине прямого угла треугольника.

Вариации и обобщение

Четырёхугольники с перпендикулярными парами элементов: с 2 перпендикулярными сторонами и с 2 перпендикулярными диагоналями,- вырождаются в прямоугольный треугольник, если длина одной нужной стороны (из их 4 сторон), лежащей вблизи прямого угла или же опирающейся концами на этот угол, стремится к нулю.

Если в прямоугольном треугольнике провести отрезок, параллельный его гипотенузе, то он разрежет этот треугольник на подобный ему же прямоугольный треугольник и трапецию. При этом сумма углов при одном из оснований трапеции будет равна 90°, а продолжения боковых сторон трапеции пересекутся под прямым углом. Тогда отрезок, соединяющий середины оснований указанной трапеции, равен полуразности оснований. Данное утверждение обобщает свойство: медиана прямоугольного треугольника, опущенная из вершины прямого угла на гипотенузу, равна половине длины гипотенузы.

Примечания

↑ Wentworth p. 156
↑ Voles, Roger, «Integer solutions of $a^{{-2}}+b^{{-2}}=d^{{-2}}$ ,» Mathematical Gazette 83, July 1999, 269—271.
↑ Richinick, Jennifer, «The upside-down Pythagorean Theorem, » Mathematical Gazette 92, July 2008, 313—317.
↑ Andreescu, Titu and Andrica, Dorian, «Complex Numbers from A to…Z», Birkhäuser, 2006, pp. 109—110.
↑ Posamentier, Alfred S., and Salkind, Charles T. Challenging Problems in Geometry, Dover, 1996.
↑ Bailey, Herbert, and DeTemple, Duane, «Squares inscribed in angles and triangles», Mathematics Magazine 71(4), 1998, 278—284.

Ссылки

Calculator for right triangles
Weisstein, Eric W. Right Triangle (англ.) на сайте Wolfram MathWorld.
Wentworth, G.A. A Text-Book of Geometry (неопр.). — Ginn & Co., 1895.

Эта страница в последний раз была отредактирована 21 мая 2022 в 14:24.

Как только страница обновилась в Википедии она обновляется в Вики 2.
Обычно почти сразу, изредка в течении часа.

Источник

«Прямоугольный треугольник»

Прямоугольный треугольник — треугольник, имеющий прямой угол. Стороны, образующие прямой угол, называют катетами, а сторону, противолежащую к прямому углу, называют гипотенузой.

Свойства прямоугольного треугольника:
1. Катет меньше гипотенузы.
2. Квадрат гипотенузы равен сумме квадратов катетов (теорема Пифагора): с² = а² + b².
3. Сумма острых углов прямоугольного треугольника равна 90°.
4. Медиана,проведенная к гипотенузе,равна половине гипотенузы (радиусу окружности, описанной около треугольника).
5. Радиус окружности, вписанной в прямоугольный треугольник ,можно вычислить по формуле: r = (a + b — c)/2.
6. Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы.
7. Если катет прямоугольного треугольника равен 1/2 гипотенузы, то угол, лежащий против этого катета, равен 30°.

Признаки равенства прямоугольных треугольников

Два прямоугольных треугольника равны если:
• два катета одного треугольника равны двум катетам другого;
• катет и острый угол одного треугольника равны катету и острому углу другого треугольника;
• гипотенуза и острый угол одного треугольника равны гипотенузе и острому углу другого треугольника;
• гипотенуза и катет одного треугольника равны гипотенузе и катету другого треугольника.

Это конспект по теме «Прямоугольные треугольники». Выберите дальнейшие действия:

Перейти к следующему конспекту: ЗАДАЧИ по теме Прямоугольные треугольники
Вернуться к Списку конспектов по геометрии

Источник

Содержание:

Определение прямоугольного треугольника
Свойство прямоугольного треугольника
Примеры решения задач

Определение прямоугольного треугольника

Определение

Прямоугольным называется треугольник, у которого один из углов прямой (на рисунке это $angle C$ ).

Стороны, которые образуют прямой угол ( $A C$ и $B C$ ), называются катетами, а сторона,
лежащая против прямого угла — гипотенузой ( $A B$ ).

Свойство прямоугольного треугольника

В прямоугольном треугольнике, катет, лежащий против угла в $30^{circ}$, равен половине гипотенузы.

Примеры решения задач

Пример

Задание. В треугольниках $A B C$, $K L M$ и $D E F$, заданны по два угла:

1) $angle A=50^{circ}, angle B=40^{circ}$

2) $angle L=37^{circ}, angle M=53^{circ}$

3) $angle D=23^{circ}, angle E=78^{circ}$

Определить есть ли среди них прямоугольный треугольник.

Решение. Найдем для каждого треугольника, чему равен третий угол, используя свойство, что в
треугольнике сумма всех углов
равна $180^{circ}$:

1) $angle C=180^{circ}-angle A-angle B Rightarrow angle C=180^{circ}-50^{circ}-40^{circ}=90^{circ}$

2) $angle K=180^{circ}-angle L-angle M Rightarrow angle K=180^{circ}-37^{circ}-53^{circ}=90^{circ}$

3) $angle F=180^{circ}-angle D-angle E Rightarrow angle F=180^{circ}-23^{circ}-78^{circ}=79^{circ}$

Так как у треугольников $A B C$ и
$K L M$ третий угол прямой ( $angle C=90^{circ}$ и $angle K=90^{circ}$ ), то эти треугольники прямоугольные.

Ответ. $Delta A B C$ и $Delta K I M$ — прямоугольные треугольники.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Дан прямоугольный треугольник
$A B C$, $angle C=90^{circ}, angle B=60^{circ}, A B=6$ см. Найти сторону $B C$.

Решение. В заданном прямоугольном треугольнике сторона
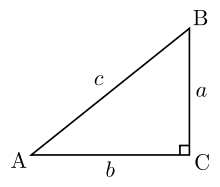
$A B$ лежит против прямого угла $C$, то есть является гипотенузой (рис. 1). Стороны $B C$ и $A C$ — катеты. Найдем, чему равен
$angle A$. Так сумма всех углов треугольника равна $180^{circ}$, то

$$angle A=180^{circ}-angle C-angle B Rightarrow angle A=180^{circ}-90^{circ}-60^{circ}=30^{circ}$$

Искомая сторона $B C$ является катетом,
который лежит против угла $angle A=30^{circ}$, поэтому равна половине гипотенузы:

$B C=frac{1}{2} A B Rightarrow B C=frac{6}{2} Rightarrow B C=3$ (см)

Ответ. $B C=3$ см

Читать дальше: что такое равносторонний треугольник.

Источник