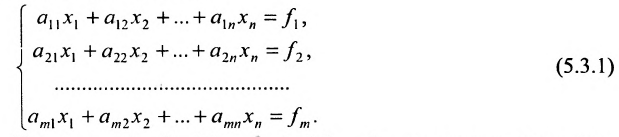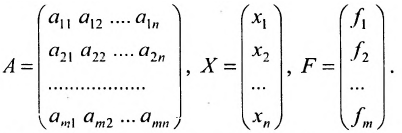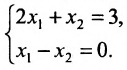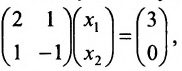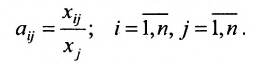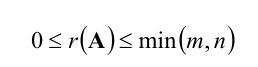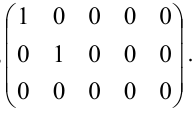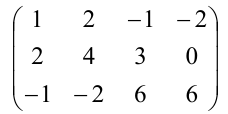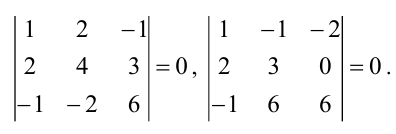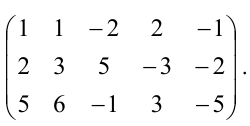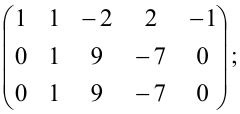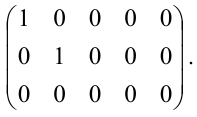В данной статье пойдет речь о таком понятии, как ранг матрицы и необходимых дополнительных понятиях. Мы приведем примеры и доказательства нахождения ранга матрицы, а также расскажем, что такое минор матрицы, и почему он так важен.
Минор матрицы
Чтобы понять, что такое ранг матрицы, необходимо разобраться с таким понятием, как минор матрицы.
Минор k-ого порядка матрицы — определитель квадратной матрицы порядка k×k, которая составлена из элементов матрицы А, находящихся в заранее выбранных k-строках и k-столбцах, при этом сохраняется положение элементов матрицы А.
Проще говоря, если в матрице А вычеркнуть (p-k) строк и (n-k) столбцов, а из тех элементов, которые остались, составить матрицу, сохраняя расположение элементов матрицы А, то определитель полученной матрицы и есть минор порядка k матрицы А.
Из примера следует, что миноры первого порядка матрицы А и есть сами элементы матрицы.
Можно привести несколько примеров миноров 2-ого порядка. Выберем две строки и два столбца. Например, 1-ая и 2 –ая строка, 3-ий и 4-ый столбец.
При таком выборе элементов минором второго порядка будет -1302=(-1)×2-3×0=-2
Другим минором 2-го порядка матрицы А является 0011=0
Предоставим иллюстрации построения миноров второго порядка матрицы А:
Минор 3-го порядка получается, если вычеркнуть третий столбец матрицы А:
003112-1-40=0×1×0+0×2×(-1)+3×1×(-4)-3×1×(-1)-0×1×0-0×2×(-4)=-9
Иллюстрация, как получается минор 3-го порядка матрицы А:
Для данной матрицы миноров выше 3-го порядка не существует, потому что
k≤min(p, n)=min (3, 4)=3
Сколько существует миноров k-ого порядка для матрицы А порядка p×n?
Число миноров вычисляют по следующей формуле:
Cpk×Cnk, где Сpk=p!k!(p-k)! и Cnk=n!k!(n-k)! — число сочетаний из p по k, из n по k соответственно.
После того, как мы определились, что такое миноры матрицы А, можно переходить к определению ранга матрицы А.
Ранг матрицы: методы нахождения
Ранг матрицы — наивысший порядок матрицы, отличный от нуля.
Rank (A), Rg (A), Rang (A).
Из определения ранга матрицы и минора матрицы становиться понятно, что ранг нулевой матрицы равен нулю, а ранг ненулевой матрицы отличен от нуля.
Нахождение ранга матрицы по определению
Метод перебора миноров — метод, основанный на определении ранга матрицы.
Алгоритм действий способом перебора миноров:
Необходимо найти ранг матрицы А порядка p×n. При наличии хотя бы одного элемента, отличного от нуля, то ранг матрицы как минимум равен единице (т.к. есть минор 1-го порядка, который не равен нулю).
Далее следует перебор миноров 2-го порядка. Если все миноры 2-го порядка равны нулю, то ранг равен единице. При существовании хотя бы одного не равного нулю минора 2-го порядка, необходимо перейти к перебору миноров 3-го порядка, а ранг матрицы, в таком случае, будет равен минимум двум.
Аналогичным образом поступим с рангом 3-го порядка: если все миноры матрицы равняются нулю, то ранг будет равен двум. При наличии хотя бы одного ненулевого минора 3-го порядка, то ранг матрицы равен минимум трем. И так далее, по аналогии.
Найти ранг матрицы:
А=-11-1-202260-443111-7
Поскольку матрица ненулевая, то ее ранг минимум равен единице.
Минор 2-го порядка -1122=(-1)×2-1×2=4 отличен от нуля. Отсюда следует, что ранг матрицы А не меньше двух.
Перебираем миноры 3-го порядка: С33×С53=15!3!(5-3)!= 10 штук.
-11-12264311=(-1)×2×11+1×6×4+(-1)×2×3-(-1)×2×4-1×2×11-(-1)×6×3=0
-11-2220431=(-1)×2×1+1×0×4+(-2)×2×3-(-2)×2×4-1×2×1-(-1)×0×3=0
-1-1-22604111=(-1)×6×1+(-1)×0×4+(-2)×2×11-(-2)×6×4-(-1)×2×1-(-1)×0×11=0
-11-2220431=(-1)×2×1+1×0×4+(-2)×2×3-(-2)×2×4-1×2×1-(-1)×0×3=0
-1-1026-4411-7=(-1)×6×(-7)+(-1)×(-4)×4+0×2×11-0×6×4-(-1)×2×(-7)-(-1)×(-4)×11=0
1-1026-4311-7=1×6×(-7)+(-1)×(-4)×3+0×2×11-0×6×3-(-1)×2×(-7)-1×(-4)×11=0
1-2020-431-7=1×0×(-7)+(-2)×(-4)×3+0×2×1-0×0×3-(-2)×2×(-7)-1×(-4)×1=0
-1-2060-4111-7=(-1)×0×(-7)+(-2)×(-4)×11+0×6×1-0×0×11-(-2)×6×(-7)-(-1)×(-4)×1=0
Миноры 3-го порядка равны нулю, поэтому ранг матрицы равен двум.
Ответ: Rank (A) = 2.
Нахождение ранга матрицы методом окаймляющих миноров
Метод окаймляющих миноров — метод, который позволяет получить результат при меньшей вычислительной работе.
Окаймляющий минор — минор Mok(k+1) -го порядка матрицы А, который окаймляет минор M порядка k матрицы А, если матрица, которая соответствует минору Mok , «содержит» матрицу, которая соответствует минору М.
Проще говоря, матрица, которая соответствует окаймляемому минору М, получается из матрицы, соответствующей окаймляющему минору Mok , вычеркиванием элементов одной строки и одного столбца.
Найти ранг матрицы:
А=120-13-2037134-21100365
Для нахождения ранга берем минор 2-го порядка М=2-141
Записываем все окаймляющие миноры:
12-1-207341,20-10374-21,2-13071411,12-1341006,20-14-21036,2-13411065.
Чтобы обосновать метод окаймляющих миноров, приведем теорему, формулировка которой не требует доказательной базы.
Если все миноры, окаймляющие минор k-ого порядка матрицы А порядка p на n, равны нулю, то все миноры порядка (k+1) матрицы А равна нулю.
Алгоритм действий:
Чтобы найти ранг матрицы, необязательно перебирать все миноры, достаточно посмотреть на окаймляющие.
Если окаймляющие миноры равняются нулю, то ранг матрицы нулевой. Если существует хотя бы один минор, который не равен нулю, то рассматриваем окаймляющие миноры.
Если все они равны нулю, то Rank(A) равняется двум. При наличии хотя бы одного ненулевого окаймляющего минора, то приступаем к рассматриванию его окаймляющих миноров. И так далее, аналогичным образом.
Найти ранг матрицы методом окаймляющих миноров
А=210-134210-12111-40024-14
Как решить?
Поскольку элемент а11 матрицы А не равен нулю, то возьмем минор 1-го порядка. Начнем искать окаймляющий минор, отличный от нуля:
2142=2×2-1×4=02041=2×1-0×4=2
Мы нашли окаймляющий минор 2-го порядка не равный нулю 2041.
Осуществим перебор окаймляющих миноров — (их(4-2)×(5-2)=6 штук).
210421211=0; 20-1410211=0; 20341-121-4=0;210421002=0; 20-1410024=0; 20341-102-14=0
Ответ: Rank(A) = 2.
Нахождение ранга матрицы методом Гаусса (с помощью элементарных преобразований)
Вспомним, что представляют собой элементарные преобразования.
Элементарные преобразования:
- путем перестановки строк (столбцов) матрицы;
- путем умножение всех элементов любой строки (столбца) матрицы на произвольное ненулевое число k;
путем прибавления к элементам какой-либо строки (столбца) элементов, которые соответствуют другой стоки (столбца) матрицы, которые умножены на произвольное число k.
Нахождение ранга матрицы методом Гаусса — метод, который основывается на теории эквивалентности матриц: если матрица В получена из матрицы А при помощи конечного числа элементарных преобразований, то Rank(A) = Rank(B).
Справедливость данного утверждения следует из определения матрицы:
- в случае перестановки строк или столбцов матрицы ее определитель меняет знак. Если он равен нулю, то и при перестановке строк или столбцов остается равным нулю;
- в случае умножения всех элементов какой-либо строки (столбца) матрицы на произвольное число k, которое не равняется нулю, определитель полученной матрицы равен определителю исходной матрицы, которая умножена на k;
в случае прибавления к элементам некоторой строки или столбца матрицы соответствующих элементов другой строки или столбца, которые умножены на число k, не изменяет ее определителя.
Суть метода элементарных преобразований: привести матрицу ,чей ранг необходимо найти, к трапециевидной при помощи элементарных преобразований.
Для чего?
Ранг матриц такого вида достаточно просто найти. Он равен количеству строк, в которых есть хотя бы один ненулевой элемент. А поскольку ранг при проведении элементарных преобразований не изменяется, то это и будет ранг матрицы.
Проиллюстрируем этот процесс:
- для прямоугольных матриц А порядка p на n, число строк которых больше числа столбцов:
А~1b12b13⋯b1n-1b1n01b23⋯b2n-2b2n⋮⋮⋮⋮⋮⋮000⋯1bn-1n000⋯01000⋯00⋮⋮⋮⋮⋮⋮000⋯00, Rank(A)=n
или
А~1b12b13⋯b1kb1k+1⋯b1n01b23⋯b2kb2k+1⋯b2n⋮⋮⋮⋮⋮⋮⋮⋮000⋯1bkk+1⋯bkn000⋯00⋯0⋮⋮⋮⋮⋮⋮⋮⋮000⋯00⋯0, Rank(A)=k
- для прямоугольных матриц А порядка p на n, число строк которых меньше числа столбцов:
А~1b12b13⋯b1pb1p+1⋯b1n01b23⋯b2pb2p+1⋯b2n⋮⋮⋮⋮⋮⋮⋮⋮000⋯1bpp+1⋯bpn, Rank(A)=p
или
А~1b12b13⋯b1kb1k+1⋯b1n01b23⋯b2kb2k+1⋯b2n⋮⋮⋮⋮⋮⋮⋮⋮000⋯1bkk+1⋯bkn000⋯00⋯0⋮⋮⋮⋮⋮⋮⋮⋮000⋯00⋯0
- для квадратных матриц А порядка n на n:
А~1b12b13⋯b1n-1b1n01b23⋯b2n-1b2n⋮⋮⋮⋮⋮⋮000⋯1bn-1n000⋯01, Rank(A)=n
или
A~1b12b13⋯b1kb1k+1⋯b1n01b23⋯b2kb2k+1⋯b2n⋮⋮⋮⋮⋮⋮⋮⋮000⋯1bkk+1⋯bkn000⋯00⋯0⋮⋮⋮⋮⋮⋮⋮⋮000⋯00⋯0, Rank(A)=k, k<n
Найти ранг матрицы А при помощи элементарных преобразований:
А=21-26300-11-12-75-24-1572-411
Как решить?
Поскольку элемент а11 отличен от нуля, то необходимо умножить элементы первой строки матрицы А на 1а11=12:
А=21-26300-11-12-75-24-1572-411~
Прибавляем к элементам 2-ой строки соответствующие элементы 1-ой строки, которые умножены на (-3). К элементам 3-ей строки прибавляем элементы 1-ой строки, которые умножены на (-1):
~А(1)=112-13300-11-12-75-24-1572-411~А(2)==112-133+1(-3)0+12(-3)0+(-1)(-3)-1+3(-3)1+1(-3)-1+12(-3)2+(-1)(-1)-7+3(-1)5+1(-5)-2+12(-5)4+(-1)(-5)-15+3(-5)7+1(-7)2+12(-7)-4+(-1)(-7)11+3(-7)=
=112-130-323-100-323-100-929-300-323-10
Элемент а22(2) отличен от нуля, поэтому мы умножаем элементы 2-ой строки матрицы А на А(2) на 1а22(2)=-23:
А(3)=112-1301-22030-323-100-929-300-323-10~А(4)=112-1301-22030-32+1323+(-2)32-10+203×320-92+1929+(-2)92-30+203×920-32+1323+(-2)32-10+203×32==112-1301-2203000000000000
- К элементам 3-ей строки полученной матрицы прибавляем соответствующие элементы 2-ой строки ,которые умножены на 32;
- к элементам 4-ой строки — элементы 2-ой строки, которые умножены на 92;
- к элементам 5-ой строки — элементы 2-ой строки, которые умножены на 32.
Все элементы строк равны нулю. Таким образом, при помощи элементарных преобразований ,мы привели матрицу к трапецеидальному виду, откуда видно, что Rank (A(4))=2 . Отсюда следует, что ранг исходной матрицы также равен двум.
Если проводить элементарные преобразования, то не допускаются приближенные значения!
Перед тем как начать знакомство с темой, необходимо повторить правила нахождения определителей второго, третьего и высших порядков. Также необходимо знать, что детерминант 1-го порядка — число. Рассмотрим 2 метода вычисления ранга матриц.
Онлайн-калькулятор
Метод окаймляющих миноров
Для нахождения ранга матрицы данным методом требуется уметь находить миноры матриц.
Рангом матрицы QQ называется наивысший порядок миноров, среди которых есть хотя бы один отличный от 00.
При этом ранг матрицы не может превышать порядка матрицы: 0⩽rang Qm×n⩽min(m,n)0leqslant rang Q_{mtimes n}leqslant min (m, n).
Обозначить ранг матрицы QQ можно следующим образом: rang Qrang Q или r(Q)r(Q).
Если ранг матрицы QQ равен rr, то это означает, что в матрице QQ имеется отличный от нуля минор порядка rr. При этом всякий минор порядка больше, чем rr равен нулю.
Исходя из определения ранга матрицы, следует, что если все миноры первого порядка (т. е. элементы матрицы QQ) равны 00, то rang Q=0rang Q=0. Если один из миноров первого порядка отличен от 00, а все миноры второго порядка равны 00, то rang Q=1rang Q=1. Если все миноры kk-го порядка равны 00, или миноров kk-го порядка не существует, то rang Q=k−1rang Q=k-1.
Рассмотрим примеры нахождения ранга матриц данным методом.
Пример 1
Найти ранг матрицы методом окаймляющих миноров
F=(03−1210−2−10)F=begin{pmatrix}0&3&-1\2&1&0\-2&-1&0end{pmatrix}.
Данная матрица имеет размер 3×33times3, поэтому ее ранг не может быть больше 33, т.е. rang F⩽3rang Fleqslant3.
Перейдем к вычислению ранга матрицы.
Среди миноров 1-го порядка (т.е. элементов определителя) есть хотя бы один, не равный 00, поэтому rang F≥1rang Fgeq1.
Перейдем к проверке миноров 2-го порядка. Например, на пересечении строк №1 и №2 и столбцов №1 и №2 получим минор: ∣0321∣=0⋅1−2⋅3=0−6=−6begin{vmatrix}0&3\2&1end{vmatrix}=0cdot1-2cdot3=0-6=-6. Значит, среди миноров 2-го порядка есть хотя бы один, не равный 00 и поэтому rang F≥2rang Fgeq2.
Перейдем к проверке миноров 3-го порядка. Минор 3-го порядка — определитель матрицы FF, поскольку она состоит из 3 строк и 3 столбцов: ∣03−1210−2−10∣=0begin{vmatrix}0&3&-1\2&1&0\-2&-1&0end{vmatrix}=0. Значит, ранг матрицы FF равен 22, или rang F=2rang F=2.
Пример 2
Найти ранг матрицы методом окаймляющих миноров
K=(21−23−121213−15−2−21243−31)K=begin{pmatrix}2&1&-2&3\-1&2&1&2\1&3&-1&5\-2&-2&1&2\4&3&-3&1end{pmatrix}.
Данная матрица имеет размер 5×45times4. Из чисел 55 и 44 минимальным является 44, поэтому ее ранг не может быть больше 44, а значит rang K⩽4rang Kleqslant4.
Перейдем к вычислению ранга матрицы.
Среди миноров 1-го порядка (т.е. элементов определителя) есть хотя бы один, не равный 00, поэтому rang K≥1rang Kgeq1.
Перейдем к проверке миноров 2-го порядка. Например, на пересечении строк №1 и №2 и столбцов №1 и №2 получим минор: ∣21−12∣=2⋅2−(−1)⋅1=4+1=5begin{vmatrix}2&1\-1&2end{vmatrix}=2cdot2-(-1)cdot1=4+1=5. Значит, среди миноров 2-го порядка есть хотя бы один, не равный 00 и поэтому rang K≥2rang Kgeq2.
Перейдем к проверке миноров 3-го порядка. Например, на пересечении строк №1, №3 и №5 и столбцов №2, №3 и №4 получим минор:
∣1−233−153−31∣=1⋅(−1)⋅1+(−2)⋅5⋅3+3⋅(−3)⋅3−3⋅(−1)⋅3−(−2)⋅1⋅3−1⋅5⋅(−3)=−1−30−27+9+6+15=−28begin{vmatrix}1&-2&3\3&-1&5\3&-3&1end{vmatrix}=1cdot(-1)cdot1+(-2)cdot5cdot3+3cdot(-3)cdot3-3cdot(-1)cdot3-(-2)cdot1cdot3-1cdot5cdot(-3)=-1-30-27+9+6+15=-28.
Значит, среди миноров 3-го порядка есть хотя бы один, не равный 00 и поэтому rang K≥3rang Kgeq3.
Перейдем к проверке миноров 4-го порядка. Например, на пересечении строк №1, №2, №3 и №4 и столбцов №1, №2, №3 и №4 получим минор:
∣21−23−121213−15−2−212∣=2(−1)1+1∣2123−15−212∣−(−1)2+1∣1−233−15−212∣+(−1)3+1∣1−23212−212∣−2(−1)4+1∣1−232123−15∣=2(−1)2∣2123−15−212∣−(−1)3∣1−233−15−212∣+(−1)4∣1−23212−212∣−2(−1)5∣1−232123−15∣=2∣2123−15−212∣+∣1−233−15−212∣+∣1−23212−212∣+2∣1−232123−15∣=2(−4+6−10−4−10−6)−2+9+20−6−5+12+2+6+8+6−2+8+2(5−6−12−9+2+20)=−56+56+0=0begin{vmatrix}2&1&-2&3\-1&2&1&2\1&3&-1&5\-2&-2&1&2end{vmatrix}=2(-1)^{1+1}begin{vmatrix}2&1&2\3&-1&5\-2&1&2end{vmatrix}-(-1)^{2+1}begin{vmatrix}1&-2&3\3&-1&5\-2&1&2end{vmatrix}+(-1)^{3+1}begin{vmatrix}1&-2&3\2&1&2\-2&1&2end{vmatrix}-2(-1)^{4+1}begin{vmatrix}1&-2&3\2&1&2\3&-1&5end{vmatrix}=2(-1)^{2}begin{vmatrix}2&1&2\3&-1&5\-2&1&2end{vmatrix}-(-1)^{3}begin{vmatrix}1&-2&3\3&-1&5\-2&1&2end{vmatrix}+(-1)^{4}begin{vmatrix}1&-2&3\2&1&2\-2&1&2end{vmatrix}-2(-1)^{5}begin{vmatrix}1&-2&3\2&1&2\3&-1&5end{vmatrix}=2begin{vmatrix}2&1&2\3&-1&5\-2&1&2end{vmatrix}+begin{vmatrix}1&-2&3\3&-1&5\-2&1&2end{vmatrix}+begin{vmatrix}1&-2&3\2&1&2\-2&1&2end{vmatrix}+2begin{vmatrix}1&-2&3\2&1&2\3&-1&5end{vmatrix}=2(-4+6-10-4-10-6)-2+9+20-6-5+12+2+6+8+6-2+8+2(5-6-12-9+2+20)=-56+56+0=0.
Остальные миноры 4-го порядка также равны нулю:
∣21−23−121213−1543−31∣=0begin{vmatrix}2&1&-2&3\-1&2&1&2\1&3&-1&5\4&3&-3&1end{vmatrix}=0,
∣21−23−1212−2−21243−31∣=0begin{vmatrix}2&1&-2&3\-1&2&1&2\-2&-2&1&2\4&3&-3&1end{vmatrix}=0,
∣21−2313−15−2−21243−31∣=0begin{vmatrix}2&1&-2&3\1&3&-1&5\-2&-2&1&2\4&3&-3&1end{vmatrix}=0,
∣−121213−15−2−21243−31∣=0begin{vmatrix}-1&2&1&2\1&3&-1&5\-2&-2&1&2\4&3&-3&1end{vmatrix}=0.
Значит, ранг матрицы KK равен 33, или rang K=3rang K=3.
Данный метод не всегда удобен, поскольку связан с вычислением большого количества определителей. Рассмотрим метод нахождения ранга матриц, который наиболее часто применяется на практике.
Метод Гаусса (метод элементарных преобразований)
Метод основан на элементарных преобразованиях матриц, под которыми будем понимать такие преобразования, в результате которых сохраняется эквивалентность матриц:
- перестановка местами любых двух рядов (строк или столбцов) матрицы;
- умножение любого ряда матрицы (строки или столбца) на некоторое число, отличное от нуля;
- прибавление к любому ряду (строке или столбцу) матрицы другого ряда (строки или столбца), умноженного на некоторое число, отличное от нуля.
Рангом матрицы называется количество ненулевых строк матрицы после ее приведения к ступенчатому виду при помощи элементарных преобразований над строками и столбцами.
Рассмотрим суть данного метода на примерах.
Пример 1
Найти ранг матрицы методом Гаусса F=(03−1210−2−10)F=begin{pmatrix}0&3&-1\2&1&0\-2&-1&0end{pmatrix}.
Приведем матрицу FF с помощью элементарных преобразований к ступенчатому виду.
Поменяем местами строки №1 и №2:
(03−1210−2−10)∼(21003−1−2−10)begin{pmatrix}0&3&-1\2&1&0\-2&-1&0end{pmatrix}sim begin{pmatrix}2&1&0\0&3&-1\-2&-1&0end{pmatrix}.
Прибавим к строке №3 строку №1, умноженную на 1:
(21003−1−2−10)∼(21003−1000)begin{pmatrix}2&1&0\0&3&-1\-2&-1&0end{pmatrix}simbegin{pmatrix}2&1&0\0&3&-1\0&0&0end{pmatrix}.
С помощью элементарных преобразований мы привели матрицу FF к ступенчатому виду. В ней остались 2 ненулевые строки, следовательно, rang F=2rang F=2.
Пример 2
Найти ранг матрицы методом Гаусса
K=(21−23−121213−15−2−21243−31)K=begin{pmatrix}2&1&-2&3\-1&2&1&2\1&3&-1&5\-2&-2&1&2\4&3&-3&1end{pmatrix}.
Приведем матрицу KK с помощью элементарных преобразований к ступенчатому виду.
Поменяем местами строки №1 и №2:
(21−23−121213−15−2−21243−31)∼(−121221−2313−15−2−21243−31)begin{pmatrix}2&1&-2&3\-1&2&1&2\1&3&-1&5\-2&-2&1&2\4&3&-3&1end{pmatrix}sim begin{pmatrix}-1&2&1&2\2&1&-2&3\1&3&-1&5\-2&-2&1&2\4&3&-3&1end{pmatrix}.
Поменяем местами строки №2 и №4:
(−121221−2313−15−2−21243−31)∼(−1212−2−21213−1521−2343−31)begin{pmatrix}-1&2&1&2\2&1&-2&3\1&3&-1&5\-2&-2&1&2\4&3&-3&1end{pmatrix}sim begin{pmatrix}-1&2&1&2\-2&-2&1&2\1&3&-1&5\2&1&-2&3\4&3&-3&1end{pmatrix}.
Поменяем местами строки №3 и №4:
(−1212−2−21213−1521−2343−31)∼(−1212−2−21221−2313−1543−31)begin{pmatrix}-1&2&1&2\-2&-2&1&2\1&3&-1&5\2&1&-2&3\4&3&-3&1end{pmatrix}sim begin{pmatrix}-1&2&1&2\-2&-2&1&2\2&1&-2&3\1&3&-1&5\4&3&-3&1end{pmatrix}.
Поменяем местами строки №4 и №5:
(−1212−2−21221−2313−1543−31)∼(−1212−2−21221−2343−3113−15)begin{pmatrix}-1&2&1&2\-2&-2&1&2\2&1&-2&3\1&3&-1&5\4&3&-3&1end{pmatrix}sim begin{pmatrix}-1&2&1&2\-2&-2&1&2\2&1&-2&3\4&3&-3&1\1&3&-1&5end{pmatrix}.
Прибавим к строке №2 строку №1, умноженную на -2:
(−1212−2−21221−2343−3113−15)∼(−12120−6−1−221−2343−3113−15)begin{pmatrix}-1&2&1&2\-2&-2&1&2\2&1&-2&3\4&3&-3&1\1&3&-1&5end{pmatrix}sim begin{pmatrix}-1&2&1&2\0&-6&-1&-2\2&1&-2&3\4&3&-3&1\1&3&-1&5end{pmatrix}.
Прибавим к строке №3 строку №1, умноженную на 2:
(−12120−6−1−221−2343−3113−15)∼(−12120−6−1−2050743−3113−15)begin{pmatrix}-1&2&1&2\0&-6&-1&-2\2&1&-2&3\4&3&-3&1\1&3&-1&5end{pmatrix}sim begin{pmatrix}-1&2&1&2\0&-6&-1&-2\0&5&0&7\4&3&-3&1\1&3&-1&5end{pmatrix}.
Прибавим к строке №4 строку №1, умноженную на 4:
(−12120−6−1−2050743−3113−15)∼(−12120−6−1−205070111913−15)begin{pmatrix}-1&2&1&2\0&-6&-1&-2\0&5&0&7\4&3&-3&1\1&3&-1&5end{pmatrix}sim begin{pmatrix}-1&2&1&2\0&-6&-1&-2\0&5&0&7\0&11&1&9\1&3&-1&5end{pmatrix}.
Прибавим к строке №5 строку №1, умноженную на 1:
(−12120−6−1−205070111913−15)∼(−12120−6−1−20507011190507)begin{pmatrix}-1&2&1&2\0&-6&-1&-2\0&5&0&7\0&11&1&9\1&3&-1&5end{pmatrix}sim begin{pmatrix}-1&2&1&2\0&-6&-1&-2\0&5&0&7\0&11&1&9\0&5&0&7end{pmatrix}.
Прибавим к строке №2 строку №3, умноженную на 1:
(−12120−6−1−20507011190507)∼(−12120−1−150507011190507)begin{pmatrix}-1&2&1&2\0&-6&-1&-2\0&5&0&7\0&11&1&9\0&5&0&7end{pmatrix}sim begin{pmatrix}-1&2&1&2\0&-1&-1&5\0&5&0&7\0&11&1&9\0&5&0&7end{pmatrix}.
Прибавим к строке №5 строку №3, умноженную на -1:
(−12120−1−150507011190507)∼(−12120−1−150507011190000)begin{pmatrix}-1&2&1&2\0&-1&-1&5\0&5&0&7\0&11&1&9\0&5&0&7end{pmatrix}sim begin{pmatrix}-1&2&1&2\0&-1&-1&5\0&5&0&7\0&11&1&9\0&0&0&0end{pmatrix}.
Прибавим к строке №3 строку №2, умноженную на 5:
(−12120−1−150507011190000)∼(−12120−1−1500−532011190000)begin{pmatrix}-1&2&1&2\0&-1&-1&5\0&5&0&7\0&11&1&9\0&0&0&0end{pmatrix}sim begin{pmatrix}-1&2&1&2\0&-1&-1&5\0&0&-5&32\0&11&1&9\0&0&0&0end{pmatrix}.
Прибавим к строке №4 строку №2, умноженную на 11:
(−12120−1−1500−532011190000)∼(−12120−1−1500−53200−10640000)begin{pmatrix}-1&2&1&2\0&-1&-1&5\0&0&-5&32\0&11&1&9\0&0&0&0end{pmatrix}sim begin{pmatrix}-1&2&1&2\0&-1&-1&5\0&0&-5&32\0&0&-10&64\0&0&0&0end{pmatrix}.
Прибавим к строке №4 строку №3, умноженную на -2:
(−12120−1−1500−53200−10640000)∼(−12120−1−1500−53200000000)begin{pmatrix}-1&2&1&2\0&-1&-1&5\0&0&-5&32\0&0&-10&64\0&0&0&0end{pmatrix}sim begin{pmatrix}-1&2&1&2\0&-1&-1&5\0&0&-5&32\0&0&0&0\0&0&0&0end{pmatrix}.
С помощью элементарных преобразований мы привели матрицу KK к ступенчатому виду. В ней остались 3 ненулевые строки, следовательно, rang K=3rang K=3.
Любым из рассмотренных методов можно найти ранг матрицы.
Наши эксперты готовы оказать вам помощь с решением задачи онлайн по самым низким ценам!
Тест по теме «Ранг матрицы»
In linear algebra, the rank of a matrix A is the dimension of the vector space generated (or spanned) by its columns.[1][2][3] This corresponds to the maximal number of linearly independent columns of A. This, in turn, is identical to the dimension of the vector space spanned by its rows.[4] Rank is thus a measure of the «nondegenerateness» of the system of linear equations and linear transformation encoded by A. There are multiple equivalent definitions of rank. A matrix’s rank is one of its most fundamental characteristics.
The rank is commonly denoted by rank(A) or rk(A);[2] sometimes the parentheses are not written, as in rank A.[i]
Main definitions[edit]
In this section, we give some definitions of the rank of a matrix. Many definitions are possible; see Alternative definitions for several of these.
The column rank of A is the dimension of the column space of A, while the row rank of A is the dimension of the row space of A.
A fundamental result in linear algebra is that the column rank and the row rank are always equal. (Three proofs of this result are given in § Proofs that column rank = row rank, below.) This number (i.e., the number of linearly independent rows or columns) is simply called the rank of A.
A matrix is said to have full rank if its rank equals the largest possible for a matrix of the same dimensions, which is the lesser of the number of rows and columns. A matrix is said to be rank-deficient if it does not have full rank. The rank deficiency of a matrix is the difference between the lesser of the number of rows and columns, and the rank.
The rank of a linear map or operator 
where 

Examples[edit]
The matrix
has rank 2: the first two columns are linearly independent, so the rank is at least 2, but since the third is a linear combination of the first two (the first column minus the second), the three columns are linearly dependent so the rank must be less than 3.
The matrix
has rank 1: there are nonzero columns, so the rank is positive, but any pair of columns is linearly dependent. Similarly, the transpose
of A has rank 1. Indeed, since the column vectors of A are the row vectors of the transpose of A, the statement that the column rank of a matrix equals its row rank is equivalent to the statement that the rank of a matrix is equal to the rank of its transpose, i.e., rank(A) = rank(AT).
Computing the rank of a matrix[edit]
Rank from row echelon forms[edit]
A common approach to finding the rank of a matrix is to reduce it to a simpler form, generally row echelon form, by elementary row operations. Row operations do not change the row space (hence do not change the row rank), and, being invertible, map the column space to an isomorphic space (hence do not change the column rank). Once in row echelon form, the rank is clearly the same for both row rank and column rank, and equals the number of pivots (or basic columns) and also the number of non-zero rows.
For example, the matrix A given by
can be put in reduced row-echelon form by using the following elementary row operations:
The final matrix (in row echelon form) has two non-zero rows and thus the rank of matrix A is 2.
Computation[edit]
When applied to floating point computations on computers, basic Gaussian elimination (LU decomposition) can be unreliable, and a rank-revealing decomposition should be used instead. An effective alternative is the singular value decomposition (SVD), but there are other less expensive choices, such as QR decomposition with pivoting (so-called rank-revealing QR factorization), which are still more numerically robust than Gaussian elimination. Numerical determination of rank requires a criterion for deciding when a value, such as a singular value from the SVD, should be treated as zero, a practical choice which depends on both the matrix and the application.
Proofs that column rank = row rank[edit]
Proof using row reduction[edit]
The fact that the column and row ranks of any matrix are equal forms is fundamental in linear algebra. Many proofs have been given. One of the most elementary ones has been sketched in § Rank from row echelon forms. Here is a variant of this proof:
It is straightforward to show that neither the row rank nor the column rank are changed by an elementary row operation. As Gaussian elimination proceeds by elementary row operations, the reduced row echelon form of a matrix has the same row rank and the same column rank as the original matrix. Further elementary column operations allow putting the matrix in the form of an identity matrix possibly bordered by rows and columns of zeros. Again, this changes neither the row rank nor the column rank. It is immediate that both the row and column ranks of this resulting matrix is the number of its nonzero entries.
We present two other proofs of this result. The first uses only basic properties of linear combinations of vectors, and is valid over any field. The proof is based upon Wardlaw (2005).[9] The second uses orthogonality and is valid for matrices over the real numbers; it is based upon Mackiw (1995).[4] Both proofs can be found in the book by Banerjee and Roy (2014).[10]
Proof using linear combinations[edit]
Let A be an m × n matrix. Let the column rank of A be r, and let c1, …, cr be any basis for the column space of A. Place these as the columns of an m × r matrix C. Every column of A can be expressed as a linear combination of the r columns in C. This means that there is an r × n matrix R such that A = CR. R is the matrix whose ith column is formed from the coefficients giving the ith column of A as a linear combination of the r columns of C. In other words, R is the matrix which contains the multiples for the bases of the column space of A (which is C), which are then used to form A as a whole. Now, each row of A is given by a linear combination of the r rows of R. Therefore, the rows of R form a spanning set of the row space of A and, by the Steinitz exchange lemma, the row rank of A cannot exceed r. This proves that the row rank of A is less than or equal to the column rank of A. This result can be applied to any matrix, so apply the result to the transpose of A. Since the row rank of the transpose of A is the column rank of A and the column rank of the transpose of A is the row rank of A, this establishes the reverse inequality and we obtain the equality of the row rank and the column rank of A. (Also see Rank factorization.)
Proof using orthogonality[edit]
Let A be an m × n matrix with entries in the real numbers whose row rank is r. Therefore, the dimension of the row space of A is r. Let x1, x2, …, xr be a basis of the row space of A. We claim that the vectors Ax1, Ax2, …, Axr are linearly independent. To see why, consider a linear homogeneous relation involving these vectors with scalar coefficients c1, c2, …, cr:
where v = c1x1 + c2x2 + ⋯ + crxr. We make two observations: (a) v is a linear combination of vectors in the row space of A, which implies that v belongs to the row space of A, and (b) since Av = 0, the vector v is orthogonal to every row vector of A and, hence, is orthogonal to every vector in the row space of A. The facts (a) and (b) together imply that v is orthogonal to itself, which proves that v = 0 or, by the definition of v,
But recall that the xi were chosen as a basis of the row space of A and so are linearly independent. This implies that c1 = c2 = ⋯ = cr = 0. It follows that Ax1, Ax2, …, Axr are linearly independent.
Now, each Axi is obviously a vector in the column space of A. So, Ax1, Ax2, …, Axr is a set of r linearly independent vectors in the column space of A and, hence, the dimension of the column space of A (i.e., the column rank of A) must be at least as big as r. This proves that row rank of A is no larger than the column rank of A. Now apply this result to the transpose of A to get the reverse inequality and conclude as in the previous proof.
Alternative definitions[edit]
In all the definitions in this section, the matrix A is taken to be an m × n matrix over an arbitrary field F.
Dimension of image[edit]
Given the matrix 
defined by
The rank of 

Rank in terms of nullity[edit]
Given the same linear mapping f as above, the rank is n minus the dimension of the kernel of f. The rank–nullity theorem states that this definition is equivalent to the preceding one.
Column rank – dimension of column space[edit]
The rank of A is the maximal number of linearly independent columns 
Row rank – dimension of row space[edit]
The rank of A is the maximal number of linearly independent rows of A; this is the dimension of the row space of A.
Decomposition rank[edit]
The rank of A is the smallest integer k such that A can be factored as 
- the column rank of A is less than or equal to k,
- there exist k columns
of size m such that every column of A is a linear combination of
,
- there exist an
matrix C and a
matrix R such that
(when k is the rank, this is a rank factorization of A),
- there exist k rows
of size n such that every row of A is a linear combination of
,
- the row rank of A is less than or equal to k.
Indeed, the following equivalences are obvious: 
For example, to prove (3) from (2), take C to be the matrix whose columns are 
To prove (2) from (3), take 
It follows from the equivalence 
As in the case of the «dimension of image» characterization, this can be generalized to a definition of the rank of any linear map: the rank of a linear map f : V → W is the minimal dimension k of an intermediate space X such that f can be written as the composition of a map V → X and a map X → W. Unfortunately, this definition does not suggest an efficient manner to compute the rank (for which it is better to use one of the alternative definitions). See rank factorization for details.
Rank in terms of singular values[edit]
The rank of A equals the number of non-zero singular values, which is the same as the number of non-zero diagonal elements in Σ in the singular value decomposition 
Determinantal rank – size of largest non-vanishing minor[edit]
The rank of A is the largest order of any non-zero minor in A. (The order of a minor is the side-length of the square sub-matrix of which it is the determinant.) Like the decomposition rank characterization, this does not give an efficient way of computing the rank, but it is useful theoretically: a single non-zero minor witnesses a lower bound (namely its order) for the rank of the matrix, which can be useful (for example) to prove that certain operations do not lower the rank of a matrix.
A non-vanishing p-minor (p × p submatrix with non-zero determinant) shows that the rows and columns of that submatrix are linearly independent, and thus those rows and columns of the full matrix are linearly independent (in the full matrix), so the row and column rank are at least as large as the determinantal rank; however, the converse is less straightforward. The equivalence of determinantal rank and column rank is a strengthening of the statement that if the span of n vectors has dimension p, then p of those vectors span the space (equivalently, that one can choose a spanning set that is a subset of the vectors): the equivalence implies that a subset of the rows and a subset of the columns simultaneously define an invertible submatrix (equivalently, if the span of n vectors has dimension p, then p of these vectors span the space and there is a set of p coordinates on which they are linearly independent).
Tensor rank – minimum number of simple tensors[edit]
The rank of A is the smallest number k such that A can be written as a sum of k rank 1 matrices, where a matrix is defined to have rank 1 if and only if it can be written as a nonzero product 
Properties[edit]
We assume that A is an m × n matrix, and we define the linear map f by f(x) = Ax as above.
- The rank of an m × n matrix is a nonnegative integer and cannot be greater than either m or n. That is,
A matrix that has rank min(m, n) is said to have full rank; otherwise, the matrix is rank deficient.
- Only a zero matrix has rank zero.
- f is injective (or «one-to-one») if and only if A has rank n (in this case, we say that A has full column rank).
- f is surjective (or «onto») if and only if A has rank m (in this case, we say that A has full row rank).
- If A is a square matrix (i.e., m = n), then A is invertible if and only if A has rank n (that is, A has full rank).
- If B is any n × k matrix, then
- If B is an n × k matrix of rank n, then
- If C is an l × m matrix of rank m, then
- The rank of A is equal to r if and only if there exists an invertible m × m matrix X and an invertible n × n matrix Y such that
where Ir denotes the r × r identity matrix.
- Sylvester’s rank inequality: if A is an m × n matrix and B is n × k, then[ii]
This is a special case of the next inequality.
- The inequality due to Frobenius: if AB, ABC and BC are defined, then[iii]
- Subadditivity:
when A and B are of the same dimension. As a consequence, a rank-k matrix can be written as the sum of k rank-1 matrices, but not fewer.
- The rank of a matrix plus the nullity of the matrix equals the number of columns of the matrix. (This is the rank–nullity theorem.)
- If A is a matrix over the real numbers then the rank of A and the rank of its corresponding Gram matrix are equal. Thus, for real matrices
This can be shown by proving equality of their null spaces. The null space of the Gram matrix is given by vectors x for which
If this condition is fulfilled, we also have
[11]
- If A is a matrix over the complex numbers and
denotes the complex conjugate of A and A∗ the conjugate transpose of A (i.e., the adjoint of A), then
Applications[edit]
One useful application of calculating the rank of a matrix is the computation of the number of solutions of a system of linear equations. According to the Rouché–Capelli theorem, the system is inconsistent if the rank of the augmented matrix is greater than the rank of the coefficient matrix. If on the other hand, the ranks of these two matrices are equal, then the system must have at least one solution. The solution is unique if and only if the rank equals the number of variables. Otherwise the general solution has k free parameters where k is the difference between the number of variables and the rank. In this case (and assuming the system of equations is in the real or complex numbers) the system of equations has infinitely many solutions.
In control theory, the rank of a matrix can be used to determine whether a linear system is controllable, or observable.
In the field of communication complexity, the rank of the communication matrix of a function gives bounds on the amount of communication needed for two parties to compute the function.
Generalization[edit]
There are different generalizations of the concept of rank to matrices over arbitrary rings, where column rank, row rank, dimension of column space, and dimension of row space of a matrix may be different from the others or may not exist.
Thinking of matrices as tensors, the tensor rank generalizes to arbitrary tensors; for tensors of order greater than 2 (matrices are order 2 tensors), rank is very hard to compute, unlike for matrices.
There is a notion of rank for smooth maps between smooth manifolds. It is equal to the linear rank of the derivative.
Matrices as tensors[edit]
Matrix rank should not be confused with tensor order, which is called tensor rank. Tensor order is the number of indices required to write a tensor, and thus matrices all have tensor order 2. More precisely, matrices are tensors of type (1,1), having one row index and one column index, also called covariant order 1 and contravariant order 1; see Tensor (intrinsic definition) for details.
The tensor rank of a matrix can also mean the minimum number of simple tensors necessary to express the matrix as a linear combination, and that this definition does agree with matrix rank as here discussed.
See also[edit]
- Matroid rank
- Nonnegative rank (linear algebra)
- Rank (differential topology)
- Multicollinearity
- Linear dependence
Notes[edit]
References[edit]
- ^ Axler (2015) pp. 111-112, §§ 3.115, 3.119
- ^ a b Roman (2005) p. 48, § 1.16
- ^ Bourbaki, Algebra, ch. II, §10.12, p. 359
- ^ a b Mackiw, G. (1995), «A Note on the Equality of the Column and Row Rank of a Matrix», Mathematics Magazine, 68 (4): 285–286, doi:10.1080/0025570X.1995.11996337
- ^ Hefferon (2020) p. 200, ch. 3, Definition 2.1
- ^ Katznelson & Katznelson (2008) p. 52, § 2.5.1
- ^ Valenza (1993) p. 71, § 4.3
- ^ Halmos (1974) p. 90, § 50
- ^
Wardlaw, William P. (2005), «Row Rank Equals Column Rank», Mathematics Magazine, 78 (4): 316–318, doi:10.1080/0025570X.2005.11953349, S2CID 218542661 - ^ Banerjee, Sudipto; Roy, Anindya (2014), Linear Algebra and Matrix Analysis for Statistics, Texts in Statistical Science (1st ed.), Chapman and Hall/CRC, ISBN 978-1420095388
- ^ Mirsky, Leonid (1955). An introduction to linear algebra. Dover Publications. ISBN 978-0-486-66434-7.
Sources[edit]
- Axler, Sheldon (2015). Linear Algebra Done Right. Undergraduate Texts in Mathematics (3rd ed.). Springer. ISBN 978-3-319-11079-0.
- Halmos, Paul Richard (1974) [1958]. Finite-Dimensional Vector Spaces. Undergraduate Texts in Mathematics (2nd ed.). Springer. ISBN 0-387-90093-4.
- Hefferon, Jim (2020). Linear Algebra (4th ed.). ISBN 978-1-944325-11-4.
- Katznelson, Yitzhak; Katznelson, Yonatan R. (2008). A (Terse) Introduction to Linear Algebra. American Mathematical Society. ISBN 978-0-8218-4419-9.
- Roman, Steven (2005). Advanced Linear Algebra. Undergraduate Texts in Mathematics (2nd ed.). Springer. ISBN 0-387-24766-1.
- Valenza, Robert J. (1993) [1951]. Linear Algebra: An Introduction to Abstract Mathematics. Undergraduate Texts in Mathematics (3rd ed.). Springer. ISBN 3-540-94099-5.
Further reading[edit]
- Roger A. Horn and Charles R. Johnson (1985). Matrix Analysis. ISBN 978-0-521-38632-6.
- Kaw, Autar K. Two Chapters from the book Introduction to Matrix Algebra: 1. Vectors [1] and System of Equations [2]
- Mike Brookes: Matrix Reference Manual. [3]
In linear algebra, the rank of a matrix A is the dimension of the vector space generated (or spanned) by its columns.[1][2][3] This corresponds to the maximal number of linearly independent columns of A. This, in turn, is identical to the dimension of the vector space spanned by its rows.[4] Rank is thus a measure of the «nondegenerateness» of the system of linear equations and linear transformation encoded by A. There are multiple equivalent definitions of rank. A matrix’s rank is one of its most fundamental characteristics.
The rank is commonly denoted by rank(A) or rk(A);[2] sometimes the parentheses are not written, as in rank A.[i]
Main definitions[edit]
In this section, we give some definitions of the rank of a matrix. Many definitions are possible; see Alternative definitions for several of these.
The column rank of A is the dimension of the column space of A, while the row rank of A is the dimension of the row space of A.
A fundamental result in linear algebra is that the column rank and the row rank are always equal. (Three proofs of this result are given in § Proofs that column rank = row rank, below.) This number (i.e., the number of linearly independent rows or columns) is simply called the rank of A.
A matrix is said to have full rank if its rank equals the largest possible for a matrix of the same dimensions, which is the lesser of the number of rows and columns. A matrix is said to be rank-deficient if it does not have full rank. The rank deficiency of a matrix is the difference between the lesser of the number of rows and columns, and the rank.
The rank of a linear map or operator 
where 

Examples[edit]
The matrix
has rank 2: the first two columns are linearly independent, so the rank is at least 2, but since the third is a linear combination of the first two (the first column minus the second), the three columns are linearly dependent so the rank must be less than 3.
The matrix
has rank 1: there are nonzero columns, so the rank is positive, but any pair of columns is linearly dependent. Similarly, the transpose
of A has rank 1. Indeed, since the column vectors of A are the row vectors of the transpose of A, the statement that the column rank of a matrix equals its row rank is equivalent to the statement that the rank of a matrix is equal to the rank of its transpose, i.e., rank(A) = rank(AT).
Computing the rank of a matrix[edit]
Rank from row echelon forms[edit]
A common approach to finding the rank of a matrix is to reduce it to a simpler form, generally row echelon form, by elementary row operations. Row operations do not change the row space (hence do not change the row rank), and, being invertible, map the column space to an isomorphic space (hence do not change the column rank). Once in row echelon form, the rank is clearly the same for both row rank and column rank, and equals the number of pivots (or basic columns) and also the number of non-zero rows.
For example, the matrix A given by
can be put in reduced row-echelon form by using the following elementary row operations:
The final matrix (in row echelon form) has two non-zero rows and thus the rank of matrix A is 2.
Computation[edit]
When applied to floating point computations on computers, basic Gaussian elimination (LU decomposition) can be unreliable, and a rank-revealing decomposition should be used instead. An effective alternative is the singular value decomposition (SVD), but there are other less expensive choices, such as QR decomposition with pivoting (so-called rank-revealing QR factorization), which are still more numerically robust than Gaussian elimination. Numerical determination of rank requires a criterion for deciding when a value, such as a singular value from the SVD, should be treated as zero, a practical choice which depends on both the matrix and the application.
Proofs that column rank = row rank[edit]
Proof using row reduction[edit]
The fact that the column and row ranks of any matrix are equal forms is fundamental in linear algebra. Many proofs have been given. One of the most elementary ones has been sketched in § Rank from row echelon forms. Here is a variant of this proof:
It is straightforward to show that neither the row rank nor the column rank are changed by an elementary row operation. As Gaussian elimination proceeds by elementary row operations, the reduced row echelon form of a matrix has the same row rank and the same column rank as the original matrix. Further elementary column operations allow putting the matrix in the form of an identity matrix possibly bordered by rows and columns of zeros. Again, this changes neither the row rank nor the column rank. It is immediate that both the row and column ranks of this resulting matrix is the number of its nonzero entries.
We present two other proofs of this result. The first uses only basic properties of linear combinations of vectors, and is valid over any field. The proof is based upon Wardlaw (2005).[9] The second uses orthogonality and is valid for matrices over the real numbers; it is based upon Mackiw (1995).[4] Both proofs can be found in the book by Banerjee and Roy (2014).[10]
Proof using linear combinations[edit]
Let A be an m × n matrix. Let the column rank of A be r, and let c1, …, cr be any basis for the column space of A. Place these as the columns of an m × r matrix C. Every column of A can be expressed as a linear combination of the r columns in C. This means that there is an r × n matrix R such that A = CR. R is the matrix whose ith column is formed from the coefficients giving the ith column of A as a linear combination of the r columns of C. In other words, R is the matrix which contains the multiples for the bases of the column space of A (which is C), which are then used to form A as a whole. Now, each row of A is given by a linear combination of the r rows of R. Therefore, the rows of R form a spanning set of the row space of A and, by the Steinitz exchange lemma, the row rank of A cannot exceed r. This proves that the row rank of A is less than or equal to the column rank of A. This result can be applied to any matrix, so apply the result to the transpose of A. Since the row rank of the transpose of A is the column rank of A and the column rank of the transpose of A is the row rank of A, this establishes the reverse inequality and we obtain the equality of the row rank and the column rank of A. (Also see Rank factorization.)
Proof using orthogonality[edit]
Let A be an m × n matrix with entries in the real numbers whose row rank is r. Therefore, the dimension of the row space of A is r. Let x1, x2, …, xr be a basis of the row space of A. We claim that the vectors Ax1, Ax2, …, Axr are linearly independent. To see why, consider a linear homogeneous relation involving these vectors with scalar coefficients c1, c2, …, cr:
where v = c1x1 + c2x2 + ⋯ + crxr. We make two observations: (a) v is a linear combination of vectors in the row space of A, which implies that v belongs to the row space of A, and (b) since Av = 0, the vector v is orthogonal to every row vector of A and, hence, is orthogonal to every vector in the row space of A. The facts (a) and (b) together imply that v is orthogonal to itself, which proves that v = 0 or, by the definition of v,
But recall that the xi were chosen as a basis of the row space of A and so are linearly independent. This implies that c1 = c2 = ⋯ = cr = 0. It follows that Ax1, Ax2, …, Axr are linearly independent.
Now, each Axi is obviously a vector in the column space of A. So, Ax1, Ax2, …, Axr is a set of r linearly independent vectors in the column space of A and, hence, the dimension of the column space of A (i.e., the column rank of A) must be at least as big as r. This proves that row rank of A is no larger than the column rank of A. Now apply this result to the transpose of A to get the reverse inequality and conclude as in the previous proof.
Alternative definitions[edit]
In all the definitions in this section, the matrix A is taken to be an m × n matrix over an arbitrary field F.
Dimension of image[edit]
Given the matrix 
defined by
The rank of 

Rank in terms of nullity[edit]
Given the same linear mapping f as above, the rank is n minus the dimension of the kernel of f. The rank–nullity theorem states that this definition is equivalent to the preceding one.
Column rank – dimension of column space[edit]
The rank of A is the maximal number of linearly independent columns 
Row rank – dimension of row space[edit]
The rank of A is the maximal number of linearly independent rows of A; this is the dimension of the row space of A.
Decomposition rank[edit]
The rank of A is the smallest integer k such that A can be factored as 
- the column rank of A is less than or equal to k,
- there exist k columns
of size m such that every column of A is a linear combination of
,
- there exist an
matrix C and a
matrix R such that
(when k is the rank, this is a rank factorization of A),
- there exist k rows
of size n such that every row of A is a linear combination of
,
- the row rank of A is less than or equal to k.
Indeed, the following equivalences are obvious: 
For example, to prove (3) from (2), take C to be the matrix whose columns are 
To prove (2) from (3), take 
It follows from the equivalence 
As in the case of the «dimension of image» characterization, this can be generalized to a definition of the rank of any linear map: the rank of a linear map f : V → W is the minimal dimension k of an intermediate space X such that f can be written as the composition of a map V → X and a map X → W. Unfortunately, this definition does not suggest an efficient manner to compute the rank (for which it is better to use one of the alternative definitions). See rank factorization for details.
Rank in terms of singular values[edit]
The rank of A equals the number of non-zero singular values, which is the same as the number of non-zero diagonal elements in Σ in the singular value decomposition 
Determinantal rank – size of largest non-vanishing minor[edit]
The rank of A is the largest order of any non-zero minor in A. (The order of a minor is the side-length of the square sub-matrix of which it is the determinant.) Like the decomposition rank characterization, this does not give an efficient way of computing the rank, but it is useful theoretically: a single non-zero minor witnesses a lower bound (namely its order) for the rank of the matrix, which can be useful (for example) to prove that certain operations do not lower the rank of a matrix.
A non-vanishing p-minor (p × p submatrix with non-zero determinant) shows that the rows and columns of that submatrix are linearly independent, and thus those rows and columns of the full matrix are linearly independent (in the full matrix), so the row and column rank are at least as large as the determinantal rank; however, the converse is less straightforward. The equivalence of determinantal rank and column rank is a strengthening of the statement that if the span of n vectors has dimension p, then p of those vectors span the space (equivalently, that one can choose a spanning set that is a subset of the vectors): the equivalence implies that a subset of the rows and a subset of the columns simultaneously define an invertible submatrix (equivalently, if the span of n vectors has dimension p, then p of these vectors span the space and there is a set of p coordinates on which they are linearly independent).
Tensor rank – minimum number of simple tensors[edit]
The rank of A is the smallest number k such that A can be written as a sum of k rank 1 matrices, where a matrix is defined to have rank 1 if and only if it can be written as a nonzero product 
Properties[edit]
We assume that A is an m × n matrix, and we define the linear map f by f(x) = Ax as above.
- The rank of an m × n matrix is a nonnegative integer and cannot be greater than either m or n. That is,
A matrix that has rank min(m, n) is said to have full rank; otherwise, the matrix is rank deficient.
- Only a zero matrix has rank zero.
- f is injective (or «one-to-one») if and only if A has rank n (in this case, we say that A has full column rank).
- f is surjective (or «onto») if and only if A has rank m (in this case, we say that A has full row rank).
- If A is a square matrix (i.e., m = n), then A is invertible if and only if A has rank n (that is, A has full rank).
- If B is any n × k matrix, then
- If B is an n × k matrix of rank n, then
- If C is an l × m matrix of rank m, then
- The rank of A is equal to r if and only if there exists an invertible m × m matrix X and an invertible n × n matrix Y such that
where Ir denotes the r × r identity matrix.
- Sylvester’s rank inequality: if A is an m × n matrix and B is n × k, then[ii]
This is a special case of the next inequality.
- The inequality due to Frobenius: if AB, ABC and BC are defined, then[iii]
- Subadditivity:
when A and B are of the same dimension. As a consequence, a rank-k matrix can be written as the sum of k rank-1 matrices, but not fewer.
- The rank of a matrix plus the nullity of the matrix equals the number of columns of the matrix. (This is the rank–nullity theorem.)
- If A is a matrix over the real numbers then the rank of A and the rank of its corresponding Gram matrix are equal. Thus, for real matrices
This can be shown by proving equality of their null spaces. The null space of the Gram matrix is given by vectors x for which
If this condition is fulfilled, we also have
[11]
- If A is a matrix over the complex numbers and
denotes the complex conjugate of A and A∗ the conjugate transpose of A (i.e., the adjoint of A), then
Applications[edit]
One useful application of calculating the rank of a matrix is the computation of the number of solutions of a system of linear equations. According to the Rouché–Capelli theorem, the system is inconsistent if the rank of the augmented matrix is greater than the rank of the coefficient matrix. If on the other hand, the ranks of these two matrices are equal, then the system must have at least one solution. The solution is unique if and only if the rank equals the number of variables. Otherwise the general solution has k free parameters where k is the difference between the number of variables and the rank. In this case (and assuming the system of equations is in the real or complex numbers) the system of equations has infinitely many solutions.
In control theory, the rank of a matrix can be used to determine whether a linear system is controllable, or observable.
In the field of communication complexity, the rank of the communication matrix of a function gives bounds on the amount of communication needed for two parties to compute the function.
Generalization[edit]
There are different generalizations of the concept of rank to matrices over arbitrary rings, where column rank, row rank, dimension of column space, and dimension of row space of a matrix may be different from the others or may not exist.
Thinking of matrices as tensors, the tensor rank generalizes to arbitrary tensors; for tensors of order greater than 2 (matrices are order 2 tensors), rank is very hard to compute, unlike for matrices.
There is a notion of rank for smooth maps between smooth manifolds. It is equal to the linear rank of the derivative.
Matrices as tensors[edit]
Matrix rank should not be confused with tensor order, which is called tensor rank. Tensor order is the number of indices required to write a tensor, and thus matrices all have tensor order 2. More precisely, matrices are tensors of type (1,1), having one row index and one column index, also called covariant order 1 and contravariant order 1; see Tensor (intrinsic definition) for details.
The tensor rank of a matrix can also mean the minimum number of simple tensors necessary to express the matrix as a linear combination, and that this definition does agree with matrix rank as here discussed.
See also[edit]
- Matroid rank
- Nonnegative rank (linear algebra)
- Rank (differential topology)
- Multicollinearity
- Linear dependence
Notes[edit]
References[edit]
- ^ Axler (2015) pp. 111-112, §§ 3.115, 3.119
- ^ a b Roman (2005) p. 48, § 1.16
- ^ Bourbaki, Algebra, ch. II, §10.12, p. 359
- ^ a b Mackiw, G. (1995), «A Note on the Equality of the Column and Row Rank of a Matrix», Mathematics Magazine, 68 (4): 285–286, doi:10.1080/0025570X.1995.11996337
- ^ Hefferon (2020) p. 200, ch. 3, Definition 2.1
- ^ Katznelson & Katznelson (2008) p. 52, § 2.5.1
- ^ Valenza (1993) p. 71, § 4.3
- ^ Halmos (1974) p. 90, § 50
- ^
Wardlaw, William P. (2005), «Row Rank Equals Column Rank», Mathematics Magazine, 78 (4): 316–318, doi:10.1080/0025570X.2005.11953349, S2CID 218542661 - ^ Banerjee, Sudipto; Roy, Anindya (2014), Linear Algebra and Matrix Analysis for Statistics, Texts in Statistical Science (1st ed.), Chapman and Hall/CRC, ISBN 978-1420095388
- ^ Mirsky, Leonid (1955). An introduction to linear algebra. Dover Publications. ISBN 978-0-486-66434-7.
Sources[edit]
- Axler, Sheldon (2015). Linear Algebra Done Right. Undergraduate Texts in Mathematics (3rd ed.). Springer. ISBN 978-3-319-11079-0.
- Halmos, Paul Richard (1974) [1958]. Finite-Dimensional Vector Spaces. Undergraduate Texts in Mathematics (2nd ed.). Springer. ISBN 0-387-90093-4.
- Hefferon, Jim (2020). Linear Algebra (4th ed.). ISBN 978-1-944325-11-4.
- Katznelson, Yitzhak; Katznelson, Yonatan R. (2008). A (Terse) Introduction to Linear Algebra. American Mathematical Society. ISBN 978-0-8218-4419-9.
- Roman, Steven (2005). Advanced Linear Algebra. Undergraduate Texts in Mathematics (2nd ed.). Springer. ISBN 0-387-24766-1.
- Valenza, Robert J. (1993) [1951]. Linear Algebra: An Introduction to Abstract Mathematics. Undergraduate Texts in Mathematics (3rd ed.). Springer. ISBN 3-540-94099-5.
Further reading[edit]
- Roger A. Horn and Charles R. Johnson (1985). Matrix Analysis. ISBN 978-0-521-38632-6.
- Kaw, Autar K. Two Chapters from the book Introduction to Matrix Algebra: 1. Vectors [1] and System of Equations [2]
- Mike Brookes: Matrix Reference Manual. [3]
Содержание:
Элементарные преобразования матриц:
Рассмотрим прямоугольную матрицу:
состоящую из m строк и n столбцов. В п.3.2 отмсчалось, что каждую строку матрицы можно рассматривать как n-мсрный вектор, а каждый столбец — как m-мерный вектор. Тогда матрицу А можно записать в виде:
и, следовательно, данную матрицу можно рассматривать как систему вектор строк или вектор столбцов. Б указанных системах вектор-строк и вектор-столбцов можно выделять линейно независимые (зависимые) векторы. Тогда будем говорить, что строки (столбцы) матрицы линейно независимы (зависимы), если соответствующие им векторы независимы (зависимы).
Определения
Определение: Рангом системы строк (соответственно столбцов) матрицы А называется наибольшее число линейно независимых среди них.
Поскольку легко доказать, что ранг системы строк матрицы равен рангу системы её столбцов, то справедливо следующее
Определение: Рангом матрицы, обозначаемым r(А), называется максимальное число линейно независимых строк (столбцов) матрицы.
При транспонировании матрицы ранг её не изменяется.
Другой метод определения ранга матрицы связан с понятием определителя.
Выделим в матрице А любые k строк и k столбцов. Элементы, стоящие на их пересечении, образуют квадратную матрицу, определитель которой называется минором k-го порядка матрицы А. Ясно, что величина к должна удовлетворять двум условиям: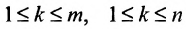
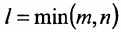
Определение: Рангом матрицы, обозначаемым r(А), называется порядок самого старшего минора этой матрицы, не равного нулю.
Из определения следует, что если ранг матрицы А равен l, то среди всех её миноров существует хотя бы один минор l-го порядка, отличный от нуля, но все миноры (l+1)-го порядков либо равны нулю, либо не могут быть составлены.
Вычисление ранга матрицы путём перебора всех её миноров весьма трудоёмко. Существует, однако, более простой способ вычисления ранга матрицы, основанный на упрощении структуры матрицы с помощью элементарных преобразований. Элементариыми преобразованиями матрицы называют следующие преобразования:
- обмен местами двух строк или двух столбцов матрицы;
- умножение всех элементов строки или столбца матрицы на произвольное число
, не равное нулю;
- прибавление ко всем элементам строки (столбца) матрицы соответствующих элементов другой строки (столбца), предварительно умноженных на одно и то же число;
- исключение из матрицы строки или столбца, состоящего из нулей.
Матрицы называются эквивалентными, если от одной из них к другой можно перейти путём конечного числа элементарных преобразований.
Ступенчатой матрицей называется матрица, удовлетворяющая тому свойству, что если в какой-либо из сё строк первый отличный от нуля элемент стоит на l-м месте, то во всех следующих строках на первых l местах стоят нули:
где элементы 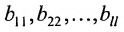
Для вычисления ранга матрицы приводят её с помощью цепочки элементарных преобразований к ступенчатому виду. Тогда ранг матрицы совпадает с числом её ненулевых диагональных элементов.
Теоремы о ранге матриц. Свойства ранга матриц
Относительно ранга матриц можно сформулировать следующие теоремы:
Теорема: Если матрица имеет минор порядка r, отличный от нуля, для которого все содержащие его миноры порядка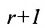
Вычисление ранга матрицы при помощи метода окаймления нужно вести от низших порядков к высшим. Сначала ищем минор первого порядка (т.е. элемент матрицы) или сразу второго порядка, отличный от нуля. Затем вычисляем окаймляющие его миноры следующего порядка, пока не найдём среди них отличного от нуля и т.д., пока не найдем минор порядка l, отличный от нуля, для которого либо все окаймляющие его миноры порядка l+1 равны нулю, либо такие миноры не могут быть составлены.
Теорема: Элементарные преобразования не меняют ранга матрицы.
Доказательство теоремы следует из определения ранга матрицы и свойств определителей.
Пример:
Найти ранг матрицы:
Решение:
Минор первого порядка в левом верхнем углу равен 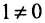
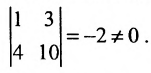
Значит ранг матрицы равен 2.
Пример:
Найти ранг матрицы:
Решение:
При помощи элементарных преобразований приведём данную матрицу к ступенчатому виду. На первом шаге умножим последовательно первую строку на 3, 3, 2 и вычтем из второй, третьей, четвёртой строк соответственно:
В эквивалентной матрице прибавим к третьей строке вторую и вычтем вторую из четвёртой строки:
(поменяем местами третью и четвертую строки)
(поменяем местами третий, четвёртый и пятый столбцы со вторым и опустим строки, состоящие из нулей) 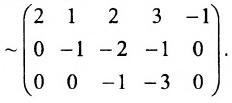
Отмстим некоторые свойства ранга матриц.
- Ранг суммы двух (или нескольких) матриц не больше суммы их рангов.
- Любую матрицу ранга r можно представить в виде суммы r матриц ранга 1, но нельзя представить в виде суммы менее чем r таких матриц.
- Любую матрицу С ранга r можно представить в виде произведения
, где А состоит из r линейно независимых столбцов, г B -из r линейно независимых строк.
- Ранг произведения матриц порядка n удовлетворяет неравенству
.
Определение системы m линейных уравнений с n неизвестными
Системой m линейных уравнений с n неизвестными 
Числа 
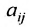
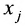
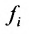
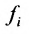
С помощью знака суммирования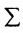
Матрица
составленная из коэффициентов системы 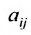
системы. Если к этой матрице добавить столбец свободных членов, то получим расширенную матрицу системы: 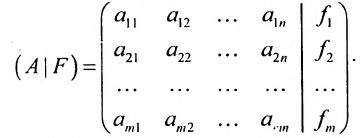
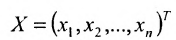
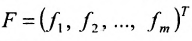

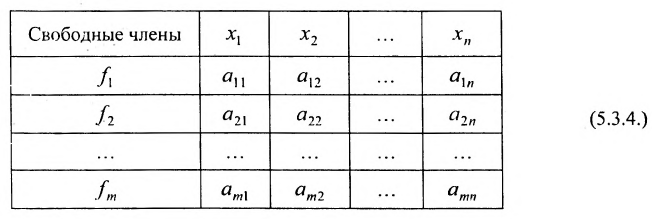
Используется также табличная форма записи системы (5.3.1):
Отметим, что (5.3.1), (5.3.2), (5.3.3), (5.3.4)- различные виды записи одной и той же системы линейных уравнений.
Решением системы (5.3.1) называется любой упорядоченный набор действительных чисел 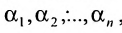
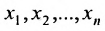
Система уравнений (5.3.1) называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет решений. Совместная система уравнений называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.
Две системы уравнений с одинаковыми наборами неизвестных 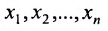
Отмстим, что для любой системы (5.3.1) возможны только три случая:
- система (5.3.1) имеет единственное решение;
- система (5.3.1) имеет бесчисленное множество решений;
- система (5.3.1) несовместна.
Множество всех решений системы (5.3.1) называется ее общим решением.
Решить систему (5.3.1) — значит найти ее общее решение.
Пример:
Пусть задана система
Тогда эту систему можно записать в матричном виде:
или в виде таблицы:
Система определенная, так как она имеет единственное решение 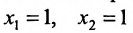
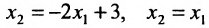
Экономические задачи, приводящие к системе линейных уравнений
Предположим, что производственные мощности для изготовления n различных видов продукции установлены в т цехах. Пусть 
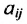
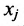
Широкий круг задач экономики приводит к составлению системы уравнений. Так в примере 4.3.2 составлялась система линейных уравнений (4.3.1) балансовой модели для трёх отраслей. В общем случае под балансовой моделью понимается система уравнений, каэ/сдое из которых выражает требование баланса между производимым количеством продукции и совокупной потребностью в этой продукции.
При построении балансовых моделей используется понятие чистой (или технологической) отрасли, т.е. условной отрасли, объединяющей всё производство данного продукта независимо от ведомственной (административной) подчинённости и форм собственности предприятий и фирм. Всё народное хозяйство представляется в виде совокупности п отраслей, каждая из которых рассматривается как производящая и как потребляющая.
Если обозначить через:
то систему уравнений баланса можно записать в виде:
или в матричной форме:
где Х- вектор-столбец валовой продукции; Y- вектор-столбец конечной продукции; А — матрица коэффициентов прямых затрат.
Основу экономико-математической модели межотраслевого баланса составляет технологическая матрица А, содержащая коэффициенты прямых затрат на производство единицы продукции:
Коэффициент!,! прямых затрат являются довольно стабильной величиной во времени.
Переписав матричное уравнение (5.4.2) в виде EX-AX = Y или (E-A)X = Y, (5.4.3) получим стандартную форму записи системы уравнений.
Определение ранга матрицы
Рассмотрим прямоугольную матрицу (4.1). Если в этой матрице выделить произвольно 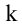
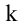
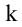
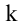
Очевидно, что выполняется соотношение
Ранг матрицы находится либо методом окаймления миноров, либо методом элементарных преобразований. При вычислении ранга матрицы первым способом следует переходить от миноров низших порядков к минорам более высокого порядка. Если уже найден минор D 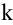
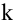
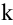
Элементарными называются следующие преобразования матрицы:
- перестановка двух любых строк (или столбцов),
- умножение строки (или столбца) на отличное от нуля число,
- прибавление к одной строке (или столбцу) другой строки (или столбца), умноженной на некоторое число.
Две матрицы называются эквивалентными, если одна из них получается из другой с помощью конечного множества элементарных преобразований.
Эквивалентные матрицы не являются, вообще говоря, равными, но их ранги равны. Если матрицы А и В эквивалентны, то это записывается так: А ~ В.
Канонической матрицей называется матрица, у которой в начале главной диагонали стоят подряд несколько единиц (число которых может равняться нулю), а все остальные элементы
равны нулю, например,
При помощи элементарных преобразований строк и столбцов любую матрицу можно привести к канонической. Ранг канонической матрицы равен числу единиц на ее главной диагонали.
- Заказать решение задач по высшей математике
Пример:
Найти методом окаймления миноров ранг матрицы
Решение:
Начинаем с миноров 1-го порядка, т.е. с элементов матрицы А. Выберем, например, минор (элемент) 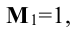
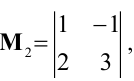
Переходим теперь к минорам 3-го порядка, окаймляющим 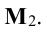
Таким образом, асе окаймляющие миноры третьего порядка оказались равными нулю. Ранг матрицы А равен двум.
Пример:
Найти ранг матрицы 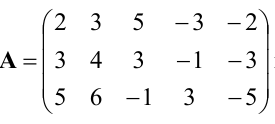
Решение:
Из второй строки вычтем первую и переставим эти строки:
Теперь из второй и третьей строк вычтем первую, умноженную соответственно на 2 и 5:
из третьей строки вычтем первую; получим матрицу 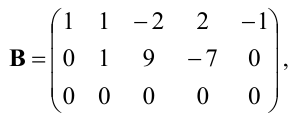
Вычисление ранга матрицы
Для исследования разрешимости систем линейных уравнений важную роль играет понятие ранга матрицы. Рассмотрим прямоугольную матрицу А
Выделим k произвольных строк и k произвольных столбцов этой матрицы. Определитель k-го порядка, составленный из элементов матрицы А, расположенных на пересечении выделенных строк и столбцов, называется минором k-го порядка матрицы А.
Рангом матрицы А называется наибольший порядок ее миноров, отличных от нуля. Обозначение: rank А,
Базисным минором матрицы называется всякий отличный от нуля ее минор, порядок которого равен рангу матрицы.
Рассмотрим некоторые методы вычисления ранга матрицы.
Метод окаймляющих миноров
Минор порядка k+1, содержащий в себе минор порядка k, называется окаймляющим минором.
Вычисляя ранг матрицы, удобнее переходить от миноров меньших порядков к минорам больших порядков. Если найден минор k-го порядка, отличный от нуля, а все окаймляющие его миноры порядка k+1 равны нулю, то ранг матрицы равен k.
- Определители второго и третьего порядков и их свойства
- Метод Гаусса — определение и вычисление
- Прямая линия на плоскости и в пространстве
- Плоскость в трехмерном пространстве
- Кратный интеграл
- Ряды в математике
- Дифференциальные уравнения с примерами
- Обратная матрица — определение и нахождение
Ранг матрицы.
Определение.
Рангом системы строк (столбцов) называется максимальное количество линейно независимых строк (столбцов) этой системы.
Теорема.
Ранг системы строк матрицы равен её рангу системы столбцов.
Определение.
Рангом матрицы A называется ранг её системы строк или столбцов.
Обычно ранг матрицы A обозначается rank(A) или rang(A)
Свойства матрицы связанные с рангом
Методы вычисления ранга матрицы
Метод элементарных преобразований
Используя свойства матрицы связанные с ее рангом, получен метод расчета ранга наиболее часто использующийся на практике.
Метод 1.
Ранг матрицы равен количеству ненулевых строк после приведения матрицы к ступенчатому виду, используя элементарные преобразования над строками и столбцами матрицы.
Метод окаймления миноров
Теорема.
Ранг матрицы равен наибольшему порядку не равного нулю минора.
Метод 2.
Если в матрице A найден ненулевой минор k-го порядка M. Рассмотрим все миноры (k + 1)-го порядка, включающие в себя (окаймляющие) минор M; если все они равны нулю, то ранг матрицы равен k. Если среди окаймляющих миноров найдется ненулевой, то вся процедура повторяется.
Пример.
Вычислить ранг матрицы A, где
| A = | 4 | 2 | 0 | 1 | ||
| 2 | 1 | 2 | 3 | |||
| 0 | 3 | 10 | 1 | |||
| 4 | 2 | 4 | 6 |
Решение:
От 1-ой строки отнимем 2-ую умноженную на 2, от 4-той отнимем 2-ую умноженную на 2
| 4 | 2 | 0 | 1 | ~ | 0 | 0 | -4 | -5 | ~ | ||||
| 2 | 1 | 2 | 3 | 2 | 1 | 2 | 3 | ||||||
| 0 | 3 | 10 | 1 | 0 | 3 | 10 | 1 | ||||||
| 4 | 2 | 4 | 6 | 0 | 0 | 0 | 0 |
Поменяем местами строки
| ~ | 2 | 1 | 2 | 3 | ||
| 0 | 3 | 10 | 1 | |||
| 0 | 0 | -4 | -5 | |||
| 0 | 0 | 0 | 0 |
полученная матрица есть является ступенчатой, значит rank(A) = 3.
Ответ: rank(A) = 3.
Нахождение ранга матрицы — примеры решения
Содержание:
- Что такое ранг матрицы — понятие, для чего используется
-
Как определить ранг матрицы, примеры
- Нахождение ранга матрицы по определению
- Нахождение ранга матрицы методом окаймляющих миноров
- Отыскание ранга матрицы способом элементарных преобразований (методом Гаусса)
Что такое ранг матрицы — понятие, для чего используется
Возьмем случайную матрицу (underset{mtimes n}A) и натуральное число k, меньшее или равное числам m и n. Вычеркивая в ней произвольным образом (m — k) строк и (n — k) столбцов, мы получим квадратные подматрицы меньше размера исходной, k-го порядка. Определители таких подматриц будут минорами k-го порядка матрицы (underset{mtimes n}A.)
Минор k-го порядка матрицы A — это определитель k-го порядка с элементами, которые расположены на пересечении любых k строк и любых k столбцов.
Всего из матрицы (underset{mtimes n}A) получится выделить (C_m^kC_n^k) миноров k-го порядка.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Например, из (underset{3times 4}A) мы получим 12 миноров 1-го порядка, 18 — 2-го и 4 — 3-го.
Если среди матричных элементов (a_{ij}) (i = 1, 2 … m; j = 1, 2 … n) есть отличные от нуля, то существует натуральное число r, которое обладает следующими свойствами:
- У матрицы А есть ненулевой минор r-го порядка.
- Любой из миноров этой матрицы порядка r + 1 или выше будет нулевым.
Число r с такими характеристиками — ранг матрицы A.
Ранг матрицы — это наивысший порядок ее ненулевых миноров.
Устоявшегося обозначения ранга не существует, чаще всего его записывают как (r (A)) или rang A, где А — обозначение матрицы. Понятие ранга обычно используют в ситуациях, когда необходима проверка совместимости системы линейных уравнений.
В случае, когда базисный минор матрицы (underset{3times 4}A) имеет порядок r < m, то как минимум одна ее строка будет не базисной. Согласно теореме о базисном миноре, в таком случае строки рассматриваемой матрицы (underset{3times 4}A) линейно зависимы. В случае, когда r = m, все строки являются базисными и линейно независимыми.
Из этого можно сделать следующие выводы:
- Когда ранг матрицы A меньше числа ее строк, они линейно зависимы. В случае, когда он равен числу строк, все они линейно независимы.
- Всякие r + 1 строк матрицы A ранга r линейно зависимы.
- Ранг любой матрицы равняется максимальному числу ее линейно независимых строк.
Теорема 1
Максимальное число линейно независимых столбцов матрицы равно максимальному количеству ее линейно независимых строк и равно ее рангу.
Следствие
Ранг не меняется при транспонировании.
Как определить ранг матрицы, примеры
Нахождение ранга матрицы по определению
Определить ранг можно, перебрав все миноры.
Теорема 2
Если из элементов матрицы можно составить ненулевой минор n-го порядка, то ранг равен n.
С учетом данной теоремы перебор производится по следующему алгоритму:
- Перебрать миноры 1-го порядка. Если наличествует хоть один ненулевой минор 1-го порядка, ранг как минимум равен 1.
- Перебрать миноры 2-го порядка. Если все они нулевые, ранг — единичный. В противном случае переходим к пункту 3.
- Перебрать миноры 3-го порядка. Если все они нулевые, ранг — два. В противном случае переходим к минорам 4-го, 5-го порядков и т. д.
Нахождение ранга матрицы методом окаймляющих миноров
Этот метод дает возможность сократить вычисления.
Окаймляющий минор — минор (n+1)-го порядка матрицы А. Он окаймляет минор n-го порядка, если матрица, соответствующая минору (n+1)-го порядка, содержит матрицу, которая соответствует упомянутому минору n-го порядка. Таким образом, чтобы получить окаймляемый минор, надо взять окаймляющий его и вычеркнуть одну строку и один столбец.
Пример № 1
Вычислить ранг матрицы
(begin{pmatrix}2&3&7&11\1&2&4&7\5&0&10&5end{pmatrix}.)
Решение:
В матрице есть элементы, отличные от нуля, значит, ее ранг больше единицы.
(М_2;=;begin{pmatrix}2&3\1&2end{pmatrix};=;4;-;3;=;1; neq 0. )
Раз ранг больше двух, нужно рассмотреть миноры 3-го порядка, содержащие вышеприведенный минор (М_2.)
(М_3;=;begin{pmatrix}2&3&7\1&2&4\5&0&10end{pmatrix};=;5;times;begin{pmatrix}3&7\2&4end{pmatrix};+;10;times;begin{pmatrix}2&3\1&2end{pmatrix}=;5;times;(12;-;14);+;10;times;(4;-;3);=;-;10;+;10;=;0.)
(М_3;=;begin{pmatrix}2&3&11\1&2&7\5&0&5end{pmatrix};=;5;times;begin{pmatrix}3&11\2&7end{pmatrix};+;5;times;begin{pmatrix}2&3\1&2end{pmatrix}=;5;times;(21;-;22);+;5;times;(4;-;3);=;-;5;+;5;=;0.)
Как мы видим, все миноры 3-го порядка нулевые, значит, наибольший ненулевой минор относится ко 2-му порядку.
Ответ: 2.
Отыскание ранга матрицы способом элементарных преобразований (методом Гаусса)
В большинстве случаев нахождение ранга перебором миноров требует долгих вычислений. Более простой способ решения этой задачи базируется на элементарных преобразованиях по методу Гаусса, сохраняющих ранг исходной матрицы A и приводящих ее к ступенчатому виду. К таким преобразованиям относятся:
- Вычеркивание нулевой строки или столбца. Нулевая строка не может быть базисной строкой, ведь в таком случае базисные строки были бы линейно зависимы, а это противоречит теореме о базисном миноре.
- Перестановка двух строк между собой. Другие строки в этом случае не меняются. Это утверждение непосредственно следует из теоремы о базисном миноре, согласно которой ранг равняется максимальному числу линейно независимых строк.
- Умножение любой строки на число( lambda neq 0).
- Вычеркивание строки, которая является линейной комбинацией других строк.
- Прибавление к одной строке другой строки, умноженной на число (lambda neq 0).
- Транспонирование.
Проведем подробный разбор пункта 5. Представим, что к q-й строке прибавлена p-я строка, умноженная на (lambda neq 0). В итоге появится новая матрица A′. Если q-я и p-я строки — базисные, это преобразование не изменит значения базисного минора. В случае, когда только p-я строка — базисная, q-я строка является их линейной комбинацией. Умножение на (lambda) это не изменит, и такую строку допустимо удалить при преобразовании.
Если q-я строка — базисная, а p-я — нет, то после преобразования (r_{q} rightarrow r_{q} + lambda r_{p}) базисный минор (triangle_{r}) перейдет в минор (triangle’_{r}) матрицы A′, который отличается от (triangle_{r}) тем, что вместо элементов строки (r_{q}) содержит элементы строки( r_{q} + lambda r_{p}). Согласно теореме о линейности, (triangle’_r=triangle_r+lambda;triangle_r^{(1)}.)
Определитель r-го порядка (triangle_r^{(1)}) в этом выражении отличается от (triangle_r) тем, что вместо элементов q-й строки содержит соответствующие элементы строки( r_{p}.)
Так как p-я строка — не базисная, она может быть представлена в виде линейной комбинации r базисных строк, то (triangle_r^{(1)} = 0) и (triangle_r^{(1)} = triangle_r.)
Как мы видим, при преобразовании( r_{q} rightarrow r_{q} + lambda r_{p}) базисный минор ни при каких условиях не изменяется. Из этого делаем вывод, что r (A) = r (A′).
Примечание
Матрицы A и B эквивалентны по рангу и обозначаются A ∼ B в том случае, когда B можно получить из A путем элементарных преобразований, перечисленных выше.
Пример № 2
Вычислить ранг матрицы
(В;=;begin{pmatrix}4&0&-1\0&2&4\4&4&1end{pmatrix}.)
Решение:
Прибавим первую строку матрицы B, умноженную на -1, к ее третьей строке. После произведения необходимых расчетов получим:
(В;sim;begin{pmatrix}4&0&-1\0&2&4\0&4&2end{pmatrix}.)
Умножим вторую строку получившейся матрицы на -2 и прибавим результат умножения к третьей строке:
(В;sim;begin{pmatrix}4&0&-1\0&2&4\0&0&-6end{pmatrix}.)
Итак, исходная матрица 3-го порядка является невырожденной, поскольку ее определитель равен
(4 times 2 times (-6) = -48 neq 0.)
Ответ: 3.




























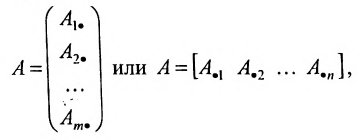
 , не равное нулю;
, не равное нулю;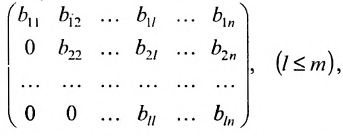
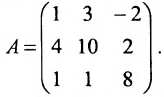
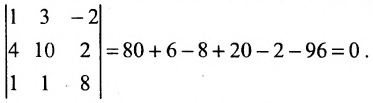

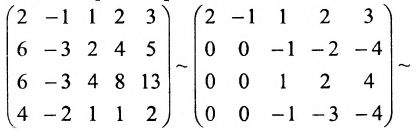


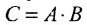 , где А состоит из r линейно независимых столбцов, г B -из r линейно независимых строк.
, где А состоит из r линейно независимых столбцов, г B -из r линейно независимых строк.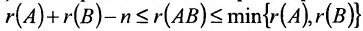 .
.