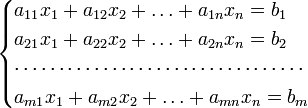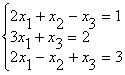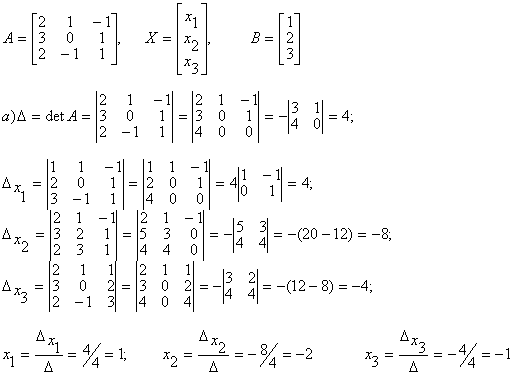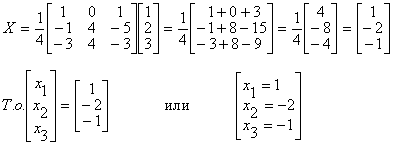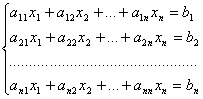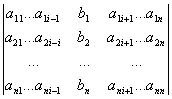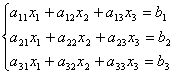Как пишется расширенная матрица - Правописание и грамматика

Система линейных алгебраических уравнений

В данной публикации мы рассмотрим определение системы линейных алгебраических уравнений (СЛАУ), как она выглядит, какие виды бывают, а также как ее представить в матричной форме, в том числе расширенной.

Определение системы линейных уравнений

Система линейных алгебраических уравнений (или сокращенно “СЛАУ”) – это система, которая в общем виде выглядит так:

Индексы коэффициентов ( a_ij ) формируются следующим образом:

i – номер линейного уравнения;
j – номер переменной, к которой относится коэффициент.

Решение СЛАУ – такие числа c₁, c₂,…, c_n , при постановке которых вместо x₁, x₂,…, x_n , все уравнения системы превратятся в тождества.

Виды СЛАУ

Однородная – все свободные члены системы равны нулю ( b₁ = b₂ = … = b_m = 0 ).

В зависимости от количества решений, СЛАУ может быть:

Совместная – имеет хотя бы одно решение. При этом если оно единственное, система называется определенной, если решений несколько – неопределенной.

СЛАУ выше является совместной, т.к. есть хотя бы одно решение: , y = 3 .
Несовместная – система не имеет решений.

Правые части уравнений одинаковые, а левые – нет. Таким образом, решений нет.

Матричная форма записи системы

СЛАУ можно представить в матричной форме:

Пример
Представим систему уравнений ниже в матричном виде:

Пользуясь формами выше, составляем основную матрицу с коэффициентами, столбцы с неизвестными и свободными членами.

Полная запись заданной системы уравнений в матричном виде:

Расширенная матрица СЛАУ

Если к матрице системы A добавить справа столбец свободных членов B , разделив данные вертикальной чертой, то получится расширенная матрица СЛАУ.

Для примера выше получается так:

– обозначение расширенной матрицы.

Расширенная матрица

Расширенная матрица представляет собой краткое обозначение системы линейных алгебраических уравнений (SLAE).

Пусть множество SLAU

Матрица А, составленная из коэффициентов для неизвестных ,называется главной матрицей системы или матрицы системы:

Матрица , полученная из основной матрицы, путем добавления столбца свободных членов вправо, называется расширенной матрицей SLAE:

Примеры решения задач с расширенными матрицами

Выписать основные и расширенные матрицы следующей системы линейных уравнений

Мы составляем основную матрицу коэффициентов с неизвестными

Добавив столбец свободных членов справа от основной матрицы, получим расширенную матрицу:

Методы решения систем линейных алгебраических уравнений (СЛАУ) с примерами

Содержание:

Методы решения систем линейных алгебраических уравнений (СЛАУ)

Метод Крамера

Определение: Системой линейных алгебраических уравнений (СЛАУ) называется выражение

Определение: Определитель, составленный из коэффициентов при неизвестных, называется главным определителем системы

Крамер предложил следующий метод решения СЛАУ: умножим главный определитель на для этого умножим все элементы первого столбца на эту неизвестную:

Второй столбец умножим на третий столбец — на -ый столбец — на и все эти произведения прибавим к первому столбцу, при этом произведение не изменится:

Согласно записи СЛАУ первый столбец получившегося определителя представляет собой столбец свободных коэффициентов, т.е.

Определение: Определитель называется первым вспомогательным определителем СЛАУ.

Поступая аналогично тому, как описано выше, найдем все вспомогательные определители СЛАУ:

31. Для того чтобы найти вспомогательный определитель i, надо в главном определителе СЛАУ заменить столбец i на столбец свободных коэффициентов.

Определение: Полученные выше соотношения называются формулами Крамера. Используя формулы Крамера, находят неизвестные величины Проанализируем полученные формулы:

Пример:

Решить СЛАУ методом Крамера

Решение:

Прежде всего, обращаем внимание на то, что в последнем уравнении переменные записаны в неправильном порядке, в этом случае говорят, что СЛАУ записана в ненормализованном виде. Нормализуем СЛАУ, для чего запишем неизвестные в последнем уравнении системы в правильном порядке, чтобы одноименные неизвестные были записаны друг под другом

Найдем главный определитель СЛАУ (раскрываем по первой строке)

Так как главный определитель системы отличен от нуля, то СЛАУ имеет единственное решение. Найдем три вспомогательных определителя

Воспользуемся формулами Крамера

Замечание: После нахождения решения СЛАУ надо обязательно провести проверку, для чего найденные числовые значения неизвестных подставляется в нормализованную систему линейных алгебраических уравнений.

Выполним проверку Отсюда видно, что СЛАУ решена верно.

Матричный способ решения СЛАУ

Для решения СЛАУ матричным способом введем в рассмотрение матрицу, составленную из коэффициентов при неизвестных матpицы-столбцы неизвестных и свободных коэффициентов

Тогда СЛАУ можно записать в матричном виде Матричный способ решения СЛАУ состоит в следующем: умножим слева матричное уравнение на обратную матрицу к матрице А, получим в силу того, что произведение найдем Таким образом, для нахождения неизвестных матричным способом, надо найти обратную к А матрицу после чего надо умножить эту матрицу на матрицу-столбец свободных коэффициентов.

Пример:

Решить СЛАУ матричным способом

Решение:

Введем в рассмотрение следующие матрицы

Найдем матрицу (см. Лекцию № 2): найдем детерминант матрицы А.

Пример:

Решение:

Найдем алгебраические дополнения всех элементов Запишем обратную матрицу (в правильности нахождения обратной матрицы убедиться самостоятельно). Подействуем пай денной матрицей на матрицу-столбец свободных коэффициентов В:

Отсюда находим, что х = 1; y = l; z = l.

Метод Гаусса

Метод Гаусса или метод исключения неизвестных состоит в том, чтобы за счет элементарных преобразований привести СЛАУ к треугольному виду. Покажем использование расширенной матрицы, составленной из коэффициентов при неизвестных и расширенной за счет столбца свободных коэффициентов, для приведения СЛАУ к треугольному виду на примере системы, рассматриваемой в этой лекции. Расширенная матрица для СЛАУ имеет вид:

Замечание: В методе Гаусса желательно, чтобы первая строка расширенной матрицы начиналась с единицы.

Обменяем в расширенной матрице первую и вторую строки местами, получим Приведем матрицу к треугольному виду, выполнив следующие преобразования: умножим элементы первой строки на (-2) и прибавим к соответствующим элементам второй строки Разделим все элементы второй строки на (-5), получим эквивалентную матрицу

Умножим элементы первой строки на (—1) и прибавим к соответствующим элементам третьей строки Разделим все элементы третьей строки на (-3), получим Таким образом, эквивалентная СЛАУ имеет вид (напомним, что первый столбец это коэффициенты при неизвестной х, второй — при неизвестной у, третий — при неизвестной z, а за вертикальной чертой находится столбец свободных коэффициентов):

Из первого уравнения находим, что х = 1.

Вывод: Из вышеизложенного материала следует, что вне зависимости от

способа решения СЛАУ всегда должен получаться один и тот же ответ.

Замечание: После нахождения решения СЛАУ надо обязательно выполнить проверку, то есть подставить полученные значения неизвестных в заданную СЛАУ и убедиться в тождественности левой части всех равенств системы соответствующим правым частям. Отметим, что задание СЛАУ всегда верно, то есть, если проверка показывает нарушение оговоренной тождественности, то надо искать ошибку в проведенных вычислениях.

Ранг матрицы. Теорема Кронекера-Капелли

Определение: Рангом матрицы называется наивысший порядок отличного от нуля минора этой матрицы.

Если то среди всевозможных миноров этой матрицы есть хотя бы один минор порядка r, который отличен от нулю, а все миноры порядков больших, чем r, равны нулю.

При вычислении ранга необходимо начинать вычислять миноры 2 порядка, затем миноры 3 порядка и так далее, пока не будут найдены миноры, обращающиеся в нуль. Если все миноры порядка p равны нулю, то и все миноры, порядок которых больше p, равны нулю.

Пример:

Найти ранг матрицы

Решение:

Очевидно, что среди миноров второго порядка есть миноры отличные от нуля, например, среди миноров третьего порядка также есть миноры, которые не равны нулю, например, Очевидно, что определитель четвертого порядка равен нулю, так как он будет содержать строку, состоящую из одних нулей (см. свойство для определителей). Следовательно, ранг матрицы А равен 3.

Теорема Кронекера-Капелли (критерий совместности СЛАУ). Для совместности системы линейных алгебраических уравнений (СЛАУ) необходимо и достаточно, чтобы ранг расширенной матрицы совпадал с рангом основной матрицы, составленной из коэффициентов при неизвестных величинах.

Следствия из теоремы Кронекера — Капелли

Следствие: Если ранг матрицы совместной системы равен числу неизвестных, то система имеет единственное решение (то есть она определенная).

Следствие: Если ранг матрицы совместной системы меньше числа неизвестных, то система имеет бесчисленное множество решений (т.е. она неопределенная).

В случае неопределенной системы решения ищут следующим образом: выбираются главные неизвестные, число которых равно рангу, а остальные неизвестные считаются свободными; далее главные неизвестные выражаются через свободные и получают множество решений, зависящих от свободных неизвестных. Это множество решений называется общим решением системы. Придавая свободным неизвестным различные произвольные значения, получим бесчисленное множество решений, каждое из которых называется частным решением системы.

Рекомендую подробно изучить предметы:

Математика
Алгебра
Линейная алгебра
Векторная алгебра
Высшая математика
Дискретная математика
Математический анализ
Математическая логика

Ещё лекции с примерами решения и объяснением:

Скалярное произведение и его свойства
Векторное и смешанное произведения векторов
Преобразования декартовой системы координат
Бесконечно малые и бесконечно большие функции
Критерий совместности Кронекера-Капелли
Формулы Крамера
Матричный метод
Экстремум функции

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

источники:

http://www.homework.ru/spravochnik/rasshirennaya-matrica/

http://www.evkova.org/metodyi-resheniya-sistem-linejnyih-algebraicheskih-uravnenij-slau

Источник

Расширенная матрица

ОПРЕДЕЛЕНИЕ

Расширенная матрица представляет собой краткое обозначение системы линейных алгебраических уравнений (SLAE).

Пусть множество SLAU

Примеры решения задач с расширенными матрицами

ПРИМЕР 1

Задача

Выписать основные и расширенные матрицы следующей системы линейных уравнений

Решение.

Мы составляем основную матрицу коэффициентов с неизвестными

Добавив столбец свободных членов справа от основной матрицы, получим расширенную матрицу:

Ответ

Источник

Основная
матрица — это матрица, составленная из
соответствующих чисел по левую сторону
уравнений при неизвестных. В
расширенную матрицу входят и числа с
правой стороны.

Матричный
способ записи:

Систему
из m уравнений
с n неизвестными

можно
представить в матричном виде

и
тогда всю систему можно записать так:

AX = B,
где A имеет
смысл таблицы коэффициентов a_ij системы
уравнений.

3) Теоорема о решении невыражденной слау методом обратной матрицы (с доказательством).

Если
матрица СЛАУ невырожденная, то решение
СЛАУ может

быть
найдено по формуле: X
= A^-1B

где
матрица А^-1
вычисляется по формуле:
,
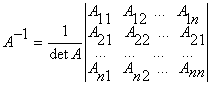
либо методом элементарных преобразований.

Пример.
Решить СЛАУ

а)
по формулам Крамера;

б)
методом обратной матрицы

Запишем
матрицу системы А,
матрицу-столбец неизвестных X и

матрицу-столбец
свободных членoв Х
:

б)Воспользуемся
формулой Х
=А^-1В,
где матрица A^-1
вычислена

2)
Предположим, что матрица СЛАУ имеет
размерность m*n. В этом случае СЛАУ

имеет
вид

a₁₁x₁+a₁₂x₂+…+a₁_nx_n=b₁

a₂₁x₁+a₂₂x₂+…+a₂_nx_n=b₂

…
… … …

a_m1x₁+a_m2x₂+…+a_m_nx_n=b_m

Запишем
расширенную матрицу системы А.

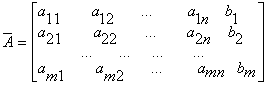
4) Теорема Крамера (с доказательством).

Теорема.
Система
из n
уравнений с n
неизвестными

в
случае, если определитель матрицы
системы не равен нулю, имеет единственное
решение и это решение находится по
формулам:

x_i
= D_i/D,
где

D
= det
A,
а D_i
– определитель матрицы, получаемой из
матрицы системы заменой столбца i
столбцом свободных членов b_i.

D_i
=

Пример.

A
= ;
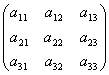
D₁=
;
D₂=
;
D₃=
;

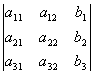
x₁
= D₁/detA;
x₂
= D₂/detA;
x₃
= D₃/detA;

5)
Решение невырожденных СЛАУ методом
Гауса: эквивалентные (элементарные)
преобразования матриц, начальный и
конечный вид расширенной матрицы
системы, прямой и обратный ход, как по
конечному виду расширенной матрицы
определить решение.

Пусть
исходная система выглядит следующим
образом

Матрица
A
называется основной матрицей системы,
b —
столбцом свободных членов.

Тогда
согласно свойству элементарных
преобразований
над строками основную матрицу этой
системы можно привести к ступенчатому
виду(эти же преобразования нужно
применять к столбцу свободных членов):

При
этом будем считать, что базисный
минор
(ненулевой минор
максимального порядка) основной матрицы
находится в верхнем левом углу, то есть
в него входят только коэффициенты при
переменных
^[3].

Тогда
переменные
называются
главными
переменными.
Все остальные называются свободными.

Если
хотя бы одно число
,
где i
> r,
то рассматриваемая система несовместна.

Пусть

для
любых i
> r.

Перенесём
свободные переменные за знаки равенств
и поделим каждое из уравнений системы
на свой коэффициент при самом левом

(,
где
—
номер строки):

,
где

Если
свободным переменным системы (2) придавать
все возможные значения и решать новую
систему относительно главных неизвестных
снизу вверх (то есть от нижнего уравнения
к верхнему), то мы получим все решения
этой СЛАУ.
Так как эта система получена путём
элементарных
преобразований
над исходной системой (1), то по теореме
об эквивалентности при элементарных
преобразованиях системы (1) и (2)
эквивалентны, то есть множества их
решений совпадают.

Следствия:1:
Если в совместной системе все переменные
главные, то такая система является
определённой.

2:
Если количество переменных в системе
превосходит число уравнений, то такая
система является либо неопределённой,
либо несовместной

Алгоритм
решения СЛАУ
методом Гаусса подразделяется на два
этапа.

На
первом этапе осуществляется так
называемый прямой ход, когда путём
элементарных
преобразований
над строками систему приводят к
ступенчатой или треугольной
форме,
либо устанавливают, что система
несовместна. А именно, среди элементов
первого столбца матрицы выбирают
ненулевой, перемещают его на крайнее
верхнее положение перестановкой строк
и вычитают получившуюся после перестановки
первую строку из остальных строк,
домножив её на величину, равную отношению
первого элемента каждой из этих строк
к первому элементу первой строки, обнуляя
тем самым столбец под ним. После того,
как указанные преобразования были
совершены, первую строку и первый столбец
мысленно вычёркивают и продолжают пока
не останется матрица нулевого размера.
Если на какой-то из итераций среди
элементов первого столбца не нашёлся
ненулевой, то переходят к следующему
столбцу и проделывают аналогичную
операцию.

На
втором этапе осуществляется так
называемый обратный ход, суть которого
заключается в том, чтобы выразить все
получившиеся базисные переменные через
небазисные и построить фундаментальную
систему решений,
либо, если все переменные являются
базисными, то выразить в численном виде
единственное решение системы линейных
уравнений. Эта процедура начинается с
последнего уравнения, из которого
выражают соответствующую базисную
переменную (а она там всего одна) и
подставляют в предыдущие уравнения, и
так далее, поднимаясь по «ступенькам»
наверх. Каждой строчке соответствует
ровно одна базисная переменная, поэтому
на каждом шаге, кроме последнего (самого
верхнего), ситуация в точности повторяет
случай последней строки.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Расширенная матрица

Из Википедии, бесплатной энциклопедии

Перейти к навигации
Перейти к поиску

В линейной алгебре , расширенная матрица представляет собой матрица , полученная путем добавления столбцов двух заданных матриц, как правило , с целью выполнения тех же операций элементарно строк на каждом из заданных матриц.

Для матриц A и B , где

расширенная матрица ( A | B ) записывается как

Это полезно при решении систем линейных уравнений .

Для заданного количества неизвестных количество решений системы линейных уравнений зависит только от ранга матрицы, представляющей систему, и ранга соответствующей расширенной матрицы. В частности, согласно теореме Руше – Капелли , любая система линейных уравнений несовместима (не имеет решений), если ранг расширенной матрицы больше, чем ранг матрицы коэффициентов ; если, с другой стороны, ранги этих двух матриц равны, система должна иметь хотя бы одно решение. Решение уникально тогда и только тогда, когда ранг равен количеству переменных. В противном случае общее решение имеет k свободных параметров, где k— разница между количеством переменных и рангом; следовательно, в таком случае решений бесконечно много.

Расширенная матрица также может использоваться, чтобы найти обратную матрицу, комбинируя ее с единичной матрицей .

Чтобы найти обратную матрицу

Пусть C — квадратная матрица 2 × 2.

Чтобы найти обратное к C, мы создаем ( C | I ), где I — единичная матрица 2 × 2 . Затем мы уменьшаем часть ( C | I ), соответствующую C, до единичной матрицы, используя только элементарные операции со строками на ( C | I ).

правая часть которой является обратной по отношению к исходной матрице.

Существование и количество решений

Рассмотрим систему уравнений

Матрица коэффициентов:

а расширенная матрица

Поскольку оба они имеют одинаковый ранг, а именно 2, существует по крайней мере одно решение; и поскольку их ранг меньше, чем количество неизвестных, последнее равно 3, существует бесконечное количество решений.

Напротив, рассмотрим систему

Матрица коэффициентов:

а расширенная матрица

В этом примере матрица коэффициентов имеет ранг 2, а расширенная матрица — ранг 3; так что эта система уравнений не имеет решения. Действительно, увеличение количества линейно независимых строк сделало систему уравнений противоречивой .

Решение линейной системы

Как используется в линейной алгебре, расширенная матрица используется для представления коэффициентов и вектора решения каждого набора уравнений. Для системы уравнений

коэффициенты и постоянные члены дают матрицы

и, следовательно, дадим расширенную матрицу

Обратите внимание, что ранг матрицы коэффициентов, равный 3, равен рангу расширенной матрицы, поэтому существует по крайней мере одно решение; и поскольку этот ранг равен количеству неизвестных, существует ровно одно решение.

Чтобы получить решение, операции со строками могут быть выполнены над расширенной матрицей, чтобы получить единичную матрицу с левой стороны, в результате чего

поэтому решение системы ( x , y , z ) = (4, 1, -2).

Ссылки

Марвин Маркус и Хенрик Минк, Обзор теории матриц и матричных неравенств , Dover Publications , 1992, ISBN 0-486-67102-X . Стр.31.

Источник

Содержание:

Определение СЛАУ
Виды систем
Матричная запись систем уравнений
Расширенная матрица системы

Определение СЛАУ

Определение

Системой линейных алгебраических уравнений (СЛАУ) называется система вида:

$$left{begin{array}{l}
a_{11} cdot x_{1}+a_{12} cdot x_{2}+ldots+a_{1 n} cdot x_{n}=b_{1} \
a_{21} cdot x_{1}+a_{22} cdot x_{2}+ldots+a_{2 n} cdot x_{n}=b_{2} \
ldots ldots ldots ldots ldots ldots ldots ldots ldots ldots ldots ldots ldots ldots . . \
a_{m 1} cdot x_{1}+a_{m 2} cdot x_{2}+ldots+a_{m n} cdot x_{n}=b_{m}
end{array}right.$$

Упорядоченный набор значений $$left{x_{1}^{0}, x_{2}^{0}, ldots, x_{n}^{0}right}$$ называется решением системы, если при подстановке в уравнения все уравнения превращаются в тождество.

Пример

Задание. Проверить, является ли набор ${0,3}$
решением системы $left{begin{array}{l}
3 x-2 y=-6 \
5 x+y=3
end{array}right.$

Решение. Подставляем в каждое из уравнений системы
$x=0$ и $y=3$:

$$left{begin{array}{l}
3 x-2 y=-6 \
5 x+y=3
end{array}right.$$

$$5 x+y=3 Rightarrow 5 cdot 0+3=3 Rightarrow 3=3$$

Так как в результате подстановки получили верные равенства, то делаем вывод, что заданный набор является
решением указанной
СЛАУ.

Ответ. Набор ${0,3}$ является решением
системы $left{begin{array}{l}
3 x-2 y=-6 \
5 x+y=3
end{array}right.$

Виды систем

Определение

СЛАУ называется совместной, если она имеет, хотя бы одно решение.

В противном случае система называется несовместной.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Система $left{begin{array}{l}
3 x-2 y=-6 \
5 x+y=3
end{array}right.$ является совместной, так как она
имеет, по крайней мере, одно решение $x=0$, $y=3$

Пример

Система $left{begin{array}{l}
5 x+y=-6 \
5 x+y=3
end{array}right.$ является несовместной, так
как выражения, стоящие в левых частях уравнений системы равны, но правые части не равны друг другу. Ни для каких
наборов ${x,y}$ это не выполняется.

Определение

Система называется определённой, если она совместна и имеет единственное решение.

В противном случае (т.е. если система совместна и имеет более одного решения) система называется неопределённой.

Определение

Система называется однородной, если все правые части уравнений, входящих в нее, равны нулю одновременно.

Пример

$$left{begin{array}{l}
x-y+z-4 t=0 \
5 x+y+t=0
end{array}right.$$

Определение

Система называется квадратной, если количество уравнений равно количеству неизвестных.

Пример

Система $left{begin{array}{l}
3 x-2 y=-6 \
5 x+y=3
end{array}right.$ квадратная, так как неизвестных
две и это число равно количеству уравнений системы.

Матричная запись систем уравнений

Исходную СЛАУ можно записать в матричном виде:

$$A…X=B$$

где матрица $A=left(begin{array}{ccc}
a_{11} & ldots & a_{1 n} \
ldots & ldots & ldots \
a_{m 1} & ldots & a_{m n}
end{array}right)$ называется матрицей системы, это
матрица, составленная из коэффициентов при неизвестных;
$$X=left(begin{array}{c}
x_{1} \
vdots \
x_{n}
end{array}right)$$ — вектором-столбцом неизвестных,
$$B=left(begin{array}{c}
b_{1} \
vdots \
b_{n}
end{array}right)$$ — вектором-столбцом правых частей или
свободных коэффициентов.

Пример

Задание. Систему $left{begin{array}{l}
x-y+z-4 t=0 \
5 x+y+t=-11
end{array}right.$
записать в матричной форме и выписать все матрицы, которые ей соответствуют.

Решение. Заданную СЛАУ записываем в
матричной форме $A…X=B$ , где матрица системы:

$$A=left(begin{array}{rrrr}
1 & -1 & 1 & -4 \
5 & 1 & 0 & 1
end{array}right)$$

вектор-столбец неизвестных:

$$X=left(begin{array}{l}
x \
y \
z \
t
end{array}right)$$

вектор-столбец свободных коэффициентов:

$$B=left(begin{array}{c}
0 \
-11
end{array}right)$$

то есть, запись СЛАУ в матричной форме:

$$left(begin{array}{rrrr}
1 & -1 & 1 & -4 \
5 & 1 & 0 & 1
end{array}right)left(begin{array}{l}
x \
y \
z \
t
end{array}right)=left(begin{array}{c}
0 \
-11
end{array}right)$$

Расширенная матрица системы

Определение

Расширенной матрицей системы $widetilde{A}=(A mid B)$ называется матрица, полученная из матрицы системы $A$ , дописыванием справа после вертикальной черты столбца свободных членов.

Пример

Задание. Записать матрицу и расширенную матрицу системы
$left{begin{array}{l}
2 x_{1}+x_{2}-x_{3}=4 \
x_{1}-x_{2}=5
end{array}right.$

Решение. Матрица системы $A=left(begin{array}{rrr}
2 & 1 & -1 \
1 & -1 & 0
end{array}right)$ ,
тогда расширенная матрица $tilde{A}=(A mid B)=left(begin{array}{rrr|r}
2 & 1 & -1 & 4 \
1 & -1 & 0 & 5
end{array}right)$

Читать дальше: критерий совместности системы.

Источник

Как найти расширенную матрицу

Матрицей называют таблицу, состоящую из определенных значений и имеющую размерность в n столбцов и m строк. Система линейных алгебраических уравнений (СЛАУ) большого порядка может решаться с помощью связанных с ней матриц — матрицы системы и расширенной матрицы. Первая представляет собой массив А коэффициентов системы, стоящих при неизвестных переменных. При добавлении к данному массиву столбца-матрицы В свободных членов СЛАУ получается расширенная матрица (А|В). Построение расширенной матрицы является одним из этапов в решении произвольной системы уравнений.

Инструкция

В общем виде систему линейных алгебраических уравнений можно решить методом подстановки, но для СЛАУ большой размерности такое вычисление весьма трудоемко. И чаще в этом случае используют связанные матрицы, в том числе и расширенную.

Запишите заданную систему линейных уравнений. Проведите ее преобразование, упорядочив множители в уравнениях таким образом, чтобы одинаковые неизвестные переменные располагались в системе строго друг под другом. Свободные коэффициенты без неизвестных перенесите в другую часть уравнений. При перестановке слагаемых и переносе учитывайте их знак.

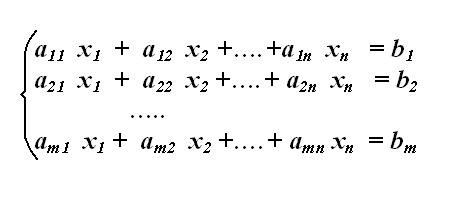
Определите матрицу системы. Для этого отдельно выпишите коэффициенты, стоящие при искомых переменных СЛАУ. Выписывать нужно в том порядке, как они расположены в системе, т.е. из первого уравнения первый коэффициент поставьте на пересечении первой строки и первого столбца матрицы. Порядок строк новой матрицы соответствует порядку уравнений системы. Если одна из неизвестных системы в данном уравнении отсутствует, значит, ее коэффициент здесь равен нулю – внесите ноль в матрицу на соответствующую позицию строки. Получаемая матрица системы должна быть квадратной (m=n).

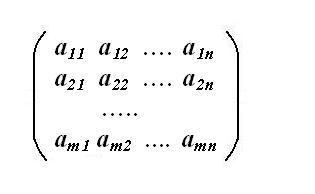
Найдите расширенную матрицу системы. Свободные коэффициенты в уравнениях системы за знаком равенства выпишите в отдельный столбец, сохраняя тот же порядок строк. В квадратной матрице системы справа от всех коэффициентов поставьте вертикальную черту. За чертой допишите полученный столбец свободных членов. Это и будет расширенная матрица исходной СЛАУ размерностью (m, n+1), где m – число строк, n – число столбцов.

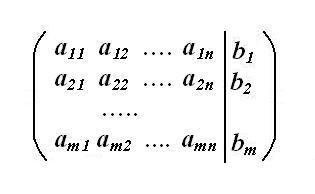
Обратите внимание

Именно по расширенной матрице согласно методу Гаусса вычисляются корни системы линейных алгебраических уравнений. Метод Гаусса является одним из наиболее активно используемых способов решения СЛАУ большого порядка.

Источники:

расширенная матрица системы

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Расширенная матрица системы линейных уравнений

Предмет
Высшая математика

Разместил

🤓 lownmarfcountreal1978

👍 Проверено Автор24

получается из основной матрицы (матрицы системы) путём добавления столбца из свободных членов

Научные статьи на тему «Расширенная матрица системы линейных уравнений»

Высшая математика 1 курс

Линейная алгебра
Матрицы и действия над ними
Рассматриваются матрицы, которые содержат m строк и n столбцов…
Ранг матрицы
Ранг матрицы рассматривается как максимальное число линейно-зависимых строк матрицы и наибольшее…
Метод Гаусса
Вводится понятие расширенной матрицы, совместной и определенной системы уравнений, равносильных…
систем уравнений, однородной системы линейных уравнений….
Правило решения системы уравнений:
Найти ранг основной ($rA$) и расширенной ($r bar{A}$):

Если $rA

Статья от экспертов

Регуляризация неустойчивых задач наименьших квадратов на основе расширенных систем

Рассматривается метод решения неустойчивых задач наименьших квадратов по приближенным данным. Метод основан на преобразовании исходной задачи наименьших квадратов к эквивалентной расширенной системе линейных уравнений с симметричной матрицей.

Решение системы уравнений методом Гаусса-Зейделя

линейных уравнений….
линейных алгебраических уравнений)….
, когда ранг матрицы и ранг расширенной матрицы, полученной добавлением «к» столбца свободных членов…
равны) или совсем не иметь решения (в случае, когда ранг матрицы и расширенной матрицы отличаются)….
Предположим, что имеется система из трех линейных уравнений.

Статья от экспертов

Метод расширенных нормальных уравнений для задач регуляризации Тихонова с дифференцирующим оператором

Рассматривается новый метод решения плохо обусловленных линейных алгебраических систем с применением дифференцирующего оператора. Такого вида задачи возникают при решении интегральных уравнений Фредгольма первого рода. Основная сложность данного метода состоит в том, что матрица дискретного аналога оператора дифференцирования является матрицей неполного ранга. Для решения подобного класса задач используются методы, основанные на обобщенном сингулярном разложении. Этот подход имеет очень высокую вычислительную сложность, а также приводит к возникновению дополнительной погрешности в вычислениях. Предложенный в данной работе метод основан на преобразовании исходной задачи регуляризации к эквивалентной расширенной регуляризованной нормальной системе уравнений с применением дискретного аналога оператора дифференцирования. Весьма актуальной является проблема исследования спектра матрицы расширенной регуляризованной нормальной системы уравнений с матрицей дискретного оператора дифференциро…

Повышай знания с онлайн-тренажером от Автор24!

Напиши термин
Выбери определение из предложенных или загрузи свое
Тренажер от Автор24 поможет тебе выучить термины с помощью удобных и приятных
карточек

Источник