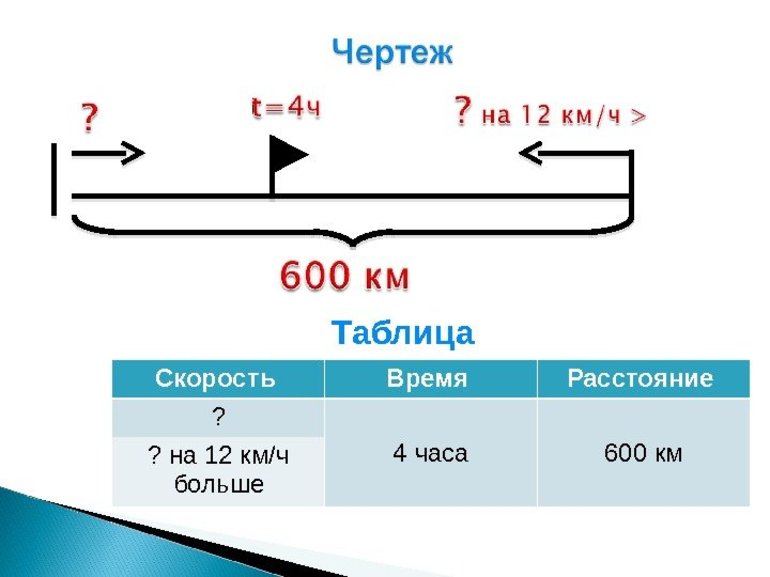
Памятка
по математике 4 класс по теме
«Скорость, время, расстояние»
S – расстояние ( путь); измеряется в км, м и т.д.
V – скорость ( это расстояние, преодолеваемое за единицу времени); измеряется в км/ч, м/ мин и т.д.
t- время; измеряется в часах, минутах и т.д.
- Чтобы найти расстояние, нужно скорость умножить на время. S =V х t
- Чтобы найти скорость, нужно расстояние разделить на время.
V = S : t
- Чтобы найти время, нужно расстояние разделить на скорость.
t = S :V
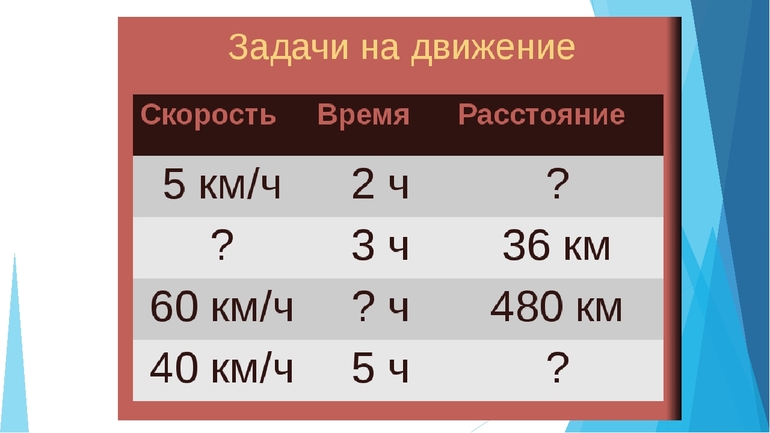
Задача на нахождение расстояния
Пешеход шёл со скоростью 5 километров в час. Какой путь он пройдёт за 3 часа?
5 х 3 = 15 ( км)
Ответ: 15 километров пройдёт пешеход.
Задача на нахождение скорости
Пешеход за 3 часа прошёл 15 километров. С какой скоростью шёл пешеход?
15 : 3 = 5 ( км/ч)
Ответ: 5 км/ ч скорость пешехода.
Задача на нахождение времени
Пешеход шёл со скоростью 5 километров в час и прошёл 15 километров. Сколько времени шёл пешеход?
15 : 5 = 3 ( ч)
Ответ: 3 часа шёл пешеход.
Загрузить PDF
Загрузить PDF
Расстояние (обозначим как d) – это длина прямой между двумя точками. Расстояние можно найти между двумя неподвижными точками, а можно найти расстояние, пройденное движущимся телом. В большинстве случаев расстояние может быть вычислено по следующим формулам: d = s × t, где d — расстояние, s – скорость, t – время; d = √((x2 — x1)2 + (y2 — y1)2, где (x1, y1) и (x2, y2) – координаты двух точек.
-
1
Чтобы вычислить расстояние, пройденное движущимся телом, вам необходимо знать скорость тела и время в пути, чтобы подставить их в формулу d = s × t.
- Пример. Автомобиль едет со скоростью 120 км/ч в течение 30 минут. Необходимо вычислить пройденное расстояние.
-
2
Перемножьте скорость и время и вы найдете пройденное расстояние.
- Обратите внимание на единицы измерения величин. Если они различны, вам необходимо конвертировать одну из них так, чтобы она соответствовала другой единице. В нашем примере скорость измеряется в километрах в час, а время – в минутах. Поэтому необходимо конвертировать минуты в часы; для этого значение времени в минутах необходимо разделить на 60 и вы получите значение времени в часах: 30/60 = 0,5 часов.
- В нашем примере: 120 км/ч х 0,5 ч = 60 км. Обратите внимание, что единица измерения «час» сокращается и остается единица измерения «км» (то есть расстояние).
-
3
Описанную формулу можно использовать для вычисления входящих в нее величин. Для этого обособьте нужную величину на одной стороне формулы и подставьте в нее значения двух других величин. Например, для вычисления скорости используйте формулу s = d/t, а для вычисления времени – t = d/s.
- Пример. Автомобиль проехал 60 км за 50 минут. В этом случае его скорость равна s = d/t = 60/50 = 1,2 км/мин.
- Обратите внимание, что результат измеряется в км/мин. Чтобы конвертировать эту единицу измерения в км/ч, умножьте результат на 60 и получите 72 км/ч.
-
4
Данная формула вычисляет среднюю скорость, то есть предполагается, что в течение всего времени в пути тело имеет постоянную (неизменную) скорость. Это годится в случае абстрактных задач и моделирования движения тел. В реальной жизни скорость тела может меняться, то есть тело может ускоряться, замедляться, останавливаться или двигаться в обратном направлении.
- В предыдущем примере мы нашли, что автомобиль, проехавший 60 км за 50 минут, ехал со скоростью 72 км/ч. Это справедливо только при условии, что с течением времени скорость автомобиля не менялась. Например, если в течение 25 минут (0,42 часов) автомобиль ехал со скорость 80 км/ч, а в течение еще 25 минут (0,42 часов) – со скоростью 64 км/час, он тоже проедет 60 км за 50 минут (80 х 0,42 + 64 х 0,42 = 60).
- Для решения задач, включающих меняющуюся скорость тела, лучше использовать производные, а не формулу для вычисления скорости по расстоянию и времени.
Реклама
-
1
Найдите две точки пространственных координат. Если вам даны две неподвижные точки, то, чтобы вычислить расстояние между этими точками, необходимо знать их координаты; в одномерном пространстве (на числовой прямой) вам понадобятся координаты x1 и x2, в двумерном пространстве – координаты (x1,y1) и (x2,y2), в трехмерном пространстве – координаты (x1,y1,z1) и (x2,y2,z2).
-
2
Вычислите расстояние в одномерном пространстве (точки лежат на одной горизонтальной прямой) по формуле: d = |x2 — x1|, то есть вы вычитаете «х» координаты, а затем находите модуль полученного значения.
- Обратите внимание, что в формулу включены скобки модуля (абсолютного значения). Модуль числа – это неотрицательное значение этого числа (то есть модуль отрицательного числа равен этому числу со знаком плюс).
- Пример. Машина находится между двумя городами. До города, который находится перед ней, 5 км, а до города за ней – 1 км. Вычислите расстояние между городами. Если взять машину за точку отсчета (за 0), то координата первого города x1 = 5, а второго x2 = -1. Расстояние между городами:
- d = |x2 — x1|
- = |-1 — 5|
- = |-6| = 6 км.
-
3
Вычислите расстояние в двумерном пространстве по формуле: d = √((x2 — x1)2 + (y2 — y1)2). То есть вы вычитаете «х» координаты, вычитаете «у» координаты, возводите полученные значения в квадрат, складываете квадраты, а затем из полученного значения извлекаете квадратный корень.
- Формула для вычисления расстояния в двумерном пространстве основана на теореме Пифагора, которая гласит, что гипотенуза прямоугольного треугольника равна квадратному корню из суммы квадратов обоих катетов.
- Пример. Найдите расстояние между двумя точками с координатами (3, -10) и (11, 7) (центр окружности и точка на окружности, соответственно).
- d = √((x2 — x1)2 + (y2 — y1)2)
- d = √((11 — 3)2 + (7 — -10)2)
- d = √(64 + 289)
- d = √(353) = 18,79
-
4
Вычислите расстояние в трехмерном пространстве по формуле: d = √((x2 — x1)2 + (y2 — y1)2 + (z2 — z1)2). Эта формула является видоизмененной формулой для вычисления расстояния в двумерном пространстве с добавлением третьей координаты «z».
- Пример. Космонавт находится в открытом космосе недалеко от двух астероидов. Первый из них расположен в 8 километрах перед космонавтом, в 2 км справа от него и в 5 км ниже него; второй астероид находится в 3 км позади космонавта, в 3 км слева от него, и в 4 км выше него. Таким образом, координаты астероидов (8,2,-5) и (-3,-3,4). Расстояние между астероидами вычисляется следующим образом:
- d = √((-3 —
2 + (-3 — 2)2 + (4 — -5)2)
- d = √((-11)2 + (-5)2 + (9)2)
- d = √(121 + 25 + 81)
- d = √(227) = 15,07 км
Реклама
Похожие статьи
Об этой статье
Эту страницу просматривали 60 513 раз.
Была ли эта статья полезной?
Содержание материала
- Формула времени. Решение задач
- Видео
- Формулы для расчета пути и времени движения при неравномерном движении тела
- Скорость
- График пути равномерного движения
- Единицы измерения времени
- Первые часы
- Как люди измеряли время?
- Способы вычисления расстояния и времени
Формула времени. Решение задач
Скорость, время и расстояние — физические величины, взаимосвязаны процессом движения. Виды движений: 1) равномерное (прямолинейное, криволинейное и по окружности), 2) равноускоренное (с постоянным ускорением), 3) гармоническое. Для каждого вида движения своя формула времени.
Время обозначается как t. Единица измерения времени – с (секунды).
Самая простая формула при равномерном прямолинейном движении. Время, необходимое для прохождения пути равняется частному от деления пути на скорость равномерного прямолинейного движения: t = S / v.
При равноускоренном движении время равняется частному от деления разницы конечной и начальной скорости на ускорение: t = (v — v) / a или частному от деления пути на разность конечной и начальной скорости: t = S / (v — v).
Видео
Формулы для расчета пути и времени движения при неравномерном движении тела
При неравномерном движении мы используем определение средней скорости, которую можем найти по формуле
$$upsilon_{ср} = frac{S}{t}$$
Чтобы определить путь при неравномерном движении, нужно среднюю скорость движения умножить на время:
$$large S = upsilon_{ср} t$$
Также мы можем рассчитать время, разделив путь, пройденный телом, на среднюю скорость его движения:
$$t = frac{s}{upsilon_{ср}}$$
Скорость
Двигаться со скоростью черепахи — значит медленно, а со скоростью света — значит очень быстро. Сейчас узнаем, как пишется скорость в математике и как ее найти по формуле.
Скорость определяет путь, который преодолеет объект за единицу времени. Скорость обозначается латинской буквой v.
Проще говоря, скоростью называют расстояние, пройденное телом за единицу времени.
Впервые формулу скорости проходят на математике в 5 классе. Сейчас мы ее сформулируем и покажем, как ее использовать.
Формула скорости
Чтобы найти скорость, нужно разделить путь на время:
v = s : t
Показатели скорости чаще всего выражаются в м/сек или км/час.
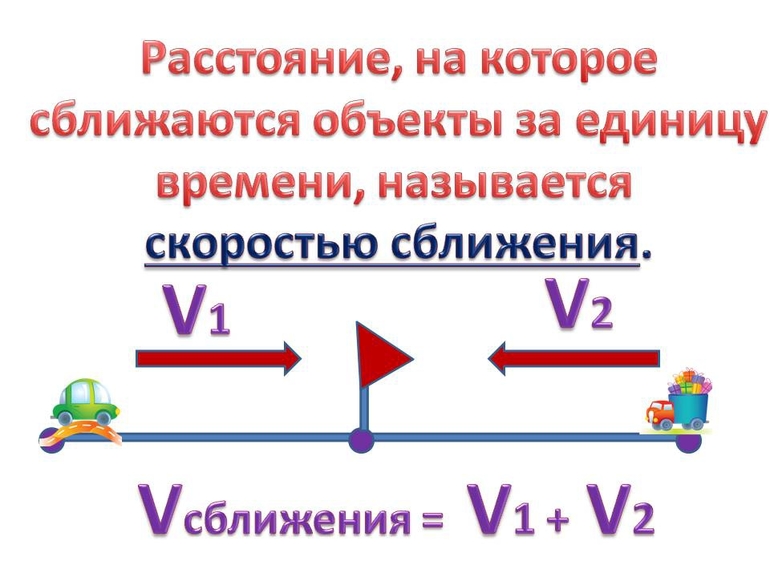
Скорость сближения — это расстояние, на которое сблизились два объекта за единицу времени. Чтобы найти скорость сближения двух объектов, которые движутся навстречу друг другу, надо сложить скорости этих объектов.
Скорость удаления — расстояние, на которое отдалились друг от друга два объекта за единицу времени.
Чтобы найти скорость удаления объектов, которые движутся в противоположных направлениях, нужно сложить скорости этих объектов.
Чтобы найти скорость удаления при движении с отставанием или скорость сближения при движении вдогонку, нужно из большей скорости вычесть меньшую.
Онлайн-курсы по математике для детей — отличный способ разобраться в сложных темах под руководством внимательного преподавателя.
График пути равномерного движения
Пример графика зависимости пути равномерного движения представлен на рисунке 3.
Здесь $S$ — ось пройденных путей, $t$ — ось времени. По этому графику мы можем найти путь, пройденный телом за определенный промежуток времени. Например, за 1 с тело проходит путь длиной 2 м, за 2 с – 4 м, за 3 с – 6 м.
Зная путь и время, мы можем рассчитать скорость. Для удобства расчета возьмем самый первый отрезок пути: $t = 1 с, s = 2 м$. Тогда,
$upsilon = frac{s}{t} = frac{2 м}{1 с} = 2 frac{м}{с}$.
Единицы измерения времени
Основной единицей измерения момента силы в системах СИ и СГС является: [t]=c
Единицы измерения времени основываются на периоде вращения Земли около своей оси и вокруг Солнца, Луни вокруг Земли. Внесистемные единицы измерения времени: час, минута, сутки и т.д.
Первые часы
Сначала было достаточно палочки, на которой каменным топором можно делать зарубки и тем самым отсчитывать прошедшие дни. Но это скорее был календарь, а не часы.
Первые и самые древние часы – солнечные. Их действие основано на изменении длины тени предметов по мере того, как солнце движется по небосводу. Такие часы представляли собой гномон – длинный шест, воткнутый в землю. Солнечные часы применялись в Древнем Египте и Китае. О них было доподлинно известно уже в 1200 году до нашей эры.
Затем появились водяные, песочные и огненные часы. Работа этих механизмов не была привязана к движению небесных светил. Долгое время водяные часы были главным инструментом для измерения времени.
Первые механические часы были изготовлены китайскими мастерами в 725 году нашей эры. Однако широкое распространение они получили относительно недавно.
В средневековой Европе механические часы устанавливались в башнях соборов и имели только одну стрелку – часовую. Карманные часы появились только в 1675 году (изобретение запатентовал Гюйгенс), а наручные – намного позже.
Как люди измеряли время?
Для измерения времени нужны какие-либо повторяющиеся с одинаковым периодом события. Например, смена дня и ночи. Солнце каждый день встает на востоке и садится на западе, а Луна каждый синодический месяц проходит весь цикл фаз освещенности солнцем — от тоненького серпа полумесяца до полнолуния.
Древним людям ничего не оставалось, как привязать отсчет времени к движению небесных тел и событиям, связанным с ним. А именно – к смене дней, ночей и сезонов года.
В году 4 сезона и 12 месяцев. Именно столько раз за весну, лето, осень и зиму Луна меняет свои фазы.
По мере развития прогресса методы измерения времени совершенствовались, появились солнечные, водяные, песочные, огненные, механические, электронные и, наконец, молекулярные часы.
Способы вычисления расстояния и времени
Можно и наоборот, зная скорость, найти значение расстояния или времени. Например:
S=v*t, где v — понятно что такое,
S — расстояние, которое требуется найти,
t — время, за которое объект прошел это расстояние.
Таким образом вычисляется значение расстояния.
Или вычисляем значение времени, за которое пройдено расстояние:
t=S/v, где v — все та же скорость,
S — расстояние, пройденный путь,
t — время, значение которого в данном случае нужно найти.
Для нахождения средних значений этих параметров существует довольно много представлений как данной формулы, так и всех остальных. Главное, знать основные правила перестановок и вычислений. А еще главнее знать сами формулы и лучше наизусть. Если же запомнить не получается, тогда лучше записывать. Это поможет, не сомневайтесь.
Пользуясь такими перестановками можно с легкостью найти время, расстояние и другие параметры, используя нужные, правильные способы их вычисления.
И это еще не предел!
Теги
Расстояние
Мы постоянно ходим пешком и ездим на транспорте из одной точки в другую. Давайте узнаем, как можно посчитать это пройденное расстояние.
Расстояние — это длина от одного пункта до другого.
- Например: расстояние от дома до школы 3 км, от Москвы до Петербурга 705 км.
Расстояние обозначается латинской буквой s.
Единицы расстояния чаще всего выражаются в метрах (м), километрах (км).
Формула пути
Чтобы найти расстояние, нужно умножить скорость на время движения:
s = v × t
Демоурок по математике
Узнайте, какие темы у вас «хромают», а после — разбирайте их без зубрежки формул и скучных лекций.
Скорость
Двигаться со скоростью черепахи — значит медленно, а со скоростью света — значит очень быстро. Сейчас узнаем, как пишется скорость в математике и как ее найти по формуле.
Скорость определяет путь, который преодолеет объект за единицу времени. Скорость обозначается латинской буквой v.
Проще говоря, скоростью называют расстояние, пройденное телом за единицу времени.
Впервые формулу скорости проходят на математике в 5 классе. Сейчас мы ее сформулируем и покажем, как ее использовать.
Формула скорости
Чтобы найти скорость, нужно разделить путь на время:
v = s : t
Показатели скорости чаще всего выражаются в м/сек или км/час.
Скорость сближения — это расстояние, на которое сблизились два объекта за единицу времени. Чтобы найти скорость сближения двух объектов, которые движутся навстречу друг другу, надо сложить скорости этих объектов.
Скорость удаления — расстояние, на которое отдалились друг от друга два объекта за единицу времени.
Чтобы найти скорость удаления объектов, которые движутся в противоположных направлениях, нужно сложить скорости этих объектов.
Чтобы найти скорость удаления при движении с отставанием или скорость сближения при движении вдогонку, нужно из большей скорости вычесть меньшую.
Онлайн-курсы по математике для детей — отличный способ разобраться в сложных темах под руководством внимательного преподавателя.
Время
Время — самое дорогое, что у нас есть. Но кроме философии, у времени есть важная роль и в математике.
Время — это продолжительность каких-то действий, событий.
- Например: от метро до дома — 10 минут, от дома до дачи — 2 часа.
Время движения обозначается латинской буквой t.
Чаще всего вам будут встречаться такие единицы времени, как секунды, минуты и часы.
Формула времени
Чтобы найти время, нужно разделить расстояние на скорость:
t = s : v
Эта формула пригодится, если нужно узнать, за какое время тело преодолеет то или иное расстояние.
Взаимосвязь скорости, времени, расстояния
Скорость, время и расстояние связаны между собой очень крепко. Одно без другого даже сложно представить.
Если известны скорость и время движения, то можно найти расстояние. Оно равно скорости, умноженной на время: s = v × t.
Задачка 1. Мы вышли из дома и направились в гости в соседний двор. Мы дошли до соседнего двора за 15 минут. Фитнес-браслет показал, что наша скорость была 50 метров в минуту. Какое расстояние мы прошли?
Как рассуждаем:
Если за одну минуту мы прошли 50 метров, то сколько таких пятьдесят метров мы пройдем за 10 минут? Умножив 50 метров в минуту на 15 минут, мы определим расстояние от дома до магазина:
v = 50 м/мин
t = 15 мин
s = v × t = 50 × 15 = 750 (м)
Ответ: мы прошли 750 метров.
Если известно время и расстояние, то можно найти скорость: v = s : t.
Задачка 2. Двое школьников решили проверить, кто быстрее добежит от двора до спортплощадки. Расстояние между двором и площадкой — 100 метров. Первый школьник добежал за 25 секунд, второй за 50 секунд. Кто добежал быстрее?
Как рассуждаем:
Быстрее добежал тот, кто за 1 секунду пробежал большее расстояние. Говорят, что у него скорость движения больше. В этой задаче скорость школьников — это расстояние, которое они пробегают за 1 секунду.
Чтобы найти скорость, нужно расстояние разделить на время движения. Найдем скорость первого школьника: для этого разделим 100 метров на время движения первого школьника, то есть на 25 секунд:
100 : 25 = 4
Если расстояние дано в метрах, а время движения в секундах, то скорость измеряется в метрах в секунду (м/с). Если расстояние дано в километрах, а время движения в часах, скорость измеряется в километрах в час (км/ч).
В нашей задаче расстояние дано в метрах, а время в секундах. Значит, будем измерять скорость в метрах в секунду (м/с).
100 м : 25 с = 4 м/с
Так мы узнали, что скорость движения первого школьника 4 метра в секунду.
Теперь найдем скорость движения второго школьника. Для этого разделим расстояние на время движения второго школьника, то есть на 50 секунд:
100 : 50 = 2
Значит, скорость движения второго школьника составляет 2 метра в секунду.
Сейчас можно сравнить скорости движения каждого школьника и узнать, кто добежал быстрее.
4 (м/с) > 2 (м/с)
Скорость первого школьника больше. Значит, он добежал до спортивной площадки быстрее.
Ответ: первый школьник добежал быстрее.
Если известны скорость и расстояние, то можно найти время: t = s : v.
Задачка 3. От школы до стадиона 500 метров. Мы должны дойти до него пешком. Наша скорость будет 100 метров в минуту. За какое время мы дойдем до стадиона из школы?
Как рассуждаем:
Если за одну минуту мы будем проходить 100 метров, то сколько таких минут со ста метрами будет в 500 метрах?
Чтобы ответить на этот вопрос, нужно 500 метров разделить на расстояние, которое мы будем проходить за одну минуту, то есть на 100. Тогда мы получим время, за которое дойдем до стадиона:
s = 500 м
v = 100 м/мин
t = s : v = 500 : 100 = 5 (мин)
Ответ: от школы до стадиона мы дойдем за 5 минут.
Специально для уроков математики можно распечатать или нарисовать самостоятельно такую таблицу, чтобы быстрее запомнить и применять формулы скорости, времени, расстояния.
Математика
5 класс
Урок № 35
Задачи на движение
Перечень вопросов, рассматриваемых в теме:
- Понятия скорости, времени, расстояния.
- Формулы нахождения скорости, времени, расстояния.
- Понятия скорости сближения, скорости удаления.
Глоссарий по теме
Расстояние – это длина от одного пункта до другого.
Большие расстояния, в основном, измеряются в метрах и километрах.
Расстояние обозначается латинской буквой S.
Чтобы найти расстояние, надо скорость умножить на время движения:
S = v ∙ t
Скорость – это расстояние, пройденное телом за единицу времени. Под единицей времени подразумевается 1 час, 1 минута или 1 секунда.
Скорость обозначается латинской буквой v.
Чтобы найти скорость, нужно расстояние разделить на время движения:
v = S : t
Время – это продолжительность каких-то действий, событий.
Время движения обозначается маленькой латинской буквой t.
Чтобы найти время, нужно расстояние разделить на скорость движения:
t = S : v
Скорость сближения – это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.
Чтобы найти скорость сближения, нужно сложить скорости объектов.
Скорость удаления – это расстояние, которое увеличивается за единицу времени между двумя объектами, двигающимися в противоположных направлениях.
Чтобы найти скорость удаления, нужно сложить скорости объектов.
Чтобы найти скорость удаления при движении в одном направлении, нужно из большей скорости вычесть меньшую скорость.
Основная литература
1. Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К., Потапов, Н. Н. Решетников и др. — М.: Просвещение, 2017. — 258 с.
2. Потапов М. К., Шевкин А. В. Математика. Книга для учителя. 5 – 6 классы — М.: Просвещение, 2010
Дополнительная литература
1. Чесноков А. С., Нешков К. И. Дидактические материалы по математике 5 кл. – М.: Академика учебник, 2014
2. Бурмистрова Т. А. Математика. Сборник рабочих программ. 5–6 классы // Составитель Бурмистрова Т. А.
3. Потапов М. К. Математика: дидактические материалы. 6 кл. // Потапов М. К., Шевкин А. В. — М.: Просвещение, 2010
Теоретический материал для самостоятельного изучения
Очень часто нам встречаются задачи на нахождение скорости, времени и расстояния. Что же всё это такое? Сейчас нам предстоит в этом разобраться.
Расстояние – это длина от одного пункта до другого. (Например, расстояние от дома до школы 2 километра). В основном большие расстояния измеряются в метрах и километрах. Общепринятое обозначение расстояния – заглавная латинская буква S.
Скоростью называют расстояние, пройденное телом за единицу времени. Под единицей времени подразумевается 1 час, 1 минута или 1 секунда. Скорость обозначается маленькой латинской буквой v.
Рассмотрим задачу:
Двое школьников решили проверить, кто быстрее добежит от двора до спортплощадки. Расстояние от двора до спортплощадки 200 метров. Первый школьник добежал за 50 секунд. Второй за 100 секунд. Кто из ребят бежал быстрее?
Решение:
Быстрее бежал тот, кто за 1 секунду пробежал большее расстояние. Говорят, что у него скорость движения больше. Чтобы найти скорость, нужно расстояние разделить на время движения.
Давайте найдём скорость первого школьника. Для этого разделим 200 метров на время движения первого школьника, то есть на 50 секунд:
200 м : 50 с = 4
Если расстояние дано в километрах, а время движения в часах, скорость измеряется в километрах в час (км/ч).
У нас расстояние дано в метрах, а время в секундах. Значит, скорость измеряется в метрах в секунду:
200 м : 50 с = 4 (м/с)
Скорость движения первого школьника составляет 4 метра в секунду.
Теперь найдём скорость движения второго школьника. Для этого разделим расстояние на время движения второго школьника:
200 м : 100 c = 2 (м/с)
Скорость движения первого школьника – 4 (м/с).
Скорость движения второго школьника – 2 (м/с).
4 (м/с) > 2 (м/с)
Скорость первого школьника больше. Значит, он бежал до спортплощадки быстрее.
Иногда возникает ситуация, когда требуется узнать, за какое время тело преодолеет то или иное расстояние. Время движения обозначается маленькой латинской буквой t.
Рассмотрим задачу:
От дома до спортивной секции 1200 метров. Мы должны доехать туда на велосипеде. Наша скорость будет 600 метров в минуту. За какое время мы доедем до спортивной секции?
Решение:
Если за одну минуту мы будем проезжать 600 метров, то сколько таких минут нам понадобится для преодоления тысячи двухсот метров? Очевидно, что надо разделить 1200 метров на то расстояние, которое мы будем проезжать за одну минуту, то есть на 600 метров. Тогда мы получим время, за которое мы доедем до спортивной секции:
1200 : 600 = 2 (мин)
Ответ: мы доедем до спортивной секции за 2 минуты.
Скорость, время и расстояние связаны между собой.
Если известны скорость и время движения, то можно найти расстояние. Оно равно скорости, умноженной на время:
S = v ∙ t
Рассмотрим задачу:
Мы вышли из дома и направились в магазин. Мы дошли до магазина за 15 минут. Наша скорость была 60 метров в минуту. Какое расстояние мы прошли?
Решение:
Если за одну минуту мы прошли 60 метров, то сколько таких отрезков по шестьдесят метров мы пройдём за 15 минут? Очевидно, что умножив 60 метров на 15 минут, мы определим расстояние от дома до магазина:
v = 60 (м/мин)
t = 15 (минут)
S = v ∙ t = 60 ∙ 15 = 900 (метров)
Ответ: мы прошли 900 метров.
Если известно время и расстояние, то можно найти скорость:
v = S : t
Рассмотрим задачу:
Расстояние от дома до школы 800 метров. Школьник дошёл до этой школы за 8 минут. Какова была его скорость?
Скорость движения школьника – это расстояние, которое он проходит за одну минуту. Если за 10 минут он преодолел 800 метров, то какое расстояние он преодолевал за одну минуту?
Чтобы ответить на этот вопрос, нужно разделить расстояние на время движения школьника:
S = 800 метров
t = 8 минут
v = S : t = 800 : 8 = 100 (м/мин)
Ответ: скорость школьника была 100 м/мин.
Если известна скорость и расстояние, то можно найти время:
t = S : v
Рассмотрим задачу:
От дома до спортивной секции 600 метров. Мы должны дойти до неё пешком. Наша скорость будет 120 метров в минуту (120 м/мин). За какое время мы дойдём до спортивной секции?
Если за одну минуту мы будем проходить 120 метров, то сколько таких минут со ста двадцатью метрами будет в шестистах метрах?
Чтобы ответить на этот вопрос, нужно 600 метров разделить на расстояние, которое мы будем проходить за одну минуту, то есть на 120. Тогда мы получим время, за которое мы дойдём до спортивной секции:
S = 600 метров
v = 120 (м/мин)
t = S : v = 600 : 120 = 5 (минут).
Ответ: мы дойдём до спортивной секции за 5 минут.
Итак, все рассмотренные нами формулы мы можем представить в виде треугольника для лучшего запоминания:
Теперь рассмотрим типы задач на движение.
Задачи на сближение.
Скорость сближения – это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.
Например, если из двух пунктов навстречу друг другу отправятся два пешехода, причём скорость первого будет 100 метров в минуту, а второго – 105 метров в минуту, то скорость сближения будет составлять 100 плюс 105, то есть 205 метров в минуту. Значит, каждую минуту расстояние между пешеходами будет уменьшаться на 205 метров.
Чтобы найти скорость сближения, нужно сложить скорости объектов.
Задача.
Из двух пунктов навстречу друг другу выехали одновременно два велосипедиста. Скорость первого велосипедиста 13 км/ч, а скорость второго – 15 км/ч. Через 3 часа они встретились. Определите расстояние между населёнными пунктами.
Решение:
- Найдём скорость сближения велосипедистов:
13 км/ч + 15 км/ч = 28 км/ч
- Определим расстояние между населёнными пунктами. Для этого скорость сближения умножим на время движения:
28 ∙ 3 = 84 км
Ответ: расстояние между населёнными пунктами 84 км.
Задачи на скорость удаления.
Скорость удаления – это расстояние, которое увеличивается за единицу времени между двумя объектами, двигающимися в противоположных направлениях.
Например, если два пешехода отправятся из одного и того же пункта в противоположных направлениях, причём скорость первого будет 4 км/ч, а скорость второго 6 км/ч, то скорость удаления будет составлять 4 плюс 6, то есть 10 км/ч. Каждый час расстояние между двумя пешеходами будет увеличиваться на 10 километров.
Чтобы найти скорость удаления, нужно сложить скорости объектов.
Рассмотрим задачу:
С причала одновременно в противоположных направлениях отправились теплоход и катер. Скорость теплохода составляла 60 км/ч, скорость катера 130 км/ч. Какое расстояние будет между ними через 2 часа?
Решение:
- Определим скорость удаления. Для этого сложим их скорости:
60 + 130 = 190 км/ч.
Получили скорость удаления равную 190 км/ч. Данная скорость показывает, что за час расстояние между теплоходом и катером будет увеличиваться на 190 километров.
- Чтобы узнать какое расстояние будет между ними через два часа, нужно 190 умножить на 2:
190 ∙ 2 = 380 км.
Ответ: через 2 часа расстояние между теплоходом и катером будет составлять 380 километров.
Задачи на движение объектов в одном направлении.
В предыдущих пунктах мы рассматривали задачи, в которых объекты (люди, машины, лодки) двигались либо навстречу друг другу, либо в противоположных направлениях. В первом случае мы находили скорость сближения – в ситуации, когда два объекта двигались навстречу друг другу. Во втором случае мы находили скорость удаления – в ситуации, когда два объекта двигались в противоположных направлениях. Но объекты также могут двигаться в одном направлении, причём с различной скоростью.
Чтобы найти скорость удаления при движении в одном направлении, нужно из большей скорости вычесть меньшую скорость.
Рассмотрим задачу:
Из города в одном и том же направлении выехали легковой автомобиль и автобус. Скорость автомобиля 130 км/ч, а скорость автобуса 90 км/ч. Какое расстояние будет между ними через 1 час? Через 3 часа?
Решение:
- Найдём скорость удаления. Для этого из большей скорости вычтем меньшую:
130 км/ч − 90 км/ч = 40 км/ч
- Каждый час легковой автомобиль отдаляется от автобуса на 40 километров. За один час расстояние между автомобилем и автобусом будет 40 км. За 3 часа в три раза больше:
40 ∙ 3 = 120 км
Ответ: через один час расстояние между автомобилем и автобусом будет 40 км, через три часа – 120 км.
Рассмотрим ситуацию, в которой объекты начали своё движение из разных пунктов, но в одном направлении.
Задача.
Пусть на одной улице имеется дом, школа и аттракцион. Дом находится на одном конце улицы, аттракцион на другом, школа между ними. От дома до школы 900 метров. Два пешехода отправились в аттракцион в одно и то же время. Причём первый пешеход отправился в аттракцион от дома со скоростью 90 метров в минуту, а второй пешеход отправился в аттракцион от школы со скоростью 85 метров в минуту. Какое расстояние будет между пешеходами через 3 минуты? Через сколько минут после начала движения первый пешеход догонит второго?
Решение:
- Определим расстояние, пройденное первым пешеходом за 3 минуты. Он двигался со скоростью 90 метров в минуту. За три минуты он пройдёт в три раза больше, то есть 270 метров:
90 ∙ 3 = 270 метров
- Определим расстояние, пройденное вторым пешеходом за 3 минуты. Он двигался со скоростью 85 метров в минуту. За три минуты он пройдёт в три раза больше, то есть 255 метров:
85 ∙ 3 = 255 метров
- Теперь найдём расстояние между пешеходами. Чтобы найти расстояние между пешеходами, можно к расстоянию от дома до школы (900м) прибавить расстояние, пройденное вторым пешеходом (255м), и из полученного результата вычесть расстояние, пройденное первым пешеходом (270м):
900 + 255 = 1155 м
1155 – 270 = 885 м
Либо из расстояния от дома до школы (900 м) вычесть расстояние, пройденное первым пешеходом (270 м), и к полученному результату прибавить расстояние, пройденное вторым пешеходом (255 м):
900 – 270 = 630 м
630 + 255 = 885 м
Таким образом, через три минуты расстояние между пешеходами будет составлять 885 метров.
- Теперь давайте ответим на вопрос: через сколько минут после начала движения первый пешеход догонит второго?
В самом начале пути между пешеходами было расстояние 900 м. Через минуту после начала движения расстояние между ними будет составлять 895 метров, поскольку первый пешеход двигается на 5 метров в минуту быстрее второго:
90 ∙ 1 = 90 м
85 ∙ 1 = 85 м
900 + 85 – 90 = 985 – 90 = 895 м
Через три минуты после начала движения расстояние уменьшится на 15 метров и будет составлять 885 метров. Это был наш ответ на первый вопрос задачи:
90 ∙ 3 = 270 м
85 ∙ 3 = 255 м
900 + 255 – 270 = 1155 – 270 = 885 м
Можно сделать вывод, что каждую минуту расстояние между пешеходами будет уменьшаться на 5 метров.
А раз изначальные 900 метров с каждой минутой уменьшаются на одинаковые 5 метров, то мы можем узнать сколько раз 900 метров содержат по 5 метров, тем самым определяя через сколько минут первый пешеход догонит второго:
900 : 5 = 180 минут.
Ответ: через три минуты расстояние между пешеходами будет составлять 885 метров, первый пешеход догонит второго через 180 минут = 3 часа.
Разбор решения заданий тренировочного модуля
№1. Тип задания: ввод с клавиатуры пропущенных элементов в тексте
Заполните таблицу:
|
S |
v |
t |
|
|
1. |
135 км |
9 км/ч |
____ ч |
|
2. |
____ м |
12 м/с |
4 с |
|
3. |
132 м |
____ м/мин |
11 мин |
Для заполнения пропусков воспользуемся формулами нахождения скорости, времени, расстояния:
- Надо найти время: t = S : v
135 : 9 = 15 часов.
- Надо найти расстояние: S = v ∙ t
12 ∙ 4 = 48 м.
- Надо найти скорость: v = S : t
132 : 11 = 12 м/мин.
Верный ответ:
|
S |
v |
t |
|
|
1. |
135 км |
9 км/ч |
15 часов |
|
2. |
48 м |
12 м/с |
4 с |
|
3. |
132 м |
12 м/мин |
11 мин |
№2. Тип задания: единичный / множественный выбор
Выберите верный ответ к задаче:
Из пунктов А и В, расстояние между которыми 300 км, отправились одновременно навстречу друг другу мотоциклист и автомобилист. Скорость автомобиля 60 км/ч, а мотоцикла 30 км/ч. Какое расстояние будет между ними через 3 часа?
Варианты ответов:
- 70
- 30
- 270
- 240
Эта задача относится к типу задач на сближение, т.е. нам надо:
- сложить скорости мотоциклиста и автомобилиста:
60 + 30 = 90 км/ч – скорость сближения;
- узнать, сколько километров они пройдут за 3 часа вместе. Для этого:
90 ∙ 3 = 270 км;
- из общего расстояния нам осталось вычесть пройденное:
300 – 270 = 30 км
Верный ответ: 2. 30 км.
Метрическое пространство может не иметь счётной базы, но всегда удовлетворяет первой аксиоме счётности — имеет счётную базу в каждой точке.
- Более того, каждый компакт в метрическом пространстве имеет счётную базу окрестностей.
- Сверх того, в каждом метрическом пространстве существует такая база, что каждая точка пространства принадлежит лишь счётному множеству её элементов — точечно-счётная база (но это свойство слабее метризуемости даже в присутствии паракомпактности и хаусдорфовости).
Вариации и обобщения [ | ]
- Для данного множества M <displaystyle M>, функция d : M × M → R <displaystyle dcolon Mtimes Mto mathbb > называется псевдометрикой или полуметрикой на M <displaystyle M>если для любых точек x , y , z <displaystyle x,;y,;z>из M <displaystyle M>она удовлетворяет следующим условиям:
- d ( x , x ) = 0 <displaystyle d(x,x)=0>;
- d ( x , y ) = d ( y , x ) <displaystyle d(x,y)=d(y,x)>(симметрия);
- d ( x , z ) ⩽ d ( x , y ) + d ( y , z ) <displaystyle d(x,z)leqslant d(x,y)+d(y,z)>(неравенство треугольника).
- Для данного множества M <displaystyle M>функция d : M × M → R <displaystyle dcolon Mtimes Mto mathbb > называется квазиметрикой, если для любых точек x <displaystyle x>, y <displaystyle y>, z <displaystyle z>из M <displaystyle M>она удовлетворяет следующим условиям:
- d ( x , x ) = 0 <displaystyle d(x,x)=0>;
- d ( x , y ) ⩽ c ⋅ d ( y , x ) <displaystyle d(x,y)leqslant ccdot d(y,x)>(квазисимметрия);
- d ( x , z ) ⩽ c ⋅ ( d ( x , y ) + d ( y , z ) ) <displaystyle d(x,z)leqslant ccdot (d(x,y)+d(y,z))>(обобщённое неравенство треугольника).
- Метрика на пространстве называется ультраметрикой, если она удовлетворяет сильному неравенству треугольника: Для всех x <displaystyle x>, y <displaystyle y>и z <displaystyle z>в M <displaystyle M>d ( x , z ) ⩽ max ( d ( x , y ) , d ( y , z ) ) <displaystyle d(x,z)leqslant max(d(x,y),d(y,z))>.
- Иногда удобно рассматривать ∞ <displaystyle infty >-метрики, то есть метрики со значениями [ 0 ; ∞ ] <displaystyle [0;infty ]>. Для любой ∞ <displaystyle infty >-метрики можно построить конечную метрику, которая определяет ту же топологию. Например, d ′ ( x , y ) = d ( x , y ) 1 + d ( x , y ) <displaystyle d'(x,y)=<frac <1+d(x,y)>>> или d ″ ( x , y ) = min ( 1 , d ( x , y ) ) . <displaystyle d»(x,y)=min <(1,d(x,y))>.>
- Иногда квазиметрика определяется как функция, удовлетворяющая всем аксиомам для метрики за возможным исключением симметрии [3][4] . Название этого обобщения не вполне устоялось [5] . В своей книге Смит [4] называет их «полуметриками». Тот же термин используется часто также для двух других обобщений метрик.
- d ( x , y ) ⩾ 0 <displaystyle d(x,y)geqslant 0>(положительность)
- d ( x , y ) = 0 ⟺ x = y <displaystyle d(x,y)=0iff x=y>(положительная определённость)
- d(x, y)=d(y, x) (симметрия вычеркнута)
- d ( x , z ) ⩽ d ( x , y ) + d ( y , z ) <displaystyle d(x,z)leqslant d(x,y)+d(y,z)>(неравенство треугольника)
- В метаметрике все аксиомы метрики выполняются, за исключением того, что расстояние между идентичными точками не обязательно равно нулю. Другими словами, аксиомами для метаметрики являются:
- d ( x , y ) ⩾ 0
- из d ( x , y ) = 0 <displaystyle d(x,y)=0>следует x = y <displaystyle x=y>(но не наоборот.)
- d ( x , y ) = d ( y , x )
- d ( x , z ) ⩽ d ( x , y ) + d ( y , z ) <displaystyle d(x,z)leqslant d(x,y)+d(y,z)>.
- Ослабление последних трёх аксиом ведёт к понятию преметрики, то есть функции, удовлетворяющей условиям:
- d ( x , y ) ⩾ 0
- d ( x , x ) = 0
- Префиксы псевдо-, квази- и полу- могут комбинироваться, например, псевдоквазиметрика (иногда называемая гемиметрикой) ослабляет как аксиому неразличимости, так и аксиому симметрии, и является просто преметрикой, удовлетворяющей неравенству треугольника. Для псевдоквазиметрических пространств открытые r <displaystyle r>-шары образуют базис открытых множеств. Простейшим примером псевдоквазиметрического пространства служит множество < 0 , 1 ><displaystyle <0,1>> с преметрикой, задаваемой функцией d <displaystyle d>, такой что d ( 0 , 1 ) = 1 <displaystyle d(0,1)=1>и d ( 1 , 0 ) = 0 <displaystyle d(1,0)=0>. Ассоциированное топологическое пространство является пространством Серпинского.
Линейное метрическое пространство [ | ]
- x n → x , y n → y ⇒ x n + y n → x + y <displaystyle x_to x,y_to yRightarrow x_+y_to x+y>
- x n → x , λ n → λ ⇒ λ n x n → λ x <displaystyle x_to x,lambda _to lambda Rightarrow lambda _x_to lambda x>
- Линейное пространство всех комплексных последовательностей можно превратить в линейное метрическое пространство при помощи введения расстояния между его элементами с помощью формулы:
История [ | ]
Морис Фреше впервые ввёл понятие метрического пространства [13] в связи с рассмотрением функциональных пространств.
Как обозначают время в математике?
Если при решении задачи по физике или математике необходимо обозначить время, то это пишется буквой так: t (читается: [тэ]), а если расстояние — пишется буквой так: s (читается: [эс]). Для обозначения пути обычно используется строчная (маленькая) буква [эль], т.
Как обозначаются скорость время расстояние в математике?
Скорость принято обозначать маленькой латинской буквой v, время движения – маленькой буквой t, пройденное расстояние – маленькой буквой s. Скорость, время и расстояние связаны между собой. Например, мы вышли из дома и направились в магазин. Мы дошли до магазина за 10 минут.
Как обозначается время расстояние?
Время. Расстояние. Эти три величины обозначают вот так: S – расстояние (путь); t – время, за которое пройдено расстояние S ; v – скорость движения. 2 Скорость – это расстояние, пройденное за единицу времени.
Что нужно сделать чтобы узнать время в математике?
Чтобы узнать скорость движения, нужно расстояние разделить на время. Чтобы узнать расстояние, нужно скорость умножить на время. Чтобы найти время, нужно расстояние разделить на скорость.
Как обозначается время в задачах?
Время – это продолжительность каких-то действий, событий. Время движения обозначается маленькой латинской буквой t. Скорость сближения – это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени. Чтобы найти скорость сближения, нужно сложить скорости объектов.
Как пишется скорость?
Скорость обозначается латинской буквой v. Проще говоря, скоростью называют расстояние, пройденное телом за единицу времени. Впервые формулу скорости проходят на математике в 5 классе.
Как найти скорость если есть время и расстояние?
- V = S / T. V — величина скорости; S — величина пройденного пути; Т — время в пути. .
- S = V * T. Т. е величину пройденного пути находим как произведение скорости на время в пути. Если известно расстояние и скорость, определить время можно по формуле:
- T = S / V. т. е.
Как находят скорость время расстояние?
В 4 классе ученики решают много задач по математике с примением формулы нахождения скорости, времени или расстояния при равномерном движении. Эта формула выглядит так: S = V×t. В данной формуле S — это путь, V — скорость, а t — время.
Как определить скорость течения реки?
Необходимо отметить, что собственная скорость водного суда – это скорость в стоячей воде. Чтобы найти скорость по течению, надо к скорости течения прибавить собственную. Для того чтобы найти скорость против течения, надо из собственной скорости вычесть скорость течения.
Как обозначается общая площадь?
В математике и в физике площадь обозначается буквой S заглавной (читается: [эс]). Так, в геометрии этой буквой обозначается площадь любых фигур (треугольника, прямоугольника, квадрата, ромба и т.
Как узнать время в пути?
- Чтобы найти расстояние, нужно скорость умножить на время.
- Чтобы найти время, надо расстояние разделить на скорость.
- Чтобы найти скорость, надо расстояние разделить на время.
Как найти время формула 5 класс?
S = V·t. В данной формуле S – это путь, V – скорость, а t – время.
Как решать задачи на расстояние скорость и время?
- если мы умножаем скорость на время, то получаем расстояние;
- если расстояние делим на время, то получаем скорость;
- если расстояние делим на скорость, то получаем время ;
Как найти время формула 4 класс?
В 4 классе ученики решают много задач по математике с примением формулы нахождения скорости, времени или расстояния при равномерном движении. Эта формула выглядит так: S = V×t. В данной формуле S — это путь, V — скорость, а t — время.
Как найти расстояние которое прошло тело?
Чтобы определить путь, который прошло тело при равномерном движении, необходимо скорость движения тела умножить на время которое это тело двигалось. S=V*t.
Расстояние — Distance
Расстояние — это числовое измерение того, насколько далеко друг от друга находятся объекты или точки. В физике или повседневном использовании расстояние может относиться к физической длине или оценке, основанной на других критериях (например, «на два округа больше»). Расстояние от точки A до точки B иногда обозначается как . В большинстве случаев «расстояние от A до B» взаимозаменяемо с «расстоянием от B до A». В математике функция расстояния или метрика — это обобщение концепции физического расстояния; это способ описания того, что значит для элементов некоторого пространства быть «близко» или «далеко» друг от друга. В психологии и социальных науках расстояние — это нечисловое измерение; Психологическая дистанция определяется как «различные способы, которыми объект может быть удален от себя» по таким измерениям, как «время, пространство, социальная дистанция и гипотетичность». | А B |
СОДЕРЖАНИЕ
Обзор и определения
Физические расстояния
Физическое расстояние может означать несколько разных вещей:
- Пройденное расстояние: длина определенного пути, пройденного между двумя точками, например расстояние, пройденное при навигации по лабиринту.
- Прямолинейное (евклидово) расстояние: длина кратчайшего возможного пути в пространстве между двумя точками, который можно было бы пройти, если бы не было препятствий (обычно формализируется как евклидово расстояние ).
- Геодезическое расстояние: длина кратчайшего пути между двумя точками, оставаясь на некоторой поверхности, например, расстояние по дуге вдоль кривой Земли.
- Длина определенного пути, который возвращается к начальной точке, например, мяч, брошенный вверх, или Земля, когда он завершает один оборот по орбите .
«Круговое расстояние» — это расстояние, пройденное колесом, которое может быть полезно при проектировании транспортных средств или механических передач. Окружность колеса равна 2 π × радиус, и если принять радиус равным 1, то каждый оборот колеса эквивалентен расстоянию 2 π радиан. В технике часто используется ω = 2 πƒ , где ƒ — частота .
Необычные определения расстояния могут быть полезны для моделирования определенных физических ситуаций, но также используются в теоретической математике:
- « Манхэттенское расстояние » — это прямолинейное расстояние, названное в честь количества кварталов (в северном, южном, восточном или западном направлениях), по которым такси должно проехать, чтобы добраться до пункта назначения на сетке улиц в некоторых частях Нью-Йорка. .
- «Расстояние до шахматной доски», формализованное как расстояние Чебышева , — это минимальное количество ходов, которое король должен сделать на шахматной доске , чтобы пройти между двумя клетками.
Теоретические расстояния
Термин «расстояние» также используется по аналогии для измерения нефизических объектов определенными способами.
В информатике есть понятие « расстояние редактирования » между двумя строками. Например, слова «собака» и «точка», которые различаются только одной буквой, ближе, чем «собака» и «кошка», которые различаются на три буквы. Эта идея используется в средствах проверки орфографии и в теории кодирования и математически формализована несколькими различными способами, такими как:
В математике метрическое пространство — это набор, для которого определены расстояния между всеми членами набора. Таким образом, можно вычислить множество различных типов «расстояний», например, для обхода графиков , сравнения распределений и кривых, а также с использованием необычных определений «пространства» (например, с использованием многообразия или отражений ). Понятие расстояния в теории графов использовалось для описания социальных сетей , например, с помощью числа Эрдёша или числа Бэкона — количество отношений сотрудничества на расстоянии от человека — от плодовитого математика Пола Эрдёша и актера Кевина Бэкона соответственно.
В психологии, географии человека и социальных науках расстояние часто рассматривается не как объективный показатель, а как субъективный опыт.
Расстояние в зависимости от направленного расстояния и смещения
И расстояние, и смещение измеряют движение объекта. Расстояние не может быть отрицательным и никогда не уменьшается. Расстояние — это скалярная величина или величина , тогда как смещение — это векторная величина, имеющая как величину, так и направление . Он может быть отрицательным, нулевым или положительным. Направленное расстояние не измеряет движение; он измеряет расстояние между двумя точками и может быть положительным, нулевым или отрицательным вектором.
Расстояние , пройденное транспортным средством (например , в виде записанного с помощью одометр ), человека, животного или объекта вдоль изогнутой траектории от точки А до точки Б , следует отличать от прямолинейного расстояния от A до B . Например, независимо от расстояния, пройденного за время пути от A до B и обратно до A , смещение равно нулю, поскольку начальная и конечная точки совпадают. В общем, расстояние по прямой не равно пройденному расстоянию, за исключением поездок по прямой.
Направленное расстояние
Направленные расстояния можно определять по прямым и изогнутым линиям.
Направленные расстояния вдоль прямых линий — это векторы, которые определяют расстояние и направление между начальной и конечной точками. Направленное расстояние точки C от точки A в направлении B на прямой AB в евклидовом векторном пространстве — это расстояние от A до C, если C падает на луч AB , но является отрицательным для этого расстояния, если C падает на луч BA (т. е. если C не находится на той же стороне от A, что и B ). Например, направленное расстояние от флагштока Главной библиотеки Нью-Йорка до флагштока Статуи Свободы:
- Отправная точка: флагшток библиотеки
- Конечная точка: статуя флагштока.
- Направление: -38 °
- Расстояние: 8.72 км
Другой вид направленного расстояния — это расстояние между двумя разными частицами или точечными массами в данный момент времени. Например, расстояние от центра тяжести Земли A до центра тяжести Луны B (что не означает строго движение от A к B ) попадает в эту категорию.
Направленное расстояние вдоль изогнутой линии не является вектором и представлено сегментом этой изогнутой линии, определяемой конечными точками A и B , с некоторой конкретной информацией, указывающей смысл (или направление) идеального или реального движения от одной конечной точки сегмент к другому (см. рисунок). Например, простая маркировка двух конечных точек как A и B может указывать на смысл, если предполагается упорядоченная последовательность ( A , B ), что подразумевает, что A является начальной точкой.
Смещение
Смещение (см. Выше) — это особый вид направленного расстояния, определенный в механике . Направленное расстояние называется смещением, когда это расстояние по прямой (минимальное расстояние) от A и B , и когда A и B — позиции, занятые одной и той же частицей в два разных момента времени. Это подразумевает движение частицы. Расстояние, пройденное частицей, всегда должно быть больше или равно ее смещению, причем равенство имеет место только тогда, когда частица движется по прямой траектории.
Математика
Геометрия
В аналитической геометрии , то евклидово расстояние между двумя точками на плоскости ху , можно найти , используя формулу расстояния. Расстояние между ( x 1 , y 1 ) и ( x 2 , y 2 ) определяется по формуле:
Аналогично, для заданных точек ( x 1 , y 1 , z 1 ) и ( x 2 , y 2 , z 2 ) в трехмерном пространстве расстояние между ними равно:
Эти формулы легко выводятся путем построения прямоугольного треугольника с опорой на гипотенузе другого (с другой ноги , ортогональной к плоскости , содержащей 1 — треугольник) и применяя теорему Пифагора . Эта формула расстояния также может быть расширена до формулы длины дуги . Другие расстояния с другими формулами используются в неевклидовой геометрии .
Расстояние в евклидовом пространстве
В евклидовом пространстве R n расстояние между двумя точками обычно определяется евклидовым расстоянием ( расстояние с двумя нормами). Иногда вместо них используются другие расстояния, основанные на других нормах .
Для точки ( x 1 , x 2 , . x n ) и точки ( y 1 , y 2 , . y n ) расстояние Минковского порядка p ( p -нормальное расстояние ) определяется как :
| 1-нормальное расстояние | знак равно ∑ я знак равно 1 п | Икс я — у я | < displaystyle = sum _ ^ left | x_ -y_ right |> |
| 2-нормальное расстояние | знак равно ( ∑ я знак равно 1 п | Икс я — у я | 2 ) 1 / 2 < displaystyle = left ( sum _ ^ left | x_ -y_ right | ^ <2> right) ^ <1/2>> |
| p — нормальное расстояние | знак равно ( ∑ я знак равно 1 п | Икс я — у я | п ) 1 / п < displaystyle = left ( sum _ ^ left | x_ -y_ right | ^
right) ^ <1 / p>> |
| бесконечное нормальное расстояние | знак равно Lim п → ∞ ( ∑ я знак равно 1 п | Икс я — у я | п ) 1 / п < displaystyle = lim _
left ( sum _ ^ left | x_ -y_ right | ^
right ) ^ <1 / p>> |
| знак равно Максимум ( | Икс 1 — у 1 | , | Икс 2 — у 2 | , … , | Икс п — у п | ) . < displaystyle = max left (| x_ <1>-y_ <1>|, | x_ <2>-y_ <2>|, ldots, | x_ -y_ | right) .> |
p не обязательно должно быть целым числом, но оно не может быть меньше 1, потому что в противном случае неравенство треугольника не выполняется.
Расстояние с двумя нормами — это евклидово расстояние , обобщение теоремы Пифагора на более чем две координаты . Это то, что было бы, если бы расстояние между двумя точками было измерено линейкой : «интуитивное» представление о расстоянии.
Расстояние в 1 норму более красочно называется нормой для такси или манхэттенским расстоянием , потому что это расстояние, которое автомобиль проехал бы в городе, разбитом на квадратные кварталы (если нет улиц с односторонним движением).
Расстояние с бесконечной нормой также называется расстоянием Чебышева . В 2D, это минимальное количество ходов короли требуют , чтобы перемещаться между двумя квадратами на шахматной доске .
Р -норма редко используется для значений р , кроме 1, 2 и бесконечности, но видеть суперэллипс .
В физическом пространстве евклидово расстояние в некотором смысле является наиболее естественным, потому что в этом случае длина твердого тела не изменяется при вращении .
Вариационная формулировка расстояния
Евклидово расстояние между двумя точками в пространстве ( и ) может быть записано в вариационной форме, где расстояние является минимальным значением интеграла: А знак равно р → ( 0 ) < Displaystyle А = < vec > (0)> B знак равно р → ( Т ) < Displaystyle B = < vec > (T)>
Вот траектория (путь) между двумя точками. Значение интеграла (D) представляет длину этой траектории. Расстояние является минимальным значением этого интеграла и получается, когда где — оптимальная траектория. В известном евклидовом случае (указанный выше интеграл) эта оптимальная траектория представляет собой просто прямую линию. Хорошо известно, что кратчайший путь между двумя точками — это прямая линия. Формально прямые линии можно получить, решив уравнения Эйлера – Лагранжа для указанного выше функционала . В неевклидовых многообразиях (искривленных пространствах), где природа пространства представлена метрическим тензором, подынтегральное выражение должно быть изменено на , где использовалось соглашение Эйнштейна о суммировании . р → ( т ) < Displaystyle < vec > (т)> р знак равно р * < Displaystyle г = г ^ <*>> р * < displaystyle r ^ <*>> грамм а б < displaystyle g_ > грамм а c р ˙ c грамм а б р ˙ б < displaystyle < sqrt < dot > _ g_ < dot > ^ >>>
Обобщение на многомерные объекты
Евклидово расстояние между двумя объектами также может быть обобщено на случай, когда объекты больше не являются точками, а представляют собой многомерные многообразия , такие как пространственные кривые, поэтому в дополнение к разговору о расстоянии между двумя точками можно обсудить концепции расстояния между двумя струны. Поскольку новые объекты, с которыми имеют дело, являются расширенными объектами (больше не точками), дополнительные концепции, такие как нерасширяемость, ограничения кривизны и нелокальные взаимодействия, которые обеспечивают непересечение, становятся центральными в понятии расстояния. Расстояние между двумя многообразиями — это скалярная величина, которая получается в результате минимизации обобщенного функционала расстояния, который представляет преобразование между двумя многообразиями:
Вышеупомянутый двойной интеграл представляет собой обобщенный функционал расстояния между двумя полимерными конформациями. является пространственным параметром и является псевдовремени. Это означает, что это конформация полимер / струна во время, параметризованная по длине струны на . Точно так же и траектория бесконечно малого отрезка струны при преобразовании всей струны из конформации в конформацию . Член с кофактором является множителем Лагранжа, и его роль заключается в обеспечении того, чтобы длина полимера оставалась неизменной во время преобразования. Если два дискретных полимера нерастяжимы, тогда преобразование минимального расстояния между ними больше не включает чисто прямолинейное движение даже в евклидовой метрике. У такого обобщенного расстояния есть потенциальное применение к проблеме сворачивания белка . s < displaystyle s>т < displaystyle t>р → ( s , т знак равно т я ) < displaystyle < vec > (s, t = t_ )> т я < displaystyle t_ > s < displaystyle s>р → ( s знак равно S , т ) < Displaystyle < vec > (s = S, t)> р → ( s , 0 ) < displaystyle < vec > (s, 0)> р → ( s , Т ) < displaystyle < vec > (s, T)> λ
Это обобщенное расстояние аналогично действию Намбу – Гото в теории струн , однако нет точного соответствия, потому что евклидово расстояние в трехмерном пространстве не эквивалентно пространственно-временному расстоянию, минимизированному для классической релятивистской струны.
Алгебраическое расстояние
Это показатель, часто используемый в компьютерном зрении, который может быть минимизирован методом наименьших квадратов . [1] [2] Для кривых или поверхностей, заданных уравнением (например, коники в однородных координатах ), алгебраическое расстояние от точки до кривой просто . Это может служить «начальным предположением» для геометрического расстояния для уточнения оценок кривой с помощью более точных методов, таких как нелинейный метод наименьших квадратов . Икс Т C Икс знак равно 0 < displaystyle x ^ < text > Cx = 0> Икс ′ < displaystyle x ‘>Икс ′ Т C Икс ′ < displaystyle x ‘^ < text > Cx’>
Общая метрика
В математике , в частности в геометрии , функция расстояния на заданном множестве M — это функция d : M × M → R , где R обозначает множество действительных чисел , которая удовлетворяет следующим условиям:
- d ( x , y ) ≥ 0 и d ( x , y ) = 0 тогда и только тогда, когдаx = y . (Расстояние между двумя разными точками положительно и равно нулю точно от точки до самой себя.)
- Он симметричен : d ( x , y ) = d ( y , x ) . (Расстояние между x и y одинаково в обоих направлениях.)
- Он удовлетворяет неравенству треугольника : d ( x , z ) ≤ d ( x , y ) + d ( y , z ) . (Расстояние между двумя точками — это кратчайшее расстояние по любому пути). Такая функция расстояния известна как метрика . Вместе с набором он составляет метрическое пространство .
Например, обычное определение расстояния между двумя действительными числами x и y : d ( x , y ) = | х — у | . Это определение удовлетворяет трем условиям выше, и соответствует стандартной топологии на прямой . Но расстояние на данном множестве — выбор определения. Другой возможный выбор — определить: d ( x , y ) = 0, если x = y , и 1 в противном случае. Это также определяет метрику, но дает совершенно другую топологию, « дискретную топологию »; с этим определением числа не могут быть сколь угодно близкими.
Расстояния между наборами и между точкой и набором
Между объектами возможны различные определения расстояний. Например, между небесными телами не следует путать расстояние от поверхности до поверхности и расстояние от центра до центра. Если первое намного меньше второго, как для низкой околоземной орбиты , обычно указывается первое (высота), в противном случае, например, для расстояния Земля – Луна, второе.
Есть два общих определения расстояния между двумя непустыми подмножествами данного метрического пространства :
- Одна из версий расстояния между двумя непустыми множествами — это нижняя грань расстояний между любыми двумя из их соответствующих точек, что является повседневным значением этого слова, т. Е.
- Расстояние Хаусдорфа — это большее из двух значений, одно из которых является супремумом , для точки, лежащей в пределах одного набора, нижнего предела, для второй точки, лежащей над другим набором, расстояния между точками, а другое значение аналогично определены, но роли двух наборов поменялись местами. Это расстояние делает само множество непустых компактных подмножеств метрического пространства метрическим пространством .
Расстояние между точкой и множеством является нижней гранью расстояний между точкой и те , в наборе. Это соответствует расстоянию, в соответствии с первым упомянутым выше определением расстояния между наборами, от набора, содержащего только эту точку, до другого набора.
В терминах этого определение расстояния Хаусдорфа можно упростить: это большее из двух значений, одно из которых является супремумом, для точки, находящейся в пределах одного набора, расстояния между точкой и набором, а другое значение определены аналогично, но роли двух наборов поменялись местами.
Теория графов
В теории графов расстояние между двумя вершинами представляет собой длину самого короткого пути между этими вершинами.
Статистические расстояния
В статистике и информационной геометрии существует много видов статистических расстояний , особенно расхождения , особенно расхождения Брегмана и f- расхождения . Они включают и обобщают многие понятия «разницы между двумя распределениями вероятностей » и позволяют изучать их геометрически, как статистические многообразия . Самым элементарным является квадрат Евклидова расстояния , который составляет основу наименьших квадратов ; это самое основное расхождение Брегмана. Наиболее важным в теории информации является относительная энтропия ( дивергенция Кульбака – Лейблера ), которая позволяет аналогичным образом изучать оценку максимального правдоподобия геометрически; это самая основная f- дивергенция, а также дивергенция Брегмана (и единственная дивергенция, которая является обеими). Статистические многообразия, соответствующие расходимости Брегмана, являются плоскими многообразиями в соответствующей геометрии, что позволяет использовать аналог теоремы Пифагора (которая традиционно верна для квадрата евклидова расстояния) для линейных обратных задач при выводе теории оптимизации .
Другие важные статистические расстояния включают расстояние Махаланобиса , энергетическое расстояние и многие другие.
Другие математические «расстояния»
- Канберрское расстояние — взвешенная версия манхэттенского расстояния, используемая в информатике.
В психологии
Психологическая дистанция определяется как «различные способы, которыми объект может быть удален от себя» по таким измерениям, как «время, пространство, социальная дистанция и гипотетичность». Взаимосвязь между психологической дистанцией и степенью абстрактности или конкретного мышления описывается в теории конструктивного уровня , которая представляет собой основу для принятия решений .
Найдите правильный ответ на вопрос ✅ «Как пишется расстояние математическое буквой …» по предмету 📘 Математика, а если вы сомневаетесь в правильности ответов или ответ отсутствует, то попробуйте воспользоваться умным поиском на сайте и найти ответы на похожие вопросы.
Смотреть другие ответы
Какую цифру можно поставить вместо звёздочки 347*, что бы полученное число делилось нацело и на 2 и на 3?
Ответы (5)
Найти площадь трапеции со сторонами 13,20,37, 60
Ответы (2)
Двигаясь вверх по реке, рыбак проплыл на лодке S=6 km за t1=6 ч Потом он заснул и и проснувшись через 3 ч, обнаружил что находиться в том же самом месте, с которого он начал движение.
Ответы (1)
3. Винни Пух должен прийти к Кролику в 12 ч 35 мин. Путь от его дома до дома Кролика занимает 25 минут. По дороге Винни Пух зашёл в гости к Сове.
Ответы (2)
3 бригады производили прополку кукурузы. 1 бригада прополола 30 процентов всей прощади, 2 60 процентов того, что прополола 1, а 3 остальную прощадь. Сколько гиктаров прополола все бригады вместе если 3 бригада прополола на 198 га больше, чем 1
Ответы (1)
0 интересует
0 не интересует
130 просмотров
Как обозначается расстояние в математике (какой буквой)
- обозначается
- расстояние
- математике
- 1 — 4 классы
- математика
спросил
17 Апр, 18
от
Alinacraft_zn
(30 баллов)
в категории Математика
1 Ответ
0 интересует
0 не интересует
ответил
17 Апр, 18
от
Printeska55_zn
(28 баллов)
V-скорость
T-время
S-растояние
вроде так
Добро пожаловать на сайт Школьные решения и ответы. У нас вы можете задавать задачи и получать решения от других членов сообщества.
- Расстояние в математике
-
Метри́ческим простра́нством называется множество, в котором определено расстояние между любой парой элементов.
Формальное определение
Метрическое пространство M есть множество точек с функцией расстояния (также называется метрикой)
(где
обозначает множество вещественных чисел). Для любых точек x,y,z из M эта функция должна удовлетворять следующим условиям:
(аксиома тождества).
- d(x,y) = d(y,x) (аксиома симметрии).
(аксиома треугольника или неравенство треугольника).
Эти аксиомы отражают интуитивное понятие расстояния. Например, расстояние должно быть неотрицательно, то есть
(это вытекает из аксиомы треугольника при z = x) и расстояние от x до y такое же, как и от y до x. Неравенство треугольника означает, что пройти от x до z можно короче, или хотя бы не длиннее, чем сначала пройти x до y, а потом от y до z.
Обозначения
Обычно расстояние между точками x и y в метрическом пространстве M обозначается
- d(x,y),
- | xy | или | xy | M , если необходимо подчеркнуть что речь идет о M,
- xy
- | x − y |
Примеры
- Дискретная метрика: d(x,y) = 0, если x = y, и d(x,y) = 1 во всех остальных случаях.
- Вещественные числа с функцией расстояния d(x,y) = | y − x | и евклидово пространство являются полными метрическими пространствами.
- Манхеттенская, или городская метрика: координатная плоскость, на которой расстояние определено как сумма расстояний между координатами. Более общий пример: любое нормированное пространство можно превратить в метрическое, определив функцию расстояния
, в случае конечной размерности это называется пространством Минковского[1] (не надо путать с другим пространством Минковского).
- Так называемая Французская железнодорожная метрика является примером, который нередко приводят в качестве примера метрики, не порожденной нормой.
- Любое связное риманово многообразие M можно превратить в метрическое пространство, определив расстояние как точную нижнюю грань длин путей, соединяющих пару точек.
- Множество вершин любого связного графа G можно превратить в метрическое пространство, определив расстояние как минимальное число рёбер в пути, соединяющем вершины.
- Множество компактных подмножеств K(M) любого метрического пространства M можно превратить в метрическое пространство, определив расстояние с помощью так называемой метрики Хаусдорффа. В этой метрике два подмножества близки друг к другу, если для любой точки одного множества можно найти близкую точку в другом подмножестве. Вот точное определение:
- Множество всех компактных метрических пространств (с точностью до изометрии) можно превратить в метрическое пространство, определив расстояние с помощью так называемой метрики Громова — Хаусдорффа.
Связанные определения
- Метрическое пространство называется полным, если любая фундаментальная последовательность в нём сходится к некоторому элементу этого пространства.
- Метрика d на M называется внутренней, если любые две точки x и y в M можно соединить кривой с длиной, произвольно близкой к d(x,y).
- Любое метрическое пространство обладает естественной топологией, базой для которой служит множество открытых шаров, т.е. множеств следующего типа:
-
,
- где x есть точка в M и r — положительное вещественное число, называемое радиусом шара. Иначе говоря, множество O является открытым, если для любой точки
найдётся положительное число r, такое, что множество точек на расстоянии меньше r от x принадлежит O.
- Две метрики, определяющие одну и ту же топологию, называются эквивалентными.
- Топологическое пространство, которое может быть получено таким образом, называется метризируемым.
- Расстояние d(x,S) от точки x до подмножества S в M определяется по формуле:
-
- Тогда d(x,S) = 0, только если x принадлежит замыканию S.
Свойства
- Метрическое пространство компактно тогда и только тогда, когда из любой последовательности точек можно выбрать сходящуюся подпоследовательность (секвенциальная компактность).
- Метрическое пространство может не иметь счётной базы, но всегда удовлетворяет первой аксиоме счётности — имеет счётную базу в каждой точке.
- Более того, каждый компакт в метрическом пространстве имеет счётную базу окрестностей.
- Сверх того, в каждом метрическом пространстве существует такая база, что каждая точка пространства принадлежит лишь счётному множеству её элементов — точечно-счётная база (но это свойство слабее метризуемости даже в присутствии паракомпактности и хаусдорфовости).
Вариации и обобщения
Для данного множества
, функция
называется псевдометрикой или полуметрикой на
если для любых точек
из
она удовлетворяет следующим условиям:
;
(симметрия);
(неравенство треугольника).
То есть, в отличие от метрики, различные точки в
могут находится на нулевом расстоянии. Псевдометрика естественно определяет метрику на факторпространстве
где
.
Метрика на пространстве называется ультраметрикой, если она удовлетворяет сильному неравенству треугольника:
-
-
-
- Для всех
,
и
в
.
- Для всех
-
-
Иногда рассматривают метрики со значениями
, соответствующие пространства называются
-метрическими пространствами. Для любой такой метрики можно рассмотреть конечную метрику
или
. Эти метрические пространства имеют одну и ту же топологию.
История
Морис Фреше впервые ввёл понятие метрического пространства[2] в связи с рассмотрением функциональных пространств.
Примечания
- ↑ К. Лейхтвейс, Выпуклые множества, Определение 11.2
- ↑ M. Fréchet, Sur quelques points du calcul fonctionnel, Rendic. Circ. Mat. Palermo 22(1906) 1-74,
См. также
- Индуцированная метрика
Литература
- Н.Васильев,
- Метрические пространства Квант, №1, 1990;
- Метрические пространства Квант, №10, 1970.
- В.А.Скворцов, Примеры метрических пространств, Библиотека «Математическое просвещение», выпуск 9, (2001).
- Ю.А.Шрейдер Что такое расстояние?, «Популярные лекции по математике», Выпуск 38, Физматгиз 1963 г., 76 стр.
Ссылки
Wikimedia Foundation.
2010.
Полезное
Смотреть что такое «Расстояние в математике» в других словарях:
-
Расстояние — В этой статье не хватает ссылок на источники информации. Информация должна быть проверяема, иначе она может быть поставлена под сомнение и удалена. Вы можете отредактировать эту статью, добавив ссылки на авторитетные источники. Эта отметка… … Википедия
-
Расстояние Левенштейна — (также редакционное расстояние или дистанция редактирования) между двумя строками в теории информации и компьютерной лингвистике это минимальное количество операций вставки одного символа, удаления одного символа и замены одного символа на… … Википедия
-
Популярные лекции по математике — «Популярные лекции по математике» серия брошюр на разные математические темы, выпускавшихся в СССР. Многие выпуски неоднократно переиздавались. Выпуски 1 26 вышли в издательстве «Гостехиздат», затем они выходили в издательстве «Физматгиз» и… … Википедия
-
Популярные лекции по математике (книжная серия) — «Популярные лекции по математике» серия брошюр на разные математические темы, выпускавшихся в СССР. Многие выпуски неоднократно переиздавались. Выпуски 1 26 вышли в издательстве «Гостехиздат», затем они выходили в издательстве «Физматгиз» и… … Википедия
-
Плоскость (в математике) — Две пересекающиеся плоскости Плоскость одно из основных понятий геометрии. При систематическом изложении геометрии понятие плоскости обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется аксиомами геометрии … Википедия
-
КООРДИНАТЫ (в математике) — КООРДИНАТЫ (от лат. co совместно и ordinatus упорядоченный, определенный), числа, заданием которых определяется положение точки на плоскости, на поверхности или в пространстве. Прямоугольные (декартовы) координаты точки на плоскости суть… … Энциклопедический словарь
-
Фокус (в математике) — Конические сечения: окружность, эллипс, парабола (плоскость сечения параллельна образующей конуса), гипербола. Коническое сечение или коника есть пересечение плоскости с круговым конусом. Существует три главных типа конических сечений: эллипс,… … Википедия
-
Координаты в математике — величины, определяющие положение точки. В Декартовых прямоугольных К. положение точки определяется тремя расстояниями ее от трех взаимно перпендикулярных плоскостей; пересечения этих плоскостей представляют собой три прямые, выходящие из одной… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
-
Координаты, в математике — величины, определяющие положение точки. В Декартовых прямоугольных К. положение точки определяется тремя расстояниями ее от трех взаимно перпендикулярных плоскостей; пересечения этих плоскостей представляют собой три прямые, выходящие из одной… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
-
Евклидово расстояние — В математике термин евклидово пространство может обозначать один из сходных и тесно связанных объектов: В обоих случаях, n мерное евклидово пространство обычно обозначается , хотя часто используется не вполне приемлемое обозначение . 1.… … Википедия
Вопрос:
Как пишется расстояние математическое буквой
Ответы:
s-скорость
t-время
v-расстояние
S-эс расстояние t-время те V-скорость
Как пишется расстояние математическое буквой
- пишется
- расстояние
- математическое
- 1 — 4 классы
- математика
спросил
13 Апр, 18
от
Arevik2_zn
(57 баллов)
в категории Математика
2 Ответы
ответил
13 Апр, 18
от
Катя6531_zn
Начинающий
(138 баллов)
Лучший ответ
S-скорость
t-время
v-расстояние
0 голосов
ответил
13 Апр, 18
от
Focfoc54_zn
Одаренный
(3.9k баллов)
S-эс расстояние t-время те V-скорость
Добро пожаловать на сайт Ответы онлайн, где вы можете задавать вопросы и получать ответы от других членов сообщества.
…
Инфоурок
›
Другое
›Другие методич. материалы›Математика.Памятка на тему : Скорость,время,расстояние.
Математика.Памятка на тему : Скорость,время,расстояние.
Скачать материал
Скачать материал


- Сейчас обучается 2426 человек из 85 регионов


- Сейчас обучается 103 человека из 42 регионов




Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 054 754 материала в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Другие материалы
Рейтинг:
5 из 5
- 11.02.2018
- 1474
- 38
- 11.02.2018
- 359
- 0
Рейтинг:
5 из 5
- 11.02.2018
- 941
- 6
- 11.02.2018
- 2717
- 9
- 11.02.2018
- 386
- 0
- 11.02.2018
- 638
- 0
- 11.02.2018
- 330
- 0
Рейтинг:
5 из 5
- 11.02.2018
- 2652
- 45
Вам будут интересны эти курсы:
-
Курс повышения квалификации «Возрастные особенности детей младшего школьного возраста»
-
Курс профессиональной переподготовки «Методика организации образовательного процесса в начальном общем образовании»
-
Курс повышения квалификации «Организация проектно-исследовательской деятельности учащихся в рамках реализации ФГОС»
-
Курс повышения квалификации «Использование мини-проектов в школьном: начальном, основном и среднем общем и среднем профессиональном естественнонаучном образовании в условиях реализации ФГОС»
-
Курс повышения квалификации «Тайм-менеджмент — персональная эффективность преподавателя»
-
Курс профессиональной переподготовки «Организация инклюзивного обучения в сфере образования»
-
Курс повышения квалификации «Формирование мотивации учебной деятельности младших школьников с ограниченными возможностями здоровья»
-
Курс повышения квалификации «Система работы учителя-дефектолога при обучении и воспитании детей с особыми образовательными потребностями (ООП) в общеобразовательном учреждении»
-
Курс повышения квалификации «Активизация познавательной деятельности младших школьников с ограниченными возможностями здоровья (ОВЗ) как стратегия повышения успешной учебной деятельности»
-
Курс повышения квалификации «Применение методов арт-терапии в работе со старшими дошкольниками и младшими школьниками»
-
Курс повышения квалификации «Продуктивность учебной деятельности младших школьников общеобразовательного учреждения в рамках реализации ФГОС НОО»
-
Курс повышения квалификации «Проективные методики в начальной школе в соответствии с ФГОС»
-
Курс повышения квалификации «Система диагностики предметных и метапредметных результатов в начальной школе»
-
Курс профессиональной переподготовки «Оказание психолого-педагогической помощи лицам с ОВЗ»
-
Курс профессиональной переподготовки «Музыка: теория и методика преподавания в сфере начального общего, основного общего, среднего общего образования»
-
Скачать материал
-
11.02.2018
2063
-
DOCX
14.9 кбайт -
47
скачиваний - Оцените материал:
-
-
Настоящий материал опубликован пользователем Cарышева Линара Ильинична. Инфоурок является
информационным посредником и предоставляет пользователям возможность размещать на сайте
методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них
сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайтЕсли Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с
сайта, Вы можете оставить жалобу на материал.Удалить материал
-
- На сайте: 6 лет и 3 месяца
- Подписчики: 0
- Всего просмотров: 151943
-
Всего материалов:
82
Distance is a numerical or occasionally qualitative measurement of how far apart objects or points are. In physics or everyday usage, distance may refer to a physical length or an estimation based on other criteria (e.g. «two counties over»). Since spatial cognition is a rich source of conceptual metaphors in human thought,[1] the term is also frequently used metaphorically to mean a measurement of the amount of difference between two similar objects (such as statistical distance between probability distributions or edit distance between strings of text) or a degree of separation (as exemplified by distance between people in a social network). Most such notions of distance, both physical and metaphorical, are formalized in mathematics using the notion of a metric space.
In the social sciences, distance can refer to a qualitative measurement of separation, such as social distance or psychological distance.
Distances in physics and geometry[edit]
The distance between physical locations can be defined in different ways in different contexts.
Straight-line or Euclidean distance[edit]
The distance between two points in physical space is the length of a straight line between them, which is the shortest possible path. This is the usual meaning of distance in classical physics, including Newtonian mechanics.
Straight-line distance is formalized mathematically as the Euclidean distance in two- and three-dimensional space. In Euclidean geometry, the distance between two points A and B is often denoted 
Similarly, given points (x1, y1, z1) and (x2, y2, z2) in three-dimensional space, the distance between them is:[2]
This idea generalizes to higher-dimensional Euclidean spaces.
Measurement[edit]
There are many ways of measuring straight-line distances. For example, it can be done directly using a ruler, or indirectly with a radar (for long distances) or interferometry (for very short distances). The cosmic distance ladder is a set of ways of measuring extremely long distances.
Shortest-path distance on a curved surface[edit]
Airline routes between Los Angeles and Tokyo approximately follow a direct great circle route (top), but use the jet stream (bottom) when heading eastwards. The shortest route appears as a curve rather than a straight line because the map projection does not scale all distances equally compared to the real spherical surface of the Earth.
The straight-line distance between two points on the surface of the Earth is not very useful for most purposes, since we cannot tunnel straight through the Earth’s mantle. Instead, one typically measures the shortest path along the surface of the Earth, as the crow flies. This is approximated mathematically by the great-circle distance on a sphere.
More generally, the shortest path between two points along a curved surface is known as a geodesic. The arc length of geodesics gives a way of measuring distance from the perspective of an ant or other flightless creature living on that surface.
Effects of relativity[edit]
In the theory of relativity, because of phenomena such as length contraction and the relativity of simultaneity, distances between objects depend on a choice of inertial frame of reference. On galactic and larger scales, the measurement of distance is also affected by the expansion of the universe. In practice, a number of distance measures are used in cosmology to quantify such distances.
Other spatial distances[edit]
Unusual definitions of distance can be helpful to model certain physical situations, but are also used in theoretical mathematics:
- In practice, one is often interested in the travel distance between two points along roads, rather than as the crow flies. In a grid plan, the travel distance between street corners is given by the Manhattan distance: the number of east–west and north–south blocks one must traverse to get between those two points.
- Chessboard distance, formalized as Chebyshev distance, is the minimum number of moves a king must make on a chessboard in order to travel between two squares.
Metaphorical distances[edit]
Many abstract notions of distance used in mathematics, science and engineering represent a degree of difference or separation between similar objects. This page gives a few examples.
Statistical distances[edit]
In statistics and information geometry, statistical distances measure the degree of difference between two probability distributions. There are many kinds of statistical distances, typically formalized as divergences; these allow a set of probability distributions to be understood as a geometrical object called a statistical manifold. The most elementary is the squared Euclidean distance, which is minimized by the least squares method; this is the most basic Bregman divergence. The most important in information theory is the relative entropy (Kullback–Leibler divergence), which allows one to analogously study maximum likelihood estimation geometrically; this is an example of both an f-divergence and a Bregman divergence (and in fact the only example which is both). Statistical manifolds corresponding to Bregman divergences are flat manifolds in the corresponding geometry, allowing an analog of the Pythagorean theorem (which holds for squared Euclidean distance) to be used for linear inverse problems in inference by optimization theory.
Other important statistical distances include the Mahalanobis distance and the energy distance.
Edit distances[edit]
In computer science, an edit distance or string metric between two strings measures how different they are. For example, the words «dog» and «dot», which differ by just one letter, are closer than «dog» and «cat», which have no letters in common. This idea is used in spell checkers and in coding theory, and is mathematically formalized in a number of different ways, including Levenshtein distance, Hamming distance, Lee distance, and Jaro–Winkler distance.
Distance in graph theory[edit]
In a graph, the distance between two vertices is measured by the length of the shortest edge path between them. For example, if the graph represents a social network, then the idea of six degrees of separation can be interpreted mathematically as saying that the distance between any two vertices is at most six. Similarly, the Erdős number and the Bacon number—the number of collaborative relationships away a person is from prolific mathematician Paul Erdős and actor Kevin Bacon, respectively—are distances in the graphs whose edges represent mathematical or artistic collaborations.
[edit]
In psychology, human geography, and the social sciences, distance is often theorized not as an objective numerical measurement, but as a qualitative description of a subjective experience.[4] For example, psychological distance is «the different ways in which an object might be removed from» the self along dimensions such as «time, space, social distance, and hypotheticality».[5] In sociology, social distance describes the separation between individuals or social groups in society along dimensions such as social class, race/ethnicity, gender or sexuality.
Mathematical formalization[edit]
Most of the notions of distance between two points or objects described above are examples of the mathematical idea of a metric. A metric or distance function is a function d which takes pairs of points or objects to real numbers and satisfies the following rules:
- The distance between an object and itself is always zero.
- The distance between distinct objects is always positive.
- Distance is symmetric: the distance from x to y is always the same as the distance from y to x.
- Distance satisfies the triangle inequality: if x, y, and z are three objects, then
This condition can be described informally as «intermediate stops can’t speed you up.»
As an exception, many of the divergences used in statistics are not metrics.
Distance between sets[edit]
The distances between these three sets do not satisfy the triangle inequality:
There are multiple ways of measuring the physical distance between objects that consist of more than one point:
- One may measure the distance between representative points such as the center of mass; this is used for astronomical distances such as the Earth–Moon distance.
- One may measure the distance between the closest points of the two objects; in this sense, the altitude of an airplane or spacecraft is its distance from the Earth. The same sense of distance is used in Euclidean geometry to define distance from a point to a line, distance from a point to a plane, or, more generally, perpendicular distance between affine subspaces.
- Even more generally, this idea can be used to define the distance between two subsets of a metric space. The distance between sets A and B is the infimum of the distances between any two of their respective points:
This does not define a metric on the set of such subsets: the distance between overlapping sets is zero, and this distance does not satisfy the triangle inequality for any metric space with two or more points (consider the triple of sets consisting of two distinct singletons and their union).
- The Hausdorff distance between two subsets of a metric space can be thought of as measuring how far they are from perfectly overlapping. Somewhat more precisely, the Hausdorff distance between A and B is either the distance from A to the farthest point of B, or the distance from B to the farthest point of A, whichever is larger. (Here «farthest point» must be interpreted as a supremum.) The Hausdorff distance defines a metric on the set of compact subsets of a metric space.
[edit]
Further information: Length
The word distance is also used for related concepts that are not encompassed by the description «a numerical measurement of how far apart points or objects are».
Distance travelled[edit]
The distance travelled by an object is the length of a specific path travelled between two points,[6] such as the distance walked while navigating a maze. This can even be a closed distance along a closed curve which starts and ends at the same point, such as a ball thrown straight up, or the Earth when it completes one orbit. This is formalized mathematically as the arc length of the curve.
The distance travelled may also be signed: a «forward» distance is positive and a «backward» distance is negative.
Circular distance is the distance traveled by a point on the circumference of a wheel, which can be useful to consider when designing vehicles or mechanical gears (see also odometry). The circumference of the wheel is 2π × radius; if the radius is 1, each revolution of the wheel causes a vehicle to travel 2π radians.
Displacement and directed distance[edit]
Distance along a path compared with displacement. The Euclidean distance is the length of the displacement vector.
The displacement in classical physics measures the change in position of an object during an interval of time. While distance is a scalar quantity, or a magnitude, displacement is a vector quantity with both magnitude and direction. In general, the vector measuring the difference between two locations (the relative position) is sometimes called the directed distance.[7] For example, the directed distance from the New York City Main Library flag pole to the Statue of Liberty flag pole has:
- A starting point: library flag pole
- An ending point: statue flag pole
- A direction: -38°
- A distance: 8.72 km
Signed distance[edit]
In mathematics and its applications, the signed distance function (or oriented distance function) is the orthogonal distance of a given point x to the boundary of a set Ω in a metric space, with the sign determined by whether or not x is in the interior of Ω. The function has positive values at points x inside Ω, it decreases in value as x approaches the boundary of Ω where the signed distance function is zero, and it takes negative values outside of Ω.[8] However, the alternative convention is also sometimes taken instead (i.e., negative inside Ω and positive outside).[9]
See also[edit]
Wikiquote has quotations related to Distance.
- Absolute difference
- Astronomical system of units
- Color difference
- Closeness (mathematics)
- Distance geometry problem
- Dijkstra’s algorithm
- Distance matrix
- Distance set
- Engineering tolerance
- Multiplicative distance
- Optical path length
- Orders of magnitude (length)
- Proper length
- Proxemics – physical distance between people
- Signed distance function
- Similarity measure
- Social distancing
- Vertical distance
Library support[edit]
- Python (programming language)
- Interspace -A package for finding the distance between two vectors, numbers and strings.
- SciPy -Distance computations (
scipy.spatial.distance)
- Julia (programming language)
- Julia Statistics Distance -A Julia package for evaluating distances (metrics) between vectors.
References[edit]
- ^ Schnall, Simone (2014). «Are there basic metaphors?». The power of metaphor: Examining its influence on social life. American Psychological Association. pp. 225–247. doi:10.1037/14278-010.
- ^ a b Weisstein, Eric W. «Distance». mathworld.wolfram.com. Retrieved 2020-09-01.
- ^ «Distance Between 2 Points». www.mathsisfun.com. Retrieved 2020-09-01.
- ^ «SOCIAL DISTANCES». www.hawaii.edu. Retrieved 2020-07-20.
- ^ Trope Y, Liberman N (April 2010). «Construal-level theory of psychological distance». Psychological Review. 117 (2): 440–63. doi:10.1037/a0018963. PMC 3152826. PMID 20438233.
- ^ «What is displacement? (article)». Khan Academy. Retrieved 2020-07-20.
- ^ «The Directed Distance» (PDF). Information and Telecommunication Technology Center. University of Kansas. Archived from the original (PDF) on 10 November 2016. Retrieved 18 September 2018.
- ^ Chan, T.; Zhu, W. (2005). Level set based shape prior segmentation. IEEE Computer Society Conference on Computer Vision and Pattern Recognition. doi:10.1109/CVPR.2005.212.
- ^ Malladi, R.; Sethian, J.A.; Vemuri, B.C. (1995). «Shape modeling with front propagation: a level set approach». IEEE Transactions on Pattern Analysis and Machine Intelligence. 17 (2): 158–175. CiteSeerX 10.1.1.33.2443. doi:10.1109/34.368173.
Bibliography[edit]
- Deza E, Deza M (2006). Dictionary of Distances. Elsevier. ISBN 0-444-52087-2.
Distance is a numerical or occasionally qualitative measurement of how far apart objects or points are. In physics or everyday usage, distance may refer to a physical length or an estimation based on other criteria (e.g. «two counties over»). Since spatial cognition is a rich source of conceptual metaphors in human thought,[1] the term is also frequently used metaphorically to mean a measurement of the amount of difference between two similar objects (such as statistical distance between probability distributions or edit distance between strings of text) or a degree of separation (as exemplified by distance between people in a social network). Most such notions of distance, both physical and metaphorical, are formalized in mathematics using the notion of a metric space.
In the social sciences, distance can refer to a qualitative measurement of separation, such as social distance or psychological distance.
Distances in physics and geometry[edit]
The distance between physical locations can be defined in different ways in different contexts.
Straight-line or Euclidean distance[edit]
The distance between two points in physical space is the length of a straight line between them, which is the shortest possible path. This is the usual meaning of distance in classical physics, including Newtonian mechanics.
Straight-line distance is formalized mathematically as the Euclidean distance in two- and three-dimensional space. In Euclidean geometry, the distance between two points A and B is often denoted 
Similarly, given points (x1, y1, z1) and (x2, y2, z2) in three-dimensional space, the distance between them is:[2]
This idea generalizes to higher-dimensional Euclidean spaces.
Measurement[edit]
There are many ways of measuring straight-line distances. For example, it can be done directly using a ruler, or indirectly with a radar (for long distances) or interferometry (for very short distances). The cosmic distance ladder is a set of ways of measuring extremely long distances.
Shortest-path distance on a curved surface[edit]
Airline routes between Los Angeles and Tokyo approximately follow a direct great circle route (top), but use the jet stream (bottom) when heading eastwards. The shortest route appears as a curve rather than a straight line because the map projection does not scale all distances equally compared to the real spherical surface of the Earth.
The straight-line distance between two points on the surface of the Earth is not very useful for most purposes, since we cannot tunnel straight through the Earth’s mantle. Instead, one typically measures the shortest path along the surface of the Earth, as the crow flies. This is approximated mathematically by the great-circle distance on a sphere.
More generally, the shortest path between two points along a curved surface is known as a geodesic. The arc length of geodesics gives a way of measuring distance from the perspective of an ant or other flightless creature living on that surface.
Effects of relativity[edit]
In the theory of relativity, because of phenomena such as length contraction and the relativity of simultaneity, distances between objects depend on a choice of inertial frame of reference. On galactic and larger scales, the measurement of distance is also affected by the expansion of the universe. In practice, a number of distance measures are used in cosmology to quantify such distances.
Other spatial distances[edit]
Unusual definitions of distance can be helpful to model certain physical situations, but are also used in theoretical mathematics:
- In practice, one is often interested in the travel distance between two points along roads, rather than as the crow flies. In a grid plan, the travel distance between street corners is given by the Manhattan distance: the number of east–west and north–south blocks one must traverse to get between those two points.
- Chessboard distance, formalized as Chebyshev distance, is the minimum number of moves a king must make on a chessboard in order to travel between two squares.
Metaphorical distances[edit]
Many abstract notions of distance used in mathematics, science and engineering represent a degree of difference or separation between similar objects. This page gives a few examples.
Statistical distances[edit]
In statistics and information geometry, statistical distances measure the degree of difference between two probability distributions. There are many kinds of statistical distances, typically formalized as divergences; these allow a set of probability distributions to be understood as a geometrical object called a statistical manifold. The most elementary is the squared Euclidean distance, which is minimized by the least squares method; this is the most basic Bregman divergence. The most important in information theory is the relative entropy (Kullback–Leibler divergence), which allows one to analogously study maximum likelihood estimation geometrically; this is an example of both an f-divergence and a Bregman divergence (and in fact the only example which is both). Statistical manifolds corresponding to Bregman divergences are flat manifolds in the corresponding geometry, allowing an analog of the Pythagorean theorem (which holds for squared Euclidean distance) to be used for linear inverse problems in inference by optimization theory.
Other important statistical distances include the Mahalanobis distance and the energy distance.
Edit distances[edit]
In computer science, an edit distance or string metric between two strings measures how different they are. For example, the words «dog» and «dot», which differ by just one letter, are closer than «dog» and «cat», which have no letters in common. This idea is used in spell checkers and in coding theory, and is mathematically formalized in a number of different ways, including Levenshtein distance, Hamming distance, Lee distance, and Jaro–Winkler distance.
Distance in graph theory[edit]
In a graph, the distance between two vertices is measured by the length of the shortest edge path between them. For example, if the graph represents a social network, then the idea of six degrees of separation can be interpreted mathematically as saying that the distance between any two vertices is at most six. Similarly, the Erdős number and the Bacon number—the number of collaborative relationships away a person is from prolific mathematician Paul Erdős and actor Kevin Bacon, respectively—are distances in the graphs whose edges represent mathematical or artistic collaborations.
[edit]
In psychology, human geography, and the social sciences, distance is often theorized not as an objective numerical measurement, but as a qualitative description of a subjective experience.[4] For example, psychological distance is «the different ways in which an object might be removed from» the self along dimensions such as «time, space, social distance, and hypotheticality».[5] In sociology, social distance describes the separation between individuals or social groups in society along dimensions such as social class, race/ethnicity, gender or sexuality.
Mathematical formalization[edit]
Most of the notions of distance between two points or objects described above are examples of the mathematical idea of a metric. A metric or distance function is a function d which takes pairs of points or objects to real numbers and satisfies the following rules:
- The distance between an object and itself is always zero.
- The distance between distinct objects is always positive.
- Distance is symmetric: the distance from x to y is always the same as the distance from y to x.
- Distance satisfies the triangle inequality: if x, y, and z are three objects, then
This condition can be described informally as «intermediate stops can’t speed you up.»
As an exception, many of the divergences used in statistics are not metrics.
Distance between sets[edit]
The distances between these three sets do not satisfy the triangle inequality:
There are multiple ways of measuring the physical distance between objects that consist of more than one point:
- One may measure the distance between representative points such as the center of mass; this is used for astronomical distances such as the Earth–Moon distance.
- One may measure the distance between the closest points of the two objects; in this sense, the altitude of an airplane or spacecraft is its distance from the Earth. The same sense of distance is used in Euclidean geometry to define distance from a point to a line, distance from a point to a plane, or, more generally, perpendicular distance between affine subspaces.
- Even more generally, this idea can be used to define the distance between two subsets of a metric space. The distance between sets A and B is the infimum of the distances between any two of their respective points:
This does not define a metric on the set of such subsets: the distance between overlapping sets is zero, and this distance does not satisfy the triangle inequality for any metric space with two or more points (consider the triple of sets consisting of two distinct singletons and their union).
- The Hausdorff distance between two subsets of a metric space can be thought of as measuring how far they are from perfectly overlapping. Somewhat more precisely, the Hausdorff distance between A and B is either the distance from A to the farthest point of B, or the distance from B to the farthest point of A, whichever is larger. (Here «farthest point» must be interpreted as a supremum.) The Hausdorff distance defines a metric on the set of compact subsets of a metric space.
[edit]
Further information: Length
The word distance is also used for related concepts that are not encompassed by the description «a numerical measurement of how far apart points or objects are».
Distance travelled[edit]
The distance travelled by an object is the length of a specific path travelled between two points,[6] such as the distance walked while navigating a maze. This can even be a closed distance along a closed curve which starts and ends at the same point, such as a ball thrown straight up, or the Earth when it completes one orbit. This is formalized mathematically as the arc length of the curve.
The distance travelled may also be signed: a «forward» distance is positive and a «backward» distance is negative.
Circular distance is the distance traveled by a point on the circumference of a wheel, which can be useful to consider when designing vehicles or mechanical gears (see also odometry). The circumference of the wheel is 2π × radius; if the radius is 1, each revolution of the wheel causes a vehicle to travel 2π radians.
Displacement and directed distance[edit]
Distance along a path compared with displacement. The Euclidean distance is the length of the displacement vector.
The displacement in classical physics measures the change in position of an object during an interval of time. While distance is a scalar quantity, or a magnitude, displacement is a vector quantity with both magnitude and direction. In general, the vector measuring the difference between two locations (the relative position) is sometimes called the directed distance.[7] For example, the directed distance from the New York City Main Library flag pole to the Statue of Liberty flag pole has:
- A starting point: library flag pole
- An ending point: statue flag pole
- A direction: -38°
- A distance: 8.72 km
Signed distance[edit]
In mathematics and its applications, the signed distance function (or oriented distance function) is the orthogonal distance of a given point x to the boundary of a set Ω in a metric space, with the sign determined by whether or not x is in the interior of Ω. The function has positive values at points x inside Ω, it decreases in value as x approaches the boundary of Ω where the signed distance function is zero, and it takes negative values outside of Ω.[8] However, the alternative convention is also sometimes taken instead (i.e., negative inside Ω and positive outside).[9]
See also[edit]
Wikiquote has quotations related to Distance.
- Absolute difference
- Astronomical system of units
- Color difference
- Closeness (mathematics)
- Distance geometry problem
- Dijkstra’s algorithm
- Distance matrix
- Distance set
- Engineering tolerance
- Multiplicative distance
- Optical path length
- Orders of magnitude (length)
- Proper length
- Proxemics – physical distance between people
- Signed distance function
- Similarity measure
- Social distancing
- Vertical distance
Library support[edit]
- Python (programming language)
- Interspace -A package for finding the distance between two vectors, numbers and strings.
- SciPy -Distance computations (
scipy.spatial.distance)
- Julia (programming language)
- Julia Statistics Distance -A Julia package for evaluating distances (metrics) between vectors.
References[edit]
- ^ Schnall, Simone (2014). «Are there basic metaphors?». The power of metaphor: Examining its influence on social life. American Psychological Association. pp. 225–247. doi:10.1037/14278-010.
- ^ a b Weisstein, Eric W. «Distance». mathworld.wolfram.com. Retrieved 2020-09-01.
- ^ «Distance Between 2 Points». www.mathsisfun.com. Retrieved 2020-09-01.
- ^ «SOCIAL DISTANCES». www.hawaii.edu. Retrieved 2020-07-20.
- ^ Trope Y, Liberman N (April 2010). «Construal-level theory of psychological distance». Psychological Review. 117 (2): 440–63. doi:10.1037/a0018963. PMC 3152826. PMID 20438233.
- ^ «What is displacement? (article)». Khan Academy. Retrieved 2020-07-20.
- ^ «The Directed Distance» (PDF). Information and Telecommunication Technology Center. University of Kansas. Archived from the original (PDF) on 10 November 2016. Retrieved 18 September 2018.
- ^ Chan, T.; Zhu, W. (2005). Level set based shape prior segmentation. IEEE Computer Society Conference on Computer Vision and Pattern Recognition. doi:10.1109/CVPR.2005.212.
- ^ Malladi, R.; Sethian, J.A.; Vemuri, B.C. (1995). «Shape modeling with front propagation: a level set approach». IEEE Transactions on Pattern Analysis and Machine Intelligence. 17 (2): 158–175. CiteSeerX 10.1.1.33.2443. doi:10.1109/34.368173.
Bibliography[edit]
- Deza E, Deza M (2006). Dictionary of Distances. Elsevier. ISBN 0-444-52087-2.
На чтение 10 мин. Просмотров 1k. Опубликовано 19 декабря 2022
Вычислить скорость, время и расстояние часто бывает необходимо в повседневной жизни, когда мы рассчитываем время на дорогу. Все эти величины (время, расстояние и скорость) связаны между собой математической формулой и зная две из них всегда можно найти третью. Мы с вами рассмотрим, что понимается под этими величинами, как их найти, решим несколько задач.
Скорость, время и расстояние — это ключевые параметры при решении задач на движение. Эти задачи есть и в ЕГЭ и в ОГЭ по математике. Сегодня мы подробнее остановимся на этих величинах.
Расстояние
Расстояние — это физическая величина, означающая длину между двумя объектами. Расстояние обозначается буквой S и измеряется в единицах длины: метрах. Метр — это международно-принятая единица измерения длины. Однако встречаются и другие единицы длины — километр, сантиметр, миллиметр. В этом случае целесообразно перевести единицы длины в международную систему единиц (СИ).
Например: расстояние от Земли до Солнца равно 149 597 870 700 метров.
Расстояние связано со скоростью и временем:
S=v cdot t
Вот тут таблица длин и их перевода в международную систему единиц — то есть в метры.
| Единицы длины | СИ |
| 1 сантиметр | 0,01 м |
| 1 километр | 1000 м |
| 1 дециметр | 0,1 м |
| 1 миллиметр | 0,001 м |
| 1 микрометр | 1·10-6 м |
| 1 миля | 1609,34 м |
| 1 фут | 0,3048 м |
| 1 ярд | 0,9144 м |
| 1 дюйм | 0,0254 м |
| 1 морская миля | 1852 м |
Время
Время — это физическая величина, которая обозначает непрерывное и необратимое (возможно) движение от прошлого к будущему через настоящее. Это фундаментальная физическая величина, единица измерения времени — секунда. Однако, в задачах могут использоваться и другие единицы времени — часы, минуты, дни.
Время можно найти по формуле:
t=frac{S}{v}
Ученые о времени
По словам греческого философа Парменида (ок. 450 г. до н.э.), время и движение были иллюзиями. Его ученик Зенон Элейский разработал два знаменитых парадокса: «Ахиллес и черепаха» и «Парадокс летящей стрелы», чтобы доказать его утверждения. Платон, живший на пару поколений позже, считал, что время создано вместе со вселенной и существует независимо. Он рассматривал время как пустой контейнер, который можно заполнить движущимися вещами и событиями. Его ученик Аристотель считал, что время не существует независимо от событий, но время есть изменение и движение.
Аристотель пришел к выводу, что время не состоит из последовательных неделимых моментов «сейчас», как пытался сказать Зенон с помощью своего парадокса стрелы. Согласно Аристотелю, не существует серии моментов «сейчас», потому что такие моменты не могли бы исчезнуть в течение их собственной длительности или в следующий момент «сейчас». Исааку Ньютону (1642–1726) время понадобилось в качестве переменной в его уравнениях, и он начал думать о времени с научной точки зрения. Ньютон поддерживал идею Платона о независимости времени. Он разделил время на абсолютное (математическое) время и относительное (обычное) время.
Абсолютное время, или продолжительность, является реальным и математическим, и оно течет неуклонно, независимо от чего-либо внешнего. Относительное время кажущееся и является внешней мерой длительности, которая может быть обнаружена органами чувств с помощью движения, которое может быть точным или неточным.
Готфрид Лейбниц (1646–1716) был согласен с Аристотелем и думал, что без событий и перемен не было бы времени. Физик- теоретик Ли Смолин писал в 2010 году, что исследования квантовой гравитации подтверждают, что четырехмерное пространство-время имеет смысл только в том случае, если время реально, фундаментально и даже является единственным аспектом реальности, который мы непосредственно ощущаем.
Скорость
Скорость обозначается буквой — это физическая величина, которая обозначает какое расстояние проходит объект в единицу времени. Единица измерения скорости — м/с. Однако, встречаются также и км/ч и см/с (эти измерения не входят в международную систему единиц измерения). Скорость показывает как быстро изменяется расстояние во времени.
Например, выражение 9 м/с означает, что тело за 1 секунду проходит 9 метров. То есть за 1 секунду 9 метров, за 2 секунду еще 9 метров, итого за 2 секунду — 18 метров. В курсе школьной математики мы считаем, что скорость равномерная во времени. То есть тело за равные промежутки времени проходит равные расстояния. То есть 9 м/с означает 9 метров в любую из секунд движения тела. Однако, в реальности движение бывает равномерное и неравномерное. Мы не рассматриваем неравномерное движение в курсе математики (1-6 класс), однако в курсе алгебры элементы кинематики с неравномерным движением рассматриваются.
Еще примеры: скорость 100 км/ч — это прохождение расстояния в 100 километров за 1 час.
Формула скорости
Скорость можно найти через расстояние и время по формуле:
v=frac{S}{t}
Средняя скорость
Если движение тела можно разбить на несколько участков и в пределах каждого участка скорость тела не меняется, то целесообразно говорить о средней скорости.
Формула средней скорости:
v=frac{S_{весь ; путь}}{t_{всё ; время}}=frac{S_1+S_2+…+ S_n}{t_1+t_2+…+ t_n}
То есть средняя скорость это отношение всего пути, ко всему времени.
Скорости сближения и удаления
Понятие скорости ученики изучают еще в 4 классе, а далее это понятие расширяется и уточняется. Вводятся такие понятия как скорость сближения и скорость удаления. Не все педагоги используют эти понятия в своей работе, поскольку эти понятия можно использовать только при решении небольшого класса задач на движение и они ограничивают решение задач и другими условиями (например, если тела удаляются или сближаются не по одной прямой, а по перпендикулярным прямым). И все же, давайте мы уточним, о чем вообще идет речь.
Скорость удаления
Если два тела удаляются друг от друга, двигаясь по одной прямой, то в таких случаях говорят о скорости удаления. То есть скорость удаления характеризует расстояние, которое увеличивается по мере удаления двух тел в единицу времени.
Допустим есть два пешехода, которые удаляются друг от друга, первый пешеход удаляется со скоростью 3 км/ч, а второй пешеход со скоростью 4 км/ч. Тогда скорость удаления будет:
3+4=7 км/ч.
Действительно, расстояние, пройденное первым пешеходом за один час будет 3 километра, а расстояние, пройденное вторым пешеходом за то же время будет 4 километра. Тогда при удалении пешеходов друг от друга расстояние между ними увеличивается на 7 километров в каждый час или наши пешеходы удаляются со скоростью 7 км/ч. Мы должны сложить скорости объектов.
Формула скорости удаления:
v_{удаления}=v_1+v_2
где
— скорость одного тела,
— скорость другого тела.
Напомним, что это понятие можно использовать только если тела двигаются в разных направлениях, располагаемых на одной прямой.
Скорость сближения двух тел
Аналогично, рассмотрим ситуацию, если два пешехода двигаются навстречу друг к другу. Один пешеход за один час проходит расстояние 2 км, а второй пешеход за то же время проходит 5 км.
Значит, расстояние между ними будем уменьшаться со скоростью 5+2 = 7 км/ч.
Формула скорости сближения:
v_{сближения}=v_1+v_2
где
— скорость одного тела,
— скорость другого тела.
Если один пешеход догоняет другого. То скорость сближения при движении в одном направлении можно определить, если вычесть из большей скорости меньшую.
То есть, если у нас второго пешехода (=3км/ч) догоняет первый пешеход (
=5 км/ч), то скорость их сближения будет 2 км/ч:
Формула скорости сближения при движении вдогонку:
v_{сближения}=v_1-v_2
где
— скорость одного тела,
— скорость другого тела. При этом
Таблица «скорость, время, расстояние» при решении задач на движение
При решении задач на движение очень удобно пользоваться такой таблицей, в которой три столбца с данными по скорости, времени движения тел и расстоянию, которое они проходят. Эта таблица, кстати помогает легко запомнить формулы скорости, времени и расстояния, если представить что первый столбец — это первый множитель, второй столбец — второй множитель, а третий столбец — произведение.
| Скорость, v, м/с | Время, t, с | Расстояние, S, м |
Простой пример, найти скорость велосипедиста, если за 5 часов он прошел 45 километров.
Составляем таблицу и записываем в нее данные:
| Скорость, v, км/ч | Время, t, ч | Расстояние, S, км |
| ? | 5 | 45 |
Теперь видно, что неизвестна скорость в первом столбце, значит, неизвестен первый множитель. Чтобы определить неизвестный множитель надо произведение разделить на известный множитель: = 45/5 = 9 км/ч.
Важно! В задачах все единицы измерения должны быть приведены либо к международной системе единиц (метр, секунда, м/с) либо к одним единицам измерения (то есть если в задаче есть и м/с и км/ч можно привести всё либо к м/с (тогда и время в секундах и расстояние в метрах), либо к км/ч (тогда и время в часах будет и расстояние в километрах))
Рассмотрим теперь некоторые примеры решения задач
Примеры задач на движение
Задача 1
Школьник идет домой со скоростью 2 км/ч. Расстояние от школы до дома 1 км. За какое время школьник дойдет до дома?
Решение:
Найдем время по формуле: displaystyle t=frac{S}{v}=frac{1}{2}ч.
Школьник дойдет до дома за полчаса.
Ответ: 0,5 ч.
Задача 2
Автомобилист и велосипедист выехали в город из деревни одновременно. Скорость автомобилиста 50 км/ч. Расстояние до города 100 км. Какова скорость велосипедиста, если известно, что он прибыл в город на 8 часов позже автомобилиста?
Решение: Составим таблицу
| Скорость, v, км/ч | Время, t, ч | Расстояние, S, км | |
| Автомобилист | 50 | 100/50 | 100 |
| Велосипедист | x | 100/x | 100 |
Пусть скорость велосипедиста x. В таблице мы сразу смогли написать соотношения для времени движения. По условию задачи дано, что велосипедист прибыл в город на 8 часов позже автомобилиста. Запишем это:
displaystyle frac{100}{x}-frac{100}{50}=8
Мы отнимаем от времени, которое потратил велосипедист (он же потратил больше времени) время, которое потратил автомобилист и получаем 8 часов.
Решим полученное уравнение.
displaystyle frac{100}{x}-2=8
displaystyle frac{100}{x}=10
x=10
Ответ: 10 км/ч
Задача 3
Стрела пролетает 180 метров за 0,05 минуты. Найдите ее скорость.
Решение: прежде чем решать задачу, переведем все единицы в одну систему единиц. Минуты переведем в секунды.
В одной минуте 60 секунд. Значит, чтобы узнать сколько секунд в 0,05 минутах, умножим 0,05 на 60, получим:
0,05 cdot 60=3 c.
Тогда displaystyle v= frac{180}{3}=60 м/с.
Ответ: 60 м/с
Задача 4
Турист прошел лесной участок длиной 10 км со скоростью 5 км/ч, а затем шел по полю 20 км, со скоростью 4 км/ч. Какова средняя скорость туриста?
Решение:
Определим весь путь который прошел турист:
displaystyle S_{весь ; путь}=S_1+S_2=10+20=30 км.
Для прохождения лесного участка турист потратил: displaystyle t_1= frac{S_1}{v_1}=frac{10}{5}=2ч, а на второй участок времени ушло: displaystyle t_2= frac{S_2}{v_2}=frac{20}{4}=5ч
Все время: displaystyle t_{всё ; время}=t_1+t_2=2+5=7ч
Тогда найдем среднюю скорость:
displaystyle v_{ср}= frac{S_{весь ; путь}}{t_{всё ; время}}=frac{30}{7}=4 frac{2}{7} км/ч.
Ответ: displaystyle v_{ср}=4 frac{2}{7}
Задача 5
Лиса гонится за зайцем. Скорость лисы 20 м/с, а скорость зайца 15 м/с. Догонит ли лиса зайца, если заяц находится на расстоянии 300 метров от безопасного места, а лиса находится на расстоянии 200 метров от зайца?
Решение:
Заяц добежит до норы за displaystyle t= frac{300}{15}=20 секунд.
Лиса же за 20 секунд пробежит расстояние displaystyle S= 20 cdot 20=400 метров.
Лиса не догонит зайца.
Действительно, скорость сближения лисы и зайца:
displaystyle v=v_{лисы}-v_{зайца}=20-15=5 м/с
То есть, чтобы преодолеть расстояние 200 метров, которое изначально существует между лисой и зайцем, лисе понадобиться displaystyle t=frac{200}{5}=40 с
Заяц же уже 20 секунд будет в безопасном месте.
Ответ: лиса зайца не догонит.
В этом уроке мы рассмотрим три физические величины, а именно расстояние, скорость и время.
Расстояние
Расстояние мы уже изучали в уроке единицы измерения. Говоря простым языком, расстояние это длина от одного пункта до другого. (Пример: расстояние от дома до школы 2 километра).
Имея дело с большими расстояниями, в основном они будут измеряться в метрах и километрах. Расстояние обозначается латинской буквой S. Можно обозначить и другой буквой, но буква S общепринята.
Скорость
Скоростью называют расстояние, пройденное телом за единицу времени. Под единицей времени подразумевается 1 час, 1 минута или 1 секунда.
Предположим, что двое школьников решили проверить, кто быстрее добежит от двора до спортплощадки. Расстояние от двора до спортплощадки 100 метров. Первый школьник добежал за 25 секунд. Второй за 50 секунд. Кто добежал быстрее?
Быстрее добежал тот, кто за 1 секунду пробежал бóльшее расстояние. Говорят, что у него скорость движения больше. В данном случае скорость школьников это расстояние, которое они пробегают за 1 секунду.
Чтобы найти скорость, нужно расстояние разделить на время движения. Давайте найдём скорость первого школьника. Для этого разделим 100 метров на время движения первого школьника, то есть на 25 секунд:
100 м : 25 с = 4
Если расстояние дано в метрах, а время движения в секундах, то скорость измеряется в метрах в секунду (м/с). Если расстояние дано в километрах, а время движения в часах, скорость измеряется в километрах в час (км/ч).
У нас расстояние дано в метрах, а время в секундах. Значит скорость измеряется в метрах в секунду (м/с)
100м : 25с = 4 (м/с)
Итак, скорость движения первого школьника составляет 4 метра в секунду (м/с).
Теперь найдем скорость движения второго школьника. Для этого разделим расстояние на время движения второго школьника, то есть на 50 секунд:
100 м : 50 c = 2 (м/с)
Значит скорость движения второго школьника составляет 2 метра в секунду (м/с).
Скорость движения первого школьника — 4 (м/с)
Скорость движения второго школьника — 2 (м/с)
4 (м/с) > 2 (м/с)
Скорость первого школьника больше. Значит он добежал до спортплощадки быстрее. Скорость обозначается латинской буквой v.
Время
Иногда возникает ситуация, когда требуется узнать за какое время тело преодолеет то или иное расстояние.
Например, от дома до спортивной секции 1000 метров. Мы должны доехать туда на велосипеде. Наша скорость будет 500 метров в минуту (500м/мин). За какое время мы доедем до спортивной секции?
Если за одну минуту мы будем проезжать 500 метров, то сколько таких минут с пятью ста метрами будет в 1000 метрах?
Очевидно, что надо разделить 1000 метров на то расстояние, которое мы будем проезжать за одну минуту, то есть на 500 метров. Тогда мы получим время, за которое доедем до спортивной секции:
1000 : 500 = 2 (мин)
Время движения обозначается маленькой латинской буквой t.
Взаимосвязь скорости, времени, расстояния
Скорость принято обозначать маленькой латинской буквой v, время движения – маленькой буквой t, пройденное расстояние – маленькой буквой s. Скорость, время и расстояние связаны между собой.
Если известны скорость и время движения, то можно найти расстояние. Оно равно скорости, умноженной на время:
s = v × t
Например, мы вышли из дома и направились в магазин. Мы дошли до магазина за 10 минут. Наша скорость была 50 метров в минуту. Зная свою скорость и время, мы можем найти расстояние.
Если за одну минуту мы прошли 50 метров, то сколько таких пятьдесят метров мы пройдем за 10 минут? Очевидно, что умножив 50 метров на 10, мы определим расстояние от дома до магазина:
v = 50 (м/мин)
t = 10 минут
s = v × t = 50 × 10 = 500 (метров до магазина)
Если известно время и расстояние, то можно найти скорость:
v = s : t
Например, расстояние от дома до школы 900 метров. Школьник дошел до этой школы за 10 минут. Какова была его скорость?
Скорость движения школьника это расстояние, которое он проходит за одну минуту. Если за 10 минут он преодолел 900 метров, то какое расстояние он преодолевал за одну минуту?
Чтобы ответить на этот, нужно разделить расстояние на время движения школьника:
s = 900 метров
t = 10 минут
v = s : t = 900 : 10 = 90 (м/мин)
Если известна скорость и расстояние, то можно найти время:
t = s : v
Например, от дома до спортивной секции 500 метров. Мы должны дойти до неё пешком. Наша скорость будет 100 метров в минуту (100 м/мин). За какое время мы дойдем до спортивной секции?
Если за одну минуту мы будем проходить 100 метров, то сколько таких минут со ста метрами будет в 500 метрах?
Чтобы ответить на этот вопрос нужно 500 метров разделить на расстояние, которое мы будем проходить за одну минуту, то есть на 100. Тогда мы получим время, за которое мы дойдем до спортивной секции:
s = 500 метров
v = 100 (м/мин)
t = s : v = 500 : 100 = 5 (минут до спортивной секции)
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже

Понятие о времени
Существует характеристика, с которой приходится сталкиваться каждый день вне зависимости от возраста, социального статуса, различных способностей и умений. С её помощью определяют будущее, прошедшее и настоящее. По сути, это маркер, определяющий событие. Называют его временем. Рассматривая движение, всегда учитывают эту характеристику, как и её прогрессию.
Время является частью пространственной координаты. Но если относительно других осей можно перемещаться в различных направлениях, относительно него движение определяется только вперёд или назад. Неотъемлемой частью, связанной со временем, является пространство, благодаря которому и возможно понять суть параметра.
Исследованием характеристики занимались философы и учёные в различные периоды существования человечества. Видеть и слышать время невозможно, в отличие от осязаемого пространства, которое возможно наблюдать сразу и везде. Причём в нём можно перемещаться.
Дискуссии, как правильно воспринимать время, не утихают до сих пор. Платон считал, что оно есть не что иное, как движение. Аристотель предполагал, что время — количественное измерение перемещения. Оно было добавлено к классической геометрии Евклида, действующей на ограниченное число измерений. В итоге стало рассматриваться четырёхмерное пространство.
Сегодня так и нет ответов на следующие вопросы о времени:
- из-за чего происходит его течение;
- почему оно определяется только в одном направлении;
- является ли параметр одномерным, как многие учёные считают;
- можно ли обнаружить кванты характеристики.
В классической физике для определения временного изменения используется специальная координата пространство-время. Принято будущие события обозначать знаком плюс, а прошедшие минусом. Единица измерения времени связана с вращением планеты вокруг своей оси и Солнца. Этот выбор был сделан условно и привязан к удобству жизнедеятельности человечества.
В Международной системе единиц принято за секунду принимать интервал, равный 9 192 631 770 периодам излучения атома цезия-133 в покое при нуле градусов по Кельвину. Обозначают параметр латинской буквой t. Таким образом, время — физическая величина, связанная с перемещением какого-либо тела относительно выбранной системы координат.
Расстояние и скорость
Положение каждой физической точки можно описать с помощью координатных осей. Другими словами, системой, которая по отношению к исследуемому телу остаётся неизменной. Изменение положения относительно другого объекта можно представить пройденным расстоянием. Фактически это путь, для которого известно начало и конец. С физической точки зрения, расстояние — величина, являющаяся размерностью длины, и выражающаяся в её единицах.
В математике мера пройденного пути тесно связана с метрическим пространством, то есть положением, где существует пара (x, d), определённая в декартовом произведении. Соответственно, если координату принять за x, y, можно сказать следующее:
- начало пути и его конец обозначают точками с координатами d (x, y) и p (x, y);
- пройденное расстояние можно определить, отняв из конечных координат начальные;
- изменение положения будет нулевым, когда d = p.
В физике расстояние измеряют единицами длины. В соответствии с СИ за размерность берут метр. Расстояние — мера пройденного пути, то есть длина. Если необходимо просто определить изменение положения без учёта, когда и как оно произошло, используют координатные оси. Но при нахождении пройденного пути за время в формуле для расстояния должна учитываться ещё одна величина — скорость.
Обозначают эту характеристику символом V. Характеризует она быстроту перемещения в выбранной системе отсчёта. По определению скорость равняется производной радиус-вектора точки по времени. Иными словами, это значение, задающееся положением в пространстве относительно неизменной координаты, за которую чаще всего принимается начало.
Одно и то же расстояние можно преодолеть за разное время. Например, чтобы пройти 7 километров человеку понадобится затратить порядка одного часа, на автомобиле же этот путь можно преодолеть за 10 минут, а то и меньше. Вот как раз эти отличия и зависят от скорости движения.
Но на самом деле не всё так однозначно. Скорость необязательно должна быть одинаковой на всём пути. На определённых промежутках она может увеличиваться или уменьшаться, поэтому в математике под её значением понимают среднюю величину. Считается, что тело движется равномерно при прохождении установленного расстояния.
Общая формула
Скорость, время, расстояние — это 3 фундаментальных величины, связанные друг с другом. Исследуя одну характеристику, обязательно нужно учитывать две других. Фактически скорость — это физическая величина, определяющая, какую длину преодолеет физическое тело за единицу времени. Например, значение 120 км/ч показывает, что объект сможет преодолеть 120 километров за один час. В математическом виде связь между тремя характеристиками может быть записана в виде следующей формулы:
S = V * t, где:
- S — пройденное объектом расстояние;
- V — средняя скорость тела;
- t — время, затраченное на преодоление пути.
Зная это равенство и любых 2 параметра, можно выполнить расчёт третьего, так для времени она будет иметь вид t = S / V, а скорости V = S / t. Проверить правильность формулы для скорости времени и расстояния можно путём анализа размерности. Если в выражение подставить единицы измерения, то после сокращения должна получиться величина, соответствующая определяемой. S = V * t = (м / с) * с = м (метр). Что и требовалось получить. Аналогично можно проверить и 2 оставшиеся формулы: t = s / v = м / (м/с) = м * с / м = с (секунда) и V = S / t = м / с (метр на секунду).
Действительно, пусть имеется физическое тело, находящееся в каком-то месте. Через некоторое время, неважно по каким причинам, оно переместилось в другую точку, при этом не выходя за пределы установленного пространства. Если тело представить в декартовой плоскости, причём за начало принять координату (0, 0), через время объект изменит своё положение, определяющееся значением (x1, y2). В двухмерном же пространстве это изменение можно описать как переход из точки A в Б.
Значит, чтобы тело достигло второй координаты, ему необходимо затратить время. При этом пройденный путь будет находиться в прямой зависимости от него. Расстояние и время должны связываться третьей величиной, которой как раз и является скорость. То есть параметр, определяющий, за сколько тело сможет преодолеть определённую длину.
Как видно, выражение, связывающее 3 величины, довольно простое. Но оно не учитывает, что скорость может быть непостоянной, поэтому если объект проходит свой путь неравномерно, в выражение подставляют среднее значение. Находится оно как сумма всех отдельных скоростей на неравномерных участках: Vср = ΔS / Δt.
Решение задач
Чтобы уметь решать простые задания в средних классах по математике, связанных с движением, нужно знать всего одну формулу. При этом необходимо пристальное внимание уделять размерности. Все вычисления осуществляются в СИ. Вот некоторые из типовых заданий, используемые при обучении школьников в четвёртом классе средней школы:
- Из населённого пункта А в точку Б выехала колонна грузовиков. Навстречу им отправился легковой автомобиль. Скорость грузоперевозчиков составляет 80 км/ч, а пассажирской машины 60 км/ч. Встретились они в точке C через полтора часа. Определить расстояние между А и Б. Решение этой задачи будет состоять из нескольких шагов. На первом можно найти путь, который проехала колона: 80 * 1,2 = 96 км. На втором вычислить пройденное расстояние второй: 60 * 1,2 = 72 км. Отсюда общий путь будет равен сумме: АС + СБ = 72 + 96 = 168 км.
- Корабль, скорость которого в стоячих водах равна 30 км/ч, идёт по течению, а после возвращается. Скорость реки равняется трём километрам в час, промежуточная остановка занимает 5 часов. Путь от начала до возврата корабль проходит за 30 часов. Найти, сколько километров составляет весь рейс. Чтобы решить задачу, удобно составить таблицу. В столбцах нужно записать расстояние, скорость и время, а в строках расчётные данные для таких событий, как стоянка, ход по и против течения. Учитывая условие, рабочая формула примет вид: (S / 28) + (S / 22) + 5 = 30. Выражение можно упростить. В итоге должно получиться: 25 * S / 308 = 25 → S = 308. Так как путь корабля состоял из двух одинаковых расстояний, искомое расстояние будет: P = 2 * S = 308 * 2 = 616 км.
- Железнодорожный состав проезжает мост за 45 секунд. Длина переправы составляет 450 метров. При этом стрелочник, смотря прямо, видит проходящий поезд всего 15 секунд. Найти длину состава и скорость его движения. Если принять, что поезд движется со скоростью V, то его длина будет равняться D = 15 * V. Так как состав за 45 секунд проходит расстояние 45 * V = 450 + 15 * V, из равенства легко определить скорость: V = 45 * V – 15 * V = 450 → V = 450 / 3 0 = 15 м / с. Следовательно, длина состава: D = 15 * 15 = 225 м.
Все задачи на движение можно разделить на несколько типов: перемещение навстречу, движение вдогонку, нахождение параметров относительно неподвижного объекта. Но, несмотря на их виды, все они решаются по одинаковому алгоритму, поэтому для удобства можно сделать памятку, указав в ней формулы и размерность величин.
С древних времен людей беспокоит мысль о достижении сверх скоростей, так же как не дают покоя раздумья о высотах, летательных аппаратах. На самом деле это два очень сильно связанных между собой понятия. То, насколько быстро можно добраться из одного пункта в другой на летательном аппарате в наше время, зависит полностью от скорости. Рассмотрим же способы и формулы расчета этого показателя, а также времени и расстояния.
Как же рассчитать скорость?
На самом деле, рассчитать ее можно несколькими способами:
- через формулу нахождения мощности;
- через дифференциальные исчисления;
- по угловым параметрам и так далее.
В этой статье рассматривается самый простой способ с самой простой формулой — нахождение значения этого параметра через расстояние и время. Кстати, в формулах дифференциального расчета также присутствуют эти показатели. Формула выглядит следующим образом:
v=S/t, где
- v — скорость объекта,
- S — расстояние, которое пройдено или должно быть пройдено объектом,
- t — время, за которое пройдено или должно быть пройдено расстояние.
Как видите, в формуле первого класса средней школы нет ничего сложного. Подставив соответствующие значения вместо буквенных обозначений, можно рассчитать быстроту передвижения объекта. Например, найдем значение скорости передвижения автомобиля, если он проехал 100 км за 1 час 30 минут. Сначала требуется перевести 1 час 30 минут в часы, так как в большинстве случаев единицей измерения рассматриваемого параметра считается километр в час (км/ч). Итак, 1 час 30 минут равно 1,5 часа, потому что 30 минут есть половина или 1/2 или 0,5 часа. Сложив вместе 1 час и 0,5 часа получим 1,5 часа.
Теперь нужно подставить имеющиеся значения вместо буквенных символов:
v=100 км/1,5 ч=66,66 км/ч
Здесь v=66,66 км/ч, и это значение очень приблизительное (незнающим людям об этом лучше прочитать в специальной литературе), S=100 км, t=1,5 ч.
Таким нехитрым способом можно найти скорость через время и расстояние.
А что делать, если нужно найти среднее значение? В принципе, вычисления, показанные выше, и дают в итоге результат среднего значение искомого нами параметра. Однако можно вывести и более точное значение, если известно, что на некоторых участках по сравнению с другими скорость объекта была непостоянной. Тогда пользуются таким видом формулы:
vср=(v1+v2+v3+…+vn)/n, где v1, v2, v3, vn — значения скоростей объекта на отдельных участках пути S, n — количество этих участков, vср — средняя скорость объекта на всем протяжении всего пути.
Эту же формулу можно записать иначе, используя путь и время, за которое объект прошел этот путь:
- vср=(S1+S2+…+Sn)/t, где vср — средняя скорость объекта на всем протяжении пути,
- S1, S2, Sn — отдельные неравномерные участки всего пути,
- t — общее время, за которое объект прошел все участки.
Можно записать использовать и такой вид вычислений:
- vср=S/(t1+t2+…+tn), где S — общее пройденное расстояние,
- t1, t2, tn — время прохождения отдельных участков расстояния S.
Но можно записать эту же формулу и в более точном варианте:
vср=S1/t1+S2/t2+…+Sn/tn, где S1/t1, S2/t2, Sn/tn — формулы вычисления скорости на каждом отдельном участке всего пути S.
Таким образом, очень легко найти искомый параметр, используя данные выше формулы. Они очень просты, и как уже было указано, используются в начальных классах. Более сложные формулы базируются на этих же формулах и на тех же принципах построения и вычисления, но имеют другой, более сложный вид, больше переменных и разных коэффициентов. Это нужно для получения наиболее точного значения показателей.
Другие способы вычисления
Существую и другие способы и методы, которые помогают вычислить значения рассматриваемого параметра. В пример можно привести формулу вычисления мощности:
N=F*v*cos α , где N — механическая мощность,
F — сила,
v — скорость,
cos α — косинус угла между векторами силы и скорости.
Способы вычисления расстояния и времени
Можно и наоборот, зная скорость, найти значение расстояния или времени. Например:
S=v*t, где v — понятно что такое,
S — расстояние, которое требуется найти,
t — время, за которое объект прошел это расстояние.
Таким образом вычисляется значение расстояния.
Или вычисляем значение времени, за которое пройдено расстояние:
t=S/v, где v — все та же скорость,
S — расстояние, пройденный путь,
t — время, значение которого в данном случае нужно найти.
Для нахождения средних значений этих параметров существует довольно много представлений как данной формулы, так и всех остальных. Главное, знать основные правила перестановок и вычислений. А еще главнее знать сами формулы и лучше наизусть. Если же запомнить не получается, тогда лучше записывать. Это поможет, не сомневайтесь.
Пользуясь такими перестановками можно с легкостью найти время, расстояние и другие параметры, используя нужные, правильные способы их вычисления.
И это еще не предел!
Видео
В нашем видео вы найдете интересные примеры решения задач на нахождение скорости, времени и расстояния.









 2 + (-3 — 2)2 + (4 — -5)2)
2 + (-3 — 2)2 + (4 — -5)2)








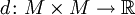 (где
(где  обозначает множество вещественных чисел). Для любых точек
обозначает множество вещественных чисел). Для любых точек 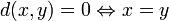 (аксиома тождества).
(аксиома тождества).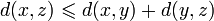 (аксиома треугольника или неравенство треугольника).
(аксиома треугольника или неравенство треугольника).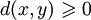 (это вытекает из аксиомы треугольника при
(это вытекает из аксиомы треугольника при  , в случае конечной размерности это называется пространством Минковского[1] (не надо путать с другим пространством Минковского).
, в случае конечной размерности это называется пространством Минковского[1] (не надо путать с другим пространством Минковского).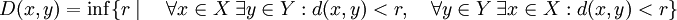
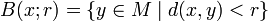 ,
,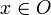 найдётся положительное число
найдётся положительное число 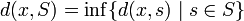
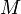 , функция
, функция  из
из 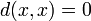 ;
;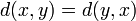 (симметрия);
(симметрия);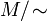 где
где 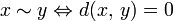 .
.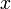 ,
, 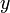 и
и 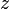 в
в 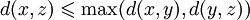 .
.![[0;infty]](https://dic.academic.ru/pictures/wiki/files/54/6ac441d46ab9a3b004180c27a3d5361f.png) , соответствующие пространства называются
, соответствующие пространства называются  -метрическими пространствами. Для любой такой метрики можно рассмотреть конечную метрику
-метрическими пространствами. Для любой такой метрики можно рассмотреть конечную метрику 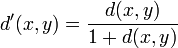 или
или 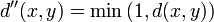 . Эти метрические пространства имеют одну и ту же топологию.
. Эти метрические пространства имеют одну и ту же топологию.