Найдите правильный ответ на вопрос ✅ «Как пишется расстояние математическое буквой …» по предмету 📘 Математика, а если вы сомневаетесь в правильности ответов или ответ отсутствует, то попробуйте воспользоваться умным поиском на сайте и найти ответы на похожие вопросы.
Смотреть другие ответы
Какую цифру можно поставить вместо звёздочки 347*, что бы полученное число делилось нацело и на 2 и на 3?
Ответы (5)
Найти площадь трапеции со сторонами 13,20,37, 60
Ответы (2)
Двигаясь вверх по реке, рыбак проплыл на лодке S=6 km за t1=6 ч Потом он заснул и и проснувшись через 3 ч, обнаружил что находиться в том же самом месте, с которого он начал движение.
Ответы (1)
3. Винни Пух должен прийти к Кролику в 12 ч 35 мин. Путь от его дома до дома Кролика занимает 25 минут. По дороге Винни Пух зашёл в гости к Сове.
Ответы (2)
3 бригады производили прополку кукурузы. 1 бригада прополола 30 процентов всей прощади, 2 60 процентов того, что прополола 1, а 3 остальную прощадь. Сколько гиктаров прополола все бригады вместе если 3 бригада прополола на 198 га больше, чем 1
Ответы (1)
0 интересует
0 не интересует
130 просмотров
Как обозначается расстояние в математике (какой буквой)
- обозначается
- расстояние
- математике
- 1 — 4 классы
- математика
спросил
17 Апр, 18
от
Alinacraft_zn
(30 баллов)
в категории Математика
1 Ответ
0 интересует
0 не интересует
ответил
17 Апр, 18
от
Printeska55_zn
(28 баллов)
V-скорость
T-время
S-растояние
вроде так
Добро пожаловать на сайт Школьные решения и ответы. У нас вы можете задавать задачи и получать решения от других членов сообщества.
- Расстояние в математике
-
Метри́ческим простра́нством называется множество, в котором определено расстояние между любой парой элементов.
Формальное определение
Метрическое пространство M есть множество точек с функцией расстояния (также называется метрикой)
(где
обозначает множество вещественных чисел). Для любых точек x,y,z из M эта функция должна удовлетворять следующим условиям:
(аксиома тождества).
- d(x,y) = d(y,x) (аксиома симметрии).
(аксиома треугольника или неравенство треугольника).
Эти аксиомы отражают интуитивное понятие расстояния. Например, расстояние должно быть неотрицательно, то есть
(это вытекает из аксиомы треугольника при z = x) и расстояние от x до y такое же, как и от y до x. Неравенство треугольника означает, что пройти от x до z можно короче, или хотя бы не длиннее, чем сначала пройти x до y, а потом от y до z.
Обозначения
Обычно расстояние между точками x и y в метрическом пространстве M обозначается
- d(x,y),
- | xy | или | xy | M , если необходимо подчеркнуть что речь идет о M,
- xy
- | x − y |
Примеры
- Дискретная метрика: d(x,y) = 0, если x = y, и d(x,y) = 1 во всех остальных случаях.
- Вещественные числа с функцией расстояния d(x,y) = | y − x | и евклидово пространство являются полными метрическими пространствами.
- Манхеттенская, или городская метрика: координатная плоскость, на которой расстояние определено как сумма расстояний между координатами. Более общий пример: любое нормированное пространство можно превратить в метрическое, определив функцию расстояния
, в случае конечной размерности это называется пространством Минковского[1] (не надо путать с другим пространством Минковского).
- Так называемая Французская железнодорожная метрика является примером, который нередко приводят в качестве примера метрики, не порожденной нормой.
- Любое связное риманово многообразие M можно превратить в метрическое пространство, определив расстояние как точную нижнюю грань длин путей, соединяющих пару точек.
- Множество вершин любого связного графа G можно превратить в метрическое пространство, определив расстояние как минимальное число рёбер в пути, соединяющем вершины.
- Множество компактных подмножеств K(M) любого метрического пространства M можно превратить в метрическое пространство, определив расстояние с помощью так называемой метрики Хаусдорффа. В этой метрике два подмножества близки друг к другу, если для любой точки одного множества можно найти близкую точку в другом подмножестве. Вот точное определение:
- Множество всех компактных метрических пространств (с точностью до изометрии) можно превратить в метрическое пространство, определив расстояние с помощью так называемой метрики Громова — Хаусдорффа.
Связанные определения
- Метрическое пространство называется полным, если любая фундаментальная последовательность в нём сходится к некоторому элементу этого пространства.
- Метрика d на M называется внутренней, если любые две точки x и y в M можно соединить кривой с длиной, произвольно близкой к d(x,y).
- Любое метрическое пространство обладает естественной топологией, базой для которой служит множество открытых шаров, т.е. множеств следующего типа:
-
,
- где x есть точка в M и r — положительное вещественное число, называемое радиусом шара. Иначе говоря, множество O является открытым, если для любой точки
найдётся положительное число r, такое, что множество точек на расстоянии меньше r от x принадлежит O.
- Две метрики, определяющие одну и ту же топологию, называются эквивалентными.
- Топологическое пространство, которое может быть получено таким образом, называется метризируемым.
- Расстояние d(x,S) от точки x до подмножества S в M определяется по формуле:
-
- Тогда d(x,S) = 0, только если x принадлежит замыканию S.
Свойства
- Метрическое пространство компактно тогда и только тогда, когда из любой последовательности точек можно выбрать сходящуюся подпоследовательность (секвенциальная компактность).
- Метрическое пространство может не иметь счётной базы, но всегда удовлетворяет первой аксиоме счётности — имеет счётную базу в каждой точке.
- Более того, каждый компакт в метрическом пространстве имеет счётную базу окрестностей.
- Сверх того, в каждом метрическом пространстве существует такая база, что каждая точка пространства принадлежит лишь счётному множеству её элементов — точечно-счётная база (но это свойство слабее метризуемости даже в присутствии паракомпактности и хаусдорфовости).
Вариации и обобщения
Для данного множества
, функция
называется псевдометрикой или полуметрикой на
если для любых точек
из
она удовлетворяет следующим условиям:
;
(симметрия);
(неравенство треугольника).
То есть, в отличие от метрики, различные точки в
могут находится на нулевом расстоянии. Псевдометрика естественно определяет метрику на факторпространстве
где
.
Метрика на пространстве называется ультраметрикой, если она удовлетворяет сильному неравенству треугольника:
-
-
-
- Для всех
,
и
в
.
- Для всех
-
-
Иногда рассматривают метрики со значениями
, соответствующие пространства называются
-метрическими пространствами. Для любой такой метрики можно рассмотреть конечную метрику
или
. Эти метрические пространства имеют одну и ту же топологию.
История
Морис Фреше впервые ввёл понятие метрического пространства[2] в связи с рассмотрением функциональных пространств.
Примечания
- ↑ К. Лейхтвейс, Выпуклые множества, Определение 11.2
- ↑ M. Fréchet, Sur quelques points du calcul fonctionnel, Rendic. Circ. Mat. Palermo 22(1906) 1-74,
См. также
- Индуцированная метрика
Литература
- Н.Васильев,
- Метрические пространства Квант, №1, 1990;
- Метрические пространства Квант, №10, 1970.
- В.А.Скворцов, Примеры метрических пространств, Библиотека «Математическое просвещение», выпуск 9, (2001).
- Ю.А.Шрейдер Что такое расстояние?, «Популярные лекции по математике», Выпуск 38, Физматгиз 1963 г., 76 стр.
Ссылки
Wikimedia Foundation.
2010.
Полезное
Смотреть что такое «Расстояние в математике» в других словарях:
-
Расстояние — В этой статье не хватает ссылок на источники информации. Информация должна быть проверяема, иначе она может быть поставлена под сомнение и удалена. Вы можете отредактировать эту статью, добавив ссылки на авторитетные источники. Эта отметка… … Википедия
-
Расстояние Левенштейна — (также редакционное расстояние или дистанция редактирования) между двумя строками в теории информации и компьютерной лингвистике это минимальное количество операций вставки одного символа, удаления одного символа и замены одного символа на… … Википедия
-
Популярные лекции по математике — «Популярные лекции по математике» серия брошюр на разные математические темы, выпускавшихся в СССР. Многие выпуски неоднократно переиздавались. Выпуски 1 26 вышли в издательстве «Гостехиздат», затем они выходили в издательстве «Физматгиз» и… … Википедия
-
Популярные лекции по математике (книжная серия) — «Популярные лекции по математике» серия брошюр на разные математические темы, выпускавшихся в СССР. Многие выпуски неоднократно переиздавались. Выпуски 1 26 вышли в издательстве «Гостехиздат», затем они выходили в издательстве «Физматгиз» и… … Википедия
-
Плоскость (в математике) — Две пересекающиеся плоскости Плоскость одно из основных понятий геометрии. При систематическом изложении геометрии понятие плоскости обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется аксиомами геометрии … Википедия
-
КООРДИНАТЫ (в математике) — КООРДИНАТЫ (от лат. co совместно и ordinatus упорядоченный, определенный), числа, заданием которых определяется положение точки на плоскости, на поверхности или в пространстве. Прямоугольные (декартовы) координаты точки на плоскости суть… … Энциклопедический словарь
-
Фокус (в математике) — Конические сечения: окружность, эллипс, парабола (плоскость сечения параллельна образующей конуса), гипербола. Коническое сечение или коника есть пересечение плоскости с круговым конусом. Существует три главных типа конических сечений: эллипс,… … Википедия
-
Координаты в математике — величины, определяющие положение точки. В Декартовых прямоугольных К. положение точки определяется тремя расстояниями ее от трех взаимно перпендикулярных плоскостей; пересечения этих плоскостей представляют собой три прямые, выходящие из одной… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
-
Координаты, в математике — величины, определяющие положение точки. В Декартовых прямоугольных К. положение точки определяется тремя расстояниями ее от трех взаимно перпендикулярных плоскостей; пересечения этих плоскостей представляют собой три прямые, выходящие из одной… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
-
Евклидово расстояние — В математике термин евклидово пространство может обозначать один из сходных и тесно связанных объектов: В обоих случаях, n мерное евклидово пространство обычно обозначается , хотя часто используется не вполне приемлемое обозначение . 1.… … Википедия
Вопрос:
Как пишется расстояние математическое буквой
Ответы:
s-скорость
t-время
v-расстояние
S-эс расстояние t-время те V-скорость
Как пишется расстояние математическое буквой
- пишется
- расстояние
- математическое
- 1 — 4 классы
- математика
спросил
13 Апр, 18
от
Arevik2_zn
(57 баллов)
в категории Математика
2 Ответы
ответил
13 Апр, 18
от
Катя6531_zn
Начинающий
(138 баллов)
Лучший ответ
S-скорость
t-время
v-расстояние
0 голосов
ответил
13 Апр, 18
от
Focfoc54_zn
Одаренный
(3.9k баллов)
S-эс расстояние t-время те V-скорость
Добро пожаловать на сайт Ответы онлайн, где вы можете задавать вопросы и получать ответы от других членов сообщества.
…
- Более того, каждый компакт в метрическом пространстве имеет счётную базу окрестностей.
- Сверх того, в каждом метрическом пространстве существует такая база, что каждая точка пространства принадлежит лишь счётному множеству её элементов — точечно-счётная база (но это свойство слабее метризуемости даже в присутствии паракомпактности и хаусдорфовости).
Вариации и обобщения [ | ]
- Для данного множества M <displaystyle M>, функция d : M × M → R <displaystyle dcolon Mtimes Mto mathbb > называется псевдометрикой или полуметрикой на M <displaystyle M>если для любых точек x , y , z <displaystyle x,;y,;z>из M <displaystyle M>она удовлетворяет следующим условиям:
- d ( x , x ) = 0 <displaystyle d(x,x)=0>;
- d ( x , y ) = d ( y , x ) <displaystyle d(x,y)=d(y,x)>(симметрия);
- d ( x , z ) ⩽ d ( x , y ) + d ( y , z ) <displaystyle d(x,z)leqslant d(x,y)+d(y,z)>(неравенство треугольника).
- Для данного множества M <displaystyle M>функция d : M × M → R <displaystyle dcolon Mtimes Mto mathbb > называется квазиметрикой, если для любых точек x <displaystyle x>, y <displaystyle y>, z <displaystyle z>из M <displaystyle M>она удовлетворяет следующим условиям:
- d ( x , x ) = 0 <displaystyle d(x,x)=0>;
- d ( x , y ) ⩽ c ⋅ d ( y , x ) <displaystyle d(x,y)leqslant ccdot d(y,x)>(квазисимметрия);
- d ( x , z ) ⩽ c ⋅ ( d ( x , y ) + d ( y , z ) ) <displaystyle d(x,z)leqslant ccdot (d(x,y)+d(y,z))>(обобщённое неравенство треугольника).
- Метрика на пространстве называется ультраметрикой, если она удовлетворяет сильному неравенству треугольника: Для всех x <displaystyle x>, y <displaystyle y>и z <displaystyle z>в M <displaystyle M>d ( x , z ) ⩽ max ( d ( x , y ) , d ( y , z ) ) <displaystyle d(x,z)leqslant max(d(x,y),d(y,z))>.
- Иногда удобно рассматривать ∞ <displaystyle infty >-метрики, то есть метрики со значениями [ 0 ; ∞ ] <displaystyle [0;infty ]>. Для любой ∞ <displaystyle infty >-метрики можно построить конечную метрику, которая определяет ту же топологию. Например, d ′ ( x , y ) = d ( x , y ) 1 + d ( x , y ) <displaystyle d'(x,y)=<frac <1+d(x,y)>>> или d ″ ( x , y ) = min ( 1 , d ( x , y ) ) . <displaystyle d»(x,y)=min <(1,d(x,y))>.>
- Иногда квазиметрика определяется как функция, удовлетворяющая всем аксиомам для метрики за возможным исключением симметрии [3][4] . Название этого обобщения не вполне устоялось [5] . В своей книге Смит [4] называет их «полуметриками». Тот же термин используется часто также для двух других обобщений метрик.
- d ( x , y ) ⩾ 0 <displaystyle d(x,y)geqslant 0>(положительность)
- d ( x , y ) = 0 ⟺ x = y <displaystyle d(x,y)=0iff x=y>(положительная определённость)
- d(x, y)=d(y, x) (симметрия вычеркнута)
- d ( x , z ) ⩽ d ( x , y ) + d ( y , z ) <displaystyle d(x,z)leqslant d(x,y)+d(y,z)>(неравенство треугольника)
- В метаметрике все аксиомы метрики выполняются, за исключением того, что расстояние между идентичными точками не обязательно равно нулю. Другими словами, аксиомами для метаметрики являются:
- d ( x , y ) ⩾ 0
- из d ( x , y ) = 0 <displaystyle d(x,y)=0>следует x = y <displaystyle x=y>(но не наоборот.)
- d ( x , y ) = d ( y , x )
- d ( x , z ) ⩽ d ( x , y ) + d ( y , z ) <displaystyle d(x,z)leqslant d(x,y)+d(y,z)>.
- Ослабление последних трёх аксиом ведёт к понятию преметрики, то есть функции, удовлетворяющей условиям:
- d ( x , y ) ⩾ 0
- d ( x , x ) = 0
- Префиксы псевдо-, квази- и полу- могут комбинироваться, например, псевдоквазиметрика (иногда называемая гемиметрикой) ослабляет как аксиому неразличимости, так и аксиому симметрии, и является просто преметрикой, удовлетворяющей неравенству треугольника. Для псевдоквазиметрических пространств открытые r <displaystyle r>-шары образуют базис открытых множеств. Простейшим примером псевдоквазиметрического пространства служит множество < 0 , 1 ><displaystyle <0,1>> с преметрикой, задаваемой функцией d <displaystyle d>, такой что d ( 0 , 1 ) = 1 <displaystyle d(0,1)=1>и d ( 1 , 0 ) = 0 <displaystyle d(1,0)=0>. Ассоциированное топологическое пространство является пространством Серпинского.
Линейное метрическое пространство [ | ]
- x n → x , y n → y ⇒ x n + y n → x + y <displaystyle x_to x,y_to yRightarrow x_+y_to x+y>
- x n → x , λ n → λ ⇒ λ n x n → λ x <displaystyle x_to x,lambda _to lambda Rightarrow lambda _x_to lambda x>
- Линейное пространство всех комплексных последовательностей можно превратить в линейное метрическое пространство при помощи введения расстояния между его элементами с помощью формулы:
История [ | ]
Морис Фреше впервые ввёл понятие метрического пространства [13] в связи с рассмотрением функциональных пространств.
Как обозначают время в математике?
Если при решении задачи по физике или математике необходимо обозначить время, то это пишется буквой так: t (читается: [тэ]), а если расстояние — пишется буквой так: s (читается: [эс]). Для обозначения пути обычно используется строчная (маленькая) буква [эль], т.
Как обозначаются скорость время расстояние в математике?
Скорость принято обозначать маленькой латинской буквой v, время движения – маленькой буквой t, пройденное расстояние – маленькой буквой s. Скорость, время и расстояние связаны между собой. Например, мы вышли из дома и направились в магазин. Мы дошли до магазина за 10 минут.
Как обозначается время расстояние?
Время. Расстояние. Эти три величины обозначают вот так: S – расстояние (путь); t – время, за которое пройдено расстояние S ; v – скорость движения. 2 Скорость – это расстояние, пройденное за единицу времени.
Что нужно сделать чтобы узнать время в математике?
Чтобы узнать скорость движения, нужно расстояние разделить на время. Чтобы узнать расстояние, нужно скорость умножить на время. Чтобы найти время, нужно расстояние разделить на скорость.
Как обозначается время в задачах?
Время – это продолжительность каких-то действий, событий. Время движения обозначается маленькой латинской буквой t. Скорость сближения – это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени. Чтобы найти скорость сближения, нужно сложить скорости объектов.
Как пишется скорость?
Скорость обозначается латинской буквой v. Проще говоря, скоростью называют расстояние, пройденное телом за единицу времени. Впервые формулу скорости проходят на математике в 5 классе.
Как найти скорость если есть время и расстояние?
- V = S / T. V — величина скорости; S — величина пройденного пути; Т — время в пути. .
- S = V * T. Т. е величину пройденного пути находим как произведение скорости на время в пути. Если известно расстояние и скорость, определить время можно по формуле:
- T = S / V. т. е.
Как находят скорость время расстояние?
В 4 классе ученики решают много задач по математике с примением формулы нахождения скорости, времени или расстояния при равномерном движении. Эта формула выглядит так: S = V×t. В данной формуле S — это путь, V — скорость, а t — время.
Как определить скорость течения реки?
Необходимо отметить, что собственная скорость водного суда – это скорость в стоячей воде. Чтобы найти скорость по течению, надо к скорости течения прибавить собственную. Для того чтобы найти скорость против течения, надо из собственной скорости вычесть скорость течения.
Как обозначается общая площадь?
В математике и в физике площадь обозначается буквой S заглавной (читается: [эс]). Так, в геометрии этой буквой обозначается площадь любых фигур (треугольника, прямоугольника, квадрата, ромба и т.
Как узнать время в пути?
- Чтобы найти расстояние, нужно скорость умножить на время.
- Чтобы найти время, надо расстояние разделить на скорость.
- Чтобы найти скорость, надо расстояние разделить на время.
Как найти время формула 5 класс?
S = V·t. В данной формуле S – это путь, V – скорость, а t – время.
Как решать задачи на расстояние скорость и время?
- если мы умножаем скорость на время, то получаем расстояние;
- если расстояние делим на время, то получаем скорость;
- если расстояние делим на скорость, то получаем время ;
Как найти время формула 4 класс?
В 4 классе ученики решают много задач по математике с примением формулы нахождения скорости, времени или расстояния при равномерном движении. Эта формула выглядит так: S = V×t. В данной формуле S — это путь, V — скорость, а t — время.
Как найти расстояние которое прошло тело?
Чтобы определить путь, который прошло тело при равномерном движении, необходимо скорость движения тела умножить на время которое это тело двигалось. S=V*t.
Расстояние — Distance
Расстояние — это числовое измерение того, насколько далеко друг от друга находятся объекты или точки. В физике или повседневном использовании расстояние может относиться к физической длине или оценке, основанной на других критериях (например, «на два округа больше»). Расстояние от точки A до точки B иногда обозначается как . В большинстве случаев «расстояние от A до B» взаимозаменяемо с «расстоянием от B до A». В математике функция расстояния или метрика — это обобщение концепции физического расстояния; это способ описания того, что значит для элементов некоторого пространства быть «близко» или «далеко» друг от друга. В психологии и социальных науках расстояние — это нечисловое измерение; Психологическая дистанция определяется как «различные способы, которыми объект может быть удален от себя» по таким измерениям, как «время, пространство, социальная дистанция и гипотетичность». | А B |
СОДЕРЖАНИЕ
Обзор и определения
Физические расстояния
Физическое расстояние может означать несколько разных вещей:
- Пройденное расстояние: длина определенного пути, пройденного между двумя точками, например расстояние, пройденное при навигации по лабиринту.
- Прямолинейное (евклидово) расстояние: длина кратчайшего возможного пути в пространстве между двумя точками, который можно было бы пройти, если бы не было препятствий (обычно формализируется как евклидово расстояние ).
- Геодезическое расстояние: длина кратчайшего пути между двумя точками, оставаясь на некоторой поверхности, например, расстояние по дуге вдоль кривой Земли.
- Длина определенного пути, который возвращается к начальной точке, например, мяч, брошенный вверх, или Земля, когда он завершает один оборот по орбите .
«Круговое расстояние» — это расстояние, пройденное колесом, которое может быть полезно при проектировании транспортных средств или механических передач. Окружность колеса равна 2 π × радиус, и если принять радиус равным 1, то каждый оборот колеса эквивалентен расстоянию 2 π радиан. В технике часто используется ω = 2 πƒ , где ƒ — частота .
Необычные определения расстояния могут быть полезны для моделирования определенных физических ситуаций, но также используются в теоретической математике:
- « Манхэттенское расстояние » — это прямолинейное расстояние, названное в честь количества кварталов (в северном, южном, восточном или западном направлениях), по которым такси должно проехать, чтобы добраться до пункта назначения на сетке улиц в некоторых частях Нью-Йорка. .
- «Расстояние до шахматной доски», формализованное как расстояние Чебышева , — это минимальное количество ходов, которое король должен сделать на шахматной доске , чтобы пройти между двумя клетками.
Теоретические расстояния
Термин «расстояние» также используется по аналогии для измерения нефизических объектов определенными способами.
В информатике есть понятие « расстояние редактирования » между двумя строками. Например, слова «собака» и «точка», которые различаются только одной буквой, ближе, чем «собака» и «кошка», которые различаются на три буквы. Эта идея используется в средствах проверки орфографии и в теории кодирования и математически формализована несколькими различными способами, такими как:
В математике метрическое пространство — это набор, для которого определены расстояния между всеми членами набора. Таким образом, можно вычислить множество различных типов «расстояний», например, для обхода графиков , сравнения распределений и кривых, а также с использованием необычных определений «пространства» (например, с использованием многообразия или отражений ). Понятие расстояния в теории графов использовалось для описания социальных сетей , например, с помощью числа Эрдёша или числа Бэкона — количество отношений сотрудничества на расстоянии от человека — от плодовитого математика Пола Эрдёша и актера Кевина Бэкона соответственно.
В психологии, географии человека и социальных науках расстояние часто рассматривается не как объективный показатель, а как субъективный опыт.
Расстояние в зависимости от направленного расстояния и смещения
И расстояние, и смещение измеряют движение объекта. Расстояние не может быть отрицательным и никогда не уменьшается. Расстояние — это скалярная величина или величина , тогда как смещение — это векторная величина, имеющая как величину, так и направление . Он может быть отрицательным, нулевым или положительным. Направленное расстояние не измеряет движение; он измеряет расстояние между двумя точками и может быть положительным, нулевым или отрицательным вектором.
Расстояние , пройденное транспортным средством (например , в виде записанного с помощью одометр ), человека, животного или объекта вдоль изогнутой траектории от точки А до точки Б , следует отличать от прямолинейного расстояния от A до B . Например, независимо от расстояния, пройденного за время пути от A до B и обратно до A , смещение равно нулю, поскольку начальная и конечная точки совпадают. В общем, расстояние по прямой не равно пройденному расстоянию, за исключением поездок по прямой.
Направленное расстояние
Направленные расстояния можно определять по прямым и изогнутым линиям.
Направленные расстояния вдоль прямых линий — это векторы, которые определяют расстояние и направление между начальной и конечной точками. Направленное расстояние точки C от точки A в направлении B на прямой AB в евклидовом векторном пространстве — это расстояние от A до C, если C падает на луч AB , но является отрицательным для этого расстояния, если C падает на луч BA (т. е. если C не находится на той же стороне от A, что и B ). Например, направленное расстояние от флагштока Главной библиотеки Нью-Йорка до флагштока Статуи Свободы:
- Отправная точка: флагшток библиотеки
- Конечная точка: статуя флагштока.
- Направление: -38 °
- Расстояние: 8.72 км
Другой вид направленного расстояния — это расстояние между двумя разными частицами или точечными массами в данный момент времени. Например, расстояние от центра тяжести Земли A до центра тяжести Луны B (что не означает строго движение от A к B ) попадает в эту категорию.
Направленное расстояние вдоль изогнутой линии не является вектором и представлено сегментом этой изогнутой линии, определяемой конечными точками A и B , с некоторой конкретной информацией, указывающей смысл (или направление) идеального или реального движения от одной конечной точки сегмент к другому (см. рисунок). Например, простая маркировка двух конечных точек как A и B может указывать на смысл, если предполагается упорядоченная последовательность ( A , B ), что подразумевает, что A является начальной точкой.
Смещение
Смещение (см. Выше) — это особый вид направленного расстояния, определенный в механике . Направленное расстояние называется смещением, когда это расстояние по прямой (минимальное расстояние) от A и B , и когда A и B — позиции, занятые одной и той же частицей в два разных момента времени. Это подразумевает движение частицы. Расстояние, пройденное частицей, всегда должно быть больше или равно ее смещению, причем равенство имеет место только тогда, когда частица движется по прямой траектории.
Математика
Геометрия
В аналитической геометрии , то евклидово расстояние между двумя точками на плоскости ху , можно найти , используя формулу расстояния. Расстояние между ( x 1 , y 1 ) и ( x 2 , y 2 ) определяется по формуле:
Аналогично, для заданных точек ( x 1 , y 1 , z 1 ) и ( x 2 , y 2 , z 2 ) в трехмерном пространстве расстояние между ними равно:
Эти формулы легко выводятся путем построения прямоугольного треугольника с опорой на гипотенузе другого (с другой ноги , ортогональной к плоскости , содержащей 1 — треугольник) и применяя теорему Пифагора . Эта формула расстояния также может быть расширена до формулы длины дуги . Другие расстояния с другими формулами используются в неевклидовой геометрии .
Расстояние в евклидовом пространстве
В евклидовом пространстве R n расстояние между двумя точками обычно определяется евклидовым расстоянием ( расстояние с двумя нормами). Иногда вместо них используются другие расстояния, основанные на других нормах .
Для точки ( x 1 , x 2 , . x n ) и точки ( y 1 , y 2 , . y n ) расстояние Минковского порядка p ( p -нормальное расстояние ) определяется как :
| 1-нормальное расстояние | знак равно ∑ я знак равно 1 п | Икс я — у я | < displaystyle = sum _ ^ left | x_ -y_ right |> |
| 2-нормальное расстояние | знак равно ( ∑ я знак равно 1 п | Икс я — у я | 2 ) 1 / 2 < displaystyle = left ( sum _ ^ left | x_ -y_ right | ^ <2> right) ^ <1/2>> |
| p — нормальное расстояние | знак равно ( ∑ я знак равно 1 п | Икс я — у я | п ) 1 / п < displaystyle = left ( sum _ ^ left | x_ -y_ right | ^
right) ^ <1 / p>> |
| бесконечное нормальное расстояние | знак равно Lim п → ∞ ( ∑ я знак равно 1 п | Икс я — у я | п ) 1 / п < displaystyle = lim _
left ( sum _ ^ left | x_ -y_ right | ^
right ) ^ <1 / p>> |
| знак равно Максимум ( | Икс 1 — у 1 | , | Икс 2 — у 2 | , … , | Икс п — у п | ) . < displaystyle = max left (| x_ <1>-y_ <1>|, | x_ <2>-y_ <2>|, ldots, | x_ -y_ | right) .> |
p не обязательно должно быть целым числом, но оно не может быть меньше 1, потому что в противном случае неравенство треугольника не выполняется.
Расстояние с двумя нормами — это евклидово расстояние , обобщение теоремы Пифагора на более чем две координаты . Это то, что было бы, если бы расстояние между двумя точками было измерено линейкой : «интуитивное» представление о расстоянии.
Расстояние в 1 норму более красочно называется нормой для такси или манхэттенским расстоянием , потому что это расстояние, которое автомобиль проехал бы в городе, разбитом на квадратные кварталы (если нет улиц с односторонним движением).
Расстояние с бесконечной нормой также называется расстоянием Чебышева . В 2D, это минимальное количество ходов короли требуют , чтобы перемещаться между двумя квадратами на шахматной доске .
Р -норма редко используется для значений р , кроме 1, 2 и бесконечности, но видеть суперэллипс .
В физическом пространстве евклидово расстояние в некотором смысле является наиболее естественным, потому что в этом случае длина твердого тела не изменяется при вращении .
Вариационная формулировка расстояния
Евклидово расстояние между двумя точками в пространстве ( и ) может быть записано в вариационной форме, где расстояние является минимальным значением интеграла: А знак равно р → ( 0 ) < Displaystyle А = < vec > (0)> B знак равно р → ( Т ) < Displaystyle B = < vec > (T)>
Вот траектория (путь) между двумя точками. Значение интеграла (D) представляет длину этой траектории. Расстояние является минимальным значением этого интеграла и получается, когда где — оптимальная траектория. В известном евклидовом случае (указанный выше интеграл) эта оптимальная траектория представляет собой просто прямую линию. Хорошо известно, что кратчайший путь между двумя точками — это прямая линия. Формально прямые линии можно получить, решив уравнения Эйлера – Лагранжа для указанного выше функционала . В неевклидовых многообразиях (искривленных пространствах), где природа пространства представлена метрическим тензором, подынтегральное выражение должно быть изменено на , где использовалось соглашение Эйнштейна о суммировании . р → ( т ) < Displaystyle < vec > (т)> р знак равно р * < Displaystyle г = г ^ <*>> р * < displaystyle r ^ <*>> грамм а б < displaystyle g_ > грамм а c р ˙ c грамм а б р ˙ б < displaystyle < sqrt < dot > _ g_ < dot > ^ >>>
Обобщение на многомерные объекты
Евклидово расстояние между двумя объектами также может быть обобщено на случай, когда объекты больше не являются точками, а представляют собой многомерные многообразия , такие как пространственные кривые, поэтому в дополнение к разговору о расстоянии между двумя точками можно обсудить концепции расстояния между двумя струны. Поскольку новые объекты, с которыми имеют дело, являются расширенными объектами (больше не точками), дополнительные концепции, такие как нерасширяемость, ограничения кривизны и нелокальные взаимодействия, которые обеспечивают непересечение, становятся центральными в понятии расстояния. Расстояние между двумя многообразиями — это скалярная величина, которая получается в результате минимизации обобщенного функционала расстояния, который представляет преобразование между двумя многообразиями:
Вышеупомянутый двойной интеграл представляет собой обобщенный функционал расстояния между двумя полимерными конформациями. является пространственным параметром и является псевдовремени. Это означает, что это конформация полимер / струна во время, параметризованная по длине струны на . Точно так же и траектория бесконечно малого отрезка струны при преобразовании всей струны из конформации в конформацию . Член с кофактором является множителем Лагранжа, и его роль заключается в обеспечении того, чтобы длина полимера оставалась неизменной во время преобразования. Если два дискретных полимера нерастяжимы, тогда преобразование минимального расстояния между ними больше не включает чисто прямолинейное движение даже в евклидовой метрике. У такого обобщенного расстояния есть потенциальное применение к проблеме сворачивания белка . s < displaystyle s>т < displaystyle t>р → ( s , т знак равно т я ) < displaystyle < vec > (s, t = t_ )> т я < displaystyle t_ > s < displaystyle s>р → ( s знак равно S , т ) < Displaystyle < vec > (s = S, t)> р → ( s , 0 ) < displaystyle < vec > (s, 0)> р → ( s , Т ) < displaystyle < vec > (s, T)> λ
Это обобщенное расстояние аналогично действию Намбу – Гото в теории струн , однако нет точного соответствия, потому что евклидово расстояние в трехмерном пространстве не эквивалентно пространственно-временному расстоянию, минимизированному для классической релятивистской струны.
Алгебраическое расстояние
Это показатель, часто используемый в компьютерном зрении, который может быть минимизирован методом наименьших квадратов . [1] [2] Для кривых или поверхностей, заданных уравнением (например, коники в однородных координатах ), алгебраическое расстояние от точки до кривой просто . Это может служить «начальным предположением» для геометрического расстояния для уточнения оценок кривой с помощью более точных методов, таких как нелинейный метод наименьших квадратов . Икс Т C Икс знак равно 0 < displaystyle x ^ < text > Cx = 0> Икс ′ < displaystyle x ‘>Икс ′ Т C Икс ′ < displaystyle x ‘^ < text > Cx’>
Общая метрика
В математике , в частности в геометрии , функция расстояния на заданном множестве M — это функция d : M × M → R , где R обозначает множество действительных чисел , которая удовлетворяет следующим условиям:
- d ( x , y ) ≥ 0 и d ( x , y ) = 0 тогда и только тогда, когдаx = y . (Расстояние между двумя разными точками положительно и равно нулю точно от точки до самой себя.)
- Он симметричен : d ( x , y ) = d ( y , x ) . (Расстояние между x и y одинаково в обоих направлениях.)
- Он удовлетворяет неравенству треугольника : d ( x , z ) ≤ d ( x , y ) + d ( y , z ) . (Расстояние между двумя точками — это кратчайшее расстояние по любому пути). Такая функция расстояния известна как метрика . Вместе с набором он составляет метрическое пространство .
Например, обычное определение расстояния между двумя действительными числами x и y : d ( x , y ) = | х — у | . Это определение удовлетворяет трем условиям выше, и соответствует стандартной топологии на прямой . Но расстояние на данном множестве — выбор определения. Другой возможный выбор — определить: d ( x , y ) = 0, если x = y , и 1 в противном случае. Это также определяет метрику, но дает совершенно другую топологию, « дискретную топологию »; с этим определением числа не могут быть сколь угодно близкими.
Расстояния между наборами и между точкой и набором
Между объектами возможны различные определения расстояний. Например, между небесными телами не следует путать расстояние от поверхности до поверхности и расстояние от центра до центра. Если первое намного меньше второго, как для низкой околоземной орбиты , обычно указывается первое (высота), в противном случае, например, для расстояния Земля – Луна, второе.
Есть два общих определения расстояния между двумя непустыми подмножествами данного метрического пространства :
- Одна из версий расстояния между двумя непустыми множествами — это нижняя грань расстояний между любыми двумя из их соответствующих точек, что является повседневным значением этого слова, т. Е.
- Расстояние Хаусдорфа — это большее из двух значений, одно из которых является супремумом , для точки, лежащей в пределах одного набора, нижнего предела, для второй точки, лежащей над другим набором, расстояния между точками, а другое значение аналогично определены, но роли двух наборов поменялись местами. Это расстояние делает само множество непустых компактных подмножеств метрического пространства метрическим пространством .
Расстояние между точкой и множеством является нижней гранью расстояний между точкой и те , в наборе. Это соответствует расстоянию, в соответствии с первым упомянутым выше определением расстояния между наборами, от набора, содержащего только эту точку, до другого набора.
В терминах этого определение расстояния Хаусдорфа можно упростить: это большее из двух значений, одно из которых является супремумом, для точки, находящейся в пределах одного набора, расстояния между точкой и набором, а другое значение определены аналогично, но роли двух наборов поменялись местами.
Теория графов
В теории графов расстояние между двумя вершинами представляет собой длину самого короткого пути между этими вершинами.
Статистические расстояния
В статистике и информационной геометрии существует много видов статистических расстояний , особенно расхождения , особенно расхождения Брегмана и f- расхождения . Они включают и обобщают многие понятия «разницы между двумя распределениями вероятностей » и позволяют изучать их геометрически, как статистические многообразия . Самым элементарным является квадрат Евклидова расстояния , который составляет основу наименьших квадратов ; это самое основное расхождение Брегмана. Наиболее важным в теории информации является относительная энтропия ( дивергенция Кульбака – Лейблера ), которая позволяет аналогичным образом изучать оценку максимального правдоподобия геометрически; это самая основная f- дивергенция, а также дивергенция Брегмана (и единственная дивергенция, которая является обеими). Статистические многообразия, соответствующие расходимости Брегмана, являются плоскими многообразиями в соответствующей геометрии, что позволяет использовать аналог теоремы Пифагора (которая традиционно верна для квадрата евклидова расстояния) для линейных обратных задач при выводе теории оптимизации .
Другие важные статистические расстояния включают расстояние Махаланобиса , энергетическое расстояние и многие другие.
Другие математические «расстояния»
- Канберрское расстояние — взвешенная версия манхэттенского расстояния, используемая в информатике.
В психологии
Психологическая дистанция определяется как «различные способы, которыми объект может быть удален от себя» по таким измерениям, как «время, пространство, социальная дистанция и гипотетичность». Взаимосвязь между психологической дистанцией и степенью абстрактности или конкретного мышления описывается в теории конструктивного уровня , которая представляет собой основу для принятия решений .
Со времен возникновения различных наук и математических расчетов ученые начали использовать множество символов и сокращений. Это вполне оправданное решение, ведь длинные формулы, записанные при помощи слов, отнимали бы много времени. По какому принципу выбираются эти обозначения, в частности буквы, указывающие на скорость и расстояние?
Как обозначают физические величины и понятия?
В физике существует общепринятый список обозначений. Он включает латинские и греческие буквы, кириллицу (редко), специальные символы, надстрочные и подстрочные знаки, скобки и др. В качестве самостоятельной науки физика зародилась в 17-м веке во время научной революции, но многие идеи, физические воззрения появились еще в античный период. Отсюда и использование латыни, греческого языка.
Количество физических величин довольно большое – букв в алфавитах недостаточно для обозначения их всех. Поэтому одни и те же буквы могут обозначать разные понятия. Важно различать и стиль написания.
Например, латинские символы обычно пишутся курсивом, греческие – обыкновенным прямым начертанием. Строчными буквами обозначают интенсивные величины (не зависят от размеров системы, например, температура), заглавными – экстенсивные.
Интересный факт: среди всех латинских букв для обозначения понятий из области физики реже всего встречается буква о.
Ввиду исторических причин множество обозначений с использованием латинских букв – это сокращения слов, которые указывают на данные понятия. Чаще всего это латинские, английские, немецкие и французские слова. Во избежание путаницы почти не используются греческие заглавные буквы, если они похожи на латинские по манере написания.
Почему в физике расстояние обозначается буквой s?
Расстояние в физике измеряется единицами длины (метр в международной системе единиц) и имеет два значения:
- степень удаленности объектов друг от друга;
- длина пути, которую прошел объект.
Расстояние – один из тех случаев, когда обозначающая буква является первой в слове-определении. Некоторые источники по-разному объясняют происхождение буквы s:
- От английского слова «space», которое означает расстояние, пространство, площадь.
- От латинского «spatium» – пространство между двумя предметами, протяжение в длину и ширину.
Фактически оба варианта являются правильными. Согласно этимологии слова «space», оно вошло в употребление в 1300-х годах и происходит от французского «espace», а оно, в свою очередь, от латинского «spatium». В значении космического пространства «space» начало употребляться лишь с конца 17-го века, после того как появилось в художественном произведении Джона Мильтона.
Почему в физике скорость обозначается буквой v?
Для обозначения скорости в физике используют строчную букву v тоже не случайно. Это первая буква в латинском слове «velocitas», французском «vitesse» и английском «velocity». Все они означают скорость, быстроту, стремительность.
Возникает другой вопрос: почему именно «velocity» стало определением скорости, а не другие английские слова с похожим значением, например, «speed»? Дело в том, что в физике скорость является векторной величиной, которая отображает быстроту и направление перемещения объекта относительно заданной системы отсчета.
Слово «speed» указывает на скалярную скорость – величину, которая не зависит от системы координат. Например, скорость света – постоянная величина, поэтому на английском данный термин будет выглядеть как «the speed of light».
Кроме того, скорость и расстояние – взаимосвязанные величины наряду со временем. Эта связь в физике выражается формулой. Зная две величины, можно рассчитать и третью. Использование одинаковых букв нецелесообразно.
Если Вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
В этом уроке мы рассмотрим три физические величины, а именно расстояние, скорость и время.
Расстояние
Расстояние мы уже изучали в уроке единицы измерения. Говоря простым языком, расстояние это длина от одного пункта до другого. (Пример: расстояние от дома до школы 2 километра).
Имея дело с большими расстояниями, в основном они будут измеряться в метрах и километрах. Расстояние обозначается латинской буквой S. Можно обозначить и другой буквой, но буква S общепринята.
Скорость
Скоростью называют расстояние, пройденное телом за единицу времени. Под единицей времени подразумевается 1 час, 1 минута или 1 секунда.
Предположим, что двое школьников решили проверить, кто быстрее добежит от двора до спортплощадки. Расстояние от двора до спортплощадки 100 метров. Первый школьник добежал за 25 секунд. Второй за 50 секунд. Кто добежал быстрее?
Быстрее добежал тот, кто за 1 секунду пробежал бóльшее расстояние. Говорят, что у него скорость движения больше. В данном случае скорость школьников это расстояние, которое они пробегают за 1 секунду.
Чтобы найти скорость, нужно расстояние разделить на время движения. Давайте найдём скорость первого школьника. Для этого разделим 100 метров на время движения первого школьника, то есть на 25 секунд:
100 м : 25 с = 4
Если расстояние дано в метрах, а время движения в секундах, то скорость измеряется в метрах в секунду (м/с). Если расстояние дано в километрах, а время движения в часах, скорость измеряется в километрах в час (км/ч).
У нас расстояние дано в метрах, а время в секундах. Значит скорость измеряется в метрах в секунду (м/с)
100м : 25с = 4 (м/с)
Итак, скорость движения первого школьника составляет 4 метра в секунду (м/с).
Теперь найдем скорость движения второго школьника. Для этого разделим расстояние на время движения второго школьника, то есть на 50 секунд:
100 м : 50 c = 2 (м/с)
Значит скорость движения второго школьника составляет 2 метра в секунду (м/с).
Скорость движения первого школьника — 4 (м/с)
Скорость движения второго школьника — 2 (м/с)
4 (м/с) > 2 (м/с)
Скорость первого школьника больше. Значит он добежал до спортплощадки быстрее. Скорость обозначается латинской буквой v.
Время
Иногда возникает ситуация, когда требуется узнать за какое время тело преодолеет то или иное расстояние.
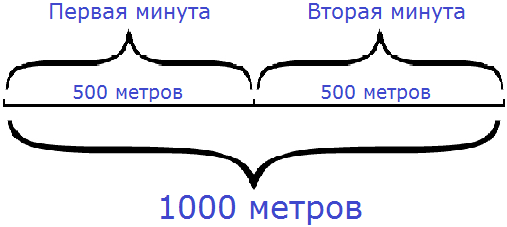
Например, от дома до спортивной секции 1000 метров. Мы должны доехать туда на велосипеде. Наша скорость будет 500 метров в минуту (500м/мин). За какое время мы доедем до спортивной секции?
Если за одну минуту мы будем проезжать 500 метров, то сколько таких минут с пятью ста метрами будет в 1000 метрах?
Очевидно, что надо разделить 1000 метров на то расстояние, которое мы будем проезжать за одну минуту, то есть на 500 метров. Тогда мы получим время, за которое доедем до спортивной секции:
1000 : 500 = 2 (мин)
Время движения обозначается маленькой латинской буквой t.
Взаимосвязь скорости, времени, расстояния
Скорость принято обозначать маленькой латинской буквой v, время движения – маленькой буквой t, пройденное расстояние – маленькой буквой s. Скорость, время и расстояние связаны между собой.
Если известны скорость и время движения, то можно найти расстояние. Оно равно скорости, умноженной на время:
s = v × t
Например, мы вышли из дома и направились в магазин. Мы дошли до магазина за 10 минут. Наша скорость была 50 метров в минуту. Зная свою скорость и время, мы можем найти расстояние.
Если за одну минуту мы прошли 50 метров, то сколько таких пятьдесят метров мы пройдем за 10 минут? Очевидно, что умножив 50 метров на 10, мы определим расстояние от дома до магазина:
v = 50 (м/мин)
t = 10 минут
s = v × t = 50 × 10 = 500 (метров до магазина)
Если известно время и расстояние, то можно найти скорость:
v = s : t
Например, расстояние от дома до школы 900 метров. Школьник дошел до этой школы за 10 минут. Какова была его скорость?
Скорость движения школьника это расстояние, которое он проходит за одну минуту. Если за 10 минут он преодолел 900 метров, то какое расстояние он преодолевал за одну минуту?
Чтобы ответить на этот, нужно разделить расстояние на время движения школьника:
s = 900 метров
t = 10 минут
v = s : t = 900 : 10 = 90 (м/мин)
Если известна скорость и расстояние, то можно найти время:
t = s : v
Например, от дома до спортивной секции 500 метров. Мы должны дойти до неё пешком. Наша скорость будет 100 метров в минуту (100 м/мин). За какое время мы дойдем до спортивной секции?
Если за одну минуту мы будем проходить 100 метров, то сколько таких минут со ста метрами будет в 500 метрах?
Чтобы ответить на этот вопрос нужно 500 метров разделить на расстояние, которое мы будем проходить за одну минуту, то есть на 100. Тогда мы получим время, за которое мы дойдем до спортивной секции:
s = 500 метров
v = 100 (м/мин)
t = s : v = 500 : 100 = 5 (минут до спортивной секции)
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже

Относительные размеры
объектов, lg м
-20 —
–
-18 —
–
-16 —
–
-14 —
–
-12 —
–
-10 —
–
-8 —
–
-6 —
–
-4 —
–
-2 —
–
0 —
–
2 —
–
4 —
–
6 —
–
8 —
–
10 —
–
12 —
–
14 —
–
16 —
–
18 —
–
20 —
–
22 —
–
24 —
–
26 —
–
28 —
–
30 —
←
Размер водяной капли в
тумане — 5·10-6
←
Средний радиус орбиты
Земли — 1,5·1011
Расстоя́ние, в широком смысле, степень (мера) удалённости объектов друг от друга.
Расстояние является фундаментальным понятием геометрии. Термин часто используется в других науках и дисциплинах: астрономия, география, геодезия, навигация и других. В различных дисциплинах как термин имеет различное определение, представленное ниже.
Расстояние в математике
Расстояние в алгебре
Содержание термина «расстояние» в алгебре связано с понятием метрики и метрического пространства.
Метрическим пространством называется множество X, если дано такое отображение, называемое метрикой, X² в множество неотрицательных чисел, что для любых элементов a, b, c множества X выполняются следующие аксиомы, называемые аксиомами Фреше:
1) 
2) 
3) 
Для третьей аксиомы частным случаем является неравенство треугольника.
Расстояние в множестве действительных чисел
Введение метрики
Для множества всех действительных чисел расстояние от числа a до числа b математики считают число 
Легко убедиться, что множество действительных чисел с данной метрикой будет являться метрическим пространством.
Доказательство
Первое условие выполняется, так как модуль любого действительного числа из определения — число неотрицательное, притом модуль числа равен нулю тогда и только тогда, когда выражение под модулем равно нулю, откуда, если равенство выполняется, то числа равны.
Второе свойство верно, так как из свойств модуля числа: 
Третье свойство выполняется, так как само свойство равносильно 

Расстояние в множестве пар действительных чисел
Из основных метрик в множестве пар действительных чисел (а в графической интерпретации — множестве всех точек плоскости) выделяют две: метрику Декарта и метрику Евклида.
Метрика Декарта
Введение метрики
Для множества пар действительных чисел дана метрика Декарта:

Убедимся, что множество пар действительных чисел (R²) с введенной метрикой Декарта является метрическим пространством.
Доказательство
Первое свойство очевидно выполняется, так как сумма модулей, каждый из которых является неотрицательным числом — также число неотрицательное. Притом равенство выполняется тогда и только тогда, когда оба выражения под модулем равны нулю, но тогда и рассматриваемые элементы-пары множества также равны.
Второе свойство выполняется, так как 
Докажем третье свойство:
Пусть даны три пары действительных чисел, (a; b), (c; d), (e; f). Тогда требуемое неравенство можно записать в следующем виде:



Метрика Евклида
Введение метрики
Для множества пар действительных чисел дана метрика Евклида:

Убедимся, что множество R² с введенной метрикой Евклида является метрическим пространством.
Доказательство
Первое свойство выполняется, так как арифметический корень из неотрицательного числа всегда неотрицателен. Если же выполняется равенство нулю, то оба выражения возводимые в квадрат, равны нулю, откуда требуемое очевидно.
Второе свойство выполняется, так как 
Докажем третье свойство:
Пусть даны три пары действительных чисел, (a; b), (c; d), (e; f). Тогда требуемое неравенство можно записать в следующем виде:


Расстояние в геометрии
В геометрии расстояние между фигурами — минимально возможная длина отрезка между точкой, принадлежащей первой фигуре, и точкой, принадлежащей второй фигуре.
Расстояние в технике
Расстояние между объектами — длина отрезка прямой, соединяющей два объекта. Расстояние в этом смысле является физической величиной с размерностью длины, значение расстояния выражается в единицах длины.
Расстояние в физике
Основная статья: Длина
В физике расстояние меряется единицами длины, которые в большинстве систем измерений являются одной из основных единиц измерения. В международной системе единиц (СИ) за единицу длины принят метр. Расстоянием также называют длину пути, пройденного объектом. В этом случае производной расстояния (радиус-вектора) по времени является скорость.
Другие использования
В проксемике понятие расстояния используют для описания личного пространства человека.
См. также
- Расстояние Левенштейна
- Промежуток (математика)
- Отрезок
- Интервал
- Путь
Примечания
Литература
- Зенитное расстояние // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
Эта страница в последний раз была отредактирована 28 февраля 2023 в 19:38.
Как только страница обновилась в Википедии она обновляется в Вики 2.
Обычно почти сразу, изредка в течении часа.

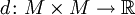 (где
(где  обозначает множество вещественных чисел). Для любых точек
обозначает множество вещественных чисел). Для любых точек 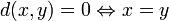 (аксиома тождества).
(аксиома тождества).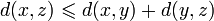 (аксиома треугольника или неравенство треугольника).
(аксиома треугольника или неравенство треугольника).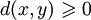 (это вытекает из аксиомы треугольника при
(это вытекает из аксиомы треугольника при  , в случае конечной размерности это называется пространством Минковского[1] (не надо путать с другим пространством Минковского).
, в случае конечной размерности это называется пространством Минковского[1] (не надо путать с другим пространством Минковского).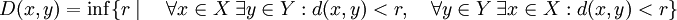
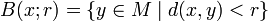 ,
,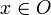 найдётся положительное число
найдётся положительное число 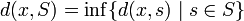
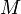 , функция
, функция  из
из 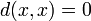 ;
;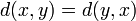 (симметрия);
(симметрия);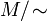 где
где 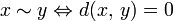 .
.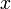 ,
, 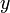 и
и 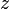 в
в 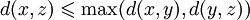 .
.![[0;infty]](https://dic.academic.ru/pictures/wiki/files/54/6ac441d46ab9a3b004180c27a3d5361f.png) , соответствующие пространства называются
, соответствующие пространства называются 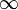 -метрическими пространствами. Для любой такой метрики можно рассмотреть конечную метрику
-метрическими пространствами. Для любой такой метрики можно рассмотреть конечную метрику 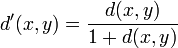 или
или 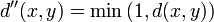 . Эти метрические пространства имеют одну и ту же топологию.
. Эти метрические пространства имеют одну и ту же топологию.