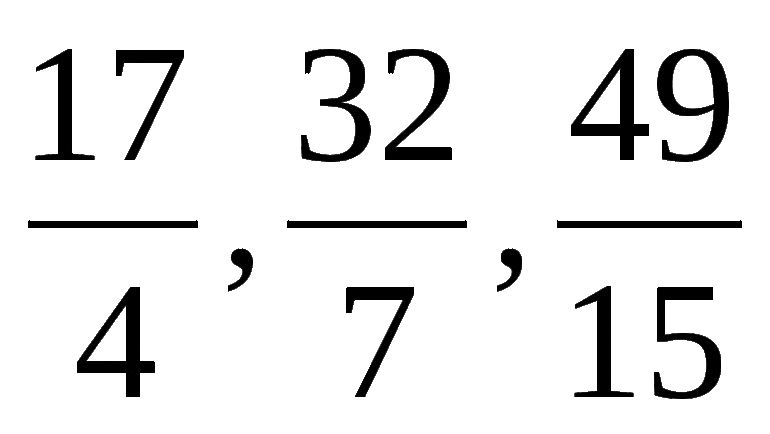Как вы уже заметили дроби бывают разные. Например, (frac<1><2>, frac<3><5>, frac<5><7>, frac<7><7>, frac<13><5>, …)
Делятся дроби на два вида правильные дроби и неправильные дроби.
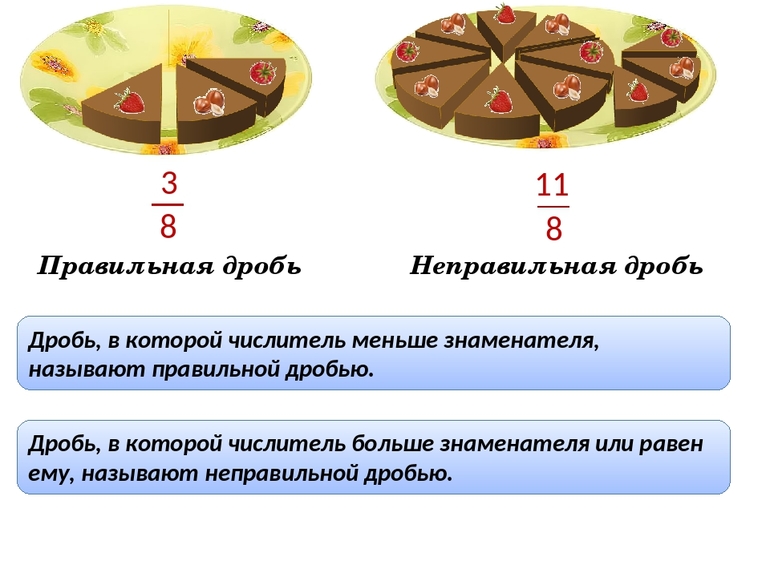
В правильной дроби числитель меньше знаменателя, например, (frac<1><2>, frac<3><5>, frac<5><7>, …)
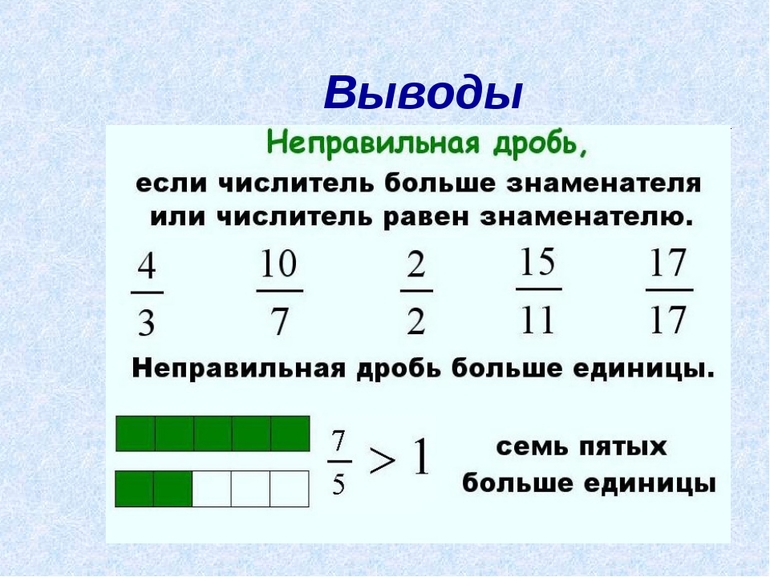
В неправильной дроби числитель больше или равен знаменателю, например, (frac<7><7>, frac<9><4>, frac<13><5>, …)
Правильная дробь всегда меньше единицы. Рассмотрим пример:
Знаменатели одинаковые равны числу 3, далее сравниваем числители.
Вопросы по теме “Правильные или неправильные дроби”:
Может ли правильная дробь быть больше 1?
Ответ: нет.
Может ли правильная дробь равна 1?
Ответ: нет.
Может ли неправильная дробь меньше 1?
Ответ: нет.
Пример №1:
Напишите:
а) все правильные дроби со знаменателем 8;
б) все неправильные дроби с числителем 4.
Решение:
а) У правильных дробей знаменатель больше числителя. Нам нужно в числитель поставить числа меньшие 8.
(frac<1><8>, frac<2><8>, frac<3><8>, frac<4><8>, frac<5><8>, frac<6><8>, frac<7><8>.)
б) В неправильной дроби числитель больше знаменателя. Нам нужно в знаменатель поставить числа меньшие 4.
(frac<4><4>, frac<4><3>, frac<4><2>, frac<4><1>.)
Пример №2:
При каких значениях b дробь:
а) (frac<12>) будет правильной;
б) (frac<9>) будет не правильной.
Решение:
а) b может принимать значения 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11.
б) b может принимать значения 1, 2, 3, 4, 5, 6, 7, 8, 9.
Задача №1:
Сколько минут в часе? Какую часть часа составляет 11 мин.?
Ответ: В часе 60 минут. Три минуты составят (frac<11><60>) часа.
Источник
Общие сведения
Слово «дробь» в обиход ввёл математик средневековой Европы Фибоначчи. На Руси под этим понятием понимались доли чисел. В дословном переводе на русский с арабского термин обозначает «ломать» или «раздроблять». Вид записи выражения, который применяется и сегодня, предложили арабы. Но фундамент теории заложили греческие и индийские учёные.
В математике под дробным отношением понимают число, образованное из некоторой части единицы. Простыми словами это можно объяснить на наглядном примере. Пусть на столе лежит две круглые пиццы. Каждую из них разрезали на восемь равных частей. Всего получилось шестнадцать долей. Через какое-то время было съедено одиннадцать кусков. Соответственно на столе осталось пять. В математической записи такое действие будет выглядеть как 11 / 8.
Число, стоящее в верхней части выражения, называют делимым или числителем, а в нижней делителем или знаменателем. В зависимости от их числового значения все дроби разделяют на три класса:
Кроме этого, выделяют ещё одну группу выражений. Дроби, относящиеся к ней, называют десятичными. Это такие отношения, у которых знаменатель — это десятичное число, стоящее в любой натуральной степени. Для записи десятичных выражений используют не дробную черту, а запятую. Например, 12 / 10 = 1,2.
Суть отношения
Обыкновенная дробь может быть правильной или неправильной. Например, 19 / 21 — правильное выражение, так как результат деления будет меньше единицы. В то же время обыкновенные числа 32 / 6 и 90 / 90 — неправильные, так как ответ, получаемый при делении, будет больше единицы в первом случае и равен ей во втором.
Чтобы разобраться, почему же дробные выражения, у которых числитель превосходит или равняется знаменателю называют «неправильными» можно порассуждать следующим образом.
Пусть имеется неправильная дробь 10 / 10. Эта запись обозначает, что взято десять долей чего-то состоящего из такого же числа частей. Иными словами, из имеющихся десяти долей можно сложить целый предмет. Неправильное выражение вида 10 / 10, по сути, означает целый предмет. Значит, можно записать, что 10 / 10 =1. Следовательно, такое отношение можно заменить натуральным числом.
Теперь можно рассмотреть неправильные отношения 7 / 3 и 12 / 4. Совершенно очевидно, что из этих семи третьих долей легко составляется два целых числа. Одно из них будет содержать три части. Значит, для оставшихся двух долей понадобится шесть частей: 3 + 3 = 6. При этом останется ещё одна доля — третья. Таким образом, выражение семь третьих означает две целые части и ещё одну третью от них. Аналогично из двенадцати четвёртых можно сформировать три целых числа по четыре доли в каждом. То есть дробное отношение 12 / 4 означает, по сути, три целых предмета.
Если провести анализ полученных результатов, то можно сделать вывод о том, что неправильные дроби, могут быть представлены в двух видах:
Особенный интерес вызывает представление неправильной дроби в виде суммы натурального числа и правильной части. Это действие называется выделением целой доли из неправильного отношения. Причём такая операция может быть выполнена и в обратном направлении — трансформация выражения в смешанное.
Превращение дробей
По смыслу неправильные выражения представляют собой целую и дробную часть, записанную в виде отношения. Поэтому любую смешанную дробь можно превратить в правильную, и наоборот. Деление целого числа на такое же можно объяснить так. Пусть нужно разделить четыре на пять. Значит, единицу понадобится разделить на пять равных частей, то есть 1 / 5. Четыре же единицы дадут 1 / 5 + 1/ 5 + 1 / 5 + 1 / 5 = 4 / 5. В этом случае получается правильное выражение. Но бывает, что числитель количественно превышает знаменатель. Значит, для более понятной формы записи нужно из такого выражения выделить целую часть.
Например, нужно преобразовать число 25 / 8. Это действие подразумевает нахождение целых единиц, содержащихся в выражении. Рассуждать нужно следующим образом. Одна единица может быть представлена как 8 / 8, две — 16 / 8, три — 24 / 8. Значит, число состоит из трёх единиц и оставшейся 1 / 8 части. Поэтому записать его можно так: 3 (1 / 8).
Такого вида преобразования часто приходится выполнять при решении примеров с дробями в 5 классе. Поэтому понять принцип превращения лучше всего на конкретное задание. При этом можно использовать следующий алгоритм:
Итак, пусть имеется выражение 3 (5 / 7). Так как фактически это сумма трёх и пяти седьмых, то следуя алгоритму, можно решение расписать так: 3 + 5 / 7 = (3 * 7 + 5) / 7 = (21 + 5) / 7 = 26 / 7. Аналогичный результат мог быть получен при простом сложении двух частей смешанного числа: 3 / 1 + 5 / 7 = (3 * 7) / 1 * 7 + 5 / 7 = 21 / 7 + 5 / 7 = (21 + 5) / 7 = 26 / 7. Первый вариант, конечно же, более удобен. Его можно выразить формулой: a (c / d) = (a * d + c) / d.
Эту выражение нужно обязательно запомнить, так как его придётся довольно часто использовать при решении задач различной сложности.
Выполнение действий
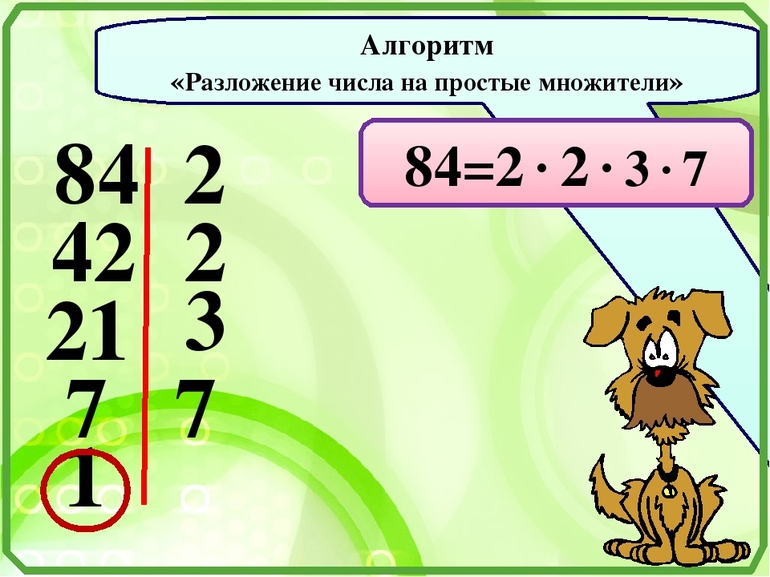
Отличие неправильной дроби от правильной заключается в том, что первая равна или больше единицы, а вторая меньше её. Поэтому правило выполнения арифметических действий одинаковое для этих двух групп. Для того чтобы ребёнок понял, как правильно решать простые и сложные задания объяснение в 5 классе неправильных дробей и действий над ними начинают с повторения правила разложения числа на простые множители.
Выполняется оно за несколько шагов. Вначале ищут минимальную величину, на которую можно разделить исходное без остатка. Далее, находят результат деления и повторяют действие, но уже для полученного числа. Операцию повторяют до тех пор, пока в ответе не получится единица.
Разложение на простые множители используется при поиске наименьшего знаменателя при сложении или вычитании неправильных дробей с разными делителями. Существует алгоритм, придерживаясь которого можно выполнить любое арифметическое действие над двумя и более дробными выражениями. Он заключается в следующем:
Например, 4 / 3 + 9 / 7 = (7 * 4) / 21 + (3 * 9) / 21 = 28 / 21 + 27 / 21 = (28 + 27) / 21 = 55 / 21 = 2 (13 / 21) и 56 / 9 — 6 / 9 = (56 — 6) / 9 = 50 / 9 = 5 (5 / 9).
Неправильные выражения можно не только складывать, но и вычитать. Для того чтобы их перемножить следует отдельно найти произведение делимых и делителей. Затем в числитель записать первый результат, а в знаменатель второй. То есть действие нужно выполнять по формуле: f / n * s / m = (f * s) / (n * m). Выполнить деление также просто. Для этого действия в вычитаемом выражении меняется местами аргументы и выполняется умножение: (f / n) / (s / m) = (f * m) / (n * s).
Источник
Обыкновенные дроби
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Доля целого
Доля — это каждая равная часть, из суммы которых состоит целый предмет.
Для примера возьмем два мандарина. Когда мы их почистим, то получим в каждом мандарине разное количество долек или долей. В одном может быть 6, а в другом — целых 9. Размеры долей у каждого мандарина тоже разные.
У каждой доли есть свое название: оно зависит от количества долей в конкретном предмете. Если в мандарите шесть долей — каждая из них будет определяться, как одна шестая от целого.
Понятие доли можно применить не только к предметам, но и величинам. Так, например, картина занимает четверть стены — при этом ее ширина треть метра.
Чтобы быстрее запомнить соотношения частей и целого, можно использовать наглядную табличку:
Понятие дроби
Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которой можно представить число. Есть два формата записи:
Виды дробей:
Какие еще бывают дроби:
Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 4/9 и 23/57.
Неправильная дробь — та, у которой числитель больше знаменателя или равен ему. Например, 13/5. Такое число называют смешанным — читается так: «две целых три пятых», а записывается — 2 35.
Выделение целой части из неправильной дроби — это запись неправильной дроби в виде суммы натурального числа и правильной дроби. Например, 11/5 = 2 + 1/5.
Онлайн-курсы математики для детей помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Как устроена обыкновенная дробь
Обыкновенная дробь — это запись вида m/n, где m и n любые натуральные числа.
Такие дроби записываются с помощью двух натуральных чисел и горизонтальной черты, которая называется чертой дроби. Иногда ставится не горизонтальная черта, а косая.
Числитель обыкновенной дроби m/n — это натуральное число m, которое стоит над чертой. Числитель это делимое — то, что мы делим.
Знаменатель обыкновенной дроби m/n — натуральное число n, которое стоит под чертой. Знаменатель это делитель — то, на сколько делим.
Черта между числителем и знаменателем — символ деления.
Равные обыкновенные дроби — обыкновенные дроби a/b и c/d, для которых справедливо равенство: a * d = b * c. Пример равных дробей: 1/2 и 2/4, так как 1 * 4 = 2 * 2.
Неравные обыкновенные дроби — обыкновенные дроби a/b и c/d, для которых равенство: a * d = b * c не является верным.
Как устроена десятичная дробь
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. Выходит, что десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
Свойства дробей
Основное свойство дроби: если числитель и знаменатель дроби умножить или разделить на одно и то же отличное от нуля число, то получится дробь, равная данной. Формула выглядит так:

Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:
У нас есть отличные курсы по математике для учеников с 1 по 11 классы, записывайтесь!
Действия с дробями
С дробями можно выполнять те же действия, что и с обычными числами: складывать, вычитать, умножать и делить. А еще дроби можно сокращать и сравнивать между собой. Давайте попробуем.
Сравнение дробей
Из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше.
Сравним 1/5 и 4/5. Как рассуждаем:
Чтобы сравнить дроби с разными знаменателями, нужно привести дроби к общему знаменателю. А после приведения дробей к общему знаменателю, можно применить правило сравнения дробей с одинаковыми знаменателями.
Пример. Сравнить 2/7 и 1/14.
Важно запомнить: любая неправильная дробь больше любой правильной. Потому что неправильная дробь всегда больше или равна 1, а правильная дробь всегда меньше 1.
Чтобы сравнить дроби с разными числителями и знаменателями, нужно:
Чтобы привести дроби к наименьшему общему знаменателю, нужно:
Сокращение дробей
Сокращение дроби — это деление числителя и знаменателя дроби на одно и то же натуральное число. Сократить дробь значит сделать ее короче и проще для восприятия. Например, дробь 1/3 выглядит намного проще и красивее, чем 27/81.
Сокращение дроби выглядит так: зачеркивают числитель и знаменатель, а рядом записывают результаты деления числителя и знаменателя на одно и то же число.
В этом примере делим обе части дроби на двойку.
Можно никуда не спешить и сокращать дроби последовательно, в несколько действий.
Сложение и вычитание дробей
При сложении и вычитании дробей с одинаковыми знаменателями к числителю первой дроби прибавляют числитель второй дроби (из числителя первой вычитают числитель второй) и оставляют тот же знаменатель.
Не забудьте проверить, можно ли сократить дробь и выделить целую часть.
При сложении и вычитании дробей с разными знаменателями нужно найти наименьший общий знаменатель, сложить или вычесть полученные дроби (используем предыдущее правило).
Для этого запишем в столбик числа, которые в сумме дают значения делителей. Далее перемножаем полученное и получаем НОК.
НОК (15, 18) = 3 * 2 * 3 * 5 = 90
Полученные числа запишем справа сверху над числителем.
Ход решения одной строкой:
Сложение или вычитание смешанных чисел можно привести к отдельному сложению их целых частей и дробных частей. Для этого нужно действовать поэтапно:
Необходимо приводить к общему, если знаменатели разные. Для этого воспользуемся знаниями из предыдущего примера.
Если при сложении дробных частей получилась неправильная дробь, нужно выделить ее целую часть и прибавить к полученной ранее целой части.
Умножение и деление дробей
Произведение двух дробей равно дроби, числитель которой равен произведению числителей, а знаменатель — произведению знаменателей:
Не забываем про сокращение. Это может облегчить вычисления.
Чтобы умножить два смешанных числа, надо:
Чтобы разделить дробь на дробь нужно выполнить следующую последовательность действий:
Другими словами это правило звучит так: чтобы разделить одну дробь на другую, надо первую умножить на обратную от второй.
Числа, произведение которых равно 1, называют взаимно обратными.
Как делить дроби с разными знаменателями? На самом деле одинаковые или разные знаменатели у дробей — неважно, потому что все дроби делятся по правилу, описанному выше.
Для деления смешанных чисел необходимо:
Источник
Неправильная дробь
Что такое неправильная дробь
Неправильной называется дробь, числитель которой по своей величине превышает знаменатель либо одинаков с ним.
Основные математические действия с неправильными дробями
Неправильная дробь — полноценный представитель числового множества, поэтому с ней можно производить основные математические действия:
Сравнение
6 / 5 7 / 5 ; 9 / 7 > 8 / 7 ; 5 / 5 = 5 / 5
Однако, бывает необходимо вычислить, насколько значение неправильной дроби больше (либо меньше) значения другой неправильной дроби с иным знаменателем.
Сложение
Определить сумму двух неправильных дробей с одинаковым знаменателем легко: 5/4+7/4=12/4=3
Схематически это можно записать с помощью формулы:
Сложение неправильных дробей с различными знаменателями. Для таких случаев существует два варианта: перевести дроби в смешанные либо использовать правило для перехода к общему знаменателю.
Переход к смешанным дробям осуществляется путем деления числителя на знаменатель (бывает, что с остатком):
Тактика приведения к общему знаменателю при сложении неправильных дробей (и их вычитании) следующая:
Аналогичным образом поступают, когда необходимо провести вычитание с неправильными дробями.
Умножение
При умножении друг на друга двух неправильных дробей получается дробь, числитель которой равен произведению числителей первоначальных дробей, а знаменатель — произведению знаменателей.
Деление
При делении неправильных дробей деление имеет обратное свойство. Делитель необходимо записать наоборот: числитель и знаменатель поменять местами. Когда это проведено, делимое умножают на делитель и получают искомый результат.
Перевод неправильной дроби в смешанную дробь и обратно
Неправильную дробь можно легко перевести в смешанную, произведя следующие действия:
Например, необходимо превратить в смешанную дробь 13/8.
Разделив 13 на 8, получаем 1 и 5/8. Разделив 5 на 8, получаем 0,625. В итоге 1,625.
Бывают случаи, когда нужно произвести обратное действие: превратить смешанную дробь в неправильную. Объяснение изложено в следующей формуле:
Подставим в эту формулу значения. 21 / 3 = ( 1 + 2 * 3 ) / 3 = 7 / 3
Примеры задач
Рассмотрим приведенные выше правила на примерах.
Сложение с одинаковым знаменателем: 8 / 5 + 7 / 5 = 15 / 5 = 3
Объяснение: приводим слагаемые к общему знаменателю. Для этого на знаменатель правой дроби умножаем числитель левой, а знаменатель левой — на числитель правой. В знаменателе дроби-произведения стоит произведение обоих знаменателей. После проведения расчетов получается смешанная дробь 3,625.
Объяснение: приводим вычитаемые к общему знаменателю. Для этого на знаменатель правой дроби умножаем числитель левой, а знаменатель левой — на числитель правой. В знаменателе дроби-частного стоит произведение обоих знаменателей. После проведения расчетов получается смешанная дробь 3,875.
Задача на умножение:
7 / 5 * 9 / 4 = 63 / 20
8 / 6 * 10 / 9 = 80 / 54
Объяснение: умножаем числитель на знаменатель и получаем искомое произведение.
4 / 7 : 2 / 5 = 4 / 7 * 5 / 2 = ( 4 * 5 ) / ( 7 * 2 ) = 20 / 14 = 16 / 14
Поменяв местами числитель и знаменатель в делителе, производим действие умножения двух дробей. После этого в числителе итоговой дроби ставится произведение двух числителей, а в ее знаменателе — произведение двух знаменателей.
Источник
Дроби
Что такое дробь
Дроби нужны для обозначения нецелых количеств. Они образуются как результат деления натуральных чисел, когда делимое не кратно делителю.
Дробная черта равносильна знаку деления. То есть (4:6=frac46) (четыре шестых), (7:2=frac72) (семь вторых). Числитель дроби играет роль делимого, а знаменатель — делителя.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Знаменатель дроби не может быть нулем.
Основные свойства дробей
Несократимой называют дробь, числитель и знаменатель которой взаимно просты, то есть не имеют общих делителей, кроме 1 (-1).
Существует два вида дробей: правильные и неправильные.
Неправильные дроби всегда больше правильных: (frac <39>
Правильные дроби
Правильная дробь — это обыкновенная дробь, числитель которой меньше знаменателя.
Правильная дробь называется так, поскольку выражает «правильную» часть единицы, то есть часть, которая меньше целого: ( frac25
Таким образом, отличить правильную дробь от неправильной можно при сравнении дробей с единицей. Это различие не влияет на арифметические действия, но важно при сравнении дробей.
Смешанные дроби
Неправильные дроби не принято оставлять в результате вычислений. Лучше преобразовывать их в смешанные числа. Любую неправильную дробь можно представить в виде смешанного числа.
Смешанное число — это число, содержащее целую и дробную часть.
Для составления смешанной дроби необходимо:
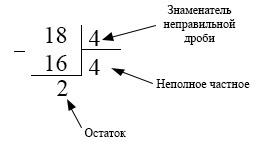
Записать неправильную дробь (frac<18>4) в виде смешанной.
Тогда искомая смешанная дробь (frac<18>4=4frac24.) Эту дробь можно сократить, поделив числитель и знаменатель дробной части на общий делитель 2:
Смешанное число можно записать в виде неправильной дроби. Для этого необходимо целую часть умножить на знаменатель дробной части. К полученному числу нужно прибавить числитель дробной части. Эту сумму записать в числитель, а знаменатель дробной части оставить без изменений.
Смешанное число (6frac25) записать в виде неправильной дроби.
Как перевести правильную дробь в неправильную
Перевести правильную дробь в неправильную или наоборот невозможно. Это разные категории чисел.
Любое натуральное число можно представить в виде неправильной дроби: (2=frac21.)
Дробь с числителем p и знаменателем 1 — это другая форма записи натурального числа p. Это правило можно представить в виде формулы: (p=frac p1.)
Действия с дробями, как решать примеры
Приведение к общему знаменателю
Чтобы решать большинство примеров с дробями, необходимо приводить их к общему знаменателю. Чтобы привести дроби (frac ab) и (frac cd) к общему знаменателю, необходимо:
Сравнение
Чтобы сравнить обыкновенные дроби, следует привести их к общему знаменателю и сравнить числители. Дробь с большим числителем больше.
(frac34>frac13,) поскольку (frac9<12>>frac4<12>.)
Если сравниваются смешанные числа, в первую очередь необходимо смотреть на целую часть. Больше то число, целая часть которого больше.
К примеру, (8frac16>5frac23.)
Если целые части смешанных чисел равны, то сравнивают дробные части по правилу сравнения обыкновенных дробей. Число с наибольшей дробной частью будет больше: (5frac23>5frac13.)
Сложение и вычитание
Чтобы сложить обыкновенные дроби, необходимо привести их к общему знаменателю, сложить числители, а знаменатели оставить без изменений. При необходимости привести дробь в вид смешанного числа.
При сложении смешанных чисел целые и дробные части складываются отдельно.
Чтобы вычесть одну дробь из другой, также необходимо привести их к общему знаменателю, после чего вычесть числители, а знаменатели оставить без изменений.
Умножение и деление
Чтобы умножить обыкновенные дроби, необходимо перемножить их числители и знаменатели.
(frac abcdotfrac cd=frac)
Умножить дробь (frac35) на (frac23.)
При умножении дроби на натуральное число, нужно умножить числитель на это число, а знаменатель оставить тем же. Так происходит, поскольку любое натуральное число можно представить в виде (p=frac p1.)
(frac abcdot p=frac abcdotfrac p1=fracb.)
Чтобы умножить смешанные числа, необходимо сперва представить их в виде обыкновенных дробей и лишь затем совершать действие.
Чтобы поделить одну дробь на другую, нужно умножить первую дробь на дробь, обратную второй. При этом оба знаменателя и числитель второй дроби не должны быть равны нулю.
(frac ab:frac cd=frac abcdotfrac dc=frac.)
Поделить дробь (frac34) на (frac23.)
При делении смешанных чисел, как и при умножении, их необходимо сперва привести к виду обыкновенной дроби.
Источник
неправильная дробь
- неправильная дробь
- непра́вильная дробь
дробь, бо́льшая единицы или равная ей.
* * *
НЕПРАВИЛЬНАЯ ДРОБЬ
НЕПРА́ВИЛЬНАЯ ДРО́БЬ, дробь, большая единицы или равная ей.
Энциклопедический словарь.
2009.
Смотреть что такое «неправильная дробь» в других словарях:
-
НЕПРАВИЛЬНАЯ ДРОБЬ — дробь, большая единицы или равная ей … Большой Энциклопедический словарь
-
неправильная дробь — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN improper fraction … Справочник технического переводчика
-
НЕПРАВИЛЬНАЯ ДРОБЬ — дробь, бблыпая единицы или равная ей … Естествознание. Энциклопедический словарь
-
Неправильная дробь — Четверти Рациональное число (лат. ratio отношение, деление, дробь) число, представляемое обыкновенной дробью , где m целое число, а n натуральное число. При этом число m называется числителем, а число n знаменателем дроби . Таку … Википедия
-
Неправильная дробь — арифметическая Дробь, числитель которой больше знаменателя (или равен ему), например 5/3, 4/2, 7/7. Н. д. можно представить, выделяя из неё целую часть, в виде смешанного числа, т. е. числа, имеющего целую и дробную части, например… … Большая советская энциклопедия
-
ДРОБЬ — ДРОБЬ, дроби, жен. 1. только ед., собир. Мелкие свинцовые шарики (употр. для стрельбы из охотничьего ружья). В утку попал весь заряд дроби. 2. Число, состоящее из частей единицы (мат.). Правильная дробь (меньше единицы). Неправильная дробь… … Толковый словарь Ушакова
-
дробь — и; ж. см. тж. дробью, дробовой, дробный 1) собир. Мелкие свинцовые шарики для стрельбы из охотничьего ружья. Зарядить ружьё дробью. Стрелять мелкой дробью. Вложить в ружьё заряд дроби. 2) собир … Словарь многих выражений
-
дробь — и, ж. 1. собир. Мелкие свинцовые шарики, употребляемые обычно для стрельбы из охотничьего ружья. Зарядить ружье дробью. □ Мы подстерегали стайки перелетных скворцов и стреляли в них мелкой дробью. Чехов, Моя жизнь. Какой то охотник всадил мне в… … Малый академический словарь
-
дробь — и; ж. 1. собир. Мелкие свинцовые шарики для стрельбы из охотничьего ружья. Зарядить ружьё дробью. Стрелять мелкой дробью. Вложить в ружьё заряд дроби. 2. собир. Частые, ритмически повторяющиеся звуки от ударов по чему л. Д. дождя, града. Слышна… … Энциклопедический словарь
-
дробь — ДРОБЬ, и, жен., собир. Мелкие свинцовые шарики для стрельбы из охотничьего ружья. | прил. дробовой, ая, ое. II. ДРОБЬ, и, мн. дроби, ей, жен. Число, представленное как состоящее из частей единицы. Правильная д. (меньше единицы). Неправильная д.… … Толковый словарь Ожегова
На букву Н Со слова «неправильная»
Фраза «неправильная дробь»
Фраза состоит из двух слов и 17 букв без пробелов.
- Написание фразы наоборот
- Написание фразы в транслите
- Написание фразы шрифтом Брайля
- Передача фразы на азбуке Морзе
- Произношение фразы на дактильной азбуке
- Остальные фразы со слова «неправильная»
- Остальные фразы из 2 слов

Математика 5 класс. Правильные и неправильные дроби

5 класс, 25 урок, Правильные и неправильные дроби

Выделение целой части из неправильной дроби. Математика 5 класс.

14 — Что такое правильная дробь, неправильная дробь и смешанное число ( Математика — 5 класс )

Перевод смешанного числа в неправильную дробь. Математика 5 класс.

Преобразование неправильной дроби
Написание фразы «неправильная дробь» наоборот
Как эта фраза пишется в обратной последовательности.
ьборд яаньливарпен 😀
Написание фразы «неправильная дробь» в транслите
Как эта фраза пишется в транслитерации.
в латинской🇬🇧 nepravilnaya drob
Как эта фраза пишется в пьюникоде — Punycode, ACE-последовательность IDN
xn--80aafkrsjfnk0lpb xn--90af4ah6d
Как эта фраза пишется в английской Qwerty-раскладке клавиатуры.
ytghfdbkmyfzlhj,m
Написание фразы «неправильная дробь» шрифтом Брайля
Как эта фраза пишется рельефно-точечным тактильным шрифтом.
⠝⠑⠏⠗⠁⠺⠊⠇⠾⠝⠁⠫⠀⠙⠗⠕⠃⠾
Передача фразы «неправильная дробь» на азбуке Морзе
Как эта фраза передаётся на морзянке.
– ⋅ ⋅ ⋅ – – ⋅ ⋅ – ⋅ ⋅ – ⋅ – – ⋅ ⋅ ⋅ – ⋅ ⋅ – ⋅ ⋅ – – ⋅ ⋅ – ⋅ – ⋅ – – ⋅ ⋅ ⋅ – ⋅ – – – – ⋅ ⋅ ⋅ – ⋅ ⋅ –
Произношение фразы «неправильная дробь» на дактильной азбуке
Как эта фраза произносится на ручной азбуке глухонемых (но не на языке жестов).
Передача фразы «неправильная дробь» семафорной азбукой
Как эта фраза передаётся флажковой сигнализацией.
Остальные фразы со слова «неправильная»
Какие ещё фразы начинаются с этого слова.
- неправильная галактика
- неправильная диета
- неправильная дорога
- неправильная жизнь
- неправильная интерпретация
- неправильная информация
- неправильная линия
- неправильная музыка
- неправильная осанка
- неправильная оценка
- неправильная парковка
- неправильная переменная звезда
- неправильная пища
- неправильная позиция
- неправильная постановка вопроса
- неправильная проверка ввода
- неправильная работа
- неправильная речь
- неправильная тактика
- неправильная точка зрения
- неправильная форма
- неправильная цель
Ваша фраза добавлена!
Остальные фразы из 2 слов
Какие ещё фразы состоят из такого же количества слов.
- а вдобавок
- а вдруг
- а ведь
- а вот
- а если
- а ещё
- а именно
- а капелла
- а каторга
- а ну-ка
- а приятно
- а также
- а там
- а то
- аа говорит
- аа отвечает
- аа рассказывает
- ааронов жезл
- аароново благословение
- аароново согласие
- аб ово
- абажур лампы
- абазинская аристократия
- абазинская литература
Комментарии

11:35
Что значит фраза «неправильная дробь»? Как это понять?..
Ответить

13:52

×
Здравствуйте!
У вас есть вопрос или вам нужна помощь?
Спасибо, ваш вопрос принят.
Ответ на него появится на сайте в ближайшее время.
А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ъ Ы Ь Э Ю Я
Транслит Пьюникод Шрифт Брайля Азбука Морзе Дактильная азбука Семафорная азбука
Палиндромы Сантана

Народный словарь великого и могучего живого великорусского языка.
Онлайн-словарь слов и выражений русского языка. Ассоциации к словам, синонимы слов, сочетаемость фраз. Морфологический разбор: склонение существительных и прилагательных, а также спряжение глаголов. Морфемный разбор по составу словоформ.
По всем вопросам просьба обращаться в письмошную.
Значение словосочетания «неправильная дробь»

-
Неправильная дробь (
мат.) — дробь, числитель которой больше знаменателя или равен ему.См. также неправильный.
Источник (печатная версия): Словарь русского языка: В 4-х
т. / РАН,
Ин-т лингвистич.
исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.;
Полиграфресурсы,
1999;
(электронная версия): Фундаментальная
электронная
библиотека
-
Неправильная дробь (мат.)
— см. дробь.См. также неправильный.
Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940);
(электронная версия): Фундаментальная
электронная
библиотека
Делаем Карту слов лучше вместе
Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать
Карту слов. Я отлично
умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!
Спасибо! Я стал чуточку лучше понимать мир эмоций.
Вопрос: ада — это что-то нейтральное, положительное или отрицательное?
Ассоциации к слову «неправильный»
Ассоциации к слову «дробь»
Синонимы к слову «неправильный»
Синонимы к слову «дробь»
Предложения со словосочетанием «неправильная дробь»
- Если дробная часть уменьшаемого будет меньше дробной части вычитаемого, то превращаем в неправильную дробь, за счёт уменьшения на единицу целой части уменьшаемого.
- (все предложения)
Афоризмы русских писателей со словом «неправильный»
- В погоне за красотой я постоянно грешил против точности описаний, неправильно ставил вещи, неверно освещал людей.
- Их (писателей) не должно утешать то, что сейчас многие «признанные» писатели тоже плохо знают родной язык.
Почти у каждого можно отметить неправильную расстановку слов; запутанность фразы, неточность её. Это значит, что автор плохо видит то, о чем он пишет. - Нельзя уйти от жизненных проблем… Слабые люди преодолевают жизнь, мужественные — осваивают… Если живешь неправильно, рано или поздно что-то случится.
- (все афоризмы русских писателей)
Отправить комментарий
Дополнительно
Значение слова «НЕПРАВИЛЬНАЯ ДРОБЬ» найдено в 23 источниках
НЕПРАВИЛЬНАЯ ДРОБЬ
арифметическая Дробь, числитель которой больше знаменателя (или равен ему), например 5/3, 4/2, 7/7. Н. д. можно представить, выделяя из неё целую часть, в виде смешанного числа, т. е. числа, имеющего целую и дробную части, например

Обратно, всякое смешанное число можно записать в виде Н. д., например

Найдено 2 изображения:
Изображения из описаний на этой странице
неправильная дробь
שֶבֶר מְדוּמֶה ז’
frazione impropria {/trn]
НЕПРАВИЛЬНАЯ ДРОБЬ, дробь, большая единицы или равная ей.
composed fraction, improper fraction
НЕПРАВИЛЬНАЯ дробь — дробь, большая единицы или равная ей.
НЕПРАВИЛЬНАЯ ДРОБЬ , дробь, большая единицы или равная ей.
НЕПРАВИЛЬНАЯ ДРОБЬ, дробь, большая единицы или равная ей.
дробь, бблыпая единицы или равная ей.
мат. неправильний (мішаний) дріб.
— дробь, большая единицы или равная ей.
мі́шаний дріб, непра́вильний дріб
Что такое «неправильная дробь»? Значение словосочетания в словарях и простыми словами, примеры употребления в тексте
Cловосочетание НЕПРАВИЛЬНАЯ ДРОБЬ означает:
дробь, большая единицы или равная ей.
Источник: Большой Энциклопедический Словарь
Cловосочетание «неправильная дробь» является ответом на вопросы
- Вопросы, в которых ответом является словосочетание «неправильная дробь» не найдены.
Разбор частей речи
Далее давайте разберем морфологические признаки каждой из частей речи русского языка на примерах. Согласно лингвистике русского языка, выделяют три группы из 10 частей речи, по общим признакам:
1. Самостоятельные части речи:
- существительные (см. морфологические нормы сущ. );
- глаголы:
-
- причастия;
- деепричастия;
- прилагательные;
- числительные;
- местоимения;
- наречия;
2. Служебные части речи:
- предлоги;
- союзы;
- частицы;
3. Междометия.
Ни в одну из классификаций (по морфологической системе) русского языка не попадают:
- слова да и нет, в случае, если они выступают в роли самостоятельного предложения.
- вводные слова: итак, кстати, итого, в качестве отдельного предложения, а так же ряд других слов.
Морфологический разбор существительного
План морфологического разбора существительного
Пример:
«Малыш пьет молоко.»
Малыш (отвечает на вопрос кто?) – имя существительное;
- начальная форма – малыш;
- постоянные морфологические признаки: одушевленное, нарицательное, конкретное, мужского рода, I -го склонения;
- непостоянные морфологические признаки: именительный падеж, единственное число;
- при синтаксическом разборе предложения выполняет роль подлежащего.
Морфологический разбор слова «молоко» (отвечает на вопрос кого? Что?).
- начальная форма – молоко;
- постоянная морфологическая характеристика слова: среднего рода, неодушевленное, вещественное, нарицательное, II -е склонение;
- изменяемые признаки морфологические: винительный падеж, единственное число;
- в предложении прямое дополнение.
Приводим ещё один образец, как сделать морфологический разбор существительного, на основе литературного источника:
«Две дамы подбежали к Лужину и помогли ему встать. Он ладонью стал сбивать пыль с пальто. (пример из: «Защита Лужина», Владимир Набоков).»
Дамы (кто?) — имя существительное;
- начальная форма — дама;
- постоянные морфологические признаки: нарицательное, одушевленное, конкретное, женского рода, I склонения;
- непостоянная морфологическая характеристика существительного: единственное число, родительный падеж;
- синтаксическая роль: часть подлежащего.
Лужину (кому?) — имя существительное;
- начальная форма — Лужин;
- верная морфологическая характеристика слова: имя собственное, одушевленное, конкретное, мужского рода, смешанного склонения;
- непостоянные морфологические признаки существительного: единственное число, дательного падежа;
- синтаксическая роль: дополнение.
Ладонью (чем?) — имя существительное;
- начальная форма — ладонь;
- постоянные морфологические признаки: женского рода, неодушевлённое, нарицательное, конкретное, I склонения;
- непостоянные морфо. признаки: единственного числа, творительного падежа;
- синтаксическая роль в контексте: дополнение.
Пыль (что?) — имя существительное;
- начальная форма — пыль;
- основные морфологические признаки: нарицательное, вещественное, женского рода, единственного числа, одушевленное не охарактеризовано, III склонения (существительное с нулевым окончанием);
- непостоянная морфологическая характеристика слова: винительный падеж;
- синтаксическая роль: дополнение.
(с) Пальто (С чего?) — существительное;
- начальная форма — пальто;
- постоянная правильная морфологическая характеристика слова: неодушевленное, нарицательное, конкретное, среднего рода, несклоняемое;
- морфологические признаки непостоянные: число по контексту невозможно определить, родительного падежа;
- синтаксическая роль как члена предложения: дополнение.
Морфологический разбор прилагательного
Имя прилагательное — это знаменательная часть речи. Отвечает на вопросы Какой? Какое? Какая? Какие? и характеризует признаки или качества предмета. Таблица морфологических признаков имени прилагательного:
- начальная форма в именительном падеже, единственного числа, мужского рода;
- постоянные морфологические признаки прилагательных:
-
- разряд, согласно значению:
-
- — качественное (теплый, молчаливый);
- — относительное (вчерашний, читальный);
- — притяжательное (заячий, мамин);
- степень сравнения (для качественных, у которых этот признак постоянный);
- полная / краткая форма (для качественных, у которых этот признак постоянный);
- непостоянные морфологические признаки прилагательного:
-
- качественные прилагательные изменяются по степени сравнения (в сравнительных степенях простая форма, в превосходных — сложная): красивый-красивее-самый красивый;
- полная или краткая форма (только качественные прилагательные);
- признак рода (только в единственном числе);
- число (согласуется с существительным);
- падеж (согласуется с существительным);
- синтаксическая роль в предложении: имя прилагательное бывает определением или частью составного именного сказуемого.
План морфологического разбора прилагательного
Пример предложения:
Полная луна взошла над городом.
Полная (какая?) – имя прилагательное;
- начальная форма – полный;
- постоянные морфологические признаки имени прилагательного: качественное, полная форма;
- непостоянная морфологическая характеристика: в положительной (нулевой) степени сравнения, женский род (согласуется с существительным), именительный падеж;
- по синтаксическому анализу — второстепенный член предложения, выполняет роль определения.
Вот еще целый литературный отрывок и морфологический разбор имени прилагательного, на примерах:
Девушка была прекрасна: стройная, тоненькая, глаза голубые, как два изумительных сапфира, так и заглядывали к вам в душу.
Прекрасна (какова?) — имя прилагательное;
- начальная форма — прекрасен (в данном значении);
- постоянные морфологические нормы: качественное, краткое;
- непостоянные признаки: положительная степень сравнения, единственного числа, женского рода;
- синтаксическая роль: часть сказуемого.
Стройная (какая?) — имя прилагательное;
- начальная форма — стройный;
- постоянные морфологические признаки: качественное, полное;
- непостоянная морфологическая характеристика слова: полное, положительная степень сравнения, единственное число, женский род, именительный падеж;
- синтаксическая роль в предложении: часть сказуемого.
Тоненькая (какая?) — имя прилагательное;
- начальная форма — тоненький;
- морфологические постоянные признаки: качественное, полное;
- непостоянная морфологическая характеристика прилагательного: положительная степень сравнения, единственное число, женского рода, именительного падежа;
- синтаксическая роль: часть сказуемого.
Голубые (какие?) — имя прилагательное;
- начальная форма — голубой;
- таблица постоянных морфологических признаков имени прилагательного: качественное;
- непостоянные морфологические характеристики: полное, положительная степень сравнения, множественное число, именительного падежа;
- синтаксическая роль: определение.
Изумительных (каких?) — имя прилагательное;
- начальная форма — изумительный;
- постоянные признаки по морфологии: относительное, выразительное;
- непостоянные морфологические признаки: множественное число, родительного падежа;
- синтаксическая роль в предложении: часть обстоятельства.
Морфологические признаки глагола
Согласно морфологии русского языка, глагол — это самостоятельная часть речи. Он может обозначать действие (гулять), свойство (хромать), отношение (равняться), состояние (радоваться), признак (белеться, красоваться) предмета. Глаголы отвечают на вопрос что делать? что сделать? что делает? что делал? или что будет делать? Разным группам глагольных словоформ присущи неоднородные морфологические характеристики и грамматические признаки.
Морфологические формы глаголов:
- начальная форма глагола — инфинитив. Ее так же называют неопределенная или неизменяемая форма глагола. Непостоянные морфологические признаки отсутствуют;
- спрягаемые (личные и безличные) формы;
- неспрягаемые формы: причастные и деепричастные.
Морфологический разбор глагола
- начальная форма — инфинитив;
- постоянные морфологические признаки глагола:
-
- переходность:
-
- переходный (употребляется с существительными винительного падежа без предлога);
- непереходный (не употребляется с существительным в винительном падеже без предлога);
- возвратность:
-
- возвратные (есть -ся, -сь);
- невозвратные (нет -ся, -сь);
- вид:
-
- несовершенный (что делать?);
- совершенный (что сделать?);
- спряжение:
-
- I спряжение (дела-ешь, дела-ет, дела-ем, дела-ете, дела-ют/ут);
- II спряжение (сто-ишь, сто-ит, сто-им, сто-ите, сто-ят/ат);
- разноспрягаемые глаголы (хотеть, бежать);
- непостоянные морфологические признаки глагола:
-
- наклонение:
-
- изъявительное: что делал? что сделал? что делает? что сделает?;
- условное: что делал бы? что сделал бы?;
- повелительное: делай!;
- время (в изъявительном наклонении: прошедшее/настоящее/будущее);
- лицо (в настоящем/будущем времени, изъявительного и повелительного наклонения: 1 лицо: я/мы, 2 лицо: ты/вы, 3 лицо: он/они);
- род (в прошедшем времени, единственного числа, изъявительного и условного наклонения);
- число;
- синтаксическая роль в предложении. Инфинитив может быть любым членом предложения:
-
- сказуемым: Быть сегодня празднику;
- подлежащим :Учиться всегда пригодится;
- дополнением: Все гости просили ее станцевать;
- определением: У него возникло непреодолимое желание поесть;
- обстоятельством: Я вышел пройтись.
Морфологический разбор глагола пример
Чтобы понять схему, проведем письменный разбор морфологии глагола на примере предложения:
Вороне как-то Бог послал кусочек сыру… (басня, И. Крылов)
Послал (что сделал?) — часть речи глагол;
- начальная форма — послать;
- постоянные морфологические признаки: совершенный вид, переходный, 1-е спряжение;
- непостоянная морфологическая характеристика глагола: изъявительное наклонение, прошедшего времени, мужского рода, единственного числа;
- синтаксическая роль в предложении: сказуемое.
Следующий онлайн образец морфологического разбора глагола в предложении:
Какая тишина, прислушайтесь.
Прислушайтесь (что сделайте?) — глагол;
- начальная форма — прислушаться;
- морфологические постоянные признаки: совершенный вид, непереходный, возвратный, 1-го спряжения;
- непостоянная морфологическая характеристика слова: повелительное наклонение, множественное число, 2-е лицо;
- синтаксическая роль в предложении: сказуемое.
План морфологического разбора глагола онлайн бесплатно, на основе примера из целого абзаца:
— Его нужно предостеречь.
— Не надо, пусть знает в другой раз, как нарушать правила.
— Что за правила?
— Подождите, потом скажу. Вошел! («Золотой телёнок», И. Ильф)
Предостеречь (что сделать?) — глагол;
- начальная форма — предостеречь;
- морфологические признаки глагола постоянные: совершенный вид, переходный, невозвратный, 1-го спряжения;
- непостоянная морфология части речи: инфинитив;
- синтаксическая функция в предложении: составная часть сказуемого.
Пусть знает (что делает?) — часть речи глагол;
- начальная форма — знать;
- постоянные морфологические признаки: несовершенный вид, невозвратный, переходный, 1-го спряжения;
- непостоянная морфология глагола: повелительное наклонение, единственного числа, 3-е лицо;
- синтаксическая роль в предложении: сказуемое.
Нарушать (что делать?) — слово глагол;
- начальная форма — нарушать;
- постоянные морфологические признаки: несовершенный вид, невозвратный, переходный, 1-го спряжения;
- непостоянные признаки глагола: инфинитив (начальная форма);
- синтаксическая роль в контексте: часть сказуемого.
Подождите (что сделайте?) — часть речи глагол;
- начальная форма — подождать;
- постоянные морфологические признаки: совершенный вид, невозвратный, переходный, 1-го спряжения;
- непостоянная морфологическая характеристика глагола: повелительное наклонение, множественного числа, 2-го лица;
- синтаксическая роль в предложении: сказуемое.
Вошел (что сделал?) — глагол;
- начальная форма — войти;
- постоянные морфологические признаки: совершенный вид, невозвратный, непереходный, 1-го спряжения;
- непостоянная морфологическая характеристика глагола: прошедшее время, изъявительное наклонение, единственного числа, мужского рода;
- синтаксическая роль в предложении: сказуемое.