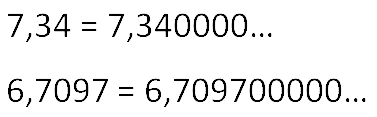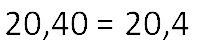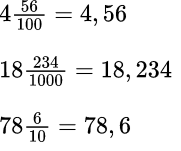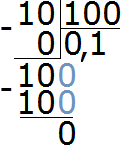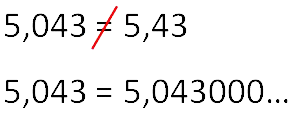Как читать десятичные дроби
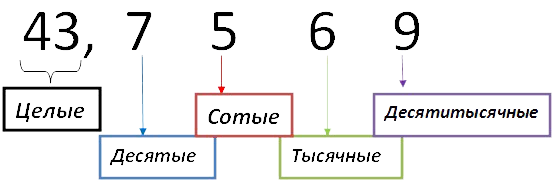
В первую очередь обсудим вид десятичной дроби. Каждая цифра после запятой имеет своё название.
Десятые, сотые, тысячные, десятитысячные…
Десятые, сотые и тысячные
Попробуем прочитать десятичную дробь из примера выше. Чтобы правильно прочитать десятичную дробь нужно:
Прочитать число слева от запятой и добавить слово «целыx», так как слева от запятой находится целая часть десятичной дроби. Читаем: «сорок три целых».
Затем прочитать число справа от запятой: «семь тысяч пятьсот шестьдесят девять».
Добавить в конце название самой правой цифры.
У нас это 9 , которая стоит на месте десятитысячных (см. рис. выше): «десятитысячных».
Значит, полное название дроби звучит так:
43,7569 — сорок три целых семь тысяч пятьсот шестьдесят девять десятитысячных.
Справа от запятой после самой последней правой цифры отличной от нуля можно добавлять сколько угодно нулей. От этого значение десятичной дроби не изменится.
Таким же образом если в конце десятичной дроби отбросить ноль, то мы получим такую же по значению десятичную дробь.
Поэтому, если при расчётах получили десятичную дробь 20,40 , отбрасываем ноль на конце и записываем:
Нули можно добавлять (убирать) только после самой последней правой отличной от нуля цифры. Нули между цифрами в числе убирать нельзя.
Источник статьи: http://math-prosto.ru/?page=pages/decimal/decimal2.php
Чтение десятичных дробей
Десятичная дробь в обязательном порядке содержит запятую. Та числовая часть дроби, которая располагается левее запятой, называется целой; правее – дробной:
Дробная часть десятичной дроби состоит из десятичных знаков (десятичных разрядов):
- десятые – 0,1 (одна десятая);
- сотые – 0,01 (одна сотая);
- тысячные – 0,001 (одна тысячная);
- десятитысячные – 0,0001 (одна десятитысячная);
- стотысячные – 0,00001 (одна стотысячная);
- миллионные – 0,000001 (одна миллионная);
- десятимиллионные – 0,0000001 (одна десятимиллионная);
- стомиллионные – 0,00000001 (одна стомиллионная);
- миллиардные – 0,000000001 (одна миллиардная) и т. д.
Как правильно читать десятичную дробь:
- прочитать число, составляющее целую часть дроби и добавить слово “целых“;
- прочитать число, составляющее дробную часть дроби и добавить название младшего разряда.
- 0,25 – ноль целых двадцать пять сотых;
- 9,1 – девять целых одна десятая;
- 18,013 – восемнадцать целых тринадцать тысячных;
- 100,2834 – сто целых две тысячи восемьсот тридцать четыре десятитысячных.
Запись десятичных дробей
Чтобы записать десятичную дробь, необходимо:
- записать целую часть дроби и поставить запятую (число, означающее целую часть дроби всегда заканчивается словом “целых“);
- записать дробную часть дроби таким образом, чтобы последняя цифра попала в нужный разряд (при отсутствии значащих цифр в определенных десятичных разрядах они заменяются нулями).
- двадцать целых девять десятых – 20,9 – в этом примере все просто;
- пять целых одна сотая – 5,01 – слово “сотая” означает, что после запятой должны стоять две цифры, но, поскольку в числе 1 нет разряда десятых, он заменяется нулем;
- ноль целых восемьсот восемь тысячных – 0,808;
- три целых пятнадцать десятых – такую десятичную дробь записать невозможно, потому, что в произношении дробной части допущена ошибка – число 15 содержит два разряда, а слово “десятых” подразумевает только один. Правильно будет три целых пятнадцать сотых (или тысячных, десятитысячных и т. д.).
Сравнение десятичных дробей
Сравнение десятичных дробей проводится аналогично сравнению натуральных чисел.
- сначала сравниваются целые части дробей – больше будет та десятичная дробь у которой больше ее целая часть;
- если целые части дробей равны, сравнивают поразрядно дробные части, слева направо, начиная от запятой: десятые, сотые, тысячные и т.д. Сравнение ведут до первого несовпадения – больше будет та десятичная дробь у которой будет больше неравная цифра в соответствующем разряде дробной части. Например: 1,283 > 1,279, т. к. в сотых разрядах у первой дроби стоит 8, а у второй 7.
Если вам понравился сайт, будем благодарны за его популяризацию 🙂 Расскажите о нас друзьям на форуме, в блоге, сообществе. Это наша кнопочка:
Код кнопки: 
Политика конфиденциальности Об авторе
Источник статьи: http://prosto-o-slognom.ru/matematika/007-desyatichnaya_drob.html
СПАДИЛО.РУ
теория по математике 📈 числа и вычисления
Десятичная дробь — дробь, которая представляет собой способ представление числа в виде записи числа с запятой, где цифры перед запятой называются целой частью, а цифры после запятой – дробной частью (десятичной частью).
Десятичные дроби получают из записи обыкновенных дробей со знаменателем 10, 100, 1000 и так далее. Например, десятичные дроби:
4,56 – четыре целых пятьдесят шесть сотых 18,234 – восемнадцать целых двести тридцать четыре тысячных 78,6 – семьдесят восемь целых шесть десятых
Чтение десятичных дробей
Чтение десятичной части (десятых, сотых и так далее) зависит от количества цифр после запятой. Если цифра одна, то читают – десятых (в числе десять — один нуль, это соответствует одной цифре). Если две цифры после запятой, то читают – сотых (в сотне два нуля).
Десятичные дроби получаются из обыкновенных дробей:
Сложение (вычитание) десятичных дробей
Чтобы сложить (вычесть) в столбик две десятичные дроби нужно:
- Записать их друг под другом так, чтобы при записи запятая оказалась под запятой и соответствующий разряд под соответствующим.
- Уравнять количество знаков после запятой, добавляя недостающие нулями.
- Выполнить сложение (вычитание) в столбик, не обращая внимания на запятую.
- Поставить запятую под запятыми.
Если складывают (вычитают) целое число и десятичную дробь, то нужно поставить запятую после целого числа и приписать необходимое количество нулей после запятой.
Пример №1. Запись, где запятая под запятой и соответствующий разряд под соответствующим.
34,145 + 5,678 = 39,823
Пример №2. Запись, где также запятая под запятой, а во втором числе дописан нуль, чтобы уравнять количество знаков после запятой.
Пример №3. В первом слагаемом нет десятичной части, поэтому, после числа 56 поставили запятую и добавили нужное количество нулей.
Умножение десятичных дробей
При умножении двух десятичных дробей в столбик необходимо:
- Написать числа одно под другим, не обращая внимания на запятую
- Выполнить умножение в столбик
- В ответе отделить столько цифр справа запятой, сколько их в обоих множителях вместе. Если в одном из чисел нет запятой, то считать цифры только в одном числе.
Пример №4. Запись выполнена так, что цифры по правому краю записаны ровно одна под одной, то есть как при обычном умножении чисел в столбик. Умножение выполнено без учета запятой. В ответе справа отделены 4 цифры запятой, так как в первом множителе их 3 после запятой, а во втором – одна, в двух множителях вместе – четыре.
0,125 × 2,3 00375 0250 0,2875
Пример №5. Здесь показано умножение десятичной дроби и целого числа. Умножение выполнено без учета запятой. В ответе отделена справа запятой только одна цифра, так как только в первом множителе есть десятичная часть с одной цифрой после запятой.
Умножение десятичных дробей на 10, 100, 1000…
Чтобы умножить десятичную дробь на 10, 100, 1000 и так далее, нужно перенести запятую вправо на столько цифр, сколько нулей у множителя. Умножение в данном случае выполняется в строчку.
Пример №6. 2,456 × 10 = 24,56 Запятую в десятичной дроби перенесли вправо на 1 цифру, так как у 10 один нуль.
Пример №7. 0,45678 × 100 = 45,678 Запятую перенесли вправо на 2 цифры, так как у 100 два нуля. Нуль, стоящий в начале десятичной дроби, убрали, так как впереди целой части, отличной от нуля он не пишется.
Пример №8. 9,46 × 1000 = 9460 в данном случае при переносе запятой на три цифра не хватило одной, поэтому в конце числа приписали нуль, и в ответе получилось целое число.
Умножение десятичной дроби на разрядную единицу 0,1; 0,01; 0,001…
При умножении десятичной дроби на разрядную единицу 0,1; 0,01; 0,001 (и так далее) нужно перенести запятую на столько цифр влево, сколько цифр в данной разрядной единице после запятой. Умножение обычно выполняется в строчку устно.
Пример №9. 983,7821 × 0,01= 9,837821 Переносим запятые влево на 2 цифры, так как в числе 0,01 две цифры после запятой.
Пример №10. 8,7654 × 0,1 = 0,87654 Перенесли на 1 цифру влево, так как в числе 0,1 одна цифра после запятой. В данном случае перед 8 появился нуль, так как при переносе запятой слева цифр не оказалось.
Пример №11. 7,98 × 0,0001 = 0,000798 При переносе влево на 4 цифры не хватило трех, поэтому впереди поставили нули, а также нуль образуется и в целой части.
Деление десятичных дробей
- При делении десятичной дроби на целое число выполняют сначала деление целой части, а затем десятичной.
- При делении десятичной дроби на другую десятичную дробь необходимо в делителе убрать запятую, а в делимом передвинуть ее вправо на столько цифр, сколько их в делителе после запятой. Затем выполнить деление на целое число.
- Есть случаи, когда цифр после запятой при переносе запятой у дроби не хватает. Тогда необходимо дополнить число нулями.
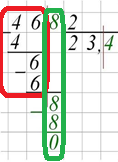
Пример №12. Деление десятичной дроби на целое число. 46,8 : 2 = 23,4
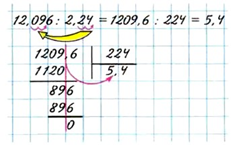
Пример №13. Деление десятичной дроби на десятичную дробь. 12,096 : 2,24 = 5,4 Из данного примера видно, что деление десятичных дробей обязательно сводится к делению на целое число.
Пример №14. 276,3 : 0,003 = 276300 : 3 = 92100. Здесь видно, что не хватает двух цифр в числе 276,3 и поэтому при переносе запятой к нему приписали два нуля. Затем выполнили деление двух целых чисел.
Деление десятичной дроби на 10, 100, 1000…
При делении десятичной дроби на 10,100, 1000 и так далее нужно перенести запятую на столько цифр влево, сколько нулей в данном числе. Деление выполняется в строчку устно.
Пример №16. 134,987 : 1000 = 0,134987 Перенесли запятую на три цифры влево, так как у 1000 три нуля. В целой части поставили нуль, так как цифр не хватило.
Пример №17. 7,234 : 100 = 0,07234 Перенесли запятую влево на две цифры. Так как цифр не хватало, то недостающие заменили нулями.
Деление десятичной дроби на разрядную единицу 0,1; 0,01; 0,001…
При делении десятичной дроби на разрядную единицу 0,1; 0,01; 0,001 и так далее нужно перенести запятую на столько цифр вправо, сколько цифр в данной разрядной единице после запятой. Деление обычно выполняется в строчку устно.
Пример №19. 41,234 : 0,01 = 4123,4 Перенос запятой на 2 цифры вправо, так как в числе 0,01 две цифры после запятой.
Пример №20. 56,91 : 0,001 = 56910 При переносе запятой на три цифры вправо приписали один нуль, так как одной цифры не хватило.
Источник статьи: http://spadilo.ru/desyatichnye-drobi/
Морфемный разбор слова:
Однокоренные слова к слову:
Поиск ответа
Как произносится числительное в предложении «А больше Б в 1,72 раза»
Ответ справочной службы русского языка
Произносится: в один и семьдесят две сотых раза.
Добрый день, уважаемые эксперты. Я патрулирующий русской Википедии. В своей работе нередко сталкиваюсь с числительными, а именно с денежными наименованиями. Постоянно возникают трудности с десятичными дробями. Не знаю как склонять существительные рядом с ними. Например, 2,89 миллиардА или миллиардОВ доллара(-ов). Обычно проверяю себя, проговаривая дробное число: «Две целых восемьдесят девять сотЫХ миллиардОВ долларОВ», но не знаю, правильно ли это. Можете, пожалуйста, объяснить и просклонять данное число и, например одна целая тридцать одна сотая. Благодарю.
Ответ справочной службы русского языка
Правило простое: при дробных числительных существительное употребляется в форме единственного числа родительного падежа: 4,3 рубля, 67,84 километра, 2,89 миллиарда. Слово доллар уже не зависит напрямую от числительного, поэтому ставится во множественном числе: 2,89 миллиарда (чего?) долларов.
Поэтому верно: Две целых восемьдесят девять сотых миллиарда долларов; одна целая тридцать одна сотая миллиарда долларов.
Добрый день! Как правильно: 59,99 долларов США (т.е. 59 долларов и 99 центов) или 59,99 доллара США (т.е. 59 целых 99 сотых )?
Ответ справочной службы русского языка
Верно: 59,99 доллара; 59 долларов 99 центов.
Добрый день! Как правильно прописью написать математическое число 18 800,50 граммов?
Ответ справочной службы русского языка
Восемнадцать тысяч восемьсот и пятьдесят сотых грамма.
Ответ справочной службы русского языка
Поскольку здесь используется дробное числительное, существительное ставится в форме единственного числа родительного падежа: барреля.
Скажите, пожалуйста. где можно найти подробное правило о согласовании дробных числительных с прилагательным и существительным ( например: 0,68 сотых квадратных метров? квадратного метра?)?
Ответ справочной службы русского языка
При смешанном числе существительным управляет дробь, а не целое число. Правильно: 0,68 квадратного метра.
Ответ справочной службы русского языка
Существительным управляет дробная часть: 4,67 календарного дня (шестьдесят семь сотых календарного дня).
Как правильно писать 56 789,56 рубля или 56 789,56 рублей? На что ориентироваться: на количество целых, количество сотых или на то, что сотые всегда одного рубля?
Ответ справочной службы русского языка
Правильно: 56 789,56 рубля. Существительным управляет дробная часть: пятьдесят шесть сотых рубля.
Добрый день!
Подскажите, как верно указывать окончание слова «рубль» при следующей расшифровке стоимости:
243 111,87 (Двести сорок три тысячи сто одиннадцать и 87/100) рубля или рублей и почему.
Спасибо.
Ответ справочной службы русского языка
Правильно: 243 111,87 рубля (существительным управляет дробная часть: восемьдесят семь сотых рубля ) или 243 111 рублей 87 копеек.
Как правильно писать 12348, 56 рубля или 12348,56 рублей?
Ответ справочной службы русского языка
Правильно: рубля. Существительным управляет дробная часть: пятьдесят шесть сотых рубля.
Добрый день! Подскажите пожалуйста, как правильно писать 0,96 процента/процентов,
8,3496 процента/процентов? Мнения в коллективе разошлись.
Ответ справочной службы русского языка
Подскажите, пожалуйста, правильно ли употребление существительных с числительными: 2,38 года и 76,1 лет.
Ответ справочной службы русского языка
Добрый день. Скажите, пожалуйста, правильно ли я понимаю, если после цифры следует запятая (т.е. дробная часть) всегда к числу указываем балла, а не баллов?
Например: 0,12 балла или 2,1 балла.
Ответ справочной службы русского языка
Да, существительным управляет дробная часть: 0,12 балла, 2,1 балла (читаем: двенадцать сотых балла, одна десятая балла).
Стоимость билета на проезд в автобусе внутри города составит 6,90 рублей вместо 6,60 рублей.
Рубля или рублей? (когда с десятыми) Спасибо!
Ответ справочной службы русского языка
Существительным управляет дробная часть: 6,90 рубля (девяносто сотых рубля). Но лучше: 6 рублей 90 копеек.
Прошу ответить, вопрос крайне важен!
Как сокращается в русском языке слово «карат»? Бриллиант в 2,11 карат? А если это относится к золоту?
Спасибо заранее!
Ответ справочной службы русского языка
В счетной форме (т. е. в конструкциях с количественным значением) правильно: каратов и карат: 5 каратов и 5 карат.
Однако в рассматриваемом примере верно: 2,11 карата. Существительным управляет дробная часть: одиннадцать сотых карата.
Источник
одна сотая
Смотреть что такое «одна сотая» в других словарях:
Сотая — I ж. жен. к сущ. сотый I II прил. разг. Очень малая, незначительная, небольшая часть, доля чего либо. III числ. разг. Часть, доля, полученная от деления чего либо на сто равных частей; одна сотая. Толковый словарь Ефремовой. Т. Ф. Ефремова. 2000 … Современный толковый словарь русского языка Ефремовой
Сотая — I ж. жен. к сущ. сотый I II прил. разг. Очень малая, незначительная, небольшая часть, доля чего либо. III числ. разг. Часть, доля, полученная от деления чего либо на сто равных частей; одна сотая. Толковый словарь Ефремовой. Т. Ф. Ефремова. 2000 … Современный толковый словарь русского языка Ефремовой
Сотая — I ж. жен. к сущ. сотый I II прил. разг. Очень малая, незначительная, небольшая часть, доля чего либо. III числ. разг. Часть, доля, полученная от деления чего либо на сто равных частей; одна сотая. Толковый словарь Ефремовой. Т. Ф. Ефремова. 2000 … Современный толковый словарь русского языка Ефремовой
сотая — см. сотый 2); ой; ж. Одна со/тая рубля. Шесть сотых гектара … Словарь многих выражений
Базисный пункт — Одна сотая часть процента. Употребляется применительно к рынку долговых обязательств. Наименьшая единица, используемая при котировании доходности. Каждый процент доходности равен 100 базисным пунктам. Базисные пункты также используются… … Инвестиционный словарь
Сантиметр — одна сотая часть метра, около одной четвертой части вершка … Популярный политический словарь
Список разменных денежных единиц — перечень единиц измерения денежных сумм, равных определённой доле базовой денежной единицы (валюты). Как правило, это монеты, реже банкноты или не имеющие физической формы счётные единицы, которые используется для мелких расчётов и называются… … Википедия
метрическая система — система мер и весов, получившая широкое распространение в различных странах и называемая поэтому международной. Впервые метрическая система была введена во Франции в 1793 году. В России до 1918 года метрическая система допускалась к применению… … Справочный коммерческий словарь
Разменные денежные единицы — Разменная (производная) денежная единица (номинал, монета) денежный знак (как правило, монета, реже банкнота) или не имеющая физической формы счётная единица, которая является составной (как правило, 1/100) частью базовой валюты страны и… … Википедия
Существующие разменные денежные единицы — Существующие разменные денежные единицы находящиеся в обращении разменные (производные, дробные) денежные единицы (номиналы, монеты). Как правило, существуют в форме монет, реже банкнот или не имеющих физической формы счётных единиц,… … Википедия
Цент — У этого термина существуют и другие значения, см. Цент (значения). Цент (лат. centum сто) производная денежная единица и разменная монета достоинством в одну сотую базовой валюты 55 стран. Содержание 1 Этимология … Википедия
Источник
Как написать одна сотая
Если Вы хотите просто узнать, как пишется число прописью, то можете воспользоваться онлайн сервисом:
Имена числительные в русском языке не имеют единой системы склонения. Изменение по падежам зависит от разряда. Некоторые числительные могут изменяться по родам и числам. При склонении числительных следует уделять внимание и правильности согласования с ним существительного, чтобы не допускать в речи и на письме грамматических ошибок.
Порядковые имена числительные
К разряду порядковых относят числительные, обозначающие порядок при счете и отвечающие на вопросы который? которая? которое? Например: девятый вал, вторая передача, сорок второе открытие. Их делят на простые (состоящие из одного слова) и составные (из двух и более слов).
Склонение порядковых числительных схоже с изменением по числам, родам и падежам имен прилагательных. При склонении составных числительных изменяется только последнее слово. В первом и во втором случае сочетаемое существительное также будет изменяться по падежам. При этом в винительном падеже окончания у числительных, которые согласуются с одушевленными существительными, будут отличаться от тех, которые согласуются с существительными неодушевленными.
Первый вагон (неодуш.), пассажир (одуш.)
Двадцать второй автобус (неодуш.), человек (одуш.)
Первого вагона, пассажира
Двадцать второго автобуса, человека
Первому вагону, пассажиру
Двадцать второму автобусу, человеку
Первый вагон, первого пассажира
Двадцать второй автобус, двадцать второго человека
Первым вагоном, пассажиром
Двадцать вторым автобусом, человеком
О первом вагоне, пассажире
О двадцать втором автобусе, человеке
Внимание! При указании даты изменяется только порядковое числительное. Имя существительное, обозначающее название месяца, всегда будет употребляться только в форме родительного падежа: поздравить с восьмым (т. п.) марта (р. п.), подготовиться к первому (д. п.) сентября (р. п.), рассказать о двадцать третьем (п. п.) февраля (р. п.).
Количественные числительные
К этой группе относятся числительные, обозначающие количество предметов: две руки, пять пальцев, тридцать два зуба, четверо друзей. По количеству слов делятся на простые (одно слово) и составные (два и более слов).
Простые количественные числительные представляют собой обширную группу, которая имеет несколько видов склонения.
От 1 до 4
Числительное один имеет падежные окончания прилагательного, бывает единств. и множеств. числа (один – одни), мужского, женского и среднего рода (один, одна, одно).
Следует помнить, что у числительных, которые согласуются с одушевленными существительными единственного и множественного числа мужского рода и среднего рода, а также множественного числа женского рода, окончания совпадают в формах родительного и винительного падежа. Если существительное неодушевленное, то окончания будут совпадать в формах именительного и винительного падежей.
Для единственного числа женского рода этот показатель не будет признаком одушевленности-неодушевленности.
Источник
Сумма прописью онлайн
Чтобы узнать результат перевода, введите сумму
Бесплатный калькулятор “Сумма прописью онлайн” поможет быстро перевести сумму, записанную цифрами, в сумму прописью по всем правилам орфографии. Правописание числительных — обширная тема с массой нюансов, не все помнят ее со школы. Наш простой калькулятор покажет суммы прописью на русском языке без ошибок. Вам нужно только ввести цифровое значение в поле.
При заполнении финансовых, бухгалтерских и налоговых документов нужно написать денежный показатель цифрами и продублировать его прописью — то есть, прописать словами. Это делается в зарплатных ведомостях, договорах, кассовых ордерах, применяется для банковского чека — деньги фигурируют почти во всех бумагах. Основная цель прописывания сумм — желание избежать подделки. Внешний вид цифр легко изменить, а вот словесное написание исправить трудно.
Перевод цифровых значений в словесные — утомительное занятие. Если вам приходится заполнять много документов, то возрастает и риск ошибки. Чтобы легко и бесплатно перевести сумму в правильный прописной вариант, воспользуйтесь нашим калькулятором.
Как работает калькулятор «Сумма прописью онлайн»
Введите числовой вариант суммы в рублях в поле калькулятора. Программа отреагирует на введение числа автоматически и предложит словесную формулировку суммы. Она будет писаться ниже числового поля сразу же после ввода цифр. Дополнительно ничего нажимать не нужно.
Прописная расшифровка появляется именно в том варианте, который принят для финансовых документов: рубли указываются прописью, копейки — цифрами, это правило. Сумма пишется с заглавной буквы, значение суммы в рублях и копейках не разделяется запятой или другим знаком препинания (точка, скобка). Например: “Двадцать тысяч пятьсот один рубль 51 копейка”.
Если нужно указать число копеек в сумме, пишите их после запятой или точки в составе числа. Пробел для этой цели использовать не удастся. Например: “20500,56” или “346.5”.
Если сумма целая, без копеек, пишите число без запятой и нулевых показателей после нее. Например: “3000000”. Калькулятор все поймет сам и предложит прописной вариант суммы с дополнением: “00 копеек”. Но и указание суммы в виде десятичной дроби с нулевыми значениями после запятой тоже допустимо. Например: “100,00”. Третий знак после запятой (точки) поставить не удастся.
Будьте внимательны, прописывая большие числа, особенно с несколькими нулями подряд.
Источник
Поиск ответа
Здравствуйте! Прошу помощи! Как правильно написать: «мы обзавелись 1 3/4 десятин(-ы)(-ами)» (имеется в виду одна целая и три четверти). СПАСИБО!
Ответ справочной службы русского языка
Здравствуйте! Как правильно: девяносто один целых семь десятых, девяносто одна целая семь десятых или девяносто одна целая и семь десятых?
Ответ справочной службы русского языка
Корректны второй и третий варианты, предпочтителен второй.
Как правильно писать: 1541,1 (одна тысяча пятьсот сорок одна целая одна десятая) квадратных метра. Или 1541,1 (одна тысяча пятьсот сорок один целый одна десятая) квадратных метра.
Ответ справочной службы русского языка
Верно: одна тысяча пятьсот сорок один и одна десятая квадратного метра.
Как правильно писать: 1541,1 (одна тысяча пятьсот сорок одна целая одна десятая) квадратных метра. Или 1541,1 (одна тысяча пятьсот сорок один целый одна десятая) квадратных метра.
Ответ справочной службы русского языка
Верно: 1541,1 (одна тысяча пятьсот сорок одна целая одна десятая) квадратного метра.
Добрый день, уважаемые эксперты. Я патрулирующий русской Википедии. В своей работе нередко сталкиваюсь с числительными, а именно с денежными наименованиями. Постоянно возникают трудности с десятичными дробями. Не знаю как склонять существительные рядом с ними. Например, 2,89 миллиардА или миллиардОВ доллара(-ов). Обычно проверяю себя, проговаривая дробное число: «Две целых восемьдесят девять сотЫХ миллиардОВ долларОВ», но не знаю, правильно ли это. Можете, пожалуйста, объяснить и просклонять данное число и, например одна целая тридцать одна сотая. Благодарю.
Ответ справочной службы русского языка
Правило простое: при дробных числительных существительное употребляется в форме единственного числа родительного падежа: 4,3 рубля, 67,84 километра, 2,89 миллиарда. Слово доллар уже не зависит напрямую от числительного, поэтому ставится во множественном числе: 2,89 миллиарда (чего?) долларов.
Поэтому верно: Две целых восемьдесят девять сотых миллиарда долларов; одна целая тридцать одна сотая миллиарда долларов.
Что-то я так и не увидел ответ на свой вопрос. Повторю его в кратком виде: как написать правильно: более 1,5 тысячи пар или более 1,5 тысяч пар если иметь ввиду не полторы тысячи, а одна целая пять десятых тысяч? P.S. Ошибку ссылки в одном из ответов вы также так и не исправили.
Ответ справочной службы русского языка
Правильно: более 1500 пар. В этом случае нет необходимости в использовании дробного числа (что затрудняет прочтение текста).
Здравствуйте. Как правильно прочитать 1,4 млрд.руб. так или нет: 1миллиард 4 миллиона рублей?
Ответ справочной службы русского языка
Возможны два варианта: одна целая четыре десятых миллиарда рублей и один миллиард четыреста миллионов рублей.
51,1 квадратная километра или квадратного километра, ведь- 51, 1десятая процента.
Большое спасибо.
Ответ справочной службы русского языка
Правильно: 51,1 (пятьдесят одна целая и одна десятая) чего? квадратного километра.
Будьте добры. Поскажите как произноситься 321,2; 125,589; 879,2354
Ответ справочной службы русского языка
Триста двадцать одна целая две десятых; сто двадцать пять целых пятьсот восемьдесят девять тысячных; восемьсот семьдесят девять целых две тысячи триста пятьдесят четыре десятитысячных.
Как будет правильно написать: » Одна целая три тысячных грамма» или «Одна целых и три тысячных грамм». Спасибо
Ответ справочной службы русского языка
Правильно: одна целая три тысячных грамма.
Добрый день!
Прошу сообщить как правильно писать: двадцать ОДНА ЦЕЛАЯ четыре десятых метра или двадцать ОДИН ЦЕЛЫЙ четыре десятых метра?
Спасибо.
Ответ справочной службы русского языка
Ответ справочной службы русского языка
Эта фамилия склоняется по первому школьному склонению (как слово мама ).
Как правильно произнести?
Один целЫЙ и восемь десятых процентОВ или одна целАЯ и восемь десятых процентА
Ответ справочной службы русского языка
Правильно: одна целая и восемь десятых процента.
как правильно написать словами «1001,44 евро»: 1) «одна тысяча один целых сорок четыре сотых евро» или 2) «одна тысяча одна целая сорок четыре сотых евро»?
Ответ справочной службы русского языка
Подскажите, пожалуйста, как правильно писать: Одна целая метра или одна целых метра?
Ответ справочной службы русского языка
Источник
Теперь вы знаете какие однокоренные слова подходят к слову Как написать одна сотая, а так же какой у него корень, приставка, суффикс и окончание. Вы можете дополнить список однокоренных слов к слову «Как написать одна сотая», предложив свой вариант в комментариях ниже, а также выразить свое несогласие проведенным с морфемным разбором.
Процент сотая часть числа
— Если, например, в городе 45 тысяч жителей, то 450 человек составляют один П. населения. Предположим, что на какое-нибудь предприятие истрачено 20 тыс. руб. и чистого дохода получено 3 тыс. руб. В этом случае доход составляет 15/100 частей капитала или 15 П., что, обыкновенно, обозначают так: 15%. Если не желают участвовать в рисках предприятия, то дают деньги взаймы, довольствуясь небольшим доходом, получая, например, 4% или 5%. Это значит, что в продолжение года
доход составляет 4/100 или 5/100 частей капитала, отданного взаймы. Этот доход называется процентными деньгами.
В обыденной речи употребляют выражение «получать проценты» вместо правильного «получать процентные деньги».
Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона. — С.-Пб.: Брокгауз-Ефрон
.
1890-1907
.
Смотреть что такое «Процент сотая часть числа» в других словарях:
Если, например, в городе 45 тысяч жителей, то 450 человек составляют один П. населения. Предположим, что на какое нибудь предприятие истрачено 20 тыс. руб. и чистого дохода получено 3 тыс. руб. В этом случае доход составляет 15/100 частей… …
ПРОЦЕНТ
— сотая часть числа, принимаемого за единицу; обозначается знаком % … Большая политехническая энциклопедия
— (лат.). Цифра, означающая прибыль или плату с сотни. В химии: выраженное в числах отношение различных составных частей вещества. В статистике: отношение народонаселения и т. д. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А … Словарь иностранных слов русского языка
— % Процент (лат. per cent на сотню) одна сотая доля. Обозначается знаком «%». Используется для обозначения доли чего либо по отношению к целому. Например, 17 % от 500 кг означает 17 частей по 5 кг каждая, то есть… … Википедия
ИНВЕСТИРОВАНИЕ
— INVESTINGПод И. понимается вложение капитала с целью получения прибыли. Ожидаемая прибыль может быть в виде дивидендов, процентов или увеличения реального капитала. Попытка извлечь выгоду из кратковременных изменений стоимости актива называется… … Энциклопедия банковского дела и финансов
Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Древность не знала ныне всюду распространенных видов водки (Eau de vie, Branntwein, Schnaps, Brandy, whiskey, см. Водка), как перегнанного крепкого, или спиртового, напитка, потому что искусство перегонки (см. это сл.) выработано в эпоху… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
У этого термина существуют и другие значения, см. Автомат Калашникова (значения). Автомат Калашникова … Википедия
CHF
— (Швейцарский франк) Национальная валюта Швейцарии, история появления, развития Информация о швейцарском франке, истории появления и развитияю месте франка в современной экономике Содержание денежная единица. Швейцарский Франк — это(код по… … Энциклопедия инвестора
Процент это один из интересных и часто применяемых на практике инструментов. Проценты частично или полностью применяются в любой науке, на любой работе и даже в повседневном общении. Человек, который хорошо разбирающийся в процентах, создаёт впечатление умного и образованного. В данном уроке мы узнаем, что такое процент и какие действия можно с ним выполнять.
Содержание урока
Что такое процент?
В повседневной жизни дроби встречаются наиболее часто. Они даже получили свои названия: половина, треть и четверть соответственно.
Но есть ещё одна дробь, которая тоже встречается часто. Это дробь (одна сотая). Данная дробь получила название процент
. А что означает дробь одна сотая ? Эта дробь означает, что чего-либо разделено на сто частей и оттуда взята одна часть. Значит процентом является одна сотая часть чего-либо.
Процентом называется одна сотая часть чего-либо
Например, от одного метра составляет 1 см. Один метр разделили на сто частей, и взяли одну часть (вспоминаем, что 1 метр это 100 см). А одна часть из этих ста частей составляет 1 см. Значит один процент от одного метра составляет 1 см.
От одного метра уже составляет 2 сантиметра. В этот раз один метр разделили на сто частей и взяли оттуда не одну, а две части. А две части из ста составляют два сантиметра. Значит два процента от одного метра составляет 2 сантиметра.
Еще пример, от одного рубля составляет одну копейку. Рубль разделили на сто частей, и взяли оттуда одну часть. А одна часть из этих ста частей составляет одну копейку. Значит один процент от одного рубля составляет одну копейку.
Проценты встречались настолько часто, что люди заменили дробь на специальный значок, который выглядит следующим образом:
Эта запись читается как «один процент». Она заменяет собой дробь . Также она заменяет собой десятичную дробь 0,01 потому что если перевести обычную дробь в десятичную дробь, то мы получим 0,01. Стало быть между этими тремя выражениями можно поставить знак равенства:
1% = = 0,01
Два процента в дробном виде будут записаны как , в виде десятичной дроби как 0,02 а с помощью специального значка два процента записывается как 2%.
2% = = 0,02
Как найти процент?
Принцип нахождения процента такой же, как и обычное нахождение дроби от числа. Чтобы найти процент от чего-либо, нужно это чего-либо разделить на 100 частей и полученное число умножить на нужный процент.
Например, найти 2% от 10 см.
Что означает запись 2% ? Запись 2% заменяет собой запись . Если перевести это задание на более понятый язык, то оно будет выглядеть следующим образом:
Найти от 10 см
А как решать подобные задания мы уже знаем. Это обычное нахождение дроби от числа. Чтобы найти дробь от числа, нужно это число разделить на знаменатель дроби, и полученный результат умножить на числитель дроби.
Итак, делим число 10 на знаменатель дроби
Получили 0,1. Теперь 0,1 умножаем на числитель дроби
0,1 × 2 = 0,2
Получили ответ 0,2. Значит 2% от 10 см составляет 0,2 см. А если , то получим 2 миллиметра:
0,2 см = 2 мм
Значит 2% от 10 см составляют 2 мм.
Пример 2.
Найти 50% от 300 рублей.
Чтобы найти 50% от 300 рублей, нужно эти 300 рублей разделить на 100, и полученный результат умножить на 50.
Итак, делим 300 рублей 100
300: 100 = 3
Теперь полученный результат умножаем на 50
3 × 50 = 150 руб.
Значит 50% от 300 рублей составляет 150 рублей.
Если на первых порах сложно привыкнуть к записи со значком %, можно заменять эту запись на обычную дробную запись.
Например, те же 50% можно заменить на запись . Тогда задание будет выглядеть так: Найти от 300 рублей, а решать такие задачи для нас пока проще
300: 100 = 3
3 × 50 = 150
В принципе, ничего сложного здесь нет. Если возникают сложности, советуем остановиться и заново изучить и .
Пример 3.
Швейная фабрика выпустила 1200 костюмов. Из них 32% составляют костюмы нового фасона. Сколько костюмов нового фасона выпустила фабрика?
Здесь нужно найти 32% от 1200. Найденное число будет ответом к задаче. Воспользуемся правилом нахождения процента. Разделим 1200 на 100 и полученный результат умножим на искомый процент, т.е. на 32
1200: 100 = 12
12 × 32 = 384
Ответ: 384 костюмов нового фасона выпустила фабрика.
Второй способ нахождения процента
Второй способ нахождения процента намного проще и удобнее. Он заключается в том, что число от которого ищется процент сразу умножит на нужный процент, выраженный в виде десятичной дроби.
Например, решим предыдущую задачу этим способом. Найти 50% от 300 рублей.
Запись 50% заменяет собой запись , а если перевести эти в десятичную дробь, то мы получим 0,5
Теперь для нахождения 50% от 300, достаточно будет умножить число 300 на десятичную дробь 0,5
300 × 0,5 = 150
Кстати, по этому же принципу работает механизм нахождения процента на калькуляторах. Чтобы найти процент с помощью калькулятора, нужно ввести в калькулятор число от которого ищется процент, затем нажать клавишу умножения и ввести искомый процент. Затем нажать клавишу процента %
Нахождения числа по его проценту
Зная процент от числа, можно узнать всё число. Например, предприятие выплатило нам 60000 рублей за работу, и это составляет 2% от общей прибыли, полученной предприятием. Зная свою долю, и сколько процентов она составляет, мы можем узнать общую прибыль.
Сначала нужно узнать сколько рублей составляет один процент. Как это сделать? Попробуйте догадаться внимательно изучив следующий рисунок:
Если два процента от общей прибыли составляют 60 тысяч рублей, то нетрудно догадаться, что один процент составляет 30 тысяч рублей. А чтобы получить эти 30 тысяч рублей, нужно 60 тысяч разделить на 2
60 000: 2 = 30 000
Мы нашли один процент от общей прибыли, т.е. . Если одна часть это 30 тысяч, то для определения ста частей, нужно 30 тысяч умножить на 100
30 000 × 100 = 3 000 000
Мы нашли общую прибыль. Она составляет три миллиона.
Попробуем сформировать правило нахождения числа по его проценту.
Чтобы найти число по его проценту, нужно известное число разделить на данный процент, и полученный результат умножить на 100.
Пример 2.
Число 35 это 7% от какого-то неизвестного числа. Найти это неизвестное число.
Читаем первую часть правила:
Чтобы найти число по его проценту, нужно известное число разделить на данный процент
У нас известное число это 35, а данный процент это 7. Разделим 35 на 7
35: 7 = 5
Читаем вторую часть правила:
и полученный результат умножить на 100
У нас полученный результат это число 5. Умножим 5 на 100
5 × 100 = 500
500 это неизвестное число, которое требовалось найти. Можно сделать проверку. Для этого находим 7% от 500. Если мы всё сделали правильно, то должны получить 35
500: 100 = 5
5 × 7 = 35
Получили 35. Значит задача была решена правильно.
Принцип нахождения числа по его проценту такой же, как и обычное нахождение целого числа по его дроби. Если проценты на первых порах смущают и сбивают с толку, то запись с процентом можно заменять на дробную запись.
Например, предыдущая задача может быть изложена так: число 35
это от какого-то неизвестного числа. Найти это неизвестное число. Как решать такие задачи мы уже знаем. Это нахождение числа по дроби. Для нахождения числа по дроби, мы это число делим на числитель дроби и полученный результат умножаем на знаменатель дроби. В нашем примере число 35 нужно разделить на 7 и полученный результат умножить на 100
35: 7 = 5
5 × 100 = 500
В будущем мы будем решать задачи на проценты, часть из которых будут сложными. Чтобы на первых порах не усложнять обучение, достаточно уметь находить процент от числа, и число по проценту.
Задания для самостоятельного решения
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Если, например, в городе 45 тысяч жителей, то 450 человек составляют один П. населения. Предположим, что на какое нибудь предприятие истрачено 20 тыс. руб. и чистого дохода получено 3 тыс. руб. В этом случае доход составляет 15/100 частей… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
I ж. жен. к сущ. сотый I II прил. разг. Очень малая, незначительная, небольшая часть, доля чего либо. III числ. разг. Часть, доля, полученная от деления чего либо на сто равных частей; одна сотая. Толковый словарь Ефремовой. Т. Ф. Ефремова. 2000 … Современный толковый словарь русского языка Ефремовой
I ж. жен. к сущ. сотый I II прил. разг. Очень малая, незначительная, небольшая часть, доля чего либо. III числ. разг. Часть, доля, полученная от деления чего либо на сто равных частей; одна сотая. Толковый словарь Ефремовой. Т. Ф. Ефремова. 2000 … Современный толковый словарь русского языка Ефремовой
Сотая часть процента В таких единицах принято измерять разницу в процентных ставках. Например, если ставка процента повысилась с 10,4 % до 10,8 %, то она изменилась на 40 базисных пунктов … Энциклопедический словарь экономики и права
ПУНКТ, БАЗИСНЫЙ
— сотая часть процента; показатель, используемый для характеристики разницы в процентных ставках изменения дохода по ценным бумагам и т.д. Например, если казначейский вексель приносит доход в 7,17% и его цена меняется так, что он теперь приносит… … Большой экономический словарь
базисный пункт
— сотая часть процента. В таких единицах принято характеризовать, измерять разницу в процентных ставках. Например, если ставка процента повысилась с 6,2% до 6,5%, то она изменилась на 20 базисных пунктов … Словарь экономических терминов
Процент
— сотая часть чего нибудь, обозначается % … Популярный политический словарь
Перечень единиц измерения денежных сумм, равных определённой доле базовой денежной единицы (валюты). Как правило, это монеты, реже банкноты или не имеющие физической формы счётные единицы, которые используется для мелких расчётов и называются… … Википедия
— (лат.). Цифра, означающая прибыль или плату с сотни. В химии: выраженное в числах отношение различных составных частей вещества. В статистике: отношение народонаселения и т. д. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А … Словарь иностранных слов русского языка
Книги
- 11 месяцев в пути, или Как проехать две Америки на велосипеде , Почаев Е.. В дневнике искателя приключений и настоящего героя нашего времени Евгения Почаева рассказывается о покорении на велосипеде самого длинного непрерывного маршрутана планете — двух Америк, от…
Если, например, в городе 45 тысяч жителей, то 450 человек составляют один П. населения. Предположим, что на какое-нибудь предприятие истрачено 20 тыс. руб. и чистого дохода получено 3 тыс. руб. В этом случае доход составляет 15/100 частей капитала или 15 П., что, обыкновенно, обозначают так: 15%. Если не желают участвовать в рисках предприятия, то дают деньги взаймы, довольствуясь небольшим доходом, получая, например, 4% или 5%. Это значит, что в продолжение года
доход составляет 4/100 или 5/100 частей капитала, отданного взаймы. Этот доход называется процентными деньгами.
В обыденной речи употребляют выражение «получать проценты» вместо правильного «получать процентные деньги».
- — фиброзная капсула; трабекула; эллипсоиды; лимфоидные узелки; кисточковые артериолы; центральная артерия; периартериальные лимфоидные муфты; красная пульпа; ворота селезенки; селезеночная вена…
Атлас анатомии человека
- — Фармакологические группы: Детоксицирующие средства, включая антидоты›› Средства, препятствующие образованию и способствующие растворению конкрементов›› Слабительные средства›› Стимуляторы моторики ЖКТ, в том…
Медицинские препараты
- — Единица относительной величины…
Словарь мер
- — ПРОЦЕНТ Плата, взимаемая за заем суммы денег…
Финансовый словарь
- — 1. сотая доля какого-либо числа, принимаемого за целое, за единицу; 2. доход в процентах, получаемый кредитором от заемщика за пользование деньгами: 3…
Большой бухгалтерский словарь
- — см….
Справочный коммерческий словарь
- — плата, получаемая кредитором от заемщика за пользование денежной ссудой…
Терминологический словарь библиотекаря по социально-экономической тематике
- — сотая доля числа; обозначается знаком %. Так, 3% от 18 есть 3 сотых от этого числа, т.е. 0,54. П. применяются в хоз. расчётах…
Естествознание. Энциклопедический словарь
- — Плата, взимаемая за заем суммы денег…
Словарь бизнес терминов
- — Плата, взимаемая за кредит, помимо выплаты заимствованной суммы. Ставка процента является дополнительной оплатой за единицу ссуды; обычно рассчитывается в виде годовой ставки…
Экономический словарь
- — Если, например, в городе 45 тысяч жителей, то 450 человек составляют один П. населения…
Энциклопедический словарь Брокгауза и Евфрона
- — см. Дробная и целая части числа…
Большая Советская энциклопедия
- — СО́ТЫЙ, -ая,…
Толковый словарь Ожегова
-
Толковый словарь Ефремовой
- — со́тая I ж. жен. к сущ. сотый I II прил. разг. Очень малая, незначительная, небольшая часть, доля чего-либо. III числ. разг. Часть, доля, полученная от деления чего-либо на сто равных частей; одна сотая…
Толковый словарь Ефремовой
- — со́тая I ж. жен. к сущ. сотый I II прил. разг. Очень малая, незначительная, небольшая часть, доля чего-либо. III числ. разг. Часть, доля, полученная от деления чего-либо на сто равных частей; одна сотая…
Толковый словарь Ефремовой
«Процент сотая часть числа» в книгах
Сотая «Сэвидж»
Из книги
Разговоры с Раневской
автора
Сотая «Сэвидж»
«Сэвидж» прошла в сотый раз. Публика приветствовала артистов, на сцену вынесли огромную корзину от месткома и поставили ее у ног Ф. Г. «Бурные аплодисменты, переходящие в овацию», как писали раньше газеты о явлении Сталина народу, на этот раз сотрясли
СОТАЯ «СЭВИДЖ»
Из книги
Фаина Раневская. Фуфа Великолепная, или с юмором по жизни
автора
Скороходов Глеб Анатольевич
СОТАЯ «СЭВИДЖ»
«Сэвидж» прошла в сотый раз. Публика приветствовала артистов, на сцену вынесли огромную корзину от месткома и поставили ее у ног Ф. Г. «Бурные аплодисменты, переходящие в овацию», как писали раньше газеты о явлении Сталина народу, на этот раз сотрясли
XIX. ПРОЦЕНТ
Из книги
Человеческая деятельность. Трактат по экономической теории
автора
Мизес Людвиг фон
XIX. ПРОЦЕНТ
1. Феномен процента
Выше было показано, что временное предпочтение является категорией, присущей любому человеческому действию. Временное предпочтение проявляет себя в феномене первоначального процента, т.е. скидки на будущие блага по сравнению с
§ 3 Процент
Из книги
Основы экономики
автора
Борисов Евгений Филиппович
[в) Масси. Процент как часть прибыли. Объяснение высоты процента уровнем прибыли]
Из книги
Том 26, ч.1
автора
Энгельс Фридрих
[в) Масси. Процент как часть прибыли. Объяснение высоты процента уровнем прибыли]
An Essay on the Governing Causes of the Natural Rate of Interest; wherein the Sentiments of Sir William Petty and Mr. Locke, on that Head, are considered. London, 1750.«Из приведенных выдержек видно следующее: господин Локк полагает, что естественный
Процент
Из книги
Большая Советская Энциклопедия (ПР)
автора
БСЭ
Целая часть числа
Из книги
Большая Советская Энциклопедия (ЦЕ)
автора
БСЭ
Из книги
Цифровой журнал «Компьютерра» № 164
автора
Журнал «Компьютерра»
Сотая колонка: попытка перевести дух, осмотреться и понять, что и зачем я делаю
Дмитрий Шабанов
Опубликовано 15 марта 2013
Я пишу колонки для КомпьютеррыOnline, которая сейчас превратилась снова просто в Компьютерру, вот уже два года без маленького
ЧАСТЬ ВТОРАЯ Числа и кролики
Из книги
Искатели необычайных автографов
автора
Левшин Владимир Артурович
ЧАСТЬ ВТОРАЯ
Числа и кролики
Четвертая часть Безопасно там, где числа
Из книги
Даже не ошибка
автора
Коллинз Пол
Четвертая часть
Безопасно там, где числа
Сотая обезьянка — современный миф
Из книги
Боги в каждом мужчине [Архетипы, управляющие жизнью мужчин]
автора
Болен Джин Шинода
Сотая обезьянка — современный миф
«Сотая обезьянка» — это название современного мифа. Эта история стала известна и описана лишь пару десятилетий назад, и с тех пор ее рассказывают и пересказывают во всем мире. Миф об обезьянке возник совсем недавно, однако, как и в
Часть II. Числа, знаки и узоры
Из книги
Самоучитель по толкованию снов
автора
Врублевская Галина
Часть II. Числа, знаки и узоры
ЧислаЧисла, появляющиеся в сновидениях, наиболее трудны для толкования. Это связано с тем, что коллективное (архетипическое) их значение часто оказывается слабее, чем личное восприятие числа сновидцем.Любой предмет быта (допустим, тарелка) и в
Из книги
Познание России. Заветные мысли (сборник)
автора
Менделеев Дмитрий Иванович
Часть первая
ВАЖНЕЙШИЕ ЧИСЛА, ОТНОСЯЩИЕСЯ КО ВСЕЙ РОССИИ И К ЕЕ ЧАСТЯМ ПО ПЕРЕПИСИ 1897 г.
Извлеченные из переписи числа приведены в табл. 1–3, которые — для удобства сличений — расположены и напечатаны тождественным образом.В табл. 1 даются первейшие сведения о составе
Часть первая ВАЖНЕЙШИЕ ЧИСЛА, ОТНОСЯЩИЕСЯ КО ВСЕЙ РОССИИ И К ЕЕ ЧАСТЯМ ПО ПЕРЕПИСИ 1897 г.
Из книги
К познанию России
автора
Менделеев Дмитрий Иванович
Часть первая
ВАЖНЕЙШИЕ ЧИСЛА, ОТНОСЯЩИЕСЯ КО ВСЕЙ РОССИИ И К ЕЕ ЧАСТЯМ ПО ПЕРЕПИСИ 1897 г.
Извлеченные из переписи числа приведены в табл. 1–3, которые – для удобства сличений – расположены и напечатаны тождественным образом.В табл. 1 даются первейшие сведения о составе
Глава 6. Часть числа?
Из книги
Хижина
автора
Янг Уильям Пол
Глава 6. Часть числа?
Неважно, какой силой может быть Бог, первым аспектом Бога никогда не станет Повелитель всего, Всемогущий. Это аспект того Бога, который ставит себя на один уровень с человеком и ограничивает себя.
Жак Эллюль. «Анархия и христианство»
— Нy, Макензи, не
Здесь можно быстро перевести число в строку
Введите целое или дробное число:
Примеры: 135; 10 434; 0,58; 12.659, 12659,0004
Результат (число прописью):
Отзывы, обсуждения, предложения
(по инструменту Цифры прописью)
Какое самое большое число?
Лекция про самые большие числа мира
Процент — это специальный математический знак, применяемый для обозначения относительных величин. Какова его история и как рассчитать процент от числа — об этом пойдет речь в статье.
Процент — что это такое?
Процент — это понятие, которое используется в нескольких значениях и сферах деятельности:
- В математике: это одна сотая часть какого-либо числа, представленная в виде целого.
- В метрологии: это единица измерения, выраженная в сотых долях какой-либо величины.
- В экономике и банковском деле: величина дохода, получаемая субъектом финансовых отношений от каждой сотни денежных единиц.
Как мы видим, данное понятие используется в различных областях, а потому необходимо знать, как посчитать процент от числа.
Процент как единица измерения
Этот термин имеет латинское происхождение: «per cent» можно перевести как «на сотню». По сути, это одна сотая часть чего-то. В математике и информатике имеет свое обозначение — «%». То есть 10 килограмм от одной тонны (что составляет, как известно, 1000 кг) — это будет как раз 1 %. В школах понятие процента очень часто объясняют на примере пирога. Так, целый пирог — это единица (или 100 %). Если мы отрежем от него половину — то это будет 50 %, если четверть — то 25 % и так далее.
История процента
О процентах знали (и активно их применяли в качестве своеобразной системы исчисления) еще в древнеримском государстве. Тогда использовались дроби в качестве определения размера налога на товары (его величина составляла одну сотую).
Как свидетельствуют многочисленные источники, такая дробная система активно использовалась и позже, уже в Средние Века. С её помощью вычисляли размер процентных ставок, а также величину доходов и убытков. Начиная с 17 века эта система стала общестандартной для подобных исчислений. На территории нашей страны процентная система прижилась во времена великого реформатора Петра Первого. Однако можно утверждать, что она существовала и раньше в виде привязки денег (монет) к стандарту 1:100 (ведь русский рубль издавна и не случайно делился именно на 100 копеек).
Математический знак процента и история его происхождения
Как же возник этот математический знак, который обозначает «проценты» и известен сегодня во всем мире? Оказывается, история его происхождения очень любопытна, а возник он вследствие простой опечатки! Так, французский математик в 1685 году издает труд под названием «Руководство по коммерческой арифметике». При этом для обозначения процента он пользовался сокращением «cto». Когда же он отдал свою рукопись в печать, то человек, набиравший его текст, воспринял это сокращение как дробь и в книге напечатал его именно так: » 0 / 0 «. Вот так и родился этот знак — в результате банальной опечатки наборщика! И очень быстро он стал популярным и узнаваемым по всей планете.
Как вычислить процент от числа?
Каждый человек практически ежедневно может столкнуться с необходимостью произвести математическое действие с процентами. Как посчитать процент от числа правильно? Сделать это совсем несложно. К примеру, вам нужно определить величину, которая равняется 35 % от числа 1500. Для этого необходимо исходное число разделить на 100 и умножить полученный результат на 35. Получаем ответ: 525.
Как посчитать процент от числа с помощью калькулятора?
Если у вас есть калькулятор, то произвести такую математическую операцию тоже не составит труда. Так, в поле счетной машинки нужно ввести «1500», затем нажать «умножить», ввести «35» и в конце нажать специальную кнопку «%». В результате мы получим то же числовое значение: 525.
Правила использования знака при компьютерном наборе
Этот знак используется исключительно вместе с цифрой. До 1982 года ГОСТом было принято не разрывать знак «%» и числовое значение, идущее перед ним. Однако потом правила набора изменились, теперь между числом и знаком процента нужно ставить так называемый неразрывный пробел. Это пробел, который не разрывает два соседних символа на разные строки документа. Исключением является лишь тот случай, когда знак применяется на письме для обозначения слова «процентный», или «процентная». Так, например, при написании фразы «5%-й раствор глюкозы» пробел между числом и знаком не ставится.
В заключение
Процент — это понятие, о котором знали еще древние римляне. Процентная система активно использовалась ими для различных экономических расчетов. Применяется она и в наши дни в разных науках и сферах деятельности общества. Надеемся, что наша статья помогла вам разобраться с тем, как посчитать процент от числа быстро и легко.
Если, например, в городе 45 тысяч жителей, то 450 человек составляют один П. населения. Предположим, что на какое-нибудь предприятие истрачено 20 тыс. руб. и чистого дохода получено 3 тыс. руб. В этом случае доход составляет 15/100 частей капитала или 15 П., что, обыкновенно, обозначают так: 15%. Если не желают участвовать в рисках предприятия, то дают деньги взаймы, довольствуясь небольшим доходом, получая, например, 4% или 5%. Это значит, что в продолжение года
доход составляет 4/100 или 5/100 частей капитала, отданного взаймы. Этот доход называется процентными деньгами.
В обыденной речи употребляют выражение «получать проценты» вместо правильного «получать процентные деньги».
- — фиброзная капсула; трабекула; эллипсоиды; лимфоидные узелки; кисточковые артериолы; центральная артерия; периартериальные лимфоидные муфты; красная пульпа; ворота селезенки; селезеночная вена…
Атлас анатомии человека
- — Фармакологические группы: Детоксицирующие средства, включая антидоты›› Средства, препятствующие образованию и способствующие растворению конкрементов›› Слабительные средства›› Стимуляторы моторики ЖКТ, в том…
Медицинские препараты
- — Единица относительной величины…
Словарь мер
- — ПРОЦЕНТ Плата, взимаемая за заем суммы денег…
Финансовый словарь
- — 1. сотая доля какого-либо числа, принимаемого за целое, за единицу; 2. доход в процентах, получаемый кредитором от заемщика за пользование деньгами: 3…
Большой бухгалтерский словарь
- — см….
Справочный коммерческий словарь
- — плата, получаемая кредитором от заемщика за пользование денежной ссудой…
Терминологический словарь библиотекаря по социально-экономической тематике
- — сотая доля числа; обозначается знаком %. Так, 3% от 18 есть 3 сотых от этого числа, т.е. 0,54. П. применяются в хоз. расчётах…
Естествознание. Энциклопедический словарь
- — Плата, взимаемая за заем суммы денег…
Словарь бизнес терминов
- — Плата, взимаемая за кредит, помимо выплаты заимствованной суммы. Ставка процента является дополнительной оплатой за единицу ссуды; обычно рассчитывается в виде годовой ставки…
Экономический словарь
- — Если, например, в городе 45 тысяч жителей, то 450 человек составляют один П. населения…
Энциклопедический словарь Брокгауза и Евфрона
- — см. Дробная и целая части числа…
Большая Советская энциклопедия
- — СО́ТЫЙ, -ая,…
Толковый словарь Ожегова
-
Толковый словарь Ефремовой
- — со́тая I ж. жен. к сущ. сотый I II прил. разг. Очень малая, незначительная, небольшая часть, доля чего-либо. III числ. разг. Часть, доля, полученная от деления чего-либо на сто равных частей; одна сотая…
Толковый словарь Ефремовой
- — со́тая I ж. жен. к сущ. сотый I II прил. разг. Очень малая, незначительная, небольшая часть, доля чего-либо. III числ. разг. Часть, доля, полученная от деления чего-либо на сто равных частей; одна сотая…
Толковый словарь Ефремовой
«Процент сотая часть числа» в книгах
Сотая «Сэвидж»
Из книги
Разговоры с Раневской
автора
Сотая «Сэвидж»
«Сэвидж» прошла в сотый раз. Публика приветствовала артистов, на сцену вынесли огромную корзину от месткома и поставили ее у ног Ф. Г. «Бурные аплодисменты, переходящие в овацию», как писали раньше газеты о явлении Сталина народу, на этот раз сотрясли
СОТАЯ «СЭВИДЖ»
Из книги
Фаина Раневская. Фуфа Великолепная, или с юмором по жизни
автора
Скороходов Глеб Анатольевич
СОТАЯ «СЭВИДЖ»
«Сэвидж» прошла в сотый раз. Публика приветствовала артистов, на сцену вынесли огромную корзину от месткома и поставили ее у ног Ф. Г. «Бурные аплодисменты, переходящие в овацию», как писали раньше газеты о явлении Сталина народу, на этот раз сотрясли
XIX. ПРОЦЕНТ
Из книги
Человеческая деятельность. Трактат по экономической теории
автора
Мизес Людвиг фон
XIX. ПРОЦЕНТ
1. Феномен процента
Выше было показано, что временное предпочтение является категорией, присущей любому человеческому действию. Временное предпочтение проявляет себя в феномене первоначального процента, т.е. скидки на будущие блага по сравнению с
§ 3 Процент
Из книги
Основы экономики
автора
Борисов Евгений Филиппович
[в) Масси. Процент как часть прибыли. Объяснение высоты процента уровнем прибыли]
Из книги
Том 26, ч.1
автора
Энгельс Фридрих
[в) Масси. Процент как часть прибыли. Объяснение высоты процента уровнем прибыли]
An Essay on the Governing Causes of the Natural Rate of Interest; wherein the Sentiments of Sir William Petty and Mr. Locke, on that Head, are considered. London, 1750.«Из приведенных выдержек видно следующее: господин Локк полагает, что естественный
Процент
Из книги
Большая Советская Энциклопедия (ПР)
автора
БСЭ
Целая часть числа
Из книги
Большая Советская Энциклопедия (ЦЕ)
автора
БСЭ
Из книги
Цифровой журнал «Компьютерра» № 164
автора
Журнал «Компьютерра»
Сотая колонка: попытка перевести дух, осмотреться и понять, что и зачем я делаю
Дмитрий Шабанов
Опубликовано 15 марта 2013
Я пишу колонки для КомпьютеррыOnline, которая сейчас превратилась снова просто в Компьютерру, вот уже два года без маленького
ЧАСТЬ ВТОРАЯ Числа и кролики
Из книги
Искатели необычайных автографов
автора
Левшин Владимир Артурович
ЧАСТЬ ВТОРАЯ
Числа и кролики
Четвертая часть Безопасно там, где числа
Из книги
Даже не ошибка
автора
Коллинз Пол
Четвертая часть
Безопасно там, где числа
Сотая обезьянка — современный миф
Из книги
Боги в каждом мужчине [Архетипы, управляющие жизнью мужчин]
автора
Болен Джин Шинода
Сотая обезьянка — современный миф
«Сотая обезьянка» — это название современного мифа. Эта история стала известна и описана лишь пару десятилетий назад, и с тех пор ее рассказывают и пересказывают во всем мире. Миф об обезьянке возник совсем недавно, однако, как и в
Часть II. Числа, знаки и узоры
Из книги
Самоучитель по толкованию снов
автора
Врублевская Галина
Часть II. Числа, знаки и узоры
ЧислаЧисла, появляющиеся в сновидениях, наиболее трудны для толкования. Это связано с тем, что коллективное (архетипическое) их значение часто оказывается слабее, чем личное восприятие числа сновидцем.Любой предмет быта (допустим, тарелка) и в
Из книги
Познание России. Заветные мысли (сборник)
автора
Менделеев Дмитрий Иванович
Часть первая
ВАЖНЕЙШИЕ ЧИСЛА, ОТНОСЯЩИЕСЯ КО ВСЕЙ РОССИИ И К ЕЕ ЧАСТЯМ ПО ПЕРЕПИСИ 1897 г.
Извлеченные из переписи числа приведены в табл. 1–3, которые — для удобства сличений — расположены и напечатаны тождественным образом.В табл. 1 даются первейшие сведения о составе
Часть первая ВАЖНЕЙШИЕ ЧИСЛА, ОТНОСЯЩИЕСЯ КО ВСЕЙ РОССИИ И К ЕЕ ЧАСТЯМ ПО ПЕРЕПИСИ 1897 г.
Из книги
К познанию России
автора
Менделеев Дмитрий Иванович
Часть первая
ВАЖНЕЙШИЕ ЧИСЛА, ОТНОСЯЩИЕСЯ КО ВСЕЙ РОССИИ И К ЕЕ ЧАСТЯМ ПО ПЕРЕПИСИ 1897 г.
Извлеченные из переписи числа приведены в табл. 1–3, которые – для удобства сличений – расположены и напечатаны тождественным образом.В табл. 1 даются первейшие сведения о составе
Глава 6. Часть числа?
Из книги
Хижина
автора
Янг Уильям Пол
Глава 6. Часть числа?
Неважно, какой силой может быть Бог, первым аспектом Бога никогда не станет Повелитель всего, Всемогущий. Это аспект того Бога, который ставит себя на один уровень с человеком и ограничивает себя.
Жак Эллюль. «Анархия и христианство»
— Нy, Макензи, не
Процент это один из интересных и часто применяемых на практике инструментов. Проценты частично или полностью применяются в любой науке, на любой работе и даже в повседневном общении. Человек, который хорошо разбирающийся в процентах, создаёт впечатление умного и образованного. В данном уроке мы узнаем, что такое процент и какие действия можно с ним выполнять.
Содержание урока
Что такое процент?
В повседневной жизни дроби встречаются наиболее часто. Они даже получили свои названия: половина, треть и четверть соответственно.
Но есть ещё одна дробь, которая тоже встречается часто. Это дробь (одна сотая). Данная дробь получила название процент
. А что означает дробь одна сотая ? Эта дробь означает, что чего-либо разделено на сто частей и оттуда взята одна часть. Значит процентом является одна сотая часть чего-либо.
Процентом называется одна сотая часть чего-либо
Например, от одного метра составляет 1 см. Один метр разделили на сто частей, и взяли одну часть (вспоминаем, что 1 метр это 100 см). А одна часть из этих ста частей составляет 1 см. Значит один процент от одного метра составляет 1 см.
От одного метра уже составляет 2 сантиметра. В этот раз один метр разделили на сто частей и взяли оттуда не одну, а две части. А две части из ста составляют два сантиметра. Значит два процента от одного метра составляет 2 сантиметра.
Еще пример, от одного рубля составляет одну копейку. Рубль разделили на сто частей, и взяли оттуда одну часть. А одна часть из этих ста частей составляет одну копейку. Значит один процент от одного рубля составляет одну копейку.
Проценты встречались настолько часто, что люди заменили дробь на специальный значок, который выглядит следующим образом:
Эта запись читается как «один процент». Она заменяет собой дробь . Также она заменяет собой десятичную дробь 0,01 потому что если перевести обычную дробь в десятичную дробь, то мы получим 0,01. Стало быть между этими тремя выражениями можно поставить знак равенства:
1% = = 0,01
Два процента в дробном виде будут записаны как , в виде десятичной дроби как 0,02 а с помощью специального значка два процента записывается как 2%.
2% = = 0,02
Как найти процент?
Принцип нахождения процента такой же, как и обычное нахождение дроби от числа. Чтобы найти процент от чего-либо, нужно это чего-либо разделить на 100 частей и полученное число умножить на нужный процент.
Например, найти 2% от 10 см.
Что означает запись 2% ? Запись 2% заменяет собой запись . Если перевести это задание на более понятый язык, то оно будет выглядеть следующим образом:
Найти от 10 см
А как решать подобные задания мы уже знаем. Это обычное нахождение дроби от числа. Чтобы найти дробь от числа, нужно это число разделить на знаменатель дроби, и полученный результат умножить на числитель дроби.
Итак, делим число 10 на знаменатель дроби
Получили 0,1. Теперь 0,1 умножаем на числитель дроби
0,1 × 2 = 0,2
Получили ответ 0,2. Значит 2% от 10 см составляет 0,2 см. А если , то получим 2 миллиметра:
0,2 см = 2 мм
Значит 2% от 10 см составляют 2 мм.
Пример 2.
Найти 50% от 300 рублей.
Чтобы найти 50% от 300 рублей, нужно эти 300 рублей разделить на 100, и полученный результат умножить на 50.
Итак, делим 300 рублей 100
300: 100 = 3
Теперь полученный результат умножаем на 50
3 × 50 = 150 руб.
Значит 50% от 300 рублей составляет 150 рублей.
Если на первых порах сложно привыкнуть к записи со значком %, можно заменять эту запись на обычную дробную запись.
Например, те же 50% можно заменить на запись . Тогда задание будет выглядеть так: Найти от 300 рублей, а решать такие задачи для нас пока проще
300: 100 = 3
3 × 50 = 150
В принципе, ничего сложного здесь нет. Если возникают сложности, советуем остановиться и заново изучить и .
Пример 3.
Швейная фабрика выпустила 1200 костюмов. Из них 32% составляют костюмы нового фасона. Сколько костюмов нового фасона выпустила фабрика?
Здесь нужно найти 32% от 1200. Найденное число будет ответом к задаче. Воспользуемся правилом нахождения процента. Разделим 1200 на 100 и полученный результат умножим на искомый процент, т.е. на 32
1200: 100 = 12
12 × 32 = 384
Ответ: 384 костюмов нового фасона выпустила фабрика.
Второй способ нахождения процента
Второй способ нахождения процента намного проще и удобнее. Он заключается в том, что число от которого ищется процент сразу умножит на нужный процент, выраженный в виде десятичной дроби.
Например, решим предыдущую задачу этим способом. Найти 50% от 300 рублей.
Запись 50% заменяет собой запись , а если перевести эти в десятичную дробь, то мы получим 0,5
Теперь для нахождения 50% от 300, достаточно будет умножить число 300 на десятичную дробь 0,5
300 × 0,5 = 150
Кстати, по этому же принципу работает механизм нахождения процента на калькуляторах. Чтобы найти процент с помощью калькулятора, нужно ввести в калькулятор число от которого ищется процент, затем нажать клавишу умножения и ввести искомый процент. Затем нажать клавишу процента %
Нахождения числа по его проценту
Зная процент от числа, можно узнать всё число. Например, предприятие выплатило нам 60000 рублей за работу, и это составляет 2% от общей прибыли, полученной предприятием. Зная свою долю, и сколько процентов она составляет, мы можем узнать общую прибыль.
Сначала нужно узнать сколько рублей составляет один процент. Как это сделать? Попробуйте догадаться внимательно изучив следующий рисунок:
Если два процента от общей прибыли составляют 60 тысяч рублей, то нетрудно догадаться, что один процент составляет 30 тысяч рублей. А чтобы получить эти 30 тысяч рублей, нужно 60 тысяч разделить на 2
60 000: 2 = 30 000
Мы нашли один процент от общей прибыли, т.е. . Если одна часть это 30 тысяч, то для определения ста частей, нужно 30 тысяч умножить на 100
30 000 × 100 = 3 000 000
Мы нашли общую прибыль. Она составляет три миллиона.
Попробуем сформировать правило нахождения числа по его проценту.
Чтобы найти число по его проценту, нужно известное число разделить на данный процент, и полученный результат умножить на 100.
Пример 2.
Число 35 это 7% от какого-то неизвестного числа. Найти это неизвестное число.
Читаем первую часть правила:
Чтобы найти число по его проценту, нужно известное число разделить на данный процент
У нас известное число это 35, а данный процент это 7. Разделим 35 на 7
35: 7 = 5
Читаем вторую часть правила:
и полученный результат умножить на 100
У нас полученный результат это число 5. Умножим 5 на 100
5 × 100 = 500
500 это неизвестное число, которое требовалось найти. Можно сделать проверку. Для этого находим 7% от 500. Если мы всё сделали правильно, то должны получить 35
500: 100 = 5
5 × 7 = 35
Получили 35. Значит задача была решена правильно.
Принцип нахождения числа по его проценту такой же, как и обычное нахождение целого числа по его дроби. Если проценты на первых порах смущают и сбивают с толку, то запись с процентом можно заменять на дробную запись.
Например, предыдущая задача может быть изложена так: число 35
это от какого-то неизвестного числа. Найти это неизвестное число. Как решать такие задачи мы уже знаем. Это нахождение числа по дроби. Для нахождения числа по дроби, мы это число делим на числитель дроби и полученный результат умножаем на знаменатель дроби. В нашем примере число 35 нужно разделить на 7 и полученный результат умножить на 100
35: 7 = 5
5 × 100 = 500
В будущем мы будем решать задачи на проценты, часть из которых будут сложными. Чтобы на первых порах не усложнять обучение, достаточно уметь находить процент от числа, и число по проценту.
Задания для самостоятельного решения
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Если, например, в городе 45 тысяч жителей, то 450 человек составляют один П. населения. Предположим, что на какое нибудь предприятие истрачено 20 тыс. руб. и чистого дохода получено 3 тыс. руб. В этом случае доход составляет 15/100 частей… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
I ж. жен. к сущ. сотый I II прил. разг. Очень малая, незначительная, небольшая часть, доля чего либо. III числ. разг. Часть, доля, полученная от деления чего либо на сто равных частей; одна сотая. Толковый словарь Ефремовой. Т. Ф. Ефремова. 2000 … Современный толковый словарь русского языка Ефремовой
I ж. жен. к сущ. сотый I II прил. разг. Очень малая, незначительная, небольшая часть, доля чего либо. III числ. разг. Часть, доля, полученная от деления чего либо на сто равных частей; одна сотая. Толковый словарь Ефремовой. Т. Ф. Ефремова. 2000 … Современный толковый словарь русского языка Ефремовой
Сотая часть процента В таких единицах принято измерять разницу в процентных ставках. Например, если ставка процента повысилась с 10,4 % до 10,8 %, то она изменилась на 40 базисных пунктов … Энциклопедический словарь экономики и права
ПУНКТ, БАЗИСНЫЙ
— сотая часть процента; показатель, используемый для характеристики разницы в процентных ставках изменения дохода по ценным бумагам и т.д. Например, если казначейский вексель приносит доход в 7,17% и его цена меняется так, что он теперь приносит… … Большой экономический словарь
базисный пункт
— сотая часть процента. В таких единицах принято характеризовать, измерять разницу в процентных ставках. Например, если ставка процента повысилась с 6,2% до 6,5%, то она изменилась на 20 базисных пунктов … Словарь экономических терминов
Процент
— сотая часть чего нибудь, обозначается % … Популярный политический словарь
Перечень единиц измерения денежных сумм, равных определённой доле базовой денежной единицы (валюты). Как правило, это монеты, реже банкноты или не имеющие физической формы счётные единицы, которые используется для мелких расчётов и называются… … Википедия
— (лат.). Цифра, означающая прибыль или плату с сотни. В химии: выраженное в числах отношение различных составных частей вещества. В статистике: отношение народонаселения и т. д. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А … Словарь иностранных слов русского языка
Книги
- 11 месяцев в пути, или Как проехать две Америки на велосипеде , Почаев Е.. В дневнике искателя приключений и настоящего героя нашего времени Евгения Почаева рассказывается о покорении на велосипеде самого длинного непрерывного маршрутана планете — двух Америк, от…
Проценты
Процент
— это одна сотая часть числа. Один процент (пишут 1%) от некоторого числа.
Количество процентов может выражаться не только целыми, но и дробными числами.
Например, 0,1% (ноль целых одна десятая процента) есть одна десятая часть от
одной сотой части.
Пример 1. (Определение процента от
числа). Найдём 3% от 400. Сначала найдём один процент. Это будет одна
сотая, т.е. 400/100 = 4. Один процент – это 4. И умножаем 4 на три. Получим 12.
Следовательно, 3% от 400 – это 12.
Пример 2. Найти 25% от 120.
Решение:
1)
25% = 0,25;
2)
120 . 0,25 = 30.
Ответ:
30.
Пример 3. (Определение числа по
известной его части, выраженной в процентах). Найти число, если 15% его равны
30.
Решение:
1)
15% = 0,15;
2)
30 : 0,15 = 200.
или:
х
— данное число;
0,15.х
= 300;
х
= 200.
Ответ:
200.
Пример 4. В классе 24 ученика. Во время
контрольной работы отсутствовало 12,5% учащихся. Найди, сколько учеников
отсутствовало?
Решение 1. Целое в этой задаче – общее
количество учащихся (24).
12,5%
= 0,125
24*0,125
= 3
Решение
2. Пусть х учеников отсутствовали, что составляет 12,5%. Если 24
ученика –общее количество учеников (100%), то
24
ученика – 100%
х
учеников – 12,5%
х
=24*12,5/100
Ответ: В классе отсутствовало 3 ученика.
Пример 5. Проезд на автобусе стоит 14 рублей. В дни
школьных каникул для учащихся ввели скидку 25%. Сколько стоит проезд на
автобусе в дни школьных каникул?
Решение. Сначала найдем один процент
от 14 рублей. 14/100 = 0,14 рубля. А таких процентов у нас 25. Вот и умножим
0,14 рубля на 25. Получим 3,5 рублей. А теперь узнаем новую стоимость проезда:
14
– 3,5 = 10,5.
Ответ: 10,5.
Пример 6. Ширина прямоугольника 20м, а
длина 32м. Сколько % составляет ширина от длины? (Длина является основой для
сравнения)
Решение: В этой задаче длина
прямоугольника 32м составляет 100%, тогда ширина 20м составляет х%. Составим и
решим пропорцию:
32 метра – 100 %
20 метров – х %
х
= 20*100/32
х=62,5%
Ответ: Ширина составляет от длины 62,5%.
Задачи для
самостоятельного решения.
1.
Вычислить: 76% от 100; 33% от 50; 20% от 40; 52% от 3; 25%
от 8.
2.
Вычислить: 154% от 7; 268% от 49; 450% от 16
3.
Сколько минут составляет 30% часа? 75% часа?
4.
Увеличить: 60 на 10%, 44 на 50%, 80 на 25%, 10 на 75%.
5.
Уменьшить: 100 на 13%, 12 на 10%, 60 на 25%, 34 на 56%.
6.
Почтальон Печкин вышел на пенсию и теперь может
покупать товары в спортивном магазине с 5%-ной скидкой. Сколько он заплатит за
новый велосипед, который стоит 2000 рублей?
7.
В нашем районе площадь посевов составляет 69940 га., что составляет
23,3% общей площади района. Какова общая площадь района?
8.
В районе сельхозугодия занимаю 126288 гектаров. Из
них 78208 гектаров
– пашня. Сколько процентов земли занимают пашни?
9.
Население Буздякского района составляет 29955 человек.
Из них лиц башкирской национальности – 40,2 % , русской национальности – 7,1 %
, других национальностей – 1,4%. Сколько лиц татарской национальности?
10.
Население Буздякского района составляет 29955 человек.
Из них лиц трудоспособного возраста – 15878 человек. Доля работающих в
субъектах малого предпринимательства 19,8 % от общей численности
трудоспособного населения района. Сколько человек работают в субъектах малого предпринимательства?
→
сотые — прилагательное, именительный п., мн. ч.
↳
сотые — прилагательное, винительный п., мн. ч.
→
сотые — прилагательное, именительный п., мн. ч.
↳
сотые — прилагательное, винительный п., мн. ч.
↳
сотые — существительное, именительный п., мн. ч.
↳
сотые — существительное, винительный п., мн. ч.
→
сотые — прилагательное, именительный п., мн. ч.
↳
сотые — прилагательное, винительный п., мн. ч.
↳
сотые — существительное, именительный п., мн. ч.
↳
сотые — существительное, винительный п., мн. ч.
↳
сотые — числительное, поряд., именительный п., мн. ч.
↳
сотые — числительное, поряд., винительный п., мн. ч.
Часть речи: числительное
Часть речи: существительное
Часть речи: прилагательное
Положительная степень:
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
For the band from South Carolina, see Hundredth (band).
|
|
This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. |
In arithmetic, a hundredth is a single part of something that has been divided equally into a hundred parts. For example, a hundredth of 675 is 6.75. In this manner it is used with the prefix «centi» such as in centimeter.
A hundredth is the reciprocal of 100.
A hundredth is written as a decimal fraction as 0.01, and as a vulgar fraction as 1/100.
“Hundredth” is also the ordinal number that follows “ninety-ninth” and precedes “hundred and first.” It is written as 100th.
See also[edit]
- Basis point
- Cent (currency)
- Cent (music)
- Hundredth is an American rock band from Myrtle Beach, South Carolina, that formed in 2008.
- Order of magnitude (numbers)
- Orders of magnitude
- Percentage
- Point (gemstone)
| Preceded by Tenth |
Decimal orders of magnitude |
Succeeded by Thousandth |
Orders of magnitude |
|
|---|---|
| Quantity |
|
| See also |
|
| Related |
|
|
|
This article about a number is a stub. You can help Wikipedia by expanding it. |
- v
- t
- e
For the band from South Carolina, see Hundredth (band).
|
|
This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. |
In arithmetic, a hundredth is a single part of something that has been divided equally into a hundred parts. For example, a hundredth of 675 is 6.75. In this manner it is used with the prefix «centi» such as in centimeter.
A hundredth is the reciprocal of 100.
A hundredth is written as a decimal fraction as 0.01, and as a vulgar fraction as 1/100.
“Hundredth” is also the ordinal number that follows “ninety-ninth” and precedes “hundred and first.” It is written as 100th.
See also[edit]
- Basis point
- Cent (currency)
- Cent (music)
- Hundredth is an American rock band from Myrtle Beach, South Carolina, that formed in 2008.
- Order of magnitude (numbers)
- Orders of magnitude
- Percentage
- Point (gemstone)
| Preceded by Tenth |
Decimal orders of magnitude |
Succeeded by Thousandth |
Orders of magnitude |
|
|---|---|
| Quantity |
|
| See also |
|
| Related |
|
|
|
This article about a number is a stub. You can help Wikipedia by expanding it. |
- v
- t
- e
Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается
только за счет дохода от рекламы.
Пожалуйста, добавьте нас в исключения блокировщика.
на главную
Как читать десятичные дроби
Поддержать сайт
В первую очередь обсудим вид десятичной дроби.
Каждая цифра после запятой имеет своё название.
Десятые, сотые, тысячные, десятитысячные…
Десятые, сотые и тысячные
Попробуем прочитать десятичную дробь из примера выше.
Чтобы правильно прочитать десятичную дробь нужно:
-
Прочитать число слева от запятой и добавить слово «целыx», так как слева от запятой находится
целая часть десятичной дроби. Читаем: «сорок три целых». -
Затем прочитать число справа от запятой: «семь тысяч пятьсот шестьдесят девять».
-
Добавить в конце название самой правой цифры.
У нас это
9, которая стоит на месте десятитысячных
(см. рис. выше):
«десятитысячных».
Значит, полное название дроби звучит так:
43,7569 — сорок три целых семь тысяч пятьсот шестьдесят девять десятитысячных.
Справа от запятой после самой последней
правой цифры отличной от нуля можно добавлять сколько угодно
нулей. От этого значение десятичной дроби не изменится.
Таким же образом если в конце десятичной дроби отбросить ноль, то мы получим
такую же по значению десятичную дробь.
Поэтому, если при расчётах получили десятичную дробь 20,40 , отбрасываем
ноль на конце и записываем:
Запомните!
Нули можно добавлять (убирать) только после самой последней правой отличной от нуля
цифры. Нули между цифрами в числе убирать нельзя.
Процент, сотая часть числа
- Процент, сотая часть числа
-
Если, например, в городе 45 тысяч жителей, то 450 человек составляют один П. населения. Предположим, что на какое-нибудь предприятие истрачено 20 тыс. руб. и чистого дохода получено 3 тыс. руб. В этом случае доход составляет 15/100 частей капитала или 15 П., что, обыкновенно, обозначают так: 15%. Если не желают участвовать в рисках предприятия, то дают деньги взаймы, довольствуясь небольшим доходом, получая, например, 4% или 5%. Это значит, что в продолжение года доход составляет 4/100 или 5/100 частей капитала, отданного взаймы. Этот доход называется процентными деньгами. В обыденной речи употребляют выражение «получать проценты» вместо правильного «получать процентные деньги».
Д. С.
Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона. — С.-Пб.: Брокгауз-Ефрон.
1890—1907.
Смотреть что такое «Процент, сотая часть числа» в других словарях:
-
Процент сотая часть числа — Если, например, в городе 45 тысяч жителей, то 450 человек составляют один П. населения. Предположим, что на какое нибудь предприятие истрачено 20 тыс. руб. и чистого дохода получено 3 тыс. руб. В этом случае доход составляет 15/100 частей… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
-
ПРОЦЕНТ — сотая часть числа, принимаемого за единицу; обозначается знаком % … Большая политехническая энциклопедия
-
ПРОЦЕНТ — (лат.). Цифра, означающая прибыль или плату с сотни. В химии: выраженное в числах отношение различных составных частей вещества. В статистике: отношение народонаселения и т. д. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А … Словарь иностранных слов русского языка
-
Процент — % Процент (лат. per cent на сотню) одна сотая доля. Обозначается знаком «%». Используется для обозначения доли чего либо по отношению к целому. Например, 17 % от 500 кг означает 17 частей по 5 кг каждая, то есть… … Википедия
-
ИНВЕСТИРОВАНИЕ — INVESTINGПод И. понимается вложение капитала с целью получения прибыли. Ожидаемая прибыль может быть в виде дивидендов, процентов или увеличения реального капитала. Попытка извлечь выгоду из кратковременных изменений стоимости актива называется… … Энциклопедия банковского дела и финансов
-
Винокурение* — древность не знала ныне всюду распространенных видов водки (Eau de vie, Branntwein, Schnaps, Brandy, whiskey, см. Водка), как перегнанного крепкого , или спиртового, напитка, потому что искусство перегонки (см. это сл.) выработано в эпоху… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
-
Винокурение — древность не знала ныне всюду распространенных видов водки (Eau de vie, Branntwein, Schnaps, Brandy, whiskey, см. Водка), как перегнанного крепкого , или спиртового, напитка, потому что искусство перегонки (см. это сл.) выработано в эпоху… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
-
Автомат Калашникова — У этого термина существуют и другие значения, см. Автомат Калашникова (значения). Автомат Калашникова … Википедия
-
CHF — (Швейцарский франк) Национальная валюта Швейцарии, история появления, развития Информация о швейцарском франке, истории появления и развитияю месте франка в современной экономике Содержание денежная единица . Швейцарский Франк – это(код по… … Энциклопедия инвестора