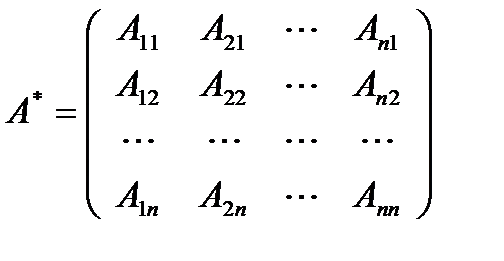Содержание материала
- Повторение: умножение матриц
- Видео
- Метод элементарных преобразований
- Нахождение обратной матрицы методом алгебраических дополнений (союзной матрицы)
- Нахождение обратной матрицы методом линейных преобразований
Повторение: умножение матриц
Прежде всего договоримся об обозначениях. Матрицей $A$ размера $left[ mtimes n right]$ называется просто таблица из чисел, в которой ровно $m$ строк и $n$ столбцов:
[A=left[ mtimes n right]=underbrace{left[ begin{matrix} {{a}_{11}} & {{a}_{12}} & … & {{a}_{1n}} \ {{a}_{21}} & {{a}_{22}} & … & {{a}_{2n}} \ … & … & … & … \ {{a}_{m1}} & {{a}_{m2}} & … & {{a}_{mn}} \end{matrix} right]}_{n}]
Чтобы случайно не перепутать строки и столбцы местами (поверьте, на экзамене можно и единицу с двойкой перепутать — что уж говорить про какие-то там строки), просто взгляните на картинку:
Что происходит? Если разместить стандартную систему координат $OXY$ в левом верхнем углу и направить оси так, чтобы они охватывали всю матрицу, то каждой клетке этой матрицы можно однозначно сопоставить координаты $left( x;y right)$ — это и будет номер строки и номер столбца.
Почему система координат размещена именно в левом верхнем углу? Да потому что именно оттуда мы начинаем читать любые тексты. Это очень просто запомнить.
А почему ось $x$ направлена именно вниз, а не вправо? Опять всё просто: возьмите стандартную систему координат (ось $x$ идёт вправо, ось $y$ — вверх) и поверните её так, чтобы она охватывала матрицу. Это поворот на 90 градусов по часовой стрелке — его результат мы и видим на картинке.
В общем, как определять индексы у элементов матрицы, мы разобрались. Теперь давайте разберёмся с умножением.
Определение. Матрицы $A=left[ mtimes n right]$ и $B=left[ ntimes k right]$, когда количество столбцов в первой совпадает с количеством строк во второй, называются согласованными.
Именно в таком порядке. Можно сумничать и сказать, мол, матрицы $A$ и $B$ образуют упорядоченную пару $left( A;B right)$: если они согласованы в таком порядке, то совершенно необязательно, что $B$ и $A$, т.е. пара $left( B;A right)$ — тоже согласована.
Умножать можно только согласованные матрицы.
Определение. Произведение согласованных матриц $A=left[ mtimes n right]$ и $B=left[ ntimes k right]$ — это новая матрица $C=left[ mtimes k right]$, элементы которой ${{c}_{ij}}$ считаются по формуле:
[{{c}_{ij}}=sumlimits_{k=1}^{n}{{{a}_{ik}}}cdot {{b}_{kj}}]
Другими словами: чтобы получить элемент ${{c}_{ij}}$ матрицы $C=Acdot B$, нужно взять $i$-строку первой матрицы, $j$-й столбец второй матрицы, а затем попарно перемножить элементы из этой строки и столбца. Результаты сложить.
Да, вот такое суровое определение. Из него сразу следует несколько фактов:
- Умножение матриц, вообще говоря, некоммутативно: $Acdot Bne Bcdot A$;
- Однако умножение ассоциативно: $left( Acdot B right)cdot C=Acdot left( Bcdot C right)$;
- И даже дистрибутивно: $left( A+B right)cdot C=Acdot C+Bcdot C$;
- И ещё раз дистрибутивно: $Acdot left( B+C right)=Acdot B+Acdot C$.
Дистрибутивность умножения пришлось отдельно описывать для левого и правого множителя-суммы как раз из-за некоммутативности операции умножения.
Если всё же получается так, что $Acdot B=Bcdot A$, такие матрицы называются перестановочными.
Среди всех матриц, которые там на что-то умножаются, есть особые — те, которые при умножении на любую матрицу $A$ снова дают $A$:
Определение. Матрица $E$ называется единичной, если $Acdot E=A$ или $Ecdot A=A$. В случае с квадратной матрицей $A$ можем записать:
[Acdot E=Ecdot A=A]
Единичная матрица — частый гость при решении матричных уравнений. И вообще частый гость в мире матриц.:)
А ещё из-за этой $E$ кое-кто придумал всю ту дичь, которая будет написана дальше.
Видео
Метод элементарных преобразований
Данный метод еще называют методом Гаусса и мы будем его еще применять при решении систем линейных уравнений.
К элементарным преобразования относятся:
- перестановки строк (столбцов);
- умножение строки (столбца) на некоторое число, отличное от нуля;
- прибавление к элементам строки (столбца) соответствующих элементов другой строки (столбца), предварительно умноженные на некоторое число.
Пример №3 Найти обратную матрицу методом элементарных преобразований
Составляем расширенную матрицу 
Теперь наша задача состоит в том, чтобы первая часть матрицы (до черты) стала единичной, т.е. 


Займемся первым столбцом
Число в первой строке нужно превратить в 

Чтобы во второй строке получить 

Чтобы в третьей строке получить 

Все действия делаем от исходной расширенной матрицы, получаем:
Первый столбец теперь соответствует единичной матрице, поэтому
Займемся вторым столбцом
Теперь мы работаем уже с полученной матрицей, после преобразований первого столбца.
Чтобы в первой строке получить 

Чтобы во второй строке получить 

Чтобы в третьей строке получить 
Выполнив данные действия, получаем:
Работаем дальше с третьим столбцом:
Чтобы в первой строке получить 

Чтобы получить 

Чтобы в третьей строке получить 

Получаем:
В первой части матрицы мы получили единичную матрицу, а вторая часть матрицы (после черты) и будет нашей обратной матрицей:
Оба способа нахождения обратной матрицы, довольно простые, если в них вникнуть, самое главное — не допустить ошибок в вычислениях, а остальное придет со временем.
Нахождение обратной матрицы методом алгебраических дополнений (союзной матрицы)
Для неособенной квадратной матрицы Аобратной является матрица

где 

Разберём ключевые понятия, которые потребуются для решения задач — союзная матрица, алгебраические дополнения и транспонированная матрица.
Пусть существует квадратная матрица A:
Транспонированная относительно матрицы A матрица A’ получается, если из строк матрицы A сделать столбцы, а из её столбцов — наоборот, строки, то есть заменить строки столбцами:
Остановимся на минорах и алгебраических дополнениях.
Пусть есть квадратная матрица третьего порядка:

Её определитель:
Вычислим алгебраическое дополнение элемента 
Для этого нужно сначала найти минор этого элемента. Он получается вычёркиванием из определителя строки и столбца, на пересечении которых стоит указанный элемент. В результате останется следующий определитель, который и является минором элемента 

Алгебраическое дополнение элемента 



По этой инструкции нужно вычислить алгебраические дополнения всех элементов матрицы A’, транспонированной относительно матрицы матрица A.
И последнее из значимых для нахождение обратной матрицы понятий. Союзной с квадратной матрицей A называется матрица 

Алгоритм нахождения обратной матрицы методом алгебраических дополнений
1. Найти определитель данной матрицы A. Если определитель равен нулю, нахождение обратной матрицы прекращается, так как матрица вырожденная и обратная для неё не существует.
2. Найти матрицу, транспонированную относительно A.
3. Вычислить элементы союзной матрицы как алгебраические дополнения марицы, найденной на шаге 2.
4. Применить формулу (2): умножить число, обратное определителю матрицы A, на союзную матрицу, найденную на шаге 4.
5. Проверить полученный на шаге 4 результат, умножив данную матрицу A на обратную матрицу. Если произведение этих матриц равно единичной матрицы, значит обратная матрица была найдена верно. В противном случае начать процесс решения снова.
Пример 1. Для матрицы
найти обратную матрицу.
Решение. Для нахождения обратной матрицы необходимо найти определитель матрицы А . Находим по правилу треугольников:
Следовательно, матрица А – неособенная (невырожденная, несингулярная) и для неё существует обратная.
Найдём матрицу, союзную с данной матрицей А.
Найдём матрицу 
Вычисляем элементы союзной матрицы как алгебраические дополнения матрицы, транспонированной относительно матрицы A:
Следовательно, матрица 
Замечание. Порядок вычисления элементов и транспонирования матрицы может быть иным. Можно сначала вычислить алгебраические дополнения матрицы A, а затем транспонировать матрицу алгебраических дополнений. В результате должны получиться те же элементы союзной матрицы.
Применяя формулу (2), находим матрицу, обратную матрице А:
Проверить решение можно с помощью онлайн калькулятора для нахождения обратной матрицы.
Нахождение обратной матрицы методом линейных преобразований
Матрицы теснейшим образом связаны с системами линейных уравнений. Каждой матрице соответствует система линейных уравнений, коэффициенты в которой есть элементы матрицы. И наоборот, системе линейных уравнений соответствует некоторая матрица.
Поэтому существует метод линейных преобразований для нахождения обратной матрицы. Для решения задач нам будет достаточно знать, что линейное преобразование — это система линейных уравнений, вид которой будет приведён ниже в алгоритме.
Алгоритм нахождения обратной матрицы методом линейных преобразований
1. Для данной невырожденной матрицы A составить линейное преобразование — систему линейных уравнений вида

где aij — элементы матрицы A.
2. Решить полученную систему относительно y — найти для предыдущего линейного преобразование обратное линейное преобразование

в котором Aij — алгебраические дополнения элементов матрицы A, Δ — определитель матрицы A. Внимание! Алгебраические дополнения располагаются как в транспонированной матрице, то есть для элементов строки — в столбце, а для элементов столбца — в строке.
3. Находим коэффициенты при y: 
4. Пользуясь элементами, найденными на шаге 3, записать найденную обратную матрицу.
Наиболее наблюдательные могли заметить, что по сути метод линейных преобразований — это тот же метод алгебраических преобразований (союзной матрицы), но с другой формой записи. Для кого-то метод линейных преобразований может оказаться более удобным как более компактный.
Пример 4. Найти обратную матрицу для матрицы

Сначала проверим, не равен ли нулю определитель данной матрицы. Он не равен нулю, следовательно, обратная матрица существует.
Для данной матрицы записываем линейное преобразование:

Находим линейное преобразование, обратное предыдущему, для этого потребуется находить алгебраические дополнения (урок откроется в новом окне). Запишем обратное линейное преобразование:
Коэффициенты при иксах в обратном линейном преобразовании — это элементы обратной матрицы для матрицы A. Таким образом нашли обратную матрицу:
Проверить решение можно с помощью онлайн калькулятора для нахождения обратной матрицы.
Теги
Алгоритм вычисления обратной матрицы с помощью алгебраических дополнений: метод присоединённой (союзной) матрицы.
Матрица $A^{-1}$ называется обратной по отношению к квадратной матрице $A$, если выполнено условие $A^{-1}cdot A=Acdot A^{-1}=E$, где $E$ – единичная матрица, порядок которой равен порядку матрицы $A$.
Невырожденная матрица – матрица, определитель которой не равен нулю. Соответственно, вырожденная матрица – та, у которой равен нулю определитель.
Обратная матрица $A^{-1}$ существует тогда и только тогда, когда матрица $A$ – невырожденная. Если обратная матрица $A^{-1}$ существует, то она единственная.
Есть несколько способов нахождения обратной матрицы, и мы рассмотрим два из них. На этой странице будет рассмотрен метод присоединённой матрицы, который полагается стандартным в большинстве курсов высшей математики. Второй способ нахождения обратной матрицы (метод элементарных преобразований), который предполагает использование метода Гаусса или метода Гаусса-Жордана, рассмотрен во второй части.
Метод присоединённой (союзной) матрицы
Пусть задана матрица $A_{ntimes n}$. Для того, чтобы найти обратную матрицу $A^{-1}$, требуется осуществить три шага:
- Найти определитель матрицы $A$ и убедиться, что $Delta Aneq 0$, т.е. что матрица А – невырожденная.
- Составить алгебраические дополнения $A_{ij}$ каждого элемента матрицы $A$ и записать матрицу $A_{ntimes n}^{*}=left(A_{ij} right)$ из найденных алгебраических дополнений.
- Записать обратную матрицу с учетом формулы $A^{-1}=frac{1}{Delta A}cdot {A^{*}}^T$.
Матрицу ${A^{*}}^T$ часто именуют присоединённой (взаимной, союзной) к матрице $A$.
Если решение происходит вручную, то первый способ хорош лишь для матриц сравнительно небольших порядков: второго (пример №2), третьего (пример №3), четвертого (пример №4). Чтобы найти обратную матрицу для матрицы высшего порядка, используются иные методы. Например, метод Гаусса, который рассмотрен во второй части.
Пример №1
Найти матрицу, обратную к матрице $A=left( begin{array} {cccc} 5 & -4 &1 & 0 \ 12 &-11 &4 & 0 \ -5 & 58 &4 & 0 \ 3 & -1 & -9 & 0 end{array} right)$.
Решение
Так как все элементы четвёртого столбца равны нулю, то $Delta A=0$ (т.е. матрица $A$ является вырожденной). Так как $Delta A=0$, то обратной матрицы к матрице $A$ не существует.
Ответ: матрицы $A^{-1}$ не существует.
Пример №2
Найти матрицу, обратную к матрице $A=left(begin{array} {cc} -5 & 7 \ 9 & 8 end{array}right)$. Выполнить проверку.
Решение
Используем метод присоединённой матрицы. Сначала найдем определитель заданной матрицы $A$:
$$
Delta A=left| begin{array} {cc} -5 & 7\ 9 & 8 end{array}right|=-5cdot 8-7cdot 9=-103.
$$
Так как $Delta A neq 0$, то обратная матрица существует, посему продолжим решение. Находим алгебраические дополнения каждого элемента заданной матрицы:
begin{aligned}
& A_{11}=(-1)^2cdot 8=8; ; A_{12}=(-1)^3cdot 9=-9;\
& A_{21}=(-1)^3cdot 7=-7; ; A_{22}=(-1)^4cdot (-5)=-5.\
end{aligned}
Составляем матрицу из алгебраических дополнений: $A^{*}=left( begin{array} {cc} 8 & -9\ -7 & -5 end{array}right)$.
Транспонируем полученную матрицу: ${A^{*}}^T=left( begin{array} {cc} 8 & -7\ -9 & -5 end{array}right)$ (полученная матрица часто именуется присоединённой или союзной матрицей к матрице $A$).
Используя формулу $A^{-1}=frac{1}{Delta A}cdot {A^{*}}^T$, имеем:
$$
A^{-1}=frac{1}{-103}cdot left( begin{array} {cc} 8 & -7\ -9 & -5 end{array}right)
=left( begin{array} {cc} -8/103 & 7/103\ 9/103 & 5/103 end{array}right)
$$
Итак, обратная матрица найдена:
$$A^{-1}=left( begin{array} {cc} -8/103 & 7/103\ 9/103 & 5/103 end{array}right).$$
Чтобы проверить истинность результата, достаточно проверить истинность одного из равенств: $A^{-1}cdot A=E$ или $Acdot A^{-1}=E$. Проверим выполнение равенства $A^{-1}cdot A=E$. Дабы поменьше работать с дробями, будем подставлять матрицу $A^{-1}$ не в форме $left( begin{array} {cc} -8/103 & 7/103\ 9/103 & 5/103 end{array}right)$, а в виде $-frac{1}{103}cdot left( begin{array} {cc} 8 & -7\ -9 & -5 end{array}right)$:
$$
A^{-1}cdot{A}
=-frac{1}{103}cdot left( begin{array} {cc} 8 & -7\ -9 & -5 end{array}right)cdotleft(begin{array} {cc} -5 & 7 \ 9 & 8 end{array}right)
=-frac{1}{103}cdotleft(begin{array} {cc} -103 & 0 \ 0 & -103 end{array}right)
=left(begin{array} {cc} 1 & 0 \ 0 & 1 end{array}right)
=E
$$
Проверка пройдена успешно, обратная матрица $A^{-1}$ найдена верно.
Ответ: $A^{-1}=left( begin{array} {cc} -8/103 & 7/103\ 9/103 & 5/103 end{array}right)$.
Пример №3
Найти обратную матрицу для матрицы $A=left( begin{array} {ccc} 1 & 7 & 3 \ -4 & 9 & 4 \ 0 & 3 & 2end{array} right)$. Выполнить проверку.
Решение
Начнём с вычисления определителя матрицы $A$. Итак, определитель матрицы $A$ таков:
$$
Delta A=left| begin{array} {ccc} 1 & 7 & 3 \ -4 & 9 & 4 \ 0 & 3 & 2end{array} right| = 18-36+56-12=26.
$$
Так как $Delta Aneq 0$, то обратная матрица существует, посему продолжим решение. Находим алгебраические дополнения каждого элемента заданной матрицы:
$$
begin{aligned}
& A_{11}=(-1)^{2}cdotleft|begin{array}{cc} 9 & 4\ 3 & 2end{array}right|=6;;
A_{12}=(-1)^{3}cdotleft|begin{array}{cc} -4 &4 \ 0 & 2end{array}right|=8;;
A_{13}=(-1)^{4}cdotleft|begin{array}{cc} -4 & 9\ 0 & 3end{array}right|=-12;\
& A_{21}=(-1)^{3}cdotleft|begin{array}{cc} 7 & 3\ 3 & 2end{array}right|=-5;;
A_{22}=(-1)^{4}cdotleft|begin{array}{cc} 1 & 3\ 0 & 2end{array}right|=2;;
A_{23}=(-1)^{5}cdotleft|begin{array}{cc} 1 & 7\ 0 & 3end{array}right|=-3;\
& A_{31}=(-1)^{4}cdotleft|begin{array}{cc} 7 & 3\ 9 & 4end{array}right|=1;;
A_{32}=(-1)^{5}cdotleft|begin{array}{cc} 1 & 3\ -4 & 4end{array}right|=-16;;
A_{33}=(-1)^{6}cdotleft|begin{array}{cc} 1 & 7\ -4 & 9end{array}right|=37.
end{aligned}
$$
Составляем матрицу из алгебраических дополнений и транспонируем её:
$$
A^*=left( begin{array} {ccc} 6 & 8 & -12 \ -5 & 2 & -3 \ 1 & -16 & 37end{array} right); ;
{A^*}^T=left( begin{array} {ccc} 6 & -5 & 1 \ 8 & 2 & -16 \ -12 & -3 & 37end{array} right).
$$
Используя формулу $A^{-1}=frac{1}{Delta A}cdot {A^{*}}^T$, получим:
$$
A^{-1}=frac{1}{26}cdot left( begin{array} {ccc} 6 & -5 & 1 \ 8 & 2 & -16 \ -12 & -3 & 37end{array} right)=
left( begin{array} {ccc} 3/13 & -5/26 & 1/26 \ 4/13 & 1/13 & -8/13 \ -6/13 & -3/26 & 37/26 end{array} right)
$$
Чтобы проверить истинность результата, достаточно проверить истинность одного из равенств: $A^{-1}cdot A=E$ или $Acdot A^{-1}=E$. Проверим выполнение равенства $Acdot A^{-1}=E$. Дабы поменьше работать с дробями, будем подставлять матрицу $A^{-1}$ не в форме $left( begin{array} {ccc} 3/13 & -5/26 & 1/26 \ 4/13 & 1/13 & -8/13 \ -6/13 & -3/26 & 37/26 end{array} right)$, а в виде $frac{1}{26}cdot left( begin{array} {ccc} 6 & -5 & 1 \ 8 & 2 & -16 \ -12 & -3 & 37end{array} right)$:
$$
Acdot{A^{-1}}
=left( begin{array}{ccc}
1 & 7 & 3 \
-4 & 9 & 4\
0 & 3 & 2end{array} right)cdot
frac{1}{26}cdot left( begin{array} {ccc} 6 & -5 & 1 \ 8 & 2 & -16 \ -12 & -3 & 37end{array} right)
=frac{1}{26}cdotleft( begin{array} {ccc} 26 & 0 & 0 \ 0 & 26 & 0 \ 0 & 0 & 26end{array} right)
=left( begin{array} {ccc} 1 & 0 & 0 \ 0 & 1 & 0 \ 0 & 0 & 1end{array} right)
=E
$$
Проверка пройдена успешно, обратная матрица $A^{-1}$ найдена верно.
Ответ: $A^{-1}=left( begin{array} {ccc} 3/13 & -5/26 & 1/26 \ 4/13 & 1/13 & -8/13 \ -6/13 & -3/26 & 37/26 end{array} right)$.
Пример №4
Найти матрицу, обратную матрице $A=left( begin{array} {cccc} 6 & -5 & 8 & 4\ 9 & 7 & 5 & 2 \ 7 & 5 & 3 & 7\ -4 & 8 & -8 & -3 end{array} right)$.
Решение
Для матрицы четвёртого порядка нахождение обратной матрицы с помощью алгебраических дополнений несколько затруднительно. Однако такие примеры в контрольных работах встречаются.
Чтобы найти обратную матрицу, для начала нужно вычислить определитель матрицы $A$. Лучше всего в данной ситуации это сделать с помощью разложения определителя по строке (столбцу). Выбираем любую строку или столбец и находим алгебраические дополнения каждого элемента избранной строки или столбца.
Например, для первой строки получим:
$$
A_{11}=left|begin{array}{ccc} 7 & 5 & 2\ 5 & 3 & 7\ 8 & -8 & -3 end{array}right|=556;;
A_{12}=-left|begin{array}{ccc} 9 & 5 & 2\ 7 & 3 & 7 \ -4 & -8 & -3 end{array}right|=-300;
$$
$$
A_{13}=left|begin{array}{ccc} 9 & 7 & 2\ 7 & 5 & 7\ -4 & 8 & -3 end{array}right|=-536;;
A_{14}=-left|begin{array}{ccc} 9 & 7 & 5\ 7 & 5 & 3\ -4 & 8 & -8 end{array}right|=-112.
$$
Определитель матрицы $A$ вычислим по следующей формуле:
$$
Delta{A}=a_{11}cdot A_{11}+a_{12}cdot A_{12}+a_{13}cdot A_{13}+a_{14}cdot A_{14}=6cdot 556+(-5)cdot(-300)+8cdot(-536)+4cdot(-112)=100.
$$
А далее продолжаем находить алгебраические дополнения:
$$
begin{aligned}
& A_{21}=-77;;A_{22}=50;;A_{23}=87;;A_{24}=4;\
& A_{31}=-93;;A_{32}=50;;A_{33}=83;;A_{34}=36;\
& A_{41}=473;;A_{42}=-250;;A_{43}=-463;;A_{44}=-96.
end{aligned}
$$
Матрица из алгебраических дополнений:
$$A^*=left(begin{array}{cccc} 556 & -300 & -536 & -112\ -77 & 50 & 87 & 4 \ -93 & 50 & 83 & 36\ 473 & -250 & -463 & -96end{array}right)$$
Присоединённая матрица:
$${A^*}^T=left(begin{array} {cccc} 556 & -77 & -93 & 473\ -300 & 50 & 50 & -250 \ -536 & 87 & 83 & -463\ -112 & 4 & 36 & -96end{array}right)$$
Обратная матрица:
$$
A^{-1}=frac{1}{100}cdot left( begin{array} {cccc} 556 & -77 & -93 & 473\ -300 & 50 & 50 & -250 \ -536 & 87 & 83 & -463\ -112 & 4 & 36 & -96 end{array} right)=
left( begin{array} {cccc} 139/25 & -77/100 & -93/100 & 473/100 \ -3 & 1/2 & 1/2 & -5/2 \ -134/25 & 87/100 & 83/100 & -463/100 \ -28/25 & 1/25 & 9/25 & -24/25 end{array} right)
$$
Проверка, при желании, может быть произведена так же, как и в предыдущих примерах.
Ответ: $A^{-1}=left( begin{array} {cccc} 139/25 & -77/100 & -93/100 & 473/100 \ -3 & 1/2 & 1/2 & -5/2 \ -134/25 & 87/100 & 83/100 & -463/100 \ -28/25 & 1/25 & 9/25 & -24/25 end{array} right)$.
Во второй части будет рассмотрен иной способ нахождения обратной матрицы, который предполагает использование преобразований метода Гаусса или метода Гаусса-Жордана.
Содержание:
- Нахождение обратной матрицы с помощью присоединённой матрицы
- Нахождение обратной матрицы с помощью союзной матрицы
- Облегченный способ для матрицы второго порядка
Обратную матрицу
можно найти с помощью двух ниже описанных методов.
Нахождение обратной матрицы с помощью присоединённой матрицы
Пример
Задание. Для матрицы $ A=left( begin{array}{ll}{7} & {4} \ {5} & {3}end{array}right) $
найти обратную методом присоединенной матрицы.
Решение. Приписываем к заданной матрице

единичную матрицу второго порядка:
$$ Aleft|E=left( begin{array}{cc|cc}{7} & {4} & {1} & {0} \ {5} & {3} & {0} & {1}end{array}right)right. $$
От первой строки отнимаем вторую (для этого от элемента первой строки отнимаем соответствующий элемент второй строки):
$$ Aleft|E = left( begin{array}{rr|rr}{2} & {1} & {1} & {-1} \ {5} & {3} & {0} & {1}end{array}right)right. $$
От второй строки отнимаем две первых:
$$ Aleft|E sim left( begin{array}{rr|rr}{2} & {1} & {1} & {-1} \ {1} & {1} & {-2} & {3}end{array}right)right. $$
Первую и вторую строки меняем местами:
$$ Aleft|E sim left( begin{array}{rr|rr}{1} & {1} & {-2} & {3} \ {2} & {1} & {1} & {-1}end{array}right)right. $$
От второй строки отнимаем две первых:
$$ Aleft|E sim left( begin{array}{rr|rr}{1} & {1} & {-2} & {3} \ {0} & {-1} & {5} & {-7}end{array}right)right. $$
Вторую строку умножаем на (-1), а к первой строке прибавляем вторую:
$$ Aleft|E sim left( begin{array}{rr|rr}{1} & {0} & {3} & {-4} \ {0} & {1} & {-5} & {7}end{array}right)right. $$
Итак, слева получили единичную матрицу, а значит матрица, стоящая в
правой части (справа от вертикальной черты), является обратной к исходной.
Таким образом, получаем, что $ A^{-1}=left( begin{array}{rr}{3} & {-4} \ {-5} & {7}end{array}right) $
Ответ. $ A^{-1}=left( begin{array}{rr}{3} & {-4} \ {-5} & {7}end{array}right) $
Замечание
Если на некотором этапе в «левой» матрице получается
нулевая строка, то это
означает, что исходная матрица обратной не имеет.
Облегченный способ для матрицы второго порядка
Для матрицы второго порядка можно немного облегчить нахождение обратной, используя следующий алгоритм:
Шаг 1. Находим определитель $ Delta $ заданной матрицы,
если он равен нулю, то делаем вывод, что обратной матрицы не существует, иначе переходим к следующему шагу.
Шаг 2. Элементы, стоящие на
главной диагонали меняем местами, а у элементов
побочной диагонали меняем знак на противоположный.
Шаг 3. Делим все элементы на $ Delta $ и получаем обратную матрицу.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти обратную матрицу для
$ A=left( begin{array}{ll}{1} & {2} \ {2} & {4}end{array}right) $
Решение. Шаг 1. $ Delta=left| begin{array}{ll}{1} & {2} \ {2} & {4}end{array}right|=4-4=0 $ ,
тогда обратной матрицы не существует.
Ответ. Так как
определитель матрицы $A$ равен нулю,
то она не имеет обратной.
Пример
Задание. Найти обратную матрицу для $ A=left( begin{array}{ll}{1} & {1} \ {1} & {2}end{array}right) $
Решение. Шаг 1. Находим определитель: $ Delta=left| begin{array}{ll}{1} & {1} \ {1} & {2}end{array}right|=2-1=1 neq 0 $
Шаг 2. $ A^{prime}=left( begin{array}{rr}{2} & {-1} \ {-1} & {1}end{array}right) $
Шаг 3. $ A^{-1}=frac{1}{Delta} cdot A^{prime}=left( begin{array}{rr}{2} & {-1} \ {-1} & {1}end{array}right) $
Ответ. $ A^{-1}=left( begin{array}{rr}{2} & {-1} \ {-1} & {1}end{array}right) $
Нахождение обратной матрицы с помощью союзной матрицы
Определение
Матрица $ tilde{A} $ называется lt strong>союзной lt /strong> к квадратной матрице $A$ ,
если элементы матрицы $ tilde{A} $ равны
алгебраическим дополнениям соответствующих
элементов матрицы $A$ .
$$ A=left( begin{array}{ccc}{a_{11}} & {a_{12}} & {a_{13}} \ {a_{21}} & {a_{22}} & {a_{23}} \ {a_{31}} & {a_{32}} & {a_{33}}end{array}right) Rightarrow tilde{A}=left( begin{array}{ccc}{A_{11}} & {A_{12}} & {A_{13}} \ {A_{21}} & {A_{22}} & {A_{23}} \ {A_{31}} & {A_{32}} & {A_{33}}end{array}right) $$
Имеет место следующее свойство: $ A cdot widetilde{A}^{T}=|A| cdot E $
Тогда, если $ |A| neq 0 $ , то
$ A cdot tilde{A}^{T} cdot frac{1}{|A|}=E $ , а тогда
$ A^{-1}=frac{1}{|A|} cdot tilde{A}^{T} $
Таким образом, матрица имеет союзную тогда и только тогда, когда она
невырожденная.
Пример
Задание. Найти обратную матрицу к матрице $ A=left( begin{array}{rrr}{1} & {0} & {2} \ {2} & {-1} & {1} \ {1} & {3} & {-1}end{array}right) $
Решение. Вычисляем определитель матрицы:
$$ Delta=left| begin{array}{rrr}{1} & {0} & {2} \ {2} & {-1} & {1} \ {1} & {3} & {-1}end{array}right|=1 cdot(-1) cdot(-1)+2 cdot 3 cdot 2+0 cdot 1 cdot 1- $$
$$ -1 cdot(-1) cdot 2-3 cdot 1 cdot 1-2 cdot 0 cdot(-1)=1+12+0+2-3+0=12 neq 0 $$
Так как определитель не равен нулю, то матрица имеет обратную.
Обратная матрица $A^{-1}$ к матрице
$A$ находится по формуле:
$$ A^{-1}=frac{1}{Delta} cdot widetilde{A}^{T} $$
Найдем союзную матрицу $ tilde{A} $ , для этого вычислим алгебраические
дополнения к элементам матрицы $A$ :
$$ A_{11}=(-1)^{1+1} left| begin{array}{rr}{-1} & {1} \ {3} & {-1}end{array}right|=(-1) cdot(-1)-3 cdot 1=1-3=-2 $$
$$ A_{12}=(-1)^{1+2} left| begin{array}{rr}{2} & {1} \ {1} & {-1}end{array}right|=-[2 cdot(-1)-1 cdot 1]=-(-2-1)=3 $$
$$ A_{13}=(-1)^{1+3} left| begin{array}{rr}{2} & {-1} \ {1} & {3}end{array}right|=2 cdot 3-1 cdot(-1)=6+1=7 $$
$$ A_{21}=(-1)^{2+1} left| begin{array}{rr}{0} & {2} \ {3} & {-1}end{array}right|=-[0 cdot(-1)-3 cdot 2]=-(0-6)=6 $$
$$ A_{22}=(-1)^{2+2} left| begin{array}{rr}{1} & {2} \ {1} & {-1}end{array}right|=1 cdot(-1)-1 cdot 2=-1-2=-3 $$
$$ A_{23}=(-1)^{2+3} left| begin{array}{cc}{1} & {0} \ {1} & {3}end{array}right|=-[1 cdot 3-1 cdot 0]=-(3-0)=-3 $$
$$ A_{31}=(-1)^{3+1} left| begin{array}{rr}{0} & {2} \ {-1} & {1}end{array}right|=0 cdot 1-(-1) cdot 2=0+2=2 $$
$$ A_{32}=(-1)^{3+2} left| begin{array}{cc}{1} & {2} \ {2} & {1}end{array}right|=-[1 cdot 1-2 cdot 2]=-(1-4)=3 $$
$$ A_{33}=(-1)^{3+3} left| begin{array}{rr}{1} & {0} \ {2} & {-1}end{array}right|=1 cdot(-1)-2 cdot 0=-1-0=-1 $$
Таким образом, $ tilde{A}=left( begin{array}{rrr}{-2} & {3} & {7} \ {6} & {-3} & {-3} \ {2} & {3} & {-1}end{array}right) $
Транспонируем эту матрицу (т.е. строки матрицы делаем столбцами с тем же номером):
$$ widetilde{A}^{T}=left( begin{array}{rrr}{-2} & {6} & {2} \ {3} & {-3} & {3} \ {7} & {-3} & {-1}end{array}right) $$
Итак, $ A^{-1}=frac{1}{12} left( begin{array}{rrr}{-2} & {6} & {2} \ {3} & {-3} & {3} \ {7} & {-3} & {-1}end{array}right) $
Ответ. $ A^{-1}=frac{1}{12} left( begin{array}{rrr}{-2} & {6} & {2} \ {3} & {-3} & {3} \ {7} & {-3} & {-1}end{array}right) $
Читать дальше: линейно зависимые и линейно независимые строки.
Обратная матрица и её свойства
15 февраля 2018
- Домашняя работа
- Ответы
Эта тема является одной из самых ненавистных среди студентов. Хуже, наверное, только определители.
Фишка в том, что само понятие обратного элемента (и я сейчас не только о матрицах) отсылает нас к операции умножения. Даже в школьной программе умножение считается сложной операцией, а уж умножение матриц — вообще отдельная тема, которой у меня посвящён целый параграф и видеоурок.
Сегодня мы не будем вдаваться в подробности матричных вычислений. Просто вспомним: как обозначаются матрицы, как они умножаются и что из этого следует.
Повторение: умножение матриц
Прежде всего договоримся об обозначениях. Матрицей $A$ размера $left[ mtimes n right]$ называется просто таблица из чисел, в которой ровно $m$ строк и $n$ столбцов:
[A=left[ mtimes n right]=underbrace{left[ begin{matrix} {{a}_{11}} & {{a}_{12}} & … & {{a}_{1n}} \ {{a}_{21}} & {{a}_{22}} & … & {{a}_{2n}} \ … & … & … & … \ {{a}_{m1}} & {{a}_{m2}} & … & {{a}_{mn}} \end{matrix} right]}_{n}]
Чтобы случайно не перепутать строки и столбцы местами (поверьте, на экзамене можно и единицу с двойкой перепутать — что уж говорить про какие-то там строки), просто взгляните на картинку:
Что происходит? Если разместить стандартную систему координат $OXY$ в левом верхнем углу и направить оси так, чтобы они охватывали всю матрицу, то каждой клетке этой матрицы можно однозначно сопоставить координаты $left( x;y right)$ — это и будет номер строки и номер столбца.
Почему система координат размещена именно в левом верхнем углу? Да потому что именно оттуда мы начинаем читать любые тексты. Это очень просто запомнить.
А почему ось $x$ направлена именно вниз, а не вправо? Опять всё просто: возьмите стандартную систему координат (ось $x$ идёт вправо, ось $y$ — вверх) и поверните её так, чтобы она охватывала матрицу. Это поворот на 90 градусов по часовой стрелке — его результат мы и видим на картинке.
В общем, как определять индексы у элементов матрицы, мы разобрались. Теперь давайте разберёмся с умножением.
Определение. Матрицы $A=left[ mtimes n right]$ и $B=left[ ntimes k right]$, когда количество столбцов в первой совпадает с количеством строк во второй, называются согласованными.
Именно в таком порядке. Можно сумничать и сказать, мол, матрицы $A$ и $B$ образуют упорядоченную пару $left( A;B right)$: если они согласованы в таком порядке, то совершенно необязательно, что $B$ и $A$, т.е. пара $left( B;A right)$ — тоже согласована.
Умножать можно только согласованные матрицы.
Определение. Произведение согласованных матриц $A=left[ mtimes n right]$ и $B=left[ ntimes k right]$ — это новая матрица $C=left[ mtimes k right]$, элементы которой ${{c}_{ij}}$ считаются по формуле:
[{{c}_{ij}}=sumlimits_{k=1}^{n}{{{a}_{ik}}}cdot {{b}_{kj}}]
Другими словами: чтобы получить элемент ${{c}_{ij}}$ матрицы $C=Acdot B$, нужно взять $i$-строку первой матрицы, $j$-й столбец второй матрицы, а затем попарно перемножить элементы из этой строки и столбца. Результаты сложить.
Да, вот такое суровое определение. Из него сразу следует несколько фактов:
- Умножение матриц, вообще говоря, некоммутативно: $Acdot Bne Bcdot A$;
- Однако умножение ассоциативно: $left( Acdot B right)cdot C=Acdot left( Bcdot C right)$;
- И даже дистрибутивно: $left( A+B right)cdot C=Acdot C+Bcdot C$;
- И ещё раз дистрибутивно: $Acdot left( B+C right)=Acdot B+Acdot C$.
Дистрибутивность умножения пришлось отдельно описывать для левого и правого множителя-суммы как раз из-за некоммутативности операции умножения.
Если всё же получается так, что $Acdot B=Bcdot A$, такие матрицы называются перестановочными.
Среди всех матриц, которые там на что-то умножаются, есть особые — те, которые при умножении на любую матрицу $A$ снова дают $A$:
Определение. Матрица $E$ называется единичной, если $Acdot E=A$ или $Ecdot A=A$. В случае с квадратной матрицей $A$ можем записать:
[Acdot E=Ecdot A=A]
Единичная матрица — частый гость при решении матричных уравнений. И вообще частый гость в мире матриц.:)
А ещё из-за этой $E$ кое-кто придумал всю ту дичь, которая будет написана дальше.
Что такое обратная матрица
Поскольку умножение матриц — весьма трудоёмкая операция (приходится перемножать кучу строчек и столбцов), то понятие обратной матрицы тоже оказывается не самым тривиальным. И требующим некоторых пояснений.
Ключевое определение
Что ж, пора познать истину.
Определение. Матрица $B$ называется обратной к матрице $A$, если
[Acdot B=Bcdot A=E]
Обратная матрица обозначается через ${{A}^{-1}}$ (не путать со степенью!), поэтому определение можно переписать так:
[Acdot {{A}^{-1}}={{A}^{-1}}cdot A=E]
Казалось бы, всё предельно просто и ясно. Но при анализе такого определения сразу возникает несколько вопросов:
- Всегда ли существует обратная матрица? И если не всегда, то как определить: когда она существует, а когда — нет?
- А кто сказал, что такая матрица ровно одна? Вдруг для некоторой исходной матрицы $A$ найдётся целая толпа обратных?
- Как выглядят все эти «обратные»? И как, собственно, их считать?
Насчёт алгоритмов вычисления — об этом мы поговорим чуть позже. Но на остальные вопросы ответим прямо сейчас. Оформим их в виде отдельных утверждений-лемм.
Основные свойства
Начнём с того, как в принципе должна выглядеть матрица $A$, чтобы для неё существовала ${{A}^{-1}}$. Сейчас мы убедимся в том, что обе эти матрицы должны быть квадратными, причём одного размера: $left[ ntimes n right]$.
Лемма 1. Дана матрица $A$ и обратная ей ${{A}^{-1}}$. Тогда обе эти матрицы — квадратные, причём одинакового порядка $n$.
Доказательство. Всё просто. Пусть матрица $A=left[ mtimes n right]$, ${{A}^{-1}}=left[ atimes b right]$. Поскольку произведение $Acdot {{A}^{-1}}=E$ по определению существует, матрицы $A$ и ${{A}^{-1}}$ согласованы в указанном порядке:
[begin{align} & left[ mtimes n right]cdot left[ atimes b right]=left[ mtimes b right] \ & n=a end{align}]
Это прямое следствие из алгоритма перемножения матриц: коэффициенты $n$ и $a$ являются «транзитными» и должны быть равны.
Вместе с тем определено и обратное умножение: ${{A}^{-1}}cdot A=E$, поэтому матрицы ${{A}^{-1}}$ и $A$ тоже согласованы в указанном порядке:
[begin{align} & left[ atimes b right]cdot left[ mtimes n right]=left[ atimes n right] \ & b=m end{align}]
Таким образом, без ограничения общности можем считать, что $A=left[ mtimes n right]$, ${{A}^{-1}}=left[ ntimes m right]$. Однако согласно определению $Acdot {{A}^{-1}}={{A}^{-1}}cdot A$, поэтому размеры матриц строго совпадают:
[begin{align} & left[ mtimes n right]=left[ ntimes m right] \ & m=n end{align}]
Вот и получается, что все три матрицы — $A$, ${{A}^{-1}}$ и $E$ — являются квадратными размером $left[ ntimes n right]$. Лемма доказана.
Что ж, уже неплохо. Мы видим, что обратимыми бывают лишь квадратные матрицы. Теперь давайте убедимся, что обратная матрица всегда одна.
Лемма 2. Дана матрица $A$ и обратная ей ${{A}^{-1}}$. Тогда эта обратная матрица — единственная.
Доказательство. Пойдём от противного: пусть у матрицы $A$ есть хотя бы два экземпляра обратных —$B$ и $C$. Тогда, согласно определению, верны следующие равенства:
[begin{align} & Acdot B=Bcdot A=E; \ & Acdot C=Ccdot A=E. \ end{align}]
Из леммы 1 мы заключаем, что все четыре матрицы — $A$, $B$, $C$ и $E$ — являются квадратными одинакового порядка: $left[ ntimes n right]$. Следовательно, определено произведение:
[Bcdot Acdot C]
Поскольку умножение матриц ассоциативно (но не коммутативно!), мы можем записать:
[begin{align} & Bcdot Acdot C=left( Bcdot A right)cdot C=Ecdot C=C; \ & Bcdot Acdot C=Bcdot left( Acdot C right)=Bcdot E=B; \ & Bcdot Acdot C=C=BRightarrow B=C. \ end{align}]
Получили единственно возможный вариант: два экземпляра обратной матрицы равны. Лемма доказана.
Приведённые рассуждения почти дословно повторяют доказательство единственность обратного элемента для всех действительных чисел $bne 0$. Единственное существенное дополнение — учёт размерности матриц.
Впрочем, мы до сих пор ничего не знаем о том, всякая ли квадратная матрица является обратимой. Тут нам на помощь приходит определитель — это ключевая характеристика для всех квадратных матриц.
Лемма 3. Дана матрица $A$. Если обратная к ней матрица ${{A}^{-1}}$ существует, то определитель исходной матрицы отличен от нуля:
[left| A right|ne 0]
Доказательство. Мы уже знаем, что $A$ и ${{A}^{-1}}$ — квадратные матрицы размера $left[ ntimes n right]$. Следовательно, для каждой из них можно вычислить определитель: $left| A right|$ и $left| {{A}^{-1}} right|$. Однако определитель произведения равен произведению определителей:
[left| Acdot B right|=left| A right|cdot left| B right|Rightarrow left| Acdot {{A}^{-1}} right|=left| A right|cdot left| {{A}^{-1}} right|]
Но согласно определению $Acdot {{A}^{-1}}=E$, а определитель $E$ всегда равен 1, поэтому
[begin{align} & Acdot {{A}^{-1}}=E; \ & left| Acdot {{A}^{-1}} right|=left| E right|; \ & left| A right|cdot left| {{A}^{-1}} right|=1. \ end{align}]
Произведение двух чисел равно единице только в том случае, когда каждое из этих чисел отлично от нуля:
[left| A right|ne 0;quad left| {{A}^{-1}} right|ne 0.]
Вот и получается, что $left| A right|ne 0$. Лемма доказана.
На самом деле это требование вполне логично. Сейчас мы разберём алгоритм нахождения обратной матрицы — и станет совершенно ясно, почему при нулевом определителе никакой обратной матрицы в принципе не может существовать.
Но для начала сформулируем «вспомогательное» определение:
Определение. Вырожденная матрица — это квадратная матрица размера $left[ ntimes n right]$, чей определитель равен нулю.
Таким образом, мы можем утверждать, что всякая обратимая матрица является невырожденной.
Как найти обратную матрицу
Сейчас мы рассмотрим универсальный алгоритм нахождения обратных матриц. Вообще, существует два общепринятых алгоритма, и второй мы тоже сегодня рассмотрим.
Тот, который будет рассмотрен сейчас, очень эффективен для матриц размера $left[ 2times 2 right]$ и — частично — размера $left[ 3times 3 right]$. А вот начиная с размера $left[ 4times 4 right]$ его лучше не применять. Почему — сейчас сами всё поймёте.
Алгебраические дополнения
Готовьтесь. Сейчас будет боль. Нет, не переживайте: к вам не идёт красивая медсестра в юбке, чулках с кружевами и не сделает укол в ягодицу. Всё куда прозаичнее: к вам идут алгебраические дополнения и Её Величество «Союзная Матрица».
Начнём с главного. Пусть имеется квадратная матрица размера $A=left[ ntimes n right]$, элементы которой именуются ${{a}_{ij}}$. Тогда для каждого такого элемента можно определить алгебраическое дополнение:
Определение. Алгебраическое дополнение ${{A}_{ij}}$ к элементу ${{a}_{ij}}$, стоящего в $i$-й строке и $j$-м столбце матрицы $A=left[ ntimes n right]$ — это конструкция вида
[{{A}_{ij}}={{left( -1 right)}^{i+j}}cdot M_{ij}^{*}]
Где $M_{ij}^{*}$ — определитель матрицы, полученной из исходной $A$ вычёркиванием той самой $i$-й строки и $j$-го столбца.
Ещё раз. Алгебраическое дополнение к элементу матрицы с координатами $left( i;j right)$ обозначается как ${{A}_{ij}}$ и считается по схеме:
- Сначала вычёркиваем из исходной матрицы $i$-строчку и $j$-й столбец. Получим новую квадратную матрицу, и её определитель мы обозначаем как $M_{ij}^{*}$.
- Затем умножаем этот определитель на ${{left( -1 right)}^{i+j}}$ — поначалу это выражение может показаться мозговыносящим, но по сути мы просто выясняем знак перед $M_{ij}^{*}$.
- Считаем — получаем конкретное число. Т.е. алгебраическое дополнение — это именно число, а не какая-то новая матрица и т.д.
Саму матрицу $M_{ij}^{*}$ называют дополнительным минором к элементу ${{a}_{ij}}$. И в этом смысле приведённое выше определение алгебраического дополнения является частным случаем более сложного определения — того, что мы рассматривали в уроке про определитель.
Важное замечание. Вообще-то во «взрослой» математике алгебраические дополнения определяются так:
- Берём в квадратной матрице $k$ строчек и $k$ столбцов. На их пересечении получится матрица размера $left[ ktimes k right]$ — её определитель называется минором порядка $k$ и обозначается ${{M}_{k}}$.
- Затем вычёркиваем эти «избранные» $k$ строчек и $k$ столбцов. Снова получится квадратная матрица — её определитель называется дополнительным минором и обозначается $M_{k}^{*}$.
- Умножаем $M_{k}^{*}$ на ${{left( -1 right)}^{t}}$, где $t$ — это (вот сейчас внимание!) сумма номеров всех выбранных строчек и столбцов. Это и будет алгебраическое дополнение.
Взгляните на третий шаг: там вообще-то сумма $2k$ слагаемых! Другое дело, что для $k=1$ мы получим лишь 2 слагаемых — это и будут те самые $i+j$ — «координаты» элемента ${{a}_{ij}}$, для которого мы ищем алгебраическое дополнение.
Таким образом сегодня мы используем слегка упрощённое определение. Но как мы увидим в дальнейшем, его окажется более чем достаточно. Куда важнее следующая штука:
Определение. Союзная матрица $S$ к квадратной матрице $A=left[ ntimes n right]$ — это новая матрица размера $left[ ntimes n right]$, которая получается из $A$ заменой ${{a}_{ij}}$ алгебраическими дополнениями ${{A}_{ij}}$:
[A=left[ begin{matrix} {{a}_{11}} & {{a}_{12}} & … & {{a}_{1n}} \ {{a}_{21}} & {{a}_{22}} & … & {{a}_{2n}} \ … & … & … & … \ {{a}_{n1}} & {{a}_{n2}} & … & {{a}_{nn}} \end{matrix} right]Rightarrow S=left[ begin{matrix} {{A}_{11}} & {{A}_{12}} & … & {{A}_{1n}} \ {{A}_{21}} & {{A}_{22}} & … & {{A}_{2n}} \ … & … & … & … \ {{A}_{n1}} & {{A}_{n2}} & … & {{A}_{nn}} \end{matrix} right]]
Первая мысль, возникающая в момент осознания этого определения — «это сколько же придётся всего считать!» Расслабьтесь: считать придётся, но не так уж и много.:)
Что ж, всё это очень мило, но зачем это нужно? А вот зачем.
Основная теорема
Вернёмся немного назад. Помните, в Лемме 3 утверждалось, что обратимая матрица $A$ всегда не вырождена (т.е. её определитель отличен от нуля: $left| A right|ne 0$).
Так вот, верно и обратное: если матрица $A$ не вырождена, то она всегда обратима. И даже существует схема поиска ${{A}^{-1}}$. Зацените:
Теорема об обратной матрице. Пусть дана квадратная матрица $A=left[ ntimes n right]$, причём её определитель отличен от нуля: $left| A right|ne 0$. Тогда обратная матрица ${{A}^{-1}}$ существует и считается по формуле:
[{{A}^{-1}}=frac{1}{left| A right|}cdot {{S}^{T}}]
А теперь — всё то же самое, но разборчивым почерком. Чтобы найти обратную матрицу, нужно:
- Посчитать определитель $left| A right|$ и убедиться, что он отличен от нуля.
- Составить союзную матрицу $S$, т.е. посчитать 100500 алгебраических дополнений ${{A}_{ij}}$ и расставить их на месте ${{a}_{ij}}$.
- Транспонировать эту матрицу $S$, а затем умножить её на некое число $q={1}/{left| A right|};$.
И всё! Обратная матрица ${{A}^{-1}}$ найдена. Давайте посмотрим на примеры:
Задача. Найдите обратную матрицу:
[left[ begin{matrix} 3 & 1 \ 5 & 2 \end{matrix} right]]
Решение. Проверим обратимость. Посчитаем определитель:
[left| A right|=left| begin{matrix} 3 & 1 \ 5 & 2 \end{matrix} right|=3cdot 2-1cdot 5=6-5=1]
Определитель отличен от нуля. Значит, матрица обратима. Составим союзную матрицу:
[S=left[ begin{matrix} {{A}_{11}} & {{A}_{12}} \ {{A}_{21}} & {{A}_{22}} \end{matrix} right]]
Посчитаем алгебраические дополнения:
[begin{align} & {{A}_{11}}={{left( -1 right)}^{1+1}}cdot left| 2 right|=2; \ & {{A}_{12}}={{left( -1 right)}^{1+2}}cdot left| 5 right|=-5; \ & {{A}_{21}}={{left( -1 right)}^{2+1}}cdot left| 1 right|=-1; \ & {{A}_{22}}={{left( -1 right)}^{2+2}}cdot left| 3 right|=3. \ end{align}]
Обратите внимание: определители |2|, |5|, |1| и |3| — это именно определители матриц размера $left[ 1times 1 right]$, а не модули. Т.е. если в определителях стояли отрицательные числа, убирать «минус» не надо.
Итого наша союзная матрица выглядит так:
[S=left[ begin{array}{*{35}{r}}2 & -5 \ -1 & 3 \end{array} right]]
Осталось посчитать обратную:
[{{A}^{-1}}=frac{1}{left| A right|}cdot {{S}^{T}}=frac{1}{1}cdot {{left[ begin{array}{*{35}{r}} 2 & -5 \ -1 & 3 \end{array} right]}^{T}}=left[ begin{array}{*{35}{r}} 2 & -1 \ -5 & 3 \end{array} right]]
Ну вот и всё. Задача решена.
Ответ. $left[ begin{array}{*{35}{r}} 2 & -1 \ -5 & 3 \end{array} right]$
Задача. Найдите обратную матрицу:
[left[ begin{array}{*{35}{r}} 1 & -1 & 2 \ 0 & 2 & -1 \ 1 & 0 & 1 \end{array} right]]
Решение. Опять считаем определитель:
[begin{align} & left| begin{array}{*{35}{r}} 1 & -1 & 2 \ 0 & 2 & -1 \ 1 & 0 & 1 \end{array} right|=begin{matrix} left( 1cdot 2cdot 1+left( -1 right)cdot left( -1 right)cdot 1+2cdot 0cdot 0 right)- \ -left( 2cdot 2cdot 1+left( -1 right)cdot 0cdot 1+1cdot left( -1 right)cdot 0 right) \end{matrix}= \ & =left( 2+1+0 right)-left( 4+0+0 right)=-1ne 0. \ end{align}]
Определитель отличен от нуля — матрица обратима. А вот сейчас будет самая жесть: надо посчитать аж 9 (девять, мать их!) алгебраических дополнений. И каждое из них будет содержать определитель $left[ 2times 2 right]$. Полетели:
[begin{matrix} {{A}_{11}}={{left( -1 right)}^{1+1}}cdot left| begin{matrix} 2 & -1 \ 0 & 1 \end{matrix} right|=2; \ {{A}_{12}}={{left( -1 right)}^{1+2}}cdot left| begin{matrix} 0 & -1 \ 1 & 1 \end{matrix} right|=-1; \ {{A}_{13}}={{left( -1 right)}^{1+3}}cdot left| begin{matrix} 0 & 2 \ 1 & 0 \end{matrix} right|=-2; \ … \ {{A}_{33}}={{left( -1 right)}^{3+3}}cdot left| begin{matrix} 1 & -1 \ 0 & 2 \end{matrix} right|=2; \ end{matrix}]
Короче, союзная матрица будет выглядеть так:
[S=left[ begin{matrix} 2 & -1 & -2 \ 1 & -1 & -1 \ -3 & 1 & 2 \end{matrix} right]]
Следовательно, обратная матрица будет такой:
[{{A}^{-1}}=frac{1}{-1}cdot left[ begin{matrix} 2 & -1 & -2 \ 1 & -1 & -1 \ -3 & 1 & 2 \end{matrix} right]=left[ begin{array}{*{35}{r}}-2 & -1 & 3 \ 1 & 1 & -1 \ 2 & 1 & -2 \end{array} right]]
Ну и всё. Вот и ответ.
Ответ. $left[ begin{array}{*{35}{r}} -2 & -1 & 3 \ 1 & 1 & -1 \ 2 & 1 & -2 \end{array} right]$
Как видите, в конце каждого примера мы выполняли проверку. В связи с этим важное замечание:
Не ленитесь выполнять проверку. Умножьте исходную матрицу на найденную обратную — должна получиться $E$.
Выполнить эту проверку намного проще и быстрее, чем искать ошибку в дальнейших вычислениях, когда, например, вы решаете матричное уравнение.
Альтернативный способ
Как я и говорил, теорема об обратной матрице прекрасно работает для размеров $left[ 2times 2 right]$ и $left[ 3times 3 right]$ (в последнем случае — уже не так уж и «прекрасно»), а вот для матриц больших размеров начинается прям печаль.
Но не переживайте: есть альтернативный алгоритм, с помощью которого можно невозмутимо найти обратную хоть для матрицы $left[ 10times 10 right]$. Но, как это часто бывает, для рассмотрения этого алгоритма нам потребуется небольшая теоретическая вводная.
Элементарные преобразования
Среди всевозможных преобразований матрицы есть несколько особых — их называют элементарными. Таких преобразований ровно три:
- Умножение. Можно взять $i$-ю строку (столбец) и умножить её на любое число $kne 0$;
- Сложение. Прибавить к $i$-й строке (столбцу) любую другую $j$-ю строку (столбец), умноженную на любое число $kne 0$ (можно, конечно, и $k=0$, но какой в этом смысл? Ничего не изменится же).
- Перестановка. Взять $i$-ю и $j$-ю строки (столбцы) и поменять местами.
Почему эти преобразования называются элементарными (для больших матриц они выглядят не такими уж элементарными) и почему их только три — эти вопросы выходят за рамки сегодняшнего урока. Поэтому не будем вдаваться в подробности.
Важно другое: все эти извращения нам предстоит выполнять над присоединённой матрицей. Да, да: вы не ослышались. Сейчас будет ещё одно определение — последнее в сегодняшнем уроке.
Присоединённая матрица
Наверняка в школе вы решали системы уравнений методом сложения. Ну, там, вычесть из одной строки другую, умножить какую-то строку на число — вот это вот всё.
Так вот: сейчас будет всё то же, но уже «по-взрослому». Готовы?
Определение. Пусть дана матрица $A=left[ ntimes n right]$ и единичная матрица $E$ такого же размера $n$. Тогда присоединённая матрица $left[ Aleft| E right. right]$ — это новая матрица размера $left[ ntimes 2n right]$, которая выглядит так:
[left[ Aleft| E right. right]=left[ begin{array}{rrrr|rrrr}{{a}_{11}} & {{a}_{12}} & … & {{a}_{1n}} & 1 & 0 & … & 0 \{{a}_{21}} & {{a}_{22}} & … & {{a}_{2n}} & 0 & 1 & … & 0 \… & … & … & … & … & … & … & … \{{a}_{n1}} & {{a}_{n2}} & … & {{a}_{nn}} & 0 & 0 & … & 1 \end{array} right]]
Короче говоря, берём матрицу $A$, справа приписываем к ней единичную матрицу $E$ нужного размера, разделяем их вертикальной чертой для красоты — вот вам и присоединённая.:)
В чём прикол? А вот в чём:
Теорема. Пусть матрица $A$ обратима. Рассмотрим присоединённую матрицу $left[ Aleft| E right. right]$. Если с помощью элементарных преобразований строк привести её к виду $left[ Eleft| B right. right]$, т.е. путём умножения, вычитания и перестановки строк получить из $A$ матрицу $E$ справа, то полученная слева матрица $B$ — это обратная к $A$:
[left[ Aleft| E right. right]to left[ Eleft| B right. right]Rightarrow B={{A}^{-1}}]
Вот так всё просто! Короче говоря, алгоритм нахождения обратной матрицы выглядит так:
- Записать присоединённую матрицу $left[ Aleft| E right. right]$;
- Выполнять элементарные преобразования строк до тех пор, пока права вместо $A$ не появится $E$;
- Разумеется, слева тоже что-то появится — некая матрица $B$. Это и будет обратная;
- PROFIT!:)
Конечно, сказать намного проще, чем сделать. Поэтому давайте рассмотрим парочку примеров: для размеров $left[ 3times 3 right]$ и $left[ 4times 4 right]$.
Задача. Найдите обратную матрицу:
[left[ begin{array}{*{35}{r}} 1 & 5 & 1 \ 3 & 2 & 1 \ 6 & -2 & 1 \end{array} right]]
Решение. Составляем присоединённую матрицу:
[left[ begin{array}{rrr|rrr} 1 & 5 & 1 & 1 & 0 & 0 \ 3 & 2 & 1 & 0 & 1 & 0 \ 6 & -2 & 1 & 0 & 0 & 1 \end{array} right]]
Поскольку последний столбец исходной матрицы заполнен единицами, вычтем первую строку из остальных:
[begin{align} & left[ begin{array}{rrr|rrr} 1 & 5 & 1 & 1 & 0 & 0 \ 3 & 2 & 1 & 0 & 1 & 0 \ 6 & -2 & 1 & 0 & 0 & 1 \end{array} right]begin{matrix} downarrow \ -1 \ -1 \end{matrix}to \ & to left[ begin{array}{rrr|rrr} 1 & 5 & 1 & 1 & 0 & 0 \ 2 & -3 & 0 & -1 & 1 & 0 \ 5 & -7 & 0 & -1 & 0 & 1 \end{array} right] \ end{align}]
Больше единиц нет, кроме первой строки. Но её мы не трогаем, иначе в третьем столбце начнут «размножаться» только что убранные единицы.
Зато можем вычесть вторую строку дважды из последней — получим единицу в левом нижнем углу:
[begin{align} & left[ begin{array}{rrr|rrr} 1 & 5 & 1 & 1 & 0 & 0 \ 2 & -3 & 0 & -1 & 1 & 0 \ 5 & -7 & 0 & -1 & 0 & 1 \end{array} right]begin{matrix} \ downarrow \ -2 \end{matrix}to \ & left[ begin{array}{rrr|rrr} 1 & 5 & 1 & 1 & 0 & 0 \ 2 & -3 & 0 & -1 & 1 & 0 \ 1 & -1 & 0 & 1 & -2 & 1 \end{array} right] \ end{align}]
Теперь можно вычесть последнюю строку из первой и дважды из второй — таким образом мы «занулим» первый столбец:
[begin{align} & left[ begin{array}{rrr|rrr} 1 & 5 & 1 & 1 & 0 & 0 \ 2 & -3 & 0 & -1 & 1 & 0 \ 1 & -1 & 0 & 1 & -2 & 1 \end{array} right]begin{matrix} -1 \ -2 \ uparrow \end{matrix}to \ & to left[ begin{array}{rrr|rrr} 0 & 6 & 1 & 0 & 2 & -1 \ 0 & -1 & 0 & -3 & 5 & -2 \ 1 & -1 & 0 & 1 & -2 & 1 \end{array} right] \ end{align}]
Умножим вторую строку на −1, а затем вычтем её 6 раз из первой и прибавим 1 раз к последней:
[begin{align} & left[ begin{array}{rrr|rrr} 0 & 6 & 1 & 0 & 2 & -1 \ 0 & -1 & 0 & -3 & 5 & -2 \ 1 & -1 & 0 & 1 & -2 & 1 \end{array} right]begin{matrix} \ left| cdot left( -1 right) right. \ \end{matrix}to \ & to left[ begin{array}{rrr|rrr} 0 & 6 & 1 & 0 & 2 & -1 \ 0 & 1 & 0 & 3 & -5 & 2 \ 1 & -1 & 0 & 1 & -2 & 1 \end{array} right]begin{matrix} -6 \ updownarrow \ +1 \end{matrix}to \ & to left[ begin{array}{rrr|rrr} 0 & 0 & 1 & -18 & 32 & -13 \ 0 & 1 & 0 & 3 & -5 & 2 \ 1 & 0 & 0 & 4 & -7 & 3 \end{array} right] \ end{align}]
Осталось лишь поменять местами строки 1 и 3:
[left[ begin{array}{rrr|rrr} 1 & 0 & 0 & 4 & -7 & 3 \ 0 & 1 & 0 & 3 & -5 & 2 \ 0 & 0 & 1 & -18 & 32 & -13 \end{array} right]]
Готово! Справа — искомая обратная матрица.
Ответ. $left[ begin{array}{*{35}{r}}4 & -7 & 3 \ 3 & -5 & 2 \ -18 & 32 & -13 \end{array} right]$
Задача. Найдите обратную матрицу:
[left[ begin{matrix} 1 & 4 & 2 & 3 \ 1 & -2 & 1 & -2 \ 1 & -1 & 1 & 1 \ 0 & -10 & -2 & -5 \end{matrix} right]]
Решение. Снова составляем присоединённую:
[left[ begin{array}{rrrr|rrrr} 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \ 1 & -2 & 1 & -2 & 0 & 1 & 0 & 0 \ 1 & -1 & 1 & 1 & 0 & 0 & 1 & 0 \ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \end{array} right]]
Немного позалимаем, попечалимся от того, сколько сейчас придётся считать… и начнём считать. Для начала «обнулим» первый столбец, вычитая строку 1 из строк 2 и 3:
[begin{align} & left[ begin{array}{rrrr|rrrr} 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \ 1 & -2 & 1 & -2 & 0 & 1 & 0 & 0 \ 1 & -1 & 1 & 1 & 0 & 0 & 1 & 0 \ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \end{array} right]begin{matrix} downarrow \ -1 \ -1 \ \end{matrix}to \ & to left[ begin{array}{rrrr|rrrr} 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \ 0 & -6 & -1 & -5 & -1 & 1 & 0 & 0 \ 0 & -5 & -1 & -2 & -1 & 0 & 1 & 0 \ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \end{array} right] \ end{align}]
Наблюдаем слишком много «минусов» в строках 2—4. Умножим все три строки на −1, а затем «выжжем» третий столбец, вычитая строку 3 из остальных:
[begin{align} & left[ begin{array}{rrrr|rrrr} 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \ 0 & -6 & -1 & -5 & -1 & 1 & 0 & 0 \ 0 & -5 & -1 & -2 & -1 & 0 & 1 & 0 \ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \end{array} right]begin{matrix} \ left| cdot left( -1 right) right. \ left| cdot left( -1 right) right. \ left| cdot left( -1 right) right. \end{matrix}to \ & to left[ begin{array}{rrrr|rrrr} 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \ 0 & 6 & 1 & 5 & 1 & -1 & 0 & 0 \ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \ 0 & 10 & 2 & 5 & 0 & 0 & 0 & -1 \end{array} right]begin{matrix} -2 \ -1 \ updownarrow \ -2 \end{matrix}to \ & to left[ begin{array}{rrrr|rrrr} 1 & -6 & 0 & -1 & -1 & 0 & 2 & 0 \ 0 & 1 & 0 & 3 & 0 & -1 & 1 & 0 \ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \end{array} right] \ end{align}]
Теперь самое время «поджарить» последний столбец исходной матрицы: вычитаем строку 4 из остальных:
[begin{align} & left[ begin{array}{rrrr|rrrr} 1 & -6 & 0 & -1 & -1 & 0 & 2 & 0 \ 0 & 1 & 0 & 3 & 0 & -1 & 1 & 0 \ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \end{array} right]begin{matrix} +1 \ -3 \ -2 \ uparrow \end{matrix}to \ & to left[ begin{array}{rrrr|rrrr} 1 & -6 & 0 & 0 & -3 & 0 & 4 & -1 \ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \ 0 & 5 & 1 & 0 & 5 & 0 & -5 & 2 \ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \end{array} right] \ end{align}]
Финальный бросок: «выжигаем» второй столбец, вычитая строку 2 из строки 1 и 3:
[begin{align} & left[ begin{array}{rrrr|rrrr} 1 & -6 & 0 & 0 & -3 & 0 & 4 & -1 \ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \ 0 & 5 & 1 & 0 & 5 & 0 & -5 & 2 \ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \end{array} right]begin{matrix} 6 \ updownarrow \ -5 \ \end{matrix}to \ & to left[ begin{array}{rrrr|rrrr} 1 & 0 & 0 & 0 & 33 & -6 & -26 & -17 \ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \ 0 & 0 & 1 & 0 & -25 & 5 & 20 & -13 \ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \end{array} right] \ end{align}]
И снова слева единичная матрица, значит справа — обратная.:)
Ответ. $left[ begin{matrix} 33 & -6 & -26 & 17 \ 6 & -1 & -5 & 3 \ -25 & 5 & 20 & -13 \ -2 & 0 & 2 & -1 \end{matrix} right]$
Ну вот и всё. Проверку сделайте сами — мне в лом.:)
Смотрите также:
- Определитель
- Дополнительные соображения
- Тест к уроку «Площади многоугольников на координатной сетке» (легкий)
- Четырехугольная пирамида в задаче C2
- Задача B5: площадь кольца
- Случай четырехугольной пирамиды

Исходная матрица:
Где:
Обозначение
См. также
- Обратная матрица
- Алгебраическое дополнение
- Линейная алгебра
Литература
- Гантмахер Ф. Р. Теория матриц. — 2-е изд. — М.: Наука, 1966.
), для которой выполняется условие:
В случае если входная матрица a не является квадратной или вычисление обратной матрицы невозможно, то вызывается исключение LinAlgError.
Параметры: a — массив NumPy или подобнй массиву объект. Это может быть толко «квадратный» двумерный массив, т.е. квадратная матрица. Если это многомерный массив, то две его последние оси должны быть равны, в этом случае он рассматривается как массив матриц и обратная матрица вычисляется отдельно для каждой из них. Возвращает: результат — массив NumPy Обратная матрица или массив обратных матриц.
Примеры
Мы можем проверить правильность результата, опираясь на основное свойство обратной матрицы, т.е. np.dot(a, ainv) = np.dot(ainv, a) = np.eye(a.shape[0])
Понятие обратной матрицы может быть обобщено и для матриц над полем комплексных чисел:
Линейная алгебра на Python. [Урок 5]. Обратная матрица и ранг матрицы
Обратной матрицей A -1 матрицы A называют матрицу, удовлетворяющую следующему равенству:
где – E это единичная матрица.
Для того, чтобы у квадратной матрицы A была обратная матрица необходимо и достаточно чтобы определитель |A| был не равен нулю. Введем понятие союзной матрицы . Союзная матрица A* строится на базе исходной A путем замены всех элементов матрицы A на их алгебраические дополнения.
Союзная ей матрица A*:
Транспонируя матрицу A*, мы получим так называемую присоединенную матрицу A* T :
Теперь, зная как вычислять определитель и присоединенную матрицу, мы можем определить матрицу A -1 , обратную матрице A:
Пример вычисления обратной матрицы. Пусть дана исходная матрица A, следующего вида:
Для начала найдем определитель матрицы A:
Как видно из приведенных вычислений, определитель матрицы не равен нулю, значит у матрицы A есть обратная.
Союзная матрица будет иметь следующий вид:
Присоединенная матрица получается из союзной путем транспонирования:
Находим обратную матрицу:
➤ Пример на Python
Решим задачу определения обратной матрицы на Python. Для получения обратной матрицы будем использовать функцию inv():
Рассмотрим свойства обратной матрицы.
Свойство 1 . Обратная матрица обратной матрицы есть исходная матрица:
➤Пример на Python
Свойство 2 . Обратная матрица транспонированной матрицы равна транспонированной матрице от обратной матрицы:
➤ Пример на Python
Свойство 3 . Обратная матрица произведения матриц равна произведению обратных матриц:
➤ Пример на Python
Ранг матрицы
Ранг матрицы является еще одной важной численной характеристикой.
Вычислим ранг матрицы с помощью Python. Создадим единичную матрицу:
Ранг такой матрицы равен количеству ее столбцов (или строк), в нашем случае ранг будет равен четырем, для его вычисления на Python воспользуемся функцией matrix_rank():
Если мы приравняем элемент в нижнем правом углу к нулю, то ранг станет равен трем:
P.S.
Вводные уроки по “Линейной алгебре на Python” вы можете найти соответствующей странице нашего сайта . Все уроки по этой теме собраны в книге “Линейная алгебра на Python”.
Если вам интересна тема анализа данных, то мы рекомендуем ознакомиться с библиотекой Pandas.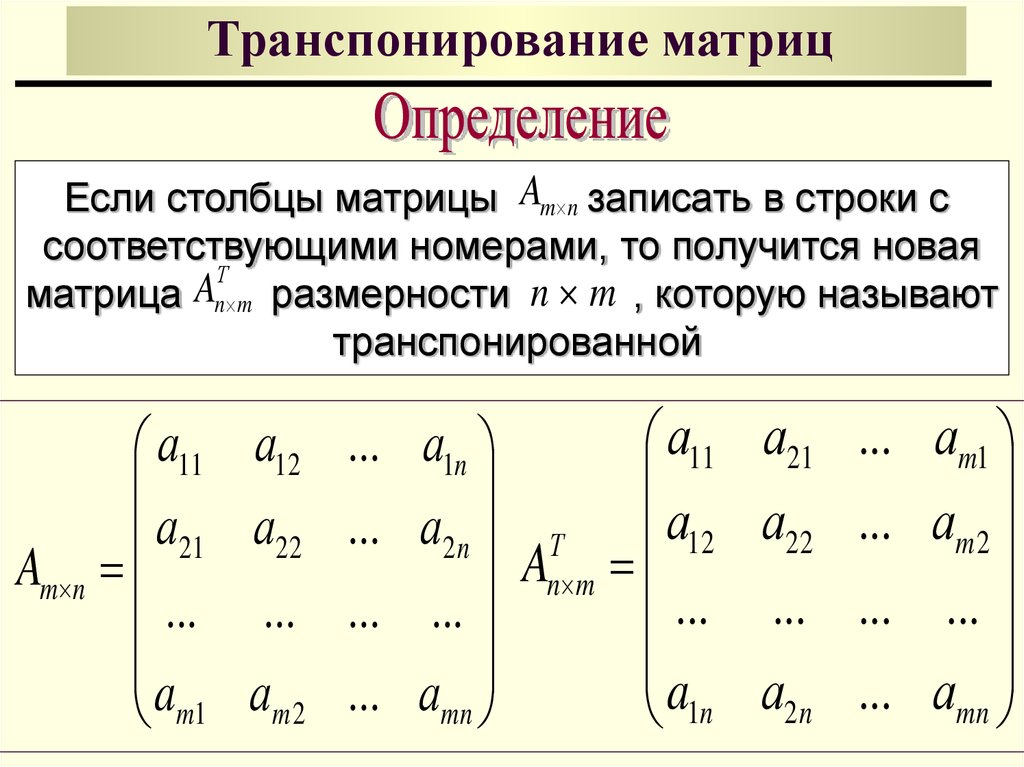
Линейная алгебра на Python. [Урок 5]. Обратная матрица и ранг матрицы : 1 комментарий
i want that help me
1) написать программу вычисляющую обратную матрицу
Работа с Matrix в Python
Для работы с Matrix Python нам необходимо импортировать модуль numpy. Матрица используется для операций с матрицей, которая может использоваться для научных целей, обработки изображений и т.д.
Как создать матрицу?
Согласно Википедии, матрица – это прямоугольный массив чисел, символов или выражений, упорядоченный по строкам и столбцам. Итак, в следующем коде мы будем инициализировать различные типы матриц.
Обычно матрица создается с помощью функции numpy.matix(). Мы можем использовать numpy.shape, чтобы узнать размер матрицы. Смотрите следующий пример кода матрицы.
Вы получите результат, как на следующем изображении.
Добавление матрицы
Код для сложения матриц достаточно сложен для написания вручную. Благодаря модулю numpy мы можем просто использовать оператор + для добавления матрицы. Итак, в следующем примере кода мы увидим, как писать код сложения вручную, а также с помощью оператора +.
Умножение и транспонирование матриц, обратная матрица
В предыдущем разделе мы обсудили преимущество Python Matrix в том, что он просто упрощает для нас задачу. Таким образом, мы можем просто умножить две матрицы, получить инверсию и транспонирование матрицы.
Как мы видели ранее, оператор + добавляет две матрицы, здесь мы можем просто использовать оператор * для умножения матриц. При этом количество столбцов в первой матрице должно быть равно количеству строк во второй матрице.
Мы можем получить инверсию матрицы, используя функцию getI() и использовать getT() для транспонирования матрицы. Давайте посмотрим на пример:
Поскольку мы использовали случайные значения. Таким образом, элементы матрицы будут разными.
«Обратная матрица» для студентов 2 курса СПО
Дисциплина – «Элементы высшей математики»
Курс -2
Практическая работа
Тема: «Обратная матрица»
Цель: формирование умений вычислять обратные матрицы;
закрепление умений вычислять определители второго и третьего порядков, составлять и вычислять алгебраические дополнения к элементам матрицы.
формирование общих компетенций, включающими в себя способность:
ОК 2. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.
ОК 3. Принимать решения в стандартных и нестандартных ситуациях.
ОК 6. Работать в коллективе и в команде, эффективно общаться с коллегами, руководством, потребителями.
Методические указания и теоретические сведения к практической работе
Алгоритм вычисления обратной матрицы с помощью алгебраических дополнений: метод присоединённой (союзной) матрицы.
А зачем нужно искать обратную матрицу?
Ели обратная матрица известна, то решение системы уравнений сводится к операции простого умножения матриц. При программировании задач 3D-графики и компьютерных игр обратные матрицы также находят широкое применение.
Матрица называется обратной по отношению к квадратной матрице A, если выполнено условие , где E – единичная матрица, порядок которой равен порядку матрицы A.
Невырожденная матрица – матрица, определитель которой не равен нулю. Вырожденная матрица – матрица, определитель которой равен нулю.
Обратная матрица существует тогда и только тогда, когда матрица A – невырожденная.
Метод присоединённой (союзной) матрицы
Пусть задана матрица An×n. Для того, чтобы найти обратную матрицу A−1, требуется осуществить три шага:
Найти определитель матрицы A и убедиться, что ΔA≠0, т.е. что матрица А – невырожденная.
Составить алгебраические дополнения каждого элемента матрицы A и записать матрицу из найденных алгебраических дополнений.
Записать обратную матрицу по формуле
Матрица называется присоединённой (взаимной, союзной) к матрице A.
Союзной или присоединенной к матрице A называют матрицу , которая получается из матрицы A, если все ее элементы заменить соответствующими алгебраическими дополнениями и к полученной матрице применить операцию транспонирования. (Присоединенная матрица – это транспонированная матрица, составленная из алгебраических дополнений к элементам данной матрицы)
Пример 1.
Найти обратную матрицу к матрице
Решение. Вычисляем определитель матрицы:
Так как определитель не равен нулю, то матрица имеет обратную. Обратная матрица к матрице находится по формуле:
Найдем (присоединенную) союзную матрицу , для этого вычислим алгебраические дополнения к элементам матрицы :
Таким образом, – матрица, составленная из алгебраических дополнений к элементам матрицы .
Транспонируем эту матрицу (т.е. строки матрицы делаем столбцами с тем же номером), поучим присоединенную (союзную)матрицу :
Итак, ,
Ответ:
Дисциплина – «Элементы высшей математики»
Курс -2
Практическая работа
Тема: «Обратная матрица»
Задание 1.
Задание 2. Выполните проверку для задания 1.
Указание. Используйте формулу:
Задание 3. Докажите равенство для матриц из задания 1.
Задание 4. Определите, при каких x значениях существует матрица, обратная данной:
а)
; б) .
Задание 5. Показать, что матрица А является обратной для матрицы В, если:
а)
а) , .
б) .
Задание 6. Найти , если: а) ; б) /
Задание 7. Выполните проверку для матриц из задания 6.
Отчет о практической работе
1.Тема практической работы
2.Цель практической работы
3.
В ходе выполнения практической работы я научился (закрепил умения) вычислять…
Я получил (совершенствовал) практические навыки…
4.Знания
5.Выводы
Мне было сложно выполнять…, потому, что…
Мне было несложно выполнять…, потому, что…
Теоретические вопросы
1.Вырожденные и невырожденные матрицы
2.Присоединенная (союзная) матрица
3.Обратная матрица
4.Алгоритм нахождения обратной матрицы
Опубликовано 23.06.18 в 09:47 в группе «УРОК.РФ: группа для участников конкурсов»
обратная матрица.py · GitHub
| a=[[7,2,0],[3,1,0],[1,1,1]] | |
| b=[[0,2,3],[1,0,-2],[3,1,1]] | |
| # !/usr/bin/python | |
| # -*- coding: CP866 -*- | |
| # Нахождение обратной матрицы, и Детерминанта, примеры на Python | |
| import math # подключаем модуль математических функций | |
| def determinant(dim, data): # функция вычисления детерминанты | |
| if dim == 0: | |
| det = 0 | |
| if dim == 1: | |
| det = data[0] | |
| if dim == 2: | |
| det = data[0] * data[3] — data[2] * data[1] | |
| if dim == 3: | |
| det = data[0] * data[4] * data[8] + data[1] * data[5] * data[6] + data[2] * data[3] * data[7] — data[6] * data[ | |
| 4] * data[2] — data[7] * data[5] * data[0] — data[8] * data[3] * data[1] | |
| if dim > 3: | |
| det = 0 | |
| i = 0 | |
| for j in range(dim): | |
| det += data[i * dim + j] * cofactor(dim, data, i, j) | |
| return det | |
| def minor(dim, data, i, j): | |
| new_matrix = [] | |
| for k in range(dim * dim): | |
if (math. floor(k / dim) != i and k % dim != j): floor(k / dim) != i and k % dim != j): |
|
| new_matrix.append(data[k]) | |
| return determinant(dim — 1, new_matrix) | |
| def cofactor(dim, data, i, j): # функция вычисления кофактора | |
| return math.pow(-1, i + j) * minor(dim, data, i, j) | |
| def cofactor_matrix(dim, data): # функция вычисления кофакторной матрицы | |
| new_matrix = [] | |
| for i in range(dim): | |
| for j in range(dim): | |
new_matrix. append(cofactor(dim, data, i, j)) append(cofactor(dim, data, i, j)) |
|
| return new_matrix | |
| def transpose_matrix(dim, data):#транспонирование | |
| new_matrix = [] | |
| for i in range(dim): | |
| for j in range(dim): | |
| new_matrix.append(data[j * dim + i]) | |
| return new_matrix | |
| def adjoint_matrix(dim, data):#союзная матрица | |
| return transpose_matrix(dim, cofactor_matrix(dim, data)) | |
| matix = [[2, 2, 1, 2, 5], [1, 3, 3, 1, 3], [1, 2, 2, 1, 3], [4, 2, 2, 3, 8], [1, 5, 2, 1, 1]] # Пример матрицы | |
| matix = a | |
| data = [] # создаем пустую матрицу | |
| for i in range(len(matix)): # создаем счетчик итераций на основе размера матрицы matix | |
| for j in range(len(matix)): # создаем счетчик итераций на основе размера матрицы matix | |
| data = data + [matix[i][j]] # переводим квадратную матрицу matix в плоскую | |
| dim = len(matix) # размер матрицы | |
| dim2 = dim * dim # находим квадрат | |
| det = determinant(dim, data) # находим детерминанту | |
| print( | |
| ‘Детерминант: |A| =: ‘, det # | |
| ) | |
| print() | |
| print( | |
| ‘Обратная матрица : ‘) | |
| print() | |
| if det != 0: # если матрица имеет детерминант не равный нулю | |
| adj_matrix = adjoint_matrix(dim, data) # находим значение строк матрицы | |
| for n in range(dim2): # создаем счетчик итерации | |
| cs = int((adj_matrix[n]) / det) # находим значение ячейки матрицы | |
| if cs < 0: # условие при котором значение меньше нуля | |
| pr = » » # 3 пробела для форматирования | |
| else: # иначе | |
| pr = » » # 4 пробела для форматирования | |
| g = pr + str(cs) + » » # конкатинация пробелов и значения ячейки матрицы | |
| print( | |
| g), # выводим значение переменной g | |
| if (n % dim == dim — 1): # | |
| print () # пустая строка | |
| else: # иначе | |
| print( | |
| ‘Это вырожденная матрица, обратную матрицу найти невозможно’ ) # выводим сообщение о том что матрица вырождена |
Математика — Квадратный корень из матрицы
Поскольку квадратный корень из общей матрицы сложен, мы сначала попробуем несколько более простых случаев:
Корень из диагональной матрицы диагонали равны нулю.
В этом случае результат прост, мы просто берем корни отдельных диагональных членов.
Корень симметричной матрицы
Симметричная матрица – это матрица, члены которой симметричны относительно диагональной оси, то есть элемент x ij имеет то же значение, что и элемент x ji
Для симметричной матрицы мы можно повернуть его, чтобы получить диагональную матрицу, затем взять корень диагональной матрицы, как указано выше, а затем повернуть ее обратно к исходным координатам.
[D] = [Q] -1 [A] [Q]
где:
- [D] = диагональная матрица, диагональные члены являются собственными векторами A
- [A] = Симметричная матрица
- [Q] = Ортогональная матрица, столбцы являются собственными векторами A
- [Q] -1 = инверсия [Q]
Для получения дополнительной информации о диагонализации матриц см. эту страницу.
Таким образом, чтобы найти квадратный корень из [A], мы используем:
√[A] = [Q] √[D] [Q] -1
Пример
Мы хотим найти квадратный корень из:
Программа
Существует ряд программ компьютерной алгебры с открытым исходным кодом.
Я выделил красным цветом пользовательский ввод:
(1) -> m := matrix[[1,0,0],[0,1,0],[0,0,1]]
+1 0 0+
| |
(1) |0 1 0|
| |
+0 0 1+
Тип: Матрица (Целое число)
(2) -> собственные значения (м)
(2) [1]
Тип: Список (Союз (Дробь (Полином (Целое))),
ТакойЧто(Символ,Полином(Целое число))))
(3) -> собственные векторы (м)
+0+ +0+ +1+
| | | | | |
(3) [[eigval= 1,eigmult= 3,eigvec= [|0|,|1|,|0|]]]
| | | | | |
+1+ +0+ +0+
Тип: Список (Запись (eigval: Union (Дробь (Полином (Целое))),
Такой(Символ,Полином(Целое)))),
eigmult: NonNegativeInteger, eigvec:
Список(Матрица(Дробь(Многочлен(Целое))))))
(4) -> собственная матрица (m)
+1 0 0+
| |
(4) |0 1 0|
| |
+0 0 1+
Тип: Union(Matrix(Expression(Integer)),. ..)
(5) ->
..)
(5) ->
Итак, в этом примере
√[A] = [Q] √[D] [Q] -1
, поскольку √1 = ±1
|
Однако этот метод, похоже, не находит других возможных корней, таких как: |
или |
Они также возводятся в соответствие с требуемым значением, как мы можем видеть здесь:
(5) -> a := matrix[[0,0,1],[0,1,0],[1, 0,0]]
+0 0 1+
| |
(5) |0 1 0|
| |
+1 0 0+
Тип: Матрица (Целое число)
(6) -> а*а
+1 0 0+
| |
(6) |0 1 0|
| |
+0 0 1+
Тип: Матрица (Целое число)
(7) ->
Таким образом, в этом случае мы можем переупорядочить собственные векторы, чтобы сформировать другую собственную матрицу, но не все порядки являются корнями, например, это не соответствует требуемому значению:
(7) -> b := матрица [[0,0,1],[1,0,0],[0,1,0]]
+0 0 1+
| |
(7) |1 0 0|
| |
+0 1 0+
Тип: Матрица (Целое число)
(8) -> б*б
+0 1 0+
| |
(8) |0 0 1|
| |
+1 0 0+
Тип: Матрица (Целое число)
(9) ->
Корень общей матрицы
Я еще не придумал, как это сделать.
Оплачивайте счета через Интернет, лично и по телефону
От оплаты автомобиля до оплаты коммунальных услуг и ипотеки — оплата счетов через Western Union выполняется быстро, удобно и надежно, независимо от того, как вы решите платить.
Начать
Пригласи друга!
Вы оба получите электронный подарочный код Amazon.com на 20 долларов * .
Принять условия.
Подробнее
Простые шаги для онлайн-оплаты счетов
1
Зарегистрируйтесь и подтвердите свой бесплатный профиль
Войдите или Зарегистрируйтесь и подтвердите свой бесплатный профиль, чтобы оплачивать счета онлайн. Вы можете подтвердить свой профиль, используя водительские права США, паспорт или удостоверение личности государственного образца.
2
Найдите своего биллера
Найдите своего биллера, введя имя. От вашей ипотеки до счета за воду наша сеть, скорее всего, покроет вас.
3
Заполните обязательные поля
Просто укажите номер своего счета и сумму, которую вы хотите оплатить в счет.
4
Выберите безопасный способ оплаты
Наши услуги по оплате счетов позволяют удобно оплачивать кредитной/дебетовой картой 1 .
5
Готово! Счет оплачен
Мы вышлем вам электронное письмо с подтверждением и контрольным номером денежного перевода (MTCN) вашей транзакции для ваших записей.
Готов оплатить счета?
Начало работы
Дополнительные способы оплаты счетов с помощью Western Union
Оплачивайте счета на ходу
Оплачивайте счета в любое время и в любом месте с помощью приложения Western Union ® .
Загрузите приложение
Произведите платеж лично
Посетите одно из 55 000 отделений агентов в США 2 , чтобы оплатить счет. Начните с приложения, и вы сможете сэкономить время при оплате в магазине — никаких форм для заполнения.
Поиск локаций
Оплатить по телефону
Нужно оплатить счет сейчас? Позвоните по номеру 1-800-634-3422 со своего домашнего или мобильного телефона и оплатите кредитной/дебетовой картой 1 .
Узнать больше
Зарегистрируйтесь, чтобы начать оплачивать счета сегодня
Зарегистрируйтесь сейчас
Быстрая и простая регистрация
Все, что вам нужно, это действующий адрес электронной почты и номер мобильного телефона, чтобы начать оплачивать счета через приложение , на WU.com или лично сегодня.
Отслеживание платежей
Мы предоставляем электронное письмо с подтверждением или квитанцию с номером отслеживания вашей транзакции.
Оплачивайте как вам удобно
Оплачивайте счета с помощью кредитной/дебетовой карты 1 онлайн или наличными в магазине.
Удобное расположение
Оплачивайте счета лично в ближайшем отделении Western Union ® .
Зарегистрируйтесь сейчас
Оплачивайте счета быстро в нашем приложении
Оплачивайте счета или начните оплачивать счета и оплачивайте в магазине.
Отслеживайте свои платежи в режиме реального времени.
Touch ID экономит ваше время благодаря быстрому входу в систему.
Отсканируйте QR-код, чтобы загрузить приложение WU.
Рейтинг на 15 сентября 2020 г.
Часто задаваемые вопросы об оплате счетов с помощью Western Union
Как оплачивать счета с помощью приложения Western Union ® ?
1. Если у вас уже есть приложение Western Union ® , войдите в систему, используя Touch ID или свои учетные данные. Если у вас еще нет нашего приложения, просто загрузите его в Apple App Store или Google Play Store. Новые пользователи могут выполнить шаги, чтобы зарегистрировать профиль с вашим адресом электронной почты. Вы можете подтвердить свой профиль, используя водительские права, паспорт или удостоверение личности государственного образца.
2. Когда вы войдете в наше приложение, выберите «Оплатить счета» и найдите своего биллера, введя его имя.
3. Укажите номер своего счета и сумму, которую вы хотите оплатить по счету.
4. Введите данные своей кредитной/дебетовой карты1.
5. Мы отправим вам электронное письмо с подтверждением и контрольным номером денежного перевода (MTCN) вашей транзакции для вашего учета.
Скачать приложение
Как оплачивать счета лично?
1. Найдите ближайшее отделение Western Union®.
2. Подойдите прямо к стойке и сообщите свой номер телефона, название компании, которую вы хотите оплатить, и номер вашего счета.
3. Оплата наличными или дебетовой картой, выпущенной банком США.
4. Мы отправим вам электронное письмо с подтверждением и контрольным номером денежного перевода (MTCN) вашей транзакции для вашего учета.
Ближайшее отделение Western Union®
Как оплачивать счета по телефону?
1. Позвоните по номеру 1-800-634-3422 (для испанского языка 1-800-325-4045) со своего домашнего или мобильного телефона.
2. Следуйте инструкциям по оплате по телефону. Вам понадобится номер счета, указанный в выписке по счету.
3. Оплатите счет кредитной/дебетовой картой1, выпущенной банком в США.
4. Мы предоставим вам номер для отслеживания (MTCN). Сохраните это как подтверждение платежа.
Остались вопросы?
Свяжитесь с нашей службой поддержки клиентов или посетите нашу страницу часто задаваемых вопросов для получения дополнительной информации.
1 Если вы используете кредитную карту, может взиматься комиссия эмитента карты за выдачу наличных и соответствующие проценты. Чтобы избежать этих комиссий или снизить комиссию, используйте дебетовую карту или проверьте другие способы оплаты.
2 Данные сети по состоянию на 30 июня 2020 г.
* Применяются положения и условия. Применяются ограничения, см. amazon.com/gc-legal
Ассоциативные свойства матриц
Горячая математика
Ассоциативное свойство сложения матриц.
состояния
:
Позволять
А
,
Б
а также
С
быть
м
×
н
матрицы
. Затем,
(
А
+
Б
)
+
С
знак равно
А
+
(
Б
+
С
)
.
Пример 1:
А
знак равно
[
3
2
4
−
1
0
−
5
]
,
Б
знак равно
[
−
2
3
−
1
4
2
0
]
,
С
знак равно
[
8
−
1
5
6
1
2
]
Находить
(
А
+
Б
)
+
С
а также
А
+
(
Б
+
С
)
Находить
(
А
+
Б
)
+
С
:
(
[
3
2
4
−
1
0
−
5
]
+
[
−
2
3
−
1
4
2
0
]
)
+
[
8
−
1
5
6
1
2
]
знак равно
[
1
5
3
3
2
−
5
]
+
[
8
−
1
5
6
1
2
]
знак равно
[
94
8
9
3
−
3
]
Находить
А
+
(
Б
+
С
)
:
[
3
2
4
−
1
0
−
5
]
+
(
[
−
2
3
−
1
4
2
0
]
+
[
8
−
1
5
6
1
2
]
)
знак равно
[
3
2
4
−
1
0
−
5
]
+
[
6
2
4
10
3
2
]
знак равно
[
94
8
9
3
−
3
]
Ассоциативное свойство умножения матриц
состояния:
Позволять
А
,
Б
а также
С
быть
н
×
н
матрицы.
(
А
Б
)
С
знак равно
А
(
Б
С
)
.
Пример 2:
А
знак равно
[
3
2
−
1
0
]
,
Б
знак равно
[
−
2
3
4
2
]
,
С
знак равно
[
−
1
5
1
2
]
Находить
(
А
Б
)
С
а также
А
(
Б
С
)
.
п.4. Союзная матрица.
Пусть дана квадратная матрица
– го порядка. Для каждого ее элемента
найдем его алгебраическое дополнение
и составим матрицу

стоит его алгебраическое дополнение
.
Определение. Матрица называется присоединенной по отношению к матрице А.
Транспонируем присоединенную матрицу: 
Определение. Матрица называется союзной или взаимной.
Обозначение. Союзную матрицу часто обозначают А*. Таким образом, .
Следующее утверждение носит вспомогательный характер и мы принимаем его без доказательства.
Лемма. Определитель произведения квадратных матриц равен произведению их определителей.
.
Теорема. (Необходимые и достаточные условия существования обратной матрицы.)
1. Для того, чтобы квадратная матрица была обратимой необходимо и достаточно, чтобы ее определитель был не равен нулю.
2. Обратная матрица может быть найдена по формуле:

Доказательство. а) Пусть А обратимая матрица, т.е. существует обратная к ней . Тогда
.
С одной стороны, в силу леммы,
,
а с другой стороны,
.
Получаем,
,
откуда и следует, что .
В частности, из последнего равенства следует, что
.
б) Пусть .
Из формул (6) и (7) предыдущей теоремы сразу же следует матричное равенство: .
Или в развернутом виде:

Теорема доказана.





























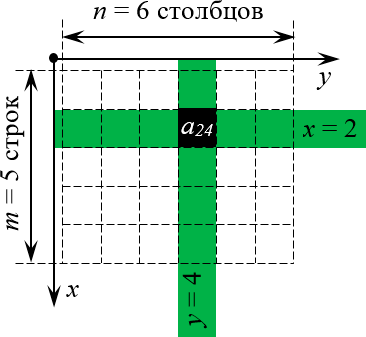




 ..)
(5) ->
..)
(5) ->