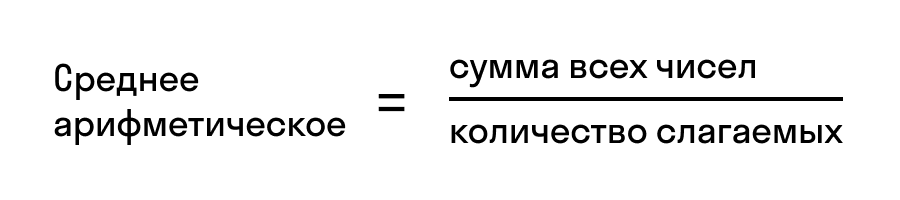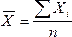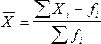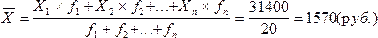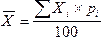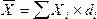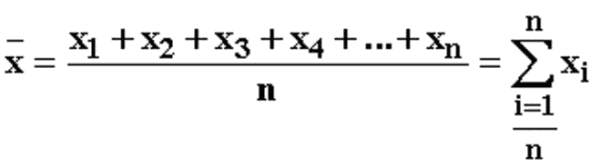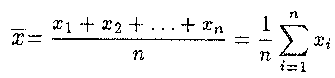Как пишется среднее значение как обозначаются

From Wikipedia, the free encyclopedia

For broader coverage of this topic, see Mean.

In mathematics and statistics, the arithmetic mean ( arr-ith-MET-ik), arithmetic average, or just the mean or average (when the context is clear), is the sum of a collection of numbers divided by the count of numbers in the collection.^[1] The collection is often a set of results from an experiment, an observational study, or a survey. The term «arithmetic mean» is preferred in some mathematics and statistics contexts because it helps distinguish it from other types of means, such as geometric and harmonic.

In addition to mathematics and statistics, the arithmetic mean is frequently used in economics, anthropology, history, and almost every academic field to some extent. For example, per capita income is the arithmetic average income of a nation’s population.

While the arithmetic mean is often used to report central tendencies, it is not a robust statistic: it is greatly influenced by outliers (values much larger or smaller than most others). For skewed distributions, such as the distribution of income for which a few people’s incomes are substantially higher than most people’s, the arithmetic mean may not coincide with one’s notion of «middle». In that case, robust statistics, such as the median, may provide a better description of central tendency.

Definition[edit]

Given a data set ${displaystyle X={x_{1},ldots ,x_{n}}}$ , the arithmetic mean (also mean or average), denoted (read bar), is the mean of the values $x_{1},ldots ,x_{n}$ .^[2]

The arithmetic mean is a data set’s most commonly used and readily understood measure of central tendency. In statistics, the term average refers to any measurement of central tendency. The arithmetic mean of a set of observed data is equal to the sum of the numerical values of each observation, divided by the total number of observations. Symbolically, for a data set consisting of the values , the arithmetic mean is defined by the formula:

${displaystyle {bar {x}}={frac {1}{n}}left(sum _{i=1}^{n}{x_{i}}right)={frac {x_{1}+x_{2}+dots +x_{n}}{n}}}$

^[3]

(For an explanation of the summation operator, see summation.)

For example, if the monthly salaries of employees are , then the arithmetic mean is:

${displaystyle {frac {2500+2700+2400+2300+2550+2650+2750+2450+2600+2400}{10}}=2530}$

If the data set is a statistical population (i.e., consists of every possible observation and not just a subset of them), then the mean of that population is called the population mean and denoted by the Greek letter . If the data set is a statistical sample (a subset of the population), it is called the sample mean (which for a data set is denoted as ).

The arithmetic mean can be similarly defined for vectors in multiple dimensions, not only scalar values; this is often referred to as a centroid. More generally, because the arithmetic mean is a convex combination (meaning its coefficients sum to ), it can be defined on a convex space, not only a vector space.

Motivating properties[edit]

The arithmetic mean has several properties that make it interesting, especially as a measure of central tendency. These include:

The arithmetic mean is independent of scale of the units of measurement, in the sense that ${displaystyle {text{avg}}(ca_{1},cdots ,ca_{n})=ccdot {text{avg}}(a_{1},cdots ,a_{n}).}$ So, for example, calculating a mean of liters and then converting to gallons is the same as converting to gallons first and then calculating the mean. This is also called first order homogeneity.

Additional properties[edit]

The arithmetic mean of a sample is always between the largest and smallest values in that sample.
The arithmetic mean of any amount of equal-sized number groups together is the arithmetic mean of the arithmetic means of each group.

Contrast with median[edit]

The arithmetic mean may be contrasted with the median. The median is defined such that no more than half the values are larger, and no more than half are smaller than it. If elements in the data increase arithmetically when placed in some order, then the median and arithmetic average are equal. For example, consider the data sample . The mean is 2.5 , as is the median. However, when we consider a sample that cannot be arranged to increase arithmetically, such as , the median and arithmetic average can differ significantly. In this case, the arithmetic average is , while the median is . The average value can vary considerably from most values in the sample and can be larger or smaller than most.

There are applications of this phenomenon in many fields. For example, since the 1980s, the median income in the United States has increased more slowly than the arithmetic average of income.^[4]

Generalizations[edit]

Weighted average[edit]

A weighted average, or weighted mean, is an average in which some data points count more heavily than others in that they are given more weight in the calculation.^[5] For example, the arithmetic mean of and is ${displaystyle {frac {3+5}{2}}=4}$ , or equivalently ${displaystyle 3{frac {1}{2}}+5{frac {1}{2}}=4}$ . In contrast, a weighted mean in which the first number receives, for example, twice as much weight as the second (perhaps because it is assumed to appear twice as often in the general population from which these numbers were sampled) would be calculated as ${displaystyle 3{frac {2}{3}}+5{frac {1}{3}}={frac {11}{3}}}$ . Here the weights, which necessarily sum to one, are ${frac {2}{3}}$ and ${frac {1}{3}}$ , the former being twice the latter. The arithmetic mean (sometimes called the «unweighted average» or «equally weighted average») can be interpreted as a special case of a weighted average in which all weights are equal to the same number ( ${frac {1}{2}}$ in the above example and ${frac {1}{n}}$ in a situation with numbers being averaged).

Continuous probability distributions[edit]

If a numerical property, and any sample of data from it, can take on any value from a continuous range instead of, for example, just integers, then the probability of a number falling into some range of possible values can be described by integrating a continuous probability distribution across this range, even when the naive probability for a sample number taking one certain value from infinitely many is zero. In this context, the analog of a weighted average, in which there are infinitely many possibilities for the precise value of the variable in each range, is called the mean of the probability distribution. The most widely encountered probability distribution is called the normal distribution; it has the property that all measures of its central tendency, including not just the mean but also the median mentioned above and the mode (the three Ms^[6]), are equal. This equality does not hold for other probability distributions, as illustrated for the log-normal distribution here.

Angles[edit]

Particular care is needed when using cyclic data, such as phases or angles. Taking the arithmetic mean of 1° and 359° yields a result of 180°.
This is incorrect for two reasons:

In general application, such an oversight will lead to the average value artificially moving towards the middle of the numerical range. A solution to this problem is to use the optimization formulation (that is, define the mean as the central point: the point about which one has the lowest dispersion) and redefine the difference as a modular distance (i.e., the distance on the circle: so the modular distance between 1° and 359° is 2°, not 358°).

Symbols and encoding[edit]

The arithmetic mean is often denoted by a bar (vinculum or macron), as in .^[2]

Some software (text processors, web browsers) may not display the «x̄» symbol correctly. For example, the HTML symbol «x̄» combines two codes — the base letter «x» plus a code for the line above (̄ or ¯).^[7]

In some document formats (such as PDF), the symbol may be replaced by a «¢» (cent) symbol when copied to a text processor such as Microsoft Word.

References[edit]

^ Jacobs, Harold R. (1994). Mathematics: A Human Endeavor (Third ed.). W. H. Freeman. p. 547. ISBN 0-7167-2426-X.
^ ^a ^b ^c Medhi, Jyotiprasad (1992). Statistical Methods: An Introductory Text. New Age International. pp. 53–58. ISBN 9788122404197.
^ Weisstein, Eric W. «Arithmetic Mean». mathworld.wolfram.com. Retrieved 21 August 2020.
^ Krugman, Paul (4 June 2014) [Fall 1992]. «The Rich, the Right, and the Facts: Deconstructing the Income Distribution Debate». The American Prospect.
^ «Mean | mathematics». Encyclopedia Britannica. Retrieved 21 August 2020.
^ Thinkmap Visual Thesaurus (30 June 2010). «The Three M’s of Statistics: Mode, Median, Mean June 30, 2010». www.visualthesaurus.com. Retrieved 3 December 2018.
^ «Notes on Unicode for Stat Symbols». www.personal.psu.edu. Retrieved 14 October 2018.
^ If AC = a and BC = b. OC = AM of a and b, and radius r = QO = OG.
Using Pythagoras’ theorem, QC² = QO² + OC² ∴ QC = √QO² + OC² = QM.
Using Pythagoras’ theorem, OC² = OG² + GC² ∴ GC = √OC² − OG² = GM.
Using similar triangles, HC/GC = GC/OC ∴ HC = GC²/OC = HM.

External links[edit]

Calculations and comparisons between arithmetic mean and geometric mean of two numbers
Calculate the arithmetic mean of a series of numbers on fxSolver

Источник

From Wikipedia, the free encyclopedia

For broader coverage of this topic, see Mean.

Definition[edit]

Given a data set ${displaystyle X={x_{1},ldots ,x_{n}}}$ , the arithmetic mean (also mean or average), denoted (read bar), is the mean of the values $x_{1},ldots ,x_{n}$ .^[2]

${displaystyle {bar {x}}={frac {1}{n}}left(sum _{i=1}^{n}{x_{i}}right)={frac {x_{1}+x_{2}+dots +x_{n}}{n}}}$

^[3]

(For an explanation of the summation operator, see summation.)

For example, if the monthly salaries of employees are , then the arithmetic mean is:

${displaystyle {frac {2500+2700+2400+2300+2550+2650+2750+2450+2600+2400}{10}}=2530}$

Motivating properties[edit]

The arithmetic mean has several properties that make it interesting, especially as a measure of central tendency. These include:

The arithmetic mean is independent of scale of the units of measurement, in the sense that ${displaystyle {text{avg}}(ca_{1},cdots ,ca_{n})=ccdot {text{avg}}(a_{1},cdots ,a_{n}).}$ So, for example, calculating a mean of liters and then converting to gallons is the same as converting to gallons first and then calculating the mean. This is also called first order homogeneity.

Additional properties[edit]

The arithmetic mean of a sample is always between the largest and smallest values in that sample.
The arithmetic mean of any amount of equal-sized number groups together is the arithmetic mean of the arithmetic means of each group.

Contrast with median[edit]

There are applications of this phenomenon in many fields. For example, since the 1980s, the median income in the United States has increased more slowly than the arithmetic average of income.^[4]

Generalizations[edit]

Weighted average[edit]

Continuous probability distributions[edit]

Angles[edit]

Particular care is needed when using cyclic data, such as phases or angles. Taking the arithmetic mean of 1° and 359° yields a result of 180°.
This is incorrect for two reasons:

Symbols and encoding[edit]

The arithmetic mean is often denoted by a bar (vinculum or macron), as in .^[2]

In some document formats (such as PDF), the symbol may be replaced by a «¢» (cent) symbol when copied to a text processor such as Microsoft Word.

References[edit]

^ Jacobs, Harold R. (1994). Mathematics: A Human Endeavor (Third ed.). W. H. Freeman. p. 547. ISBN 0-7167-2426-X.
^ ^a ^b ^c Medhi, Jyotiprasad (1992). Statistical Methods: An Introductory Text. New Age International. pp. 53–58. ISBN 9788122404197.
^ Weisstein, Eric W. «Arithmetic Mean». mathworld.wolfram.com. Retrieved 21 August 2020.
^ Krugman, Paul (4 June 2014) [Fall 1992]. «The Rich, the Right, and the Facts: Deconstructing the Income Distribution Debate». The American Prospect.
^ «Mean | mathematics». Encyclopedia Britannica. Retrieved 21 August 2020.
^ Thinkmap Visual Thesaurus (30 June 2010). «The Three M’s of Statistics: Mode, Median, Mean June 30, 2010». www.visualthesaurus.com. Retrieved 3 December 2018.
^ «Notes on Unicode for Stat Symbols». www.personal.psu.edu. Retrieved 14 October 2018.
^ If AC = a and BC = b. OC = AM of a and b, and radius r = QO = OG.
Using Pythagoras’ theorem, QC² = QO² + OC² ∴ QC = √QO² + OC² = QM.
Using Pythagoras’ theorem, OC² = OG² + GC² ∴ GC = √OC² − OG² = GM.
Using similar triangles, HC/GC = GC/OC ∴ HC = GC²/OC = HM.

External links[edit]

Calculations and comparisons between arithmetic mean and geometric mean of two numbers
Calculate the arithmetic mean of a series of numbers on fxSolver

Источник

Среднее арифметическое

В математике и статистике, среднее арифметическое (, ударение на первом и третьем слогах слова «арифметика»), или просто среднее или среднее (когда контекст ясно), представляет собой сумму набора чисел, деленную на количество чисел в коллекции. Коллекция часто представляет собой набор результатов эксперимента или наблюдательного исследования, или часто набор результатов опроса. Термин «среднее арифметическое» предпочтительнее в некоторых контекстах математики и статистики, поскольку он помогает отличить его от других средств, таких как среднее геометрическое и среднее гармоническое.

Помимо математики и статистики, среднее арифметическое часто используется во многих различных областях, таких как экономика, антропология и история, и оно используется в в той или иной степени почти во всех академических областях. Например, доход на душу населения — это средний арифметический доход населения страны.

Хотя среднее арифметическое часто используется для сообщения основных тенденций, это не надежная статистика, а это означает, что на него сильно влияют выбросы (значения, которые намного больше или меньше большинства значений). Примечательно, что для асимметричных распределений, таких как распределение доходов, для которого доходы нескольких людей существенно больше, чем у большинства людей, среднее арифметическое может не совпадать с понятием «среднего», а надежная статистика, такая как медиана, может лучше описать центральную тенденцию.

Содержание

1 Определение
2 Мотивирующие свойства
3 Контраст с медианой
4 Обобщения
- 4.1 Средневзвешенное значение
- 4.2 Непрерывное распределение вероятностей
- 4.3 Углы
5 Символы и кодирование
6 См. также
7 Ссылки
8 Дополнительная литература
9 Внешние ссылки

Определение

Учитывая набор данных X = {x 1,…, xn} { displaystyle X = {x_ {1}, ldots, x_ {n} }} ${ displaystyle X = {x_ {1}, ldots, x_ {n} }}$ , среднее арифметическое (или означает или среднее ), обозначается x ¯ { displaystyle { bar {x}}}(читается x { displaystyle x}bar) — это среднее значение n { displaystyle n}значений x 1, x 2,…, xn { displaystyle x_ {1}, x_ {2}, ldots, x_ {n}} $x_ {1}, x_ {2}, ldots, x_ {n}$ .

Среднее арифметическое — это наиболее часто используемый и легко понимаемый показатель центральной тенденции в наборе данных. В статистике термин среднее относится к любому из показателей центральной тенденции. Среднее арифметическое набора наблюдаемых данных определяется как сумма числовых значений каждого и каждого наблюдения, деленная на общее количество наблюдений. Символически, если у нас есть набор данных, состоящий из значений a 1, a 2,…, an { displaystyle a_ {1}, a_ {2}, ldots, a_ {n}} $a_ {1}, a_ {2}, ldots, a_ {n}$ , тогда среднее арифметическое A { displaystyle A}определяется по формуле:

A = 1 n ∑ i = 1 nai = a 1 + a 2 + ⋯ + ann { Displaystyle A = { frac {1} {n}} sum _ {i = 1} ^ {n} a_ {i} = { frac {a_ {1} + a_ {2} + cdots + a_ { n}} {n}}} ${ displaystyle A = { frac {1} { n}} sum _ {i = 1} ^ {n} a_ {i} = { frac {a_ {1} + a_ {2} + cdots + a_ {n}} {n}}}$

(объяснение оператора суммирования см. в разделе суммирование.)

Например, рассмотрим ежемесячную зарплату 10 сотрудников фирмы: 2500, 2700, 2400, 2300, 2550, 2650, 2750, 2450, 2600, 2400. Среднее арифметическое

2500 + 2700 + 2400 + 2300 + 2550 + 2650 + 2750 + 2450 + 2600 + 2400 10 = 2530. { displaystyle { frac {2500 + 2700 + 2400 + 2300 + 2550 + 2650 + 2750 + 2450 + 2600 + 2400} {10}} = 2530.} ${ frac {2500 + 2700 + 2400 + 2300 + 2550 + 2650 + 2750 + 2450 + 2600 + 2400} {10}} = 2530.$

Если набор данных статистическая совокупность (т. Е. Состоит из всех возможных наблюдений, а не только их подмножества), тогда среднее значение этой совокупности называется средним генеральным значением и обозначает редактируется греческой буквой μ { displaystyle mu}. Если набор данных представляет собой статистическую выборку (подмножество генеральной совокупности), то мы называем статистику, полученную в результате этого вычисления, выборочным средним (что для набора данных X { displaystyle X}обозначается как X ¯ { displaystyle { overline {X}}}).

Среднее арифметическое может быть аналогично определено для векторов в нескольких измерениях, а не только для скалярных значений; это часто называют центроидом. В более общем смысле, поскольку среднее арифметическое представляет собой выпуклую комбинацию (сумма коэффициентов равна 1), оно может быть определено на выпуклом пространстве, а не только в векторном пространстве.

Мотивирующие свойства

Среднее арифметическое имеет несколько свойств, которые делают его полезным, особенно в качестве меры центральной тенденции. К ним относятся:

Если числа x 1,…, xn { displaystyle x_ {1}, dotsc, x_ {n}} $x_ { 1}, dotsc, x_ {n}$ имеют среднее значение x ¯ { displaystyle { bar {x}}}, затем (x 1 — x ¯) + ⋯ + (xn — x ¯) = 0 { displaystyle (x_ {1} — { bar {x) }}) + dotsb + (x_ {n} — { bar {x}}) = 0} $(x_ {1} - { bar {x}}) + dotsb + (x_ {n} - { bar {x}}) = 0$ . Поскольку xi — x ¯ { displaystyle x_ {i} — { bar {x}}} $x_ {i} - { bar {x}}$ — это расстояние от заданного числа до среднего значения, один из способов интерпретировать это свойство — сказать что числа слева от среднего уравновешены числами справа от среднего. Среднее — это единственное число, для которого остатки (отклонения от оценки) равны нулю.
Если требуется использовать одно число в качестве «типичного» значения для набор известных чисел x 1,…, xn { displaystyle x_ {1}, dotsc, x_ {n}} $x_ { 1}, dotsc, x_ {n}$ , тогда среднее арифметическое чисел делает это лучше всего в том смысле, что минимизации суммы квадратов отклонений от типичного значения: сумма (xi — x ¯) 2 { displaystyle (x_ {i} — { bar {x}}) ^ {2}} $(x_ {i} - { bar {x}}) ^ {2}$ . (Отсюда следует, что выборочное среднее также является лучшим единственным предиктором в том смысле, что имеет наименьшую среднеквадратическую ошибку.) Если требуется среднее арифметическое совокупности чисел, тогда оценка этого несмещен — среднее арифметическое для выборки, взятой из генеральной совокупности.

Контраст с медианой

Среднее арифметическое может быть противопоставлено медиане. Медиана определяется таким образом, что не более половины значений больше и не более половины меньше медианы. Если элементы в данных увеличиваются арифметически при размещении в некотором порядке, то медиана и среднее арифметическое равны. Например, рассмотрим образец данных 1, 2, 3, 4 { displaystyle {1,2,3,4}}. Среднее значение равно 2,5 { displaystyle 2.5} 2,5 , как и медиана. Однако, когда мы рассматриваем выборку, которую нельзя расположить так, чтобы увеличиваться арифметически, например 1, 2, 4, 8, 16 { displaystyle {1,2,4,8,16}}, медиана и среднее арифметическое могут значительно отличаться. В этом случае среднее арифметическое составляет 6,2, а медиана — 4. В общем, среднее значение может значительно отличаться от большинства значений в выборке и может быть больше или меньше большинства из них.

Это явление можно найти во многих областях. Например, с 1980-х годов средний доход в США увеличивался медленнее, чем среднее арифметическое дохода.

Обобщения

Средневзвешенное значение

Средневзвешенное, или средневзвешенное значение — это среднее значение, в котором одни точки данных имеют больший вес, чем другие, поскольку им придается больший вес в расчетах. Например, среднее арифметическое 3 { displaystyle 3}и 5 { displaystyle 5}равно (3 + 5) 2 = 4 { displaystyle { frac {(3 + 5)} {2}} = 4} ${ frac {(3 + 5)} {2}} = 4$ или, что эквивалентно, (1 2 ⋅ 3) + (1 2 ⋅ 5) = 4 { displaystyle left ({ frac {1} {2}} cdot 3 right) + left ({ frac {1} {2}} cdot 5 right) = 4} $left ({ frac {1} {2}} cdot 3 right) + left ({ frac {1} {2}} cdot 5 right) = 4$ . Напротив, средневзвешенное значение, при котором первое число получает, например, вдвое больший вес, чем второе (возможно, потому, что предполагается, что оно встречается в два раза чаще в генеральной совокупности, из которой были взяты эти числа), будет рассчитываться как (2 3 ⋅ 3) + (1 3 ⋅ 5) = 11 3 { displaystyle left ({ frac {2} {3}} cdot 3 right) + left ({ frac {1} {3}} cdot 5 right) = { frac {11} {3}}} $left ({ frac {2} {3}} cdot 3 right) + left ({ frac {1} {3}} cdot 5 right) = { frac {11} {3}}$ . Здесь веса, которые обязательно составляют единицу, равны (2/3) { displaystyle (2/3)} (2/3) и (1/3) { displaystyle (1 / 3)} (1/3) , причем первое вдвое больше, чем второе. Среднее арифметическое (иногда называемое «невзвешенным средним» или «равновзвешенным средним») можно интерпретировать как частный случай средневзвешенного значения, в котором все веса равны друг другу (равны 1 2 { displaystyle { frac {1} {2}}} ${ frac {1} {2}}$ в приведенном выше примере и равно 1 n { displaystyle { frac {1} {n}}} ${ frac {1 } {n}}$ в ситуации с усредненными числами n { displaystyle n}).

Непрерывные распределения вероятностей

Сравнение двух логнормальных распределений с равной медианной, но разной асимметрией, что приводит к разным означает режимы и

Если числовое свойство и любой образец данных из него может принимать любое значение из непрерывного диапазона, а не, например, только целые числа, то вероятность попадания числа в некоторый диапазон возможных значений может быть описана путем интегрирования непрерывного распределения вероятностей по этому диапазону, даже если наивная вероятность для номера выборки, принимающего одно определенное значение из бесконечного множества, равна нуль. Аналог средневзвешенного значения в этом контексте, в котором существует бесконечное количество возможностей для точного значения переменной в каждом диапазоне, называется средним значением распределения вероятностей. Наиболее распространенное распределение вероятностей называется нормальным распределением ; он обладает тем свойством, что все меры его центральной тенденции, включая не только среднее значение, но также вышеупомянутую медиану и режим (три M), равны друг другу. Это равенство не выполняется для других распределений вероятностей, как показано для логнормального распределения здесь.

Углы

Следует соблюдать особую осторожность при использовании циклических данных, таких как фазы или углы. Наивное взятие среднего арифметического 1 ° и 359 ° дает результат 180 °. Это неверно по двум причинам:

Во-первых, угловые измерения определяются только до аддитивной константы 360 ° (или 2π, если измерения в радианах ). Таким образом, можно было бы так же легко назвать эти 1 ° и -1 ° или 361 ° и 719 °, так как каждый из них дает различное среднее значение.
Во-вторых, в этой ситуации 0 ° (эквивалентно 360 °) геометрически является лучшим средним значением: имеется меньшая дисперсия (точки находятся на расстоянии 1 ° от него и 179 ° от 180 °, предполагаемое среднее значение).

В общем случае такие недосмотр приведет к искусственному смещению среднего значения к середине числового диапазона. Решение этой проблемы состоит в том, чтобы использовать формулировку оптимизации (, а именно, определить среднее значение как центральную точку: точку, относительно которой имеет наименьшую дисперсию), и переопределить разницу как модульное расстояние (т. Е., расстояние по окружности: поэтому модульное расстояние между 1 ° и 359 ° составляет 2 °, а не 358 °).

Доказательство без слов неравенства среднего арифметического и геометрического :. PR — диаметр окружности с центром в O; его радиус AO равен среднему арифметическому значений a и b. Используя теорему о среднем геометрическом, треугольник PGR высота GQ является средним геометрическим. Для любого отношения a: b AO ≥ GQ.

Символы и кодировка

Среднее арифметическое часто обозначается чертой, например, как в x ¯ { displaystyle { bar {x }}}(прочтите x { displaystyle x}bar).

Некоторое программное обеспечение (текстовые процессоры, веб-браузеры ) могут неправильно отображать символ x. Например, символ x̄ в HTML на самом деле представляет собой комбинацию двух кодов — базовой буквы x и кода для вышеприведенной строки (̄ или ¯).

В некоторых текстах такие как pdfs, символ x может быть заменен символом cent (¢) (Unicode ¢) при копировании в текстовый процессор, такой как Microsoft Word.

См. Также

Геометрическое доказательство без слов, что max (a, b)>среднее квадратичное или среднеквадратичное (QM)>среднее арифметическое (AM)>среднее геометрическое (GM)>среднее гармоническое (HM)>мин (a, b) двух положительных чисел a и b

среднее по Фреше
Обобщенное среднее
Среднее геометрическое
Среднее гармоническое
Неравенство средних арифметических и геометрических
Режим
Выборочное среднее и ковариация
Стандартное отклонение
Стандартная ошибка среднего
Суммарная статистика

Ссылки

Дополнительная литература

Huff, Darrell (1993). Как лгать со статистикой. W. W. Norton. ISBN 978-0-393-31072-6.

Внешние ссылки

Расчеты и сравнения между средним арифметическим и средним геометрическим двух чисел
Вычислить среднее арифметическое ряда числа на fxSolver

Источник

У этого термина существуют и другие значения, см. среднее значение.

В математике и статистике сре́днее арифмети́ческое — одна из наиболее распространённых мер центральной тенденции, представляющая собой сумму всех наблюденных значений деленную на их количество.

Предложена (наряду со средним геометрическим и средним гармоническим) еще пифагорейцами ^[1] и является одной из наиболее распространенных мер центральной тенденции.

Частными случаями среднего арифметического являются генеральное среднее ( генеральной совокупности) и выборочное среднее ( выборки).

Содержание

1 Введение
- 1.1 Примеры
- 1.2 Непрерывная случайная величина
2 Некоторые проблемы применения среднего
- 2.1 Отсутствие робастности
- 2.2 Сложный процент
- 2.3 Направления
3 Примечания
4 См. также
5 Ссылки

Введение

Обозначим множество данных X = (x₁, x₂, …, x_n), тогда выборочное среднее обычно обозначается горизонтальной чертой над переменной (, произносится «x с чертой»).

Для обозначения среднего арифметического всей совокупности используется греческая буква μ. Для случайной величины, для которой определено среднее значение, μ есть вероятностное среднее или математическое ожидание случайной величины. Если множество X является совокупностью случайных чисел с вероятностным средним μ, тогда для любой выборки x_i из этой совокупности μ = E{x_i} есть математическое ожидание этой выборки.

На практике разница между μ и в том, что μ является типичной ненаблюдаемой переменной, потому что видеть можно скорее выборку, а не всю генеральную совокупность. Поэтому, если выборку представлять случайным образом (в терминах теории вероятностей), тогда (но не μ) можно трактовать как случайную переменную, имеющую распределение вероятностей на выборке (вероятностное распределение среднего).

Обе эти величины вычисляются одним и тем же способом:

$bar{x} = frac{1}{n}sum_{i=1}^n x_i = frac{1}{n} (x_1+cdots+x_n).$

Если X — случайная переменная, тогда математическое ожидание X можно рассматривать как среднее арифметическое значений в повторяющихся измерениях величины X. Это является проявлением закона больших чисел. Поэтому выборочное среднее используется для оценки неизвестного математического ожидания.

В элементарной алгебре доказано, что среднее n + 1 чисел больше среднего n чисел тогда и только тогда, когда новое число больше чем старое среднее, меньше тогда и только тогда, когда новое число меньше среднего, и не меняется тогда и только тогда, когда новое число равно среднему. Чем больше n, тем меньше различие между новым и старым средними значениями.

Заметим, что имеется несколько других «средних» значений, в том числе среднее степенное, среднее Колмогорова, гармоническое среднее, арифметико-геометрическое среднее и различные средне-взвешенные величины.

Примеры

Для трёх чисел сложим их и поделим на 3:

$frac{x_1 + x_2 + x_3}{3}.$

Для четырёх чисел сложим их и поделим на 4:

$frac{x_1 + x_2 + x_3 + x_4}{4}.$

Непрерывная случайная величина

Для непрерывно распределённой величины f(x) среднее арифметическое на отрезке [a;b] определяется через определённый интеграл:

$overline{f(x)}_{[a;b]} = frac1{b-a} int_{a}^b f(x) dx$

Некоторые проблемы применения среднего

Отсутствие робастности

Хотя среднее арифметическое часто используется в качестве средних значений или центральных тенденций, это понятие не относится к робастной статистике, что означает, что среднее арифметическое подвержено сильному влиянию «больших отклонений». Примечательно, что для распределений с большим коэффициентом асимметрии среднее арифметическое может не соответствовать понятию «среднего», а значения среднего из робастной статистики (например, медиана) может лучше описывать центральную тенденцию.

Классическим примером является подсчёт среднего дохода. Арифметическое среднее может быть неправильно истолковано в качестве медианы, из-за чего может быть сделан вывод, что людей с большим доходом больше, чем на самом деле. «Средний» доход истолковывается таким образом, что доходы большинства людей находятся вблизи этого числа. Этот «средний» (в смысле среднего арифметического) доход является выше, чем доходы большинства людей, так как высокий доход с большим отклонением от среднего делает сильный перекос среднего арифметического (в отличие от этого, средний доход по медиане «сопротивляется» такому перекосу). Однако, этот «средний» доход ничего не говорит о количестве людей вблизи медианного дохода (и не говорит ничего о количестве людей вблизи модального дохода). Тем не менее, если легкомысленно отнестись к понятиям «среднего» и «большинство народа», то можно сделать неверный вывод о том, что большинство людей имеют доходы выше, чем они есть на самом деле. Например, отчёт о «среднем» чистом доходе в Медине, штат Вашингтон, подсчитанный как среднее арифметическое всех ежегодных чистых доходов жителей, даст на удивление большое число из-за Билла Гейтса. Рассмотрим выборку (1, 2, 2, 2, 3, 9). Среднее арифметическое равно 3.17, но пять значений из шести ниже этого среднего.

Сложный процент

Если числа перемножать, а не складывать, нужно использовать среднее геометрическое, а не среднее арифметическое. Наиболее часто этот казус случается при расчёте окупаемости инвестиций в финансах.

Например, если акции в первый год упали на 10 %, а во второй год выросли на 30 %, тогда некорректно вычислять «среднее» увеличение за эти два года как среднее арифметическое (−10 % + 30 %) / 2 = 10 %; правильное среднее значение в этом случае дают совокупные ежегодные темпы роста, по которым годовой рост получается только 8,2 %.

Причина этого в том, что проценты имеют каждый раз новую стартовую точку: 30 % — это 30 % от меньшего числа. Если акции в начале стоили $30 и упали на 10 %, они теперь стоят $27. Если акции выросли на 30 %, они теперь стоят $35.1. Арифметическое среднее этого роста 10 %, но поскольку акции выросли за 2 года на $5.1, средний рост в 8,2 % даёт конечный результат $35.1 [$30 (1 — 10 %) (1 + 30 %) = $30 (1 + 8,2 %) (1 + 8,2 %) = $35.1]. Если же использовать таким же образом среднее арифметическое значение 10 %, мы не получим фактическое увеличение [$30 (1 + 10 %) (1 + 10 %) = $36.3].

В общем, сложный процент даёт 90 % * 130 % = 117 % общий рост, а годовой прирост , то есть 8,2 % в год.

Направления

Основная статья: Статистика направлений

Особую осторожность нужно иметь при расчёте циклических данных, таких как фазы или углы. Наивное вычисление среднего арифметического 1° и 359° даёт результат 180°. Это неверно по двум причинам:

Во-первых, угловые меры определены только до 360° (или 2π, при измерении в радианах). Таким образом, ту же пару можно записать 1° и −1°, или 1° и 719°, но каждая из которых даёт различные средние значения.
Во-вторых, в этой ситуации, 0° (эквивалентно 360°) геометрически лучшее среднее значение: меньше дисперсия (обе точки на 1° от него, и на 179° от 180°, вычисленного среднего).

В целом применение такого рассмотрения средней величины ведёт к искусственному сдвигу его к середине числового диапазона. Решение этой проблемы заключается в использовании оптимальной формализации (а именно, определение среднего в качестве центральной точки, то есть точки, от которой наименьшая дисперсия), а также переопределение вычитания как модульного расстояния (то есть как расстояние от окружности; в частности, модульное расстояние между 1° и 359° — это 2°, а не 358°).

Примечания

↑ Cantrell, David W., «Pythagorean Means» from MathWorld

См. также

Взвешенное среднее
Винсоризованное среднее
Гармоническое среднее
Геометрическое среднее
Медиана
Мода
Среднее Колмогорова
Усеченное среднее
Неравенство между средним арифметическим и средним геометрическим
Неравенство Швейцера

Ссылки

Арифметическая средняя // Энциклопедический словарь Брокгауза и Ефрона: В 86 томах (82 т. и 4 доп.). — СПб., 1890—1907.
Финансовая математика
Прикладная математика

Статистические показатели

Описательная
статистика

Непрерывные
данные

Коэффициент сдвига	Среднее (Арифметическое, Геометрическое, Гармоническое) · Медиана · Мода · Размах
Вариация	Ранг · Среднеквадратическое отклонение · Коэффициент вариации · Квантиль (Дециль, Процентиль/Перцентиль/Центиль)
Моменты	Математическое ожидание · Дисперсия · Асимметрия · Эксцесс

Дискретные
данные

Частота · Таблица контингентности

Статистический
вывод и
проверка
гипотез

Статистический вывод	Доверительный интервал (Частотная вероятность) · Достоверный интервал (Байесовский вывод) · Статистическая значимость · Мета-анализ
Планирование эксперимента	Генеральная совокупность · Планирование выборки · Районированная выборка · Репликация · Группировка · Чувствительность и специфичность
Объём выборки	Статистическая мощность · Мера эффекта · Стандартная ошибка
Общая оценка	Байесовская оценка решения · Метод максимального правдоподобия · Метод моментов нахождения оценок · Оценка минимального расстояния · Оценка максимального интервала
Статистические критерии	Z-тест · t-критерий Стьюдента · Критерий Фишера · Критерий Пирсона (Хи-квадрат) · Критерий согласия Колмогорова · Тест Вальда · U-критерий Манна — Уитни · Критерий Уилкоксона · Критерий Краскела — Уоллиса · Критерий Кохрена · Критерий Лиллиефорса
Анализ выживания	Функция выживания · Оценка Каплана — Мейера · Логранк-тест · Интенсивность отказов · Пропорциональная модель опасностей

Корреляция

Коэффициент корреляции Пирсона · Ранг корреляций (Коэффициент Спирмана для ранга корреляций, Коэффициент тау Кендалла для ранга корреляций) · Переменная смешивания

Линейные модели

Основная линейная модель · Обобщённая линейная модель · Анализ вариаций · Ковариационный анализ

Регрессия

Линейная · Нелинейная · Непараметрическая регрессия · Полупараметрическая регрессия · Логистическая регрессия

Столбчатая диаграмма · Совмещённая диаграмма · Диаграмма управления · Лесная диаграмма · Гистограмма · Q-Q диаграмма · Диаграмма выполнения · Диаграмма разброса · Стебель-листья · Ящик с усами

Источник

Понятие среднего арифметического

Среднее арифметическое нескольких чисел — это сумма этих чисел, которую разделили на количество слагаемых. Формула среднего арифметического, которую обычно проходят в 5 классе, выглядит так:

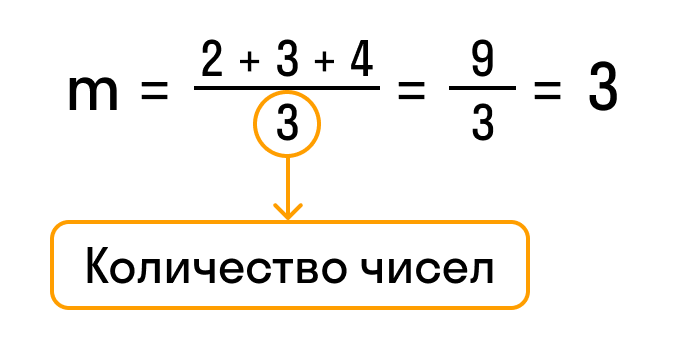
Потренируемся использовать формулу среднего арифметического.

Например, найдем среднее арифметическое чисел 2, 3 и 4. Обозначим среднее значение латинской буквой «m» и посчитаем сумму этих чисел.

2 + 3 + 4 = 9

Разделим результат на количество чисел в задании, то есть на 3, и получим ответ — 3.

Применить эти знания можно в любой сфере жизни, где нужно обобщить и дать среднюю оценку: узнать среднюю цену товара в разных магазинах, вычислить среднюю зарплату сотрудников компании, сравнить среднюю посещаемость занятий учениками 5А и 5Б.

Средняя скорость движения — это весь пройденный путь, поделенный на время движения. Формула:

Так мы рассмотрели самые основные методы нахождения среднего значения. Теперь осталось попрактиковаться на примерах, чтобы быстро решать задачки на контрольной.

Получай лайфхаки, статьи, видео и чек-листы по обучению на почту

Реши домашку по математике на 5.

Подробные решения помогут разобраться в самой сложной теме.

Примеры расчета среднего арифметического

Пример 1. Вычислить среднее арифметическое 33,3 и 55,5.

Как решаем:

Чтобы найти среднее арифметическое двух чисел, надо сложить эти числа и результат разделить на 2: (33,3 + 55,5) : 2 = 88,8 : 2 = 44,4.

Пример 2. Подсчитать среднее арифметическое 7,5 и 8 и 0,5.

Как решаем:

Чтобы найти среднее арифметическое трех чисел, надо сложить эти числа и результат разделить на 3: (7,5 + 8 + 0,5) : 3 = 16 : 3 = 5,33.

Пример 3. Найти среднее арифметическое 202, 105, 67 и 9.

Как решаем:

Чтобы найти среднее арифметическое четырех чисел, надо сложить эти числа и результат разделить на 4: (202 + 105 + 67 + 9) : 4 = 383 : 4 = 95,75.

Пример 4. Сколько в среднем тратит школьник денег в неделю, если в понедельник он потратил 80 рублей, во вторник 75 рублей, в среду и четверг по 100 рублей, в пятницу 50 рублей.

Как решаем:

Чтобы найти сколько в среднем школьник потратил за пять дней, надо сложить эти суммы и результат разделить на 5: (80 + 75 + 100 + 100 + 50) : 5 = 405 : 5 = 81.

Ответ: школьник в неделю тратит в среднем 81 рубль.

Еще больше интересных практических заданий — на курсах математики в онлайн-школе Skysmart. Вводный урок — бесплатно!

Источник

Среднее значение (μ – «мю», x̅ ) – мера центральной тенденции, служащая для описания множества значений одним-единственным числом. Меру можно охарактеризовать несколькими метриками: Cреднее (Mean), Медиана (Median), Мода (Mode). В Науке о данных (Data Science) широкое применение получили следующие его разновидности: арифметическое, геометрическое и гармоническое средние значения.

Среднее арифметическое

Среднее арифметическое (μ для совокупности, x̄ для выборки; англ. Arithmetic Mean) – показатель описательной статистики, сумма элементов Датасета (Dataset), разделенная на их количество. Рассчитывается с помощью формулы:

$$μ = frac{Σ_{i=1}^n a_i}{n}, где$$
$$μspace{–}space{среднее,}$$
$$Σ_{i=1}^n a_ispace{–}space{сумма}space{всех}space{элементов}space{выборки},$$
$$nspace{–}space{количество}space{наблюдений}$$

По умолчанию рассматривают именно с среднее арифметическое, остальные разновидности среднего рассматривают реже:

Разновидности среднего значения

В данной статье рассматриваются простые средние значения без Весовой функции (Weight Function).

Пример. Для небольшого списка [1, 6, 3, 2] средним арифметическим будет:

$$μ = frac{1 + 6 + 3 + 2}{4} = frac{12}{4} = 3$$

Понятие используется в Науке о данных множеством способов:

В сочетании с другими показателями описательной статистики для первичного представления о признаке (Feature)
Для визуальной оценки скошенности признака:

Данные скошены влево, и одного Среднего для описания признака уже недостаточно

Для индикации Выбросов (Outlier) и проч.

Среднее арифметическое и библиотека statistics

Рассчитать среднее автоматически позволит библиотека statistics. Установим библиотеку и импортируем ее для начала:

!pip install statistics

import statistics

Инициализируем список:

# Выборка: высота плодовых деревьев  
lst = [5, 16, 1, 12, 20, 5, 17, 2, 11, 3, 16, 15, 6, 9]

x = statistics.mean(lst) 
print('Арифметическое среднее: %.3f' % x)

Арифметическое среднее: 9.857

Среднее геометрическое

Среднее геометрическое (Geometric Mean) – корень N-й степени из произведения всех значений:

$$x̅_{geom} = sqrt[n]{x_1 × x_1 ×… × x_n},space{где}$$
$$x̅_{geom}space{–}spaceсреднееspace{геометрическое,}$$
$$x_nspace{–}space{n-й}space{элемент}space{выборки}$$

Если Выборка (Sample) содержит два значения, мы извлекаем квадратный корень из перемноженных элементов. Для трех значений используется кубический корень и так далее.

Пример. Как построить квадрат той же площади, что и прямоугольник 2 x 18? Вычислим среднее геометрическое:

$$x̅_{geom} = sqrt[2]{2 × 18} = 6$$

Площади равны

Наш квадрат будет иметь ту же площадь (36), и ребра, равные 6.

В Машинном обучении (ML) Критерий G-Mean (Geometric Mean) – это Среднее геометрическое, определяющее качество классификации большинства и меньшинства. Низкий G-Mean-критерий является признаком плохой работы Модели (Model) в Бинарной классификации (Binary Classification) для положительных случаев.

Среднее геометрическое и SciPy

Среднее геометрическое можно вычислить с помощью функции SciPy gmean():

from scipy.stats import gmean

# Инициализируем список данных
data = [1, 2, 3, 40, 50, 60, 0.7, 0.88, 0.9, 1000]

# Применим функцию
y = gmean(data)
print('Среднее геометрическое: %.3f' % y)

Среднее геометрическое: 7.246

Среднее гармоническое

Среднее гармоническое (Harmonic Mean) – количество значений, поделенное на сумму обратных величин:

$$x̅_{harmonic} = frac{N}{frac{1}{x_1} + frac{1}{x_2} + … + frac{1}{x_n}},space{где}$$
$$x̅_{harmonic}space{–}space{среднее}space{гармоническое,}$$
$$x_nspace{–}space{n-й}space{элемент}space{выборки}$$

В Машинном обучении Критерий F1 ( F1 Score), показатель оценки эффективности модели, – это Среднее гармоническое Точности измерений (Accuracy) и Отзыва (Recall).

Среднее гармоническое и SciPy

Среднее гармоническое значение можно вычислить с помощью функции SciPy hmean().

from scipy.stats import hmean

# Инициализируем список
data = [0.11, 0.22, 0.33, 0.44, 0.55, 0.66, 0.77, 0.88, 0.99]

z = hmean(data)
print('Среднее гармоническое: %.3f' % z)

Среднее гармоническое: 0.350

Ноутбук, не требующий дополнительной настройки на момент написания статьи, можно скачать здесь.

Фото: @peterluo0113

Источник

Среднее арифметическое

Сущность и значение средних величин.

Абсолютные и относительные величины.

Виды группировок.

В зависимости от задач, решаемых с помощью группировок выделяют следующие их виды:

— типологические

— структурные

— аналитические

Главная задача типологической состоит в классификации социально-экономических явлений путем выделения однородных к качественным отношениям групп.

Качественная однородность при этом понимается в том смысле, что в отношении изучаемого свойства все единицы совокупности подчиняются одному закону развития. Например: группировка предприятиям отраслей экономики.

Абсолютной величиной называется показатель, выражающий размеры социально-экономического явления.

Относительной величиной в статистике называется показатель, выражающий количественное соотношение между явлениями. Он получается в результате деления одной абсолютной величины на другую абсолютную величину. Величина с которой мы производим сравнения называется основанием или базой сравнения.

Абсолютные величины — всегда величины именованные.

Относительные величины выражаются в коэффициентах, процентах, промили и т.д.

Относительная величина показывает, во сколько раз, или на сколько процентов сравниваемая величина больше или меньше базы сравнения.

В статистике различают 8 видов относительных величин:

Средние величины являются одними из наиболее распространенных обобщающих статистических показателей. Они имеют своей целью одним числом охарактеризовать статистическую совокупность состоящую из меньшинства единиц. Средние величины тесно связаны с законом больших чисел. Сущность этой зависимости заключается в том, что при большом числе наблюдений случайные отклонения от общей статистики взаимопогашаются и в среднем более отчетливо проявляется статистическая закономерность.

С помощью метода средних решаются следующие основные задачи:

1. Характеристика уровня развития явлений.

2. Сравнение двух или нескольких уровней.

3. Изучение взаимосвязей социально-экономических явлений.

4. Анализ размещения социально-экономических явлений в пространстве.

Для решения этих задач статистическая методология разработала различные виды средних.

Для выяснения методики расчета средней арифметической используем следующие обозначения:

X — арифметический признак

X (X1, X2, … X3) — варианты определенного признака

n — число единиц совокупности

— средняя величина признака

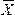
В зависимости от исходных данных средняя арифметическая может быть рассчитана двумя способами:

1. Если данные статистического наблюдения на сгруппированы, или сгруппированные варианты имеют одинаковые частоты, то рассчитывается средняя арифметическая простая:

2. Если частоты сгруппированы в данных разные, то рассчитывается среднее арифметическое взвешанное:

— численность (частоты) вариантов

— сумма частот

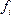
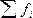
Среднее арифметическое рассчитывается по разному в дискретных и интервальных вариационных рядах.

В дискретных рядах варианты признака умножаются на частоты, эти произведения суммируются и полученная сумма произведений делится на сумму частот.

Рассмотрим пример вычисления средней арифметической в дискретном ряду:

Заработная плата, руб. Xi	Число сотрудников, чел. fi	Произведение вариант на веса (частоты) Xi*fi











Итого:

В интервальных рядах значение признака задано, как известно, в виде интервалов, поэтому, прежде чем рассчитывать среднюю арифметическую, нужно перейти от интервального ряда к дискретному.

В качестве вариантов Xi используется середина соответствующих интервалов. Они определяются как полусумма нижней и верхней границ.

Если у интервала отсутствует нижняя граница, то его середина определяется как разность между верхней границей и половиной величины следующих интервалов. При отсутствии верхних границ, середина интервала определяется как сумма нижней границы и половины величины предыдущего интервала. После перехода к дискретному ряду дальнейшие вычисления происходят по методике рассмотренной выше.

Если веса fi заданы не в абсолютных показателях, а в относительных, то формула расчета средней арифметической будет следующей:

pi — относительные величины структуры, показывающие, какой процент составляют частоты вариантов в сумме всех частот.

Если относительные величины структуры заданы не в процентах, а в долях, то среднее арифметическое будет рассчитываться по формуле:

studopedia.ru

Среднее значение

Сре́днее значе́ние — числовая характеристика множества чисел или функций (в математике); — некоторое число, заключённое между наименьшим и наибольшим из их значений.

Основные сведения

Исходным пунктом становления теории средних величин явилось исследование пропорций школой Пифагора. При этом не проводилось строгого различия между понятиями средней величины и пропорции. Значительный толчок развитию теории пропорций с арифметической точки зрения был дан греческими математиками — Никомахом Герасским (конец I — начало II в. н. э.) и Паппом Александрийским (III в. н. э.). Первым этапом развития понятия средней является этап, когда средняя стала считаться центральным членом непрерывной пропорции. Но понятие средней как центрального значения прогрессии не даёт возможности вывести понятие средней по отношению к последовательности n членов, независимо от того, в каком порядке они следуют друг за другом. Для этой цели необходимо прибегнуть к формальному обобщению средних. Следующий этап — переход от непрерывных пропорций к прогрессиям — арифметической, геометрической и гармонической (англ.)[1].

В истории статистики впервые широкое употребление средних величин связано с именем английского учёного У. Петти. У. Петти один из первых пытался придать средней величине статистический смысл, связав её с экономическими категориями. Но описания понятия средней величины, его выделения, Петти не произвёл. Родоначальником теории средних величин принято считать А. Кетле. Он одним из первых начал последовательно разрабатывать теорию средних величин, пытаясь подвести под неё математическую базу. А. Кетле выделял два вида средних величин — собственно средние и средние арифметические. Собственно средние представляют вещь, число, действительно существующие. Собственно средние или средние статистические должны выводиться из явлений однокачественных, одинаковых по своему внутреннему значению. Средние арифметические — числа, дающие возможно близкое представление о многих числах, различных, хотя и однородных[2].

Каждый из видов средней может выступать либо в форме простой, либо в форме взвешенной средней. Правильность выбора формы средней вытекает из материальной природы объекта исследования. Формулы простых средних применяются в случае, если индивидуальные значения усредняемого признака не повторяются. Когда в практических исследованиях отдельные значения изучаемого признака встречаются несколько раз у единиц исследуемой совокупности, тогда частота повторений индивидуальных значений признака присутствует в расчётных формулах степенных средних. В этом случае они называются формулами взвешенных средних.[3]

Иерархия средних значений в математике

среднее значение функции — понятие, определяемое многими способами.
- Более конкретно, но на основе произвольных функций, определяются средние Колмогорова для набора чисел.
  - среднее степенное — частный случай средних Колмогорова при ϕ ( x ) = x α {displaystyle phi (x)=x^{alpha }} . Средние различных степеней связывает между собой неравенство о средних. Наиболее распространённые частные случаи:
    1. среднее арифметическое ( α = 1 {displaystyle alpha =1} );
    2. среднее квадратическое ( α = 2 {displaystyle alpha =2} );
    3. среднее гармоническое ( α = − 1 {displaystyle alpha =-1} );
    4. по непрерывности при α → 0 {displaystyle alpha to 0} доопределяется среднее геометрическое, которое также является Колмогоровским средним при ϕ ( x ) = log ⁡ x {displaystyle phi (x)=log x}
Среднее взвешенное — обобщение средней величины на случай произвольной линейной комбинации:
- Среднее арифметическое взвешенное.
- Среднее геометрическое взвешенное.
- Среднее гармоническое взвешенное.
среднее хронологическое — обобщает значения признака для одной и той же единицы или совокупности в целом, изменяющихся во времени.
среднее логарифмическое, определяемое по формуле a ¯ = a 1 − a 2 ln ⁡ ( a 1 / a 2 ) {textstyle {bar {a}}={frac {a_{1}-a_{2}}{ln(a_{1}/a_{2})}}} , используется в теплотехнике
среднее логарифмическое, определяемое в электроизоляции соответствии с ГОСТ 27905.4-88 определяется как l o g a ¯ = log ⁡ a 1 + l o g a 2 + . . . + . . . l o g a n a 1 + a 2 + . . . + a n {textstyle log{bar {a}}={frac {log a_{1}+loga_{2}+…+…loga_{n}}{a_{1}+a_{2}+…+a_{n}}}} (логарифм по любому основанию)[4]

В теории вероятностей и статистике

Основная статья: Показатели центра распределения

непараметрические средние — мода, медиана.
среднее значение случайной величины — то же, что математическое ожидание случайной величины. По сути — среднее значение её функции распределения.

ru.wikipedia.org

Каким знаком обозначается среднее арифметическое значение?

Вот, скажем, сумма — это эпсилон прописная…

Ксения

Средняя арифметическая — это тот предел, около которого группируются отдельные значения наблюдаемых и изучаемых характеристик, Средняя арифметическая — частное от деления суммы значений кого-либо признака на число элементов совокупности. В статистике средняя арифметическая обычно обозначается через отдельные значения признака (или частные результаты опыта) – через x1, x2, x3 и т. д., а общие количество признаков (или количество опытов) — n.
При большом количестве измерений положительные и отрицательные случайные погрешности встречаются одинаково часто. По многократным измерениям какой-либо физической величины можно определить ее среднее арифметическое значение. Многократные измерения также дают возможность установить точность измерения, как для окончательного результата, так и для отдельных измерений, т. е. найти те границы, в которых находится полученный результат измеряемой величины.
При п измерениях некоторой величины мы получим п различных ее значений. Наиболее близким к истинному значению измеряемой величины будет среднее арифметическое значение всех измерений.
Если обозначить отдельные измерения через а, az, a3, ..ап, то среднеарифметическое значение измеряемой величины определится по формуле:
п
п — at + аг + • — • + Д„ _1 а,-
а _ ——————
=Y-^
^J П
Значения отдельных измерений отличаются от среднеарифметического значения а0 на следующие величины:
Абсолютные значения разностей (Да^ Даг,…) между средним арифметическим значением измеряемой величины и величиной отдельных измерений называют абсолютными погрешностями отдельных измерений. Среднее арифметическое абсолютных погрешностей всех измерений, которое необходимо для определения относительной погрешности измерений и записи окончательного результата, вычисляется по формуле:
^-. (2)
Эту погрешность называют средней абсолютной погрешностью измерения. Принимая один знак абсолютных погрешностей, мы тем самым сознательно берем наибольшую из возможных погрешностей.

Что такое среднее арифметическое? Как найти среднее арифметическое?

Формула среднего арифметического чисел?

Алекс-89

Среднее арифметическое нескольких чисел — это сумма этих чисел, делённая на их количество.

x ср = S/n

где:

x ср — среднее арифметическое

S — сумма чисел

n — количество чисел.

Например, нам нужно найти среднее арифметическое чисел 3, 4, 5 и 6.

Для этого нам нужно их сложить и полученную сумму разделить на 4:

(3 + 4 + 5 + 6) : 4 = 18 : 4 = 4,5.

Алсу — ш

Мне, как математику, интересны вопросы по данному предмету.

Начну с истории вопроса. Над средними величинами задумывались с древних времмен. Среднее арифметическое, среднее геометоическое, среднее гармоническое. Эти понятия предложены в древней Греции пифагорийцами.

А теперь интересующий нас вопрос. Что же понимается под средним арифметичским нескольких чисел:

Итак, для нахождения среднего арифметического чисел нужно прибавить все числа и разделить полученную сумму на количество слагаемых.

Имеет место формула:

Пример. Найти среднее арифметическое чисел: 100, 175, 325.

Решение.

Воспользуемся формулой нахождения среднего арифметического трех чисел (то есть вместо n будет 3; нужно сложить все 3 числа и разделить полученную сумму на их количество, т.е. на 3). Имеем: х=(100+175+325)/3=600/3=200.

Ответ: 200.

Lady v

Арифметика считается самым элементарным разделом математики и изучает простые действия с числами. Поэтому и среднее арифметическое также находится очень просто. Начнем с определения. Среднее арифметическое — это величина, которая показывает какое число наиболее близко к истине при нескольких последовательных однотипных действиях. Например при беге на сто метров человек каждый раз показывает разное время, но средняя величина будет в пределах например 12 секунд. Нахождение среднего арифметического таким образом сводится в последовательному суммированию всех чисел определенного ряда (результатов забегов) и деление этой суммы на количество этих забегов (попыток, чисел). В виде формулы это выглядит так:

Sариф = (Х1+Х2+..+Хn)/n

Mb78

Среднее арифметическое — это среднее число между несколькими числами.

Например между числами 2 и 4 среднее число 3.

Формула нахождения среднего арифметического такая:

Нужно сложить все числа и разделить на количество этих чисел:

Например у нас 3 числа: 2, 5 и 8.

Находим среднее арифметическое:

X=(2+5+8)/3=15/3=5

Область применения среднего арифметического достаточно широка.

Например можно зная координаты двух точек отрезка найти координаты середины этого отрезка.

Например координаты отрезка: (X1,Y1,Z1)-(X2,Y2,Z2).

Обозначим середину этого отрезка координатами X3,Y3,Z3.

Отдельно находим середину для каждой координаты:

X3=(X1+X2)/2;

Y3=(Y1+Y2)/2;

Z3=(Z1+Z2)/2;

Красивая поляна

Средне арифметическое число, это числа сложенные вместе и деленные на их количество, полученный ответ и есть средне арифметическое число.

Например: Катя положила в копилку 50 рублей, Максим 100 рублей, а Саша положил в копилку 150 рублей. 50 + 100 + 150 = 300 рублей в копилке, теперь делим эту сумму на три (три человека положили деньги). Итак 300 : 3 = 100 рублей. Эти 100 рублей и будет средне арифметически, каждый из них положил в копилку.

Есть такой простой пример: один человек ест мясо, другой человек ест капусту, а средне арифметически они оба едят голубцы.

Таким же образом рассчитывают среднюю зарплату…

Simpl

Среднеарифметическое-это среднее значение из заданных…

Т.е. по простому имеем количество палочек разной длины и хотим узнать их среднее значение..

Логично, что для этого мы их сводим вместе, получая длинную палку, а потом делим её на требуемое число частей..

Вот и выходит среднеарифметическое..

Вот так и выводится формула:Sa=(S(1)+..S(n))/n..

Птичка2014

Среднее арифметическое — это сумма всех значений и деленное на их количество.

Например числа 2, 3 , 5, 6 . Нужно их сложить 2+ 3+ 5 + 6 = 16

16 делим на 4 и получаем ответ 4 .

4 и есть среднее арифметическое этих чисел.

Azamatik

Средним арифметическим называют сумму чисел, разделенное на количество этих самых чисел. А найти среднее арифметическое очень просто.

Как следует из определения мы должны взять числа, сложить их и разделить на их количество.

Приведем пример: дается числа 1, 3, 5, 7 и нам надо найти среднее арифметическое этих чисел.

сначала складываем эти числа (1+3+5+7) и получаем 16
полученный результат нам надо разделить на 4 (кол — во): 16/4 и получаем результат 4.

Итак, среднее арифметическое чисел 1, 3, 5 и 7 — это 4.

Tana76

Среднее арифметическое — среднее значение среди заданных показателей.

Оно находится путем деления суммы всех показателей на их количество.

Например, у меня есть 5 яблок весом 200, 250, 180, 220 и 230 грамм.

Средний вес 1 яблока находим так:

ищем общий вес всех яблок (сумму всех показателей) — он равен 1080 граммов,
делим общий вес на количество яблок 1080:5 = 216 граммов. Это и есть среднее арифметическое.

Это наиболее часто применяемый в статистике показатель.

Зеленый чебуречек

Это мы знаем со школьной скамьи. У кого был хороший учитель по математике, то запомнить это нехитрое действие можно было с первого раза.

При нахождении среднего арифметического необходимо сложить все имеющиеся числа и разделить на их количество.

Например, я купила в магазине 1 кг яблок, 2 кг бананов, 3 кг апельсинов и 1 кг киви. Сколько килограммов в среднем я купила фруктов.

1+2+3+1=7.

7/4= 1,8 килограммов. Это и будет среднеарифметическим значением.

Бьемон эпу

Помню как итоговую контрольную по математике сдавал

Так там нужно было среднее арифметическое найти.

Хорошо что добрые люди подсказали что делать, иначе беда.

Например у нас 4 числа.

Складываем числа и делим на их количество (в данном случае 4)

Например цифры 2,6,1,1. Складываем 2+6+1+1 и делим на 4 = 2.5

Как видите ничего сложного. Так что среднее арифметическая — это среднее значение всех чисел.

bolshoyvopros.ru

Definition[edit]

Motivating properties[edit]

Additional properties[edit]

Contrast with median[edit]

Generalizations[edit]

Weighted average[edit]

Continuous probability distributions[edit]

Angles[edit]

Symbols and encoding[edit]

See also[edit]

References[edit]

Further reading[edit]

External links[edit]

Definition[edit]

Motivating properties[edit]

Additional properties[edit]

Contrast with median[edit]

Generalizations[edit]

Weighted average[edit]

Continuous probability distributions[edit]

Angles[edit]

Symbols and encoding[edit]

See also[edit]

References[edit]

Further reading[edit]

External links[edit]

Содержание

Определение

Мотивирующие свойства

Контраст с медианой

Обобщения

Средневзвешенное значение

Непрерывные распределения вероятностей

Углы

Символы и кодировка

См. Также

Ссылки

Дополнительная литература

Внешние ссылки

Содержание

Введение

Примеры

Непрерывная случайная величина

Некоторые проблемы применения среднего

Отсутствие робастности

Сложный процент

Направления

Примечания

См. также

Ссылки

Понятие среднего арифметического

Примеры расчета среднего арифметического

Среднее арифметическое

Среднее арифметическое и библиотека statistics

Среднее геометрическое

Среднее геометрическое и SciPy

Среднее гармоническое

Среднее гармоническое и SciPy

Среднее арифметическое

Среднее значение

Основные сведения

Иерархия средних значений в математике

В теории вероятностей и статистике

Каким знаком обозначается среднее арифметическое значение?

Что такое среднее арифметическое? Как найти среднее арифметическое?

Читайте также