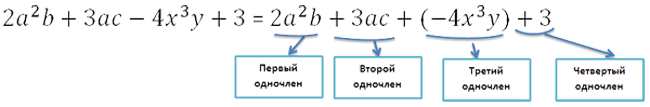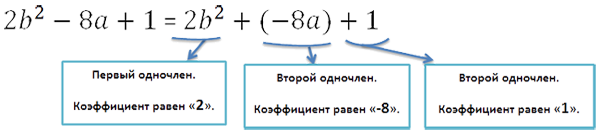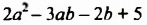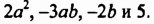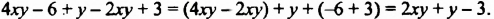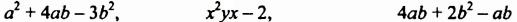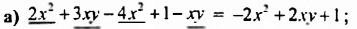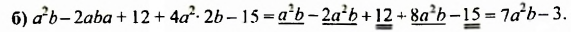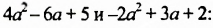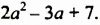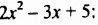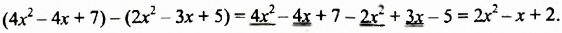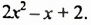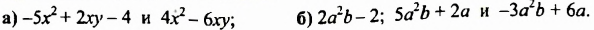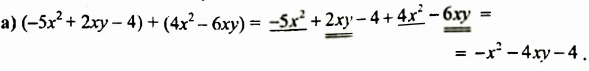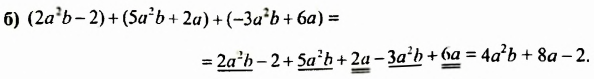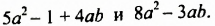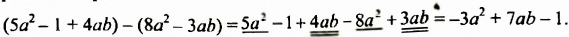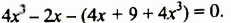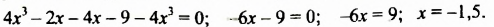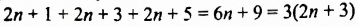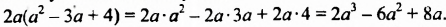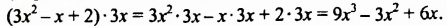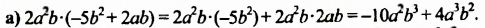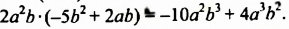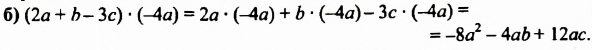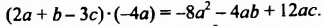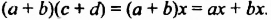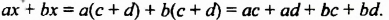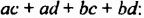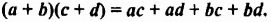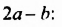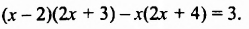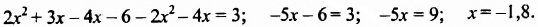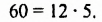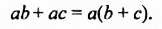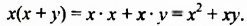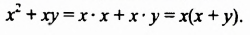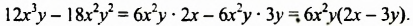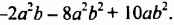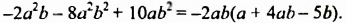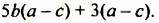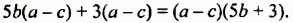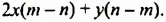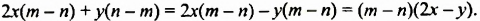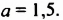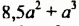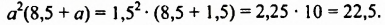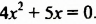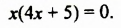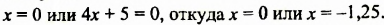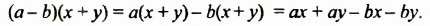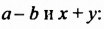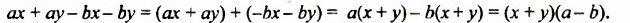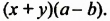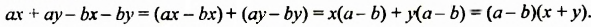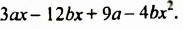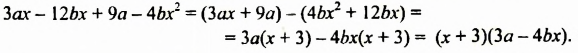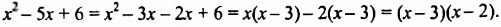После изучения одночленов переходим к многочленам. Данная статья расскажет о всех необходимых сведениях, необходимых для выполнения действий над ними. Мы определим многочлен с сопутствующими определениями члена многочлена, то есть свободный и подобный, рассмотрим многочлен стандартного вида, введем степень и научимся ее находить, поработаем с его коэффициентами.
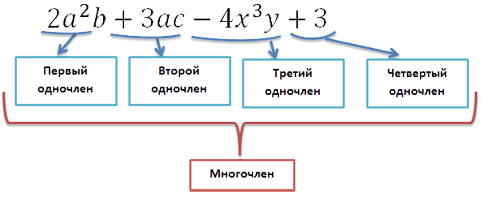
Многочлен и его члены – определения и примеры
Определение многочлена было дано еще в 7 классе после изучения одночленов. Рассмотрим его полное определение.
Многочленом считается сумма одночленов, причем сам одночлен – это частный случай многочлена.
Из определения следует, что примеры многочленов могут быть различными: 5, 0, −1, x, 5·a·b3, x2·0,6·x·(−2)·y12, -213·x·y2·323·x·x3·y·z и так далее. Из определения имеем, что 1+x, a2+b2 и выражение x2-2·x·y+25·x2+y2+5,2·y·x являются многочленами.
Рассмотрим еще определения.
Членами многочлена называются его составляющие одночлены.
Рассмотрим такой пример, где имеем многочлен 3·x4−2·x·y+3−y3, состоящий из 4 членов: 3·x4, −2·x·y, 3 и −y3. Такой одночлен можно считать многочленом, который состоит из одного члена.
Многочлены, которые имеют в своем составе 2, 3 трехчлена имеют соответственное название – двучлен и трехчлен.
Отсюда следует, что выражение вида x+y – является двучленом, а выражение 2·x3·q−q·x·x+7·b – трехчленом.
По школьной программе работали с линейным двучленом вида a·x+b, где а и b являются некоторыми числами, а х – переменной. Рассмотрим примеры линейных двучленов вида: x+1, x·7,2−4 с примерами квадратных трехчленов x2+3·x−5 и 25·x2-3x+11.
Для преобразования и решения необходимо находить и приводить подобные слагаемые. Например, многочлен вида 1+5·x−3+y+2·x имеет подобные слагаемые 1 и -3, 5х и 2х. Их подразделяют в особую группу под названием подобных членов многочлена.
Подобные члены многочлена – это подобные слагаемые, находящиеся в многочлене.
В примере, приведенном выше, имеем, что 1 и -3, 5х и 2х являются подобными членами многочлена или подобными слагаемыми. Для того, что бы упростить выражение, применяют нахождение и приведение подобных слагаемых.
Многочлен стандартного вида
У всех одночленов и многочленов имеются свои определенные названия.
Многочленом стандартного вида называют многочлен, у которого каждый входящий в него член имеет одночлен стандартного вида и не содержит подобных членов.
Из определения видно, что возможно приведение многочленов стандартного вида, например, 3·x2−x·y+1 и __formula__, причем запись в стандартном виде. Выражения 5+3·x2−x2+2·x·z и 5+3·x2−x2+2·x·z многочленами стандартного вида не является, так как первый из них имеет подобные слагаемые в виде 3·x2 и −x2, а второй содержит одночлен вида x·y3·x·z2, отличающийся от стандартного многочлена.
Если того требуют обстоятельства, иногда многочлен приводится к стандартному виду. Многочленом стандартного вида считается и понятие свободного члена многочлена.
Свободным членом многочлена является многочлен стандартного вида, не имеющий буквенной части.
Иначе говоря, когда запись многочлена в стандартном виде имеет число, его называют свободным членом. Тогда число 5 является свободным членом многочлена x2·z+5, а многочлен 7·a+4·a·b+b3 свободного члена не имеет.
Степень многочлена – как ее найти?
Определение самой степени многочлена базируется на определении многочлена стандартного вида и на степенях одночленов, которые являются его составляющими.
Степенью многочлена стандартного вида называют наибольшую из степеней, входящих в его запись.
Рассмотрим на примере. Степень многочлена 5·x3−4 равняется 3, потому как одночлены, входящие в его состав, имеют степени 3 и 0, а большее из них 3 соответственно. Определение степени из многочлена 4·x2·y3−5·x4·y+6·x равняется наибольшему из чисел, то есть 2+3=5, 4+1=5 и 1, значит 5.
Следует выяснить, каким образом находится сама степень.
Степень многочлена произвольного числа — это степень соответствующего ему многочлена в стандартном виде.
Когда многочлен записан не в стандартном виде, но нужно найти его степень, необходимо приведение к стандартному, после чего находить искомую степень.
Найти степень многочлена 3·a12−2·a·b·c·a·c·b+y2·z2−2·a12−a12.
Решение
Для начала представим многочлен в стандартном виде. Получим выражение вида:
3·a12−2·a·b·c·a·c·b+y2·z2−2·a12−a12= =(3·a12−2·a12−a12)−2·(a·a)·(b·b)·(c·c)+y2·z2= =−2·a2·b2·c2+y2·z2
При получении многочлена стандартного вида получаем, что отчетливо выделяются два из них −2·a2·b2·c2 и y2·z2. Для нахождения степеней посчитаем и получим, что 2+2+2=6 и 2+2=4. Видно, что наибольшая из них равняется 6. Из определения следует, что именно 6 является степенью многочлена −2·a2·b2·c2+y2·z2, следовательно и исходного значения.
Ответ: 6.
Коэффициенты членов многочлена
Когда все члены многочлена являются одночленами стандартного вида, то в таком случаем они имеют название коэффициентов членов многочлена. Иначе говоря, их можно называть коэффициентами многочлена.
При рассмотрении примера видно, что многочлен вида 2·x−0,5·x·y+3·x+7 имеет в своем составе 4 многочлена: 2·x, −0,5·x·y, 3·x и 7 с соответствующими их коэффициентами 2, −0,5, 3 и 7. Значит, 2, −0,5, 3 и 7 считаются коэффициентами членов заданного многочлена вида 2·x−0,5·x·y+3·x+7. При преобразовании важно обращать внимание на коэффициенты, стоящие перед переменными.
Download Article
Download Article
Polynomial means «many terms,» and it can refer to a variety of expressions that can include constants, variables, and exponents. For example, x — 2 is a polynomial; so is 25. To find the degree of a polynomial, all you have to do is find the largest exponent in the polynomial.[1]
If you want to find the degree of a polynomial in a variety of situations, just follow these steps.
-
1
Combine like terms. Combine all of the like terms in the expression so you can simplify it, if they are not combined already. Let’s say you’re working with the following expression: 3x2 — 3x4 — 5 + 2x + 2x2 — x. Just combine all of the x2, x, and constant terms of the expression to get 5x2 — 3x4 — 5 + x.[2]
-
2
Drop all of the constants and coefficients. The constant terms are all of the terms that are not attached to a variable, such as 3 or 5. The coefficients are the terms that are attached to the variable. When you’re looking for the degree of a polynomial, you can either just actively ignore these terms or cross them off. For instance, the coefficient of the term 5x2 would be 5. The degree is independent of the coefficients, so you don’t need them.
- Working with the equation 5x2 — 3x4 — 5 + x, you would drop the constants and coefficients to get x2 — x4 + x.
Advertisement
-
3
Put the terms in decreasing order of their exponents. This is also called putting the polynomial in standard form.[3]
. The term with the highest exponent should be first, and the term with the lowest exponent should be last. This will help you see which term has the exponent with the largest value. In the previous example, you would be left with
-x4 + x2 + x. -
4
Find the power of the largest term. The power is simply number in the exponent. In the example, -x4 + x2 + x, the power of the first term is 4. Since you’ve arranged the polynomial to put the largest exponent first, that will be where you will find the largest term.
-
5
Identify this number as the degree of the polynomial. You can just write that the degree of the polynomial = 4, or you can write the answer in a more appropriate form: deg (3x2 — 3x4 — 5 + 2x + 2x2 — x) = 4. You’re all done.[4]
-
6
Know that the degree of a constant is zero. If your polynomial is only a constant, such as 15 or 55, then the degree of that polynomial is really zero. You can think of the constant term as being attached to a variable to the degree of 0, which is really 1. For example, if you have the constant 15, you can think of it as 15x0, which is really 15 x 1, or 15. This proves that the degree of a constant is 0.
Advertisement
-
1
Write the expression. Finding the degree of a polynomial with multiple variables is only a little bit trickier than finding the degree of a polynomial with one variable. Let’s say you’re working with the following expression:
- x5y3z + 2xy3 + 4x2yz2
-
2
Add the degree of variables in each term. Just add up the degrees of the variables in each of the terms; it does not matter that they are different variables. Remember that the degree of a variable without a written degree, such as x or y, is just one. Here’s how you do it for all three terms:[5]
- deg(x5y3z) = 5 + 3 + 1 = 9
- deg(2xy3) = 1 + 3 = 4
- deg(4x2yz2) = 2 + 1 + 2 = 5
-
3
Identify the largest degree of these terms. The largest degree of these three terms is 9, the value of the added degree values of the first term.[6]
-
4
Identify this number as the degree of the polynomial. 9 is the degree of the entire polynomial. You can write the final answer like this: deg (x5y3z + 2xy3 + 4x2yz2) = 9.
Advertisement
-
1
Write down the expression. Let’s say you’re working with the following expression: (x2 + 1)/(6x -2).[7]
-
2
Eliminate all coefficients and constants. You won’t need the coefficients or constant terms to find the degree of a polynomial with fractions. So, eliminate the 1 from the numerator and the 6 and -2 from the denominator. You’re left with x2/x.
-
3
Subtract the degree of the variable in the denominator from the degree of the variable in the numerator. The degree of the variable in the numerator is 2 and the degree of the variable in the denominator is 1. So, subtract 1 from 2. 2-1 = 1.
-
4
Write the result as your answer. The degree of this rational expression is 1. You can write it like this: deg [(x2 + 1)/(6x -2)] = 1.
Advertisement
Add New Question
-
Question
What is the degree of a polynomial?
In the case of a polynomial with only one variable (such as 2x³ + 5x² — 4x +3, where x is the only variable),the degree is the same as the highest exponent appearing in the polynomial (in this case 3). In the case of a polynomial with more than one variable, the degree is found by looking at each monomial within the polynomial, adding together all the exponents within a monomial, and choosing the largest sum of exponents. That sum is the degree of the polynomial. For example, in the expression 2x²y³ + 4xy² — 3xy, the first monomial has an exponent total of 5 (2+3), which is the largest exponent total in the polynomial, so that’s the degree of the polynomial.
-
Question
What is degree of 1/x^4 + x^2?
1 / (x^4) is equivalent to x^(-4). So the highest (most positive) exponent in the polynomial is 2, meaning that 2 is the degree of the polynomial.
-
Question
What about a polynomial with multiple variables that has one or more negative exponents in it?
Combine the exponents found within a given monomial as you would if all the exponents were positive, but you would subtract the negative exponents.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
-
This just shows the steps you would go through in your mind. You don’t have to do this on paper, though it might help the first time. If you do it on paper, however, you won’t make a mistake.
-
By convention, the degree of the zero polynomial is generally considered to be negative infinity.
-
For the third step, linear terms like x can be written as x1 and non-zero constant terms like 7 can be written as 7x0
Thanks for submitting a tip for review!
Advertisement
References
About This Article
Article SummaryX
To find the degree of a polynomial with one variable, combine the like terms in the expression so you can simplify it. Next, drop all of the constants and coefficients from the expression. Then, put the terms in decreasing order of their exponents and find the power of the largest term. The power of the largest term is the degree of the polynomial. To find the degree of a polynomial with multiple variables, write out the expression, then add the degree of variables in each term. The power of the largest term is your answer! If you want to learn how to find the degree of a polynomial in a rational expression, keep reading the article!
Did this summary help you?
Thanks to all authors for creating a page that has been read 863,302 times.
Did this article help you?
Download Article
Download Article
Polynomial means «many terms,» and it can refer to a variety of expressions that can include constants, variables, and exponents. For example, x — 2 is a polynomial; so is 25. To find the degree of a polynomial, all you have to do is find the largest exponent in the polynomial.[1]
If you want to find the degree of a polynomial in a variety of situations, just follow these steps.
-
1
Combine like terms. Combine all of the like terms in the expression so you can simplify it, if they are not combined already. Let’s say you’re working with the following expression: 3x2 — 3x4 — 5 + 2x + 2x2 — x. Just combine all of the x2, x, and constant terms of the expression to get 5x2 — 3x4 — 5 + x.[2]
-
2
Drop all of the constants and coefficients. The constant terms are all of the terms that are not attached to a variable, such as 3 or 5. The coefficients are the terms that are attached to the variable. When you’re looking for the degree of a polynomial, you can either just actively ignore these terms or cross them off. For instance, the coefficient of the term 5x2 would be 5. The degree is independent of the coefficients, so you don’t need them.
- Working with the equation 5x2 — 3x4 — 5 + x, you would drop the constants and coefficients to get x2 — x4 + x.
Advertisement
-
3
Put the terms in decreasing order of their exponents. This is also called putting the polynomial in standard form.[3]
. The term with the highest exponent should be first, and the term with the lowest exponent should be last. This will help you see which term has the exponent with the largest value. In the previous example, you would be left with
-x4 + x2 + x. -
4
Find the power of the largest term. The power is simply number in the exponent. In the example, -x4 + x2 + x, the power of the first term is 4. Since you’ve arranged the polynomial to put the largest exponent first, that will be where you will find the largest term.
-
5
Identify this number as the degree of the polynomial. You can just write that the degree of the polynomial = 4, or you can write the answer in a more appropriate form: deg (3x2 — 3x4 — 5 + 2x + 2x2 — x) = 4. You’re all done.[4]
-
6
Know that the degree of a constant is zero. If your polynomial is only a constant, such as 15 or 55, then the degree of that polynomial is really zero. You can think of the constant term as being attached to a variable to the degree of 0, which is really 1. For example, if you have the constant 15, you can think of it as 15x0, which is really 15 x 1, or 15. This proves that the degree of a constant is 0.
Advertisement
-
1
Write the expression. Finding the degree of a polynomial with multiple variables is only a little bit trickier than finding the degree of a polynomial with one variable. Let’s say you’re working with the following expression:
- x5y3z + 2xy3 + 4x2yz2
-
2
Add the degree of variables in each term. Just add up the degrees of the variables in each of the terms; it does not matter that they are different variables. Remember that the degree of a variable without a written degree, such as x or y, is just one. Here’s how you do it for all three terms:[5]
- deg(x5y3z) = 5 + 3 + 1 = 9
- deg(2xy3) = 1 + 3 = 4
- deg(4x2yz2) = 2 + 1 + 2 = 5
-
3
Identify the largest degree of these terms. The largest degree of these three terms is 9, the value of the added degree values of the first term.[6]
-
4
Identify this number as the degree of the polynomial. 9 is the degree of the entire polynomial. You can write the final answer like this: deg (x5y3z + 2xy3 + 4x2yz2) = 9.
Advertisement
-
1
Write down the expression. Let’s say you’re working with the following expression: (x2 + 1)/(6x -2).[7]
-
2
Eliminate all coefficients and constants. You won’t need the coefficients or constant terms to find the degree of a polynomial with fractions. So, eliminate the 1 from the numerator and the 6 and -2 from the denominator. You’re left with x2/x.
-
3
Subtract the degree of the variable in the denominator from the degree of the variable in the numerator. The degree of the variable in the numerator is 2 and the degree of the variable in the denominator is 1. So, subtract 1 from 2. 2-1 = 1.
-
4
Write the result as your answer. The degree of this rational expression is 1. You can write it like this: deg [(x2 + 1)/(6x -2)] = 1.
Advertisement
Add New Question
-
Question
What is the degree of a polynomial?
In the case of a polynomial with only one variable (such as 2x³ + 5x² — 4x +3, where x is the only variable),the degree is the same as the highest exponent appearing in the polynomial (in this case 3). In the case of a polynomial with more than one variable, the degree is found by looking at each monomial within the polynomial, adding together all the exponents within a monomial, and choosing the largest sum of exponents. That sum is the degree of the polynomial. For example, in the expression 2x²y³ + 4xy² — 3xy, the first monomial has an exponent total of 5 (2+3), which is the largest exponent total in the polynomial, so that’s the degree of the polynomial.
-
Question
What is degree of 1/x^4 + x^2?
1 / (x^4) is equivalent to x^(-4). So the highest (most positive) exponent in the polynomial is 2, meaning that 2 is the degree of the polynomial.
-
Question
What about a polynomial with multiple variables that has one or more negative exponents in it?
Combine the exponents found within a given monomial as you would if all the exponents were positive, but you would subtract the negative exponents.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
-
This just shows the steps you would go through in your mind. You don’t have to do this on paper, though it might help the first time. If you do it on paper, however, you won’t make a mistake.
-
By convention, the degree of the zero polynomial is generally considered to be negative infinity.
-
For the third step, linear terms like x can be written as x1 and non-zero constant terms like 7 can be written as 7x0
Thanks for submitting a tip for review!
Advertisement
References
About This Article
Article SummaryX
To find the degree of a polynomial with one variable, combine the like terms in the expression so you can simplify it. Next, drop all of the constants and coefficients from the expression. Then, put the terms in decreasing order of their exponents and find the power of the largest term. The power of the largest term is the degree of the polynomial. To find the degree of a polynomial with multiple variables, write out the expression, then add the degree of variables in each term. The power of the largest term is your answer! If you want to learn how to find the degree of a polynomial in a rational expression, keep reading the article!
Did this summary help you?
Thanks to all authors for creating a page that has been read 863,302 times.
Did this article help you?
Часто путают понятия одночлена и многочлена.
Давайте разберемся, что называют одночленом, а что многочленом.
Прежде всего, вспомним, что называли одночленом в уроке «Одночлены».
Обратите внимание, что «внутри» одночлена (между буквами и числовым коэффициентом) есть только знак умножения.
Например, в одночлене:
3ab = 3 · a · b
Запомните!
Многочленом называется алгебраическая сумма нескольких одночленов.
Одночлены, из которых составлен многочлен, называют членами многочлена.
Примеры многочленов:
a + 2b2 − c;
3t5 − 4b;
4 − 6xy
Несложно заметить, что любой многочлен состоит из нескольких одночленов.
Рассмотрим многочлен подробнее.
Возникает вопрос, почему многочленом называют алгебраическую сумму
одночленов, если в многочлене присутствует
знак минуса.
Это объясняется тем, что на самом деле знак «−» относится к числовому коэффициенту одночлена,
который стоит справа от знака.
Любой многочлен можно записать
по правилу знаков
как сумму одночленов.
В многочлене знак, который стоит слева от одночлена относится к числовому коэффициенту самого одночлена.
Как найти степень многочлена
Запомните!
Степенью многочлена называют наибольшую из степеней входящих в него одночленов.
То есть, чтобы найти степень многочлена, нужно сначала найти
степень каждого одночлена, который входит в
состав многочлена.
Степени многочленов
| Многочлен |
Степень многочлена |
||||
|---|---|---|---|---|---|
|
a2 − 3a2b + x = a2(степень одночлена 2) |
3 | ||||
x2y2
x2y2(степень одночлена 4) |
4 | ||||
|
8x2 8x2(степень одночлена 2) |
2 |
Любой одночлен является многочленом.
В самом деле, любой одночлен, по сути, является многочленом, который состоит всего из одного одночлена.
Примеры таких многочленов: 2a2b;
−3d3; a.
Число «0» называют нулевым многочленом.
Содержание:
Многочлены
Многочлен
Выражение
Определение: Многочленом называют сумму нескольких одночленов.
Одночлены, составляющие многочлен, называют членами этого многочлена.
Например, членами многочлена 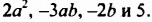
Многочлен, состоящий из двух членов, называют двучленом, многочлен, состоящий из трех членов, — трехчленом и т. д. Так,
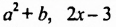
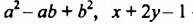
Считают, что каждый одночлен является многочленом, который состоит из одного члена.
Многочлен стандартного вида
Рассмотрим многочлен 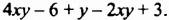
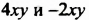
Приведем в многочлене 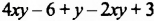
Многочлен 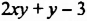
Определение:
Многочлен, являющийся суммой одночленов стандартного вида, среди которых нет подобных членов, называют многочленом стандартного вида.
Среди многочленов
только первый является многочленом стандартного вида, а два другие — нет, поскольку во втором многочлене первый член не является одночленом стандартного вида, а третий многочлен имеет подобные члены.
Степень многочлена
Многочлен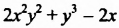
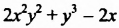
Определение:
Степенью многочлена стандартного вида называют наибольшую степень одночленов, образующих данный многочлен.
По этому определению 
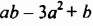
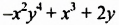
Члены многочлена можно записывать в произвольном порядке. Для многочленов стандартного вида, содержащих одну переменную, члены, как правило, записывают в порядке убывания или возрастания показателей степеней. Например:
Каждый многочлен является целым выражением. Однако не каждое целое выражение является многочленом. Например, целые выражения 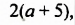
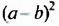
Примеры выполнения заданий:
Пример №117
Записать в стандартному виде многочлен:
Сложение и вычитание многочленов
Сложение многочленов
Сложим многочлены
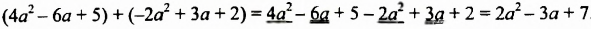
Раскрыв скобки и приведя подобные слагаемые, мы записали сумму данных многочленов в виде многочлена. Итак, суммой многочленов 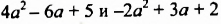
Таким же образом находят сумму трех и более многочленов. Сумму любых многочленов всегда можно записать в виде многочлена.
Вычитание многочленов
Вычтем из многочлена 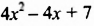
Раскрыв скобки и приведя подобные слагаемые, мы записали разность данных многочленов в виде многочлена. Итак, разностью многочленов 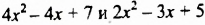
Разность любых многочленов всегда можно записать в виде многочлена.
Примеры выполнения заданий:
Пример №118
Найти сумму многочленов:
Пример №119
Найти разность многочленов
Решение:
Пример №120
Решить уравнение
Решение:
Ответ.-1,5.
Пример №121
Доказать, что сумма трех последовательных нечетных чисел делится на 3.
Решение:
Пусть из трех последовательных нечетных чисел наименьшим является 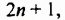
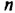
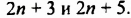
делится на 3, поскольку имеет делитель 3.
Умножение одночлена на многочлен
Умножим одночлен 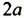
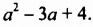
Итак, произведением одночлена 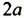
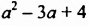
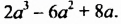
Чтобы умножить одночлен на многочлен, нужно одночлен умножить на каждый член многочлена и полученные произведения сложить.
По этому правилу можно умножать и многочлен на одночлен. Например:
Произведение любого одночлена и любого многочлена всегда можно :ать в виде многочлена.
Примеры выполнения заданий:
Пример №122
Выполнить умножение:
Сокращенная запись:
Сокращенная запись:
Пример №123
Упростить выражение
Решение:
Пример №124
Решить уравнение
Решение:
Ответ. 0,5.
Умножение многочлена на многочлен
Умножим многочлен 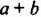
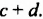
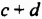
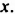
Возвращаясь к замене 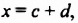
Итак, произведением многочлена 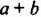
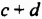
Выражение 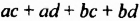
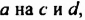
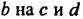
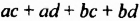
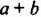
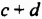
Приходим к такому правилу:
Чтобы умножить многочлен на многочлен, достаточно каждый член одного многочлена умножить на каждый член другого многочлена и полученные произведения сложить.
Умножим по этому правилу многочлен 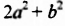
Выполняя умножение многочленов, промежуточные результаты можно не записывать:
В каждом из рассмотренных примеров произведение двух многочленов мы записывали в виде многочлена. Вообще, произведение любых многочленов всегда можно записать в виде многочлена.
- Заказать решение задач по высшей математике
Примеры выполнения заданий:
Пример №125
Выполнить умножение:
б) Найдем произведение первых двух многочленов, а потом полученное произведение умножим на третий многочлен:
Пример №126
Решить уравнение
Решение:
Ответ.-1,8.
Разложение многочленов на множители способом вынесения общего множителя за скобки
1. В шестом классе мы изучали разложение чисел на множители. Например, число 60 можно записать в виде произведения двух чисел 12 и 5:
Говорят, что число 60 разложили на два множителя 12 и 5.
На множители можно разложить и многочлены. Например,
Записав многочлен 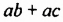
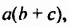
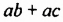
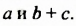
Разложить многочлен на множители значит представить его в виде произведения нескольких многочленов.
Сравните
2. Рассмотрим один из способов разложения многочленов на множители. Выполним умножение одночлена на многочлен:
Перепишем эти равенства в обратном порядке:
Многочлен 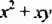
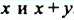
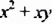
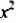
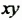
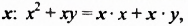
Такой способ разложения многочленов на множители называют способом вынесения общего множителя за скобки.
Примеры выполнения заданий:
Пример №127
Разложить на множителя многочлен 12х3у — 18х2у2.
Решение:
Сначала найдем общий числовой множитель для коэффициентов 12 и -18. Если коэффициентами являются целые числа, то в качестве общего числового множителя берут, как правило, наибольший общий делитель модулей этих коэффициентов. В нашем случае это число 6. Степени с основанием 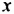
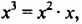
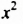
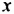
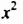
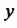
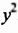
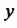
Пример №128
Разложить на множители многочлен
Решение:
Пример №129
Разложить на множители:
Решение:
Данное выражение является суммой двух слагаемых, для которых общим множителем является выражение 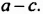
Пример №130
Разложить на множители:
Решение:
Слагаемые имеют множители 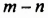
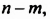
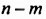
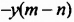
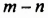
Следовательно,
Пример №131
Найти значение выражения 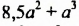
Решение:
Разложим сначала многочлен 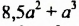
При 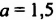
Пример №132
Решить уравнение
Решение:
Разложим левую часть уравнения на множители:
Произведение 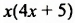
Ответ. 0; -1,25.
Разложение многочленов на множители способом группировки
Изучение этого способа разложения многочленов на множители начнем с рассмотрения примера умножения многочленов. Выполним умножение двучлена 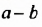
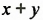
Выполняя преобразования в обратном порядке, многочлен 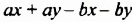
Проанализируем последние преобразования. Имеем многочлен, члены которого можно группировать так, чтобы каждая группа имела общий множитель: для группы 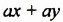
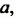
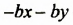
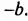
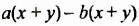
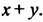
Рассмотренный способ разложения многочленов на множители называют способом группировки. При применении этого способа нужно образовывать такие группы членов, чтобы они имели общий множитель. После вынесения в каждой группе общего множителя за скобки должен образоваться общин множитель для всех групп, который также нужно вынести за скобки.
Многочлен 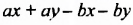
Сравните
Примеры выполнения заданий:
Пример №133
Разложить на множители многочлен
Решение:
Пример №134
Разложить на множители трехчлен
Решение:
Представим второй член 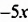
- Формулы сокращенного умножения
- Разложение многочленов на множители
- Системы линейных уравнений с двумя переменными
- Рациональные выражения
- Выражения и уравнения
- Линейное уравнение с одной переменной
- Целые выражения
- Одночлены
Степень многочлена
Что такое степень многочлена? Как определить степень одночлена?
Определение.
Степенью многочлена называют наибольшую из степеней входящих в него одночленов.
Обычно, прежде чем искать степень многочлена, его приводят к многочлену стандартного вида, хотя, вообще говоря, это не обязательно.
Итак, чтобы найти степень многочлена:
1) Можно привести многочлен к стандартному виду.
2) Найти степень всех входящих в него одночленов — членов многочлена.
3) Выбрать наибольшую из этих степеней.
Примеры.
Найти степень многочлена:
Решение:
Данный многочлен записан в стандартном виде. Степень первого члена многочлена — одночлена 7x²y — равна 2+1=3. Степень второго члена многочлена — -11xy — равна 1+1=2. Степень третьего члена многочлена — 4y — равна 1. -9 — одночлен нулевой степени.
Наибольшая из степеней одночленов — 3. Таким образом, это — многочлен третьей степени.
Здесь 10x²y³ — одночлен 5-й степени, 32x⁴ — 4-й, -12x²y² — также одночлен 4-й степени. Наибольшая из степеней одночленов — 5. Следовательно, это — многочлен 5-й степени.
3) Сначала приведем данный многочлен к стандартному виду:
14a³ — одночлен 3-й степени, -5a³b — 4-й, 16ab³ — также одночлен 4-й степени. Наибольшая из степеней входящих в многочлен одночленов — 4. Таким образом, данный многочлен имеет четвертую степень.
Хотя в алгебре принято упрощать многочлен, приводя его к стандартному виду, степень можно искать и для многочлена, не записанного в стандартном виде.
1,7x — одночлен 1-й степени, 2y — одночлен 1-й степени, -12 — одночлен 0-й степени. Значит, это — многочлен первой степени.
Одночлен считают многочленом, состоящим из одного члена. 20 — одночлен 0-й степени. Следовательно, 20 является многочленом нулевой степени.