From Wikipedia, the free encyclopedia
«Times table» redirects here. For a table of departure and arrival times, see Timetable (disambiguation).
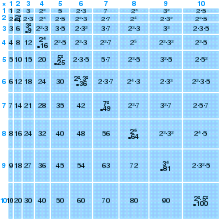
Multiplication table from 1 to 10 drawn to scale with the upper-right half labeled with prime factorisations
In mathematics, a multiplication table (sometimes, less formally, a times table) is a mathematical table used to define a multiplication operation for an algebraic system.
The decimal multiplication table was traditionally taught as an essential part of elementary arithmetic around the world, as it lays the foundation for arithmetic operations with base-ten numbers. Many educators believe it is necessary to memorize the table up to 9 × 9.[1]
History[edit]
Pre-modern times[edit]
The oldest known multiplication tables were used by the Babylonians about 4000 years ago.[2] However, they used a base of 60.[2] The oldest known tables using a base of 10 are the Chinese decimal multiplication table on bamboo strips dating to about 305 BC, during China’s Warring States period.[2]
The multiplication table is sometimes attributed to the ancient Greek mathematician Pythagoras (570–495 BC). It is also called the Table of Pythagoras in many languages (for example French, Italian and Russian), sometimes in English.[4] The Greco-Roman mathematician Nichomachus (60–120 AD), a follower of Neopythagoreanism, included a multiplication table in his Introduction to Arithmetic, whereas the oldest surviving Greek multiplication table is on a wax tablet dated to the 1st century AD and currently housed in the British Museum.[5]
In 493 AD, Victorius of Aquitaine wrote a 98-column multiplication table which gave (in Roman numerals) the product of every number from 2 to 50 times and the rows were «a list of numbers starting with one thousand, descending by hundreds to one hundred, then descending by tens to ten, then by ones to one, and then the fractions down to 1/144.»[6]
Modern times[edit]
In his 1820 book The Philosophy of Arithmetic,[7] mathematician John Leslie published a multiplication table up to 99 × 99, which allows numbers to be multiplied in pairs of digits at a time. Leslie also recommended that young pupils memorize the multiplication table up to 50 × 50.
The illustration below shows a table up to 12 × 12, which is a size commonly used nowadays in English-world schools.
| × | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 2 | 0 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 |
| 3 | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 | 33 | 36 |
| 4 | 0 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 | 44 | 48 |
| 5 | 0 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 |
| 6 | 0 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 | 66 | 72 |
| 7 | 0 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 | 77 | 84 |
| 8 | 0 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 | 88 | 96 |
| 9 | 0 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 | 99 | 108 |
| 10 | 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 110 | 120 |
| 11 | 0 | 11 | 22 | 33 | 44 | 55 | 66 | 77 | 88 | 99 | 110 | 121 | 132 |
| 12 | 0 | 12 | 24 | 36 | 48 | 60 | 72 | 84 | 96 | 108 | 120 | 132 | 144 |
In China, however, because multiplication of integers is commutative, many schools use a smaller table as below. Some schools even remove the first column since 1 is the multiplicative identity.
| 1 | 1 | ||||||||
| 2 | 2 | 4 | |||||||
| 3 | 3 | 6 | 9 | ||||||
| 4 | 4 | 8 | 12 | 16 | |||||
| 5 | 5 | 10 | 15 | 20 | 25 | ||||
| 6 | 6 | 12 | 18 | 24 | 30 | 36 | |||
| 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | ||
| 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | |
| 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 |
| × | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
The traditional rote learning of multiplication was based on memorization of columns in the table, in a form like
1 × 10 = 10
2 × 10 = 20
3 × 10 = 30
4 × 10 = 40
5 × 10 = 50
6 × 10 = 60
7 × 10 = 70
8 × 10 = 80
9 × 10 = 90
This form of writing the multiplication table in columns with complete number sentences is still used in some countries, such as Bosnia and Herzegovina,[citation needed] instead of the modern grids above.
Patterns in the tables[edit]
There is a pattern in the multiplication table that can help people to memorize the table more easily. It uses the figures below:
| → | → | ||||||||
| ↑ | 1 | 2 | 3 | ↓ | ↑ | 2 | 4 | ↓ | |
|---|---|---|---|---|---|---|---|---|---|
| 4 | 5 | 6 | |||||||
| 7 | 8 | 9 | 6 | 8 | |||||
| ← | ← | ||||||||
| 0 | 5 | 0 | |||||||
| Figure 1: Odd | Figure 2: Even |
Cycles of the unit digit of multiples of integers ending in 1, 3, 7 and 9 (upper row), and 2, 4, 6 and 8 (lower row) on a telephone keypad
Figure 1 is used for multiples of 1, 3, 7, and 9. Figure 2 is used for the multiples of 2, 4, 6, and 8. These patterns can be used to memorize the multiples of any number from 0 to 10, except 5. As you would start on the number you are multiplying, when you multiply by 0, you stay on 0 (0 is external and so the arrows have no effect on 0, otherwise 0 is used as a link to create a perpetual cycle). The pattern also works with multiples of 10, by starting at 1 and simply adding 0, giving you 10, then just apply every number in the pattern to the «tens» unit as you would normally do as usual to the «ones» unit.
For example, to recall all the multiples of 7:
- Look at the 7 in the first picture and follow the arrow.
- The next number in the direction of the arrow is 4. So think of the next number after 7 that ends with 4, which is 14.
- The next number in the direction of the arrow is 1. So think of the next number after 14 that ends with 1, which is 21.
- After coming to the top of this column, start with the bottom of the next column, and travel in the same direction. The number is 8. So think of the next number after 21 that ends with 8, which is 28.
- Proceed in the same way until the last number, 3, corresponding to 63.
- Next, use the 0 at the bottom. It corresponds to 70.
- Then, start again with the 7. This time it will correspond to 77.
- Continue like this.
In abstract algebra[edit]
Tables can also define binary operations on groups, fields, rings, and other algebraic systems. In such contexts they are called Cayley tables. Here are the addition and multiplication tables for the finite field Z5:
- for every natural number n, there are also addition and multiplication tables for the ring Zn.
|
|
For other examples, see group, and octonion.
Chinese and Japanese multiplication tables[edit]
Mokkan discovered at Heijō Palace suggest that the multiplication table may have been introduced to Japan through Chinese mathematical treatises such as the Sunzi Suanjing, because their expression of the multiplication table share the character 如 in products less than ten.[8] Chinese and Japanese share a similar system of eighty-one short, easily memorable sentences taught to students to help them learn the multiplication table up to 9 × 9. In current usage, the sentences that express products less than ten include an additional particle in both languages. In the case of modern Chinese, this is 得 (dé); and in Japanese, this is が (ga). This is useful for those who practice calculation with a suanpan or a soroban, because the sentences remind them to shift one column to the right when inputting a product that does not begin with a tens digit. In particular, the Japanese multiplication table uses non-standard pronunciations for numbers in some specific instances (such as the replacement of san roku with saburoku).
Warring States decimal multiplication bamboo slips[edit]
A bundle of 21 bamboo slips dated 305 BC in the Warring States period in the Tsinghua Bamboo Slips (清華簡) collection is the world’s earliest known example of a decimal multiplication table.[9]
A modern representation of the Warring States decimal multiplication table used to calculate 12 × 34.5
Standards-based mathematics reform in the US[edit]
In 1989, the National Council of Teachers of Mathematics (NCTM) developed new standards which were based on the belief that all students should learn higher-order thinking skills, which recommended reduced emphasis on the teaching of traditional methods that relied on rote memorization, such as multiplication tables. Widely adopted texts such as Investigations in Numbers, Data, and Space (widely known as TERC after its producer, Technical Education Research Centers) omitted aids such as multiplication tables in early editions. NCTM made it clear in their 2006 Focal Points that basic mathematics facts must be learned, though there is no consensus on whether rote memorization is the best method. In recent years, a number of nontraditional methods have been devised to help children learn multiplication facts, including video-game style apps and books that aim to teach times tables through character-based stories.
See also[edit]
- Vedic square
- IBM 1620, an early computer that used tables stored in memory to perform addition and multiplication
References[edit]
- ^ Trivett, John (1980), «The Multiplication Table: To Be Memorized or Mastered!», For the Learning of Mathematics, 1 (1): 21–25, JSTOR 40247697.
- ^ a b c Qiu, Jane (January 7, 2014). «Ancient times table hidden in Chinese bamboo strips». Nature News. doi:10.1038/nature.2014.14482. S2CID 130132289.
- ^ Wikisource:Page:Popular Science Monthly Volume 26.djvu/467
- ^ for example in An Elementary Treatise on Arithmetic by John Farrar
- ^ David E. Smith (1958), History of Mathematics, Volume I: General Survey of the History of Elementary Mathematics. New York: Dover Publications (a reprint of the 1951 publication), ISBN 0-486-20429-4, pp. 58, 129.
- ^ David W. Maher and John F. Makowski. «Literary evidence for Roman arithmetic with fractions». Classical Philology, 96/4 (October 2001), p. 383.
- ^ Leslie, John (1820). The Philosophy of Arithmetic; Exhibiting a Progressive View of the Theory and Practice of Calculation, with Tables for the Multiplication of Numbers as Far as One Thousand. Edinburgh: Abernethy & Walker.
- ^ «「九九」は中国伝来…平城宮跡から木簡出土». Yomiuri Shimbun. December 4, 2010. Archived from the original on December 7, 2010.
- ^ Nature article The 2,300-year-old matrix is the world’s oldest decimal multiplication table
From Wikipedia, the free encyclopedia
«Times table» redirects here. For a table of departure and arrival times, see Timetable (disambiguation).
Multiplication table from 1 to 10 drawn to scale with the upper-right half labeled with prime factorisations
In mathematics, a multiplication table (sometimes, less formally, a times table) is a mathematical table used to define a multiplication operation for an algebraic system.
The decimal multiplication table was traditionally taught as an essential part of elementary arithmetic around the world, as it lays the foundation for arithmetic operations with base-ten numbers. Many educators believe it is necessary to memorize the table up to 9 × 9.[1]
History[edit]
Pre-modern times[edit]
The oldest known multiplication tables were used by the Babylonians about 4000 years ago.[2] However, they used a base of 60.[2] The oldest known tables using a base of 10 are the Chinese decimal multiplication table on bamboo strips dating to about 305 BC, during China’s Warring States period.[2]
The multiplication table is sometimes attributed to the ancient Greek mathematician Pythagoras (570–495 BC). It is also called the Table of Pythagoras in many languages (for example French, Italian and Russian), sometimes in English.[4] The Greco-Roman mathematician Nichomachus (60–120 AD), a follower of Neopythagoreanism, included a multiplication table in his Introduction to Arithmetic, whereas the oldest surviving Greek multiplication table is on a wax tablet dated to the 1st century AD and currently housed in the British Museum.[5]
In 493 AD, Victorius of Aquitaine wrote a 98-column multiplication table which gave (in Roman numerals) the product of every number from 2 to 50 times and the rows were «a list of numbers starting with one thousand, descending by hundreds to one hundred, then descending by tens to ten, then by ones to one, and then the fractions down to 1/144.»[6]
Modern times[edit]
In his 1820 book The Philosophy of Arithmetic,[7] mathematician John Leslie published a multiplication table up to 99 × 99, which allows numbers to be multiplied in pairs of digits at a time. Leslie also recommended that young pupils memorize the multiplication table up to 50 × 50.
The illustration below shows a table up to 12 × 12, which is a size commonly used nowadays in English-world schools.
| × | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 2 | 0 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 |
| 3 | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 | 33 | 36 |
| 4 | 0 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 | 44 | 48 |
| 5 | 0 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 |
| 6 | 0 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 | 66 | 72 |
| 7 | 0 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 | 77 | 84 |
| 8 | 0 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 | 88 | 96 |
| 9 | 0 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 | 99 | 108 |
| 10 | 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 110 | 120 |
| 11 | 0 | 11 | 22 | 33 | 44 | 55 | 66 | 77 | 88 | 99 | 110 | 121 | 132 |
| 12 | 0 | 12 | 24 | 36 | 48 | 60 | 72 | 84 | 96 | 108 | 120 | 132 | 144 |
In China, however, because multiplication of integers is commutative, many schools use a smaller table as below. Some schools even remove the first column since 1 is the multiplicative identity.
| 1 | 1 | ||||||||
| 2 | 2 | 4 | |||||||
| 3 | 3 | 6 | 9 | ||||||
| 4 | 4 | 8 | 12 | 16 | |||||
| 5 | 5 | 10 | 15 | 20 | 25 | ||||
| 6 | 6 | 12 | 18 | 24 | 30 | 36 | |||
| 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | ||
| 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | |
| 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 |
| × | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
The traditional rote learning of multiplication was based on memorization of columns in the table, in a form like
1 × 10 = 10
2 × 10 = 20
3 × 10 = 30
4 × 10 = 40
5 × 10 = 50
6 × 10 = 60
7 × 10 = 70
8 × 10 = 80
9 × 10 = 90
This form of writing the multiplication table in columns with complete number sentences is still used in some countries, such as Bosnia and Herzegovina,[citation needed] instead of the modern grids above.
Patterns in the tables[edit]
There is a pattern in the multiplication table that can help people to memorize the table more easily. It uses the figures below:
| → | → | ||||||||
| ↑ | 1 | 2 | 3 | ↓ | ↑ | 2 | 4 | ↓ | |
|---|---|---|---|---|---|---|---|---|---|
| 4 | 5 | 6 | |||||||
| 7 | 8 | 9 | 6 | 8 | |||||
| ← | ← | ||||||||
| 0 | 5 | 0 | |||||||
| Figure 1: Odd | Figure 2: Even |
Cycles of the unit digit of multiples of integers ending in 1, 3, 7 and 9 (upper row), and 2, 4, 6 and 8 (lower row) on a telephone keypad
Figure 1 is used for multiples of 1, 3, 7, and 9. Figure 2 is used for the multiples of 2, 4, 6, and 8. These patterns can be used to memorize the multiples of any number from 0 to 10, except 5. As you would start on the number you are multiplying, when you multiply by 0, you stay on 0 (0 is external and so the arrows have no effect on 0, otherwise 0 is used as a link to create a perpetual cycle). The pattern also works with multiples of 10, by starting at 1 and simply adding 0, giving you 10, then just apply every number in the pattern to the «tens» unit as you would normally do as usual to the «ones» unit.
For example, to recall all the multiples of 7:
- Look at the 7 in the first picture and follow the arrow.
- The next number in the direction of the arrow is 4. So think of the next number after 7 that ends with 4, which is 14.
- The next number in the direction of the arrow is 1. So think of the next number after 14 that ends with 1, which is 21.
- After coming to the top of this column, start with the bottom of the next column, and travel in the same direction. The number is 8. So think of the next number after 21 that ends with 8, which is 28.
- Proceed in the same way until the last number, 3, corresponding to 63.
- Next, use the 0 at the bottom. It corresponds to 70.
- Then, start again with the 7. This time it will correspond to 77.
- Continue like this.
In abstract algebra[edit]
Tables can also define binary operations on groups, fields, rings, and other algebraic systems. In such contexts they are called Cayley tables. Here are the addition and multiplication tables for the finite field Z5:
- for every natural number n, there are also addition and multiplication tables for the ring Zn.
|
|
For other examples, see group, and octonion.
Chinese and Japanese multiplication tables[edit]
Mokkan discovered at Heijō Palace suggest that the multiplication table may have been introduced to Japan through Chinese mathematical treatises such as the Sunzi Suanjing, because their expression of the multiplication table share the character 如 in products less than ten.[8] Chinese and Japanese share a similar system of eighty-one short, easily memorable sentences taught to students to help them learn the multiplication table up to 9 × 9. In current usage, the sentences that express products less than ten include an additional particle in both languages. In the case of modern Chinese, this is 得 (dé); and in Japanese, this is が (ga). This is useful for those who practice calculation with a suanpan or a soroban, because the sentences remind them to shift one column to the right when inputting a product that does not begin with a tens digit. In particular, the Japanese multiplication table uses non-standard pronunciations for numbers in some specific instances (such as the replacement of san roku with saburoku).
Warring States decimal multiplication bamboo slips[edit]
A bundle of 21 bamboo slips dated 305 BC in the Warring States period in the Tsinghua Bamboo Slips (清華簡) collection is the world’s earliest known example of a decimal multiplication table.[9]
A modern representation of the Warring States decimal multiplication table used to calculate 12 × 34.5
Standards-based mathematics reform in the US[edit]
In 1989, the National Council of Teachers of Mathematics (NCTM) developed new standards which were based on the belief that all students should learn higher-order thinking skills, which recommended reduced emphasis on the teaching of traditional methods that relied on rote memorization, such as multiplication tables. Widely adopted texts such as Investigations in Numbers, Data, and Space (widely known as TERC after its producer, Technical Education Research Centers) omitted aids such as multiplication tables in early editions. NCTM made it clear in their 2006 Focal Points that basic mathematics facts must be learned, though there is no consensus on whether rote memorization is the best method. In recent years, a number of nontraditional methods have been devised to help children learn multiplication facts, including video-game style apps and books that aim to teach times tables through character-based stories.
See also[edit]
- Vedic square
- IBM 1620, an early computer that used tables stored in memory to perform addition and multiplication
References[edit]
- ^ Trivett, John (1980), «The Multiplication Table: To Be Memorized or Mastered!», For the Learning of Mathematics, 1 (1): 21–25, JSTOR 40247697.
- ^ a b c Qiu, Jane (January 7, 2014). «Ancient times table hidden in Chinese bamboo strips». Nature News. doi:10.1038/nature.2014.14482. S2CID 130132289.
- ^ Wikisource:Page:Popular Science Monthly Volume 26.djvu/467
- ^ for example in An Elementary Treatise on Arithmetic by John Farrar
- ^ David E. Smith (1958), History of Mathematics, Volume I: General Survey of the History of Elementary Mathematics. New York: Dover Publications (a reprint of the 1951 publication), ISBN 0-486-20429-4, pp. 58, 129.
- ^ David W. Maher and John F. Makowski. «Literary evidence for Roman arithmetic with fractions». Classical Philology, 96/4 (October 2001), p. 383.
- ^ Leslie, John (1820). The Philosophy of Arithmetic; Exhibiting a Progressive View of the Theory and Practice of Calculation, with Tables for the Multiplication of Numbers as Far as One Thousand. Edinburgh: Abernethy & Walker.
- ^ «「九九」は中国伝来…平城宮跡から木簡出土». Yomiuri Shimbun. December 4, 2010. Archived from the original on December 7, 2010.
- ^ Nature article The 2,300-year-old matrix is the world’s oldest decimal multiplication table
Как выучить таблицу умножения легко и быстро
Эти приёмы спасут лето вашего школьника.
1. Взломайте систему
Обычно таблица умножения на обратной стороне школьных тетрадок выглядит так.
Один вид этих бесконечных столбиков с цифрами способен вогнать энергичного младшеклассника в отчаяние. Поэтому без сомнений берите жирный маркер и на глазах ребёнка перечёркивайте математическую пытку. Это не просто перфоманс, а способ создать позитивный настрой.
Вместо сложных примеров предложите школьнику таблицу Пифагора.
Это и есть настоящая таблица умножения. Покажите ребёнку, насколько легко ею пользоваться.
Результат умножения двух цифр — это число, которое находится на пересечении строки и столбика с соответствующими цифрами. Например, чтобы умножить 3 на 4, достаточно мысленно провести две линии: одну горизонтальную от цифры 3 в левом столбике, и вторую вертикальную — от цифры 4 в верхней строке. Результат — 12.
2. Объясните, что задача в два раза проще, чем кажется
Вместе умножьте 3 на 4. А теперь предложите ребёнку поменять цифры местами: выбрать 3 не в вертикальном столбике, а в горизонтальной строке. А 4, соответственно, в столбике слева. Обратите внимание, что результат будет тем же. И 3 × 4, и 4 × 3 равно 12.
Это правило называется свойством коммутативности. Или детским языком «от перемены мест множителей результат не меняется».
Не надо запоминать, сколько будет 3 × 4 или 4 × 3. Достаточно выучить, что цифры 3 и 4 в любом порядке при умножении друг на друга дают 12.
Из свойства коммутативности следует простой вывод. Таблица умножения — в два раза меньше и проще, чем кажется. Если вы знаете, сколько будет 4 × 7, значит, вам автоматически известно, сколько будет 7 × 4. Вам не надо это дополнительно учить.
3. Помогите ребёнку понять физический смысл умножения
Это можно сделать, рисуя на таблице прямоугольники со сторонами, соответствующими умножаемым цифрам.
Например, вот так можно показать, что такое 2 × 4 — это два ряда по четыре клеточки в каждом.
Предложите ребёнку сосчитать, сколько клеточек помещается в получившемся прямоугольнике. Так он сам обнаружит, что 2 × 4 = 8.
Отсканируйте или распечатайте несколько копий таблицы Пифагора и вместе со школьником рисуйте другие прямоугольники — горизонтальные, вертикальные, маленькие и большие, подсчитывая, сколько в них клеточек. Таким образом вы заодно задействуете зрительную память: вспоминая, сколько будет, например, 3 × 4, ребёнок представит себе соответствующую фигуру — и легко ответит.
4. Найдите в таблице закономерности
Когда ребёнок самостоятельно обнаруживает закономерность, он запоминает её навсегда. Это более простой и эффективный способ освоить таблицу умножения, чем зубрёжка.
Вот некоторые закономерности, на которые стоит обратить внимание.
- При умножении на 1 любая цифра остаётся той же.
- Умножение на 2 — это просто цифра, к которой прибавили её же. Например, 3 × 2 означает, что к цифре 3 прибавили 3. 8 × 2 значит 8 + 8.
- Все примеры с умножением на 5 имеют результат, который оканчивается на 5 или на 0.
- Чтобы умножить на 5 любое чётное число, надо взять его половинку и приписать к ней 0. Например, 6 × 5: берём половинку от 6 — это цифра 3 — и приставляем к ней ноль: получается 30.
- При умножении на 9 сумма цифр в результате обязательно будет равна 9. Например, 2 × 9 = 18 (1 + 8 = 9). 3 × 9 = 27 (2 + 7 = 9). И так далее.
- Чтобы умножить любое число на 10, достаточно пририсовать к нему справа ноль.
5. Учите небольшими порциями
Не нужно пытаться за один присест вызубрить всё. Начните с умножения на 1, 2 и 3 и посвятите изучению каждой такой темы день или два. Так вы постепенно подготовите ребёнка к усвоению более сложной информации.
Когда школьник разобрался и усвоил самые простые столбцы, переходите к числам посложнее: сначала к умножению на 4–7, а затем — на 8–9.
6. Повторяйте
Чем чаще, тем лучше. Сначала спрашивайте по порядку, а когда ответы станут уверенными — вразброс. Следите и за темпом: поначалу давайте больше времени на размышление, но постепенно просите ребёнка отвечать быстрее.
7. Распечатайте или купите обучающие плакаты
Лучше несколько. Развесьте их в тех местах, где ребёнок проводит много времени — в детской (игровой зоне), над рабочим столом, на холодильнике.
Плакаты должны быть большими и яркими. Можно использовать и те, на которых изображена не таблица Пифагора, а стандартные примеры. В любом случае ребёнок будет цепляться взглядом за красочное изображение, и оно закрепится в памяти.
8. Научите ребёнка математическим фокусам
Вот несколько простых примеров.
Фокус с умножением на 7
Вам понадобятся несколько игральных кубиков (костей). Скажите ребёнку, что, сколько бы костей он ни выбросил, вы сразу же скажете сумму точек на их верхних и нижних гранях — даже несмотря на то, что низ кубиков не видно.
Секрет прост: кубики устроены таким образом, что сумма точек на верхней и нижней поверхностях всегда равна 7. Таким образом, чтобы узнать правильный ответ, достаточно умножить количество брошенных кубиков на 7.
Предложите ребёнку показать фокус брату или сестре, бабушке с дедушкой, друзьям. Пусть школьник меняет число кубиков. Это поможет ему закрепить в памяти умножение на 7.
Фокус с умножением на 9
Поверните обе ладони к себе. Перед вами окажутся 10 пальцев. Мысленно пронумеруйте их от 1 до 10: большой палец левой руки — 1, указательный — 2 и так далее, вплоть до большого пальца правой руки, который будет соответствовать 10. Дальше действуйте так.
- Выберите цифру, на которую хотите умножить 9.
- Прижмите соответствующий ей палец вниз.
- Посчитайте, сколько пальцев останется слева от прижатого — это будут десятки в искомом ответе. Справа — единицы.
Например, вам нужно умножить 9 на 2. Вы прижимаете второй по счёту палец — левый указательный. Справа от него остаётся 1 палец (количество десятков), слева — 8 (количество единиц). Правильный ответ: 9 × 2 = 18.
9. Покажите, что математика полезна
Детям, да и взрослым, сложно запоминать абстрактные вещи — те, что не применяются в обычной жизни. Ваша задача — продемонстрировать ребёнку, что таблица умножения очень даже полезна. Это можно сделать разными способами.
Например, предложите школьнику, собирающемуся на прогулку, угостить друзей конфетами или печеньем. «На площадке тебя ждут Катя, Вася, Платон и Ира. Каждому из них ты собираешься дать по 2 конфеты. Сколько конфет тебе надо взять?»
Другой вариант: пусть ребёнок посчитает общее количество колёс у проезжающих мимо шести автомобилей. Или выяснит, сколько людей пойдёт на пикник, если вы собираетесь встретиться четырьмя семьями, в каждой из которых по три человека.
10. Играйте в математику
Сегодня можно купить множество обучающих пособий с красочными картинками и продуманными логическими задачами. Благодаря таким упражнениям обучение превращается в увлекательную игру. Но играть можно, и не тратясь на книжки.
Используйте готовые игры с кубиками
Подойдёт любая бродилка, в которой игрок продвигается на то количество клеток, которое указывает брошенный кубик. Скажите ребёнку, что сегодня все броски считаются двойными (или, положим, тройными). Как правило, детям очень нравится идея проходить в два или три раза дальше, чем показывает кубик.
Чтобы добавить интереса в игру, регулярно пытайтесь смошенничать. Например, говорите: «Так, у меня выпало 4, значит, я должен пройти в два раза дальше… На 10 клеточек!» Пусть ребёнок вас поправляет.
Предложите ребёнку опередить калькулятор
Вам понадобятся всё те же игральные кубики (если ребёнок учит умножение от 1 до 6) или колода игральных карт без картинок (если речь об умножении цифр от 6 до 10). Пусть школьник бросает два кубика или вытягивает две карты из колоды.
Увидев цифры, вы перемножаете их на калькуляторе, а ребёнок проделывает ту же процедуру в уме. Кто быстрее справится, тот получает очко.
Игра может длиться, например, до 7 очков. Победитель получает оговорённый заранее приз.
11. Не превращайте обучение в стресс
Нередко, контролируя детскую учёбу, родители слишком увлекаются и совершают одни и те же ошибки. Вот чего нельзя делать ни в коем случае.
- Заставлять ребёнка заниматься, если он не хочет. Попытайтесь мотивировать: учёба должна быть интересной, а не превращаться в пытку.
- Ругать за ошибки и пугать плохими оценками.
- Ставить в пример одноклассников. Когда тебя с кем-то сравнивают, это неприятно. И нередко вызывает протест: «Раз я хуже, то вообще ничего учить не буду!»
- Учить сразу всё. Ребёнка легко напугать и утомить большим объёмом новой информации.
- Игнорировать успехи. Хвалите ребёнка, когда он справляется с заданиями. Это снизит стресс и вызовет стремление учиться дальше.
Этот материал впервые был опубликован в январе 2017 года. В июле 2020-го мы обновили текст.
*Деятельность Meta Platforms Inc. и принадлежащих ей социальных сетей Facebook и Instagram запрещена на территории РФ.
Табли́ца умноже́ния, она же табли́ца Пифаго́ра — таблица, где строки и столбцы озаглавлены множителями, а в ячейках таблицы находится их произведение. Используется для обучения школьников умножению.
Содержание
- 1 Изучение
- 2 Обычное представление
- 3 Как найти результат по таблице умножения
- 4 Применение
- 5 Обобщения
- 6 Таблица Кэли
- 6.1 Модулярная арифметика
- 7 См. также
- 8 Примечания
- 9 Ссылки
Изучение
В своё время введение заучиваемой наизусть таблицы умножения революционизировало устный и письменный счёт. До этого использовались разные хитрые способы вычисления произведений однозначных чисел, которые сильно замедляли весь процесс и служили источником дополнительных ошибок.
В российских школах значения традиционно доходят до 10×10. В Великобритании до 12×12, что связано в том числе с единицами английской системой мер длины (1 фут = 12 дюймов) и денежного обращения (существовавшей до 1971 г.: 1 фунт стерлингов = 20 шиллингам, 1 шиллинг = 12 пенсам).
В Советском Союзе таблицу умножения обычно «задавали на лето» после 1-го класса, а закрепляли на занятиях во 2-м классе (в возрасте 8 лет). В российских школах чаще всего проходят во 2-м классе. По стандартам английского школьного образования таблица умножения должна быть выучена к возрасту 11 лет (планируется ужесточение требования до 9 лет).[1]
Обычное представление
| × | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 | 26 | 28 | 30 | 32 | 34 | 36 | 38 | 40 |
| 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 | 33 | 36 | 39 | 42 | 45 | 48 | 51 | 54 | 57 | 60 |
| 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 | 44 | 48 | 52 | 56 | 60 | 64 | 68 | 72 | 76 | 80 |
| 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 | 100 |
| 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 | 66 | 72 | 78 | 84 | 90 | 96 | 102 | 108 | 114 | 120 |
| 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 | 77 | 84 | 91 | 98 | 105 | 112 | 119 | 126 | 133 | 140 |
| 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 | 88 | 96 | 104 | 112 | 120 | 128 | 136 | 144 | 152 | 160 |
| 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 | 99 | 108 | 117 | 126 | 135 | 144 | 153 | 162 | 171 | 180 |
| 10 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 110 | 120 | 130 | 140 | 150 | 160 | 170 | 180 | 190 | 200 |
| 11 | 11 | 22 | 33 | 44 | 55 | 66 | 77 | 88 | 99 | 110 | 121 | 132 | 143 | 154 | 165 | 176 | 187 | 198 | 209 | 220 |
| 12 | 12 | 24 | 36 | 48 | 60 | 72 | 84 | 96 | 108 | 120 | 132 | 144 | 156 | 168 | 180 | 192 | 204 | 216 | 228 | 240 |
| 13 | 13 | 26 | 39 | 52 | 65 | 78 | 91 | 104 | 117 | 130 | 143 | 156 | 169 | 182 | 195 | 208 | 221 | 234 | 247 | 260 |
| 14 | 14 | 28 | 42 | 56 | 70 | 84 | 98 | 112 | 126 | 140 | 154 | 168 | 182 | 196 | 210 | 224 | 238 | 252 | 266 | 280 |
| 15 | 15 | 30 | 45 | 60 | 75 | 90 | 105 | 120 | 135 | 150 | 165 | 180 | 195 | 210 | 225 | 240 | 255 | 270 | 285 | 300 |
| 16 | 16 | 32 | 48 | 64 | 80 | 96 | 112 | 128 | 144 | 160 | 176 | 192 | 208 | 224 | 240 | 256 | 272 | 288 | 304 | 320 |
| 17 | 17 | 34 | 51 | 68 | 85 | 102 | 119 | 136 | 153 | 170 | 187 | 204 | 221 | 238 | 255 | 272 | 289 | 306 | 323 | 340 |
| 18 | 18 | 36 | 54 | 72 | 90 | 108 | 126 | 144 | 162 | 180 | 198 | 216 | 234 | 252 | 270 | 288 | 306 | 324 | 342 | 360 |
| 19 | 19 | 38 | 57 | 76 | 95 | 114 | 133 | 152 | 171 | 190 | 209 | 228 | 247 | 266 | 285 | 304 | 323 | 342 | 361 | 380 |
| 20 | 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 | 180 | 200 | 220 | 240 | 260 | 280 | 300 | 320 | 340 | 360 | 380 | 400 |
Как найти результат по таблице умножения
Чтобы узнать результат произведения 4×8 по таблице умножения , нужно найти четвёрку в левом столбце и восьмёрку в верхней строке, провести от 4 горизонтальную линию и от 8 вертикальную. Клетка, на которой линии встречаются, является произведением (в данном случае 32).
| × | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 |
| 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 |
| 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 |
| 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
Применение
Помимо широко известного применения классической таблицы умножения для выработки практических навыков умножения натуральных чисел, её можно использовать в некоторых математических доказательствах, например, при выводе формулы суммы кубов натуральных чисел или получении подобного выражения для суммы квадратов[2].
Обобщения
Наряду с таблицей умножения, в некоторых случаях бывают удобны таблицы сложения.
Таблица Кэли
Таблица Кэли — в абстрактной алгебре, таблица, которая описывает структуру конечных алгебраических систем с одной бинарной операцией. Названа в честь английского математика Артура Кэли. Имеет важное значение в дискретной математике, в частности, в теории групп, в которой в качестве операций рассматриваются умножение и сложение. Таблица позволяет определить, является ли группа абелевой, найти центр группы и обратные элементы по отношению к другим элементам в этой группе.
В высшей алгебре таблицы Кэли могут также использоваться для определения бинарных операций в полях, кольцах и других алгебраических структурах. Также они удобны при проведении действий в данных структурах.
Модулярная арифметика
Все остатки от деления на натуральное число образуют кольцо, а от деления на простое число — поле. Это иллюстрируется таблицами умножения:
Таблица умножения в кольце вычетов по модулю 8
| × | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 2 | 0 | 2 | 4 | 6 | 0 | 2 | 4 | 6 |
| 3 | 0 | 3 | 6 | 1 | 4 | 7 | 2 | 5 |
| 4 | 0 | 4 | 0 | 4 | 0 | 4 | 0 | 4 |
| 5 | 0 | 5 | 2 | 7 | 4 | 1 | 6 | 3 |
| 6 | 0 | 6 | 4 | 2 | 0 | 6 | 4 | 2 |
| 7 | 0 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
Таблица умножения в поле вычетов по модулю 5
| × | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 2 | 3 | 4 |
| 2 | 0 | 2 | 4 | 1 | 3 |
| 3 | 0 | 3 | 1 | 4 | 2 |
| 4 | 0 | 4 | 3 | 2 | 1 |
См. также
- Умножение
- Деление (математика)
- Сложение
- Вычитание
Примечания
- ↑ Children must learn times tables by age nine… // Daily Mail, 17.12.2011
- ↑ Роу С. Геометрические упражнения с куском бумаги. — 2-е изд. — Одесса: Матезис, 1923. — С. 68—72.
Ссылки
- Способ Пифагора
Таблица умножения
Таблица умножения — таблица, где строки и столбцы озаглавлены множителями, а ячейки таблицы содержат их произведение. Таблица применяется для обучения умножению.
Таблица умножения чисел от 1 до 10
| × 1 | × 2 | × 3 | × 4 | × 5 |
| 1 × 1 = 1 1 × 2 = 2 1 × 3 = 3 1 × 4 = 4 1 × 5 = 5 1 × 6 = 6 1 × 7 = 7 1 × 8 = 8 1 × 9 = 9 1 × 10 = 10 |
2 × 1 = 2 2 × 2 = 4 2 × 3 = 6 2 × 4 = 8 2 × 5 = 10 2 × 6 = 12 2 × 7 = 14 2 × 8 = 16 2 × 9 = 18 2 × 10 = 20 |
3 × 1 = 3 3 × 2 = 6 3 × 3 = 9 3 × 4 = 12 3 × 5 = 15 3 × 6 = 18 3 × 7 = 21 3 × 8 = 24 3 × 9 = 27 3 × 10 = 30 |
4 × 1 = 4 4 × 2 = 8 4 × 3 = 12 4 × 4 = 16 4 × 5 = 20 4 × 6 = 24 4 × 7 = 28 4 × 8 = 32 4 × 9 = 36 4 × 10 = 40 |
5 × 1 = 5 5 × 2 = 10 5 × 3 = 15 5 × 4 = 20 5 × 5 = 25 5 × 6 = 30 5 × 7 = 35 5 × 8 = 40 5 × 9 = 45 5 × 10 = 50 |
| × 6 | × 7 | × 8 | × 9 | × 10 |
| 6 × 1 = 6 6 × 2 = 12 6 × 3 = 18 6 × 4 = 24 6 × 5 = 30 6 × 6 = 36 6 × 7 = 42 6 × 8 = 48 6 × 9 = 54 6 × 10 = 60 |
7 × 1 = 7 7 × 2 = 14 7 × 3 = 21 7 × 4 = 28 7 × 5 = 35 7 × 6 = 42 7 × 7 = 49 7 × 8 = 56 7 × 9 = 63 7 × 10 = 70 |
8 × 1 = 8 8 × 2 = 16 8 × 3 = 24 8 × 4 = 32 8 × 5 = 40 8 × 6 = 48 8 × 7 = 56 8 × 8 = 64 8 × 9 = 72 8 × 10 = 80 |
9 × 1 = 9 9 × 2 = 18 9 × 3 = 27 9 × 4 = 36 9 × 5 = 45 9 × 6 = 54 9 × 7 = 63 9 × 8 = 72 9 × 9 = 81 9 × 10 = 90 |
10 × 1 = 10 10 × 2 = 20 10 × 3 = 30 10 × 4 = 40 10 × 5 = 50 10 × 6 = 60 10 × 7 = 70 10 × 8 = 80 10 × 9 = 90 10 × 10 = 100 |
Таблица умножения чисел от 1 до 20
| × | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 | 26 | 28 | 30 | 32 | 34 | 36 | 38 | 40 |
| 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 | 33 | 36 | 39 | 42 | 45 | 48 | 51 | 54 | 57 | 60 |
| 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 | 44 | 48 | 52 | 56 | 60 | 64 | 68 | 72 | 76 | 80 |
| 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 | 100 |
| 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 | 66 | 72 | 78 | 84 | 90 | 96 | 102 | 108 | 114 | 120 |
| 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 | 77 | 84 | 91 | 98 | 105 | 112 | 119 | 126 | 133 | 140 |
| 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 | 88 | 96 | 104 | 112 | 120 | 128 | 136 | 144 | 152 | 160 |
| 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 | 99 | 108 | 117 | 126 | 135 | 144 | 153 | 162 | 171 | 180 |
| 10 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 110 | 120 | 130 | 140 | 150 | 160 | 170 | 180 | 190 | 200 |
| 11 | 11 | 22 | 33 | 44 | 55 | 66 | 77 | 88 | 99 | 110 | 121 | 132 | 143 | 154 | 165 | 176 | 187 | 198 | 209 | 220 |
| 12 | 12 | 24 | 36 | 48 | 60 | 72 | 84 | 96 | 108 | 120 | 132 | 144 | 156 | 168 | 180 | 192 | 204 | 216 | 228 | 240 |
| 13 | 13 | 26 | 39 | 52 | 65 | 78 | 91 | 104 | 117 | 130 | 143 | 156 | 169 | 182 | 195 | 208 | 221 | 234 | 247 | 260 |
| 14 | 14 | 28 | 42 | 56 | 70 | 84 | 98 | 112 | 126 | 140 | 154 | 168 | 182 | 196 | 210 | 224 | 238 | 252 | 266 | 280 |
| 15 | 15 | 30 | 45 | 60 | 75 | 90 | 105 | 120 | 135 | 150 | 165 | 180 | 195 | 210 | 225 | 240 | 255 | 270 | 285 | 300 |
| 16 | 16 | 32 | 48 | 64 | 80 | 96 | 112 | 128 | 144 | 160 | 176 | 192 | 208 | 224 | 240 | 256 | 272 | 288 | 304 | 320 |
| 17 | 17 | 34 | 51 | 68 | 85 | 102 | 119 | 136 | 153 | 170 | 187 | 204 | 221 | 238 | 255 | 272 | 289 | 306 | 323 | 340 |
| 18 | 18 | 36 | 54 | 72 | 90 | 108 | 126 | 144 | 162 | 180 | 198 | 216 | 234 | 252 | 270 | 288 | 306 | 324 | 342 | 360 |
| 19 | 19 | 38 | 57 | 76 | 95 | 114 | 133 | 152 | 171 | 190 | 209 | 228 | 247 | 266 | 285 | 304 | 323 | 342 | 361 | 380 |
| 20 | 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 | 180 | 200 | 220 | 240 | 260 | 280 | 300 | 320 | 340 | 360 | 380 | 400 |
Содержание
Часто родители и педагоги предпочитают обучать детей таблице умножения с помощью печатных материалов: таблиц, карточек, мнемокарточек, самодельных игр. Это особенно актуально, если ребенок проводит слишком много времени в гаджетах, ведь распечатки и игры не только позволяют родителю отвлечь ребенка от цифрового мира, но и занять его более полезной деятельностью.
- Карточки по таблице умножения
- Таблица умножения
- Примеры из таблицы умножения без ответов
- Таблица умножения без ответов вразброс
- Таблица умножения А4
- Таблица умножения на 12
- Сделай таблицу умножения
- Игра на пальцы
Карточки по таблице умножения
Карточки по таблице умножения представляют собой отличный инструмент для обучения ребенка. Они могут быть сделаны из бумаги, картона или какого-то другого материала, который вы сами посчитаете подходящим. Цвет карточек вы можете выбирать на свое усмотрение, но для работы с детьми лучше, чтобы они были цветными, т.к. черно-белые будут слишком скучными. Если говорить о размере, то для совсем малышей стоит делать карточки побольше – во-первых, на них лучше видно, что написано, а во-вторых, они будут удобнее для детских ручек, да и карточки большего размера имеют меньше шансов куда-то завалиться и быть потерянными.
Что же касается наполнения, то на таких карточках, как правило, просто пишутся примеры заданий, которые нужно решить. При желании на обратной стороне можно разместить правильные ответы. В Интернете сегодня можно найти множество уже готовых карточек, которые нужно лишь распечатать и вырезать. Но, вооружившись цветным картоном, ножницами и маркерами, вы в состоянии сделать их и своими руками. А особенно замечательно будет, если в процессе будет принимать участие ваш ребенок.
Вот несколько примеров таких карточек:
А скачать файл в формате PDF с листами А4 для распечатки и вырезания карточек вы можете тут:
Скачать карточкиdownload
Таблица умножения
Скачать горизонтальнуюdownload
Скачать вертикальнуюdownload
Распечатанная таблица умножения – еще один потрясающий вариант для занятий с ребенком. По сути, тут можно провести полную аналогию с карточками. Уже готовые таблицы можно найти в Интернете, причем в самых разных вариациях, либо сделать самостоятельно, придав им тот вид, который хочется, например, нарисовать на цветном картоне, дополнив изображениями любимых мультяшных или сказочных героев своего чада, украсив блестящими звездочками или другими элементами.
Данный вариант подходит для непосредственного запоминания правильных произведений чисел и их ответов. Кстати, распечатанные таблицы умножения можно повесить в нескольких местах своего жилища (обязательно – в детской), чтобы они сами собой попадали в поле зрения ребенка. Но здесь стоит иметь в виду, что такие распечатки (или собственные поделки) обязательно должны вызывать в малыше любопытство, а потому рекомендуется, чтобы они были красочными, яркими и привлекающими внимание.
Несколько примеров таких таблиц мы приводим ниже:

Примеры из таблицы умножения без ответов
Скачать горизонтальнуюdownload
Скачать вертикальнуюdownload
Примеры из таблицы умножения – это аналог распечатанной таблицы умножения с одной лишь разницей в том, что здесь нет ответов, а вместо них присутствуют пустые поля. И в этом случае вашему ребенку каждый раз придется вспоминать правильный ответ, глядя на таблицу. Между тем, это хороший способ тренировки памяти и решения простейших математических задач. А чтобы малышу было проще вспомнить ответ, рядом с пустыми клеточками можно разместить какие-нибудь фигуры, которые будут вызывать ассоциации в сознании ребенка (например, рядом с клеточкой, где должна стоять цифра 2, можно разместить лебедя и т.п.)
Если вас интересует озвученный вариант, таблицу умножения без ответов придется сделать самостоятельно, т.к. в Интернете подобных вариаций нет. В том же случае, если развитие ассоциативного мышления на текущем этапе для вас непринципиально, в вашем распоряжении огромное количество готовых для печати шаблонов. А сами такие распечатки можно использовать и для проверки знаний на домашних уроках, но тогда вам потребуется либо иметь на руках несколько распечаток, чтобы каждый раз выдавать ребенку новую, либо искать в магазинах варианты для письма маркером (ответы потом просто стираются). Таблицы без ответов служат отличным дополнением к таблицам с ответами.
И снова несколько примеров:

Таблица умножения без ответов вразброс
Скачать горизонтальнуюdownload
Скачать вертикальнуюdownload
Таблицы умножения без ответов вразброс – это логическое продолжение обычных таблиц без ответов. Нюанс же состоит в том, что примеры из таблицы расположены на распечатке не по порядку, а хаотично. Работая с такими таблицами, ребенок будет лучше использовать память и мышление, потому как здесь уже не дашь правильного ответа на автомате, ведь при заучивании таблицы по порядку ответы запоминаются по нарастающей от меньшего к большему, что впоследствии может приводить к трудностям.
Если же ваш ребенок начнет заниматься с таблицами, где примеры даются в любом порядке, это поможет ему избавиться от автоматизма при решении. Буквально каждый раз ему придется либо искать в голове правильный ответ, копаясь в том, что он запомнил, либо самостоятельно решать примеры. И стоит заметить, что именно последнее позволяет освоить таблицу умножения максимально эффективно, т.к. в процессе ребенок не просто вспоминает, а считает по-настоящему.
Чтобы было понятнее, о чем идет речь, взгляните на примеры:

Таблица умножения А4
Скачать с ответамиdownload
Скачать без ответовdownload
Здесь мы снова повторимся, т.к. в данном случае вы просто распечатываете таблицы умножения (черно-белые таблицы, цветные таблицы, таблицы с иллюстрациями, таблицы с ответами, таблицы без ответов, таблицы умножения вразброс) в формате А4. Этот формат очень удобен, т.к. является универсальным, и при необходимости вы можете собрать целое учебное пособие для своего ребенка.
Можно, конечно, использовать любой формат, но именно листы А4 удобно складывать в отдельные файлы и папки. Это позволяет держать все, что нужно, в одном месте, и даже носить с собой, не боясь, что что-то потеряется или «куда-то денется», как это часто бывает. А еще в формате А4 делают большинство альбомов для рисования. Поэтому и те таблицы, которые вы сделаете своими руками, вы сможете хранить вместе с распечатанными из Интернета.
Таблицы в формате А4 могут выглядеть так:

Таблица умножения до 12 для печати
Скачать с ответамиdownload
Скачать без ответовdownload
В американских школах часто учат таблицу умножения не только до 10, но и до 12. Это стандартная часть математики, которую обычно изучают в начальной школе, однако, некоторые школы учат таблицу умножения до 20 и даже до 100. Обучение таблице умножения является важным этапом развития умений выполнять арифметические операции и понимать понятие множественности.
А подробнее про то, как выучить таблицу умножения до двенадцати, читайте в этом материале.
Сделай таблицу умножения
Самодельная таблица умножения хороша тем, что практически не ограничивает фантазию своего создателя. Она может быть любого цвета, любого размера и любого наполнения, и при этом ее вовсе не обязательно именно рисовать. Так, вместе со своим ребенком вы можете сделать коллаж, составленный из вырезок из газет и журналов, вылепить цифры и знаки из пластилина и закрепить на пластиковой кухонной дощечке, собрать из конструктора или составить из маленьких игрушек из «Киндер-сюрприза».
Помимо того, что ребенок будет учить таблицу умножения, уже в процессе ее создания станут развиваться его творческое мышление и креативность, нестандартный подход к решению задач, фантазия и логическое мышление. Такая активность будет содействовать развитию мелкой моторики и правильной координации движений ребенка. А еще он будет учиться усидчивости, обязательности, умению доводить начатое до конца и, конечно же, аккуратности. Говорить о том, что это прекрасное совместное времяпрепровождение, укрепляющее отношения в семье, думаем, излишне.
А вот что вы можете сделать своими руками:


Игра на пальцы
Как вы знаете, дети очень любят играть, а если игры на самом деле необычные и забавные, то интерес ребенка будет поистине неиссякаем. И одной из таких оригинальных игр является игра на пальцы. Все, что вам нужно, – это распечатать шаблоны, вырезать их ножницами и дальше следовать инструкции.
Итак, распечатайте эти шаблоны так, чтобы они были на всю ширину листа А4:



Далее вырежьте каждый шаблон:
Согните таким образом:
Переверните шаблон на другую сторону:
Согните шаблон еще раз:
И еще раз:
Должна получиться такая конструкция:
Все! Ваше оригами для таблицы умножения готово! Осталось лишь надеть на пальцы и научиться пользоваться:
Эту поделку мы нашли на сайте petit-fernand.co.uk, и если вы хотите обратиться к оригинальной инструкции, переходите по этой ссылке.
Надеемся, теперь вы знаете, как превратить изучение таблицы умножения с ребенком в интересный и увлекательный процесс. Не боитесь экспериментировать, применять творческий подход и превращать обучение в игру – тогда и результат не заставит себя долго ждать!