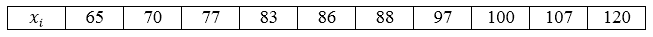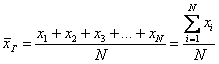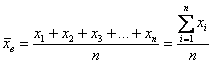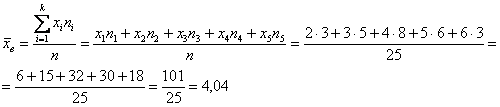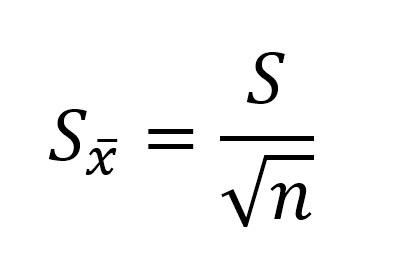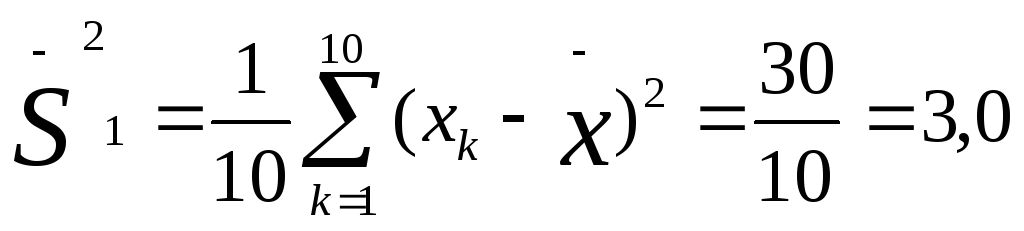Как пишется выборочное среднее - Правописание и грамматика

ВЫ́БОРОЧНЫЙ, —ая, —ое. Не сплошной, частичный. Выборочная проверка. Выборочная пахота. Выборочная рубка леса.

Все значения слова «выборочный»

СРЕ́ДНИЙ, —яя, —ее. 1. Находящийся в середине между двумя точками, линиями, предметами и т. п., равноудаленный от краев чего-л. Среднее окно. Средняя полоса России. Среднее течение реки.

Все значения слова «средний»

Выборочная средняя (ХВ) определяется как среднее арифметическое значение вариант статистического ряда.
Оказалось, что, когда процесс находится в статистически управляемом состоянии, нет необходимости вообще в проведении статистических выборочных исследований, поскольку, вопреки ожиданиям, они не добавляют информации о системе сверх той, что уже содержится в выборочном среднем и выборочном размахе, которые получены ранее (последние исследования в области контрольных карт показывают, что это утверждение справедливо при определённых допущениях о характере процессов).
Наиболее распространёнными характеристиками статистического распределения являются средние величины: мода, медиана и средняя арифметическая (или выборочная средняя).
(все предложения)

среднее геометрическое
среднее арифметическое
выборочная дисперсия
состоятельная оценка
многомерное нормальное распределение
(ещё синонимы…)

выбор
(ещё ассоциации…)

палец
средневековье
рост
посредник
середина
(ещё ассоциации…)

выборочная проверка
выборочная совокупность
выборочный контроль
(полная таблица сочетаемости…)

средний рост
мужчина средних лет
показать средний палец
(полная таблица сочетаемости…)

Разбор по составу слова «выборочный»
Разбор по составу слова «средний»

Как правильно пишется слово «выборочный»
Как правильно пишется слово «средний»

Источник

Эксперт по предмету «Математика»

Задать вопрос автору статьи

Генеральная средняя

Пусть нам дана генеральная совокупность относительно случайной величины $X$. Для начала напомним следующее определение:

Определение 1

Генеральная совокупность — совокупность случайно отобранных объектов данного вида, над которыми проводят наблюдения с целью получения конкретных значений случайной величины, проводимых в неизменных условиях при изучении одной случайной величины данного вида.

Определение 2

Генеральная средняя — среднее арифметическое значений вариант генеральной совокупности.

Пусть значения вариант $x_1, x_2,dots ,x_k$ имеют, соответственно, частоты $n_1, n_2,dots ,n_k$. Тогда генеральная средняя вычисляется по формуле:

Тренируй мозг с удовольствием

Развивай память, внимание и мышление c помощью онлайн-тренажеров

Выбрать программу

Рассмотрим частный случай. Пусть все варианты $x_1, x_2,dots ,x_k$ различны. В этом случае $n_1, n_2,dots ,n_k=1$. Получаем, что в этом случае генеральная средняя вычисляется по формуле:

Выборочная средняя

Пусть нам дана выборочная совокупность относительно случайной величины $X$. Для начала напомним следующее определение:

Определение 3

Выборочная совокупность — часть отобранных объектов из генеральной совокупности.

Определение 4

Выборочная средняя — среднее арифметическое значений вариант выборочной совокупности.

Пусть значения вариант $x_1, x_2,dots ,x_k$ имеют, соответственно, частоты $n_1, n_2,dots ,n_k$. Тогда выборочная средняя вычисляется по формуле:

Рассмотрим частный случай. Пусть все варианты $x_1, x_2,dots ,x_k$ различны. В этом случае $n_1, n_2,dots ,n_k=1$. Получаем, что в этом случае выборочная средняя вычисляется по формуле:

«Средняя выборки: генеральная, выборочная» 👇

!!! В случае, когда значение вариант не являются дискретными, а представляют из себя интервалы, то в формулах для вычисления генеральной или выборочной средних значений за значение $x_i$ принимается значение середины интервала, которому принадлежит $x_i.$

Примеры задач на нахождение средней выборки

Пример 1

В магазин завезли 10 видов шоколадных конфет. По ним проведена следующая выборка по цене за килограмм: 70, 65, 97, 83, 120, 107, 77, 88, 100, 86. Построить ряд распределения данной генеральной совокупности и найти её генеральное среднее.

Решение.

Видим, что все значения вариант различны, поэтому частоты равны единице. Ряд распределения можно записать следующим образом, перечислив значения вариант в порядке возрастания:

Рисунок 1.

Так как наша совокупность является генеральной и все варианты различны, то мы будем пользоваться следующей формулой:

[overline{x_г}=frac{sumlimits^k_{i=1}{x_i}}{n}]

Получим:

[overline{x_г}=frac{65+70+77+83+86+88+97+100+107+120}{10}=89,3]

Ответ: 89,3.

Пример 2

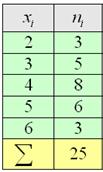
Выборочная совокупность задана следующей таблицей распределения:

Рисунок 2.

Найти среднее выборочное данной совокупности.

Решение.

Для нахождения значения выборочной средней будем пользоваться следующей формулой:

[overline{x_в}=frac{sumlimits^k_{i=1}{x_in_i}}{n}]

Обычно, для наглядности и удобности вычислений составляется расчетная таблица, в которую входят необходимые промежуточные вычисления. В нашем случае составим таблицу со следующей «шапкой»:

Рисунок 3.

Внизу таблицы также добавляется строка «итог», в которой подсчитывается сумма по всем значениям столбцов. Проведя необходимые вычисления, получим следующую расчетную таблицу:

Рисунок 4.

Используя формулу, получим:

[overline{x_в}=frac{sumlimits^k_{i=1}{x_in_i}}{n}=frac{305}{20}=15,25]

Ответ: 15,25.

Пример 3

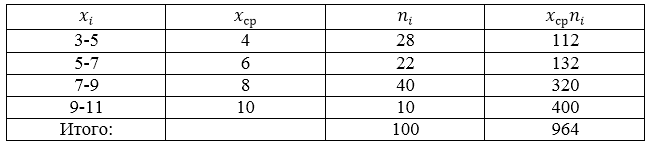
Проводится социальный опрос среди 100 пенсионеров об уровне их пенсии. Получена следующая таблица распределения результатов опроса (размер пенсии указан в тысячах рублей):

Рисунок 5.

Найти среднее выборочное данной совокупности.

Данная совокупность является выборочной, поэтому будем пользоваться следующей формулой:

[overline{x_в}=frac{sumlimits^k_{i=1}{x_in_i}}{n}]

Составим, для начала, расчетную таблицу.

Рисунок 6.

Получаем:

[overline{x_в}=frac{sumlimits^k_{i=1}{x_in_i}}{n}=frac{964}{100}=9,64]

Ответ: 9,64.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

выборочное среднее

выборочное среднее: 3.19 выборочное среднее (sample mean) :Сумма n значений х_i выборочных единиц, деленная на объем выборки п

Смотри также родственные термины:

2.25. Выборочное среднее арифметическое

где n — объем выборки;

x_i — результат измерения i-ой единицы.

Оценка х является состоятельной и несмещенной оценкой среднего значения в совокупности

2.27. Выборочное среднее квадратическое отклонение

Оценка не является несмещенной

Полезное

Смотреть что такое «выборочное среднее» в других словарях:

ВЫБОРОЧНОЕ СРЕДНЕЕ — наблюдений х1, …, хn есть В. с. является состоятельной, несмещенной, эффективной оценкой математического ожидания случайной величины X. Если совокупность распределена нормально (см. Распределение нормальное) с параметрами (a , s ), то… … Геологическая энциклопедия
выборочное среднее — математическое ожидание — [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность Синонимы математическое ожидание EN sample meanpopulation mean … Справочник технического переводчика
Выборочное среднее — Выборочное (эмпирическое) среднее это приближение теоретического среднего распределения, основанное на выборке из него. Определение Пусть выборка из распределения вероятности, определённая на некотором вероятностном пространстве .… … Википедия
Выборочное среднее арифметическое — 2.25. Выборочное среднее арифметическое где n объем выборки; xi результат измерения i ой единицы. Оценка х является состоятельной и несмещенной оценкой среднего значения в совокупности Источник … Словарь-справочник терминов нормативно-технической документации
Выборочное среднее квадратическое отклонение — 2.27. Выборочное среднее квадратическое отклонение Оценка не является несмещенной Источник … Словарь-справочник терминов нормативно-технической документации
выборочное среднее — Арифметическое среднее наблюдений, составляющих выборку, т.е. сумма всех наблюдений, деленная на их количество: (x1 x2 … xn)/n. Является одной из наиболее частых оценок среднего совокупности. Это мера положения, часто обозначается . Величина… … Словарь социологической статистики
ВЫБОРОЧНОЕ СРЕДНЕЕ — математическое ожидание эмпирического распределения … Математическая энциклопедия
Среднее арифметическое — У этого термина существуют и другие значения, см. среднее значение. В математике и статистике среднее арифметическое одна из наиболее распространённых мер центральной тенденции, представляющая собой сумму всех наблюденных значений деленную на их… … Википедия
СРЕДНЕЕ, ИСТИННОЕ (или ПОПУЛЯЦИЯ) — Теоретическое значение, представляющее среднее полного набора всех возможных рассматриваемых значений. Полученное или выборочное среднее – всегда наилучшая оценка этого истинного среднего … Толковый словарь по психологии
Среднее значение (выборочное) — среднеарифметическое из частных значений, образующих выборку независимых друг от друга и от пространственных координат величин. Источник: ГОСТ 20522 96: Грунты. Методы статистической обработки результатов испытаний … Словарь-справочник терминов нормативно-технической документации

Источник

3.1. Показатели центральной тенденции

Простейший пример такого показателя нам уже встречался – это среднее арифметическое значение. Но средней

дело не ограничивается, впрочем, обо всём по порядку:

3.1.1. Генеральная и выборочная средняя

Пусть исследуется некоторая генеральная совокупность объёма , а именно её числовая характеристика , не важно, дискретная или непрерывная.

Генеральной средней называют среднее арифметическое всех значений этой совокупности:

Если среди чисел есть одинаковые (что

характерно для дискретного ряда), то формулу можно записать в более компактном

виде:
, где:
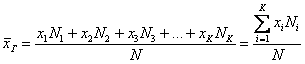
варианта повторяется раз;
варианта – раз;
варианта – раз;
…
варианта – раз.

Живой пример вычисления генеральной средней встретился в Примере 2, но чтобы не занудничать, я даже не буду

напоминать его содержание. Далее.

Как мы помним, обработка всей генеральной совокупности часто затруднена либо невозможна, и поэтому из неё организуют представительную выборку объема , и на основании исследования этой выборки делают вывод обо всей совокупности.

Выборочной средней называется среднее арифметическое всех значений выборки:

и при наличии одинаковых вариант формула запишется компактнее:
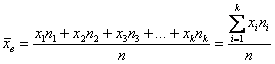
– как сумма произведений вариант на соответствующие частоты , делённая на объём совокупности .

Выборочная средняя позволяет достаточно

точно оценить истинное значение , при этом, чем

больше выборка, тем точнее будет эта оценка.

Практику начнём с дискретного вариационного ряда и знакомого условия:

Пример 8

По результатам выборочного исследования рабочих цеха были установлены их квалификационные разряды: 4, 5, 6, 4, 4, 2, 3, 5, 4,

4, 5, 2, 3, 3, 4, 5, 5, 2, 3, 6, 5, 4, 6, 4, 3.

Это числа из Примера 4, но теперь нам требуется: вычислить выборочную среднюю, и, не отходя от станка, найти моду

и медиану.

Как решать задачу? Если нам даны первичные данные (конкретные варианты ), то их можно тупо просуммировать и разделить результат на объём

выборки:
– средний квалификационный разряд рабочих

цеха.

Но здесь удобнее составить вариационный ряд:

и использовать «цивилизованную» формулу:

3.1.2. Мода

3. Основные показатели статистической совокупности

| Оглавление |

Источник

Что такое 24wiki.ru
Наш сайт — это статьи из сайта википедии, написанные на более понятном языке. Он открыт для любого пользователя. 24wiki.ru это библиотека, которая является общественной.

Основа этой страницы находится в 24wiki.ru. Текст доступен по лицензии CC BY-SA 3.0 Unported License.

Wiki® — зарегистрированный товарный знак организации Wiki Foundation, Inc. 24wiki.ru является независимой компанией и не аффилирована с Фондом Викимедиа (Wikimedia Foundation). 24wiki.ru — НЕофициальный сайт Википедии!

E-mail: admin@24wiki.ru

Источник

Представление результатов исследования

В научных публикациях важно представление результатов исследования. Очень часто окончательный результат приводится в следующем виде: M±m, где M – среднее арифметическое, m –ошибка среднего арифметического. Например, 163,7±0,9 см.

Прежде чем разбираться в правилах представления результатов исследования, давайте точно усвоим, что же такое ошибка среднего арифметического.

Ошибка среднего арифметического

Среднее арифметическое, вычисленное на основе выборочных данных (выборочное среднее), как правило, не совпадает с генеральным средним (средним арифметическим генеральной совокупности). Экспериментально проверить это утверждение невозможно, потому что нам неизвестно генеральное среднее. Но если из одной и той же генеральной совокупности брать повторные выборки и вычислять среднее арифметическое, то окажется, что для разных выборок среднее арифметическое будет разным.

Чтобы оценить, насколько выборочное среднее арифметическое отличается от генерального среднего, вычисляется ошибка среднего арифметического или ошибка репрезентативности.

Ошибка среднего арифметического обозначается как m или

Ошибка среднего арифметического рассчитывается по формуле:

где: S — стандартное отклонение, n – объем выборки; Например, если стандартное отклонение равно S=5 см, объем выборки n=36 человек, то ошибка среднего арифметического равна: m=5/6 = 0,833.

Ошибка среднего арифметического показывает, какая ошибка в среднем допускается, если использовать вместо генерального среднего выборочное среднее.

Так как при небольшом объеме выборки истинное значение генерального среднего не может быть определено сколь угодно точно, поэтому при вычислении выборочного среднего арифметического нет смысла оставлять большое число значащих цифр.

Правила записи результатов исследования

В записи ошибки среднего арифметического оставляем две значащие цифры, если первые цифры в ошибке «1» или «2».
В остальных случаях в записи ошибки среднего арифметического оставляем одну значащую цифру.
В записи среднего арифметического положение последней значащей цифры должно соответствовать положению первой значащей цифры в записи ошибки среднего арифметического.

Представление результатов научных исследований

В своей статье «Осторожно, статистика!», опубликованной в 1989 году В.М. Зациорский указал, какие числовые характеристики должны быть представлены в публикации, чтобы она имела научную ценность. Он писал, что исследователь «…должен назвать: 1) среднюю величину (или другой так называемый показатель положения); 2) среднее квадратическое отклонение (или другой показатель рассеяния) и 3) число испытуемых. Без них его публикация научной ценности иметь не будет “с. 52

В научных публикациях в области физической культуры и спорта очень часто окончательный результат приводится в виде: (М±m) (табл.1).

Таблица 1 — Изменение механических свойств латеральной широкой мышцы бедра под воздействием физической нагрузки (n=34)

	Эффективный модуль упругости (Е), кПа	Эффективный модуль вязкости (V), Па с
Этап эксперимента	Рассл.	Напряж.	Рассл.	Напряж.
До ФН	7,0±0,3	17,1±1,4	29,7±1,7	46±4
После ФН	7,7±0,3	18,7±1,4	30,9±2,0	53±6

Литература

Высшая математика и математическая статистика: учебное пособие для вузов / Под общ. ред. Г. И. Попова. – М. Физическая культура, 2007.– 368 с.
Гласс Дж., Стэнли Дж. Статистические методы в педагогике и психологии. М.: Прогресс. 1976.- 495 с.
Зациорский В.М. Осторожно — статистика! // Теория и практика физической культуры, 1989.- №2.
Катранов А.Г. Компьютерная обработка данных экспериментальных исследований: Учебное пособие/ А. Г. Катранов, А. В. Самсонова; СПб ГУФК им. П.Ф. Лесгафта. – СПб.: изд-во СПб ГУФК им. П.Ф. Лесгафта, 2005. – 131 с.
Основы математической статистики: Учебное пособие для ин-тов физ. культ / Под ред. В.С. Иванова.– М.: Физкультура и спорт, 1990. 176 с.

Источник

Выборочное среднее

Выборочное
среднее
значение как статистический показатель
представляет
собой среднюю оценку изучаемого в
эксперименте психологического качества.

Эта
оценка характеризует степень его
развития
в целом у той группы испытуемых, которая
была подвергнута
психодиагностическому обследованию.
Сравнивая непосредственно средние
значения двух или нескольких выборок,
мы
можем судить об относительной степени
развития у людей, составляющих эти
выборки, оцениваемого качества.

Выборочное
среднее определяется при помощи следующей
формулы:

где

х_ср
—выборочная
средняя величина или среднее арифметическое
значение по выборке;

п —
количество
испытуемых в выборке
или частных психодиагностических
показателей, на основе которых
вычисляется средняя величина;

x_k
— частные
значения показателей
у отдельных испытуемых. Всего таких
показателей п,
поэтому
индекс k
данной
переменной принимает значения от 1 до
п;

∑ — принятый
в математике знак суммирования величин
тех
переменных, которые находятся справа
от этого знака.

Выражение

соответственно означает сумму всех х
с индексом k
от 1 до n.

Пример.
Допустим,
что в результате применения
психодиагностической
методики для оценки некоторого
психологического
свойства у десяти испытуемых мы получили
следующие частные
показатели степени развитости данного
свойства у отдельных
испытуемых: х₁=
5,
х₂
=
4, х₃
= 5,
х₄
= 6,
х₅
= 7,
х₆
= 3,
х₇
= 6,
х₈₌
2,
х₉=
8,
х₁₀
⁼
4. Следовательно, п
= 10,
а индекс k
меняет
свои значения от 1 до 10 в приведенной
выше формуле. Для данной выборки
среднее значение¹,
вычисленное по этой формуле, будет
равно:

¹
В дальнейшем, как это и принято в
математической статистике, с целью
сокращения
текста мы будем опускать слова «выборочное»
и «арифметическое» и просто говорить
о «среднем» или «среднем значении».

В
психодиагностике и в экспериментальных
психолого-педагогических исследованиях
среднее,
как правило, не вычисляется
с точностью, превышающей один, два знака
после запятой, т.е.
с большей, чем десятые или сотые доли
единицы.

В
психодиагностических обследованиях
большая точность расчетов не требуется
и не имеет смысла, если принять во
внимание приблизительность тех оценок,
которые в них получаются, и достаточность
таких оценок для производства сравнительно
точных расчетов.

Дисперсия

Дисперсия
как статистическая, величина характеризует,
насколько
частные значения отклоняются от средней
величины в данной
выборке.

Чем
больше дисперсия, тем больше отклонения
или разброс данных. Прежде чем представлять
формулу для расчетов
дисперсии, рассмотрим пример. Воспользуемся
теми первичными
данными, которые были приведены ранее
и на основе которых вычислялась в
предыдущем примере средняя величина.
Мы видим, что все они разные и отличаются
не только друг от
друга, но и от средней величины. Меру их
общего отличия от средней
величины и характеризует дисперсия. Ее
определяют для того,
чтобы можно было отличать друг от друга
величины, имеющие
одинаковую среднюю, но разный разброс.

Представим
себе другую, отличную от предыдущей
выборку первичных значений,
например такую: 5, 4, 5, 6, 5, 6, 5, 4, 5, 5. Легко
убедиться в том, что ее средняя величина
также равна 5,0. Но в данной выборке
ее отдельные частные значения отличаются
от средней гораздо
меньше, чем в первой выборке. Выразим
степень этого отличия
при помощи дисперсии, которая определяется
по
следующей
формуле:

где

— выборочная
дисперсия, или просто дисперсия;

— выражение,
означающее, что для всех x_k
от
первого
до последнего в данной выборке необходимо
вычислить разности
между частными и средними значениями,
возвести эти разности
в квадрат и просуммировать;

п —
количество
испытуемых в выборке или первичных
значений,
по которым вычисляется дисперсия.

Заметим,
что во многих изданиях дисперсию принято
обозначать как D(x).

Определим
дисперсии для двух приведенных выше
выборок частных
значений, обозначив эти дисперсии
соответственно индексами
1 и 2:

Мы
видим, что дисперсия по второй выборке
(0,4) значительно меньше дисперсии по
первой выборке (3,0). Если бы не было
дисперсии,
то мы не в состоянии были бы различить
данные выборки.

Соседние файлы в папке МатМетоды в Психологии (литература)

#
#
13.02.201616.87 Mб1462Наследов А.Д. IBM SPSS Statistics 20 профессиональный анализ данных.pdf
#

Источник

Генеральная средняя

Выборочная средняя

Примеры задач на нахождение средней выборки

выборочное среднее

Смотри также родственные термины:

Полезное

Смотреть что такое «выборочное среднее» в других словарях:

3.1. Показатели центральной тенденции

3.1.1. Генеральная и выборочная средняя

Представление результатов исследования

Ошибка среднего арифметического

Правила записи результатов исследования

Представление результатов научных исследований

Литература

Выборочное среднее

Дисперсия