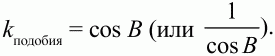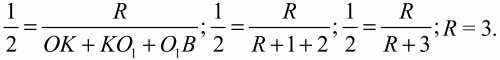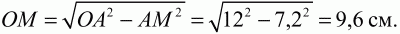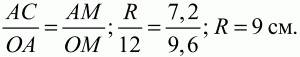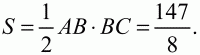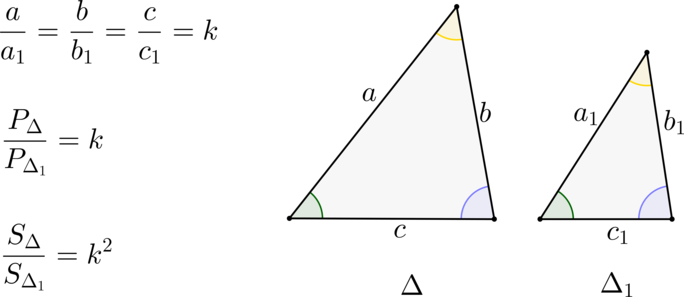Найди верный ответ на вопрос ✅ «Укажите верное написание выделенного слова. «Задача (на) подоби … треугольников. 1) Наподобие — наречие 2) Наподобии — наречие 3) На …» по предмету 📙 Русский язык, а если ответа нет или никто не дал верного ответа, то воспользуйся поиском и попробуй найти ответ среди похожих вопросов.
Искать другие ответы
Главная » ⭐️ Русский язык » Укажите верное написание выделенного слова. «Задача (на) подоби … треугольников. 1) Наподобие — наречие 2) Наподобии — наречие 3) На подобии — существительное в предложном падеже 4) На подобие — существительное в винительном падеже
23
Янв 2014
Категория: Планиметрия
Задачи на подобие треугольников
2014-01-23
2022-01-11
Рассмотрим задачи, при решении которых мы будем использовать подобие треугольников.
Уделим внимание как базовым задачам, так и задачам посложней.
В конце статье вы найдете задачи для самостоятельной работы
Задача 1. Через точки М и N, принадлежащие сторонам АВ и ВС треугольника ABC соответственно, проведена прямая МN, параллельная стороне АС. Найдите длину СN, если ВС = 6, МN = 4 и АС = 9.
Решение: + показать
Задача 2. Прямая, параллельная основанию треугольника, делит его на треугольник и трапецию, площади которых относятся как 4:5. Периметр образовавшегося треугольника равен 20 см. Найдите периметр данного треугольника.
Решение: + показать
Задача 3. Через вершину прямого угла прямоугольного треугольника с катетами 6 и 8 см проведен перпендикуляр к гипотенузе. Вычислите площади образовавшихся треугольников.
Решение: + показать
Задача 4. Из одной точки проведены к кругу две касательные. Длина касательной равна 156, а расстояние между точками касания равно 120. Найдите радиус круга.
Решение: + показать
Задача 5. В трапеции меньшая диагональ
, равная 6, перпендикулярна основаниям
и
. Найдите сумму тупых углов
и
.
Решение:+ показать
Задача 6. Основания трапеции равны a и b. Определите длину отрезка, параллельного основаниям и делящего трапецию на равновеликие части.
Решение: + показать
Задачи для самостоятельной работы
1. Через точки E и F, принадлежащие сторонам АВ и ВС треугольника ABC соответственно, проведена прямая EF, параллельная стороне АС. Найдите длину BС, если EF = 10, AC = 15 и FC = 9. (Ответ: 27).
2. В прямоугольном треугольнике проведена высота
к гипотенузе.
,
Найдите катет
. (Ответ: 20/3).
3. Прямая, параллельная основанию треугольника, отсекает от него треугольник, площадь которого в 8 раз меньше площади оставшейся части. Периметр большего треугольника равен 27. Найдите периметр меньшего треугольника. (Ответ: 9).
4. Основание треугольника 15 см, а боковые стороны 13 и 14 см. Высота разделена в отношении 2:3 (считая от вершины) и через точку деления проведена прямая, параллельная основанию. Найдите площадь образовавшейся при этом трапеции. (Ответ: 70,56 (возможно, вам потребуется формула Герона)).
5. В трапеции с основаниями
и
диагонали пересекаются в точке
. Площадь треугольника
равна 4, площадь треугольника
равна 9. Найдите площадь трапеции. (Ответ: 25).
6. Трапеция разделена диагоналями на четыре части. Определить ее площадь, если известны площади ее частей, прилежащих к основаниям и
. (Ответ:
).
Автор: egeMax |
комментариев 9
Наподобие или наподобии как правильно?
В зависимости от контекста предложения в русском языке можно употребить три варианта: наподобие, на подобие и на подобии.
Правильно
Наподобие — при слитном написании слово является неизменяемым предлогом, который образован от существительного «подобие». Пишется всегда с буквой «е» в конце слова. Является наиболее часто используемым вариантом. Синонимы: в виде, вроде, подобно чему, похоже на что-то, как.
У нее была сумка наподобие клатча (похожая на клатч).
На подоконнике сидела птичка наподобие воробья (похожая на воробья).
Облицовка сделана из материала наподобие мрамора (в виде мрамора).
Каждый солдат получил сумку, наподобие тех, какие носят почтальоны.
Мы играли в игру наподобие «Монополии»
Кусты росли наподобие высокого забора
На подобие — при таком написании имеем дело с предлогом «на» и существительным «подобие» в винительном падеже. Предлог с существительным всегда пишется раздельно, в конце существительного буква «е». В данном случае эта конструкция отвечает на вопрос «на что?» Синонимы: на схожесть, на похожесть, на сходство, на подобство.
Мы обратили внимание на подобие двух картин (или «на схожесть»).
Учитель указал на подобие методов решения задачи (или «на похожесть»).
Посмотрите на подобие этих треугольников (или «на сходство»).
На подобии — конструкция из предлога «на» и существительного «подобие» в форме предложного падежа (на чем?).
Он сидел на подобии королевского трона (что-то похожее на трон, но не трон).
Робинзон лежал на подобии матраса (лежал на чем-то, похожем на матрас).
Он писал на подобии древнеегипетского папируса (что-то, похожее на папирус).
Неправильно
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите левый Ctrl+Enter.
Наподобие или на подобие?
В разговорной речи мы часто описываем вещи или людей при помощи сравнений, чтобы придать фразе образность и донести свою мысль как можно более наглядно. Для этого нередко используем слово наподобие. Но если произнесенное вслух, это слово не вызывает никаких затруднений, то правописание довольно часто хромает. Как же правильно пишется: наподобие или на подобие? Нужен ли пробел или слово пишется слитно? Скажем сразу, что оба варианта верны, но в разных случаях пишутся по-разному: это всегда зависит от контекста.
Правописание слова наподобие
Для начала определим, какой частью речи слово выступает в предложении. Вариант первый: слово пишется слитно в случае, если оно – производный предлог. Этот предлог образован от существительного «подобие», то есть «похожесть» и предлога «на», но утратил самостоятельность и стал служебной частью речи.
Чтобы понять, что это именно предлог, нужно убедиться, что:
- после него следует существительное, которое с чем-то/кем-то сравнивают: «уши наподобие слоновьих»;
- его можно свободно заменить словами «похожий на», «такой как», «вроде» или другим синонимичным: «уши, похожие на слоновьи», «такие же, как слоновьи», «вроде слоновьих» и так далее;
- между «на» и «подобие» нельзя вставить никакое другое слово.
Если все эти условия соблюдены, значит, перед нами предлог, пишущийся всегда слитно. Кроме того, так как предлог в русском языке – неизменяемая часть речи, то он пишется всегда одинаково – с буквой Е на конце.
Примеры предложений
- Иван долго не спал, пытаясь выдать что-то наподобие стихов, но в итоге сдался и под утро уснул.
- Еж выкатился из кустов наподобие шара и замер: было видно, что он напуган.
- Павел издал звук наподобие лошадиного ржания и показал Маше язык.
- Ирина сшила платье наподобие старинного кринолина и с нетерпением ждала новогоднего вечера.
- Иван мечтал стать писателем и даже делал какие-то потуги наподобие новеллы, но безуспешно.
Правописание слов на подобие
Вариант второй: слова пишутся раздельно в случае, если это предлог «на» с самостоятельной частью речи – существительным «подобие», то есть «схожесть».
Так как предлог «на» употребляется с существительным в винительном падеже, то и в этом случае «подобие» тоже пишется в винительном падеже. При этом окончание существительного 2 склонения совпадает с окончанием в именительном падеже: «видим что? – подобие», «смотрим на что? – на подобие».
Хотя предлог наподобие и предлог с существительным на подобие схожи между собой, однако употребляются они в разных случаях, и путать их не следует. Так, если соблюдаются условия:
слова нельзя заменить синонимами «похожий на» и «такой, как»;
между предлогом «на» и существительным можно вставить прилагательное, например: «на великое подобие»,
то это именно предлог с существительным и пишется раздельно.
При этом окончание у него будет также Е. Может ли на подобие иметь окончание И? Может – в случае, когда пишется в предложном падеже: «где? На подобии». Однако подобное случаи такого употребления так редки, что им можно пренебречь и запомнить правильным правописание через Е.
Примеры предложений
- Туристы долго и с интересом любовались на маленькое подобие Тауэрской башни в городском саду.
- Юрист делал ставку на подобие между двумя домами и не прогадал.
- Чашка с кофе стояла на унылом подобии журнального столика.
Ошибочное написание
Сделать ошибку в правописании данных слов можно, перепутав части речи и написав слитно там, где нужно раздельно, и наоборот.
Также неправильно писать предлог наподобии с буквой И на конце.
Заключение
Итак, чтобы не ошибиться в написании слов наподобие и на подобие, нужно, главным образом, правильно определить часть речи и писать предлог только слитно и с буквой Е в конце.
Наподобие, наподобии или на подобие?
Производный предлог «наподобие» пишется слитно и с конечной буквой «е». Отличаем его в контексте от форм существительного с предлогом «на подобие», «на подобии».
Орфографическую трудность представляет различение омонимичных слов, принадлежащих к разным частям речи, например, производных предлогов и существительных с предлогами:
Точно также в зависимости от контекста выберем написание производного предлога «наподобие» и падежных форм существительного «на подобии» и «на подобие».
Правописание форм существительного «подобие»
Проследим, как изменяется по падежам это существительное:
- и.п. что? подоби-е
- р.п. нет чего? подоби-я
- д.п. стремлюсь к чему? к подоби-ю
- в.п. обращаю внимание на что? на подобие
- т.п. восхищен чем? подобием
- п.п. остановлюсь на чём? на подобии
Учитель обращает внимание учащихся на подобие треугольников.
На подобии этих представителей флоры тундры остановимся подробнее.
Падежные формы существительного пишутся с предлогами раздельно, так как между ними можно вставить вопрос или определение, например:
- указал на какое? подобие;
- остановимся на точном подобии.
Это существительное среднего рода оканчивается на -ие, поэтому оно имеет в форме предложного падежа окончание -и в отличие от типичного окончания -е других существительных второго склонения. Сравним:
- сидеть (на чём?) на дереве;
- гореть (в чём?) в огне;
- рассказать о призвании;
- услышать о чём? о достижении.
Производный предлог «наподобие»
Производный отымённый предлог следует отличать от одинаково звучащих форм существительного с предлогом. В контексте производный предлог употребляется вместе с существительным в форме родительного падежа. Его можно заменить синонимичными производными предлогами «в виде», «вроде», например:
Эта геометрическая фигура наподобие конуса (вроде конуса).
Расцветший цветок был наподобие тюльпана (в виде тюльпана).
Примеры предложений с предлогом «наподобие»
Цветы у гороха наподобие белых мотыльков.
Такое дерево, наподобие лиственницы, нередко встречается в наших лесах.
Она повторяла свою роль, на ходу низко кланялась и несколько раз потом качала головой, наподобие глиняных котов (А. Пушкин).
У многих рек, наподобие Волги, один берег горный, другой луговой (И. Тургенев).
Сколько я ни пытался различить вдалеке что-нибудь наподобие лодки, всё безуспешно (М. Лермонтов).
Где-то неподалёку вышла из берегов река, и вода её бокового рукава потихоньку подступила вплотную к насыпи. В укорочении, получившемся при взгляде с головокружительной высоты, казалось, что плавно идущий поезд скользит по воде наподобие сверхъестественного, фантастического корабля (Б. Пастернак).
источники:
http://correctno.ru/orfografiya/napodobie_ili_na_podobie
http://russkiiyazyk.ru/orfografiya/pravopisanie/napodobie-napodobii-na-podobie.html
Производный предлог «наподобие» пишется слитно и с конечной буквой «е». Отличаем его в контексте от форм существительного с предлогом «на подобие», «на подобии».
Орфографическую трудность представляет различение омонимичных слов, принадлежащих к разным частям речи, например, производных предлогов и существительных с предлогами:
- в заключение доклада — в заключении диплома;
- в продолжение разговора — в продолжении книги;
- в течение недели — в течении Дона;
- вследствие рассеянности — в следствии по делу.
Точно также в зависимости от контекста выберем написание производного предлога «наподобие» и падежных форм существительного «на подобии» и «на подобие».
Правописание форм существительного «подобие»
Проследим, как изменяется по падежам это существительное:
- и.п. (что?) подобие
- р.п. нет (чего?) подобия
- д.п. стремлюсь (к чему?) к подобию
- в.п. обращаю внимание (на что?) на подобие
- т.п. восхищен (чем?) подобием
- п.п. остановлюсь (на чём?) на подобии
Учитель обращает внимание учащихся на подобие треугольников.
На подобии этих представителей флоры тундры остановимся подробнее.
Падежные формы существительного пишутся с предлогами раздельно, так как между ними можно вставить вопрос или определение, например:
- указал на какое? подобие;
- остановимся на точном подобии.
Это существительное среднего рода оканчивается на -ие, поэтому оно имеет в форме предложного падежа окончание -и в отличие от типичного окончания -е других существительных второго склонения. Сравним:
- сидеть (на чём?) на дереве;
- гореть (в чём?) в огне;
- рассказать о призвании;
- услышать о чём? о достижении.
Производный предлог «наподобие»
Производный отымённый предлог следует отличать от одинаково звучащих форм существительного с предлогом. В контексте производный предлог употребляется вместе с существительным в форме родительного падежа. Его можно заменить синонимичными производными предлогами «в виде», «вроде», например:
Эта геометрическая фигура наподобие конуса (вроде конуса).
Расцветший цветок был наподобие тюльпана (в виде тюльпана).
Примеры предложений с предлогом «наподобие»
Цветы у гороха наподобие белых мотыльков.
Такое дерево, наподобие лиственницы, нередко встречается в наших лесах.
Она повторяла свою роль, на ходу низко кланялась и несколько раз потом качала головой, наподобие глиняных котов (А. Пушкин).
У многих рек, наподобие Волги, один берег горный, другой луговой (И. Тургенев).
Сколько я ни пытался различить вдалеке что-нибудь наподобие лодки, всё безуспешно (М. Лермонтов).
Где-то неподалёку вышла из берегов река, и вода её бокового рукава потихоньку подступила вплотную к насыпи. В укорочении, получившемся при взгляде с головокружительной высоты, казалось, что плавно идущий поезд скользит по воде наподобие сверхъестественного, фантастического корабля (Б. Пастернак).
Средняя оценка: 4.1.
Проголосовало: 25
Поурочное планирование по геометрии для 8 класса. Ориентировано на работу с УМК Атанасян и др. Геометрия 8 класс. Глава VII. ПОДОБНЫЕ ТРЕУГОЛЬНИКИ. Урок 36 Решение задач на применение признаков подобия треугольников. Вернуться к Списку уроков Тематического планирования.
Основные дидактические цели урока: сформировать у учащихся навыки применения признаков подобия треугольников при решении задач; совершенствовать навыки доказательств теорем.
Ход урока
I. Организационный момент.
Мотивация к учебной деятельности. (Учитель сообщает тему урока, формулирует цели урока.)
II. Актуализация знаний учащихся
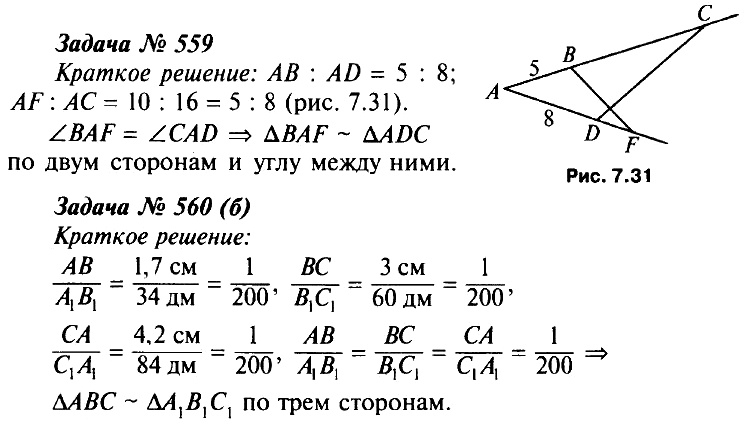
- Проверка домашнего задания. (Учитель проверяет решение задач № 559, 560 (б). Два ученика заранее готовят решение на доске.)
- Теоретический опрос. (Два ученика готовят доказательства теорем у доски.)
- Сформулируйте признаки подобия треугольников.
- Докажите теоремы, выражающие второй и третий признаки подобия треугольников.
- Работа по индивидуальным карточкам. (3—6 учеников работают по карточкам во время теоретического опроса.)
I уровень сложности
Подобны ли треугольники АВС и А1В1С1, если известно, что:
- АВ = 10 см; ВС = 5 см; АС = 7 см; А1В1 = 15 см; В1С1 = 7,5 см; A1С1 = 9,5 см?
- ∠A = 37°, ∠B = 48°, ∠C1 = 95°, ∠B1 = 48°?
- АВ = 10 см, ВС = 8 см, А1В1 = 5 см, А1С1 = 3 см, ∠C = ∠C1 = 90°?
II уровень сложности
- Прямая, параллельная стороне MN треугольника MNK, пересекает стороны КМ и KN в точках Е и F соответственно, КЕ = 6 см, KM = 10 см, KF = 9 см, KN = 15 см. Найдите отношения. a) EF: MN, б) PKMN : РКЕF, в) SKEF : SKMN.
- Точка Е — середина стороны AD параллелограмма ABCD. В каком отношении прямая BE делит диагональ АС параллелограмма? Найдите отношение площади треугольника АВЕ и четырехугольника BCDE.
III уровень сложности
- Основания трапеции равны 9 и 6 см, а высота равна 10 см. Найдите разность расстояний от точки пересечения диагоналей трапеции до ее оснований.
- Докажите признак подобия прямоугольных треугольников по гипотенузе и катету.
- Решение задач по готовым чертежам.
- 1) Рис. 7.32. Найти: ∠C1, В1С1.
- 2) Рис. 7.33. Найти: ∠C, ∠C1
- 3) Рис. 7.34. Найти: ВМ.
- 4) Рис. 7.35. Найти: ВС.
- 5) Рис. 7.36. Найти: ∠DCA.
- 6) Рис. 7.37. Найти АВ, NC.
Ответы к задачам по готовым чертежам:
- 1) ∠C1 = 71°, В1С1 = 15 см.
- 2) ∠C = ∠C1 = 60°.
- 3) ВМ = 6 см.
- 4) BC = 20/3.
- 5) Обратите внимание! Ответ автора задания ∠DCA = 90°. Однако, этот ответ нельзя признать правильным в виду каких-то опечаток в рис.7.36. Единственный вывод из рисунка: треугольники ABC и АCD подобны (по трем сторонам), но в таком случае ответ должен быть 80°, а не 90°. Но самый противоречивый момент связан с тем, что треугольники с заявленными сторонами и углами не существуют. Если считать, что стороны на рисунке указаны правильно, то вместо 80° должно быть указано 92,73°, а вместо 55° должно быть 45,52°. Тогда правильный ответ будет ∠DCA = 92,73°.
- 6) АВ = 8, NC= 8.
(После окончания самостоятельного решения задач и самопроверки по готовым ответам выполняется самооценка.) Критерии оценивания:
- оценка «5» — правильно решены пять-шесть задачи;
- оценка «4» — правильно решены четыре задачи;
- оценка «3» — правильно решены две-три задачи;
- оценка «2» — не ставится.
(Учащиеся, справившиеся со всеми задачами, решают дополнительные задачи.)
Дополнительные задачи
- Диагональ АС трапеции ABCD (АВ||CD) делит ее на два подобных треугольника. Найдите площадь трапеции ABCD, если АВ = 25 см, ВС = 20 см, АС = 15 см.
Ответ: SABCD = 204 см2.
- Угол В треугольника AВС в два раза больше угла А. Биссектриса угла В делит сторону АС на части AD = 6 см и CD = 3 см. Найдите стороны треугольника АВС.
Ответ: АС = 9 см, АВ = 6√3 см, ВС = 3√3 см.
III. Самостоятельная работа
I уровень сложности
Вариант 1
- Рис. 7.38. Доказать: ΔАВС ~ ΔА1В1С1
- Продолжения боковых сторон трапеции ABCD пересекаются в точке О. Найдите ВО и отношение площадей треугольников ВОС и AOD, AD = 5 см, ВС = 2 см, АО = 25 см.
Вариант 2
- Рис. 7.39. Доказать: ΔАВС ~ ΔА1B1С1.
- АВ и CD пересекаются в точке О, АО = 12 см, ВО = 4 см, СО = 30 см, DO = 10 см. Найдите угол САО, если ∠DBO = 61°. Найдите отношение площадей треугольников АОС и BOD.
II уровень сложности
Вариант 1.
- Рис. 7.40. Доказать: ΔАВС ~ ΔА1В1С1
- Прямая, параллельная стороне АС треугольника АВС, пересекает стороны АВ и ВС соответственно в точках М и Н. Найдите АС и отношение площадей треугольников АВС и ВМН, если МВ = 14 см, АВ = 16 см, МН = 28 см.
Вариант 2
- Рис. 7.41. Доказать: ΔМВН ~ ΔСВA.
- В треугольнике АВС АВ = 15 м, АС = 20 м, ВС = 32 м. На стороне АВ отложен отрезок AD = 9 м, а на стороне АС — отрезок АЕ = 12 м. Найдите DE и отношение площадей треугольников АВС и ADE.
III уровень сложности
Вариант 1
- Дано: ∠1 = ∠2, AD = 4, АС = 9 (рис. 7.42). Найти: АВ, SABD : SABC.
- Диагонали четырехугольника ABCD пересекаются в точке О, АО • ВО = СО • DO. Докажите, что площади треугольников ACD и ABD равны.
Вариант 2
- Дано: ВС ⊥ АС, МН ⊥ ВС, 2МС = ВС, МН = 0,5АС (рис. 7.43). Доказать: АВ||СН. Найти. SАВС : SMCH.
- В трапеции ABCD AD и ВС — основания, О — точка пересечения диагоналей, АО : ОС = 3 : 2. Найдите отношение площадей треугольников АВС и ACD.
(Ответы на самостоятельную работу смотрите в уроке 37)
IV. Рефлексия учебной деятельности
- Сформулируйте признаки подобия треугольников.
- В каком случае подобны равносторонние, равнобедренные, прямоугольные треугольники?
Домашнее задание. Решить задачи № 562, 563, 604, 605.
Вы смотрели: Поурочное планирование по геометрии для 8 класса. УМК Атанасян и др. (Просвещение). Глава VII. ПОДОБНЫЕ ТРЕУГОЛЬНИКИ. Урок 36 Решение задач на применение признаков подобия треугольников.
Вернуться к Списку уроков Тематического планирования.
Два треугольника подобны: по двум углам, по двум сторонам и углу между ними, по трём сторонам. Очень важно в задаче увидеть подобные треугольники или другие подобные фигуры. Для этого нужна хорошая практика решения задач.
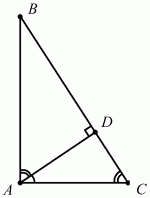
При решении задач на прямоугольный треугольник полезно знать, что высота, проведённая из прямого угла, делит его на два подобных треугольника (рис. 180):
?ABD ~ ?ADC ~ ?ABC.
Рис. 180.
Примеры решения задач
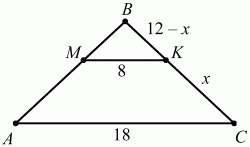
111. Через точки М и К, принадлежащие сторонам АВ и ВС треугольника ABC соответственно, проведена прямая МК, параллельная стороне АС. Найдите длину СК, если ВС = 12, МК = 8 и АС = 18 (рис. 181). (1)
Рис. 181.
Решение. Обозначим КС через х. Тогда ВК = 12 – х. Из подобия треугольников ABC и МВК следует: MK/BK = AC/BC; 8/(12 – x) = 18/12; x = 20/3.
Ответ: 20/3.
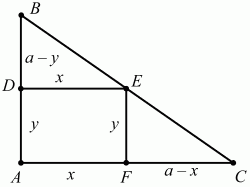
112. В прямоугольный равнобедренный треугольник вписан прямоугольник так, что угол прямоугольника совпадает с углом при вершине треугольника, а вершина противолежащего угла лежит на гипотенузе. Докажите, что периметр прямоугольника есть величина постоянная для данного треугольника (рис. 182). (1)
Рис. 182.
Решение. Пусть АВ = АС = а, DE = х; AD = у. Тогда DB = а – у; FC = а – х. Треугольник DEB подобен треугольнику FСЕ, значит, DE/DB = FC/FE; x/(a – y) = (a – x)/y; ху2= а2– ау – ах + ху; х + у = а; РADEF = 2(х + у) = 2а, т. е. не зависит от х и у.
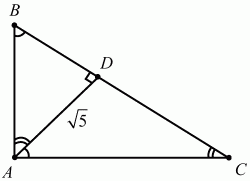
113. В прямоугольном треугольнике ABC угол А – прямой. Опущена высота AD, равная ?5. Найдите произведение BD ? DC (рис. 183). (1)
Рис. 183.
Решение. Треугольники ADB и ADC подобны (?BAD = ?ACD, ?ABD = ?DAC). Значит, BD/AD = AD/DC; BD ? DC = AD2= (?5)2= 5.
Ответ: 5.
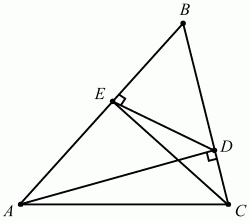
114. В треугольнике ABC проведены высоты AD и СЕ. Докажите, что треугольники ABC и DBE подобны. Чему равен коэффициент подобия (рис. 184)? (2)
Рис. 184.
Решение. Из прямоугольного треугольника ВСЕ: BE = ВС ? cos В. Из ?ABD: BD = АВ ? cos В. Значит, две стороны BD и BE треугольника BDE пропорциональны сторонам АВ и ВС треугольника ABC, а угол В (угол между пропорциональными сторонами) у треугольников общий. ?BDE ~ ?ABC по двум сторонам и углу между ними.
Значит,
Ответ: kподобия = cos B.
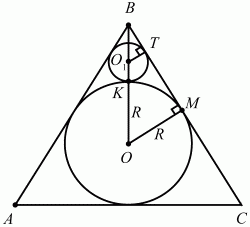
115. В равносторонний треугольник вписана окружность. Этой окружности и сторон треугольника касаются три малые окружности. Найдите сторону треугольника, если радиус малой окружности равен 1 (рис. 185). (2)
Рис. 185.
Решение. Так как в равностороннем треугольнике ABC угол ABC = 60°, то ?ОВМ = 30° (см. рис.). Из центров О и О1 проведем перпендикуляры ОМ и О1Т к стороне ВС. По условию О1Т и О1K равны 1. Длины отрезков ОМ и ОК обозначим через R. Из треугольника ВТО1 следует, что ВО1 = О1Т/sin 30° = 1/0,5 = 2. Треугольники ВТО1 и ВМО подобны по двум углам (?BTO1 = ?BMO = 90°; ?OBM – общий). Отсюда следует, что O1T/O1B = OM/OB;
Теперь мы знаем радиус вписанной в равносторонний треугольник окружности. Осталось найти длину его стороны. Из треугольника ВОМ следует ВМ = OM ? ctg ?ОВМ = 3?3. Тогда ВС = 2ВМ = 6?3.
Ответ: 6?3.
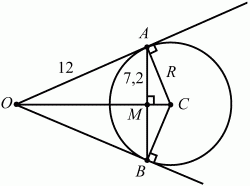
116. Из одной точки к окружности проведены две касательные. Длина каждой касательной равна 12 см, а расстояние между точками касания 14,4 см. Определите радиус окружности (рис. 186). (2)
Рис. 186.
Решение. Пусть ОА и ОВ – касательные к окружности с центром С; А и В – точки касания. Тогда СВ ? ОВ, СА ? ОА. Кроме того, ОС ? АВ и делит эту сторону пополам. ОА = 12 см, AM = 1/2 АВ = 7,2 см.
?МОА = ?АОС (углы с взаимноперпендикулярными сторонами), значит, ?ОАС подобен ?ОАМ; тогда
Ответ: 9 см.
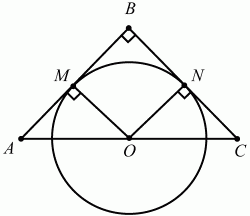
117. Центр О окружности радиуса длиной 3 лежит на гипотенузе АС прямоугольного треугольника ABC. Катеты треугольника касаются окружности. Найти площадь треугольника ABC, если известно, что длина отрезка ОС равна 5 (рис. 187). (3)
Рис. 187.
Решение. Пусть ABC – данный в условии задачи треугольник. Обозначим через M и N точки касания окружности соответственно со сторонами АВ и ВС. Соединив эти точки с центром О окружности, получим квадрат MBNO, и поэтому BN = ОМ = 3. Треугольник ONC прямоугольный, в нём ОС = 5, ON = 3. Следовательно,
Но тогда ВС = NC + NB = 7. Треугольники ONC и ABC подобны, поэтому AB/ON = BC/NC; AB/3 = 7/4; отсюда получаем, что AB = (ON ? BC)/NC = (3 ? 7)/4 = 21/4. Теперь находим S – площадь прямоугольного треугольника ABC:
Ответ: 147/8.
Задачи для самостоятельного решения
118. В равнобедренный треугольник вписан параллелограмм так, что угол параллелограмма совпадает с углом при вершине треугольника, а вершина противолежащего угла лежит на основании. Докажите, что периметр параллелограмма есть величина постоянная для данного треугольника. (1)
119. Из точки D, лежащей на катете АС прямоугольного треугольника ABC, на гипотенузу СВ опущен перпендикуляр DE. Найдите длину CD, если СВ = 15, АВ = 9, СЕ = 4. (1)
120. Точка на гипотенузе, равноудаленная от обоих катетов, делит гипотенузу на отрезки длиной 30 и 40 см. Найдите катеты треугольника. (1)
121. В параллелограмме ABCD проведена диагональ BD и отрезок AF (F ? ВС), пересекающий BD в точке О. Известно, что ВО = 6, OD = 18, FB = 4. Определите сторону параллелограмма AD. (1)
122. В острый угол, равный 60°, вписаны две окружности, извне касающиеся друг друга. Радиус меньшей окружности равен 1. Найдите радиус большей окружности. (1)
123. Найдите длину стороны квадрата, вписанного в равнобедренный треугольник с основанием а и боковой стороной b так, что две его вершины лежат на основании, а две другие вершины – на боковых сторонах. (2)
124. В параллелограмме ABCD точка М– середина стороны СВ, N – середина стороны CD. Докажите, что прямые AM и AN делят диагональ BD на три равные части. (2)
125. В трапеции, основания которой равны а и b, через точку пересечения диагоналей проведена прямая, параллельная основаниям. Найдите длину отрезка этой прямой, отсекаемого боковыми сторонами трапеции. (2)
126. В остроугольном треугольнике ABC из вершин А и С на стороны ВС и АВ опущены высоты АР и CQ. Известно, что площадь треугольника ABC равна 18, площадь треугольника BPQ равна 2, а длина отрезка PQ равна 2?2. Вычислите радиус окружности, описанной около треугольника ABC. (3)
3. Геометрия на плоскости (планиметрия). Часть I
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Треугольник: задачи на подобие
(blacktriangleright) Треугольники подобны, если их углы равны, а сходственные стороны (лежащие напротив равных углов) относятся друг к другу с одним и тем же коэффициентом (k) (пропорциональны).
(blacktriangleright) Признаки подобия:
1. Два угла одного треугольника равны двум углам другого треугольника.
2. Три стороны одного треугольника пропорциональны трем сторонам другого треугольника.
3. Две стороны одного треугольника пропорциональны двум сторонам другого, а углы между этими сторонами равны.
(blacktriangleright) Площади подобных треугольников относятся как (k^2), а периметры – как (k).
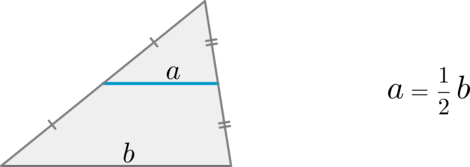
(blacktriangleright) Средняя линия треугольника – отрезок, соединяющий середины двух сторон. Она равна половине третьей стороны.
Задание
1
#3935
Уровень задания: Равен ЕГЭ
Точка (E) лежит на стороне (AC) треугольника (ABC), причём (dfrac{EC}{AE} = 2). Точка (D) лежит на (BC), причём (EDparallel AB). Найдите (AB), если (ED = dfrac{4}{3}).
Так как (EDparallel AB), то (angle CED = angle CAB), (angle CDE = angle CBA) (как соответственные при параллельных прямых и секущей), тогда треугольники (CED) и (CAB) подобны.
Так как (EC = 2cdot AE), то (AC = 3cdot AE), следовательно, [dfrac{AC}{EC} = dfrac{3cdot AE}{2cdot AE} = dfrac{3}{2}.]
Так как стороны (EC) и (AC) лежат против равных углов (в треугольниках (CED) и (CAB) соответственно), то [dfrac{AB}{ED} = dfrac{AC}{EC} = dfrac{3}{2},] откуда [AB = dfrac{3}{2}cdot ED = dfrac{3}{2}cdotdfrac{4}{3} = 2.]
Ответ:
2
Задание
2
#3937
Уровень задания: Равен ЕГЭ
Точка (E) лежит на стороне (AC) треугольника (ABC), причём (dfrac{EC}{AE} = 3). Точка (D) лежит на (BC), причём (dfrac{CD}{CB} = 0,75). Найдите (angle CED — angle CAB). Ответ дайте в градусах.
Рассмотрим треугольники (CAB) и (CED):
(angle C) – общий,
[dfrac{CA}{CE} = dfrac{AE + CE}{CE} = dfrac{AE}{CE} + 1 = dfrac{1}{3} + 1 = dfrac{4}{3} = dfrac{CB}{CD},] тогда треугольники (CAB) и (CED) подобны по пропорциональности двух сторон и равенству углов между ними.
В подобных треугольниках против пропорциональных сторон лежат равные углы, тогда (angle CED = angle CAB), откуда (angle CED — angle CAB = 0^{circ}).
Ответ:
0
Задание
3
#3943
Уровень задания: Равен ЕГЭ
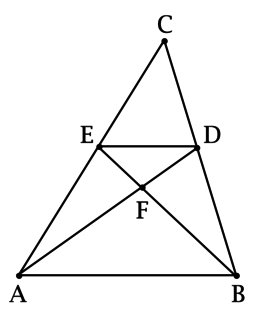
(F) – точка пересечения (AD) и (BE) – медиан треугольника (ABC). Известно, что (S_{ABF} = 1). Найдите (S_{DEF}).
(ED) – средняя линия треугольника (ABC), тогда (ED = 0,5cdot AB), (EDparallel AB).
Так как (EDparallel AB), то (angle DEF = angle ABF), (angle EDF = angle FAB) (как внутренние накрест лежащие при параллельных прямых и секущей), следовательно, треугольники (DEF) и (ABF) подобны (по двум углам). Так как (ED = 0,5cdot AB), причём стороны (ED) и (AB) лежат (в треугольниках (DEF) и (ABF) соответственно) против равных углов, то [dfrac{S_{DEF}}{S_{ABF}} = left(dfrac{ED}{AB}right)^2 = 0,5^2 = 0,25,] откуда с учётом того, что (S_{ABF} = 1) находим (S_{DEF} = 0,25).
Ответ:
0,25
Задание
4
#3936
Уровень задания: Сложнее ЕГЭ
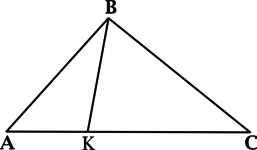
Отрезок (BK) соединяет вершину (B) треугольника (ABC) с точкой на противоположной стороне, причем (angle AKB = angle B). При этом известно, что (BK = 10), (AB = 12), (AC = 18). Найдите (BC).
Рассмотрим треугольники (ABK) и (ACB):
(angle AKB = angle B),
(angle A) – общий, тогда треугольники (ABK) и (ACB) подобны по двум углам.
В подобных треугольниках против равных углов лежат пропорциональные стороны, тогда [dfrac{BK}{BC} = dfrac{AB}{AC},] откуда (dfrac{10}{BC} = dfrac{12}{18}), следовательно (BC = 15).
Ответ:
15
Задание
5
#3938
Уровень задания: Сложнее ЕГЭ
Отрезок (BK) соединяет вершину (B) треугольника (ABC) с точкой на противоположной стороне. При этом известно, что (angle AKB = 105^{circ}), (AB = 12), (AC = 24), (AK = 6). Найдите (angle ABC). Ответ дайте в градусах.
Рассмотрим треугольники (ABK) и (ACB):
(angle A) – общий,
[dfrac{AB}{AC} = dfrac{AK}{AB},] тогда треугольники (ABK) и (ACB) подобны по пропорциональности двух сторон и равенству углов между ними.
В подобных треугольниках против пропорциональных сторон лежат равные углы, тогда (angle ABC = angle AKB = 105^{circ}).
Ответ:
105
Задание
6
#3939
Уровень задания: Сложнее ЕГЭ
На сторонах (AB), (BC) и (AC) треугольника (ABC) лежат точки (D), (E) и (F) соответственно. Известно, что (dfrac{DF}{BC} = 0,5), (AC = 2cdot DE), (AB-EF=EF) (angle DEF = 61^{circ}), (angle EFD = 55^{circ}). Найдите (angle C). Ответ дайте в градусах.
Так как (angle DEF = 61^{circ}), (angle EFD = 55^{circ}), то (angle EDF = 180^{circ} — 61^{circ} — 55^{circ} = 64^{circ}).
Рассмотрим треугольники (ABC) и (EFD): по условию
[dfrac{DF}{BC} = 0,5 = dfrac{DE}{AC} = dfrac{EF}{AB},] тогда треугольники (ABC) и (EFD) подобны по пропорциональности трех сторон.
В подобных треугольниках против пропорциональных сторон лежат равные углы, тогда (angle C = angle EDF = 64^{circ}).
Ответ:
64
Задание
7
#3940
Уровень задания: Сложнее ЕГЭ
Отрезок (BK) соединяет вершину (B) треугольника (ABC) с точкой на противоположной стороне. При этом известно, что (AB = 12), (AC = 24), (AK = 6), (BK = 10), (BC = 20). Найдите (angle AKB — angle B). Ответ дайте в градусах.
Рассмотрим треугольники (ABK) и (ACB):
[dfrac{AB}{AC} = dfrac{AK}{AB} = dfrac{BK}{BC},] тогда треугольники (ABK) и (ACB) подобны по пропорциональности трех сторон.
В подобных треугольниках против пропорциональных сторон лежат равные углы, тогда (angle B = angle AKB), следовательно (angle AKB — angle B = 0^{circ}).
Ответ:
0
Как показывает статистика, планиметрические задачи вызывают наибольшие сложности у учащихся старших классов. Именно поэтому школьникам будет полезно освежить в памяти основные принципы решения задач с подобными треугольниками при подготовке к ЕГЭ. Причем еще раз повторить эту тему стоит всем ученикам, независимо от того, профильный или базовый уровень планирует сдавать выпускник.
Вместе с образовательным порталом «Школково» вы сможете качественно подготовиться к аттестационному испытанию. Чтобы решение задач ЕГЭ по теме «Подобные треугольники» давалось легко, рекомендуем вспомнить основную теорию. Найти ее вы можете в соответствующем разделе нашего сайта. Здесь представлены основные признаки подобных треугольников (для решения заданий ЕГЭ знать их необходимо), формула отношения их площадей и другая базовая информация. Ее специалисты образовательного портала «Школково» подготовили и изложили в максимально доступной форме.
Отточить навык решения задач ЕГЭ на нахождение сторон и углов подобных треугольников, а также, например, задачи по теореме Пифагора учащиеся также смогут на нашем сайте. В разделе «Каталог» представлен широкий перечень упражнений различной сложности, который постоянно обновляется.
В каждом задании прописано решение и дан правильный ответ. Выполнять задачи с применением признаков подобия площадей подобных треугольников можно в режиме онлайн.
Любое из представленных упражнений при необходимости можно сохранить в разделе «Избранное». Таким образом, к нему возможно будет вернуться в дальнейшем, к примеру, для обсуждения с преподавателем.

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ