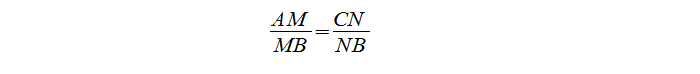Как пишется значок параллельности - Правописание и грамматика

Параллельно ∥

Значение символа

Параллельно. Математические операторы.

Символ «Параллельно» был утвержден как часть Юникода версии 1.1 в 1993 г.

Версия	1.1
Блок	Математические операторы
Тип парной зеркальной скобки (bidi)	Нет
Композиционное исключение	Нет
Изменение регистра	2225
Простое изменение регистра	2225

Кодировка	hex	dec (bytes)	dec	binary
UTF-8	E2 88 A5	226 136 165	14846117	11100010 10001000 10100101
UTF-16BE	22 25	34 37	8741	00100010 00100101
UTF-16LE	25 22	37 34	9506	00100101 00100010
UTF-32BE	00 00 22 25	0 0 34 37	8741	00000000 00000000 00100010 00100101
UTF-32LE	25 22 00 00	37 34 0 0	622985216	00100101 00100010 00000000 00000000

Наборы с этим символом

Источник

Морфемный разбор слова:

Однокоренные слова к слову:

Когда и кем была введена знак параллельности II

В евклидовой геометрии

Параллельными (иногда — равнобежными) прямыми называются прямые, которые лежат в одной плоскости и либо совпадают, либо не пересекаются. В некоторых школьных определениях совпадающие прямые не считаются параллельными, здесь такое определение не рассматривается.
[править] Свойства

1. Параллельность — бинарное отношение эквивалентности, поэтому разбивает всё множество прямых на классы параллельных между собой прямых.
2. Через любую точку можно провести ровно одну прямую, параллельную данной. Это отличительное свойство евклидовой геометрии, в других геометриях число 1 заменено другими (в геометрии Лобачевского таких прямых минимум две)
3. 2 параллельные прямые в пространстве лежат в одной плоскости.
4. При пересечении 2 параллельных прямых третьей, называемой секущей:
1. Секущая обязательно пересекает обе прямые.
2. При пересечении образуется 8 углов, некоторые характерные пары которых имеют особые названия и свойства:
1. Накрест лежащие углы равны.
2. Соответственные углы равны.
3. Односторонние углы в сумме составляют 180°.

[править] В геометрии Лобачевского
Параллельные прямые в модели Пуанкаре: две зелёные прямые параллельны синей прямой, а фиолетовая ультрапараллельна к ней

В геометрии Лобачевского в плоскости через точку C вне данной прямой AB проходит бесконечное множество прямых, не пересекающих AB. Из них параллельными к AB называются только две. Прямая CE называется равнобежной (параллельной) прямой AB в направлении от A к B, если:

Источник

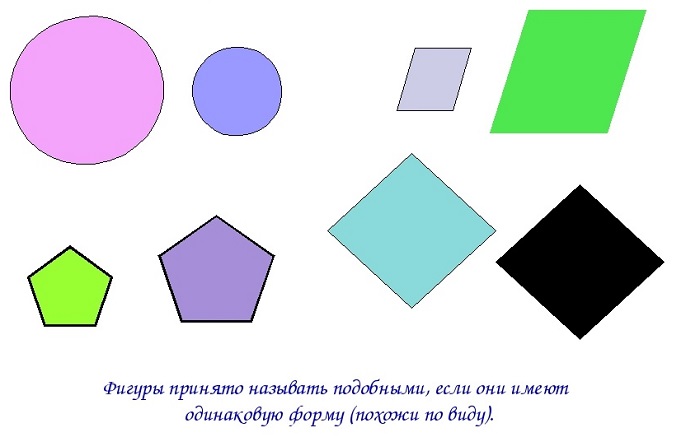
В учебниках по геометрии часто встречаются задачи на подобие фигур. Какой знак используется для обозначения подобия фигур? Какие фигуры называются подобными? Поговорим обо всем этом в нашей статье.

Определение и знак подобия в геометрии

На нижеприведенном рисунке подобные фигуры: круги, параллелограммы, пятиугольники и ромбы.

Для обозначения термина «подобие» в геометрии используют знак «тильда», который является типографским символом и обозначается волнистой чертой:

Знак «двойная тильда» ставится около чисел для демонстрации примерности или приблизительности чего-либо:

1,35 ≈ 1,4 — числа 1,35 и 1,4 приблизительно равны.

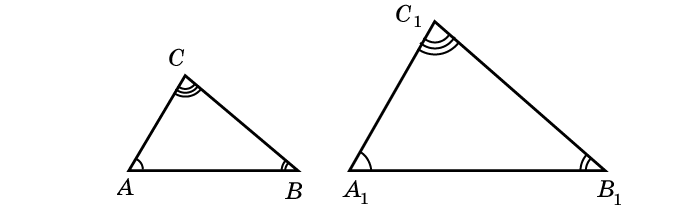
Коэффициент подобия треугольников и знак подобия

Часто сверху знака подобия выставляют коэффициент подобия треугольников:

В математических задачах и уравнениях «тильду» используют для маркирования разных типов подобия. Часто применяется для обозначения подобия, эквивалентности.

В алгебре высказываний знаком

обозначают логическую операцию «эквиваленция».

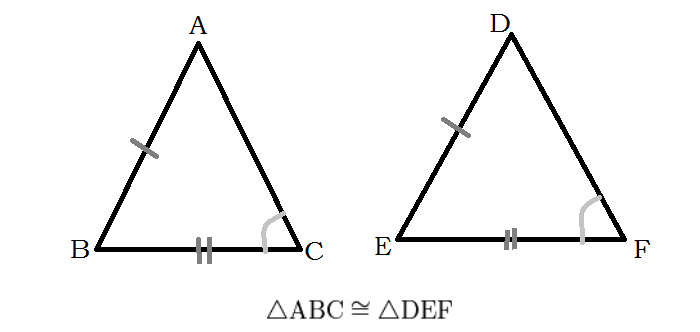
При сочетании тильды и знака равенства получают обозначение отношения конгруэнтности, определения в геометрии, применяемого в контексте обозначения равенства различных фигур и тел (углов, отрезков):

Признаки подобия прямоугольных треугольников

Острые углы: наличие равного острого угла в прямоугольных треугольниках делает их подобными.

Два катета: общая пропорциональность катетам одного прямоугольного треугольника к катетам второго делает их подобными.

Катет и гипотенуза: пропорциональность катета и гипотенузы одного прямоугольного треугольника к катету и гипотенузе второго прямоугольного треугольника делает их подобными.

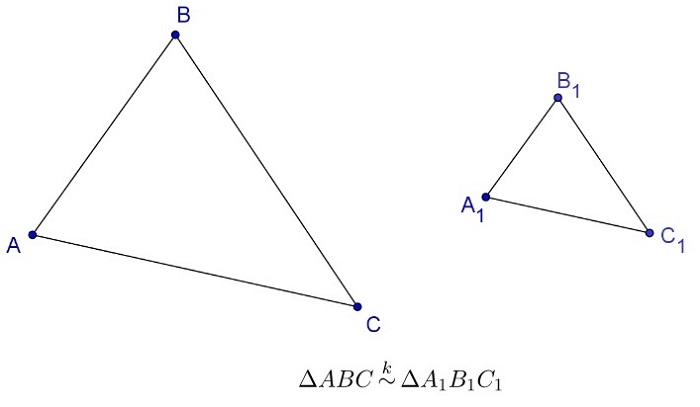
треугольник ∆ABC и треугольник ∆A₁B₁C₁ считаются подобными при равнозначности углов и пропорциональности сторон;

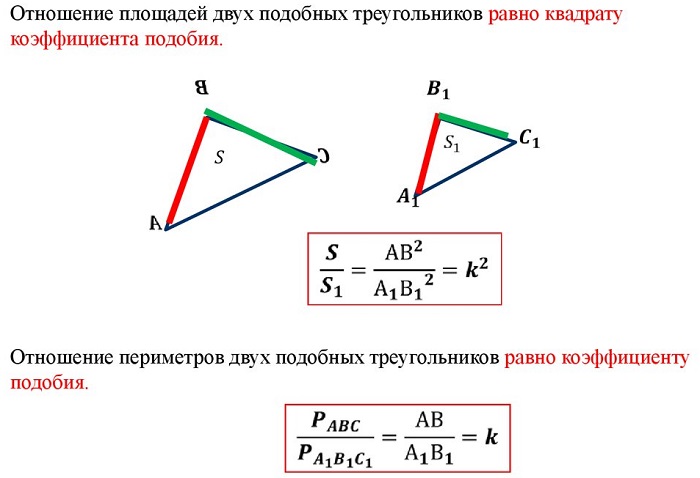
отношение площадей подобных треугольников равно квадрату коэффициента подобия.

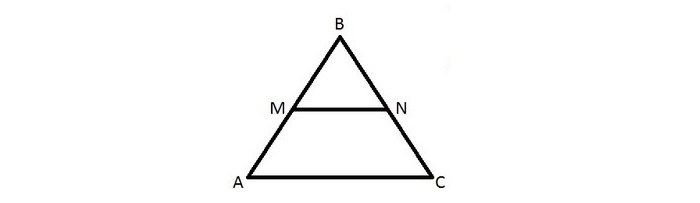
Доказательство подобия треугольников через среднюю линию

Требуется доказательство подобия треугольников ∆MBN и ∆ABC.

Посмотрев на ∆MBN и ∆ABC, видим, что угол В — общий, а отношение:

Отсюда делаем вывод, что ∆MBN

∆ABC по II признаку подобия треугольников, что и требовалось доказать.

Примеры решения задач по геометрии на тему «Подобие треугольников»

Источник

Определение и знак подобия в геометрии

На нижеприведенном рисунке подобные фигуры: круги, параллелограммы, пятиугольники и ромбы.

Знак «двойная тильда» ставится около чисел для демонстрации примерности или приблизительности чего-либо:

1,35 ≈ 1,4 — числа 1,35 и 1,4 приблизительно равны.

Коэффициент подобия треугольников и знак подобия

Часто сверху знака подобия выставляют коэффициент подобия треугольников:

В алгебре высказываний знаком

обозначают логическую операцию «эквиваленция».

Признаки подобия прямоугольных треугольников

Острые углы: наличие равного острого угла в прямоугольных треугольниках делает их подобными.

отношение площадей подобных треугольников равно квадрату коэффициента подобия.

Доказательство подобия треугольников через среднюю линию

Требуется доказательство подобия треугольников ∆MBN и ∆ABC.

Посмотрев на ∆MBN и ∆ABC, видим, что угол В — общий, а отношение:

Отсюда делаем вывод, что ∆MBN

∆ABC по II признаку подобия треугольников, что и требовалось доказать.

Примеры решения задач по геометрии на тему «Подобие треугольников»

Источник

Обозначения и символика

Для обозначения геометрических фигур и их проекций, для отображения отношения между ними, а также для краткости записей геометрических предложений, алгоритмов решения задач и доказательства теорем в курсе используется геометрический язык, составленный из обозначений и символов, принятых в курсе математики (в частности, в новом курсе геометрии в средней школе).

Все многообразие обозначений и символов, а также связи между ними могут быть подразделены на две группы:

группа I — обозначения геометрических фигур и отношений между ними;

группа II обозначения логических операций, составляющие синтаксическую основу геометрического языка.

Ниже приводится полный список математических символов, используемых в данном курсе. Особое внимание уделяется символам, которые применяются для обозначения проекций геометрических фигур.

СИМВОЛЫ, ОБОЗНАЧАЮЩИЕ ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ И ОТНОШЕНИЯ МЕЖДУ НИМИ

А. Обозначение геометрических фигур

1. Геометрическая фигура обозначается — Ф.

2. Точки обозначаются прописными буквами латинского алфавита или арабскими цифрами:

3. Линии, произвольно расположенные по отношению к плоскостям проекций, обозначаются строчными буквами латинского алфавита:

Линии уровня обозначаются: h — горизонталь; f— фронталь.

Для прямых используются также следующие обозначения:

(АВ) — прямая, проходящая через точки А а В;

[АВ) — луч с началом в точке А;

[АВ] — отрезок прямой, ограниченный точками А и В.

4. Поверхности обозначаются строчными буквами греческого алфавита:

Чтобы подчеркнуть способ задания поверхности, следует указывать геометрические элементы, которыми она определяется, например:

α(а || b) — плоскость α определяется параллельными прямыми а и b;

5. Углы обозначаются:

6. Угловая: величина (градусная мера) обозначается знаком , который ставится над углом:

— величина угла АВС;

— величина угла φ.

Прямой угол отмечается квадратом с точкой внутри

7. Расстояния между геометрическими фигурами обозначаются двумя вертикальными отрезками — ||.

|АВ| — расстояние между точками А и В (длина отрезка АВ);

|Аа| — расстояние от точки А до линии a;

|Аα| — расстояшие от точки А до поверхности α;

|аb| — расстояние между линиями а и b;

|αβ| расстояние между поверхностями α и β.

π₂ —фрюнтальная плоскость проекций.

При замене плоскостей проекций или введении новых плоскостей последние обозначают π₃, π₄ и т. д.

Постояшную прямую эпюра Монжа обозначают k.

10. Проекции точек, линий, поверхностей, любой геометрической фигуры обозначаются теми же буквами (или цифрами), что и оригинал, с добавлением верхнего индекса, соответствующего плоскости проекции, на которой они получены:

11. Следы плоскостей (поверхностей) обозначаются теми же буквами, что и горизонталь или фронталь, с добавлением подстрочного индекса _0α, подчеркивающего, что эти линии лежат в плоскости проекции и принадлежат плоскости (поверхности) α.

12. Следы прямых (линий) обозначаются заглавными буквами, с которых начинаются слова, определяющие название (в латинской транскрипции) плоскости проекции, которую пересекает линия, с подстрочным индексом, указывающим принадлежность к линии.

Например: H_a — горизонтальный след прямой (линии) а;

F_a — фронтальный след прямой (линии ) a.

13. Последовательность точек, линий (любой фигуры) отмечается подстрочными индексами _{1,2,3. n:}

Вспомогательная проекция точки, полученная в результате преобразования для получения действительной величины геометрической фигуры, обозначается той же буквой с подстрочным индексом ₀:

14. Аксонометрические проекции точек, линий, поверхностей обозначаются теми же буквами, что и натура с добавлением верхнего индекса 0 :

15. Вторичные проекции обозначаются путем добавления верхнего индекса 1 :

Для облегчения чтения чертежей в учебнике при оформлении иллюстративного материала использованы несколько цветов, каждый из которых имеет определенное смысловое значение: линиями (точками) черного цвета обозначены исходные данные; зеленый цвет использован для линий вспомогательных графических построений; красными линиями (точками) показаны результаты построений или те геометрические элементы, на которые следует обратить особое внимание.

Источник

Обозначения и символика

Все многообразие обозначений и символов, а также связи между ними могут быть подразделены на две группы:

группа I — обозначения геометрических фигур и отношений между ними;

группа II обозначения логических операций, составляющие синтаксическую основу геометрического языка.

СИМВОЛЫ, ОБОЗНАЧАЮЩИЕ ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ И ОТНОШЕНИЯ МЕЖДУ НИМИ

А. Обозначение геометрических фигур

1. Геометрическая фигура обозначается — Ф.

2. Точки обозначаются прописными буквами латинского алфавита или арабскими цифрами:

Линии уровня обозначаются: h — горизонталь; f— фронталь.

Для прямых используются также следующие обозначения:

(АВ) — прямая, проходящая через точки А а В;

[АВ) — луч с началом в точке А;

[АВ] — отрезок прямой, ограниченный точками А и В.

4. Поверхности обозначаются строчными буквами греческого алфавита:

α(а || b) — плоскость α определяется параллельными прямыми а и b;

5. Углы обозначаются:

6. Угловая: величина (градусная мера) обозначается знаком , который ставится над углом:

— величина угла АВС;

— величина угла φ.

Прямой угол отмечается квадратом с точкой внутри

7. Расстояния между геометрическими фигурами обозначаются двумя вертикальными отрезками — ||.

|АВ| — расстояние между точками А и В (длина отрезка АВ);

|Аа| — расстояние от точки А до линии a;

|Аα| — расстояшие от точки А до поверхности α;

|аb| — расстояние между линиями а и b;

|αβ| расстояние между поверхностями α и β.

π₂ —фрюнтальная плоскость проекций.

При замене плоскостей проекций или введении новых плоскостей последние обозначают π₃, π₄ и т. д.

Постояшную прямую эпюра Монжа обозначают k.

Например: H_a — горизонтальный след прямой (линии) а;

F_a — фронтальный след прямой (линии ) a.

13. Последовательность точек, линий (любой фигуры) отмечается подстрочными индексами _{1,2,3. n:}

15. Вторичные проекции обозначаются путем добавления верхнего индекса 1 :

Источник

Теперь вы знаете какие однокоренные слова подходят к слову Как пишется знак параллельно в геометрии, а так же какой у него корень, приставка, суффикс и окончание. Вы можете дополнить список однокоренных слов к слову «Как пишется знак параллельно в геометрии», предложив свой вариант в комментариях ниже, а также выразить свое несогласие проведенным с морфемным разбором.

Источник

Морфемный разбор слова:

Однокоренные слова к слову:

Параллельность прямых

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Определение параллельности прямых

Начнем с главного — определимся, какие прямые параллельны согласно евклидовой геометрии. Мы недаром упомянули Евклида, ведь именно в его трудах, написанных за 300 лет до н. э., до нас дошли первые упоминания о параллельности.

Параллельными называются прямые в одной плоскости, не имеющие точек пересечения, даже если их продолжать бесконечно долго. Обозначаются они следующим образом: a II b.

Казалось бы, здесь все просто, но со времен Евклида над определением параллельных прямых и признаками параллельности прямых бились лучшие умы. Особый интерес вызывал 5-й постулат древнегреческого математика: через точку, которая не относится к прямой, в той же плоскости можно провести только одну прямую, параллельную первой. В XIX веке российский математик Н. Лобачевский смог опровергнуть постулат и указать на условия, при которых возможно провести как минимум 2 параллельные прямые через одну точку.

Впрочем, поскольку школьная программа ограничена евклидовой геометрией, вышеуказанное утверждение мы принимаем как аксиому.

На плоскости через любую точку, не принадлежащую некой прямой, можно провести единственную прямую, которая была бы ей параллельна.

Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.

Свойства и признаки параллельных прямых

Есть ряд признаков, по которым можно определить, что одна прямая параллельна другой. К счастью, свойства и признаки параллельности прямых тесно связаны, поэтому не придется запоминать много информации.

Начнем со свойств. Для этого проведем третью прямую, пересекающую параллельные прямые — она будет называться секущей. В результате у нас образуется 8 углов.

Если секущая проходит через две параллельные прямые, то:

∠4 + ∠6 = 180°; ∠3 + ∠5 = 180°.

∠1 = ∠5, ∠3 = ∠7, ∠4 = ∠8, ∠2 = ∠6.

Если секущая образует перпендикуляр с одной из параллельных прямых, то она будет перпендикулярна и другой.

Вышеуказанные свойства являются одновременно признаками, по которым мы можем сделать вывод о параллельности прямых. Причем достаточно установить и доказать лишь один признак — остальные будут к нему прилагаться.

А сейчас посмотрим, как все это помогает решать задачи и практиковаться в определении параллельности двух прямых.

Задача 1

Прямые MN и KP пересекают две другие прямые, образуя несколько углов. Известно, что ∠1 = 73°; ∠3 = 92°; ∠2 = 73°. Требуется найти величину ∠4.

Решение

Поскольку ∠1 и ∠2 являются соответственными, их равенство говорит о том, что MN II KP. Следовательно, ∠3 = ∠MPK = 92°.

Согласно другому свойству параллельных прямых ∠4 + ∠MPK = 180°.

Задача 2

Две параллельные прямые а и b удалены друг от друга на расстояние 27 см. Секущая к этим прямым образует с одной из них угол в 150°. Требуется найти величину отрезка секущей, расположенного между а и b.

Решение

Поскольку а II b, значит ∠MKD + ∠KDN = 180°.

Теперь рассмотрим треугольник KDM. Мы знаем, что отрезок DM представляет собой расстояние между прямыми а и b, а значит, DM ┴ b и наш треугольник является прямоугольным.

Поскольку катет, противолежащий углу в 30°, равен ½ гипотенузы, DM = 1/2DK.

Источник

Параллельность прямых

Определение параллельности прямых

Свойства и признаки параллельных прямых

Если секущая проходит через две параллельные прямые, то:

∠4 + ∠6 = 180°; ∠3 + ∠5 = 180°.

∠1 = ∠5, ∠3 = ∠7, ∠4 = ∠8, ∠2 = ∠6.

Если секущая образует перпендикуляр с одной из параллельных прямых, то она будет перпендикулярна и другой.

Задача 1

Решение

Согласно другому свойству параллельных прямых ∠4 + ∠MPK = 180°.

Задача 2

Решение

Поскольку а II b, значит ∠MKD + ∠KDN = 180°.

Поскольку катет, противолежащий углу в 30°, равен ½ гипотенузы, DM = 1/2DK.

Источник

знак параллельности

ТолкованиеПереводзнак параллельности мат. parallel mark, parallel sign

Смотреть что такое “знак параллельности” в других словарях:

Parallel — Знак параллельности || параллельный … Краткий толковый словарь по полиграфии

История математических обозначений — Математические обозначения это символы, используемые для компактной записи математических уравнений и формул[1]. Помимо цифр и букв различных алфавитов (латинского, в том числе в готическом начертании, греческого и еврейского),… … Википедия

ЗНАКИ МАТЕМАТИЧЕСКИЕ — условные обозначения, предназначенные для записи математич. понятий и выкладок. Напр., понятие квадратный корень из числа, равного отношению длины окружности к ее диаметру обозначается кратко а предложение отношение длины окружности к ее диаметру … Математическая энциклопедия

Знаки математические — условные обозначения, предназначенные для записи математических понятий, предложений и выкладок. Например, √2 (квадратный корень из двух), 3 > 2 (три больше двух) и т.п. Развитие математической символики было тесно… … Большая советская энциклопедия

ПОЛЯРИЗОВАННЫЕ НЕЙТРОНЫ — совокупность нейтронов, спины s к рых имеют преимуществ. ориентацию по отношению к к. л. выделенному направлению в пространстве, обычно направлению магн. поля Н. Т. к. нейтрон обладает спином 1/2, то в поле Н возможны две ориентации спина:… … Физическая энциклопедия

сталь — 2.1 сталь: Материал (сплав железа с углеродом),в котором массовая доля железа больше, чем массовая доля какого либо другого элемента, а массовая доля углерода составляет менее 2 %, и в состав которого входят также и другие химические элементы. У… … Словарь-справочник терминов нормативно-технической документации

ГОСТ 380-71: Сталь углеродистая обыкновенного качества. Марки и общие технические требования — Терминология ГОСТ 380 71: Сталь углеродистая обыкновенного качества. Марки и общие технические требования оригинал документа: 2.2. Сталь группы А. 2.2.1. Нормируемые показатели для стали группы А указаны в табл. 1. Таблица 1 Категории стали Марки … Словарь-справочник терминов нормативно-технической документации

бессоюзные сложные предложения — Один из двух основных структурных типов сложного предложения в русском языке, выделяемый по формальному признаку. При бессоюзии мобилизуются в противовес союзам другие средства связи: 1) интонация; 2) видо временные отношения в предикативных… … Словарь лингвистических терминов Т.В. Жеребило

бессоюзные сложные предложения — Один из двух основных структурных типов сложного предложения в русском языке, выделяемый по формальному признаку. При бессоюзии мобилизуются в противовес союзам другие средства связи: 1) интонация; 2) видо временные отношения в… … Синтаксис: Словарь-справочник

Отред, Уильям — Уильям Отред William Oughtred … Википедия

Отред — Отред, Уильям Уильям Отред Уильям Отред (англ. William Oughtred, 5 марта 1575 30 июня 1660) английский математи … Википедия

Для обозначения геометрических фигур и их проекций, для отображения отношения между геометрическими фигурами, а также для краткости записей геометрических предложений, алгоритмов решения задач и доказательства теорем используются символьные обозначения.

Символьные обозначения, все их многообразие, может быть подразделено на две группы: – Первая группа – обозначения геометрических фигур и отношения между ними; – Вторая группа – обозначения логических операций, составляющая синтаксическую основу геометрического языка.

Символьные обозначения – Первая группа

Символы, обозначающие геометрические фигуры и отношения между ними

Обозначения геометрических фигур: Φ – геометрическая фигура; A, B, C, D, …, L, M, N, … – точки расположенные в пространстве; 1, 2, 3, 4, …, 12, 13, 14, … – точки расположенные в пространстве; a, b, c, d, …, l, m, n, … – линии, произвольно расположенные по отношению к плоскостям проекций; h, υ(f), ω – линии уровня (горизонталь, фронталь, профильная прямая соответственно); (AB) – прямая проходящая через точки A и B; [AB) – луч с началом в точке A; [AB] – отрезок прямой, ограниченный точками A и B; α, β, γ, δ, …, ζ, η, θ – поверхность; ∠ABC – угол с вершиной в точке B; ∠α, ∠β, ∠γ – угол α, угол β, угол γ соответственно; |AB| – расстояние от точки A до точки B (длина отрезка AB); |Aa| – расстояние от точки A до линии a; |Aα| – расстояние от точки A до поверхности α; |ab| – расстояние между прямыми a и b; |αβ| – расстояние между поверхностями α и β; H, V, W – координатные плоскости проекций (именуемые как горизонтальная, фронтальная, профильная соответственно); П₁, П₂, П₃ – координатные плоскости проекций (именуемые как горизонтальная, фронтальная, профильная соответственно); x, y, z – координатные оси проекций (ось абсцисс, ось ординат, ось аппликат); k_o – постоянная прямая эпюра Монжа;O – точка пересечения осей проекций; `, “, `” – верхние индексы для проекций точек, прямых, углов, фигур, поверхностей на плоскости проекций (именуемые как горизонтальную, фронтальную, профильную соответственно); 1, 2, 3 – верхние индексы для проекций точек, прямых, углов, фигур, поверхностей на плоскости проекций (именуемые как горизонтальную, фронтальную, профильную соответственно); α_H, α_V, α_W – след поверхности оставляемый на горизонтальной, на фронтальной, на профильной плоскости проекций соответственно; α_H, α_V, α_W – след поверхности α оставляемый на горизонтальной, на фронтальной, на профильной плоскости проекций соответственно; a_H, a_V, a_W – след прямой a оставляемый на горизонтальной, на фронтальной, на профильной плоскости проекций соответственно;

Проекции точек, линий, поверхностей любой геометрической фигуры обозначаются теми же буквами (или цифрами), что и оригинал, с добавлением верхнего индекса A`, A”, A`” или 1`, 1″, 1`”, соответствующего плоскости проекции, на которой они получены: A`, B`, C`, D`, …, L`, M`, N`, … – горизонтальные проекции точек; A”, B”, C”, D”, …, L”, M”, N”, … – фронтальные проекции точек; A`”, B`”, C`”, D`”, …, L`”, M`”, N`”, … – профильные проекции точек; a`, b`, c`, d`, …, l`, m`, n`, … – горизонтальные проекции линий; a”, b”, c”, d”, …, l”, m”, n”, … – фронтальные проекции линий; a`”, b`”, c`”, d`”, …, l`”, m`”, n`”, … – профильные проекции линий; α`, β`, γ`, δ`, …, ζ`, η`, θ`, … – горизонтальные проекции поверхностей; α”, β”, γ”, δ”, …, ζ”, η”, θ”, … – фронтальные проекции поверхностей; α`”, β`”, γ`”, δ`”, …, ζ`”, η`”, θ`”, … – профильные проекции поверхностей;

Символы взаиморасположения геометрических объектов

ΔDEF – треугольники ABC и DEF подобны. ≅ конгруэнтность ΔАВС ≅ /АВ/ = /CD/ – отрезки АВ и CD равны. = равенство, результат действия /АВ/ = /CD/ – длины отрезков AB и CD равны; k ∩ l = M – прямые k и l пересекаются в точке M. / отрицание А ∉ l – точка А не принадлежит прямой l. → ← отображение, преобразование V/H → V1/H– система ортогональных плоскостей V/H преобразуется в систему плоскостей V1/H

Символьные обозначения – Вторая группа

Источник

Теперь вы знаете какие однокоренные слова подходят к слову Как пишется знак параллельности в геометрии, а так же какой у него корень, приставка, суффикс и окончание. Вы можете дополнить список однокоренных слов к слову «Как пишется знак параллельности в геометрии», предложив свой вариант в комментариях ниже, а также выразить свое несогласие проведенным с морфемным разбором.

Источник

знак параллельности

Большой англо-русский и русско-английский словарь . 2001 .

знак параграфа
знак перевода строки

Смотреть что такое «знак параллельности» в других словарях:

Parallel — Знак параллельности || параллельный … Краткий толковый словарь по полиграфии

бессоюзные сложные предложения — Один из двух основных структурных типов сложного предложения в русском языке, выделяемый по формальному признаку. При бессоюзии мобилизуются в противовес союзам другие средства связи: 1) интонация; 2) видо временные отношения в… … Синтаксис: Словарь-справочник

Отред, Уильям — Уильям Отред William Oughtred … Википедия

Источник

Математика,

вопрос задал mishhenko05,

5 лет назад

Как пишется знак параллели Очень срочно нужно пожалуйста

Ответы на вопрос

Ответил AlinaMarco

знак параллельности пишется вот так ||

Ответил HelpaniteMenya

Две черточки || вот так

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Алгебра,
4 года назад

4.С башни выпустили вверх стрелу из лука. Если начальная скорость стрелы равна 30 м/с и t — время полёта стрелы (в секундах), то расстояние h (в метрах) стрелы от поверхности земли можно найти по…

Физика,
4 года назад

—
материальное
10. Объясните, как вы понимаете смысл фразы: «А колесо, как известно,
воплощение операции поворота».
В своём объяснении используйте следующие словосочетания: центр ко-…

История,
5 лет назад

почему в 16 веке таманский п-ов называли «шахским островом? а) здесь находилось резиденция турецкого сераскира б) турецкий султан любил здесь охотится в) турецкий султан был отсюда родом г) из-за…

История,
5 лет назад

Казахстан период Великой Отечественной войны? Помогите пожалуйста…..

История,
6 лет назад

Если бы ты могла Какое событие эпохи новейшего времени ты бы не допустила…

Математика,
6 лет назад

От двух станций,расстояние между которыми 56 км,отошли одновременно в противоположных направлениях два поезда. Скорость одного поезда 45 км/ч,скорость второго на 12 км/ч больше. Какое расстояние…

Источник

Две прямые на плоскости называются параллельными, если они не пересекаются.

Для обозначения параллельности прямых используется символ ll. Запись а ll b читается: «Прямая a параллельна прямой b».

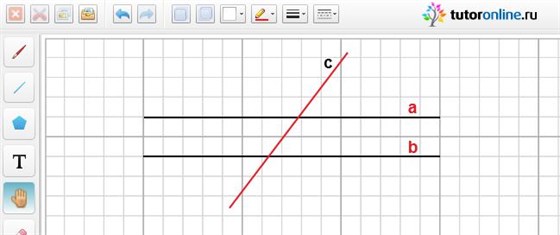
Свойства параллельных прямых

Через точку, не лежащую на прямой, можно провести на плоскости не более одной прямой параллельной данной.

Две прямые, параллельные третьей, параллельны друг другу.

Если две прямые на плоскости перпендикулярны третьей прямой, то они параллельны друг другу.

Признаки параллельности прямых

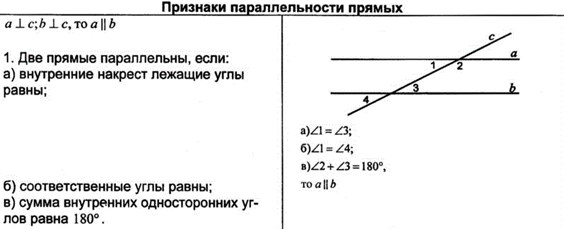
Пусть АВ и СD – две прямые. Пусть АС – третья прямая, пересекающая прямые АВ и СD. Прямая АС по отношению к прямым АВ и СD называется секущей. Образованные этими прямыми углы часто рассматриваются попарно. Пары углов получили специальные названия. Так если точки В и D лежат в разных полуплоскостях относительно прямой АС, то углы ВАС и DСА называются внутренними односторонними углами. Если точки B и D лежат в разных полуплоскостях относительно прямой АС, то углы ВАС и DCА называются внутренними накрест лежащими углами.

Секущая АС образует с прямыми АВ и СD две пары внутренних односторонних и две пары внутренних накрест лежащих углов.

Если внутренние накрест лежащие углы равны или сумма внутренних односторонних углов равна 180˚, то прямые параллельны.

Верно и обратное утверждение: если две параллельные прямые пересечены третьей прямой. То внутренние и накрест лежащие углы равны, а сумма внутренних односторонних углов равна 180˚.

Остались вопросы?

Задайте свой вопрос и получите ответ от профессионального преподавателя.

Источник

Ниже представлена таблица с основными математическими символами и знаками, которые используются в геометрии с 7 класса и старше.


Знак	Название	Значение/описание	Пример
∠	угол	фигура, состоящая из двух лучей и вершины	∠ABC = 30°
	острый угол	угол от 0 до 90 градусов	∠AOB = 60°
	прямой угол	угол, равный 90 граусам	∠AOB = 90°
	тупой угол	угол от 90 до 180 градусов	∠AOB = 120°
	развернутый угол	угол, равный 180 градусам	∠AOB = 180°
° (или deg)	градус	единица измерения угла, равна 1/360 окружности	45°
′	минута	единица измерения угла, 1° = 60′	α = 70°59′
″	секунда	единица измерения угла, 1′ = 60″	α = 70°59′59″
	линия	бесконечная прямая без начала и конца
	отрезок	участок на прямой между точками A и B
	луч	бесконечная прямая, имеющая начало в точке A, но не имеющая конца
	дуга	дуга, образованная между точками A и B
⊥	перпендикулярность	линии (прямые), расположенные под углом 90° по отношению друг к другу	AC ⊥ BC
\|\|	параллельность	непересекающиеся прямые (линии)	AB \|\| CD
∩	пересечение	множество одинаковых элементов, принадлежащих как множеству A, так и B	A ∩ B
∈ / ∉	принадлежность/ непринадлежность	элемент является/не является элементом заданного множества	a ∈ S
≅	конгуэнтность	эквивалентность геометрических форм и размеров	∆ABC ≅ ∆XYZ
~	подобие	та же форма, но разные размеры	∆ABC ~ ∆XYZ
Δ	треугольник	фигура треугольника	ΔABC ≅ ΔBCD
\|x-y\|	дистанция	дистанция между точками X и Y	\| x-y \| = 5
π	константа «Пи»	отношение длины окружности к диаметру круга, π = C/d	π = 3.141592654…
рад (rad) или ^c	радиан	единица измерения угла	360° = 2π ^c

microexcel.ru

Источник