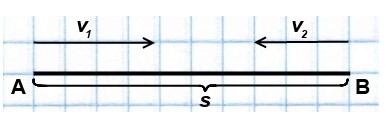
Как обозначается в математике скорость время расстояние
Скорость: V Время: t Расстояние: S
Скорость: V
Время: t
Расстояние: S
Время-t
Скорость-v
Расстояние-s
V — скорость
S — расстояние
t — время
Скорость: V
Время: t
Расстояние: S
скорость V
время t
расстояние S
Скорость: V
Время: t
Расстояние: S
Скорость: V
Время: t
Расстояние: S
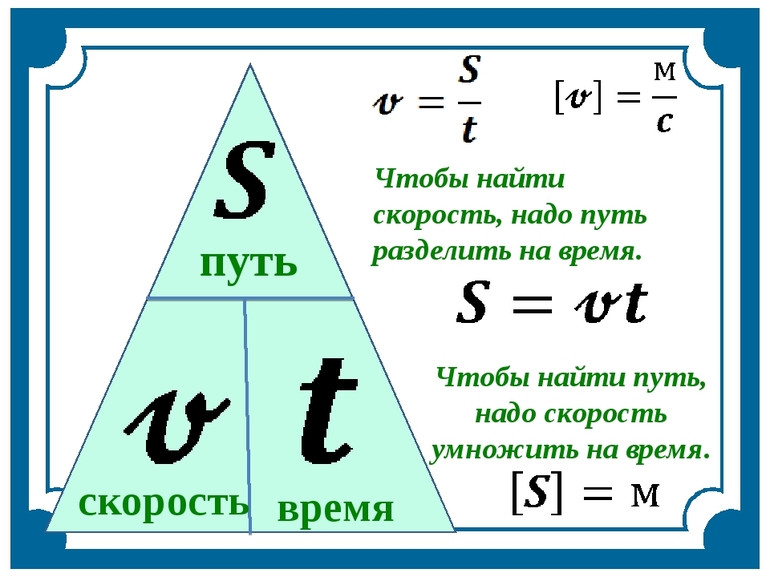
Чтобы найти расстояние нужно время умножить на скорость и получится:
S=V*T
Чтобы найти время нужно расстояние разделить на скорость и получится:
T= S/V
Чтобы найти скорость нужно расстояние разделить на время и получится:
V=S/T
Скорость: V
Время: t
Расстояние: S
Скорость: V
Время: t
Расстояние: S
Скорость: V
Время: t
Расстояние: S
Скорсость v
время t
растояние s
Скорость-V
Время-t
Расстояние-S
Скорость: V
Время: t
Расстояние: S
Скорость: V
Время: t
Расстояние: S
Скорость: V
Время: t
Расстояние: S
Скорость-V
время-t
расстояние (путь) -S
Скорость: V
Время: t
Расстояние: S
Скорость: V
Время: t
Расстояние: S
Скорость — V
Расстояние — S
Время — t
Буквой «S» в математике обычно обозначают площадь — «square». На эту букву существует ещё огромное количество других латинских и английских слов.
Расстояние в математике обычно обозначают буквой «d» — distance.
Но в твоём случае буква «S»
Скорость: V
Время: t
Расстояние: S
Скорость: V
Время: t
Расстояние: S
V — скорость
S — расстояние
t — время
Скорость: V
Время: t
Расстояние: S
Скорость: V
Время: t
Расстояние: S
Чтобы найти расстояние нужно время умножить на скорость и получится:
S=V*T
Чтобы найти время нужно расстояние разделить на скорость и получится:
T= S/V
Чтобы найти скорость нужно расстояние разделить на время и получится:
V=S/T
V — скорость
S — расстояние
t — время
Скорость: V
Время: t
Расстояние: S
Скорость V
Время T
Путь (расстояние) S
Скорость-Sкм
Время-Vч
расстояние-Sкмч
Скорость: V
Время: t
Расстояние: S
Расстояние: S
Скорость: V
Время: t
Войдите, чтобы написать ответ
|
Амирбаева Гаухар Амирбаевна учитель начальных классов Махамбетская средняя школа им. Есенбая Агелеуова, село Махамбет, Махамбетский район Атырауская область |
Цель: продолжить формировать представление о новой величине «скорость, время, расстояние» и единицах ее измерения.
Задачи:
- Создать условия для осознания детьми зависимости между величинами, характеризующими движение тел — скоростью, временем и расстоянием.
- Познакомить детей с понятием скорости и единицами её измерения.
- Отрабатывать вычислительные навыки, обучать детей работе с графическими моделями.
- Развивать познавательную активность детей, способности к самооценке и самоконтролю, формировать коммуникативные умения.
Оборудование: карточки, карточки для работы в парах, интерактивная доска, название единиц времени на карточках, рабочая тетрадь, компьютер, проектор, экран
учебник.
Тип урока: урок закрепления и развития знаний, умений и навыков.
Методы: формы познавательной деятельности учащихся на уроке, индивидуальная работа, работа в парах.
Планируемые достижения учащихся на уроке:
- знать понятие скорости, времени и расстоянии как новой единицы измерения, уметь решать задачи на нахождение скорости движения по известным расстоянию и времени движения;
- закрепить табличные и внетабличные случаи умножения и деления, знание единиц длины и времени.
Ход урока
Организационный момент
Психологический настрой
Прозвенел заливистый школьный звонок.
Начинается новый урок.
Мы готовы считать и задачи решать.
Учитель: Я улыбнулась вам, и вы улыбнитесь друг другу, и подумайте, как хорошо, что мы сегодня все вместе. Мы спокойны, добры и приветливы. Глубоко вдохните и выдохните. Выдохните вчерашнюю обиду и злость, беспокойство. Забудьте о них. Я желаю вам хорошего настроения.
Сообщение темы и цели урока
Сегодня на уроке мы с вами вспомним о величинах, с которыми познакомились на предыдущих уроках и решали с ними задачи на движение и ставить свои ответы на листах самооценки.
(Ответы учащихся) Верно, это скорость, время, расстояние. Какими латинскими буквами они обозначаются. (s, v, t).
Слайд № 1
Девиз нашего урока: «Один за всех, все за одного»
Работа в парах
На партах карточки с примерами:
Увеличь произведение чисел 805 и 5 на 1025 (5050)
Из 10000 вычти частное число 40025 и 5 (1995)
Увеличь частное чисел 4025 и 5 в 100 раз (80500)
Прибавь к числу 1207 частное чисел 51300 и 9 (6907)
Из произведения чисел 480 и 7 вычти число 1406 (1954)
Произведение чисел 4070 и 6 уменьши на 4420 (20000)
Записать ответы в порядке возрастания
(ответ записан на интерактивной доске)
Минутка чистописания
Слайд № 2
2 4 6 8 10 (образец в тетради)
Прочитайте числа. Какие это числа? В каком порядке они расположены? Как они увеличиваются? Прочитайте число целиком. Сколько цифр использовано? В обратном направлении можем прочитать? Прочитайте. Запишите числа в порядке возрастания, через клеточку в порядке убывания. Прочитайте их, сравните. Запишите еще раз в порядке возрастания, найдите сумму этих четных чисел. Как вы это сделали?
Индивидуальная работа по карточкам
(4 ученика решают № 7)
Устная работа с остальными учениками:
В саду растут груши и ивы. На груше росло 69 груш, а на иве на 100 груш больше. Сколько груш росло на иве?
Мама варила одно яйцо 5 минут. Сколько времени будет варить 3 яйца?
Масса 1 мешка сахара 50 кг. Сколько кг в 4 таких мешках?
За 1 с человек делает 2 шага. Сколько шагов он сделает за 5 с.? За 10 с?
Слайд № 3
Физминутка
Слайд № 4
Качу, лечу во весь опор. (Выполняют ходьбу на месте.)
Я сам — шофер (Имитируют управление автомобильным рулем.)
И сам — мотор. (Круговые движения плечами вперед-назад.)
Нажимаю на педаль, (Имитируют нажимание на педаль.)
И машина мчится вдаль! (Бег на месте.)
Первичное закрепление
Слайд № 5
Орел летел со скоростью 20 км/ч. За сколько часов он пролетит 80 км?
Cкорость полета космического спутника 8 км/сек. Сколько км он пролетит за 10 сек?
Слайд № 6
Решение задачи № 2
Автобус
S — 90 км 90: 45= 2 часа
T — ?
V — 45 км/ч
Легковая машина
S — 270 км 270: 90 = 3 часа
T — ?
V — 90 км/ч
Самостоятельная работа по учебнику
№ 8, № 9
Итог урока
Давайте подведем итог урока
— Чем занимались на уроке?
— Что запомнили?
Рефлексия
Окрасьте сегодняшний урок (Дети рисуют сердечко своего настроения от урока) Учитель объясняет значении выбранного цвета.
- Красный — радость
- Жёлтый — приятное
- Зелёный — спокойное
- Синий — грустное
- Фиолетовый — тревожный
- Оранжевый — удовлетворение
- Чёрный — неудовлетворение
И на память об уроке солнышко дарит вам частичку своего тепла и хорошего настроения.
Наш закончен урок —
Спасибо за внимание,
Будем рады новой встрече,
Всем Вам до свидания!
Домашнее задание
№ 5, 6
Комментирование оценок
Морфемный разбор слова:
Однокоренные слова к слову:
Формула скорости — обозначение, единицы измерения и примеры нахождения
Довольно часто в точных науках приходится сталкиваться с понятием скорость. Формула, дающаяся в школе на уроке математики, справедлива лишь для частного случая, при котором перемещение остаётся всегда постоянным. По сути, термин обозначает быстроту изменения чего-либо. Существует несколько видов движения и методов расчета.
Понятие и основные термины
Под скоростью понимается величина, определяющая быстроту и направление перемещения материальной точки в выбранной системе отсчёта. Термин широко применяется в математике, физике, химии. Так, с его помощью описывают реакции, изменения температуры, передвижение тел, используют как производную рассматриваемой величины.
Слово «скорость» произошло от латинского «velocitas», обозначающее движение. В качестве единицы измерения, согласно Международной системе единиц (СИ), для неё выбран метр, делённый на секунду (м/с). Обозначается скорость буквой V, вне зависимости от науки, в которой её применяют. Простейшая формула, с помощью которой определяют величину, выглядит следующим образом: V = S: t. Где:
Это обобщённое уравнение, но в то же время позволяющее получить представление о понятии. Часто это неравенство называют уравнением пути. Формула используется для вычисления только в том случае, если движение не изменяется на всём исследуемом участке.
Впервые с выражением знакомят учащихся на уроках математики в пятом классе. Учитель предлагает научиться решать простые задачи на нахождение характеристики при известной длине пройденного пути и потраченного на это времени. Например, автомобиль за четыре часа проехал 16 километров. Необходимо найти, с какой скоростью он двигался. Решение задачи сводится к двум действиям. В первом все заданные величины переводятся в систему СИ: 4 часа = 240 минут = 10240 секунд; 16 километров = 16000 метров. Во втором действии данные подставляют в формулу и вычисляют ответ: V = 16000/10240 = 1,6 м/с.
Но, помимо равномерного движения, то есть при котором скорость является константой, есть ещё и другие виды перемещений. Использовать обобщённое уравнение для них нельзя. Для каждого вида движения применяется своя формула. Существующую скорость разделяют на следующие виды:
Равноускоренное движение
Если в течение времени положение тела изменяется относительно предметов, находящихся в покое, то считается, что оно движется. При этом в качестве основного параметра, описывающего перемещение, используется скорость. Движение тела или точки можно представить в виде линии, повторяющей путь прохождения. Называется она траекторией. Если линия прямая, то движение считается прямолинейным.
Неравномерное движение характеризуется перемещением по различной траектории с непостоянной величиной скорости. При этом изменение положения может быть равноускоренным, то есть параметр на одинаковых промежутках увеличивается или уменьшается на одно и то же значение. В качестве примера можно привести падение камня.
В произвольно взятой точке скорость перемещения равна ускорению свободного падения.
Таким образом, если векторы V и ускорения A лежат вдоль прямой, то в проекциях такое направление можно рассматривать как алгебраические величины. При равноускоренном движении по прямой траектории скорость точки вычисляется по формуле: V = V0 + A*t. Где:
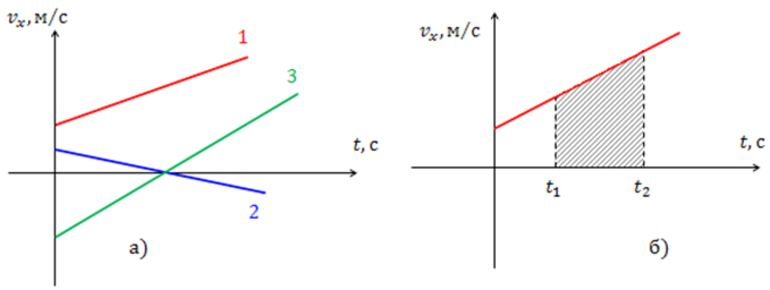
Это основная формула в физике. На графике она изображается как прямая линия v (t). По оси ординат откладывается время, а абсцисс — скорость. Построив график, по наклону прямой можно определить ускорение точки A. Для этого используется формула нахождения сторон треугольника: A = (v-v0) / t.
Среднее значение
В кинематике для нахождения характеристики используется усреднённый параметр. Используют его при изучении движения материальной точки или любого физического тела. Для определения средней скорости используют две величины: скалярную и векторную. Первой обозначают путевое движение, а второй — перемещение.
Путевая скорость определяется как отношение расстояния пройденного тела ко времени, затраченному на его прохождение: V = Σs / Σt.
По сути, среднее значение находится как среднеарифметическое от всех скоростей, если рассматриваемая точка передвигалась одинаковые отрезки времени. В ином же случае найденная величина будет взвешенной среднеарифметической величиной.
Математически формулу средней скорости записывают так: V (t + Δ t) = Δ s/ Δ t = (s (t + Δ t) — s (t)) / Δ t. Учитывая, что Δs зависит от длины пути, которую преодолела точка за время Δt, верной будет запись: Δ s = s (t + Δt) — s (t). Если же затраченное время стремится к нулю, получится формула, совпадающая с выражением для нахождения мгновенной скорости.
Вектор материальной точки находится из отношения положения тела к отрезку времени: V (t + Δt) = Δr / Δt = (r (t + Δt) — r (t)) / Δt, где r — радиус-вектор. Когда тело выполняет равномерно-прямолинейное перемещение, то справедливым будет равенство: = V.
Например, мяч первую половину пути длиной 100 метров катился с одной скоростью в течение двадцати секунд, а вторую с другой и одну минуту. Необходимо вычислить среднюю скорость. Согласно формулам, интервал движения на первом участке пути будет равен: t1 = s/2*V1, а на втором t2 = s/2*V2. Решением задачи будет: Vср = s/(t1+t2) = s/(s/2*v1 + s/2*v2) = 2*V1*V2/(V1+V2) = 100/(20 +60) = 1,25 м/с.
Угловая скорость
Проявляется этот вид при вращении тела вокруг оси. Траектория представляет собой круговое движение. Основным параметром, учитывающимся при его нахождении, является угол поворота (f). Все элементарные угловые движения являются векторами. Обычный поворот равен углу вращения тела df за небольшой отрезок времени dt в противоположную сторону от хода часовой стрелки.
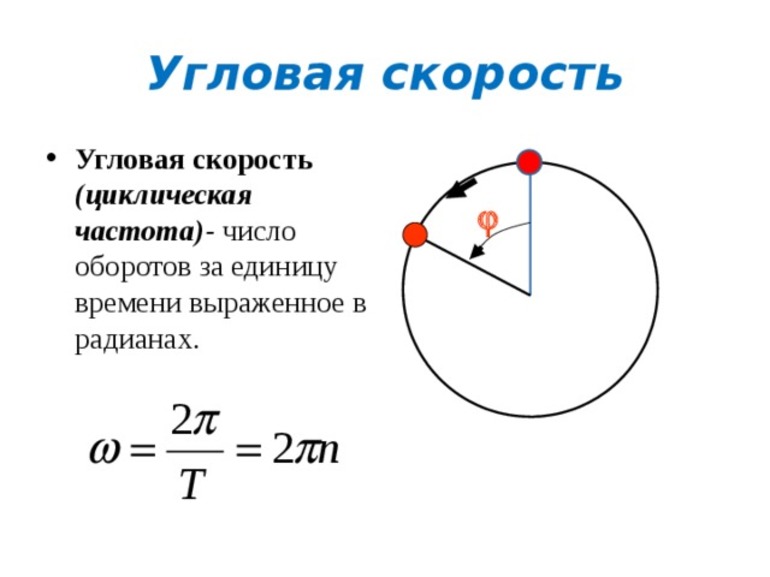
В математике формулу для нахождения углового параметра записывают как w = df/dt. Угловая скорость — аксиальная величина, располагающаяся вдоль мгновенной оси и совпадающая с поступательным вращением правого винта. Равномерное вращение, то есть движение, при котором происходит поворот на один и тот же угол, называют равномерным. Модуль угловой скорости определяют по формуле: w = f/t, где f — угол поворота, t — время, в течение которого происходило вращение. Учитывая, что Δf = 2p, формулу можно переписать до вида: w = 2p/T, то есть с использованием периода.
Существует связь между угловой скоростью и числом оборотов: w = 2*p*v. Это понятие используется для решения заданий при описании неравномерного вращения. Есть также выражение, связывающее линейную скорость с угловой: v = [w*R], где R — компонента, проведённая перпендикулярно к радиус-вектору. В качестве единицы измерения параметра используется радиан, делённый на секунду (рад/с).
Например, необходимо определить угловую скорость вариатора в тот момент, когда подвешенная масса пройдёт расстояние, равное 10 метрам. Радиус плеча составляет 40 сантиметров. В начальный момент подвес находится в состоянии покоя, а затем начинает опускаться с ускорением A = 0,04 м/с2.
Учитывая, что линейная скорость вариатора совпадает с движением груза по прямой, можно записать: V = (2*a*S)½. Должен получится ответ: V = (4*0,04*10)½ = 1,26 м/с. Угловую же скорость находят по формуле: w = v/R, так как R = 40 см = 0,4 м, то W = 1,26/0,4 = 3,15 рад/с.
Закон сложения
Для разных систем отсчёта движения материальных точек существует закон, связывающий их между собой. Согласно ему, скорость чего-либо относительно системы, находящейся в покое, определяется суммой силы перемещения скоростей в подвижной области и более быстрой системы отсчёта по отношению к неподвижной.
Чтобы понять суть закона, лучше всего рассмотреть простой пример. Пусть по железной дороге движется вагон со скоростью 80 км/ч. В этом вагоне перемещается пассажир со скоростью 3 км/ч. Приняв за систему отсчёта неподвижный железнодорожный путь, можно утверждать, что скорость пассажира относительно неё равна сумме скорости вагона и человека.
Если движение вагона и пассажира происходит в одном направлении, то значения просто складываются, V = 80+3 = 83 км/ч, в противоположном — вычитаются V = 80−3 = 77 км/ч. Но это правило будет верным лишь тогда, когда перемещение происходит по одной линии. Поэтому, если человек будет передвигаться в вагоне под углом, следует учитывать и этот фактор, так как по своей сути искомый параметр — величина векторная. Фактически рассчитываются две скорости: сближения и удаления.
Рассматриваемое событие происходит за время Δt. За этот промежуток человек преодолеет расстояние ΔS1, вагон же сможет проехать путь ΔS2. Используя закон, перемещение пассажира будет определяться по формуле: ΔS = ΔS1 + ΔS2. Собственное движение человека относительно железнодорожного пути будет равно V = ΔS1 / Δ t. Выразив значение из формулы нахождения ΔS, можно найти скорость вагона относительно железной дороги: V2 = ΔS2 / Δt.
Использование онлайн-калькулятора
В интернете существуют сервисы, позволяющие находить параметр даже тем, кто не знает формулы или слабо ориентируется в теме. С их помощью можно решать довольно сложные задания, которые требуют скрупулёзного расчёта и немалой затраты времени. Онлайн-вычисление обычно занимает не более нескольких секунд, а за достоверность результата можно не беспокоиться.
Воспользоваться сайтами-калькуляторами сможет любой пользователь, имеющий подключение к интернету и установленный веб-браузер с поддержкой Flash-технологии. Никакой регистрации или указания личных данных сервисы, предлагающие такого рода услуги, не требуют. Система автоматически рассчитает ответ.
Из множества сайтов можно выделить три наиболее популярных среди потребителей:
Все они имеют интуитивно понятный интерфейс и, что примечательно, на своих страницах содержат таблицы всех формул, используемых для решения заданий, правильные условные обозначения и описания процессов вычисления.
Расчёт скорости любого тела несложен. Главное, знать формулы и правильно определить вид перемещения. При этом всегда можно воспользоваться услугами онлайн-калькуляторов. Через них решить поставленную задачу или проверить свои расчёты.
Источник
Понятие и основные термины
Под скоростью понимается величина, определяющая быстроту и направление перемещения материальной точки в выбранной системе отсчёта. Термин широко применяется в математике, физике, химии. Так, с его помощью описывают реакции, изменения температуры, передвижение тел, используют как производную рассматриваемой величины.
Слово «скорость» произошло от латинского «velocitas», обозначающее движение. В качестве единицы измерения, согласно Международной системе единиц (СИ), для неё выбран метр, делённый на секунду (м/с). Обозначается скорость буквой V, вне зависимости от науки, в которой её применяют. Простейшая формула, с помощью которой определяют величину, выглядит следующим образом: V = S: t. Где:
Это обобщённое уравнение, но в то же время позволяющее получить представление о понятии. Часто это неравенство называют уравнением пути. Формула используется для вычисления только в том случае, если движение не изменяется на всём исследуемом участке.
Впервые с выражением знакомят учащихся на уроках математики в пятом классе. Учитель предлагает научиться решать простые задачи на нахождение характеристики при известной длине пройденного пути и потраченного на это времени. Например, автомобиль за четыре часа проехал 16 километров. Необходимо найти, с какой скоростью он двигался. Решение задачи сводится к двум действиям. В первом все заданные величины переводятся в систему СИ: 4 часа = 240 минут = 10240 секунд; 16 километров = 16000 метров. Во втором действии данные подставляют в формулу и вычисляют ответ: V = 16000/10240 = 1,6 м/с.
Но, помимо равномерного движения, то есть при котором скорость является константой, есть ещё и другие виды перемещений. Использовать обобщённое уравнение для них нельзя. Для каждого вида движения применяется своя формула. Существующую скорость разделяют на следующие виды:
Равноускоренное движение
Если в течение времени положение тела изменяется относительно предметов, находящихся в покое, то считается, что оно движется. При этом в качестве основного параметра, описывающего перемещение, используется скорость. Движение тела или точки можно представить в виде линии, повторяющей путь прохождения. Называется она траекторией. Если линия прямая, то движение считается прямолинейным.
Неравномерное движение характеризуется перемещением по различной траектории с непостоянной величиной скорости. При этом изменение положения может быть равноускоренным, то есть параметр на одинаковых промежутках увеличивается или уменьшается на одно и то же значение. В качестве примера можно привести падение камня.
В произвольно взятой точке скорость перемещения равна ускорению свободного падения.
Таким образом, если векторы V и ускорения A лежат вдоль прямой, то в проекциях такое направление можно рассматривать как алгебраические величины. При равноускоренном движении по прямой траектории скорость точки вычисляется по формуле: V = V0 + A*t. Где:
Это основная формула в физике. На графике она изображается как прямая линия v (t). По оси ординат откладывается время, а абсцисс — скорость. Построив график, по наклону прямой можно определить ускорение точки A. Для этого используется формула нахождения сторон треугольника: A = (v-v0) / t.
Среднее значение
В кинематике для нахождения характеристики используется усреднённый параметр. Используют его при изучении движения материальной точки или любого физического тела. Для определения средней скорости используют две величины: скалярную и векторную. Первой обозначают путевое движение, а второй — перемещение.
Путевая скорость определяется как отношение расстояния пройденного тела ко времени, затраченному на его прохождение: V = Σs / Σt.
По сути, среднее значение находится как среднеарифметическое от всех скоростей, если рассматриваемая точка передвигалась одинаковые отрезки времени. В ином же случае найденная величина будет взвешенной среднеарифметической величиной.
Математически формулу средней скорости записывают так: V (t + Δ t) = Δ s/ Δ t = (s (t + Δ t) — s (t)) / Δ t. Учитывая, что Δs зависит от длины пути, которую преодолела точка за время Δt, верной будет запись: Δ s = s (t + Δt) — s (t). Если же затраченное время стремится к нулю, получится формула, совпадающая с выражением для нахождения мгновенной скорости.
Вектор материальной точки находится из отношения положения тела к отрезку времени: V (t + Δt) = Δr / Δt = (r (t + Δt) — r (t)) / Δt, где r — радиус-вектор. Когда тело выполняет равномерно-прямолинейное перемещение, то справедливым будет равенство: = V.
Например, мяч первую половину пути длиной 100 метров катился с одной скоростью в течение двадцати секунд, а вторую с другой и одну минуту. Необходимо вычислить среднюю скорость. Согласно формулам, интервал движения на первом участке пути будет равен: t1 = s/2*V1, а на втором t2 = s/2*V2. Решением задачи будет: Vср = s/(t1+t2) = s/(s/2*v1 + s/2*v2) = 2*V1*V2/(V1+V2) = 100/(20 +60) = 1,25 м/с.
Угловая скорость
Проявляется этот вид при вращении тела вокруг оси. Траектория представляет собой круговое движение. Основным параметром, учитывающимся при его нахождении, является угол поворота (f). Все элементарные угловые движения являются векторами. Обычный поворот равен углу вращения тела df за небольшой отрезок времени dt в противоположную сторону от хода часовой стрелки.
В математике формулу для нахождения углового параметра записывают как w = df/dt. Угловая скорость — аксиальная величина, располагающаяся вдоль мгновенной оси и совпадающая с поступательным вращением правого винта. Равномерное вращение, то есть движение, при котором происходит поворот на один и тот же угол, называют равномерным. Модуль угловой скорости определяют по формуле: w = f/t, где f — угол поворота, t — время, в течение которого происходило вращение. Учитывая, что Δf = 2p, формулу можно переписать до вида: w = 2p/T, то есть с использованием периода.
Существует связь между угловой скоростью и числом оборотов: w = 2*p*v. Это понятие используется для решения заданий при описании неравномерного вращения. Есть также выражение, связывающее линейную скорость с угловой: v = [w*R], где R — компонента, проведённая перпендикулярно к радиус-вектору. В качестве единицы измерения параметра используется радиан, делённый на секунду (рад/с).
Например, необходимо определить угловую скорость вариатора в тот момент, когда подвешенная масса пройдёт расстояние, равное 10 метрам. Радиус плеча составляет 40 сантиметров. В начальный момент подвес находится в состоянии покоя, а затем начинает опускаться с ускорением A = 0,04 м/с2.
Учитывая, что линейная скорость вариатора совпадает с движением груза по прямой, можно записать: V = (2*a*S)½. Должен получится ответ: V = (4*0,04*10)½ = 1,26 м/с. Угловую же скорость находят по формуле: w = v/R, так как R = 40 см = 0,4 м, то W = 1,26/0,4 = 3,15 рад/с.
Закон сложения
Для разных систем отсчёта движения материальных точек существует закон, связывающий их между собой. Согласно ему, скорость чего-либо относительно системы, находящейся в покое, определяется суммой силы перемещения скоростей в подвижной области и более быстрой системы отсчёта по отношению к неподвижной.
Чтобы понять суть закона, лучше всего рассмотреть простой пример. Пусть по железной дороге движется вагон со скоростью 80 км/ч. В этом вагоне перемещается пассажир со скоростью 3 км/ч. Приняв за систему отсчёта неподвижный железнодорожный путь, можно утверждать, что скорость пассажира относительно неё равна сумме скорости вагона и человека.
Если движение вагона и пассажира происходит в одном направлении, то значения просто складываются, V = 80+3 = 83 км/ч, в противоположном — вычитаются V = 80−3 = 77 км/ч. Но это правило будет верным лишь тогда, когда перемещение происходит по одной линии. Поэтому, если человек будет передвигаться в вагоне под углом, следует учитывать и этот фактор, так как по своей сути искомый параметр — величина векторная. Фактически рассчитываются две скорости: сближения и удаления.
Рассматриваемое событие происходит за время Δt. За этот промежуток человек преодолеет расстояние ΔS1, вагон же сможет проехать путь ΔS2. Используя закон, перемещение пассажира будет определяться по формуле: ΔS = ΔS1 + ΔS2. Собственное движение человека относительно железнодорожного пути будет равно V = ΔS1 / Δ t. Выразив значение из формулы нахождения ΔS, можно найти скорость вагона относительно железной дороги: V2 = ΔS2 / Δt.
Использование онлайн-калькулятора
В интернете существуют сервисы, позволяющие находить параметр даже тем, кто не знает формулы или слабо ориентируется в теме. С их помощью можно решать довольно сложные задания, которые требуют скрупулёзного расчёта и немалой затраты времени. Онлайн-вычисление обычно занимает не более нескольких секунд, а за достоверность результата можно не беспокоиться.
Воспользоваться сайтами-калькуляторами сможет любой пользователь, имеющий подключение к интернету и установленный веб-браузер с поддержкой Flash-технологии. Никакой регистрации или указания личных данных сервисы, предлагающие такого рода услуги, не требуют. Система автоматически рассчитает ответ.
Из множества сайтов можно выделить три наиболее популярных среди потребителей:
Все они имеют интуитивно понятный интерфейс и, что примечательно, на своих страницах содержат таблицы всех формул, используемых для решения заданий, правильные условные обозначения и описания процессов вычисления.
Расчёт скорости любого тела несложен. Главное, знать формулы и правильно определить вид перемещения. При этом всегда можно воспользоваться услугами онлайн-калькуляторов. Через них решить поставленную задачу или проверить свои расчёты.
Источник
Основная особенность используемых в настоящее время систем единиц состоит в том, что между единицами разных величин имеются определенные соотношения. Эти соотношения установлены теми физическими законами (определениями), которыми связываются между собой измеряемые величины. Так, единица скорости выбрана таким образом, что она выражается через единицы расстояния и времени. При выборе единиц скорости используется определение скорости. Единицу силы, например, устанавливают при помощи второго закона Ньютона.
При построении определенной системы единиц, выбирают несколько физических величин, единицы которых устанавливают независимо друг от друга. Единицы таких величин называют основными. Единицы остальных величин выражают через основные, их называют производными.
Таблица единиц измерения «Пространство и время»
Физическая величина
Символ
Единица измерения физической величины
Ед. изм. физ. вел.
Описание
Примечания
l, s, d
Протяжённость объекта в одном измерении.
Протяженность объекта в двух измерениях.
Протяжённость объекта в трёх измерениях.
α, φ
Величина изменения направления.
α, β, γ
Быстрота изменения координат тела.
метр в секунду в квадрате
м/с 2
Быстрота изменения скорости объекта.
рад/с =
Скорость изменения угла.
радиан на секунду в квадрате
рад/с 2 =
Быстрота изменения угловой скорости
Таблица единиц измерения «Механика»
Физическая величина
Символ
Единица измерения физической величины
Ед. изм. физ. вел.
Описание
Примечания
Величина, определяющая инерционные и гравитационные свойства тел.
килограмм на кубический метр
кг/м 3
Масса на единицу объёма.
Масса на единицу площади.
кг/м 2
Отношение массы тела к площади его поверхности
Масса на единицу длины.
Отношение массы тела к его линейному параметру
кубический метр на килограмм
м 3 /кг
Объём, занимаемый единицей массы вещества
килограмм в секунду
Масса вещества, которая проходит через заданную площадь поперечного сечения потока за единицу времени
кубический метр в секунду
м 3 /с
Объёмный расход жидкости или газа
килограмм-метр в секунду
кг•м/с
Произведение массы и скорости тела.
экстенсивная, сохраняющаяся величина
килограмм-метр в квадрате в секунду
кг•м 2 /с
Мера вращения объекта.
килограмм-метр в квадрате
кг•м 2
Мера инертности объекта при вращении.
Действующая на объект внешняя причина ускорения.
Произведение силы на длину перпендикуляра, опущенного из точки на линию действия силы.
Произведение силы на время её действия
Давление, механическое напряжение
Па = (кг/(м·с 2 ))
Сила, приходящаяся на единицу площади.
Дж = (кг·м 2 /с 2 )
Скалярное произведение силы и перемещения.
Дж = (кг·м 2 /с 2 )
Способность тела или системы совершать работу.
экстенсивная, сохраняющаяся величина, скаляр
Вт = (кг·м 2 /с 3 )
Скорость изменения энергии.
Таблица единиц измерения «Периодические явления, колебания и волны»
Физическая величина
Символ
Единица измерения физической величины
Ед. изм. физ. вел.
Описание
Примечания
Промежуток времени, за который система совершает одно полное колебание
Частота периодического процесса
Число повторений события за единицу времени.
Циклическая (круговая) частота
рад/с
Циклическая частота электромагнитных колебаний в колебательном контуре.
секунда в минус первой степени
Периодический процесс, равный числу полных циклов, совершённых за единицу времени.
Расстояние между двумя ближайшими друг к другу точками в пространстве, в которых колебания происходят в одинаковой фазе.
метр в минус первой степени
Пространственная частота волны
Таблица единиц измерения «Тепловые явления»
Физическая величина
Символ
Единица измерения физической величины
Ед. изм. физ. вел.
Описание
Примечания
Средняя кинетическая энергия частиц объекта.
кельвин в минус первой степени
Зависимость электрического сопротивления от температуры
gradT
Изменение температуры на единицу длины в направлении распространения теплоты.
Теплота (количество теплоты)
Дж = (кг·м 2 /с 2 )
Энергия, передаваемая от одного тела к другому немеханическим путём
джоуль на килограмм
Дж/кг
Кол-во теплоты, которое необходимо подвести к веществу, взятому при температуре плавления, чтобы расплавить его.
Кол-во теплоты, поглощаемой (выделяемой) телом в процессе нагревания.
джоуль на килограмм-кельвин
Дж/(кг•К)
Теплоёмкость единичной массы вещества.
джоуль на килограмм
Дж/кг
Мера необратимого рассеивания энергии или бесполезности энергии.
Таблица единиц измерения «Молекулярная физика»
Физическая величина
Символ
Единица измерения физической величины
Описание
Примечания
моль
Количество однотипных структурных единиц, из которых состоит вещество.
M, μ
кг/моль
Отношение массы вещества к количеству молей этого вещества.
Дж/моль
Энергия термодинамической системы.
джоуль на моль-кельвин
Дж/(моль•К)
Теплоёмкость одного моля вещества.
метр в минус третьей степени
Число молекул, содержащихся в единице объема.
килограмм на кубический метр
кг/м 3
Отношение массы компонента, содержащегося в смеси, к объёму смеси.
моль на кубический метр
моль/м 3
Содержание компонента относительно всей смеси.
В, μ
квадратный метр на вольт-секунду
м 2 /(В•с)
Коэффициент пропорциональности между дрейфовой скоростью носителей и приложенным внешним электрическим полем.
Таблица единиц измерения «Электричество и магнетизм»
Физическая величина
Символ
Единица измерения физической величины
Ед. изм. физ. вел.
Описание
Примечания
Протекающий в единицу времени заряд.
ампер на квадратный метр
А/м 2
Сила электрического тока, протекающего через элемент поверхности единичной площади.
Кл = (А·с)
Способность тел быть источником электромагнитных полей и принимать участие в электромагнитном взаимодействии.
экстенсивная, сохраняющаяся величина
Электрический дипольный момент
Электрические свойства системы заряженных частиц в смысле создаваемого ею поля и действия на неё внешних полей.
кулон на квадратный метр
Кл/м 2
Процессы и состояния, связанные с разделением каких-либо объектов, преимущественно в пространстве.
Изменение потенциальной энергии, приходящееся на единицу заряда.
Работа сторонних сил (некулоновских) по перемещению заряда.
Отношение силы F, действующей на неподвижный точечный заряд, помещённый в данную точку поля, к величине этого заряда q
Мера способности проводника накапливать электрический заряд
Ом = (м 2 ·кг/(с 3 ·А 2 ))
сопротивление объекта прохождению электрического тока
Удельное электрическое сопротивление
Способность материала препятствовать прохождению электрического тока
Способность тела (среды) проводить электрический ток
Векторная величина, являющаяся силовой характеристикой магнитного поля
Величина, учитывающая интенсивность магнитного поля и занимаемую им область.
Напряженность магнитного поля
Разность вектора магнитной индукции B и вектора намагниченности M
А•м 2
Величина, характеризующая магнитные свойства вещества
Величина, характеризующая магнитное состояние макроскопического физического тела.
Коэффициент пропорциональности между электрическим током, текущим в каком-либо замкнутом контуре, и полным магнитным потоком
Дж = (кг·м 2 /с 2 )
Энергия, заключенная в электромагнитном поле
Объемная плотность энергии
джоуль на кубический метр
Дж/м 3
Энергия электрического поля конденсатора
Мощность в цепи переменного тока
Величина, характеризующая нагрузки, создаваемые в электротехнических устройствах колебаниями энергии электромагнитного поля в цепи переменного тока
Суммарная мощность с учетом активной и реактивной ее составляющих, а также отклонения формы тока и напряжения от гармонической
Таблица единиц измерения «Оптика, электромагнитное излучение»
Физическая величина
Символ
Единица измерения физической величины
Ед. изм. физ. вел.
Описание
Примечания
Количество световой энергии, излучаемой в заданном направлении в единицу времени.
Световая, экстенсивная величина
Физическая величина, характеризующая количество «световой» мощности в соответствующем потоке излучения
Физическая величина, характеризует способность энергии, переносимой светом, вызывать у человека зрительные ощущения
Отношение светового потока, падающего на малый участок поверхности, к его площади.
люмен на квадратный метр
лм/м 2
Световая величина, представляющая собой световой поток
кандела на квадратный метр
кд/м 2
Сила света, излучаемая единицей площади поверхности в определенном направлении
Дж = (кг·м 2 /с 2 )
Энергия, переносимая оптическим излучением
Таблица единиц измерения «Акустика»
Физическая величина
Символ
Единица измерения физической величины
Ед. изм. физ. вел.
Описание
Примечания
Переменное избыточное давление, возникающее в упругой среде при прохождении через неё звуковой волны
кубический метр в секунду
м 3 /с
Отношение объема сырья, подаваемого в реактор в час к объему катализатора
Скорость распространения упругих волн в среде
ватт на квадратный метр
Вт/м 2
Величина, характеризующая мощность, переносимую звуковой волной в направлении распространения
скалярная физическая величина
паскаль-секунда на кубический метр
Па•с/м 3
Отношение амплитуды звукового давления в среде к колебательной скорости её частиц при прохождении через среду звуковой волны
ньютон-секунда на метр
Указывает силу, необходимую для движения тела при каждой частоте
Физическая величина
Символ
Единица измерения физической величины
Ед. изм. физ. вел.
Описание
Примечания
Масса объекта, находящегося в состоянии покоя.
Величина, выражающая влияние внутренних взаимодействий на массу составной частицы
Элементарный электрический заряд
Минимальная порция (квант) электрического заряда, наблюдающегося в природе у свободных долгоживущих частиц
Дж = (кг·м 2 /с 2 )
Разность между энергией состояния, в котором составляющие части системы бесконечно удалены
Период полураспада, среднее время жизни
Время, в течение которого система распадается в примерном отношении 1/2
Величина, характеризующая вероятность взаимодействия элементарной частицы с атомным ядром или другой частицей
Величина, равная отношению общего числа распадов радиоактивных ядер нуклида в источнике ко времени распада
Энергия ионизирующего излучения
Дж = (кг·м 2 /с 2 )
Вид энергии, высвобождаемой атомами в форме электромагнитных волн (гамма- или рентгеновское излучение) или частиц
Поглощенная доза ионизирующего излучения
Доза, при которой массе 1 кг передаётся энергия ионизирующего излучения в 1 джоул
Эквивалентная доза ионизирующего излучения
Поглощенная доза любого ионизирующего излучения, равная 100 эрг на 1 грамм облученного вещества
Экспозиционная доза рентгеновского и гамма-излучения
кулон на килограмм
Кл/кг
отношение суммарного электрического заряда ионов одного знака от внешнего гамма-излучения
Обозначения в физике с несколькими буквами
Специальные символы
Для удобства написания и чтения в среде ученых физиков принято использовать специальные символы, характеризующие те или иные явления и свойства.
Скобки
В физике принято использовать не только формулы, которые применяют в математике, но и специализированные скобки.
Диакритические знаки
Диакритические знаки добавляются к символу физической величины для обозначения определённых различий. Ниже диакритические знаки добавлены для примера к букве x.
Источник
Теперь вы знаете какие однокоренные слова подходят к слову Как пишется и читается символ скорости принятый в физике, а так же какой у него корень, приставка, суффикс и окончание. Вы можете дополнить список однокоренных слов к слову «Как пишется и читается символ скорости принятый в физике», предложив свой вариант в комментариях ниже, а также выразить свое несогласие проведенным с морфемным разбором.
Со времен возникновения различных наук и математических расчетов ученые начали использовать множество символов и сокращений. Это вполне оправданное решение, ведь длинные формулы, записанные при помощи слов, отнимали бы много времени. По какому принципу выбираются эти обозначения, в частности буквы, указывающие на скорость и расстояние?
Как обозначают физические величины и понятия?
В физике существует общепринятый список обозначений. Он включает латинские и греческие буквы, кириллицу (редко), специальные символы, надстрочные и подстрочные знаки, скобки и др. В качестве самостоятельной науки физика зародилась в 17-м веке во время научной революции, но многие идеи, физические воззрения появились еще в античный период. Отсюда и использование латыни, греческого языка.
Количество физических величин довольно большое – букв в алфавитах недостаточно для обозначения их всех. Поэтому одни и те же буквы могут обозначать разные понятия. Важно различать и стиль написания.
Например, латинские символы обычно пишутся курсивом, греческие – обыкновенным прямым начертанием. Строчными буквами обозначают интенсивные величины (не зависят от размеров системы, например, температура), заглавными – экстенсивные.
Интересный факт: среди всех латинских букв для обозначения понятий из области физики реже всего встречается буква о.
Ввиду исторических причин множество обозначений с использованием латинских букв – это сокращения слов, которые указывают на данные понятия. Чаще всего это латинские, английские, немецкие и французские слова. Во избежание путаницы почти не используются греческие заглавные буквы, если они похожи на латинские по манере написания.
Почему в физике расстояние обозначается буквой s?
Расстояние в физике измеряется единицами длины (метр в международной системе единиц) и имеет два значения:
- степень удаленности объектов друг от друга;
- длина пути, которую прошел объект.
Расстояние – один из тех случаев, когда обозначающая буква является первой в слове-определении. Некоторые источники по-разному объясняют происхождение буквы s:
- От английского слова «space», которое означает расстояние, пространство, площадь.
- От латинского «spatium» – пространство между двумя предметами, протяжение в длину и ширину.
Фактически оба варианта являются правильными. Согласно этимологии слова «space», оно вошло в употребление в 1300-х годах и происходит от французского «espace», а оно, в свою очередь, от латинского «spatium». В значении космического пространства «space» начало употребляться лишь с конца 17-го века, после того как появилось в художественном произведении Джона Мильтона.
Почему в физике скорость обозначается буквой v?
Для обозначения скорости в физике используют строчную букву v тоже не случайно. Это первая буква в латинском слове «velocitas», французском «vitesse» и английском «velocity». Все они означают скорость, быстроту, стремительность.
Возникает другой вопрос: почему именно «velocity» стало определением скорости, а не другие английские слова с похожим значением, например, «speed»? Дело в том, что в физике скорость является векторной величиной, которая отображает быстроту и направление перемещения объекта относительно заданной системы отсчета.
Слово «speed» указывает на скалярную скорость – величину, которая не зависит от системы координат. Например, скорость света – постоянная величина, поэтому на английском данный термин будет выглядеть как «the speed of light».
Кроме того, скорость и расстояние – взаимосвязанные величины наряду со временем. Эта связь в физике выражается формулой. Зная две величины, можно рассчитать и третью. Использование одинаковых букв нецелесообразно.
Если Вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
Среди прочих обозначений наиболее часто школьников интересует вопрос о том, как в математике обозначается скорость, время, расстояние. Связано это с тем, что обозначения этих величин (особенно — скорости) в учебниках по математике и физике можно увидеть различные: с чертой над буквой v (читается: [вэ]), со стрелкой над буквой v, а также буквы v, выделенные курсивом или жирным шрифтом.
Скорость в математике обозначается буквой v, но её написание принято различным для рукописного и печатного текста.
В рукописном тексте скорость движения обычно обозначается строчной (т.е. маленькой) прописной (т.е. не печатной, как в тексте из газеты, а написанной от руки так, как если бы писали письмо) буквой v. В учебниках по математике (т.е. в печатном тексте) обычно скорость движения обозначается печатной буквой v, прямой или выделенной курсивом. Такое обозначение принимается практически во всех задачах по математике, исключение составляют лишь задачи, иллюстрирующие тему «Векторы» (в этом случае обозначение принимается таким же, как и в физике).
В физике (а точнее – в её разделе «механика») обозначение скорости зависит от того, нужно ли в данной задаче учитывать тот факт, что скорость – величина векторная. Там, где учитывать это не нужно, скорость обозначается строчной буквой v (печатной или прописной, так же, как и в математике). Если же необходимо учитывать то, что скорость характеризуется не только модулем (т.е. величиной), но и направлением, скорость изображается либо прописной буквой v с направленной слева направо стрелкой над этой буквой, либо той же прописной буквой v с горизонтальной чертой над этой буквой. В печатном тексте в этом случае обычно скорость обозначают либо печатной строчной буквой v со стрелкой или чертой над буквой, либо печатной буквой v, выделенной жирным шрифтом (т.е. так: v).
Буквой v обозначают скорость движения тел. Для обозначения скорости света и скорости звука принята другая, отличная от обозначения скорости движения тел, буква. Скорость света обозначается буквой «с» (скорость света в вакууме составляет с = 2,9979х108 м/с = 2,9979х105 км/с). Скорость звука так же обозначается буквой с (читается: [цэ]).
Ускорение обозначается буквой а (исключение составляет лишь ускорение свободного падения, эта величина обозначается буквой g (читается [жэ]), g = 9,81 м/с2). Если необходимо подчеркнуть, что эта величина – векторная (например, это часто требуется в физике), то над буквой «а» изображается либо горизонтальная черта, либо горизонтальная стрелка (так же, как и при обозначении скорости). В печатном тексте для обозначения ускорения как векторной величины может использоваться и буква «а», выделенная жирным шрифтом.
Если при решении задачи по физике или математике необходимо обозначить время, то это пишется буквой так: t (читается: [тэ]), а если расстояние — пишется буквой так: s (читается: [эс]). Для обозначения пути обычно используется строчная (маленькая) буква [эль], т.е. l, реже — заглавная (большая) буква [эль], т.е. L. Чтобы обозначение пути «l» не было похоже на «единицу», эту букву пишут курсивом, т.е. с наклоном.
Вообще, вопросы «как в математике пишется скорость», «как в математике пишется время», «как в математике пишется расстояние» некорректны. Лучше формулировать такой вопрос, употребляя не слово «пишется», а слово «обозначается».
Источники:
- Яворский Б.М., Детлаф А.А., Лебедев А.К. Справочник по физике для инженеров и студентов вузов
- Справочник по элементарной математике. Геометрия, тригонометрия, векторная алгебра/ Под ред. П.Ф. Фильчакова
- Каплан И.А. Практические занятия по высшей математике
Дополнительная информация:
- ru.wikipedia.org – Список обозначений в физике
- azbyka.kz — Урок математики «Скорость, время, расстояние»
This article is about the property of moving bodies. For other uses, see Speed (disambiguation).
| Speed | |
|---|---|

Speed can be thought of as the rate at which an object covers distance. A fast-moving object has a high speed and covers a relatively large distance in a given amount of time, while a slow-moving object covers a relatively small amount of distance in the same amount of time. |
|
|
Common symbols |
v |
| SI unit | m/s, m s−1 |
| Dimension | L T−1 |
In everyday use and in kinematics, the speed (commonly referred to as v) of an object is the magnitude of the change of its position over time or the magnitude of the change of its position per unit of time; it is thus a scalar quantity.[1] The average speed of an object in an interval of time is the distance travelled by the object divided by the duration of the interval;[2] the instantaneous speed is the limit of the average speed as the duration of the time interval approaches zero. Speed is not the same as velocity.
Speed has the dimensions of distance divided by time. The SI unit of speed is the metre per second (m/s), but the most common unit of speed in everyday usage is the kilometre per hour (km/h) or, in the US and the UK, miles per hour (mph). For air and marine travel, the knot is commonly used.
The fastest possible speed at which energy or information can travel, according to special relativity, is the speed of light in a vacuum c = 299792458 metres per second (approximately 1079000000 km/h or 671000000 mph). Matter cannot quite reach the speed of light, as this would require an infinite amount of energy. In relativity physics, the concept of rapidity replaces the classical idea of speed.
Definition
Historical definition
Italian physicist Galileo Galilei is usually credited with being the first to measure speed by considering the distance covered and the time it takes. Galileo defined speed as the distance covered per unit of time.[3] In equation form, that is
where 


Instantaneous speed
Speed at some instant, or assumed constant during a very short period of time, is called instantaneous speed. By looking at a speedometer, one can read the instantaneous speed of a car at any instant.[3] A car travelling at 50 km/h generally goes for less than one hour at a constant speed, but if it did go at that speed for a full hour, it would travel 50 km. If the vehicle continued at that speed for half an hour, it would cover half that distance (25 km). If it continued for only one minute, it would cover about 833 m.
In mathematical terms, the instantaneous speed 


If 


In the special case where the velocity is constant (that is, constant speed in a straight line), this can be simplified to 
Average speed
Different from instantaneous speed, average speed is defined as the total distance covered divided by the time interval. For example, if a distance of 80 kilometres is driven in 1 hour, the average speed is 80 kilometres per hour. Likewise, if 320 kilometres are travelled in 4 hours, the average speed is also 80 kilometres per hour. When a distance in kilometres (km) is divided by a time in hours (h), the result is in kilometres per hour (km/h).
Average speed does not describe the speed variations that may have taken place during shorter time intervals (as it is the entire distance covered divided by the total time of travel), and so average speed is often quite different from a value of instantaneous speed.[3] If the average speed and the time of travel are known, the distance travelled can be calculated by rearranging the definition to
Using this equation for an average speed of 80 kilometres per hour on a 4-hour trip, the distance covered is found to be 320 kilometres.
Expressed in graphical language, the slope of a tangent line at any point of a distance-time graph is the instantaneous speed at this point, while the slope of a chord line of the same graph is the average speed during the time interval covered by the chord. Average speed of an object is
Vav = s÷t
Difference between speed and velocity
Speed denotes only how fast an object is moving, whereas velocity describes both how fast and in which direction the object is moving.[5] If a car is said to travel at 60 km/h, its speed has been specified. However, if the car is said to move at 60 km/h to the north, its velocity has now been specified.
The big difference can be discerned when considering movement around a circle. When something moves in a circular path and returns to its starting point, its average velocity is zero, but its average speed is found by dividing the circumference of the circle by the time taken to move around the circle. This is because the average velocity is calculated by considering only the displacement between the starting and end points, whereas the average speed considers only the total distance travelled.
Tangential speed
Linear speed is the distance travelled per unit of time, while tangential speed (or tangential velocity) is the linear speed of something moving along a circular path.[6] A point on the outside edge of a merry-go-round or turntable travels a greater distance in one complete rotation than a point nearer the center. Travelling a greater distance in the same time means a greater speed, and so linear speed is greater on the outer edge of a rotating object than it is closer to the axis. This speed along a circular path is known as tangential speed because the direction of motion is tangent to the circumference of the circle. For circular motion, the terms linear speed and tangential speed are used interchangeably, and both use units of m/s, km/h, and others.
Rotational speed (or angular speed) involves the number of revolutions per unit of time. All parts of a rigid merry-go-round or turntable turn about the axis of rotation in the same amount of time. Thus, all parts share the same rate of rotation, or the same number of rotations or revolutions per unit of time. It is common to express rotational rates in revolutions per minute (RPM) or in terms of the number of «radians» turned in a unit of time. There are little more than 6 radians in a full rotation (2π radians exactly). When a direction is assigned to rotational speed, it is known as rotational velocity or angular velocity. Rotational velocity is a vector whose magnitude is the rotational speed.
Tangential speed and rotational speed are related: the greater the RPMs, the larger the speed in metres per second. Tangential speed is directly proportional to rotational speed at any fixed distance from the axis of rotation.[6] However, tangential speed, unlike rotational speed, depends on radial distance (the distance from the axis). For a platform rotating with a fixed rotational speed, the tangential speed in the centre is zero. Towards the edge of the platform the tangential speed increases proportional to the distance from the axis.[7] In equation form:
where v is tangential speed and ω (Greek letter omega) is rotational speed. One moves faster if the rate of rotation increases (a larger value for ω), and one also moves faster if movement farther from the axis occurs (a larger value for r). Move twice as far from the rotational axis at the centre and you move twice as fast. Move out three times as far, and you have three times as much tangential speed. In any kind of rotating system, tangential speed depends on how far you are from the axis of rotation.
When proper units are used for tangential speed v, rotational speed ω, and radial distance r, the direct proportion of v to both r and ω becomes the exact equation
Thus, tangential speed will be directly proportional to r when all parts of a system simultaneously have the same ω, as for a wheel, disk, or rigid wand.
Units
Units of speed include:
- metres per second (symbol m s−1 or m/s), the SI derived unit;
- kilometres per hour (symbol km/h);
- miles per hour (symbol mi/h or mph);
- knots (nautical miles per hour, symbol kn or kt);
- feet per second (symbol fps or ft/s);
- Mach number (dimensionless), speed divided by the speed of sound;
- in natural units (dimensionless), speed divided by the speed of light in vacuum (symbol c = 299792458 m/s).
Conversions between common units of speed
| m/s | km/h | mph | knot | ft/s | |
|---|---|---|---|---|---|
| 1 m/s = | 1 | 3.600000 | 2.236936* | 1.943844* | 3.280840* |
| 1 km/h = | 0.277778* | 1 | 0.621371* | 0.539957* | 0.911344* |
| 1 mph = | 0.44704 | 1.609344 | 1 | 0.868976* | 1.466667* |
| 1 knot = | 0.514444* | 1.852 | 1.150779* | 1 | 1.687810* |
| 1 ft/s = | 0.3048 | 1.09728 | 0.681818* | 0.592484* | 1 |
(* = approximate values)
Examples of different speeds
| Speed | m/s | ft/s | km/h | mph | Notes |
|---|---|---|---|---|---|
| Global average sea level rise | 0.00000000011 | 0.00000000036 | 0.0000000004 | 0.00000000025 | 3.5 mm/year[8] |
| Approximate rate of continental drift | 0.0000000013 | 0.0000000042 | 0.0000000045 | 0.0000000028 | 4 cm/year. Varies depending on location. |
| Speed of a common snail | 0.001 | 0.003 | 0.004 | 0.002 | 1 millimetre per second |
| A brisk walk | 1.7 | 5.5 | 6.1 | 3.8 | |
| A typical road cyclist | 4.4 | 14.4 | 16 | 10 | Varies widely by person, terrain, bicycle, effort, weather |
| A fast martial arts kick | 7.7 | 25.2 | 27.7 | 17.2 | Fastest kick recorded at 130 milliseconds from floor to target at 1 meter distance. Average velocity speed across kick duration[9] |
| Sprint runners | 12.2 | 40 | 43.92 | 27 | Usain Bolt’s 100 metres world record. |
| Approximate average speed of road race cyclists | 12.5 | 41.0 | 45 | 28 | On flat terrain, will vary |
| Typical suburban speed limit in most of the world | 13.8 | 45.3 | 50 | 30 | |
| Taipei 101 observatory elevator | 16.7 | 54.8 | 60.6 | 37.6 | 1010 m/min |
| Typical rural speed limit | 24.6 | 80.66 | 88.5 | 56 | |
| British National Speed Limit (single carriageway) | 26.8 | 88 | 96.56 | 60 | |
| Category 1 hurricane | 33 | 108 | 119 | 74 | Minimum sustained speed over 1 minute |
| Average peak speed of a cheetah | 33.53 | 110 | 120.7 | 75 | |
| Speed limit on a French autoroute | 36.1 | 118 | 130 | 81 | |
| Highest recorded human-powered speed | 37.02 | 121.5 | 133.2 | 82.8 | Sam Whittingham in a recumbent bicycle[10] |
| Average speed of Human sneeze | 44.44 | 145.82 | 160 | 99.42 | |
| Muzzle velocity of a paintball marker | 90 | 295 | 320 | 200 | |
| Cruising speed of a Boeing 747-8 passenger jet | 255 | 836 | 917 | 570 | Mach 0.85 at 35000 ft (10668 m) altitude |
| Speed of a .22 caliber Long Rifle bullet | 326.14 | 1070 | 1174.09 | 729.55 | |
| The official land speed record | 341.1 | 1119.1 | 1227.98 | 763 | |
| The speed of sound in dry air at sea-level pressure and 20 °C | 343 | 1125 | 1235 | 768 | Mach 1 by definition. 20 °C = 293.15 kelvins. |
| Muzzle velocity of a 7.62×39mm cartridge | 710 | 2330 | 2600 | 1600 | The 7.62×39mm round is a rifle cartridge of Soviet origin |
| Official flight airspeed record for jet engined aircraft | 980 | 3215 | 3530 | 2194 | Lockheed SR-71 Blackbird |
| Space Shuttle on re-entry | 7800 | 25600 | 28000 | 17,500 | |
| Escape velocity on Earth | 11200 | 36700 | 40000 | 25000 | 11.2 km·s−1 |
| Voyager 1 relative velocity to the Sun in 2013 | 17000 | 55800 | 61200 | 38000 | Fastest heliocentric recession speed of any humanmade object.[11] (11 mi/s) |
| Average orbital speed of planet Earth around the Sun | 29783 | 97713 | 107218 | 66623 | |
| The fastest recorded speed of the Helios probes | 70,220 | 230,381 | 252,792 | 157,078 | Recognized as the fastest speed achieved by a man-made spacecraft, achieved in solar orbit. |
| Orbital speed of the Sun relative to the center of the galaxy | 251000 | 823000 | 904000 | 561000 | |
| Speed of the Galaxy relative to the CMB | 550000 | 1800000 | 2000000 | 1240000 | |
| Speed of light in vacuum (symbol c) | 299792458 | 983571056 | 1079252848 | 670616629 | Exactly 299792458 m/s, by definition of the metre |
Psychology
According to Jean Piaget, the intuition for the notion of speed in humans precedes that of duration, and is based on the notion of outdistancing.[12] Piaget studied this subject inspired by a question asked to him in 1928 by Albert Einstein: «In what order do children acquire the concepts of time and speed?»[13] Children’s early concept of speed is based on «overtaking», taking only temporal and spatial orders into consideration, specifically: «A moving object is judged to be more rapid than another when at a given moment the first object is behind and a moment or so later ahead of the other object.»[14]
See also
- Air speed
- Land speed
- List of vehicle speed records
- Typical projectile speeds
- Speedometer
- V speeds
References
Wikiquote has quotations related to Speed.
Wikimedia Commons has media related to Speed.
- Richard P. Feynman, Robert B. Leighton, Matthew Sands. The Feynman Lectures on Physics, Volume I, Section 8–2. Addison-Wesley, Reading, Massachusetts (1963). ISBN 0-201-02116-1.
- ^ Wilson, Edwin Bidwell (1901). Vector analysis: a text-book for the use of students of mathematics and physics, founded upon the lectures of J. Willard Gibbs. Yale bicentennial publications. C. Scribner’s Sons. p. 125. hdl:2027/mdp.39015000962285. This is the likely origin of the speed/velocity terminology in vector physics.
- ^ a b c Elert, Glenn. «Speed & Velocity». The Physics Hypertextbook. Retrieved 8 June 2017.
- ^ a b c Hewitt (2006), p. 42
- ^ «IEC 60050 — Details for IEV number 113-01-33: «speed»«. Electropedia: The World’s Online Electrotechnical Vocabulary. Retrieved 2017-06-08.
- ^ Wilson, Edwin Bidwell (1901). Vector analysis: a text-book for the use of students of mathematics and physics, founded upon the lectures of J. Willard Gibbs. Yale bicentennial publications. C. Scribner’s Sons. p. 125. hdl:2027/mdp.39015000962285. This is the likely origin of the speed/velocity terminology in vector physics.
- ^ a b Hewitt (2006), p. 131
- ^ Hewitt (2006), p. 132
- ^ NASA’s Goddard Space Flight Center. «Satellite sea level observations». Global Climate Change. NASA. Retrieved 20 April 2022.
- ^ «Improve Kicking Speed for Martial Arts | Get Fast Kicks!». Archived from the original on 2013-11-11. Retrieved 2013-08-14.
- ^ «The Recumbent Bicycle and Human Powered Vehicle Information Center». Archived from the original on 2013-08-11. Retrieved 2013-10-12.
- ^ Darling, David. «Fastest Spacecraft». Retrieved August 19, 2013.
- ^ Jean Piaget, Psychology and Epistemology: Towards a Theory of Knowledge, The Viking Press, pp. 82–83 and pp. 110–112, 1973. SBN 670-00362-x
- ^ Siegler, Robert S.; Richards, D. Dean (1979). «Development of Time, Speed, and Distance Concepts» (PDF). Developmental Psychology. 15 (3): 288–298. doi:10.1037/0012-1649.15.3.288.
- ^ Early Years Education: Histories and Traditions, Volume 1. Taylor & Francis. 2006. p. 164. ISBN 9780415326704.
This article is about the property of moving bodies. For other uses, see Speed (disambiguation).
| Speed | |
|---|---|

Speed can be thought of as the rate at which an object covers distance. A fast-moving object has a high speed and covers a relatively large distance in a given amount of time, while a slow-moving object covers a relatively small amount of distance in the same amount of time. |
|
|
Common symbols |
v |
| SI unit | m/s, m s−1 |
| Dimension | L T−1 |
In everyday use and in kinematics, the speed (commonly referred to as v) of an object is the magnitude of the change of its position over time or the magnitude of the change of its position per unit of time; it is thus a scalar quantity.[1] The average speed of an object in an interval of time is the distance travelled by the object divided by the duration of the interval;[2] the instantaneous speed is the limit of the average speed as the duration of the time interval approaches zero. Speed is not the same as velocity.
Speed has the dimensions of distance divided by time. The SI unit of speed is the metre per second (m/s), but the most common unit of speed in everyday usage is the kilometre per hour (km/h) or, in the US and the UK, miles per hour (mph). For air and marine travel, the knot is commonly used.
The fastest possible speed at which energy or information can travel, according to special relativity, is the speed of light in a vacuum c = 299792458 metres per second (approximately 1079000000 km/h or 671000000 mph). Matter cannot quite reach the speed of light, as this would require an infinite amount of energy. In relativity physics, the concept of rapidity replaces the classical idea of speed.
Definition
Historical definition
Italian physicist Galileo Galilei is usually credited with being the first to measure speed by considering the distance covered and the time it takes. Galileo defined speed as the distance covered per unit of time.[3] In equation form, that is
where 


Instantaneous speed
Speed at some instant, or assumed constant during a very short period of time, is called instantaneous speed. By looking at a speedometer, one can read the instantaneous speed of a car at any instant.[3] A car travelling at 50 km/h generally goes for less than one hour at a constant speed, but if it did go at that speed for a full hour, it would travel 50 km. If the vehicle continued at that speed for half an hour, it would cover half that distance (25 km). If it continued for only one minute, it would cover about 833 m.
In mathematical terms, the instantaneous speed 


If 


In the special case where the velocity is constant (that is, constant speed in a straight line), this can be simplified to 
Average speed
Different from instantaneous speed, average speed is defined as the total distance covered divided by the time interval. For example, if a distance of 80 kilometres is driven in 1 hour, the average speed is 80 kilometres per hour. Likewise, if 320 kilometres are travelled in 4 hours, the average speed is also 80 kilometres per hour. When a distance in kilometres (km) is divided by a time in hours (h), the result is in kilometres per hour (km/h).
Average speed does not describe the speed variations that may have taken place during shorter time intervals (as it is the entire distance covered divided by the total time of travel), and so average speed is often quite different from a value of instantaneous speed.[3] If the average speed and the time of travel are known, the distance travelled can be calculated by rearranging the definition to
Using this equation for an average speed of 80 kilometres per hour on a 4-hour trip, the distance covered is found to be 320 kilometres.
Expressed in graphical language, the slope of a tangent line at any point of a distance-time graph is the instantaneous speed at this point, while the slope of a chord line of the same graph is the average speed during the time interval covered by the chord. Average speed of an object is
Vav = s÷t
Difference between speed and velocity
Speed denotes only how fast an object is moving, whereas velocity describes both how fast and in which direction the object is moving.[5] If a car is said to travel at 60 km/h, its speed has been specified. However, if the car is said to move at 60 km/h to the north, its velocity has now been specified.
The big difference can be discerned when considering movement around a circle. When something moves in a circular path and returns to its starting point, its average velocity is zero, but its average speed is found by dividing the circumference of the circle by the time taken to move around the circle. This is because the average velocity is calculated by considering only the displacement between the starting and end points, whereas the average speed considers only the total distance travelled.
Tangential speed
Linear speed is the distance travelled per unit of time, while tangential speed (or tangential velocity) is the linear speed of something moving along a circular path.[6] A point on the outside edge of a merry-go-round or turntable travels a greater distance in one complete rotation than a point nearer the center. Travelling a greater distance in the same time means a greater speed, and so linear speed is greater on the outer edge of a rotating object than it is closer to the axis. This speed along a circular path is known as tangential speed because the direction of motion is tangent to the circumference of the circle. For circular motion, the terms linear speed and tangential speed are used interchangeably, and both use units of m/s, km/h, and others.
Rotational speed (or angular speed) involves the number of revolutions per unit of time. All parts of a rigid merry-go-round or turntable turn about the axis of rotation in the same amount of time. Thus, all parts share the same rate of rotation, or the same number of rotations or revolutions per unit of time. It is common to express rotational rates in revolutions per minute (RPM) or in terms of the number of «radians» turned in a unit of time. There are little more than 6 radians in a full rotation (2π radians exactly). When a direction is assigned to rotational speed, it is known as rotational velocity or angular velocity. Rotational velocity is a vector whose magnitude is the rotational speed.
Tangential speed and rotational speed are related: the greater the RPMs, the larger the speed in metres per second. Tangential speed is directly proportional to rotational speed at any fixed distance from the axis of rotation.[6] However, tangential speed, unlike rotational speed, depends on radial distance (the distance from the axis). For a platform rotating with a fixed rotational speed, the tangential speed in the centre is zero. Towards the edge of the platform the tangential speed increases proportional to the distance from the axis.[7] In equation form:
where v is tangential speed and ω (Greek letter omega) is rotational speed. One moves faster if the rate of rotation increases (a larger value for ω), and one also moves faster if movement farther from the axis occurs (a larger value for r). Move twice as far from the rotational axis at the centre and you move twice as fast. Move out three times as far, and you have three times as much tangential speed. In any kind of rotating system, tangential speed depends on how far you are from the axis of rotation.
When proper units are used for tangential speed v, rotational speed ω, and radial distance r, the direct proportion of v to both r and ω becomes the exact equation
Thus, tangential speed will be directly proportional to r when all parts of a system simultaneously have the same ω, as for a wheel, disk, or rigid wand.
Units
Units of speed include:
- metres per second (symbol m s−1 or m/s), the SI derived unit;
- kilometres per hour (symbol km/h);
- miles per hour (symbol mi/h or mph);
- knots (nautical miles per hour, symbol kn or kt);
- feet per second (symbol fps or ft/s);
- Mach number (dimensionless), speed divided by the speed of sound;
- in natural units (dimensionless), speed divided by the speed of light in vacuum (symbol c = 299792458 m/s).
Conversions between common units of speed
| m/s | km/h | mph | knot | ft/s | |
|---|---|---|---|---|---|
| 1 m/s = | 1 | 3.600000 | 2.236936* | 1.943844* | 3.280840* |
| 1 km/h = | 0.277778* | 1 | 0.621371* | 0.539957* | 0.911344* |
| 1 mph = | 0.44704 | 1.609344 | 1 | 0.868976* | 1.466667* |
| 1 knot = | 0.514444* | 1.852 | 1.150779* | 1 | 1.687810* |
| 1 ft/s = | 0.3048 | 1.09728 | 0.681818* | 0.592484* | 1 |
(* = approximate values)
Examples of different speeds
| Speed | m/s | ft/s | km/h | mph | Notes |
|---|---|---|---|---|---|
| Global average sea level rise | 0.00000000011 | 0.00000000036 | 0.0000000004 | 0.00000000025 | 3.5 mm/year[8] |
| Approximate rate of continental drift | 0.0000000013 | 0.0000000042 | 0.0000000045 | 0.0000000028 | 4 cm/year. Varies depending on location. |
| Speed of a common snail | 0.001 | 0.003 | 0.004 | 0.002 | 1 millimetre per second |
| A brisk walk | 1.7 | 5.5 | 6.1 | 3.8 | |
| A typical road cyclist | 4.4 | 14.4 | 16 | 10 | Varies widely by person, terrain, bicycle, effort, weather |
| A fast martial arts kick | 7.7 | 25.2 | 27.7 | 17.2 | Fastest kick recorded at 130 milliseconds from floor to target at 1 meter distance. Average velocity speed across kick duration[9] |
| Sprint runners | 12.2 | 40 | 43.92 | 27 | Usain Bolt’s 100 metres world record. |
| Approximate average speed of road race cyclists | 12.5 | 41.0 | 45 | 28 | On flat terrain, will vary |
| Typical suburban speed limit in most of the world | 13.8 | 45.3 | 50 | 30 | |
| Taipei 101 observatory elevator | 16.7 | 54.8 | 60.6 | 37.6 | 1010 m/min |
| Typical rural speed limit | 24.6 | 80.66 | 88.5 | 56 | |
| British National Speed Limit (single carriageway) | 26.8 | 88 | 96.56 | 60 | |
| Category 1 hurricane | 33 | 108 | 119 | 74 | Minimum sustained speed over 1 minute |
| Average peak speed of a cheetah | 33.53 | 110 | 120.7 | 75 | |
| Speed limit on a French autoroute | 36.1 | 118 | 130 | 81 | |
| Highest recorded human-powered speed | 37.02 | 121.5 | 133.2 | 82.8 | Sam Whittingham in a recumbent bicycle[10] |
| Average speed of Human sneeze | 44.44 | 145.82 | 160 | 99.42 | |
| Muzzle velocity of a paintball marker | 90 | 295 | 320 | 200 | |
| Cruising speed of a Boeing 747-8 passenger jet | 255 | 836 | 917 | 570 | Mach 0.85 at 35000 ft (10668 m) altitude |
| Speed of a .22 caliber Long Rifle bullet | 326.14 | 1070 | 1174.09 | 729.55 | |
| The official land speed record | 341.1 | 1119.1 | 1227.98 | 763 | |
| The speed of sound in dry air at sea-level pressure and 20 °C | 343 | 1125 | 1235 | 768 | Mach 1 by definition. 20 °C = 293.15 kelvins. |
| Muzzle velocity of a 7.62×39mm cartridge | 710 | 2330 | 2600 | 1600 | The 7.62×39mm round is a rifle cartridge of Soviet origin |
| Official flight airspeed record for jet engined aircraft | 980 | 3215 | 3530 | 2194 | Lockheed SR-71 Blackbird |
| Space Shuttle on re-entry | 7800 | 25600 | 28000 | 17,500 | |
| Escape velocity on Earth | 11200 | 36700 | 40000 | 25000 | 11.2 km·s−1 |
| Voyager 1 relative velocity to the Sun in 2013 | 17000 | 55800 | 61200 | 38000 | Fastest heliocentric recession speed of any humanmade object.[11] (11 mi/s) |
| Average orbital speed of planet Earth around the Sun | 29783 | 97713 | 107218 | 66623 | |
| The fastest recorded speed of the Helios probes | 70,220 | 230,381 | 252,792 | 157,078 | Recognized as the fastest speed achieved by a man-made spacecraft, achieved in solar orbit. |
| Orbital speed of the Sun relative to the center of the galaxy | 251000 | 823000 | 904000 | 561000 | |
| Speed of the Galaxy relative to the CMB | 550000 | 1800000 | 2000000 | 1240000 | |
| Speed of light in vacuum (symbol c) | 299792458 | 983571056 | 1079252848 | 670616629 | Exactly 299792458 m/s, by definition of the metre |
Psychology
According to Jean Piaget, the intuition for the notion of speed in humans precedes that of duration, and is based on the notion of outdistancing.[12] Piaget studied this subject inspired by a question asked to him in 1928 by Albert Einstein: «In what order do children acquire the concepts of time and speed?»[13] Children’s early concept of speed is based on «overtaking», taking only temporal and spatial orders into consideration, specifically: «A moving object is judged to be more rapid than another when at a given moment the first object is behind and a moment or so later ahead of the other object.»[14]
See also
- Air speed
- Land speed
- List of vehicle speed records
- Typical projectile speeds
- Speedometer
- V speeds
References
Wikiquote has quotations related to Speed.
Wikimedia Commons has media related to Speed.
- Richard P. Feynman, Robert B. Leighton, Matthew Sands. The Feynman Lectures on Physics, Volume I, Section 8–2. Addison-Wesley, Reading, Massachusetts (1963). ISBN 0-201-02116-1.
- ^ Wilson, Edwin Bidwell (1901). Vector analysis: a text-book for the use of students of mathematics and physics, founded upon the lectures of J. Willard Gibbs. Yale bicentennial publications. C. Scribner’s Sons. p. 125. hdl:2027/mdp.39015000962285. This is the likely origin of the speed/velocity terminology in vector physics.
- ^ a b c Elert, Glenn. «Speed & Velocity». The Physics Hypertextbook. Retrieved 8 June 2017.
- ^ a b c Hewitt (2006), p. 42
- ^ «IEC 60050 — Details for IEV number 113-01-33: «speed»«. Electropedia: The World’s Online Electrotechnical Vocabulary. Retrieved 2017-06-08.
- ^ Wilson, Edwin Bidwell (1901). Vector analysis: a text-book for the use of students of mathematics and physics, founded upon the lectures of J. Willard Gibbs. Yale bicentennial publications. C. Scribner’s Sons. p. 125. hdl:2027/mdp.39015000962285. This is the likely origin of the speed/velocity terminology in vector physics.
- ^ a b Hewitt (2006), p. 131
- ^ Hewitt (2006), p. 132
- ^ NASA’s Goddard Space Flight Center. «Satellite sea level observations». Global Climate Change. NASA. Retrieved 20 April 2022.
- ^ «Improve Kicking Speed for Martial Arts | Get Fast Kicks!». Archived from the original on 2013-11-11. Retrieved 2013-08-14.
- ^ «The Recumbent Bicycle and Human Powered Vehicle Information Center». Archived from the original on 2013-08-11. Retrieved 2013-10-12.
- ^ Darling, David. «Fastest Spacecraft». Retrieved August 19, 2013.
- ^ Jean Piaget, Psychology and Epistemology: Towards a Theory of Knowledge, The Viking Press, pp. 82–83 and pp. 110–112, 1973. SBN 670-00362-x
- ^ Siegler, Robert S.; Richards, D. Dean (1979). «Development of Time, Speed, and Distance Concepts» (PDF). Developmental Psychology. 15 (3): 288–298. doi:10.1037/0012-1649.15.3.288.
- ^ Early Years Education: Histories and Traditions, Volume 1. Taylor & Francis. 2006. p. 164. ISBN 9780415326704.
В этом уроке мы рассмотрим три физические величины, а именно расстояние, скорость и время.
Расстояние
Расстояние мы уже изучали в уроке единицы измерения. Говоря простым языком, расстояние это длина от одного пункта до другого. (Пример: расстояние от дома до школы 2 километра).
Имея дело с большими расстояниями, в основном они будут измеряться в метрах и километрах. Расстояние обозначается латинской буквой S. Можно обозначить и другой буквой, но буква S общепринята.
Скорость
Скоростью называют расстояние, пройденное телом за единицу времени. Под единицей времени подразумевается 1 час, 1 минута или 1 секунда.
Предположим, что двое школьников решили проверить, кто быстрее добежит от двора до спортплощадки. Расстояние от двора до спортплощадки 100 метров. Первый школьник добежал за 25 секунд. Второй за 50 секунд. Кто добежал быстрее?
Быстрее добежал тот, кто за 1 секунду пробежал бóльшее расстояние. Говорят, что у него скорость движения больше. В данном случае скорость школьников это расстояние, которое они пробегают за 1 секунду.
Чтобы найти скорость, нужно расстояние разделить на время движения. Давайте найдём скорость первого школьника. Для этого разделим 100 метров на время движения первого школьника, то есть на 25 секунд:
100 м : 25 с = 4
Если расстояние дано в метрах, а время движения в секундах, то скорость измеряется в метрах в секунду (м/с). Если расстояние дано в километрах, а время движения в часах, скорость измеряется в километрах в час (км/ч).
У нас расстояние дано в метрах, а время в секундах. Значит скорость измеряется в метрах в секунду (м/с)
100м : 25с = 4 (м/с)
Итак, скорость движения первого школьника составляет 4 метра в секунду (м/с).
Теперь найдем скорость движения второго школьника. Для этого разделим расстояние на время движения второго школьника, то есть на 50 секунд:
100 м : 50 c = 2 (м/с)
Значит скорость движения второго школьника составляет 2 метра в секунду (м/с).
Скорость движения первого школьника — 4 (м/с)
Скорость движения второго школьника — 2 (м/с)
4 (м/с) > 2 (м/с)
Скорость первого школьника больше. Значит он добежал до спортплощадки быстрее. Скорость обозначается латинской буквой v.
Время
Иногда возникает ситуация, когда требуется узнать за какое время тело преодолеет то или иное расстояние.
Например, от дома до спортивной секции 1000 метров. Мы должны доехать туда на велосипеде. Наша скорость будет 500 метров в минуту (500м/мин). За какое время мы доедем до спортивной секции?
Если за одну минуту мы будем проезжать 500 метров, то сколько таких минут с пятью ста метрами будет в 1000 метрах?
Очевидно, что надо разделить 1000 метров на то расстояние, которое мы будем проезжать за одну минуту, то есть на 500 метров. Тогда мы получим время, за которое доедем до спортивной секции:
1000 : 500 = 2 (мин)
Время движения обозначается маленькой латинской буквой t.
Взаимосвязь скорости, времени, расстояния
Скорость принято обозначать маленькой латинской буквой v, время движения – маленькой буквой t, пройденное расстояние – маленькой буквой s. Скорость, время и расстояние связаны между собой.
Если известны скорость и время движения, то можно найти расстояние. Оно равно скорости, умноженной на время:
s = v × t
Например, мы вышли из дома и направились в магазин. Мы дошли до магазина за 10 минут. Наша скорость была 50 метров в минуту. Зная свою скорость и время, мы можем найти расстояние.
Если за одну минуту мы прошли 50 метров, то сколько таких пятьдесят метров мы пройдем за 10 минут? Очевидно, что умножив 50 метров на 10, мы определим расстояние от дома до магазина:
v = 50 (м/мин)
t = 10 минут
s = v × t = 50 × 10 = 500 (метров до магазина)
Если известно время и расстояние, то можно найти скорость:
v = s : t
Например, расстояние от дома до школы 900 метров. Школьник дошел до этой школы за 10 минут. Какова была его скорость?
Скорость движения школьника это расстояние, которое он проходит за одну минуту. Если за 10 минут он преодолел 900 метров, то какое расстояние он преодолевал за одну минуту?
Чтобы ответить на этот, нужно разделить расстояние на время движения школьника:
s = 900 метров
t = 10 минут
v = s : t = 900 : 10 = 90 (м/мин)
Если известна скорость и расстояние, то можно найти время:
t = s : v
Например, от дома до спортивной секции 500 метров. Мы должны дойти до неё пешком. Наша скорость будет 100 метров в минуту (100 м/мин). За какое время мы дойдем до спортивной секции?
Если за одну минуту мы будем проходить 100 метров, то сколько таких минут со ста метрами будет в 500 метрах?
Чтобы ответить на этот вопрос нужно 500 метров разделить на расстояние, которое мы будем проходить за одну минуту, то есть на 100. Тогда мы получим время, за которое мы дойдем до спортивной секции:
s = 500 метров
v = 100 (м/мин)
t = s : v = 500 : 100 = 5 (минут до спортивной секции)
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже

На чтение 10 мин. Просмотров 1k. Опубликовано 19 декабря 2022
Вычислить скорость, время и расстояние часто бывает необходимо в повседневной жизни, когда мы рассчитываем время на дорогу. Все эти величины (время, расстояние и скорость) связаны между собой математической формулой и зная две из них всегда можно найти третью. Мы с вами рассмотрим, что понимается под этими величинами, как их найти, решим несколько задач.
Скорость, время и расстояние — это ключевые параметры при решении задач на движение. Эти задачи есть и в ЕГЭ и в ОГЭ по математике. Сегодня мы подробнее остановимся на этих величинах.
Расстояние
Расстояние — это физическая величина, означающая длину между двумя объектами. Расстояние обозначается буквой S и измеряется в единицах длины: метрах. Метр — это международно-принятая единица измерения длины. Однако встречаются и другие единицы длины — километр, сантиметр, миллиметр. В этом случае целесообразно перевести единицы длины в международную систему единиц (СИ).
Например: расстояние от Земли до Солнца равно 149 597 870 700 метров.
Расстояние связано со скоростью и временем:
S=v cdot t
Вот тут таблица длин и их перевода в международную систему единиц — то есть в метры.
| Единицы длины | СИ |
| 1 сантиметр | 0,01 м |
| 1 километр | 1000 м |
| 1 дециметр | 0,1 м |
| 1 миллиметр | 0,001 м |
| 1 микрометр | 1·10-6 м |
| 1 миля | 1609,34 м |
| 1 фут | 0,3048 м |
| 1 ярд | 0,9144 м |
| 1 дюйм | 0,0254 м |
| 1 морская миля | 1852 м |
Время
Время — это физическая величина, которая обозначает непрерывное и необратимое (возможно) движение от прошлого к будущему через настоящее. Это фундаментальная физическая величина, единица измерения времени — секунда. Однако, в задачах могут использоваться и другие единицы времени — часы, минуты, дни.
Время можно найти по формуле:
t=frac{S}{v}
Ученые о времени
По словам греческого философа Парменида (ок. 450 г. до н.э.), время и движение были иллюзиями. Его ученик Зенон Элейский разработал два знаменитых парадокса: «Ахиллес и черепаха» и «Парадокс летящей стрелы», чтобы доказать его утверждения. Платон, живший на пару поколений позже, считал, что время создано вместе со вселенной и существует независимо. Он рассматривал время как пустой контейнер, который можно заполнить движущимися вещами и событиями. Его ученик Аристотель считал, что время не существует независимо от событий, но время есть изменение и движение.
Аристотель пришел к выводу, что время не состоит из последовательных неделимых моментов «сейчас», как пытался сказать Зенон с помощью своего парадокса стрелы. Согласно Аристотелю, не существует серии моментов «сейчас», потому что такие моменты не могли бы исчезнуть в течение их собственной длительности или в следующий момент «сейчас». Исааку Ньютону (1642–1726) время понадобилось в качестве переменной в его уравнениях, и он начал думать о времени с научной точки зрения. Ньютон поддерживал идею Платона о независимости времени. Он разделил время на абсолютное (математическое) время и относительное (обычное) время.
Абсолютное время, или продолжительность, является реальным и математическим, и оно течет неуклонно, независимо от чего-либо внешнего. Относительное время кажущееся и является внешней мерой длительности, которая может быть обнаружена органами чувств с помощью движения, которое может быть точным или неточным.
Готфрид Лейбниц (1646–1716) был согласен с Аристотелем и думал, что без событий и перемен не было бы времени. Физик- теоретик Ли Смолин писал в 2010 году, что исследования квантовой гравитации подтверждают, что четырехмерное пространство-время имеет смысл только в том случае, если время реально, фундаментально и даже является единственным аспектом реальности, который мы непосредственно ощущаем.
Скорость
Скорость обозначается буквой — это физическая величина, которая обозначает какое расстояние проходит объект в единицу времени. Единица измерения скорости — м/с. Однако, встречаются также и км/ч и см/с (эти измерения не входят в международную систему единиц измерения). Скорость показывает как быстро изменяется расстояние во времени.
Например, выражение 9 м/с означает, что тело за 1 секунду проходит 9 метров. То есть за 1 секунду 9 метров, за 2 секунду еще 9 метров, итого за 2 секунду — 18 метров. В курсе школьной математики мы считаем, что скорость равномерная во времени. То есть тело за равные промежутки времени проходит равные расстояния. То есть 9 м/с означает 9 метров в любую из секунд движения тела. Однако, в реальности движение бывает равномерное и неравномерное. Мы не рассматриваем неравномерное движение в курсе математики (1-6 класс), однако в курсе алгебры элементы кинематики с неравномерным движением рассматриваются.
Еще примеры: скорость 100 км/ч — это прохождение расстояния в 100 километров за 1 час.
Формула скорости
Скорость можно найти через расстояние и время по формуле:
v=frac{S}{t}
Средняя скорость
Если движение тела можно разбить на несколько участков и в пределах каждого участка скорость тела не меняется, то целесообразно говорить о средней скорости.
Формула средней скорости:
v=frac{S_{весь ; путь}}{t_{всё ; время}}=frac{S_1+S_2+…+ S_n}{t_1+t_2+…+ t_n}
То есть средняя скорость это отношение всего пути, ко всему времени.
Скорости сближения и удаления
Понятие скорости ученики изучают еще в 4 классе, а далее это понятие расширяется и уточняется. Вводятся такие понятия как скорость сближения и скорость удаления. Не все педагоги используют эти понятия в своей работе, поскольку эти понятия можно использовать только при решении небольшого класса задач на движение и они ограничивают решение задач и другими условиями (например, если тела удаляются или сближаются не по одной прямой, а по перпендикулярным прямым). И все же, давайте мы уточним, о чем вообще идет речь.
Скорость удаления
Если два тела удаляются друг от друга, двигаясь по одной прямой, то в таких случаях говорят о скорости удаления. То есть скорость удаления характеризует расстояние, которое увеличивается по мере удаления двух тел в единицу времени.
Допустим есть два пешехода, которые удаляются друг от друга, первый пешеход удаляется со скоростью 3 км/ч, а второй пешеход со скоростью 4 км/ч. Тогда скорость удаления будет:
3+4=7 км/ч.
Действительно, расстояние, пройденное первым пешеходом за один час будет 3 километра, а расстояние, пройденное вторым пешеходом за то же время будет 4 километра. Тогда при удалении пешеходов друг от друга расстояние между ними увеличивается на 7 километров в каждый час или наши пешеходы удаляются со скоростью 7 км/ч. Мы должны сложить скорости объектов.
Формула скорости удаления:
v_{удаления}=v_1+v_2
где
— скорость одного тела,
— скорость другого тела.
Напомним, что это понятие можно использовать только если тела двигаются в разных направлениях, располагаемых на одной прямой.
Скорость сближения двух тел
Аналогично, рассмотрим ситуацию, если два пешехода двигаются навстречу друг к другу. Один пешеход за один час проходит расстояние 2 км, а второй пешеход за то же время проходит 5 км.
Значит, расстояние между ними будем уменьшаться со скоростью 5+2 = 7 км/ч.
Формула скорости сближения:
v_{сближения}=v_1+v_2
где
— скорость одного тела,
— скорость другого тела.
Если один пешеход догоняет другого. То скорость сближения при движении в одном направлении можно определить, если вычесть из большей скорости меньшую.
То есть, если у нас второго пешехода (=3км/ч) догоняет первый пешеход (
=5 км/ч), то скорость их сближения будет 2 км/ч:
Формула скорости сближения при движении вдогонку:
v_{сближения}=v_1-v_2
где
— скорость одного тела,
— скорость другого тела. При этом
Таблица «скорость, время, расстояние» при решении задач на движение
При решении задач на движение очень удобно пользоваться такой таблицей, в которой три столбца с данными по скорости, времени движения тел и расстоянию, которое они проходят. Эта таблица, кстати помогает легко запомнить формулы скорости, времени и расстояния, если представить что первый столбец — это первый множитель, второй столбец — второй множитель, а третий столбец — произведение.
| Скорость, v, м/с | Время, t, с | Расстояние, S, м |
Простой пример, найти скорость велосипедиста, если за 5 часов он прошел 45 километров.
Составляем таблицу и записываем в нее данные:
| Скорость, v, км/ч | Время, t, ч | Расстояние, S, км |
| ? | 5 | 45 |
Теперь видно, что неизвестна скорость в первом столбце, значит, неизвестен первый множитель. Чтобы определить неизвестный множитель надо произведение разделить на известный множитель: = 45/5 = 9 км/ч.
Важно! В задачах все единицы измерения должны быть приведены либо к международной системе единиц (метр, секунда, м/с) либо к одним единицам измерения (то есть если в задаче есть и м/с и км/ч можно привести всё либо к м/с (тогда и время в секундах и расстояние в метрах), либо к км/ч (тогда и время в часах будет и расстояние в километрах))
Рассмотрим теперь некоторые примеры решения задач
Примеры задач на движение
Задача 1
Школьник идет домой со скоростью 2 км/ч. Расстояние от школы до дома 1 км. За какое время школьник дойдет до дома?
Решение:
Найдем время по формуле: displaystyle t=frac{S}{v}=frac{1}{2}ч.
Школьник дойдет до дома за полчаса.
Ответ: 0,5 ч.
Задача 2
Автомобилист и велосипедист выехали в город из деревни одновременно. Скорость автомобилиста 50 км/ч. Расстояние до города 100 км. Какова скорость велосипедиста, если известно, что он прибыл в город на 8 часов позже автомобилиста?
Решение: Составим таблицу
| Скорость, v, км/ч | Время, t, ч | Расстояние, S, км | |
| Автомобилист | 50 | 100/50 | 100 |
| Велосипедист | x | 100/x | 100 |
Пусть скорость велосипедиста x. В таблице мы сразу смогли написать соотношения для времени движения. По условию задачи дано, что велосипедист прибыл в город на 8 часов позже автомобилиста. Запишем это:
displaystyle frac{100}{x}-frac{100}{50}=8
Мы отнимаем от времени, которое потратил велосипедист (он же потратил больше времени) время, которое потратил автомобилист и получаем 8 часов.
Решим полученное уравнение.
displaystyle frac{100}{x}-2=8
displaystyle frac{100}{x}=10
x=10
Ответ: 10 км/ч
Задача 3
Стрела пролетает 180 метров за 0,05 минуты. Найдите ее скорость.
Решение: прежде чем решать задачу, переведем все единицы в одну систему единиц. Минуты переведем в секунды.
В одной минуте 60 секунд. Значит, чтобы узнать сколько секунд в 0,05 минутах, умножим 0,05 на 60, получим:
0,05 cdot 60=3 c.
Тогда displaystyle v= frac{180}{3}=60 м/с.
Ответ: 60 м/с
Задача 4
Турист прошел лесной участок длиной 10 км со скоростью 5 км/ч, а затем шел по полю 20 км, со скоростью 4 км/ч. Какова средняя скорость туриста?
Решение:
Определим весь путь который прошел турист:
displaystyle S_{весь ; путь}=S_1+S_2=10+20=30 км.
Для прохождения лесного участка турист потратил: displaystyle t_1= frac{S_1}{v_1}=frac{10}{5}=2ч, а на второй участок времени ушло: displaystyle t_2= frac{S_2}{v_2}=frac{20}{4}=5ч
Все время: displaystyle t_{всё ; время}=t_1+t_2=2+5=7ч
Тогда найдем среднюю скорость:
displaystyle v_{ср}= frac{S_{весь ; путь}}{t_{всё ; время}}=frac{30}{7}=4 frac{2}{7} км/ч.
Ответ: displaystyle v_{ср}=4 frac{2}{7}
Задача 5
Лиса гонится за зайцем. Скорость лисы 20 м/с, а скорость зайца 15 м/с. Догонит ли лиса зайца, если заяц находится на расстоянии 300 метров от безопасного места, а лиса находится на расстоянии 200 метров от зайца?
Решение:
Заяц добежит до норы за displaystyle t= frac{300}{15}=20 секунд.
Лиса же за 20 секунд пробежит расстояние displaystyle S= 20 cdot 20=400 метров.
Лиса не догонит зайца.
Действительно, скорость сближения лисы и зайца:
displaystyle v=v_{лисы}-v_{зайца}=20-15=5 м/с
То есть, чтобы преодолеть расстояние 200 метров, которое изначально существует между лисой и зайцем, лисе понадобиться displaystyle t=frac{200}{5}=40 с
Заяц же уже 20 секунд будет в безопасном месте.
Ответ: лиса зайца не догонит.
Как обозначается скорость
Понятие скорости широко используется в науке: математике, физике, механике. Школьники начинают знакомиться с ним уже в третьем классе. Более подробно это происходит в 7-8 классах. В общепринятом смысле скорость — это величина, которая характеризует, насколько быстро предмет перемещается в пространстве за единицу времени. В зависимости от области применения, скорость обозначается разными символами.
1
Как обозначается скорость в математике
В учебниках по математике принято использовать строчную прописную латинскую букву v. Скорость взаимосвязана с пройденным путем и временем, за который оно пройдено.
При равномерном движении величина v=S/t, где:
- S – пройденный телом путь,
- t – время движения.
2
Как обозначается скорость в физике
В разделе физики, именуемом механикой, также изучается скорость. Обозначение скорости зависит от того, векторная это величина или обычная. В первом случае над буквой v ставится стрелочка, направленная вправо →. Если же нет необходимости учитывать направление, то применяют обычный символ v.
3
Единицы измерения скорости
В международной системе единиц измерения принято оперировать метрами в секунду (м/с). В то же время общепризнанными единицами измерения являются километр в час (км/ч), узел (морская миля в час).
4
Как обозначается скорость света и звука
Учеными доказано, что скорость света является абсолютной величиной, с которой могут перемещаться информация и энергия. Этот показатель постоянен и равен 299 792 458 ± 1,2 м/с. Его символом выбрали латинскую букву с.
Скорость звука зависит от плотности и упругости среды, в которой распространяются звуковые волны. Ее измеряют в Махах. Например, сверхзвуковая скорость находится в границах от 1,2 до 5 Махов. А все что выше, называют гиперзвуковой скоростью.
Очевидно, что символ, которым обозначается скорость, зависит от математического или физического смысла, которым наполняется данное понятие.
Как обозначается скорость
Понятие скорости широко используется в науке: математике, физике, механике. Школьники начинают знакомиться с ним уже в третьем классе. Более подробно это происходит в 7-8 классах. В общепринятом смысле скорость — это величина, которая характеризует, насколько быстро предмет перемещается в пространстве за единицу времени. В зависимости от области применения, скорость обозначается разными символами.
1
Как обозначается скорость в математике
В учебниках по математике принято использовать строчную прописную латинскую букву v. Скорость взаимосвязана с пройденным путем и временем, за который оно пройдено.
При равномерном движении величина v=S/t, где:
- S – пройденный телом путь,
- t – время движения.
2
Как обозначается скорость в физике
В разделе физики, именуемом механикой, также изучается скорость. Обозначение скорости зависит от того, векторная это величина или обычная. В первом случае над буквой v ставится стрелочка, направленная вправо →. Если же нет необходимости учитывать направление, то применяют обычный символ v.
3
Единицы измерения скорости
В международной системе единиц измерения принято оперировать метрами в секунду (м/с). В то же время общепризнанными единицами измерения являются километр в час (км/ч), узел (морская миля в час).
4
Как обозначается скорость света и звука
Учеными доказано, что скорость света является абсолютной величиной, с которой могут перемещаться информация и энергия. Этот показатель постоянен и равен 299 792 458 ± 1,2 м/с. Его символом выбрали латинскую букву с.
Скорость звука зависит от плотности и упругости среды, в которой распространяются звуковые волны. Ее измеряют в Махах. Например, сверхзвуковая скорость находится в границах от 1,2 до 5 Махов. А все что выше, называют гиперзвуковой скоростью.
Очевидно, что символ, которым обозначается скорость, зависит от математического или физического смысла, которым наполняется данное понятие.
Среди прочих обозначений наиболее часто школьников интересует вопрос о том, как в математике обозначается скорость, время, расстояние. Связано это с тем, что обозначения этих величин (особенно — скорости) в учебниках по математике и физике можно увидеть различные: с чертой над буквой v (читается: [вэ]), со стрелкой над буквой v, а также буквы v, выделенные курсивом или жирным шрифтом.
Скорость в математике обозначается буквой v, но её написание принято различным для рукописного и печатного текста.
В рукописном тексте скорость движения обычно обозначается строчной (т.е. маленькой) прописной (т.е. не печатной, как в тексте из газеты, а написанной от руки так, как если бы писали письмо) буквой v. В учебниках по математике (т.е. в печатном тексте) обычно скорость движения обозначается печатной буквой v, прямой или выделенной курсивом. Такое обозначение принимается практически во всех задачах по математике, исключение составляют лишь задачи, иллюстрирующие тему «Векторы» (в этом случае обозначение принимается таким же, как и в физике).
В физике (а точнее – в её разделе «механика») обозначение скорости зависит от того, нужно ли в данной задаче учитывать тот факт, что скорость – величина векторная. Там, где учитывать это не нужно, скорость обозначается строчной буквой v (печатной или прописной, так же, как и в математике). Если же необходимо учитывать то, что скорость характеризуется не только модулем (т.е. величиной), но и направлением, скорость изображается либо прописной буквой v с направленной слева направо стрелкой над этой буквой, либо той же прописной буквой v с горизонтальной чертой над этой буквой. В печатном тексте в этом случае обычно скорость обозначают либо печатной строчной буквой v со стрелкой или чертой над буквой, либо печатной буквой v, выделенной жирным шрифтом (т.е. так: v).
Буквой v обозначают скорость движения тел. Для обозначения скорости света и скорости звука принята другая, отличная от обозначения скорости движения тел, буква. Скорость света обозначается буквой «с» (скорость света в вакууме составляет с = 2,9979х108 м/с = 2,9979х105 км/с). Скорость звука так же обозначается буквой с (читается: [цэ]).
Ускорение обозначается буквой а (исключение составляет лишь ускорение свободного падения, эта величина обозначается буквой g (читается [жэ]), g = 9,81 м/с2). Если необходимо подчеркнуть, что эта величина – векторная (например, это часто требуется в физике), то над буквой «а» изображается либо горизонтальная черта, либо горизонтальная стрелка (так же, как и при обозначении скорости). В печатном тексте для обозначения ускорения как векторной величины может использоваться и буква «а», выделенная жирным шрифтом.
Если при решении задачи по физике или математике необходимо обозначить время, то это пишется буквой так: t (читается: [тэ]), а если расстояние — пишется буквой так: s (читается: [эс]). Для обозначения пути обычно используется строчная (маленькая) буква [эль], т.е. l, реже — заглавная (большая) буква [эль], т.е. L. Чтобы обозначение пути «l» не было похоже на «единицу», эту букву пишут курсивом, т.е. с наклоном.
Вообще, вопросы «как в математике пишется скорость», «как в математике пишется время», «как в математике пишется расстояние» некорректны. Лучше формулировать такой вопрос, употребляя не слово «пишется», а слово «обозначается».
Источники:
- Яворский Б.М., Детлаф А.А., Лебедев А.К. Справочник по физике для инженеров и студентов вузов
- Справочник по элементарной математике. Геометрия, тригонометрия, векторная алгебра/ Под ред. П.Ф. Фильчакова
- Каплан И.А. Практические занятия по высшей математике
Дополнительная информация:
- ru.wikipedia.org – Список обозначений в физике
- azbyka.kz — Урок математики «Скорость, время, расстояние»